Изобретение относится к области гидроакустики и может быть использовано для градуировки и калибровки приемных гидроакустических измерительных систем, в частности гидроакустических антенн в закрытых узких гидрокамерах в лабораторных условиях и на гидроакустических полигонах в натурных условиях.
Известен способ аналогичного назначения, применяемый в натурном водоеме для градуировки и калибровки гидроакустических измерительных антенн [1]. Способ заключается в том, что с помощью специального источника опорных сигналов в натуральном водоеме создают "калиброванное поле", воздействующее на средство измерений.
Недостатками известного способа являются узкие возможности в моделировании различных акустических полей и ограниченность его применения случаем натурного водоема.
Известен способ моделирования плоских акустических волн, используемый в устройстве для калибровки линейных гидроакустических антенных решеток [2]. Способ заключается в расположении в закрытой узкой гидрокамере опорных гидрофонов и акустических излучателей, которые возбуждались электрическими сигналами. Данный способ принят за прототип.
В прототипе в лабораторных условиях в узкой гидрокамере с помощью гидроакустических излучателей моделируют плоскую волну, падающую под некоторым углом к калибруемой гидроакустической антенне. Изменяя угол падения волны и ее амплитуду, определяют характеристику направленности и чувствительность антенны.
Недостатками прототипа являются возможность моделировать только плоские волны, сложность определения величин сигналов, подаваемых на излучатели, а также отсутствие информации о величине погрешности величины давления в генерируемом акустическом поле, а следовательно, и неизвестная точность измерений.
Техническим результатом, получаемым от внедрения изобретения, является упрощение процесса моделирования гидроакустических волн и повышение точности и достоверности проводимых измерений. Кроме этого, появляется возможность моделировать произвольные акустические поля с конечным спектром пространственных частот.
Данный технический результат достигается за счет того, что в известном способе моделирования акустических полей, заключающемся в расположении в требуемом объеме гидроакустических излучателей и воздействии на них электрическими сигналами, гидроакустические излучатели в требуемом объеме располагаются таким образом, чтобы максимальное расстояние между любыми соседними излучателями не превышало величины π /kmax, где kmax - максимальное волновое число в спектральном разложении по пространственным частотам моделируемого акустического поля, а возбуждающие гидроакустические излучатели электрические сигналы удовлетворяют математическому соотношению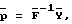
где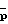 - вектор с элементами pn=unEn, un - электрический сигнал, подаваемый на n-й излучатель, а En - его чувствительность;
- вектор с элементами pn=unEn, un - электрический сигнал, подаваемый на n-й излучатель, а En - его чувствительность;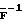 - матрица, обратная к матрице
- матрица, обратная к матрице  с элементами
с элементами  , где
, где  - радиус-вектор точки, в которой размещен m-й излучатель,
- радиус-вектор точки, в которой размещен m-й излучатель,  - решение волнового уравнения для требуемого объема в случае, когда в нем работает только n-й излучатель;
- решение волнового уравнения для требуемого объема в случае, когда в нем работает только n-й излучатель; - вектор с элементами
- вектор с элементами  - функция распределения давления в моделируемом акустическом поле.
- функция распределения давления в моделируемом акустическом поле.
Способ основан на следующих предпосылках.
Как известно, пространственное распределение давления в акустическом поле однозначно определяет это поле, поэтому для моделирования акустических полей будем моделировать распределение давления в требуемом акустическом поле.
Пусть в объеме V с границами S необходимо моделировать акустическое поле с распределением акустического давления 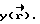 . Таким объемом может быть бесконечное полупространство, заполненное водой, некоторый плоский слой воды, реально существующий залив или произвольная гидрокамера, закрытая или частично открытая.
. Таким объемом может быть бесконечное полупространство, заполненное водой, некоторый плоский слой воды, реально существующий залив или произвольная гидрокамера, закрытая или частично открытая.
Необходимым условием моделирования является требование ограниченности спектра в спектральном разложении по пространственным частотам моделируемого акустического поля. Пространственная частота - это величина, обратная длине волны, аналогом круговой пространственной частоты является волновое число k, которое в общем случае является вектором  = (kx, ky, kz). В этом случае в соответствии с теоремой Котельникова о дискретизации сигналов с ограниченным спектром требуемое распределение давления может быть воспроизведено по значениям в ряде точек, расстояние между которыми не превышает известной величины, зависящей от максимального значения пространственной частоты в моделируемом акустическом поле.
= (kx, ky, kz). В этом случае в соответствии с теоремой Котельникова о дискретизации сигналов с ограниченным спектром требуемое распределение давления может быть воспроизведено по значениям в ряде точек, расстояние между которыми не превышает известной величины, зависящей от максимального значения пространственной частоты в моделируемом акустическом поле.
Выберем в объеме V N точек  , n=1,...,N, таких что для любого n
, n=1,...,N, таких что для любого n
Оптимальный выбор этих точек зависит от требуемой погрешности моделирования, формы объема и вида моделируемого поля, и поэтому алгоритма выбора точек, удовлетворяющего всем задачам моделирования, не существует. Отметим только, что эквидистантное расположение точек не всегда является оптимальным.
Сгенерировав произвольным способом в этих точках давление, равное давлению в требуемом акустическом поле, мы тем самым смоделируем требуемое поле. Для этого расположим в этих точках гидроакустические ненаправленные излучатели с известными комплексными чувствительностями на излучение En. Размеры излучателей должны быть таковы, чтобы последние не вносили существенных изменений в распределение акустического давления в моделирующем поле. Подав на каждый из излучателей свой электрический сигнал un, получим, что акустическое давление, генерируемое n-ным излучателем, можно записать в следующем виде:
pn=unEn.
В случае аддитивности акустического поля в объеме и в отсутствии взаимного влияния излучателей друг на друга суммарное акустическое давление, генерируемое всеми излучателями, равно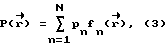
где 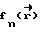 - решение волнового уравнения для объема V с заданными граничными условиями на границе 3 для случая работы в нем только n-ого излучателя.
- решение волнового уравнения для объема V с заданными граничными условиями на границе 3 для случая работы в нем только n-ого излучателя.
Следовательно, задача моделирования требуемого акустического поля сводится к задаче интерполяции функции  в точках
в точках  , n=1,...,N функцией
, n=1,...,N функцией 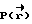 , зависящей от параметров pn, n=1,..,N. Эту задачу можно решать методом коллокации [3] . Потребуем, чтобы в точках интерполяции выполнялось точное равенство требуемой и интерполяционной функций
, зависящей от параметров pn, n=1,..,N. Эту задачу можно решать методом коллокации [3] . Потребуем, чтобы в точках интерполяции выполнялось точное равенство требуемой и интерполяционной функций
Имеем линейную систему N уравнений с N неизвестными, которую проще записывать в матричном виде
где 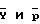 - вектора с элементами
- вектора с элементами 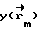 и pm соответственно, а
и pm соответственно, а  - квадратная матрица с элементами
- квадратная матрица с элементами  .
.
Решение этой системы уравнений
где  - матрица, обратная к матрице
- матрица, обратная к матрице 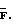
И тогда интерполяционную функцию можно записать в виде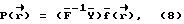
где 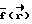 - вектор функций
- вектор функций  .
.
Все величины, использованные выше для учета фазовых соотношений, нужно считать комплексными.
Отметим, что выполнение равенства (4), а также неравенств (1) являются совокупностью необходимых и достаточных условий моделирования не только амплитудных, но и фазовых пространственных зависимостей в требуемом объеме.
Величина погрешности моделирования может быть точно вычислена на ЭВМ до начала измерений, кроме этого, возможен анализ дополнительной погрешности, вносимой ошибками в оценках параметров измерительной аппаратуры и характеристик объема (комплексные чувствительности излучателей, скорость звука в объеме, коэффициент отражения на его границах и т.п.).
Проиллюстрируем реализацию способа для установки, аналогичной описанной в прототипе. В этом случае в узкой закрытой гидрокамере моделируется одномерное акустического поле (поле плоской волны, падающей под некоторым углом к оси гидрокамеры) с распределением давления
y(x) = y0exp[i(kaxsinθ-wt)], (9)
где
y0 - амплитуда моделируемой плоской волны;
kв - волновое число в моделируемой плоской волне;
x - расстояние от левого края гидрокамеры;
θ - угол падения моделируемой плоской волны;
w - круговая частота;
t - время.
Для простоты выкладок, не ограничивая общности, ниже будем опускать временной экспоненциальный множитель exp(-iwt).
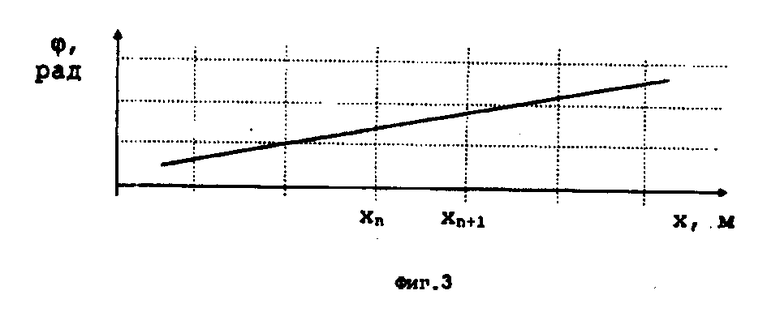
На фиг. 1 представлена схема гидростенда; на фиг. 2 и 3 - зависимости соответственно амплитуды и фазы акустического давления от продольной координаты в гидрокамере, поясняющие существо способа.
Вдоль гидрокамеры 1 длиной L эквидистантно с шагом d расположены N излучателей 2. Гидрокамера выполнена в виде узкой трубы с жесткими стенками, и поэтому решение волнового уравнения для случая работы только n-ого излучателя можно записать в следующем виде [4]:
где
k - волновое число в гидрокамере;
xn - координата n-ого излучателя.
Эти два выражения можно записать в одном
Следовательно, в данном случае - элементы вектора 
ym= y0exp(-ikaxmsin(θ)), (11)
элементы матрицы 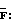

Таким образом для моделирования в такой гидрокамере плоской волны, падающей под углом θ к оси гидрокамеры, на излучатели нужно подавать электрические сигналы un, определяемые из выражения
где 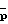 - вектор с элементами pn=unEn.
- вектор с элементами pn=unEn.
При этом распределение акустического давления вдоль гидрокамеры будет определяться выражением
где элементы вектора функций  определяются выражением (10).
определяются выражением (10).
Несмотря на кажущуюся сложность выражения (14), график зависимости акустического давления от продольной координаты в гидрокамере выглядит очень просто (фиг. 2).
Максимальное значение акустическое давление принимает в точках, расположенных посередине отрезков между соседними излучателями, минимальное значение - в точках расположения излучателей.
Тогда величину давления в любой точке гидрокамеры можно оценить как P= Pср± ΔP, используя следующие величины среднего давления и его разброса:
Pср=(Pmax+Pmin)/2,
ΔP = (Pmax-Pmin)/2.
Относительная погрешность этой оценки
δP = ΔP/Pcp,
которая максимальна при θ, равном нулю, т.е. в случае параллельности фронта воображаемой плоской волны, падающей на оси гидрокамеры. В этом случае
δP = tg2(kd/4).
Величина этой погрешности зависит от частоты и расстояния между излучателями или, что эквивалентно, от частоты и количества излучателей.
Выбором N всегда можно добиться такой величины погрешности, при которой во всем частотном диапазоне неравномерность акустического давления в гидрокамере не будет превышать требуемой величины. Так при N=200 имеем величину погрешности, не превышающей на частотах до 500 Гц 0,15 дб, что является для гидроакустических измерений малой величиной.
Зависимость фазы акустического давления от координаты (фиг. 3) является практически линейной, что полностью соответствует моделируемому полю - полю плоской волны.
Таким образом, с точностью до погрешностей в гидрокамере генерируется одинаковое акустическое давление с линейной зависимостью фазы от продольной координаты. Следовательно, в гидрокамере формируется акустическое поле, моделирующее на оси гидрокамеры поле плоской волны, падающее под априорно задаваемым углом падения.
Источники информации
1. Патент РФ N 2010456, кл. H 04 R 1/44, 1994.
2. Патент США N 4468760, кл. 367-13 (H 04 R 29/00), 1984 - прототип.
3. Корн Г., Корн Т. Справочник по математике. - М.: Наука, 1977, 832 с.
4. Исакович М.А. Общая акустика. - М.: Наука, 1973, 496 с.

Изобретение предназначено для градуировки и калибровки приемных гидроакустических измерительных систем, в частности гидроакустических антенн в закрытых гидрокамерах в лабораторных условиях и на гидроакустических полигонах в натурных условиях. В требуемом объеме располагают гидроакустические излучатели таким образом, чтобы максимальное расстояние между любыми соседними излучателями не превышало величины π /Kmax, где Kmax - максимальное волновое число в моделируемом акустическом поле, а воздействующие на гидроакустические излучатели электрические сигналы удовлетворяют математическому соотношению
где - вектор с элементами pn = UnEn, где Un - электрический сигнал, подаваемый на n-й излучатель, а En - его чувствительность;
- вектор с элементами pn = UnEn, где Un - электрический сигнал, подаваемый на n-й излучатель, а En - его чувствительность; 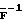 - матрица, обратная к матрице
- матрица, обратная к матрице 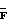 с элементами
с элементами  где
где  - радиус-вектор точки, в которой размещен m-й излучатель,
- радиус-вектор точки, в которой размещен m-й излучатель,  - решение волнового уравнения для требуемого объема в случае, когда в нем работает только n-й излучатель;
- решение волнового уравнения для требуемого объема в случае, когда в нем работает только n-й излучатель;  - вектор с элементами
- вектор с элементами  - функция распределения давления в моделируемом акустическом поле. Способ позволяет моделировать произвольные акустические поля с конечным спектром пространственных частот. 3 ил.
- функция распределения давления в моделируемом акустическом поле. Способ позволяет моделировать произвольные акустические поля с конечным спектром пространственных частот. 3 ил.
Способ моделирования акустических полей, заключающийся в расположении в требуемом объеме гидроакустических излучателей и воздействии на них электрическими сигналами, отличающийся тем, что гидроакустические излучатели в требуемом объеме располагают так, чтобы максимальное расстояние между любыми соседними излучателями не превышало величины π кmax, где кmax - максимальное волновое число в моделируемом акустическом поле, а воздействующие на гидроакустические излучатели электрические сигналы удовлетворяют математическому соотношению
где  вектор с элементами pn = unЕn, где un - электрический сигнал, подаваемый на n-й излучатель, а Еn - его чувствительность;
вектор с элементами pn = unЕn, где un - электрический сигнал, подаваемый на n-й излучатель, а Еn - его чувствительность; матрица, обратная к матрице
матрица, обратная к матрице  с элементами
с элементами  где
где  радиус-вектор точки, в которой размещен m-й излучатель,
радиус-вектор точки, в которой размещен m-й излучатель,  решение волнового уравнения для требуемого объема в случае, когда в нем работает только n-й излучатель;
решение волнового уравнения для требуемого объема в случае, когда в нем работает только n-й излучатель;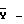 вектор с элементами
вектор с элементами  функция распределения давления в моделируемом акустическом поле.
функция распределения давления в моделируемом акустическом поле.
| RU, патент, 2010456, кл | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| US, патент, 4468760, кл | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
Авторы
Даты
1998-07-27—Публикация
1997-04-17—Подача