Изобретение относится к настольным играм, а более конкретно - к шахматным играм на классической 64-клеточной доске.
Шахматная игра создавалась на протяжении многих веков. Наряду с классическими шахматами на квадратной доске с 64 квадратными полями известно немало национальных разновидностей шахмат. Самой древней шахматной игрой считается чатуранга, пришедшая из Индии и затем превратившаяся в шатрандж у арабов и шатранг у персов, а позднее - в классические шахматы, практически, у народов всего мира. До сих пор играют в японские шахматы (шоги), китайские (цюнь ки), корейские (тьян-кеун), армянские (тама), монгольские (шатар) и т. д.
Обязательными атрибутами шахматных игр служат доска и фигуры.
Доска может быть обычной и необычной. Обычной (или классической) считается квадратная доска с квадратными полями, число которых равно 64. Необычные доски отличаются от обычной размером и формой доски и полей.
Шахматными играми на необычных досках являются, например, следующие игры [Гик Е.Я. Занимательные математические игры. -М.: Знание, 1987]:
1) Максишахматы Капабланки на прямоугольной доске размером 16х12 с удвоенным комплектом обычных фигур;
2) "Великие" шахматы с прямоугольной доской 121х12, колыбелью которых была Индия. Каждый игрок в этих шахматах имел по 12 фигур и по 12 пешек. Фигуры носили экзотические названия - крокодилы, жирафы, львы, единороги и т. п.;
3) Образцовые шахматы системы Тамерлана на доске 11х10 (одиннадцать фигур расположены на ней в три ряда);
4) Шахматы на параллельных досках, игра в которые ведется на двух параллельных досках с перемещением фигур с одной доски на другую;
5) Шахматы на цилиндрической, тороидальной, сферической, конусоидальной и в виде листа Мебиуса досках;
6) Проективные шахматы на проективной доске, в которых используются некоторые свойства проективной геометрии;
7) Объемные шахматы на объемных досках, поля на которых определяются тремя и более координатами;
8) Гексагональные (шестигранные) шахматы с шестиугольной плоской доской и шестиугольными полями;
9) Шахматы для нескольких игроков с соответствующей конфигурацией доски и другие.
Различные шахматные игры получаются не только на основе тех или иных преобразований шахматной доски. Новые игры можно получать на обычной доске в результате изменения правил или введения необычных фигур.
Таковыми можно считать, например, следующие игры [Гик Е.Я. Занимательные математические игры. -М.: Знание, 1987]:
1) Шахматы с шахами и без шахов. В игре "с шахами" все, как в настоящих шахматах, только выигрывает тот, кто первым объявляет шах. В игре "без шахов" фигуры ходят обычным образом, но объявлять простой шах запрещено - первый же шах должен быть и матом;
2) Двухходовые шахматы. В этой игре каждый ход белых и черных состоит из двух обычных ходов;
3) Поддавки, основная задача игроков в которой - избавится от всех фигур;
4) с измененной начальной позицией фигур и, возможно, пешек;
5) Шахматы с магараджей, которая объединяет в себе ходы ферзя и коня;
6) Шахматы с так называемыми сказочными фигурами;
7) Шахматы, представляющие смесь шашек и шахмат, и другие.
Из этого, далеко не исчерпывающего, но достаточно представительного, перечня различных шахматных игр видно, что в основе подавляющего числа вновь предложенных (после классических шахмат) шахматных игр лежат те или иные вариации внешних свойств основных атрибутов рассматриваемого класса игр или их некоторые сочетания с привнесенными извне элементами других настольных игр.
Напротив, в основание предлагаемого изобретения, как будет показано, положены некоторые внутренние структурные зависимости между основными элементами шахматной игры, носящие фундаментальный характер и явным образом обнаруживаемые в классических шахматах.
Именно поэтому прототипом (ближайшим аналогом) по отношению к предлагаемой супершахматной игре выбраны классические шахматы, содержащие 64 клеточную шахматную доску и комплект из 32 шахматных фигур - 16 светлых, например белых, и 16 темных, например черных [Фирсова Л.М. Игры и развлечения, Кн. 2. -М.: Молодая гвардия, 1990, с.69].
В классических шахматах набор фигур и пешек в комплекте одного цвета в качественном отношении представляется следующим образом:
а) элементарные (одинарные) фигуры: ладья (Л), слон (С), конь (К),
б) сложные (двойные) фигуры: ферзь (Ф) и король (Кр) (с ходом ферзя на один шаг по всем составляющим);
в) пешки - с ходом только на свободное поле: вперед, как ладья, - на один шаг; с ходом только при взятии фигуры или пешки противника; вперед, влево или вправо, как слон, - на один шаг.
В количественном отношении набор фигур и пешек в комплекте одного цвета классических шахмат представляется в виде следующего распределения (табл. 1).
Структура классических шахмат по (элементарным) ладейной (nл; Nл), слоновой 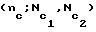 и коневой (nк; Nк) составляющим с учетом всех фигур одного цвета (без короля) может быть представлена в виде следующих векторов:
и коневой (nк; Nк) составляющим с учетом всех фигур одного цвета (без короля) может быть представлена в виде следующих векторов:
1) nл, nс; кn = (3,3.2) - статическая структурная характеристика;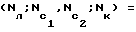 (3; 2. 2; 2) - динамическая структурная характеристика, где
(3; 2. 2; 2) - динамическая структурная характеристика, где
nл, nс, nк - суммарные числа элементарных (ладейной, слоновой и коневой) составляющих некоторого комплекта фигур (в данном случае, комплекта фигур видна {2Л, 2К, 2С, Ф}); - суммарные числа ударов, которые могут быть нанесены по некоторому полю шахматной доски однородными фигурами по ладейной (Nл), слоновой
- суммарные числа ударов, которые могут быть нанесены по некоторому полю шахматной доски однородными фигурами по ладейной (Nл), слоновой 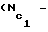 - с использованием белопольного слона,
- с использованием белопольного слона,  - использованием чернопольного слона), коневой (Nк) составляющим некоторого комплекта фигур (в данном случае, комплекта фигур вида {2Л, 2К, 2С, Ф}).
- использованием чернопольного слона), коневой (Nк) составляющим некоторого комплекта фигур (в данном случае, комплекта фигур вида {2Л, 2К, 2С, Ф}).
Первоначальное положение фигур на шахматной доске в классических шахматах изображено на фиг. 1 [Шахматный кодекс СССР. -М.: Физкультура и спорт. 1977; Спутник шахматиста: Справочник. -М.: Воениздат 1992].
Ходом в классических шахматах (за исключением рокировки) называется передвижение фигуры с одного поля на другое, свободное или занятое фигурой партнера.
Ни одна из фигур, за исключением ладьи во время рокировки и коня, не может пересекать поле, занятое другой фигурой.
Фигура, передвигаемая на поле, занятое фигурой партнера, берет этим ходом данную фигуру, которая снимается с доски.
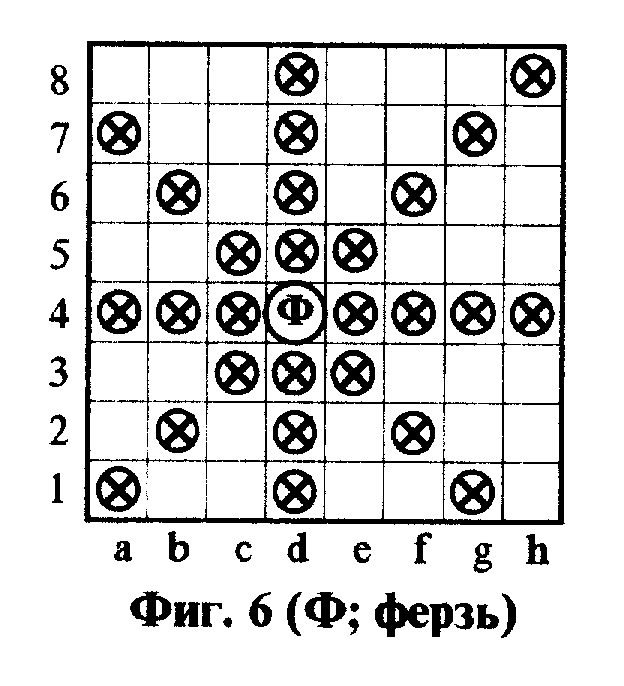
На фиг. 2oC7 изображены множества возможных ходов всех фигур и пешек в классических шахматах, при этом ход только со взятием обозначается x, , ход только на свободное поле - ○ а ход на свободное поле и со взятием - ⊗
В классических шахматах допускается так называемая рокировка. При рокировке король идет со своего поля на одно или другое поле той же горизонтали, того же цвета, наиболее близкое к нему, вслед за тем ладья, в направление которой двигался король, встает на поле, только что пересеченное королем. Рокировка невозможна в обе стороны, если король уже двигался. Рокировка также невозможна с ладьей, которая уже двигалась.
Рокировка (временно) невозможна:
а) если поле, на котором находится король, или поле, которое он должен пересечь или занять, находится под ударом фигуры партнера;
б) если между королем и ладьей, к которой должен направляться король, находятся другие фигуры.
В классических шахматах возможен ход пешки, который называется ходом со "взятием на проходе". Этот ход возможен в случае, если пешка, угрожающая полю, через которое проходит пешка партнера, совершающая ход со своей первоначальной позиции сразу на два поля, может брать, но только очередным ходом, данную пешку партнера, как если бы последняя переместилась лишь на одно поле.
Шахматная партия в классических шахматах ведется двумя партнерами, которые играют по очереди, делая каждый раз один ход. Партнер, имеющий белые фигуры, начинает партию.
Партия считается выигранной шахматистом, который дал мат королю партнера, а также тем из партнеров, противник которого сдался.
Партия может иметь ничейный исход. Все случаи, в которых заканчивается вничью, указаны, например в [Шахматный кодекс СССР. - М.: Физкультура и спорт. 1977].
Дальнейшему изложению, в частности, изложению недостатков прототипа, предпошлем некоторые определения и утверждения относительно так называемого золотого сечения и средней мощности используемых в шахматах фигур.
Золотое сечение - деление отрезка (длины l), при котором большая часть (длины x) является средней пропорциональной между всем отрезком (длины l) и меньшей его частью (длины l - x), то есть l:x = x:(l-x).
В результате получаем квадратное уравнение x2+x-1=0, решение которого дает число  которое также называется золотым сечением.
которое также называется золотым сечением.
Условие l:x=x:(l-x) можно переписать и так x=(l/(l+x).
Так как ϕ - - решение уравнения  то из последнего представления исходного уравнения следует, что
то из последнего представления исходного уравнения следует, что ,
,
то есть
ϕ определяется в виде непрерывной дроби, подходящими дробями которой являются числа последовательности ,
,
где
{ ui} = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,...} - последовательность та называемых чисел Фибоначчи [Математическая энциклопедия, т. 2. -М.: Советская энциклопедия 1979].
Золотое сечение было известно еще в древности. В дошедшей до нас античной литературе золотое сечение впервые встречается в "Началах" Евклида (3 вес до н.э.).
Термин "золотое сечение" ввел Леонардо да Винчи (конец 15 - начало 16 веков). Принципы золотого сечения легли в основу композиционного построения многих произведений мирового искусства (главным образом произведений архитектуры античности и Возрождения), в том числе, как будет показано ниже, в основу построения ряда фигур (Ф, Л, С, К) классических шахмат.
Ряд чисел (In, In-1, ..., I2, I1) таких, что Ik > Ik-1, 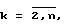 I1 > 0, называется ϕсовершенным, если
I1 > 0, называется ϕсовершенным, если  ,
,  , или, что эквивалентно,
, или, что эквивалентно,  ,
,  (так как
(так как  ).
).
Ряд чисел  таких как, что
таких как, что  , называется ϕεсовершенным, если для некоторого достаточно малого числа ε>0
, называется ϕεсовершенным, если для некоторого достаточно малого числа ε>0 ,
,
или, что эквивалентно, ,
,
где .
.
Имеют место следующее утверждение.
Если ряд чисел (In, In-1, ..., I1), In > In-1 > ... > I1 > 0, является ϕ - - совершенным, то Ik-1 + Ik = Ik+1, 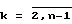 .
.
Пусть (Фn,Фn-1,...,Ф1), , n = N/2, есть упорядоченный набор различных фигур N2-клеточной шахматной игры с комплектом фигур одного цвета (без короля) вид  , ki≠kj, i≠j, ki,kj∈{1,2,...,n-1}, ,
, ki≠kj, i≠j, ki,kj∈{1,2,...,n-1}, ,  , в котором фигура Фn является самой мощной.
, в котором фигура Фn является самой мощной.
Набору фигур (Фn,Фn-1,...,Ф1) соответствует ряд чисел  , упорядоченных по величине
, упорядоченных по величине  и характеризующих так называемые средние мощности фигур Фk, , k = 1, n.
и характеризующих так называемые средние мощности фигур Фk, , k = 1, n.
Средняя мощность фигуры  , определяется в соответствии с соотношением
, определяется в соответствии с соотношением ,
,
где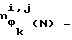 - число полей N2-клеточной доски, которые могут быть атакованы фигурой
- число полей N2-клеточной доски, которые могут быть атакованы фигурой 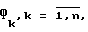 , если она находится на поле с координатами (i, j),
, если она находится на поле с координатами (i, j),  .
.
Ряд фигур (ФnФn-1,...,Ф1), , n = N/2, и соответствующая этому ряду фигур N2-клеточная игра с комплектом фигур (одного цвета без короля) вида 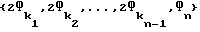 являются ϕ(ϕε) - - совершенными, если ϕ(ϕε) - - свершенным является упорядоченный по убыванию ряд чисел
являются ϕ(ϕε) - - совершенными, если ϕ(ϕε) - - свершенным является упорядоченный по убыванию ряд чисел  - значение средней мощности фигуры
- значение средней мощности фигуры  , на N2-клеточной доске.
, на N2-клеточной доске.
При этом, ϕ - -совершенную игру будет называть идеальной и обозначать Г0 ( ε = 0), а ϕε - совершенную игру будет обозначать Гε в общем случае и  для каждой конкретной игры с самой мощной фигурой Фn .
для каждой конкретной игры с самой мощной фигурой Фn .
Если игра 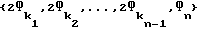 или соответствующий ей ряд фигур (Фn,Фn-1,...,Ф1) являются ϕε - - совершенными, то величину ε - - отклонения этой игры
или соответствующий ей ряд фигур (Фn,Фn-1,...,Ф1) являются ϕε - - совершенными, то величину ε - - отклонения этой игры 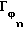 от идеальной Г0 ( ϕ - -совершенной) или евклидово расстояние
от идеальной Г0 ( ϕ - -совершенной) или евклидово расстояние  от игры
от игры  до идеальной Г0 можно вычислить в соответствии с соотношением
до идеальной Г0 можно вычислить в соответствии с соотношением ,
,
где .
.
Классические шахматы  = (2Л, 2К, 2С, Ф) на 64-клеточной доски (N= 8) являются ϕε - - совершенной игрой, так как значения средней мощности фигур из упорядочного множества (Ф4,Ф3,Ф2,Ф1) = = (Ф, Л, С, К) образуют числовой ряд
= (2Л, 2К, 2С, Ф) на 64-клеточной доски (N= 8) являются ϕε - - совершенной игрой, так как значения средней мощности фигур из упорядочного множества (Ф4,Ф3,Ф2,Ф1) = = (Ф, Л, С, К) образуют числовой ряд  , который является
, который является  - совершенным с
- совершенным с  (8,75/5,25 = 1,(6); 14,0/8,75 = 1,6;22,75/14,0 = 1,625).
(8,75/5,25 = 1,(6); 14,0/8,75 = 1,6;22,75/14,0 = 1,625).
Действительно, в общем случае (относительно параметра N-размера шахматной доски), имеем: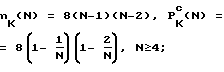 ;
; ;
;
nЛ(N) = 2(N-1)N2, P .
.
При N = 8 nК(8) = 336, nС(8) = 560, nл = 896, nФ(8) = 1456 и, следовательно, (Р
Нетрудно видеть, что (nФ, nЛ, nС, nК) = (1456, 896, 560, 336) = 24(91, 56, 35, 21) и, следовательно, 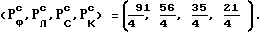 .
.
Отсюда видно, что тройка чисел  является связной подпоследовательностью последовательности подходящих дробей для непрерывной дроби, представляющей число ϕ. .
является связной подпоследовательностью последовательности подходящих дробей для непрерывной дроби, представляющей число ϕ. .
Однако, тройка чисел  обеспечивает аппроксимацию числа ϕ с абсолютной погрешностью в пределах от 0,00265 до 0,01803 и относительной погрешностью в пределах от 0,43 до 2,92%, то есть весьма грубую аппроксимацию (с относительной погрешностью в несколько процентов).
обеспечивает аппроксимацию числа ϕ с абсолютной погрешностью в пределах от 0,00265 до 0,01803 и относительной погрешностью в пределах от 0,43 до 2,92%, то есть весьма грубую аппроксимацию (с относительной погрешностью в несколько процентов).
Этим фактом выявляется первый недостаток классических шахмат как  -совершенной игры. Иначе говоря, классические шахматы являются
-совершенной игры. Иначе говоря, классические шахматы являются 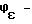 -совершенной игрой лишь в первом приближении. Конечно, этот недостаток следует считать весьма условным, так как свойство ϕV - -совершенности классических шахмат достигается элементарными средствами.
-совершенной игрой лишь в первом приближении. Конечно, этот недостаток следует считать весьма условным, так как свойство ϕV - -совершенности классических шахмат достигается элементарными средствами.
Докажем теперь, что оптимальный (в ϕV - -смысле) размер шахматной доски для пары фигур (Л, С) (следовательно, и для пары (Ф, Л), так как Р
Для доказательства этого утверждения найдем числа N1 = N , где ϕ = = 0,6180339 - золотое сечение.
, где ϕ = = 0,6180339 - золотое сечение.
Для пары (С, Л) имеет: .
.
Из уравнения 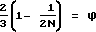 относительно N получаем:
относительно N получаем: .
.
Принимая во внимание то, что N∈{2,4,6,8...} (размер доски N является четным числом), получаем, что оптимальный (в ϕ-смысле) размер доски для пары фигур (С, Л) (следовательно, и для (Ф, Л)) равен  , где
, где  - операция округления числа x до ближайшего четного числа.
- операция округления числа x до ближайшего четного числа.
Для пары (К, С) имеем: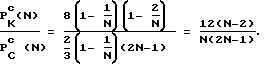 .
.
Приравнивая  числу ϕ,, получаем уравнение
числу ϕ,, получаем уравнение ,
,
решением которого является пара чисел (N1, N2) = (2,528; 7,680). Так как N ≥ 4 (см. соотношение для nК(N)), то  = N2 = 7,680.
= N2 = 7,680.
Принимая во внимание то, что N∈{2,4,6,8...}, , получаем, что оптимальный (в ϕ - -смысле) размер доски для пары фигур (С, К) равен  = <7,680> = 8, где
= <7,680> = 8, где  - операция округления числа x до ближайшего четного числа.
- операция округления числа x до ближайшего четного числа.
Таким образом, использование фигур Ф, Л, С на классической 64-клеточной шахматной доске не является оптимальным (в ϕ - -смысле), что является вторым достаточно серьезным недостатком классических шахмат.
Целью настоящего изобретения является преодоление указанных недостатков классических шахмат.
Как результат достижения поставленной уели предложена новая шахматная игра - супершахматы, содержащие 64-клеточную шахматную доску и комплект из 32 шахматных фигур - 16 светлых, например, белых, и 16 темных, например, черных, отличающихся тем, что шахматная доска выполнена четырех цветной с попеременной чередующимися светлыми полями двух оттенков, и темными полями двух оттенков, при этом поля b1, b3, b5, b7, d1, d3, d5, d7, f1, f3, f5, f7, h1, h3, h5, h7 выполнены светлыми одного оттенка, поля a2, a4, a6, a8, c2, c4, c6, c8, e,2 e4, e6, e8, g2, g4, g6, g8 выполнены светлыми другого оттенка, поля a1, a3, a5, a7, c1, c3, c5, c7, e1, e3, e5, e7, g1, g3, g5, g7 выполнены темными одного оттенка, а поля b2, b4, b6, b8, d2, d4, d6, d8, f2, f4, f6, f8, h2, h4, h6, h8 выполнены темными другого оттенка.
Супершахматы не только лишены отмеченных недостатков классических шахмат, но по важнейшим количественным параметрам и качественным признакам существенно их превосходят.
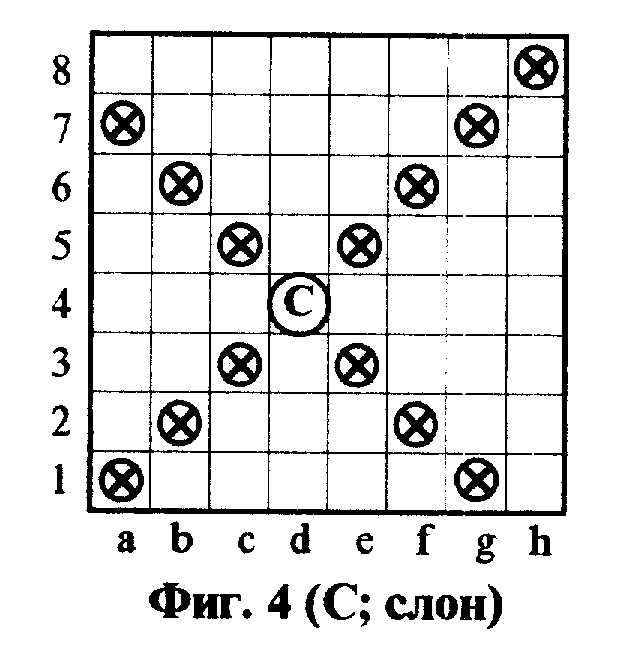
Рассмотрим множество элементарных шахматных фигур вида M1 = (Л, С, К, П, Х, К2, П2, Х2}, где Л, С, К - элементарные фигуры классических шахмат, П, Х, К2, П2, Х2 - новые элементарные фигуры.
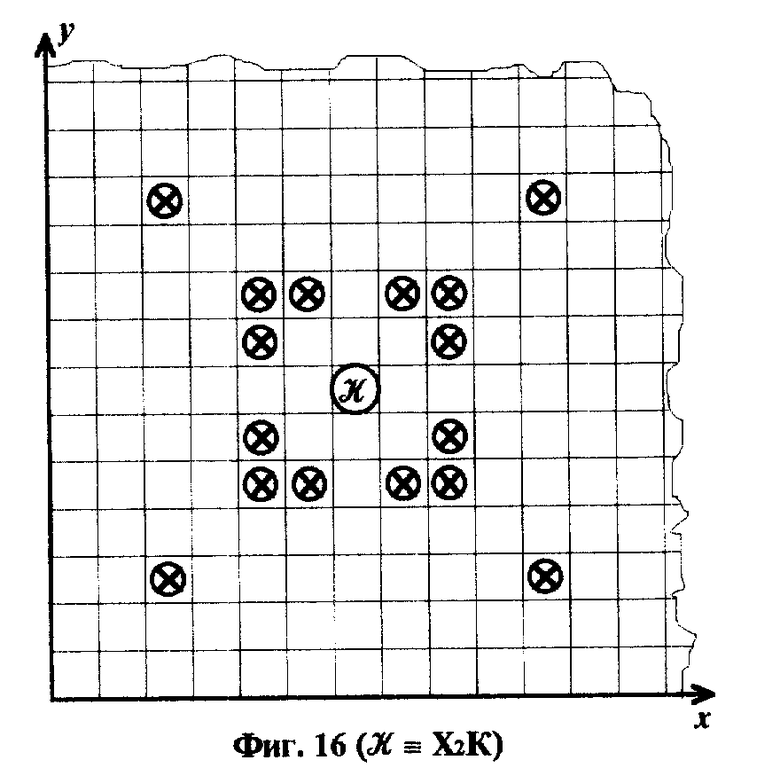
На фиг. 8 oC 13 с использованием шахматной координатной плоскости изображены множества возможных ходов элементарных фигур К (для единообразия), П, Х, К2, П2, Х2 из множества M1. Поле, которое может быть атаковано, помечено на фиг. значком "x". .
Пусть ∑(M1) - = множество всех подмножеств множества M1. Тогда каждому множеству {Ф1...,Фk}⊂∑(M1) соответствует однозначно определенная фигура F = Ф1Ф2...Фk, сочетающая ходы элементарных фигур 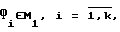 , средняя мощность P
, средняя мощность P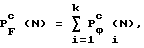 ,
,
где - средняя мощность элементарной фигуре
- средняя мощность элементарной фигуре  ,
,
N - размер доски N2-клеточной шахматной игры.
Ниже приводятся соотношения, позволяющие при любом приемлемом значении N размера доски вычислить среднюю мощность элементарных фигур из (эквивалентного множеству M1) множества M(1) = {Л, С, К, П, Х, К(2), П(2), Х(2)} , где К(2) = К2/К, П(2) = П2/П, Х(2) = Х2/Х, 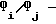 - разность двух множеств (фигур) Фi и Фj (при теоретико-множественных операциях над фигурами предполагается, что они отождествлены с множествами атакуемых ими полей):
- разность двух множеств (фигур) Фi и Фj (при теоретико-множественных операциях над фигурами предполагается, что они отождествлены с множествами атакуемых ими полей):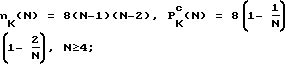 ;
; ;
; ;
; ;
;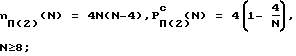 ;
; ;
;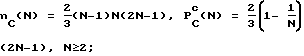 ;
;
nЛ(N) = 2(N-1)N2, P
Так как К2 = К + К(2), П2 = П + П(2), Х2 = Х + Х(2), где A + B - теоретико-множественное объединение двух непересекающихся множеств (фигур) A и B, то на основании вышеприведенных соотношений получаем: ;
; ;
;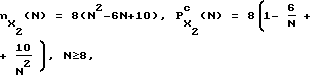 .
.
В таблице 3 (при N = 8) приведены упорядоченных по величине на соответствующих подмножествах значения  средней мощности фигур Фi∈M = σ(M1)⊂∑(M1), , где
средней мощности фигур Фi∈M = σ(M1)⊂∑(M1), , где 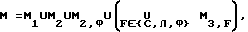 , M1 = {Л, С, К, П, Х, К2, П2, Х2}, M2 = {ФiФj| ФiФj∈M1}, , M2,Ф = {ФiФj| Фi∈M1}, , Ф = ЛС, M3,F = {ФiF| Фi∈M2}, , F∈{С,Л,Ф}, , |M| = 75 - - число различных элементов в множестве M = σ(M1) .
, M1 = {Л, С, К, П, Х, К2, П2, Х2}, M2 = {ФiФj| ФiФj∈M1}, , M2,Ф = {ФiФj| Фi∈M1}, , Ф = ЛС, M3,F = {ФiF| Фi∈M2}, , F∈{С,Л,Ф}, , |M| = 75 - - число различных элементов в множестве M = σ(M1) .
Из таблицы 2 видно, что множество M = σ(M1) всех рассматриваемых фигур представляет в виде M = M1,2∪MC∪MЛ∪MФ, , где M1,2 - множество фигур без Л-, С-компонент, MC - множество фигур с С-компонентой, MЛ - множество фигур с Л-компонентой, MФ - множество фигур с Ф-компонентой (|M1,2| = 18,|MФ| = |MЛ| = |MС| = 19). .
Поиск ϕε-совершенного ряда фигур  и минимальным значением ε- -отклонения от идеального ( (ϕ- -совершенного) ряда фигур изначально обусловлен следующими соотношениями включения:
и минимальным значением ε- -отклонения от идеального ( (ϕ- -совершенного) ряда фигур изначально обусловлен следующими соотношениями включения:
Ф4∈MФ,Ф3∈MЛ,Ф2∈MС,Ф1∈M1,2. .
Число вариантов, удовлетворяющих указанным соотношениям включения, очень велико. Однако, очевидно, что подавляющее большинство из них нет смысла рассматривать, так как они заведомо плохи в ϕ - -смысле, то есть имеют большие значения величины ε - -отклонения.
Существенное уменьшение числа рассматриваемых вариантов (без потери лучшего из них) достигается следующим образом.
Вычислим ϕ-совершенный ряд чисел, начиная с 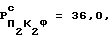 , то есть мажоранту. Имеем:
, то есть мажоранту. Имеем: .
.
Вычислим ϕ- -совершенный ряд чисел, начиная с P .
.
В результате для каждой из фигур искомого ϕε - -совершенного ряда (Ф4,Ф3,Ф2,Ф1) мы получаем так называемые области притяжения: ,
,
которые конструктивно представляются следующим образом: .
.
Нетрудно видеть, что критическим является множество  , число элементов в котором минимально (равно 5).
, число элементов в котором минимально (равно 5).
Вычисляя для каждой из пяти фигур множества  все возможные ϕ- -совершенные числовые ряды вида
все возможные ϕ- -совершенные числовые ряды вида  , где
, где  ,
,  ,
, 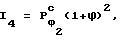 , и подбирая соответствующие этим числовым рядам ϕε- -совершенные ряды фигур
, и подбирая соответствующие этим числовым рядам ϕε- -совершенные ряды фигур  , в результате находим ϕ - -совершенный числовой ряд (35,9980; 22,2480;
, в результате находим ϕ - -совершенный числовой ряд (35,9980; 22,2480;  = 13,75; 8,4980), которому соответствует ϕε - -совершенный ряд фигур (Ф4,Ф3,Ф2,Ф1) = (П2К2Ф, К2Л, П2С, Х2К) с
= 13,75; 8,4980), которому соответствует ϕε - -совершенный ряд фигур (Ф4,Ф3,Ф2,Ф1) = (П2К2Ф, К2Л, П2С, Х2К) с 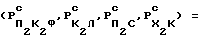 = (36,0; 22,25; 13,75; 8,50), для которого величина эпсилон-отклонения от идеального
= (36,0; 22,25; 13,75; 8,50), для которого величина эпсилон-отклонения от идеального  (13,75/8,5 = 1,61765; 22,25/13,75 = 1,61818; 36,0/22,25 = 1,61798) и
(13,75/8,5 = 1,61765; 22,25/13,75 = 1,61818; 36,0/22,25 = 1,61798) и  ,
,  .
.
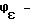 -Совершенный фигурный ряд вида (П2К2Ф, К2Л, П2С, Х2К) является наилучшим среди всех возможных фигурных рядов, рассмотренных на множестве
-Совершенный фигурный ряд вида (П2К2Ф, К2Л, П2С, Х2К) является наилучшим среди всех возможных фигурных рядов, рассмотренных на множестве  , где AxB - декартово произведение множеств A, B. Следовательно, он является наилучшим и на всем множестве фигур M = σ(M1). .
, где AxB - декартово произведение множеств A, B. Следовательно, он является наилучшим и на всем множестве фигур M = σ(M1). .
Таким образом, найден вариант ϕε - -совершенных 64-клеточных шахмат (по мощности фигур - супершахмат) вида 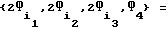 = {2К2Л, 2Х2К, 2П2С, П2К2Ф}, который, будучи превосходным в структурном отношении, намного ближе к идеальным ( ϕ - -совершенным) шахматам, чем классические:
= {2К2Л, 2Х2К, 2П2С, П2К2Ф}, который, будучи превосходным в структурном отношении, намного ближе к идеальным ( ϕ - -совершенным) шахматам, чем классические: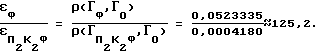 .
.
Так как  = (36,0; 22,25; 13,75; 8,5) и
= (36,0; 22,25; 13,75; 8,5) и 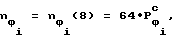 , то
, то  (2304; 1424; 880; 554). Нетрудно видеть, что (2304; 1424; 880; 554) = 24(144, 89, 55, 34).
(2304; 1424; 880; 554). Нетрудно видеть, что (2304; 1424; 880; 554) = 24(144, 89, 55, 34).
Следовательно,  . Отсюда следует, что
. Отсюда следует, что  является конечной связной подпоследовательностью последовательности подходящих дробей для непрерывной дроби, представляющей число ϕ , каждый элемент которой аппроксимирует число ϕ с абсолютной погрешностью в пределах от 0,000022 до 0,000148 и относительной погрешностью в пределах от 0,0035 до 0,0239%, то есть с погрешностью более чем на два порядка меньше той, которая имеет место в классических шахматах.
является конечной связной подпоследовательностью последовательности подходящих дробей для непрерывной дроби, представляющей число ϕ , каждый элемент которой аппроксимирует число ϕ с абсолютной погрешностью в пределах от 0,000022 до 0,000148 и относительной погрешностью в пределах от 0,0035 до 0,0239%, то есть с погрешностью более чем на два порядка меньше той, которая имеет место в классических шахматах.
Таким образом, предлагаемая новая шахматная игра (супершахматы) лишена отмеченного выше первого недостатка классических шахмат. Иначе говоря, в отличие от классических шахмат, супершахматы являются ϕε - -совершенной игрой, как минимум, во втором приближении, то есть предлагаемые супершахматы намного ближе к идеальным ( ϕ - -совершенным), чем классические шахматы.
Докажем теперь, что оптимальный (в ϕ - -смысле) размер доски для всех пар фигур ряда (П2К2Ф, К2Л, П2С, Х2К) предлагаемых супершахмат вида {2К2Л, 2Х2К, 2П2С, П2К2Ф} равен 8 (64-клеточная доска).
Для доказательства приведенного утверждения найдем числа  и
и  такие, что
такие, что и
и  ,
,
где
ϕ = = 0,6180339 - золотое сечение.
Для пары (К2Л, П2С) имеем: .
.
Найдем 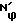 такое, что
такое, что  .
.
Интерес представляет только целочисленное решение задачи при четных N≥8. Поэтому вместо решения уравнения ϕ0(N) =1+ϕ достаточно вычислить .
.
Так как ϕ0(8) = 2136/1320 = 1,61818; ϕ0(10) = 4140/2550 = 1,62353; ϕ0(12) = = 7032/4332 = 1,62327; ϕ0(14) = = 10956/6762 = 1,62023; ϕ0(16) = 16056/9936 = 1,61594, то получаем, что 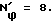 .
.
Для пары (П2С, Х2К) имеем: .
.
Найдем  такое, что
такое, что  . Имея ввиду то, что нас интересует целочисленное решение задачи при четных N≥8, достаточно вместо решения уравнения ϕ1(N) = 1+ϕ вычислить
. Имея ввиду то, что нас интересует целочисленное решение задачи при четных N≥8, достаточно вместо решения уравнения ϕ1(N) = 1+ϕ вычислить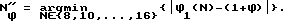 .
.
Так как ϕ1(8) = 1320/816 = 1,617647; ϕ1(10) = 2550/1464 = 1,7418; ϕ1(12) = = 4332/2304 = 1,88 и ϕ1(N) > ϕ1(12) при N>12, то получаем, что  .
.
Таким образом, оптимальный (в ϕ - -смысле) размер доски для К2Л и П2С (следовательно, и для П2К2Ф и К2Л, так как  , а также для П2С и Х2К равен 8 (64-клеточная доска). Следовательно, в предлагаемом варианте супершахмат отсутствует отмеченный выше второй недостаток, которым обладают классические шахматы.
, а также для П2С и Х2К равен 8 (64-клеточная доска). Следовательно, в предлагаемом варианте супершахмат отсутствует отмеченный выше второй недостаток, которым обладают классические шахматы.
В предлагаемых супершахматах набор фигур и пешек в комплекте одного цвета в качественном отношении представляется следующим образом:
а) сложные (двойные) фигуры: К2-ладья (К2Л), П2 - слон (П2С), Х2 - конь (Х2К);
б) сверхсложные (тройные) фигуры: П2К2 - ферзь (П2К2Ф) и ПК - король (ПККр) (с ходом П2К2-ферзя на один шаг по всем составляющим);
в) пешки (ПК-пешки; ПКп);
- с ходом на свободное поле: вперед, на один шаг, либо как ладья, либо как П-фигура, либо как конь, влево или вправо, на соседние вертикали;
- с ходом при взятии фигур или пешек противника: вперед, на один шаг, влево или вправо, как слон, или как конь, влево или вправо, на следующую горизонталь.
В количественном отношении набор фигур и пешек в комплекте одного цвета предлагаемых супершахмат может быть представлен в виде следующего распределения (табл. 3).
Структура предлагаемого варианта супершахмат по (элементарным) ладейной (nЛ; NЛ), слоновой 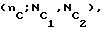 , корневой (nК; NК), К2-коневой
, корневой (nК; NК), К2-коневой  , П2-фигурной
, П2-фигурной 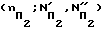 и X2-фигурной
и X2-фигурной  составляющим с учетом всех фигур одного цвета (без короля) может быть представлена в виде следующих векторов:
составляющим с учетом всех фигур одного цвета (без короля) может быть представлена в виде следующих векторов:
1) 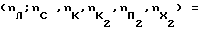 = (3, 3, 2, 3, 3, 2) - статическая структурная характеристика;
= (3, 3, 2, 3, 3, 2) - статическая структурная характеристика;
2)  (3; 2, 2; 2; 3; 2, 2; 2) - динамическая структурная характеристика.
(3; 2, 2; 2; 3; 2, 2; 2) - динамическая структурная характеристика.
Итак, с множеством фигур предлагаемых супершахмат мы определились. Теперь расставим их на доске в исходной позиции, удовлетворяющей соответствующему набору предварительных требований.
Во-первых, доска должна быть 64-клеточной (так как фигур, включая королей, по восемь с каждой стороны) с теми же обозначениями, что и в классических шахматах, горизонталей и вертикалей.
Во-вторых, пешки (ПК-пешки), как и в классических шахматах, должны быть расставлены во второй (белые) и седьмой (черные) горизонталях, по восемь на каждой.
В-третьих, король (ПК-король) и П2К2-ферзь в исходной позиции всех анализируемых вариантов для отбора искомого (лучшего) варианта исходной позиции должны занимать два центральных поля соответствующих горизонталей: белые d1 (П2К2-ферзь), el (король); черные - d8 (П2К2-ферзь), e8 (король), а K2 - ладьи - два крайних поля соответствующих горизонталей: белые - a1, n1; черные - a8, h8.
В результате, после выполнения этих требований, остается решить проблему симметричной расстановки четырех фигур (двух П2-слонов и двух X2-коней) в позиции белых и, зеркально симметрично, - в позиции черных. Всего, в силу симметричности расстановки, требуется рассмотреть два варианта исходной позиции.
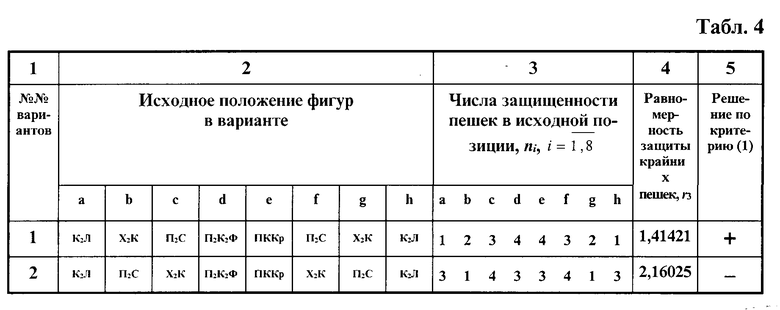
Задача выбора одного (лучшего) варианта из двух является простой. Для решения этой задачи можно ограничиться использованием следующего одного критерия: (1) предпочтение отдается варианту с максимально возможной равномерностью распределения чисел защищенности трех самых крайних пешек в исходной позиции. В классических шахматах числа защищенности трех крайних пешек имеют абсолютно равномерное распределение ((ni (1,1,1,4,4,1,1,1)).
(1,1,1,4,4,1,1,1)).
Отбор искомого варианта по критерию (1) осуществляется с использованием табличного представления данных (см. табл. 4).
Величина r3 в табл. 4 (столбец 4) вычисляется в соответствии с соотношением
где ;
;
n1 - число защищенности i-й пешки в исходной позиции;
Таким образом, как видно из табл. 4, по критерию (1) отбракован второй вариант исходной позиции.
Следовательно, вариант 1 (K2Л, Х2К, П2С, П2К2Ф, ПККр, П2С, Х2К, К2Л) является единственным искомым решением задачи выбора лучшего варианта исходной позиции фигур в предлагаемых фигур в предлагаемых супершахматах на основе перечисленных выше требований и критерия (1).
На этом завершается, в принципиальном отношении, решение проблемы создания новой ϕε--совершенной супершахматной игры на классической 64-клеточной шахматной доске с целью преодоления двух указанных выше существенных недостатков классических шахмат.
Исходная позиция фигур в предлагаемых супершахматах, а также их структура показывают, что вновь предлагаемая игра является супершахматной не только в силу большей мощности новых шахматных фигур и пешек, но и потому, что предлагаемая шахматная игра является в теоретико-игровом смысле метарасширением классических шахмат, а классические шахматы являются собственной подыгрой предлагаемой шахматной игры.
На фиг. 14 изображена исходная позиция фигур и пешек предлагаемой супершахматной игры на классической 64-клеточной шахматной доске.
На фиг. 14 приняты следующие обозначения:
На фиг. 15oC20 с использованием шахматной координатной плоскости изображены множества возможных ходов всех фигур и пешек предлагаемой супершахматной игры, при этом ход только со взятием обозначается ×, , ход только на свободное поле - ○, , а ход на свободное поле и со взятием - ⊗. .
Также доказано, что эта игра является единственно лучшей по отношению к классическим шахматам и неулучшаемой на всем пространстве возможных шахматных игр на любых квадратных шахматных досках с квадратными полями (на классических досках) с использованием любых шахматных фигур с центрально-симметричными множествами атакуемых ими полей на координатной шахматной плоскости, то есть установлено, что на всем пространстве возможных шахматных игр на классических досках с любыми шахматными фигурами существует только две шахматные игры, а именно, классические шахматы и вновь открытые супершахматы.
В предлагаемой супершахматной игре король ходит на любое "соседнее" для него поле, которое не атаковано и на которое он может попасть, делая ход либо как ладья, либо как слон, либо как конь, либо как П-фигура по соответствующему направлению на один шаг. Рокировка, как и в классических шахматах, может быть короткой (Кр - на gl (П-ход), К2Л - на f1) или длинной (Кр - на cl (П-ход), К2Л - на d1), конечно, при соблюдении всех необходимых для этого условий (тех же, что и в классических шахматах при рокировке).
В супершахматах ходы фигур П2К2Ф, К2Л, П2С, Х2К по К2-, П2- и Х2-направлениям возможны на второе поле любого из выбранных направлений тогда и только тогда, когда свободно первое поле соответствующего выбранного направления.
Так как в супершахматах пешка имеет П-ход, то утрачивает смысл имеющее место в классических шахматах замечание относительно хода пешки до линии демаркации из начальной позиции.
В предлагаемых супершахматах допускается взятие пешки на проходе, причем регулярно, то есть всегда при ее К- и П-ходах из любой позиции, включая исходную; при П-ходе на свободное поле, если бьется промежуточное поле на вертикали, по которой перемещается пешка; при К-ходе на свободное поле, если бьется промежуточное поле на соседней вертикали, на которую перемещается пешка.
В отличие от классических шахмат, в которых ни одна из фигур, за исключением ладьи во время рокировки и коня, не может пересекать поле, занятое другой фигурой, в предлагаемых супершахматах подобные ограничения накладываются лишь при перемещениях фигур по Л- и С-составляющим; во всех же других случаях, то есть при перемешиваниях фигур по К-, П-, Х-, К2-, П2-, Х2-составляющим, все фигуры (в том числе конь) и пешки (ПК-пешки) в супершахматах могут пересекать поля, занятые другими фигурами.
Некоторые фигуры предлагаемых супершахмат, такие, как Ф ≡ П2К2Ф, Кр ≡ ПККр,С ≡ П2С,К ≡ Х2К (в том числе, и п ≡ ПКп), содержат П2-, Х2- и П-фигурное компоненты, которые надевают указанные фигуры тем свойством, что при каждом из перемещения по шахматной доске в любом из определяемом отмеченными компонентами направлении сохраняются как цвет, так и четность поля, на котором любая из этих фигур находилась до этого перемещения. Этим полем может быть либо поле в исходной позиции, как это имеет место для фигуры ϑ ≡ П2С, либо поле в любой другой позиции, включая исходную, как это имеет место для фигур Ф ≡ П2К2Ф,К ≡ Х2К,Кр ≡ ПККр (в том числе, и для 
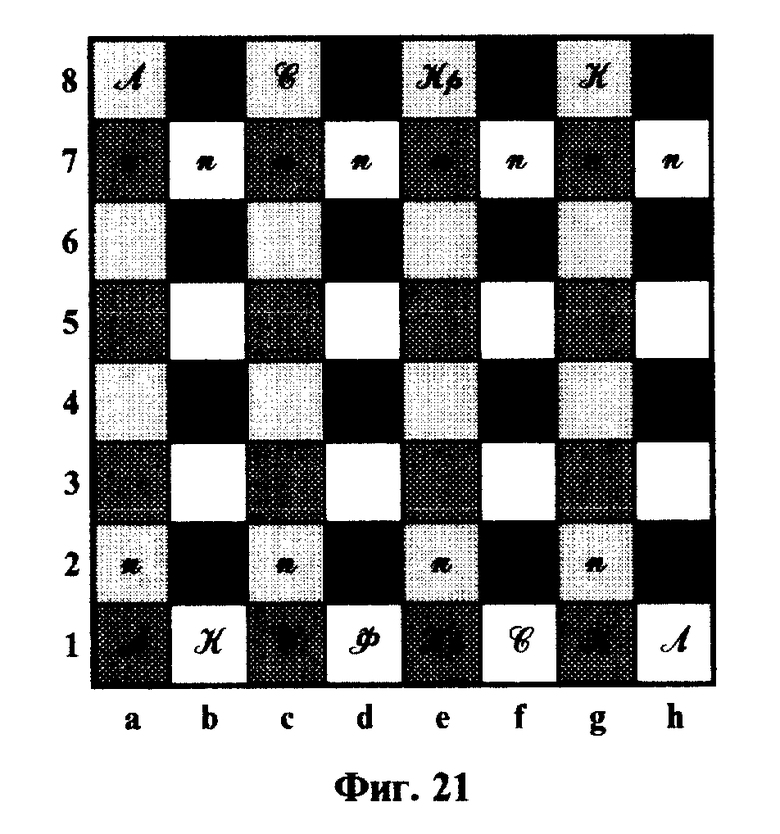
Это свойство делает весьма желательным использование в предлагаемой супершахматной игре четырех цветной 64-клеточной шахматной доски в виде, изображенном на фиг. 21 (светлые поля: b1, b3, b5, b7; d1, b3, d5, d7; f1, f3, f5, f7; h1, h3, h5, h7; темно-светлые поля; a2, a4, a6, a8; c2, c4, c6, c8; e2, e4, e6, e8; g2, g4, g6, g8; светло-темные поля; a1, a3, a5, a7; c1, c3, c5, c1; e3, e5, e7; g1, g3, g5, g7; темные поля; b2, b4, b6, b8; d2, d4, d6, d8; f2, f4, f6, f8; h2, h4, h6, h8), при этом, светлые и темно-светлые поля считаются, по определению, белыми, а светло-темные и темные поля считаются, по определению, черными полями.
Ранее отмечено, что в теоретико-игровом супершахматы являются метарасширением классических шахмат, а классические шахматы являются подыгрой предлагаемых супершахмат. В связи с этим структура супершахмат может быть представлена в виде статической и динамической характеристик не только на уровне элементарных компонент, как это сделано ранее, но и на обобщенном уровне сложных компонент (Л≡ К2Л,С ≡ П2С,К ≡ Х2К): :
а) (nЛ,nС,nК) = (3,3,2) - - обобщенная статическая структурная характеристика;
б)  - обобщенная динамическая структурная характеристика.
- обобщенная динамическая структурная характеристика.
Далее в табличной форме приводится сравнительная информация о характеристиках мощности фигур и пешек в классических шахматах и в предлагаемых супершахматах.
Мощность может быть абсолютной - с привязкой к некоторому полю шахматной доски (равной числу полей, которые может атаковать фигура с заданного поля), относительной - с привязкой к некоторому полю (равной частному от деления абсолютной мощности на число полей шахматной доски) и средней (определена выше).
Результаты сравнения мощности для набора различных фигур с привязкой к полю е4 сведены в табл. 5.
Из результатов табл. 5 следует, что по полному набору различных фигур предлагаемые супершахматы мощнее классических шахмат в 1,776 раза.
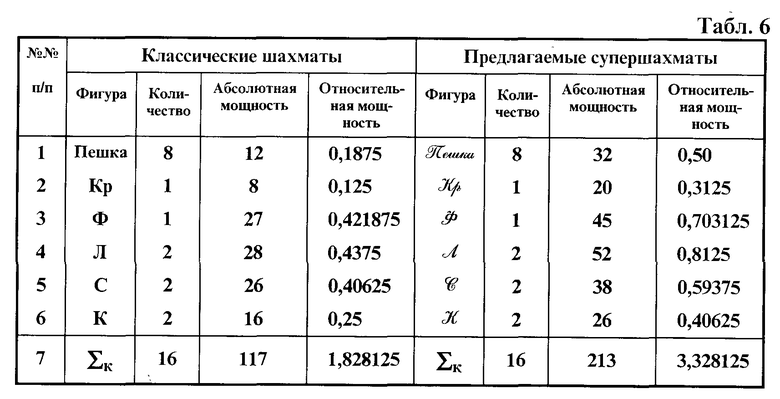
Результаты сравнения мощности для комплекта фигур одного цвета с привязкой к полю е4 сведены в табл. 6.
Как видно из результатов табл. 6, мощность комплекта фигур супершахматной игры превышает ту же величину для классических шахмат в 1,821 раза.
Результаты сравнения мощности для множества возможных ходов в начальной позиции сведены в табл. 7.
Из результатов табл. 7 видно, что по мощности множества возможных ходов в начальной позиции супершахматы сильнее классических шахмат в 2,75 раза.
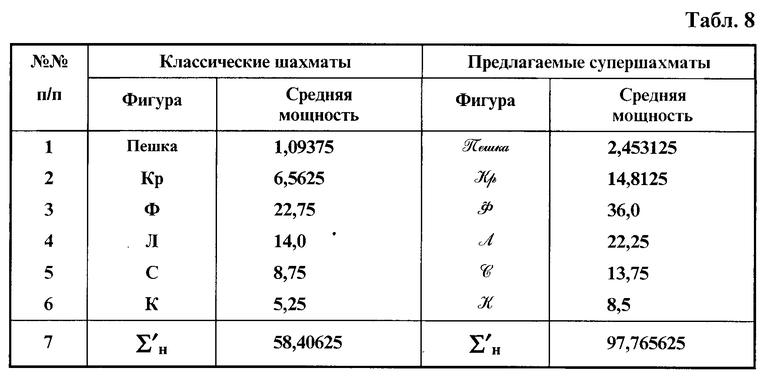
Результаты сравнения средней мощности для набора различных фигур сведены в табл. 8.
Из результатов табл. 8 следует, что средняя мощность набора различных фигур супершахматной игры превышает ту же величину для классических шахмат в 1,673 раза.
Результаты сравнения средней мощности для комплекта фигур одного цвета сведены в табл. 9.
Как видно из результатов табл. 9, средняя мощность комплекта фигур предлагаемой супершахматной игры превышает среднюю мощность комплекта фигур классических шахмат в 1,695 раза.
Шахматная партия в предлагаемых супершахматах, как и в классических шахматах, ведется между двумя партнерами на квадратной доске (шахматной) посредством передвижения фигур.
Шахматная доска состоит из 6 одинаковых клеток (полей), которые могут быть либо попеременно светлыми (белые поля) и темными (черные поля) (классическая шахматная доска), либо попеременно светлыми и темно-светлыми (белые поля), а также темными и светло-темными (черные поля), как это показано на фиг, 21 (супершахматная доска).
Шахматная доска при игре в супершахматы располагается между партнерами также, как и при игре в классические шахматы, то есть таким образом, чтобы угловое поле справа каждого шахматиста было белым.
Перед началом игры один из партнеров располагает 16 светлыми фигурами (суперфигурами) (белые), другой - 16 темными фигурами (суперфигурами) (черные).
Первоначальное положение суперфигур на классической шахматной доске (на супершахматной доске - аналогично) показано на фиг.22.
Знаки  нанесенные на изображения суперфигур приведенных в перечне, а также на фиг.22, интерпретируются следующим образом:
нанесенные на изображения суперфигур приведенных в перечне, а также на фиг.22, интерпретируются следующим образом:  суперферзь наряду с основной Ф-компонентов имеет дополнительную П2К2-компоненту; суперкороль наряжу с основной Кр-компонентой имеет дополнительную ПК-компоненту; суперпешка наряду с основной п-компонентов имеет дополнительную ПК-компоненту;
суперферзь наряду с основной Ф-компонентов имеет дополнительную П2К2-компоненту; суперкороль наряжу с основной Кр-компонентой имеет дополнительную ПК-компоненту; суперпешка наряду с основной п-компонентов имеет дополнительную ПК-компоненту;  суперладья наряду с основной Л-компонентой имеет дополнительную К2-компоненту;
суперладья наряду с основной Л-компонентой имеет дополнительную К2-компоненту;  суперслон наряду с основной С-компонентой имеет дополнительную П2-компоненту;
суперслон наряду с основной С-компонентой имеет дополнительную П2-компоненту;  суперконь наряду с основной К-компонентой имеет дополнительную Х2-компоненту.
суперконь наряду с основной К-компонентой имеет дополнительную Х2-компоненту.
Два партнера, ведущие шахматную партию в предлагаемые супершахматы, как и в классических шахматах, должны играть по очереди, делая каждый раз один ход. Партнер, имеющий белые фигуры, начинает партию.
Партия в предлагаемые супершахматы считается выигранной шахматистом, который дал мат королю партнера. Партия также считается выигранной тем из партнеров, противник которого сдался.
Партия в супершахматы может иметь ничейный исход. Партия заканчивается вничью:
1) В положении, где возможность выигрыша исключена (суперкороль против суперкороля, суперкороль против суперкороля с суперслоном или суперконем, суперкороль с суперслоном против суперкороля с суперслоном при одноцветных суперслонах).
2) Если суперкороль играющего (то есть партнера, имеющего право хода) не находится под шахом, но этот играющий не может сделать ни одного хода. Такое положение называется патом.
3) При взаимно согласии партнеров.
4) По требованию играющего, если одна и та же позиция возникает три раза, причем очередь хода каждый раз будет за играющим. Условия, при которых позиция считается повторенной, те же, что и в классических шахматах.
5) Когда играющий до совершения хода доказывает, что обеими сторонами сделано по меньшей мере 50 ходов, в течение которых ни одна суперфигура не была взята и ни одна суперпешка не сделала хода. Для некоторых отдельных позиций, по мере накопления опыта игры в супершахматы, число в 50 ходов может быть увеличено.
Рокировка в супершахматах осуществляется также, как в классических шахматах. При рокировке король (суперкороль) делает П-ход на поле той же горизонтали, на которой он находился в начальном положении, вслед за тем суперладья, в направлении которой переместился король, встает на поле, только что пересеченное королем. Условия, при которых рокировка возможна, те же, что и в классических шахматах.
Ходы фигур (суперфигур) в предлагаемых супершахматах отражены на фиг. 15oC20.
На фиг. 23oC25 схематически изображены элементы суперфигур предлагаемых супершахмат, позволяющие внешне отличить их от фигур классических шахмат.
Все шахматные фигуры классических шахмат конструктивно состоят из трех частей: нижняя часть (основание), средняя часть (шейка) и верхняя часть (вершина).
Суперфигуры в предлагаемых супершахматах отличаются от фигур классических шахмат в основании и средней части. Поэтому на указанных фиг. приведены фрагменты лишь этих частей суперфигур.
Суперфигуры вида Кр ≡ ПККр,Ф ≡ П2К2Ф,С ≡ П2С,п ≡ ПКп имеют основание, изображенное на фиг. 24.
Суперфигура вида К ≡ Х2К (суперконь) имеет основание, изображенное на фиг. 24.
Суперфигуры вида Кр ≡ ПККр,Ф ≡ П2К2Ф,Л ≡ К2Л,п ≡ ПКп имеют среднюю часть, изображенную на фиг, 25.
Об использовании предлагаемого изобретения можно сказать следующее.
Человеческая культура возникает и развертывается в игре и как игра, так что игра, таким образом, старше культуры [Йохан Хейзинга, Homo ludens: Опыт определения игрового элемента культуры. - М.: Издательская группа "Прогресс-Академия", 1992].
Общечеловеческий опыт свидетельствует, что классические шахматы (как игра, в широком смысле слова) имеют склонность быть красивыми. Этот эстетический фактор, по всей вероятности, тождествен стремлению человека творить, что оживляет шахматную игру во всех ее проявлениях и обликах. Слова, с помощью которых мы именуем элементы и моменты шахматной игры, принадлежат большей частью сфере эстетического. Это те же термины, которыми мы обозначаем проявления прекрасного: напряжение, равновесие, балансирование, чередование, контраст, вариантность, завязка и развязка, разрешение. Игра связывает и освобождает. Она исполнена тех двух благороднейших и прекраснейших качеств, которые человек способен замечать в вещах окружающего мира и сам может выразить: ритма и гармонии.
В этом и многих других аспектах о шахматной игре можно говорить бесконечно.
Предлагаемые супершахматы, как показано, имеют композиционную основу в качественном отношении более богатую и в метрическом отношении более совершенную, чем классические шахматы. Это может служить вполне достаточным основанием для того, чтобы предположить, что супершахматы и в своем внешнем проявлении, то есть как игра, станут более мощными и чистым источником прекрасного, чем классические шахматы. Это тем более вероятно, если учесть, что классические шахматы являются в строгом теоретико-игровом смысле подыгрой, то есть собственной частью, предлагаемых супершахмат. Т
| название | год | авторы | номер документа |
|---|---|---|---|
| НАСТОЛЬНАЯ ИГРА "СТОКЛЕТОЧНЫЕ ШАХМАТЫ" (ВЕРСИЯ В.И.ДУБРОВСКОГО) | 2002 |
|
RU2207178C1 |
| УСТРОЙСТВО ДЛЯ ИГРЫ В ШАХМАТЫ "ШАХМАТЫ ЧЕРНИКОВА" | 1998 |
|
RU2129897C1 |
| НАСТОЛЬНАЯ ИГРА "РУССКИЕ ТАВРЕЛИ" | 1996 |
|
RU2091110C1 |
| НАСТОЛЬНАЯ ИГРА | 1993 |
|
RU2097087C1 |
| ШАХМАТЫ С ПОДВИЖНЫМИ КЛЕТКАМИ ИГРОВОГО ПОЛЯ | 2019 |
|
RU2707590C1 |
| СПОСОБ ИГРЫ В ВОЕННЫЕ ШАХМАТЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1997 |
|
RU2123371C1 |
| ИГРА "ШАХМАТЫ 12 • 12" | 1995 |
|
RU2111784C1 |
| ШАХМАТЫ "АЛАНСКИЕ" | 2011 |
|
RU2475289C1 |
| УСТРОЙСТВО ДЛЯ ОБЪЕМНЫХ ЛОГИЧЕСКИХ ИГР "СПЕЙС ЧЕСС" | 1992 |
|
RU2097086C1 |
| Шахматно-шашечная доска | 1956 |
|
SU106997A1 |



























Шахматы относятся к настольным играм и могут быть использованы в шахматных играх на классической 64-клеточной доске. Шахматы содержат 64-клеточную шахматную доску и комплект шахматных фигур, состоящий из 16 светлых и 16 темных фигур. Шахматная доска выполнена четырехцветной с попеременно чередующимися светлыми полями двух оттенков и темными полями двух оттенков. Поля b1, b3, b5, b7, d1, d3, d5, d7, f1, f3, f5, f7, h1, h3, h5, h7 выполнены светлыми одного оттенка, а поля a2, a4, a6, a8, c2, c4, c6, c8, e2, e4, e6, e8, g2, g4, g6, g8 выполнены светлыми другого оттенка, при этом поля a1, a3, a5, a7, c1, c3, c5, c7, e1, e3, e5, e7, g1, g3, g5, g7 выполнены темными одного оттенка, а поля b2, b4, b6, b8, d2, d4, d6, d8, f2, f4, f6, f8, h2, h4, h6, h8 выполнены темными другого оттенка. Шахматы в качественном и метрическом отношениях имеют более богатую и более совершенную композиционную основу соответственно. 25 ил., 9 табл.
Шахматы, содержащие 64-клеточную шахматную доску и комплект из 32 шахматных фигур - 16 светлых, например белых, и 16 темных, например черных, отличающиеся тем, что шахматная доска выполнена четырехцветной с попеременно чередующимися светлыми полями двух оттенков и темными полями двух оттенков, при это поля b1, b3, b5, b7, d1, d3, d5, d7, f1, f3, f5, f7, h1, h3, h5, h7 выполнены светлыми от одного оттенка, поля a2, a4, a6, a8, c2, c4, c6, c8, e2, e4, e6, e8, g2, g4, g6, g8 выполнены светлыми другого оттенка, поля a1, a3, a5, a7, c1, c3, c5, c7, e1, e3, e5, e7, g1, g3, g5, g7 выполнены темными одного оттенка, а поля b2, b4, b6, b8, d2, d4, d6, d8, f2, f4, f6, f8, h2, h4, h6, h8 выполнены темными другого оттенка.
| Фирсова Л.М | |||
| Игры и развлечения | |||
| - М.: Молодая гвардия, 1990, кн.2, с769 | |||
| US 4093237 A, 06.06.78 | |||
| Шахматы | 1957 |
|
SU112692A1 |
| ОПОРНЫЙ ЭЛЕМЕНТ ЛЫЖНОЙ ПАЛКИ | 2007 |
|
RU2436612C2 |
Авторы
Даты
1998-09-10—Публикация
1997-02-05—Подача