Изобретение относится к радиотехнике, а именно к области радиотехнических устройств и систем, и в частности, заявленный реактивный фильтр с заданными частотами характеристиками может быть использован при разработке систем структурной развязки высокочастотных трактов (ВЧТ) радиопередатчиков декаметрового диапазона.
Известны реактивные фильтры с заданными частотными характеристиками, состоящие из минимально-фазовых звеньев, которые обеспечивают требуемую характеристику затухания (см. Трифонов И.И. Расчет электронных цепей с заданными частотными характеристиками. -М.: Радио и связь, 1988, с. 151-153).
Известны реактивные фильтры с заданными частотными характеристиками, состоящие из каскадно соединенных минимально-фазового и неминимально-фазового звеньев, реализованные в базисе реактивных сосредоточенных элементов, которые обеспечивают требуемые характеристики затухания и фазы (см. Трифонов И.И. Расчет электронных цепей с заданными частотными характеристиками. -М.: Радио и связь, 1988, с.196 - 206).
Недостатком этих реактивных фильтров с заданными частотными характеристиками является то, что реактивные взаимные четерхполюсники, к числу которых относятся реактивные фильтры, полностью определяются тремя независимыми параметрами (см. Фельдштейн А.Л., Явич Л.Р. Синтез четырехполюсников и восьмиполюсников на СВЧ. -М.: Связь, 1971, с. 52-53), а применительно к диапазону частот - тремя частотными характеристиками этих параметров. При синтезе же реактивных фильтров с заданными частотными характеристиками, имеющих структуры описанные выше, не представляется возможным обеспечить выполнение требований по частотным характеристикам всех трех параметров, характеризующих фильтр.
Наиболее близким аналогом (прототипом) к заявляемому устройству по своей технической сущности является известный реактивный фильтр с заданными амплитудно-частотной и фазочастотной характеристиками, описание которого приведено в книге: Трифонов И.И. Расчет электронных цепей с заданными частотными характеристиками. -М.: Радио и связь, 1988, с. 196 - 198 и рис. 4.34. Устройство - прототип содержит амплитудный четырехполюсник (на примере - два минимально-фазовых звена) и фазовый четерхполюсник (на примере - неминимально-фазовое сдвоенное звено).
Под амплитудным четырехполюсником (АЧП) здесь и ниже поднимается четырехполюсник с заданной амплитудно-частотной характеристикой. Под фазовым четырехполюсником (ФЧП) - четырехполюсник с заданной фазочастотной характеристикой и 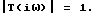
При этом, выход АЧП подключен к входу ФЧП, выход которого является выходом фильтра.
Это устройство обеспечивает выполнение требований по двум характеристикам: частотным зависимостям модуля и аргумента нормированной передаточной функции (характеристикам затухания и фазы) фильтра.
Недостатком прототипа является невозможность выполнения требований к полной совокупности независимых параметров: частотным характеристикам модуля и аргумента нормированной передаточной функции и частотной характеристике аргумента коэффициента отражения от входа фильтра при номинальной нагрузке его выхода, что необходимо, например, при использовании такого фильтра в системе структурной развязки радиопередающих устройств декаметрового диапазона.
Целью изобретения является разработка реактивного фильтра с заданными частотными характеристиками, обеспечивающего выполнение требований к полной совокупности независимых характеристик: частотным характеристикам модуля и аргумента нормированной передаточной функции и частотной характеристике аргумента отражения от входа фильтра при номинальной нагрузке его выхода.
Поставленная цель достигается тем, что в известном реактивном фильтре с заданными частотными характеристиками, содержащем АЧП, выход которого подключен к входу ФЧП, выход которого является выходом фильтра, подключен дополнительный ФЧП. Вход дополнительного ФЧП подключен к входу АПЧ. Причем ФЧП и АЧП выбраны с частотными характеристиками, удовлетворяющими условию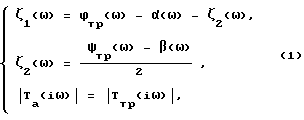
где
ζ1(ω), ζ2(ω) - фазочастотные характеристики фазовых четырехполюсников; ϕтр(ω) - заданная частотная характеристика аргумента нормированной передаточной функции фильтра; α(ω) - фазочастотная характеристика амплитудного четырехполюсника; ψтр(ω) - заданная частотная характеристика аргумента коэффициента отражения от входа фильтра при нормальной нагрузке его выхода; β(ω) - частотная характеристика аргумента коэффициента отражения от входа амплитудного четырехполюсника при нормальной нагрузке его выхода; |Tтр(iω) | - заданная частотная характеристика модуля нормированной передаточной функции фильтра; |Ta(iω)| - частотная характеристика модуля нормированной передаточной функции амплитудного четырехполюсника.
Такое построение реактивного фильтра с заданными частотными характеристиками позволяет обеспечить выполнение требований к трем частотным характеристикам заявляемого устройства: модуля и аргумента нормированной передаточной функции фильтра и аргумента коэффициента отражения от входа фильтра при нормальной нагрузке его выхода, в результате чего реализуется поставленная цель.
Заявляемое устройство поясняется чертежами, на которых показаны:
- на фиг. 1 структурная схема заявляемого реактивного фильтра с заданными частотными характеристиками;
- на фиг. 2 - заданная частотная зависимость модуля передаточной функции заявляемого фильтра;
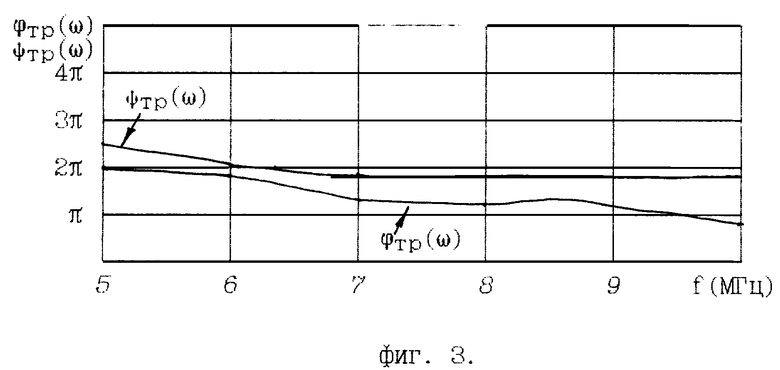
- на фиг. 3 - заданные частотные зависимости аргумента передаточной функции фильтра и аргумента коэффициента отражения от входа фильтра при нормальной нагрузке выхода;
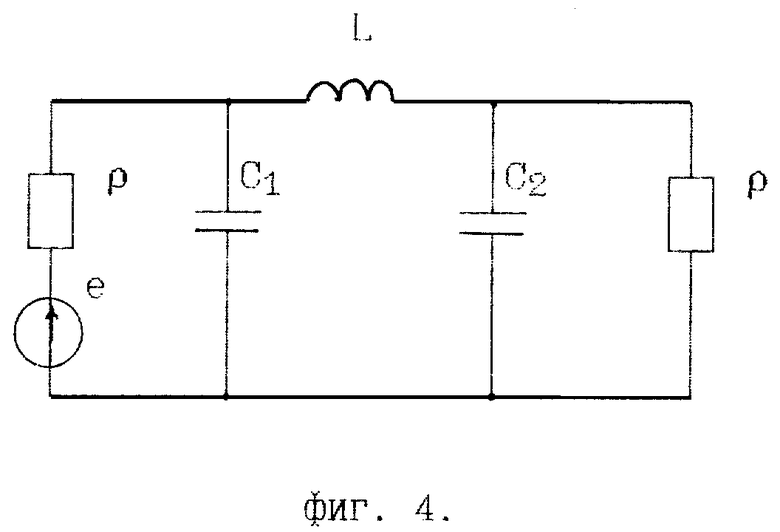
- на фиг. 4 - схема амплитудного четырехполюсника в режиме двухсторонней нагрузки;
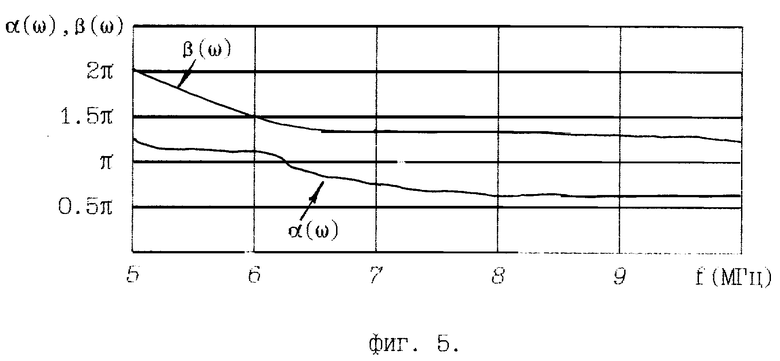
- на фиг. 5 - частотные зависимости аргумента передаточной функции амплитудного четырехполюсника и аргумента коэффициента отражения от входа амплитудного четырехполюсника при номинальной нагрузке выхода;
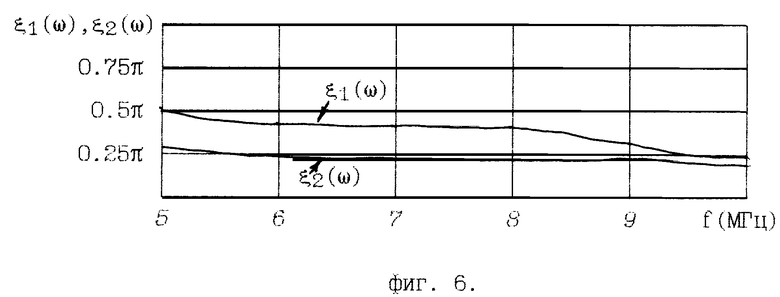
- на фиг. 6 - частотные зависимости аргументов передаточных функций фазовых четырехполюсников;
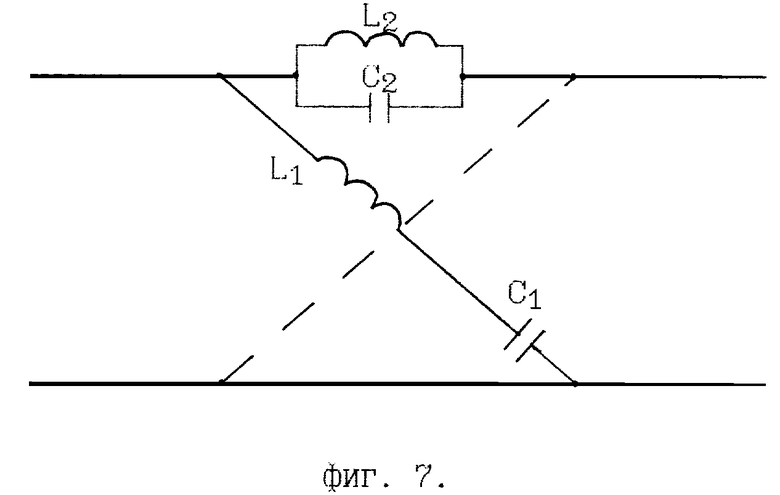
- на фиг. 7 - пример схемы фазовых четырехполюсников;
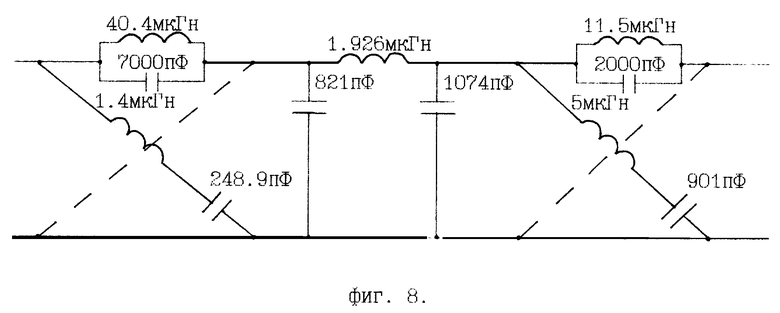
- на фиг. 8 - вариант построения схемы заявляемого устройства.
Реактивный фильтр с заданными частотными характеристиками, показанный на фиг. 1, состоит из двух ФЧП 1 и 2 и АЧП 3. Входом фильтра является вход ФЧП 2. Выход ФЧП 2 подключен к входу АЧП 3. Выход АЧП 3 подключен к входу ФЧП 1. Выход ФЧП 1 является выходом фильтра.
Заявляемое устройство работает следующим образом. Для пояснения возможности воспроизведения трех заданных частотных характеристик заявляемым реактивным фильтром, состоящим из каскадно соединенных АЧП 3 и двух ФЧП 1 и 2, как показано на фиг. 1 запишем параметры этих четырехполюсников в виде матриц рассеяния (см. Фельдштейн А.Л., Явич Л.Р. Синтез четырехполюсников и восьмиполюсников на СВЧ. -М.: Связь, 1971, - с. 30 - 33) Sа, Sф1, Sф2 соответственно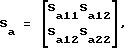 (2)
(2)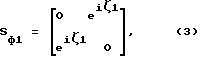
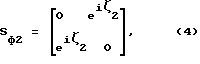
где
sа12 = |Ta(iω)|; sа11 - коэффициент отражения от входа АЧП при номинальной нагрузке его выхода; sа22 - коэффициент отражения от выхода АЧП при номинальной нагрузке его входа; ζ1 и ζ2 - аргументы передаточных функций ФЧП 1 и 2.
Используя выражения (2) - (4) , а также соотношение между элементами матриц S и T (см. Фельдштейн А.Л., Явич Л.Р. Синтез четырехполюсников и восьмиполюсников на СВЧ. -М. : Связь, 1971, с.37) определим цепные параметры четырехполюсников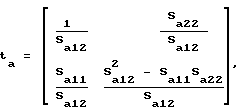
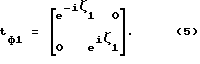
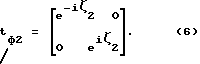
Цепная матрица каскадно соединенных четырехполюсников 2, 3 и 1 иметь вид: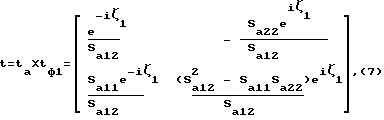
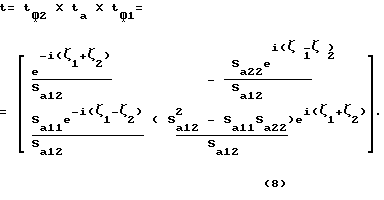
Произведя обратное преобразование, получим матрицу рассеяния результирующего четырехполюсника: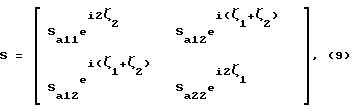
где
sа11, sа12 и sа22 элементы матрицы рассеяния АЧП 3;
ζ1 и ζ2 - - аргументы коэффициента передачи ФЧП 1, 2.
Выразим элементы матрицы рассеяния sа через три параметра:
q = |sа12|,
α = = arg{sа12},
β = = arg{sа11},
Получим: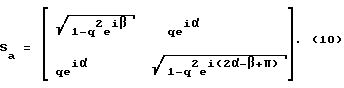
После подстановки (10) в (9) матрица рассеяния результирующего четырехполюсника примет вид: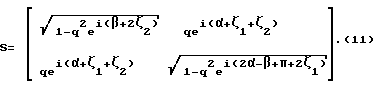
Таким образом, параметры результирующего четырехполюсника ϕ, ψ, |S12| можно выразить через параметры четырехполюсника 1, 2 и 3:
|S12| = q,
ϕ = α + ζ1 + ζ2,
ψ = β + 2ζ2.
Имея в качестве исходных данных заданные частотные характеристики 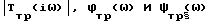 можно синтезировать реактивный фильтр, воспринимающий их. Из (12) следует, что
можно синтезировать реактивный фильтр, воспринимающий их. Из (12) следует, что
|Tтр(iω)| = |Ta(iω)|,
ϕтр(ω) = ζ1(ω) + ζ2(ω) + α(ω),
ψтр(ω) = β(ω) + 2ζ2(ω).
Следовательно, частотные характеристики аргументов передаточных функций ФЧП 1 и 2 можно определить по формулам: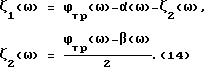
Модуль нормированной передаточной функции этих четырехполюсников |T(iω)| = 1.
Таким образом, для синтеза реактивного фильтра с заданными частотными характеристиками необходимо:
1. По заданной характеристике |Tтр(iω)| синтезировать АЧП 3.
2. Рассчитать значения параметров α и β АЧП 3 в диапазоне частот.
3. По требуемым и рассчитанным частотным характеристикам ϕтр(ω), ψтр(ω), α(ω) и β(ω) рассчитать требуемые частотные характеристики ФЧП 1, 2 - ζ1(ω) и ζ2(ω)..
4. По рассчитанным частотным характеристикам ζ1(ω) и ζ2(ω) синтезировать ФЧП 1 и 2.
Методики синтеза АЧП и ФЧП приведены в книге: Трифонов И.И. Расчет электронных цепей с заданными частотными характеристиками. - М.: Радио и связь, 1988. - с. 37-41 и 84 - 89.
Пример:
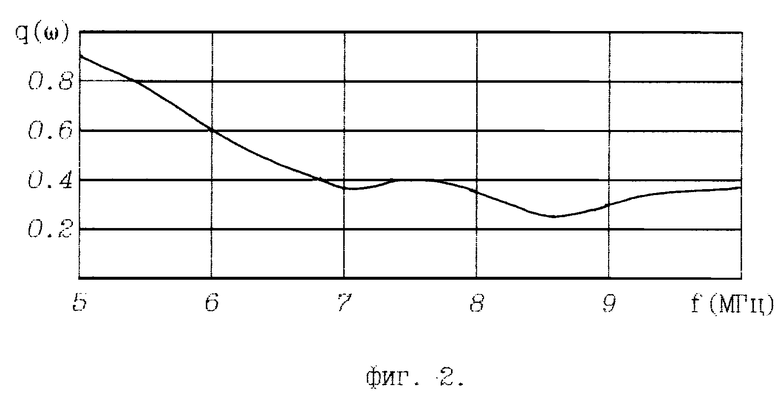
Пусть заданные частотные характеристики |Tтр(iω)|, ϕтр(ω) и ψтр(ω) изображенные на фиг. 2 и фиг. 3. Требуется рассчитать реактивный фильтр, воспроизводящий заданные характеристики.
1. Синтезируем АЧП 3, воспроизводящий требуемую частотную зависимость нормированной передаточной функции фильтр |Tтр(iω)| = q(ω), представленную на фиг. 2.
Произведем аппроксимацию функции q(ω). . Учитывая ее монотонно убывающий характер, сделаем предположение, что требуемую зависимость можно воспроизвести с высокой точностью функцией вида
представляющей собой модуль передаточной функции лестничных цепей типа ФНЧ. Зададимся порядком функции m = 3. Тогда система уравнений (3.6) (Трифонов И. И. Расчет электронных цепей с заданными частотными характеристиками. - М.: Радио и связь, 1988. - с. 86) примет вид: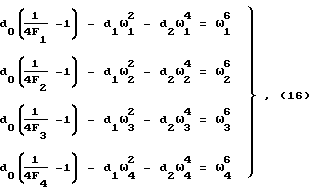
где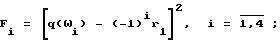
r1 - точность воспроизведения частотной зависимости q(ω) (максимальное отклонение аппроксимирующей функции от исходной по абсолютной величине).
Оптимизируя положение точек на частотной оси, соответствующих частотам ω1 ÷ ω4, и решая систему (16), добьемся, чтобы максимальные отклонения аппроксимирующей функции от исходной по абсолютной величине были равны. Данное требование выполняется при
ω1 = 2π•5•106,
ω2 = 2π•6,5•106,
ω3 = 2π•8,6•106, ω4 = 2π•107.
Значения коэффициентов d и r1 при этом соответственно равны:
d0 = 2,465 • 1044; d1 = 1,286 • 1030; d2 = 1,814 • 1015; r1 = 0,031.
Для нахождения передаточной функции искомой цепи необходимо определить коэффициенты полинома Гурвица. С этой целью в выражении (15) произведем замену переменных ω2 на -p2 . Затем, приравняв знаменатель нулю
d0 - d1p2 + d2p4 - p6 = 0,
найдет корни данного уравнения и определим полином Гурвица: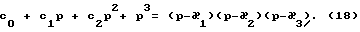
где
æ1,æ2,æ3 - - корни уравнения (17), лежащие в левой полуплоскости p. В результате получаем передаточную функцию АЧП 3:
Реализовать данную функцию можно Т-образной или П-образной цепью лестничной структуры. Решим задачу реализации для П-образной цепи, изображенной на фиг. 4. Запишем аналитическое выражение ее передаточной функции: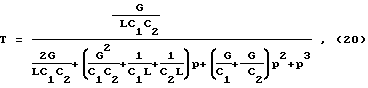
где G = 1/ρ. . Используя метод уравнивания коэффициентов, составим систему уравнений: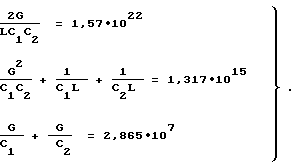
В результате решения системы (21) при ρ = 75 Ом получим:
C1 = 821 пФ, C2 = 1074 пФ, L = 1,926 мкГн.
2. Определим параметры α (аргумент передаточной функции) и (аргумент коэффициента отражения от входа при номинальной нагрузке выхода) рассчитанного АЧП.
Параметр α определяется непосредственно из выражения передаточной функции:
α(ω) = arg{Tтр(iω)}. (22)
График частотной зависимости α(ω) представлен на фиг. 5.
Для определения параметра β, рассмотрим полученную цепь в режиме двусторонней нагрузки (см. фиг. 4). При подключении к входным зажимам источника e = 1 с внутренним сопротивлением ρ и номинальной нагрузке, коэффициент отражения на входе цепи будет равен:
s11 = 2U1 - 1,
где
U1 - напряжение на входных зажимах цепи. Значение U1 найдем из выражения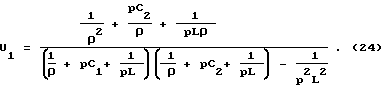
Подставляя формулу (23) и (24) и заменив переменную p на iω, найдет искомый параметр:
β(ω) = arg{S11} (25)
График зависимости Β(ω) представлен на фиг. 5.
3. Частотные зависимости аргументов передаточных функций ФЧП 1 и 2, обеспечивающие выполнение равенств (13), определим по формулам (14). Графики функций ζ1(ω), ζ2(ω) представлены на фиг. 6.
4. Решим задачу синтеза ФЧП по заданной частотной характеристике.
Произведем аппроксимацию полученной зависимости ζ1(ω), отображенной графиком на фиг. 6. Зададимся порядком аппроксимирующей функции n = 2. Система уравнений (2.11) (Трифонов И.И. Расчет электронных цепей с заданными частотными характеристиками. - М.: Радио и связь, 1988, - с. 38) примет вид: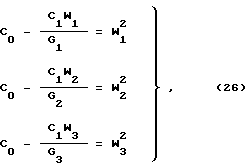
Решая систему, определим значения коэффициентов полинома Гурвица передаточной функции ФПЧ 1.
При ω1 = 2π•5,5•106, ω2 = 2π•8•106, ω3= 2π•10•106 элементы вектора c примут значения: c0 = 9,614 • 1013, c1 = 6,498 • 106. Абсолютная величина погрешности аппроксимации требуемой ФПЧ 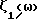 при этом не превышает 0,016 [рад.].
при этом не превышает 0,016 [рад.].
Для реализации ФПЧ 1 и 2 выберем структуру фазового контура (фиг. 7). Тогда номиналы элементов ФПЧ 1 будут следующими (Трифонов И.И. Расчет электронных цепей с заданными частотными характеристиками. - М.: Радио и связь, 1988. - с. 27 - 31):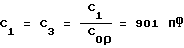
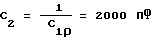
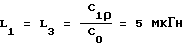
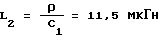
В результате решения задачи аппроксимации для ФЧП 2 получим:
c0 = 9,946 • 1013; c1 = 1,857 • 106.
Абсолютная величина погрешности аппроксимации требуемой ФЧХ ζ2(ω) при этом не превышает 0,0,27 [рад.].
Номиналы элементов ФЧП 2:
C1=C3 = 248,9 пФ; C2 = 7000 пФ; L1 = L3 = 1,4 мкГн; L2 = 40,4 мкГн.
Вариант построения схемы реактивного фильтра с заданными частотными характеристиками, обеспечивающего выполнение требований по модулю и аргументу передаточной функции и по аргументу коэффициента отражения от входа при номинальной нагрузке его выхода (фиг. 2, фиг. 3), представлена на фиг. 8.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНОГО СИГНАЛА И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2568931C1 |
| СПОСОБ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНОГО СИГНАЛА И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2589864C1 |
| АНАЛИЗАТОР ЧАСТОТНО-ВРЕМЕННОГО РАСПРЕДЕЛЕНИЯ МОЩНОСТИ | 1996 |
|
RU2108591C1 |
| СПОСОБ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНОГО СИГНАЛА И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2589304C1 |
| СПОСОБ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНОГО СИГНАЛА И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2494529C2 |
| СПОСОБ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНОГО СИГНАЛА И УСТРОЙСТВО ЕГО РЕАЛИЗЦИИ | 2011 |
|
RU2496225C2 |
| СПОСОБ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНОГО СИГНАЛА И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2496223C2 |
| СПОСОБ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНОГО СИГНАЛА И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2496224C2 |
| СПОСОБ ДЕМОДУЛЯЦИИ И ФИЛЬТРАЦИИ ФАЗОМОДУЛИРОВАННЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2488950C2 |
| СПОСОБ ДЕМОДУЛЯЦИИ И ФИЛЬТРАЦИИ ФАЗОМОДУЛИРОВАННЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2491711C2 |
Реактивный фильтр относится к радиотехнике, а именно к области радиотехнических устройств и систем. Реактивный фильтр с заданными частотными характеристиками состоит из двух фазовых четырехполюсников (1) и (2) и амплитудного четырехполюсника (3). Входом фильтра является вход фазового четырехполюсника (2), выход фазового четырехполюсника (2) подключен к выходу амплитудного четырехполюсника (3), выход амплитудного четырехполюсника (3) подключен к входу фазового четырехполюсника (1), выход фазового четырехполюсника (1) является выходом фильтра, при этом фазовые и амплитудный четырехполюсники выбраны с соответствующими частотными характеристиками. Технический результат: разработан реактивный фильтр с заданными частотными характеристиками, обеспечивающий выполнение требований к полной совокупности независимых характеристик: частотным характеристикам модуля и аргумента нормированной передаточной функции и частотной характеристике аргумента коэффициента отображения от входа фильтра при номинальной нагрузке его выхода. 8 ил.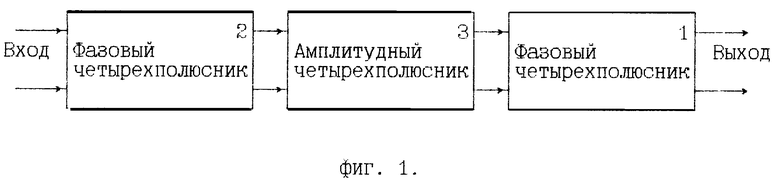
Реактивный фильтр с заданными частотными характеристиками, содержащий амплитудный четырехполюсник, выход которого подключен к входу фазового четырехполюсника, выход которого является выходом фильтра, отличающийся тем, что к входу амплитудного четырехполюсника подключен выход дополнительного фазового четырехполюсника, вход которого является входом фильтра, причем фазовые четырехполюсники и амплитудный четырехполюсник выбраны с частотными характеристиками, удовлетворяющими условию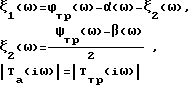
где ξ1(ω), ξ2(ω) - фазочастотные характеристики фазовых четырехполюсников;
ϕтр(ω) - заданная частотная характеристика аргумента нормированной передаточной функции фильтра;
α(ω) - фазочастотная характеристика амплитудного четырехполюсника;
ψтр(ω)- заданная частотная характеристика аргумента коэффициента отражения от входа фильтра при номинальной нагрузке его выхода;
β(ω) - частотная характеристика аргумента коэффициента отражения от входа амплитудного четырехполюсника при номинальной нагрузке его выхода; - заданная частотная характеристика модуля нормированной передаточной функции фильтра;
- заданная частотная характеристика модуля нормированной передаточной функции фильтра; 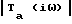 - частотная характеристика модуля нормированной передаточной функции амплитудного четырехполюсника.
- частотная характеристика модуля нормированной передаточной функции амплитудного четырехполюсника.
| Трифонов И.И | |||
| Расчет электронных цепей с заданными частотными характеристиками | |||
| М.: Радио и связь, 1988, с.199, рис.4.34 | |||
| Лосев А.К | |||
| Теория линейных электрических цепей | |||
| М.: Высшая школа, 1997, с.447, рис.9.51 | |||
| Артым А.Д | |||
| Электрические корректирующие цепи и усилители, М.- Л | |||
| Энергия, 1965, с.179-181 | |||
| Устройство для компенсации затухания и сдвига фазы четырехполюсника | 1954 |
|
SU99907A1 |
| ФАЗОВЫЙ КОРРЕКТОР СТАНДАРТНЫХ КАНАЛОВ ТОНАЛЬНОЙ ЧАСТОТЫ | 0 |
|
SU320068A1 |
| Приспособление для автоматической односторонней разгрузки железнодорожных платформ | 1921 |
|
SU48A1 |
| Способ изготовления звездочек для французской бороны-катка | 1922 |
|
SU46A1 |
| Способ изготовления звездочек для французской бороны-катка | 1922 |
|
SU46A1 |
| Способ смешанной растительной и животной проклейки бумаги | 1922 |
|
SU49A1 |
| GB 1113980 A, 15.05.68 | |||
| US 2916708 A, 08.12.59. | |||
Авторы
Даты
1998-10-20—Публикация
1996-11-10—Подача