Изобретение относится к электротехнике и может быть использовано в системах контроля уровня несинусоидальности напряжения и в прочих устройствах, где предполагается спектральный анализ периодически изменяющихся величин.
Известно преобразование Фурье, при помощи которого и выполняют спектральный анализ периодически изменяющихся величин [1].
Однако преобразование Фурье позволяет достоверно определить спектральный состав периодически изменяющейся величины лишь при условии, что эта величина составлена из целочисленных высших гармонических составляющих. А в спектрах токов и напряжений, имеющих место в современных электротехнических установках, нередко присутствуют субгармонические и дробные гармонические составляющие, то есть гармонические составляющие, частота периодических изменений которых меньше частоты основной гармоники, а также гармонические составляющие, частота которых некратна частоте основной гармоники. Математически для периодически изменяющегося напряжения это выглядит так: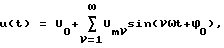
где
ν - номер гармонической составляющей, равный отношению частоты изменения этой составляющей к частоте основной гармоники: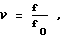
определяется лишь натуральными числами (ν = 1,2,3...).
Наиболее близким техническим решением к предлагаемому способу является графоаналитическое разложение, периодически изменяющееся, удовлетворяющее условию Дирихле, основанное на дискретном преобразовании Фурье [2].
Целью изобретения является получение количественной оценки субгармонических и дробных высших гармонических составляющих периодически изменяющихся величин.
Это достигается при учете изменения периода изменяющейся величины при появлении в ее спектре дробных гармонических составляющих. На чертеже показана структура алгоритма реализации предлагаемого способа количественной оценки субгармонических и дробных высших гармонических составляющих периодически изменяющихся величин. Реализацию этого алгоритма целесообразнее всего выполнять с помощью средств вычислительной техники.
Наличие в спектре периодически изменяющейся величины гармонической составляющей, номер которой может быть представлен лишь как некая дробная величина типа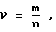
где
m и n - натуральные числа,
влечет за собой увеличение периода изменения анализируемой величины в n раз. Поэтому в блоке 1 структура алгоритма выполняется определением периода изменения анализируемой величины, то есть определением наименьшего диапазона выполнения равенства
f(χ) = f(χ+T),
где
χ - аргумент изменяющейся функции (величины);
T - период.
В электротехнике функция f(χ) чаще всего предстает в виде u(t) или i(t). Частота основной гармонической составляющей в России равна 50 Гц. Этой частоте соответствует период величиной 0,02 c.
Уже на этом этапе можно определить номер наименьшей по частоте гармонической составляющей: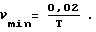
Если фактический период изменяющейся величины более периода основной гармонической составляющей
T > 0,02,
то в спектре анализируемой величины присутствует дробная гармоническая составляющая или субгармоника, номер которой определяется по формуле (I). В общем случае номер гармонической составляющей анализируемой величины определяется так: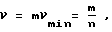
то есть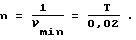
В блоке 2 происходит разложение аналоговой кривой, задаваемой чаще в виде временной диаграммы U(t) или i(t) на дискретные значения. Для этого анализируемую кривую разбивают на протяжении всего определенного ранее периода на равные временные промежутки (квантование). Число этих квантований за период, согласно следствиям теоремы Котельникова, целесообразнее всего избрать кратным 2k, где k - любое натуральное число. Для описанной операции лучше всего использовать аналого-цифровой преобразователь.
Далее в блоке 3 определяется постоянная составляющая периодически изменяющейся величины по формуле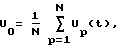
где
N - число квантований функции U(t) в периоде;
Up(t) - дискретное значение функции U(t) в момент p-го квантования;
T - период изменения анализируемой величины, задаваемый либо в градусах, либо в радианах.
В блоке 4 определяются амплитуды синусных составляющих каждой гармоники тригонометрического ряда Фурье: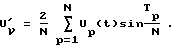
В блоке 5 определяются амплитуды косинусных составляющих каждой гармоники ряда Фурье: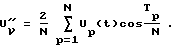
В блоке 6 определяется амплитудное значение каждой гармонической составляющей: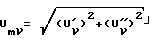
В блоке 7 определяются углы сдвига каждой гармонической составляющей относительно начального момента анализа периодически изменяющейся величины (p = 0) по формуле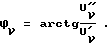
В блоке 8 формируется окончательный результат количественной оценки каждой субгармонической и дробной высшей гармонической составляющей периодически изменяющейся величины. При необходимости этот результата может быть выведен на какой-либо регистрирующий орган (дисплей, знакопечатающее устройство и т.п.).
Таким образом описываемый способ позволяет получить информацию о полном спектральном составе периодически изменяющейся величины, в частности тока или напряжения. При этом получается информация о целочисленных и дробных высших и низших гармонических составляющих анализируемой величины.
Источники информации
1. Корн Г., Корн Т. Справочник по математике. Для научных работников и инженеров. - М.: Наука, 1973. - 832 с.
Минин Г.П. Несинусоидальные токи и их измерение. - М.: Энергия, 1979, - 112 с.
Изобретение относится к электротехнике и может быть использовано в системах контроля уровня несинусоидальности напряжения и в прочих устройствах, где предполагается спектральный анализ периодически изменяющихся величии. Техническим результатом изобретения является получение количественной оценки субгармонических и дробных высших гармонических составляющих периодически изменяющихся величин. Способ количественной опенки субгармонических и дробных высших гармонических составляющих периодически изменяющихся величин позволяет оценивать гармонические составляющие тока и напряжения, частоты которых не кратны частоте основной гармоники, за счет увеличения пределов интегрирования при графоаналитическом разложении этих периодически изменяющихся величин. 1 ил.
Способ количественной оценки субгармонических и дробных высших гармонических составляющих периодически изменяющихся величин, заключающийся в том, что выполняется графоаналитическое разложение спектрального состава периодически изменяющихся напряжения или тока, при графоаналитическом разложении учитывается увеличение периода колебаний этих величин из-за присутствия в их спектральном составе субгармонических и дробных высших гармонических составляющих, при этом выполняется определение периода изменения анализируемой величины, определяется номер гармонической составляющей, определяется амплитудное значение каждой гармонической составляющей, определяются углы сдвига каждой гармонической составляющей относительно начального момента анализа периодически изменяющейся величины и формируется окончательный результат количественной оценки каждой субгармонической и дробной высшей гармонической составляющей периодически изменяющейся величины.
| Минин Г.П | |||
| Несинусоидальные токи и их измерение | |||
| - М.: Энергия, 1975, с | |||
| Паровоз для отопления неспекающейся каменноугольной мелочью | 1916 |
|
SU14A1 |
| Корн Г., Корн Т | |||
| Справочник по математике | |||
| Для научных работников и инженеров | |||
| - М.: Наука, 1973, 146 - 156 | |||
| Способ разложения сложного спектра на составляющие | 1977 |
|
SU693125A1 |
| US 3756721 A, 1974 | |||
| ИСКУССТВЕННЫЙ СФИНКТЕР | 1999 |
|
RU2162308C1 |
Авторы
Даты
1998-11-20—Публикация
1996-06-14—Подача