Изобретение относится к области игр, а более конкретно к способам образования случайных чисел, преимущественно для игр в кости.
Из предшествующего уровня техники известно, что были предприняты попытки по созданию альтернативных способов определения равновероятных игровых показателей для игр в кости.
Так, известен способ определения случайного игрового показателя (US, N 4678190, A 63 F 9/04, 1987), включающий формирование шести различных групп по шесть базовых равновероятных случайных сигналов в каждой группе, генерацию по одному случайному сигналу из каждой группы базовых равновероятных случайных сигналов, каждый из которых представляет собой совокупность из двух или трех целых чисел, а случайный игровой показатель от 6 до 36 или от 6 до 49 определяют на основании полученной совокупности случайных базовых сигналов.
Недостатками известного способа являются: узкий диапазон изменения значений случайного игрового показателя, большое число групп базовых равновероятных случайных сигналов, а также сложная структура каждого базового равновероятного случайного сигнала. Вследствие этого известный способ имеет ограниченную область использования.
Известен также способ определения случайного игрового показателя (US, N 4743025, A 63 F 9/04, 1988), взятый в качестве прототипа и включающий формирование нескольких одинаковых групп по шесть базовых равновероятных случайных сигналов в каждой группе, генерацию по одному случайному сигналу из каждой группы базовых равновероятных случайных сигналов, каждый из которых представляет собой одно целое число от 1 до 6, а случайный игровой показатель определяют на основании полученной совокупности случайных базовых сигналов.
Основной недостаток известного способа определения случайного игрового показателя заключается в том, что верхнее значение диапазона возможных значений случайного игрового показателя может изменяться только с очень большой кратностью, равной шести (36, 216, 1296 и т.д.), что существенно ограничивает область использования известного способа. Кроме того, само определение случайного игрового показателя на основании полученной совокупности случайных базовых сигналов является трудоемкой операцией, поскольку предусматривает использование специальных таблиц, а также специальной кодировки сигналов, соответствующих различным группам базовых сигналов.
Настоящее изобретение направлено на решение технической задачи по расширению множества значений дискретного распределения верхней границы диапазона возможных значений случайного игрового показателя при одновременном уменьшении интервала между указанными выше значениями. Достигаемый при этом технический результат заключается в расширении области использования предлагаемого способа.
Поставленная задача, согласно первому варианту, решена тем, что в способе определения случайного игрового показателя, согласно которому генерируют по одному случайному сигналу из каждой конечной группы равновероятных дискретных целочисленных случайных сигналов, а на основании полученной совокупности случайных сигналов определяют случайный игровой показатель, согласно изобретению, генерируют по одному случайному сигналу из N ≥ 2 различных групп равновероятных дискретных целочисленных, включая ноль, случайных сигналов, удовлетворяющих соотношению
где Cn j - j-й целочисленный случайный сигнал в n-й группе сигналов (n = 1,2,...,N);
Pi ≥ 2 - число различных значений случайных сигналов в i-й группе сигналов (i = 1,2,...,n-1);
kn j - коэффициент, принимающий значения 0,1,2,...,(Pn - 1) соответственно при j = 1,2,3,...,(Pn;
m - любое наперед заданное число от 1 до N;
а случайный игровой показатель, имеющий значение от 1 до  , определяют путем суммирования значений N генерированных случайных сигналов.
, определяют путем суммирования значений N генерированных случайных сигналов.
Дискретная функция δmn впервые была введена П. Дираком (см. П. Дирак, Принципы квантовой механики, пер. с 4-го английского издания, М., "Наука", 1979 г., с. 89).
Согласно второму варианту, поставленная задача решена тем, что в способе определения случайного игрового показателя, согласно которому генерируют по одному случайному сигналу из каждой конечной группы равновероятных дискретных целочисленных случайных сигналов, а на основании полученной совокупности случайных сигналов определяют случайный игровой показатель, согласно изобретению, генерируют по одному случайному сигналу из N ≥ 2 различных групп равновероятных дискретных целочисленных, включая ноль, случайных сигналов, удовлетворяющих соотношению
где Cn j - j-й целочисленный случайный сигнал в n-й группе сигналов (n = 1,2,...,N);
Pi ≥ 2 - число различных значений случайных сигналов в i-й группе сигналов (i = 1,2,...,n-1);
kn j - коэффициент, принимающий значения 0,1,2,...,(Pn - 1) соответственно при j = 1,2,3,...,(Pn;
а случайный игровой показатель, имеющий значение от 1 до 
определяют путем суммирования значений N генерированных случайных сигналов.
Преимущество предлагаемого способа заключается в том, что благодаря реализации совокупности новых условий осуществления известных операций генерирования случайных сигналов, а именно:
- наличие N ≥ 2 различных групп равновероятных дискретных целочисленных случайных сигналов (базовых сигналов),
- наличие в каждой группе, по крайней мере, двух или двух подгрупп равновероятных дискретных целочисленных, включая ноль, сигналов, имеющих различные значения (Pi ≥ 2),
- наличие взаимооднозначного соответствия между номером группы равновероятных дискретных целочисленных случайных сигналов и целочисленными значениями сигналов в соответствующей группе (зависимость [1] или [2]),
обеспечивается расширение множества значений дискретного распределения верхней границы диапазона возможных значений случайного игрового показателя, определяемым теперь выражением [2α×3β×4γ×5ξ×6ε×...] для первого варианта осуществления способа либо выражением [(2α×3β×4γ×5ξ×6ε×...)-1] - для второго варианта, при этом α,β,γ,ξ,ε,... - любые целые числа, включая ноль, удовлетворяющие условию α+β+γ+ξ+ε+...= N. Более того, отсутствует необходимость в дополнительном кодировании сигналов, соответствующих одной и той же группе. Таким образом, наименьшее верхнее значение диапазона возможных значений случайного игрового показателя равно не 36, как в прототипе, а 4 (α = 2 = N), при этом каких-либо ограничений сверху нет. Кроме того, существенно сужается интервал между рядом расположенными верхними значениями диапазона возможных значений случайного игрового показателя. Действительно, для представляющего безусловно практический интерес случая Pi = 2, 3 и 6 множество верхних значений диапазона возможных значений случайного игрового показателя включает все множество целых чисел, за исключением простых и кратных им.
Целесообразно в ряде случаев, чтобы игровой показатель имел и нулевое значение. Второй вариант осуществления предлагаемого способа демонстрирует эту возможность.
Таким образом, обеспечивается достижение технического результата, заключающегося в расширении области использования (комнатные игры, азартные игры, массовые развлечения) способа определения случайного игрового показателя.
В дальнейшем, изобретение поясняется чертежами и описанием к ним.
На фиг. 1 изображена блок-схема устройства для осуществления предложенного способа; на фиг. 2, 3, 4 и 5 - развертки в плоскости соответственно первой, второй, третьей и четвертой шестигранной игральной кости для значений случайного игрового показателя от 1 до 36; на фиг. 6 и 7 - развертки в плоскости соответственно первой и второй четырехгранной игральной кости для значений случайного игрового показателя от 1 до 36; на фиг. 8, 9 и 10 - развертки в плоскости, соответственно первой и второй шестигранной и третьей - четырехгранной игральной кости для значений случайного игрового показателя от 1 до 36; на фиг. 11 и 12 - развертки в плоскости соответственно первой и второй шестигранной игральной кости для значений случайного игрового показателя от 1 до 36; на фиг 13 и 14 - развертки в плоскости соответственно третьей и четвертой шестигранной игральной кости для значений случайного игрового показателя от 1 до 1296; на фиг. 15, 16 и 17 - развертки в плоскости соответственно первой, второй и третьей шестигранной игральной кости для значений случайного игрового показателя от 0 до 215.
Устройство для осуществления предлагаемого способа содержит N-входной сумматор 1, N блоков 21 - 2N памяти, N мультиплексоров 31 - 3N, N генераторов 41 - 4N равномерно распределенных случайных двоичных чисел, блок 5 запуска и индикатор 6. Блоки 21 - 2N памяти имеют соответствующие входы 71 - 7N, а выходы каждого блока 21 - 2N памяти соединены с информационными входами соответствующего мультиплексора 31 - 3N. Выходы каждого генератора 41 - 4N соединены с адресными входами соответствующего мультиплексора 31 - 3N, выходы которых соединены с соответствующими входами N-входного сумматора 1. Выход N-входного сумматора 1 соединен с входом индикатора 7, а выход блока 5 запуска соединен с управляющими входами генераторов 41 - 4N равномерно распределенных случайных двоичных числе.
Кроме того, на чертежах обозначены развертки 8-23 игральных костей, имеющих четыре или шесть граней.
Предложенный способ осуществляется следующим образом.
Предварительноm исходя из требуемого диапазона изменения случайного игрового показателя определяют число групп равновероятных дискретных целочисленных сигналов. Для этого задают такие значения показателей степени в выражении [2α×3β×4γ×5ξ×6ε×...] (3), если нижняя граница указанного выше диапазона равна единице, при которых выражение в квадратных скобках равно верхней границе диапазона изменения случайного игрового показателя. Например, для верхней границы, равной 1296, выражение в квадратных скобках может быть представлено в следующем виде: [2 • 33 • 4 • 6]. Другими словами, α = 1, β = 3, γ = 1, ξ = 0, ε = 1, а остальные показатели степени равны нулю. Сумма показателей степени (α+β+γ+ε) есть число различных групп N=6 равновероятных дискретных целочисленных случайных сигналов, а 2, 3, 4 и 6 - число неповторяющихся сигналов соответственно в первой (второй, третьей и четвертой - поскольку β = 3), а также в пятой и шестой группах. Далее в соответствии с соотношением (1) производится вычисление значений равновероятных дискретных целочисленных случайных сигналов (групп базовых сигналов). После этого по входу 71 в блок 21 памяти записываются значения целочисленных сигналов первой группы. По входу 72 в блок 22 памяти записываются значения целочисленных сигналов второй группы. И так далее. После этого по команде "Пуск" на выходе блока 5 запуска формируют управляющий импульс, который запускает генератор, 41 - 4N равномерно распределенных случайных чисел. По окончании управляющего импульса на выходах генераторов 41 - 4N появляются сигналы, соответствующие генерируемым случайным числам. Эти сигналы с выходов генераторов 41 - 4N подаются на адресные входы соответствующих мультиплексоров 31 - 3N. При этом на выходе каждого мультиплексора 31 - 3N появится сигнал с того информационного входа, номер которого соответствует двоичному числу (коду) на его адресных входах. Поскольку на информационные входы каждого мультиплексора 31 - 3N поданы сигналы, записанные в ячейках соответствующего блока 21 - 2N памяти, то на выходы N-входового сумматора 1 будут поданы сигналы, генерированные случайно из каждой группы базовых сигналов. Таким образом, на выходе сумматора 1 появится сигнал, значение которого будет соответствовать случайному игровому показателю.
Образование следующего игрового показателя осуществляется при подаче повторной команды "Пуск" на блок 5 запуска.
Если нижняя граница диапазона значений случайного игрового показателя равна нулю, то вместо выражения (3) используется выражение [(2α×3β×4γ×5ξ×6ε×...)-1] (4). Остальные действия аналогичны вышеописанным.
Кроме описанных выше средств для осуществления предлагаемого способа могут быть использованы, по крайней мере, две (поскольку N ≥ 2) игральные кости, например, наиболее часто используемые - шестигранные. В этом случае цифровые информационные метки, нанесенные на грани одной и той же игральной кости, образуют группу равновероятных дискретных целочисленных случайных сигналов (базовых), а выпавшие в результате выбрасывания костей (с помощью любого из числа известных устройств, например, описанных в патентах GB-1-2145638, GB-A-2195089) цифровые информационные метки образуют совокупность N генерированных случайных сигналов, по которым определяют (путем суммирования значений генерированных сигналов) значение случайного игрового показателя.
В зависимости от требуемого диапазона возможных значений случайного игрового показателя определяют необходимое число игральных костей (различных групп равновероятных дискретных целочисленных случайных сигналов), а также сами значения указанных выше сигналов в соответствии с выражениями (1) или (2).
Пример 1. Для верхнего значения диапазона возможных значений случайного игрового показателя, равного 36, возможны следующие три варианта для Pi = 2,3,4,6:
1) 22 • 32 = 36; 2) 32 • 4 = 36; 3) 62 = 36.
В первом случае требуется четыре кости (α = 2, β = 2, α+β = N = 4); во втором случае - три кости (β = 2, γ = 1, β+γ = N = 4) , а в третьем - две кости (ε = 2 = N).
Пусть нижнее значение диапазона возможных значений случайного игрового показателя равно единице. В этом случае целочисленные случайные сигналы в каждой группе определяются из соотношения (1). Для m = 1 имеет для первого случая:
n = 1; C1 1 = 1; C1 2 = 2;
n = 2; C2 1 = 0; C2 2 = 2;
n = 3; C3 1 = 0; C3 2 = 4; C3 3 = 8;
n = 4; C4 1 = 0; C4 2 = 12; C4 3 = 24.
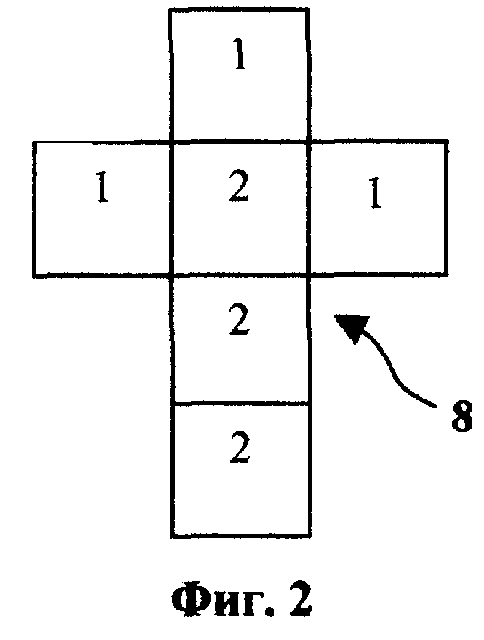
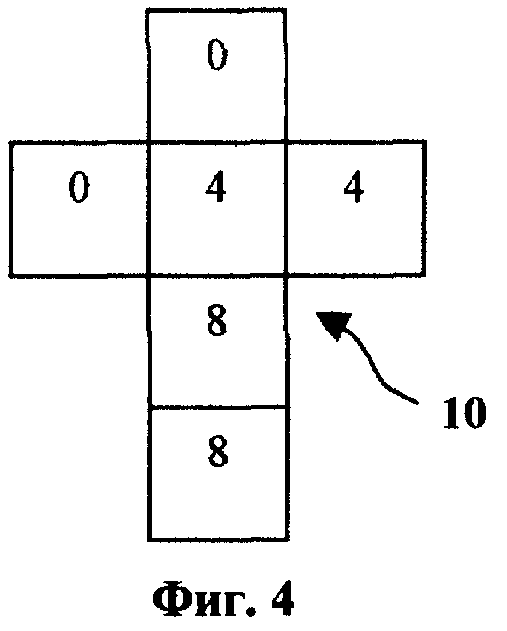
В случае использования шестигранных костей общее число равновероятных случайных сигналов в каждой группе сигналов равно числу граней игральной кости, иными словами, шести. Для обеспечения равной вероятности для двух различных сигналов группа из шести равновероятных случайных сигналов должна содержать две подгруппы сигналов, при этом первая подгруппа содержит три одинаковых сигнала C1 1 или C2 1, а вторая подгруппа - также три одинаковых сигнала соответственно C1 2 или C2 12 (фиг. 2 и 3). Аналогично для обеспечения равной вероятности для трех различных сигналов (n = 3, 4) группа из шести равновероятных случайных сигналов должна содержать три подгруппы из двух одинаковых сигналов (0, 0, 4, 4, 8, 8 для n = 3) и (0, 0, 12, 12, 24, 24 для n = 4), как показано соответственно на фиг. 4 и 5. Вместо шестигранных костей для n = 1 и n = 2 могут быть использованы и четырехгранные игральные кости (тетраэдры). В этом случае каждая подгруппа будет содержать по два одинаковых сигнала (фиг. 6 и 7).
Во втором случае для m = 2 имеем следующие три группы равновероятных случайных сигналов:
n = 1; C1 1 = 0; C1 2 = 1; C1 3 = 2;
n = 2; C2 1 = 1; C2 2 = 4; C2 3 = 7;
n = 3; C3 1 = 0; C3 2 = 9; C3 3 = 18; C3 4 = 27.
В этом случае для генерации случайных сигналов первой и второй групп (n = 1, 2) сигналов используются шестигранные игральные кости (фиг. 8 и 9), а для сигналов из третьей группы - четырехгранная игральная кость (фиг. 10).
В третьем случае для m = 1 имеем следующие две группы равновероятных случайных сигналов:
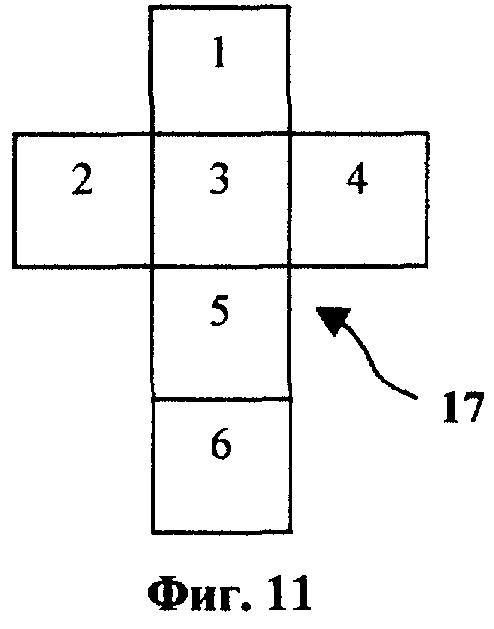
n = 1; C1 1 = 1; C1 2 = 3; C1 3 = 3; C1 4 = 4; C1 5 = 5; C1 6 = 6;
n = 2; C2 1 = 0; C2 2 = 6; C2 3 = 12; C2 4 = 18; C2 5 = 24; C2 6 = 30;
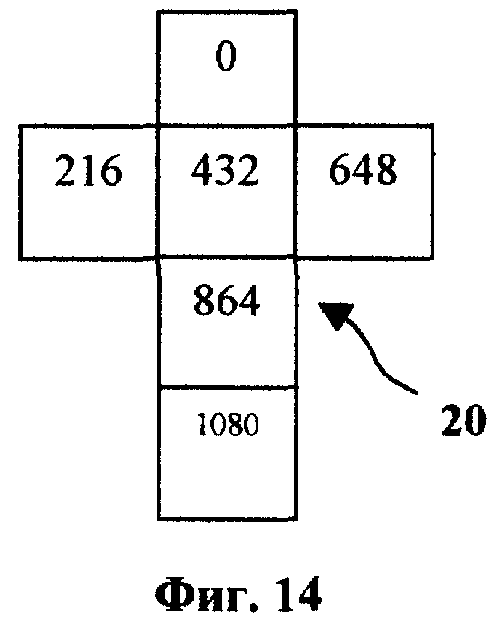
для генерации которых используются две шестигранные кости (фиг. 11 и 12). Использование же игральных костей с числом граней больше шести не представляется целесообразным, поскольку использование только четырех шестигранных костей обеспечивает верхнее значение диапазона изменения величины случайного игрового показателя, равного 1296, что вполне достаточно в подавляющем числе случаев. На фиг. 11 - 14 изображены развертки в плоскости четырех шестигранных костей для диапазона изменения случайного игрового показателя от 1 до 1296.
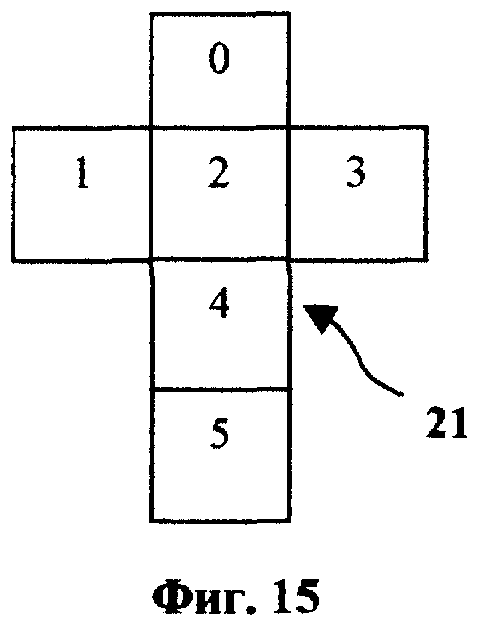
Пример 2. В случае, когда нижнее значение диапазона возможных значений случайного игрового показателя равно нулю, целочисленные случайные сигналы в каждой группе определяются из соотношения (2). Одним из возможных вариантов для реализации диапазона изменения случайного игрового показателя от 0 до 215 является набор из трех групп равновероятных случайных сигналов (ε = 3 = N):
n = 1; C1 1 = 0; C1 2 = 1; C1 3 = 2; C1 4 = 3; C1 5 = 4; C1 6 = 5;
n = 2; C2 1 = 0; C2 2 = 6; C2 3 = 12; C2 4 = 18; C2 5 = 24; C2 6 = 30;
n = 3; C3 1 = 0; C3 2 = 36; C3 3 = 72; C3 4 = 108; C3 5 = 144; C3 6 = 180.
Поскольку в каждой группе содержится по шесть равновероятных случайных сигналов, то для реализации указанного выше диапазона изменения случайного игрового показателя требуется три шестигранные игральные кости (фиг. 15 - 17).
Предлагаемый способ может быть использован при проведении как комнатных игр, в том числе и азартных, так и различных массовых развлечений, в частности экспресс-лотерей, либо в специально оборудованных стационарных или передвижных помещениях, либо на открытом воздухе, например в луна-парках.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МАССОВЫХ РАЗВЛЕЧЕНИЙ | 1997 |
|
RU2120818C1 |
| СПОСОБ МАССОВЫХ РАЗВЛЕЧЕНИЙ | 1997 |
|
RU2119810C1 |
| СПОСОБ МАССОВЫХ РАЗВЛЕЧЕНИЙ | 1997 |
|
RU2120321C1 |
| СПОСОБ МАССОВЫХ РАЗВЛЕЧЕНИЙ | 1997 |
|
RU2119811C1 |
| СПОСОБ МАССОВЫХ РАЗВЛЕЧЕНИЙ | 1997 |
|
RU2119812C1 |
| МОЮЩЕЕ СРЕДСТВО | 1999 |
|
RU2172771C1 |
| ИГРА В КОСТИ "ТЕРНАРИС" И УСТРОЙСТВО ДЛЯ ИГРЫ ТАКИМ СПОСОБОМ (ВАРИАНТЫ) | 2016 |
|
RU2682764C2 |
| ИГРОВОЙ АВТОМАТ С ВЫДАЧЕЙ МОНЕТ ИЛИ ЖЕТОНОВ | 1991 |
|
RU2020587C1 |
| АДАПТИВНАЯ РАДИОЛИНИЯ ПЕРЕДАЧИ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 1991 |
|
RU2010430C1 |
| ИГРА "ВЕДА ДИД-ЛАДО" | 2007 |
|
RU2337741C1 |












Изобретение относится к области игр, а также к способам образования случайных чисел преимущественно для игр в кости. Сущность изобретения: генерируют по одному случайному сигналу из N≥2 различных групп равновероятных дискретных целочисленных, включая ноль, случайных сигналов, удовлетворяющих соотношению, в котором учитывается целочисленный случайный сигнал в группе сигналов, а также число различных значений случайных сигналов в группе сигналов. На основании полученной совокупности случайных сигналов определяют значение игрового показателя путем суммирования значения генерированных случайных сигналов. Данное изобретение позволяет расширить множество значений дискретного распределения верхней границы диапазона возможных значений случайного игрового показателя при одновременном уменьшении интервала между указанными выше значениями, что расширяет область использования данного способа. 2 с.п.ф-лы, 17 ил.
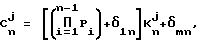
где Cj n - j-й целочисленный случайный сигнал в n-й группе сигналов (n = 1, 2, ..., N);
Pi ≥ 2 - число различных значений случайных сигналов в i-й группе сигналов (i = 1, 2, ..., n-1);
K
m - любое наперед заданное число от 1 до N,
а случайный игровой показатель, имеющий значение от 1 до 
определяют путем суммирования значений N генерированных случайных сигналов.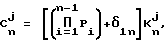
где Cj n - j-й целочисленный случайный сигнал в n-й группе сигналов (n = 1, 2, ..., N);
Pi ≥ 2 - число различных значений случайных сигналов в i-й группе сигналов (i = 1, 2, ..., n-1);
K
а случайный игровой показатель, имеющий значение от 0 до 
определяют путем суммирования значений N генерированных случайных сигналов.
| US 4743025 A, 10.05.88 | |||
| US 4713787 A, 15.12.87 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕЖФАЗНОГО НАТЯЖЕНИЯ МЕЖДУ ДВУМЯ ФЛЮИДАМИ | 2019 |
|
RU2722896C1 |
| НАСТОЛЬНАЯ ИНТЕЛЛЕКТУАЛЬНАЯ ИГРА "ЛЕТУЧИЙ ГОЛЛАНДЕЦ" | 1996 |
|
RU2113879C1 |
| Приспособление в пере для письма с целью увеличения на нем запаса чернил и уменьшения скорости их высыхания | 1917 |
|
SU96A1 |
| ДАТЧИК СЛУЧАЙНЫХ ЧИСЕЛ С РАВНОМЕРНЫМ РАСПРЕДЕЛЕНИЕМ | 1994 |
|
RU2103725C1 |
| RU 94019263 A1, 27.02.96. | |||
Авторы
Даты
1999-12-10—Публикация
1999-04-21—Подача