Изобретение относится к области оптико-электронного приборостроения и может быть использовано в скоростных дифрактометрах.
Известен способ измерения расстояния между минимумами (квазипериода) дифракционного распределения (ДР) когерентного излучения от узких щелей или отверстий, базирующийся на регистрации распределения многоэлементным фотоприемником (МЭФ), аппроксимации цифровых отсчетов сигнала в окрестности минимума кубическим полиномом, нахождении координат минимумов путем решения квадратного уравнения, получающегося при дифференцировании аппроксимирующей функции, и определении величины квазипериода по разности координат минимумов соседних порядков [1]. Недостатком данного способа является низкое быстродействие, обусловленное необходимостью обработки больших объемов информации по сложным разнородным алгоритмам.
Известен также [2] способ измерения параметров ДР, основанный на выравнивании пространственного распределения интенсивности ДР с помощью оптического элемента с убывающим к краям поглощением, регистрации пространственного распределения ДР, расчета спектра изображения ДР и определения параметров ДР по расстоянию между спектральными составляющими. Недостатком данного способа является сложность реализации и ограниченность диапазона измерений.
Из известных технических решений наиболее близким по технической сущности к заявляемому объекту является способ регистрации и измерения параметров спектральных распределений излучения на выходе оптических Фурье-спектрометров с помощью многоэлементных фотоприемников и вычислительных устройств [3]. В этом способе вычислительное устройство производит дискретное преобразование Фурье (ДПФ) N цифровых отсчетов сигнала МЭФ, в результате которого формируется N/2 отсчетов спектрального распределения. Недостатком данного способа также является низкое быстродействие, обусловленное большим количеством отсчетов спектрального распределения, для которых необходим расчет по методу ДПФ (N/2 = 512,1024).
Сущность изобретения заключается в том, что для повышения скорости измерения квазипериода ДР когерентного излучения от узкой щели производится совмещение центров ДР излучения с центром многоэлементного фотоприемника, регистрация и квантование изображения ДР, расчет амплитудного спектра значимых гармоник (превышающих пороговый уровень, нормированный к амплитуде первой гармоники) с помощью дискретного преобразования Фурье цифрового массива отсчетов сигнала МЭФ и расчет ширины спектра путем линейной аппроксимации значимых отсчетов амплитудного спектра. Квазипериод ДР определяется как величина, обратная ширине спектра.
Перечисленные признаки обеспечивают достижение поставленной цели.
В электронике известны способы регистрации оптических изображений многоэлементными фотоприемниками, операции дискретного преобразования Фурье и линейной аппроксимации данных. Однако использование перечисленных операций в указанной выше последовательности применительно к регистрируемому также указанным выше образом ДР когерентного излучения от узкой щели позволяет получить новое качество - повышение скорости измерения квазипериода. Это качество не является результатом суммирования положительных эффектов, получаемых от введения отдельных операций регистрации и обработки, а достигается именно за счет учета особенностей регистрируемого ДР и его ДПФ. Эта особенность состоит в том, что амплитудный спектр центральной части ДР, полученный в результате ДПФ, будет иметь огибающую, близкую к линейной. При этом вследствие квадратичного убывания огибающей самого ДР число регистрируемых квазипериодов и, соответственно, ширина амплитудного спектра ДПФ, определяемая по числу значимых гармоник, амплитуда которых превышает определенный порог, составляющий, например, 5% от амплитуды первой гармоники, не будет превышать 5 - 10. Число рассчитываемых гармоник с учетом синусной и косинусной составляющих будет больше приведенных значений в два раза, однако это число существенно меньше указанных выше значений гармоник, для которых производится расчет по алгоритму ДПФ в способе - прототипе. Такое уменьшение числа гармоник в сочетании с однородностью алгоритма ДПФ позволяет повысить скорость расчета ширины спектра за счет использования аппаратных решений и, соответственно, скорость измерения квазипериода дифракционного распределения.
Поскольку среди известных способов измерения квазипериода ДР от узкой щели не выявлено способов измерения со сходными признаками, которые бы решали ту же задачу тем же путем (т.е. регистрацией центральной части ДР с помощью МЭФ, квантованием и расчетом амплитудного спектра значимых гармоник с помощью дискретного преобразования Фурье цифрового массива отсчетов изображения ДР, линейной аппроксимацией амплитудного спектра, расчетом ширины спектра по координате точки пересечения аппроксимирующей линией оси частот и расчетом квазипериода как величины, обратной ширине спектра), предлагаемое решение соответствует критерию "новизна".
Изобретение поясняется чертежами, где на фиг. 1 в левом окне приведено изображение центральной части ДР от узкой щели, на фиг. 1 в правом окне - изображение амплитудного спектра ДР с аппроксимирующей прямой, пересекающей ось частот в точке Fгр. На фиг. 2 приведена возможная функциональная схема устройства, с помощью которого возможна реализация предложенного способа измерения.
Известно [4], что ДР от узкой щели описывается следующей функцией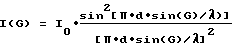 (1)
(1)
где Io - интенсивность излучения в максимуме, d - ширина щели, G - угловая координата, λ - длина волны излучения.
При переходе в плоскость приемника излучения, в частности в плоскость МЭФ с дискретными элементами, выражение (1) с учетом линейного преобразования интенсивности излучения I в сигнал U для малых углов G может быть записано в следующем виде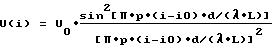 (2)
(2)
где U(i) - сигнал i-ого элемента МЭФ, i = 1-N, L - расстояние от щели до плоскости МЭФ, io - координата центра изображения ДР, выраженная в элементах МЭФ, p - шаг расположения элементов.
Изображение ДР, рассчитанное на ЭВМ в соответствии с выражением (2) при N = 1024 и io = 512, приведено в левом окне на фиг. 1.
Расстояние между минимумами ДР ΔX = Δi•p (квазипериод) соответствует изменению аргумента в квадратных скобках на π. Такая зависимость позволяет по величине квазипериода рассчитывать и измерять величину щели
d = (λ•L)/(Δi•p) (3)
Экспериментально величина квазипериода, выраженная в элементах МЭФ, может быть определена по разности координат минимумов.
В то же время из теории сигналов [5] известно, что сигнал, описываемый функцией вида sin2(x)/x2, имеет треугольный амплитудный спектр. Ширина этого спектра Fгр, определяемая как точка пересечения оси частот огибающей амплитудного спектра, связана с величиной квазипериода ΔX непрерывной функции соотношением
Fгр = K/ΔX, (4)
где K - масштабирующий коэффициент.
При регистрации центральной части ДР с помощью МЭФ происходит выделение ограниченной области ДР и ее пространственная дискретизация элементами МЭФ. Математически результат первой операции определяется произведением функции, описывающей ДР, и прямоугольного окна, размер которого равен размеру МЭФ, а второй - сверткой ДР с функцией, описывающей пространственное распределение чувствительности элемента МЭФ и выборкой результата свертки через шаг дискретизации [6]. Дискретизация ДР элементами МЭФ не оказывает какого-либо влияния на точность ее регистрации вследствие большого отношения квазипериода ДР к шагу расположения элементов МЭФ (порядка 200 - 100). Дискретизированное таким образом изображение ДР может быть с помощью АЦП представлено в виде цифровых отсчетов и преобразовано в соответствии с алгоритмами ДПФ для расчета амплитудного спектра ДР. В случае принятия размера МЭФ за период первой гармоники и частоты первой гармоники за единицу выражения для расчета синусной и косинусной составляющих k-ой гармоники будут выглядеть следующим образом: (5)
(5)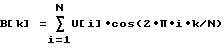 (6)
(6)
Амплитуда k-ой гармоники рассчитывается квадратичным суммированием синусной и косинусной составляющих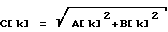 (7)
(7)
На фиг. 1 в правом окне приведен амплитудный спектра ДР, изображенного в левом окне, для квазипериода Δi = 115 при N = 1024.
Количество значимых гармоник М, для которых необходим расчет по формулам (5)-(7), зависит от числа квазипериодов ДР, укладывающихся на размере МЭФ. Количество этих гармоник может быть определено по превышению амплитудой M-й гармоники определенного, например, 5% уровня (порога) от амплитуды первой гармоники.
Полученный амплитудный спектр для расчета граничной частоты, т.е. частоты, на которой огибающая амплитудного спектра пересекает ось частот, необходимо исходя из указанного выше характера огибающей этого спектра аппроксимировать линейной функцией. При аппроксимации по методу наименьших квадратов коэффициенты 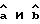 линейной зависимости
линейной зависимости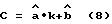
будут рассчитываться в соответствии со следующими выражениями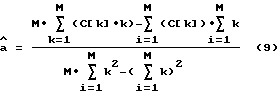

При этом Fгр может быть определена из уравнения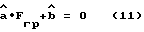


Таким образом, после выполнения ДПФ и расчета C[k], расчет Fгр сводится к несложному расчету сумм и коэффициентов. Время расчетов по формулам (7)-(12) будет незначительным вследствие ограниченности числа значимых гармоник. По этой же причине будет невелико и время выполнения ДПФ.
В качестве примера целесообразно рассмотреть аппаратную реализацию ДПФ на базе умножителя-аккумулятора 1518ВЖ1 [7], выполняющего умножение с накоплением 16-разрядных двоичных чисел за 155 нс. Функциональная схема такого устройства, приведенная на фиг. 2, помимо собственно умножителя-аккумулятора 7 включает ОЗУ 4 на базе 573РУ10, с которого на умножитель подаются отсчеты сигнала, ППЗУ 5 на базе 537РФ8, с которого подаются отсчеты гармонической функции, адресный счетчик 6, блок управления и синхронизации (БУС) 3, МЭФ 1, АЦП 2 и микропроцессорный контроллер 8. При этом операция умножения-накопления одного отсчета будет включать интервал выборки отсчетов из ОЗУ и ПЗУ и записи в умножитель (300 - 400) нс, а также интервал умножения и записи результата (200 - 300) нс. Таким образом, единичная операция умножения-накопления может быть выполнена за время не более 1 мкс, а все преобразование изображения ДР, зарегистрированное, например, с помощью отечественного МЭФ ФУК1Л2 [8] с числом элементов 1024, по алгоритму ДПФ для числа значимых гармоник М = 10 может быть выполнено за время не более 20 мс.
Время регистрации ДР при высокой освещенности и скорости считывания и аналого-цифрового преобразования сигнала может быть доведено до нескольких миллисекунд и не будет оказывать существенного влияния на общее время измерения квазипериода ДР.
При выбранной размерности первой гармоники пространственного спектра ДР коэффициент K в выражении (4) будет равен числу элементов МЭФ и величина квазипериода в принятых единицах будет рассчитываться следующим образом:
ΔX = p•N/Fгр (13)
Погрешность измерения квазипериода будет определяться как инструментальной погрешностью вследствие неоднородности чувствительности элементов, которая, в принципе, может быть скомпенсирована, и методической погрешностью, обусловленной отклонением огибающей амплитудного спектра от линейной зависимости. Модельные оценки этой погрешности свидетельствуют, что ее относительное значение при М>5 не превышает 1%. Так, в частности, разность между истинной (N/Δi = 9) и расчетной (Fгр = 9,03) граничными частотами для ДР, приведенного на фиг. 1, составляет 0,03, т.е. относительная погрешность, имеющая систематический характер, составляет около 0,3%.
Таким образом, использование предложенного метода измерения квазипериода ДР, базирующегося на скоростной регистрации его центральной части, содержащей несколько квазипериодов, с помощью многоэлементного фотоприемника, квантовании и расчете амплитудного спектра значимых гармоник, амплитуда которых превышает порог, заданный относительно первой гармоники, с помощью дискретного преобразования Фурье изображения ДР, определении значимых гармоник амплитудного спектра, расчета коэффициентов линейной функции, аппроксимирующей амплитудный спектр, расчета граничной частоты и квазипериода как параметра, обратного граничной частоте, позволяет решить поставленную задачу, а именно повысить быстродействие измерения квазипериода ДР. Оценки быстродействия при аппаратной реализации ДПФ на указанной элементной базе и выполнении расчетов по формулам (7)-(13) с помощью микропроцессорных контроллеров позволяют говорить о возможности достижения быстродействия порядка нескольких десятков измерений в секунду, т.е. о возможности выполнения измерений для подавляющего большинства приложений в реальном масштабе времени.
Литература
1. Суранов А.Я. Измерение квазипериода колебаний дифракционного распределения от узкой щели с помощью многоэлементного фотоприемника.// Докл. Второй Междунар. конф. "Датчик-95", Барнаул, 1995, с. 117-119.
2. Евсеенко Н.И., Козачок А.Г., Солодкий Ю.Н. Анализ дифракционных способов измерения линейных размеров.// Метрология, 1984, N 2, с. 17-23.
3. Okamoto Т. , Kawata S., Minami S. Optical method for resolution enhancement in photodiode array Fourier transform spectroscopy.// Applied Optics, Vol. 24, No. 23, p. 4221 - 4225.
4. Калитиевский Н.И.Волновая оптика. Учебное пособие для ун-тов. - М.: Высшая школа, 1978.
5. Денисенко А.Н., Стеценко О.А. Теоретическая радиотехника: Справочное пособие. Ч. 1: Детерминированные сигналы (методы анализа)- М.: Изд-во стандартов, 1993.
6. Макс Ж. Методы и техника обработки сигналов при физических измерениях: В 2-х томах.Пер. с франц. - М.:Мир, 1983. Т. 1.
7. Гамкрелидзе С.А., Завьялов А.В., Мальцев П.П., Соколов В.Г. Цифровая обработка информации на основе быстродействующих БИС. - М.: Энергоатомиздат, 1988.
8. Многоэлементное ФПУ ФУК1Л2. Этикетка предприятия-изготовителя.

Изобретение относится к оптико-электронному приборостроению и может использоваться в скоростных дифрактометрах. Сущность изобретения заключается в регистрации центральной части дифракционного распределения от узкой щели с помощью многоэлементного фотоприемника (МЭФ), квантовании и расчете с помощью дискретного преобразования Фурье отсчетов сигнала МЭФ амплитудного спектра значимых гармоник, амплитуда которых превышает заданный порог, нормированный к амплитуде первой гармоники, расчете коэффициентов линейной функции, аппроксимирующей значимые гармоники амплитудного спектра, расчете граничной частоты как частного от деления коэффициентов аппроксимирующей функции и расчете квазипериода как величины, обратной граничной частоте. С помощью данного способа обеспечивается повышение быстродействия. 2 ил.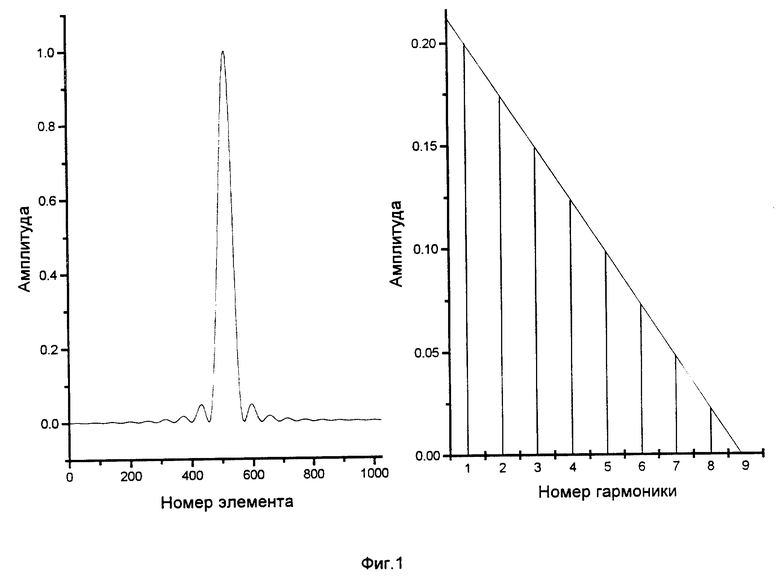
Способ измерения квазипериода дифракционного распределения излучения от узкой щели, включающей регистрацию дифракционного распределения с помощью многоэлементного фотоприемника, квантование сигналов элементов многоэлементного фотоприемника и их обработку по методу дискретного преобразования Фурье для расчета амплитудного спектра, отличающийся тем, что регистрация производится при совмещении центров многоэлементного фотоприемника и дифракционного распределения и при выборе масштаба проецирования дифракционного распределения из условия регистрации 5 - 10 квазипериодов, а обработка отсчетов амплитудного спектра включает определение числа значимых гармоник по порогу, нормированному к амплитуде первой гармоники, расчет коэффициентов линейной функции, аппроксимирующей значимые отсчеты амплитудного спектра, расчет граничной частоты как частного от деления коэффициентов аппроксимирующей функции и расчет квазипериода как величины, обратной граничной частоте.
| Okamoto T., Kawata S., Minami S | |||
| Optikal method for resolution enhancement in photodiode array Fourier transform spectroscopy | |||
| Applied Optics | |||
| Vol | |||
| Пишущая машина для тюркско-арабского шрифта | 1922 |
|
SU24A1 |
| Аппарат для печатания кинолент | 1925 |
|
SU4221A1 |
| Евсеенко Н.И., Козачок А.Г., Солодкий Ю.Н | |||
| Анализ дифракционных способов измерения линейных размеров | |||
| Метрология, 1984, N 2, с | |||
| Печь для сжигания твердых и жидких нечистот | 1920 |
|
SU17A1 |
| Суранов А.Я | |||
| Измерение квазипериода колебаний дифракционного распределения от узкой щели с помощью многоэлементного фотоприемника/Докл | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Барнаул, 1995, с | |||
| Аппарат для испытания прессованных хлебопекарных дрожжей | 1921 |
|
SU117A1 |
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| US 5424828 А, 13.06.95. | |||
Авторы
Даты
2000-01-27—Публикация
1997-10-02—Подача