Изобретение относится к области зубообработки и может быть использовано на машиностроительных заводах, где для изготовления и контроля зубьев цилиндрических эвольвентных колес применяется инструмент, работающий по методу обкатки (долбяки, дисковые шеверы, червячные фрезы, абразивные червяки, измерительные колеса, зубонакатные валки, резцы для зуботочения).
Зубообрабатывающий инструмент должен обеспечивать в станочном зацеплении с обрабатываемой деталью установленные чертежом (технологией) основной шаг, коэффициент смещения исходного контура (толщину зуба), диаметр впадин, положение граничной точки, форму и параметры переходной кривой, модификацию вершины, а также определенный радиальный зазор и отсутствие интерференции. Стандартный инструмент не всегда удовлетворяет вышеизложенным требованиям. Поэтому используется специальный инструмент со смещением исходного контура (коррекцией). Коррекция инструмента приводит к изменению станочного межосевого расстояния и, следовательно, к изменению угла давления в торцовой плоскости детали в полюсе, зацепления.
Известен способ определения коррекции инструмента, заключающийся в предварительном задании величины коррекции и основных параметров инструмента с последующей проверкой, получающихся в результате обработки параметров зубьев колеса. При неудовлетворительных результатах производятся неоднократные корректировки инструмента и практические проверки до получения положительных результатов. Известные способы определения коррекции и методы расчета ее величины по существу являются проверочными и положительный результат во многом зависит от квалификации исполнителя (См. Романов В.Ф. "Расчеты зуборезных инструментов" издательство Машиностроение, 1969 г., Москва).
Известен способ определения коррекции инструментов с помощью блокирующих контуров, приведенных в ГОСТе 16532-70 "Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет геометрии", который взят за прототип.
Приведенные в ГОСТе 16532-70 блокирующие контуры построены для прямозубых передач со стандартным исходным контуром по ГОСТ 13755-81 и с некоторым приближением используются для определения коррекции зубчатой пары "колесо-инструмент". Обычно коррекция предварительно назначается по блокирующим контурам и после проведения испытаний неоднократно меняется. Окончательное определение коррекции осуществляется по результатам наладочных работ после изготовления пробной партии деталей.
Такой способ определения коррекции инструмента не учитывает особенностей кинематики двухпрофильного зацепления, связанных с наличием перепадов удельного давления в местах контакта инструмента с деталью, возникающих в результате изменения количества контактных точек при их чередовании на линиях зацепления.
В работе Калашникова Н. А. "Точность в машиностроении и ее законы" (Машиностроение, 1950 г.) погрешности реального зацепления сводятся к одному параметру - к изменению мгновенного радиуса основной окружностью по углу поворота колеса: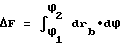
Характер чередования контактных точек в динамике теоретического двухпрофильного зацепления предлагается рассматривать с помощью решетчатых диаграмм. Расчетные зависимости для построения решетчатых диаграмм, приведенные в работе Тайца Б. А. "Точность и контроль зубчатых колес" (Машиностроение, Москва, 1972 г.) распространяются на частный случай, когда угол давления в полюсе совпадает с профильным углом исходного контура.
Известен способ изготовления цилиндрических зубчатых колес внешнего и внутреннего зацепления с эвольвентным профилем зуба, включающий обработку инструментом, имеющим смещение исходного контура (см. Семенченко И.И. и др. "Проектирование металлорежущих инструментов", М., Машгиз, 1962, с. 748).
Задача изобретения состоит в том, чтобы обеспечить повышение точности изготовления зубчатых колес путем уменьшения перепадов удельного давления в контактных точках при их чередовании на линиях зацепления инструмента и обрабатываемого колеса.
Для решения поставленной задачи смещение исходного контура инструмента осуществляют в соответствии с углом давления в торцовой плоскости обрабатываемого колеса в полюсе зацепления с инструментом, определяемым из выражения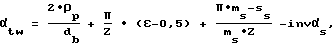
где m - модуль торцовый;
Z - число зубьев обрабатываемого колеса;
αs - профильный угол исходного контура в торцовой плоскости;
Ss - толщина зуба по дуге делительной окружности в торцовой плоскости (для внутреннего зацепления - ширина впадины);
ε - коэффициент перекрытия торцовый;
ρp - радиус кривизны в нижней точке рабочего профиля колеса для наружного зацепления (для внутреннего зацепления - ρa - на диаметре вершин);
db - диаметр основной.
На фиг. 1 изображена решетчатая диаграмма двухпрофильного зацепления колеса с инструментом для случая, когда полюс, зацепления располагается на делительной окружности, при этом угол давления в полюсе колеса - 20o.
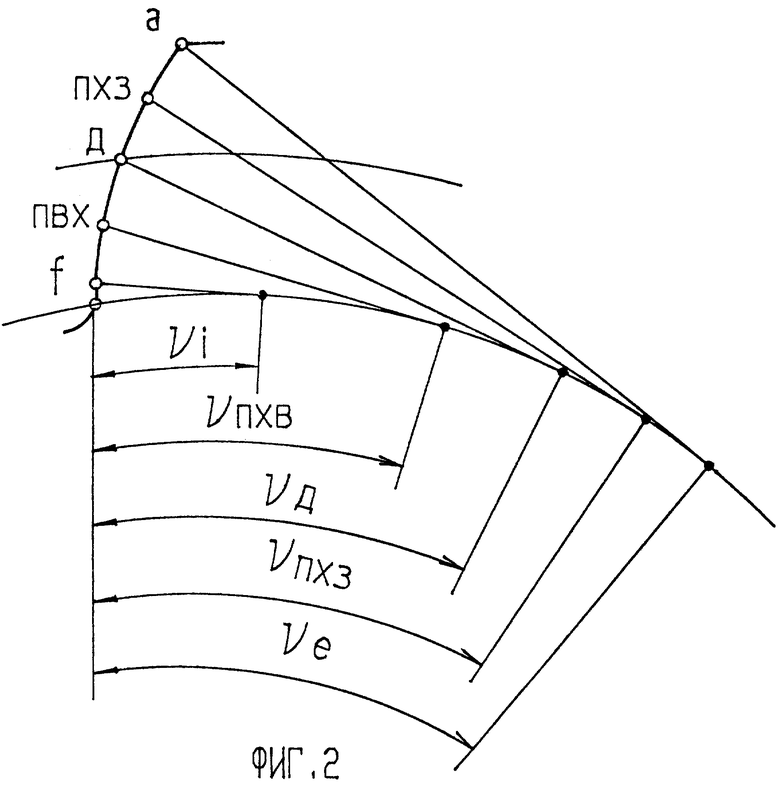
На фиг. 2 изображен профиль зуба колеса и углы развернутости эвольвенты, соответствующие характерным линиям решетчатой диаграммы фиг. 1.
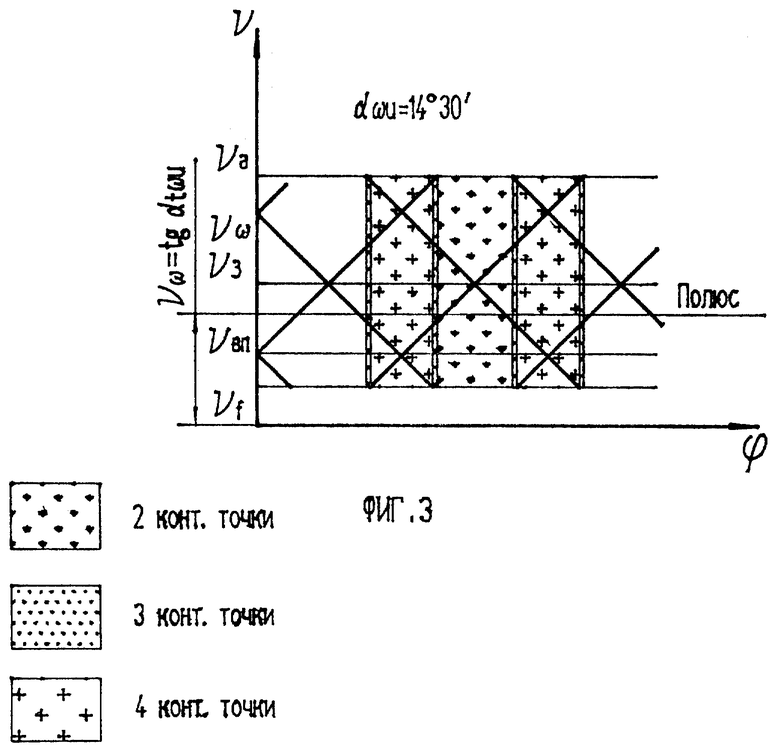
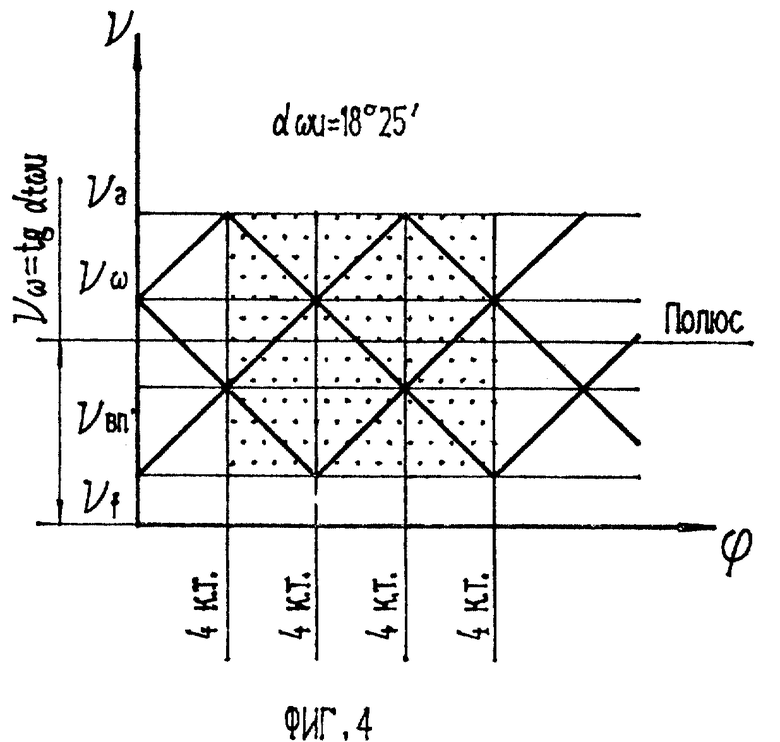
На фиг. 3 и фиг. 4 изображены решетчатые диаграммы двухпрофильного зацепления одного и того же колеса с инструментом, коррекция которого выполнена в соответствии с углами давления колеса в полюсе 14o30' и 18o25'.
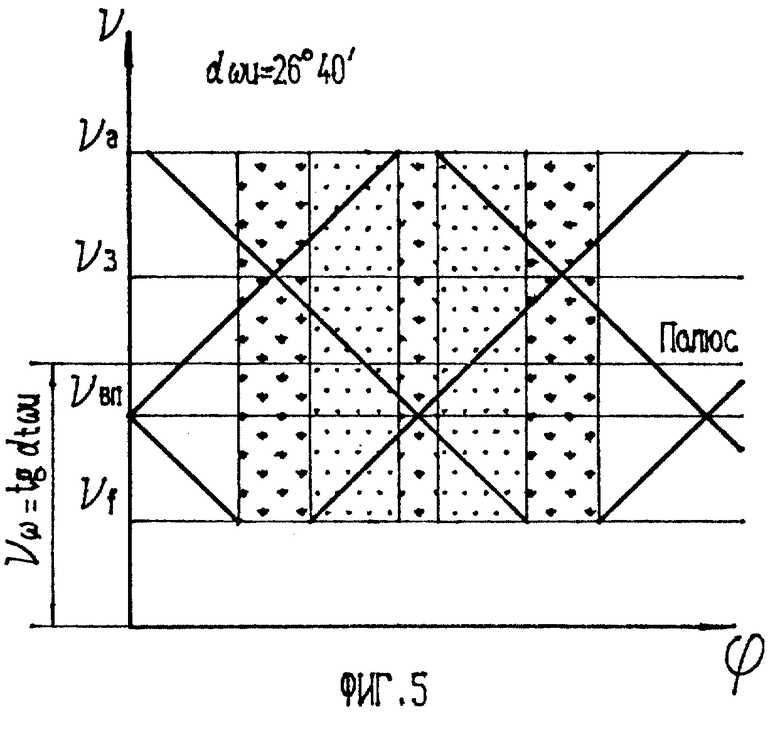
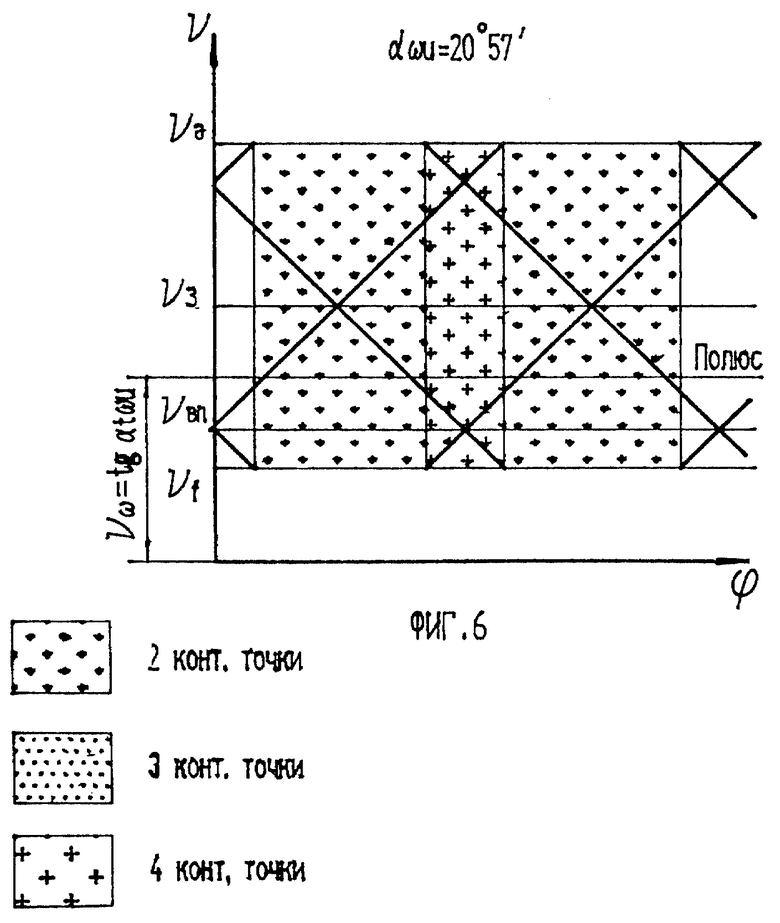
На фиг. 5 и фиг. 6 изображены решетчатые диаграммы двухпрофильного зацепление другого колеса с инструментом, коррекция инструмента при этом соответствует углам давления в полюсе колеса 20o57' и 26o40'.
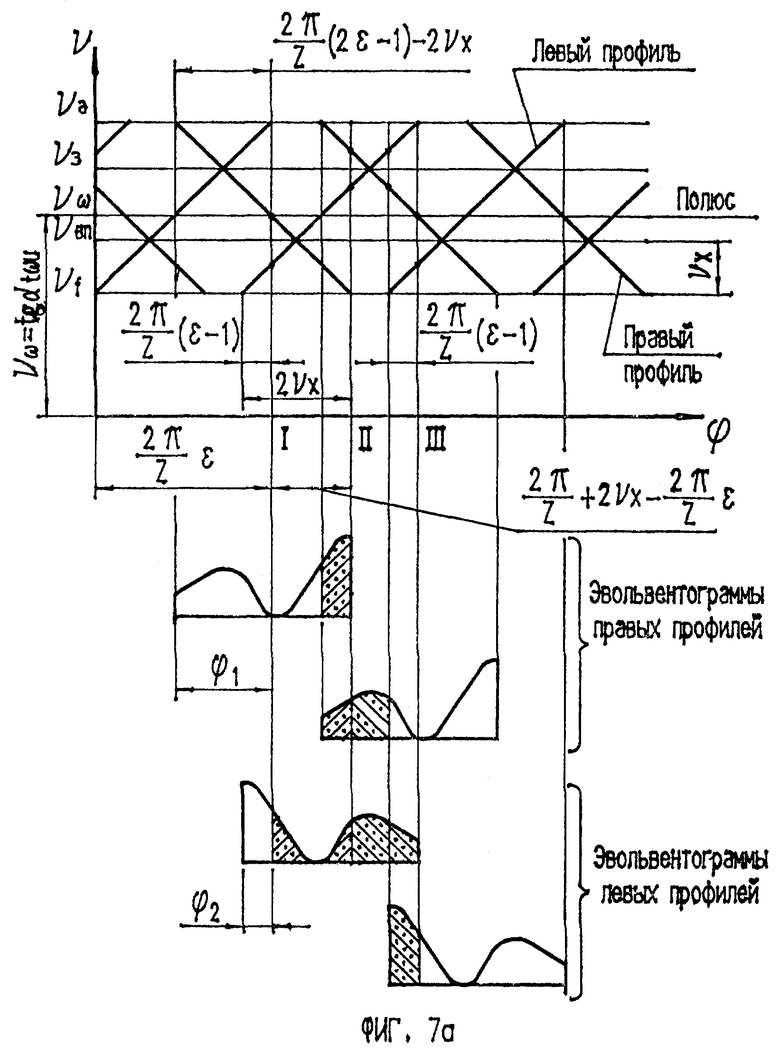
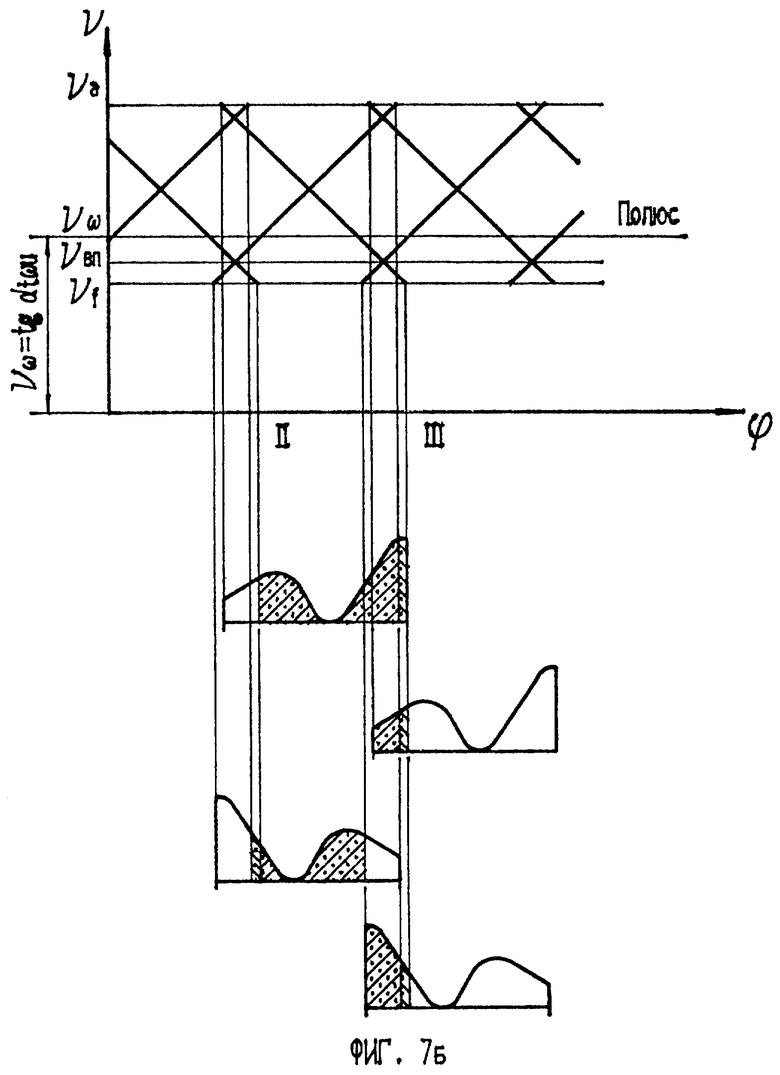
На фиг. 7а и 7б изображены решетчатые диаграммы двухпрофильного зацепления колеса с инструментом и скоординированные относительно них эвольвентограммы профилей.
Решетчатая диаграмма позволяет легко устанавливать все точки, находящиеся одновременно в зацеплении при угловом положении колеса. Для этого достаточно провести вертикальную линию при любом задаваемом значении угла ϕ и рассматривать точки ее пересечения с наклонными прямыми.
С другой стороны, по диаграмме может быть определен угол поворота, разделяющий моменты зацепления двух точек одного или разных профилей. Этот угол отсчитывается по оси абсцисс как расстояние между двумя вертикальными прямыми, проходящими через рассматриваемые точки решетчатой диаграммы.
Проведем на диаграмме фиг. 1 вертикальные линии I, II и III, соответствующие некоторым значениям углов поворота зубчатого колеса ϕI,ϕII,ϕIII.
В сечениях I и II на линиях зацепления находятся по две контактные точки, принадлежащие разным профилям зуба, а в сечении III таких точек - три: две точки на левой стороне профиля зуба и одна на правой.
В результате при вращении такого зубчатого колеса в двухпрофильном зацеплении с другим колесом, например с измерительным, количество точек контакта по линиям зацепления будет чередоваться 2-3-2-3 и т.д.
Диаграмма см. фиг. 3, показывает чередование точек контакта 3-4-3-2-3-4-3-2. .., а на фиг. 4 число контактных точек преимущественно равно 3 и лишь при некоторых очень малых значениях углов ϕ в зацеплении будут находиться 4 точки.
Характер чередования контактных точек:
фиг. 5 2-4-2-4 ...
фиг. 6 2-3-2-3 ...
Решетчатая диаграмма для каждой конкретной пары зубчатых колес индивидуальна, ее размеры и характер чередования контактных точек на линиях зацепления зависят от параметров колес пары: угла развернутости в начале рабочего участка, а следовательно, коэффициента перекрытия; от коррекции колес, а следовательно, от угла зацепления в паре.
Изменение угла зацепления в паре за счет изменения одного из колес (например, шевера, долбяка или измерительного колеса) приводит к сдвигу решетки по оси ординат в плюс или минус (в зависимости от увеличения или уменьшения коррекции), при этом изменяется характер чередования контактных точек. Плавное изменение угла зацепления пары создает эффект движения решетки по оси ординат.
Выявленная с помощью решетчатых диаграмм последовательность чередования контактных точек справедлива для двухпрофильного зацепления пары теоретических колес. В действительности неизбежны отклонения от теоретического представления о чередовании контактных точек. Поэтому важно выявить и оценить погрешности зубчатого колеса, найти пути их уменьшения.
Для теоретического зацепления радиус кривизны в точке контакта "X"
ρx= rx·tgϕx
где ϕx - угол давления в точке контакта;
Для реального зацепления:
Δρ+ρx= (Δrb+rb)·tgϕx
Δrb= Δρ·ctgϕx и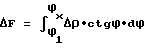
Если Δρ = 0. (т.е. погрешность профиля ffr = 0 и погрешность шага зацепления fpbr = 0), то Δ F = 0
Если Δρ = const ≠ 0 (ограничимся случаем ffr = 0, fpbr = const ≠ 0), то
ΔF = Δρ(ln|sinϕx|-ln|sinϕ1|)
Следовательно, систематическая погрешность шага зацепления приводит к нарастанию абсолютного значения дефектного перемещения при повороте зубчатого колеса на угол от ϕ1 до ϕx в пределах одного профиля. При этом величина дефектного перемещения
Δ F > 0 при Δρ < 0
и Δ F < 0 при Δρ > 0.
Однако не следует рассматривать погрешности шага зацепления отдельно от других ошибок эвольвенты.
Диаграмма профиля - эвольвентограмма - дает представление о систематических погрешностях радиуса основной окружности и о погрешностях угла профиля исходного контура режущего инструмента, которым было изготовлено проверяемое колесо.
Эвольвентограмма отражает также другие неточности средств изготовления. Поэтому для оценки дефектных приращений по линиям действия, характеризующих колебание измерительного межосевого расстояния на одном зубе (скачок), достаточно рассматривать эвольвентограммы правой и левой сторон зуба детали, правильно скоординированные относительно решетчатых диаграмм, построенных в том же масштабе, что и углы развернутости (фиг. 7а, 7б).
Рассмотрим проявление погрешностей эвольвент в контактных точках при двухпрофильном зацеплении с измерительным колесом. При угловом положении I (фиг. 7а)), когда вершина зуба левого профиля вышла из зацепления, на линиях зацепления одновременно находятся 2 контактные точки. Точка, принадлежащая правому профилю ножки зуба, является носителем погрешностей, характеризуемых площадью эвольвентограммы на участке ϕ1. Точка, принадлежащая левому профилю ножки соседнего зуба, является носителем погрешностей, характеризуемых площадью эвольвентограммы на участке ϕ2. Сумма площадей эвольвентограмм на участках ϕ1 и ϕ2 характеризует мгновенное межосевое расстояние. При повороте детали от углового положения I до углового положения II сумма погрешностей эвольвент нарастает.
Вступление на линию зацепления контактной точки, принадлежащей правому профилю вершины зуба, приводит к более интенсивному нарастанию суммы погрешностей.
При угловом положении II, когда контактная точка правого профиля ножки зуба выходит из зацепления, происходит уменьшение суммы погрешностей эвольвент. При повороте до углового положения III сумма ошибок эвольвент в контактных точках увеличивается до тех пор, пока вершина зуба левого профиля не выйдет из зацепления. Сумма площадей эвольвентограмм, заключенная между угловыми положениями I и II, II и III, характеризует изменение межосевого расстояния.
Аналогично исследуя те же эвольвентограммы, скоординированные относительно другой решетчатой диаграммы (фиг. 7б), отмечаем значительное увеличение суммы погрешностей эвольвент на участке ϕII-ϕIII.
Из этого анализа следуют два практических вывода:
1. Погрешности изготовления зубчатого венца по разному проявляются при двухпрофильном зацеплении в зависимости от последовательности чередования и количества контактных точек. При повороте зубчатого колеса число контактных точек изменяется и сумма погрешностей эвольвент также изменяется. Сумма погрешностей скачкообразно изменяется в моменты выхода из зацепления очередной контактной точки.
2. Если двухпрофильное зацепление пары зубчатых колес происходит под действием постоянной радиальной силы, например при шевинговании, то удельное давление, а следовательно, и съем металла, меняется в зависимости от числа контактных точек.
Изменение количества контактных точек, одновременно находящихся на линиях зацепления, а также изменение удельного давления в местах съема металла неизбежны.
Способ определения коррекции инструмента осуществляется следующим образом.
Угол зацепления, детали с режущим инструментом выбирается из условия минимально возможной разности количества контактных точек на линиях зацепления.
Например: 4-3-4-3..., 3-2-3-2...
Несоблюдение этого условия приводит к искажению профиля зуба колеса.
Для случая αtw≠ α зависимости углов развернутости и параметров колеса будут иметь вид: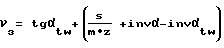 - угол развернутости в точках зуба, одновременно вступающих на линии зацепления.
- угол развернутости в точках зуба, одновременно вступающих на линии зацепления.
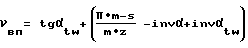 - угол развернутости в точках впадины, одновременно вступающих на линии зацепления.
- угол развернутости в точках впадины, одновременно вступающих на линии зацепления.
Угол развернутости в полюсе
νw= tgαtw
и состоит из трех составляющих:
1. Угла развернутости в начале активного участка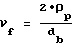
2. Угла νx, определяющего положение контактных точек впадины, одновременно вступающих на линии зацепления. Для уменьшения перепадов удельного давления в контактных точках должно соблюдаться условие равенства отрезков на решетчатой диаграмме (фиг. 7а)
и после преобразования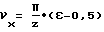
3. Разности углов развернутости, равной углу поворота детали на половину ширины впадины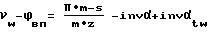
Суммируя значения этих составляющих получим:
И после преобразования: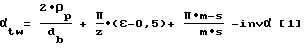
Определение коррекции зубообрабатывающего инструмента, осуществляемое в соответствии с углом зацепления (уравнение [1]), продиктовано необходимостью учета силовых факторов станочного зацепления.
Эксплуатационные погрешности колес проявляются в однопрофильном зацеплении, а выявляются в двухпрофильном зацеплении с измерительными колесами.
Чтобы максимально исключить методическую погрешность двухпрофильного измерения, необходимо использовать измерительные колеса с определенной коррекцией.
Как уже отмечалось, площади эвольвентограмм по правым и левым профилям, скоординированные относительно соответствующих наклонных линий на решетчатой диаграмме, характеризуют дефектное изменение номинального межосевого расстояния в двухпрофильном зацеплении зубчатого колеса с измерительным колесом.
Погрешностями измерительного колеса (в силу их малости) в дальнейшем анализе пренебрегаем. Площади эвольвентограмм будем определять как произведение усредненной погрешности профиля ff и угла поворота зубчатого колеса ϕ, численно равного длине соответствующей эвольвентограммы.
В этом случае величина мгновенного дефектного изменения межосевого расстояния будет зависеть от суммы углов поворота зубчатого колеса, численно равной сумме длин соответствующих этим углам эвольвентограмм профилей, находящихся в зацеплении.
Поэтому в дальнейшем целесообразно рассматривать углы ϕ в качестве характеристик величины дефектного изменения межосевого расстояния.
Для углового положения II сумма таких углов (фиг. 7а) составляет:
Для углового положения III
или после преобразования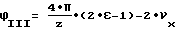
Дефектное изменение межосевого расстояния при повороте детали от углового положения II до углового положения III характеризуется площадью эвольвентограмм по правым и левым профилям на участке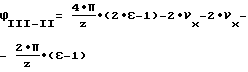
или после преобразования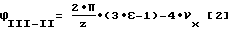
В однопрофильном зацеплении (при эксплуатации детали в передаче) на правильность работы зацепления влияет сумма погрешностей эвольвент, характеризуемых площадью эвольвентограммы на длине активного участка зуба, соответствующей углу поворота колеса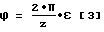
Условимся, что погрешности зубчатого колеса, выявляемые при двухпрофильном зацеплении должны соответствовать их проявлению в эксплуатации при однопрофильном зацеплении зубчатой передачи, т.е.
ϕIII-II= ϕ
Приравнивая правые части [2] и [3], получим
и после преобразования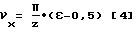
Аналогично можно получить уравнение для других угловых положений, например ϕI-II.
При угловом положении I сумма погрешностей эвольвент в контактных точках есть площадь эвольвентограмм по правому и левому профилям на участке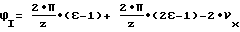
и после преобразования: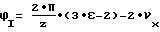
При угловом положении II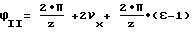
и после преобразования: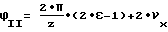
Дефектное изменение межосевого расстояния при повороте от углового положения I до углового положения II характеризуется площадью эвольвентограмм по правым и левым профилям на участке (5)
(5)
и после преобразования;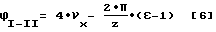
Приравнивая правые части уравнений [3] и [6], имеем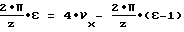
откуда
Сопоставление уравнений (4) и (7) показывает независимость величины νx от углового положения зубчатого колеса.
Рассмотрим возможный диапазон изменения угла νx и связанный с ним диапазон изменения характеристик выявляемых погрешностей.
Если в уравнении [2] ϕIII-II= 0, то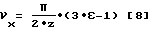
Заменив в уравнении [5] значение νx из [8] получим: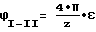
При условии ϕI-II= 0 из уравнения [5]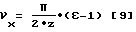
Подставим значение νx из уравнения [9] в уравнение [2], после упрощения получим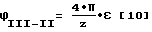
Сопоставляя [8] и [9], получаем:
- величина угла νx находится в пределах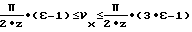
- диапазон изменения характеристик выявляемых погрешностей находится в пределах 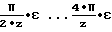 соответственно.
соответственно.
Следовательно, для одного и того же зубчатого колеса в двухпрофильном зацеплении с различными измерительными колесами изменение угла νx на решетчатой диаграмме и, соответственно, изменение угла зацепления, приводит к значительному изменению величин (в 2 раза), выявленных при контроле погрешностей, а произвольно назначенный угол зацепления является причиной появления дополнительной методической погрешности измерения.
Величина угла νx, определенная из условия равенства погрешностей колеса, выявленных при двухпрофильном зацеплении с измерительным колесом, и проявляемых погрешностей однопрофильного зацепления передачи, равна величине угла νx, определенной из условия минимизации перепадов удельного давления в контактных точках при их чередовании на линиях зацепления при обработке (см. 2-ую составляющую уравнения [1]). Поэтому уравнение [1] позволяет определить угол двухпрофильного зацепления зубчатого колеса с измерительным, при котором контроль колебаний измерительного межосевого расстояния осуществляется без дополнительной методической погрешности. Уравнение [1] справедливо для прямозубых зубчатых колес внешнего зацепления.
Для прямозубых зубчатых колес внутреннего зацепления и косозубых колес ход приведенных выше рассуждений не меняется и в конечном итоге уравнения для определения угла двухпрофильного зацепления имеют вид:
- для косозубых колес
- для прямозубых зубчатых колес внутреннего зацепления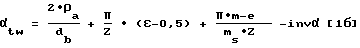
Уравнение [1] справедливо также для определения угла зацепления в торцовой плоскости детали с режущим инструментом (шевером, долбяком средней изношенности и т.п.)
Возможные перемещения решетчатой диаграммы по оси ординат ограничиваются условием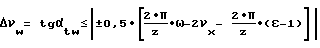
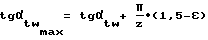
Следовательно, допускаемые пределы изменения угла зацепления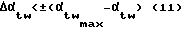
Для нового инструмента допускаемое увеличение угла зацепления ограничивается величиной, определяемой из выражения [11] для учета переточек.
Построение решетчатых диаграмм для зацепления нового и изношенного инструмента с деталью дают наглядную картину чередования контактных точек и позволяют уточнить диапазон возможных переточек с целью уменьшения неравномерности распределения удельного давления в зонах резания и переноса дополнительных погрешностей инструмента на деталь.
Уравнения [1], [1а], [1б] позволяют без предварительного построения решетчатых диаграмм автоматически выходить на рациональную диаграмму чередования контактных точек. В тех случаях, когда по конструктивным причинам (например, не проходит проверка на радиальный зазор) нельзя принять рассчитанный угол αtw, его значение можно изменить на величину 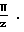 При этом решетчатая диаграмма сместится по оси ординат в плюс или минус на половину углового шага и характер чередования контактных точек не изменится.
При этом решетчатая диаграмма сместится по оси ординат в плюс или минус на половину углового шага и характер чередования контактных точек не изменится.
Такое изменение αtw рекомендуется для колес числом зубьев z ≥ 17.
Для зубчатых колес с числом зубьев z < 17 возможный диапазон изменения угла αtw по отношению к расчетному определяется по решетчатой диаграмме.
При неудовлетворительных результатах чередования точек контакта зубчатого колеса с инструментом (т.е., если разница между наибольшим и наименьшим количеством точек больше 1) целесообразно уточнение параметров зубчатого колеса, главным образом, диаметра впадин или высоты зуба колеса.
Окончательное решение о принятии значения угла зацепления αtw обрабатываемого (измеряемого) зубчатого колеса с инструментом принимается по результатам выполнения всех проверок, предусмотренных методиками расчета соответствующих инструментов, построенными на основе использования уравнения [1], а величина коррекции инструмента соответствует принятому αtw.
Проводились производственные испытания червячных фрез и шеверов, параметры которых определены в станочном зацеплении с обрабатываемой деталью из условия обеспечения угла зацепления в торцовой плоскости детали, определяемого из уравнения [1]. Обрабатываемое изделие - вал - шестерня бортредуктора трактора Т-170.
Исходные параметры шестерни на операции зубофрезерования:
m = 9, z = 10, α = 20o, β = 0, da = 116, df = 76, ρp= 7,8, W = 44,467
Обработка производилась на зубофрезерном полуавтомате ЕЗА-056.53, предварительно проверенном на технологическую точность.
Основные параметры профиля зуба червячной фрезы:
α0= 26°28′38″, sno = 13,248-0,05, hao = 9,241,
Модификация головки:
αOM= 25°36′; hom = 8,58; Rao = 1
Станочный угол зацепления в торцовой плоскости детали равен углу профиля фрезы αtwo= 26°28′38″.
Исходные параметры детали на операции зубошевингования: W = 44,467
Остальные см. операцию зубофрезерования.
Обработка производилась на зубошевинговальном полуавтомате АВС-02-7032, предварительно проверенном на технологическую точность.
Параметры шевера:
m = 9, z0 = 23, α = 20o, β0= 12°, x0 = 0,351
da0 = 236,349, s0 = 16,436, hao = 12,4
Станочный угол зацепления в торцовой плоскости детали αtwo= 25°40′6″
Изготовленные детали были обмерены поэлементно и в двухпрофильном зацеплении с измерительным колесом, коррекция и параметры которого были определены в соответствии с уравнением [1]. Достоверность результатов комплексного контроля подтверждена поэлементной проверкой.
Производственные испытания зуборезного инструмента показали повышение точности зубчатого венца по нормам кинематики и плавности в 1.6 ... 2 раза по сравнению с деталями, обработанными серийным инструментом, выполненным без учета уменьшения перепадов удельного давления в контактных точках при их чередовании на линиях зацепления.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЦИКЛОИДАЛЬНО-ЭВОЛЬВЕНТНОЕ ЗУБЧАТОЕ ЗАЦЕПЛЕНИЕ | 1993 |
|
RU2113643C1 |
| РОТОРНО-ВРАЩАТЕЛЬНАЯ МАШИНА | 1996 |
|
RU2113622C1 |
| РОТОРНО-ВРАЩАТЕЛЬНАЯ МАШИНА | 1993 |
|
RU2062907C1 |
| ПРЯМОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1999 |
|
RU2160403C1 |
| СПОСОБ ОБРАБОТКИ ЭВОЛЬВЕНТНЫХ ПРОФИЛЕЙ КРУГОВЫХ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ КОЛЕС | 1992 |
|
RU2049608C1 |
| ЭВОЛЬВЕНТНАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1999 |
|
RU2160858C1 |
| ЗУБЧАТАЯ ПЕРЕДАЧА | 1995 |
|
RU2108509C1 |
| КОСОЗУБАЯ ЦИЛИНДРИЧЕСКАЯ ЗУБЧАТАЯ ПЕРЕДАЧА ВНЕШНЕГО ЗАЦЕПЛЕНИЯ | 2002 |
|
RU2224154C1 |
| СПОСОБ И ИНСТРУМЕНТ ДЛЯ ИЗГОТОВЛЕНИЯ ПЛОСКИХ ЗУБЧАТЫХ КОЛЕС | 2010 |
|
RU2542040C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЦИКЛИЧЕСКОЙ ПОГРЕШНОСТИ ЗУБЦОВОЙ ЧАСТОТЫ В ЗУБЧАТОЙ ПЕРЕДАЧЕ | 2004 |
|
RU2265199C1 |
Изобретение относится к изготовлению зубчатых колес методом обкатки в двухпрофильном зацеплении. Способ включает обработку инструментом, имеющим смещение исходного контура. Для повышения точности изготовления зубчатых колес путем уменьшения перепадов удельного давления в контактных точках при их чередовании на линии зацепления инструмента и обрабатываемого колеса указанное смещение выбрано в соответствии с углом давления в торцовой плоскости обрабатываемого колеса в полюсе зацепления с инструментом по приведенному выражению в зависимости от торцового модуля, числа зубьев обрабатываемого колеса, профильного угла исходного контура в торцовой плоскости, толщины зуба по дуге делительной окружности (для внутреннего зацепления - ширина впадины), торцового коэффициента перекрытия, радиуса кривизны в нижней точке рабочего профиля колеса, основного диаметра. 7 ил.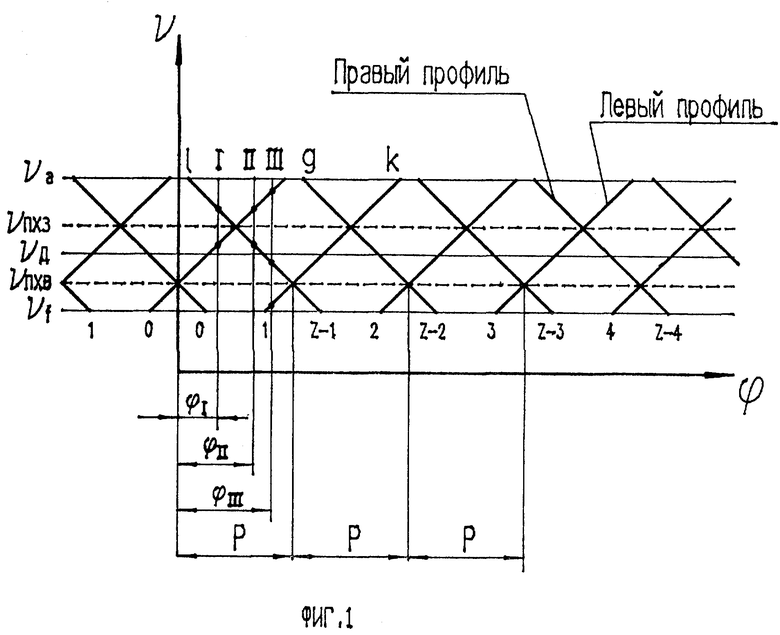
Способ изготовления цилиндрических зубчатых колес внешнего и внутреннего зацепления с эвольвентным профилем зуба, включающий обработку инструментом, имеющим смещение исходного контура, отличающийся тем, что упомянутое смещение выбирают в соответствии с углом давления (αtw) в торцовой плоскости обрабатываемого колеса в полюсе зацепления с инструментом из выражения
где ms - модуль торцовый;
Z - число зубьев обрабатываемого колеса;
αs - профильный угол исходного контура в торцовой плоскости;
Ss - толщина зуба по дуге по делительной окружности в торцовой плоскости (для внутреннего зацепления - ширина впадины);
ε - коэффициент перекрытия торцовый;
ρp - радиус кривизны в нижней точке рабочего профиля колеса;
db - диаметр основной.
| СЕМЕНЧЕНКО И.И | |||
| и др | |||
| Проектирование металлорежущих инструментов | |||
| - М.: Машгиз, 1962, с.748.SU 153006, 15.02.1963.SU 1641535 А1, 15.04.1991 | |||
| Экономайзер | 0 |
|
SU94A1 |
| Бутылочный затвор | 1929 |
|
SU16532A1 |
| Передачи зубчатые цилиндрические эвольвентные внешнего зацепления | |||
| Расчет геометрии | |||
| - М.: Государственный комитет стандартов Совета Министров СССР, 1970, с.55, 56, таблица 1 | |||
| РОМАНОВ В.Ф | |||
| Расчеты зуборезных инструментов | |||
| - М.: Машиностроение, 1969. | |||
Авторы
Даты
2001-04-20—Публикация
1999-03-22—Подача