СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗАДЕРЖКИ ДИСКРЕТИЗАЦИИ В ВЫБОРКАХ ПОЛУЧЕННОГО СИГНАЛА В СИСТЕМЕ СОТОВОЙ СВЯЗИ Российский патент 2001 года по МПК H04L7/33 

Изобретение относится к восстановлению тактовой синхронизации и цикловой синхронизации в системах связи. Изобретение применимо к любой системе связи, имеющей известную последовательность сигналов или слов синхронизации и, главным образом, к описываемой ниже системе сотовой связи с многопостанционным доступом и временным разделением каналов (TDMA), которая совместима с системой EIA/TIA, описываемой в документе IS-54-B: "Стандарт совместимости при работе мобильной станции с базовой станцией в двойном режиме". Для удобства и краткости изложения, такого рода система называется ниже просто как система IS-54. В такой системе данные передаются во временных отрезках, каждый из которых содержит слово синхронизации из 14 знаков, за которым следует информационная последовательность.

Известно, что в системах связи необходимо восстанавливать синхронизацию при уплотнении с временным разделением каналов (TDM) принятого цифрового сигнала данных с тем, чтобы выборки сигнала были получены при оптимальном временном режиме для дальнейшей обработки и извлечения передаваемой информации. Точно так же хорошо известно, что восстановление тактовой синхронизации, цикловая синхронизация и необходимая обработка выборок затруднена при низком отношении "сигнал-шум" (SNR) и то, что сотовые системы связи часто обладают низким отношением "сигнал-шум".

Обозначая интервал между знаками полученного сигнала и, следовательно, период между последовательными выборками, как T и обозначая задержку дискретизации, т.е. период между оптимальным и реальным временем выборки полученного сигнала как τ с помощью цикловой синхронизации стремятся добиться того, что задержка дискретизации τ лежит в пределах одного знакового интервала, т. е. τ находится в пределах от - T/2 до T/2, и 3 восстановление тактовой синхронизации используется для снижения задержки дискретизации τ почти до нуля. На практике можно использовать сигнал управления задержкой дискретизации, т. е. регулировать фактическое время выборки или, что то же самое, управлять интерполятором, на который подаются фактические выборки, чтобы получить интерполированные выборки при оптимальном времени дискретизации, благодаря чему обеспечивается цикловая синхронизация и восстановление тактовой синхронизации.

Целью настоящего изобретения является обеспечение улучшенной цикловой синхронизации и восстановление синхронизации в системе связи.

Краткое описание изобретения
Согласно одному аспекту, предлагается способ определения задержки дискретизации в выборках принятого сигнала, содержащий следующие стадии: оценка с использованием максимального критерия правдоподобия и косвенных переменных линейного комплексного вектора, который аппроксимирует полученные выборки сигнала, причем косвенные переменные, содержат информацию о задержке дискретизации, и определение задержки дискретизации из оцененных косвенных переменных для восстановление тактовой синхронизации принятого сигнала сообщения.

Предпочтительно, каждая составляющая линейного комплексного вектора содержит линейную комбинацию предопределенной пары функций, зависящих от задержки дискретизации, и пару функций, предпочтительно содержащих функции cos πτ и sin πτ, где τ представляет собой задержку дискретизации. Каждая косвенная переменная предпочтительно оценивается путем фильтрации выборок принятого сигнала, используя фильтры с конечной импульсной характеристикой.

Задержка дискретизации может быть определена из оцененных косвенных переменных, по меньшей мере, следующим образом, используя компромисс между точностью и сложностью вычислений:
i) путем умножения оцененных косвенных переменных на действительные элементы предопределенных хранящихся в памяти матриц;
ii) путем выполнения одиночного нелинейного преобразования оцененных косвенных переменных;
iii) расчетом в соответствии с функцией (1/π)atan действительной части произведения сопряженной матрицы первой оцененной косвенной переменной и второй оцененной косвенной переменной, деленной на квадрат амплитуды первой оцененной косвенной переменной;
iv) последовательностью операций, включающих первоначальный расчет оценки задержки дискретизации в соответствии с предопределенной функцией оцененной косвенной переменной и итеративно один или несколько раз: оценка комплексного коэффициента замирания выборок полученного сигнала в зависимости от оценки задержки дискретизации и оценки косвенных переменных и повторной оценки задержки дискретизации в зависимости от оцененного комплексного коэффициента замирания и оцененных косвенных переменных.

Для того, чтобы обеспечить цикловую синхронизацию и восстановление тактовой синхронизации, указанный способ должен также включать следующие стадии: добавку к определенной задержке дискретизации для восстановления тактовой синхронизации полученного сигнала сообщения, задержку дискретизации, включающую целое число i интервалов дискретизации T для цикловой синхронизации принятого сигнала связи и определение числа i с помощью следующих операций: определение, в зависимости от оцененных косвенных переменных и определенной задержки дискретизации для восстановления синхронизации, амплитуд сигнала множества полученных выборок и выбор числа i, соответствующего максимальной амплитуде выборки. Операция определения амплитуд сигналов может включать итеративное определение амплитуд сигнала в зависимости от итеративного определения задержки дискретизации для восстановления тактовой синхронизации.

Другим аспектом предлагаемого изобретения является способ цикловой синхронизации и восстановления тактовой синхронизации в выборках принятого сигнала связи, включающий следующие стадии: используя максимальный критерий правдоподобия, определяются косвенные переменные линейного комплексного вектора, который аппроксимирует выборки принятого сигнала, причем косвенные переменные включают информацию о задержке дискретизации для каждого из множества принятых выборок сигналов; определение первой задержки дискретизации из оцененных косвенных переменных, причем первая задержка дискретизации по времени меньше интервала дискретизации; определение, в зависимости от оцененных косвенных переменных и в соответствии с первой задержкой дискретизации, амплитуды сигнала в каждой из множества полученных выборок сигналов; идентификация индекса максимума найденных амплитуд сигналов относительно текущей выборки; сложение первой задержки дискретизации для выборки, идентифицируемой указанным индексом, с произведением интервала дискретизации, умноженного на индекс для получения итоговой задержки цикловой синхронизации и восстановления тактовой синхронизации.

Стадии определения первой задержки дискретизации и амплитуд сигнала могут быть выполнены итеративно.

Изобретение также предусматривает устройство для определения задержки дискретизации для выборки принятого сигнала связи, содержащее: множество фильтров с конечной импульсной характеристикой, реагирующих на принятые выборки сигнала для множества косвенных переменных линейного комплексного вектора, который аппроксимирует полученные выборки сигнала в соответствии с максимальным критерием правдоподобия, и калькулятор, который реагирует на множество косвенных переменных для вычисления оцененной задержки дискретизации. Множество фильтров с конечной импульсной характеристикой и расчетный узел выполнены в виде, по меньшей мере, одного цифрового процессора обработки сигнала.

Краткое описание чертежей
Сущность изобретения будет понятна из следующего описания со ссылкой на соответствующие чертежи, на которых:
Фиг. 1 представляет собой блок-схему узлов беспроводного цифрового приемника системы связи;
Фиг. 2 представляет собой блок-схему устройства восстановления тактовой синхронизации в соответствии с настоящим изобретением;
Фиг. 3, 4 и 5 представляют более подробную схему восстановления тактовой синхронизации в соответствии с одним вариантом изобретения;
Фиг. 6 представляет устройство для восстановление тактовой и цикловой синхронизации в соответствии с другим вариантом изобретения.

Подробное описание изобретения
Ниже описываются модели сигналов и наблюдения для системы IS-54, за которым следует описание процессов, которые могут быть использованы в соответствии со способом изобретения. Далее, со ссылкой на прилагаемые чертежи, подробно описывается физическое осуществление восстановления тактовой и цикловой синхронизации. Хотя это описание относится конкретно к системе IS-54, нужно подчеркнуть, что это лишь один пример осуществления изобретения и что изобретение применимо к другим системам связи с известными последовательностями синхронизации.

Модели сигналов и наблюдения
В системе IS-54 используется дифференциальная квадратурная фазовая манипуляция (DQPSK) со сдвигом фазы π/4 сигналов, которая может быть описана следующими уравнениями: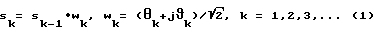

где k представляет собой положительное целое число, отождествляющее знак s_k, a w_k является комплексной величиной, представляющей двоичную информацию с действительными и мнимыми частями θ_k и ν_k, соответственно θ_k,ν_k, {-1.1} (т. е. каждая из θ_k,ν_k является набором величин -1 и 1, (т.е. либо -1, либо 1); и |s_k| = 1 для любой k (т.е. амплитуда s_k = 1). 14 комплексных величин, которые составляют слово синхронизации системы IS-54, представляют собой набор { w₁, w₂, ...w_м} при М=14, a (s₀, s₁,...s_м) представляет собой набор знаков сигнала в слове синхронизации при s₀ = 1.

При дискретизации, как правило, с двойной скоростью передачи знаков, дискретная модель наблюдения полученных выборок сигнала имеет вид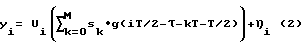

где y_i, представляет собой комплексную выборку, идентифицированную индексом i, который может быть целым числом от 1 до 2M+1, T представляет собой знак интервала, τ представляет собой задержку дискретизации, U_i - неизвестный комплексный коэффициент замирания, g(t) представляет собой импульсную характеристику фильтров канала (комбинация фильтров на передающей и приемной стороне), описываемая выражением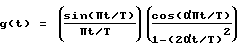

где α представляет собой коэффициент избирательности фильтра и η_i представляет собой последовательность комплексных Гауссовых случайных переменных с нулевым средним, дисперсия 2σ_η, и корреляционная функция 2σ_ηg(i-j)T)/2) между двумя случайными переменными η_i и η_j.
Способ восстановления тактовой синхронизации
Модель наблюдения, описываемая уравнением (2), аппроксимирована линейным вектором модели наблюдения, включающей косвенные переменные, которые содержат информацию о задержке дискретизации τ. Эти косвенные переменные оценены по максимальному критерию правдоподобия. Задержка дискретизации затем восстанавливается из оцененных косвенных переменных.

Модель наблюдения лицейного вектора
При [] ^T, представляющем сопряженную транспонированную матрицу в квадратных скобках, выразим (2M+1)-размерный вектор наблюдения выборок принятого сигнала через
Y_n=[y_2n+1, y_2n+2,...y_2n+2M, y_2n+2M+1]^T (3)
где (M+1)-размерный вектор известных знаков слова синхронизации является
S=[s₀, s₁,...s_M-1, s_M]^T (4)
а (2M+1)-размерный вектор наблюдения выборок помех выражен как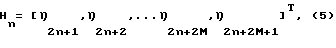

Обозначая матрицу импульсной характеристики выражениями

мы можем выразить модель уравнения (2) в векторном виде
Y_n=G τ SU_n+H_n (7)
Для того чтобы линеаризовать эту модель каждый компонент g₀(τ) этой матрицы G(τ) аппроксимирован линейной комбинацией плюс постоянным членом некоторой пары функции ω₁(τ) и ω₂(τ), так чтобы
g_ij(τ) = a_1ijϕ₁(τ)+a_2ijϕ₂(τ)+a_3ij
где a_1ij, a_2ij, и a_3ij - коэффициенты матрицы для матриц A₁, A₂ и A₃ соответственно.

После этого можно выполнить следующую аппроксимацию для матрицы G(τ)
G(τ) = A₁ϕ₁(τ)+A₂ϕ₂(τ)+A₃ (8)
в интервале от -T/2 до T/2 для задержки дискретизации τ.
Можно использовать несколько пар функций, например представленные ниже следующие пары уравнений от (9) до (13), для линеаризации и обеспечить достаточную точность аппроксимации. В паре уравнений (11) g(τ) представляет собой преобразование Гильберта функции g(τ) :
ϕ₁(τ) = cos(πτ), ϕ₂(τ) = sin(πτ) (9)
ϕ₁(τ) = cos(πτ/2), ϕ₂(τ) = sin(πτ/2) (10)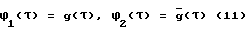

ϕ₁(τ) = g(τ), ϕ₂(τ) = dg(τ)/dτ (12)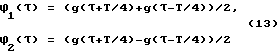

Хотя могут быть использованы любая эта или другая возможная пара функций, первая пара функции (9) обеспечивает хорошую точность и наименьшую вычислительную сложность и поэтому наиболее предпочтительна. Только эта пара функций далее рассматривается более подробно.

Используя аппроксимацию в уравнении (8), модель наблюдения уравнения (7) становится
Y_n= (A₁ϕ₁(τ)+A₂ϕ₂(τ)+A₃)SU_n+H_n (14)
или, соответственно,
Y_n= A₁SU_nϕ₁+A₂SU_nϕ₂+A₃SU_n+H_n (15)
Если Ф_n представляет собой переменную, которая представляет собой трехмерный комплексный вектор, образованный перестановкой трех косвенных переменных Ф_1,n, Ф_2,n и Ф_3,n т.е. Ф_n= [Ф_1,n, Ф_2,n, Ф_3,n]^T, когда Ф_1,n= U_nω₁, Ф_2,n= U_nω₂ и Ф_3,n = U_n при B, представляющей собой известную постоянную матрицу, B=[A₁S, A₂S, A₃S], уравнение (15) может быть написано как:
Y_n=BФ_n+H_n (16)
Оценка косвенных переменных
Если V_η представляет собой известную корреляционную матрицу аддитивного вектора Гауссова шума H_η, из уравнения (16) мы можем видеть, что функция правдоподобия для оценки вектора косвенной переменной Ф_n дается условной вероятностью 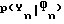(т.е. вероятности Y_n, заданной условием Ф_n):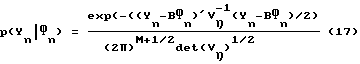

суффикс ' указывает на сопряженную транспонированную матрицу. Представляя оцененные значения диакритическим знаком ^ , максимальная оценка правдоподобия 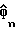для вектора косвенной переменной Ф_n может быть определена как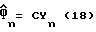

C = (B′V-η

¹B)^-1B′V-η¹ представляет собой матрицу 3 х (2M+1), которая может быть рассчитана из B и V_η (оба они известны) и хранятся в памяти в виде справочной таблицы.

Следующим шагом является извлечение задержки дискретизации τ из оценки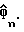
Восстановление задержки дискретизации
Для восстановления задержки дискретизации можно использовать несколько процедур, выбор которых зависит от компромисса между точностью оценки и сложностью вычислений. Ниже описывается оптимальная оценка и три субоптимальных, но вычислительно простых оценки.

Оптимальная оценка
Из уравнения (17) можно получить новое уравнение наблюдения для косвенных переменных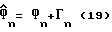

где Г_n представляет собой трехмерный вектор сложных случайных Гауссовых переменных с известной корреляционной матрицей V_γ= (B′V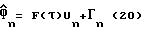-η

¹B)^-1. Уравнение (19) может быть написано в виде:

где F(τ) = [ω₁(τ),ω₂(τ),1]^T. Шум наблюдения в уравнении (20) является гауссовым шумом, так что функция правдоподобия наблюдения может быть получена как: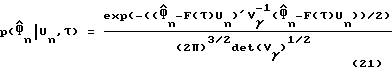

и усреднена по комплексной переменной U_n, чтобы определить следующее уравнение для функции правдоподобия по отношению к τ: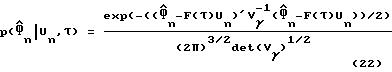

где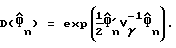
Согласно максимальному критерию правдоподобия оптимальная оценка задержки дискретизации τ должна максимизировать эту функцию правдоподобия. Следовательно, можно определить оптимальную оценку задержки дискретизации во временном интервале от - T/1 до T/2 как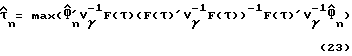

Выполнив следующую аппроксимацию: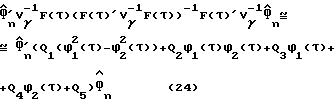

где Q₁-Q₅ являются матрицами расширения, имеющими действительные элементы, которые могут рассчитываться и храниться в справочной таблице в памяти. Затем, используя пару функций (9), можно вычислить оптимальную задержку дискретизации 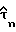как: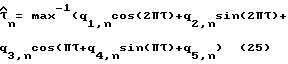

где 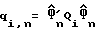для I = 1,3,4 и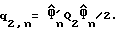
Уравнение (25) содержит нелинейную максимизацию и по этой причине ее практическое осуществление может быть связано со сложными вычислениями. Следующие три субоптимальные альтернативные процедуры устраняют этот недостаток и легко выполнимы.

Одноступенчатое нелинейное преобразование
Оценка трех косвенных переменных может быть выражена в виде 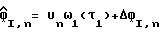для i = 1, 2, 3, где Δф_I,n представляет собой оценку ошибки, внесенную уравнением (18). Если ощибка небольшая, то оцененная задержка дискретизации 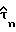может быть аппроксимирована одноступенчатым нелинейным преобразованием в виде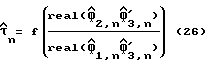

где функция f() зависит от пары функций ω₁ и ω₂. Используя пару функций (9), уравнение (23) пишется в виде:

Использование этого первого решения для задержки дискретизации описано ниже со ссылкой на фиг. 3 и требует 6М+5 комплексных умножений, 6М комплексных сложений, 1-го вещественного деления и 1-го не скалярного преобразования.

Рекурсивная процедура
Описываемая ниже альтернативная процедура рекурсивной оценки задержки дискретизации основана на максимизации функции правдоподобия по отношению к переменным ω₁ и ω₂ при допущении, что U_n известно, с последующим рассмотрением оценки U_n, предполагая, что задержка дискретизации τ также известна.

Во первых, из уравнения (21) мы получаем следующую функцию правдоподобия: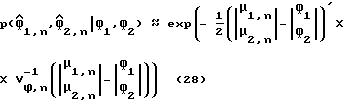

при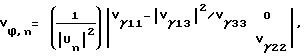


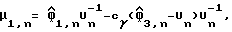
и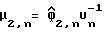
где V_γij - элементы матрицы V_γ и c_γ= V_γ13/V_γ33. При решении предполагается, что V_γ12= V_γ21= V_γ23= V_γ32= 0.
Из уравнения (28) следует, что 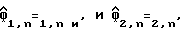и оцененная задержка дискретизации дается следующим нелинейным преобразованием: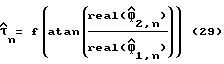

Во-вторых, из уравнения (21), функция правдоподобия для U_n, предполагая, что задержка дискретизации τ известна, может быть получена как: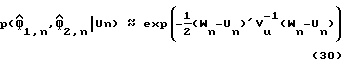

где V_u= (F(τ)′V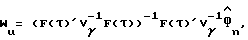-γ

¹F(τ))^-1
отсюда следует, что оценка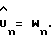
Затем рекурсивная процедура суммируется, как содержащая следующий следующие четыре последовательных шага для каждой итерации k:
Шаг 1: первоначальная оценка задержки дискретизации в соответствии с уравнением (31):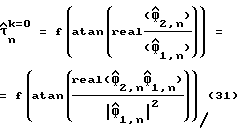

Шаг 2: оценка коэффициента замирания в соответствии с уравнением (32)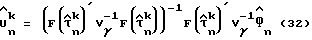

Шаг 3: повторная оценка задержки дискретизации в соответствии с уравнением (33):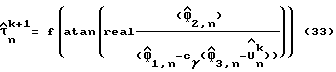

Шаг 4: прекращение дальнейших вычислений, если достигнуто предопределенное максимальное число итераций, в противном случае - возврат к шагу 2.

Осуществление этой рекурсивной процедуры для задержки дискретизации описано ниже со ссылкой на фиг. 5.

Упрошенная процедура
Простой вариант "вышеупомянутой рекурсивной процедуры заключается в остановке после шага 1, без выполнения операций 2-4. В этом случае задержка дискретизации оценивается с помощью уравнения: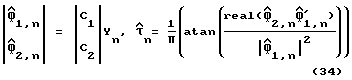

где C_i, представляет собой i-й элемент известной матрицы C.

Осуществление этой простой процедуры для определения задержки дискретизации описано ниже со ссылкой на фиг. 4.

Цикловая синхронизация
Вышеописанные способы восстановления тактовой синхронизации применяются, когда задержка дискретизации τ находится в интервале от -T/2 до T/2. Цикловая синхронизация отвечает этому требованию, когда абсолютная или общая задержка дискретизации τ_s лежит вне интервала -T/2 - T/2, но в пределах числа L интервала знака T. Таким образом, τ_s= τ+iT, где τ - интервал от -(L-1)/2 до T/2 и i - индекс в диапазоне -(L-1)/2, где L является нечетным числом. Цикловая синхронизация служит для проверки всех интервалов от -T/2 + iT до T/2 + iT и для выбора максимального критерия правдоподобия из этих интервалов, т.е. максимального критерия правдоподобия выбора индекса i
Цикловая синхронизация основана на интервале наблюдения, соответствующего неопределенности интервалов знака L задержки дискретизации t, так чтобы это было применено к набору векторов наблюдения Y, каждый из который имеет вид уравнения (2), причем этот набор описывается как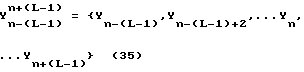

При использовании принципов максимального правдоподобия задача цикловой синхронизации и восстановления тактовой синхронизации сводится к определению максимума функции правдоподобия: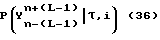

которая может быть разделена на задачу цикловой синхронизации для определения максимума средней функции правдоподобия: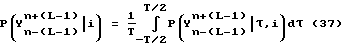

и задачу восстановления синхронизации при определении максимума функции правдоподобия:

где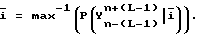
Вместо прямого вычисления функции правдоподобия в уравнении (37) можно использовать косвенный подход, как показано ниже. Для каждого значения индекса i в диапазоне от -(L-1)/2 до (L-1)/2 уравнения (7), (16), (18) и (20) могут быть выражены как:
Y_n+2i=G(τ) SU+H_n+2i;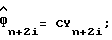

Y_n+2iBФ+H_n+2i;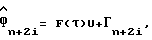

из которых может быть получена следующая функция правдоподобия: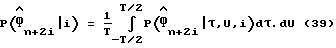

при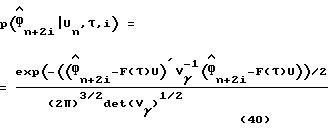

Вместо усреднения по переменной τ, уравнение (39) упрощено путем использования оцененной задержки дискретизации 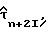полученной путем использования любого способа восстановления синхронизации из описанных выше. Посредством усреднения по переменной U_n получаем следующее: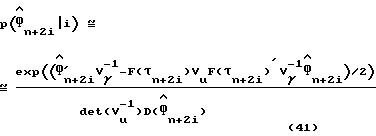

где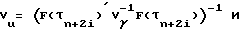
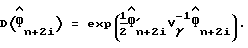
Применяя рекурсивную процедуру, описанную выше, для получения оценки 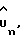функция правдоподобия в уравнении (41) может быть написана как: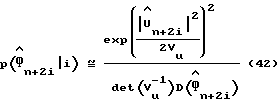

где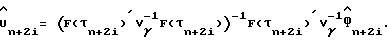
Игнорируя зависимость V_u от получаем следующие результаты: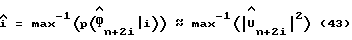

Таким образом, задача цикловой синхронизации сводится к оценке амплитуды сигнала для каждого значения индекса i и выбора такого значения индекса i, который соответствует максимальной амплитуде сигнала.

Комбинированнмй способ цикловой синхронизации и восстановления тактовой синхронизации
Сочетая этот способ цикловой синхронизации с описанной выше рекурсивной процедурой для восстановления тактовой синхронизации с описываемой ниже рекурсивной процедурой, которая предполагает использование упомянутой выше пары функций (9) для комбинации цикловой синхронизации и восстановления тактовой синхронизации, выполняются следующие шаги:
Шаг 1: для каждого значения индекса i в диапазоне от - (L-1)/2 до (L-1)/2, выполняем следующие операции 1A-1C:
1A: Оценка вектора косвенной переменной в соответствии с уравнением (44):

1B: Первоначально (для счетчика k = 1) оценивают амплитуду сигнала и задержку дискретизации в соответствии с уравнениями (45) и (46):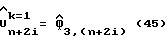


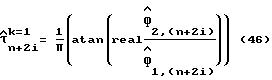
1C: Итеративно (для k = 2 для максимального числа K итераций) оценивают амплитуду сигнала и задержку дискретизации в соответствии с уравнениями (47) и (48):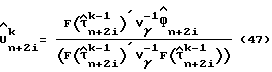


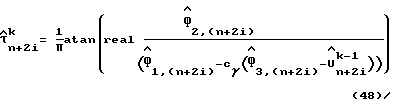
Шаг 2: для каждого значения индекса i в диапазоне от - (L-1)/2 до (L-1)/2 определяют индекс i максимума оцененной амплитуды сигнала, определенной в шаге 1, и определяют общую задержку дискретизации из этого индекса и оцененную в шаге 1 задержку дискретизации в соответствии с уравнениями (49) и (50):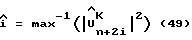


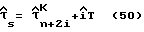
Сложность этой процедуры зависит от числа итераций K и от количества L. Эта процедура значительно упрощается с небольшим снижением точности аналогично тому, как определяется только восстановление синхронизации, путем исключения шага рекурсии 1, так что шаг 1 включает только операции 1A и 1B. Уравнения (44) - (46), (49) и (50), используемые, как описано выше, с K = 1, и с парой функций (9) уравнение (45) становится уравнением: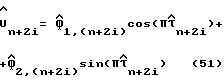

Осуществление этой комбинированной и упрощенной процедуры цикловой синхронизации и восстановления тактовой синхронизации описано ниже со ссылкой на фиг. 6.

Физическое осуществление изобретения
На фиг. 1 представлена блок-схема беспроводного цифрового приемника связи, в котором цифровой радиосигнал проходит через радиочастотную (РЧ) цепь 20 приемника на преобразователь 22 с понижением частоты, чтобы получить сигнал, который дискретизируется схемой выборки 24; выборки преобразуются в цифровую форму аналого-цифровым преобразователем 26. Оцифрованные выборки интерполируются интерполятором 28 в соответствии с восстановленной и оцененной задержкой дискретизации 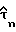для получения выборок Y_n при оцененных оптимальных временах дискретизации для дальнейшей обработки сигнала. В качестве альтернативы использованию интерполятора 28 оцененная задержка дискретизации 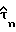может быть использована непосредственно для регулировки времени дискретизации схемы выборки 24. Интерполятор 28 образует часть цифровых цепей 30, которые удобно встроить в процессор цифрового сигнала в виде интегральной схемы, которая также включает блок 32 восстановления тактовой синхронизации и цикловой синхронизации. Блок 32 обеспечивает оцененную задержку дискретизации как описано ниже. Система содержит также блок 34 восстановления несущей, который здесь не описывается. Выборки Y_n из интерполятора 28 подаются, как входные сигналы, на блоки 32 и 34.

Блок 32 предпочтительно выполняет функции цикловой синхронизации и восстановления тактовой синхронизации, используя описанные выше операции способом, который описан ниже со ссылкой на фиг. 6. Однако операция восстановления тактовой синхронизации может выполнятся отдельно от операции цикловой синхронизации и, с этой целью, ниже описывается только функции цикловой синхронизации со ссылкой на фиг. 2-5. Предполагается, что в этих случаях задержка дискретизации находится в интервале от - T/2 до T/2.

Восстановление тактовой синхронизации
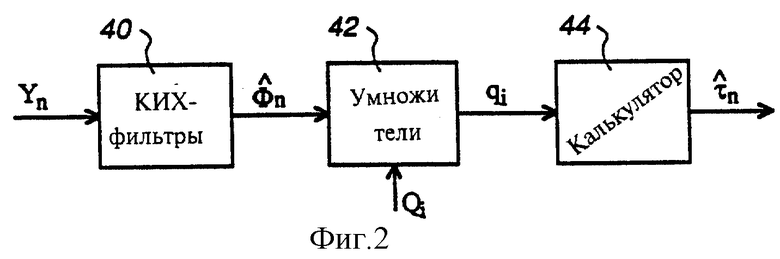
На фиг. 2 представлена блок-схема узлов блока 32, осуществляющих восстановление тактовой синхронизации для выполнения оцененной задержки дискретизации 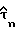из выборок Y_n полученного сигнала в соответствии с вышеописанной оптимальной процедурой оценки. Этот вариант изобретения включает фильтр с конечной импульсной характеристикой (КИХ-фильтр) 40, умножитель 42 и калькулятор 44. КИХ-фильтр 40 поставляется с выборками сигнала Y_n и фильтрует эти выборки для получения оценки 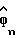в соответствии с уравнением (18), приведенным выше. Умножитель 42 выдает произведение в соответствии с вышеприведенным уравнением (24) из оценки и матриц Qi, для чисел i от 1 до 5, полученных, как указано выше, из справочных таблиц, причем выход умножителя 42 включает постоянные скалярные величины q_i. Они подаются на калькулятор 44, который производит оценку задержки дискретизации 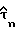в соответствии с уравнением (25).

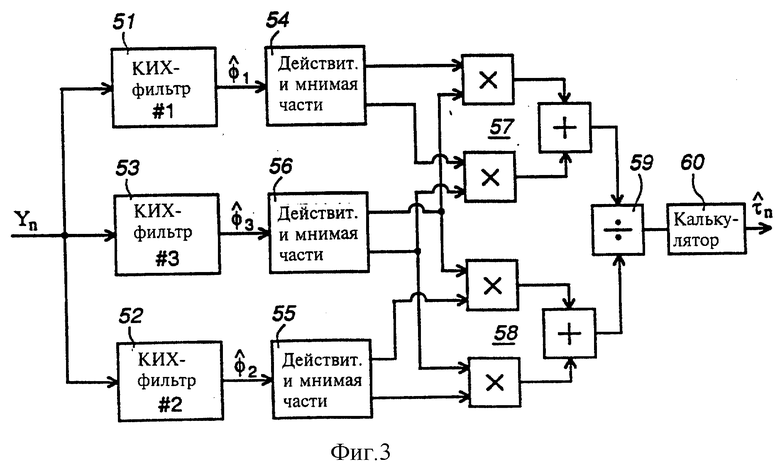
На фиг. 3 показана блок-схема узлов блока 32, осуществляющих восстановление тактовой синхронизации для выделения оцененной задержки дискретизации из полученных выборок сигнала Y_n в соответствии с одноступенчатой нелинейной процедурой преобразования, описанной выше. В этом варианте выборки сигнала Y_n поступают на три фильтра с конечной импульсной характеристикой 51, 52 и 53 для получения косвенных оценок переменной 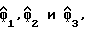соответственно, согласно уравнению (18).

Действительные и мнимые части этих оценок разделены узлами 54, 55 и 56, соответственно, и используются в остальной части цепи, представленной на фиг. 3, для выполнения управляющих функций (27). Эта часть цепи содержит два комплексных умножителя 57 и 58, каждый из которых содержит два умножителя для умножения действительных и мнимых составляющих и сумматор для суммирования произведений этих умножителей с получением, соответственно, знаменателя и числителя в уравнении (27). Блок деления 59 служит для выполнения деления числителя на знаменатель, и калькулятор 60, предназначен для выполнения функции (1/π atan() уравнения (27) и, следовательно, для получения оцененной задержки дискретизации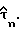
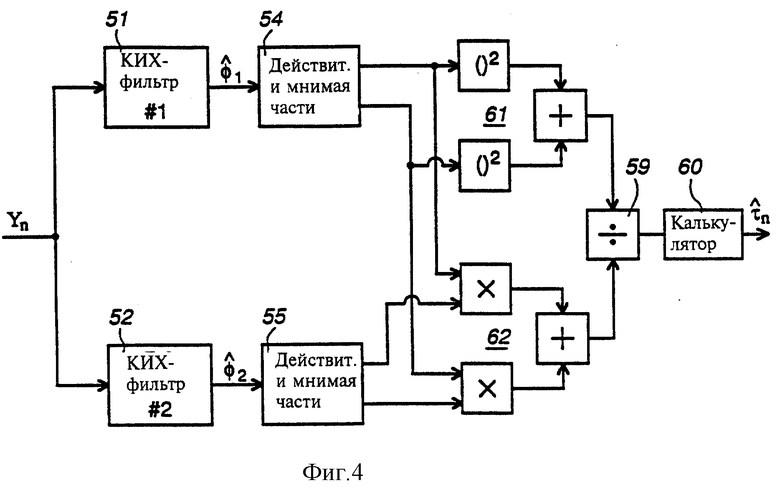
На фиг. 4 представлена блок-схема узлов блока 32, осуществляющих восстановление тактовой синхронизации для получения оцененной задержки дискретизации из полученных выборок сигнала Y_n в соответствии с простой процедурой, описанной выше. Те же ссылки используются в фиг. 3 для обозначения аналогичных частей. На фиг. 4 выборки сигнала Y_n подаются на два КИХ-фильтра 51 и 52 для получения оценок косвенной переменной 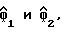соответственно, согласно уравнению (18). Действительные и мнимые части этих оценок разделены узлами 54 и 55, соответственно, и используются остальной частью цепи, представленной на фиг. 4, для выполнения управляющих функций (34). Эта часть цепи содержит комплексный квадратор 61 (содержащий два квадратора и сумматор) и комплексный умножитель 62 (содержащий два множителя и сумматор), обеспечивающие получение, соответственно, знаменателя и числителя в уравнении (34); блок деления 59, предназначенный для деления числителя на знаменатель, и калькулятор 60, предназначенный для выполнения функции (1/πatan() уравнения (34) и, следовательно, для получения оцененной задержки дискретизации
На фиг. 5 представлена блок-схема устройства блока 32 для восстановления тактовой синхронизации и извлечения оцененной задержки дискретизации 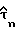из выборок принятого сигнала Y_n в соответствии с рекурсивной процедурой, описанной выше. Это устройство включает цепь фиг. 4, показанный как узел 64, для получения оценок 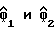косвенной переменной и оцененной задержки дискретизации 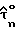(т.е. первоначально оцененной задержки шага 1 рекурсивной процедуры, для которой k = 0) и КИХ-фильтр 53 фиг. 3, предназначенный для получения оценки 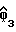косвенной переменной. Цепь также содержит узлы 65-71 и переключатель 72, функции которых описываются ниже.

Шаг 1 рекурсивной процедуры выполняется узлом 64, как описано выше, чтобы обеспечить начальную оцененную задержку дискретизации для k = 0, тем самым решая уравнение (31) (или (34)), причем переключатель 72 находится в положении для подачи этой оценки на выход узла и к калькулятору 65. На калькулятор 65 также поступают оценки 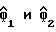косвенной переменной и матрица Y_γ. Узел 65 рассчитывает оценку 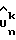(Шаг 2 рекурсивной процедуры) в соответствии с уравнением (32). Узлы 66-71 используют уравнение (33), соответствующее шагу 3 рекурсивной процедуры, чтобы обеспечить оцененную задержку дискретизации для последующего более высокого значения k, для которого k > 0, так что, как показано на фиг. 5, выключатель 72 переброшен в свое другое положение чтобы обеспечить новую оцененную задержку дискретизации, подаваемую на выход и на калькулятор 65.

Как можно видеть из фиг. 5 и уравнения (33), узел 66 является сумматором с вычитающим входом, который выполняет вычитание в скобках в знаменателе уравнения (33), разница умножается на c_γ умножителе 67 и произведение вычитается из в сумматоре 68 для получения знаменателя в уравнении (33). Узел 69 представляет собой блок деления, который выполняет деление в уравнении (33), узел 70 обеспечивает вещественную часть результата деления, а узел 71 представляет собой калькулятор, который выполняет функцию (1/π atan(). Предпочтительно выполнить калькуляторы 71 и 60 (в узле 64) в виде одного узла, элементы которого меняются с помощью переключателя 72.

Моделирование результатов восстановления синхронизации
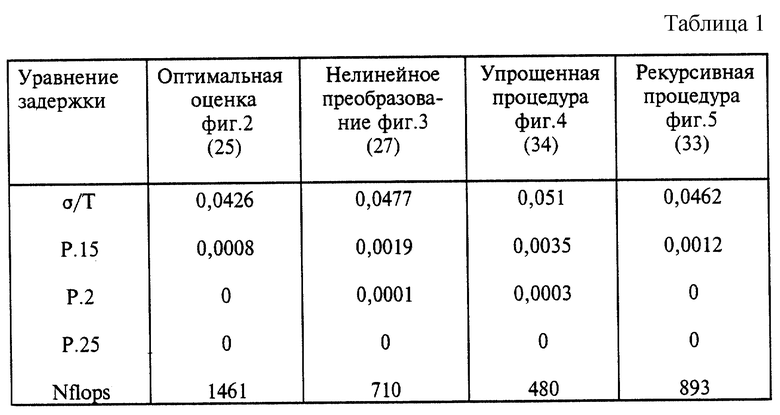
Результаты компьютерного моделирования различных описанных выше процессов изложены в табл. 1, приведенной ниже на примере отношения "сигнал-шум" порядка 8 дБ. Выбор слова синхронизации из 6 слов синхронизации, приведенных в IS-54, не оказал существенного влияния на эти результаты. При моделировании использовалась пара функций уравнения (9) в аппроксимации уравнения (8). Коэффициенты постоянных аппроксимирующих матриц A_i.

(i = 1 до 3) уравнения (8) и постоянных матриц расширения Qi (i = 1 до 5) уравнения (24) были вычислены раздельно. Для каждой из описанных выше процедур в табл. 1, указано стандартное отклонение оцененной задержки дискретизации (σ/T), причем вероятность ошибки выборки вне интервалов от - 0,15T до 0,15T, от - 0,2T до 0,2T и от - 0,25T до 0,25T, обозначенных P.15, P.2, и P. 25, соответственно, и числа операций с плавающий запятой обозначено как Nflops для каждого моделирования. С другими отношениями "сигнал/шум" последнее число, в основном, остается неизменным.

Из табл. 1 можно видеть, что оптимальная оценка обеспечивает наилучшие результаты за счет повышения сложности вычислений (высокой Nflops). Субоптимальные процедуры значительно проще для вычислений и при использовании рекурсивных процедур уравнений (31) - (33), представленных на фиг. 5, обеспечивают ныне предпочтительный компромисс между точностью и сложностью вычислений.

Комбинация цикловой синхронизации и восстановления тактовой
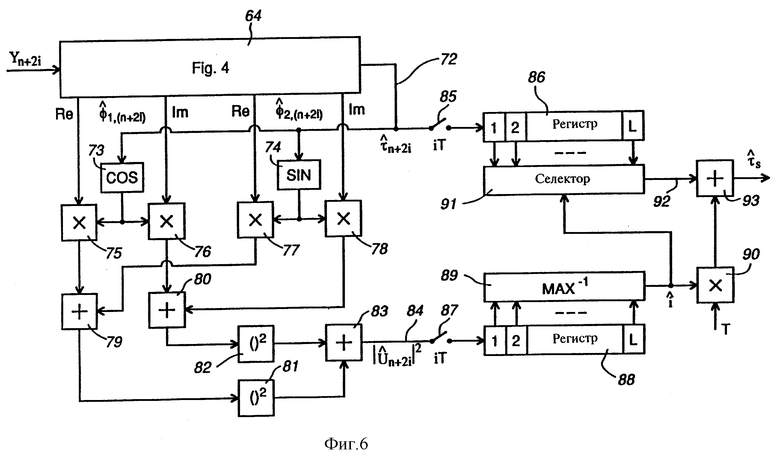
На фиг. 6 представлена блок-схема осуществления комбинированной операции цикловой синхронизации и функций восстановления синхронизации узлом 32 для получения оцененной задержка дискретизации τ_n из полученных выборок сигнала Y_n+2i в соответствии с первым шагом рекурсивной процедуры, описанной выше. Эта схема включает цепь фиг. 4, показанную как узел 64, который производит действительную (Re) и мнимую (Im) составляющие оценок косвенной переменной 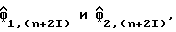в также оцененную задержку дискретизации 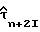на линии 72, как указано выше и в соответствии с уравнением (46).

Цепь, показанная на фиг. 6, также содержит узлы 73 к 83, которые служат для получения линии 84 амплитуд прямоугольных сигналов 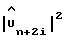в соответствии с уравнением (51). Узлы 73 и 74 содержат операторы cos и sin (например, справочные таблицы в памяти), которые получены с оцененной задержкой дискретизации 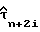из линии 72 и генерируют на своих выходах величины 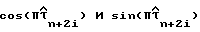соответственно, используя уравнение (51). Узлы 75 и 78 являются умножителями, которые перемножают действительные и мнимые составляющие оценок косвенной переменной 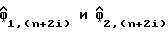из узла 64 на выходы узлов 73 и 74, чтобы получить произведения в уравнении (51). Узлы 79 и 80 являются сумматорами, предназначенными для сложения действительных и мнимых составляющих этих произведений, узлы 81 и 82 являются устройствами для возведения в квадрат выходов сумматоров 79 и 80, соответственно, а узел 83 является сумматором, предназначенным для суммирования выходов устройств 81 и 82, производя тем самым возведение в квадрат оцененные амплитуды сигнала 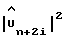на линии 84.

В остальных частях цепи, показанной на фиг. 6, оценки 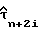на линии 72 дискретизируются дискретизатором 85 с временем выборки iT и эти выборки подаются на ступень L регистра сдвига 86 и, аналогичным образом, оценки 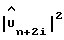нa линии 84 дискретизируются дискретизатором 87 с временем выборки iT и эти выборки направляются на ступень L регистра сдвига 88. Например, L = 5. Узел 89 предназначен для определения каждого отрезка времени дискретизации и, в соответствии с уравнением (49), индекса i максимума квадратурной амплитуды на стадиях L регистра сдвига 88 и для подачи этого индекса в качестве выхода на умножитель 90 и на управляющий вход селектора 91. Селектор 91 имеет оценки которые хранятся в ступенях L регистра сдвига 86, и предназначен для подачи к линии 92 той из указанных оценок, которая соответствует индексу i на управляющем входе селектора. Умножитель 90 перемножает индекс i со знаком интервала T, и сумматор 93 суммирует произведение iT с выходом селектора 91 для получения общей оцененной задержки дискретизации τ_s в соответствии с уравнением (50).

Хотя вышеупомянутое описание относится только к простой процедуре цикловой синхронизации, ясно, что она применима и к рекурсивной процедуре аналогично тому, как это описано выше по отношению к фиг. 5 только для восстановления тактовой синхронизации. Точно так же понятно, что любая из процедур для цикловой синхронизации может быть объединена с любой из процедур для восстановления тактовой синхронизации, описанной выше.

Результаты моделирования комбинированной цикловой синхронизации и восстановление тактовой синхронизации
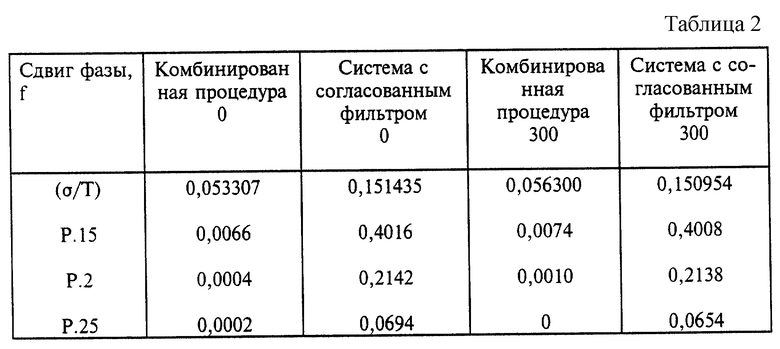
Компьютерное моделирование, аналогичное описанному выше моделированию восстановления тактовой синхронизации, приведено ниже в табл. 2 на примере отношения "сигнал/шум" порядка 8 дБ. В табл. 2 сравниваются результаты для комбинированной цикловой синхронизации и восстановление тактовой синхронизации, как описано выше, используя пару функций (9) в уравнении аппроксимации (8), с результатами для обычных согласованных фильтров с обозначением для сдвига f нулевой несущей частоты и несущей частоты 300 Гц стандартного отклонения оцененной задержки дискретизации (σ/T) и вероятности ошибки Р.15, Р. 2 и Р.25. Снова было подтверждено, что выбор слова синхронизации не оказывает значительного влияния на результаты. Для более высоких отношений сигнал-шум улучшение этой комбинированной цикловой синхронизации и восстановления тактовой синхронизации для обычных согласованных фильтров даже выше.

Хотя настоящее изобретение описано выше применительно к паре функций уравнения (9), ясно, что могут быть использованы любые другие пары функций в уравнениях (10) - (13), или другие пары функций для использования в аппроксимации уравнения (8). Кроме того, хотя подробно описаны конкретные варианты изобретения, специалистам ясно, что могут иметь место многочисленные другие модификации и изменения в пределах объема данного изобретения, как они определены в патентных притязаниях.

Сущность изобретения: восстановление тактовой синхронизации с или без цикловой синхронизации в системе сотовой связи с многопостанционным доступом и временным разделением каналов (TDMA) осуществляется способом, включающим операции оценки косвенных переменных, которые включают информацию о задержке дискретизации линейного комплексного вектора, используя критерий максимального правдоподобия и извлечение задержки дискретизации из оцененных косвенных переменных. Для извлечения задержки дискретизации используется оптимальная процедура и три субоптимальных, которые проще в смысле вычислений. Эти процедуры раскрыты в описании изобретения вместе с описанием устройства для его физической реализации. Для цикловой синхронизации задержка дискретизации при восстановлении синхронизации дополняется рядом интервалов выборок, определенных максимальной амплитудой сигнала множества выборок, вычисленных из оцененных косвенных переменных, и задержкой дискретизации. Техническим результатом является обеспечение улучшенной цикловой синхронизации и восстановление синхронизации в системе связи. 3 с. и 16 з.п. ф-лы, 6 ил., 2 табл.

1. Способ определения задержки дискретизации в выборках полученного сигнала в системе сотовой связи, характеризующийся тем, что оценивают с использованием максимального критерия правдоподобия косвенные переменные линейного комплексного вектора, который аппроксимирует полученные выборки сигнала и косвенные переменные, содержащие информацию о задержке дискретизации, определяют задержки дискретизации из оцененных косвенных переменных для восстановления тактовой синхронизации сигнала связи. 2. Способ по п.1, отличающийся тем, что каждая составляющая линейного комплексного вектора содержит линейную комбинацию предопределенной пары функций, зависящих от задержки дискретизации. 3. Способ по п.2, отличающийся тем, что пара функций содержит функции Cos (πτ) и Sin (πτ), где τ представляет собой задержку дискретизации. 4. Способ по любому из пп.1 - 3, отличающийся тем, что операция оценки каждой косвенной переменной включает фильтрацию полученных выборок сигнала с использованием характеристики фильтра с конечной импульсной характеристикой. 5. Способ по любому из пп.1 - 4, отличающийся тем, что определение задержки дискретизации из оцененных косвенных переменных включает умножение оцененных косвенных переменных на вещественные элементы предопределенных и хранящихся в памяти матриц. 6. Способ по любому из пп.1 - 5, отличающийся тем, что определение задержки дискретизации из оцененных косвенных переменных включает выполнение одиночного нелинейного преобразования оцененных косвенных переменных. 7. Способ по любому из пп.1 - 5, отличающийся тем, что определение задержки дискретизации из оцененных косвенных переменных включает вычисление задержки дискретизации в соответствии с предопределенной функцией действительной части произведения комплексной сопряженной функции первой оцененной косвенной переменной и второй оцененной косвенной переменной, деленной на квадрат амплитуды первой оцененной косвенной переменной. 8. Способ по п.7, отличающийся тем, что предопределенная функция является функцией

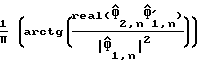
9. Способ по любому из пп.1 - 5, отличающийся тем, что определение задержки дискретизации из оцененных косвенных переменных включает стадии первоначального расчета оценки задержки дискретизации в соответствии с предопределенной функцией оцененных косвенных переменных, итеративно один или несколько раз: оценку комплексного коэффициента замирания полученных выборок сигнала в зависимости от оценки задержки дискретизации и оцененных косвенных переменных, повторную оценку задержки дискретизации в зависимости от оцененного комплексного коэффициента затухания и оцененных косвенных переменных.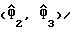 10. Способ по любому из пп.1 - 5, отличающийся тем, что дополнительно осуществляют сложение найденной задержки дискретизации для восстановления тактовой синхронизации полученного сигнала связи с задержкой дискретизации, содержащей целое число i интервалов выборок для цикловой синхронизации полученного сигнала связи, определение числа i шагами, определение амплитуд сигнала множества полученных выборок сигнала в зависимости от оцененных косвенных переменных, выбор числа i, соответствующего максимальной амплитуде выборки. 11. Способ по п.10, отличающийся тем, что определение амплитуд сигнала включает итеративное определение амплитуд сигнала в зависимости от итеративного определения задержки дискретизации для восстановления тактовой синхронизации. 12. Способ цикловой синхронизации и восстановление тактовой синхронизации путем определения задержки дискретизации принятого сигнала связи, характеризующийся тем, что, используя максимальный критерий правдоподобия, производят оценку косвенных переменных линейного комплексного вектора, который аппроксимирует полученные выборки сигнала, причем косвенные переменные включают информацию о задержке дискретизации, и для каждой из множества полученных выборок сигнала: определяют первую задержку дискретизации из оцененных косвенных переменных, причем первая задержка дискретизации короче интервала выборки, определяют в зависимости от оцененных косвенных переменных и соответствующей первой задержки дискретизации амплитуды сигнала каждого из множества полученных выборок сигнала, идентифицируют индекс максимума определенных амплитуд сигнала относительно текущей выборки, добавляют первую задержку дискретизации для выборки, идентифицированной индексом произведения при умножении интервала выборки на указанный индекс для получения комбинированной задержки дискретизации для цикловой синхронизации и восстановления тактовой синхронизации. 13. Способ по п.12, отличающийся тем, что определение первой задержки дискретизации и амплитуды сигнала выполняют итеративно. 14. Устройство дискретизации полученного сигнала сообщения в системе сотовой связи, характеризующееся тем, что содержит множество фильтров с конечной импульсной характеристикой, реагирующих на полученные выборки сигналов для получения множества косвенных переменных линейного комплексного вектора, который аппроксимирует полученные выборки сигнала по максимальному критерию правдоподобия; калькулятор, реагирующий на множество косвенных переменных для вычисления оцененной задержки дискретизации. 15. Устройство по п.14, отличающееся тем, что калькулятор реализует умножитель для умножения множества косвенных переменных на действительные элементы предопределенных матриц из блока памяти. 16. Устройство по п.14, отличающееся тем, что калькулятор реализует функции для вычисления оцененной задержки дискретизации, как функции вещественных
вещественных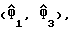
где представляют собой множество косвенных переменных, а 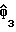является сопряженной матрицей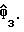
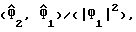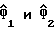17. Устройство по п.14, отличающееся тем, что калькулятор реализует функции расчета оцененной задержки дискретизации как функции atan вещественной где представляют собой множество косвенных переменных, а 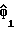является сопряженной функцией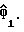
18. Устройство по любому из пп.14 - 17, отличающееся тем, что калькулятор также реализует функции для расчета оцененного комплексного коэффициента замирания выборок полученного сигнала в зависимости от множества косвенных переменных и оцененной задержки дискретизации и для рекурсивного вычисления оцененной задержки дискретизации в зависимости от множества косвенных переменных и оцененного комплексного коэффициента замирания. 19. Устройство по любому из пп.14 - 18, отличающееся тем, что множество фильтров с конечной импульсной характеристикой и калькулятор выполнены в виде, по меньшей мере, одного цифрового процессора сигнала.

Приоритет по пунктам:
23.08.95. по пп.1 - 9, 14 - 19;
23.10.95 по пп.10 - 13.