Область техники, к которой относится настоящее изобретение
В настоящем документе раскрываются способы приема, устройства приема, способы передачи, устройства передачи и приемопередающие системы.
Предшествующий уровень техники настоящего изобретения
Существует большое количество разнообразных технологий, относящихся к системам связи; при этом эти технологии привели к техническим изменениям в связи; автор настоящего изобретения предложил приемопередающую систему, в которой применены схемы с временным разделением и частотным разделением (см., например, список патентных документов [1]-[6] и список непатентных документов [1]-[32]):
Список источников
Патентная литература
Источники
[1] JT 2016-189500;
[2] WO 2012/153732 A1;
[3] WO 2014/034664 A1;
[4] WO 2013/183722 А1;
[5] JP 2016-189501 A;
[6] JP 2016-189502 A;
[7] JP 2013-251902 A;
[8] JP 2012-170083 A.
Непатентная литература
Источники
[1] D. Gabor, "Theory of Communication", in Proc. Inst. Elect. Engr,, pt. III, 93, 429-41, 1946
[2] D. Gabor, "Lectures on communication theory", in Technical Report., No., 238. Research Laboratoty of Electronics, Massachusettes Institute of technology Cambribge, 1-48, 1952.
[3] L.W. Couch, II, Digital and Analog Communication Systems, 8th Ed.," Pearson, 2013.
[4] G.B. Folland, Harmonic Analysis in Phase Space, Annals of Mathematics Studies Princeton Univ. Press, 1989.
[5] Howe, R. On the role of the Heisenberg groups in harmonic analysis," Bulltein of the American Mathematical Society, 3-2, 821-840 (1980)
[6] Rosenberg, J. A selective history of the Stone-von Neumann theorem, Contemporary Mathematics, 365. American Mathematical Society (2004)
[7] I. Daubechies, Time-frequency localization operators: a geometric phase space approach," IEEE Trans. Information Theory, 34-4, 605-612, 1988.
[8] I. Daubechies, The wavelet transform, time-frequency localization and signal analysis," IEEE Trans. Information Theory, 36-5, 961-1005, 1990.
[9] B.Le. Floch, M. Alard & C. Berrou, "coded OFDM: Coded Orthgonal Frequency Division Multiplex," Proc. of IEEE, 83-6, 982-996, 1995.
[10] P. Siohan, C. Sciclet,& N. Lacaille, "OFDM/OQAM: Analysis and Design of OFDM/OQAM Systems, based on Filterbank Theory," IEEE, Trans. Sig. 50-5, 1170-1183, May, 2002.
[11] Sciclet, C., Siohan, P. & Pinchon, D. Perfect reconstruction conditions and design of oversampled DFT-based transmultiplexers, EURASIP J. on Applied Signal Processing, 2006, Article ID 15756, 1-14, 2006.
[12] B.F. Boroujeny, "OFDM Versus Filter Bank Multicarrier," IEEE Signal Processing Magazine, 28-3, 92-112, 2011.
[13] P.P. Vaidyanathan, "Multirate Systems and Filter Banks," Prentice-Hall, 1993.
[14] J. Ville, "Theorie et application de la notion de signal analytique," Cables et transmission, no. 2, pp. 61-74. 1948. (J. Ville: "Theory and Applications of the notion of complex signal", translated from the French by I. Stein, T-92, 8-1-58, U.S. Air Force Project Rand, 1958)
[15] P.M. Woodward, Probability and Information Theory, with Applications to Radar, Pergamon Press, New York, 1953.
[16] C.H. Wilcox, "The synthesis problem for radar ambiguity function," MRC Technical Report, No. 157, pp. 1-46. Mathematics Reaearch Center, U.S. Army, Univ. Wisconsin, Madison, 1960.
[17] L. Auslander and R. Tolimieri, "Radar Ambiguity Functions and Group Theory, SIAM J. Math. Anal., 16-3, 577-601, 1985.
[18] C.W. Helstrom, Elements of Signal Detection and Estimation," PTR Prentice-Hall, 1995.
[19] N. Levanson and E. Mozeson, "Radar Signals," Wiley interscience, 2004
[20] Sakurai, J.J. Modern quantum mechanics, S.F. Tuan editor, Rev. ed., Addison-Wesley Pub. Comp. 1994.
[21] J. von Neumann, The Geometry of Operators, vol. II (Ann. Math. Studies, no. 22), 1950.
[22] Youla, D.C Generalized image restoration by the method of alternating orthogonal projections, IEEE Trans. Circuits and Systems, CAS-25-9, 694-702, 1978.
[23] Stark, H., Cahana, D. & Webb, H. Restoration of arbitrary finiteenergy optical objects from limited spatial and spectral information, J. Opt. Soc. Amer., 71-6, 635-642, 1981.
[24] Kohda, T., Jitsumatsu, Y. & Aihara, K. Separability of time-frequency synchronization, Proc. Int. Radar Symp., 964-969, 2013.
[25] T. Kohda, Y Jitsumatsu, and K. Aihara, "Gabor division/spread spectrum system is separable in time and frequency synchronization," Proc. VTC 2013 Fall, 1-5, 2013.
[26] Y. Jitsumatsu, T. Kohda, and K. Aihara, "Spread Spectrum-based Cooperative and individual time-frequency synchronization," Proc. (ISWCS), 1-5 2013.
[27] Jitsumatsu, Y., Kohada, T. & Aihara, K. Delay-Doppler space division-based multiple-access solves multiple-target detection, Jonnsson, M., et al, (eds.) MACOM2013, LNCS8310, Springer, 39-53, 2013
[28] T. Kohada, Y. Jitsumatsu, and K. Aihara, "Recovering noncoherent MPSK signal with unknown delay and Doppler using its ambiguity function," 4th International workshop on recent Advanced in Broadband Access NetWork, (RABAN2013), 251-256, 2013.
[29] T. Kohda, Y. Jitsumatsu and K. Aihara "Phase-tuned layers with multiple 2D SS codes realize 16PSK communication," 2014 2014 IEEE Wireless Commun. Networking Conference, WCNC 2014, 469-474 (2014).
[30] Jitsumatsu, Y & Kohda, T. Digital phase updating loop and delay-Doppler space division multiplexing for higher order MPSK, Jonnsson, M., et al, (eds.) MACOM2014, LNCS8715, Springer, 1-15, 2014.
[31] T. Kohda, Y. Jitsumatsu, and K. Aihara, "Frequency-division spread spectrum makes frequency synchronisation easy," Proc. IEEE Globecom 2012, 3952-3958, 2012.
[32] T. Kohda, Y Jitsumatsu, and K. Aihara, "Frequency synchronisation using SS technique," Proc. The ninth Int. Sympo. on Wireless Communication Systems, 855-859, 2012.
[33] J.F. Daughman, "Two-dimensional analysis of cortical receptive field profiles," Vision Research, 20, 846-856, 1980.
[34] J.F. Daughman, "Image analysis by local 2-D spectral signatures," J. Opt. Soc. Amer. (A), 2, p. P74, 1985.
[35] J.F. Daughman, "Complete Discrete 2-D Gabor Transform by Neural Networks for Image Analysis and Compression," IEEE Trans. Acoustics, Speech and Signal Processing, 36-7, 1169-1179, 1988.
[36] Movella, Javier R "Tutorial on Gabor filters". Archived from on 2009-04-19, Retrieved 2008-05-14.
[37] Hans G. Feichtinger and Thomas Strohmer: Gabor Analysis and Algorithms, Birkhauser, 1998.
[38] Jones, J.P. and Palmer, L.A. "An evaluation of the two-dimensional gabor filter model of simple receptive fields in cat striate cortex". J. Neurophysiol. 58(6): 1233-1258. 1987
[39] Tai Sing Lee, "Image representation using 2d Gabor wavelets," IEEE Trans. on pattern analysis and machine intelligence, 18-10, 1-13, 1996.
[40] W.D. Montgomery, "Optical applications of von Neumann's alternating projection theorem," Optics Letters, 7-1, 1-3, 1982.
[41] W.D. Montgomery "Restoration of images processing a finite Fourier series," Optics Letters, 7-2, 54-56, 1982.
[42] A.V. Oppenheim and J.S. Lim, "Importance of phase in Signals," 1980, Proc of the IEEE, 96-5, 529-541, 1981.
Краткое раскрытие настоящего изобретения
Проблемы, которые должно решить настоящее изобретение
Автор настоящего изобретения заметил то, что оператор частотно-временного сдвига (TFSO), представляющий некоммутативное свойство (NCP) частотно-временных сдвигов (TFS) в частотно-временной плоскости (TFP), играет важную роль в обнаружении и оценке сигнала, и сделал вывод о том, что необходимо обратить внимание на NCP, присущее TFSO.
В соответствии с вариантом осуществления настоящего изобретения для решения вышеупомянутой проблемы предложенный способ по существу основывается на вышеуказанном, и целью настоящего изобретения является обеспечение эффективных способа приема, приемника, способа передачи, передатчика и приемопередающей системы.
Решение проблемы
Для решения вышеупомянутой проблемы способ приема сигнала в соответствии с вариантом осуществления настоящего изобретения представляет собой способ приема сигнала, предусматривающий стадию оценки для осуществления оценки временного сдвига и частотного сдвига, которые заключены в принятом сигнале, при этом стадия оценки обращается к пространству параметров некоммутативных частотно-временных сдвигов коразмерности 2.
Для решения вышеупомянутой проблемы принимающее устройство в соответствии с вариантом осуществления настоящего изобретения представляет собой принимающее устройство для приема сигнала, содержащее оценивающую часть для осуществления оценки временного сдвига и частотного сдвига, которые заключены в принятом сигнале, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2.
Для решения вышеупомянутой проблемы способ передачи сигнала в соответствии с вариантом осуществления настоящего изобретения представляет собой способ передачи сигнала, предусматривающий стадию сдвига для осуществления частотно-временного сдвига сигнала, подлежащего передаче, с обращением к пространству параметров некоммутативных частотно-временных сдвигов коразмерности 2.
Для решения вышеупомянутой проблемы передающее устройство в соответствии с вариантом осуществления настоящего изобретения представляет собой передающее устройство для передачи сигнала, содержащее часть, выполняющую частотно-временной сдвиг, для осуществления частотно-временного сдвига сигнала, подлежащего передаче, с обращением к пространству параметров некоммутативных частотно-временных сдвигов коразмерности 2.
Для решения вышеупомянутой проблемы способ приема сигнала изображения в соответствии с вариантом осуществления настоящего изобретения представляет собой способ приема сигнала изображения, предусматривающий стадию оценки для осуществления оценки пространственного сдвига и сдвига пространственной частоты, которые заключены в принятом изображении, с обращением к пространству параметров, при этом каждый из пространственного сдвига и сдвига пространственной частоты характеризуется размерностью ≥2.
Для решения вышеупомянутой проблемы способ передачи сигнала изображения в соответствии с вариантом осуществления настоящего изобретения представляет собой способ передачи сигнала изображения, предусматривающий стадию сдвига для осуществления пространственного сдвига и сдвига пространственной частоты сигнала изображения, подлежащего передаче, с обращением к пространству параметров, при этом каждый из пространственного сдвига и сдвига пространственной частоты характеризуется размерностью ≥2.
Преимущественные эффекты настоящего изобретения
Настоящее изобретение позволяет реализовать эффективный способ приема, приемник, способ передачи, передатчик и приемопередающую систему.
Описание фигур
[Фиг. 1] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображено три типа разделений частотно-временной плоскости (TFP): (а) показано временное разделение (TD), (b) частотное разделение (FD) и (с) разделение Габора (GD) [1]. Жирными линиями в (а) показаны разделения данных длительностью Т; тонкими линиями показаны подразделения по фазовому коду (PC) во временной области (TD); точечными линиями в (b) показаны разделения данных с шириной полосы частот F; штриховыми линиями показаны подразделения по PC в частотной области (FD).
В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображено представление некоммутативного свойства (NCP) временных и частотных сдвигов (TFS): NCP проявляется в выражении, представляющем произведение операторов сдвига,
 его левая часть (LHS) соответствует треугольнику на фигуре; правая часть (RHS) соответствует квадрату; появляется фазовое искажение (PD)
его левая часть (LHS) соответствует треугольнику на фигуре; правая часть (RHS) соответствует квадрату; появляется фазовое искажение (PD)  круг на фигуре изображает симметричный оператор частотно-временного сдвига (TFSO) [26]
круг на фигуре изображает симметричный оператор частотно-временного сдвига (TFSO) [26]

[Фиг. 3] В соответствии с вариантом осуществления настоящего изобретения а) показывает функцию Габора, расположенную на TFP, и связанные с ней результаты: а0) изображает гауссов сигнал 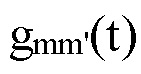 чипа, расположенный на TFP, и его преобразование Фурье (FT)
чипа, расположенный на TFP, и его преобразование Фурье (FT)  a1) показывает вещественную и мнимую части TD-шаблона, комбинацию
a1) показывает вещественную и мнимую части TD-шаблона, комбинацию  взвешенного посредством FD-PC
взвешенного посредством FD-PC 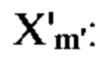 а2) показывает вещественную и мнимую части FD-шаблона, комбинацию
а2) показывает вещественную и мнимую части FD-шаблона, комбинацию  взвешенного посредством TD-PC Xm; b) изображает NN' функций кросскорреляции (CCF), N' сумм по столбцам значений множества TD-CCF, и N сумм по строкам значений множества FD-CCF; с) изображает альтернативную проекцию, ортогонально проецирующуюся на временную область с ограничением по времени (TL-TD) и на частотную область с ограничением по полосе частот (BL-FD), на основании теоремы альтернативного проецирования (APT), оцененные
взвешенного посредством TD-PC Xm; b) изображает NN' функций кросскорреляции (CCF), N' сумм по столбцам значений множества TD-CCF, и N сумм по строкам значений множества FD-CCF; с) изображает альтернативную проекцию, ортогонально проецирующуюся на временную область с ограничением по времени (TL-TD) и на частотную область с ограничением по полосе частот (BL-FD), на основании теоремы альтернативного проецирования (APT), оцененные

и сходящиеся значения td, fD.
[Фиг. 4] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен набор фильтров для синтеза сигнала (SFB), который содержит TD-, FD-PC Xm, 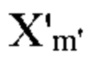 и m'-ый TD-шаблон
и m'-ый TD-шаблон

и генерирует TD-сигнатуру v[k] в (25), (67).
[Фиг. 5] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен SFB, который содержит TD-, FD-PC Xm,  и m'-ый FD-шаблон
и m'-ый FD-шаблон

и генерирует FD-сигнатуру в (25), (67)

[Фиг. 6] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен SFB с входными комплекснозначными данными с адресом р, р'
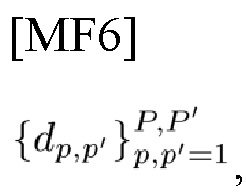
который генерирует на выходе соответствующую TD-комплексную огибающую (СЕ) в (27), (71)

[Фиг. 7] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен SFB с входными комплекснозначными данными
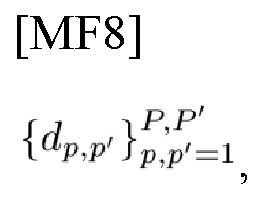
который генерирует на выходе FD-CE в (27), (71)

[Фиг. 8] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен набор фильтров для разложения сигналов (AFB), который представляет собой массив из N' TD-кросскорреляций (CCR) для декодирования комплекснозначных данных

[Фиг. 9] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен AFB, который представляет собой массив из N FD-CCR для декодирования комплекснозначных данных

[Фиг. 10] В соответствии с вариантом осуществления настоящего изобретения показано: а) массив из N' TD-CCR, с) массив из N FD-CCR и b) представление того, что оценки максимального правдоподобия (MLE) получаются посредством этих двух типов массивов CCR и поочередно обновляются друг другом согласно теоремы альтернативного проецирования фон Неймана (APT).
[Фиг. 11] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображено представление APT фон Неймана, где временная область с ограничением по времени (TL-TD) и частотная область с ограничением по полосе частот (BL-FD) обозначают два подпространства гильбертова пространства; подпространство TL-TD представляет собой LΔt (или Ts) TL-TD; подпространство BL-FD представляет собой LΔf (или Fs) BL-FD; стрелкой на фигуре показано ортогональное проецирование на соответствующее подпространство; это приводит к получению оценки максимального правдоподобия (MLE) и кардинальных чисел CCF.
[Фиг. 12] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображена блочная диаграмма системы, состоящей из двух альтернативных передатчиков, управляемых переключателями, которые выполняют эффективную и совместную оценку задержки и доплеровского смещения частоты с высокой точностью, с (или без) снабжением

-арной связью с фазовой манипуляцией (PSK-связь) и ее передатчиком (кодером), способным осуществлять эффективную и точную совместную оценку задержки и доплеровского смещения частоты.
[Фиг. 13] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображена блочная диаграмма системы, состоящей из двух альтернативных приемников, управляемых переключателями, которые выполняют эффективную и совместную оценку задержки и доплеровского смещения частоты с высокой точностью, с (или без) снабжением


-арной PSK-связью и ее приемником-синхронизатором (декодером), способным к эффективной и точной совместной оценке задержки и доплеровского смещения частоты.
[Фиг. 14] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен пример распределения значений вещественной части CCF в зависимости от задержки τ и доплеровского смещения частоты υ основного канала (МС).
[Фиг. 15] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображен пример распределения значений вещественной части CCF на пространстве задержка τ-доплеровское смещение частоты υ при добавлении искусственного канала (АС) к основному каналу (МС).
[Фиг. 16] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображено деление частотно-временной плоскости (TFP) символа с применением пространства параметров некоммутативных АС-сдвигов коразмерности 2. Разделение TFP-S с длительностью Ts и шириной полосы частот FS (т.е. разделение Габора): (S(0), S(1), S(2), S(3)) изображает вертикальную ось, перпендикулярно прикрепленную к указанной плоскости, со шкалой некоммутативных АС-сдвигов
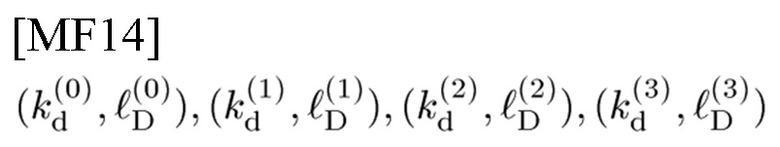
и связанными с ними 2-D PC-кодами согласно разделению

[Фиг. 17] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображено разделение TFP с применением пространства параметров некоммутативных сдвигов, где каждая из AC0-TFP, AC1-TFP, AC2-TFP и AC3-TFP сдвинута посредством соответствующего ей некоммутативного сдвига.
[Фиг. 18] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображена блочная диаграмма передающего и принимающего устройств.
[Фиг. 19] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображена блок-схема обработки сигнала в передающем и принимающем устройствах.
[Фиг. 20] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображена блочная диаграмма передающего и принимающего устройств.
[Фиг. 21] В соответствии с вариантом осуществления настоящего изобретения на этой фигуре изображена блок-схема обработки сигнала в передающем и принимающем устройствах.
Описание предпочтительного варианта осуществления
[Вариант осуществления 1] Автор настоящего изобретения со ссылками на фигуры поясняет некоторые аспекты приемопередающей системы согласно одному варианту осуществления настоящего изобретения. Автор настоящего изобретения начинает с выражения теоретических положений, стоящих за предложенным способом и примером варианта осуществления. Далее, автор настоящего изобретения приводит аспекты предложенного способа, изложенные в прилагаемой формуле изобретения.
В описании настоящего изобретения процитировано несколько источников путем ссылки на патентные источники и непатентные источники, причем указанные источники ссылкой включены в это описание настоящего изобретения.
Эти источники приведены для ссылки на технические термины и проблемы, которые необходимо решить, а также на уровень техники, относящийся к настоящему изобретению. Таким образом, упоминание этих источников не влияет на патентоспособность настоящего изобретения.
<<Краткое изложение теоретических точек зрения: Связь, в которой используется NCP, присущее операторам TFSO - Схемы передатчика, способного к совместной оценке задержки и доплеровского смещения частоты, и схемы его приемника->>
Нелегко выполнить синхронизацию систем связи с TD- и FD-разделением, которые разработаны для эффективной передачи символа данных с длительностью Ts и шириной полосы частот Fs. Остается нерешенной проблема радиолокации, касающаяся оценки задержки td и доплеровского смещения частоты fD из принятого эхосигнала. Эти сложности обусловлены фазовыми искажениями (PD)

которые генерируются операторами TFSO и являются аналогичными хорошо известным алгебраическим соотношениям для операторов положения и импульса в квантовой механике [4].
Основной целью радиолокации является обнаружение интересующего объекта, называемое обнаружением цели, и предоставление информации, касающейся местоположения, движения и других параметров объекта, называемое оценкой параметров. Таким образом, радиолокационные станции основаны на статистической проверке гипотез для обнаружения и оценки сигнала. Определение задержки и доплеровского смещения частоты является задачей оценки из PD с двумя неизвестными. Ни задержка, ни доплеровское смещение частоты не могут быть успешно обнаружены и оценены с высокой точностью из зашумленного принятого сигнала без помощи теории группы Вейля-Гейзенберга (WHG). Описание настоящего изобретения сводится к следующим 5 пунктам.
(Краткое изложение 1) Когда создается сигнал передачи, сигнал в TD и его преобразование Фурье (FT), т.е. сигнал в FD, должны быть обработаны симметрично. Более того, подтверждено, что симметричный оператор частотного и временного сдвига (TFSO), удовлетворяющий свойству частотно-временной симметричности (TFSP), является таким оператором, что адрес мультиплексированного сигнала проявляется некоммутативным свойством (NCP), присущим TFS (см. (39), (44), (51), (56)).
(Краткое изложение 2) Гауссовы импульсы с частотно-временным сдвигом, т.е. функции Габора, подвергнутые модуляции с 2-D двоичной манипуляцией с фазовым сдвигом (BPSK) с помощью TD- и FD-PC периодов N, N', являются полезными для оценок максимального правдоподобия (MLE) параметров td, fD среди N', N гипотез в FD- и TD-функционалах вероятности (LF), соответственно.
TD- и FD-PC обычно называют "2-D кодами расширенного спектра (SS)" (при этом характеристика "SS" является не совсем правильной), однако автор настоящего изобретения называет это 2-D PC для BPSK-модуляции; следует обратить внимание на то, что BPSK-модуляции присущи как преимущества, так и недостатки. Многие исследователи были плохо осведомлены о важных ролях BPSK-модуляции. Далее в настоящем описании приводятся преимущества и недостатки BPSK-модуляции, которые не были отмечены.
TD- и FD-CE (27), широкополосные сигналы, называемые "сигнатуры", содержат PD, обусловленные BPSK-модуляцией. Модуляция приводит к тому, что N СЕ TD-шаблона типа 3 (29) (или типа 1 (49)) с ее носителем [0, Ts]×[0, LΔf] (или [0, LΔt]×[0, Fs]) и N' СЕ FD-шаблона типа 4 (33) (или типа 2 (54)) с носителем [0, LΔt]×[0, Fs] (или [0, Ts]×[0, LΔf]) являются автоматически заключенными в эти TD- и FD-CE как показатели соответствия. Следовательно, эти PD играют важную роль в проверке гипотез с использованием CCR (см. (30), Предположение 4 и (35), Предположение 5).
(Краткое изложение 3) Фазовая информация сигнала не была эффективно использована в обычных MLE, однако автор настоящего изобретения определяет 4 типа TD- и FD-функций кросскорреляции (CCF) между принятым сигналом и шаблонами: СЕ TD-шаблона типа 3 (или типа 1) и СЕ FD-шаблона типа 4 (или типа 2) в качестве разновидности оптимальных приемников. Доказано, что эти CCF имеют строгие выражения в виде произведения функции неоднозначности (AF) и нескольких поворачивающих множителей, которые определены сигналом, дискретизированным по времени и частоте с выборками Δt, Δf=(LΔt)-1, при согласованном использовании BPSK-модуляции с TD- и FD-PC, и выражены как
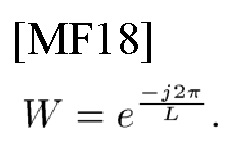
PD, обусловленные NCP, присущим TFS, могут быть оценены по степеням поворачивающих множителей, т.е. суммирование PD по адресу чипа может быть строго представлено в форме DFT и IDFT; таким образом, это выражение имеет вид произведения трех функций (см. (41) в лемме 2, (45) в лемме 4 и (52), (57)). В соответствии с вариантом осуществления настоящего изобретения может быть гарантировано эффективное вычисление посредством DSP.
(Краткое изложение 4) Используя способ реконструкции сигнала Юла [22], автор настоящего изобретения дает подтверждение алгоритма цикла фазового обновления (PUL), основанного на APT, который определен и представлен в патентном источнике, документе [1].
Во-первых, определим TD-пространство с ограничением по времени (TL) Ts (или LΔt), Е3 (или E1) и FD-пространство с ограничением по полосе частот (BL) Fs (или LΔf), Е4 (или Е2) как подпространства гильбертова пространства.
Во-вторых, согласно массивам из N' TD-CCF и N FD-CCF, определим 4 оператора проецирования (РО), осуществляющие ортогональное проецирование на Е3 (или E1) и на Е4 (или Е2), которые обозначены как Р3 (или P1) и Р4 (или Р2), соответственно.
В-третьих, в соответствии с вариантом осуществления настоящего изобретения автор настоящего изобретения определяет оператор теоремы альтернативного проецирования (АРТО) на основе теоремы альтернативного проецирования (APT), определяемый как
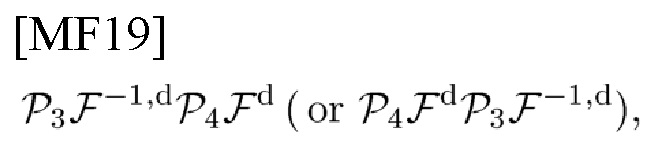
где F-1,d, Fd обозначают IDFT, DFT. В-четвертых, автор настоящего изобретения приводит выражение (59) для обновления MLE коэффициента усиления  канала как функцию оценок
канала как функцию оценок
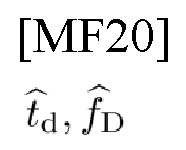
и два выражения (60), (61) для обновления MLE

Используя эти три выражения для обновления MLE, автор настоящего изобретения приходит к выводу, что (td, fD) оцениваются в пределах области сходимости оператора APT, т.е. прямоугольнике, образованном длительностью LΔt чип-импульса и шириной полосы частот LΔf чипа с адресами чипа и данных ((ρ,ρ'), р→), и доказывает, что MLE
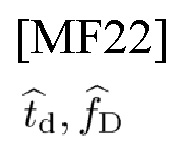
оцениваются в пределах LΔt×LΔf, и порядок вычислительной сложности составляет

вместо
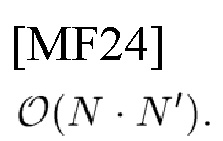
То есть этот оператор APT выделяет некоторый прямоугольник в частотно-временной плоскости (TFP) и отфильтровывает другие области. Такой оператор называется оператором фазо-пространственной (или частотно-временной) локализации [7] и, таким образом, играет важную роль в фильтрах, заменяющих традиционные фильтры с крутым срезом, применяемые обычно в DSP.
Функция Гаусса не используется в большинстве систем связи в первую очередь потому, что она не удовлетворяет условию Найквиста. Однако, показано, что некоторые благоприятные свойства гауссиан в TFP полезны для нашей задачи (td, fD)-оценки и, следовательно, гауссианы имеют решающее значение.
Алгоритм PUL представляет собой итерацию для поиска (td, fD), без ограничения диапазона (td, fD), если может быть доступен ресурс длительности PTs и ширины полосы частот P'Fs для адреса уровня данных

Соответственно, показано, что использование комбинации передатчика 2-D PC-модулированного сигнала TD-, FD-функций Гаусса и приемника, в котором PUL реализован в массивах TD-, FD-CCF, делает возможным обеспечить систему связи, способную к высокоточной и высокоскоростной оценке параметров. Другими словами, использование вышеописанной конфигурации представляет сдвиг парадигмы в системах связи, использующих NCP.
(Краткое изложение 5) Автор настоящего изобретения представляет систему кодирования-декодирования для PSK-связи с высоким значением

совместно с установлением синхронизации.
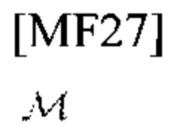
-PSK-связь доступна для автомобильной радиолокационной станции, способной как к оцениванию задержки и доплеровского смещения частоты, так и к обмену данными с другим объектом. Непросто передать

прежде всего, потому, что идентификация фазы

сложно выполнима среди фазовых ошибок и фазового шума; но является важной модуляцией для эффективного использования радиоресурсов (число

передается за раз). Однако известно, что реализация этой модуляции/демодуляции затруднена.
Для решения этой задачи, как показано в нижней части (промежуточный блок между переключателями 1-1 и 1-2) на фиг. 12, передатчик
1) разлагает целое число ("информация") k, представленное как

2) делит пространство параметров задержки и доплеровского смещения частоты, называемое целевым пространством, поровну на

подпространства параметров и приписывает 2-D PC (TD- и FD-PC) каждому подпространству, где

Кроме того, передатчик 1) выполняет 2-D BPSK-модуляцию чип-импульса с помощью

-го 2-D PC; 2) объединяет его для получения
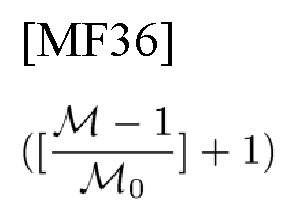
-кодово-мультиплексированного сигнала;
3) осуществляет частотно-временной сдвиг полученного в результате сигнала (называемого сигнатурой) приблизительно вокруг центра j-го подпространства параметров, т.е. посредством временной задержки

и посредством частотной задержки

где

называется сдвигом j-го искусственного канала (АС);
4) выполняет M0-PSK-модуляцию сигнатуры с частотно-временным сдвигом с помощью j'-го

и передает модулированный сигнал. Впоследствии

-смещенная сигнатура снова искажается при прохождении через основной канал (МС) со сдвигами
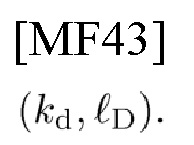
Автор настоящего изобретения разрабатывает CCF между оцененным и принятым шаблоном и принятой СЕ следующим образом. Как показано в центральном блоке, соединенном с переключателем 2-1 на фиг. 13, приемник
1') разлагает оценку k

как

2') выполняет 2-D BPSK-модуляцию чип-импульса с помощью

3') осуществляет его частотно-временной сдвиг посредством

4') и выполняет M0-PSK-демодуляцию полученного в результате сигнала посредством

Полученный в результате сигнал представляет собой оцененный и принятый шаблон.
Максимизация вещественных частей N' TD-CCF и N FD-CCF с использованием соответствующих им LF, в формах массива, проводится в терминах кардинальных чисел CCF, как функция адреса уровня чипа (ρ',ρ) и адреса уровня данных
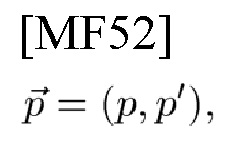
и пары оцененных декодирующих целых чисел из k:
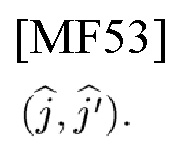
Приемник 1) выбирает

2-D PC; 2) исключает фазу данных dp→ с адресом

посредством PSK-сигнала
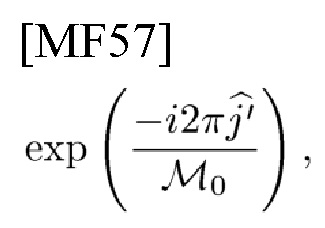
3) максимизирует вещественные части 2 CCF на основании алгоритма PUL, как показано в нижнем блоке, соединенном с переключателем 2-2, на фиг. 13, в терминах

и
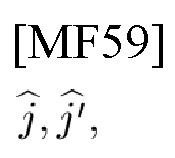
и 4) получает MLE k

Это реализуется посредством создания кодирующе-декодирующей системы на основе PSK-модуляции с низким

и объединения системы вместе с использованием

АС с некоммутативными частотно-временными сдвигами. Это обеспечивает систему связи с PSK-модуляцией с высоким

А именно, эта система может быть использована также для синхронизатора (или радиолокационной станции) для оценивания параметров, в сочетании с декодером k, из выходного сигнала одного выбранного АС согласно k из
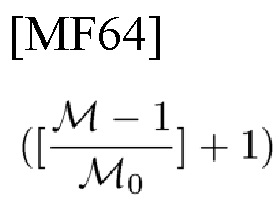
АС с некоммутативными сдвигами, каждый из которых соединен с МС со сдвигами

Таким образом, мультиплексированная система, использующая некоммутативные сдвиги АС, может представлять собой сдвиг парадигм. Следует отметить, что вычислительная сложность
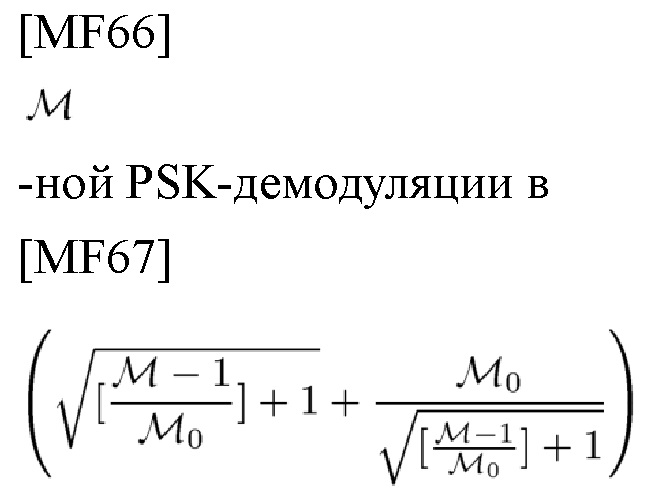
раз больше, чем у синхронизатора (или радиолокационной станции), O(N+N'):
<<Подробное описание теоретических вопросов, касающихся настоящего документа, и примеров варианта осуществления систем связи>>
В соответствии с вариантом осуществления настоящего изобретения автор настоящего изобретения описывает подробности теоретических вопросов, касающихся систем связи, и конкретные примеры варианта осуществления систем связи.
<1. Предпосылки создания изобретения>
Одной из важных задач, которые надо решить в области связи, является разработка беспроводной системы связи, которая может вместить больше трафика в пределах ограниченного объема радиочастотного спектра [1]. Мультиплексирование с ортогональным частотным разделением каналов (OFDM) являлось основной технологией в качестве мультиплексированной системы с TD- и FD-разделением для передачи данных времени Ts и ширины полосы частот Fs (см. фиг. 1); но ей присущи недостатки в том, что вследствие временных и частотных смещений нарушается ортогональность.
На фиг. 1 изображено три типа разделений частотно-временной плоскости (TFP): (а) показано временное разделение, (b) частотное разделение и (с) разделение Габора [1]. Жирными линиями в (а) показаны разделения данных длительностью Т; тонкими линиями показаны подразделения по фазовому коду (PC) во временной области (TD); точечными линиями в (b) показаны разделения данных с шириной полосы частот F; штриховыми линиями показаны подразделения по PC в частотной области (FD).
"Синхронизация" является первой процедурой для связи по каналу с td, fD. Однако, за фазовыми искажениями (PD), обусловленными оператором частотного и временного сдвига (TFSO), необходимым для мультиплексирования с разделением по TD и FD

следует PD канала
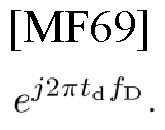
Таким образом, установить синхронизацию нелегко. Более того, отсутствует эффективное решение задачи, состоящей в оценке td, fD из эхосигнала радиолокационных станций.
Автор настоящего изобретения, во-первых, модулирует TD-сигнал и его FT, т.е. FD-сигнал, удовлетворяющий свойству частотно-временной симметричности (TFSP), в терминах td, fD (см. фиг. 2), посредством TD- и FD-PC для создания TD- и FD-сигнатур.
На фиг. 2 изображено представление NCP, присущего TFS (см. [0014]), изображено представление некоммутативного свойства (NCP) временных и частотных сдвигов (TFS): NCP проявляется в выражении, представляющем произведение операторов сдвига  его левая часть (LHS) соответствует треугольнику на фигуре; правая часть (RHS) соответствует квадрату; появляется фазовое искажение (PD)
его левая часть (LHS) соответствует треугольнику на фигуре; правая часть (RHS) соответствует квадрату; появляется фазовое искажение (PD)  круг на фигуре изображает симметричный оператор частотно-временного сдвига (TFSO) [26]
круг на фигуре изображает симметричный оператор частотно-временного сдвига (TFSO) [26]
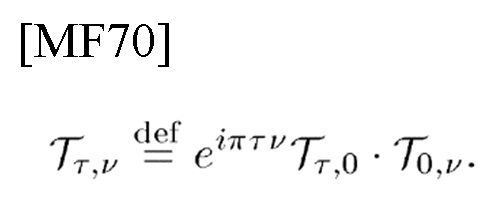
Во-вторых, автор настоящего изобретения определяет массивы из TD- и FD-CCF (см. фиг. 3b) в виде AF [15] как оптимальные приемники для обнаружения шаблонов на основании того факта, что PD заключены в сигнатуры как шаблоны.
Как показано в [27]-[32], патентных документах [1]-[6], предложенный способ оценки, во-первых, определяет td, fD и кардинальные числа TD- и FD-CCF, максимизируя вещественные части TD- и FD-CCF, без предварительной информации о td, fD, и, во-вторых, обновляет оценки td, fD в качестве альтернативы. Кроме того, показано, что этот способ становится хорошим решением для проблемы радиолокации. На фиг. 3а представлена функция Габора, расположенная на TFP, и связанные с ней вопросы: На фиг. 3а0 представлены гауссов сигнал 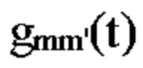 чипа, расположенный на TFP, и его преобразование Фурье (FT)
чипа, расположенный на TFP, и его преобразование Фурье (FT)  На фиг. 3а1 представлены вещественная и мнимая части TD-шаблона, комбинация
На фиг. 3а1 представлены вещественная и мнимая части TD-шаблона, комбинация  взвешенного посредством FD PC
взвешенного посредством FD PC  На фиг. 3а2 представлены вещественная и мнимая части FD-шаблона, комбинация
На фиг. 3а2 представлены вещественная и мнимая части FD-шаблона, комбинация 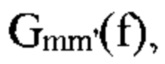 взвешенного посредством TD PC Xm; На фиг. 3b представлены функции кросскорреляции (CCF) NN', суммы по столбцам N' множества значений TD-CCF, и суммы по строкам N значений множества FD-CCF; На фиг. 3с представлены альтернативная проекция, ортогонально проецирующаяся на временную область с ограничением по времени (TL-TD) и на частотную область с ограничением по полосе частот (BL-FD), на основании теоремы альтернативного проецирования (APT), оцененные
взвешенного посредством TD PC Xm; На фиг. 3b представлены функции кросскорреляции (CCF) NN', суммы по столбцам N' множества значений TD-CCF, и суммы по строкам N значений множества FD-CCF; На фиг. 3с представлены альтернативная проекция, ортогонально проецирующаяся на временную область с ограничением по времени (TL-TD) и на частотную область с ограничением по полосе частот (BL-FD), на основании теоремы альтернативного проецирования (APT), оцененные
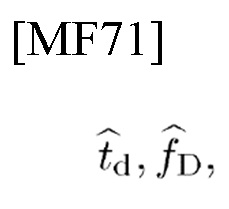
и сходящиеся значения td, fD.
Задача оценки td, fD из эхосигнала эквивалентна определению двух неизвестных из PD, обусловленных NCP, присущим TFS. Следовательно, это относится к категории обнаружения и оценки сигналов на основе теории группы Вейля-Гейзенберга (WHG). Однако, если не принимать во внимание документ Аусландера (Auslander) и Толимиери (Tolimieri) [17], многие исследователи в области радиолокации еще не получили эффективные способы оценки с высокой точностью, потому что в их способах оценки не учитывалось NCP, присущее TFS. Напротив, настоящее изобретение основано на убеждении автора настоящего изобретения в том, что NCP, присущее TFS, служит только для повышения эффективности систем связи, включая радиолокационные станции. Вейвлет-преобразование [8] с использованием функции смещения по времени и частоте, т.е. элементарных функций Габора

рассматривает представления в виде

и прежде всего касается коэффициентов 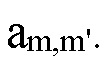 В беспроводной связи, стандарт 5G, стандарты, потенциально приходящие на смену 5G: OFDM/OQAM, стандарт с несколькими несущими в наборе фильтров (FBMC) и GFDM [9, 10, 12], проявляют интерес к разработке мультиплексированного сигнала f(t) с информацией
В беспроводной связи, стандарт 5G, стандарты, потенциально приходящие на смену 5G: OFDM/OQAM, стандарт с несколькими несущими в наборе фильтров (FBMC) и GFDM [9, 10, 12], проявляют интерес к разработке мультиплексированного сигнала f(t) с информацией  подлежащей передаче, и элементарным импульсом g(t). А именно, основным вопросом является форма g(t), которая сводит к нулю межсимвольные помехи (ISI) и межканальные помехи (ICI), и ортогональность
подлежащей передаче, и элементарным импульсом g(t). А именно, основным вопросом является форма g(t), которая сводит к нулю межсимвольные помехи (ISI) и межканальные помехи (ICI), и ортогональность 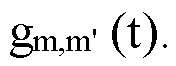
В беспроводной связи необходима синхронизация, устойчивая к временным и частотным смещениям. Однако были предприняты несколько попыток оценить td, fD. Кроме того, большинство инженеров в области связи считает, что PD, обусловленное TFS mτ0, m'ν0,

может быть несущественным. Тем не менее, теоретико-групповое свойство WHG говорит нам, что за PD канала

следует PD, обусловленное TFS,

и PD, обусловленное технологией с несколькими несущими,

возникает одновременно. Механизм возникновения фазовых ошибок является сложным.
Нужно начать с решения следующих трех задач, присущих проблеме радиолокации. Следует отметить, что линейная частотно модулированная (FM) непрерывная волна с сигналом с линейной частотной модуляцией, сжатый импульс, модулированный кратковременный импульс и его версия с несколькими несущими используются в качестве сигнала передачи в обычных радиолокационных станциях [19].
(Задача 1) Проблема радиолокации отношении в дальности и скорости является по существу задачей с двумя неизвестными td, fD; большинство приемников основано на поиске пиков величины комплексной функции неоднозначности (AF) двух переменных, называемых поверхностью неоднозначности, или использовании AF-характеристики сигнала с линейной частотной модуляцией; естественно полагать, что при решении проблемы, связанной с данной функцией двух неизвестных, способ совместного решения с (независимыми) некоторыми другими функциями неизвестных может быть лучшим способом решения.
(Задача 2) Проблеме радиолокации присуще негативное влияние PD

обусловленного NCP, присущего TFS. Подобная этому ситуация, обусловленная NCP, присущим операторам положения и импульса, наблюдается в квантовой механике. Последовательность импульсов с линейной частотной модуляцией с интервалом времени Тр и частотным сдвигом Fp генерирует PD
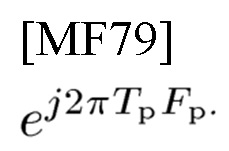
Кроме того, система связи, мультиплексированная посредством неперекрытого наложения сигнала на TFP для передачи символов данных с длительностью Ts и шириной полосы частот Fs через канал с td, fD, вызывает PD

за которым следует PD
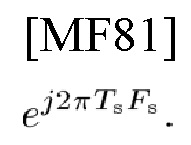
(Задача 3) При подробном рассмотрении задачи 2 не просто понять механизм возникновения PD. То есть, в системах связи и радиолокационных станциях два оператора сдвига обычно определены как
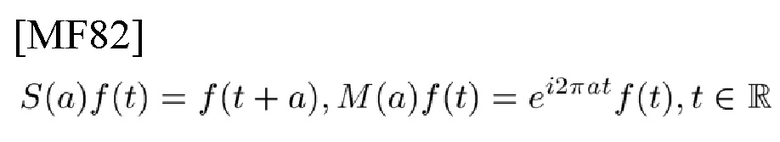
и предоставляют NCP, представленное как  т.е. NCP проявляется как
т.е. NCP проявляется как 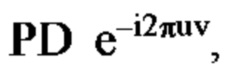 другими словами, фазовая составляющая произведения двух сдвигов исходит из того факта, что u, v потенцированы. Это наблюдение совпадает с математической основой для введения группы Гейзенберга в квантовую механику, которая предложена Вейлем. Следовательно, такое PD является важной подсказкой для решения проблемы радиолокации или синхронизации и является чисто символическим. Экспоненциальная функция, т.е.
другими словами, фазовая составляющая произведения двух сдвигов исходит из того факта, что u, v потенцированы. Это наблюдение совпадает с математической основой для введения группы Гейзенберга в квантовую механику, которая предложена Вейлем. Следовательно, такое PD является важной подсказкой для решения проблемы радиолокации или синхронизации и является чисто символическим. Экспоненциальная функция, т.е. 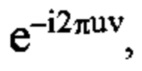 должна быть тщательно рассмотрена. Это приводит к симметричному TFSO (см. фиг. 2 и (4), (24)), что является основным вопросом в настоящем изобретении.
должна быть тщательно рассмотрена. Это приводит к симметричному TFSO (см. фиг. 2 и (4), (24)), что является основным вопросом в настоящем изобретении.
<2. Симметричные операторы частотно-временного сдвига>
Пусть s(t) обозначает вещественнозначный импульс, и пусть σ(t) обозначает преобразование Гильберта, применяемое к s(t). Затем получают комплексный сигнал, называемый аналитическим сигналом, определяемый как ψ(t)=s(t)+iσ(t) [1]. Типичный эхо сигнал может быть представлен в виде

где ψ(t) представляет собой комплексную огибающую (СЕ) импульса,

обозначают его амплитуду, время прибытия, несущую частоту, фазу его несущей и изменение в его несущей частоте, называемое доплеровским сдвигом опорной несущей Ωr=2πfr. Для краткости предположим, что на мгновение Ωr=0. Пусть

обозначает преобразование Фурье (FT) и
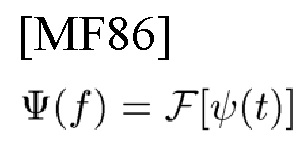
обозначает FT, применяемое к ψ(t), тогда FT, применяемое к re(t; td, fD), будет иметь вид
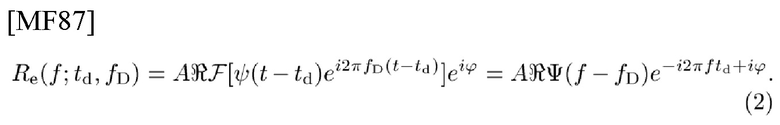
Пара re(t; td, fD) и Re(f; td, fD) не является симметричной в td и fD, так как произведение неизвестных td и fD фигурирует только в TD-функции (1).
Но она может быть представлена в незначительно измененном виде [24, 26]

Если TD-функция x(t) и ее FD-функция

являются симметричными в отношении td и fD, то это свойство называется свойством частотно-временной симметричности (TFSP) (см. фиг. 2). Таким образом, можно определить симметричные операторы частотно-временного сдвига (TFSO), удовлетворяющие TFSP, заданные как

и получить тривиальную идентичность между двумя операторами
(Свойство 1 симметричных TFSO):

Обычно используются оператор временного сдвига S(-td)x(t)=x(t-td) и оператор модуляции
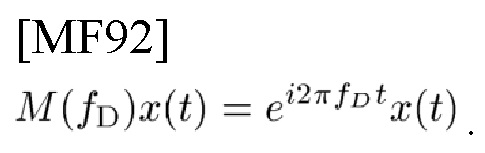
Напротив, сдвиги

в TD-сигнале x(t) и

в его FD-сигнале X(f) в (4), называемые "половинные сдвиги", представляются некоторыми незначительными модификациями к обычным частотно-временным представлениям сигнала:

Но такие половинные сдвиги представляют собой намерение получить эффективные представления радиолокационного сигнала и принятого сигнала, чтобы их фазовые коэффициенты полностью отслеживались как в TD, так и в FD, как показано ниже.
Предположение 1: TFSO (4) идентичен каноническим коммутативным соотношениям фон Неймана (обычно сокращенно CCR) в квантовой механике [4, 6], которые называются теоремой Стоун-фон Неймана [5, 4, 25] и определяются как двухпараметрическое семейство унитарных операторов S(a, b)=е-1/2 iabU(a)V(b) с его теоретико-групповым свойством, где U(a), V(b) определены ниже. Дальше Tτ,ν и  называются TFSO фон Неймана.
называются TFSO фон Неймана.
Коммутационное соотношение Гейзенберга, называемое принципом неопределенности Гейзенберга, задается как [4, 5]

Предположение 2: Предположим, что Q и Р могут быть потенцированы для однопараметрических унитарных групп U(a)=exp(iaQ), V(b)=exp(ibP) соответственно (a, b - вещественные) и сопоставим Q, Р с TFSO Тτ,0, T0,ν, соответственно, тогда

Таким образом, классический предел, т.е. предел

[20] соответствует
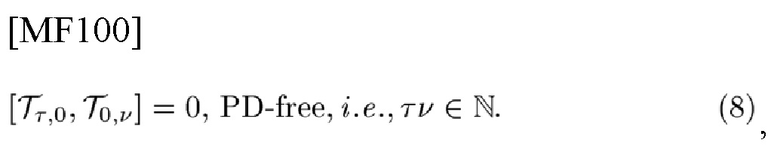
где
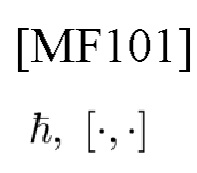
обозначает приведенную постоянную Планка
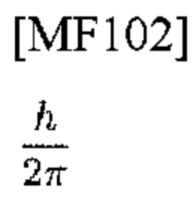
и коммутатор квантовой механики.
Сочетание TFSO

дает
(Свойство 2 симметричных TFSO):

Уравнение (7) является примером первого уравнения в уравнении (9).
Тот факт, что произведение неизвестных td и fD появляется симметрично в показателе степени PD TD- и FD-функций из их свойства симметричности, является наиболее важным свойством симметричных TFSO. Также в показателе степени PD присутствовали адреса уровня чипа и уровня данных мультиплексированного сигнала. Произведение таких показателей степени позволяет легко оценить параметры, как описано ниже. Например, в беспроводной связи [9, 10] сигнал мультиплексирования с ортогональным частотным разделением каналов (OFDM)
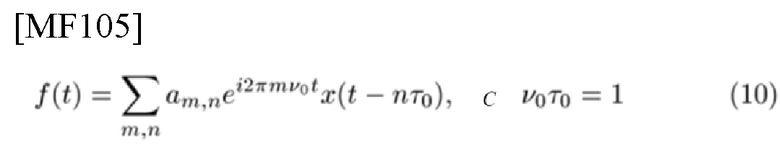
является основным предметом, где коэффициенты am,n принимают комплексные значения, представляющие закодированные передаваемые данные, a x(t) является функцией-прототипом. OFDM-сигнал перезаписывается как
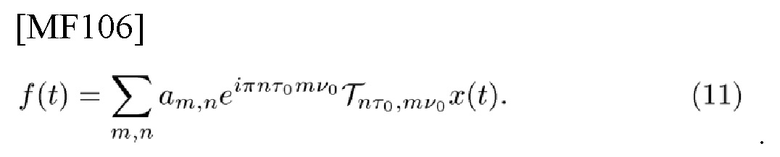
Таким образом, 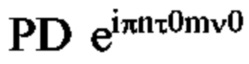 не изменяет am,n, за исключением его знака, поскольку выполняется условие τ0ν0=1 (см. (8)). Но если есть смещения, такие как τ'=τ0+ετ и ν'=ν0+εν, то неизбежно возникает PD
не изменяет am,n, за исключением его знака, поскольку выполняется условие τ0ν0=1 (см. (8)). Но если есть смещения, такие как τ'=τ0+ετ и ν'=ν0+εν, то неизбежно возникает PD

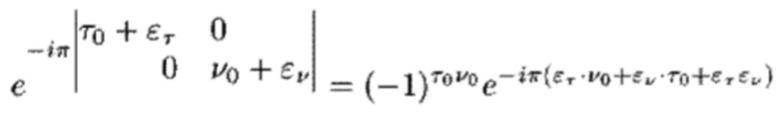
с последующим PD

через канал с двойной дисперсией с td и fD. То есть мы должны столкнуться с искаженным по фазе сигналом
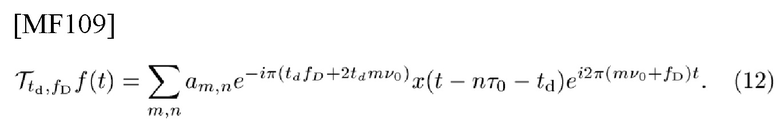
Обычное неперекрывающееся наложение сигнала в TFP [1, 2, 9, 10, 12], определенное как в (10), вызывает накопление PD

из-за его теоретико-группового свойства типа (12). Следовательно, PD напрямую ослабляют выходной сигнал приемника и приводят к серьезному ухудшению "синхронизации", необходимой в цифровых системах связи [3]. Напротив, основным вопросом является разработка функции-прототипа x(t) для уменьшения межсимвольных помех (ISI) и межканальных помех (ICI). Такое простое наблюдение обеспечивает отправную точку для этого исследования.
<3. Функционалы правдоподобия и функции кросскорреляции>
Для начала нам необходимо изучить краткий обзор статистического подхода Вудворда (Woodward) [15] к анализу и проектированию оптимальных радиолокационных систем, а также комплексное исследование Хельстрома (Helstrom) [18] по теории и практике обнаружения и оценки сигналов.
Важным наблюдением является то, что в этих подходах использовался только абелев гармонический анализ, как в статье Аусландера (Auslander) и Толимиери (Tolimieri) об исследовании Уилкокса (Wilcox) [16].
Однако основы теории радиолокации лежат в следующей теории обнаружения сигналов и оценки параметров.
<3.1 Обнаружение сигналов>
Когда в приемнике появляется радиолокационный сигнал, его обнаружение выполняется неопределенным образом из-за одновременного присутствия шума.
Рассмотрим простейшую проблему обнаружения сигнала, которая заключается в определении того, поступил ли сигнал s(t) заданной формы в определенное время среди гауссова шума n(t). Входной сигнал w(t) приемника измеряется в течение интервала наблюдения
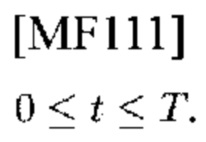
На основании этого вводного сигнала наблюдатель должен выбрать одну из двух гипотез, Н0, "сигнал отсутствует", т.е. w(t)=n(t), и H1, "сигнал присутствует", т.е. w(t)=s(t)+n(t). Если wk=w(tk) измеряется в момент времени t=tk в течение интервала наблюдения, n выборок wk являются случайными переменными, имеющими совместную функцию плотности вероятности (p.d.f.) pi(w) по гипотезам Hi, i=0, 1, и решение наблюдателя лучше всего сделать на основе отношения правдоподобия 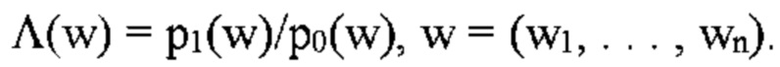
Для фиксированного уровня 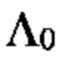 решений наблюдатель выбирает гипотезу Н0, если
решений наблюдатель выбирает гипотезу Н0, если  H1, если
H1, если 
Радиолокационный сигнал может быть просто записан как [15, 18]

где ψ(t) представляет собой его СЕ, а Ω=2πfc представляет собой несущую частоту. Если спектр сигнала s(t)

демонстрирует два узких пика, один около частоты fc, и другой около -fc, и если значения ширины полос частот намного меньше, чем Ω, сигнал называется узкополосным (NB) или квазигармоническим.
Предположим, что входной сигнал для приемника

является NB, и СЕ

может быть измерена смесителем.
При наличии стационарного NB белого гауссова шума с функцией автоковариации
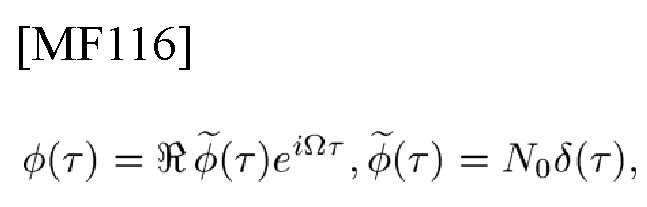
детектор оптимума NB сигнала
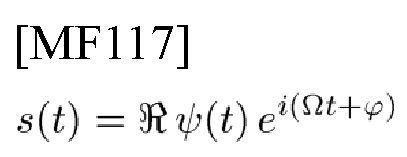
имеет логарифм своего LF (LLF) [18, стр. 106]

в котором N0 - односторонняя спектральная плотность белого шума, g, генерируемого посредством пропускания входного сигнала ψw(t) через фильтр [19], который согласован с сигналом ψ(t), который должен быть обнаружен, и d2 называется статистическим показателем и отношением сигнал-шум (SNR) 
<3.2 Оценка параметров сигнала>
Принцип проверки гипотез может быть применен к выбору из нескольких гипотез следующим образом. Предположим, что передатчик отправляет сигнал, используя один из М сигналов. Приемник должен определить, какой из этих М сигналов присутствует в течение интервала наблюдения (0, Т). В частности, по гипотезе Hk, "сигнал sk(t) был оправлен", входной сигнал приемника

где ψk(t) представляет собой NB СЕ, fk представляет собой несущую,

обозначает фазу sk(t), и n(t) представляет собой случайный шум.
Приемник выбирает одну из М гипотез на основе измерений своего входного сигнала w(t). Предположим, что приемник делает n измерений w1, …, wn своего входного сигнала w(t). Пусть pk(w) будет совместной функцией плотности вероятности (PDF) этих данных по гипотезе Hk и пусть ζk будет априорной вероятностью этой гипотезы. Отношение правдоподобия для обнаружения k-го сигнала в присутствии n(t) определяется как 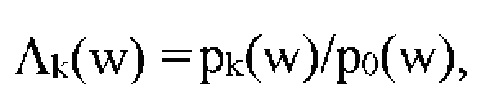 где p0(w) обозначает PDF по фиктивной гипотезе. Для простоты, предположим, что ζk=М-1, при ортогональности сигналов sk(t)
где p0(w) обозначает PDF по фиктивной гипотезе. Для простоты, предположим, что ζk=М-1, при ортогональности сигналов sk(t)

(Ei представляет собой энергию i-го сигнала), затем приемник просто определяет Hk, если  для всех k≠j.
для всех k≠j.
Обозначим неизвестные параметры сигнала как θ1, …, θm и представим их вектором θ=(θ1, …, θm) в m-мерном пространстве параметров, обозначенном как Θ.
Радиолокационный эхосигнал может быть представлен в виде

где  обозначает коэффициент ослабления, А обозначает его амплитуду, td обозначает его время прибытия, fc обозначает его несущую частоту, κ обозначает фазу его несущей, и fD обозначает доплеровский сдвиг его опорной несущей fr. Неизвестные параметры в эхосигнале (15) представлены как θ=(А, κ, td, fD). Если
обозначает коэффициент ослабления, А обозначает его амплитуду, td обозначает его время прибытия, fc обозначает его несущую частоту, κ обозначает фазу его несущей, и fD обозначает доплеровский сдвиг его опорной несущей fr. Неизвестные параметры в эхосигнале (15) представлены как θ=(А, κ, td, fD). Если

и шум является белым с односторонней спектральной плотностью N0, то LLF [18, стр. 251] является следующим
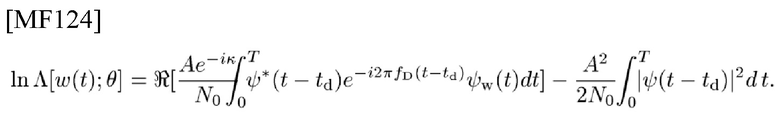
Используем замену переменных, такую как

Здесь
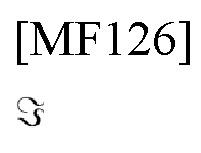
обозначает мнимую часть комплексного числа, следующего за ней. Таким образом, можно получить оценку максимального правдоподобия (MLE) А, κ, содержащего θ'=(td, fD), представленную как [18, стр. 251].

MLE остальных параметров θ' являются теми, которые максимизируют [18, стр. 251]
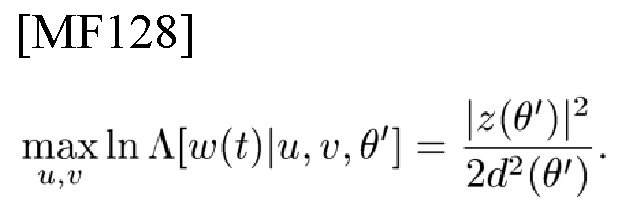
Следовательно, можно сосредоточить усилия на оценке θ'. Для одного из набора значений доплеровского сдвига с малым шагом

MLE θ' может быть получена путем создания набора параллельных фильтров, каждый из которых соответствует сигналу вида

где WD представляет собой максимальный диапазон ожидаемого доплеровского сдвига. Однако, непросто проверить статистику, создав набор параллельных NB-фильтров. Этот факт приводит к разложению задачи с 2 неизвестными параметрами на 2 задачи с одним неизвестным параметром.
Перепишем (15) и его FT в виде
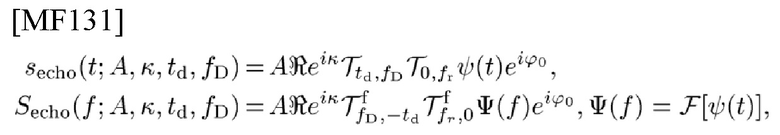
где
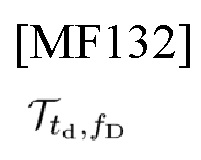
представляет собой TFSO фон Неймана с td и fD, где
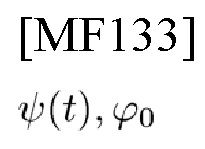
обозначает СЕ, которая должна быть создана, и ее фазу (ее детали здесь опущены), и

представляет собой сигнал полосы пропускания, сдвинутый от СЕ базовой полосы частот на опорную частоту
fr.
Используя технологии импульсного кодирования с TD-PC с периодом N и FD-PC с периодом N', можно уточнить точное местоположение (td, fD) в 2-мерной сетке

в TFP, где Тс=Ts/N, Fc=Fs/N', Ts и Fs обозначают интервал между чип-импульсами, интервал между (под)несущими чипа, длительность сигнала (или данных) и интервал между несущими, разделить пространство Θ' параметров (td, fD) на большое количество NN' мелких прямоугольных областей 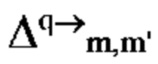 с адресом данных
с адресом данных

определенных как
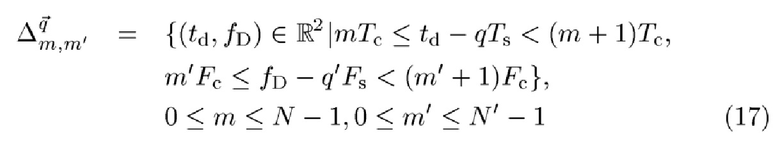
и обозначить с помощью  предположение "Набор θ' параметров лежит в области
предположение "Набор θ' параметров лежит в области
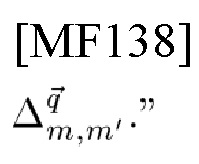
Однако, NN' таких гипотез  могут быть разложены на N' гипотез для оценки fD в TD-сигнале Secho(t; А, κ, td, fD) и N гипотез для оценки td в FD-сигнале Secho(f; А, κ, td, fD), как рассмотрено ниже.
могут быть разложены на N' гипотез для оценки fD в TD-сигнале Secho(t; А, κ, td, fD) и N гипотез для оценки td в FD-сигнале Secho(f; А, κ, td, fD), как рассмотрено ниже.
При условии, что сигналы sk(t; θ') являются ортогональными, в гипотезе Hk, соответствующей (14), для СЕ ψk(t) и фазы

рассмотрим k-й NB эхосигнал
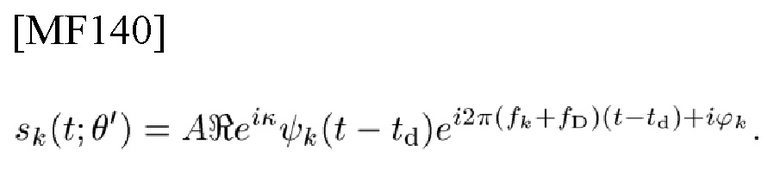
Если шум является белым и гауссовым с односторонней спектральной плотностью N0, то его TD-LLF [18, стр. 129, стр. 251] является следующим

Пусть k=k0 будет целым числом, удовлетворяющим
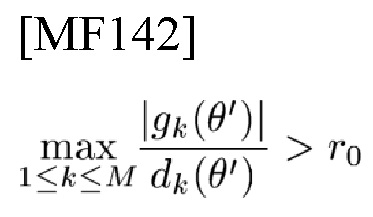
для данного уровня r0 решений; тогда приемник определяет, что прибыл k-й сигнал; если все статистические значения gk лежат ниже r0, приемник определяет, что сигнал не был передан. Это называется ML-приемником. Таким образом, построение ортогональных сигналов sk(t) имеет решающее значение. Уравнение (18) предполагает два способа максимизации |gk(θ')|: один представляет собой максимизацию интегрируемого, а другой представляет собой исключение фазовых коэффициентов eiκ несущей и

сигнала sk(t). Однако фазовый коэффициент, как правило, поглощается в

вследствие переопределения; более того, просто оценивается не gk(θ'), a |gk(θ')|. Эти стратегии уничтожают информацию о фазе. Вудворд (Woodward) [15] использовал двумерную CCF, называемую функцией неоднозначности (AF), которая ранее была определена Вилле (Ville) [14] и которая играет центральную роль в построении радиолокационного сигнала. Это представлено определением

Некоммутативные и теоретико-групповые свойства сигналов, сдвинутых по времени и частоте на основе WHG, проявляются в циссоидальных коэффициентах в (9).
Более того, можно получить:
Предположение 3 [Свойство 3 симметричных TFSO]: Для TD-сигнала z(t) и его FT

внутренние произведения (IP) сигналов с частотно-временным сдвигом в TD и FD могут быть выражены как

где

обозначает IP r(t) и s(t) в TD, и IP в FD

для

и
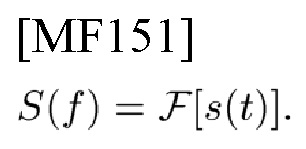
Уравнение (19) показывает, что: i) обе вещественные части IP в TD и FD максимизируются при t2=t1 и f2=f1, для которых достигается максимум AF; ii) если левая и правая составляющие IP рассматриваются как входной сигнал ψw(t) и сигнал ψ(t), который необходимо обнаружить, соответственно статистике g в LLF (13), то ψ(t) может исключить PD входного сигнала для улучшения статистики g. В предположении 3 подчеркивается важность "фазы" модулированного сигнала, подобной "фазорам", используемым в анализе переменных токов и напряжений в электротехнике [18, xv, стр. 91], и говорится о том, что в фазовой составляющей всегда присутствуют две величины td и fD. Это важный шаг к (td, fD)-оценкам в TD и FD, основанным на теории WHG, в отличие от традиционных способов с использованием согласованных фильтров [18], осуществляемых только в TD. Если можно спроектировать сигнал так, чтобы его фазовые составляющие были наделены легкой прослеживаемостью, можно использовать оба PD ψw(t), ψ(t) из статистики в TD- и FD-LLF.
Габор (Gabor) [1] подчеркнул важность анализа в TFP и полезность гауссовой волны  для достижения нижней границы отношения неопределенности времени и частоты.
для достижения нижней границы отношения неопределенности времени и частоты.
Он предоставил частотно-временное представление функции f:
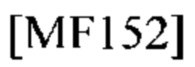

Хорошо известно [9, стр. 985], что набор функций Гаусса gm,n(t) образует базис L2(R), обладающий хорошими свойствами в отношении локализации времени и частоты, но этот базис не ортонормирован, а набор функций даже не является кадром [7]. См. источники [7, 9] для обзора представления двойных рядов (20). Большинство инженеров в области связи не используют функцию Гаусса в первую очередь потому, что она не удовлетворяет условию Найквиста. Однако, в нашей задаче (td, fD)-оценки несколько благоприятных свойств гауссианов в TFP играют важную роль.
<4. Сигнатурные сигналы и шаблоны в TD и FD>
Технологии TD-PC, т.е. технологии расширения спектра (SS) [3], могут обеспечить одновременное использование широкой полосы частот с помощью технологий множественного доступа с кодовым разделением (CDMA), в которых сигнал s(t), подлежащий передаче, модулируется независимым импульсным кодом c(t), так что его ширина полосы частот намного больше, чем ширина полосы частот информативного сигнала m(t), например, s(t)=m(t)c(t), и каждому пользователю назначается импульсный код, такой что сигналы являются ортогональными.
Для того чтобы СЕ
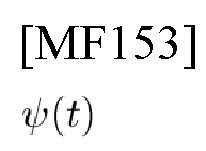
удовлетворяла свойству частотно-временной симметричности (TFSP), ее FT Ψ(f) также должно быть кодировано по фазе.
Вместо непрерывных сигналов в

рассмотрим дискретные по времени сигналы в
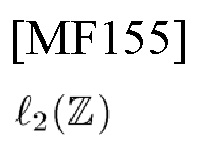
и предположим, что TD-сигнал s(t) дискретизирован с интервалом дискретизации Δt, в то время как дискретный по частоте сигнал получен с помощью L-точечного дискретного преобразования Фурье (DFT). Следовательно, частотный интервал между двумя соседними частотными бинами в FD составляет Δf=1/(LΔt).
Пусть
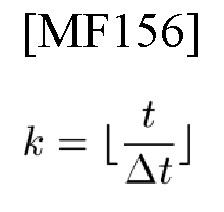
(усечение дроби

и
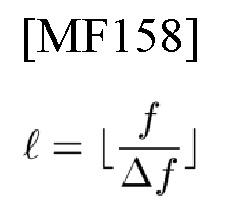
(усечение дроби

представляют собой дискретные переменные времени t и частоты f. Для ортогональности чип-импульса предположим

и пусть
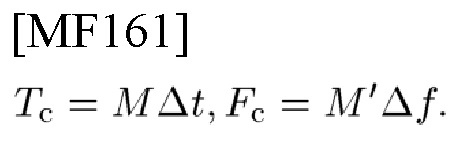
Таким образом, можно определить L-точечный поворачивающий множитель
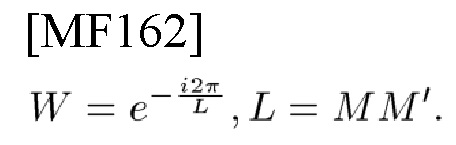
Определим следующие 7 разных типов дискретных по времени и дискретных по частоте сигналов:

где  представляет собой TD-PC периода N,
представляет собой TD-PC периода N,
 представляет собой TD-PC периода N', и χ=(Х,Х').
представляет собой TD-PC периода N', и χ=(Х,Х').
Для непрерывного чип-импульса g(t), имеющего носитель [-LΔt/2, LΔt/2], т.е. длительность LΔt, можно получить его обычный дискретный по времени LΔt-ограниченный по времени (TL) чип-импульс g[k] с задержкой [10] (D/2)Δt, D=L-1, L=(ΔtΔf)-1=MM'

и определить его дискретный по частоте LΔf-ограниченный по полосе частот (BL) чип-импульс  имеющий носитель [-LΔf/2, LΔf/2], т.е. ширину полосы частот LΔf, посредством DFT g[k]
имеющий носитель [-LΔf/2, LΔf/2], т.е. ширину полосы частот LΔf, посредством DFT g[k]

Теперь введем дискретную по времени TD-сигнатуру v[k;χ] и FD-сигнатуру 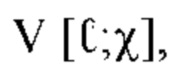 определенные как
определенные как
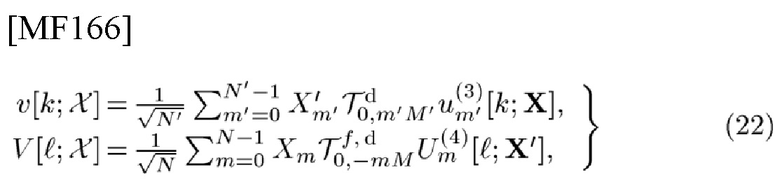
в терминах TD-шаблона типа 3
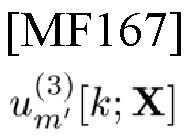
и FD-шаблона типа 4

соответственно определенные как

где
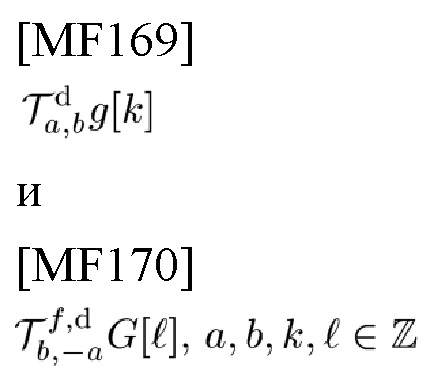
обозначают дискретные аналоги TFSO фон Неймана в TD и FD в (4), соответственно определенные как

TD-сигнатура v[k;χ] содержит N' TD-шаблонов типа 3

тогда как FD-сигнатура

содержит N FD-шаблонов типа 4

так что CCF между такой сигнатурой и заключенным в нее шаблоном может иметь большое значение по причине фазового кодирования. Следует отметить, что TD-шаблон

имеет прямоугольный носитель NMΔt×LΔf в TFP, тогда как FD-шаблон

имеет носитель LΔt×N'M'Δf. Подстановка сочетаний TFSO

(соотв.

) в (22) показывает, что TD-сигнатура и FD-сигнатура

совершенно симметричны. Предположим, что радиолокационный TD-сигнал s[k; χ] со своей СЕ
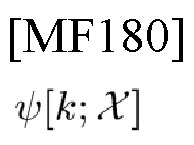
и несущей

и своим FT, FD-сигналом  имеют следующий вид
имеют следующий вид
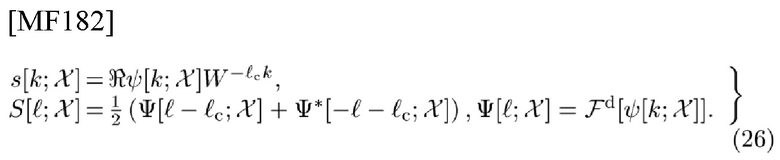
Записав СЕ и его DFT в виде
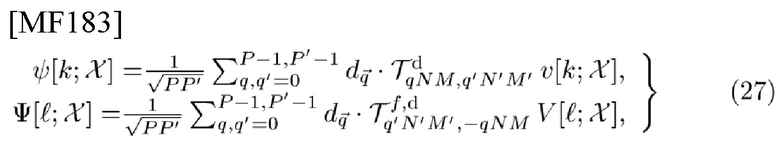
можно создать радиолокационные TD- и FD-сигналы
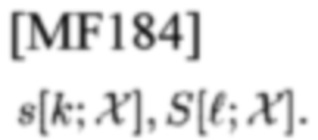
Это двумерный ряд РР' неперекрытых сигнатур

(соотв.

с длительностью Ts=NMΔt и интервалом между несущими Fs=N'M'Δf, где

представляет собой символ данных на сетке
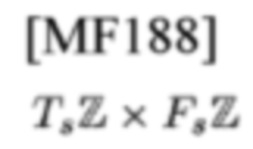
TFP, с адресом
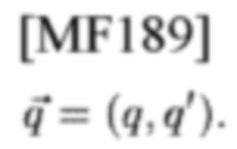
А именно, радиолокационная система требует PTs×P'Fs длительность-ширина полосы частот для поиска целей, у которых задержка td∈(0, PTs) и доплеровский сдвиг
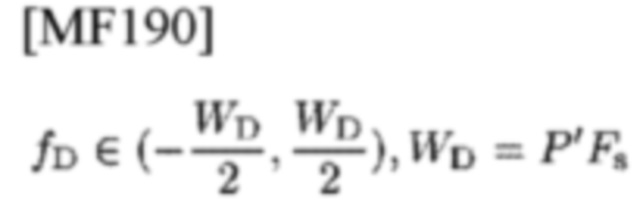
не известны заранее (просто задано dq→=1), в то время как система связи для передачи данных отправляет Р⋅Р'

(например,
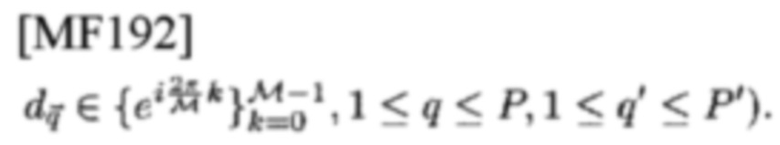
Теперь предположим, что такой сигнал s[k;χ] передается через канал с

Используя
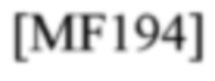
модуляцию  и демодуляцию
и демодуляцию 
можно получить принятый TD-сигнал, демодулируемый в смесителе или гомодинном приемнике
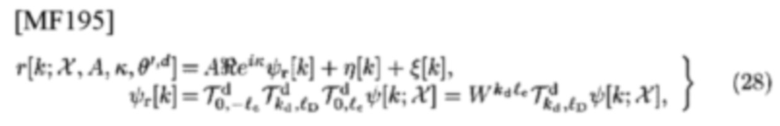
где

представляет собой составляющую СЕ сигнала в принятом сигнале, η[k] представляет собой помехи, и ξ[k] представляет собой гауссовый шум. Выражение FD, его DFT
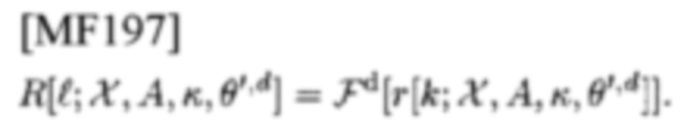
здесь опущено. Его PD

может быть поглощено в eiK вследствие переопределения, но должно быть исключено в корреляционном приемнике, как описано ниже. Такие принятые TD- и FD-сигналы обеспечивают данные w и их DFT W, наблюдаемые в смесителе.
Независимые и одинаково распределенные (i.i.d.) TD- и FD-PC дают независимые N' TD-шаблонов
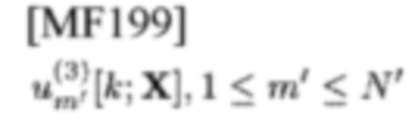
и N FD-шаблонов

в М-арном обнаружении. Следует отметить, что PC имеют две функции: рандомизация сигнала и генерирование нескольких PD, обусловленных NCP, присущим TFS; к счастью, такое PD само по себе обеспечивает хорошее указание для оценки параметров в том смысле, что передаваемый сигнал наделен легкой прослеживаемостью. Это показывает преимущества и недостатки использования PC. На самом деле, ширина полосы частот систем с кодированием по фазе должна быть намного больше, чем у классической радиолокационной системы; технология с несколькими несущими, т.е. FD-PC, умножает эту ширину полосы частот на количество поднесущих и поэтому требует сверхширокополосного сигнала.
<5. М-арное обнаружение и оценка TD- и FD-сигналов>
Давайте использовать М-арную стратегию обнаружения
с использованием TD-CE в (27)

(соотв. FD-CE


для обнаружения радиолокационного сигнала в (26)

(соотв.

Рассмотрим стратегию, согласно которой приемник выбирает среди NN' гипотез Hm,m', соответствующих (17). Достаточно найти те значения параметров θ',d, для которых LLF (или вещественная часть соответствующей ему CCF) в TD (соотв. FD) является максимальным. Рассмотрим первую проблему обнаружения принятой СЕ TD-шаблона

с ее адресом
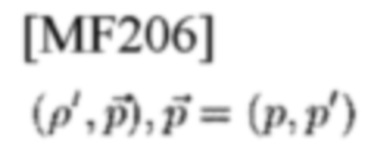
сетки в TFP

где

представляет собой СЕ TD-шаблона типа 3 (см. (22), (27)) с ρ'-м TD-шаблоном
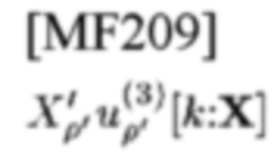
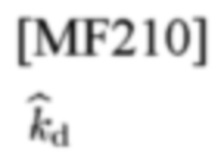
обозначает целочисленную оценку kd,

обозначает целочисленный параметр для оценки

Эта СЕ заключена в оцененной и принятой СЕ

соответствующей
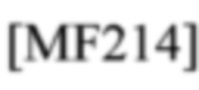

в (27) (см. ψr[k] в (28)), в которой используется отношение

Уравнение (29) показывает, что СЕ содержит последующую фазу, обусловленную несколькими PD, как указано ниже. Такая фаза должна быть исключена в CCF. Обозначим СЕ, комплементарную

как

определенную как

Уравнения (22) и (27) указывают, что N' TD-шаблонов типа 3

доступны, и приемник должен использовать N' СЕ TD-шаблона типа 3

и определять, какой из N' TD-LLF является наибольшим.
i) Проблема обнаружения дискретного по времени сигнала и ML-оценки доплеровского смещения частоты в TD:
Исходя из измеренных значений NT случайных переменных w=(w[0], …, w[NT-1]), приемник должен выбирать между двумя гипотезами,
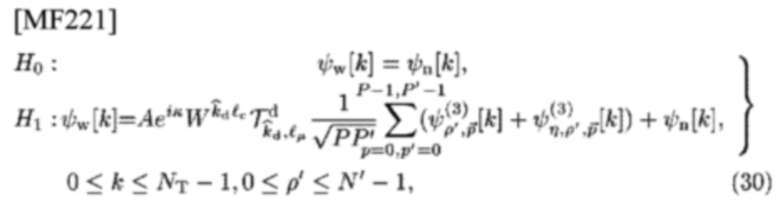
где
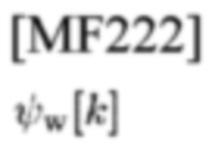
представляет собой NB СЕ данных наблюдений
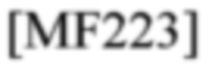
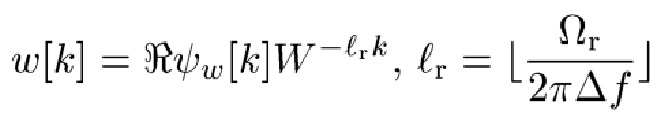
в момент времени k,
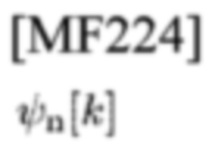
NB СЕ белого гауссова шума
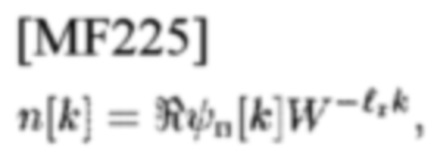
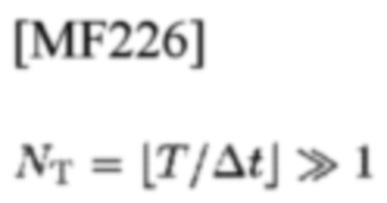
номер выборок во время длительности наблюдения (0, Т). Следует отметить, что составляющая сигнала в гипотезе H1 равна
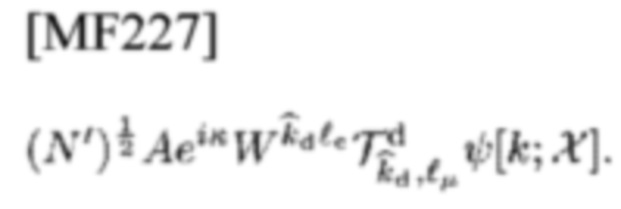
Предположим, что N' СЕ TD-шаблона типа 3
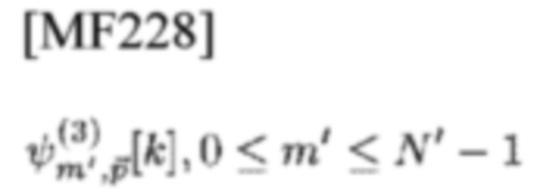
равных энергий являются квазиортогональными в том смысле, что
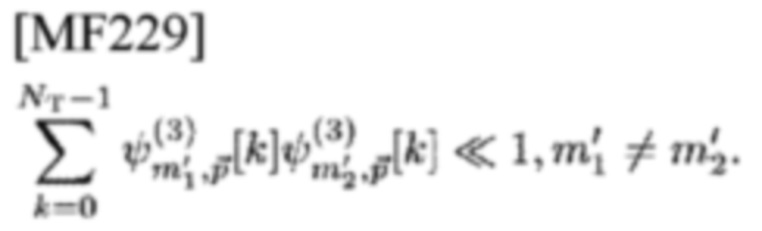
Тогда можно получить:
Предположение 4: ii) Проблема обнаружения сигнала и ML-оценки доплеровского смещения частоты в TD:
Исходя из наблюдаемых данных w=(w[0], …, w[NT-1]) в присутствии белого гауссова шума с односторонней спектральной плотностью N0, логарифм

-го TD-LF для обнаружения и оценки СЕ TD-шаблона типа 3

представлен как [21]
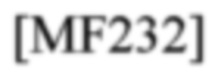
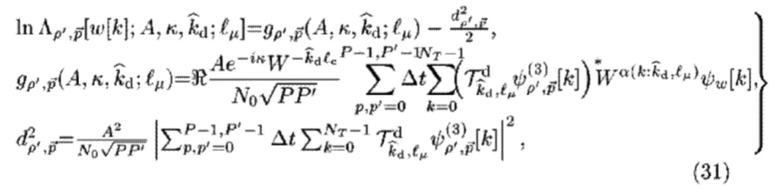
где
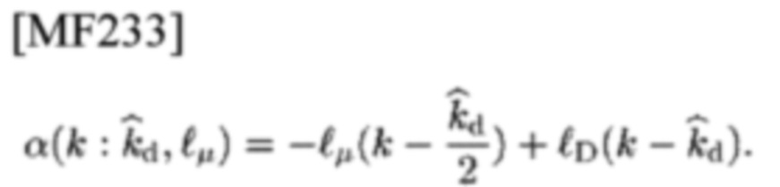
Пусть

будут целыми числами для данного уровня го решений, удовлетворяющими
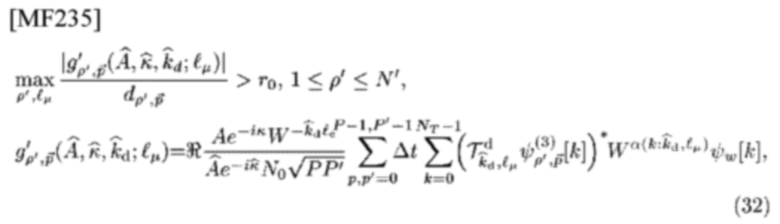
где

является компенсированным вариантом статистики в (31)

по MLE в (16)
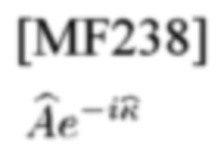
относительно Ае_iκ. Тогда приемник определяет, что
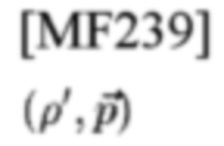
-я СЕ была получена по адресу (р',р→) сетки

в TFP, и если все статистики
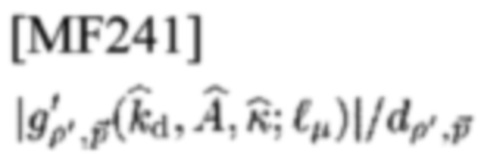
лежат ниже r0, приемник определяет, что сигнал не был передан. Таким образом,

является ML-оценкой

для данного

в котором использование оператора

требует фазовой функции

Далее следует проблема обнаружения и оценки задержки в FD с использованием DFT измеренного w,

Рассмотрим проблему обнаружения принятой СЕ FD-шаблона

с ее адресом

сетки

где

является СЕ FD-шаблона типа 4 (см. (22), (27)) с ρ-м FD-шаблоном типа 4
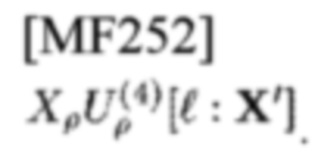
Эта СЕ заключена в оцененной и принятой FD-CE

для FD-CE, т.е. DFT в (27)
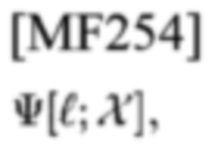
где

представляет собой целочисленную оценку

kσ представляет собой целочисленный параметр для осуществления оценки kd, и используется отношение

Обозначим СЕ, комплементарную

как

Уравнения (22) и (27) предполагают, что N FD-шаблонов типа 4

доступны, и приемник должен использовать N СЕ FD-шаблона типа 4
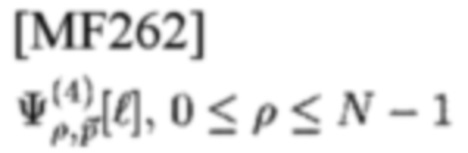
и определять, какой из N LLF является наибольшим (фиг. 3b).
ii) Проблема обнаружения сигнала и ML-оценки в FD:
На основании наблюдаемого W=(W[0], …, W[NT-1]), приемник должен выбирать между двумя гипотезами в FD,

где

является DFT наблюдаемых данных w[k] с NB СЕ


DFT шума n[k] с NB СЕ

количество выборок для ширины полосы частот В, для простоты NB=NT;

спектр сигнала
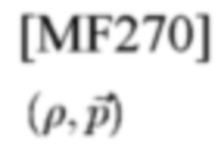
-го шаблона с его СЕ FD-шаблона типа 4 в (33)

и
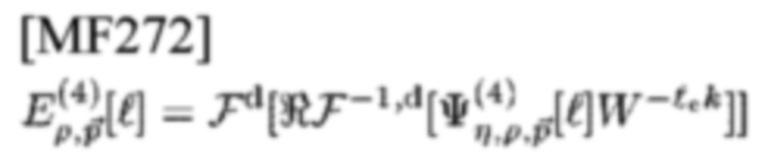
его дополняющий спектр с СЕ в (34)

Следует отметить, что составляющая сигнала в гипотезе H'1 равна

Предположим, что N СЕ FD-шаблона типа 4 (см. (22), (27))

равных энергий являются квазиортогональными в том смысле, что

Тогда можно получить:
Предположение 5: На основании данных

в присутствии белого гауссова шума с односторонней спектральной плотностью N0, логарифм

-го FD-LF для обнаружения и оценки

представлен как
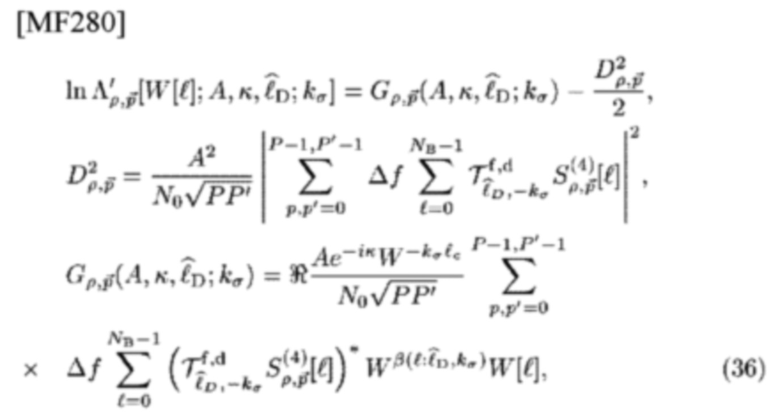
где

Пусть
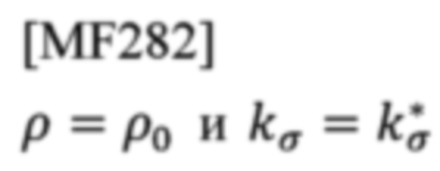
будут целыми числами, удовлетворяющими

для данного уровня r'0 решений. Тогда приемник определяет, что (ρ,р→)-й сигнал прибыл по адресу
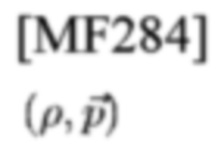
сетки в TFP

и если все статистики
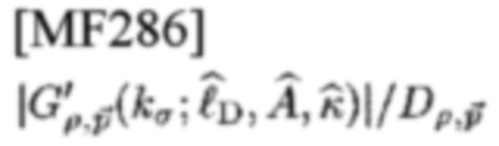
лежат ниже r'0, приемник определяет, что сигнал не был передан. Таким образом,

является ML-оценкой kd для данного
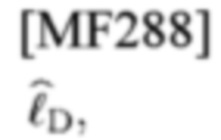
в котором использование оператора

требует фазовой функции

FD-аналог
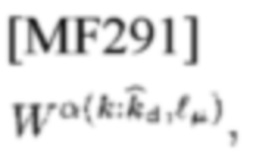
так что можно получить (36) и (37).
<6. TD- и FD-кросскорреляции для оценки параметров>
<6.1 TD- и FD-кросскорреляции>
Предположим, что наблюдаемый входной сигнал
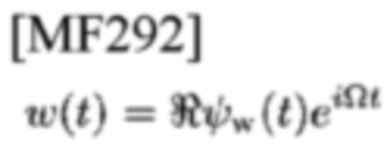
является NB, и вещественная и мнимая части СЕ
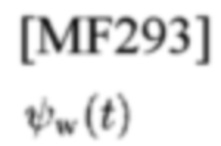
могут быть измерены отдельно [18, 3].
Чтобы исключить фазовые коэффициенты

(соотв.

и получить симметричную статистику по времени и частоте,
вместо статистики в (31)

имеющего
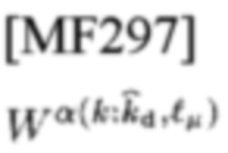
(соотв. статистики в (36)

имеющего

можно использовать соответствующую ему CCF, которая будет определена ниже (см. фиг. 3b):
Лемма 1: Предположим, что в двух гипотезах Н0 и H1 в (30) СЕ

является гауссианом. Тогда

где 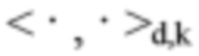 обозначает IP в пространстве
обозначает IP в пространстве

дискретных по времени TD-функций. Таким образом, можно определить CCF, называемую коррелятором типа 3, между принятой СЕ

(а именно составляющей сигнала принятой СЕ в (28)

с коэффициентом

вместо СЕ входного сигнала
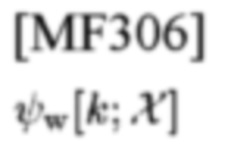
в приемник, и комплексной импульсной характеристикой NB-фильтра, согласованного с оцениваемой СЕ шаблона с адресом


представленной как
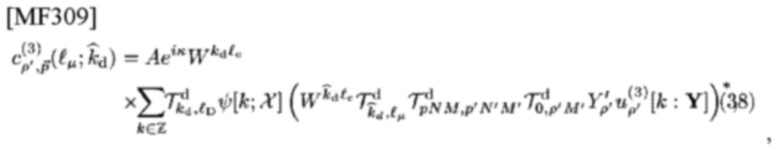
где СЕ TD-шаблона типа 3 в (29)

и коды Х'ρ',Х заменены Y'ρ',Y.
[0099] Несложно обнаружить, что эта CCF типа 3 представлена как
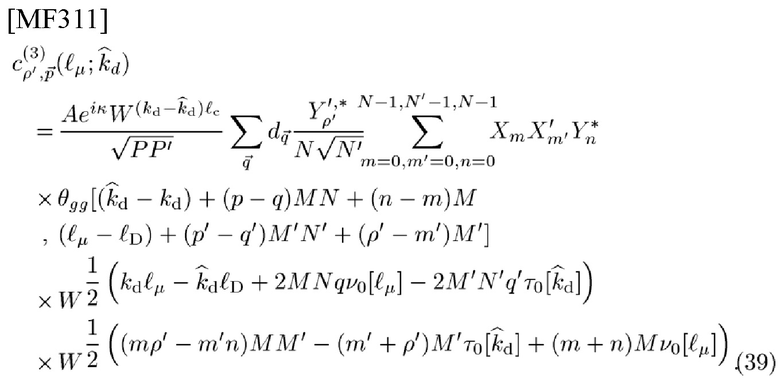
К сожалению, AF θgg(τ,υ) и ΘGG(υ,-τ) в целом имеют много боковых лепестков. Однако, гауссов чип-импульс g(t) дает радикальное решение проблем оценки, поскольку он имеет свою отделимую и экспоненциально убывающую AF в терминах τ и υ
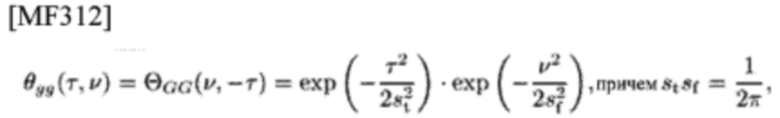
где
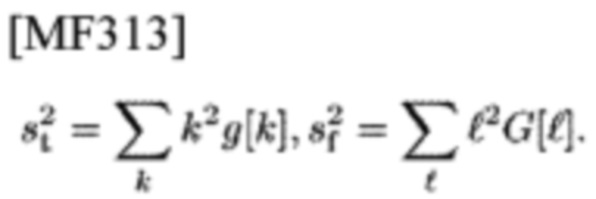
Для N, N'>>1, первый и второй аргументы 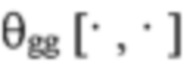 должны быть
должны быть
относительно небольшими, т.е. q→=p→, чтобы

имело большое значение; все члены с

в (39) могут быть несущественными. Это свойство гауссиана играет центральную роль в определении 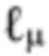 для максимизации
для максимизации

Оценка тройного суммирования PC с циссоидальным коэффициентом приводит нас к определению суммирования типа IDFT
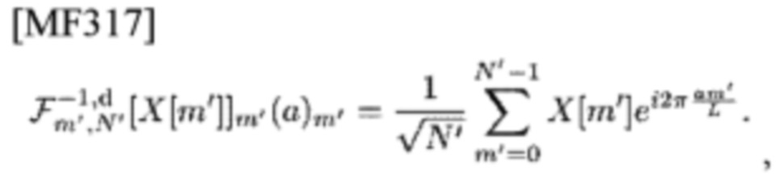
которое символически обозначено парой квадратных скобок

и круглых скобок (а)m' с его обычным обозначением  и суммирования типа DFT
и суммирования типа DFT
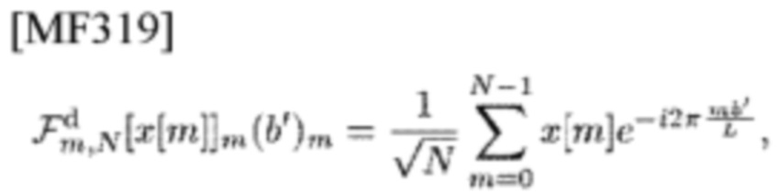
которое символически обозначено парой обычных обозначений

Используя обозначения:
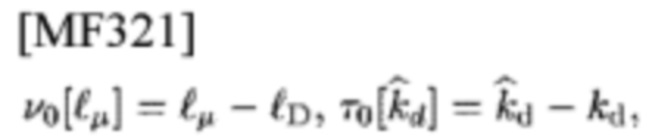
можно получить
Лемма 2: Если приемник типа 3 имеет свой адрес

и Y=X, Y'=X', тогда его CCF становится

Таким образом, известно, что необходимыми условиями для того, чтобы
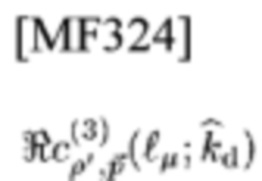
имело большое значение, являются

Обоснование. Используя символы круглой скобки в суммированиях типа IDFT и типа DFT, можно переставить 5 составляющих из 6 составляющих во втором поворачивающем множителе в (39)
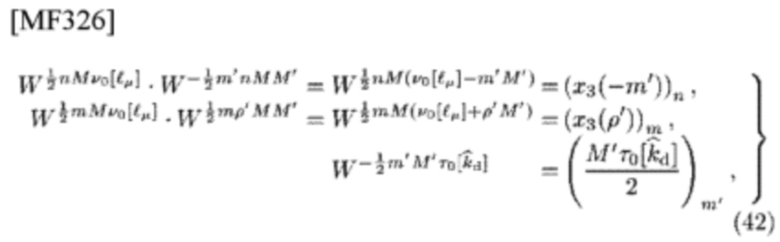
и переместить его остаточный член 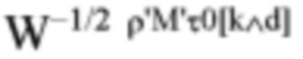 из 6 составляющих в первый поворачивающий множитель в (39). Использование отделимости AF гауссиана доказывает (41).
из 6 составляющих в первый поворачивающий множитель в (39). Использование отделимости AF гауссиана доказывает (41).
Лемма 3: Предположим, что в двух гипотезах Н'0 и H'1 в (35)

является гауссианом. Тогда CCF

где угловые скобки  обозначают IP в пространстве
обозначают IP в пространстве

дискретных по частоте FD-функций.
Тогда можно определить CCF, называемую коррелятором типа 4, между принятой FD-CE
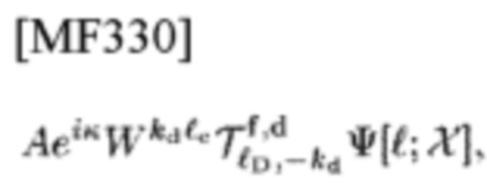
т.е. DFT составляющей сигнала принятой СЕ в (28)
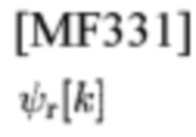
с коэффициентом

вместо СЕ входного сигнала

в приемник, и FD комплексной импульсной характеристикой NB-фильтра в FD, согласованного с оцениваемой СЕ шаблона в FD в (33) с адресом

представленной как
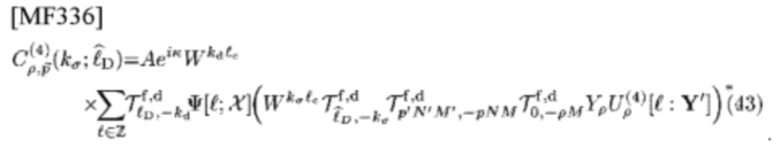
Эта CCF имеет вид

Аналогично, для N,N'>>1, можно задать
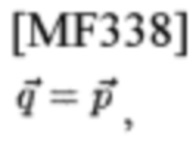
чтобы сделать

большим; все члены в (44) с

могут быть несущественным. Тогда можно получить сумму трех показателей степени в поворачивающем множителе, как указано выше. Оценивая тройное суммирование PC вместе с циссоидальным фактором, можно получить
Лемма 4: Если приемник типа 4 имеет свой адрес
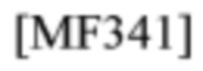

и Y=X, Y'=X', тогда его CCF становится
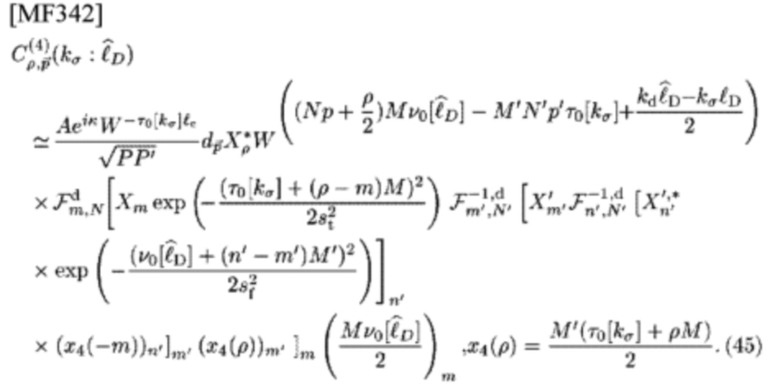
Таким образом, известно, что необходимыми условиями для того, чтобы
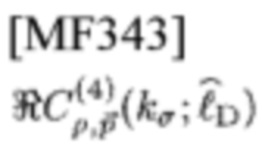
имело большое значения, являются
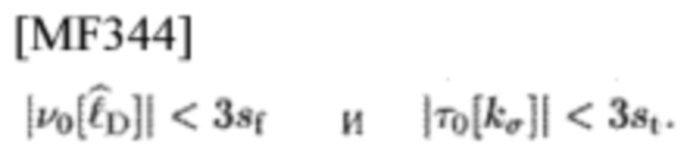
Обоснование. Аналогично, используя символы круглой скобки в суммированиях типа IDFT и типа DFT, можно переставить 5 составляющих из 6 составляющих во втором поворачивающем множителе в (44)
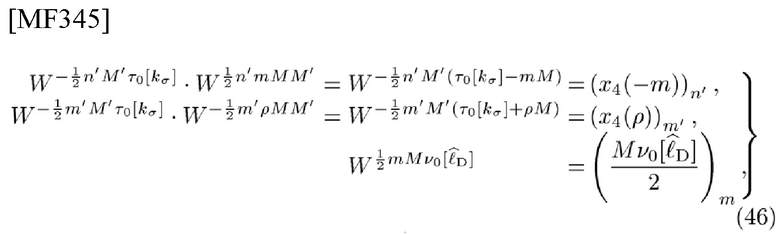
и переместить его остаточный член  из 6 составляющих в первый поворачивающий множитель в (44). Использование отделимости AF гауссиана доказывает (45).
из 6 составляющих в первый поворачивающий множитель в (44). Использование отделимости AF гауссиана доказывает (45).
Уравнения (41) и (45) демонстрируют, что коррелятор типа 3

и типа 4

являются совершенно симметричными в терминах

Взаимная замена TD-PC и FD-PC в паре типа 3
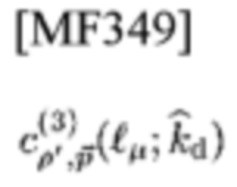
и типа 4
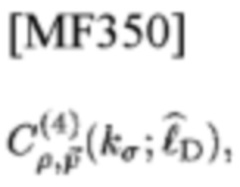
которую называют комплементарной парой (CP) [27], дает другую пару типа 1
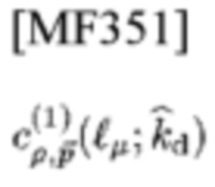
и типа 2
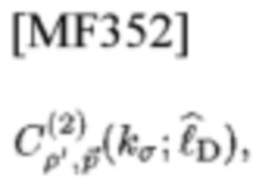
которую называют исходной парой (ОР) [24, 30], определенной следующим образом. [Исходная пара (OP) TD- и FD-корреляторов]
Рассмотрим другое разложение v[k;χ] и

представленные как
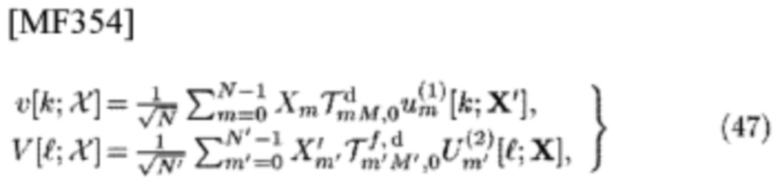
чьи TD-шаблон типа 1

и FD-шаблон типа 2

соответственно определены как

Во-первых, пусть
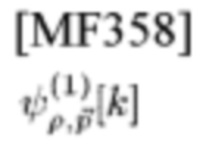
будет (ρ,ρ→)-ой оцененной и принятой СЕ, имеющей TD-шаблон

с адресом

сетки

определенной СЕ TD-шаблона типа 1
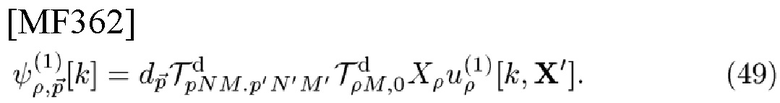
Тогда можно получить соответствующую ей CCF, называемую коррелятором типа 1

и получить

Пусть Y=X, Y'=X, и отбросим все члены

кроме члена, удовлетворяющего

Тогда можно получить
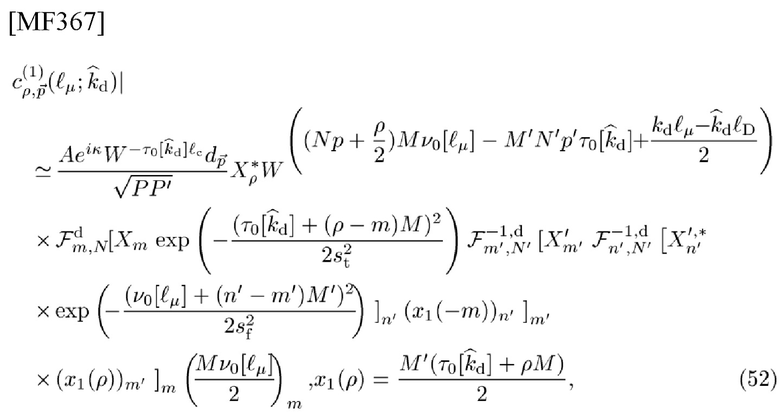
где при помощи символов круглых скобок в суммированиях типа IDFT и типа DFT можно переставить 5 составляющих из 6 составляющих во втором поворачивающем множителе в (51)

и переместить его остаточный член 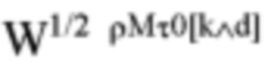 из 6 составляющих в первый поворачивающий множитель в (51). Использование отделимости AF гауссиана дает (52).
из 6 составляющих в первый поворачивающий множитель в (51). Использование отделимости AF гауссиана дает (52).
Во-вторых, пусть

будет (ρ,р→)-ой оцененной и принятой СЕ, имеющей FD-шаблон

с адресом
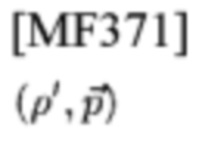
сетки

определенной CD FD-шаблона типа 2

Тогда можно получить соответствующий ей FD-коррелятор, называемый коррелятором типа 2

и получить

Пусть Y=X, Y'=X', и отбросим все члены
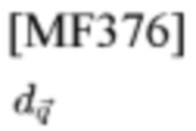
кроме члена, удовлетворяющего

Тогда можно получить

где при помощи символов круглых скобок в суммированиях типа IDFT и типа DFT можно переставить 5 составляющих из 6 составляющих во втором поворачивающем множителе в (56)

и переместить его остаточный член  из 6 составляющих в первый поворачивающий множитель в (56). Использование отделимости АР гауссиана дает (57).
из 6 составляющих в первый поворачивающий множитель в (56). Использование отделимости АР гауссиана дает (57).
<6.2 Петля обновления фазы и теорема альтернативного проецирования фон Неймана>
Если можно получить точные оценки

которые делают так, что все

в лемме 2 и
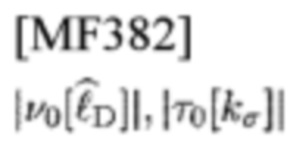
в лемме 4 находятся в пределах ширины полосы частот и длительности чип-импульса, то две CCF

отфильтруют помехи

соответственно содержащиеся в

и восстановят
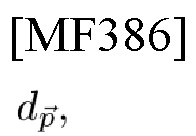
вместо использования традиционных фильтров с крутым срезом. Это является радикальным решением для цифровой обработки сигналов для связи.
Простым способом обновления оценок

в обоих парах корреляторов является следующий алгоритм, называемый петлей фазового обновления (PUL), который отличается от традиционной "петли фазовой синхронизации" для синхронизации в системах связи:
[Алгоритм PUL с обновлением правила для коэффициента ослабления-MLE]:
Пусть

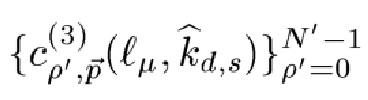
и

будут CP массивов корреляторов типа 3 и типа 4, и пусть
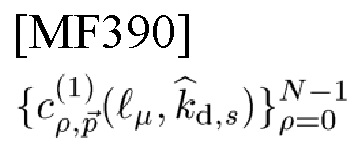
и

будут ОР массивов корреляторов типа 1 и типа 2. Для простоты зададим

пока алгоритм PUL не завершился. Пусть

будет s-ой MLE коэффициента ослабления

с s-ой оценкой в цифровой форме

параметра θ'=(td, fD), который определен в (16), где

заменены

соответственно, представленной как

Тогда можно обновить целочисленную пару

как 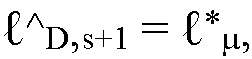 если s четное (соотв. нечетное), и
если s четное (соотв. нечетное), и 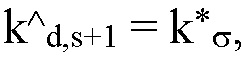 если s нечетное (соотв. четное),
если s нечетное (соотв. четное),
где

и начальное значение

выбирается произвольно, например,

Выберем

в качестве кандидатов
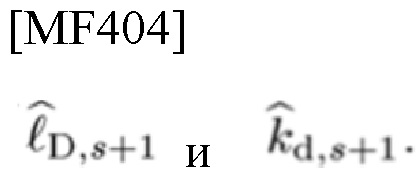
Процедура оценки (s+1)-го шага заканчивается, если для чип-импульса g[k] (или G[1]) длительность LΔt и ширина полосы частот LΔf,
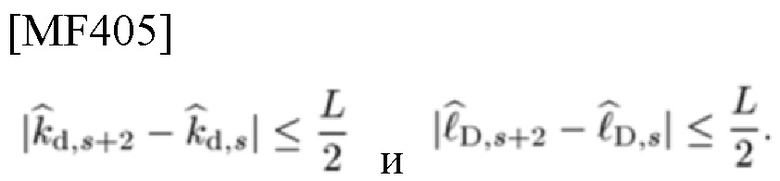
Тогда такие оценки являются ML-оценками, и оба из двух корреляторов становятся ML-приемниками. Этот алгоритм может быть записан в виде реконструкции Юла (Youla) [22] сигнала, как представлено в теореме ниже.
Восстановление или реконструкция сигнала, который был искажен, является одной из наиболее важных проблем в обработке сигнала. Юл [22] дал ответы на проблемы реконструкции. Умелое использование [23] некоторых математических механизмов, введенных Юлом [22], приведет нас к тому, чтобы показать, что сходимость алгоритма PUL зависит оттого, насколько хорошо работает APT [21] фон Неймана.
Рассмотрим гильбертово пространство

состоящее из всего пространства  квадратично-суммируемых непрерывных и дискретных по времени (или дискретных по частоте) функций с IP, определяемым как
квадратично-суммируемых непрерывных и дискретных по времени (или дискретных по частоте) функций с IP, определяемым как

(или

и нормой
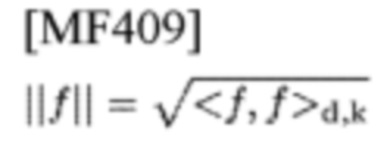
или

Пусть ε будет любым замкнутым линейным многообразием (CLM) в гильбертовом пространстве

Теорема проецирования [22] говорит нам о том, что если ε' и ε'' являются ортогональными подпространствами

тогда каждая f∈ε обладает уникальным разложением f=g+h, g∈ε', h∈ε'', где g, h являются проекциями f на ε' и ε'', соответственно, выраженными как g=Pf, h=Qf; P обозначает соответствующий оператор проецирования (РО), проецирующий на ε', Q=I-Р обозначает соответствующий ей РО, проецирующий на ε'', и I обозначает тождественный оператор.
Пусть ε1 (соотв. ε3) будет набором всех
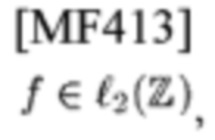
которые являются LΔt-TL (соотв. Ts-TL) сигналами. Наоборот, обозначим набор из всех
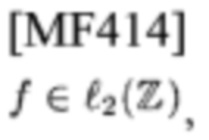
которые являются LΔf-BL сигналами, как ε2, и которые являются Fs-BL сигналами, как ε4. Каждое из

является CLM [22].
[0112] Пусть Pi будет РО, проецирующим на

и Qi=I-Pi будет РО, проецирующим на ортогональное дополнение εi, записанное как

каждое из которых определено ниже. CCF играет роль РО в том смысле, что для любых двух сигналов r и s, сигнал r∈ε в имеет уникальное разложение вида
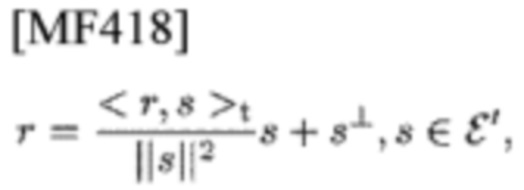
где

ортогонально s. Коэффициент

рассматривается как РО, проецирующий на ε'.
CP корреляторов типа 3, типа 4 и ОР корреляторов типа 1, типа 2 также дают РО, записанные как:
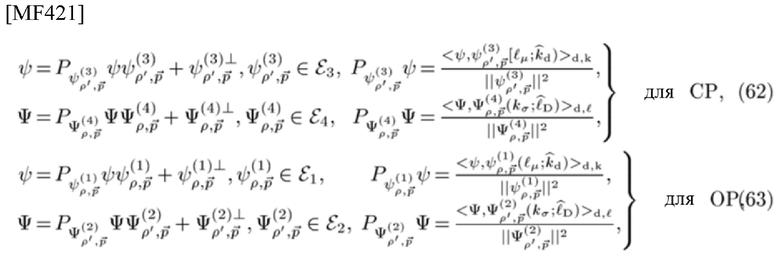
где

являются ортогональными дополнениями

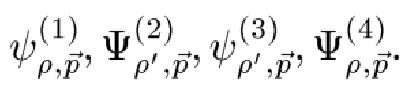
Теорема альтернативного проецирования (APT) [21, стр. 55, теорема 13.7] (фиг. 11)
говорит нам о том, что:
если Е и F являются проекциями на CLM
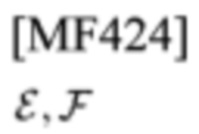
в гильбертовом пространстве, соответственно, тогда последовательность операторов Е, FE, EFE, FEFE, … имеет предел G, последовательность F, EF, FEF, … имеет такой же предел G, и G является проекцией на

(Условие EF=FE не должно выполняться.)
С использованием APT получается следующий результат:
Теорема: Сходимость петли фазового обновления (PUL) (см. фиг. 3с):
Рассмотрим 4 РО в TD и FD, которые содержат оценки (s+1)-шага
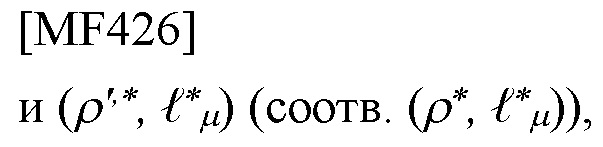
определенные посредством операций argmax в терминах  (соотв.
(соотв.  ) с оценкой s-шага
) с оценкой s-шага

в (60) (соотв. (61)), и (ρ*,k*σ) (соотв. (ρ',*,k*σ)), определенные посредством операций argmax в терминах (ρ,kσ) (соотв. (ρ',kσ)) с оценкой s-шага

в (60) (соотв. (61)). Запишем эти РО символически как

и

Тогда алгоритм PUL сходится.
[Обоснование]: Рассмотрим только формулу рекурсии для CP, потому что для ОР все аналогично, за исключением обмена между TD-PC X и FD-PC X', то есть между суффиксами (3, 4) и (1, 2). Два разных порядка оператора Р3 усечения времени и оператора Р4 с ограничением по полосе частот предоставляют два разных итерационных уравнения;
Во-первых, рассмотрим алгоритм для восстановления

следующим образом: если

тогда

и

Таким образом,

удовлетворяет операторному уравнению

Рекурсия, определенная как

позволяет нам иметь итеративное уравнение в TD [22, 23]
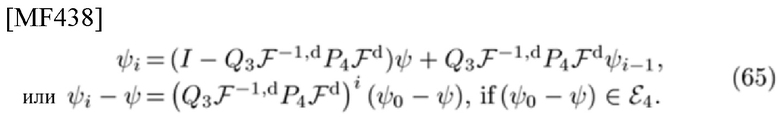
По APT
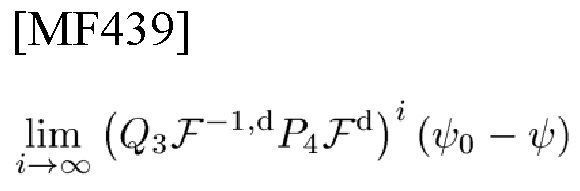
становится проекцией

на CLM 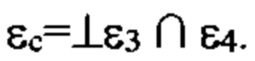 εс содержит только тривиальную функцию [22, стр. 699], [23, стр. 637]; т.е.
εс содержит только тривиальную функцию [22, стр. 699], [23, стр. 637]; т.е.
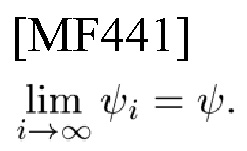
Это один из основных результатов Юла [22]. Таким образом, оператор
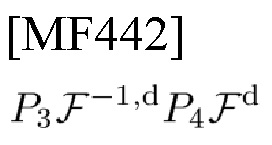
выделяет прямоугольник из длительности LΔt чип-импульса и ширины полосы частот LΔf чипа с адресами уровня чипа и уровня данных

т.е. пересечение прямоугольного носителя соответствующей ему СЕ

с тем же для СЕ
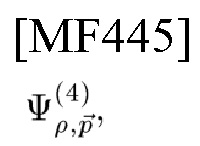
т.е.
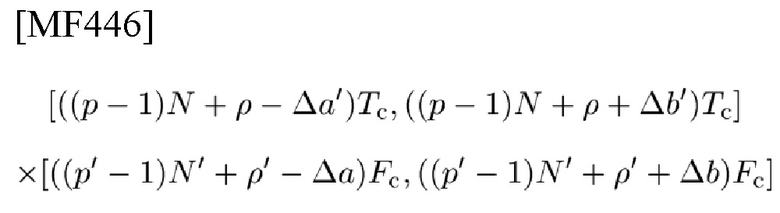
сетки
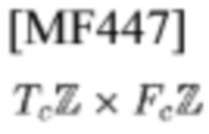
и отфильтровывает остальное в TFP, где Δа', Δb', Δа, и Δb являются целыми числами, удовлетворяющими Δa'+Δb'=М' и Δa+Δb=М. Такой оператор называется оператором локализации фазового пространства (или частотно-временной локализации) [7]. Таким образом, СЕ ψ [k] восстанавливается так, что параметры

оцениваются в пределах LΔt и LΔf. Следует отметить, что в отличие от обычных прямоугольников оператора со строгим TL (соотв. BL) [23], оператор Р3 усечения времени (соотв. оператор Р4 с ограничением по полосе частот) определяется с использованием шаблона, т.е. неперекрытого наложения N кодированных гауссовых чип-импульсов g[k] в TD (соотв. N' кодированных гауссовых чип-импульсов в FD

без защитного интервала.
Наоборот, в FD, если ψ ∈ ε3, тогда

и
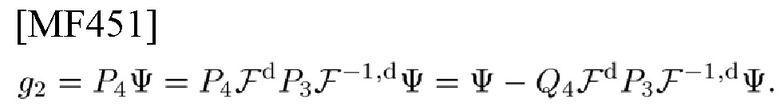
То есть, ψ удовлетворяет операторному уравнению [23]
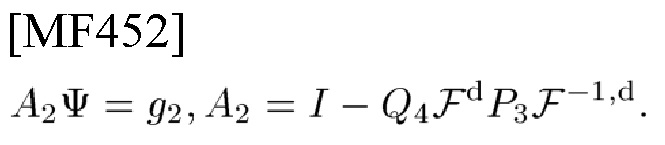
Это дает итеративное уравнение

По APT,
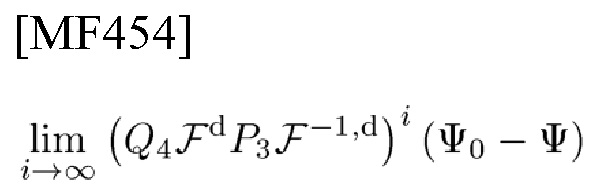
становится проекцией (ψ0-ψ) на CLM
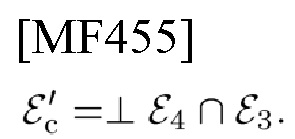
Это CLM содержит только тривиальную функцию. Таким образом, limi→∞ ψi=ψ.
[0118] FD-CE

восстанавливается так, что параметры

оцениваются в пределах LΔt и LΔf. Аналогично, оператор

т.е. другой оператор локализации выделяет прямоугольник из LΔt×LΔf с адресами уровня чипа и уровня данных

т.е. пересечение прямоугольного носителя СЕ
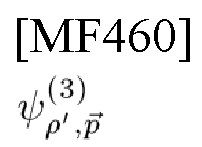
с тем же для СЕ


сетки
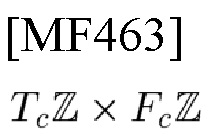
и отфильтровывает остальное в TFP. [Конец обоснования]
[0119] <7. Двойная система набора фильтров с несколькими несущими>
<7.1 Передатчики для генерирования сигнатуры и радиолокационного сигнала>
Рассмотрим набор фильтров с несколькими несущими для генерирования TD-сигнатуры v[k;χ] и FD-сигнатуры

определенной в (25). Используя повторение TD-PC Xm периода N для получения бесконечной кодовой последовательности в момент времени: -∞, …, -Тс, 0, Тс, …, ∞, и повторение FD-PC Х'm' периода N' для получения бесконечной кодовой последовательности при частоте: -∞, …, -Fc, 0, Fc, …, ∞, можно получить: Предположение 6: Запишем v[k;χ] и

в (25) соответственно как
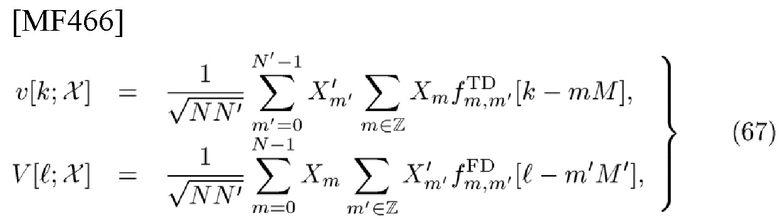
где

являются модулированными фильтрами, определенными как

Для входного сигнала x[k] и выходного сигнала y[n] Вайдьянатан (Vaidyanathan) [13, стр. 117] определил отношение входа к выходу в TD с использованием трех типов многорежимных фильтров с коэффициентом фильтрации h[⋅]: Mf-кратный прореживающий фильтр:

Lf-кратный интерполяционный фильтр:

и Mf/Lf-кратный прореживающий фильтр:
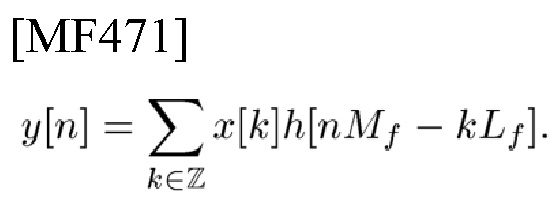
[Обоснование]: TD-сигнатура υ[k;χ] в (25) (соотв. FD-сигнатура

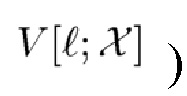
выглядит как выражение сигнала, полученного на выходе набора фильтров для синтеза сигнала (SFB) [10, 12] с N'(соотв. N) подполосами частот и с коэффициентом расширения, равным М (соотв. М'), и кодированного по фазе с помощью FD-PC X'm' (соотв. TD-PC Xm) на каждой подполосе частот. На самом деле, если
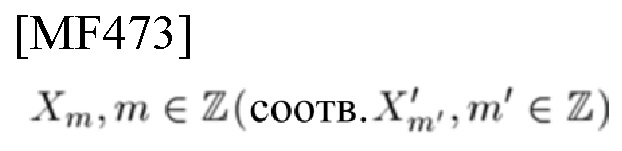
является входным сигналом и

является фильтром на (m, m')-ой подполосе частот этого SFB, тогда выходной сигнал

может быть записан как (67). [Конец обоснования]
Вместе с символами lcm[M, N']=M0N'=MN'0, lcm[М', N]=М'0 N=M'N0 [13], [10], [11], используя M0N', М'0 N многофазную составляющую

можно получить многофазные фильтры (многофазный фильтр тип 1 Вайдьянатана [13, стр. 121])

Для lm=lcm[M, N'], gd=gcd[M, N'], существуют N'0, M0, удовлетворяющие lm=MN'0=N'M0. С другой стороны, в силу тождества выполняются lm⋅gd=М⋅N', М=gd⋅M0,N'=gdN'0.
Таким образом, можно получить SFB 2-D модулированной  с помощью TD-, FD-PC, как показано на фиг. 4, 5, соответственно.
с помощью TD-, FD-PC, как показано на фиг. 4, 5, соответственно.
Фигура 4 изображает SFB с TD-, FD-PC Xm, X'm' для генерирования TD-сигнатуры v[k] в (25), (67), содержащей m'-ый TD-шаблон

Фигура 5 изображает SFB с TD-, FD-PC Xm, X'm' для генерирования FD-сигнатуры

в (25), (67), содержащей m-ый FD-шаблон

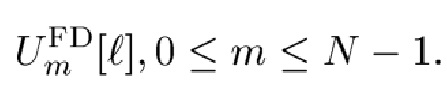
При этом уравнение (27) предоставляет SFB для генерирования

и

Предположение 7: СЕ ψ[k;χ] и

могут быть записаны соответственно как

где

являются модулированными фильтрами соответствующих им SFB, которые определены следующим образом
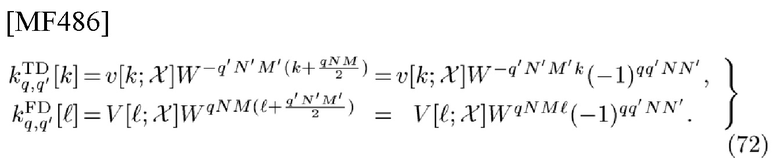
[Обоснование]: Уравнение (71) показывает, что если

(соотв.

обозначает входной сигнал, и

(соотв.

является фильтром на (q, q')-ой подполосе частот соответствующего ей SFB, то

(соотв.

является выходным сигналом его SFB с РР' подполосами частот и с коэффициентом расширения, равным NM (соотв. N'M') на каждой подполосе частот. [Конец обоснования]
Таким образом, можно получить SFB для генерирования сигнала передачи, который содержит символы данных, как показано на фиг. 6, 7. Традиционные SFB не используют процесс генерирования сигнатуры, как показано на фиг. 4, 5. На фиг. 6, 7 показан случай, в котором N=N'=1 соответствует обычным SFB. Используя следующие модулированные фильтры (MF) для передачи данных, представленные как

можно получить многофазные фильтры (многофазный фильтр тип 1 Вайдьянатана [13, стр. 121])

где Р'0, Р0 обозначает целые числа, удовлетворяющие P'0MN=lcm[P', MN], P0MN=lcm[P, MN]. [Конец обоснования]
На фиг. 6 изображен SFB для генерирования комплексной огибающей (СЕ) в TD в (26)

с входными комплекснозначными данными

На фигуре 7 изображен SFB для генерирования FD-CE в (26)

с входными комплекснозначными данными

<7.2 AFB: приемники и схема кодера>
Помимо коэффициентов ослабления Aeik, возрастает PD из-за некоммутативности операций модуляции/демодуляции над несущей lc, сопровождаемых задержкой k^d,
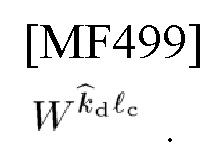
Принятый сигнал в (28)

(соотв. его FT
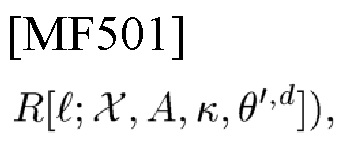
(просто обозначенном как
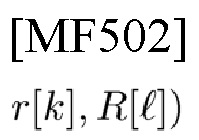
содержит эти PD.
Определим CCF типа 3 (соотв. типа 4) между принятым сигналом r[k] (соотв. R[l] в (28) и оцененной СЕ TD-шаблона типа 3 в (29)

(соотв. FD-CE в (33)

соответственно как

где фазовый коэффициент

(соотв.

предназначен для исключения коэффициента

в составляющей сигнала r[k] в (28), (38) (см.

(соотв. это же для
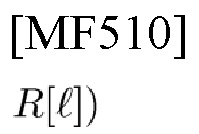
(см. в (28), (43)
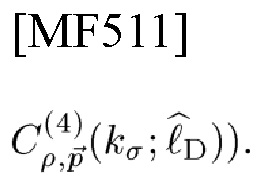
Тогда можно получить набор фильтров для разложения сигналов (AFB) в TD (соотв. FD) [10, 12]:
Предположение 8: CCF типа 3 и типа 4 могут быть переписаны для реализации AFB, соответственно как
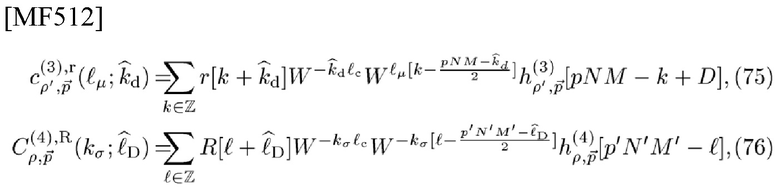
где D=L-1 и
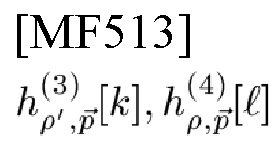
являются модулированными фильтрами AFB в TD и FD
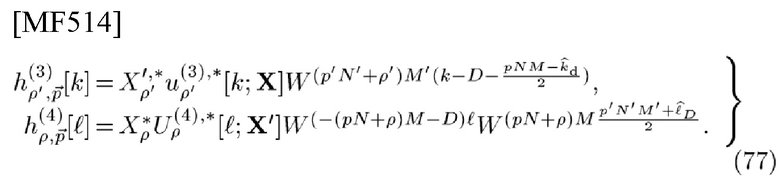
(Когда Р×Р'

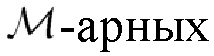 символов передаются,
символов передаются,
можно оценить выходной сигнал по адресу

в массиве корреляторов р-полосы частот, р'-длительности для оценки

[Обоснование]: Если модулированный по фазе принятый TD-сигнал,
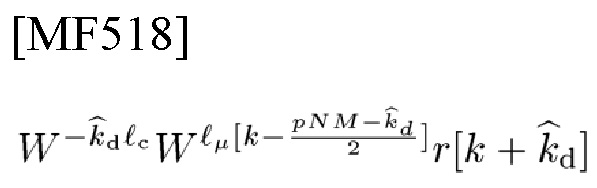
(соотв. FD-сигнал

обозначает входной сигнал
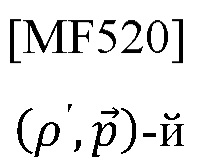
(соотв.
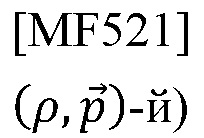
подполосы частот набора AFB с Р' (соотв. Р) подполосами частот с коэффициентом прореживания, равным NM (соотв. N'M') на каждой подполосе частот, представленным в (75) (соотв. (76)), тогда два факта:
i) один представляет собой свойство симметричности TD [10] (см. (21))

и ii) другой представляет собой свойство FD-сигнала

которое влечет за собой симметрия TD, доказывают, что связанный с ним фильтр

(соотв.
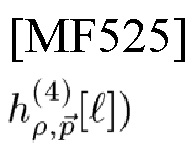
определен (77). [Конец обоснования]
Следует отметить, что два типа фильтров, приведенных в патентном документе [2], не содержат ни PD 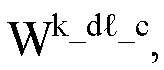 ни исключающие его члены
ни исключающие его члены 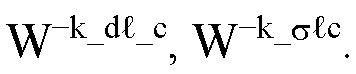
Если фильтр AFB в (77) и P'0MN, P0M'N' многофазные составляющие:
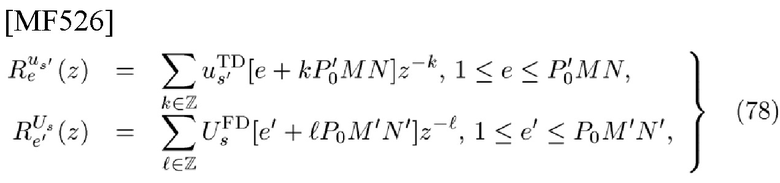
тогда можно получить N',N многофазных фильтров (многофазный фильтр тип 2 Вайдьянатана [13])

Таким образом, можно получить AFB, как показано на фиг. 8, 9. (Случай, в котором N=N'=1, N0=N'0=1 соответствует обычным AFB [12, 13].) Две CCF (75) и (76) являются FBMC-реализациями 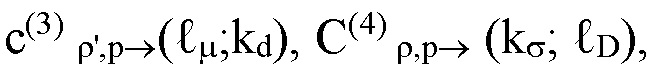 соответственно;
соответственно;
Выходной биполярный символ TD-AFB (соотв. FD-AFB) задан как знак

(соотв. знак для

где

является MLE коэффициента ослабления 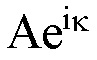 с MLE
с MLE

(см. (59)). Такая пара SFB и AFB, симметричных в TD и FD, называется "двойная-FBMC".
На фигуре 8 изображен AFB, снабженный массивом TD-корреляторов для декодирования символов комплекснозначных данных

На фигуре 9 изображен AFB, снабженный массивом FD-корреляторов для декодирования символов комплекснозначных данных
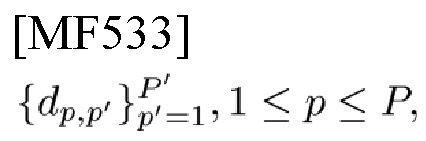
где TD-коррелятор

и FD-коррелятор

на фиг. 8 и 9 соответствуют соответственно

Следует отметить, что если алгоритм PUL реализован в интерфейсе между TD- и FD-AFB, как показано на фиг. 10, тогда результирующий интерфейс с изменяющимися во времени или адаптивными AFB становится блоком оценки параметров для радиолокационной станции и синхронизатором [3] для систем связи после схождения алгоритма PUL. Более того, он также играет роль кодера передаваемого

 символа
символа 
для связи для передачи данных на основе комплекснозначных CCF
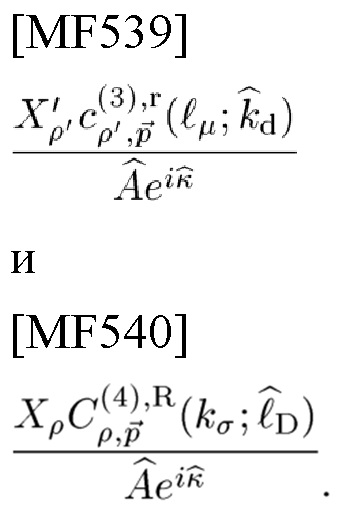
Все фильтры, определенные (68), (72) и (77), в этой FBMC могут быть реализованы многофазными фильтрами (называемыми многофазными фильтрами Вайдьянатана типа 1 или типа 2 [13]). Но это выходит за рамки нашего раскрытия, и поэтому не будут рассматриваться в настоящем документе.
На фигуре 10а и 10с изображены AFB с массивом TD-корреляторов и массивом FD-корреляторов, соответственно, и на фигуре 10b представлен альтернативный процесс обновления между MLE двух массивов на основании APT фон Неймана.
<8. Другие примеры связи, использующей некоммутативность временных и частотных сдвигов>
В технологии радиолокационного обнаружения в качестве типичного примера связи, использующей некоммутативное свойство (NCP) временных и частотных сдвигов (TFS), пара TFSO типа 3 с td, fD

и TFSO типа 4

с оцененными параметрами

в приемнике, показала, что предварительные половинные сдвиги td, fD играют важную роль в оценке этих параметров. Другие примеры систем связи, которые используют NCP TFS, приведены далее.
Наше обсуждение для простоты было ограничено одной целевой проблемой. Конечно, простой способ обнаружения нескольких целей состоит в том, чтобы адекватно использовать уровень го решений статистики для оценки доплеровского смещения частоты и r'0 статистики для задержки, соответственно в (32), (37), и чтобы зарегистрировать несколько целей как функций r0.r'0.
<8.1 Обнаружение нескольких целей с использованием CDMT>
Рассмотрим другой подход к решению проблем нескольких целей. Пусть 
 будет Npath парами задержки и доплеровского смещения частоты. Разделим целевое пространство Θ'=[0,Т)×[0,F) на 4 области:
будет Npath парами задержки и доплеровского смещения частоты. Разделим целевое пространство Θ'=[0,Т)×[0,F) на 4 области:
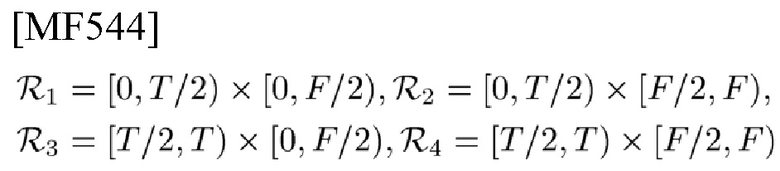
и назначим TD- и FD-PC:
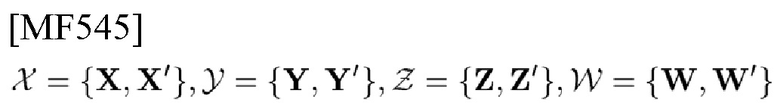
для каждой области. Предположим, что 2-D PC
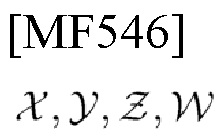
имеют свои наборы адресов чипов, определенные как
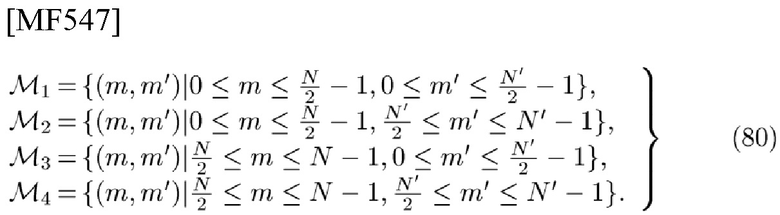
и соответствующие им сигнатурные сигналы, определенные
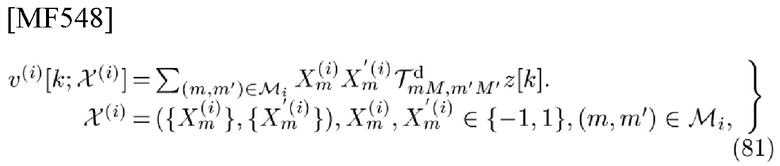
где χ(1), χ(2), χ(3), χ(4) соответствуют

Тогда СЕ радиолокационного сигнала имеет форму, соответствующую нескольким целям

Если эта СЕ передается через Npath каналов с двойной дисперсией с задержкой, доплеровским смещением частоты и коэффициентом ослабления, соответственно обозначенными как

тогда составляющая принятого сигнала представлена как

Пока приемник использует 2-D PC
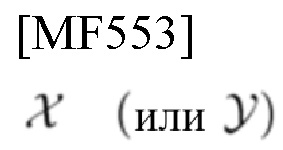
для СЕ TD-шаблона типа 3 и СЕ FD-шаблона типа 4

в (29), (33) и ограничивает диапазон управления

соответственно CCR типа 3 в (38) и CCR типа 4 в (43):

до
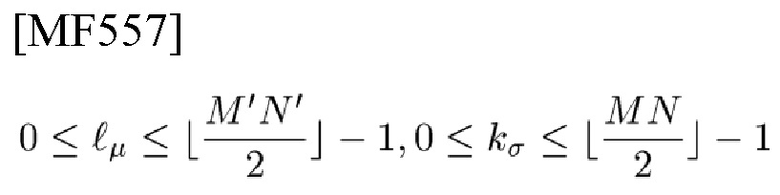
для R1 и до
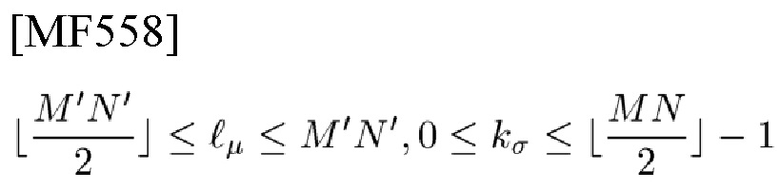
для R2, он получает MLE для целевых подпространств R1, R2. Аналогично приемник получает MLE для других областей R3, R4. Эта технология основана на принципах, лежащих в основе CDMA, и поэтому называется технологией обнаружения нескольких целей с кодовым разделением (CDMT).
Численное моделирование с N=N'=64, Npath=4, SNR≥5 дБ показало, что 3, 4 цели успешно обнаруживаются с вероятностью 80% с использованием алгоритма PUL.
<8.2 Обнаружение нескольких целей с использованием искусственной задержки и доплеровского смещения частоты>
Как показано в обосновании сходимости алгоритма PUL, TD-CCF типа 3 и FD-CCF типа 4
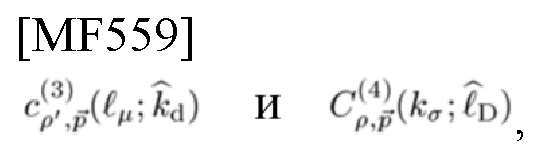
соответственно использующие ортогональные операторы проецирования: Р3 на TD-пространство с ограничением по времени (TL) Ts и Р4 на FD-пространство с ограничением по полосе частот (BL) Fs, говорят нам о том, что пара TFSO типа 3 и типа 1:

(или пара частотного двойника TFSO типа 3 и TFSO типа 2:
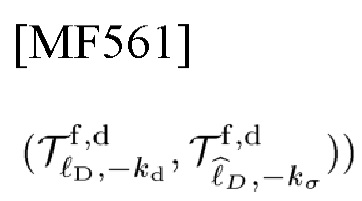
является характерным оператором, обусловленным NCP задержки и доплеровского смещения частоты, и таким образом играет важную роль в радиолокационных и мультиплексированных системах связи, поскольку такая пара содержит или пару из двух неизвестных

или пару из двух контрольных параметров

для получения пары из двух MLE

Напротив, TFSO модуляции и демодуляции
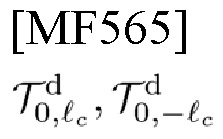
и TFSO уровня данных и уровня чипа
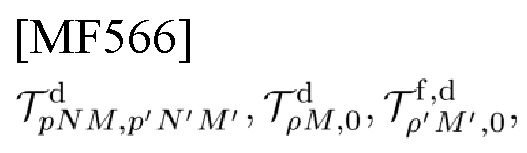
с адресами уровня данных и уровня чипа

являются независимыми от 
При этом пара TD- и FD-CCF в (41), (45)
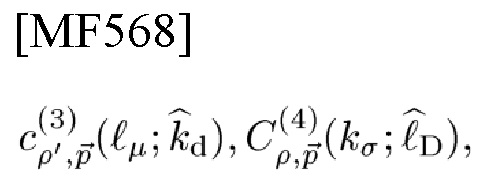
с адресными параметрами

содержит данные
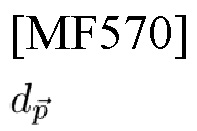
вместе с несколькими PD.
Это говорит о том, что если искусственные параметры

(для простоты задав

заключены в

тогда эти параметры доступны для проблемы нескольких целей. Например, рассмотрим системы связи на основе NCP задержки и доплеровского смещения частоты, использующие Npath пар TD-TFSO и TD-CCF и Npath пар FD-TFSO и FD-CCF, определенных как

с Npath парами параметров

Такие системы используют Npath пар TD-, FD-шаблонов, заключенных в TD- и FD-сигнатуры, и алгоритм PUL для оценки

где алгоритм PUL был назван "активным" PUL [25, 30] в том смысле, что обновление выполняется в передатчике; но характеристика "активный" была не совсем правильной, поскольку обновление применимо только к приемнику. Вышеупомянутая MLE основана на идентификации Npath пар известных сдвигов

из сигналов с заключенными сдвигами. А именно, это относительно отличается от проблемы одной цели. Таким образом, вышеупомянутая PUL является обычной PUL.
Технология CDMT может быть применена к
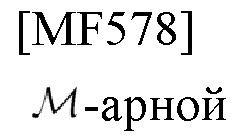
связи с манипуляцией с фазовым сдвигом (PSK) с данными

Используя Npath 2-D PC и два поворачивающих множителя
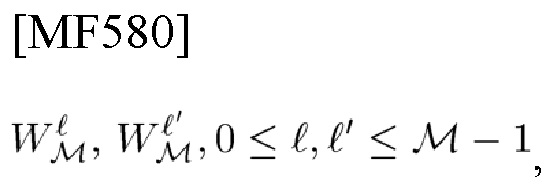
помещенные перед массивами из N' TD-CCF и N FD-CCF

называемыми "подстроенным по фазе слоем (PTL)" и заменяющими

операции для MLE в PUL на

за счет прибавления двух PTL-переменных

можно получить PTL, который играет роль замены

пары CCF в (41), (45) на

с таким результатом, что фазовые ошибки в вещественных частях CCF имеют гауссово распределение со средним 0.
Автор настоящего изобретения может получить хорошие результаты численного моделирования с N=N'=16,

и SNR 30 дБ. Однако, когда

боковые лепестки возникают слева и справа от основного лепестка в распределении, из чего следует, что могут возникнуть ошибки декодирования. Таким образом, только использование простых способов исключения PD ограничивается установкой

Таким образом, чтобы попробовать М-арную связь с
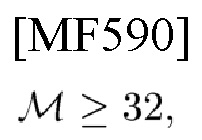
можно разделить пространство Θ' задержки и доплеровского смещения частоты и TFP S сигнала на

подпространств задержки и доплеровского смещения частоты и под-TFP и назначить

каждой под-TFP. Более того, предположим, что искусственные сдвиги

находятся вокруг центра i-го подпространства задержки и доплеровского смещения частоты и используют PTL W8=ехр(-i2π/8) и WM=ехр(-i2π/М), помещенные перед TD- и FD-CCF, а именно,

Это приводит к следующей замене PTL на
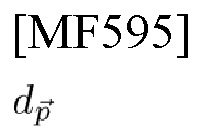
и операции arg max

Следовательно, в общем необходимо

CCF. Таким образом, можно получить результаты моделирования числового декодирования для 128-PSK, 256-PSK с использованием 16, 32 2-D PC. Эта М-арная PSK-связь реализовала новый класс мультиплексной связи, названный "мультиплекс с пространственным разделением по задержке и доплеровскому смещению частоты (dD-SDM)" [35, 34]. Однако разрешение по фазе этой системы остается в пределах WM=ехр(-i2π/М). И поэтому невозможно реализовать PSK-связь с высоким

Далее предлагается новая технология реализации PSK-связи с высоким М.
Автор настоящего изобретения может предоставить системы связи с модуляцией и демодуляцией с PSK с высоким

в сочетании с установлением синхронизации, которые могут быть использованы также в качестве синхронизатора для связи и/или радиолокационной станции. Прежде всего, можно дать следующие пояснения к фиг. 12-17, относящимся к
-арному PSK-кодеру и декодеру.
На фигуре 12 изображена блочная диаграмма передатчика (или кодера), который может быть использован также в качестве эффективной радиолокационной станции с высоким разрешением, оснащенной
-арной PSK-связью.
Есть два разных типа состояний: один тип представляет собой состояние синхронизатора/радиолокационной станции (когда данные dq→ находятся на верхних сторонах переключателей 1-1, 1-2), и другой тип представляет собой состояние
-арной PSK-связи (когда данные dq→ подключены к нижним сторонам переключателей 1-1, 1-2). Каждое состояние управляется переключателями. Если
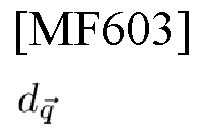
является

-арной PSK, т.е. состояние связи для передачи данных, переключатели находятся в нижнем положении.
Самая левая часть передатчика является входным сигналом

Когда передатчик пребывает в состоянии синхронизатора/радиолокационной станции, он выполняет четыре процедуры над сигналом чипа:

при этом, когда передатчик пребывает в состоянии связи для передачи данных, он выполняет шесть процедур над сигналом чипа:

Далее, в блоке k-кодера, состоящего из j'-го АС, выбранного из

параллельных АС, где символ

обозначает набор АС, а точка "." - просто один из набора.
В соответствии с вариантом осуществления настоящего изобретения кодер-переключатели 1-3, 1-4 выбирают j-ый АС в блоке k-кодера, согласно j, и передатчик модулирует по фазе выходной сигнал кодера j'-ым PSK-символом
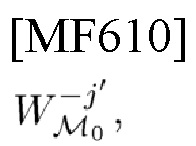
который определен посредством кодирования k с помощью целых чисел j, j', определенного как
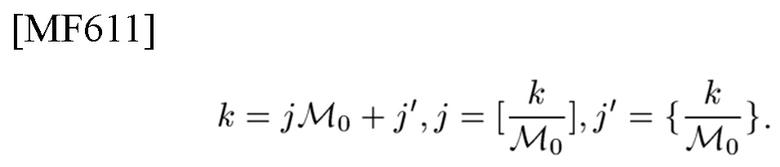
Когда переключатель 1-2 находится на верхней и нижней сторонах, соответственно

в (27) и

как определено ниже в (87), соответственно, могут быть пропущены через переключатель. Кроме того, в соответствии с вариантом осуществления настоящего изобретения передатчик (или кодер) модулирует эти СЕ при помощи несущей

передает полученный в результате сигнал полосы пропускания (РВ) через основной канал (МС) со сдвигами

и демодулирует зашумленный РВ-сигнал, загрязненный шумом, с помощью несущей

с получением в результате принятого сигнала.
Объяснение блочной диаграммы, изображенной на фиг. 12, окончено.
Если модулированный посредством PSK с высоким
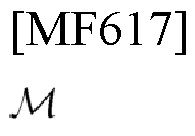
символ

передается и загрязняется фазовым шумом и дополнительным шумом, тогда сигнал

должен быть разложен. Однако, его разложение нереализуемо. Для его разложения в k-кодере (правый блок в нижней части фиг. 12) передатчик кодирует k в форме
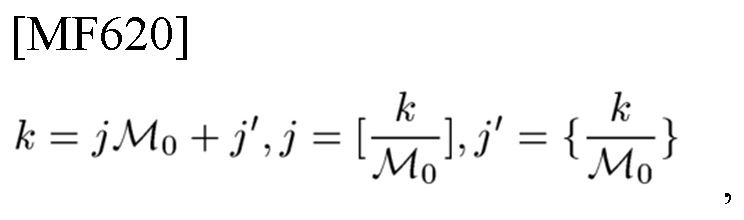
чтобы передать модулированный посредством PSK с низким

символ

При этом для передачи кодированного целого числа

передатчик в значительной степени опирается на способ совместной оценки задержки и доплеровского смещения частоты с высокой точностью, предложенный в этом раскрытии. А именно, передатчик, во-первых, делит пространство Θ' параметров (td, fD) и частотно-временную плоскость (TFP) S сигнала поровну на

подпространств 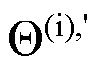 параметров и под-TFP S(i); во-вторых, назначает 2-D PC χ(i) каждой под-TFP; в-третьих, выполняет 2-D BPSK-модуляцию сигнала чипа с помощью
параметров и под-TFP S(i); во-вторых, назначает 2-D PC χ(i) каждой под-TFP; в-третьих, выполняет 2-D BPSK-модуляцию сигнала чипа с помощью
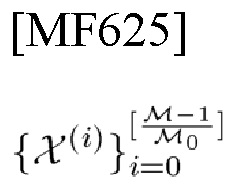
2-D PC; в-четвертых, комбинирует эти BPSK-модулированные сигналы посредством

-мультиплексирования; в-пятых, предполагает такую ситуацию, что полученный в результате мультиплексированный сигнал передается в j-ый канал, называемый j-ый искусственный канал (АС), выбранный из
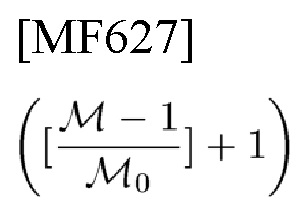
параллельных АС, согласно j, так что этот мультиплексированный сигнал представляет собой сигнал с частотно-временным сдвигом вокруг центра подпространства  параметров; в-шестых, модулирует с PSK выходной сигнал j-ого АС посредством j'-ого
параметров; в-шестых, модулирует с PSK выходной сигнал j-ого АС посредством j'-ого
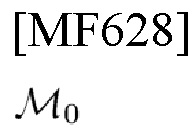
-PSK-символа

для получения СЕ передачи. Передатчик модулирует эту СЕ несущей
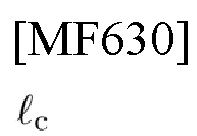
и выдает полученный в результате РВ-сигнал в МС со сдвигами
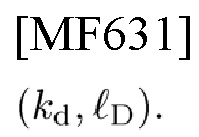
Внешний шум добавляется к выходному сигналу МС. Передатчик демодулирует зашумленный РВ-сигнал с помощью несущей

Полученный в результате ВВ-сигнал дает принятую СЕ.
Далее приведено объяснение блочной диаграммы, показанной на фиг. 13.
На фигуре 13 изображена блочная диаграмма приемника/синхронизатора (или декодера) системы связи, которая может быть использована также в качестве эффективной радиолокационной станции с высоким разрешением, оснащенной
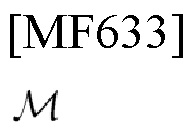
-арной PSK-связью.
Когда приемник пребывает в состоянии синхронизатора/радиолокационной станции (т.е. переключатель 2-1 находится на верхней стороне), он выполняет две процедуры над сигналом чипа:

причем когда приемник пребывает в состоянии связи для передачи данных (т.е. переключатель 2-1 находится на нижней стороне), он, во-первых, декодирует k в k-декодере, обозначенном k^ и определенном как
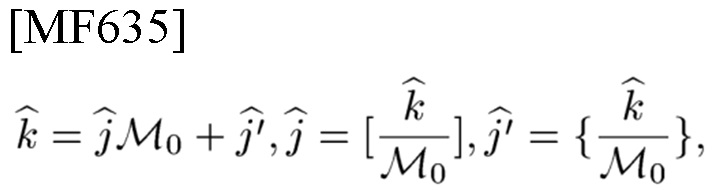
и, во-вторых, выполняет две процедуры над сигналом чипа:

чтобы выбрать j^-ый АС из

параллельных АС, где символ
обозначает набор АС, а точка "." - просто один из набора.
[0172] В соответствии с вариантом осуществления настоящего изобретения, когда переключатель 2-1 находится на нижней стороне, декодер выбирает

-ый АС в блоке k-декодера, согласно j^, и приемник модулирует по фазе выходной сигнал AC j^'-ым PSK-символом
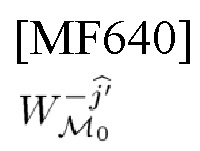
для получения СЕ шаблона. Приемник вычисляет CCR между принятой СЕ и этой СЕ шаблона в COR-блоке нижней части диаграммы на фиг. 13.
Обозначение COR означает корреляцию. Большой блок справа от COR показывает блок оценки максимального правдоподобия

и  восстановления
восстановления
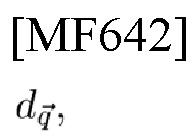
и декодирования k^ для выбранных адресов уровня чипа (ρ', ρ). Когда приемник пребывает в состоянии синхронизатора/радиолокационной станции (т.е. переключатель 2-2 находится на верхней стороне), он выполняет
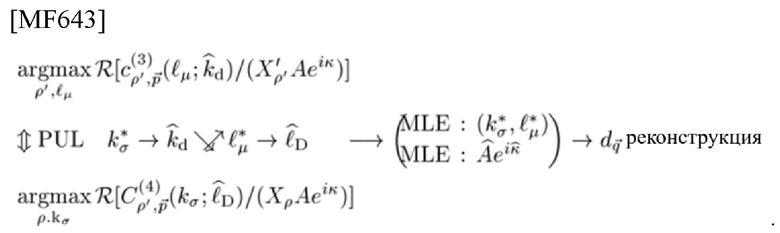
Причем когда приемник пребывает в состоянии связи для передачи данных (т.е. переключатель 2-2 находится на нижней стороне), он выполняет

Объяснение блочной диаграммы, изображенной на фиг. 13, окончено.
Далее рассмотрим такую ситуацию, что выполнена 2-D BPSK-демодуляция принятой СЕ с помощью сигнала чипа, модулированного по фазе с помощью 2-D PC. Когда приемник пребывает в состоянии связи для передачи данных (т.е. переключатель 2-1 находится на нижней стороне), он выполняет 2-D BPSK-модуляцию сигнала чипа с помощью оцененного

-го 2-D PC

и выдает 2-D BPSK-модулированный сигнал в

-ый АС, выбранный из
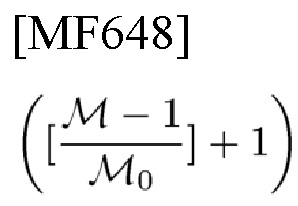
параллельных АС, и выполняет

-PSK-демодуляцию выходного сигнала АС с помощью символа
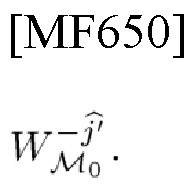
На конечной стадии в блоке MLE вещественные части TD-CCF и FD-CCF, нормализованные с помощью PC и коэффициента ослабления

максимизируются в терминах 4 переменных
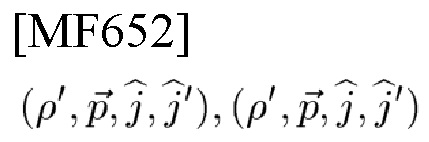
для получения MLE для

Если алгоритм PUL сходится, тогда приемник получает сходимость

Таким образом, сходимость является обычной в двух состояниях. Когда приемник пребывает в состоянии синхронизатора/радиолокационной станции (т.е. переключатель 2-2 находится на верхней стороне), он восстанавливает

при этом когда приемник пребывает в состоянии связи для передачи данных (т.е. переключатель 2-2 находится на нижней стороне), он декодирует k в виде

с использованием MLE для

Следует отметить, что даже когда приемник пребывает в обычном состоянии синхронизатора/радиолокационной станции (т.е. переключатель 2-2 находится на верхней стороне), он способен к модулированию/демодулированию с PSK с низким

для передачи данных
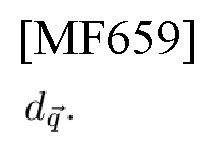
например,
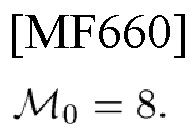
На фигуре 14 изображено распределение величин вещественных частей CCF на пространстве параметров задержки τ и доплеровского смещения частоты τ основного канала (МС). Она показывает, что основной лепесток изолирован.
Когда передатчик пребывает в состоянии синхронизатора/радиолокационной станции, основной лепесток расположен в

и он отличается от боковых лепестков, при этом двухволновой символ обозначает фоновый шум.
На фигуре 15 изображено распределение величин вещественных частей CCF на плоскости τ-ν, когда три параллельные АС добавлены к МС.
Три параллельные АС соединены последовательно перед МС, чтобы кодировать k с использованием

-PSK-модулированного сигнала. МС по-прежнему остается в

Однако когда АС добавляются к МС и трем последовательным каналам, МС+АС0, МС+АС1, МС+АС2 располагаются в
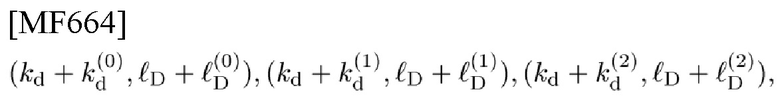
соответственно.
Временные сдвиги и частотные сдвиги являются просто аддитивными в количественном выражении. Однако одновременно возникает несколько новых PD, которые сопровождаются теоретико-групповым свойством. Чтобы получить распределение, как показано на фиг. 15, требуется тщательная оценка нескольких PD и максимизация вещественной части CCF с использованием MLE совместно с прибавлением параметрических переменных j, j' для исключения PD, как приведено в описании настоящего изобретения. Прибавленные переменные j, j' могут принимать

разных значений, соответственно.
На фигуре 16 изображена основная TFP S [0, Ts)×[0, Fs) символа и ее 4 разделенные под-TFP S(i). Это разделение предназначено для использования пространства параметров АС коразмерности 2 с NCP, присущим TFS, где термин "коразмерность" означает размер пространства параметров.
На фиг. 16 показано разделение на 4 части (разделение Габора) TFP сигнала с длительностью Ts и шириной полосы частот Fs (S(0), S(1), S(2), S(3)), при этом вертикальная ось добавлена перпендикулярно к TFP, где на нее нанесена шкала из 4 пар АС-сдвигов
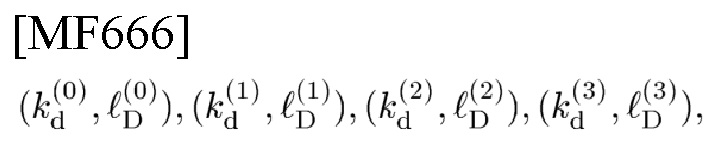
соответствующая третьей переменной TFP, помимо координатных осей Т и F.
На фигуре 17 также изображены разделенные на 4 под-TFP S(i) с соответствующим PC X(i), который предназначен для использования пространства параметров АС коразмерности 2 с NCP, присущим TFS.
Как показано на фиг. 17, каждое S(i) имеет частотно-временной сдвиг (k(i)d, 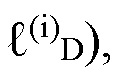 0≤i≤3. TFP S сигнала может быть идентифицировано с помощью целевого пространства параметра МС
0≤i≤3. TFP S сигнала может быть идентифицировано с помощью целевого пространства параметра МС

имеющего свою основную единичную плоскость

То есть, если цель существует вокруг TFP с адресом уровня данных

т.е. вокруг окрестности под-TFP [(p-1)Ts.pTs)×[(p'-1)Fs,p'Fs), тогда цель должна быть дискриминирована в пределах адреса уровня данных
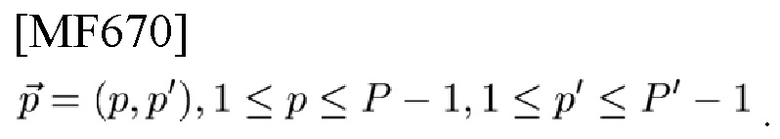
Таким образом, операция argmax над двумя вещественными частями CCF на фиг. 13 требует адрес уровня данных

независимо от использования связи для передачи данных.
Как рассмотрено выше, в передатчике и приемнике, соответственно на фиг. 12 и 13, верхняя и нижняя системы переключаются поочередно.
Системы, подключенные к верхним сторонам переключателей 1-1, 1-2, 2-1, 2-2 на фиг. 12 и 13, являются системами, соответствующими варианту осуществления из патентного документа [6], тогда как согласно варианту осуществления настоящего изобретения системы, подключенные к нижним сторонам этих переключателей, являются мультиплексированными системами связи, основанными на кодере/декодере, использующем NCP, присущее TFS.
Фигуры 12 и 13 позволяют нам отличить синхронизатор/радиолокационную станцию, не оснащенную связью с высоким М, и показать новизну настоящего изобретения.
В соответствии с вариантом осуществления этого изобретения в приемопередающей системе, чтобы передать модулированный посредством PSK
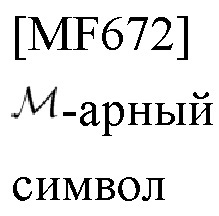

и эффективно включить "информацию" k в ее сигнал передачи, для целого числа

передатчик подготавливает

пар 2-D BPSK-кодов, т.е. пар TD-PC периода N

и FD-PC периода N'
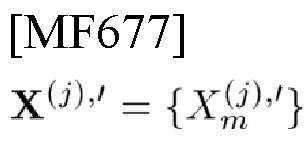
и делит основную единичную плоскость Θ'=[0,Ts)×[-Fs/2, Fs/2) пространства параметров задержки и доплеровского смещения частоты

и TFP S=[0,Ts)×[0,Fs) сигнала поровну на

подпространств параметров и под-TFP, соответственно обозначенных как

где Ts=NMΔt, Fs=N'M'Δf обозначают длительность и ширину полосы частот символа

Tmax=PTs, Fmax=P'Fs обозначают максимальные значения задержки и доплеровского смещения частоты, которые необходимо обнаружить с помощью целых чисел Р, Р' и интервалов дискретизации Δt, Δf.
Далее передатчик разлагает информацию k, представленную как

и передает пару целых чисел (j, j'), т.е. целочисленную часть

и ее дробную часть

вместо k. Для передачи кодированной целочисленной пары (j, j') передатчик 1) выполняет 2-D BPSK-модуляцию сигнала чипа с длительностью Тс=MΔt и шириной полосы частот Fc=MΔf с помощью 2-D PC X(j); 2) получает 2-D-модулированный по фазе сигнал, называемый TD-сигнатурой, и его преобразование Фурье (FT), называемое FD-сигнатурой; 3) выполняет частотно-временной сдвиг за счет сдвига (Ts, Fs) уровня данных и комбинирует эти сигнатуры с частотно-временными сдвигами в неперекрывающемся виде для получения
 -сигнатурно мультиплексированного
-сигнатурно мультиплексированного
сигнала. Далее передатчик предполагает, что мультиплексированный сигнал может передаваться по искусственному каналу (АС) с задержкой и доплеровскими сдвигами

расположенными вокруг центра подпространства 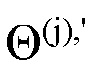 параметров. Для моделирования такой ситуации передатчик заставляет два TFSO типа 4
параметров. Для моделирования такой ситуации передатчик заставляет два TFSO типа 4

воздействовать на мультиплексированные TD- и FD-сигналы, соответственно. В-третьих, передатчик выполняет PSK-модуляцию полученного в результате TD-сигнала с частотно-временным сдвигом с помощью



(т.е. умножает PSK-модулированный сигнал на символ

), и комбинирует эти (Р/Р') сигналы в неперекрывающемся виде на TFP для генерирования TD-CE и ее DFT, FD-CE (см. фиг. 12), снабженные

-арной PSK-связью, вместо (27), представленной как

где

обозначает TD- и FD-сигнатуры (см. (25)), определенные как

где
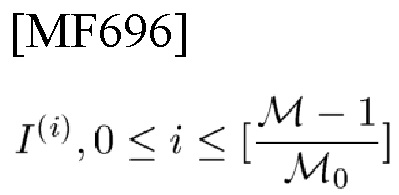
обозначает i-ый поднабор набора  адресов чипа S, который связан с i-ой под-TFP S(i), как показано на фиг. 16 и 17, и
адресов чипа S, который связан с i-ой под-TFP S(i), как показано на фиг. 16 и 17, и

TD- и FD-CE в (87) предназначены для передачи кодированных целых чисел (j, j') из k, в приемники по МС. Однако М-арная связь заставляет нас устанавливать периоды TD-PC и FD-PC приблизительно равными

их кратных для синхронизации связи или обнаружения цели для сохранения точности оценки (ситуация, в которой переключатели (1-1, 1-2, 2-1, 2-2) находятся на нижней и верхней сторонах на фиг. 12 и 13, соответствует ситуации с использованием связи для передачи данных или без нее).
Уравнение (87) говорит нам о том, что TD- и FD-сигнатуры

во-первых, 2-D BPSK-модулированы с помощью 2-D PC X(i) и, во-вторых, полученные в результате модулированные по фазе сигнатуры комбинируются в неперекрывающемся виде, так как
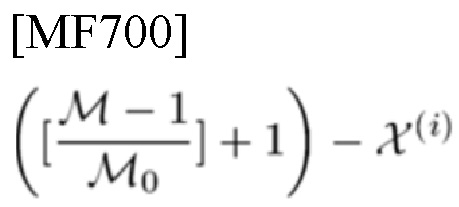 и сигнатурно мультиплексированный
и сигнатурно мультиплексированный
сигнал, и, в-третьих, такой дважды мультиплексированный сигнал является PSK-модулированным


и, в-четвертых, PSK-модулированный сигнал передается через j-ый АС со сдвигами

и, в-пятых, является PSK-модулированным

символом данных

Конечный сигнал является TD-CE

и ее DFT, т.е. FD-CE

где

с адресом q→=(q, q') уровня данных имеет значение 1.
В приемнике, оцененное k, обозначенное k^

разлагается с помощью декодированной пары целых чисел
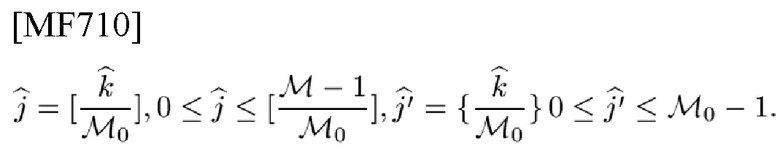
Приемник, во-первых, заставляет оцененные TD- и FD-TFSO типа 4

представляющие j^-ый АС со сдвигами

воздействовать на такие TD- и FD-сигнатуры, соответственно, и, во-вторых, выполняет PSK-демодуляцию этих TD- и FD-сигнатур с частотно-временными сдвигами при помощи

для исключения фазы PSK-модуляции (см. фиг. 13).
CCF типа 3 и типа 4, использующие АС-сдвиги, с кодированными целочисленными парами (j, j') и ее прибавленной парой для операций argmax

конкретно представлены соответственно вместо (38) и (43)

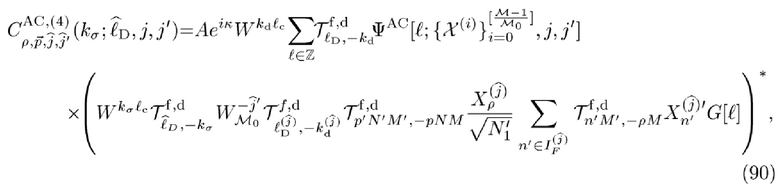
каждая из которых называется коррелятором типа 3 с АС-сдвигами и коррелятором типа 4 с АС-сдвигами, соответственно. В части сигнала передатчика (см. (87)) двух CCF выше (т.е. входной части статистики g (13)) TFSO типа 4 (или его частотный двойник)
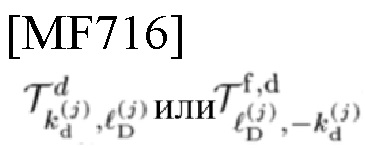
вставлен между произведением обеспечивающего сдвиг уровня чипа и данных TFSO типа 4 (или его частотного двойника) в передатчике (см. υ [k; Х(i)], 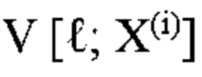 в (88))
в (88))
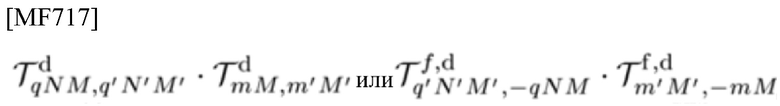
и TFSO типа 3, который представляет МС со сдвигами


При этом в части сигнала приемника двух CCF (89), (90) (т.е. части сигнала, подлежащего обнаружению, статистики g(13)), для

-арной PSK-модуляции, присутствуют

разных пар АС-сдвигов

Затем определяются соответствующие оцененные TFSO типа 3, представляющие эти АС

(или их частотные двойники
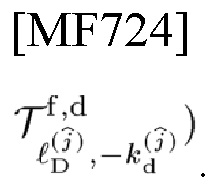
Эти TFSO вставлены между оцененным TFSO типа 1

(или оцененным TFSO типа 2

для оценки МС-сдвигов

и произведением обеспечивающих сдвиг уровня чипа и данных TFSO типа 4 или его частотного двойника в приемнике
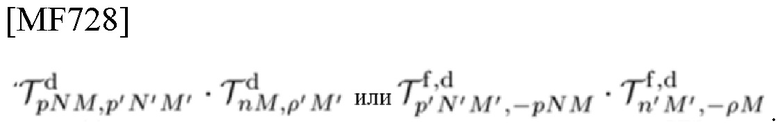
Система передатчик/приемник, показанная на фиг. 12 и 13, которая может быть использована также в качестве эффективной радиолокационной станции с высоким разрешением, оснащенной
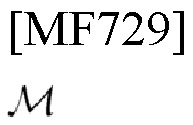
-арной PSK-связью, является типичным примером мультиплексирующих систем связи, использующим некоммутативные задержку и доплеровские сдвиги пространств параметров МС и АС коразмерности 2, где основная единичная плоскость Θ' пространства параметров задержки и доплеровского смещения частоты МС является исключительно разделенной и обозначена  Таким образом, очевидно, что термин "мультиплексирование с пространственным разделением по задержке и доплеровскому смещению частоты (dD-SDM)" [30], патентный документ [6], используется для обозначения такой мультиплексированной системы.
Таким образом, очевидно, что термин "мультиплексирование с пространственным разделением по задержке и доплеровскому смещению частоты (dD-SDM)" [30], патентный документ [6], используется для обозначения такой мультиплексированной системы.
В этой системе, вместо передачи
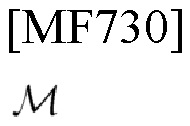
-арных данных k, передатчик отправляет сигнал, содержащий кодированные целые числа

Целое число j восстановлено посредством использования PD, обусловленного сдвигом задержки

и доплеровским сдвигом

расположенными вокруг центра  (см. фиг. 14, 15). Для включения (j, j') в сигнал передатчик, во-первых, выполняет 2-D BPSK-модуляцию сигнала чипа с помощью разных 2-D PC χ(i), во-вторых, комбинирует эти модулированные сигналы (сигнатуры) в неперекрытом виде посредством
(см. фиг. 14, 15). Для включения (j, j') в сигнал передатчик, во-первых, выполняет 2-D BPSK-модуляцию сигнала чипа с помощью разных 2-D PC χ(i), во-вторых, комбинирует эти модулированные сигналы (сигнатуры) в неперекрытом виде посредством

-мультиплексирования, в-третьих, вводит его в

-ый АС, и, в-четвертых, выполняет

-PSK-демодуляцию выходного сигнала АС символом

Для

разных значений

передатчик требует

параллельных АС и набор соответствующих им 2-D PC
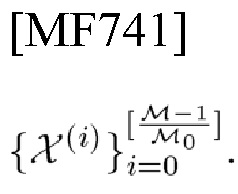
При этом в приемнике для обнаружения шаблона из четырехкрано-мультиплексированного сигнала чипа приемник выбирает оцененный

-ый АС и создает оценки максимального правдоподобия

PSK-связь с высоким
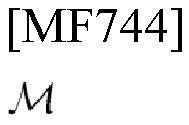
в передатчике реализована с помощью

мультиплексированных PSK-модуляций с низким

на основании использования некоммутативных АС-сдвигов и 2-D PC.
Такая мультиплексированная система, называемая "мультиплексирование с пространственным разделением по задержке и доплеровскому смещению частоты (dD-SDM)", является системой по разделению пространства S=[0, Ts)×[0, Fs) сигналов на несколько под-TFP и назначения 2-D PC каждой под-TFP для 2-D BPSK-модуляции. Использование 2-D PC приводит к добавлению новой оси, перпендикулярной TFP, в качестве третьей оси (см. фиг. 16 и 17). В частности, эта третья ось представляет ось сдвига, унаследовавшую NCP от АС-сдвигов коразмерности 2. Поэтому dD-SDM радикально отличается от обычного множественного доступа с кодовым разделением (DMA): TDMA, FDMA, CDMA и многочастотная (MC)-CDMA. Код с расширенным спектром (SS), используемый в последних двух, упрощает DMA за счет ортогональности прямоугольного чип-импульса с кодовой модуляцией. Алгоритм PUL, основанный на APT фон Неймана, позволяет нам совместно оценивать задержку и доплеровское смещение частоты с высокой точностью и может использоваться также для эффективной радиолокационной станции с высоким разрешением. Такая М-арная PSK-модуляция является предложением и простым методом в оптической связи, потому что понятие АС с некоммутативными сдвигами применимо к "физическому" оптическому волокну. Такая мультиплексированная система, называемая "мультиплексирование с пространственным разделением по задержке и доплеровскому смещению частоты (dD-SDM)", является системой, использующей пространство параметров некоммутативных сдвигов коразмерности 2. Она имеет трехмерное частотно-временное пространство (TFS), наслоенное АС-сдвигами (см. фиг. 16 и 17), в котором координатная ось, перпендикулярная символьному пространству, частотно-временной плоскости (TFP) [0, Ts)×[0, Fs), (которая идентифицирована посредством единичной плоскости целевого пространства), является осью сдвига со шкалой некоммутативных АС-сдвигов. Таким образом, dD-SDM отличается от обычных разделений сигнальной TFP: TDMA и FDMA. Алгоритм PUL, основанный на APT, которая позволяет нам оценить параметры с высокой скоростью и высокой точностью, является фундаментальной технологией. Следует отметить, что PSK-модуляция с более высоким М является многообещающей и простой технологией, которая применима к оптической связи, поскольку АС с некоммутативными сдвигами могут быть заменены несколькими типами физических линий передачи.
В источнике [30] и патентном документе [6] рассматривали проблему нескольких целей с

как применение обнаружения нескольких целей с кодовым разделением (CDMT) и предоставили способ обнаружения целей с использованием Npath 2-D PC и TFSO со сдвигами

вместе с фазовыми исключениями за счет произведения двух поворачивающих множителей

Однако этот способ заставляет нас разлагать небольшое количество фаз

Таким образом, когда

ошибки декодирования возникают из-за фазового шума и фазовых искажений. Кроме того, в приведенных выше источниках без использования TFSO типа 3

представляющего МС-сдвиги
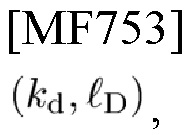
и его оцененного TFSO типа 4

была реализована

-арная связь. Более того, этот подход не годился для проблем нескольких целей в отношении сигнала с двойными задержкой и доплеровским сдвигом и не имел алгоритма оценки с гарантированным подтверждением.
Для решения этого, в соответствии с вариантом осуществления настоящего изобретения, автор настоящего изобретения определяет две новые CCF, использующие NCP, присущее АС-сдвигам
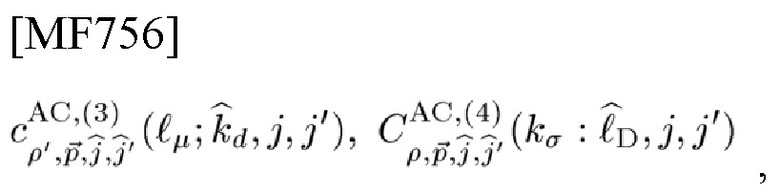
соответственно определенным (89), (90), в которых точно и строго оцениваются и исключаются несколько PD. Непросто восстановить

заключенное в TD-CE в (87)

(или FD-CE

как
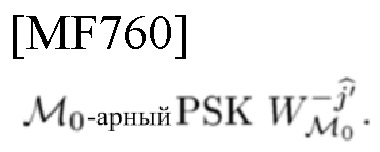
Подробности громоздких вычислений (89), (90) здесь опущены. Однако, две CCF для PSK-демодуляции с высоким

необходимы при использовании

2-D PC

и замене

в передатчике и

в приемнике. Эта замена сопровождается возникновением нескольких новых PD. Таким образом, необходимо заменить 2 переменные для MLE-операции над 2 переменными

(или

на одну из 4 переменных

(или
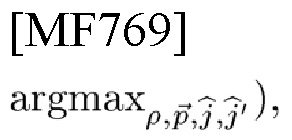
где

(или

Можно получить обобщенные версии (39), (44):

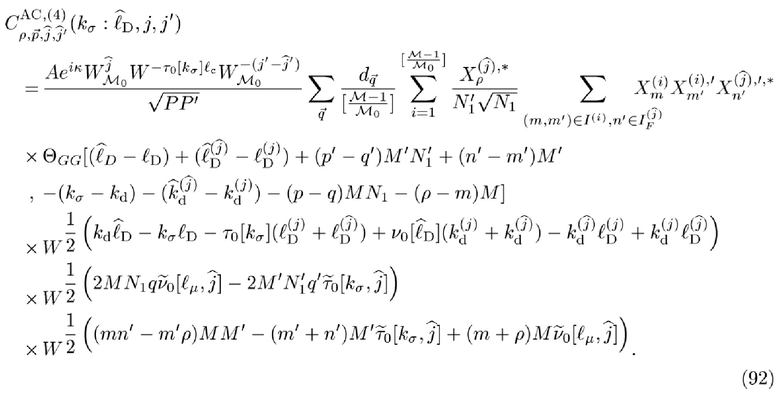
где


обозначают наборы TD- и FD-адресов n, n' чипов, соответствующие j^-ой под-TFP

и произведение наборов адресов
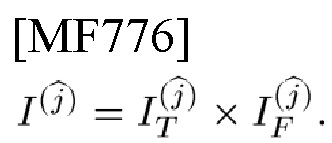
Функции неоднозначности (AF):θgg[τ, υ] и ΘGG[τ, υ] соответственно в (91) и (92) с функциями Гаусса g, G отделимы и экспоненциально убывают в терминах τ, υ. Это хорошо известное свойство и непересекающиеся наборы адресов чипов
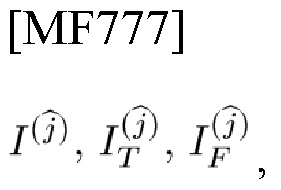
а также тот факт, что

находится вокруг центра Θ(j), говорит нам, что среди первого и второго аргументов AF всеми членами, относящимися к (p-q)MN1; (p'-q')M'N1' с р'≠q', р≠q и

с i≠j^ можно пренебречь. Таким образом, члены с р'=q', р=q и

остаются и, таким образом, только член, равный

выбирается из суммирования

идентифицируется посредством функций 
По этой причине передатчик делит исключительно Θ, выполняет 2-D BPSK-модуляцию сигнала чипа с помощью 2-D PC χ(i) и комбинирует эти модулированные сигнатуры в неперекрытом виде для осуществления

-мультиплексирования на основе

параллельных АС, которые предназначены для введения некоммутативных сдвигов. При этом
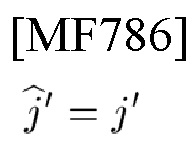
определяется членом исключения PD

Две вышеупомянутые CCF используют независимые 2-D PC

и PD, обусловленные некоммутативными АС-сдвигами

как функции оцененных целых чисел

для кодированного целого числа

целого числа k.
TD- и FD-CCF обеспечивают нам способ декодирования, использующий MLE на основе PUL. Этот способ может гарантировать разрешение по фазе по меньшей мере
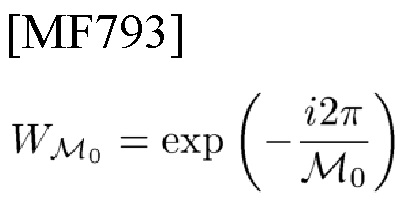
и поэтому устойчив к фазовому шуму.
Естественной является точная оценка задержки и доплеровского смещения частоты радиолокационной станции и установление синхронизации систем связи перед кодированием и декодированием

-арных PSK-данных. Так как нужно столкнуться с реальной ситуацией, когда передаваемый сигнал через МС со сдвигами
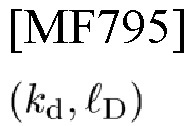
обрабатывается в приемнике, нам необходимы две CCF с АС-сдвигами в (91) и в (92). Такие приемники, когда переключатели находятся на верхней стороне на фиг. 12, 13, работают как синхронизатор (т.е. захват и отслеживание), а когда переключатели находятся на нижней стороне, сочетают синхронизатор и декодер для
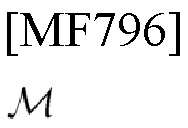
-арной PSK-связи и работают как радиолокационная станция, оснащенная передачей данных. Эта система является

-арной PSK-связью без амплитудной манипуляции (ASK) и обеспечивает секретную систему беспроводной связи, секретными ключами которой являются 2-D PC

Основная причина того, что приемники используют модуляцию без ASK, имеет два аспекта: (1) адаптивная и динамическая оценка коэффициента ослабления Aeik; (2) упрощение декодера. Оценка и исключение PD позволяют нам реализовать PSK-связь с высоким

в качестве эффективного использования радиоресурсов. Следует отметить, что использование

2-DPC подразумевает

-пользовательскую мультиплексированную связь.
<8.3 Обработка сигнала, использующая многомерные некоммутативные пространственные сдвиги и сдвиги пространственной частоты>
Даугман (Daughman) [33, 34] предоставил 2-D версию элементарных функций Габора
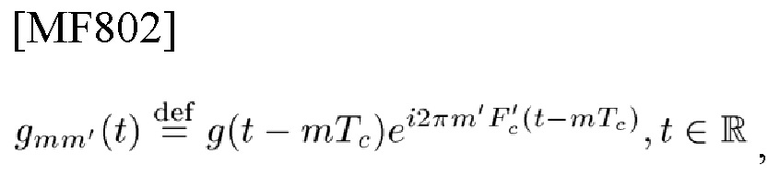
и указал на то, что 2-D представление Габора (будет определено далее) полезно для анализа и сегментации изображений. Прежде чем обсуждать исследование Даугмана, следует обратиться к теории группы Гейзенберга, рассмотренной Хоу (Howe) [5].
Для

определим два оператора сдвига
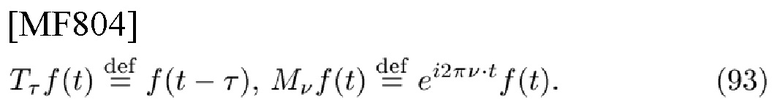
где ν⋅t обозначает внутреннее произведение. Для

введем скалярный оператор
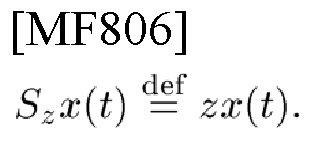
Тогда набор
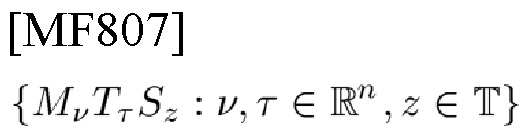
представляет собой группу унитарных операторов на

Рассмотрим набор
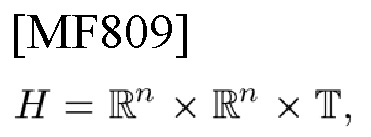
называемый (сокращенной) группой Гейзенберга степени n, и определим на нем закон комбинации

Определим карту ρ, т.е. точное унитарное представление Н, и автоформизм r для Н по правилу

Тогда можно мгновенно проверить, что в FT, обозначенном как ^, друг с другом переплетены два представления Н

То есть [5]

Даугман [35] указал на то, что модель профилей 2-D рецептивного поля, обнаруженная экспериментально в кортикальных простых клетках, которая отражает их характерные свойства настройки пространственной локализации, селективности ориентации, пространственной избирательности частоты и квадратурных фазовых отношений, является параметризованным семейством "2-D фильтров Габора". В терминах пространственной (SD) функции импульсного отклика (или комплексной функции Габора) g(x) с SD-переменными
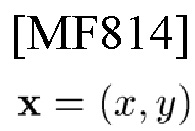
и соответствующего ей 2-D FT, т.е. функции области пространственной частоты (SFD)

с SFD-переменными
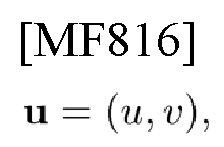
общая функциональная форма семейства 2-D фильтров Габора определена в [35, 36]
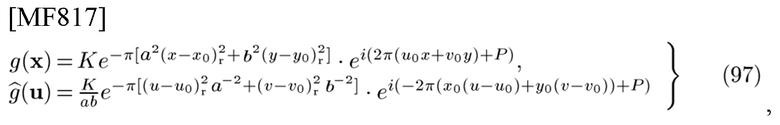
где Р обозначает фазу синусоиды, так что составляющая dc равна нулю, и

выражает поворот по часовой стрелке операции на θ, так что

SD-функция g(x), SFD-функция

являются совершенно симметричными и имеют свои сдвиги

при которых 2-D гауссова огибающая имеет пиковое значение. Важным свойством семейства 2-D фильтров Габора является достижение теоретической нижней границы совместной неопределенности в двух совместных областях х и u. Определяя неопределенность в каждой из четырех переменных по нормализованным вторым моментам

относительно основных осей, существует фундаментальный принцип неопределенности [35, 36]:

и нижняя граница неравенства достигается семейством 2-D фильтров Габора (97), где

являются модуляционными масштабирующими параметрами гауссиана.
Он предложил простую архитектуру нейронной сети (NN) для нахождения оптимальных значений коэффициентов в произвольных 2-D преобразованиях сигнала, которые в общем случае не могут быть ни полными, ни ортогональными, как указано ниже.
Рассмотрим некоторый дискретный 2-D сигнал I[х], скажем, изображение, поддерживаемое на [256×256] пикселях в х, которое нужно проанализировать или сжать путем представления его как набора коэффициентов расширения {ai} на некотором наборе 2-D элементарных функций

Попытка представить I[х] точно или в некотором оптимальном смысле, проецируя его на выбранный набор векторов  сводится к нахождению коэффициентов
сводится к нахождению коэффициентов  проекции, так что полученный в результате вектор Н[х]
проекции, так что полученный в результате вектор Н[х]

минимизирует квадрат нормы разностного вектора  Если данное изображение I[х] рассматривается как вектор в n-D векторном пространстве (например, n=65 536), тогда оптимальные коэффициенты
Если данное изображение I[х] рассматривается как вектор в n-D векторном пространстве (например, n=65 536), тогда оптимальные коэффициенты

определяются системой из n совместных уравнений с n неизвестными; но решение этой огромной системы практически нецелесообразно. Таким образом, он предложил NN архитектур с силой соединения

и входным изображением I[х]. Были предложены 2-D представления Габора для анализа и сжатия изображений, обнаружения краев, детекторов признаков и т.д. [37, 38, 39].
В этом описании автор настоящего изобретения указывает, что 2-D расширение Габора (100) можно рассматривать как совместное 2-D пространственное/частотно-пространственное представление (S/SF), использующее некоммутативные сдвиги (x0i, u0i) в терминах 2-D функций Габора
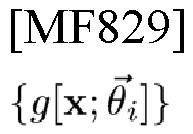
со сдвигами (x0i,u0i). В соответствии с важным прецедентом для обработок 1-D сигнала, использующих некоммутативность частотно-временных сдвигов, представленных в предыдущих частях этого описания, естественно рассматривать SD-представление (100) и соответствующее ему SFD представление симметрично. Для этого, пусть 2-D FT I[х] и Н[х]
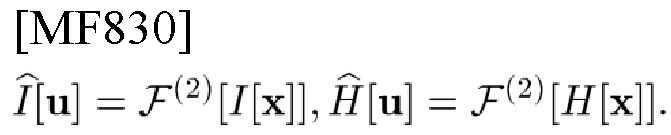
Тогда совместное пространственное/частотно-пространственное представление, вместо (100), определяется как

и пусть ε, ε' будут двумя подпространствами гильбертова пространства. Предположим, что

Квадратные нормы ошибок
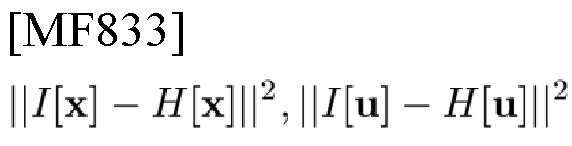
минимизируются путем использования двух ортогональных операторов проецирования (РО), проецирующих на εi, ε'i (определено ниже), соответственно

Теорема проецирования [27] говорит нам, что

обладают своим уникальным разложением

где 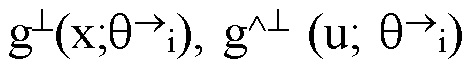 являются ортогональными дополнениями
являются ортогональными дополнениями  соответственно. Поэтому важно выбрать набор шаблонов
соответственно. Поэтому важно выбрать набор шаблонов

Например, пусть εi будет набором всех  которые являются (L1Δx×L2Δy) ограниченными в пространстве (SL) сигналами, и пусть ε'i будет набором из (L1Δu×L2Δv) ограниченных по пространственной частоте (SFL) сигналов.
которые являются (L1Δx×L2Δy) ограниченными в пространстве (SL) сигналами, и пусть ε'i будет набором из (L1Δu×L2Δv) ограниченных по пространственной частоте (SFL) сигналов.
Предположим, что

Тогда

являются РО, проецирующими на εi,ε'i; соответственно. Применим APT фон Неймана к двум РО и используем 2 2×2-D оператора локализации (LO), которые определены как

тогда можно получить оптимизированные коэффициенты расширения, представленные как
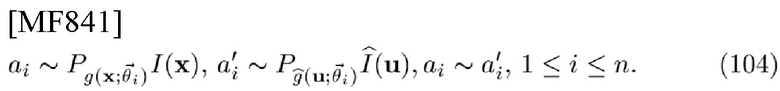
Такие 2-D LO выбирают ограниченный 4-D куб

вокруг адреса (x0i, u0i) пика в 4-D пространственной/частотно-пространственной плоскости и отфильтровывают остальное, где
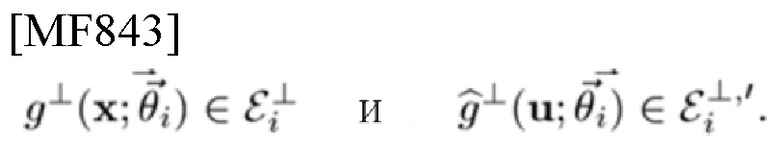

являются ортогональными дополнениями
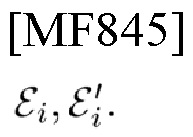
В отличие от операторов сдвига Хоу (93), для SD- и SFD-сигналов

автор настоящего изобретения вводит "полусдвиги" для симметричного свойства

и использует 2 × 2-D симметричные операторы пространственного сдвига и сдвига пространственной частоты (SSFSO) фон Неймана с этими полусдвигами, определенные с помощью
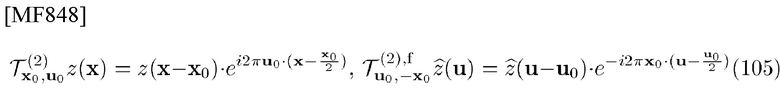
для 2-D функции Габора с адресами пика х0=(х0, у0), u0=(u0, v0)∈R2 в 2×2-D SD-SFD-пространстве

и его FT

Таким образом, автор настоящего изобретения может переписать функции Габора как

Рассмотрим DFT вышеупомянутых сигналов. Пусть (Δх, Δу) будут интервалами дискретизации 2-D пространственных переменных
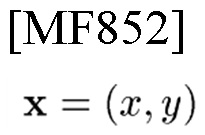
с размерами (L1, L2) декартовой сетки. Пусть

будет дискретной SD-функцией, дискретная пространственная переменная которой выражена как

Тогда интервал дискретизации 2-D пространственных частот

соответствующих пространственной сетке L1, L2, представлен как

и его дискретная переменная пространственной частоты представлена как

Используя 2 поворачивающих множителя

и 2-D DFT

можно получить соотношения между SFD-функцией

и SD-функцией


Таким образом, SD-функция

(или SFD-функция

имеет носитель
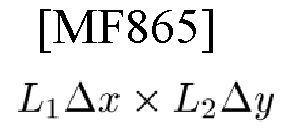
(или
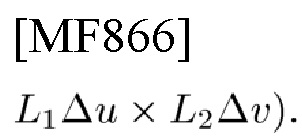
Если пространство адреса x0i (или u0i) пика на SD-пространстве (или SFD-пространстве) представляет собой

и задано условие нормализации
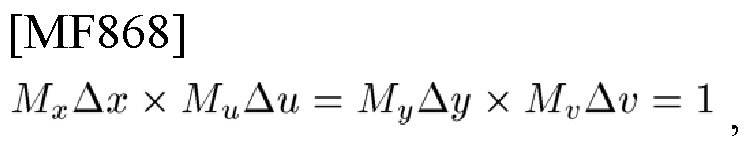
тогда
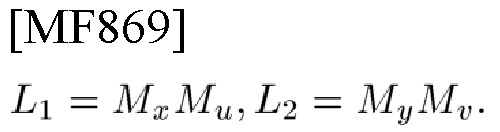
Если дискретные пространственные/частотно-пространственные сдвиги

представлены как

тогда 2×2-D дискретных SSFSO фон Неймана становятся

Эти 2×2-D симметричные SSFSO содержат 2-D половинные сдвиги

соответственно, как фазовые составляющие SD- и SFD-сигналов

Таким образом, SFSO (108) могут быть полезны для анализа изображений, извлечения признаков и сжатия данных, поскольку

эффективно извлекаются благодаря внутреннему произведению коэффициентов проекции в (102). Следует отметить, что анализ изображений, который включает временное изменение, считается предметом обработки сигналов с использованием трехмерного NCP.
<9 Отличительные признаки настоящего изобретения, а также способ и процесс его изготовления и применения>
Варианты осуществления, математические формулы и фигуры, описанные в описании настоящего изобретения, а также способ и процесс его изготовления и применения, являются всего лишь одними из примеров процесса и/или способа настоящего изобретения. Автор настоящего изобретения может честно сказать, что некоторые из вариантов осуществления являются реализованными примерами систем связи, которые используют NCP, присущее TFS, которые Габор преднамеренно исследовал в статье 1952 года [2].
Неперекрывающееся наложение сигналов на TFP обязательно влечет за собой PD из-за NCP, присущего TFS. Однако большинство исследователей в области связи имеют ограниченное представление о TFS с NCP или вовсе не имеют его. В такой ситуации ожидается, что системы связи, использующие NCP, присущее TFS, обеспечат новый класс цифровых мультиплексированных систем связи.
Системы связи, использующие NCP, присущее TFS, представленные в этом описании, могут быть пересмотрены с пяти следующих точек зрения.
(Точка зрения 1)
Симметричный оператор частотного и временного сдвига (TFSO), определенный и введенный в приведенных выше источниках (патентный документ [1] и [26, 27, 30]), имеет свойства: (i) его "половинные сдвиги", т.е. TD- и FD-PD, которые заключены в TD- и FD-сигнатурах, ясно показывают важную роль сдвига в оценке параметров; (ii) PD, обусловленное модуляцией и демодуляцией с помощью несущей lc, сопровождаемых задержкой kd,

возникает всегда; (iii) тот факт, что любые PD, встроенные в сигнал, могут быть компактно выражены в терминах степеней поворачивающего множителя

упрощает оценку нескольких PD и исключение PD.
(Точка зрения 2)
Модуляция с помощью TD- и FD-PC, т.е. 2-D двоичная манипуляция с фазовым сдвигом (BPSK)), является хорошо известной технологией модуляции. Однако если рассматривать это как пример того, что TFSO доступны, то можно увидеть, что TD- и FD-шаблоны заключены в широкополосный сигнал, модулированный посредством 2D-PC.
(Точка зрения 3)
Неперекрывающееся наложение сигналов на TFP является обычным способом эффективного использования радиоресурсов. Однако это наложение требует использования TFSO, который вызывает PD уровня данных. К счастью, такое PD играет важную роль в оценке параметров.
(Точка зрения 4)
В отличие от обычного использования только TD-функционалов (ML) максимального правдоподобия, TD- и FD-функционалы ML определяют массивы TD- и FD-CCF соответственно для обнаружения TD- и FD-шаблонов. TD- и FD-CCF определяют ортогональные операторы проецирования (РО) Р3, Р4 (или P1, Р2), соответственно проецирующие на пространства с ограничением по времени (TL) и ограничением по полосе частот (BL) как подпространства гильбертова пространства. Эти РО обеспечивают основу, на которой может быть построено более глубокое понимание APT.
(Точка зрения 5)
Вопреки распространенному мнению, что гауссиан, не удовлетворяющий условию Найквиста, является бесполезным,
альтернативные РО, представляющие соединение двух РО

(или
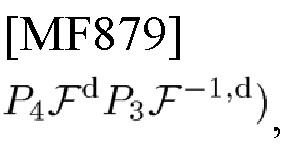
становятся оператором локализации совместно с использованием гауссиана, имеющего свойства: самодуальность FT, отделимая и экспоненциально убывающая AF гауссиана в терминах задержки и доплеровского смещения частоты. Это приводит к тому, что массивы TD- и FD-CCF дают отличные приемники.
Автор настоящего изобретения проясняет все вышеперечисленные точки зрения после публикаций в патентах и непатентных источниках. Настоящее изобретение демонстрирует свою собственную новизну. Все признаки новизны описаны следующим образом
(Пункт 1 новизны)
Предоставлены мультиплексированные системы связи, использующие NCP, присущие TFS на TFP. Кроме того, алгоритмы для оценки PD, обусловленного TFS, и для исключения их PD представлены на основании симметричных TFSO в (4), (24). Более того, показано, что такая пара операций заключения и исключения PD имеет решающее значение.
(Пункт 2 новизны)
TD- и FD-функционалы правдоподобия оценки доплеровского смещения частоты и задержки, соответственно, позволяют нам получать блоки ML-оценки параметров и осуществлять исключение PD с помощью соответствующих им MLE-корреляторов.
(Пункт 3 новизны)
Показано, что классическая BPSK-модуляция вызывает PD, обусловленные NCP, присущим ее TFS, но, к счастью, эти PD предоставляют подсказку по оценке параметров и восстановлении сигнала.
(Пункт 4 новизны)
Как неперекрывающееся наложение сигналов на TFP, так и модуляция (или демодуляция) для сигнала базовой полосы частот (или полосы пропускания), сопровождаемая задержкой, как традиционная технология в связи, вызывают PD, обусловленные NCP их TFS. К счастью, технологии заключения и исключения PD играют важную роль в обнаружении сигнала уровня данных. (Пункт 5 новизны)
Все из вышеуказанных PD исключаются с помощью TD- и FD-CCF. Эти CCF задействуют TD- и FD-PO, проецирующие на TL- и BL-пространства сигналов, соответственно как подпространства гильбертова пространства. Применение теоремы альтернативного проецирования (APT) фон Неймана к двум подпространствам определяет комбинированный оператор из двух РО, называемый оператором локализации (LO) на TFP. (Пункт 6 новизны)
Способ реконструкции сигнала Юла с использованием APT позволяет нам доказать, что LO гарантирует сходимость альтернативного алгоритма обновления параметров, называемого PUL. Это подразумевает, что LO, как функция адресов уровня данных и чипа, становится новым видом фильтров вместо обычного фильтра с крутым срезом в DSP и хорошо работает для радиолокационной станции без ограничения максимума задержки и доплеровского смещения частоты. (Пункт 7 новизны)
2-D сигнал, т.е. изображение обычно описывается с помощью совместных пространственных (8)/спектрально-частотных (SF) представлений, в частности 2-D представлений Габора. Тем не менее, многие исследователи, использующие традиционные методы, не знают, что 2-D S- и SF-сдвиги (SSFS), неявно включенные в 2-D функции Габора, неожиданно вызывают PD, обусловленные их NCP, как 1-D TFS. Автор настоящего изобретения работает с сигналом S области (SD) и сигналами SF области (SFD) симметрично и вводит совместные S/SF-представления размерности 2×2 в терминах 2-D функций Габора и их 2-D FT, определенные как (101), вместо проблемы представления изображения в терминах 2-D функций Габора (100).
Такая новая симметричная совместная проблема представления изображения (101) может быть решена за счет SD- и SFD- разложения (102) с использованием ортогональных операторов проецирования (РО), проецирующих на SD- и SFD-ограниченные пространства как подпространства гильбертова пространства, соответственно определенные как

2-D функции Габора определяются с использованием симметричных операторов пространственного сдвига и сдвига пространственной частоты (SSFSO) (105) (или (108)). Кроме того, комбинированные 2×2-D операторы локализации (LO) (103) из двух РО, к которым может быть применена APT фон Неймана, обеспечивают основы теории обработки 2-D сигнала, использующей NCP, присущее SSFS, для таких целей как анализ изображений, извлечение признаков и сжатие данных.
<<Пример 1 вариантов осуществления приемопередающей системы>>
Пример как вариант осуществления приемопередающих систем, основанных на вышеописанных теоретических аспектах, приведен вместе с приведенными фигурами.
Согласно варианту осуществления настоящего изобретения на фиг. 18 изображена блочная диаграмма, представляющая приемопередающую систему под номером 1, привязанным к окружающей ее пунктирной линии. Система связи под номером 1 содержит передающее устройство 100 и принимающее устройство 200. Эта приемопередающая система под номером 1 используется как для радиолокационной станции, так и для системы связи (например, приемопередающей системы для передачи голосовых данных и/или данных изображений).
(Передающее устройство 100)
Передающее устройство 100 представляет собой устройство, которое выполняет программу, заложенную в передатчик, как описано в вышеприведенном описании.
Как показано на фиг. 18, в качестве примера, передающее устройство 100 содержит часть 101 для сбора передаваемых данных, часть 102 для генерирования передаваемого сигнала и передающую часть 103.
(Часть 101 для сбора передаваемых данных)
Часть 101 для сбора передаваемых данных выполняет сбор данных, подлежащих передаче; передаваемые данные представляют собой, например, акустические данные, данные изображения и могут быть текстовыми данными, такими как любые оцифрованные данные.
Если приемопередающая система под номером 1 используется для радиолокационной станции, тогда передаваемые данные могут быть радиолокационным импульсным сигналом.
(Часть 102 для генерирования передаваемого сигнала)
Часть 102 для генерирования передаваемого сигнала выполняет обработку сигнала передаваемых данных, полученных частью 101 для сбора передаваемых данных, и генерирует передаваемый сигнал.
Как пример, часть 102 для генерирования передаваемого сигнала содержит SFB, как показано на фиг. 4-7, или по меньшей мере один из них.
Как упомянуто выше, примером обработки для генераторов сигнала, подлежащего передаче, является модуляция с помощью TD- и FD-фазовых кодов (PC) периодов N, N', т.е. 2-D BPSK-модуляция.
Примерами передаваемого сигнала, генерируемого частью 102 для генерирования сигнала, подлежащего передаче, являются, например, как упомянуто выше

Автор настоящего изобретения может перечислить обработку, описанную в подразделе<4. Сигнатурные сигналы и шаблоны в TD и FD>, как конкретные примеры обработки в части для генерирования передаваемого сигнала.
Часть для генерирования сигнала, подлежащего передаче, под номером 102 может представлять собой устройство, которое выполняет программу, заложенную в передатчик, как описано в подразделе <7.1 Передатчики для генерирования сигнатуры и радиолокационного сигнала>. Альтернативно, часть для генерирования сигнала, подлежащего передаче, под номером 102 может представлять собой устройство, которое выполняет программу, заложенную в передающее устройство, как описано в подразделах <8.1 Обнаружение нескольких целей с использованием CDMT> и <8.2 Обнаружение нескольких целей с использованием искусственной задержки и доплеровского смещения частоты>.
(Передающая часть 103)
Передающая часть 103 передает передаваемый сигнал, генерируемый частью для генерирования сигнала, подлежащего передаче, под номером 102. (Принимающее устройство 200)
Принимающее устройство 200 представляет собой устройство, которое выполняет программу, заложенную в приемник, как описано в вышеприведенном описании.
Как показано на фиг. 18, принимающее устройство 200, например, содержит принимающую часть 201, часть 202 оценки сдвигов и извлечения принятых данных и часть 203 принятия решения относительно принятых данных. (Принимающая часть 201)
Принимающая часть 201 принимает передаваемый сигнал, который поступает от передающего устройства 100. Примерами принятого сигнала, который принимающая часть 201 принимает, являются, например, как упомянуто выше,

Часть 202 оценки сдвигов и извлечения принятых данных (просто называемая оценивающей частью) выполняет сдвиг сигнала, принятого принимающей частью 201, посредством оцененных сдвигов и извлекает принятые данные.
Часть 202 оценки сдвигов и извлечения принятых данных содержит, например, по меньшей мере один AFB, показанный на фиг. 8-10. Часть 202 оценки сдвигов и извлечения принятых данных выполняет несколько программ, например, как описано в подразделах <5. М-арное обнаружение и оценка TD- и РТЭ-сигналов> и <6. TD- и FD-кросскорреляции для оценки параметров>.
Часть 202 оценки сдвигов и извлечения принятых данных представляет собой устройство, которое выполняет программу, как описано в подразделе <7.2 AFB; схема приемников и кодера>. Более того, часть 102 для генерирования сигнала, подлежащего передаче, представляет собой устройство, которое выполняет программу, как описано в подразделе <8.2 PSK-связь с высоким М на основе использования некоммутативных частотно-временных сдвигов>.
Таким образом, часть 202 оценки сдвигов и извлечения принятых данных реализует способ приема сигнала и выполняет программу согласно стадии оценки для осуществления оценки временного сдвига и частотного сдвига из принятого сигнала (см. фиг. 13 и (38), (43) (или (89), (90)) в соответствии с переключателями 2-1, 2-2 на верхней (или нижней) стороне с обращением к пространству параметров некоммутативных сдвигов коразмерности 2 (см. фиг. 17).
Часть 102 для генерирования сигнала, подлежащего передаче, выполняет программу согласно стадии сдвига для частотно-временного сдвига сигнала, подлежащего передаче (см. фиг. 12 и (25), (27) (или (87), (88))), в соответствии с переключателями 1-1, 1-2 на верхней (или нижней) стороне с обращением к пространству параметров некоммутативных сдвигов коразмерности 2 (см. фиг. 17).
Пространство параметров некоммутативных сдвигов коразмерности 2 является 3-мерной пространственной версией 2-D частотно-временной плоскости с временными и частотными координатами с прибавлением некоммутативных частотно-временных сдвигов в качестве третьей координаты (см. фиг. 17).
Как упомянуто выше, пара неизвестных задержки и доплеровского смещения частоты

сама по себе является парой некоммутативных сдвигов в пространстве параметров коразмерности 2, подобно паре АС-сдвигов. Пространство параметров относится к операциям сдвига, действующим на сигнал на частотно-временной плоскости (TFP); такая "плоскость сдвига" должна быть дискриминирована относительно TFP (фиг. 16). А именно, чтобы провести различие между четырьмя фундаментальными арифметическими операциями, а также дифференциальным и интегральным исчислением в терминах переменных времени t, частоты f, и операциями некоммутативного сдвига для вычисления фазовых членов, следует отметить, что NCP операции сдвига является особенностью предлагаемого частотно-временного анализа (например, третья координата фиг. 17).
Несколько комментариев к патентным документам [6]-[8] перечислены далее.
a) Фазовое искажение (PD)

(или его дискретизированная версия

которое вызывают модуляция и демодуляция с помощью несущей fc, сопровождаемые задержкой td (или kd), в вышеприведенных патентных документах не учитывалось. Тогда как в настоящем описании эти PD и PD eiκ коэффициента ослабления Aeiκ совместно и согласованно исключаются. Причина, по которой необходима согласованная обработка PD, является следующей: во-первых, каждое PD не является независимым друг от друга, во-вторых, PD распространяется благодаря своему теоретико-групповому свойству; таким образом, точное исключение этих PD является непростой задачей. Следовательно, действия по обновлению оценок временных и частотных сдвигов должны выполняться в сочетании с фазовыми исключениями (т.е. необходима одновременная и параллельная обработка: например, (59)).
b) Временные и частотные сдвиги в этом описании упоминаются как переменные пространства параметров коразмерности 2, связанные с двумя переменными: временем и частотой на TFP сигнала, соответственно. Операции некоммутативного сдвига вызывают PD. При этом временные и частотные смещения в связи представляют собой отклонения от периода импульса и несущей, соответственно.
(1) Оцененные временные и частотные смещения в патентных документах [7, 8] и временные и частотные смещения в системе связи на основе OFDM в патентном документе [7] являются отклонениями от периода чип-импульса и несущей, соответственно, и соответствуют временному сдвигу td и частотному сдвигу fD в этом описании, соответственно. А именно, оба из вышеупомянутых двух патентных документов могут быть рассмотрены как обычные способы сбора и отслеживания для синхронизации, поскольку они не содержат информации о некоммутативности td, fD.
(2) Чтобы избежать путаницы между предполагаемыми сдвигами и смещениями, автор настоящего изобретения использует термин: не смещения, а "полусдвиги показателя степени экспоненциальной функции" (в том смысле, что обычные сдвиги делятся пополам). Один из главных признаков в этом описании состоит в том, чтобы разработать передаваемый сигнал так, чтобы его фазовая функция всегда заранее содержала половинные сдвиги, и чтобы исключить PD на основании теоретико-группового свойства NCP, присущего TFS.
c) В патентном документе [8] рассматривалась преамбула принятого сигнала как шаблонный сигнал только в TD, но в нем не было информации о сигналах в FD и был предоставлен традиционный способ оценки канала без информации о NCP.
(1) Чтобы обеспечить доказательство сходимости алгоритма петли фазового обновления (PUL), предложенном в патентном документе [6], автор настоящего изобретения 1) определяет подпространства гильбертова пространства εi, 1≤i≤4, которому принадлежит шаблон; 2) показывает, что каждая из N' TD-CCF, CCF типа 3 (или CCF типа 1) дает оператор проецирования Р3 (или P1), проецирующий на NMΔt- (или LΔt-) ограниченное по времени (TL) гильбертово подпространство ε3 (или ε1), и что каждая из N FD-CCF, CCF типа 4 (или CCF типа 2) дает оператор проецирования Р4 (или Р2), проецирующий на N'M'Δf- (или LΔf-) ограниченное по полосе частот (BL) гильбертово подпространство ε4 (или ε2); 3) доказывает, что алгоритм PUL, использующий оператор локализации (LO), т.е. оператор P3F-1,dP4Fd (или P4FdP3F-1,d) теоремы альтернативного проецирования (APT) фон Неймана для сопоставления 2-D шаблонов на TFP сходится на пересечении TL гильбертова подпространства и BL гильбертова подпространства (F-1,d, Fd обозначает IDFT и DFT); кроме того, 4) показывает, что взаимодействие является пустым по теореме Юла и что PUL может давать оценки td, fD с точностью в пределах длительности LΔt и ширины полосы частот LΔf гауссова сигнала чипа и с вычислительной сложностью O[N+N'], но не O[N×N'], где N, N' обозначает количества TD- и FD-CCF (L=(ΔtΔf)-1=ММ').
(2) Алгоритм MMSE для оценки характеристик канала, предложенный в патентном документе [8], основан на правиле Бейеса и способе оценки с 2 параметрами. Таким образом, этот алгоритм имеет вычислительную сложность O[N×N']. При этом настоящее описание использует большое количество функционалов вероятности (LF), которое содержит N' TD-LF для оценки доплеровского смещения частоты и N FD-LF для оценки задержки. Каждый LF основан на правиле Бейеса. Один TD-LF среди множества TD-LF и FD-LF среди множества FD-LF в TL-TD и BL-FD гильбертовых подпространствах, соответственно, выбираются альтернативно и в смысле оценки максимального правдоподобия (MLE). Таким образом, альтернативный алгоритм с вычислительной сложностью O[N+N'] радикально отличается от традиционных способов.
Часть 202 оценки сдвигов и извлечения принятых данных выполняет программу, например, программу согласно стадии оценки для осуществления оценки временного сдвига и частотного сдвига из принятого сигнала, как описано в (84) и связанным с ним описанием. Стадия оценки использует TFSO типа 1 с оцененным временным сдвигом и частотным сдвигом

и TFSO типа 2 с временным сдвигом и оцененным частотным сдвигом

и оценивает временной сдвиг и частотный сдвиг, которые заключены в принятом сигнале.
Стадия оценки, упомянутая выше, использует 4 разных типа TFSO: TFSO типа 1 с оцененным временным сдвигом, частотным сдвигом и фазовой составляющей, представляющей половинный сдвиг оцененного временного сдвига,

TFSO типа 2 с временным сдвигом, оцененным частотным сдвигом и фазовой составляющей, представляющей половинный сдвиг оцененного частотного сдвига,
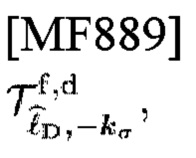
TFSO типа 3 с наблюдаемым временным сдвигом, подлежащим оценке, наблюдаемым частотным сдвигом, подлежащим оценке, и фазовой составляющей, представляющей половинный сдвиг временного сдвига, подлежащего оценке,
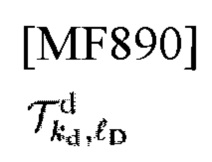
(или частотный двойник TFSO типа 3

и TFSO типа 4, представляющий оцененный временной сдвиг, оцененный частотный сдвиг и фазовую составляющую из-за половинного сдвига оцененного временного сдвига,

(или частотный двойник TFSO типа 4

и оценивает временной сдвиг и частотный сдвиг, которые заключены в принятом сигнале.
Фазовая функция TD-сигнала, подлежащего передаче, содержит фазовую составляющую, представляющую половинные сдвиги одного или более параметров временного сдвига; фазовая функция FD-сигнала, подлежащего передаче, содержит фазовую составляющую, представляющую половинные сдвиги одного или более параметров частотного сдвига.
Принимающее устройство 200, упомянутое выше, может реализовывать приемное устройство с высокой эффективностью. Например, когда приемник 200 используется для приемника радиолокационной станции, он становится высокоскоростным приемным устройством.
Например, как описано в (84) и связанном с ним описанием, на стадии оценки в программе, которую выполняет часть 202 оценки сдвигов и извлечения принятых данных, приемник использует CCF типа 1 (см. MF309, (38)), которая представлена с использованием TFSO типа 1, упомянутого выше,

и CCF типа 2 (см. MF336, (43)), которая представлена с использованием TFSO типа 2, упомянутого выше,

обращается к этим CCF, и оценивает временной сдвиг и частотный сдвиг, которые заключены в принятом сигнале.
Как упомянуто выше, вышеупомянутая CCF типа 1 может быть представлена как (см. MF309, (38))
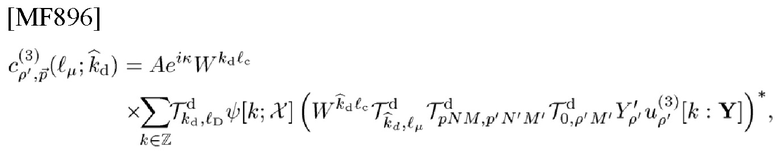
и вышеупомянутая CCF типа 2 может быть представлена как (см. MF336, (43))

На стадии оценки в программе принимающее устройство 1) использует CCF типа 1 с АС-сдвигами, которые представлены с использованием TFSO типа 1, типа 3 и типа 4, упомянутых выше (см. MF715, (89)).

и упомянутую выше CCF типа 2 с АС-сдвигами, которые представлены с использованием TFSO типа 2, типа 3 и типа 4, упомянутых выше (см. MF715, (90)).

2) обращается к этим CCF, и 3) оценивает временной сдвиг и частотный сдвиг, которые заключены в принятом сигнале.
Как описано выше, TD-CCF типа 1 с АС-сдвигами (см. MF715, (89)) и FD-CCF типа 2 с АС-сдвигами (см. MF715, (90)) содержат PD, обусловленное NCP модуляции и демодуляции с помощью несущей fc (или lc), сопровождаемых задержкой td (или kd),
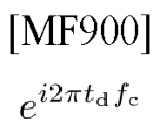
или его дискретизированную версию

и PD, обусловленное фазовой составляющей eiκ коэффициента ослабления Aeiκ.
Как описано в MF400 (см. (60), (61)) и в связанном с ним описании, часть 202 оценки сдвигов и извлечения принятых данных обновляет пару оцененной задержки и оцененного доплеровского смещения частоты

или

с использованием рекурсивной формулы для CP (АС-сдвиг (60), MF400, но версия с АС-сдвигом формулы для ОР (61) опущена)

и подставляет пару MLE

в пару из двух оценок

Кроме того, операции в части 202 оценки сдвигов и извлечения принятых данных должны
1) обращаться к TD-CCF типа 1 с АС-сдвигами (см. MF715, MF898, (89))
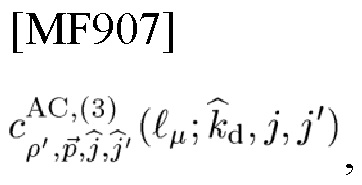
вещественная часть которой максимизируется путем изменения 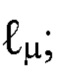 2) определять MLE
2) определять MLE

и 3) подставлять его в
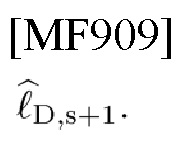
Другие операции в части 202 должны 1) обращаться к FD-CCF типа 2 с АС-сдвигами (см. MF715, MF899, (90))

вещественная часть которой максимизируется путем изменения kσ; 2) определять MLE

и 3) подставлять его в

Таким образом, функционирование части 202 оценки сдвигов и извлечения принятых данных заключается в альтернативном обновлении оценок временного сдвига и частотного сдвига.
На вышеупомянутой стадии оценки в части 202 оценки сдвигов и извлечения принятых данных оценивается временной сдвиг и частотный сдвиг, которые заключены в сигнале, с использованием MLE частотного сдвига для обнаружения N' TD-шаблонов и MLE временного сдвига для обнаружения N FD-шаблонов.
Кроме того, на вышеупомянутой стадии оценки в части 202 оценки сдвигов и извлечения принятых данных при обращении к TD-CCF типа 1 с АС-сдвигами (см. MF715, MF898, (89))

и FD-CCF типа 2 с АС-сдвигами (см. MF715, MF899, (90))

принимающее устройство, во-первых, заменяет правую часть первого уравнения (60)

и правую часть второго уравнения (60)

соответствующими CCF с АС-сдвигами, и, во-вторых, применяет операцию argmax к этим CCF с АС-сдвигами, и, в-третьих, дополняет переменные операции argmax парой из двух оцененных целых чисел (см. MF904, (109))
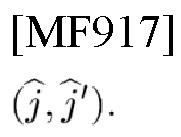
Приемное устройство на вышеупомянутой стадии оценки в части 202 оценки сдвигов и извлечения принятых данных является принимающей частью, принимающей сигнал

который является выходным сигналом j-го АС с задержкой и доплеровскими сдвигами
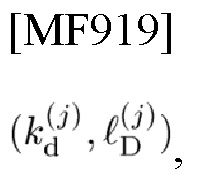
имеющими целое число j, одно из двух целых чисел, кодированных посредством кодера к для
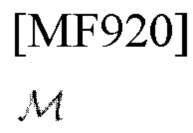
-арной связи.
В соответствии с вариантом осуществления настоящего изобретения, как рассмотрено выше, приемное устройство, которое представляет собой устройство приема сигнала, содержит оценивающую часть для оценки временного сдвига и частотного сдвига, которые заключены в сигнале, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2.
Кроме того, в MLE, передаваемые TD- и FD-CE сигналы (87) (или (27)) (согласно состоянию, в котором переключатели 1-1, 1-2 в передатчике, изображенном на фиг. 12, находятся на нижней или верхней стороне, соответственно, степень мультиплексирования изменяется) предоставляются путем мультиплексирования соответствующих им TD- и FD-сигнатур (88) (или (25)); в то время как сами сигнатуры получаются путем 2-D BPSK-модуляции функции Гаусса и FD-функции с помощью 2-D PC. Как показано в (87), передаваемые TD- и FD-CE сигналы для

-арной связи получаются следующим образом; TD- и FD-сигнатуры, во-первых, мультиплексируются с использованием 2-D BPSK-модуляции с помощью j-го PC, выбранного среди набора независимых 2-D PC

согласно кодированной целочисленной паре из к


и во-вторых, проходят в АС-канал с соответствующими ему временным и частотным сдвигами

или эквивалентно передатчик заставляет соответствующие TFSO

воздействовать на мультиплексированную TD- или FD-сигнатуру.
В соответствии с вариантом осуществления настоящего изобретения, как рассмотрено выше, способ передачи, который представляет собой способ передачи сигнала, подлежащего передаче, предусматривает стадию сдвига для частотно-временного сдвига сигнала, подлежащего передаче, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2.
Кроме того, на вышеупомянутой стадии MLE при использовании CCF в (89), (90), которые являются кросскорреляциями между принятым сигналом
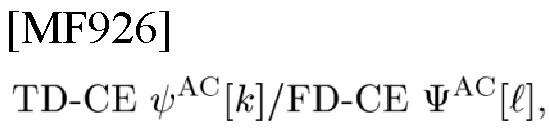
проходящим через АС-канал с соответствующими ему временным и частотным сдвигами

характеризующимися кодером к для

-арной связи, и оцененным принятым шаблоном (первый и второй члены правых частей (89), (90), обозначают передаваемый сигнал и оцененный принятый шаблон, соответственно), следует отметить тот факт, что символ Σ в (87)-(90) подразумевает мультиплексирование, эквивалентное неперекрывающемуся наложению сигнала, и что такое мультиплексирование может быть смоделировано с использованием нескольких типов TFSO. В процессе генерирования передаваемого сигнала на фиг. 12 выполняется несколько типов мультиплексирования. В (87), (88) TD- и FD-сигнатуры получаются путем мультиплексирования 2-D BPSK-модулированных TD- и FD-сигналов чипа с помощью 2-D PC

соответственно периодов

Передаваемые TD- и FD-CE получаются путем частотно-временного сдвига полученных в результате TD- и FD-сигнатур за счет сдвигов уровней данных и мультиплексирования этих сигнатур. Если наложение сигналов легковыполнимо без использования временного и частотного сдвигов, то обнаружение шаблонов затруднено; нужно расплачиваться за PD, обусловленные операциями сдвига. Тем не менее, очевидно, что, к счастью, PD являются ценными ключами в обнаружении шаблонов и, следовательно, TFSO являются важными инструментами для точной оценки PD и исключения PD. Кроме того, правые части (89), (90) содержат PD, обусловленные модуляцией и демодуляцией с помощью несущей 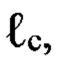 сопровождаемых задержкой kd,
сопровождаемых задержкой kd,
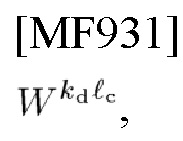
и компенсацию

за исключение PD, обусловленного фазовой модуляцией посредством кодированного целого]' из к

Как показано выше, на стадии сдвига генерируется сигнал, подлежащий передаче, путем PSK-модуляции сигнала чип-импульса в TD с помощью TD-PC периода N и PSK-модуляции TD-PSK-модулированного TD-импульсного сигнала с помощью FD-PC периода N' для генерирования версии с несколькими несущими TD-PSK-модулированного TD-импульсного сигнала, который представляет собой передаваемый сигнал.
В соответствии с вариантом осуществления настоящего изобретения в устройстве передачи в соответствии с вариантом осуществления настоящего изобретения передатчик, когда переключатели 1-1, 1-2 находятся в нижней стороне на фиг. 12, во-первых, выполняет PSK-модулирование TD-сигнала чипа с помощью TD-PC периода N, и, во-вторых, выполняет PSK-модулирование PSK-модулированного сигнала с помощью FD-PC периода N', в-третьих, мультиплексирует дважды модулированный сигнал с несколькими несущими с помощью символов данных, и, в-четвертых, пропускает мультиплексированный сигнал данных через АС со сдвигами
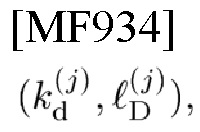
имеющими кодированное целое число j из k


Выходной сигнал АС дает
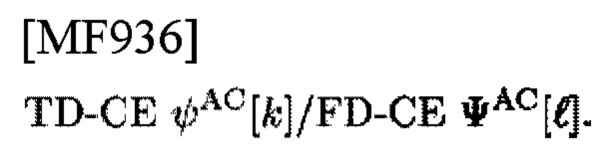
В соответствии с вариантом осуществления настоящего изобретения в принимающем устройстве в соответствии с вариантом осуществления настоящего изобретения приемник, когда переключатели 2-1, 2-2 переключены вниз на фиг. 13, приемник выполняет максимизацию вещественных частей CCF (см. MF715, (89), (90)) в терминах 4 переменных операции argmax

Если алгоритм PUL для обновления MLE

сходится, тогда может быть восстановлен символ данных

и может быть выполнено декодирование k.
В соответствии с вариантом осуществления настоящего изобретения обобщение нескольких устройств с практическими применениями к изображениям в подразделе 8.3 представляет собой естественное 2-D расширение 1-D сигнала с использованием половинных сдвигов из-за NCP пространственных сдвигов и сдвигов пространственной частоты (SSFS) (см. (102)-(108)).
(Расширенная версия варианта осуществления для изображений)
В соответствии с вариантом осуществления настоящего изобретения в этом описании предложен способ приема изображения, который предусматривает стадию оценки для осуществления оценки пространственного сдвига и сдвига пространственной частоты, которые заключены в принятом сигнале изображения, с обращением к пространству параметров коразмерности 2, где каждый из пространственного сдвига и сдвига пространственной частоты имеет размерность ≥2.
(Расширенная версия варианта осуществления для изображений)
В соответствии с вариантом осуществления настоящего изобретения приемник на вышеупомянутой стадии оценки обращается к 2×2-D симметричным SSFS-операторам (SSFSO)
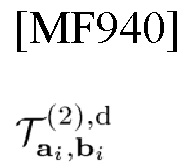
и их частотному двойнику


и оценивает пространственные сдвиги и сдвиги пространственной частоты.
(Расширенная версия варианта осуществления для изображений)
В соответствии с вариантом осуществления настоящего изобретения в этом описании предложен способ передачи сигнала изображения, предусматривающий стадию сдвига для применения пространственного сдвига и сдвига пространственной частоты в отношении сигнала изображения, подлежащего передаче, с обращением к пространству параметров, при этом каждый из пространственного сдвига и сдвига пространственной частоты имеет размерность ≥2.
(Расширенная версия варианта осуществления для изображений)
В соответствии с вариантом осуществления настоящего изобретения передатчик на вышеупомянутой стадии оценки обращается к 2×2-D симметричным SSFS-операторам (SSFSO)
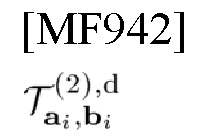
и их частотному двойнику

и выполняет пространственный сдвиг и сдвиг пространственной частоты в отношении изображения.
(Часть 203 вывода принятых данных)
Часть 203 вывода принятых данных выводит данные, извлеченные частью 202 оценки сдвигов и извлечения принятых данных.
<Блок-схема прохождения сигнала между передатчиком и приемником>
На фиг. 19 изображена блок-схема "передатчик-приемник", использующая приемопередающую систему под номером 1.
(S101)
На стадии S101 часть 101 для сбора данных получает данные, подлежащие передаче. Конкретные процедуры, выполняемые частью 101, были описаны выше.
(S102)
На стадии S102 часть 102 для генерирования сигнала генерирует сигнал, подлежащий передаче. Конкретные процедуры, выполняемые частью 102, были описаны выше.
(S103)
На стадии S103 передающая часть 103 передает сигнал, подлежащий передаче. Конкретные процедуры, выполняемые частью 103, были описаны выше.
(S201)
На этой стадии принимающая часть 201 принимает сигнал, переданный передающей частью S103. Конкретные процедуры, выполняемые частью 201, были описаны выше.
(S202)
На стадии S202 часть 202 оценки сдвигов и извлечения принятых данных оценивает сдвиги и одновременно извлекает принятые данные. Конкретные процедуры в части 202 оценки сдвигов и вывода принятых данных являются такими, как описано выше. (S203)
На стадии S203 часть 203 вывода принятых данных выводит принятые данные, извлеченные частью 202 оценки сдвигов и извлечения принятых данных. Конкретные процедуры в части 203 вывода принятых данных являются такими, как описано выше.
<<Пример 2 вариантов осуществления систем связи>>
Пример 1 вариантов осуществления систем связи, который основан на теоретической основе, как объяснено выше, поясняется вместе с приведенными фигурами.
На фигуре 20 изображена блочная диаграмма, представляющая приемопередающую систему под номером 1а, привязанным к окружающей ее пунктирной линии, согласно варианту осуществления настоящего изобретения. Как показано на фиг. 20, система под номером 1а содержит передающее устройство 100а и принимающее устройство 200а. Приемопередающая система под номером 1а, подобно приемопередающей системе под номером 1 на фиг. 18, как рассмотрено выше, может быть использована как для радиолокационной станции, так и для системы связи (например, приемопередающей системы для передачи голосовых данных и/или данных изображений). Другие части обозначены тем же номерами, что и их соответствующие части в приемопередающей системе под номером 1 и, следовательно, их подробное описание не требуется.
<Передающее устройство 100а>
Передающее устройство 100а представляет собой устройство, которое выполняет программу, заложенную в передатчик, как описано в вышеприведенном описании.
Как показано на фиг. 20, передающее устройство 100а в качестве примера содержит часть 101 для сбора передаваемых данных, часть 102а для генерирования передаваемого сигнала и передающую часть 103.
(Часть 102а для генерирования передаваемого сигнала)
Часть 102а для генерирования передаваемого сигнала содержит часть 102 для генерирования передаваемого сигнала, относящуюся к примеру 1 вариантов осуществления приемопередающей системы, а также часть 110 для заключения сдвига.
Как рассмотрено в (84), часть 110 для заключения сдвига генерирует передаваемый сигнал, в который заключен набор из Npath параметров задержки и доплеровского смещения частоты

Часть 102а для генерирования передаваемого сигнала выполняет частотно-временной сдвиг сигнала, подлежащего передаче, с использованием одного временного сдвига (или нескольких временных сдвигов) и одного частотного сдвига (или нескольких частотных сдвигов)


<Принимающее устройство 200а>
Принимающее устройство 200а представляет собой устройство, которое выполняет программу, заложенную в приемник, как описано в вышеприведенном описании.
Как показано на фиг. 20, например, принимающее устройство 200а содержит принимающую часть 201, часть 202а оценки сдвигов и извлечения принятых данных и часть 203 принятия решения относительно принятых данных.
(Часть 202а оценки сдвигов и извлечения принятых данных)
Как пример, часть 202а оценки сдвигов и извлечения принятых данных содержит части, аналогичные частям, которые содержит часть 202 оценки сдвигов и извлечения принятых данных, относящаяся к примеру 1 вариантов осуществления приемопередающей системы.
<Блок-схема прохождения сигнала между передатчиком и приемником>
На фиг. 21 изображена блок-схема "передатчик-приемник", использующая приемопередающую систему под номером 1а. Стадии S101, S103, S201 и S203 аналогичны стадиям на фиг. 19, и, следовательно, их объяснение не требуется.
(S102a)
На стадии S102a часть 102а для генерирования передаваемого сигнала с частью ПО для заключения сдвига генерирует передаваемый сигнал. Конкретные процедуры, выполняемые частью 102а для генерирования передаваемого сигнала, были описаны выше.
(S202a)
На стадии S202a часть 202а оценки сдвигов и извлечения принятых данных оценивает сдвиги и извлекает принятые данные, одновременно. Конкретные процедуры в части 202а оценки сдвигов и извлечения принятых данных являются такими, как описано выше.
<<Пример 3 вариантов осуществления систем связи>>
Приемопередающая система, которая объясняется со ссылкой на фиг. 18-21, может быть вариантом осуществления, который выполняет программы, как описано в подразделе <8.3 Обработка сигнала, использующая многомерные некоммутативные пространственные сдвиги и сдвиги пространственной частоты>.
Например, как описано в подразделе <8.3 Обработка сигнала, использующая многомерные некоммутативные пространственные сдвиги и сдвиги пространственной частоты>, принимающее устройство 200 выполняет стадию оценки для осуществления оценки SSFS, которые заключены в принятых изображениях, с обращением к пространству параметров, т.е. пространству параметров SSFS коразмерности ≥2.
Как описано в подразделе <8.3 Обработка сигнала, использующая многомерные некоммутативные пространственные сдвиги и сдвиги пространственной частоты>, на вышеупомянутом стадии оценки приемник обращается к 2×2-D симметричным операторам пространственного сдвига и сдвига пространственной частоты (SSFS) (SSFSO), представляющим PD половинного сдвига, обусловленные NCP, присущим SSFS,

и их частотному двойнику

и оценивает SSFS.
Аналогично, в соответствии с вариантом осуществления настоящего изобретения, передатчик, т.е. способ передачи изображения, обращается к пространству параметров SSFS коразмерности ≥2 и содержит 2 разных SSFSO, которые представляют осуществление пространственного сдвига и сдвига пространственной частоты изображения, подлежащего передаче, и PD, обусловленное полусдвигом сдвига пространственной частоты (или PD, обусловленное полусдвигом пространственного сдвига).
На вышеупомянутом стадии сдвига передатчик обращается к симметричным SSFSO
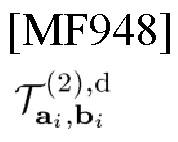
и их частотному двойнику
и оценивает SSFS.
[0300] [Пример вариантов осуществления с использованием программного обеспечения]
Блок управления в передающих устройствах 100, 100а и принимающих устройствах 200, 200а (в частности, частях 102, 102а для генерирования передаваемого сигнала и частях 202, 202а оценки сдвигов и извлечения принятых данных) может быть реализован с помощью логических схем, выполненных в виде интегральных схем (интегральных микросхем), или с помощью программного обеспечения.
В случае выполнения с помощью программного обеспечения передающие устройства 100, 100а и принимающие устройства 200, 200а снабжаются электронной вычислительной машиной, которая выполняет программы для каждой из нескольких функций; например, электронная вычислительная машина содержит несколько процессоров и машиночитаемых запоминающих устройств. Электронная вычислительная машина выполняет программы, которые процессоры считывают из запоминающих устройств, чтобы она могла реализовать цель настоящего изобретения. В качестве запоминающих устройств используются постоянные запоминающие устройства, например память, доступная только для чтения (ROM), лента, диск, карта, микросхема памяти, программируемые логические схемы и т.п. Электронная вычислительная машина может быть снабжена запоминающим устройством с произвольной выборкой (RAM) для выполнения вышеупомянутых программ. Вышеупомянутые программы могут быть установлены посредством любой среды передачи (такой как сеть связи, радиовещание, радиоволна) и предоставлены вышеупомянутой электронной вычислительной машиной. В соответствии с вариантом осуществления настоящего изобретения вышеупомянутая программа может содержаться в заключенном в несущей волне сигнале данных в результате электронной передачи и может быть реализована.
Программные продукты, используемые электронной вычислительной машиной, которые реализуют несколько функций передающих устройств 100, 100а и принимающих устройств 200, 200а, включают в себя один из вариантов осуществления настоящего изобретения. Вышеупомянутый программный продукт, используемый электронной вычислительной машиной, загружает программы, предоставляемые любой средой передачи, с использованием по меньшей мере одной электронной вычислительной машины и заставляет электронную вычислительную машину выполнять по меньшей мере одну программу. Таким образом, по меньшей мере один процессор, связанный с электронной вычислительной машиной, выполняет по меньшей мере одну программу. Следовательно, может быть реализована каждая из функций передающих устройств 100, 100а и принимающих устройств 200, 200а. Программный продукт, используемый электронной вычислительной машиной, заставляет по меньшей мере одну из электронных вычислительных машин с установленными программами выполнять стадии в процессе передачи (способе передачи) и процессе приема (способе приема).
В соответствии с вариантом осуществления настоящего изобретения вышеупомянутые варианты осуществления не имеют ограничений. Модификации и изменения вариантов осуществления приведены в формуле изобретения. Сочетание нескольких способов или технологий, предоставленных в разных вариантах осуществления, приводит к варианту осуществления, относящемуся к настоящему патентному документу, и включает в себя один из способов, относящихся к настоящему патентному документу. Кроме того, надлежащее сочетание нескольких способов или технологий, предоставленное в разных вариантах осуществления, может обеспечивать новый технический признак.
Промышленная применимость
Настоящее изобретение идеально подходит для беспроводных приемопередающих систем связи и радарных систем.
Перечень обозначений для частей, относящихся к варианту осуществления:
1,1а: приемопередающая система;
100, 100а: передающее устройство;
101: часть для сбора передаваемых данных;
102, 102а: часть для генерирования передаваемого сигнала;
103: передающая часть;
110: часть для заключения сдвига;
200, 200а: принимающее устройство;
201: принимающая часть;
202, 202а: часть оценки сдвигов и извлечения принятых данных (оценивающая часть);
203: часть принятия решения относительно принятых данных.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРИЕМА ОПОРНОГО СИГНАЛА В СИСТЕМЕ БЕСПРОВОДНОЙ СВЯЗИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2017 |
|
RU2713407C1 |
| УСТРОЙСТВО ПЕРЕДАЧИ, УСТРОЙСТВО ПРИЕМА И СПОСОБ ПЕРЕДАЧИ В РЕЖИМЕ OFDM | 2008 |
|
RU2479132C2 |
| КОДИРОВАНИЕ И МУЛЬТИПЛЕКСИРОВАНИЕ УПРАВЛЯЮЩЕЙ ИНФОРМАЦИИ В СИСТЕМЕ БЕСПРОВОДНОЙ СВЯЗИ | 2011 |
|
RU2471295C1 |
| КОДИРОВАНИЕ И МУЛЬТИПЛЕКСИРОВАНИЕ УПРАВЛЯЮЩЕЙ ИНФОРМАЦИИ В СИСТЕМЕ БЕСПРОВОДНОЙ СВЯЗИ | 2008 |
|
RU2446590C2 |
| КОДИРОВАНИЕ И МУЛЬТИПЛЕКСИРОВАНИЕ УПРАВЛЯЮЩЕЙ ИНФОРМАЦИИ В СИСТЕМЕ БЕСПРОВОДНОЙ СВЯЗИ | 2011 |
|
RU2472291C1 |
| СПОСОБ ИЗМЕРЕНИЯ ХАРАКТЕРИСТИК АКУСТИЧЕСКИХ КОЛЕБАНИЙ, ИЗЛУЧАЕМЫХ ПОДВИЖНЫМ ОБЪЕКТОМ, И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1992 |
|
RU2050598C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПЕРЕДАЧИ И ПРИЕМА СИГНАЛОВ С ОГРАНИЧЕННЫМ СПЕКТРОМ (ВАРИАНТЫ) | 2004 |
|
RU2265278C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТИПА ЗАМКНУТОЙ ТРАЕКТОРИИ ДВИЖЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ | 2023 |
|
RU2840399C2 |
| ПРИЕМНИК СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 1997 |
|
RU2118054C1 |
| ПЕРЕДАТЧИК И ПРИЕМНИК И СООТВЕТСТВУЮЩИЕ СПОСОБЫ | 2018 |
|
RU2733419C1 |



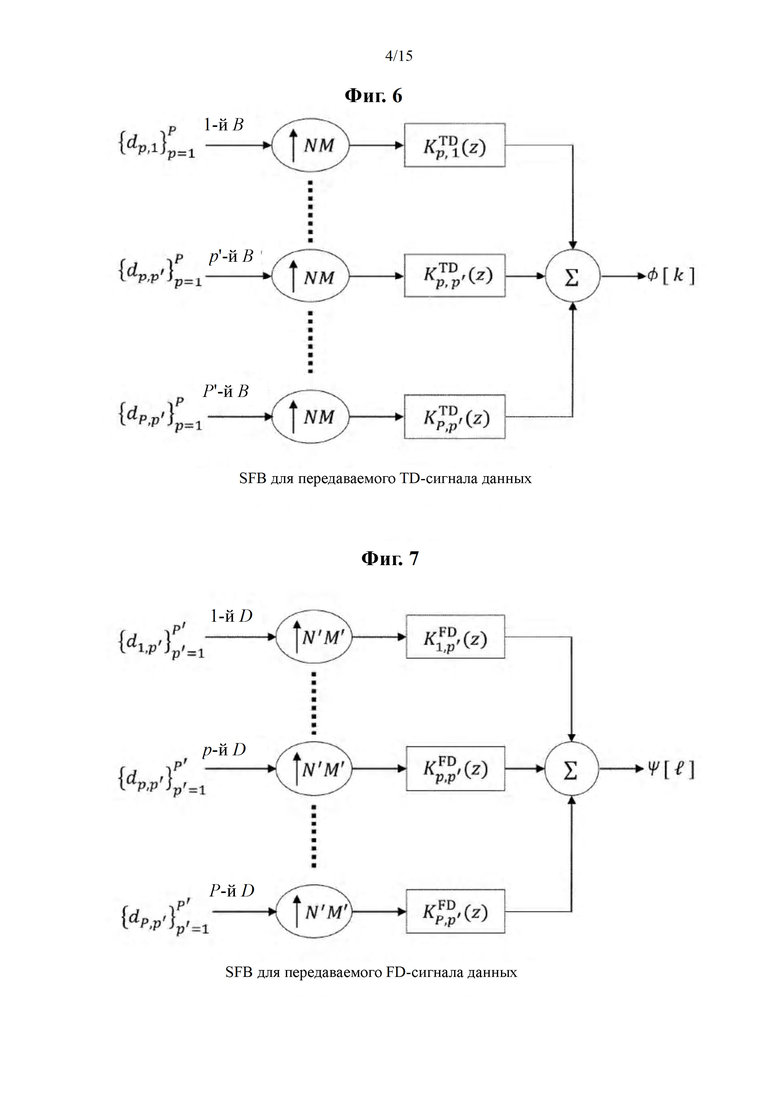




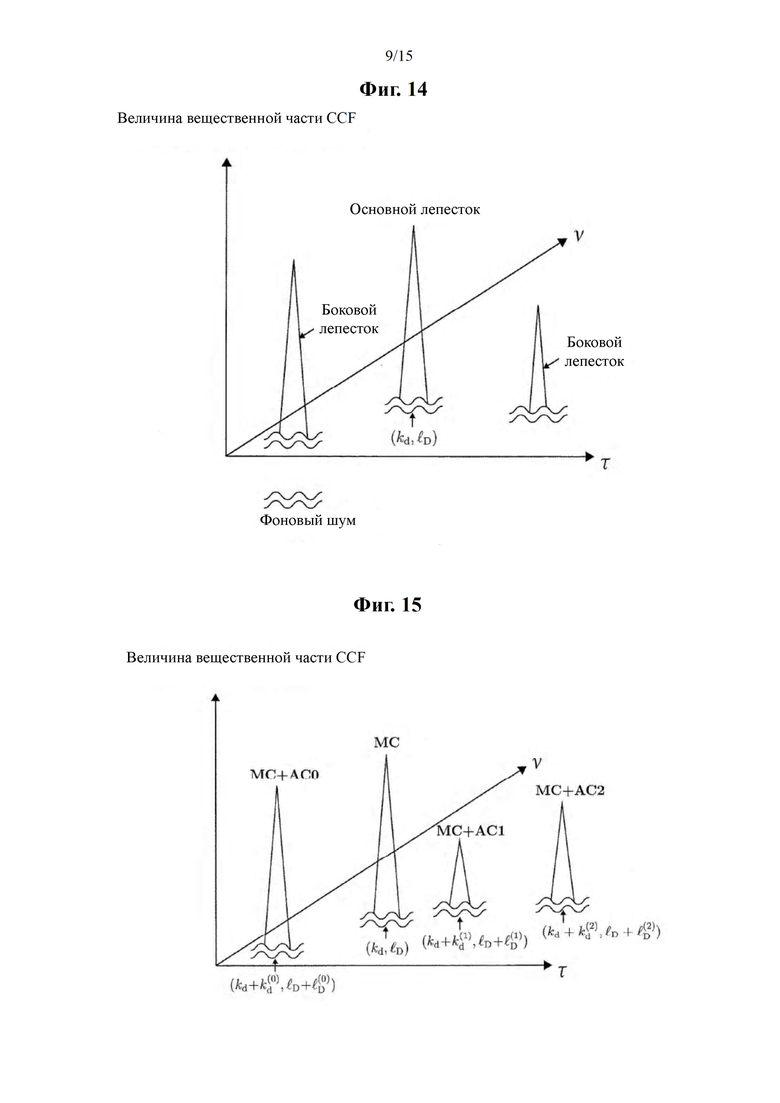




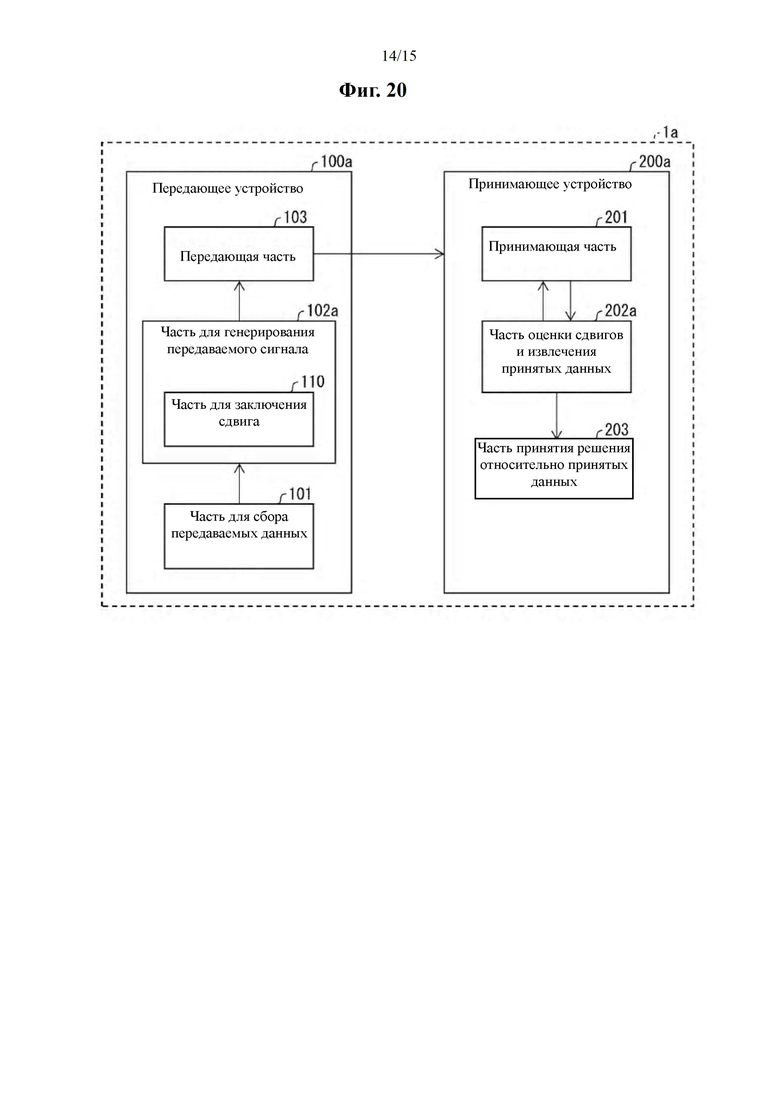

Изобретение относится к технике связи и может использоваться в системах беспроводной связи. Технический результат состоит в повышении помехоустойчивости передачи. Для этого в соответствии с вариантом осуществления настоящего изобретения предлагается способ приема сигнала, предусматривающий стадию оценки для осуществления оценки временного и частотного сдвигов, которые заключены в принятом сигнале, чтобы исключить сдвиги, при этом способ обращается к пространству параметров некоммутативных сдвигов коразмерности 2. 7 н. и 9 з.п. ф-лы, 21 ил.
1. Способ приема сигнала, предусматривающий стадию оценки для осуществления оценки временного сдвига и частотного сдвига, которые заключены в сигнале, при этом стадия оценки обращается к пространству параметров некоммутативных сдвигов коразмерности 2.
2. Способ по п. 1, в котором пространство параметров некоммутативных сдвигов коразмерности 2 является пространством, полученным путем перевода в трехмерное пространство плоскости, которая определена первой осью, указывающей время, и второй осью, указывающей частоту, посредством присоединения к этой плоскости третьей оси, указывающей частотно-временные сдвиги.
3. Способ по п. 1 или 2, в котором на стадии оценки оценивают временной сдвиг и частотные сдвиги, которые заключены в сигнале, с использованием оператора частотно-временного сдвига (TFSO) типа 1, представляющего оцененный временной сдвиг, частотный сдвиг и фазовую составляющую из-за половинного сдвига оцененного временного сдвига,

TFSO типа 2, представляющего временной сдвиг, оцененный частотный сдвиг и фазовую составляющую из-за половинного сдвига оцененного частотного сдвига,

TFSO типа 3, представляющего наблюдаемый временной сдвиг, подлежащий оценке, наблюдаемый частотный сдвиг, подлежащий оценке, и фазовую составляющую из-за половинного сдвига временного сдвига, подлежащего оценке,

или частотного двойника TFSO типа 3

и TFSO типа 4, представляющего оцененный временной сдвиг, оцененный частотный сдвиг и фазовую составляющую из-за половинного сдвига оцененного временного сдвига,

или частотного двойника TFSO типа 4
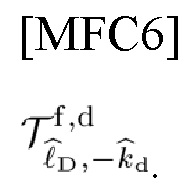
4. Способ по п. 3, в котором на стадии оценки оценивают временной сдвиг и частотный сдвиг, которые заключены в сигнале, с использованием функции кросскорреляции во временной области (TD-CCF) типа 1, представленной в терминах TFSO типа 1, типа 3 и типа 4, и функции кросскорреляции в частотной области (FD-CCF) типа 2, представленной в терминах TFSO типа 2, типа 3 и типа 4.
5. Способ по п. 4, в котором TD-CCF типа 1 и FD-CCF типа 2 содержат фазовое искажение (PD), обусловленное операцией некоммутативного сдвига между модуляцией и демодуляцией с помощью несущей fc и временного сдвига td
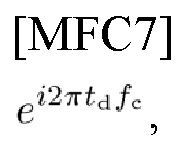
или дискретизированную версию PD

и PD, обусловленное фазовой составляющей еiк коэффициента ослабления Аiк.
6. Способ по п. 4 или 5, в котором стадия оценки включает в себя две альтернативных стадии обновления: (1) обновление оцененного частотного сдвига с обращением к TD-CCF типа 1 и (2) обновление оцененного временного сдвига с обращением к FD-CCF типа 2.
7. Способ по п. 1 или 2, в котором на стадии оценки оценивают временной сдвиг и частотный сдвиг, которые заключены в сигнал, с использованием оценок максимального правдоподобия (MLE) частотного сдвига для обнаружения N' шаблонов во временной области (TD) и MLE временного сдвига для обнаружения N шаблонов в частотной области (FD).
8. Приемное устройство для приема сигнала, содержащее оценивающую часть для осуществления оценки временного сдвига и частотного сдвига, которые заключены в сигнале, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2.
9. Способ передачи сигнала, предусматривающий стадию сдвига для осуществления частотно-временного сдвига сигнала, подлежащего передаче, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2.
10. Способ по п. 9, в котором на стадии сдвига генерируют сигнал, подлежащий передаче, путем модуляции с манипуляцией с фазовым сдвигом (PSK) сигнала чип-импульса во временной области (TD) с помощью TD-фазового кода (PC) периода N и PSK-модуляции TD-PSK-модулированного TD-импульсного сигнала с помощью FD-PC периода N' для генерирования версии с несколькими несущими TD-PSK-модулированного TD-импульсного сигнала.
11. Передающее устройство для передачи сигнала, содержащее часть, выполняющую частотно-временной сдвиг, для осуществления частотно-временного сдвига сигнала, подлежащего передаче, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2.
12. Приемопередающая система, содержащая:
передающее устройство; и
принимающее устройство, причем
передающее устройство содержит часть, выполняющую частотно-временной сдвиг, для осуществления частотно-временного сдвига сигнала, подлежащего передаче, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2,
принимающее устройство содержит оценивающую часть для осуществления оценки временного сдвига и частотного сдвига, которые заключены в сигнале, подлежащем передаче, с обращением к пространству параметров некоммутативных сдвигов коразмерности 2.
13. Способ приема сигнала изображения, предусматривающий стадию оценки для осуществления оценки пространственного сдвига и сдвига пространственной частоты (SSFS), которые заключены в сигнале изображения, с обращением к пространству параметров коразмерности 2, при этом
каждый пространственный сдвиг и сдвиг пространственной частоты имеет размерность ≥2.
14. Способ по п. 13, в котором на стадии оценки оценивают SSFS с обращением к 2-D симметричным SSF-операторам (SSFSO)

или частотному двойнику 2-D симметричных SSFSO

15. Способ передачи сигнала изображения, предусматривающий стадию сдвига для осуществления пространственного сдвига и сдвига пространственной частоты сигнала изображения, подлежащего передаче, с обращением к пространству параметров, при этом каждый из пространственного сдвига и сдвига пространственной частоты имеет размерность ≥2.
16. Способ по п. 15, в котором на стадии сдвига осуществляют пространственный сдвиг и сдвиг пространственной частоты сигнала изображения, подлежащего передаче, с обращением к 2-D симметричным SSFSO
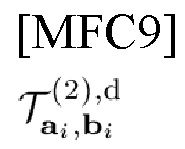
и частотному двойнику 2-D симметричных SSFSO

| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИКИ КАЧЕСТВА КАНАЛА | 2010 |
|
RU2549359C2 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
Авторы
Даты
2020-01-14—Публикация
2018-06-28—Подача