Изобретение относится к прикладной физике и может быть использовано для разработки тестовых генераторов в метрологии фрактальных сигналов. Фрактальный сигнал является самоподобным (или самоаффинным), а его размерность Хаусдорфа-Безиковича является дробной [1] (Федер Е., "Фракталы", М.: Мир, 1991).
Известны генераторы случайных сигналов различных конструкций, принцип действия которых основан на преобразовании естественных флуктуаций внешнего или внутреннего источника в электрический сигнал. Много примеров построения таких генераторов приведено в [2] (Бобнев M.П. Генерирование случайных сигналов. М.: Энергия, 1971).
Недостатком генераторов является то, что случайный сигнал не является в полном смысле фрактальным сигналом с контролируемой размерностью Хаусдорфа, а его флуктуационное происхождение не позволяет управлять размерностью сигнала.
Известен генератор фрактального сигнала [3] (Кузнецов А.П., Кузнецов В. П. Генератор фрактального сигнала. Письма в ЖТФ, 1992, т. 18, N 24, с. 19), содержащий последовательную цепочку счетчиков, каждый из которых связан со своим двухполюсником, а также входные и выходные клеммы.
Принцип действия такого генератора основан на пересчете итерационной последовательности определенного типа, в результате чего на его выходе появляется сигнал с дробной размерностью Хаусдорфа. Размерность Хаусдорфа этого сигнала D может лежать в диапазоне 0 < D < 1, так как итерационная последовательность и выходной сигнал, реализованные в известном генераторе, порождаются двухмасштабным множеством Кантора.
Недостатком известного генератора фрактального сигнала является тот факт, что сигналы с D > 1 в нем получить нельзя, в то время как фрактальные сигналы природного происхождения являются аналоговыми и имеют размерность D > 1.
В связи с этим техническая задача заключается в создании генератора фрактального сигнала с D > 1, который можно использовать для генерирования тестовых сигналов, моделирующих фрактальные сигналы природного происхождения, например сигналы с ленгмюровских зондов в плазме со структурной турбулентностью.
Техническим результатом является возможность получения с помощью предлагаемого генератора фрактальных сигналов с заданной размерностью Хаусдорфа из диапазона 1 < D < 2.
Этот результат достигается тем, что в генератор фрактального сигнала, содержащий N делителей частоты (где N > 2), введены генератор сигнала типа "меандр" с коэффициентом заполнения 0,5, N полосовых фильтров, N усилителей с регулируемым коэффициентом усиления и аналоговый сумматор сигналов, при этом выход генератора сигнала типа "меандр" соединен со входами делителей частоты, выход каждого из которых через соответствующий полосовой фильтр соединен со входом соответствующего усилителя с регулируемым коэффициентом усиления, выход которого соединен с соответствующим входом аналогового сумматора сигналов, причем коэффициенты деления βn делителей частоты установлены в соответствии с выражением
βn = A-1qn-1,
где n = 1, 2, ..., N, A - постоянная величина, A > 1; q - постоянная величина, q > 1;
а центральная частота fn, полосовых фильтров удовлетворяет выражению
fn = A-1qn-1f0,
где f0 - частота генератора сигнала типа "меандр".
Указанная совокупность признаков позволяет получить фрактальный сигнал с заданной размерностью Хаусдорфа за счет того что генератор, собранный по такой схеме, может генерировать сигнал F(t), форма которого порождается функцией Вейерштрасса: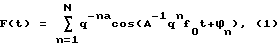
где 0 < a < 1 - постоянная, которая определяет величину размерности Хаусдорфа в соответствии с соотношением
D = 2 - a,
величина kус = q-na задается установленной заранее величиной коэффициента усиления в усилителе n-й цепочки, выходная частота делителя частоты задается в соответствии с формулой Вейерштрасса так, чтобы выполнялось fп = A-1qn-1f0.
Фрактальные свойства функции Вейерштрасса, порождающей сигнал в предлагаемом генераторе, известны и описаны в [1]. Требование N ≥ 3 связано с тем, что в противном случае диапазон масштабов времени, на котором у функции (1) проявляются фрактальные свойства с размерностью (2), является нулевым.
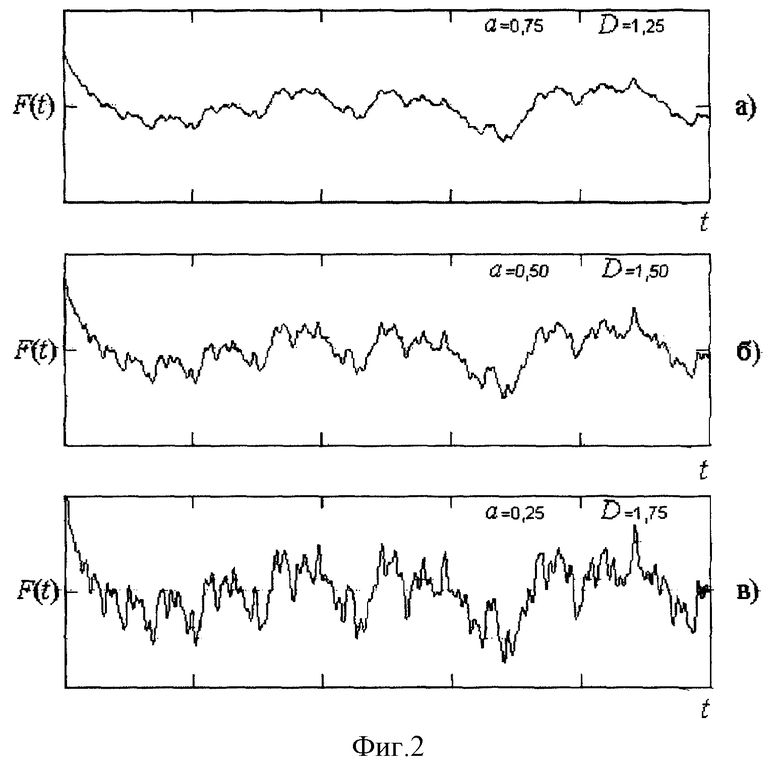
На фиг. 1 показана блок-схема генератора фрактального сигнала; на фиг. 2 - примеры осциллограмм генерируемых фрактальных сигналов с различной величиной размерности Хаусдорфа.
Генератор фрактального сигнала содержит генератор 1 сигнала типа "меандр" с коэффициентом заполнения 0,5, амплитудой ~4,5 В (уровень "0" - 0 - 0,75 В; уровень "1" - 4,3 - 5 В) и частотой f0 = 256 МГц, выполненный, например, на основе высокостабильного кварцевого генератора. К генератору 1 последовательно подключены, например, 10 параллельных цепочек, в каждой из которых последовательно соединены делитель 2 частоты, полосовой фильтр 3, усилитель 4. Для случая q = 2 и А = 100 делители частоты 2 могут быть выполнены в виде счетчиков, начальные состояния которых устанавливаются независимо для каждого счетчика перед запуском всего генератора фрактального сигнала. Начальные состояния счетчиков определяют начальные фазы Φn (см. выражение (1)) с точностью ΔΦ = πA-1q-n-1. Полосовые пассивные фильтры 3 выполнены на основе известных RLC-схем и при условии ΔΦn/Φn < 10-2 и наклоном АЧХ в полосах подавления 40 дБ/декаду преобразуют сигнал типа "меандр" в гармонический (синусоидальный) сигнал. Усилители 4 с регулируемым коэффициентом усиления kус могут быть выполнены на основе операционных усилителей. Выходы усилителей 4 подключены к соответствующим входам аналогового сумматора 5, выход которого является выходом генератора фрактального сигнала.
Генератор фрактального сигнала работает следующим образом. Подготовка к работе генератора фрактального сигнала заключается в установке начальных условий делителей частоты (счетчиков) 2 и коэффициентов kус усиления усилителей 4.
С выхода генератора 1 на входы счетчиков 2 поступает сигнал типа "меандр" с частотой 256 МГц. Счетчики 2 пересчитывают поступающий в них сигнал и на их выходах появляется сигнал типа "меандр" с частотами: 2,56 МГц; 1,28 МГц; 640 кГц; 320 кГц; 160 кГц; 80 кГц; 40 кГц; 20 кГц; 10 кГц; 5 кГц с начальными фазами, соответствующими начальным условиям на счетчиках. Эти сигналы поступают на входы полосовых фильтров 3 с узкой полосой пропускания, которые преобразуют сигналы типа "меандр" в гармонический сигнал с частотой, равной частоте "меандра". С выходов фильтров 3 гармонические сигналы поступают на входы усилителей 4 с заранее установленными коэффициентами усиления в соответствии с (1).
Далее с выходов усилителей 4 сигналы поступают на входы аналогового сумматора 5, где они суммируются. Выход сумматора 5 является выходом генератора фрактального сигнала в целом и с него выводится фрактальный сигнал.
На фиг 2 а, б, в приведены примеры осциллограмм выходного сигнала, указана постоянная a, которая определяет величину размерности Хаусдорфа в соответствии с соотношением (2), приведены значения D.
Таким образом, в предлагаемом генераторе фрактального сигнала поставленная техническая задача полностью решена, то есть на его выходе получается фрактальный сигнал в виде функции Вейерштрасса с заданной размерностью Хаусдорфа-Безиковича из диапазона 1 < D < 2.
| название | год | авторы | номер документа |
|---|---|---|---|
| РЕГУЛЯТОР КОНЦЕНТРАЦИИ ОЗОНА | 2000 |
|
RU2189070C2 |
| ТАЙМЕР С КОНТРОЛЕМ | 1995 |
|
RU2113007C1 |
| ТАЙМЕР С КОНТРОЛЕМ | 1999 |
|
RU2173938C2 |
| РЕЛЕ ВРЕМЕНИ | 1997 |
|
RU2119245C1 |
| ДЕЛИТЕЛЬ ЧАСТОТЫ С ИЗМЕНЯЕМЫМ КОЭФФИЦИЕНТОМ ДЕЛЕНИЯ | 1996 |
|
RU2134485C1 |
| УСТРОЙСТВО ДЛЯ СЧЕТА ИМПУЛЬСОВ | 1997 |
|
RU2151463C1 |
| СПОСОБ ЗАЩИТЫ ИНФОРМАЦИИ ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА В ВОЛОКОННО-ОПТИЧЕСКИХ ЛИНИЯХ СВЯЗИ | 1995 |
|
RU2110894C1 |
| ЭЛЕКТРОННОЕ КОДОВОЕ УСТРОЙСТВО | 2000 |
|
RU2179223C2 |
| Устройство для генерирования случайного сигнала с фрактальными свойствами | 2015 |
|
RU2609754C1 |
| ГЕНЕРАТОР ИМПУЛЬСОВ | 1995 |
|
RU2102833C1 |
Изобретение относится к области прикладной физики и может быть использовано для разработки тестовых генераторов в метрологии фрактальных сигналов. Генератор фрактального сигнала содержит N делителей частоты (где N > 2), генератор сигнала типа "меандр" с коэффициентом заполнения 0,5, N полосовых фильтров, N усилителей, сумматор сигналов, при этом выход генератора сигнала типа "меандр" соединен со входами делителей частоты, выход каждого из которых через соответствующий полосовой фильтр соединен со входом соответствующего усилителя с регулируемым коэффициентом усиления, выход которого соединен с соответствующим входом аналогового сумматора сигналов, причем коэффициенты деления βn делителей частоты установлены в соответствии с выражением βn= A-1qn-1, где n = 1,2,..., N, A - постоянная величина, A > 1, q - постоянная величина, q > 1, а центральная частота fn полосовых фильтров удовлетворяет выражению fn = An-1 f0, где f0 - частота генератора сигнала типа "меандр". Достигаемый технический результат: получение на выходе сигнала в виде функции Вейерштрасса с заданной размерностью Хаусдорфа-Безиковича из диапазона 1 < D < 2. 2 ил.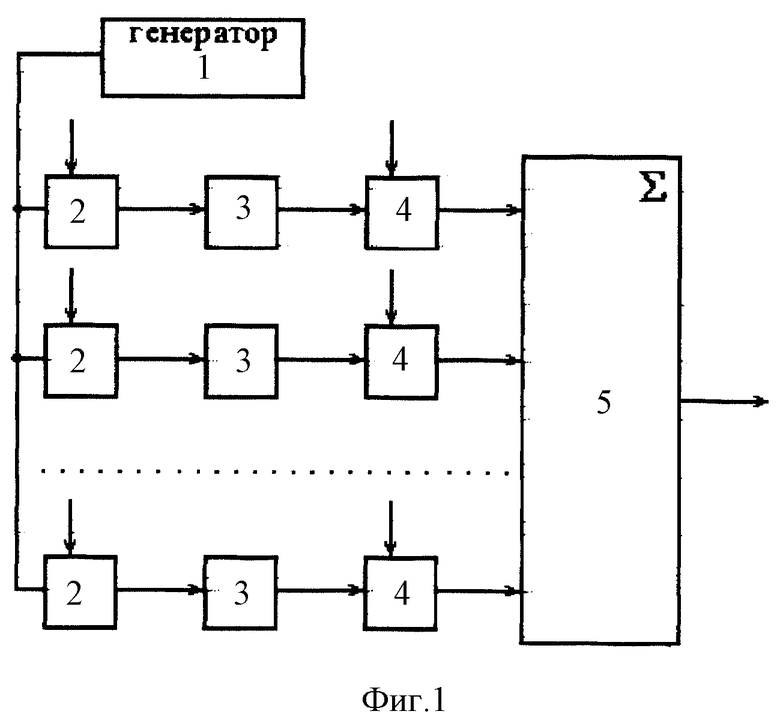
Генератор фрактального сигнала, содержащий N делителей частоты ( где N > 2), отличающийся тем, что введены генератор сигнала типа "меандр" с коэффициентом заполнения 0,5, N полосовых фильтров, N усилителей с регулируемым коэффициентом усиления и аналоговый сумматор сигналов, при этом выход генератора сигнала типа "меандр" соединен со входами делителей частоты, выход каждого из которых через соответствующий полосовой фильтр соединен со входом соответствующего усилителя с регулируемым коэффициентом усиления, выход которого соединен с соответствующим входом аналогового сумматора сигналов, причем коэффициенты деления βn делителей частоты установлены в соответствии с выражением
βn= A-1qn-1,
где n = 1, 2, ..., N;
А - постоянная величина, А > 1;
q - постоянная величина, q > 1,
а центральная частота fn полосовых фильтров удовлетворяет выражению
fn = A-1qn-1fo,
где fo - частота генератора сигнала типа "меандр".
| Генератор шума | 1972 |
|
SU445125A1 |
| Генератор случайной цифровой последовательности | 1983 |
|
SU1107264A1 |
| Генератор случайных сигналов | 1983 |
|
SU1117823A1 |
| US 4684903, 04.08.1987 | |||
| 0 |
|
SU251908A1 | |
Авторы
Даты
2001-06-10—Публикация
1999-08-27—Подача