Изобретение относится к робототехнике и может быть использовано при разработке систем управления манипуляционными роботами, обеспечивающих решение траекторных задач при предъявлении дополнительных требований к максимизации контурной (траекторией) скорости.
Все возрастающая необходимость интенсификации режимов работы манипуляционных роботов (МР) предъявляет все более жесткие требования к системам управления ими. Круг задач, для которых необходима работа в предельных, в смысле быстродействия, режимах достаточно широк. В первую очередь это относиться к режимам функционирования МР в экстремальных условиях: в случае радиационного заражения среды; при активном противодействии внешней среды; при согласовании работы МР с другими роботами и устройствами; при обходе препятствий и т. д. В любом из этих случаев помимо оптимизации критерия быстродействия ставиться задача отслеживания заданной траектории, которая может быть задана как в функции внешних (рабочих) координат, так и в пространстве обобщенных координат МР. Последнее обстоятельство требует аналитического или численного решения обратной задачи кинематики, что в свою очередь связано с известными трудностями и проблемами [Фу К., Гонсалес Р., Ли К. "Робототехника", М. , Мир, 1989, 624 с., с.69-93, Тимофеев А.В. Управление роботами. Л., из-во ЛГУ, 1986, 240 с., с.77].
Не менее важной при такой постановке задачи является необходимость учета нелинейных свойств динамики МР, наиболее характерных для таких режимов [Вукобратович М., Стокич К., Кирчански Н. Неадаптивное и адаптивное управление манипуляционными роботами. М.: Мир, 1989, 376 с., с.59-60], и помимо указанных факторов необходимость обеспечения асимптотической устойчивости в целом планируемых траекторий определяет актуальность разработки новых структурно-алгоритмических решений систем траекторного управления, определяемых в классе оптимальных или субоптимальных систем.
Известны алгоритмы траекторного управления роботами и соответствующая им структурная схема [А.В. Тимофеев. Управление роботами. М., из-во Ленинградского университета, 1986, 240 с., с.83-86], которая предполагает наличие блока планировщика траекторий и содержит два вычислительных блока, два блока суммирования и интегратор.
Устройство управления, реализуемое предоставленной структурой, позволяет организовать движение вдоль прямой линии в пространстве внешних координат, соединяющей начальное и конечное положения схвата, с постоянной скоростью и не требует решения обратной задачи кинематики.
Признаки аналога, общие с заявляемым техническим решением, следующие: блок исполнительных механизмов, блок механической системы, представимые двумя интеграторами, блоком матрицы управления, блоком суммирования и блоком нелинейных элементов, планировщик траекторий в пространстве внешних координат, блок датчиков, вычислительные блоки, блоки перемножения и блоки суммирования.
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем: полученные структурные решения не позволяют организовать движение по широкому спектру траекторий или предполагают аппроксимацию сложных траекторий отрезками прямых линий и наличия соответствующего блока аппроксимации. Кроме того, структурно-алгоритмические решения аналога не позволяют организовать движение рабочего органа манипуляционного робота с максимальной траекторией скоростью, что, соответственно, не позволяет достичь максимально возможной на данной траектории производительности.
Известны процедура траекторного, оптимального по быстродействию управления манипуляционным роботом (Н.Н. Болотник, Ф.Л. Черноусько. Оптимизация управления манипуляционными роботами. "Техническая кибернетика", 1, 1990, с.189-238] и соответствующая ей структура системы управления, которая предполагает наличие блока исполнительных механизмов, блока механической системы, представимых двумя интеграторами, блоком матрицы управления, блоком суммирования и блоком нелинейных элементов, планировщика траекторий в пространстве внешних координат, блока вычисления кривой максимальной скорости, блока интегрирования, блоков суммирования и блока компараторов.
Устройство управления, реализуемое структурой аналога, позволяет организовать движение манипуляционного робота вдоль заданной траектории с максимально возможной траекторной (контурной) скоростью. Кроме того, представленная процедура позволяет учесть нелинейные свойства и многосвязность динамической модели робота, наиболее характерные для режимов быстрых перемещений манипулятора.
Признаки аналога, общие с заявляемым техническим решением, следующие: блок исполнительных механизмов, блок механической системы, представимые двумя интеграторами, блоком матрицы управления, блоком суммирования и блоком нелинейных элементов, планировщик траекторий в пространстве внешних координат, блок датчиков, блок вычисления кривой максимальной скорости, блоки суммирования, блоки компараторов, вычислительные блоки и блоки перемножения.
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем: реализуемые алгоритмы управления требуют предварительного расчета моментов переключения управляющих воздействий, что требует соответствующей программно-аппаратной поддержки, и также требуется дополнительное время, снижающее производительность функционирования манипуляционного робота при оперативной смене желаемых траекторий движения. Кроме того, представляемые алгоритмы управления реализуются в классе разомкнутых систем, что, как известно [Клюев А.С., Колесников А.А. Оптимизация автоматических систем управления по быстродействию. М. , Энергоиздат, 1982, 239 с.], не всегда позволяет организовать движение робота вдоль заданных траекторий с требуемым качеством.
Известно устройство контурного (траекторного) управления манипуляционным роботом [Пшихопов В. Х., Колесников А.А. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000], которое содержит планировщик траекторий в пространстве внешних координат, блок исполнительных механизмов, блок датчиков, блок механической системы робота, блок вычисления управлений, включающий в себя следующие блоки: блок вычисления нелинейных элементов, блок вычисления матрицы коэффициентов управления, блок вычисления якобиана решения прямой задачи кинематики, блок вычисления производной по времени от якобиана решения прямой задачи кинематики, блок вычисления решения прямой задачи кинематики, блоки вычисления якобиана желаемых траекторий, блок вычисления производной по времени от якобиана желаемых траекторий, блок вычисления векторного коэффициента, блок транспонирования, блоки обращения матриц, блоки перемножения и блоки суммирования.
Устройство управления, реализуемое структурой прототипа, позволяет исключить из структуры системы управления блок решения обратной задачи кинематики, которое заменено решением обратной задачи динамики, не требуется наличия аппроксимирующих устройств и интерполяторов в структуре системы управления роботом, что позволяет исключить соответствующие составляющие погрешности задания, связанные с приближенностью расчетов [Бурдаков С.Ф., Дьяченко В. А., Тимофеев А.Н. Проектирование манипуляторов промышленных роботов и роботизированных комплексов. М., Высшая школа, 1986, 246 с., с.60], и, следовательно, снизить погрешность отработки планируемых траекторий движения, а также организовать движение робота во всем классе квадратичных форм внешних или обобщенных координат.
Признаки прототипа, общие с заявляемым техническим решением, следующие: блок исполнительных механизмов, блок механической системы, представимые двумя интеграторами, блоком матрицы управления, блоком суммирования и блоком нелинейных элементов, планировщик траекторий в пространстве внешних координат, блок датчиков, блок вычисления якобиана решения прямой задачи кинематики, блок вычисления производной по времени от якобиана решения прямой задачи кинематики, блок вычисления решения прямой задачи кинематики, блоки вычисления якобиана желаемых траекторий, блок вычисления производной по времени от якобиана желаемых траекторий, блоки суммирования, вычислительные блоки и блоки перемножения.
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем: алгоритмы управления, реализуемые прототипом, позволяют организовать движение робота вдоль заданных траекторий только с постоянной траекторией (контурной) скоростью, значение которой может принимать только наименьшее из значений кривой максимальной скорости [Н.Н. Болотник, Ф. Л. Черноусько. Оптимизация управления манипуляционными роботами. "Техническая кибернетика", 1, 1990, с.189-238]. Т.е. имеющиеся энергетические возможности приводов используются не в полной мере, и манипуляционный робот не достигает максимально возможной производительности.
Задачей изобретения является повышение производительности манипуляционных роботов при отработке траекторий, определяемых технологической задачей.
Технический результат, достигаемый при осуществлении предлагаемого устройства, заключается в том, что предлагаемые алгоритмы управления обеспечивают движение рабочего органа манипуляционного робота вдоль заданной в пространстве внешних или обобщенных координат траектории с максимально возможной траекторной скоростью. При этом не требуется организации предварительных расчетов поверхностей или линий переключения, а также предварительного определения моментов переключения управляющих воздействий для случая разомкнутого управления.
Технический результат достигается тем, что в устройство, содержащее планировщик траекторий в пространстве внешних координат, блок датчиков, блок вычисления управлений, первый блок суммирования, первый и второй интеграторы, блок формирования нелинейных элементов, блок матрицы управления, выходы которого связаны с первыми входами первого блока суммирования, вторые входы которого подключены к выходам блока формирования нелинейных элементов, первые входы которого связаны с выходами первого интегратора, входы которого подключены к выходам первого блока суммирования, со вторыми входами блока датчиков и входами второго интегратора, а вторые входы блока формирования нелинейных элементов связаны с выходами второго интегратора и первыми входами блока датчиков, первые выходы которого связаны с первыми входами планировщика траекторий в пространстве внешних координат и четвертыми входами блока вычисления управлений, а вторые выходы блока датчиков подключены ко вторым входам планировщика траекторий в пространстве внешних координат, вторые выходы которого связаны с шестыми входами блока вычисления управлений, и к пятым входам блока вычисления управлений, выходы которого связаны со входами блока матрицы управления, введены блок торможения, блок дифференцирования, блок формирования кривой максимальной скорости.
Первые входы последнего связаны со вторыми выходами блока датчиков, со вторыми входами блока дифференцирования, со вторыми входами планировщика траекторий в пространстве внешних координат, с первыми входами блока торможения, вторые входы которого подключены к третьим выходам планировщика траекторий в пространстве внешних координат, третьи входы которого связаны с выходами блока торможения и четвертыми входами блока формирования кривой максимальной скорости, вторые входы которого подключены к первым выходам блока датчиков, к третьим входам блока торможения, к первым входам блока дифференцирования, первые выходы которого связаны со вторыми входами блока вычисления управлений, к первым входам планировщика траекторий в пространстве внешних координат, первые выходы которого связаны с третьими входами блока формирования кривой максимальной скорости, выходы которого подключены к первым входам блока вычисления управлений и к входам блока дифференцирования, вторые выходы которого связаны с третьими входами блока вычисления управлений.
Блок вычисления управлений содержит блок вычисления коэффициентов управления, блок вычисления матричного коэффициента, блок вычисления нелинейных элементов, блок обращения матрицы, блок формирования траекторий, второй, третий, четвертый и пятый блоки суммирования, первый, второй, третий, четвертый и пятый блоки перемножения, блок вычисления произведения матриц Якоби, первые входы которого являются четвертыми входами блока вычисления управлений и подключены ко вторым входам блока вычисления коэффициентов управления, выходы которого связаны с третьими входами второго блока перемножения, ко вторым входам блока вычисления матричного коэффициента, к первым входам блока формирования траекторий и ко вторым входам блока вычисления нелинейных элементов, выходы которого связаны с первыми входами третьего блока перемножения, выходы которого подключены ко вторым входам третьего блока суммирования.
Вторые входы блока вычисления произведения матриц Якоби являются пятыми входами блока вычисления управлений и подключены к первым входам блока вычисления матричного коэффициента, выходы которого связаны со вторыми входами четвертого блока суммирования, ко вторым входам первого блока перемножения, выходы которого связаны со вторыми входами пятого блока суммирования, и к первым входам блока вычисления нелинейных элементов, третьи входы блока вычисления произведения матриц Якоби являются шестыми входами блока вычисления управлений и связаны с первыми входами блока вычисления коэффициентов управления, с третьими входами блока вычисления матричного коэффициента, с третьими входами блока вычисления нелинейных элементов, со вторыми входами второго блока перемножения, выходы которого подключены ко входам блока обращения матрицы, со вторыми входами блока формирования траекторий, выходы которого подключены к третьим входам третьего блока суммирования, с третьими входами третьего блока перемножения, вторые входы которого подключены к выходам второго блока суммирования и первым входам второго блока перемножения, со вторыми входами четвертого блока перемножения, первые входы которого являются первыми входами блока вычисления управлений, а выходы связаны с первыми входами третьего блока суммирования, выходы которого подключены к первым входам пятого блока суммирования, выходы которого связаны с первыми входами пятого блока перемножения.
Первые входы четвертого блока суммирования, выходы которого подключены к первым входам первого бока перемножения, являются вторыми входами блока вычисления управлений, первые входы второго блока суммирования являются третьими входами бока вычисления управлений, вторые входы второго блока суммирования связаны с выходами блока вычисления произведения матриц Якоби, а инверсные выходы блока обращения матрицы подключены ко вторым входам пятого блока перемножения, выходы которого являются выходами блока вычисления управлений.
Блок вычисления кривой максимальной скорости содержит первую схему сборки, блок ключей, блок схем совпадения, первый блок компараторов, блок вычисления ординат вершин, блок вычисления коэффициентов, первые, вторые и третьи входы которого являются соответственно первыми, вторыми и третьими входами блока формирования кривой максимальной скорости, а его выходы подключены ко входам блока вычисления ординат вершин, выходы которого связаны с первыми входами блока ключей и попарно во всех комбинациях со входами первого блока компараторов, прямые и инверсные выходы которого подключены к первым входам блока схем совпадения, причем прямые выходы каждого ij-го компаратора первого блока компараторов подключены к первым входам i-го элемента блока схем совпадения, а инверсные выходы каждого ij-го компаратора первого блока компараторов подключены к первым входам j-го элемента блока схем совпадения.
Вторые входы блока схем совпадения являются четвертыми входами блока формирования кривой максимальной скорости, а выходы блока схем совпадения связаны со вторыми входами блока ключей, выходы которого подключены ко входам первой схемы сборки, выходы которой являются выходами блока формирования кривой максимальной скорости.
Блок торможения содержит вторую схему сборки, второй блок компараторов, блок вычисления оставшегося пути и блок вычисления тормозного пути, первые входы которого являются первыми входами блока торможения, вторые входы являются третьими входами блока торможения, третьи входы являются вторыми входами блока торможения и связаны со входами блока вычисления оставшегося пути, выходы которого подключены к первым входам второго блока компараторов, вторые входы которого связаны с выходами блока вычисления тормозного пути, а выходы второго блока компараторов подключены ко входам второй схемы сборки, выходы которой являются выходами блока торможения.
Теоретическое доказательство наличия причинно-следственной связи между заявляемыми признаками и достигаемым техническим результатом приведено ниже.
Пусть математическая модель динамики манипуляционного робота представлена в неявном виде [М. Шахинпур, "Курс робототехники". М., Мир, 1990, 527 с., с.327]: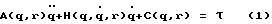
где A - (nхn)-матрица инерции; Н - (nхn)-тензор коэффициентов кориолисовых и центробежных членов; С - (nх1)-вектор гравитационных составляющих; τ - (nх1)-вектор управляющих воздействий; 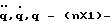 векторы обобщенных ускорений, скоростей и координат соответственно; здесь n - число степеней подвижности МР; r - параметры конкретного робота, под которым будем в дальнейшем понимать параметры, определяемые его массогабаритными показателями (длины и массы звеньев, моменты инерции звеньев и двигателей и т.п.).
векторы обобщенных ускорений, скоростей и координат соответственно; здесь n - число степеней подвижности МР; r - параметры конкретного робота, под которым будем в дальнейшем понимать параметры, определяемые его массогабаритными показателями (длины и массы звеньев, моменты инерции звеньев и двигателей и т.п.).
Зачастую представляется целесообразным рассмотрение модели (1) в форме Коши с дополнением ее решением прямой задачи кинематики [Пшихопов В.Х., Колесников А. А. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000]: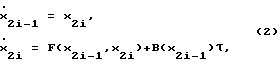
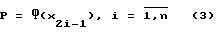
где 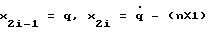 -векторы координат состояния, соответствующие обобщенным координатам и скоростям;
-векторы координат состояния, соответствующие обобщенным координатам и скоростям; 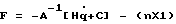 -вектор нелинейных элементов; В - (nхn)-матрица управления, В=А-1; Р - (mх1)-вектор внешних координат, элементы которого являются гладкими решениями прямой задачи кинематики, здесь n - число степеней подвижности МР.
-вектор нелинейных элементов; В - (nхn)-матрица управления, В=А-1; Р - (mх1)-вектор внешних координат, элементы которого являются гладкими решениями прямой задачи кинематики, здесь n - число степеней подвижности МР.
В дальнейшем, без потери общности рассматриваемых результатов, будем предполагать кинематическую безызбыточность МР, для которых справедливо равенство m=n.
Модели в форме (1) и (2) равнозначны и достаточно адекватно отражают динамику манипуляционных роботов. Решение прямой задачи кинематики (3) является промежуточным результатом при выводе уравнений динамики [М. Вукобратович, Д. Стокич, Н. Кирчански. Неадаптивное и адаптивное управление манипуляционными роботами. M., Мир. 1989, 376 с., с.50].
Пусть желаемые траектории движения, определяемые требованиями технологической задачи, задаются в пространстве Rm внешних координат или в пространстве Rn обобщенных координат в виде [Пшихопов В.Х., Колесников А.А. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000]:
∑
∑
где ∑ - дважды дифференцируемые функции своих аргументов. В соответствии с известными работами [Теория автоматического управления. В 2-х частях. Под ред. акад. Воронова А.А., часть 2-я "Теория нелинейных и специальных систем автоматического управления", М., "Высшая школа", 1986, 504 с., с.254] задача оптимального по быстродействию управления требует минимизации интегрального критерия вида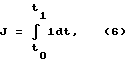
где t0, t1 - соответственно моменты начала и окончания движения.
Пусть при организации оптимального по быстродействию процесса требуется обеспечить J= Jопт= min и удовлетворить ограничениям на управляющие воздействия: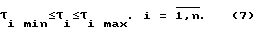
Рассмотрим подробнее вид траекторий (4) и (5). Известно, что большинство существующих методов планирования движения рабочего органа МР оперирует пространством внешних координат Rm. Причем набор этих траекторий зачастую ограничен дугами окружностей и отрезками прямых [Фу К., Гонсалес Р., Ли К. "Робототехника", М. , Мир, 1989, 624 с.]. Такое ограничение функциональных возможностей МР определяется в основном достаточно сложной процедурой трансформации траекторий (4) в пространство обобщенных координат Rn и приведением их к виду (5). Аппроксимация траекторий (4) или их интерполяция требует обязательного решения обратной задачи кинематики и поиска компромисса между точностью их задания и производительностью их отработки [Moon K. S. , Kim К. , Azadivar F. Optimum continues path operating conditions for maximum productivity of robotic manufacturing systems. "Rob. And Comput.-Integr. Manuf. ", 19-91, 8, 4, pp. 193-199.]. Уход от решения этих проблем уже обсуждался в работах [Pshikhopov V.H. Analytical Synthesis of the Nonlinear Contour Controllers for Manipulating Robots. Abstracts Book of Int. Conf. "Mathematical Theory of Network and Systems", July 6-10, 1998, Padova, Italy, Пшихопов В.Х. Аналитический синтез агрегированных регуляторов манипуляционных роботов. // В сб. "Синтез алгоритмов сложных систем", вып. 9, М., 1997, с.93-110], в которых удалось получить достаточно эффективные алгоритмы управления, позволяющие планировать траектории в виде квадратичных форм координат пространства внешних координат Rm.
Зададим требования и траектории движения в Rm в виде
где Мij - матрицы заданных коэффициентов, dim Mi1=(nхn), dim Мi2=(1хn), dim Мi3=(1х1); 01 - нулевая матрица размерности (1х1).
В частности, при m=n=3 верхние две строки вектора ∑
Любая из перечисленных кривых может быть сведена к канонической форме в соответствии с известными процедурами [Корн Г., Корн Т. "Справочник по математике для научных работников и инженеров", М., Наука, 1984, 832 с.].
При n= m≥3 вектор ∑
Возможны и другие формы задания траекторий (4), (5) как результат использования оптимизационных или иных процедур.
Сформулируем теперь требования к внешним скоростям. В силу желаемого свойства асимптотической устойчивости в целом очевидным является требование 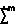 = 0, т.е. отсутствие нормальной к траектории ∑
= 0, т.е. отсутствие нормальной к траектории ∑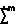 вдоль желаемой траектории (8). Иными словами, требования к траекторной скорости в пространстве внешних координат Rm могут быть заданы в виде равенства
вдоль желаемой траектории (8). Иными словами, требования к траекторной скорости в пространстве внешних координат Rm могут быть заданы в виде равенства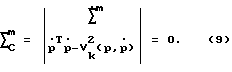
Вид функции 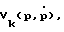 являющейся желаемой траекторной скоростью, оставим пока без обсуждения. Предположим только, что она является непрерывной на всем участке траектории [р0, рf] в Rm или на соответствующем участке | x0 2i-1, xf 2i-1| в Rn.
являющейся желаемой траекторной скоростью, оставим пока без обсуждения. Предположим только, что она является непрерывной на всем участке траектории [р0, рf] в Rm или на соответствующем участке | x0 2i-1, xf 2i-1| в Rn.
В силу предположения о дважды дифференцируемых функций ∑ и гладкости решений Ф (3), преобразования (9) могут быть представлены в пространстве обобщенных координат Rn в следующем виде: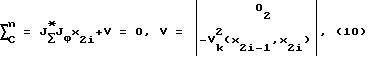
где J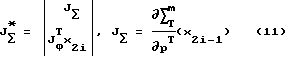
JФ - матрица Якоби вектор-функции Ф (3), dim JФ = (nхn),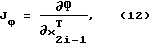
02 - нулевой вектор размерности (n-1)х1.
Очевидно [Корн Г. , Корн Т. "Справочник по математике для научных работников и инженеров", М. , Наука, 1984, 832 с.], что линия Ψ пересечения многообразия (8) и (10), при учете выражений (3), определяет желаемую траекторию движения в фазовом пространстве обобщенных координат:
Ψ = ∑
где R - положительно определенная матрица задаваемых констант, dim R= (nхn).
В работах [Пшихопов В.Х. Аналитический синтез агрегированных регуляторов манипуляционных роботов. // В сб. "Синтез алгоритмов сложных систем", вып. 9, М., 1997, с.93-110. Pshikhopov V.H. Analytical Synthesis of the Nonlinear Contour Controllers for Manipulating Robots. Abstracts Book of Int. Conf. "Mathematical Theory of Network and Systems", July 6-10, 1998, Padova, Italy. Pshikhopov V.H., Kolesnikov A.A. Synergetic Approach to the Synthesis of Multiply Connected control Systems for Perspective Aggregates. Proc VI-th SAUM Inter. Confer, on Systems, Automation Control and Measurement. Nis, Yugoslavia, pp. 423-427. Пшихопов В.Х., Колесников A.A. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000] уже обсуждалась процедура синтеза контурных регуляторов при Vk=const, обеспечивающих асимптотическую устойчивость траекторий (13) во всем фазовом пространстве Rnxn обобщенных координат и, следовательно, желаемых траекторий движения (4) и (5) и заданных скоростных многообразий (9) и (10).
Используя изложенные в этих работах процедуры, с учетом функциональной зависимости вектора V от координат пространства состояний, получим следующий алгоритм траекторного управления [Pshikhopov V. Kh. New Approach to the Design of the Near Time Optimal Path Following Controller for the Manipulating Robots. Proceedings CD and Abstracts Book of Int. Conf. "Mathematical Theory of Network and Systems", Perpignian, France, June 19-23, 2000]:
τ = -K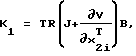
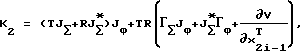
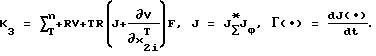
где Т - положительно определенная (nхn)-матрица задаваемых констант.
Предложенный алгоритм управления предполагает планирование траекторий в соответствующих подпространствах пространства Rmхm; последующий переход в пространство Rnхn посредством решения прямой задачи кинематики (3); синтез управляющих воздействий в соответствии с выражениями (14), которые стабилизируют желаемые фазовые траектории во всей области достижимости соответствующих пространств фазовых координат. Следует отметить, что элементы матриц Т и R определяют характер движения замкнутой системы к многообразию (13) и должны выбираться из условия максимального использования энергетических возможностей МР [Пшихопов В.Х. Аналитический синтез агрегированных регуляторов манипуляционных роботов. // В сб. "Синтез алгоритмов сложных систем", вып. 9, М., 1997, с.93-110].
Рассмотрим вопрос формирования контурной скорости Vk (10), удовлетворяющей поставленной задаче.
Известно [Huang H.P., McClamroch N.H. Time-optimal Control for a Robotic Contour following Problem. "IEEE J. Rob and Autom." 1988, 4, 2, p.p. 140-149] , что в задаче оптимального по быстродействию управления минимизация времени перемещения эквивалентна максимизации скорости движения по траектории. Процедура получения профиля максимальной скорости на траектории движения достаточно подробно рассмотрена в работах Сhеn Y., Chien S.Y.-P., Desrochers A.A. General structure of time-optimal control of robotic manipulators moving along prescribed paths. "IEEE Int. J. Control", 1992, 56, 4, pp. 767-782. Shiller Z., Dubovsky S. On the Time Optimal Control of Robotic Manipulators with Actuator and End-effector Constraints. IEEE Int. Conf. Rob. and Autom. , St. Louis, March 25-28, 1985, Silver Spring, Md, 1984, 614-620; Н. Н. Болотник, Ф.Л. Черноусько. Оптимизация управления манипуляционными роботами. "Техническая кибернетика", 1, 1990, с.189-238.
Используя в качестве параметра траектории S(t) - длину пройденного вдоль нее расстояния, обобщенные координаты q(t) можно представить в функции, зависящей от S(t):
q(t)=M(S(t)), q(t0)=M(S0), q(tf)=M(Sf), (15)
где t0, tf - начальный и конечный моменты времени; S0, Sf - начальное и конечное значения функции S(t).
Как известно [Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. М., Наука, 1967, 608 с., с. 394], если траектория (4) задается на плоскости (m=n=2) в явном виде:
у=f(х) или x=g(y), (15-а)
то длина дуги кривой, описываемой выражениями (4), соответствующая пройденному вдоль кривой (4) пути S, может быть определена как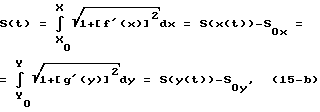
S0х=S(x(t0))=S(X0), S0y=S(y(t0))=S(Y0)
или в общем случае
S(t) = S(P(t))-S0, (15-с)
S0= S(P(t0))=S(P0),
где ' означает соответствующую производную по аргументу функций (15-а); x0, y0 - соответственно координаты точки Р0 начала движения, принадлежащей желаемой траектории (15-а), t0 - момент начала движения рабочего органа МР вдоль траектории (15-а).
Связь между траекториями вида (15-а) и траекториями вида (4) при m=n=2 является очевидной [Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. М., Наука, 1967, 608 с., с. 205-212].
Следует отметить, что при задании требований к траектории движения рабочего органа МР в более общем виде, в частности, при m=n=3 выражения (4) могут быть также сведены к виду (15-а) [Шикин Е.В., Франк-Каменецкий М.М. Кривые на плоскости и в пространстве. М., Фазис, 1997, 336 с., с. 261-262].
Таким образом, задание траектории в виде (4) или требований к траектории движения рабочего органа МР вида (8) в пространстве Rm внешних координат при задании точки Р0 начального положения схвата однозначно, в силу выражения (15-с), определяет значение параметра S(P(t)) в функции внешних координат Р.
Кроме того, учитывая выражение (3), однозначно определяющее связь между вектором внешних Р и обобщенных q=x2i-1 координат, с учетом выражения (8) можно получить функциональную зависимость параметра S от обобщенных координат q= x2i-1, определяемую кинематикой МР и желаемой траекторией движения рабочего органа, вида
S(t)=S(x2i-1(t))-S0, - (15-d)
S0=S(x2i-1(t0)).
В случае задания траекторий в виде выражений (5) зависимости вида (15-d) могут быть получены непосредственно на основании второго равенства выражения (15 -b).
Указанное обстоятельство позволяет получить функциональную зависимость вида (15), которая однозначно определяется желаемой траекторией движения рабочего органа МР (4) или (5), а также уравнениями динамики МР (1), что позволяет получить уравнение динамики МР в функции параметра траектории S.
Беря первую и вторую производные от обеих частей первого из равенств (15) и подставляя их в уравнение (1), получим [Chen Y., Chien S.Y.-P., Desrochers A. A. General structure of time-optimal control of robotic manipulators moving along prescribed paths. "IEEE Int. J. Control", 1992, 56, 4, pp. 767-782; Н.Н. Болотник, Ф.Л. Черноусько. Оптимизация управления манипуляционными роботами. "Техническая кибернетика", 1, 1990, с.189-238]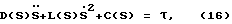
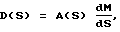
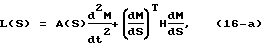
где A, H, C - матрицы соответствующих размерностей, определенные в уравнении (1).
Матричная форма записи уравнений (16) позволяет однозначно перейти к скалярной форме записи для каждого i-го звена МР. Запишем уравнение (16) в скалярной форме: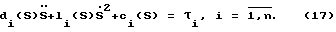
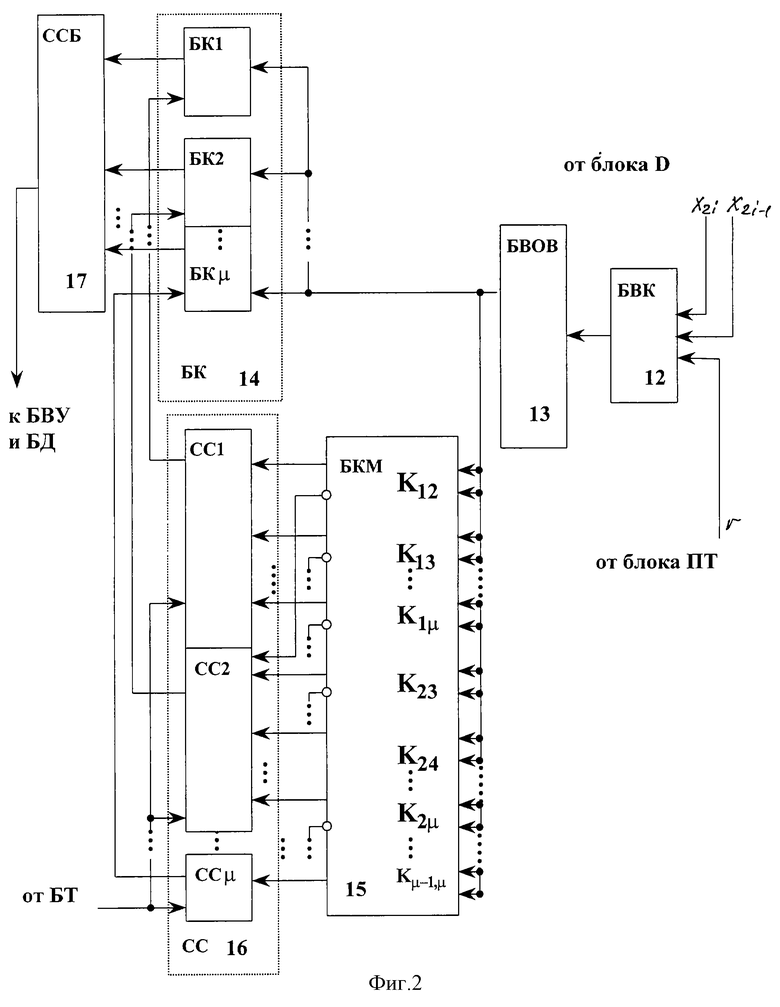
Параметры di, 1i, сi, являющиеся элементами соответствующих векторов D(S), L(S), C(S), определяемых выражениями (16-а), в силу функциональной зависимости параметра S от обобщенных координат q=x2i-1 и функциональной зависимости матриц А, Н, С от обобщенных координат q, скоростей 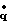 и параметров робота r [Шахинпур М. Курс робототехники. М., Мир, 1990, 527 с., с 327; Фу К. , Гонсалес Р., Ли К. Робототехника. М., Мир, 1989, 624 с., с. 117-121; Воробьев Е.И., Козырев Ю.Г., Царенко В.И. Промышленные роботы агрегатно-модульного типа. М., Машиностроение. 1989, 240 с., с. 150; Черноусько Ф.Л., Болотник Н.Н., Градецкий В.Г. Манипуляционные роботы. (Динамика, управление, оптимизация). М. , Наука, 1989, 368 с., с.73-83.] однозначно определяются текущими значениями обобщенных координат и скоростей, а также параметрами конкретного робота, определяемыми его массогабаритными показателями (длины и массы звеньев, моменты инерции двигателей и т.п.) и его кинематической схемой.
и параметров робота r [Шахинпур М. Курс робототехники. М., Мир, 1990, 527 с., с 327; Фу К. , Гонсалес Р., Ли К. Робототехника. М., Мир, 1989, 624 с., с. 117-121; Воробьев Е.И., Козырев Ю.Г., Царенко В.И. Промышленные роботы агрегатно-модульного типа. М., Машиностроение. 1989, 240 с., с. 150; Черноусько Ф.Л., Болотник Н.Н., Градецкий В.Г. Манипуляционные роботы. (Динамика, управление, оптимизация). М. , Наука, 1989, 368 с., с.73-83.] однозначно определяются текущими значениями обобщенных координат и скоростей, а также параметрами конкретного робота, определяемыми его массогабаритными показателями (длины и массы звеньев, моменты инерции двигателей и т.п.) и его кинематической схемой.
Подстановка неравенств (7) в уравнение (17) позволяет получить следующие выражения: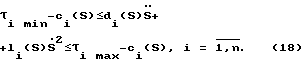
Для любого сочленения i-e неравенство (18) определяет ограниченную открытую область, образованную парой параллельных прямых на плоскости 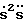 для заданного значения S. Число n таких неравенств образует на плоскости многоугольник Ω допустимых значений скоростей и ускорений [Chen Y., Chien S. Y. -P., Desrochers A.A. General structure of time-optimal control of robotic manipulators moving along prescribed paths. "IEEE Int. J. Control", 1992, 56, 4, pp.767-782].
для заданного значения S. Число n таких неравенств образует на плоскости многоугольник Ω допустимых значений скоростей и ускорений [Chen Y., Chien S. Y. -P., Desrochers A.A. General structure of time-optimal control of robotic manipulators moving along prescribed paths. "IEEE Int. J. Control", 1992, 56, 4, pp.767-782].
Движение МР может иметь место только внутри многоугольника Ω. При различных значениях S эти многоугольники имеют различный вид [Chen Y., Chien S. Y. -P., Desrochers A.A. General structure of time-optimal control of robotic manipulators moving along prescribed paths. "IEEE Int. J. Control", 1992, 56, 4, pp. 767-782].
Очевидно, что значение допустимой траекторной скорости 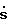 лежит между 0 и некоторой максимальной скоростью
лежит между 0 и некоторой максимальной скоростью 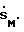 Множество всех
Множество всех 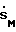 вдоль траектории S(t) образует кривую максимальной скорости на плоскости
вдоль траектории S(t) образует кривую максимальной скорости на плоскости 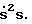
Таким образом, формируя кривую максимальной скорости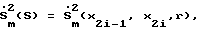
и используя ее в траекторном многообразии ∑S(9), т.е. принимая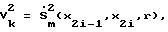
мы можем обеспечить максимальное по быстродействию траекторное управление МР, а определение глобального минимума функции максимальной скорости на интервале [S0, Sf] позволяет однозначно и корректно определить максимально возможное постоянное значение контурной скорости, необходимое для организации, например, операций лазерного кроя, дуговой сварки и т.п.
В соответствии с неравенствами (18) ординаты 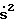 вершин многоугольника Ω могут быть вычислены в соответствии с выражениями
вершин многоугольника Ω могут быть вычислены в соответствии с выражениями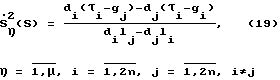
где μ= C2 2n-n - количество вершин многоугольника Ω, здесь n - число звеньев.
Максимальная из вершин, определяемых выражением (19), и является точкой кривой максимальной скорости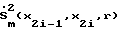
при текущем значении параметра S.
В качестве алгоритмов, используемых для определения матриц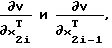
входящих в выражение (14), могут быть использованы известные численные процедуры [Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М., 1984, 833 с., с.695-696, c.112].
В частности, в соответствии с выражением (20.7-2) [Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М., 1984, 833 с., с. 695] элементы vx2i(w, e) матрицы 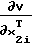 , входящей в выражение (14), при w=n, здесь n - число звеньев робота, определяются как
, входящей в выражение (14), при w=n, здесь n - число звеньев робота, определяются как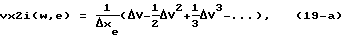
где Δxе - приращение значения е-й обобщенной скорости, 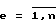 , здесь n - число звеньев МР;
, здесь n - число звеньев МР; 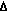 V - приращение кривой максимальной скорости
V - приращение кривой максимальной скорости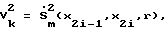
определяемой выражением (19).
Если w<n, то в силу второго равенства выражения (10) vx2i(w,e)=0.
Аналогичным образом определяются и элементы vx(w,e) матрицы 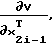 входящей в выражение (14), при w=n:
входящей в выражение (14), при w=n: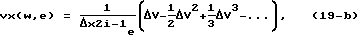
где Δх2i-1e - приращение значения е-й обобщенной координаты, 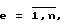 здесь n - число звеньев МР. Если w<n, то в силу второго равенства выражения (10) vx(w,e)=0.
здесь n - число звеньев МР. Если w<n, то в силу второго равенства выражения (10) vx(w,e)=0.
Количество членов, удерживаемых в выражениях (19-а), (19-b), определяется требованиями к точности вычислений.
В случае необходимости вывода рабочего органа МР в заданную технологическими требованиями точку Pf в пространстве Rm внешних координат или точку xf 2i-1 пространства Rn обобщенных координат (точки Pf и xf 2i-1 принадлежат соответственно траектории (4) или (5)) необходима организация режима торможения.
Режим торможения и, соответственно, формирование уставки VK=0 осуществляется в случае удовлетворения хотя бы одному из неравенств [Newman W. Robust Near Time-Optimal Control. IEEE Trans. Autom. Control., 1990, 35, 7, p.p. 841-844]: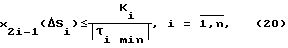
где ΔSi - параметр торможения i-го звена, ΔSi=Sf-S; Кi - кинетическая энергия i-го звена;  - модуль минимального значения управляющего воздействия. Здесь Sf - значение пройденного пути в конечной точке Pf или xf 2i-1, определяемое выражением (15-с) или (15-d) как
- модуль минимального значения управляющего воздействия. Здесь Sf - значение пройденного пути в конечной точке Pf или xf 2i-1, определяемое выражением (15-с) или (15-d) как
Sf=S(Pf)-S0, S0=S(P(t0))=S(P0)
или
Sf=S(xf 2i-1)-S0, S0=S(x2i-1(t0)). (21)
Значение S является текущим значением параметра траектории, определяемого планировщиком траекторий в пространстве внешних координат по выражениям (15-с) или (15-d).
Вычисление кинетической энергии Ki i-гo звена робота осуществляется по формуле [Фу К., Гонсалес Р., Ли К. Робототехника. М., Мир, 1989, 624 с., с. 109-110]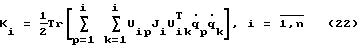
где Тr[] - операция вычисления следа матрицы [], однозначно определяемая алгоритмом п. 13.2-7 [Корн Г., Корн Т. Справочник по математике для научных работников и инженеров, М., Наука, 1984, 832 с., с.394]; Uip, Uik - вспомогательные матрицы, зависящие от обобщенных координат q=х2i-1, параметров конкретного робота r и определяемые выражениями (3.2-2)-(3.2-11) [Фу К., Гонсалес Р., Ли К. Робототехника. М., Мир, 1989, 624 с., с. 104-107]; Т- символ транспонирования; Ji - моменты инерции i-ro звена, являющиеся параметрами конкретного робота; 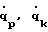 - обобщенные скорости р-го и k-го звеньев; n - число звеньев МР.
- обобщенные скорости р-го и k-го звеньев; n - число звеньев МР.
Выражение (22), являющееся функцией обобщенных координат q=х2i-1 и обобщенных скоростей 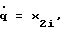 а также параметров конкретного робота r, позволяет однозначно определить кинетическую энергию каждого звена МР.
а также параметров конкретного робота r, позволяет однозначно определить кинетическую энергию каждого звена МР.
Отметим, что организация режима торможения возможна и при переключении на структуру позиционного регулятора, являющегося частным случаем управления (14) [Пшихопов В. Х. Аналитический синтез агрегированных регуляторов манипуляционных роботов. // В сб. "Синтез алгоритмов сложных систем", вып. 9, М. , 1997, с. 93-110]. Для организации режима торможения возможно использование и иных процедур.
Следует отметить, что все вычисления осуществляются в функции измеряемых фазовых координат х2i-1 (обобщенных координат) и x2i (обобщенных скоростей).
Предложенный алгоритм траекторного, оптимального по быстродействию управления и его структурная реализация позволяют организовать движение рабочего органа МР вдоль заданных траекторий с максимальной контурной (траекторной) скоростью. При этом не требуется наличия аппроксимирующих устройств и интерполяторов, а также гарантируется асимптотическая устойчивость в целом заданных, фазовых траекторий движения.
Учет нелинейных элементов моделей динамики робота (1), (3) при синтезе алгоритма управления (14) и структуры управления прототипа позволяет расширить область фазового пространства робота, т.е. обеспечить точное отслеживание быстрых траекторий [М. Вукобратович, Д. Стокич, Н. Кирчански. Неадаптивное и адаптивное управление манипуляционными роботами, М., Мир, 1989, 376 с. с. 59-60], что является немаловажным фактом при повышении требований к производительности робота. Замыкание робота управлением (14) обеспечивает асимптотическую устойчивость в целом планируемых траекторий (13). Аналогичным свойством обладают и объекты, замкнутые устройством управления прототипа.
Полученный алгоритм управления (14) не требует решения обратной задачи кинематики (ОЗК) при организации движения рабочего органа манипуляционного робота вдоль траекторий, заданных в пространстве внешних координат, которое сведено к решению обратной задачи динамики, т.е. к решению алгебраической (относительно τ) системы уравнений. Исключение блока решения ОЗК упрощает структуру системы управления роботом.
Время движения рабочего органа робота к желаемым фазовым траекториям, т. е. время отработки отклонения от желаемой траектории, определяется величиной элементов матриц Т и R и, с одной стороны, определяется энергетическими возможностями робота, с другой - требованиями технологической задачи [А.А. Колесников. Синергетическая теория управления. М., - Таганрог, 1994, 344 с., с. 99].
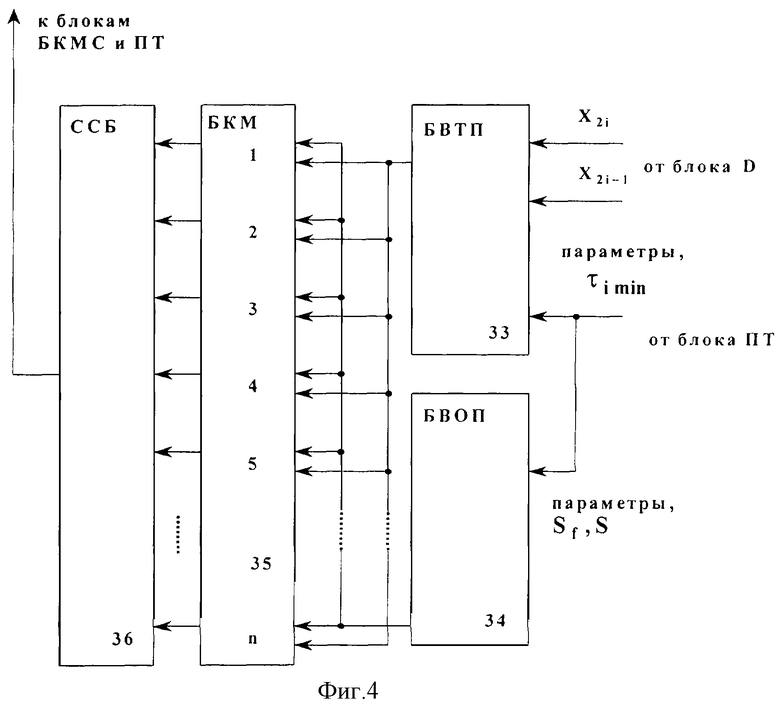
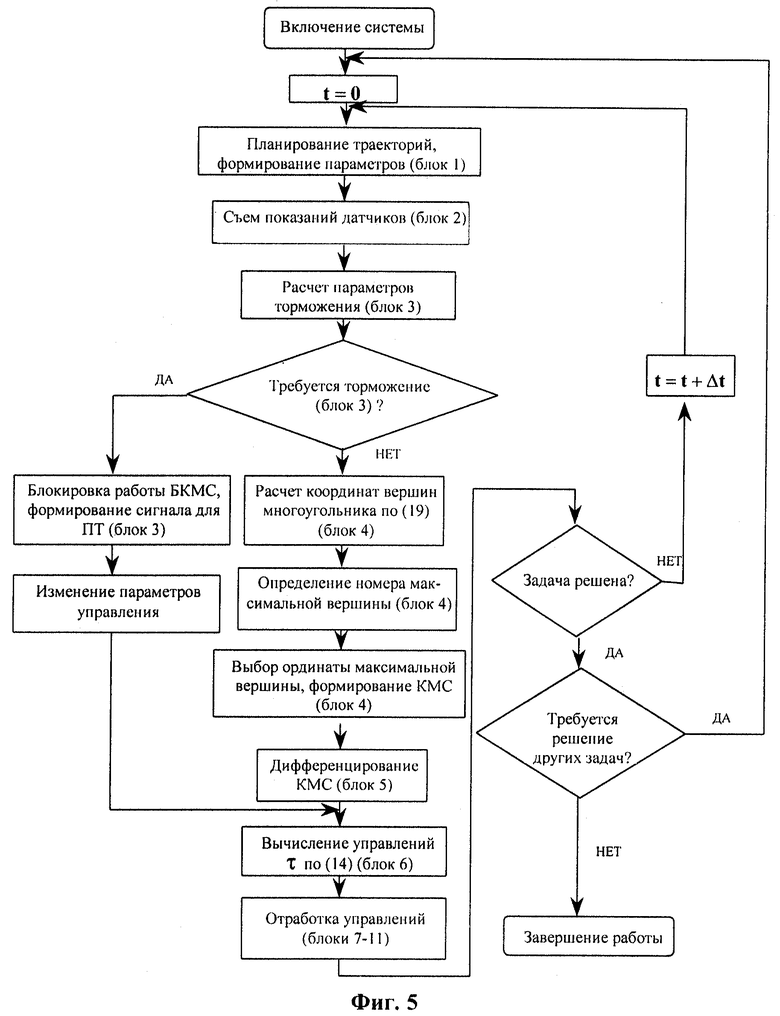
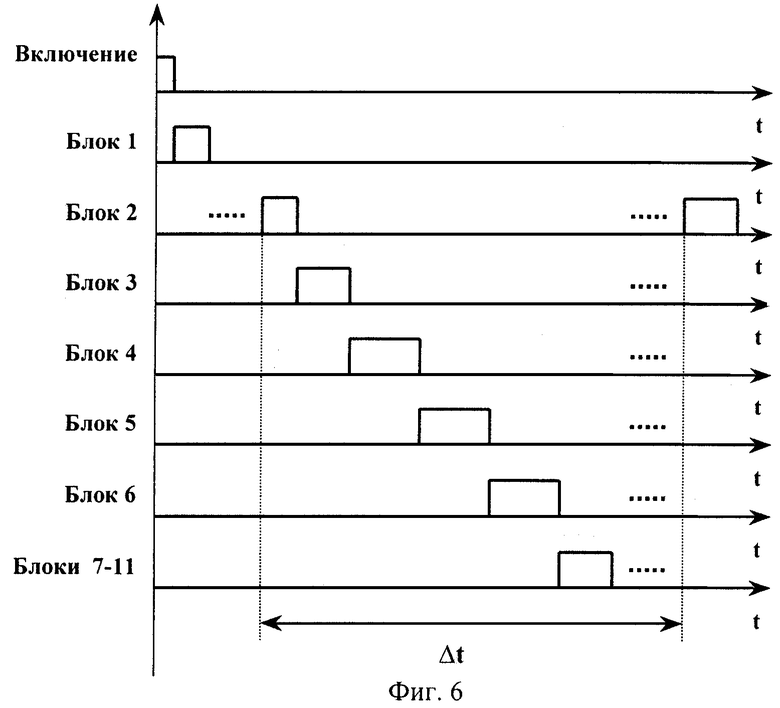
Изобретение поясняется чертежами, где на фиг.1 представлена блок-схема робота, замкнутого синтезированным устройством траекторного, оптимального по быстродействию управления, на фиг.2 - структурная схема блока формирования кривой максимальной скорости, на фиг.3 - структурная схема блока вычисления управлений, на фиг. 4 - структурная схема блока торможения, на фиг.5 - блок-схема алгоритма функционирования устройства, на фиг.6 - диаграмма работы устройства.
Устройство траекторного, оптимального по быстродействию управления роботом, представленное на фиг. 1, содержит планировщик траекторий в пространстве внешних координат (ПТ) 1, первые входы которого подключены к первым выходам блока датчиков (D) 2, третьим входам блока торможения (БТ) 3, вторым входам блока формирования кривой максимальной скорости (БКМС) 4, первым входам блока дифференцирования (БД) 5 и четвертым входам блока вычисления управлений (БВУ) 6.
Вторые входы планировщика траекторий в пространстве внешних координат 1 связаны со вторыми выходами блока датчиков 2, первыми входами блока торможения 3, первыми входами блока формирования кривой максимальной скорости 4, вторыми входами блока дифференцирования 5 и пятыми входами блока вычисления управлений 6, а его третьи входы подключены к выходам блока торможения 3 и четвертым входам блока формирования кривой максимальной скорости 4, третьи входы которого подключены к первым выходам планировщика траекторий в пространстве внешних координат 1.
Вторые выходы планировщика траекторий в пространстве внешних координат 1 связаны с шестыми входами блока вычисления управлений 6, вторые и третьи входы которого связаны соответственно с первыми и вторыми выходами блока дифференцирования 5, третьи входы которого подключены к первым входам блока вычисления управлений 6 и выходам блока формирования кривой максимальной скорости 4.
Третьи выходы планировщика траекторий в пространстве внешних координат 1 подключены ко вторым входам блока торможения 3.
Выходы блока вычисления управлений 6 подключены к входам блока матрицы управления (В) 7, выходы которого подключены к первым входам первого блока суммирования (С) 8, вторые входы которого связаны с выходами блока формирования нелинейных элементов (F) 9, а выходы блока суммирования 8 связаны со входами первого интегратора (И) 10.
Выходы первого интегратора 10 связаны с входами второго интегратора (И) 11, первыми входами блока формирования нелинейных элементов 9 и вторыми входами блока датчиков 2, первые входы которого подключены к выходам второго интегратора 11 и вторым входам блока формирования нелинейных элементов 9.
Функциональный блок 4 формирования кривой максимальной скорости, представленный на фиг.2, содержит блок вычисления коэффициентов (БВК) 12, первые, вторые, третьи входы которого являются соответственно первыми, вторыми и третьими входами блока формирования кривой максимальной скорости 4, а его выходы связаны с входами блока вычисления ординат вершин (БВОВ) 13, выходы которого связаны с первыми входами элементов блока ключей (БК) 14 и попарно с входами двухвходовых компараторов первого блока компараторов (БКМ) 15. Причем прямые выходы каждого из компараторов Кij подключены к первым входам i-го элемента блока схем совпадения (СС) 16, а инверсные выходы каждого из компараторов Кij связаны с первыми входами j-го элемента блока схем совпадения (СС) 16. Вторые входы блока схем совпадения 16 являются четвертыми входами блока формирования кривой максимальной скорости и подключены к выходам блока торможения 3. Выходы η-го элемента блока схем совпадения 16 подключены ко вторым входам η-го элемента блока ключей 14, выходы которого подключены ко входам первой схемы сборки (ССБ) 17, выходы которой являются выходами блока формирования кривой максимальной скорости 4.
Функциональный блок вычисления управлений 6, представленный на фиг.3, содержит блок вычисления произведения матриц Якоби (БВЯ) 18, первые входы которого являются четвертыми входами блока вычисления управлений и связаны со вторыми входами блока коэффициентов управления (БКУ) 19, вторыми входами блока вычисления матричного коэффициента (БВМК) 20, первыми входами блока формирования траекторий (БФТ) 21 и вторыми входами блока вычисления нелинейных элементов (БНЭ) 22. Вторые входы блока вычисления матрицы Якоби 18, являющиеся пятыми входами блока вычисления управлений 6, связаны с первыми входами блока вычисления матричного коэффициента 20, вторыми входами первого блока перемножения (П) 23 и первыми входами блока вычисления нелинейных элементов 22. Третьи входы блока вычисления матрицы Якоби 18 являются шестыми входами блока вычисления управлений 6 и связаны с первыми входами блока коэффициентов управления 19, вторыми входами второго блока перемножения (П) 24, со вторыми входами блока формирования траекторий 21, с третьими входами третьего блока перемножения (П) 25, со вторыми входами четвертого блока перемножения (П) 26, первые входы которого являются первыми входами блока вычисления управлений 6, с третьими входами блока вычисления матричного коэффициента 20 и с третьими входами блока вычисления нелинейных элементов 22, выходы которого подключены к первым входам третьего блока перемножения 25.
Выходы блока вычисления матрицы Якоби 18 связаны со вторыми входами второго блока суммирования (С) 27, первые входы которого являются третьими входами блока вычисления управлений 6, а его выходы подключены к первым входам второго блока перемножения 24 и вторым входам третьего блока перемножения 25, выходы которого связаны со вторыми входами третьего блока суммирования (С) 28, первые входы которого подключены к выходам четвертого блока перемножения 26.
Выходы блока вычисления матричного коэффициента 20 связаны со вторыми входами четвертого блока суммирования (С) 29, первые входы которого являются вторыми входами блока вычисления управлений 6, а его выходы связаны с первыми входами первого блока перемножения 23, выходы которого подключены ко вторым входам пятого блока суммирования (С) 30, первые входы которого связаны с выходом третьего блока суммирования 28, третьи входы которого подключены к выходам блока формирования траекторий 21.
Выходы блока коэффициентов управления 19 связаны с третьими входами второго блока перемножения 24, выходы которого подключены к входам блока обращения матрицы (БОМ) 31, инверсные выходы которого подключены ко вторым входам пятого блока перемножения (П) 32, первые входы которого соединены с выходами пятого блока суммирования 30, первые входы которого связаны с выходами третьего блока суммирования 28, а выходы пятого блока перемножения 32 являются выходами блока вычисления управлений.
Функциональный блок торможения (БТ) 3, представленный на фиг.4, содержит блок вычисления тормозного пути (БВТП) 33, первые, вторые и третьи входы которого соответственно являются первыми, третьими и вторыми входами блока торможения 3. Причем третьи входы блока вычисления тормозного пути 33 подключены к входам блока вычисления оставшегося пути (БВОП) 34, выходы которого связаны с первыми n входами второго блока компараторов (БКМ) 35, n вторых входов которого подключены к выходам блока вычисления тормозного пути 33, а его выходы связаны со входами второй схемы сборки (ССБ) 36, выходы которой являются выходами блока торможения 3.
Блок-схема алгоритма функционирования устройства и диаграмма его работы представлены соответственно на фиг.5 и фиг.6.
Устройство траекторного, оптимального по быстродействию управления функционирует следующим образом. Планировщик траекторий в пространстве внешних координат 1 (см. фиг.1) в зависимости от желаемой траектории формирует на своих вторых выходах соответствующие коэффициенты квадратичных форм, диагональные элементы определенно положительных матриц Т и R, определяющих динамику движения робота к линии пересечения (13) многообразий (8) и (9), и, в случае необходимости, требуемое значение постоянной контурной скорости Vk движения вдоль этих траекторий, а также параметры робота, определяющие элементы матрицы В, вектора F и матричных коэффициентов [Пшихопов В.Х., Колесников А. А. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000]. Все эти параметры передаются на шестой вход блока вычисления управлений 6 для последующего расчета управляющих воздействий.
На первых выходах планировщика траекторий в пространстве внешних координат 1 формируются параметры робота, необходимые для расчета элементов, используемых в выражении (19), которые подаются на третьи входы блока формирования кривой максимальной скорости 4, а на его третьих выходах в соответствии с выражениями (15-d), (21) формируются параметры Sf и S, задаются параметры r конкретного манипулятора (длины и массы звеньев, моменты инерции звеньев и двигателей и т.д.), необходимые для расчета кинетической энергии звеньев по выражениям (22), ограничения на управляющие воздействия  необходимые для функционирования блока торможения 3.
необходимые для функционирования блока торможения 3.
Блоком датчиков 2 снимаются показания с n выходов первого интегратора 10 и с n выходов второго интегратора 11 механической системы робота. Сигналы с n первых выходов блока датчиков 2, соответствующие вектору x2i состояния обобщенных скоростей, подаются соответственно на первые входы блока формирования кривой максимальной скорости 4, на вторые входы планировщика траекторий в пространстве внешних координат, на первые входы блока торможения 3 и на пятые входы блока вычисления управлений 6. Сигналы с n вторых выходов блока датчиков 2, соответствующие вектору x2i-1 состояния обобщенных координат, подаются соответственно на первые входы планировщика траекторий в пространстве внешних координат 1, на вторые входы блока формирования кривой максимальной скорости 4, на четвертые входы блока вычисления управлений 6 и на третьи входы блока торможения 3.
На основании показаний блока датчиков 2, подаваемых на первые и вторые входы блока торможения 3, а также заданных планировщиком траекторий в пространстве внешних координат 1 параметров блок вычисления тормозного пути 33 (см. фиг.4) блока торможения 3 формирует сигналы, соответствующие правой части неравенства (20). Алгоритм вычисления кинетической энергии звеньев в функции обобщенных координат и скоростей представлен выражением (22). Ограничения на управляющие воздействия известны для конкретного манипуляционного робота и задаются планировщиком траекторий в пространстве внешних координат 1. Одновременно блок вычисления оставшегося пути 34 блока торможения 3 на основании выражений (15) и параметров, заданных планировщиком траекторий в пространстве внешних координат 1, в соответствии с выражениями (15), (15-d), (21) рассчитывает левую часть неравенства (20). Рассчитанные данные с n выходов блока вычисления тормозного пути 33 подаются на n вторые входы второго блока компараторов 35, на первые n входы которого подаются рассчитанные данные с n выходов блока вычисления оставшегося пути 34. Второй блок компараторов 35 осуществляет сравнение данных для каждой из n обобщенных координат. И если выполняется одно из неравенств (20), то на его выходах формируется сигнал, который через схему сборки 36 подается на четвертые входы блока формирования кривой максимальной скорости 4, блокируя его работу, и на третьи входы планировщика траекторий в пространстве внешних координат 1 для последующей организации режима торможения. В этом случае планировщик траекторий в пространстве внешних координат 1 изменяет параметры по своему второму выходу и система переходит в режим торможения.
Выражения (20), (21) и (22) однозначно определяют алгоритм функционирования блока торможения 3.
Если ни одно из неравенств (20) не выполняется или режим торможения не требуется, то на выходе второй схемы сборки 36 сигнал торможения не вырабатывается и система функционирует в режиме оптимального по быстродействию движения.
В этом случае блок вычисления коэффициентов 12 блока формирования кривой максимальной скорости 4 (см. фиг.2) на основании выражений (16-а), модели (1), параметров конкретного робота, задаваемых планировщиком траекторий в пространстве внешних координат 1 и данных блока датчиков 2 вычисляет элементы выражения (19), на основании которого блок вычисления ординат вершин формирует значения ординаты каждой из μ вершин многоугольника допустимых значений, построенного в соответствии с неравенствами (18). Эти ординаты передаются на входы первого блока компараторов 15, где попарно сравниваются между собой на каждом из двухвходовых компараторов: на компараторе К12 ордината первой вершины сравнивается с ординатой второй вершины, на компараторе К13 ордината первой вершины сравнивается с ординатой третьей вершины, на компараторе Кij ордината i-й вершины сравнивается с ординатой j-й вершины и т. д. Если значение ординаты i-й вершины превышает значение ординаты в j-й вершине, то на прямом выходе компаратора Кij формируется сигнал логической единицы. В противном случае этот сигнал формируется на инверсном выходе компаратора Кij. Сигналы с выходов первого блока компараторов 15 определенным образом подаются на первые входы элементов блока схем совпадения 16: прямые сигналы компараторов Кij подаются на первые входы i-го элемента блока схем совпадения 16, а инверсные сигналы компараторов Кij подаются на первые входы j-го элемента блока схем совпадения 16. Сигнал логической единицы появляется на выходе η-го элемента блока схем совпадения 16 только в том случае, если на всех его входах присутствует сигнал логической единицы, что соответствует максимальному значению ординаты η-й вершины. Этот сигнал подается на второй вход η-го элемента блока ключей 14, открывает его и сигнал с первого входа этого ключа, соответствующий значению ординаты максимальной вершины многоугольника допустимых значений скоростей и ускорений, а следовательно, и значению максимальной траекторной скорости, через первую схему сборки 17 подается на блок дифференцирования 5 и блок вычисления управлений 6. В случае блокирования работы блока формирования кривой максимальной скорости 4 блоком торможения 3 на вторых входах каждого из элементов блока схем совпадения 16 формируется сигнал логического нуля, соответственно на выходах блока схем совпадения 16 формируются сигналы логического нуля, которые блокируют выходы блока ключей 14, и значения кривой максимальной скорости не формируются.
Таким образом, на основании модели робота (1) по выражениям (16-а) в силу функциональной зависимости (7) параметра S от обобщенных координат q= x2i-1 и функциональной зависимости матриц А, Н, С от обобщенных координат q, скоростей 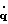 и параметров робота r, на основании показаний блока датчиков 2 и параметров конкретного робота r, задаваемых планировщиком траекторий в пространстве внешних координат 1, блоком 12 вычисляются параметры di, 1i, сi, являющиеся элементами соответствующих векторов D(S), L(S), C(S) (16-а). А блок 13 на основании вычисленных значений параметров di, li, сi и известных для каждого конкретного робота ограничений (7) определяет на основании выражений (19) ординаты вершин многоугольника.
и параметров робота r, на основании показаний блока датчиков 2 и параметров конкретного робота r, задаваемых планировщиком траекторий в пространстве внешних координат 1, блоком 12 вычисляются параметры di, 1i, сi, являющиеся элементами соответствующих векторов D(S), L(S), C(S) (16-а). А блок 13 на основании вычисленных значений параметров di, li, сi и известных для каждого конкретного робота ограничений (7) определяет на основании выражений (19) ординаты вершин многоугольника.
Выражения (16-а) и (19), а также изложенная процедура сравнения ординат, реализованная на блоках 14-17, однозначно определяет алгоритм функционирования блока 4 формирования кривой максимальной скорости (КМС).
Блок дифференцирования 5 на основании кривой максимальной скорости, формируемой на его третьем входе блоком формирования кривой максимальной скорости 4, значений обобщенных координат, формируемых на его первых входах блоком датчиков 2, и значений обобщенных скоростей, формируемых на его вторых входах блоком датчиков 2, осуществляет дифференцирование вектора V из выражения (10) по вектору обобщенных координат x2i-1 и по вектору обобщенных скоростей х2i в соответствии с алгоритмами (19-а), (19-b).
Блок вычисления управлений 6 реализует алгоритм управления по выражению (14). Блок 18 вычисления произведения матриц Якоби J из выражения (14) на основании данных планировщика траекторий в пространстве внешних координат 1, подаваемых на его третий вход, который является шестым входом блока вычисления управлений 6, данных от блока датчиков 2, подаваемых на его первые и вторые входы, которые являются соответственно четвертыми и пятыми входами блока вычисления управлений 6, формирует на своих выходах элементы матрицы J, используемой для вычисления управляющих воздействий. Более детальная реализация подобного блока приведена в Пшихопов В. Х., Колесников А.А. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000. Второй блок суммирования 27, второй блок перемножения 24 и блок коэффициентов управления 19, реализующий элементы матрицы В конкретного робота в соответствии с выражением, представленным в модели (2), формируют матричный коэффициент K1 из алгоритма (14) размерности nxn. Блок вычисления матричного коэффициента 20 и четвертый блок суммирования 29, на вторые входы которого подается сигнал производной вектора V по вектору x2i-1, формируют матричный коэффициент К2 из алгоритма (14) размерности nхn. Более детальная реализация блока вычисления матричного коэффициента 20 приведена в Пшихопов В.Х., Колесников А.А. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000. Блок вычисления нелинейных элементов 22, реализующий вычисление вектора F из модели (2), третий блок перемножения 25, четвертый блок перемножения 26, на первые входы которого от блока формирования кривой максимальной скорости подается значение максимальной траекторной скорости, блок формирования траекторий ∑
Перемножение элементов алгоритма (14) на блоке перемножения 32 позволяет сформировать на его n выходах управляющие воздействия, подаваемые на входы блока 7 матрицы управления В манипуляционного робота, который совместно с блоком суммирования 8, первым интегратором 10, вторым интегратором 11 и блоком нелинейных элементов 9 представляет собой исполнительные устройства и механическую систему манипуляционного робота, отрабатывающего рассчитанные управляющие воздействия.
Планировщик траекторий в пространстве внешних координат 1, снимая показания с блока датчиков 2, определяет необходимость дальнейшего формирования управляющих сигналов. В случае, если технологическая задача не решена, блок планировщика траекторий в пространстве внешних координат 1 повторно формирует набор тех же констант на своих выходах, которые инициализируют работу остальных блоков устройства (см. фиг.5). В противном случае работа устройства завершается и константы на выходе планировщика траекторий в пространстве внешних координат 1 не формируются или осуществляется переход к решению следующей технологической задачи, т.е. формированию нового набора констант и параметров.
Под планировщиком траекторий в пространстве внешних координат понимается совокупность блоков и модулей, формирующих желаемые траектории движения робота. Т. е. в состав блока планировщика траекторий могут быть включены ЭВМ верхнего уровня, пульт оператора, чувствительные устройства и т.п. [Управление роботами от ЭВМ. Под ред. Юревича Е.И. Л., Энергия, 1980, 264 с. , с.78].
Следует отметить, что структурная реализация блоков 19, 20, 22 однозначно определяется из известных моделей (1) или (2), (3) для каждого конкретного робота. Так, например, в соответствии с выражениями, приведенными в модели (2), процедура вычисления нелинейных элементов вектора F и матрицы коэффициентов управления В может быть реализована как последовательность элементарных операций над известными векторами С, H и матрицей А (суммирование, умножение, обращение). Структурная схема вычисления векторов С, Н и матрицы А приведена в Фу К., Гонсалес Р., Ли К. Робототехника. М., Мир, 1989, 624 с., с.152. Решение прямой задачи кинематики реализуется по выражению (3) и в зависимости от модели конкретного робота может быть представлено набором блоков суммирования, блоков перемножения, вычислителей тригонометрических функций (синус, косинус). Кроме того, выражение (3) однозначно определяет процедуру вычисления его матрицы Якоби и производной от него [Фу К., Гонсалес Р., Ли К. Робототехника. М., Мир, 1989, 624 с., с. 152 и Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М. , 1984, 833 с., с. 395]. В частности, процедура вычисления решения прямой задачи кинематики и его матрицы Якоби для шестизвенного робота Пума приведена соответственно на страницах 62 и 590-591 в работе Фу К., Гонсалес Р., Ли К. Робототехника. М., Мир, 1989, 624 с.
Структура блоков суммирования, перемножения и транспонирования матриц (векторов), обращения матриц определяется известными правилами матричного исчисления [Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М. , 1984, 833с., с.392-393]. Например, блок транспонирования матриц может представлять собой коммутатор с жесткими связями между (nхn) входами и (nхn) выходами [Пшихопов В.Х., Колесников А.А. "Устройство контурного управления манипуляционным роботом". Патент РФ 2146606, бюл. 8, 2000]. Нулевые элементы диагональных матриц структурой устройства управления не формируются. Схемы сборки 17 и 36 реализуются на элементах ИЛИ.
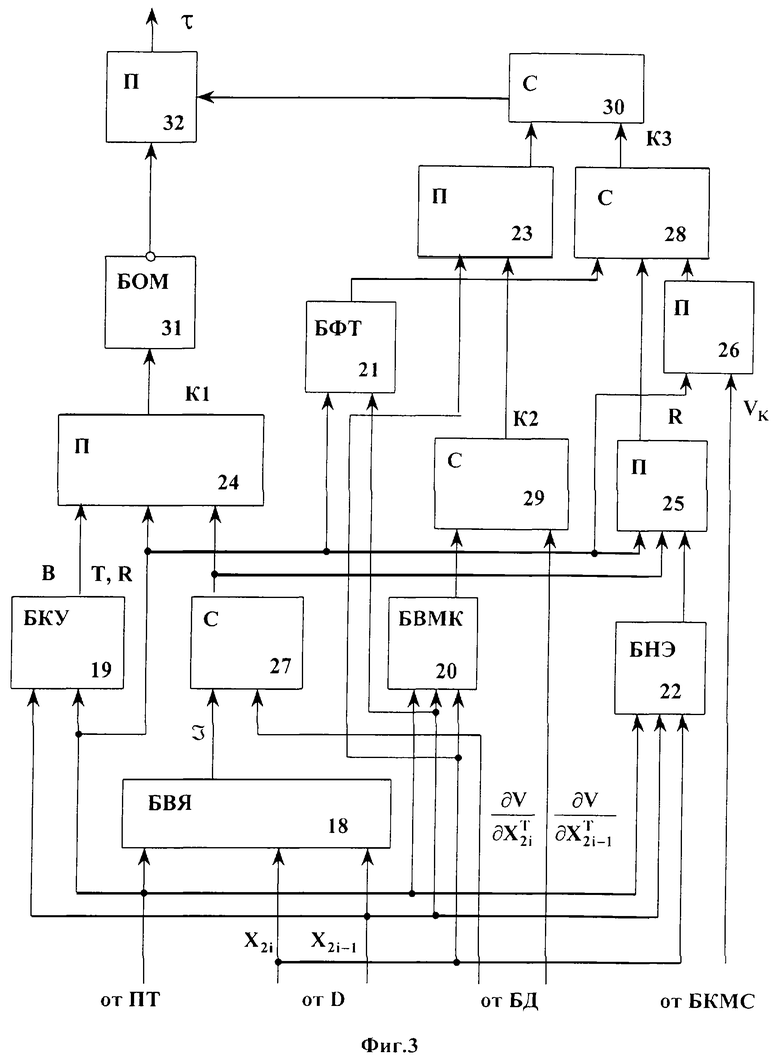
Расчет управляющих воздействий по алгоритму (14) осуществляется с частотой 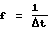 не менее 50 Гц [М. Вукобратович, Д. Стокич, Н. Кирчански. Неадаптивное и адаптивное управление манипуляционными роботами. М., из-во "Мир", 1998, 376 с., с.338-339] до полного выполнения технологического задания.
не менее 50 Гц [М. Вукобратович, Д. Стокич, Н. Кирчански. Неадаптивное и адаптивное управление манипуляционными роботами. М., из-во "Мир", 1998, 376 с., с.338-339] до полного выполнения технологического задания.
Технический результат, достигаемый при осуществлении заявляемого технического решения, заключается в том, что оно позволяет по сравнению с прототипом повысить производительность отработки планируемых траекторий. Повышение производительности манипуляционного робота обусловлено использованием в алгоритме управления значений максимально возможной траекторной скорости. При этом не требуется организации предварительных расчетов поверхностей или линий переключения, а также предварительного определения моментов переключения управляющих воздействий для случая разомкнутого управления.
Представленные алгоритмы траекторного, оптимального по быстродействию управления могут быть реализованы программно с использованием устройств микропроцессорной техники, например высокопроизводительных контроллеров (одного или нескольких) [М. Вукобратович, Д. Стокич, Н. Кирчански. Неадаптивное и адаптивное управление манипуляционными роботами. М., из-во "Мир", 1998, 376 с., с. 320-326], в соответствии с приведенными в описании выражениями, блок-схемой алгоритма, представленной на фиг.5, и диаграммой работы устройства, представленной на фиг.6.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО КОНТУРНОГО УПРАВЛЕНИЯ МАНИПУЛЯЦИОННЫМ РОБОТОМ | 1998 |
|
RU2146606C1 |
| УСТРОЙСТВО ПОЗИЦИОННО-ТРАЕКТОРНОГО УПРАВЛЕНИЯ МОБИЛЬНЫМ РОБОТОМ | 2001 |
|
RU2185279C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ АДАПТИВНЫМ МОБИЛЬНЫМ РОБОТОМ | 2000 |
|
RU2187832C2 |
| УСТРОЙСТВО УПРАВЛЕНИЯ ПОДВИЖНЫМ ОБЪЕКТОМ | 2009 |
|
RU2393522C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ АДАПТИВНЫМ МОБИЛЬНЫМ РОБОТОМ | 1998 |
|
RU2143334C1 |
| СПОСОБ УПРАВЛЕНИЯ ПОДВИЖНЫМ ОБЪЕКТОМ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2010 |
|
RU2450308C2 |
| СПОСОБ УПРАВЛЕНИЯ ПОДВИЖНЫМ ОБЪЕКТОМ | 2013 |
|
RU2538315C1 |
| СПОСОБ СЕЛЕКЦИИ ДВИЖУЩИХСЯ ЦЕЛЕЙ | 1999 |
|
RU2143709C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ ПОДВИЖНЫМ ОБЪЕКТОМ | 2013 |
|
RU2531864C1 |
| СПОСОБ УПРАВЛЕНИЯ ПОДВИЖНЫМ ОБЪЕКТОМ | 2013 |
|
RU2582868C2 |
Изобретение относится к робототехнике и может быть использовано при разработке систем управления манипуляционными роботами. Техническим результатом является обеспечение движения рабочего органа манипуляционного робота вдоль заданной в пространстве внешних или обобщенных координат траектории с максимально возможной траекторной скоростью. При этом не требуется организации предварительных расчетов поверхностей, линий или моментов переключения управляющих воздействий. Технический результат достигается тем, что в устройство, содержащее планировщик траекторий в пространстве внешних координат, блок датчиков, блок вычисления управлений, блок вычисления нелинейных элементов, блок матрицы управления, введены блок торможения, блок дифференцирования, блок формирования кривой максимальной скорости, блок вычисления матричного коэффициента, блок вычисления коэффициентов управления, блок обращения матрицы, блок вычисления нелинейных элементов, блок вычисления произведений матриц Якоби, блок формирования траекторий, схемы сборки, блоки компараторов, блок вычисления тормозного пути, блок вычисления оставшегося пути, блок схем совпадения, блок вычисления ординат вершин. Выполняемый устройством алгоритм управления не требует решения обратной задачи кинематики при организации рабочего движения вдоль заданных траекторий. 2 з.п. ф-лы, 6 ил.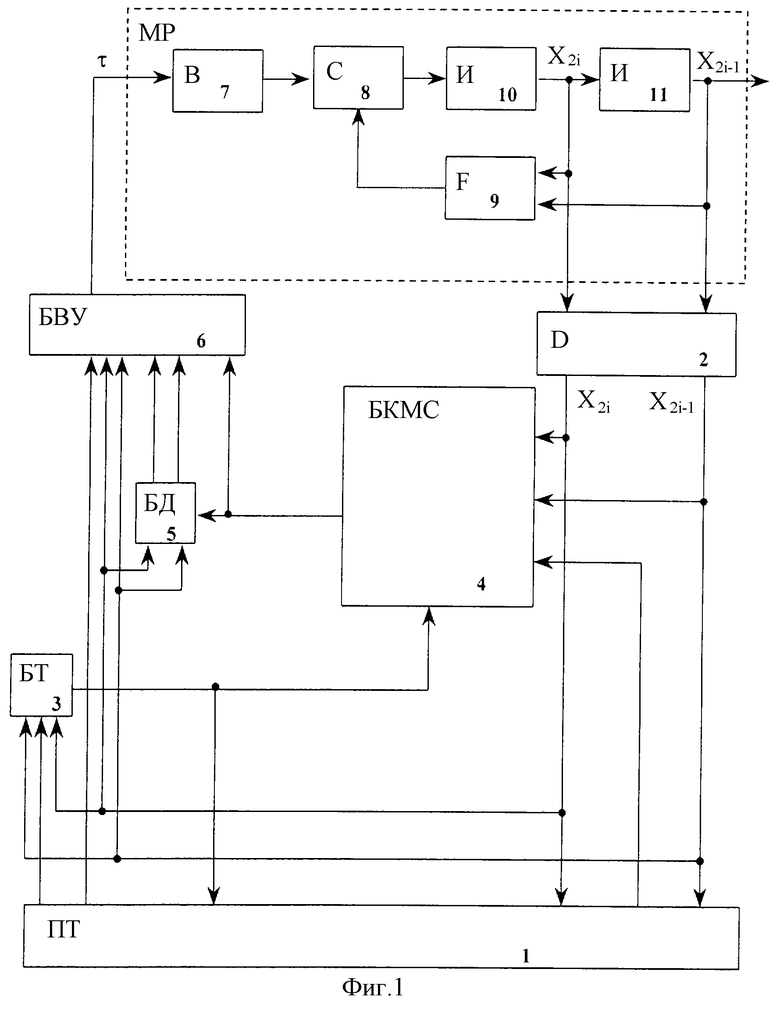
| УСТРОЙСТВО КОНТУРНОГО УПРАВЛЕНИЯ МАНИПУЛЯЦИОННЫМ РОБОТОМ | 1998 |
|
RU2146606C1 |
| US 5103404 A, 07.04.1992 | |||
| US 5530791 A, 25.06.1996 | |||
| DE 3207698 A2, 08.09.1983 | |||
| Динамометрический прибор для измерения радиальной составляющей силы резания на шлифовальных и других центровых станках | 1961 |
|
SU141717A1 |
| Дорожная спиртовая кухня | 1918 |
|
SU98A1 |
Авторы
Даты
2003-02-27—Публикация
2000-11-20—Подача