Изобретение относится к вычислительной технике и может быть использовано для повышения достоверности функционирования работы комбинационных устройств, а также устройств хранения и передачи информации (оперативных и постоянных запоминающих устройств ЭВМ и т.п.).
Известно самокорректирующееся дискретное устройство [1], содержащее исходное дискретное устройство, избыточное дискретное устройство, блок вычисления синдрома, дешифратор ошибки и корректор, входы устройства соединены с входами исходного дискретного устройства и входами избыточного дискретного устройства, информационные выходы которого подключены к входам блока вычисления синдрома, выходы которого подключены к входам дешифратора синдрома ошибки, выход которого соединен с управляющим входом первым входом корректора, информационные входы которого подключены к выходам исходного дискретного устройства, а выход является выходом устройства.
Недостатком устройства является низкая достоверность его функционирования, так как в контрольных разрядах обнаруживается только одиночная ошибка.
Наиболее близким по техническому решению является самокорректирующееся дискретное устройство [2], использующее декодирующее устройство, исправляющее модульные (байтовые) ошибки на основе применения кодов Рида-Соломона, содержащие исходную схему, кодирующее устройство, избыточную схему, декодирующее устройство, включающее схему вычисления синдрома, формирователь мнимых синдромов, дешифратор ошибки в байте, схему вычисления искаженного байта, коммутаторы ошибок, корректор ошибок, входы устройства подключены к входам исходной схемы и к входам кодирующего устройства, выходы кодирующего устройства подключены к входам избыточной схемы, выходы которой подключены к первым входам схемы вычисления синдрома, выходы исходной схемы подключены к вторым входам схемы вычисления синдрома и к первым входам корректора, выходы схемы вычисления синдрома подключены ко входам дешифратора ошибки, выходы которого подключены к вторым входам корректора, выходы корректора являются выходами устройства.
Недостатком устройства является низкая достоверность функционирования устройства, так как коды Рида-Соломона позволяют корректировать ошибку в одном байте информации и обнаруживать ошибку в двух байтах информации, кроме этого данные коды нельзя использовать при малом числе информационных разрядов.
Целью изобретения является повышение достоверности функционирования устройства за счет обеспечения коррекции в одном байте информации и обнаружения ошибок во всех остальных байтах информации.
Поставленная цель достигается тем, что устройство, содержащее исходную схему, первое кодирующее устройство, схему синдрома ошибки, дешифратор ошибки, корректор, входы устройства подключены к исходной схеме и к входам первого кодирующего устройства, выходы исходной схемы подключены к первым входам корректора, выходы которого являются выходами устройства, дополнительно содержит второе, третье и четвертое кодирующие устройства, с первой по четвертую схемы свертки, схему признака ошибки, элемент ИЛИ, причем входы устройства подключены к входам второго кодирующего устройства, а выходы исходной схемы подключены к входам третьего и четвертого кодирующих устройств, выходы с первого по четвертое кодирующих устройств подключены соответственно к входам с первой по четвертую схем свертки, выходы первой и второй схем свертки подключены к входам схемы синдрома ошибки, выходы второй и четвертой схем свертки подключены к входам схемы признака ошибки, выходы схемы синдрома ошибки и признака ошибки подключены к входам дешифратора ошибки, первая группа выходов дешифратора ошибки подключена к вторым входам корректора, а вторая группа выходов подключена к входу элемента ИЛИ, с выхода которого снимается сигнал "Отказ устройства".
На фиг. 1 представлена блок-схема устройства, на фиг.2 - схема первого кодирующего устройства 2, на фиг. 3 - первая схема 6 свертки, на фиг.4 - схема 11 признака ошибки, на фиг.5 - схема корректора.
Устройство содержит исходную схему 1, первое кодирующее устройство 2, второе кодирующее устройство 3, третье кодирующее устройство 4, четвертое кодирующее устройство 5, первую схему свертки 6, вторую схему свертки 7, третью схему свертки 8, четвертую схему свертки 9, схему синдрома ошибки 10, схему признака ошибки 11, дешифратор ошибки 12, корректор 13, элемент 14 ИЛИ, входы 15 устройства, выходы 16 устройства, выход 17 "Отказ устройства".
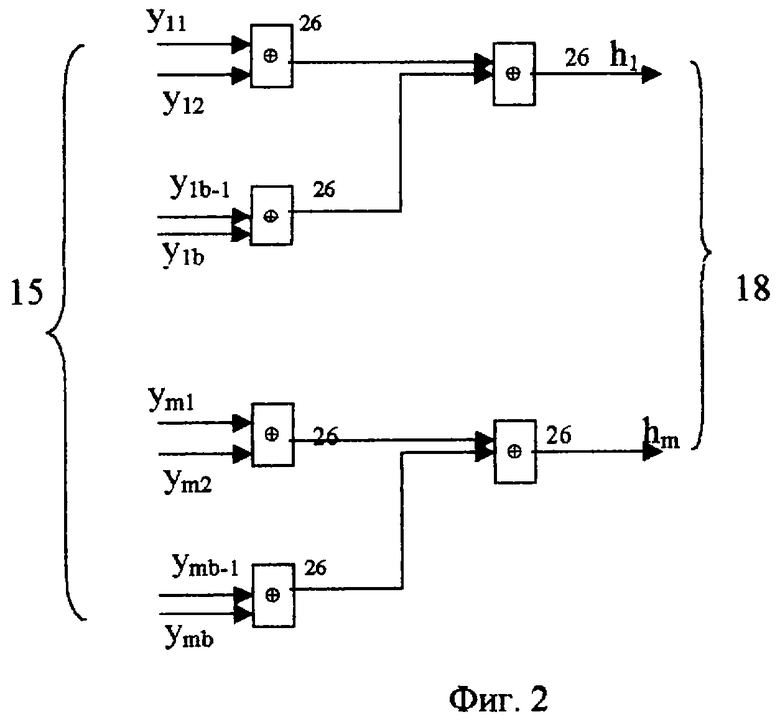
Первое кодирующее устройство 2 содержит группу элементов 26 неравнозначности.
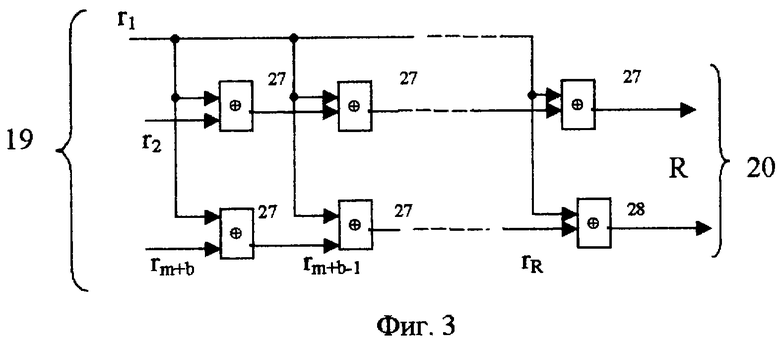
Первая схема 6 свертки содержит группу элементов 27 неравнозначности.
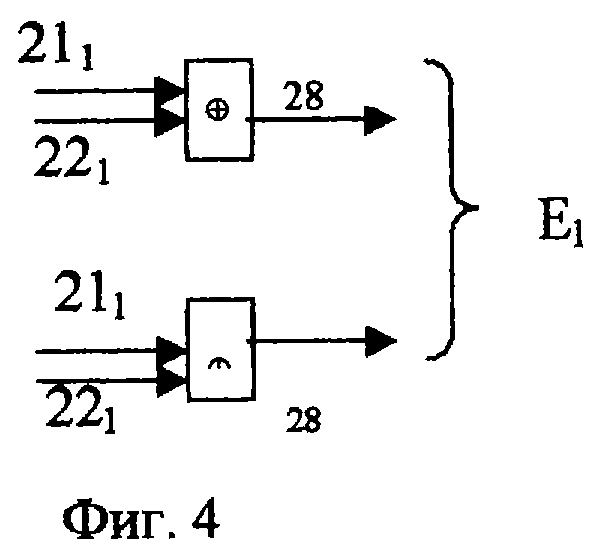
Схема 11 признака ошибки содержит группу элементов 28 неравнозначности.
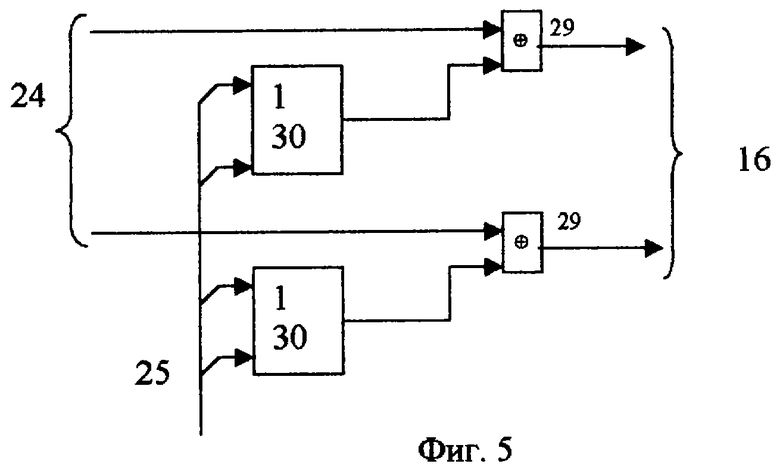
Корректор содержит группу элементов 29 неравнозначности и группу элементов 30 ИЛИ.
Входы 15 устройства подключены к входам исходной схемы 1, к входам первого кодирующего устройства 2 и к входам второго кодирующего устройства 3, выходы сходной схемы соответственно к входам третьего 4 и четвертого 5 кодирующих устройств и к первым входам корректора 13, выходы первого 2 и второго 7 кодирующих устройств подключены соответственно к входам первой 6 и второй 7 схем свертки, выходы первой схемы 6 свертки подключены к первым входам схемы 10 синдрома ошибки, выходы второй схемы 7 свертки подключены к первым входам схемы 11 признака ошибки, выходы третьего 4 и четвертого 5 кодирующих устройств подключены соответственно к вторым входам третьей 8 и четвертой 9 схем свертки, выходы которых подключены соответственно к входам схемы 10 синдрома ошибки и к входам схемы 11 признака ошибки, выходы которых подключены к входам дешифратора 12 ошибки, первая группа выходов дешифратора ошибки подключена к вторым входам корректора 13, а вторая группа выходов подключена к входам элемента 14 ИЛИ, выходы 13 корректора являются выходами устройства, с выхода 17 устройства снимается сигнал "Отказ".
Первое кодирующее устройство 2 предназначено для реализации проверок на четность (см. приложение) строк и столбцов информационной матрицы (1). На фиг.2 показан порядок формирования вектора четности строк - Н на группе сумматоров 26 по mod 2, аналогичным образом формируется вектор четности столбцов - Z.
Второе кодирующее устройство 3 реализует правые и левые диагональные проверки на четность в соответствии с правилами (5), (6), представленными в приложении.
Третье кодирующее устройство 4 выполняет одинаковые функции с первым кодирующим устройством 2, т. е. осуществляет проверку на четность строк и столбцов матрицы, построенной относительно выходных сигналов исходной схемы.
Четвертое кодирующее устройство 5 выполняет функции, одинаковые с функциями второго кодирующего устройства 3, т.е. осуществляет диагональные проверки относительно полученной информации.
Первая схема 6 (третья схема 8) свертки (фиг.3) предназначена для уменьшения числа контрольных разрядов, полученных в результате проверок на четность строк и столбцов информационной матрицы, до значения R в соответствии с выражением (11).
Вторая схема 7 (четвертая 9) свертки предназначена для уменьшения числа контрольных разрядов, полученных при организации диагональных проверок до значения R1, полученного на основе выражения (12).
Схема 10 синдрома ошибки и схема 11 признака ошибки представляют собой схему поразрядного сравнения (см. фиг.5) и предназначены для сравнения информации, передаваемой в контрольных разрядах и сформированной относительно полученной информации.
Дешифратор 12 ошибки предназначен для формирования управляющих сигналов на корректор 13 при возникновении корректируемых ошибок и выдачи сигнала "Отказ" на вход элемента 14 ИЛИ при возникновении некорректируемой ошибки.
Устройство работает следующим образом. При поступлении входной информации на входы исходной схемы 1 она одновременно поступает на входы первого 2 и второго 3 кодирующих устройств. Данная информация разбивается на блоки информации (см. приложение), т.е. представляется в виде информационной матрицы (1). Первое кодирующее устройство 2 осуществляет проверку на четность строк и столбцов информационной матрицы, а второе кодирующее устройство 3 осуществляет диагональные проверки на четность по правилам (5), (6). Первая 6 и вторая 7 схемы свертки осуществляют уменьшение числа контрольных разрядов в соответствии с выражениями (11) и (12).
Третье 4 и четвертое 5 кодирующие устройства осуществляют соответственно аналогичные функции первого 2 и второго 3 кодирующих устройств относительно выходной информации, поступающей с выходов исходной схемы 1.
Третья 8 и четвертая 9 схемы свертки выполняют функции, аналогичные первой 6 и второй 7 схем свертки.
Схема 10 синдрома ошибки формирует синдром ошибки Ес путем поразрядного сравнения информации, поступающей с первой и третьей схем свертки.
Схема 11 признака ошибки формирует признак ошибки E1 путем поразрядного сравнения информации, поступающей со второй 7 и четвертой 9 схем свертки.
При отсутствии ошибок значения синдрома и признака ошибки имеют нулевое значение.
При возникновении корректируемой ошибки дешифратор ошибки формирует управляющий сигнал, поступающий через элементы 30 ИЛИ корректора 13 (см. фиг.5) на те элементы неравнозначности, на вторые входы которых поступает ошибочный информационный разряд.
Если возникает некорректируемая ошибка, то сигнал с выхода дешифратора ошибки поступает на вход элемента 14 ИЛИ, с выхода которого снимается сигнал "Отказ".
Предлагаемый метод кодирования позволяет получить новый уровень достоверности функционирования отказоустойчивых устройств хранения информации по сравнению с существующими методами коррекции ошибок модульного типа. Так, например, при использовании кода Рида-Соломона (наиболее эффективно для коррекции модульного ошибок) для коррекции одного полубайта и обнаружения ошибок в четырех полубайтах информации 64 информационных разрядов требуется 16 контрольных разрядов [1, 2]. Предлагаемый метод кодирования требует 15 контрольных разрядов и при этом позволяет осуществлять коррекцию в одном байте информации и обнаружить ошибки во всех остальных байтах.
ПРИЛОЖЕНИЕ
Коррекция ошибок в одном байте и обнаружение ошибок в остальных байтах информации достигается на основе итеративного кода.
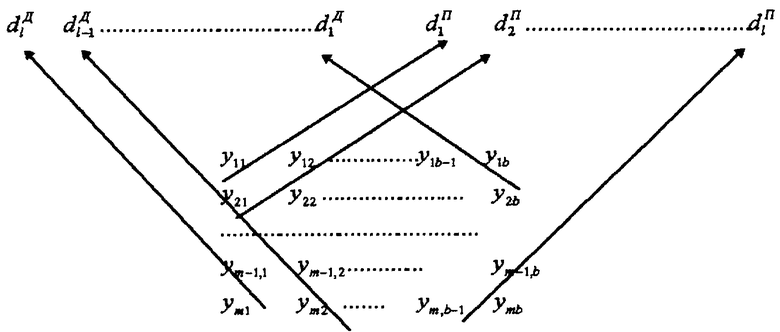
Процедура построения двумерного итеративного кода состоит в следующем [3] . Заданную совокупность информационных символов делят на группы (блоки, модули) информации по b разрядов в каждой группе. Полученные модули информации представляют в виде информационной матрицы (1)
Затем осуществляется кодирование информации по методу четности (путем сложения по mod 2 символов строк и столбцов полученной матрицы). В результате имеем двумерный итеративный код, позволяющий обнаруживать и исправлять любую одиночную ошибку
где Н=h1, h2,..., hm - вектор четности строк; Z=z1, z2,..., zb - вектор четности столбцов. Вектора четности строк и столбцов образуют совокупность контрольных разрядов R= { r1, r2, rm, rm+1,..., rb}. При получении кодовой комбинации относительно информационных разрядов повторно формируются значения контрольных разрядов RП={r1, r2, rm, rm+1,..., rb}. В данном случае разница между переданными значениями контрольных разрядов и полученными после приема информации образует вектор ошибки Е: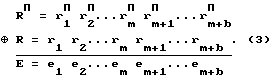
При этом разряды вектора ошибки е1е2. ..еm (полученные относительно вектора четности строк) указывают модуль информации, имеющей ошибку, а разряды еmеm+1. . .еm+b (полученные относительно вектора четности столбцов) указывают ошибочный разряд в модуле информации.
Так как кодовые комбинации строк и столбцов имеют минимальное расстояние d= 2, то минимальное расстояние данного кода d=4. Этот код позволяет исправлять любую одиночную ошибку и обнаруживать значительную долю кратных ошибок.
Структуры ошибок, не обнаруживаемых двумерным итеративным кодом, показаны на рисунке: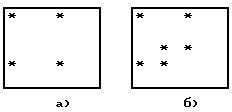
1) Структуры ошибок, не обнаруживаемых двумерным итеративным кодом: а) - ошибки кратности 4; б) - ошибки кратности 6.

2) Структуры ошибок двумерного итеративного кода, приводящие к ошибочной коррекции: а) - ошибки кратности 5; б) - ошибки кратности 7.
В общем случае можно строить итеративные коды более высокой размерности (трехмерные, четырехмерные и т.д.), где каждый информационный символ будет являться компонентой одновременно x различных кодовых слов. Параметры итеративных кодов размерности x таковы [3]:
где ni, ki, di - соответственно длина, количество информационных разрядов, минимальное расстояние кодовых наборов строк и столбцов.
Построения корректирующих кодов, исправляющих ошибки модульного типа, базируются на основе введения диагональных проверок, проводимых по правилу, показанному на схеме (см. в конце описания).
Структура диагональных проверок: d1 nd2 n...d1 n - результаты правых диагональных проверок; d1 дd2 д...d1 д - результаты левых диагональных проверок.
Результаты правых диагональных проверок образуются при суммировании значений следующих информационных разрядов:
Результаты левых диагональных проверок образуются по правилу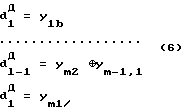
В этом случае общее число диагональных проверок равно 2l.
Утверждение 1. Существует хотя бы одна диагональная проверка информационной матрицы, позволяющая выявить четную ошибку, не обнаруживаемую двумерным итеративным кодом.
Утверждение 2. Существует хотя бы одна диагональная проверка информационной матрицы, позволяющая выявить нечетную ошибку, воспринимаемую двумерным итеративным кодом как одиночная (корректируемая).
Пример 1. Пусть рассматриваемое слово состоит из четырех информационных разрядов, которые имеют нулевые значения. Для данного кодового набора информационная матрица имеет вид
0 0
0 0
В этом случае проверки на четность строк и столбцов информационной матрицы дадут нулевые значения и, кроме этого, будут иметь нулевые значения результаты всех диагональных проверок. При возникновении ошибки во всех информационных разрядах имеем четную ошибку, не обнаруживаемую двумерным итеративным кодом, т.к. проверки на четность строк и столбцов информационной матрицы имеют нулевые значения
1* 1*
1* 1*.
В то же время правые и левые диагональные проверки дают соответственно результат 101.
Утверждение 3. Четырехмерный итеративный код, реализующий все диагональные проверки, обнаруживает все четные ошибки, не обнаруживаемые двумерным итеративным кодом, и выявляет нечетные ошибки, воспринимаемые двумерным итеративным кодом как корректируемые. Таким образом, при использовании четырехмерного итеративного кода кодовый набор передается в виде
Y=y1y2...ykr1r2...rmrm+1rm+2...rm+brm+b+1...rm+b+21. (7)
Соответственно вектор ошибки определяется выражением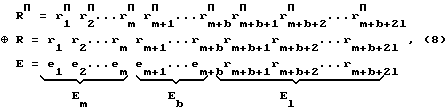
где разряды вектора ошибки Еm определяют адрес модуля, имеющего ошибку; Еb - номер разряда имеющего ошибку; El - признак ошибки.
Множество значений признака ошибки El делится на две части соответственно: EK l - множество значений признака корректируемой ошибки; EH - множество значений признака некорректируемой ошибки.
В этом случае декодирование (исправление) ошибки принимается в результате решения системы трех уравнений:
1) Em=0, Еb=0, Ei l=0 - информация принята без ошибок;
2) Еm≠0, Еb≠0, Ei l∈El K - произошла корректируемая (одиночная) ошибка;
3) Еm≠0, Еb≠0, Ei l∈El H - возникла некорректируемая нечетная ошибка;
4) Em=0, Еb=0, Ei l∈El H - произошла некорректируемая четная ошибка.
Естественно, данный код имеет слишком большую избыточность, поэтому его использование для коррекции одиночной ошибки не является оправданным. Применение диагональных проверок значительно увеличивает минимальное кодовое расстояние четырехмерного итеративного кода (см. 4), что позволяет использовать данный код для исправления ошибок модульного типа и кроме этого минимизировать число контрольных разрядов.
В этом случае разряды вектора ошибки Еm определяют адрес модуля, имеющего ошибку, разряды вектора ошибки Еb определяют конфигурацию ошибки и каждому значению ошибки в модуле информации ставится в соответствие свое значение признака корректируемой ошибки EK li.
Число возможных ошибок, возникающих в модуле информации, определяется выражением
где b - число разрядов модуля.
Соответственно общее число корректируемых ошибок равно
Q = qm, (10)
где m - число модулей информации.
Если каждой ошибке поставить в соответствие свои значения Еm и Еb, то для формирования синдрома ошибки требуемое число контрольных разрядов составит
R = log2Q. (11)
В этом случае уменьшение числа контрольных разрядов (разрядов вектора ошибки Еm и Еb) может быть выполнено путем свертки, например, путем сложения первого разряда вектора ошибки e1 с остальными разрядами (e2, e3,...,em+b). Данная процедура (сложение первого разряда полученного результата с остальными разрядами) выполняется до тех пор, пока число контрольных разрядов не станет равным R. Таким образом значение синдрома ошибки Еc может быть сформировано на R разрядах.
Уменьшение числа разрядов признака ошибки El(em+b+1...em+b+2l) может быть выполнено аналогичным образом до значения R1 на основе следующего свойства.
Свойство 1. Для одинаковых значений синдрома ошибки Еc значения признаков ошибки не совпадают (имеют разное значение), если выполняется условие
Rl = log2(mb)+1. (12)
Используя выражения (9), (10), (11), (12) получим границу числа проверочных разрядов для кода, исправляющего любую ошибку в модуле информации и обнаруживающего любые ошибки во всех остальных модулях информации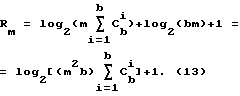
В этом случае декодирование (исправление) ошибки модульного типа принимается в результате решения системы уравнений:
1) EC=0, ЕП=0 - информация принята без ошибок;
2) ЕC≠0; EП≠0, ЕП∈El К - произошла корректируемая ошибка;
3) ЕС≠0; ЕП≠0, EП∈El H - возникла некорректируемая ошибка;
4) EС=0; EП≠0, El i ∈El H - произошла некорректируемая ошибка.
Пример 2. Рассмотрим правила формирования синдрома ошибки при кодировании четырехразрядного слова, информационная матрица которого рассматривается в примере 1.
Модуль информации содержит два информационных разряда. Возможное число ошибок в модуле составляет три ошибки (две одиночных, одна двойная). Общее число ошибок шесть. Используя выражение (11), определяем требуемое число контрольных разрядов для формирования синдрома ошибки, которое в данном случае равно трем. Число контрольных разрядов для формирования признака ошибки определяем по формуле (12), которое в данном случае также равно трем.
Пусть произошла одиночная ошибка в первом информационном разряде
1* 0
0 0
В этом случае разряды вектора ошибки имеют следующие значения: Еm=10; Eb=10; Еl=100010.
Осуществляя свертку значений Еm и Еb (сложением первого разряда с остальными значениями) и свертку значения El (также до трех разрядов), определим значения синдрома ошибки и признака ошибки ЕП. В результате имеем ЕС=101; ЕП=010.
Для одиночных ошибок второго, третьего и четвертого информационных разрядов имеем соответственно
ЕС=110; ЕП=001
ЕС=110; ЕП=100
ЕС=101 EП=101
Для двойных ошибок в первом и во втором модуле синдром ошибок и признак ошибки имеют значения
а) ЕC=011; ЕП=011; b) ЕС=011; EП=001.
Для четырехкратной ошибки имеем ЕС=000; ЕП=010.
Для двойных ошибок, возникающих в первом и третьем, втором и четвертом, первом и четвертом, втором и третьем информационных разрядах соответственно имеем следующие значения синдрома ошибки и признака ошибки:
ЕС=011; ЕП=110
ЕС=011; EП=100
ЕС=000 ЕП=111
ЕС=000 ЕП=101
Для тройных ошибок, возникающих соответственно 1,2,3; 1,2,4; 1,3,4; 2,3,4 - информационных разрядов имеем
ЕС=101; ЕП=111
ЕС=110; ЕП=110
ЕС=110 ЕП=011
ЕС=101 EП=100
Из рассмотренного примера следует, что предлагаемый метод кодирования в принципе позволяет корректировать любую возможную ошибку, за исключением таких сочетаний ошибок в информационных и контрольных разрядах, которые переводят ошибочный кодовый набор из одного смежного класса ошибок в другой, что является существенным недостатком любого линейного кода. В этом случае следует ограничиться исправлением наиболее вероятных конфигураций модульных ошибок.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. А.С. СССР 1716521, кл. G О6 F 11/14.
2. Щербаков Н. С. Достоверность работы цифровых устройств. - М.: Машиностроение, 1989, 224 с., рис. 39 и 44.
3. Хетагуров Я.А., Руднев Ю.П. Повышение надежности цифровых устройств методами избыточного кодирования. - М.: Энергия, 1974, 270 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| ОТКАЗОУСТОЙЧИВОЕ ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО | 2001 |
|
RU2211492C2 |
| ОТКАЗОУСТОЙЧИВОЕ УСТРОЙСТВО | 2004 |
|
RU2297031C2 |
| ОТКАЗОУСТОЙЧИВОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО | 2004 |
|
RU2297035C2 |
| САМОКОРРЕКТИРУЮЩЕЕСЯ УСТРОЙСТВО | 2004 |
|
RU2297033C2 |
| САМОКОРРЕКТИРУЮЩЕЕСЯ УСТРОЙСТВО ХРАНЕНИЯ ИНФОРМАЦИИ | 2004 |
|
RU2297030C2 |
| ОТКАЗОУСТОЙЧИВОЕ УСТРОЙСТВО ХРАНЕНИЯ ИНФОРМАЦИИ | 2004 |
|
RU2297034C2 |
| ОТКАЗОУСТОЙЧИВОЕ УСТРОЙСТВО | 2004 |
|
RU2297036C2 |
| САМОКОРРЕКТИРУЮЩЕЕСЯ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО | 2004 |
|
RU2297032C2 |
| САМОКОНТРОЛИРУЮЩЕЕСЯ УСТРОЙСТВО | 2004 |
|
RU2297028C2 |
| САМОКОРРЕКТИРУЮЩЕЕСЯ УСТРОЙСТВО | 2004 |
|
RU2297029C2 |
Изобретение относится к области автоматики и вычислительной техники. Технический результат заключается в повышении достоверности функционирования дискретных и запоминающих устройств и позволяет корректировать ошибку в одном модуле информации при условии обнаружения ошибок в остальных модулях информации. Технический результат достигается на основе использования четырехмерного итеративного кода за счет введения в структурную схему с первого по четвертое кодирующих устройств, реализующих проверки на четность строк и столбцов информационной матрицы, а также диагональные проверки с первой по четвертую схем свертки, схем формирования синдрома и признака ошибки, дешифратора ошибки, корректора. 5 ил.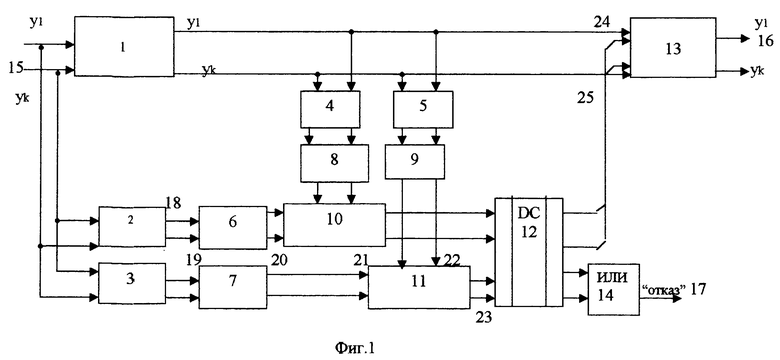
Самокорректирующееся устройство, содержащее исходную схему, первое кодирующее устройство, схему синдрома ошибки, дешифратор ошибки, корректор, входы устройства подключены к исходной схеме и к входам первого кодирующего устройства, выходы исходной схемы подключены к первым входам корректора, выходы которого являются выходами устройства, отличающееся тем, что оно дополнительно содержит второе, третье и четвертое кодирующие устройства, с первой по четвертую схемы свертки, схему признака ошибки, элемент ИЛИ, причем входы устройства подключены к входам второго кодирующего устройства, а выходы исходной схемы подключены к входам третьего и четвертого кодирующих устройств, выходы с первого по четвертое кодирующих устройств подключены соответственно к входам с первой по четвертую схем свертки, выходы первой и третьей схем свертки подключены к входам схемы синдрома ошибки, выходы второй и четвертой схем свертки подключены к входам схемы признака ошибки, выходы схемы синдрома ошибки и признака ошибки подключены к входам дешифратора ошибки, первая группа выходов дешифратора ошибки подключена к вторым входам корректора, а вторая группа выходов подключена к входу элемента ИЛИ, с выхода которого снимается сигнал "Отказ устройства".
| ЩЕРБАКОВ Н.С | |||
| Достоверность работы цифровых устройств | |||
| - М.: Машиностроение, 1989, с | |||
| Машина для разделения сыпучих материалов и размещения их в приемники | 0 |
|
SU82A1 |
| Говорящий кинематограф | 1920 |
|
SU111A1 |
| Устройство для коррекции ошибок вычислительного процесса | 1991 |
|
SU1807487A1 |
| Самокорректирующееся дискретное устройство | 1989 |
|
SU1716521A1 |
| RU 94030354 А1, 20.05.1997 | |||
| RU 2053578 С1, 27.01.1996 | |||
| US 4314350 А, 02.02.1982 | |||
| US 3471830 А, 07.10.1969. | |||
Авторы
Даты
2003-08-20—Публикация
1999-05-31—Подача