Изобретение относится к области управления синхронными электрическими машинами с электронными коммутаторами в зависимости от положения ротора.
Известен способ измерения углового положения ротора по всем фазным токам и напряжению питания для синхронного двигателя [1], заключающийся в том, что по уравнениям модели двигателя из всех фазных токов и напряжения питания определяют ЭДС, наводимую полем ротора в статорных обмотках. Далее по известному вектору ЭДС вычисляют текущее положение ротора и скорость его вращения.
Недостатками такого способа являются низкая точность при малых скоростях вращения, вследствие уменьшения ЭДС, наводимой ротором в статорных обмотках, и невозможности определения положения ротора при нулевой скорости вращения. При этом алгоритм определения ЭДС по фазным токам и напряжению питания достаточно сложен, т. к. требует решения нескольких дифференциальных (или разностных) уравнений с прогнозируемыми значениями токов для следующего момента времени.
Предлагаемый способ определения скорости вращения и положения ротора в электрических машинах с двойной зубчатостью позволяет определять скорость вращения и угловое положение ротора при любых скоростях вращения без потери точности и требует решения только одного дифференциального уравнения.
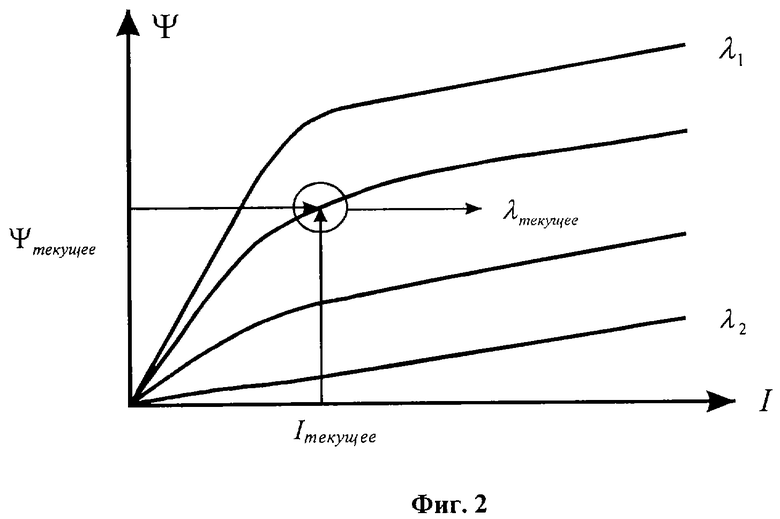
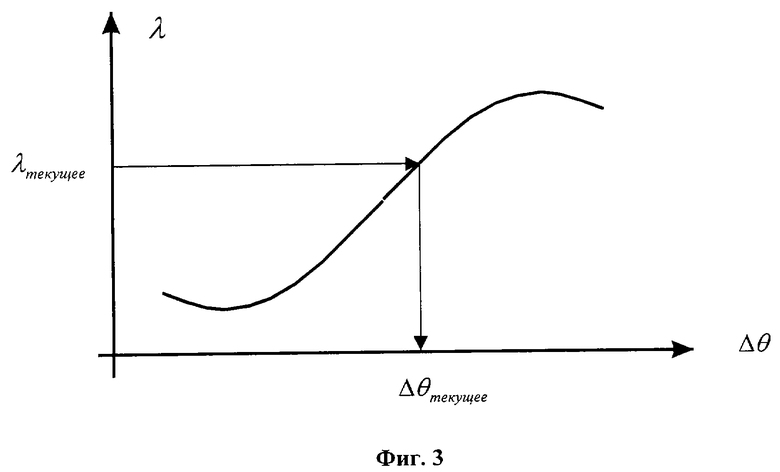
Для пояснения способа определения скорости вращения и положения ротора в электрических машинах с двойной зубчатостью приведены три чертежа. На фиг.1 изображена одна из типичных схем электрической машины с двойной зубчатостью. На фиг. 2 изображены кривые намагничивания в координатах потокоспепления и тока фазы. На фиг. 3 изображена кривая зависимости магнитной проводимости воздушного зазора от угла между зубцами полюса статора и зубцами ротора.
Для определения углового положение ротора вычисляют магнитную проводимость воздушного зазора между зубцами полюса статора и зубцами ротора. С этой целью по измеренным фазным токам и напряжению питания определяют потокосцепление для каждой фазы: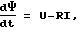
где Ψ, I, U, R - потокосцепление, ток, напряжение и активное сопротивление фазы соответственно.
Далее по аппроксимации кривых намагничивания находят магнитную проводимость воздушного зазора между зубцами полюса статора и зубцами ротора λ, см, фиг.2.
По известной магнитной проводимости воздушного зазора λ и аппроксимации ее зависимости от угла между зубцами фиг.3 определяют модуль угла положения зубцов ротора по отношению к зубцам статора |Δθ|.
Сравнивая магнитную проводимость воздушного зазора текущей рассчитываемой фазы и соседней, определяют знак угла положения зубцов ротора по отношению к зубцам статора Δθ и рассчитывают положение ротора θ по отношению к начальному (нулевому) углу, исходя из геометрии машины.
Определив значение угла по каждой фазе, итоговый результат вычисляют по формуле:
θ = k1•θ1+k2•θ2+...+kn•θn,
где n - количество фаз, θi - угловое положение ротора, определенное по i-й фазе, ki - весовые коэффициенты, сумма которых равна единице.
Введение весовых коэффициентов, позволяет контролировать положение ротора в каждый момент времени, несмотря на то, что при измерении по отдельно взятой фазе существуют зоны нечувствительности, в которых определение углового положения невозможно, вследствие малого изменения магнитной проводимости возданного зазора от угла между зубцами.
Весовые коэффициенты для фаз, работающих в данный момент на участках с малым изменением магнитной проводимости воздушного зазора между зубцами ротора и статора, приравниваются нулю. По остальным фазам суммируют токи, и весовые коэффициенты выбирают пропорционально отношению фазного тока к полученному суммарному. Такой алгоритм вычисления весовых коэффициентов позволяет исключать из рассмотрения фазы, в которых отсутствует ток или данные, от которых недостоверны.
Для повышения точности определения углового положения ротора, которая зависит от точности аппроксимации кривых намагничивания и магнитной проводимости фиг. 2 и 3, ее целесообразно проводить только на участках линейной зависимости потокосцепления от тока и линейной зависимости магнитной проводимости от угла между зубцами ротора и статора. Для этого весовые коэффициенты фаз, работающих на этих участках, выбираются во много раз большими, чем весовые коэффициенты для фаз, работающих в нелинейных областях.
Т.к. питание фазных обмоток машин рассматриваемого класса является дискретным, и в реальных условиях ток практически во всех режимах присутствует только в активной фазе (фаза, подключенная к источнику питания и создающая на данном этапе основную часть механического момента электрической машины) и в предыдущей отключаемой фазе, то для сокращения объемов вычислений определение углового положения ротора можно вести только по этим двум фазам.
Ошибку от вычисления потокосцепления сбрасывают, приравнивая потокосцепление фазы Ψ нулю при равенстве тока фазы I нулю.
Скорость вращения ротора определяют по изменению угла с использованием алгоритмов статистической обработки измерений.
Предлагаемый способ определения скорости вращения и положения ротора в электрических машинах с двойной зубчатостью применим только для синхронных электрических машин с зубцами на роторе и на статоре (вентильно-индукторные, шаговые и т.п.) фиг.1. Техническая реализация данного способа легко осуществима па базе современных микроконтроллеров.
Источники информации
1. Д. Б. Изосимов "Синтез алгоритмов цифрового управления синхронным электроприводом без датчика на валу двигателя".// "Электричество", 9, 1998 г., с. 26-32.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования электромагнитных полей и процессов в асинхронных машинах | 1989 |
|
SU1683041A1 |
| ДВУХФАЗНЫЙ НЕРЕВЕРСИВНЫЙ ВЕНТИЛЬНО-ИНДУКТОРНЫЙ ДВИГАТЕЛЬ | 2004 |
|
RU2266604C1 |
| БЕСКОНТАКТНАЯ ЭЛЕКТРИЧЕСКАЯ МАШИНА | 2004 |
|
RU2280936C2 |
| Электрический шаговый двигатель | 1990 |
|
SU1809506A1 |
| ЭЛЕКТРИЧЕСКАЯ РЕДУКТОРНАЯ МАШИНА С ПОЛЮСНЫМ ЗУБЧАТЫМ ИНДУКТОРОМ | 2009 |
|
RU2393614C1 |
| СОВМЕЩЕННЫЙ ВЕНТИЛЬНЫЙ ИНДУКТОРНО-РЕАКТИВНЫЙ ДВИГАТЕЛЬ | 2006 |
|
RU2309517C1 |
| БЕСКОНТАКТНАЯ РЕДУКТОРНАЯ МАГНИТОЭЛЕКТРИЧЕСКАЯ МАШИНА С ПОЛЮСНЫМ ЗУБЧАТЫМ ИНДУКТОРОМ | 2009 |
|
RU2392723C1 |
| РЕДУКТОРНАЯ МАГНИТОЭЛЕКТРИЧЕСКАЯ МАШИНА С ПОЛЮСНЫМ ЗУБЧАТЫМ ИНДУКТОРОМ | 2011 |
|
RU2478250C1 |
| РЕДУКТОРНАЯ ЭЛЕКТРИЧЕСКАЯ МАШИНА С ПОЛЮСНЫМ ЗУБЧАТЫМ ИНДУКТОРОМ | 2011 |
|
RU2477917C1 |
| ВЕНТИЛЬНО-ИНДУКТОРНАЯ РЕАКТИВНАЯ МАШИНА | 2021 |
|
RU2780383C1 |
Изобретение относится к области электротехники, а именно к устройствам управления синхронными машинами с электронными коммутаторами. Технический результат изобретения, заключающийся в повышении точности определения положения ротора, достигается путем того, что в способе определения положения ротора в электрических машинах с двойной зубчатостью по измеряемым фазным токам и напряжениям, положение ротора находят одновременно по всем фазам с учетом весовых коэффициентов через магнитную проводимость воздушного зазора между зубцами полюсов статора и зубцами ротора по кривым аппроксимации магнитной проводимости в зависимости от угла между зубцами полюсов статора и зубцами ротора, при этом весовые коэффициенты фаз, работающих на участках с малым изменением магнитной проводимости зазора между зубцами ротора, приравниваются к нулю, а для других выбираются пропорционально величине тока фазы, сумма весовых коэффициентов равна единице. 1 з.п. ф-лы, 3 ил.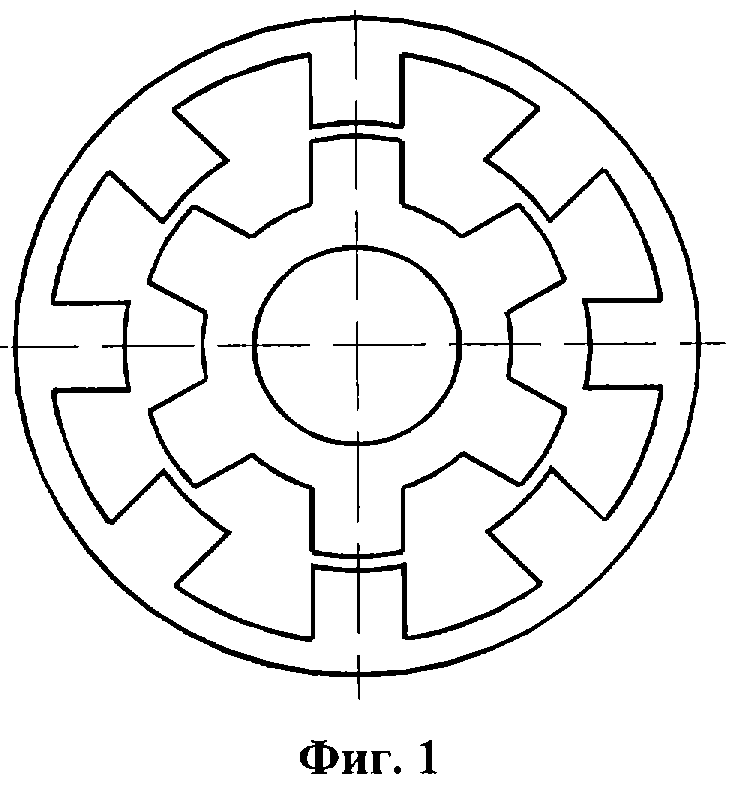
| Способ определения скорости электрической машины постоянного тока | 1948 |
|
SU77035A1 |
| СПОСОБ ИЗМЕРЕНИЯ СКОРОСТИ ВРАЩЕНИЯ ВАЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2017156C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЛИНЕЙНОГО ДВИЖЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1995 |
|
RU2089918C1 |
| ВСЕСОЮЗНАЯ Iчгйитуп^^. ^'"ГЦШ\miБИ5ЛИО~е.КА | 0 |
|
SU334180A1 |
Авторы
Даты
2003-11-27—Публикация
2000-03-10—Подача