Область техники, к которой относится изобретение
Изобретение относится к измерительной технике, а именно к стереологическому анализу размеров и размерных распределений объектов. В частности, изобретение может использоваться при изучении объектов по их плоскостным изображениям, получаемым при световой микроскопии, трансмиссионной электронной микроскопии, конфокальной лазерной сканирующей микроскопии, компьютерной рентгеновской томографии, магнитно-резонансной томографии, ультразвуковой томографии и других методах исследования. Еще одним примером области применения настоящего изобретения является анализ объектов по их проекционным изображениям, получаемым в технике и научных исследованиях.
Уровень техники
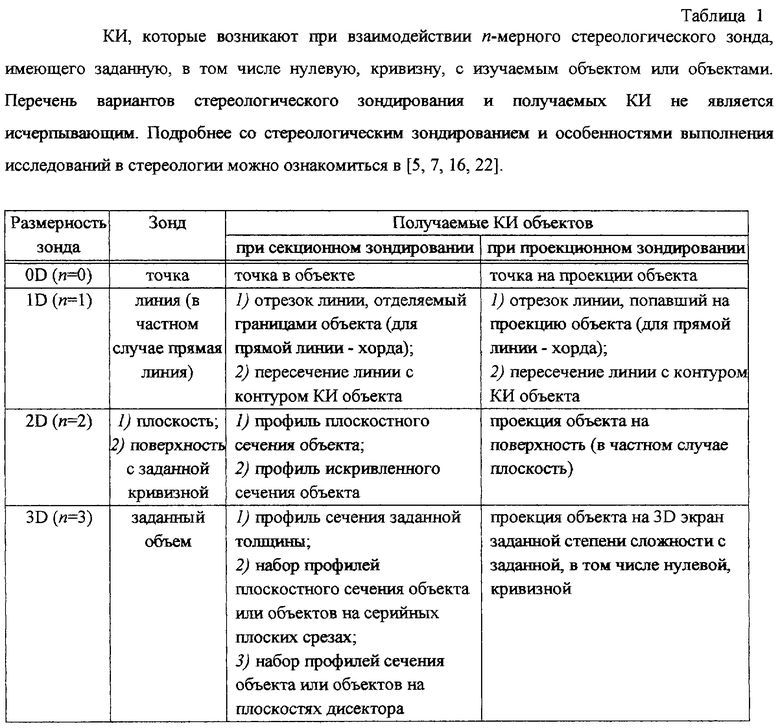
Стереологический анализ широко применяется при изучении структурной организации материалов, искусственных и естественных сред, технических объектов и живых систем. Его сущность заключается в получении информации об объектах посредством изучения стохастики их изображений, возникающих в результате взаимодействия объекта со стереологическим зондом (от англ. stereological probe). В трехмерном (3D) пространстве стереологические зонды обладают нулевой (0D), первой (1D), второй (2D) или третьей (3D) размерностью. Любой из указанных зондов может быть зондом сечения (секционным зондом) или зондом проекции (проекционным зондом). Возможны также разнообразные комбинации стереологических зондов. Получаемые при зондировании объекта изображения в зависимости от специфики выполняемой работы и личных предпочтений авторов могут называться по-разному. Применяются, в частности, такие термины, как профили сечения, профили стереологического зондирования, изображения, образы, проекции, тени и кажущиеся изображения. В настоящем описании для обозначения изображений, возникающих при взаимодействия объекта со стереологическим зондом, будет использоваться термин "кажущиеся изображения (КИ) объектов". КИ, получаемые в результате 2D зондирования плоскостью сечения, будут называться профилями плоскостного сечения. Примеры зондов различной размерности и соответствующих КИ приведены в табл. 1.
К числу наиболее распространенных в стереологии относятся задачи по восстановлению истинных размеров объектов по распределениям размеров их КИ (как правило, по распределениям размеров профилей плоскостного сечения). Истинными при этом являются размеры объектов, отражающие пространственную, или 3D, организацию последних. Поэтому истинные размеры называют также 3D размерами объектов. Способы стереологического получения точной размерной информации об объектах являются довольно трудоемкими. На практике же нередко встречаются ситуации, когда искомыми являются примерные размеры объектов, и их нужно определить с малыми затратами времени и других ресурсов. Для этих ситуаций в стереологии разрабатывают способы приближенной оценки 3D размеров объектов, к числу которых относится и предлагаемый способ. При использовании приближенных способов важно, чтобы получаемая оценка не была чрезмерно грубой и действительно отражала 3D размеры объектов, а не какие-либо неопределенно близкие к ним величины.
Известен способ определения площади просвета и других размеров поперечного сечения кровеносных микрососудов непосредственно по замерам их профилей плоскостного сечения на ультратонких срезах с контролируемым максимальным отклонением плоскости среза от направления, перпендикулярного продольной оси микрососуда (см., например, [1]). Отклонение плоскости среза при осуществлении данного способа оценивается по осевому соотношению профиля плоскостного сечения (X/Y). Поскольку предполагается, что микрососуды на ограниченных участках длины внешней поверхности имеют форму прямого круглого цилиндра, замеры проводятся лишь на профилях с достаточно близким к единице осевым соотношением (в статье [1] принято, что величина X/Y принадлежит интервалу [0,90; 1,00] ). Остальные профили плоскостного сечения рассматриваются как чрезмерно растянутые и в выборку для измерений не включаются. Известный способ является приближенным (особенно при широких интервалах X/Y) и применяется главным образом для сравнительно быстрого получения прикидочной оценки исследуемых размеров микрососудов. К его основным недостаткам относится следующее. 1) Способ предназначен к использованию только при анализе микрососудов, форма которых на ограниченных участках длины может быть с достаточной точностью аппроксимирована прямыми круглыми цилиндрами. При отклонении формы микрососудов от модельной (например, при появлении эллиптичности микрососуда или при искривлении его продольной оси) способ приобретает значительную инструментальную погрешность и перестает удовлетворять современным требованиям по точности. Также способ не может использоваться при изучении объектов нецилиндрической формы. 2) Известный способ основан на применении единственного варианта стереологического зондирования - сечения микрососудов плоскостными зондами (2D зондами сечения). В ряде случаев было бы эффективно использовать другие зонды, в частности 1D зонд сечения. Однако их применение при анализе микрососудов известным способом не описано.
Существует способ [2] анализа размерных распределений частиц (например, форменных элементов крови) посредством выполнения следующей последовательности действий. Сначала измеряют размерное распределение исследуемых частиц с помощью специальной аппаратуры. Полученное фактически размерное распределение принимают в качестве теоретического (оценочного) распределения, необходимого для обработки последующих замеров частиц. Далее находят различия между теоретическим (оценочным) распределением и фактическими размерными распределениями, которые получают при измерениях последующих проб, содержащих анализируемые частицы. Выявленные различия используют в качестве параметра, характеризующего соответствующие фактические распределения размера исследуемых частиц. Тем самым сущность известного способа заключается в оценке взаимных отклонений, получаемых при замерах распределений фактических размеров частиц. Основным недостатком способа является невозможность его использования (по крайней мере, в заявленном виде) при стереологическом анализе. Данный недостаток связан с тем, что размерные распределения объектов в стереологии оцениваются не в результате прямых замеров, а посредством реконструкции распределений КИ.
Известен также способ [3] стереологической реконструкции распределения размеров (диаметров, радиусов, осевых соотношений) частиц, аппроксимируемых по форме сферами, эллипсоидами вращения или прямоугольными параллелепипедами, по распределению тангенциальных диаметров профилей плоскостного сечения частиц. Данный способ имеет достаточно высокую точность. Его осуществляют посредством построения фактической гистограммы, содержащей размерные классы профилей реконструируемых частиц. В гистограмме выделяется размерный класс, соответствующий наибольшему значению исследуемого размера профилей плоскостного сечения частиц. Далее принимается, что наибольшее значение размера профилей является истинным (3D) значением для первого кластера частиц (частиц наибольшего размера). Для частоты наибольшего значения размера КИ выстраивается теоретическое распределение, которое могло бы быть получено при случайном 2D сечении одинаковых частиц принятого 3D размера. Полученные частоты размерных классов вычитаются из частот фактического распределения размеров профилей реконструируемых частиц. Затем вновь выделяется размерный класс, соответствующий наибольшему значению размера из оставшихся, и процедура последовательно повторяется до полного разложения фактического распределения на ряд простых теоретических распределений. Найденные при такой декомпозиции частоты значений 3D размера позволяют оценить размерное распределение реконструируемых частиц.
К существенным недостаткам известного способа относятся: 1) возможность его использования в описанном авторами виде лишь при изучении частиц, аппроксимируемых по форме сферами, эллипсоидами вращения или прямоугольными параллелепипедами, но не частиц другой формы; 2) ограниченный перечень размеров частиц, 3D распределение которых может быть получено известным способом; 3) возникновение затруднений с определением величины класса наибольших по размеру профилей, на котором базируется весь анализ фактического распределения. При принятых в стереологии объемах выборок ощутимые отклонения в оценке величины этого класса неизбежны, что сопровождается возникновением необъясненных и/или отрицательных частот в фактической гистограмме и, следовательно, дополнительным снижением точности стереологической реконструкции. Данное снижение точности может последовательно накапливаться при каждом переходе к размерному классу, соответствующему наибольшему значению размера из оставшихся. 4) Кроме того, способ имеет достаточно малую устойчивость к отклонению формы частиц от принятой модельной формы, что является дополнительным фактором, лимитирующим его применимость на практике. 5) Известный способ посвящен рассмотрению лишь случая сечения частиц плоскостными зондами (2D зондами сечения). Остальные варианты стереологического зондирования (проецирование на плоскость, на поверхность, сечение 1D и 3D зондами, приобретение секущей плоскостью кривизны, комбинированные зонды и др.) во внимание не принимаются. 6) Наконец, известный способ довольно трудоемок в исполнении и требует к тому же, чтобы применяющий его исследователь обладал определенной математической подготовкой.
Наиболее близким по технической сущности и достигаемому результату к предлагаемому является способ [4], разработанный в 70-е годы 20-го века для прикидочного определения 3D осевых соотношений (Х0/Y0) цилиндрических и эллипсоидных объектов. При осуществлении известного способа форму фактической гистограммы осевых соотношений профилей плоскостного сечения (X/Y) сравнивают с формой шести модельных гистограмм X/Y, рассчитанных для 3D изотропного сечения такой модельной фигуры, как единичный цилиндр (с X0/Y0, равным 1,0; 2,0 или 4,0) или эллипсоид вращения (X0/Y0 составляет 2,0:1,0:1,0; 1,0: 2,0: 2,0 или 1,0:8,0:8,0). При сравнении выбирают модельную гистограмму, в наибольшей мере похожую на фактическую. Осевое соотношение соответствующей модельной фигуры является оценкой X0/Y0 исследуемых объектов. Тем самым известный способ позволяет сравнительно быстро получить искомый результат при анализе двух классов объектов.
Однако и он имеет свои недостатки, основным из которых является тот факт, что 1) точность и валидность способа не удовлетворяют современным требованиям. Получаемые фактически гистограммы X/Y зачастую не могут быть аппроксимированы ни одной из представленных модельных гистограмм либо в чем-то похожи сразу на несколько из них, и возникает неясность, каким же образом оценивать 3D осевые соотношения исследуемых объектов. В таких неясных ситуациях было бы особенно уместным иметь сведения о достигаемом качестве аппроксимации фактического распределения X/Y, однако необходимые указания в описании способа отсутствуют. Причины недостаточной точности и валидности известного способа связаны главным образом с чрезмерно идеализируемым представлением изучаемых объектов. Действительно, а) даже при работе с простыми распределениями, когда X0/Y0 строго фиксированы на некоторых значениях (что едва ли встречается на практике), фактические гистограммы X/Y могут сильно отличаться от модельных, например, по причине малого количества измерений или вследствие преимущественной ориентации изучаемых объектов относительно плоскостей сечения. При этом б) модельные гистограммы рассчитаны лишь для шести значений 3D осевых соотношений объектов (по три значения X0/Y0 для цилиндров и эллипсоидов вращения). Остальные значения X0/Y0 при построении частотных гистограмм в работе не рассматриваются. В результате далеко не все фактические распределения X/Y хорошо согласуются с модельными, даже если другие условия применения способа выполняются идеально, в) При появлении же факторов, усложняющих распределение X0/Y0 (дисперсия, наличие размерных кластеров и пр. ), точность известного способа снижается в еще большей степени, поскольку модельные гистограммы построены без учета этих влияний, г) Способ приобретает дополнительную погрешность при случайных и/или систематических отклонениях формы исследуемых объектов от модельной, например, при появлении неровностей поверхности или при искривлении оси (осей) объектов.
2) Следующим недостатком известного способа является его применимость при исследовании лишь осевых соотношений объектов. Остальные размерные параметры цилиндрических и эллипсоидных объектов (радиусы, диаметры, площадь сечения цилиндра, периметр сечения цилиндра, площадь сечении эллипсоида вращения через большую/малую ось, периметр сечения эллипсоида вращения через большую/малую ось и др.) известным способом не охватываются. 3) Способ может быть использован только при изучении объектов, форма которых аппроксимируется прямыми эллиптическими (в частном случае круглыми) цилиндрами или эллипсоидами вращения с заданными значениями X0/Y0. Объекты, описываемые другими фигурами, равно как и объекты неправильной формы, известным способом исследоваться не могут. 4) Кроме того, вариантом стереологического зондирования, применяемым при осуществлении способа-прототипа, является секционное 2D зондирование. Остальные варианты стереологического зондирования авторами не рассматриваются, что дополнительно ограничивает сферу применимости известного способа.
Сущность изобретения
Сущность настоящего изобретения состоит в следующем. При взаимодействии исследуемых объектов со стереологическим зондом получают КИ. Как оказалось, распределение размера КИ имеет моду, которая равна характерному значению размера объектов. Данный эффект - далее мы будем называть его модальным эффектом - возникает в силу особенностей стохастики значений размера КИ в модальной точке при малых изменениях ориентации объекта относительно применяемого стереологического зонда (подробнее см. в Приложении). Модальный эффект позволяет сравнительно быстро получать приближенную оценку исследуемого 3D размера, что впервые применяется в данном изобретении при стереологическом анализе размеров и размерных распределений. (Для справки отметим, что под размерным распределением исследуемых объектов понимают распределение их 3D размера или размеров.) объектов. При необходимости полученная оценка 3D размера может быть использована при моделировании фактического распределения размера КИ объектов.
Изобретательский замысел, составляющий основу настоящего изобретения, направлен на достижение трех главных целей.
Первая из них заключается в универсализации и расширении возможностей стереологического подхода к изучению размеров и размерных распределений объектов, благодаря чему становится возможным оценивать размеры объектов а) различной, в том числе неправильной, формы, б) организованных в исследуемых телах, материалах или средах произвольным образом. Для анализа объектов используются КИ, получаемые при взаимодействии объектов со стереологическими зондами любого в) типа (зонды сечения, проекционные стереологические зонды, их комбинации), г) любой размерности (0D, 1D, 2D, 3D, их комбинации) и д) кривизны. При этом е) исследуемым(и) 3D размером(ами) объектов может быть любой измеряемый размер.
Вторая основная цель изобретения состоит в сохранении простоты или даже упрощении оценки размеров и размерных распределений объектов, благодаря чему снижается стоимость анализа, и он становится более доступным. Оказывается возможным оценивать 3D размеры объектов по размерным распределениям их КИ без выполнения трудоемких математических вычислений.
Вместе с тем применение способа не должно приводить к получению лишь грубой оценки исследуемого 3D размера объектов. Получаемые результаты должны быть более точными, чем при прикидочном определении размеров непосредственно по КИ объектов (см. , например, способ [1]) или при сравнении фактической гистограммы с модельными (см. прототипный способ [4]). Важно к тому же, чтобы с использованием способа была возможной оценка именно 3D размера объектов, а не каких-либо произвольным образом связанных с ним отвлеченных величин. Тем самым третьей целью изобретения является повышение точности и валидности получаемой оценки размеров и размерных распределений объектов.
Способ осуществляют следующим образом. Образец тела, материала или среды, содержащий исследуемые объекты, подготавливают к стереологическому анализу. Объекты подвергают взаимодействию с n-мерным. (В 3D пространстве n равно 0, 1, 2, 3 или их комбинации (для комбинированных зондов); в более общем случае n составляет 0, 1, 2, 3, ....) стереологическим зондом любой степени сложности с задаваемой, в частном случае нулевой, кривизной. Например, при подготовке образца биологической ткани к трансмиссионной электронной микроскопии процесс ультрамикротомирования является стереологическим зондированием, а именно его вариантом - плоскостным 2D зондированием сечения. В результате зондирования получают набор КИ объектов. Выбирают размер КИ, по распределению значений которого будут исследоваться объекты. Это может быть длина, площадь, периметр или диаметр (диаметры). (Как известно, диаметром объекта произвольной (в том числе неправильной) формы называют точную верхнюю грань расстояний между парами точек этого объекта, т.е. для замкнутых ограниченных объектов - расстояние между максимально удаленными точками объекта. Иногда диаметрами называют также максимальное и минимальное расстояния между точками объекта при измерении через геометрический центр тяжести. В этом случае используются термины "большой" и "малый" диаметры. Половины большого и малого диаметров составляют большой и малый радиусы. При исследовании всех этих размеров может использоваться модальный эффект.) КИ, максимальное, минимальное или среднее расстояние от геометрического центра тяжести КИ, максимальная, минимальная или средняя кривизна контура КИ, другой размер, а также любое соотношение перечисленных и других размеров. Перечень некоторых часто используемых размеров КИ приведен в табл. 2.
Далее выполняют замеры значений выбранного размера у полученных КИ объектов. Измерение размера КИ осуществляют общепринятыми методами (см., в частности, [5-7] ), например линейкой по микрофотографии, содержащей изображения КИ, либо с помощью современных анализаторов изображений. При необходимости КИ увеличивают с применением современных микроскопов (светового, электронного, конфокального лазерного сканирующего и др. ), томографов (компьютерного рентгеновского, магнитно-резонансного, ультразвукового и др.) или иных специальных устройств. По значениям размера выстраивают размерное распределение КИ объектов. Размерное распределение КИ объектов представляют в любом из перечисленного виде: в виде 1) частотной гистограммы (гистограммы частот) значений размера КИ, 2) графика плотности вероятности, 3) кривой функции распределения (кумулятивной кривой), 4) кумулятивной частотной гистограммы (кумулятивной гистограммы частот), 5) другого графика функции распределения, 6) другого графика производной функции распределения или 7) другого графика параметра функции распределения (подробнее с принципами работы со случайными величинами и их графическими представлениями можно ознакомиться в специальной литературе - см., в частности, [8-9]). Для полученного размерного распределения находят моду - абсциссу максимального значения плотности вероятности. При использовании гистограммы частот это будет размерный класс, имеющий наибольшую частоту. На кумулятивной гистограмме частот и кривой функции распределения модальное значение также может быть найдено (например, в виде абсциссы той точки на кривой функции распределения, касательная в которой наиболее близка к вертикальному направлению), но их использование менее удобно.
По моде распределения размера КИ объектов оценивают характерное значение соответствующего размера объектов. Если размерное распределение КИ имеет единственную хорошо выраженную моду, то найденное модальное значение равно характерному значению исследуемого 3D размера объектов. Примеры пар "измеряемый размер КИ - 3D размер объекта" при различных вариантах стереологического зондирования приведены в табл. 2. Если же распределение размера КИ имеет две или несколько хорошо различимых мод, то каждое из модальных значений позволяет аналогичным образом оценить характерное значение исследуемого 3D размера в пределах кластера объектов одинакового или близкого размера. На частотных гистограммах это проявляется в виде двух или нескольких выступающих столбиков (нередко имеющих различную высоту), "всплеск" частоты в каждом из которых не может быть объяснен случайными факторами. Следует отметить при этом, что слабо выраженные моды могут быть использованы при предлагаемом анализе объектов лишь с необходимой осторожностью. Нередко своим появлением они обязаны не особенностям размерного распределения исследуемых объектов, а стохастике применяемого стереологического зондирования, особенностям включения КИ в выборку для замеров и/или погрешностям последующего измерения КИ. Поэтому такие случайные отклонения частот не позволяют оценивать 3D размеры объектов. Для решения вопроса, является ли слабо выраженная мода следствием влияния случайных возмущающих факторов, можно использовать нахождение доверительных интервалов ожидаемых частот при моделировании, о чем будет сказано ниже.
Таким образом, по моде (модам) размерного распределения КИ объектов можно определить характерное значение (значения) исследуемого 3D размера объектов. В этом и состоит сущность предлагаемого способа определения размеров или размерных распределений объектов.
Полученное характерное значение (или характерные значения) размера объектов может быть использовано при моделировании фактического размерного распределения КИ. Это может оказаться полезным при необходимости верифицировать найденную по моде (модам) оценку (оценки) исследуемого 3D размера объектов и оценить ее достоверность. Моделирование может стать и шагом к более детальному стереологическому исследованию, в результате которого полученная оценка 3D размера может быть не только уточнена, но и дополнена, например, сведениями об особенностях пространственной ориентации исследуемых объектов. Моделирование фактического размерного распределения КИ проводят с помощью известных методов стереологии и математического анализа (является ли аппроксимация математическим анализом) (см., например, [3, 7, 11-14]). Для этого по значениям исследуемого 3D размера объектов, найденным с применением модального эффекта, рассчитывают модельное размерное распределение КИ. Модельное размерное распределение КИ сравнивают с фактическим на предмет выяснения степени соответствия между ними, т.е. определяют качество аппроксимации фактического распределения модельным. Сравнение распределений производится визуально и/или с использованием количественных критериев, таких, в частности, как статистический критерий χ2.
При сравнении могут применяться и значения моментов (среднего арфиметического, дисперсии и др.) модельного и фактического распределений, а также значения других параметров этих функций распределения. Качество аппроксимации фактического распределения модельным оценивается в этом случае с использованием соответствующих статистических критериев F Фишера, t Стьюдента и др. (вопросам статистической проверки гипотез посвящена обширная литература, см., к примеру, [8-9]). Если результаты сравнения фактического и модельного распределений свидетельствуют о достижении удовлетворительного качества аппроксимации, можно сделать вывод о том, что полученная оценка характерного размера (или размеров) объектов является в достаточной мере аккуратной. В противном случае ее можно уточнить небольшим смещением характерного значения размера объектов в пределах соответствующего класса гистограммирования. Саму процедуру аппроксимации проводят в соответствии с общими положениями, известными из источников литературы (см., например, [13-14]). В частности, следует учитывать, что аппроксимация оказывается обычно итерационной процедурой, которую ведут в направлении уменьшения выраженности различий между фактическим и модельным распределениями. Например, при использовании критерия соответствия χ2 повышение качества аппроксимации сопровождается уменьшением значения χ2 и увеличением соответствующей вероятности р. Выполнение процедуры аппроксимации заканчивают при прекращении прироста точности и/или при достижении необходимой точности аппроксимации. Если же прирост точности прекратился до достижения необходимой точности аппроксимации, повышают количество измеряемых КИ объектов. Затем процедуру аппроксимации повторяют.
В завершение отметим, что для модельного распределения размера КИ целесообразно выстраивать также доверительные интервалы ожидаемых частот. Расположение фактических значений частоты размера КИ в пределах указанных интервалов свидетельствует о том, что имеющиеся фактические отклонения можно расценивать как случайные. Модальные значения, соответствующие случайно возникающим локальным максимумам, не следует использовать для определения 3D размеров объектов предлагаемым способом.
Некоторые рекомендации по использованию предлагаемого способа
1. Использование модельной формы. Способ предназначен к использованию при анализе объектов любой формы. Если объекты имеют неправильную форму, основными размерами объектов, исследуемыми по размерам КИ с применением модального эффекта, могут быть площадь сечения или проекции, периметр сечения или проекции, диаметр (диаметры), характеристики расположения геометрического центра тяжести и некоторые другие. Вместе с тем форма исследуемых объектов нередко может быть описана правильными геометрическими фигурами (сферами, эллипсоидами, круглыми цилиндрами, эллиптическими цилиндрами, треугольными цилиндрами, кубами, параллелепипедами, тетраэдрами, многогранниками, конусами, другими фигурами, различными композициями этих и других фигур). Например, форма кровеносных и лимфатических микрососудов (артериол, прекапилляров, кровеносных капилляров, посткапилляров, венул, лимфатических капилляров и пр. ) на ограниченных участках их длины, согласно имеющимся в литературе микроанатомическим данным, может быть с приемлемой точностью аппроксимирована эллиптическими, в частном случае круглыми, цилиндрами.
При принятии предположений о форме объектов характерное значение (значения) 3D размера оценивают описанным выше образом. Далее при необходимости выстраивают модельное распределение размера КИ объектов при задаваемых форме, 3D размере (размерах), ориентации и расположении объектов, свойствах стереологического зонда и других необходимых параметрах (подробнее см. в [3, 7, 11, 12]). При задании 3D размера (размеров) объектов используют оценки, полученные по моде или модам размерного распределения КИ. Затем выполняют описанную выше процедуру аппроксимации фактического распределения размера КИ. При этом целесообразно использовать имеющиеся в литературе данные о виде функции взаимосвязи 3D размеров объектов различной формы с соответствующими размерами КИ (табл. 3). Часть функций может быть также выведена исследователем самостоятельно с использованием традиционного для стереологии математического аппарата.
Важно учитывать, что точность стереологического анализа при применении модельной формы снижается, если имеются отклонения от нее реальной формы объектов. Однако при малых отклонениях аппроксимация формы объектов обычно позволяет успешнее, чем без нее, верифицировать полученную оценку 3D размера, оценивать ее достоверность и проводить дальнейший стереологический анализ. Существенного снижения точности определения 3D размеров по моде при умеренных отклонениях формы также не происходит, поскольку модальный эффект достаточно устойчив к возмущающим воздействиям. Еще одним преимуществом принятия модельных предположений о форме исследуемых объектов является расширение перечня измеряемых 3D размеров. К тому же предметное значение 3D размеров объектов приобретает большую ясность.
Заметим, что при применении настоящего способа могут наблюдаться ситуации, при которых зондирование даже одинаковых по размеру объектов правильной формы порождает два или несколько максимумов плотности вероятности изучаемого размера КИ (например, при изучении площади случайной проекции на плоскость объектов в форме круглого конуса [10]). При анализе реальных распределений размера КИ следует ожидать наличия двух и большего количества мод. Получаемые моды связаны со значениями 3D размеров исследуемого объекта, и настоящий способ может быть осуществлен. При этом следует учитывать соотношение значений мод, возникающих при стереологическом зондировании одинаковых по размеру объектов, что позволяет вычленять спаренные модальные значения, относящиеся к кластеру объектов одинакового или близкого размера. Например, при анализе площади (S) проекции на плоскость конусообразных объектов с высотой 5,0 и радиусом основания 1,0 распределение S имеет четыре моды [10], одна из которых равна площади основания исследуемого конуса (3,14), а другая из оставшихся - площади его боковой проекции (5,00), первая из которых равна 3D. В реальном распределении при проецировании набора конусов разного размера, но имеющих фиксированное отношение высоты и радиуса основания 5:1, можно ожидать появления спаренных мод, относящихся друг к другу как 5,00:3,14.
2. Варианты представления размерного распределения КИ. По результатам измерений КИ выстраивают статистическое распределение размера КИ. Размерное распределение КИ может быть выражено в виде абсолютного числа КИ, приходящегося на заданный интервал значений размера. Могут также использоваться относительные показатели количества профилей (частота КИ, число КИ заданного интервала значений размера на единице площади среза и др.). Из перечисленных вариантов частота КИ (в процентах) представляется нам наиболее удобной при анализе. При выполнении процедуры аппроксимации модельное размерное распределение следует выстраивать в виде, аналогичном используемому при построении фактического распределения размера КИ.
Следует также заметить, что предлагаемый способ может быть использован при анализе сразу нескольких 3D размеров объектов (например, площади и периметра проекции на плоскость). Процедура анализа в этом случае лишь незначительно отличается от вышеописанной. Так, по получаемым при стереологическом зондировании КИ объектов измеряют соответствующие размеры. По ним выстраивают совместное распределение размеров КИ. Характерные значения 3D размеров объектов определяют по моде (модам) совместного распределения. При необходимости проводят аппроксимацию фактического совместного распределения размеров КИ.
3. Ограничения применимости настоящего способа. Применение модального эффекта при анализе 3D размеров объектов составляет основу предлагаемого способа. Однако в некоторых случаях характерное значение 3D размера по моде (модам) размерного распределения КИ может не определяться. Это связано с нарушениями условий, необходимых для формирования "всплеска" частоты в точке характерного значения 3D размера (подробнее см. в Приложении). Все же мода размерного распределения КИ будет и в этом случае оставаться оценкой (пусть и менее точной) характерного значения 3D размера объектов в силу своих статистических свойств как оценка среднего в распределении. Заметим, что, если имеется неясность, возможен ли модальный эффект в какой-либо конкретной ситуации анализа, целесообразно сначала подтвердить появление "всплеска" частоты размера КИ в точке характерного значения 3D размера объектов рассматриваемого класса и только затем использовать предлагаемый способ. Подтверждение возникновения "всплеска" частоты осуществляется с использованием традиционного для стереологии математического аппарата.
Иногда оценка 3D размера объектов, получаемая по моде (модам) распределения размера КИ, может быть неполной и при выполнении модального эффекта в рассматриваемых условиях стереологического зондирования объектов. Так, не все характерные значения 3D размера объектов могут быть определены, если доля объектов одного из размерных кластеров значительно меньше доли превалирующего кластера объектов. Модальный "всплеск" частоты размера КИ, соответствующий малому кластеру, будет в этом случае неразличим. Одна или некоторые из мод будут также отсутствовать на размерном распределении КИ, если распределение 3D размера объектов является более сложным, чем набор размерных кластеров с характерными значениями размера, вокруг которых концентрируются размеры отдельных объектов. Такое может быть, например, в том случае, если значения 3D размера исследуемых объектов подчиняются непрерывному равномерному закону распределения.
Таким образом, областью наиболее эффективного применения настоящего способа является оценка размеров или размерных распределений объектов, формирующих в изучаемом теле, материале или среде один или несколько (до 10-15) размерных кластеров. Кластеры при этом представлены в общей совокупности объектов примерно одинаковыми долями. Размерное распределение КИ, по которому проводится анализ, имеет одно или несколько (до 10-15) модальных значений. Каждая из мод оказывается равной характерному для кластера значению исследуемого 3D размера. Тем самым размерное распределение объектов представляется в итоге как набор дискретных значений, состоящий не менее чем из одного характерного значения 3D размера объектов.
При невыполнении перечисленных условий кластеризации применение предлагаемого способа является менее эффективным, что, однако, не исключает возможности его использования. Мода размерного распределения КИ продолжает и в этом случае оставаться оценкой (пусть и менее точной) характерного значения 3D размера в силу своих статистических свойств как оценка среднего в анализируемом фактическом распределении.
Сведения, подтверждающие возможность осуществления изобретения
Предлагаемым способом была определена характерная величина истинного, или 3D, осевого соотношения (X0/Y0) перифолликулярных кровеносных капилляров в щитовидной железе (ЩЖ) крысы. Исследование было выполнено на 6 белых крысах-самцах, достигших половой зрелости. Забор ткани ЩЖ осуществляли под эфирным наркозом. Фрагменты ЩЖ последовательно фиксировали в растворах глютаральдегида (2,5%, 2 ч.) и тетраоксида осмия (1%, 1 ч.) на какодилатном буфере (0,2 М, рН 7,4). Образцы ткани обезвоживали в спиртах восходящей концентрации и заключали в смесь смол эпон-аралдит М (Fluka Chemical Co., США). Ультратонкие срезы изготавливали на микротоме III-LKB-8800 (Швеция). Тем самым при анализе был применен стереологический 2D зонд плоскостного сечения. (Как известно, диаметр кровеносного капилляра составляет не менее 4 мкм, что значительно превышает толщину ультратонкого среза (40-60 нм). Поэтому получаемые при ультрамикротомировании профили плоскостного сечения можно считать двухмерными (2D), а используемый при изготовлении ультратонких срезов стереологический зонд - 2D зондом плоскостного сечения.) Срезы контрастировали уранилацетатом и цитратом свинца. Просмотр и фотографирование препаратов выполняли на трансмиссионном электронном микроскопе Hitachi H-300 (Япония). По микрофотографиям с конечным увеличением х1650 вручную были выполнены замеры больших (X) и малых (Y) радиусов 150 случайно отобранных профилей плоскостного сечения капилляров (по 25 профилей от каждого животного).
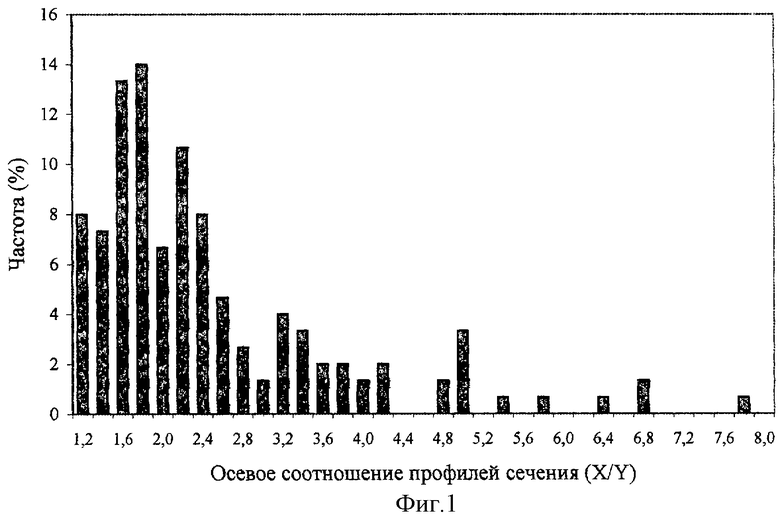
На основании полученных данных была построена частотная гистограмма осевых соотношений профилей капилляров (X/Y) с шагом гистограммирования 0,2 (Фиг. 1). На гистограмме отмечается два высоких столбика, соответствующих частотам профилей с X/Y∈[1,4; 1,6[ и X/Y∈(1,6; 1,8[. Столбики близки по высоте. Следовательно, мода распределения X/Y находится примерно в центре интервала [1,4; 1,8], т.е. в окрестности 1,6. Характерное значение 3D осевого соотношения исследуемых микрососудов, согласно изложенным выше положениям об оценке 3D размеров, равно моде и составляет 1,6 (X0/Y0≈1,6). Тем самым получена искомая оценка характерного значения X0/Y0. Данная величина X0/Y0 хорошо согласуется с характерным осевым соотношением перифолликулярных гемокапилляров в ЩЖ крысы, оцененным нами как 1,6 при выполнении процедуры стереологической реконструкции (результаты представлены в [15]).
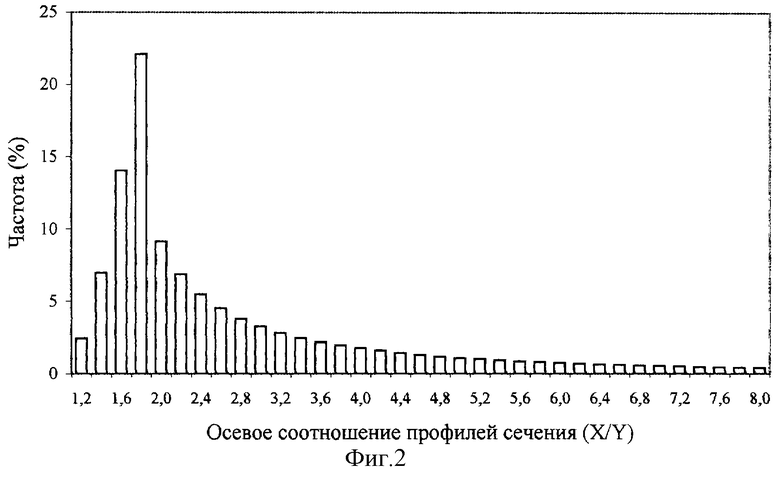
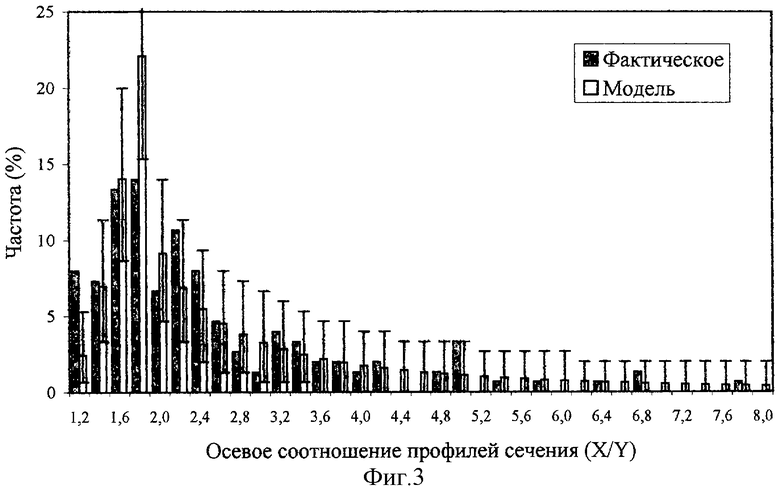
Полученная оценка X0/Y0 может быть дополнительно верифицирована посредством сравнения фактического распределения X/Y с модельным распределением, рассчитанным для эллиптических капилляров с 3D осевым соотношением 1,6 (для задания X0/Y0 модельного набора капилляров используется полученная по моде оценка X0/Y0). На Фиг.2 представлена соответствующая модельная гистограмма. При ее построении была использована методика [11] расчета плотности вероятности для 3D изотропного плоскостного сечения капилляров с формой, аппроксимируемой на ограниченных участках длины прямыми эллиптическими цилиндрами. Визуально определяется, что модельная и фактическая гистограммы X/Y близки друг другу. На Фиг.3 модельная гистограмма показана с доверительными интервалами (α=0,05) ожидаемых частот X/Y. Здесь же приведены фактические частоты X/Y. Видно, что фактические частоты находятся в пределах соответствующих доверительных интервалов X/Y. Исключение составляют лишь столбики для X/Y∈[1,0; 1,2[ и X/Y∈[1,6; 1,8[.
С учетом того, что при принятой доверительной вероятности α=0,05 отклонения частот за пределы доверительных границ возможны в 5% столбиков, имеющиеся отклонения фактических частот от ожидаемых можно в целом расценивать как случайные. Данный вывод подтверждается при выяснении степени соответствия модельной гистограммы фактическому распределению по критерию χ2(χ2 = 36,931; р= 0,335). Полученное значение доверительной вероятности р превышает 0,05, следовательно, нулевая гипотеза не может быть отвергнута, т.е. модельная гистограмма статистически не отличается от фактической. Для повышения качества аппроксимации (увеличения р) можно было бы укрупнить выборку измеряемых профилей сечения капилляров. Также можно было бы более точно подобрать моду в окрестности 1,6. Однако это не нужно в данном исследовании, поскольку найденная оценка характерного значения X0/Y0 совпала с полученной в [15]. К тому же, представленное исследование фактического материала является лишь примером, подтверждающим возможность осуществления настоящего изобретения. Завершая моделирование фактического распределения X/Y, можно сделать вывод о том, что фактическое распределение X/Y с приемлемой для примера точностью аппроксимируется модельным распределением, построенным для 3D изотропного набора эллиптических цилиндров с одинаковым осевым соотношением Х0/Y0=1,6.
Таким образом, предлагаемый способ позволил при сравнительно малых затратах времени достаточно точно определить характерное значение одного из 3D размеров исследуемых микрососудов (X0/Y0). При этом не проводилась полномасштабная стереологическая реконструкция, аналогичная описанной в способе [3] , которая потребовала бы выполнения трудоемких вычислений и, вероятнее всего, проведения большего количества замеров. Выигрышным для настоящего способа является его сравнение и со способом [4], поскольку форма фактической гистограммы (Фиг.1) недостаточно хорошо согласуется с любой из модельных гистограмм, приведенных в описании прототипа. И даже если пренебречь имеющимися расхождениями, то получаемая способом [4] оценка X0/Y0 равна 2,0, что значительно (на 25%) отличается от найденной нами (X0/Y0≈1,6). К тому же полученная предлагаемым способом оценка не потребовала принятия модельных ограничений, чрезмерно упрощающих представление формы капилляров (не были приняты предположения 1) о фиксировании X0/Y0 на значениях 1,0; 2,0 или 4,0, 2) о наличии лишь единственного размерного кластера капилляров, 3) о 3D изотропной ориентации капилляров). Найденное характерное значение X0/Y0 согласуется с результатами проведенной ранее стереологической реконструкции капилляров ЩЖ крысы [15]. Поэтому оно может расцениваться как валидное, т.е. действительно отражающее исследуемый 3D размер перифолликулярных кровеносных микрососудов в ЩЖ. На имеющемся фактическом материале могут быть определены характерные значения и других 3D размеров микрососудов, например большого и малого радиусов, площади, периметра, эксцентриситета поперечного сечения. При этом могут применяться самые различные варианты стереологического зондирования. Все это еще раз свидетельствует о преимуществах предлагаемого способа по сравнению с прототипом и другими аналогами. Заметим, что способ [1] при выполненном анализе использоваться не может, поскольку изучаемые капилляры имеют эллиптичность и, следовательно, не должны аппроксимироваться круглыми цилиндрами.
В заключение необходимо сказать, что представленным описанием не охватываются все возможные варианты использования модального эффекта при анализе размеров и размерных распределений объектов. Специалистами могут быть найдены и другие модификации настоящего способа, не выходящие за рамки прилагаемых пунктов формулы или эквивалентных им положений. При нахождении, развитии и применении таких модификаций изменений сущности настоящего изобретения не происходит.
Выражение признательности
Авторы настоящего изобретения выражают свою искреннюю признательность директору Научно-исследовательского центра Московской медицинской академии им. И. М. Сеченова член-корр. РАМН проф. Грачеву С.В. за оказанную организационную помощь при выполнении экспериментального фрагмента исследования.
Приложение. Вероятностно-геометрические основы возникновения модального эффекта
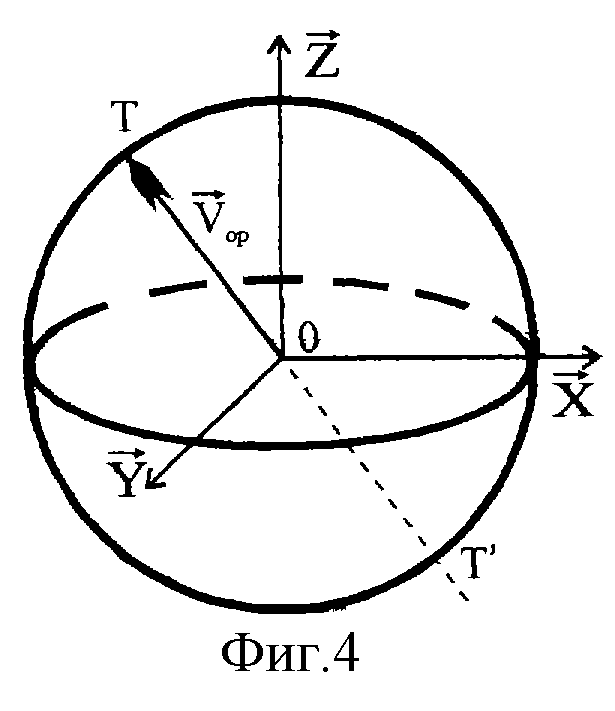
Механизм возникновения модального эффекта (равенства моды распределения размера КИ объектов характерному значению 3D размера объектов) можно пояснить следующим образом. Процесс зондирования в стереологии представляют в сферической системе координат (Фиг.4). В них направление вектора ориентации исследуемого объекта относительно стереологического зонда (вектора 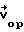 ) задается двумя углами - полярным (θ) и плоскостным (ϕ). Каждой ориентации вектора
) задается двумя углами - полярным (θ) и плоскостным (ϕ). Каждой ориентации вектора  соответствует точка Т на верхней полусфере. Изменение углов θ и ϕ при стереологическом зондировании (т.е. перемещение точки Т по поверхности полусферы) сопровождается динамикой значения соответствующего размера КИ. Значение размера КИ при этом может уменьшаться или возрастать. Для объектов заданного класса существует диапазон возможных значений размера их КИ. Экстремальное (минимальное или максимальное) из них, как правило, соответствует истинному, или 3D, значению размера. Например, при плоскостном сечении единичного цилиндра конечной длины такой размер профилей плоскостного сечения, как S (площадь КИ), может принимать значения от 3D площади сечения S0 до некоторого конечного Smax, равного площади сечения цилиндра по диагонали. Аналогичная ситуация возникает при измерении большого радиуса (X), малого радиуса (Y) или периметра (Р) сечения эллиптического цилиндра. Минимальные значения их распределений равны 3D значениям - соответственно Х0, Y0, Р0.
соответствует точка Т на верхней полусфере. Изменение углов θ и ϕ при стереологическом зондировании (т.е. перемещение точки Т по поверхности полусферы) сопровождается динамикой значения соответствующего размера КИ. Значение размера КИ при этом может уменьшаться или возрастать. Для объектов заданного класса существует диапазон возможных значений размера их КИ. Экстремальное (минимальное или максимальное) из них, как правило, соответствует истинному, или 3D, значению размера. Например, при плоскостном сечении единичного цилиндра конечной длины такой размер профилей плоскостного сечения, как S (площадь КИ), может принимать значения от 3D площади сечения S0 до некоторого конечного Smax, равного площади сечения цилиндра по диагонали. Аналогичная ситуация возникает при измерении большого радиуса (X), малого радиуса (Y) или периметра (Р) сечения эллиптического цилиндра. Минимальные значения их распределений равны 3D значениям - соответственно Х0, Y0, Р0.
Особенностью стереологического зондирования в направлении Dirextr, порождающем экстремальное значение размера КИ, является то, что при отклонениях углов θ и ϕ от Dirextr первого порядка малости значение соответствующего размера КИ испытывает изменения второго порядка малости. В результате отклонение θ и ϕ в окрестности Dirextr сопровождается нулевым градиентом исследуемого размера КИ. Частоты данного значения размера КИ наслаиваются друг на друга, и возникает "всплеск" частоты. При этом высота модального "всплеска" бесконечна. Если экстремальное значение размера КИ совпадает с 3D размером объекта, мода распределения размера КИ оказывается равной характерному значению 3D размера анализируемых объектов. Это и составляет суть модального эффекта. При стереологическом зондировании объектов одинакового размера, что может наблюдаться скорее в идеальной ситуации, чем на практике, мода размера КИ строго равна 3D размеру объектов (определяемое характерное значение 3D размера является истинным). Модальный эффект выполняется также при соотношении размеров КИ, экстремальное значение каждого из которых совпадает с 3D размером объекта (например, при анализе X0/Y0 - 3D осевых соотношений эллиптических цилиндров - по профилям их плоскостного сечения).
В силу некоторых своих особенностей модальный эффект устойчив к умеренным возмущающим воздействия, например, к неточностям измерения, стохастическим колебаниям измеряемого 3D размера при малых объемах выборок для измерений, отклонениям формы исследуемых объектов от модельной, если таковая используется. Мода обладает также свойством робастности - устойчивости к сильным возмущениям в малой доле измерений. Такая устойчивость позволяет использовать малые шаги гистограммирования при стереологическом анализе. Несмотря на то, что фактическое распределение будет иметь многочисленные пропущенные столбики, модальный эффект позволит и в этом случае оценить 3D размер объектов по моде (модам) распределения.
В завершение следует сказать об условиях возникновения модального эффекта. Мода распределения размера КИ всегда равна характерному значению 3D размера объектов, если одновременно выполняются следующие условия: 1) размер КИ является гладкой функцией взаимной ориентации объекта и зонда, 2) значение размера КИ зависит от взаимной ориентации объекта и зонда, но не от их взаимного расположения, 3) вероятность попадания точки Т в участок единичной площади на поверхности полусферы является непрерывной и нигде не обращается в ноль или бесконечность. Вместе с тем невыполнение перечисленных условий не означает, что модальный эффект не возникает. При использовании предлагаемого способа в таких случаях может лишь понадобиться предварительное подтверждение возникновения модального эффекта. При этом могут использоваться данные литературы (см. , например, табл. 2) и современный математический аппарат стереологии.
Источники информации
1. Красноперов Р.А., Грачев С.В., Глумова В.А., Рящиков С.Н., Волкова С. И. Ультраструктурная организация гемато-С-целлюлярных взаимоотношений в щитовидной железе десимпатизированных гуанетидином крыс 4-недельного возраста.// Бюлл. экспер. биол. мед. - 1996. - Т. 122, N 12. - С.678-681.
2. Kanamori S. Particle size distribution analysis. USA Pat. 4817446. Apr. 4, 1989. Prior. Jul. 25, 1986. IPC G 01 N 15/02.
3. Sahagian D.L., Proussevitch A.A. 3D particle size distributions from 2D observations: stereology for natural applications. // J. Volcanol. Geotherm. Res. - 1998. - Vol. 84, N 3-4, P.173-196.
4. Elias H. , Hyde D. M. An elementary introduction to stereology (quantitative microscopy). // Am. J. Anat. - 1980. - Vol. 159, N 4.- P. 412-446.
5. Автандилов Г.Г. Медицинская морфометрия. Руководство. М.: Медицина, 1990. - 384 с.
6. Караганов Я.Л., Алимов Г.А., Гусев С.А. Ультраструктурная морфометрия обменных микрососудов. // Тр. 2-го МОЛГМИ. - 1976. - N 2. - С.7-26.
7. Чернявский К.С. Стереология в металловедении. М.: Металлургия, 1977. - 280 с.
8. Теннант-Смит Дж. Бейсик для статистиков. Пер. с англ. М.: Мир, 1988. 208 с.
9. Freund J.E., Walpole R.E. Mathematical statistics. 4th ed. 1987. 606 p.
10. Vickers G. T. , Brown D.J. The distribution of projected area and perimeter of convex, solid particles. // Proc. Roy. Soc. A (Lond). - 2001. - Vol.457, N 2006. - P.283-306.
11. Красноперов Р.А., Герасимов А.Н. Способ определения размеров аппроксимируемых эллиптическими цилиндрами объектов по профилям их сечения. Заявка на патент РФ 2000132518 от 26.12.2000. МКИ7 G 06 Т 7/60.
12. Gundersen H.J.G., Jensen E.B. Particle sizes and their distributions estimated from line- and point-sampled intercepts. Including graphical unfolding. // J. Microsc. - 1983. - Vol. 131, Pt.3. - P.291-310.
13. Носач В.В. Решение задач аппроксимации с помощью персональных компьютеров. М.: Бином. Из серии: Современные математические методы в прикладных исследованиях (теория, алгоритмы и программы). - 1994. - 380 с.
14. Braess D. Nonlinear approximation theory. Berlin, Springer, 1986. - 290 p.
15. Krasnoperov R.A., Grachev S.V., Gerasimov A.N. Elliptical microvessel sizes derived from measurement of size distributions of section profiles. // FASEB J. - 2001. - Vol.15, N 4, Pt.1.- P.A119-A119.
16. Howard C.V., Reed M.G. Unbiased Stereology. Three-Dimensional Measurement in Microscopy. RMS Handbook 41. BIOS Scientific Publishers, Oxford, 1998. - 246 p.
17. Gille W. Chord length distributions and small-angle scattering. // Eur. Phys. J. В. - 2000. - Vol. 17, N 3. - P.371-383.
18. Saltikov S. A. The determination of the size distribution of particles in an opaque material from a measurement of me size distribution of their sections. // Stereology (Proc. 2nd Int. Congr. Stereology; Chicago, 8-13, April, 1967)./Ed. H. Elias. Berlin, Springer-Verlag, 1967. P.163-173.
19. Cruz-Orive L.M. Particle size-shape distributions: the general spheroid problem. I. Mathematical model. // J. Microsc. - 1976. - Vol. 107, Pt. 3. - P.235-253.
20. Cruz-Orive L. M. Distribution-free estimation of sphere size distributions from slabs showing overprojection and truncation, with a review of previous methods. // J. Microsc. - 1983. - Vol. 131, Pt.3. P.265-290.
21. Brown D. J. , Vickers G.T. The use of projected area distribution functions in particle shape measurement. // Powder Technol. - 1998. - Vol. 98. - P.250-257.
22. Вульфсон Н.И. Методы стереологии в геофизике. Л.: Гидрометеоиздат, 1989. 200 с.
Перечень фигур
Фиг. 1. Распределение осевых соотношений профилей плоскостного сечения кровеносных капилляров в ЩЖ крысы, полученное с использованием трансмиссионной электронной микроскопии. Размерное распределение профилей капилляров представлено в виде гистограммы частот X/Y с шагом гистограммирования (размерным классом), равным 0,2. Данные по оси абсцисс соответствуют верхней исключаемой границе размерного класса (например, первый столбик соответствует частоте профилей с X/Y∈[1,0; 1,2[). По моде распределения (по абсциссе максимума плотности вероятности) можно определить характерную величину 3D осевого соотношения (X0/Y0) капилляров как 1,6.
Фиг. 2. Модельное распределение частот X/Y, рассчитанное для изотропного набора эллиптических капилляров с фиксированным 3D осевым соотношением Х0/Y0= 1,6. Форма капилляров на ограниченных участках длины аппроксимируется прямыми эллиптическими цилиндрами. Модельное распределение в целом повторяет форму фактического распределения частот.
Фиг. 3. Модельное распределение, показанное на Фиг.2, приведено в сравнении с фактическим распределением. На столбиках модельной гистограммы имеются доверительные интервалы ожидаемых частот X/Y с пороговой вероятностью от 0,025 до 0,975 (α=0,05). Фактические частоты X/Y, как правило, находятся в указанных доверительных интервалах.
Фиг.4. В сферической системе координат с осями 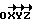 показан вектор ориентации объекта относительно стереологического зонда
показан вектор ориентации объекта относительно стереологического зонда 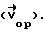 На верхней полусфере вектору соответствует точка Т. Направление данного вектора задается в 3D пространстве двумя углами - θ и ϕ. Угол θ(θ∈[0,π/2]) располагается между
На верхней полусфере вектору соответствует точка Т. Направление данного вектора задается в 3D пространстве двумя углами - θ и ϕ. Угол θ(θ∈[0,π/2]) располагается между 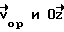 и задает кошироту точки Т, а угол ϕ(ϕ∈[0,π]) - между
и задает кошироту точки Т, а угол ϕ(ϕ∈[0,π]) - между 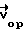 и плоскостью
и плоскостью 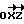 и определяет долготу точки Т. Заданной ориентации вектора
и определяет долготу точки Т. Заданной ориентации вектора 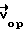 соответствует некоторое соотношение значений размера КИ и 3D размера исследуемого объекта.
соответствует некоторое соотношение значений размера КИ и 3D размера исследуемого объекта.


Изобретение относится к области стереологического анализа пространственной организации объектов, в частности, при изучении объектов по их плоскостным изображениям. Его применение в световой, электронной, конфокальной лазерной микроскопии, а также в компьютерной, магнитно-резонансной и ультразвуковой томографии позволяет получить технический результат в виде расширения возможностей при сохранении точности стереологического анализа. Этот результат достигается благодаря тому, что объекты подвергают взаимодействию с n-мерным стереологическим зондом, определяют распределение размера получаемых кажущихся изображений объектов, по моде размерного распределения кажущихся изображений оценивают характерное значение размера объектов. Степень согласования модели с фактическим распределением оценивают визуально и/или статистическими методами. 8 з.п.ф-лы, 4 ил., 3 табл.
| СПОСОБ АВТОМАТИЧЕСКОГО РАСЧЕТА ФОРМЫ ОБЪЕМНЫХ ТЕЛ | 1998 |
|
RU2158960C2 |
| СПОСОБ СТЕРЕОЛОГИЧЕСКОЙ ОЦЕНКИ ДИСТРАКЦИОННОГО ОСТЕОГЕНЕЗА, УЗЕЛ СОЕДИНЕНИЯ ОПОР АППАРАТА, ИСПОЛЬЗУЕМЫЙ ПРИ ЕГО ОСУЩЕСТВЛЕНИИ | 1996 |
|
RU2165243C2 |
| US 5825908 A, 20.10.1998 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОДОПРОЧНОСТИ ПОЧВЕННЫХ АГРЕГАТОВ | 2007 |
|
RU2344419C1 |
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
Авторы
Даты
2003-12-10—Публикация
2000-12-26—Подача