ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Изобретение относится к измерительной технике, а именно к способам количественного анализа структурной организации объектов, в частности таких ее аспектов, как расположение объектов в пространстве, размеры, форма и ориентация объектов. Изобретение относится также к способам определения геометрических признаков объектов по их изображениям и, кроме того, к способам получения изображений объектов, используемых при изучении структурной организации объектов.
Изобретение предназначено к применению при исследовании различных тел, сред, материалов и систем (в частности, живых систем), содержащих объекты, особенности структурной организации которых либо не могут быть выявлены посредством прямых измерений, либо такие измерения неэффективны, например, по причине многочисленности объектов. В частности, изобретение может использоваться при изучении объектов по их плоскостным и другим изображениям, получаемым при световой микроскопии (СМ), электронной микроскопии (ЭМ), конфокальной лазерной сканирующей микроскопии (КЛСМ), компьютерной томографии (КТ), магнитно-резонансной томографии (МРТ), позитронно-эмиссионной томографии (ПЭТ), однофотонной эмиссионной компьютерной томографии (англ. - single photon emission computed tomography, SPECT), а также с помощью ультразвуковой микроскопии (УМ), ультразвуковой томографии (УТ) и других ультразвуковых (УЗ) методов исследования. Еще одним примером области применения настоящего изобретения является анализ объектов, осуществляемый в технике и научных исследованиях по проекционным изображениям объектов.
УРОВЕНЬ ТЕХНИКИ
Стереологический анализ широко используется при изучении структурной организации тел, сред, искусственных и естественных материалов, технических объектов и живых систем. Сущность стереологического анализа заключается в получении информации о геометрических свойствах объектов посредством изучения событий (в частном случае - изображений), возникающих при взаимодействии объектов со стереологическими зондами. В трехмерном (3D) пространстве стереологические зонды обладают нулевой (0D), первой (1D), второй (2D) и третьей (3D) размерностью. Любой из указанных зондов может быть зондом сечения (секционным зондом) или зондом проекции (проекционным зондом). Возможны также разнообразные комбинации стереологических зондов. События (в частном случае - изображения), получаемые при стереологическом зондировании объектов, в зависимости от специфики выполняемой работы и личных предпочтений авторов могут называться по-разному. Применяются, в частности, такие термины, как "профили стереологического зондирования (ПСЗ)", "профили сечения", "изображения", "образы", "проекции", "тени" и "кажущиеся изображения". В настоящем описании для обозначения событий (в частном случае - изображений), возникающих при взаимодействии объектов со стереологическими зондами, будет использоваться первый из приведенных терминов. Профилями сечения будут называться ПСЗ, получаемые при плоскостном (2D) сечении объектов. Примеры зондов различной размерности и соответствующих ПСЗ приведены в табл.1.
К аспектам структурной организации объектов, исследуемых методами стереологического анализа, может относиться, в частности, любое из следующего либо любая комбинация из следующего: 1) распределение расположения (например, 3D-расположения) объектов, 2) размерное распределение объектов, 3) распределение формы объектов и 4) распределение ориентации объектов. Предлагаемый способ позволяет оценивать любой или любые из перечисленных аспектов структурной организации объектов. При этом основным предназначением способа является исследование расположения объектов. Рассмотрим подробнее те из известных решений в области стереологического анализа, которые представляют интерес в сопоставлении с предлагаемым способом.
Известен способ [Sahagian et al., 1998] стереологической реконструкции распределения размеров (диаметров, радиусов, осевых соотношений) частиц, аппроксимируемых по форме сферами, эллипсоидами вращения или прямоугольными параллелепипедами, по распределению тангенциальных диаметров профилей плоскостного сечения частиц. Данный способ осуществляют посредством построения фактической гистограммы, содержащей размерные классы профилей реконструируемых частиц. В гистограмме выделяется размерный класс, соответствующий наибольшему значению исследуемого размера профилей плоскостного сечения частиц. Далее принимается, что наибольшее значение размера профилей является истинным (3D) значением для первого кластера частиц (частиц наибольшего размера). Для частоты наибольшего значения размера ПСЗ выстраивается теоретическое распределение, которое могло бы быть получено при случайном 2D-сечении одинаковых частиц принятого 3D-размера. Полученные частоты размерных классов вычитаются из частот фактического распределения размеров профилей реконструируемых частиц. Затем вновь выделяется размерный класс, соответствующий наибольшему значению размера из оставшихся, и процедура последовательно повторяется до полного разложения фактического распределения на ряд простых теоретических распределений. Найденные при такой декомпозиции частоты значений 3D-размера позволяют оценить размерное распределение реконструируемых частиц. Известный способ имеет следующие основные недостатки. 1) Способ в описанном авторами виде применим лишь при изучении частиц, аппроксимируемых по форме сферами, эллипсоидами вращения или прямоугольными параллелепипедами, но не частиц другой формы. 2) При осуществлении способа используется единственный вариант стереологического зондирования, а именно зондирование плоскостью сечения. 3) Не рассматриваются также возможности применения движущегося зонда, представленного, например, летательным аппаратом, при изучении атмосферных потоков. 4) Способом могут быть получены сведения только о размерных распределениях объектов, но не о распределении их а) расположения, б) формы (за исключением осевых соотношений, что было использовано авторами) или в) ориентации. 5) В описанном виде способ не позволяет исследовать структурную организацию объектов во временной динамике. 6) Известным способом не предусмотрено получение изображений объектов.
Стереологический анализ находит также применение при изучении формы объектов. Известен способ определения формы объектов в гистологии [Elias et al., 1980], суть которого заключается в реализации следующего принципа. Если множество 3D-объектов одинаковой формы будут подвергнуты плоскостному сечению, распределение осевых соотношений (L/B), получаемых профилей сечения, позволит определить форму исследуемых объектов. В частности, отмечается, что при сечении сфер все профили сечения являются круглыми, т.е. имеют L/B, равное единице. Поэтому при обнаружении на гистологическом срезе только круглых профилей можно заключить о сферичности исследуемых объектов. Если же производится сечение множества случайно ориентированных круглых цилиндров, то 75% профилей их сечения имеют L/B в диапазоне [1,0; 2,0], а 25% профилей оказываются более вытянутыми. Авторами дополнительно построены шесть шаблонных гистограмм частот значений L/B для фигур несферической формы: для круглых цилиндров (истинное осевое соотношение сечения L0/B0=1,0), эллипсоидов вращения (истинное осевое соотношение 2,0:1,0:1,0; 1,0:2,0:2,0 или 1,0:8,0:8,0) и эллиптических цилиндров с L0/B0, равным 2,0 или 4,0. Если полученное фактически распределение L/B совпадает с одной из приведенных шести гистограмм, то форму изучаемых объектов можно определить по тому, для какой фигуры рассчитана эта шаблонная гистограмма - для круглого цилиндра, эллипсоида вращения или эллиптического цилиндра с L0/B0, равным 2,0 или 4,0. Основными недостатками известного способа являются следующие недостатки. 1) Способ может применяться лишь при исследовании объектов, описываемых по форме сферами, цилиндрами или эллипсоидами вращения. 2) Используемым вариантом зондирования является сечение плоскостью; остальные стереологические зонды (в том числе движущиеся) в описании не приводятся. 3) Результатом изучения объектов с применением известного способа являются сведения только об их форме. Другие аспекты структурной организации объектов [а) распределение расположения, б) размерное распределение (например, распределение L0 и В0) или в) распределение ориентации] анализу не подвергаются. 4) При этом авторы предлагают оценивать лишь характерную форму, но не распределение формы объектов, что само по себе придает результатам исследования предварительный характер. 5) Кроме того, даже с учетом свойственной способу приблизительности точность последнего, как правило, оказывается недостаточной. Получаемые фактически гистограммы L/B очень редко, если вообще когда-либо, могут быть соотнесены с любой из представленных шаблонных гистограмм, и возникает неясность, каким же образом оценивать характерную форму объектов. Действительно, а) даже при работе с простыми распределениями, когда L0/B0 объектов строго фиксированы на некоторых единственных значениях (что едва ли встречается на практике), фактические гистограммы L/B могут сильно отличаться от шаблонных, например, по причине малого количества измерений, применения иного шага гистограммирования или анизотропной ориентации объектов относительно плоскостей сечения. При этом б) шаблонные гистограммы рассчитаны лишь для шести значений истинных осевых соотношений объектов. Другие значения L0/B0 при построении шаблонных гистограмм в работе не рассматриваются. В результате, далеко не все фактические распределения L/B хорошо согласуются с шаблонными, даже если остальные условия применения способа выполняются идеально, в) при появлении же факторов, усложняющих распределение L0/B0 (дисперсия, наличие размерных кластеров и пр.), точность известного способа снижается в еще большей степени, поскольку шаблонные гистограммы построены без учета этих влияний. Следующим недостатком известного способа является тот факт, что 6) способ не позволяет исследовать структурную организацию объектов во временной динамике, например, в реальном режиме времени. К тому же, 7) способ не предполагает возможности построения изображения (в частности, 3D-изображения) изучаемых объектов, что могло бы сделать получаемые данные об их характерной форме более наглядными.
Стереологический анализ используется и при изучении ориентации объектов. Интерес к данному аспекту структурной организации объектов обусловлен тем, что механические и другие важные свойства тел, сред, материалов и систем нередко определяются особенностями ориентации содержащихся в них объектов. В 3D-пространстве объекты могут иметь изотропную ориентацию. При этом любое направление ориентации объектов является случайным и независимым относительно направлений ориентации других объектов и одновременно случайным и независимым относительно системы пространственных координат. Объекты также могут быть ориентированы анизотропно, если условия о случайности и независимости направлений их ориентации не выполняются. Подробнее с некоторыми распределениями, используемыми при описании ориентации объектов, можно ознакомиться в специальной литературе (см., например, [Howard et al., 1998; Mardia, 1972]).
Известен стереологический способ определения анизотропии ориентации частиц в металлографии, осуществляемый посредством построения полярной диаграммы (розы направлений) числа пересечений поверхностей частиц с прямыми параллельными линиями, последовательно размещаемыми на срезе или другом образце материала с некоторым шагом поворота (см., например, [Чернявский, 1977, стр.175-183]). Существенными недостатками известного способа являются 1) применимость при анализе лишь одного из аспектов структурной организации объектов, а именно распределения ориентации объектов; 2) существующий способ применим при изучении частиц по профилям их сечения 1D-зондами (прямыми тест-линиями в виде набора). Остальные варианты стереологического зондирования известным способом не предусмотрены; 3) в описании способа отсутствуют указания на использование движущегося зонда, представленного, например, пучком электромагнитного излучения или летательным аппаратом при исследованиях атмосферы. Кроме того, 4) получаемые оценки анизотропии в прямом виде не могут быть использованы при построении структурных моделей материалов даже в том случае, если форма частиц достаточно проста и представима в виде известных геометрических фигур. В частности, известный способ не позволяет оценивать 3D-распределение углов ориентации исследуемых частиц. 5) Невозможным является при применении способа в описанном виде изучение структурной организации объектов во временной динамике. 6) К тому же, при осуществлении способа не достигается графическое представление исследуемых объектов.
Существует также способ оценки распределения ориентации волокон (в частности, волокон наполнителей композитных материалов) по координатам профилей их сечения на изображениях параллельных срезов, получаемых при КЛСМ [Mattfeldt et al., 1994]. При реализации данного способа определяют координаты (значения абсцисс х и ординат у) центральных точек профилей волокон на изображениях двух или более параллельных срезов, отстоящих друг от друга на известном расстоянии. По этим координатам рассчитывают полярный (α1) и плоскостной (α2) углы 3D-ориентации исследуемого волокна. Расчеты повторяют для различных волокон, представленных на срезах. Получаемые данные об ориентации волокон в образце выражают в виде функции совместного распределения углов α1 и α2. В результате достигается сравнительно точная оценка распределения ориентации волокон в исследуемом материале. Вместе с тем, известному способу присущи следующие недостатки. 1) Способ, по крайней мере в описанном виде, применим лишь при анализе волокон и других близких по форме объектов. 2) При этом используется единственный вариант стереологического зондирования - секционное 3D-зондирование в виде набора параллельных плоскостных срезов. 3) Результатом осуществления известного способа являются сведения о распределении 3D-ориентации волокон, тогда как другие аспекты структурной организации объектов (а) распределение расположения и б) размерное распределение) исследованию не подвергаются. К тому же способ, по крайней мере в описанном виде, не предусматривает возможности 4) изучать объекты во временной динамике и 5) с построением изображений (например, 3D-изображений) объектов.
Стереологический анализ находит также применение при изучении особенностей расположения объектов. Изучение паттерна пространственного расположения объектов относится к стереологии второго порядка (см., например, [Cruz-Orive, 1989; Howard et al., 1998; Jensen ЕВ et al., 1990]). Данный подход все более широко применяется в современных исследованиях, поскольку от расположения объектов в значительной мере зависит реализация важных свойств тел, сред, материалов и систем, содержащих исследуемые объекты. Рассмотрим подробнее некоторые из известных решений в области анализа расположения объектов, учитывая при этом, что получение такого рода информации об объектах является основным предназначением настоящего способа.
Известен способ исследования 3D-расположения нервных клеток в биологической ткани [Duyckaerts et al., 1994], сущность которого заключается в выполнении следующей совокупности действий. Из изучаемой ткани, например ткани головного мозга, изготавливают гистологические срезы известной толщины. На изображении любого из них находят значения координат х и y центральных точек профилей нейронов. С помощью специальной компьютерной программы изображение поверхности среза разделяют на k-угольники, стороны которых проводят под прямым углом через центры отрезков, соединяющих центральные точки ближайших друг к другу профилей нейронов. Тем самым на срезе осуществляют реализацию точечной решетки Дирихле, в которой каждая ячейка (k-угольник, обычно k=6) содержит по одному нейрону, а ее площадь с учетом толщины среза отражает объем свободного пространства вокруг нервной клетки. Далее определяют площади (Sя) полученных ячеек и рассчитывают коэффициент вариации  данного параметра на срезе. По величине
данного параметра на срезе. По величине 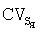 судят о паттерне 3D-расположения нейронов в изучаемой ткани. При этом учитывают результаты выполненных авторами статистических испытаний, которые свидетельствуют в целом о регулярности 3D-расположения нейронов при
судят о паттерне 3D-расположения нейронов в изучаемой ткани. При этом учитывают результаты выполненных авторами статистических испытаний, которые свидетельствуют в целом о регулярности 3D-расположения нейронов при  Величина
Величина  позволяет расценивать расположение нервных клеток как случайное, т.е. описываемое пуассоновским точечным процессом. При
позволяет расценивать расположение нервных клеток как случайное, т.е. описываемое пуассоновским точечным процессом. При  заключают о сгруппированности (наличии кластеров) нейронов в объеме исследуемой ткани. Таким образом становится возможным оценивать основные закономерности 3D-расположения изучаемых нейронов. К существенным недостаткам известного способа можно отнести следующее. 1) Способ, по крайней мере в описанном виде, предназначен к использованию лишь при анализе нейронов. 2) Способ основан на применении единственного варианта стереологического зондирования, а именно секционного 3D-зондирования с получением срезов ненулевой толщины. Перспективы использования других (в том числе движущихся) зондов авторами не рассматриваются, что ограничивает возможности известного способа. 3) Способ позволяет исследовать только особенности 3D-расположения изучаемых объектов, но не остальные аспекты их структурной организации. В частности, не проводится анализ а) размерного распределения, б) распределения формы и в) распределения ориентации нервных клеток. Кроме того, 4) получаемые с помощью известного способа данные о расположении нейронов не могут быть непосредственно интегрированы со сведениями о других аспектах их структурной организации. Следующим недостатком известного способа является 5) его ограниченная точность. Это, в частности, обусловлено тем, что а) в описанном виде способ предполагает выполнение анализа с учетом лишь приближенной связи между особенностями 3D-расположения нейронов и расположением их ПСЗ. Как отмечают сами авторы, "принадлежащее" нейрону 3D-пространство описывается k-угольниками на срезе достаточно условно. Величина возникающей при этом ошибки неизвестна и корректировке не поддается; б) точность способа ограничена еще и тем, что при нахождении пороговых значений
заключают о сгруппированности (наличии кластеров) нейронов в объеме исследуемой ткани. Таким образом становится возможным оценивать основные закономерности 3D-расположения изучаемых нейронов. К существенным недостаткам известного способа можно отнести следующее. 1) Способ, по крайней мере в описанном виде, предназначен к использованию лишь при анализе нейронов. 2) Способ основан на применении единственного варианта стереологического зондирования, а именно секционного 3D-зондирования с получением срезов ненулевой толщины. Перспективы использования других (в том числе движущихся) зондов авторами не рассматриваются, что ограничивает возможности известного способа. 3) Способ позволяет исследовать только особенности 3D-расположения изучаемых объектов, но не остальные аспекты их структурной организации. В частности, не проводится анализ а) размерного распределения, б) распределения формы и в) распределения ориентации нервных клеток. Кроме того, 4) получаемые с помощью известного способа данные о расположении нейронов не могут быть непосредственно интегрированы со сведениями о других аспектах их структурной организации. Следующим недостатком известного способа является 5) его ограниченная точность. Это, в частности, обусловлено тем, что а) в описанном виде способ предполагает выполнение анализа с учетом лишь приближенной связи между особенностями 3D-расположения нейронов и расположением их ПСЗ. Как отмечают сами авторы, "принадлежащее" нейрону 3D-пространство описывается k-угольниками на срезе достаточно условно. Величина возникающей при этом ошибки неизвестна и корректировке не поддается; б) точность способа ограничена еще и тем, что при нахождении пороговых значений 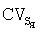 (33% и 64%) использовалось описание нервных клеток точками. Поскольку нейроны не являются 0D-объектами, применение известного способа сопровождается дополнительными погрешностями, связанными с невозможностью двух или нескольких клеток располагаться в одной точке пространства или слишком близко друг к другу. К тому же, в) авторами не приводится подтверждение правомерности выбора именно этих (33% и 64%), а, например, не близких к ним, пороговых значений
(33% и 64%) использовалось описание нервных клеток точками. Поскольку нейроны не являются 0D-объектами, применение известного способа сопровождается дополнительными погрешностями, связанными с невозможностью двух или нескольких клеток располагаться в одной точке пространства или слишком близко друг к другу. К тому же, в) авторами не приводится подтверждение правомерности выбора именно этих (33% и 64%), а, например, не близких к ним, пороговых значений 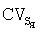 при анализе объектов реальной размерности. Можно предположить, что представление нейронов в виде точек приводило иногда при проведении статистических испытаний к появлению очень маленьких ячеек, соответствующих близко расположенным точкам, и поэтому к некоторому возрастанию
при анализе объектов реальной размерности. Можно предположить, что представление нейронов в виде точек приводило иногда при проведении статистических испытаний к появлению очень маленьких ячеек, соответствующих близко расположенным точкам, и поэтому к некоторому возрастанию 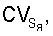 со смещением искомых пороговых значений
со смещением искомых пороговых значений  В результате влияния всех этих факторов точность известного способа не поддается существенному повышению при увеличении количества изучаемых ПСЗ или выполнении более точных измерений. Другим недостатком известного способа является тот факт, что 6) он не позволяет анализировать структурную организацию нейронов во временной динамике (клетки фиксируются при изготовлении гистологических срезов). И, наконец, 7) применение способа не сопровождается построением изображения (в частности, 3D-изображения) нейронов, что могло бы сделать процесс их исследования более наглядным.
В результате влияния всех этих факторов точность известного способа не поддается существенному повышению при увеличении количества изучаемых ПСЗ или выполнении более точных измерений. Другим недостатком известного способа является тот факт, что 6) он не позволяет анализировать структурную организацию нейронов во временной динамике (клетки фиксируются при изготовлении гистологических срезов). И, наконец, 7) применение способа не сопровождается построением изображения (в частности, 3D-изображения) нейронов, что могло бы сделать процесс их исследования более наглядным.
Наиболее близким к предлагаемому способу по технической сущности и достигаемому результату является способ исследования расположения микропор в металлических материалах [Tewari et al., 1998], при осуществлении которого изготавливают металлографический шлиф (или шлифы), ориентированный (ориентированные) вдоль продольной оси случайно отобранного образца изучаемого материала, определяют расстояния между центральными точками получаемых профилей сечения микропор и оценивают первую, вторую и третью функции распределения расстояния между центрами ближайших профилей микропор (функции NND, от англ. nearest neighbour distance distribution) (Первая функция NND характеризует здесь плотность распределения PDFm, для которой PDFm·dr равна вероятности того, что на плоскости шлифа в круге радиусом r, проведенном вокруг центра произвольно выбранного профиля микропоры, нет ни одного другого центра профиля микропоры и, вместе с тем, в круглом поясе, образованном на плоскости шлифа радиусами r и r+dr вокруг центра выбранного профиля, имеется по меньшей мере один центр профиля микропоры. Тем самым первая функция NND определяет вероятность того, что расстояние между центрами ближайших профилей микропор не больше величины r. Вторая функция NND характеризует плотность распределения PDFm*, для которой PDFm*·dr равна вероятности того, что на плоскости шлифа в круге радиусом г, проведенном вокруг центра произвольно выбранного профиля микропоры, имеется еще один центр профиля микропоры, а в круглом поясе, образованном радиусами r и r+dr вокруг выбранного центра, имеется по меньшей мере два центра профилей микропор. Соответственно, третья функция NND определяет PDFm**, для которой PDFm**·dr равна вероятности того, что в круге радиусом г, проведенном на плоскости вокруг центра произвольно выбранного профиля микропоры, имеется еще два центра профилей микропор, а в круглом поясе, образованном радиусами r и r+dr, имеется по меньшей мере три центра.) Расстояния между профилями сечения микропор находят с помощью специальной компьютерной программы по координатам х и у их центров на изображениях шлифа. Заключение об особенностях расположения микропор в исследуемом объеме делают по функциям NND, а также по соотношению Сф/м средних значений фактической и модельной NND. При этом модельная NND рассчитывается для микропор, имеющих случайное расположение и равные фактическим значения таких показателей как объемная плотность, численная плотность и размерное распределение. При Сф/м=1 микропоры в исследуемом объеме считают расположенными случайно. Если Сф/м<1, делают вывод о сгруппированности микропор в кластеры. Сф/м>1 свидетельствует о стремлении микропор "избегать" друг друга. Тем самым известный способ предполагает нахождение сначала функций NND, описывающих характерные расстояния между профилями ближайших микропор, а затем получение общего вывода о паттерне расположения микропор по Сф/м. Принимая во внимание эту двухэтапность анализа, рассмотрим основные недостатки известного способа. 1) В опубликованном виде способ предназначен к использованию лишь при анализе микропор в металлических материалах, но не при изучении других объектов. 2) Способ предполагает использование единственного варианта стереологического зондирования - 2D-зондирования сечением. Остальные варианты зондирования, включая связанные с применением движущихся зондов, авторами не рассматриваются, что ограничивает возможности практического применения известного способа. 3) Способ позволяет исследовать только особенности расположения объектов. Другие аспекты структурной организации последних остаются вне рассмотрения. В частности, не проводится анализ а) размерного распределения, б) распределения формы и в) распределения ориентации объектов. К тому же, 4) получаемые с помощью известного способа данные о расположении объектов не могут быть непосредственно интегрированы со сведениями о других аспектах их структурной организации. Следующим важным недостатком известного способа является 5) его недостаточная точность, проявляющаяся в получении оценок NND, характеризующих микропоры на плоскости шлифа, но не в 3D-пространстве. Так, например, расстояния между центрами ближайших микропор при измерении на плоскости шлифа будут иметь заниженные значения по сравнению с теми же данными, получаемыми при 3D-измерениях. Поэтому без 2D/3D-преобразования значения NND оказываются ниже действительных, что приводит к занижению и среднего арифметического NND, используемого при расчете Сф/м. Заметим, что необходимость в 2D/3D-преобразовании особенно велика при анализе вытянутых объектов (в частности, кровеносных микрососудов), когда результаты 2D- и 3D-замеров связаны менее однозначно. Кроме того, 6) анализ расположения объектов с помощью NND направлен на оценку характерных расстояний между объектами. Тем самым изучаются отношения типа "объект - объект", которые характеризуют особенности расположения объектов относительно друг друга. В то же время, зачастую остается невыясненным, как при полученной NND исследуемые объекты располагаются в объеме материала (т.е. каковы отношения типа "объект - среда"). Объекты могут находиться, например, в основном в центральной части образца материала, оставляя периферию почти свободной, что будет приводить к тем же значениям функции NND, как и при некоторых вариантах размещения объектов по всему объему образца. 7) Способ имеет также недостаток, связанный с применением соотношения Сф/м. Так, использование средних арифметических NND при расчете Сф/м может быть не вполне адекватным с позиций удовлетворительного по точности описания функции распределения NND. Данный недостаток приобретает большее значение при отклонениях фактического распределения расстояния между ближайшими микропорами от гауссовского (нормального) закона распределения, которые, кстати, имели место в выполненном авторами исследовании. Далее, 8) способ не позволяет исследовать структурную организацию объектов во временной динамике, например в реальном режиме времени. И, наконец, 9) применение известного способа не предполагает построения изображений микропор, а это могло бы повысить эффективность исследования особенностей расположения объектов и демонстративность получаемых результатов.
Значения некоторых терминов, применяемых далее в описании изобретения
Определим значения отдельных терминов, используемых в последующем описании изобретения. Под объектом будет пониматься объект любой природы, располагающийся в некотором теле, некоторой среде, некотором материале или некоторой системе. Подвергаемая исследованию часть тела, среды, материала или системы будет называться образцом. В ряде ситуаций исследованию подвергается все тело, среда, материал или система. Для унификации терминологии все тело, среду, материал или систему мы также будем в этом случае называть образцом. Под носителем будет пониматься та часть образца, которая выделяется из последнего (иногда виртуально) в процессе стереологического зондирования и в дальнейшем непосредственно подвергается анализу. К примеру, при изучении объектов с использованием трансмиссионной ЭМ блок исследуемой биологической ткани является образцом, а изготавливаемые из него ультратонкие срезы - носителями. Носители в данном случае возникают при применении стереологического зонда (а именно, при сечении образца ткани ножом ультрамикротома) и содержат ПСЗ объектов. Можно также сказать, что носители содержат изображения объектов, по которым могут быть измерены параметры ПСЗ объектов (такие, например, как координаты расположения, размеры, ориентация и количество ПСЗ объектов). Носители не являются обязательным атрибутом стереологического зондирования. Существуют зонды (в частности, представленные электромагнитным излучением), при применении которых выделение носителя из образца не происходит.
Совокупность объектов в исследуемом образце с учетом динамики их существования будет называться, как это принято в специальной литературе, процессом объектов. Как правило, процесс объектов является случайным, или вероятностным, поскольку его характеристики подвержены случайным отклонениям. Если объекты могут быть описаны точками (0D-объектами), то процесс объектов является точечным процессом, а случайный процесс объектов - случайным точечным процессом. Аналогично, существуют процессы 1D-объектов (линий), 2D-объектов (поверхностей) или 3D-объектов (объемных образований), которые обычно также оказываются случайными. Случайный процесс объектов стационарен, если его характеристики не зависят от перемещения системы координат. Расположение объектов тогда является случайным и независимым относительно друг друга (отношения типа "объект - объект"), а также относительно содержащего их пространства (отношения типа "объект - среда"). Случайный процесс объектов изотропен, если его характеристики не зависят от вращения системы координат. При этом объекты ориентированы случайно и независимо относительно друг друга (отношения "объект - объект"), а также относительно содержащего их пространства (отношения "объект - среда"). Стационарный изотропный случайный процесс объектов обладает свойством полной пространственной случайности (CSR - от англ. complete spatial randomness).
Термин "размерное распределение объектов" используется в данном описании как собирательный по отношению к терминам "распределение размера объектов" и "распределение размеров объектов". Термины "3D-расположение объектов" и "расположение объектов в объеме образца" являются синонимами и применяются нами для обозначения одного и того же аспекта структурной организации объектов. Вместе с тем, настоящий способ позволяет исследовать не только 3D, но и другие варианты расположения объектов, например, 2D- или 1D-расположение объектов. С этой точки зрения термин "пространственное расположение объектов" является более полным, так как подразумевает различные размерности пространства (в частности, 3D, 2D или 1D), в которых могут располагаться исследуемые объекты. Данный термин будет использоваться далее как основной. Следует также учитывать, что расположение объектов обычно характеризуется через расположение объектов относительно используемых стереологических зондов.
Стереологическим зондом далее будет называться единичный зонд (единичная плоскость, единичная прямая и т.д.). Поскольку в стереологии обычно используется совокупность зондов (например, набор плоскостей сечения), в описании изобретения употребляется также термин "зондирование" как собирательный по отношению ко всем ситуациям применения стереологического зонда или зондов. К таким ситуациям можно отнести, в частности, следующее: 1) однократное использование единичного зонда, 2) многократное использование единичного зонда, 3) однократное применение зонда, представляющего собой комбинацию единичных стереологических зондов и 4) многократное применение зонда, представляющего собой комбинацию единичных стереологических зондов.
Сущность изобретения
Проблематика изобретения. При исследовании тел, сред, материалов и систем имеется необходимость в оценке расположения содержащихся в них объектов. Известные решения в этой области не всегда надежны и не позволяют получать всю информацию о размещении объектов в изучаемом пространстве. Не нацелены они и на выяснение особенностей расположения объектов в определенной системе координат, без чего структурная организация объектов не может быть квантифицирована с требуемой полнотой. Существующие способы не предусматривают также возможности изучать расположение объектов в сочетании с другими аспектами их структурной организации (размерами, формой, ориентацией объектов), в том числе с учетом изменений параметров объектов во времени. Кроме того, известные способы не предполагают построения изображений, характеризующих объекты. Решение комплекса указанных проблем составляет сущность настоящего изобретения.
Сущность изобретения в кратком изложении (раскрытие изобретения). Сущность настоящего изобретения состоит в выполнении следующей совокупности действий. Объекты подвергают n-мерному стереологическому зондированию (n равно 0, 1, 2, 3 или их комбинации). Координаты расположения получаемых ПСЗ объектов измеряют. При необходимости производятся также замеры значений размера (размеров) ПСЗ, характеристики (характеристик) ориентации ПСЗ и/или количества ПСЗ объектов. Результаты замеров координат расположения и других параметров ПСЗ преобразуют в статистическое распределение (распределения) параметра (параметров) ПСЗ объектов. Получаемое распределение (распределения) аппроксимируют модельным распределением, рассчитанным при любом из следующих задаваемых условий или при любой комбинации из следующих задаваемых условий: при задаваемом 1) распределении расположения объектов в пространстве, 2) распределении расположения объектов относительно применяемых стереологических зондов, 3) распределении размера (или размеров) объектов, 4) распределении формы объектов, 5) распределении ориентации объектов, 6) распределении углов, задающих ориентацию объектов относительно стереологических зондов, 7) распределении параметров применяемых зондов, 8) распределении свойств волнового потока, используемого при проекционном стереологическом зондировании. Результатом выполнения процедуры аппроксимации является нахождение условий, позволяющих с необходимой точностью аппроксимировать фактическое распределение параметра (параметров) ПСЗ модельным распределением параметра (параметров) ПСЗ объектов. Найденные условия аппроксимации представляют собой искомую оценку соответствующего аспекта структурной организации объектов. Например, условия о распределении пространственного расположения объектов являются искомой оценкой распределения пространственного расположения объектов, найденные условия о размерном распределении объектов - оценкой размерного распределения объектов и т.д. При повторяющихся исследованиях объектов их структурная организация может быть изучена во временной динамике, например в реальном режиме времени. На основе найденных условий, характеризующих исследуемые аспекты структурной организации объектов, выстраивают изображения объектов. Способ может быть реализован - как полностью, так и частично - с применением ЭВМ (электронно-вычислительной машины), называемой также компьютером.
Цели изобретения. Изобретательский замысел, составляющий основу предлагаемого способа, направлен на достижение следующих основных целей.
Первая из них заключается в получении более полных и надежных, чем ранее, сведений об организации объектов в исследуемом теле, среде, материале или системе. Этот технический результат проявляется в том, что при осуществлении изобретения а) становится возможным оценивать функцию распределения значений координатных характеристик объектов в пространстве и не только делать по ней заключение о случайности или неслучайности расположения объектов, но и определять возможные варианты выявленных отклонений от условий CSR; б) по получаемым данным можно судить о взаимном расположении объектов (отношения типа "объект - объект"), а также о виде функции NND или других функций стереологии второго порядка. Вместе с тем, предлагаемый способ позволяет оценивать закономерности расположения объектов в исследуемом объеме (отношения типа "объект - среда"), в том числе в представлении в необходимой системе 3D-координат, что принципиально невозможно при использовании аналогичных решений; в) расположение объектов может изучаться в комплексе с другими аспектами их структурной организации - размерным распределением, распределением формы и распределением ориентации объектов. При этом изучаемыми размерами могут быть любые измеряемые размерные характеристики объектов. Анализ может быть проведен без введения предположений о форме объектов. При необходимости может быть подобран способ задания формы, с максимальной полнотой и удобством для целей выполняемого исследования отражающий особенности формы изучаемых объектов. В выборе характеристик ориентации объектов также отсутствуют какие-либо ограничения; г) определяемые параметры структурной организации объектов могут быть представлены в виде, легко интегрируемом с данными о других аспектах организации объектов, - в виде функции распределения соответствующей величины. Такое представление позволяет, кроме того, предельно полно квантифицировать изучаемые особенности структурной организации объектов. Вместе с тем, параметры объектов при необходимости могут быть выражены и другими методами, например, в виде конкретных числовых значений или моментов соответствующей функции распределения; д) полнота и надежность получаемых сведений достигается также за счет учета имеющейся в наличии дополнительной информации о структурной организации объектов; е) при реализации способа существует выбор вариантов стереологического зондирования, что позволяет подобрать такой из них, который способен обеспечить получение наиболее полной и надежной информации об исследуемых объектах; ж) при многократных исследованиях объектов их структурная организация может быть изучена во временной динамике, например в реальном режиме времени, что дополнительно повышает полноту получаемых сведений.
С первой целью изобретения связана вторая цель, которая состоит в универсализации процедуры исследования аспектов структурной организации объектов. Это выражается, в частности, в том, что изучаемыми объектами могут быть объекты а) различной природы, б) любой, в том числе неправильной, формы, произвольным образом в) расположенные и г) ориентированные в исследуемых телах, средах, материалах или системах. При этом д) объекты могут быть изучены как одномоментно, так и во временной динамике. При анализе используются ПСЗ, получаемые при взаимодействии объектов со стереологическими зондами любого е) типа (зонды сечения, проекционные зонды, их комбинации), ж) любой размерности (0D, 1D, 2D, 3D, их комбинации) и з) кривизны. Могут использоваться и) любые другие комбинированные зонды, а также к) движущиеся стереологические зонды. При проекционном зондировании может применяться л) любой волновой поток, например электромагнитное излучение, м) анализ может быть выполнен с применением современных средств визуализации (КЛСМ, КТ, МРТ, ПЭТ, SPECT, УТ и др.) или традиционными методами исследования (например, с помощью СМ). В дополнение, н) способ не предъявляет каких-либо требований к величине и размерному распределению исследуемых объектов. Могут исследоваться объекты молекулярной и субмолекулярной величины (размеры которых не превышают нескольких десятков нанометров), микрообъекты (размером до 400-500 микрометров), мезообъекты (до нескольких миллиметров), макрообъекты (до нескольких километров) и объекты более крупного размера. Частными примерами исследуемых объектов являются структуры организма человека или животных (кровеносные или лимфатические сосуды, нервные проводники, трабекулы костной ткани и др.).
Третья основная цель выражается в достижении необходимой точности анализа. При реализации способа сохраняется или даже повышается в сравнении с аналогами точность определения различных аспектов структурной организации объектов, что обеспечивается посредством а) возможности проведения исследования без принятия каких-либо заведомо невыполнимых предположений о структурной организации объектов, б) использования любых, в том числе усложненных, моделей формы объектов со сколь угодно сложным заданием функции распределения формы объектов, в) задания при необходимости любого другого параметра объектов в виде сколь угодно сложной функции распределения, г) наличия широкого выбора вариантов стереологического зондирования, позволяющего в каждом конкретном случае применять зонд, наиболее удобный в работе и обеспечивающий необходимую точность анализа, д) применения связи параметров ПСЗ объектов с истинными параметрами объектов (например, 2D/3D-связи при определении параметров структурной организации 3D-объектов по параметрам их 2D-ПСЗ), е) возможности использования специальной процедуры аппроксимации, способной сглаживать некоторые случайные ошибки измерения и контролировать систематические погрешности. Следует также отметить, что при реализации способа ж) можно соотносить достигаемый уровень точности с трудоемкостью проводимого анализа (например, с количеством измеряемых ПСЗ).
Четвертой целью является формирование удобного в работе графического представления объектов, например, в виде их 3D- или 2D-изображений. При осуществлении способа изображения выстраивают по получаемым данным о структурной организации объектов. При этом может учитываться временная динамика параметров исследуемых объектов. Тем самым достигается доступная по стоимости и сравнительно точная визуализация объектов, позволяющая схематично демонстрировать основные аспекты их структурной организации.
Осуществление изобретения. Способ осуществляют выполнением совокупности действий, состоящей из стереологического зондирования исследуемых объектов, измерения параметра (параметров) получаемых ПСЗ, преобразования результатов измерений в статистическое распределение или распределения параметра (параметров) ПСЗ объектов, аппроксимации данного распределения или распределений. При необходимости по параметрам объектов, задаваемым при аппроксимации, строят изображения исследуемых объектов. Рассмотрим перечисленные действия подробнее.
Стереологическое зондирование объектов. Образец тела, среды, материала или системы, содержащий исследуемые объекты, подготавливают к анализу общепринятым образом. Объекты подвергают n-мерному (n равно 0, 1, 2, 3 или их комбинации) стереологическому зондированию и получают ПСЗ. Основные виды используемого стереологического зондирования и особенности возникающих при этом ПСЗ объектов приведены в табл.1. Тем самым объекты изучают с применением любого из следующих стереологических зондов: 1) нульмерного (0D) зонда сечения, 2) одномерного (1D) зонда сечения с задаваемой, в частном случае нулевой, кривизной, 3) двухмерного (2D) зонда сечения с задаваемой, в частном случае нулевой, кривизной, 4) трехмерного (3D) зонда сечения с задаваемой, в частном случае нулевой, кривизной, 5) 0D-зонда проекции, 6) 1D-зонда проекции с задаваемой, в частном случае нулевой, кривизной, 7) 2D-зонда проекции с задаваемой, в частном случае нулевой, кривизной, 8) 3D- зонда проекции с задаваемой, в частном случае нулевой, кривизной, 9) любого другого стереологического зонда, 10) зонда, представляющего собой любую комбинацию из перечисленного.
В частности, при исследовании биологической ткани с применением трансмиссионной ЭМ стереологическое зондирование осуществляют посредством ультрамикротомирования залитых в смолу блоков ткани, содержащей изучаемые объекты. ПСЗ объектов представлены в данном случае на ультратонких срезах, которые рассматривают под электронным микроскопом (как правило, после специальной обработки - контрастирования). С учетом характерных размеров объектов ультратонкие срезы расценивают обычно как плоскостные, т.е. являющиеся результатом применения 2D-зонда сечения с нулевой кривизной. При использовании СМ (в частности, при СМ толстого гистологического среза) ПСЗ могут быть результатом и оптического сечения объектов (см., например, [Gundersen, 1986; Petroll et al., 1993]). ПСЗ возникают тогда в плоскости фокусировки светового или конфокального лазерного микроскопа и также имеют в необходимой степени малую толщину. Метод оптического сечения удобен тем, что плоскость фокусировки можно перемещать по толщине рассматриваемого среза. В результате плоскость сечения объектов быстро принимает нужное исследователю положение, что позволяет ускорить выполнение анализа.
В зависимости от характера изучаемых объектов и специфики выполняемого исследования ПСЗ объектов могут быть представлены и на любых других носителях. Такими носителями могут являться: 1) гистологические срезы, 2) другие срезы (в частности, срезы небиологического материала, содержащего исследуемые объекты), 3) шлифы образца минеральной породы, 4) другие шлифы, 5) металлографические реплики при изучении образца металлического материала, 6) другие реплики, 7) фольги, 8) порошковые пробы исследуемого материала, 9) другие обработанные поверхности образца изучаемого тела, среды, материала или системы, 10) томограммы, 11) сканограммы. При необходимости носители перед просмотром подвергают общепринятой обработке (к примеру, гистологические срезы - окрашиванию, просветлению и/или контрастированию).
Можно также сказать, что носители содержат изображения объектов, по которым определяют параметр или параметры ПСЗ. При этом изображения объектов могут быть получены с применением любого из перечисленного: 1) CM, 2) ЭМ, 3) КЛСМ, 4) КГ, 5) МРТ, 6) ПЭТ, 7) SPECT, 8) УМ, 9) УТ, 10) другого УЗ метода исследования, 11) другого метода получения и анализа изображений объектов. Например, при изучении гистологического среза (носитель) по изображениям объектов в поле зрения светового микроскопа могут быть оценены такие параметры 2D-профилей сечения, как координаты х и у их плоскостного расположения. При необходимости изображения объектов увеличивают в размерах. С целью проведения дальнейшего анализа получаемые с носителей изображения объектов могут быть запечатлены, в частности, в виде любого из следующего: в виде 1) фотографии, 2) цифрового снимка, 3) томограммы, 4) сканограммы, 5) видеоизображения. Аналогичным образом могут быть запечатлены изображения ПСЗ объектов.
При стереологическом зондировании расположение и направление зондов по отношению к объектам обычно выбирают случайно. Тогда ПСЗ объектов представлены на IUR (от англ. isotropic uniform random - изотропный равномерно случайный) срезах или проекциях (подробнее см. в [Howard et al., 1998] и других источниках литературы). Использоваться могут и иные дизайны стереологического зондирования. В частности, ПСЗ объектов могут быть получены на вертикальных срезах (VUR - от англ. vertical uniform random) [Baddeley et al., 1986; Howard et al., 1998], параллельных срезах, ортогональном триплете (трех взаимно перпендикулярных срезах)[Mattfeldt et al., 1985], при сечении объектов дисекторами (параллельными срезами с известным расстоянием между ними) [Sterio, 1984], сферическим зондом [Mouton et al., 2002], искривленными дисекторами, а также в результате взаимодействия объектов с комбинированными стереологическими зондами. Важно учитывать, что в стереологии расположение объектов (по крайней мере обычно) задается как расположение объектов относительно зондов. Аналогично и ориентацию объектов описывают как ориентацию объектов относительно зондов. Поэтому следует выбирать такой дизайн стереологического зондирования, который не будет "затушевывать" особенности структурной организации исследуемых объектов. Во многих случаях целесообразно использовать, например, один протяженный IUR срез через исследуемый образец. Иногда ориентация такого среза может принимать и перпендикулярное направление по отношению к направлению преимущественной ориентации объектов.
Если структурная организация объектов изучается во временной динамике, то взаимодействие объектов со стереологическим зондом (зондами) выполняют многократно для получения данных о ПСЗ объектов в различные необходимые моменты времени. Возможен также непрерывный мониторинг ПСЗ. При реализации настоящего изобретения зондирование может осуществляться и с применением движущегося стереологического зонда, проникающего через тело, среду, материал или систему. В таком случае имеет значение динамика возникновения ПСЗ исследуемых объектов, что отличает данный вариант зондирования от использования, например, поверхности сечения, которая также обычно перемещается при изготовлении среза, но параметры ПСЗ определяются без учета динамики этого процесса, т.е. в стационарных условиях. Примером движущегося зонда может являться пучок электромагнитного излучения при анализе объектов различной природы или же летательный аппарат при исследованиях атмосферы (подробнее см. в [Вульфсон, 1989] и других источниках литературы).
Следует заметить, что при стереологическом зондировании бывает целесообразным применение компьютера, к примеру, для генерации случайного направления ориентации и случайного расположения зондов. В данном качестве могут использоваться и компьютеры, встроенные в технические средства для визуализации объектов, в частности в аппараты для КЛСМ, КТ, МРТ, ПЭТ, SPECT, УМ и УТ. При динамических исследованиях в реальном режиме времени скорость выполнения стереологического зондирования особенно важна. Тогда применение компьютера при анализе может оказаться неизбежным.
Измерение параметра (параметров) ПСЗ объектов. Из получаемого при зондировании набора ПСЗ составляют выборку для замеров (в нее могут войти все полученные ПСЗ или их часть). Особенности формирования репрезентативной выборки в стереологии описаны в литературе (см., например, [Автандилов, 1990; Чернявский, 1977; Howard et al., 1998; Weibel, 1979-1980]). С учетом параметров объектов, которые требуется определить при анализе структурной организации объектов (об этих параметрах речь пойдет ниже), выделяют параметры ПСЗ объектов, по которым будет проводиться исследование. При этом измеряемыми параметрами ПСЗ являются 1) координаты расположения ПСЗ, а также при необходимости любое из следующего: 2) размер (или размеры) ПСЗ, 3) характеристика (или характеристики) ориентации ПСЗ и 4) количество ПСЗ. Рассмотрим перечисленные параметры ПСЗ объектов подробнее.
Определяемыми координатами расположения ПСЗ объектов могут быть любые из следующих координат либо любые комбинации следующих координат: 1) координаты 0D ПСЗ, 2) координаты центральной точки (например, геометрического центра тяжести) ПСЗ, 3) координаты начальной точки ПСЗ, 4) координаты конечной точки ПСЗ, 5) координаты точки максимальной кривизны ПСЗ, 6) координаты точки минимальной кривизны ПСЗ, 7) координаты точки средней кривизны ПСЗ, 8) координаты любой другой точки, связанной с кривизной ПСЗ, 9) координаты точки пересечения двух или нескольких диаметров ПСЗ, 10) координаты точки, связанной с любой из перечисленных, 11) любые другие координаты, характеризующие расположение ПСЗ. Заметим, что при определении координат расположения ПСЗ объектов могут использоваться любые системы координат (линейные, нелинейные, полярные, прямоугольные, косоугольные, плоскостные, полярные, эллиптические, цилиндрические, сферические, криволинейные координаты на поверхности и пр.). В наиболее употребимой аффинной, или общей декартовой, системе (т.е. в системе прямоугольных пространственных или плоскостных координат) координаты расположения ПСЗ объектов могут быть представлены наборами из трех координат - х, у, z; двух координат - х, у или же одной координатой, например, х. Здесь х - абсцисса выбранной точки, характеризующей расположение ПСЗ, у - ее ордината, а z - апликата.
Измеряемым размером (размерами) ПСЗ объектов может быть любой из следующих размеров ПСЗ либо любая комбинация следующих размеров ПСЗ: 1) радиус, 2) малый радиус (В), 3) большой радиус (L), 4) диаметр, 5) малый диаметр (2·В), 6) большой диаметр (2·L) (В литературе под диаметром в общем виде понимается расстояние между наиболее удаленными друг от друга точками поверхности изучаемого тела. Если плоскостной ПСЗ имеет эллиптическую форму, то на нем без труда определяются большой и малый диаметры. При этом большой диаметр эллипса - это расстояние между наиболее удаленными друг от друга точками его контура. Малым диаметром эллипса является расстояние между наименее удаленными точками его контура при измерении через центральную точку эллипса. Для тел другой (в том числе неправильной) формы большой диаметр определяется как расстояние между наиболее удаленными точками поверхности тела при измерении через окрестность центра тяжести. Аналогичным образом может быть задан и малый диаметр как расстояние между наименее удаленными точками поверхности тела при измерении через окрестность его центра тяжести.), 7) осевое соотношение (любое соотношение малого и большого радиусов либо малого и большого диаметров) (L/B или B/L), 8) площадь (S), 9) периметр (Р), 10) длина (Н), 11) показатель (показатели) эксцентриситета (в частности, отношение межфокусного расстояния эллипса к величине его большого диаметра), 12) показатель (показатели) кривизны (в частности, максимальная, минимальная и/или средняя кривизна контура ПСЗ), 13) объем ПСЗ (V), 14) любой размер (размеры), связанный (связанные) с любым из перечисленных, 15) любое соотношение перечисленных размеров, 16) любой другой размер. При исследовании полых объектов, например кровеносных микрососудов, исследоваться могут перечисленные размеры внешней поверхности, а также размеры просвета объектов.
Измеряемой характеристикой ориентации (характеристиками ориентации) ПСЗ объектов может быть любой из следующих показателей либо любая комбинация следующих показателей: 1) угол (углы), характеризующий (характеризующие) направление ПСЗ (например, 1D ПСЗ), 2) угол (углы), характеризующий (характеризующие) направление диаметра ПСЗ, 2) угол (углы), характеризующий (характеризующие) направление большого диаметра ПСЗ, 4) угол (углы), характеризующий (характеризующие) направление малого диаметра ПСЗ, 5) угол (углы), характеризующий (характеризующие) направление касательной, проведенной в точке максимальной кривизны ПСЗ, 6) угол (углы), характеризующий (характеризующие) направление касательной, проведенной в точке минимальной кривизны ПСЗ, 7) угол (углы), характеризующий (характеризующие) направление касательной, проведенной в точке средней кривизны ПСЗ, 8) угол (углы), характеризующий (характеризующие) направление касательной, проведенной в другой точке, расположение которой связано с особенностями кривизны ПСЗ, 9) угол (углы), характеризующий (характеризующие) направление плоской стороны ПСЗ, 10) угол (углы), характеризующий (характеризующие) направление плоской поверхности ПСЗ, 11) угол (углы), характеризующий (характеризующие) направление секущей линии максимальной длины, проводимой через тест-точку, попавшую на ПСЗ, 12) угол (углы), характеризующий (характеризующие) направление хорды максимальной длины, проводимой через тест-точку, попавшую на ПСЗ, 13) распределение значений длины секущей линии, проводимой под разными углами через тест-точку, попавшую на ПСЗ, 14) распределение значений длины хорды, проводимой под разными углами через тест-точку, попавшую на ПСЗ, 15) величина (величины), связанная (связанные) с любым из перечисленных показателей, 16) любая другая характеристика ориентации ПСЗ.
Количество как параметр ПСЗ объектов не требует дальнейшей детализации, поскольку не вызывает затруднений при определении. Заметим лишь, что сведения о количестве ПСЗ имеют существенное значение при использовании 0D зондов. Замеры количества ПСЗ производятся тогда для оценки размеров (обычно S) ПСЗ объектов. Вместе с тем, замеры количества ПСЗ могут быть необходимы и в других случаях. Подробнее о количестве ПСЗ объектов см., например, в [Автандилов, 1990; Чернявский, 1977; Howard et al., 1998; Weibel, 1979-1980].
При определении перечня параметров объектов, на оценку которых направлено проводимое исследование, учитывают следующее. Характеристиками пространственного расположения объектов, анализируемыми по параметрам ПСЗ, могут быть любые из перечисленных ниже координат объектов либо любые комбинации перечисленных координат: 1) координаты расположения центральных точек (например, геометрических центров тяжести) объектов, 2) координаты начальных точек объектов, 3) координаты конечных точек объектов, 4) координаты точек кривизны (например, максимальной, минимальной и/или средней кривизны) объектов, 5) координаты точек пересечения двух или нескольких диаметров объектов, 6) координаты точек объектов, связанных с любыми из перечисленных, 7) любые другие характеристики расположения объектов. Координаты объектов (точнее координаты выбранных точек объектов) будут далее обозначаться xo, уо, zо. Здесь xо - абсцисса выбранной точки, характеризующей пространственное расположение объекта (например, геометрического центров тяжести), уо - ее ордината, а zo - апликата. Как правило, характеристики расположения объектов, распределение которых оценивается в исследовании, совпадают по типу с измеряемыми характеристиками расположения ПСЗ объектов. Например, в исследовании могут производиться замеры координат расположения центральных точек ПСЗ для оценки распределения расположения центральных точек объектов в 3D-пространстве. Однако возможны и другие варианты. В частности, по распределению координат центральных точек ПСЗ может измеряться распределение координат расположения точек максимальной кривизны контура объектов.
Размером (размерами) объектов, распределение которого (которых) определяется в исследовании, может являться любой размер (любые размеры) из перечисленного: 1) радиус поперечного сечения, 2) малый радиус поперечного сечения (В0), 3) большой радиус поперечного сечения (L0), 4) диаметр поперечного сечения, 5) малый диаметр поперечного сечения (2·В0), 6) большой диаметр поперечного сечения (2·L0), 7) осевое соотношение (любое соотношение малого и большого радиусов либо малого и большого диаметров) поперечного сечения (L0/В0 или B0/L0), 8) площадь поперечного сечения (S0), 9) периметр поперечного сечения (Р0), 10) длина объекта (Н0), 11) показатель (показатели) эксцентриситета поперечного сечения, 12) показатель (показатели) кривизны контура поперечного сечения (в частности, максимальная, минимальная и/или средняя кривизна контура), 13) объем объекта (V0), 14) любой размер (размеры), связанный (связанные) с любым из перечисленных, 15) любое соотношение перечисленных размеров, 16) любой другой размер объектов, 17) любая комбинация перечисленных размеров. Как и при анализе расположения объектов, оцениваемый размер объектов обычно совпадает с типом измеряемого размера ПСЗ объектов. Например, в исследовании могут производиться замеры площади ПСЗ (5) для определения размерного распределения объектов по площади поперечного сечения (S0). Однако возможны и любые другие варианты восстановления 3D-размерных распределений. В частности, по распределению S может измеряться размерное распределение объектов по их длине (Н0). Часть вариантов анализа размерных распределений объектов, предназначенного к осуществлению в рамках настоящего изобретения, основывается на формулах, ссылки на которые приведены в табл.2. Дополнительные формулы могут быть выведены самостоятельно с использованием традиционного для стереологии математического аппарата. Необходимо также учитывать, что данное изобретение позволяет оценивать распределение формы объектов. При этом характеристики формы обычно задаются через размеры объектов. Подробнее о способах описания формы объектов см. ниже.
Исследуемой характеристикой ориентации (характеристиками ориентации) объектов может быть любой из следующих показателей либо любая комбинация следующих показателей: 1) угол направления продольной оси вытянутого объекта, 2) угол направления диаметра (например, малого и/или большого диаметра), 3) угол направления касательной, проведенной в точке кривизны (например, максимальной, минимальной и/или средней кривизны) поверхности объекта, 4) угол направления плоской стороны объекта, 5) угол направления плоской поверхности объекта, 6) величина (величины), связанная (связанные) с любыми из перечисленных показателей, 7) величина (величины), производная (производные) от любого из перечисленных показателей, 8) любые другие характеристики ориентации. Подобно тому, как было указано выше, характеристика ориентации объектов, распределение которого определяется в исследовании, обычно совпадает с измеряемой характеристикой ориентации ПСЗ объектов. Часть вариантов анализа распределений ориентации объектов основывается на формулах, ссылки на которые имеются в табл.3. Дополнительные формулы могут быть выведены самостоятельно с использованием традиционного для стереологии математического аппарата.
После того как сформированы перечень исследуемых параметров объектов и перечень параметров ПСЗ, по которым будет проводиться анализ (каждый из этих перечней может состоять из одного параметра), вошедшие в выборку ПСЗ подвергают замерам и измеряют выбранный параметр (параметры) ПСЗ объектов. Измерения выполняют любыми, в том числе общеизвестными методами (см., в частности, [Автандилов, 1990; Клюев и др., 1996; Чернявский, 1977; Howard et al., 1998; Lindquist et al., 2001; Weibel, 1979-1980]), которые включают измерения вручную или с использованием компьютера (в интерактивном, полуавтоматизированном, автоматизированном режиме). В качестве применяемого при замерах компьютера может выступать компьютер, входящий в состав современных аппаратов для СМ, ЭМ, КЛСМ, КТ, МРТ, ПЭТ, SPECT, УМ, УТ и других методов исследования. При необходимости предварительно проводят полуавтоматизированную и/или автоматизированную сегментацию изображений ПСЗ, по которым осуществляют измерения. При динамических исследованиях замеры ПСЗ выполняют в соответствующие моменты времени или непрерывно для получения временных рядов параметра (параметров) ПСЗ объектов.
В частности, координаты расположения ПСЗ объектов могут быть измерены следующим образом: 1) линейкой по фотографии (координаты х и у на плоскости), 2) по шкале предметного столика микроскопа, позволяющей отслеживать перемещение исследуемого носителя или образца (координаты х, у), 3) посредством перемещения плоскости фокусировки микроскопа по толщине исследуемого носителя или образца (координаты х, у, z) (для СМ или КЛСМ см., например, в [Howard et al., 1998]), 4) по количественным данным томографии, 5) с помощью специального анализатора изображений, 6) другими методами. При выполнении замеров следует обращать внимание на взаимное позиционирование полей зрения, в результате чего может быть получена достаточно полная информация об особенностях расположения ПСЗ объектов в определенной системе координат. При измерении координат расположения ПСЗ бывают полезными некоторые описанные в литературе решения: в частности, состыковка различных полей зрения в единую систему 3D-координат [Tewari et al., 1998], использование данных о толщине срезов для определения значений координаты z ПСЗ объектов [Mattfeldt et al., 1994], шкалирование изучаемого образца с использованием компьютерной микротомографии (микро-КТ), КЛСМ или других средств анализа для определения 3D-расположения ПСЗ (см., например, [Eberhardt et al., 2002]), коррекция краевой ошибки [Reed et al., 1997; Stoyan, 1985].
Как было отмечено выше, определение координат расположения ПСЗ объектов может быть дополнено проведением замеров значений выбранного размера (размеров), характеристики (характеристик) ориентации и/или количества получаемых ПСЗ объектов. Измерение размеров, характеристик ориентации и количества ПСЗ также осуществляют общепринятыми методами, например, с помощью любого из следующего: 1) при измерении размеров ПСЗ - а) с помощью линейки, б) по шкале микроскопа, позволяющей отслеживать перемещение исследуемого образца или носителя, в) посредством перемещения плоскости фокусировки микроскопа по толщине исследуемого образца или носителя, г) по количественным данным томографии, д) с применением анализатора изображений; 2) при измерении ориентации ПСЗ - а) с помощью транспортира или угломера, б) по количественным данным томографии, в) с применением анализатора изображений (например, по интенсивности окрашивания фрагментов ПСЗ [Lindquist et al., 2001]); 3) при измерении количества ПСЗ - а) визуальным подсчетом, б) по количественным данным томографии, в) с применением анализатора изображений.
При использовании движущегося стереологического зонда геометрические свойства объектов изучают с учетом времени, необходимого для перемещения зонда через объекты. Данное время является одним из событий, возникающих в этом случае при стереологическом зондировании, и по нему оценивают параметры ПСЗ. В частности, расположение ПСЗ в выбранной системе координат определяют по времени прохождения стереологического зонда, движущегося в известном скоростном режиме, через одну из точек объекта (например, его геометрический центр тяжести). При этом движущиеся зонды расценивают обычно как 1D-зонды сечения. Размер (размеры) ПСЗ объекта измеряют по времени, необходимому для прохождения движущегося стереологического зонда через объект. Ориентацию получаемого ПСЗ оценивают по ориентации направления движения зонда в выбранной системе координат. Количество ПСЗ объектов определяют посредством простого контроля. Замеры параметров ПСЗ иногда могут быть проведены одновременно со стереологическим зондированием объектов.
Преобразование результатов измерений в распределение или распределения параметра (параметров) ПСЗ объектов. Из полученных при замерах значений параметра или параметров ПСЗ при необходимости формируют массив данных об исследуемых объектах. Этот массив может быть сформирован с помощью компьютера, в том числе компьютера, входящего в состав аппаратов для СМ, ЭМ, КЛСМ, КТ, МРТ, ПЭТ, SPECT, УМ, УТ и других современных методов исследования. При формировании массива данных компьютер сохраняет его в запоминающем устройстве и при необходимости выводит из запоминающего устройства (например, на дисплей и/или на печатающее устройство). Если структурная организация объектов изучается во временной динамике, это учитывается при формировании массива данных, в котором отражаются динамические значения параметров ПСЗ, возникающих при взаимодействии объектов со стереологическим зондом (зондами) в различные моменты времени.
Набор (наборы) значений, соответствующих любому из изучаемых параметров ПСЗ, преобразуют в статистическое распределение или распределения общеизвестными методами [Автандилов, 1990; Славин, 1989; Теннант-Смит, 1988; Урбах, 1975; Freund et al., 1987]. В данном случае речь идет о вероятностном распределении координат расположения или других параметров ПСЗ объектов. Например, результаты измерений абсцисс х центров ПСЗ объектов по микрофотографиям могут быть представлены в виде частотной гистограммы (гистограммы частот значений координаты х ПСЗ объектов). Вместе с тем, возможны и другие варианты выражения фактического распределения данного параметра ПСЗ, в частности, в виде 1) кривой функции распределения CDFx(b) [кумулятивной кривой, или кривой CDF (от англ. cumulative distribution function)], 2) графика плотности распределения вероятностей PDFx (от англ. probability density function), 3) кумулятивной частотной гистограммы значений х, 4) другого графика функции распределения х, 5) другого графика производной функции распределения х, 6) другого графика параметра функции распределения х (подробнее с принципами работы со случайными величинами и их графическими представлениями можно ознакомиться в специальной литературе - см., в частности, [Автандилов, 1990; Славин, 1989; Теннант-Смит, 1988; Урбах, 1975; Freund et al., 1987]). Приведенные варианты выражения фактического распределения могут быть применены при представлении распределения любого другого параметра ПСЗ. При построении распределений параметров ПСЗ при динамических исследованиях объектов время следует учитывать как одну из величин, с учетом которой может выстраиваться распределение. Тем самым получают временную динамику распределения параметра (параметров) ПСЗ или же распределение параметра (параметров) ПСЗ объектов во времени.
Набор значений, соответствующих любому из изучаемых параметров ПСЗ, может быть преобразован не только в полное распределение параметра (параметров) ПСЗ объектов, но и в параметр этого распределения, а именно: в 1) моду распределения, 2) математическое ожидание, 3) дисперсию, 4) среднее квадратическое отклонение (сигму, ст), 5) коэффициент асимметрии, 6) другой момент, 7) другой параметр распределения, 8) величину, связанную с любым из перечисленного, 9) любую комбинацию из перечисленного. О конкретных приемах таких преобразований см. в специальной литературе (в частности, [Автандилов, 1990; Славин, 1989; Теннант-Смит, 1988; Урбах, 1975; Freund et al., 1987]).
При измерении сразу нескольких параметров получаемые при замерах значения параметров ПСЗ могут быть представлены как несколько распределений, выстраиваемых отдельно для каждого из параметров. Результаты измерений могут быть выражены и в виде совместного распределения (к примеру, в виде совместного распределения значений координат х и у). Совместное распределение параметров ПСЗ объектов представляют в любом из перечисленного виде: в виде 1) графика функции совместного распределения (CDF), 2) графика плотности совместного распределения вероятностей (PDF), 3) кумулятивной гистограммы частот, 4) частотной гистограммы, 5) другого графика функции совместного распределения, 6) другого графика производной функции совместного распределения, 7) другого графика параметра функции совместного распределения. Совместное распределение параметров ПСЗ может также характеризоваться параметром (параметрами) совместного распределения, например модой.
Тем самым результаты замеров ПСЗ объектов преобразуют в любое из следующего либо в любую комбинацию из следующего: 1) одиночное распределение параметра ПСЗ объектов, 2) одиночные распределения параметров ПСЗ объектов, 3) совместное распределение параметров ПСЗ объектов, 4) совместные распределения параметров ПСЗ объектов, 5) параметр (параметры) одиночного распределения параметра ПСЗ объектов, 6) параметры одиночных распределений параметров ПСЗ объектов, 7) параметр (параметры) совместного распределения параметров ПСЗ объектов, 8) параметры совместных распределений параметров ПСЗ объектов. Заметим также, что при построении распределения параметра (параметров) ПСЗ, равно как и при графическом представлении данного распределения, полезным может быть применение компьютера, в частности компьютера, входящего в состав современных аппаратов для СМ, ЭМ, КЛСМ, КТ, МРТ, ПЭТ, SPECT, УМ, УТ и других методов исследования.
Аппроксимация распределения или распределений параметра (параметров) ПСЗ объектов. Для любого из получаемых фактически распределений параметра (параметров) ПСЗ объектов рассчитывают модельное распределение параметра (параметров) ПСЗ, задавая параметры объектов и стереологического зондирования. К задаваемым параметрам объектов и стереологического зондирования относится любое из следующего либо любая комбинация из следующего: 1) распределение расположения объектов, 2) распределение расположения объектов относительно стереологического зонда (зондов), 3) распределение размера (или размеров) объектов, 4) распределение формы объектов, 5) распределение ориентации объектов, 6) распределение углов, описывающих ориентацию объектов относительно стереологического зонда (зондов), 7) тип применяемого стереологического зонда (зондов), 8) размерность применяемого стереологического зонда (зондов), 9) кривизна применяемого стереологического зонда (зондов), 10) свойства волнового потока, используемого при проекционном стереологическом зондировании, 11) любой другой параметр применяемого стереологического зонда (зондов). При динамических исследованиях учитывают также временной фактор, который может сказываться на параметрах объектов и стереологического зондирования.
Саму процедуру аппроксимации фактического распределения параметра (параметров) ПСЗ модельным распределением проводят в соответствии с общими положениями, известными из источников литературы (см., например, [Носач, 1994; Braess, 1986; Press et al., 1994]; см. также основные математические аспекты процедуры аппроксимации, приведенные в Приложении). В частности, полезным при аппроксимации представляется использование компьютера. В данном качестве может применяться компьютер, входящий в состав современных аппаратов для СМ, ЭМ, КЛСМ, КТ, МРТ, ПЭТ, SPECT, УМ, УТ и других методов исследования. При динамическом анализе объектов процедуру аппроксимации повторяют для каждого изучаемого момента или интервала времени и получают временной ряд исследуемого параметра (параметров) структурной организации объектов.
При задании распределения расположения объектов учитывают, что процессы объектов, обладающие свойством CSR, демонстрируют равномерное распределение значений любой из координат объектов в пределах содержащего их объема пространства: 
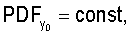
 (Нужно учитывать, что при неровностях границ содержащего объекты объема пространства распределения xo, yo, zo равномерны лишь на фрагментах данного пространства с ровными границами (например, на кубических фрагментах), направление которых совпадает с осями принятой системы координат. Поэтому правильнее рассматривать совместное распределение координат xo, yo, zo. Тогда при выполнении условия CSR имеем
(Нужно учитывать, что при неровностях границ содержащего объекты объема пространства распределения xo, yo, zo равномерны лишь на фрагментах данного пространства с ровными границами (например, на кубических фрагментах), направление которых совпадает с осями принятой системы координат. Поэтому правильнее рассматривать совместное распределение координат xo, yo, zo. Тогда при выполнении условия CSR имеем  где VR - объем содержащего объекты пространства, и (x, y, z)∈R3, VR=V(R3). При анализе принимают во внимание протяженность координатной системы, в которой были измерены координаты расположения ПСЗ объектов. Тем самым может быть получена информация об особенностях расположения объектов в определенной системе 3D-координат. Для описания стохастики расположения объектов в пространстве могут использоваться случайные точечные процессы, в том числе пуассоновский точечный процесс, марковские гомогенные и негомогенные случайные точечные процессы, гиббсовские процессы, процессы Штраусса, Матерна. При этом пуассоновский точечный процесс используется как нулевая гипотеза при анализе фактических точечных процессов. При выполнении этой гипотезы исследуемый точечный процесс обладает свойством CSR. Описание различных пространственных, плоскостных и линейных точечных процессов, а также анализ взаимосвязи между ними могут быть найдены в специальной литературе (см., например, piggle, 1983; Griffith, 1988; Koenig, 1991; Mase et al., 2001; Nikonenko et al., 2000; Ripley, 1981; Schmitz, 1998; Stoyan et al., 1994, 1995]). Необходимые уравнения могут быть также выведены самостоятельно с использованием традиционного для стереологии математического аппарата.
где VR - объем содержащего объекты пространства, и (x, y, z)∈R3, VR=V(R3). При анализе принимают во внимание протяженность координатной системы, в которой были измерены координаты расположения ПСЗ объектов. Тем самым может быть получена информация об особенностях расположения объектов в определенной системе 3D-координат. Для описания стохастики расположения объектов в пространстве могут использоваться случайные точечные процессы, в том числе пуассоновский точечный процесс, марковские гомогенные и негомогенные случайные точечные процессы, гиббсовские процессы, процессы Штраусса, Матерна. При этом пуассоновский точечный процесс используется как нулевая гипотеза при анализе фактических точечных процессов. При выполнении этой гипотезы исследуемый точечный процесс обладает свойством CSR. Описание различных пространственных, плоскостных и линейных точечных процессов, а также анализ взаимосвязи между ними могут быть найдены в специальной литературе (см., например, piggle, 1983; Griffith, 1988; Koenig, 1991; Mase et al., 2001; Nikonenko et al., 2000; Ripley, 1981; Schmitz, 1998; Stoyan et al., 1994, 1995]). Необходимые уравнения могут быть также выведены самостоятельно с использованием традиционного для стереологии математического аппарата.
Для задания размерного распределения объектов при аппроксимации фактического распределения параметра или параметров (в частном случае - размера или размеров) ПСЗ используют известные подходы, описанные, например, в [Носач, 1994; Braess, 1986; Press et al., 1994].
При задании распределения формы исследуемые объекты могут описываться известными геометрическими фигурами (сферами, цилиндрами, многогранниками, конусами, призмами, дисками, эллипсоидами, кубами и пр.) или их композициями, в том числе получаемыми при применении булевых операторов в конструктивной блочной геометрии [Kendall et al., 1999; Stoyan, 1998], имеющими при необходимости некоторые, как правило, контролируемые, отклонения по форме. Набор описывающих форму объектов фигур может состоять из одинаковых фигур и/или фигур различной формы, вводимых в модель с требующимися весовыми соотношениями. Вместе с тем, описание исследуемых объектов правильными геометрическими фигурами может и не использоваться. Тогда могут быть применены другие методы задания формы, в частности, 1) мозаичное представление [Lee, 1999], 2) представление в виде набора конечных элементов [Yeh et al., 1999], 3) описание поверхности и/или объема любого из объектов радиус-вектором [Hobolth et al., 2000], 4) контурное моделирование (англ. wireframe models) [Free et al., 2001]. Дополнительное описание различных методов задания формы объектов имеется в [Автандилов, 1990; Чернявский, 1977; Arahori et al., 2000; Dryden et al., 1998; Le et al., 1999; Stoyan et al., 1994; Wahl et al., 1984; Wang et al., 2000; Weibel, 1979-1980] и многочисленных других источниках литературы. Заметим, что при все более точном описании формы объектов структурная организация объектов изучается без упрощающих допущений, однако при этом происходит усложнение процедуры аппроксимации. Кроме того, вид функции Q (см. Приложение) может зависеть от выбранного способа задания формы объектов.
(см. Приложение) может зависеть от выбранного способа задания формы объектов.
При задании распределения ориентации объектов также используют существующие решения (см., например, [Mattfeldt et al., 1994]). В частности, при задании распределения углов, описывающих расположение объектов относительно применяемых зондов, следует учитывать дизайн стереологического зондирования, примененный при получении ПСЗ объектов (IUR срезы, IUR набор параллельных срезов, вертикальные срезы, орттрип или др.). Использование специальных дизайнов зондирования отражается при задании параметров  ,
, 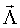 и
и  (см. Приложение).
(см. Приложение).
При задании параметров используемого стереологического зондирования принимают во внимание, в частности, 1) тип применяемого стереологического зонда (зондов) (зонд сечения, проекции, их комбинация), 2) размерность используемого стереологического зонда (зондов) (n равно 0, 1, 2, 3, их комбинации), 3) кривизну применяемого стереологического зонда (зондов).
При решении некоторых проекционных задач следует также учитывать свойства используемого при стереологическом зондировании волнового потока, такие, например, как 1) направленность излучения при получении проекционных изображений, 2) его амплитудно-частотные характеристики, 3) проникающая способность по отношению к среде, 4) проникающая способность по отношению к исследуемым объектам, 5) отражение волн излучения на границе раздела сред, 6) преломление волн излучения на границе раздела сред, 7) анизотропия свойств волнового потока, используемого при проекционном стереологическом зондировании, 8) анизотропия свойств среды, по которой проходит волновой поток, используемый при проекционном стереологическом зондировании, 9) пространственная когерентность излучения, 10) временная когерентность излучения, 11) соизмеримость длины волны используемого излучения с размерами изучаемых объектов, 12) импульсный характер излучения, 13) движение волнового потока относительно исследуемого объекта, 14) другой параметр (другие параметры) волнового потока, используемого при проекционном стереологическом зондировании, 15) любые комбинации перечисленных и/или других свойств волнового потока.
Модельное распределение параметра (параметров) ПСЗ объектов выстраивают в соответствующем фактическому распределению виде (обычно в виде гистограммы частот). Как правило, процедуру аппроксимации начинают с построения простых модельных распределений, соответствующих случаям, когда все объекты имеют равномерное расположение в пространстве, а также при необходимости некоторый одинаковый размер (конкретное числовое значение размера), одинаковую форму и/или трехмерно изотропную (3D)-ориентацию. Фактическое распределение сравнивают с модельными на предмет выбора из последних наиболее точной модели. При аппроксимации получаемого фактически распределения параметра (параметров) ПСЗ объектов модельным распределением осуществляют сравнение любого из следующего либо любой комбинации из следующего: значений 1) CDF, 2) PDF, 3) частот в кумулятивных гистограммах, 4) частот в частотных гистограммах, 5) мод распределений, б) математических ожиданий, 7) дисперсий, 8) средних квадратических отклонений (о), 9) коэффициентов асимметрии, 10) моментов функций распределения, 11) параметров функций распределения, 12) величин, связанных с любым из перечисленного. При аппроксимации совместного распределения фактических значений параметров ПСЗ также осуществляют сравнение любого из перечисленного в пунктах 1-12 настоящего абзаца.
Сравнение распределений может производиться визуально и с использованием статистических методов, например, по критерию χ2 (подробнее о работе с этим статистическим критерием можно ознакомиться в специальной литературе - см., в частности, [Славин, 1989; Теннант-Смит, 1988; Урбах, 1975; Freund et al, 1987]). При визуальном выполнении аппроксимации определяют, например, насколько сильно отклоняются значения частот фактической и теоретической гистограмм. При этом условия, принятые при построении модельного распределения и позволяющие наиболее точно и/или с необходимой точностью аппроксимировать фактическое распределение параметра (параметров) ПСЗ, являются искомой оценкой соответствующего аспекта структурной организации объектов, в чем и заключается смысл проводимой процедуры аппроксимации. Так, найденные условия о распределении расположения объектов являются искомой оценкой распределения расположения объектов, условия о распределении размера объектов - оценкой размерного распределения объектов, условия о распределении формы объектов - оценкой распределения формы объектов, а условия о распределении ориентации объектов - оценкой распределения ориентации объектов. Данные о структурной организации объектов, находимые в результате анализа, могут быть сохранены компьютером в запоминающем устройстве и при необходимости выведены из запоминающего устройства (например, на дисплей и/или печатающее устройство).
Как уже было отмечено выше, при реализации предлагаемого способа могут сравниваться не только сами фактическое и модельное распределения, представляемые, например, в виде частотных гистограмм, но и параметры этих распределений (в частности, значения математических ожиданий). При этом целесообразно использовать известные подходы к оценке статистической достоверности различий соответствующих параметров, такие, например, как основывающиеся на применении критериев Стьюдента, Фишера, Кочрена, Бартлетта, Вилкоксона-Манна-Уитни (подробнее с этими и другими статистическими критериями можно ознакомиться в специальной литературе - см., в частности, [Автандилов, 1990; Славин, 1989; Теннант-Смит, 1988; Урбах, 1975; Freund et al., 1987]). Данный подход является менее трудоемким, так как требует относительно небольшого количества замеров, достаточного для статистической оценки того или иного параметра фактического распределения параметра ПСЗ. Однако сравнение параметров распределений дает ощутимо менее точные результаты и поэтому должно использоваться лишь при получении прикидочных оценок исследуемых аспектов структурной организации объектов.
Для уточнения оценки параметра (параметров) структурной организации объектов в модель вводят усложняющие условия - более сложное распределение объектов по изучаемому параметру (параметрам). Эти усложняющие условия могут вводиться в распределение любого из исследуемых параметров объектов - т.е. в 1) распределение расположения, 2) распределение размера (размеров), 3) распределение формы, 4) распределение ориентации объектов. Введение усложняющих условий в модель, как правило, производят последовательно. Получаемые модельные распределения сравнивают с фактическим распределением для выяснения того, какая (или какие) из моделей дают наиболее точное и/или удовлетворительное по точности совпадение с фактическим распределением. Например, при использовании критерия χ2 повышение качества аппроксимации сопровождается уменьшением значения χ2 и увеличением соответствующей вероятности р. Выполнение процедуры аппроксимации заканчивают при прекращении прироста точности и/или достижении необходимой точности аппроксимации. При этом условия, взятые при построении усложненного модельного распределения, наиболее точно и/или с необходимой точностью аппроксимирующего фактическое распределение параметра (параметров) ПСЗ, являются уточненной оценкой соответствующего параметра (параметров) объектов. Если прирост точности прекратился до достижения необходимой точности аппроксимации, повышают количество измеряемых ПСЗ и/или точность измерений. Далее процедуру аппроксимации повторяют до достижения необходимого результата. При этом учитывают, что повышение количества измеряемых ПСЗ в m раз сопровождается увеличением точности аппроксимации в корень квадратный из m раз. Это приложение усиленного закона больших чисел позволяет соотносить достигаемый уровень точности анализа с трудоемкостью проводимого исследования.
При наличии имеющейся или предполагаемой информации о расположении, размере (размерах), форме и ориентации изучаемых объектов, а также о параметрах примененного стереологического зондирования, ее следует использовать при подборе модели. Так, например, могут быть заданы условия о том, насколько плотно упакованы объекты в изучаемой среде, или условия, описывающие геометрические закономерности соприкосновения поверхностей объектов (ингибирование контактного взаимодействия между объектами либо, наоборот, склонность к таковому). Дополнительная информация может найти применение при обосновании выбора наилучшей модели из нескольких альтернативных модельных распределений, описывающих с близкой точностью фактическую ситуацию. При наличии такой информации ее можно вводить в компьютер для целей автоматизированного или полуавтоматизированного осуществления процедуры аппроксимации. Вместе с тем, дополнительная информация не является обязательной при использовании предлагаемого способа.
Построение изображения (изображений) объектов. На основе условий, задаваемых при аппроксимации для описания параметров структурной организации объектов, может быть построено изображение (изображения) объектов. Построение изображений позволяет изучать объекты с большей полнотой, удобством и наглядностью, чем просто при количественной оценке соответствующих параметров объектов. Сущность построения изображений заключается в том, что по находимым условиям наилучшей и/или удовлетворительной по качеству аппроксимации (т.е. по параметрам объектов) выстраивают - вручную или с применением компьютера - графическую модель структурной организации объектов. Если, например, при исследовании объектов, описываемых по форме сферами, наряду с оценкой размерного распределения, была обнаружена равномерность распределения координат их центров xо, yо, zo, то объекты графически представляют в виде набора сфер полученного при анализе размерного распределения с центрами, случайно и независимо расположенными в объеме образца. Координаты 3D-расположения центров сфер определяют при этом как случайные и независимые величины, например, по таблице случайных чисел или с использованием генератора псевдослучайных чисел. Если же координаты расположения объектов подчиняются не равномерному, а какому-либо другому закону распределения, то в 3D-графическое представление объектов вносят соответствующие изменения, и центры объектов на изображении располагают так, как это определяется функциями распределения значений xо, yо, zo. Для объектов другой формы построение изображения выполняют аналогичным образом. В данном случае может иметь значение и распределение ориентации объектов. Для полученных 3D-изображений объектов их представление меньшей размерности (2D- и/или 1D-представление объектов) выстраивается, как правило, без затруднений. Иногда 2D- и 1D-изображения могут быть построены сразу, минуя этап создания 3D-изображения объектов.
Существенную помощь при графическом представлении объектов могут оказать известные алгоритмы построения изображений (см., в частности, [Bezrukov et al., 2001; Delarue et al., 2001; Dufresne et al, 1996; Herman et al., 2002; Louis et al., 1996; Stoyan, 1998] и работы, цитируемые в них), алгоритмы расчета распределения объектов на плоскости и в 3D-пространстве (см., например, [Reed et al., 1997]), многочисленные существующие программные продукты компьютерного дизайна и разработки (CAD/CAM - от англ. computer-aided design / computer-aided manufacturing), а также компьютерные программы, применяемые в конструктивной блочной геометрии и при моделировании случайных процессов. При наличии дополнительной информации об объектах (к примеру, об их объемной плотности или же о частоте и характере контактного взаимодействия между объектами) ее используют при построении изображений. Дополнительная информация может вводиться в компьютер для целей автоматизированного или полуавтоматизированного построения изображений объектов.
Тем самым компьютер (в том числе входящий в состав современных аппаратов для СМ, ЭМ, КЛСМ, КТ, МРТ, ПЭТ, SPECT, УМ, УТ и других методов исследования) генерирует, сохраняет и/или выводит (например, на дисплей и/или на печатающее устройство) изображение (изображения) объектов. Изображение (изображения) объектов строят любым способом из перечисленного либо с применением любой комбинации из перечисленного: 1) в монохромном (например, черно-белом) исполнении, 2) в цветном исполнении, 3) в одной, двух и/или нескольких проекциях (например, в боковой, фронтальной и/или косой проекциях), 4) в 1D, 2D- и/или 3D-представлении, 5) с использованием эффекта вращения или других эффектов анимации, 6) с использованием эффекта перспективы, 7) с использованием эффекта направленного освещения, 8) с использованием эффекта затенения. Если объекты изучаются в динамике, например, в реальном режиме времени, изображения объектов могут выстраиваться так, чтобы они отражали изменения во времени исследуемых аспектов структурной организации объектов.
Заключительные положения. В завершение следует отметить, что исследуемым аспектом (аспектами) структурной организации объектов может являться любое из следующего: 1) распределение расположения объектов; при этом заключение о данном аспекте структурной организации объектов делают по распределению расположения объектов, задаваемому при выполнении процедуры аппроксимации; 2) распределение размера (размеров) объектов; заключение о данном аспекте структурной организации объектов делают по распределению размера (размеров) объектов, задаваемому при выполнении процедуры аппроксимации; 3) распределение формы объектов; заключение о данном аспекте структурной организации объектов делают по распределению формы объектов, задаваемому при выполнении процедуры аппроксимации; 4) распределение ориентации объектов; заключение о данном аспекте структурной организации объектов делают по распределению ориентации объектов, задаваемому при выполнении процедуры аппроксимации; 5) любая комбинация из перечисленного; заключение об исследуемых аспектах структурной организации объектов делают тогда по распределению (распределениям) соответствующих параметров объектов, задаваемому (задаваемым) при выполнении процедуры аппроксимации. При любом из перечисленных видов анализа может использоваться дополнительная информация об объектах.
Тем самым предлагаемый способ может быть использован, в частности, для оценки распределения расположения объектов. В этом случае распределение расположения является единственным или одним из изучаемых аспектов структурной организации объектов. Распределение расположения объектов может исследоваться 1) по распределению расположения ПСЗ или 2) по распределению расположения ПСЗ в сочетании с любым из следующего либо в сочетании с любой комбинацией из следующего: а) распределением размера (размеров) ПСЗ, б) распределением ориентации ПСЗ, в) количеством ПСЗ объектов.
Предлагаемый способ может быть также использован для оценки размерного распределения объектов. В этом случае размерное распределение является единственным или одним из изучаемых аспектов структурной организации объектов. Размерное распределение объектов может исследоваться 1) по распределению расположения ПСЗ или 2) по распределению расположения ПСЗ в сочетании с любым из следующего либо в сочетании с любой комбинацией из следующего: а) распределением размера (размеров) ПСЗ, б) распределением ориентации ПСЗ, в) количеством ПСЗ объектов.
Предлагаемый способ может быть использован и для оценки распределения формы объектов. В этом случае распределение формы является единственным или одним из изучаемых аспектов структурной организации объектов. Распределение формы объектов может исследоваться 1) по распределению расположения ПСЗ или 2) по распределению расположения ПСЗ в сочетании с любым из следующего либо в сочетании с любой комбинацией из следующего: а) распределением размера (размеров) ПСЗ. б) распределением ориентации ПСЗ, в) количеством ПСЗ объектов.
Предлагаемый способ может быть, кроме того, использован для оценки распределения ориентации объектов. В этом случае распределение ориентации является единственным или одним из изучаемых аспектов структурной организации объектов. Распределение ориентации объектов может исследоваться 1) по распределению расположения ПСЗ или 2) по распределению расположения ПСЗ в сочетании с любым из следующего либо в сочетании с любой комбинацией из следующего: а) распределением размера (размеров) ПСЗ, б) распределением ориентации ПСЗ, в) количеством ПСЗ объектов.
СВЕДЕНИЯ, ПОДТВЕРЖДАЮЩИЕ ВОЗМОЖНОСТЬ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Предлагаемым способом был подвергнут анализу такой аспект структурной организации перифолликулярных гемокапилляров щитовидной железы (ЩЖ) крысы, как их 3D-расположение. Напомним, что именно оценка пространственного расположения объектов является основным предназначением настоящего изобретения. Исследование было выполнено на четырех белых крысах-самцах, достигших половой зрелости (масса тела 248±24,0 г, ±σ). Забор ткани ЩЖ осуществляли под эфирным наркозом. Фрагменты органа последовательно фиксировали в растворах глютаральдегида (2,5%, 2 ч.) и тетраоксида осмия (1%, 1 ч.) на какодилатном буфере (0,2 М, рН 7,4). Образцы ткани обезвоживали в спиртах восходящей концентрации и заключали в смесь смол эпон-аралдит М (Fluka Chemical Co., США) для последующего стереологического зондирования. На ультратоме LKB-8800 (LKB, Швеция) из каждой ЩЖ изготавливали по серии случайно ориентированных последовательных срезов, которые далее контрастировали уранилацетатом и цитратом свинца. (Как известно, диаметр кровеносного капилляра составляет не менее 4 мкм, что значительно превышает толщину ультратонкого среза (40-60 нм). Поэтому получаемые при ультратомировании профили сечения капилляров можно считать 2D, т.е. имеющими нулевую толщину, а используемый при изготовлении ультратонких срезов стереологический зонд - зондом плоскостного (2D) сечения. Тем самым при анализе капилляров был применен стереологический зонд плоскостного сечения.) Количественному анализу подвергали по одному случайно отобранному срезу от животного. Просмотр и фотографирование ультратонких срезов выполняли на трансмиссионном электронном микроскопе Hitachi H-300 (Hitachi, Япония). Поля зрения при съемке выбирали с сохранением условий рандомизации. На четырех микрофотографиях одинакового размера с конечным увеличением ×1650 (по одной фотография от животного) линейкой были измерены координаты х и у расположения центров профилей сечения капилляров. За начало отсчета в системе прямоугольных плоскостных координат при этом принимали левый нижний угол микрофотографии. Совместное распределение значений х и y на одной из фотографий (крыса 4) показано на Фиг.1. Полученные при замерах сведения о координатах х и y были преобразованы общеизвестным образом (см., например, [Автандилов, 1990; Славин, 1989; Теннант-Смит, 1988; Урбах, 1975; Frewid et al., 1987]) в частотные гистограммы, показанные соответственно на Фиг.2А и 2В. Затем проводилась процедура аппроксимации фактических распределений х и у.
Поскольку процедура аппроксимации может вызвать затруднения при осуществлении способа, опишем ее ход предельно подробно, хотя она и выполняется в соответствии с общими положениями, известными из многочисленных источников литературы (см., например, [Носач, 1994; Braess, 1986; Press et al., 1994]). Для условий проводимого исследования капилляров ЩЖ уравнение (1), применяемое при аппроксимации, выглядит как
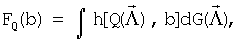
где Q - координата х или y, а функция Q выражает 2D/3D-связь координат (например, связь х с xо или y с yо). В данном случае понятия "расположение объектов в пространстве" и "расположение объектов относительно плоскости сечения" совпадают, поскольку от каждого животного изучался единственный срез. Общие соображения позволяют без детализации вида функции Q
выражает 2D/3D-связь координат (например, связь х с xо или y с yо). В данном случае понятия "расположение объектов в пространстве" и "расположение объектов относительно плоскости сечения" совпадают, поскольку от каждого животного изучался единственный срез. Общие соображения позволяют без детализации вида функции Q заключить о том, что при равномерном распределении координат объектов в объеме пространства
заключить о том, что при равномерном распределении координат объектов в объеме пространства 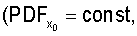

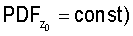 на плоскости случайного среза возникнет равномерное распределение координат профилей сечения объектов (PDFx=const, PDFy=const). С другой стороны, PDFx=const, PDFy=const может свидетельствовать о CSR расположении объектов, при котором
на плоскости случайного среза возникнет равномерное распределение координат профилей сечения объектов (PDFx=const, PDFy=const). С другой стороны, PDFx=const, PDFy=const может свидетельствовать о CSR расположении объектов, при котором 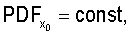

 Учитывая это, анализ следует начать с введения наиболее простых условий о распределении координат расположения центров капилляров - с принятия гипотезы о подчинении изучаемого пространственного процесса пуассоновскому закону распределения.
Учитывая это, анализ следует начать с введения наиболее простых условий о распределении координат расположения центров капилляров - с принятия гипотезы о подчинении изучаемого пространственного процесса пуассоновскому закону распределения.
Для фактических гистограмм х и y были построены модельные гистограммы PDFx=const и PDFy=const, соответствующие реализации на плоскости случайного среза пространственного процесса, обладающего свойством CSR. При этом предполагалось одновременное выполнение следующих условий: 1) центры исследуемых капилляров расположены случайно и независимо относительно друг друга и в объеме ЩЖ, 2) при анализе капилляров используется 2D-зонд плоскостного сечения, 3) плоскость среза рассекает ткань ЩЖ случайно и независимо, 4) центры капилляров расположены относительно плоскости сечения случайно и независимо. Заметим, что условие 1 является исследуемой гипотезой о паттерне 3D-организации капилляров, и центры капилляров как понятие имеют смысл, поскольку капилляры в органе обладают конечной длиной. Условия 2 и 3 определяются примененным дизайном стереологического зондирования, а условие 4 оказывается следствием совместного выполнения условий 1-3. При этом рассматривается прямоугольный фрагмент плоскости среза (микрофотография) и соответствующий ему фрагмент объема ЩЖ, ограниченный прямыми линиями, ориентация которых совпадает с применяемой системой 3D-координат. Модельные гистограммы приведены на Фиг.2А и 2В. Для иллюстративности данные по одной из микрофотографий показаны также отдельно (Фиг.2Б).
При сопоставлении фактических гистограмм с соответствующими моделями была получена достаточно высокая степень их близости. Вероятность статистического согласования в большинстве случаев превысила порог p=0,50 (табл.4), который при решении задач аппроксимации свидетельствует о том, что фактическое и модельное распределения начинают отличаться друг от друга не более чем две выборки из одного распределения. Лишь для двух распределений (координаты y для крыс 1 и 3) значения вероятности р были несколько меньше 0,50. Тем самым ни у одного животного не наблюдалось статистически значимого (р≤0,05) отклонения фактического распределения от модельного. С учетом имеющегося количества профилей капилляров на микрофотографиях (табл.4) это позволяет расценивать степень достигнутой аппроксимации как удовлетворительную и не проводить дальнейшее усложнение модельных распределений.
Из найденных условий аппроксимации фактических распределений х и y можно сделать следующий вывод. Профили капилляров расположены на фотографии статистически гомогенно. Вероятность того, что центр профиля примет на микрофотографии любое допустимое значение х и y, является в первом приближении одинаковой. Тем самым выполнение на плоскости случайного среза условий PDFx=const и PDFy=const свидетельствует о правомерности принятия в качестве итоговой модели случайного и независимого распределения капилляров относительно друг друга и в объеме ЩЖ, при котором 
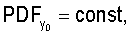
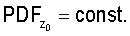 Таким образом, найдена искомая оценка исследуемого аспекта структурной организации капилляров в органе - распределения их 3D-расположения, которое, согласно условию CSR, описывается равномерным распределением любой из 3D-координат центров капилляров
Таким образом, найдена искомая оценка исследуемого аспекта структурной организации капилляров в органе - распределения их 3D-расположения, которое, согласно условию CSR, описывается равномерным распределением любой из 3D-координат центров капилляров 
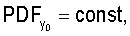
 на полных интервалах значений xо, yо, zo, определяемых размерами ЩЖ.
на полных интервалах значений xо, yо, zo, определяемых размерами ЩЖ.
На основе полученных при аппроксимации условий, характеризующих распределение расположения центров капилляров в объеме ЩЖ, было построено 2D-изображение центров капилляров, подчиняющееся пуассоновскому закону распределения с параметром λ=0,0033 (Фиг.3). При этом мы исходили из того, что пространственный пуассоновский процесс объектов, обладающий, как известно, свойством CSR, на плоскости среза также реализуется пуассоновским процессом объектов. Принималось также, что центры капилляров имеют ненулевую размерность (т.е. обладают некоторым размером), в результате чего они могут быть различимы на плоскостных изображениях. Указанное значение λ определялось как величина, близкая к среднему числу центров на единицу площади микрофотографии [например, для крысы 4 это 18-(90-72)-1]. При построении изображения использовалась программа STG 4.1, свободно распространяемая через сеть Интернет Институтом стохастики Горной академии г. Фрайберга, ФРГ (Institut fuer Stochastik, TU Bergakademie, Freiberg, BRD; адрес в Интернете - http://www.mathe.tu-freiberg.de). Задаваемая величина окна составляла 90×72 (мкм2). Как и следовало ожидать, изображение центров капилляров, полученное после удаления близко расположенных центров (Фиг.3Б), в целом согласуется по виду с совместным распределением координат х и у на случайном срезе (Фиг.1).
Следует заметить, что 2D-изображение центров капилляров ЩЖ могло также быть построено посредством задания значений соответствующих координат хo и уо с помощью таблицы случайных чисел или генератора псевдослучайных чисел (см., например, [Автандилов, 1990; Теннант-Смит, 1988; Howard et al., 1998]) и последующего размещения центров по получаемым координатам вручную или с использованием компьютера. Похожим образом может быть построено и 3D-изображение центров исследуемых капилляров. Для этого аналогично задают значения координат xо, yо, zo, по которым центры капилляров размещают в 3D-графическом пространстве.
Итак, применение предлагаемого способа позволило по распределению координат х и y расположения профилей сечения определить распределение координат xо, yо, zo расположения капилляров в объеме ЩЖ. Данная информация получена по распределению координат расположения профилей капилляров на ультратонких срезах, исследуемых общепринятым образом с помощью трансмиссионной ЭМ. При аппроксимации задавались следующие параметры объектов и стереологического зондирования: 1) распределение расположения объектов (CSR), 2) распределение расположения объектов относительно стереологического зонда (случайное и независимое), 3) тип применяемого стереологического зонда (зонд сечения), 4) размерность применяемого стереологического зонда (2D), 5) кривизна применяемого стереологического зонда (нулевая кривизна). Задание условий о других параметрах объектов не потребовалось; в частности, не принимались какие-либо предположения о форме капилляров. Проведенный анализ прост и может быть осуществлен как с применением компьютера, так и без него. Результаты исследования можно было бы дополнить с учетом того, что профили сечения капилляров имеют некоторые размеры и не способны поэтому находиться слишком близко друг к другу. Также можно было бы повысить количество анализируемых микрофотографий с совмещением их в единую координатную систему, что позволило бы уточнить функцию распределения значений координатных характеристик xо, yо, zo капилляров. Однако найденные оценки р(χ2) либо существенно превышают значение 0,50, либо близки к данному порогу, что позволяет при демонстрации осуществимости настоящего способа остановиться на анализе единственной микрофотографии от каждого животного без введения условий, характеризующих ингибирование контактного взаимодействия капилляров.
Следует заметить также, что настоящее изобретение может быть использовано в совокупности с другими способами исследования структурной организации объектов. Полученные данные, в частности, могут быть дополнены определением размерного распределения капилляров ЩЖ, распределения их формы и распределения ориентации. При этом оказывается возможным не просто суммирование разных подходов к оценке аспектов структурной организации объектов, но их интеграция с достижением таких преимуществ, как дополнительное повышение полноты и точности анализа. С учетом сведений о перифолликулярном расположении капилляров и их характерной форме может быть построено более комплексное, чем показанное на Фиг.3, графическое представление капилляров в виде 3D-изотропно ориентированных отрезков эллиптических цилиндров задаваемого осевого соотношения со случайным и независимым размещением вокруг тиреоидных фолликулов. При многократных исследованиях капилляров, каждое из которых в целом повторяет описанную схему, структурная организация капилляров может быть изучена во временной динамике, если используемый способ получения изображений, например, микро-КТ, не предполагает фиксации исследуемого органа.
При сравнении настоящего и прототипного [Tewari et al., 1998] способов обнаруживается невозможность с помощью последнего провести исследование перифолликулярных капилляров ЩЖ, поскольку прототип в описанном авторами виде не предназначен к применению при анализе вытянутых объектов, к каковым относятся капилляры. Способ [Duyckaerts et al., 1994] также не позволяет определить особенности расположения капилляров в объеме ЩЖ. Этому препятствует фолликулярная структура органа, при которой принятая авторами схема разбиения плоскости среза на ячейки лишена биологического смысла.
В завершение отметим, что приведенный пример не исчерпывает все возможности анализа структурной организации объектов по распределениям координат и других параметров ПСЗ с использованием процедуры аппроксимации, предусматривающей задание параметров объектов и стереологического зондирования. Специалистами могут быть найдены модификации настоящего изобретения, не выходящие за рамки прилагаемых пунктов формулы изобретения или эквивалентных им положений. При нахождении таких модификаций изменения сущности заявленного изобретения не происходит.
Выражение признательности. Автор изобретения выражает свою искреннюю признательность директору Научно-исследовательского центра Московской медицинской академии (ММА) им. И.М.Сеченова член-корр. РАМН проф. Грачеву Сергею Витальевичу за оказанную организационную помощь при выполнении экспериментального фрагмента исследования. Автор благодарен также заведующему кафедрой информатики и медицинской статистики ММА им. И.М.Сеченова канд. физ.-мат. наук доценту Герасимову Андрею Николаевичу за консультации и плодотворное сотрудничество в решении проблем, предшествовавших настоящему изобретению, результатом чего стало совместное оформление заявок на патенты РФ на изобретения №2000132517, №2000132518 и №2001111223.
ПРИЛОЖЕНИЕ. МАТЕМАТИЧЕСКИЕ АСПЕКТЫ АППРОКСИМАЦИИ ФАКТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ПАРАМЕТРА (ПАРАМЕТРОВ) ПСЗ МОДЕЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
Поскольку выполнение процедуры аппроксимации может вызвать затруднения при осуществлении настоящего способа, опишем ее математические аспекты подробнее, несмотря на то что она выполняется в соответствии с общими положениями, известными из многочисленных источников литературы (см., например, [Носач, 1994; Braess, 1986; Press et al., 1994]).
Как известно, "аппроксимация - [это] замена одних... объектов другими, в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов" [Стечкин, 1970]. В настоящем описании речь идет об аппроксимации распределения параметра (параметров) ПСЗ теоретическим распределением этого же параметра ПСЗ. По рассчитываемым свойствам теоретического, или модельного, распределения судят о свойствах исследуемого фактического распределения, точнее о том, какие наборы объектов (имеющие те или иные расположение в пространстве, размеры, форму, ориентацию) способны его породить.
При построении модельного распределения принимают во внимание, что в общем случае функция распределения значений Q (измеряемого параметра ПСЗ) выглядит как

где  - конечный или бесконечный набор числовых параметров изучаемого объекта, задаваемый в виде векторной величины
- конечный или бесконечный набор числовых параметров изучаемого объекта, задаваемый в виде векторной величины  аналогично,
аналогично,
 - набор числовых параметров стереологического зонда,
- набор числовых параметров стереологического зонда, 
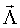 - набор координат, определяющих расположение Ω относительно Ψ,
- набор координат, определяющих расположение Ω относительно Ψ, 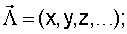 в 3D-пространстве
в 3D-пространстве 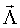 может быть представлена как
может быть представлена как 
 - углы, задающие ориентацию Ω относительно Ψ,
- углы, задающие ориентацию Ω относительно Ψ,  для описания ориентации Ω относительно Ψ в 3D-пространстве обычно используется два угла (α1 и α2);
для описания ориентации Ω относительно Ψ в 3D-пространстве обычно используется два угла (α1 и α2);
t - время (применяется при изучении объектов во временной динамике);
 - функция Хевисайда, равная 1, если
- функция Хевисайда, равная 1, если  и равная 0 в противоположном случае, для которой
и равная 0 в противоположном случае, для которой  - функция, связывающая величину Q с истинным значением изучаемого параметра Q0.
- функция, связывающая величину Q с истинным значением изучаемого параметра Q0.
Следует сказать, что  может описываться любое из следующего: 1) координаты расположения объектов в пространстве (или относительно друг друга), 2) размер или размеры объектов, 3) форма объектов и 4) ориентация объектов в пространстве (или относительно друг друга).
может описываться любое из следующего: 1) координаты расположения объектов в пространстве (или относительно друг друга), 2) размер или размеры объектов, 3) форма объектов и 4) ориентация объектов в пространстве (или относительно друг друга).
Для проекционного зондирования иногда имеют значение свойства поступающего волнового потока  и уравнение (1) принимает вид
и уравнение (1) принимает вид

где 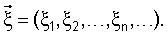 Заметим, что
Заметим, что 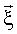 может также задаваться через
может также задаваться через  в уравнении (1).
в уравнении (1).
По определению, PDF является производной функции распределения, поэтому

Тем самым построение модельного распределения сводится к нахождению таких распределений величин, указанных в правой части уравнения (1) или (2), которые позволяют подобрать наилучший по выбранному критерию аппроксимат фактического распределения (или параметра фактического распределения) измеренного параметра ПСЗ Q. Найденные при аппроксимации распределения величин 
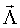 и/или
и/или  являются искомой оценкой соответственно числовых характеристик объектов, распределения координат расположения объектов относительно зонда (зондов) и распределения ориентации объектов относительно зонда (зондов). Распределение
являются искомой оценкой соответственно числовых характеристик объектов, распределения координат расположения объектов относительно зонда (зондов) и распределения ориентации объектов относительно зонда (зондов). Распределение  позволяет оценить распределение координат расположения объектов в пространстве (или относительно друг друга), распределение размера или размеров объектов, распределение формы объектов, а также распределение ориентации объектов в пространстве (или относительно друг друга). Заметим, что для целей осуществления настоящего изобретения в каждом конкретном случае может быть использована процедура аппроксимации, способная наилучшим образом сглаживать некоторые случайные ошибки измерения и контролировать систематические погрешности.
позволяет оценить распределение координат расположения объектов в пространстве (или относительно друг друга), распределение размера или размеров объектов, распределение формы объектов, а также распределение ориентации объектов в пространстве (или относительно друг друга). Заметим, что для целей осуществления настоящего изобретения в каждом конкретном случае может быть использована процедура аппроксимации, способная наилучшим образом сглаживать некоторые случайные ошибки измерения и контролировать систематические погрешности.
О задании параметров объектов при аппроксимации было сказано ранее в разделе "Сущность изобретения". В данном приложении отметим лишь, что уравнения вида  необходимые при задании распределения расположения объектов, могут быть получены из источников литературы (см., например, [Diggle, 1983; Griffith, 1988; Koenig, 1991; Mase et al., 2001; Nikonenko et al., 2000; Ripley, 1981; Schmitz, 1998; Stoyan et al., 1994, 1995]) с применением традиционного для стереологии математического аппарата. При задании размерного распределения объектов также могут быть применены уравнения, имеющиеся в литературе (см., например, табл.2) или выводимые самостоятельно. Распределение формы объектов нередко задается через один или несколько размеров. Композиции различных по форме объектов описываются распределением
необходимые при задании распределения расположения объектов, могут быть получены из источников литературы (см., например, [Diggle, 1983; Griffith, 1988; Koenig, 1991; Mase et al., 2001; Nikonenko et al., 2000; Ripley, 1981; Schmitz, 1998; Stoyan et al., 1994, 1995]) с применением традиционного для стереологии математического аппарата. При задании размерного распределения объектов также могут быть применены уравнения, имеющиеся в литературе (см., например, табл.2) или выводимые самостоятельно. Распределение формы объектов нередко задается через один или несколько размеров. Композиции различных по форме объектов описываются распределением 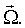 Ориентацию объектов задают с использованием известных уравнений (см., в частности, табл.3) или уравнений, получаемых самостоятельно с использованием традиционного для стереологии математического аппарата.
Ориентацию объектов задают с использованием известных уравнений (см., в частности, табл.3) или уравнений, получаемых самостоятельно с использованием традиционного для стереологии математического аппарата.
При выполнении процедуры аппроксимации любой из параметров объектов задают любым из следующего образом: в виде 1) конкретного числового значения, 2) набора конкретных числовых значений, 3) величины, принимающей значения из интервала значений с задаваемой PDF, 4) момента (моментов) функции распределения, 5) параметра (параметров) функции распределения, 6) тензорной величины, 7) векторной величины, 8) любой комбинации перечисленных способов задания параметра объектов.
В ходе выполнения процедуры аппроксимации при необходимости учитывают свойства стереологического зонда  Однако обычно функции
Однако обычно функции  используемые в уравнениях (1) и (2), приводятся в специальной литературе в виде, уже адаптированном под некоторый конкретный случай стереологического зондирования (см., в частности, табл.2-3). Наиболее часто это функции, описывающие взаимосвязь истинных (3D) размеров объектов с размерами их профилей сечения (2D) при условии изотропной ориентации и случайного независимого расположения объектов относительно плоскостей сечения. При использовании таких 2D/3D-функций отпадает необходимость каким-либо специальным образом задавать набор параметров
используемые в уравнениях (1) и (2), приводятся в специальной литературе в виде, уже адаптированном под некоторый конкретный случай стереологического зондирования (см., в частности, табл.2-3). Наиболее часто это функции, описывающие взаимосвязь истинных (3D) размеров объектов с размерами их профилей сечения (2D) при условии изотропной ориентации и случайного независимого расположения объектов относительно плоскостей сечения. При использовании таких 2D/3D-функций отпадает необходимость каким-либо специальным образом задавать набор параметров  . Кроме того, объекты в стереологии исследуются обычно не в динамике времени, поэтому временной фактор можно не учитывать. Принимая во внимание высказанные соображения, уравнение (1) следует записать как
. Кроме того, объекты в стереологии исследуются обычно не в динамике времени, поэтому временной фактор можно не учитывать. Принимая во внимание высказанные соображения, уравнение (1) следует записать как

Уравнение (4) может быть полезным при использовании имеющихся в литературе и выводимых самостоятельно уравнений, необходимых для описания функции  при задании параметра (параметров) объектов.
при задании параметра (параметров) объектов.






Основные известные типы ПСЗ, которые могут быть получены при взаимодействии n-мерных стереологических зондов с изучаемыми объектами
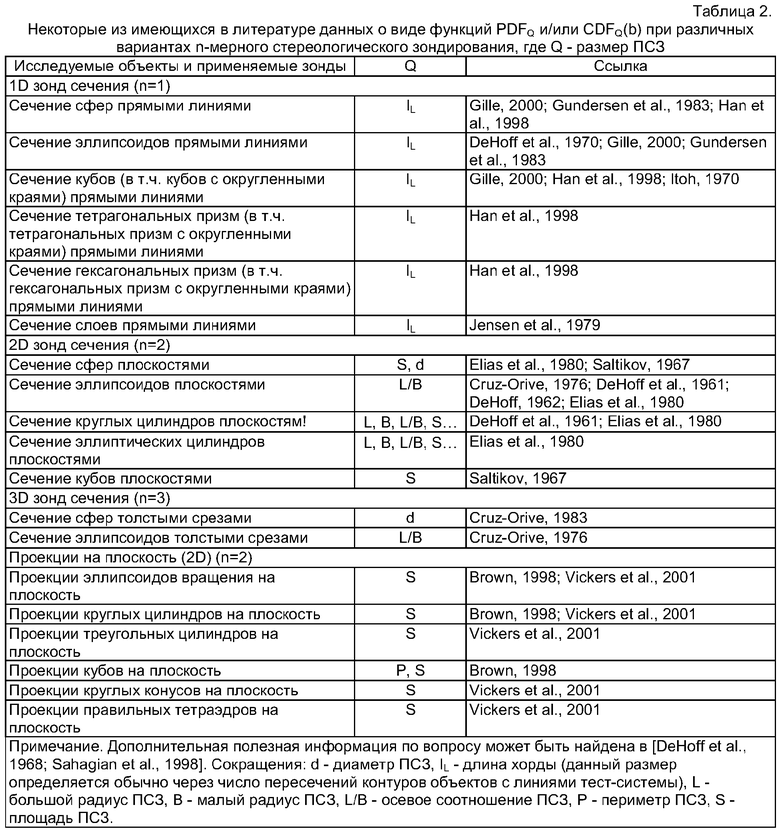
Некоторые из имеющихся в литературе данных о виде функций PDFQ и/или CDFQ(b) при различных вариантах n-мерного стереологического зондирования, где Q - ориентация ПСЗ
 - ориентация хорды максимальной длины, dir(L) - ориентация большой оси эллиптического профиля сечения по отношению к вертикальному направлению, dir(Th) - ориентация по отношению к вертикальному направлению линии, характеризующей толщину профиля сечения слоя.
- ориентация хорды максимальной длины, dir(L) - ориентация большой оси эллиптического профиля сечения по отношению к вертикальному направлению, dir(Th) - ориентация по отношению к вертикальному направлению линии, характеризующей толщину профиля сечения слоя.
Значения критерия χ2 и соответствующие доверительные вероятности р, полученные для различных животных при аппроксимации фактических распределений координат х и у центров профилей сечения капилляров равномерными распределениями PDFx=const и POFу=const. Приводятся также интервалы, на которых распределены фактические значения х и у.
ПЕРЕЧЕНЬ ФИГУР ЧЕРТЕЖЕЙ
Фиг.1. Пример совместного распределения значений координат х и у центров профилей сечения капилляров ЩЖ на микрофотографии (крыса 4).
Фиг.2. Фактические координаты х и у расположения центров профилей сечения капилляров ЩЖ представлены отдельно для каждой микрофотографии в виде частотных гистограмм х (А) иу (В) с шагом гистограммирования 20 и 15 мм соответственно. По оси абсцисс показаны верхние включаемые границы шага гистограммирования (например, первый столбик гистограммы х соответствует частоте профилей с х∈]0; 20]). При этом 10 мм на микрофотографии равны 6,061 мкм в ткани ЩЖ. Приведены также модельные гистограммы х и у, построенные на том же диапазоне значений, что и фактические гистограммы для крысы 1 или 4. Модельные гистограммы для двух других животных имеют аналогичный вид, но должны быть представлены на более коротком интервале значений (табл.4), соответственно чему укорачивается интервал значений модельной гистограммы и увеличивается высота модельных столбиков. Для иллюстративности данные х по одной из крыс (крыса 4) и модельная гистограмма х показаны в дополнение отдельно (Б). Фактические гистограммы х и у достаточно хорошо аппроксимируются равномерными распределениями PDFx=const и PDFy=const (см. также табл.4). Это означает, что расположение исследуемых капилляров в объеме ЩЖ может быть представлено как случайное и независимое (CSR), т.е. 
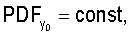

Фиг.3. Плоскостное (2D) изображение центров исследуемых капилляров, построенное по условиям удовлетворительной аппроксимации 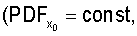
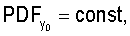
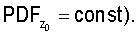 При построении изображения пространственного пуассоновского процесса центров капилляров была показана его 2D-реализация с λ=0,0033 (А). При этом принималось, что центры капилляров имеют ненулевую размерность и, следовательно, могут быть различимы на плоскости. На фиг.3Б то же изображение показано без центров, находящихся ближе чем на 5 мкм (8,25 мм на микрофотографии) к соседним. Удаление центров в группах близко расположенных профилей капилляров проводилось произвольно.
При построении изображения пространственного пуассоновского процесса центров капилляров была показана его 2D-реализация с λ=0,0033 (А). При этом принималось, что центры капилляров имеют ненулевую размерность и, следовательно, могут быть различимы на плоскости. На фиг.3Б то же изображение показано без центров, находящихся ближе чем на 5 мкм (8,25 мм на микрофотографии) к соседним. Удаление центров в группах близко расположенных профилей капилляров проводилось произвольно.


Способ исследования пространственной организации объектов основывается на выполнении следующих этапов. Объекты подвергают стереологическому зондированию. Размеры, ориентацию и/или расположение получаемых профилей стереологического зондирования измеряют. Из результатов замеров формируют массив данных об исследуемых объектах. Данные массива преобразуют в статистическое распределение координат расположения профилей стереологического зондирования объектов. Полученные распределения аппроксимируют модельными распределениями, рассчитанными для заданных параметров объектов и параметров стереологического зондирования. Технический результат - изучение структурной организации объектов во временной динамике, например в реальном режиме времени. 26 з.п. ф-лы, 4 табл., 6 ил.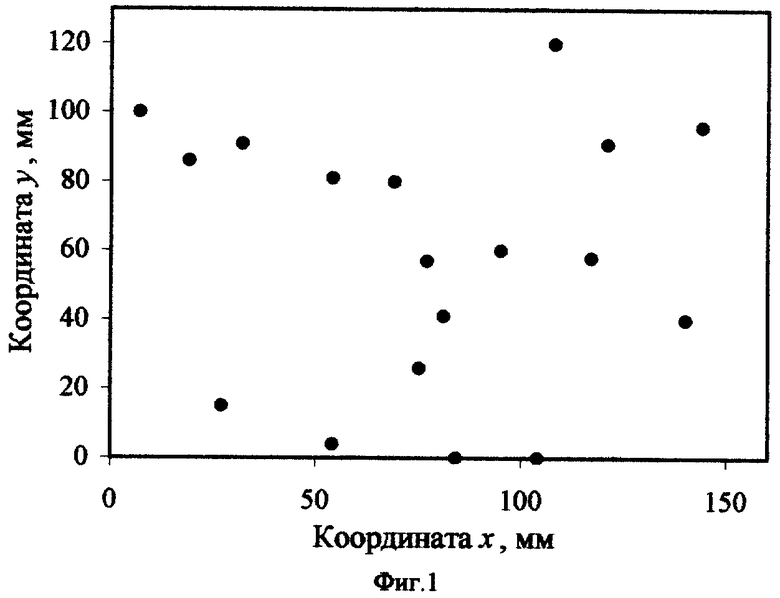
| Tewari A., Dighe M., Gokhale A.M | |||
| Quantitative characterization of spatial arrangement of micropores in cast microstructures | |||
| // Mater | |||
| Character | |||
| Способ и аппарат для получения гидразобензола или его гомологов | 1922 |
|
SU1998A1 |
| Приспособление с иглой для прочистки кухонь типа "Примус" | 1923 |
|
SU40A1 |
| СПОСОБ СТЕРЕОЛОГИЧЕСКОЙ ОЦЕНКИ ДИСТРАКЦИОННОГО ОСТЕОГЕНЕЗА, УЗЕЛ СОЕДИНЕНИЯ ОПОР АППАРАТА, ИСПОЛЬЗУЕМЫЙ ПРИ ЕГО ОСУЩЕСТВЛЕНИИ | 1996 |
|
RU2165243C2 |
| US 5825908 A, 20.10.1998 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОДОПРОЧНОСТИ ПОЧВЕННЫХ АГРЕГАТОВ | 2007 |
|
RU2344419C1 |
Авторы
Даты
2007-01-10—Публикация
2002-06-24—Подача