Область изобретения
Настоящее изобретение относится к исследованию различных равновесных случайных процессов и их регулированию для получения требуемых характеристик этих процессов.
Существующий уровень техники
Равновесными случайными процессами называются такие случайные процессы, в которых каждое отдельное случайное воздействие достаточно мало, причем эти воздействия имеют разную величину и различную направленность. В этом случае регулирование, целью которого является поддержание равновесия, должно учитывать суммарный результат случайных воздействий за конечный промежуток времени.
Примерами равновесных случайных процессов могут служить: удержание в состоянии равновесия тела, масса и плотность которого изменяются под воздействием случайных факторов (например, поддержание на заданной траектории космического корабля, внутри которого происходит перемещение масс; удержание мишени под жестким излучением в магнитном поле); удержание траектории движения объекта при сильных отклоняющих воздействиях (удержание курса морского судна во время шторма); поддержание постоянного давления в сосуде с упругими стенками, поступление и истечение текучей среды из которого подвержено случайным воздействиям (давление в газо- или нефтепроводах).
Кроме того, равновесные случайные процессы известны и в других областях. В биологии их примерами могут быть, например, поддержание кровяного давления, либо равновесие в биологических популяциях. В теории больших систем равновесными случайными процессами описывается управление потоками запросов, очередями; в психологии - поведение, основанное на соизмерении рисков; в социологии - формирование коллективных решений и предпочтений. В экономике примерами равновесных случайных процессов являются ситуации на локальных, региональных и глобальных рынках товаров, услуг, ценных бумаг, а кроме того, управление, основанное на нормах и нормативах.
Известен, например, способ управления динамической системой со стохастическим характером протекающего процесса, в котором специфическую модель процесса и управляющее воздействие формируют так, чтобы производная от логарифма получаемого при реализации события полезного эффекта, зависящего от управляющего воздействия, равнялась производной от логарифма плотности вероятности этого события во времени, определяемой моделью процесса (патент РФ №2059975, кл. G 05 В 13/00, опубл. 10.05.1996). Этот способ имеет достаточно узкие пределы применения.
Наиболее близким к заявленному является способ регулировки интегральных характеристик равновесного случайного процесса, заключающийся в том, что а) измеряют с помощью соответствующих датчиков независимые случайные величины, именуемые факторами (f) и характеризующие исследуемый равновесный случайный процесс, и исходные параметры, именуемые показателями (р) этого случайного процесса; б) для исследуемого равновесного случайного процесса в соответствии с априорной информацией о нем строят имитационные модели; в) вводят измеренные факторы (f) и исходные параметры (р) в память процессорного устройства в качестве входных сигналов для имитационных моделей (патент США №6216083, кл. G 06 F 19/00, опубл. 10.04.2001). Этот способ также имеет довольно узкие пределы применения.
Сущность изобретения
Цель настоящего изобретения состоит в создании такого способа регулировки интегральных характеристик равновесного случайного процесса, который позволил бы применять его для любых равновесных процессов.
Эта цель реализуется в способе регулировки интегральных характеристик равновесного случайного процесса, заключающемся в том, что а) измеряют с помощью соответствующих датчиков независимые случайные величины, именуемые факторами (f) и характеризующие исследуемый равновесный случайный процесс, и исходные параметры, именуемые показателями (р) этого случайного процесса; б) для исследуемого равновесного случайного процесса в соответствии с априорной информацией о нем строят имитационные модели; в) вводят измеренные факторы (f) и исходные параметры (р) в память процессорного устройства в качестве входных сигналов для имитационных моделей, - благодаря тому, что на шаге б) в качестве имитационных моделей строят первую (ρ 1) и вторую (ρ 2) имитационные модели, отображающие соответственно зависимость реализации интегральной характеристики, именуемой фактом по завышению (Fa1), и интегральной характеристики, именуемой фактом по занижению (Fa2), от факторов и показателей: Fa1=ρ 1(f, p); Fa2=ρ 2(f, р), и сохраняют первую и вторую имитационные модели ρ 1 и ρ 2 в памяти процессорного устройства; на шаге в) вводят измеренные факторы (f) и исходные параметры (р) в память процессорного устройства в качестве входных сигналов для первой и второй имитационных моделей и запускают работу этих имитационных моделей; после чего осуществляют следующие шаги: г) в течение заранее заданного промежутка времени итеративно выполняют шаги а) и в) и накапливают в памяти процессорного устройства реализации факта по завышению и факта по занижению, полученные в процессе работы соответственно первой и второй имитационных моделей; д) для исследуемого равновесного случайного процесса в соответствии с априорной информацией о нем строят на шаге б) третью (ϕ 1) и четвертую (ϕ 2) имитационные модели, отображающие соответственно зависимость интегральной характеристики, именуемой издержками завышения и характеризующей отклонение факта по завышению Fa1 от заранее неизвестного равновесного значения, именуемого планом (PL), и зависимость интегральной характеристики, именуемой издержками занижения и характеризующей отклонение факта по занижению Fa2 от упомянутого плана PL: ϕ 1(Fa1, PL), Fa1 ≤ PL - издержки завышения, ϕ 2(Fа2, PL), Fa2 ≥ PL - издержки занижения, и сохраняют третью и четвертую имитационные модели ϕ 1 и ϕ 2 в памяти процессорного устройства; е) с помощью третьей и четвертой имитационных моделей в соответствии с размещенным в памяти процессорного устройства алгоритмом эволюционно-симулятивного метода (ЭСМ) находят план PL, удовлетворяющий заранее заданному критерию на основании условий регулирования; ж) используя найденную в процессе работы в соответствии с алгоритмом ЭСМ величину плана PL, осуществляют регулирующее воздействие по изменению по меньшей мере части исходных параметров р исследуемого равновесного случайного процесса; з) возобновляют шаги г), е) и ж) на каждом следующем заранее заданном промежутке времени для обеспечения такого изменения параметров р в реальном масштабе времени, чтобы интегральные характеристики исследуемого равновесного случайного процесса или производные от них величины отвечали заранее заданным условиям.
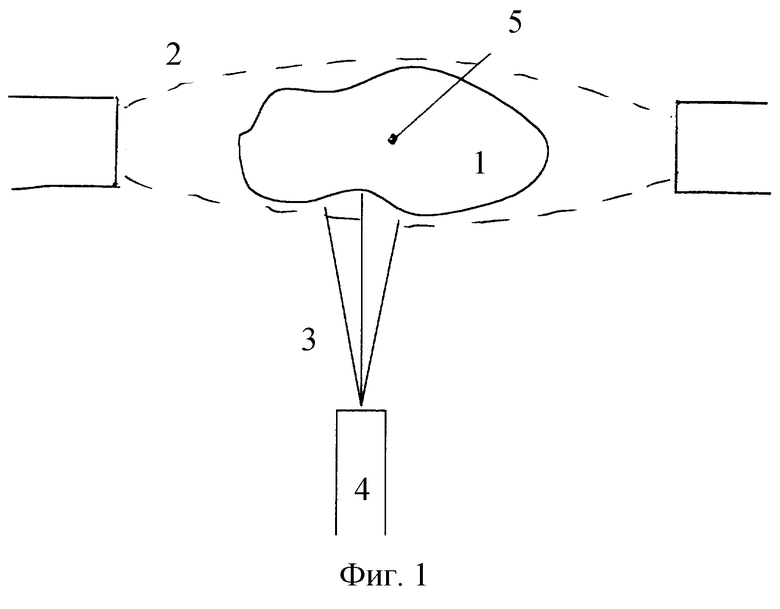
Дополнительное отличие способа по данному изобретению состоит в том, что заранее заданным критерием является равенство усредненных по всем итерациям издержек завышения, именуемых риском завышения (M{ϕ 1(Fa1, PL)}), и усредненных по всем итерациям издержек занижения, именуемых риском занижения (М{ϕ 2(Fа2, PL)}):
minPL{maxi{M{ϕ i(Fai, PL)}}},
либо заранее заданным критерием является минимум суммы риска завышения и риска занижения:
minPL M{Ф(Fa1, Fа2, PL)},
где 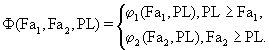
либо заранее заданным критерием является заданная вероятность превышения планом факта по завышению, именуемая надежностью по завышению (Рзав),:
(PL≥ Fa1)=Рзав,
либо заранее заданным критерием является заданная вероятность превышения фактом по занижению плана, именуемая надежностью по занижению (Рзан)
(Fа2 ≥ PL)=Рзан,
либо заранее заданным критерием является заданное отношение абсолютного значения прироста риска завышения при единичном отклонении от равновесия в сторону завышения к абсолютному приросту риска занижения при таком же отклонении в сторону занижения, именуемое Завышение/Занижение:
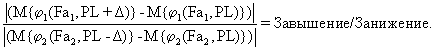
Еще одно дополнительное отличие способа по данному изобретению состоит в том, что в случае, когда равновесный случайный процесс характеризуется также комбинаторными свойствами, осуществляют следующие шаги: и) выделяют набор данных, называемых мероприятиями и содержащих конкретные численные значения стандартного для всех мероприятий набора аддитивных показателей; к) составляют сеть непротиворечивых логических связей между мероприятиями; л) выделяют один из показателей в качестве ограниченного ресурса с допустимым предельным значением; м) выделяют еще один из показателей в качестве целевого показателя; н) формируют с помощью алгоритма динамического программирования для решения булевых задач набор мероприятий, обеспечивающий заранее заданный вид экстремума для целевого показателя, не противоречащий составленной сети логических связей и требующий ограниченного ресурса, не превосходящего допустимого предельного значения; о) осуществляют регулирующее воздействие на шаге ж) с учетом найденного на шаге н) набора мероприятий.
В существующем уровне техники не выявлены объекты с таким же набором существенных признаков, что позволяет считать заявленный способ новым.
В существующем уровне техники не выявлены также объекты с набором существенных признаков, отличающих заявленный способ от наиболее близкого аналога. Это позволяет считать, что заявленный способ имеет изобретательский уровень.
Краткое описание чертежей
Настоящее изобретение иллюстрируется следующими чертежами.
Фиг.1 показывает пример системы, в которой реализуется способ р регулировки интегральных характеристик равновесного случайного процесса по настоящему изобретению.
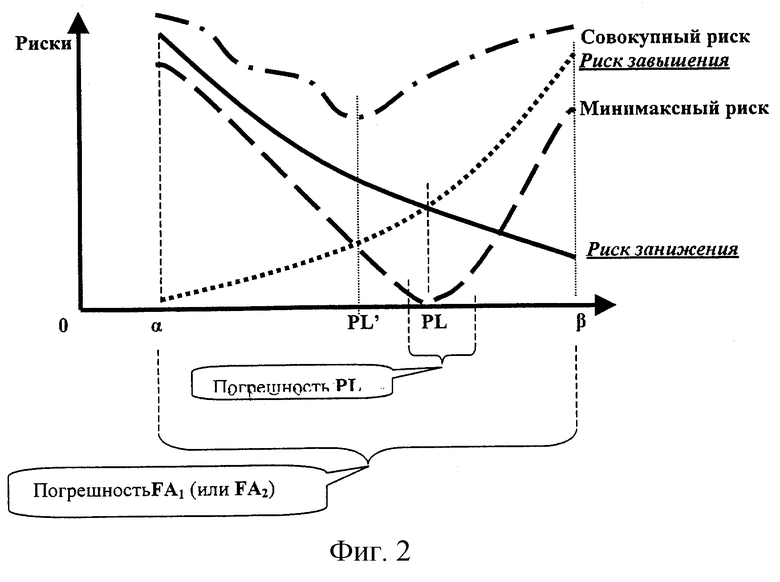
Фиг.2 иллюстрирует нахождение величины плана PL.
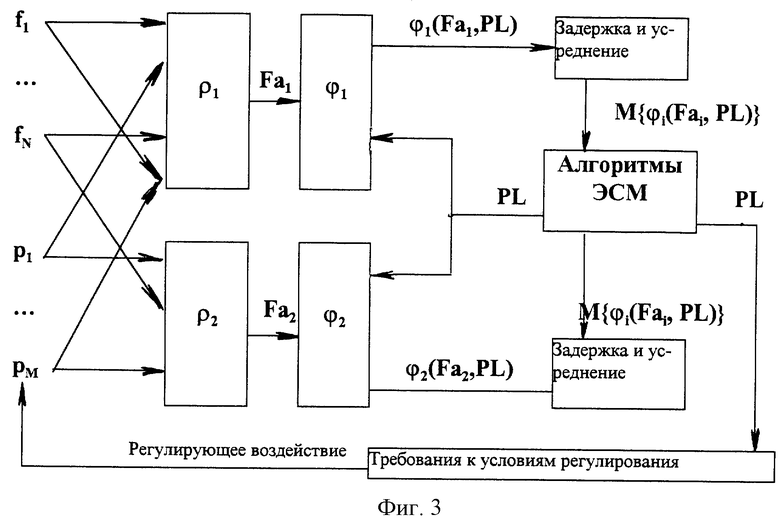
Фиг.3 является условной схемой механизма реализации способа регулировки интегральных характеристик равновесного случайного процесса в соответствии с настоящим изобретением в отсутствие в этом процессе комбинаторных свойств.
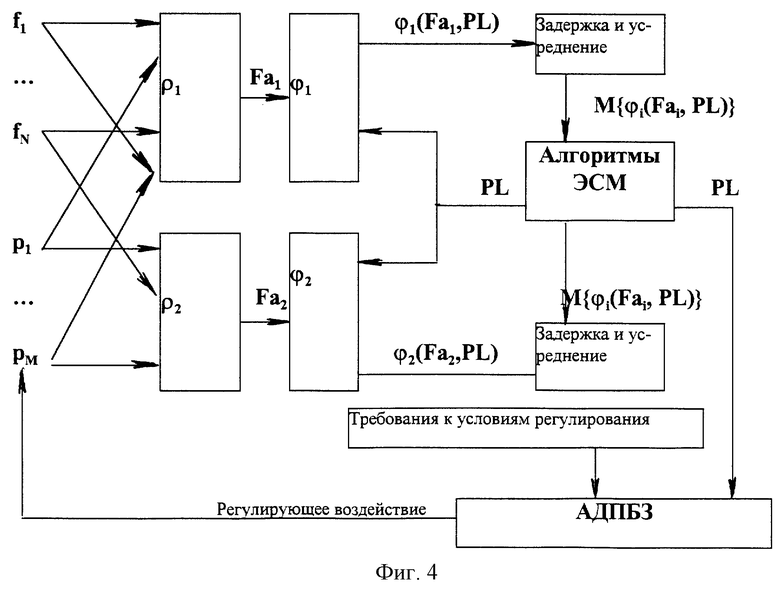
Фиг.4 является условной схемой механизма реализации способа регулировки интегральных характеристик равновесного случайного процесса в соответствии с настоящим изобретением при наличии в этом процессе комбинаторных свойств.
Подробное описание изобретения
Ниже заявленный способ раскрыт с помощью примеров его осуществления, которые приведены только для лучшего понимания настоящего изобретения и нисколько не ограничивают его объема.
Пусть имеется необходимость удерживать от вращения мишень, подвешенную в магнитном поле и обстреливаемую пучком жесткого излучения (фиг.1). В различных физических экспериментах и исследованиях возникают специфические вопросы удержания облучаемой мишени от смещения или, в некоторых случаях от вращения, с учетом того, что в роли мишени могут выступать либо очень малые количества коротко живущего вещества, либо вещества с переменной плотностью (например) плазмы. В этом случае гравитационное притяжение мишени 1 уравновешивается магнитным полем 2, но закрепление мишени 1 отсутствует. Пучок 3 жесткого излучения из пушки 4 частично рассеивается в среде, так что выбивание частиц из любого участка мишени 1 имеет ненулевую вероятность. Чтобы не возникало вращения мишени 1, среднестатистический центр пучка 3 должен быть направлен в центр 5 масс мишени 1. Однако положение этого центра 5 масс случайным образом изменяется под влиянием выбиваемых из мишени 1 частиц.
Для осуществления в этом случае способа регулирования по настоящему изобретению необходимо осуществлять импульсный процесс регулирования. Для этого нужно измерить факторы и исходные параметры данного случайного процесса.
В данном случае компонентами вектора факторов f являются: масса, координаты и частота вылета частиц, выбиваемых из мишени 1.
Компонентами вектора параметров р являются: масса, угол вылета и фокусировка (кучность) частиц, вылетающих из пушки 4.
Фактом по завышению Fa1=ρ 1(f, p) в данном случае будет отклонение точки соударения бомбардирующей частицы от неизвестного текущего центра 5 масс (т.е. плана PL) влево, а фактом по занижению Fa2=ρ 2(f, р) - отклонение точки соударения бомбардирующей частицы от PL вправо.
Издержками завышения ϕ 1(Fa1, PL), Fa1 ≤ PL будет в данном случае мгновенный левый крутящий момент, возникающий при соударении бомбардирующей частицы с мишенью 1, а издержками занижения ϕ 2(Fa2, PL), Fa2 ≥ PL - аналогичный правый крутящий момент.
Тогда риск завышения M{ϕ 1(Fa1, PL)} представляет собой усредненный за конечный промежуток времени левый крутящий момент, тогда как риск занижения M{ϕ 2(Fa2, PL)} - усредненный за тот же промежуток времени правый крутящий момент.
В данном примере регулировка интегральных характеристик равновесного случайного процесса осуществляется следующим образом.
С помощью соответствующих (например, сцинтилляционных) датчиков, установленных вокруг мишени 1, непрерывно измеряются факторы f, а с помощью других (например, индукционных или емкостных) датчиков непрерывно измеряются параметры р. Сигналы со всех датчиков поступают в процессорное устройство, запрограммированное на вычисление за конечный промежуток времени (т.е. импульсно) фактов по завышению и занижению.
Данные вычисления производятся на основании заранее составленных и введенных в память процессорного устройства первой и второй имитационных моделей ρ 1 и ρ 2, рассчитанных в соответствии с априорной информацией об исследуемом процессе. Эти имитационные модели ρ 1 и ρ 2 описываются соответствующими программами и позволяют определить зависимости реализации интегральной характеристики, именуемых фактом по завышению (Fa1) и фактом по занижению (Fa2), от факторов f и показателей р исследуемого случайного процесса. После запуска первой и второй имитационных моделей ρ 1 и ρ 2 в процессорном устройстве и итеративного выполнения вышеуказанных измерений и вычислений в памяти процессорного устройства накапливают реализации факта по завышению Fa1 и факта по занижению Fа2, полученные в процессе работы соответственно первой и второй имитационных моделей.
Помимо первой и второй имитационных моделей, в памяти процессорного устройства сохраняют также третью (ϕ 1) и четвертую (ϕ 2) имитационные модели, построенные для исследуемого равновесного случайного процесса в соответствии с априорной информацией о нем и отображающие соответственно зависимость интегральной характеристики, именуемой издержками завышения ϕ 1(Fa1, PL) и характеризующей отклонение факта по завышению Fa1 от заранее неизвестного равновесного значения, именуемого планом PL, и зависимость интегральной характеристики, именуемой издержками занижения ϕ 2(Fa2, PL) и характеризующей отклонение факта по занижению Fа2 от упомянутого плана PL. При этом вычисление плана PL осуществляют с помощью третьей и четвертой имитационных моделей ϕ 1 и ϕ 2 в соответствии с размещенным в памяти процессорного устройства алгоритмом эволюционно-симулятивного метода (ЭСМ) так, чтобы найденный план PL удовлетворял заранее заданному критерию на основании условий регулирования. Таким критерием может быть в данном примере удержание центра масс мишени 1 в заранее заданном положении с наперед заданной точностью.
Для обеспечения этого условия можно использовать различные конкретные критерии. В частности, заранее заданным критерием может выступать равенство усредненных по всем итерациям издержек завышения, именуемых риском завышения (M{ϕ 1(Fa1, PL)}), и усредненных по всем итерациям издержек занижения, именуемых риском занижения (M{ϕ 2(Fa2, PL)}), т.е. minPL{maxi{M{ϕ i(Fai, PL)}}}. Другим вариантом выражения этого заранее заданного критерия может быть минимум суммы риска завышения и риска занижения, т.е. minPL M{Ф(Fa1, Fa2, PL)},
где 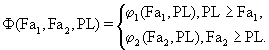
Другими возможными выражениями упомянутого заранее заданного критерия могут быть заданная вероятность превышения планом факта по завышению, именуемая надежностью по завышению (Рзав), т.е. (PL≥ Fa1)=Рзав, либо заданная вероятность превышения фактом по занижению плана, именуемая надежностью по занижению (Рзан), т.е. (Fa2 ≥ PL)=Рзан.
Еще одной возможностью для указанного заранее заданного критерия является заданное отношение абсолютного значения прироста риска завышения при единичном отклонении от равновесия в сторону завышения к абсолютному приросту риска занижения при таком же отклонении в сторону занижения, именуемое Завышение/Занижение:
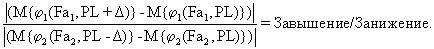
Алгоритм ЭСМ, позволяющий вычислить план PL, подробно описан в следующих книгах: В.Е. Лихтенштейн. Дискретность и случайность в экономико-математических задачах. - М.: Наука, 1973; В.Е.Лихтенштейн. Эволюционно-симулятивный метод и его применение для решения плановых и прогнозных задач. - М.: Наука, 1976; В.Е.Лихтенштейн. Эволюционно-симулятивные модели в планировании. - М.: Наука, 1980.
Эволюционно-симулятивный метод (ЭСМ) - это метод расчета равновесных характеристик случайного процесса без аппроксимации и с учетом того, что условия (правила) отклонения от равновесия в одну сторону (“влево”) могут отличаться от условий (правил) отклонения от равновесия в другую сторону (“вправо”), а следствия отклонения влево могут формироваться по иным законам (правилам), чем следствия отклонения вправо. Текущие характеристики случайного процесса могут поступать от соответствующих датчиков, либо воспроизводиться с помощью имитационных моделей, которые строятся исходя из априорной информации о процессе.
Название метода получено путем объединения двух терминов: "Эволюционный" и "Симулятивный". Эволюционный - потому, что в ЭСМ применен алгоритм оптимизации, использующий некоторые принципы естественной эволюции, которая, в свою очередь, представляет собой направленный случайный поиск. Симулятивный - потому, что ЭСМ допускает использование принципов диалогового (симулятивного) моделирования как при разработке имитационных моделей, так и непосредственно в процессе расчетов, в случае, если в течение этого процесса информация о процессе может экспортно пополняться или видоизменяться. ЭСМ включает в себя строгую структурную формулировку задачи, называемую Эволюционно-симулятивной моделью, и алгоритмы поиска ее решения.
ЭСМ соединяет достоинства некоторых других методов. В частности, подобно байесовскому подходу, стохастическому программированию и другим аналитическим методам, ЭСМ дает строгое и универсальное определение оптимума в условиях неопределенности, обобщая ряд известных формулировок. Вместе с тем, алгоритмы ЭСМ позволяют находить оптимум среди реализации случайного процесса. ЭСМ позволяет осуществлять диалог на основе нескольких вариантов прямых и обратных формулировок Эволюционно-симулятивной модели. Программной реализацией ЭСМ является модуль статистической оптимизации диалоговой компьютерной системы “Точность, Аргументированность, Надежность, Ясность” ("ТАНЯ").
В данном примере сущность этого метода можно проиллюстрировать с помощью фиг.2. На этом чертеже показаны кривые, отображающие различные риски в зависимости от значений плана PL. План PL рассчитывается, исходя из выбранного варианта для упомянутого заранее заданного критерия, например по минимуму совокупного или минимаксного риска.
После нахождения величины плана PL осуществляют регулирующее воздействие по изменению по меньшей мере части исходных параметров р исследуемого равновесного случайного процесса, чтобы интегральные характеристики исследуемого равновесного случайного процесса или производные от них величины отвечали заранее заданным условиям.
Рассмотренные операции по вычислению плана PL и регулированию параметров р возобновляют на каждом следующем заранее заданном промежутке времени.
Сказанное иллюстрируется на фиг.3, где показана условная схема механизма реализации заявленного в соответствии с настоящим изобретением способа регулировки интегральных характеристик равновесного случайного процесса.
В некоторых случаях исследуемый равновесный случайный процесс может характеризоваться еще и комбинаторными свойствами, причем при решении экономических и технических задач комбинаторные и равновесные процессы могут быть увязаны в итерационные процедуры. В частности, в рассмотренном выше примере (фиг.1) внутри мишени 1 может происходить перемещение масс, что приведет к дополнительным смещениям центра 5 масс этой мишени 1. Эти условия можно описать комбинаторными свойствами, которые могут быть присущи также и средствам регулирования. В этом случае способ регулировки равновесного случайного процесса по настоящему изобретению дополняется такими операциями:
- выделяют набор данных, называемых мероприятиями и содержащих конкретные численные значения стандартного для всех мероприятий набора аддитивных показателей;
- составляют сеть непротиворечивых логических связей между выделенными мероприятиями;
- выделяют один из показателей в качестве ограниченного ресурса с допустимым предельным значением;
- выделяют еще один из показателей в качестве целевого показателя;
- с помощью алгоритма динамического программирования для решения булевых задач (АДПБЗ) формируют набор мероприятий, обеспечивающий заранее заданный вид экстремума для целевого показателя, не противоречащий составленной сети логических связей и требующий ограниченного ресурса, не превосходящего допустимого предельного значения;
- регулирующее воздействие осуществляют с учетом найденного, как описано выше, набора мероприятий.
Иллюстрацией сказанного может служить рассмотренный на фиг.1 пример удержания от вращения мишени 1 с переменной массой в случае, если изменение параметров регулирования электронной пушки 4 имеет ряд ограничений и условий, в том числе логических. В частности, углы отклонения пушки 4 от вертикали, интенсивность излучения и его фокусировка по техническим, технологическим или иным причинам могут быть связаны различной системой условий, например:
- если отклонение в плоскости Х более, чем αi°, то интенсивность излучения не более, чем β i(X), а фокусировка не лучше, чем γ i(X), i=1,...,I;
- если отклонение в плоскости Y, ортогональной относительно X, более, чем αj°, то интенсивность излучения не более, чем β j(Y), а фокусировка не лучше, чем γ j(Y), j=1,...,J;
- если отклонение в плоскости Z, ортогональной относительно Х и Y, более, чем αk°, то интенсивность излучения не более, чем β k(Z), а фокусировка не лучше, чем γ k(Z), k=1,...,K;
- углы отклонения в ортогональных плоскостях ограничены условиями, обеспечивающими направление крутящего момента в сектор, содержащий PL, в частности:
αш°+αj°<V1, αj°+αk°<V2, αi°+αk°<V3;
- качество фокусировки ограничено условием:
γ i(X)· A+γ j(Y)· B+γ k(Z)· C<V,
где А, В, С и V константы;
- возникающий крутящий момент М зависит от всех параметров (включая углы отклонения, соответствующие интенсивность излучения и его фокусировку), т.е.:
М=F(αi°, β i(Х), γ i(X), αj°, β j(Y), γ j(Y), αk°, β k(Z), γ k(Z)).
В рассматриваемой ситуации выработка управляющего воздействия предполагает оптимальный подбор дискретных параметров αi°, i=1,...I, αj°, j=1,...,J, αk°, k=1,...,K при соблюдении указанных условий, по критерию максимума крутящего момента М→ max при каждом импульсном управляющем воздействии. Если в процессорное устройство загружен АДПБЗ, если датчики передают в процессорное устройство фактические текущие значения параметров и если в процессорное устройство загружен сервисный алгоритм определения относительных пространственных координат PL и текущего центра масс, то оптимальный подбор параметров может осуществляться в реальном масштабе времени.
Указанные выше понятия в конкретной ситуации рассмотренного примера имеют следующий физический смысл:
- мероприятие - выбор конкретного значения для αi°, или αj°, или αk°и, соответственно, зависящих от этого выбора, интенсивности излучения, его фокусировки и крутящего момента;
- параметры мероприятий - углы отклонения, интенсивность излучения, фокусировка, крутящий момент;
- логические условия - ограничения, обеспечивающие направленность крутящего момента в заданный сектор, включающий PL;
- ограниченный ресурс - взвешенная сумма параметров фокусировки;
- целевой параметр - крутящий момент.
Этот вариант осуществления заявленного по настоящему изобретению способа иллюстрируется на фиг.4, где по сравнению с фиг.3 добавлен блок, обеспечивающий выполнение АДПБЗ. Данный алгоритм известен из уже упомянутых выше книг В.Е. Лихтенштейна.
Алгоритм динамического программирования для решения булевых задач (АДПБЗ) - это алгоритм, позволяющий составлять оптимальный набор элементов (“мероприятий”) при наличии ресурсного ограничения, логических связей (ЛС) между мероприятиями и цели. В сравнении с другими методами дискретной оптимизации АДПБЗ обладает следующими основными достоинствами:
- малой чувствительностью алгоритма к размерности, в некоторых случаях с повышением (а не убыванием!) количества логических связей эффективность алгоритма возрастает;
- предоставлением всего спектра оптимальных решений для всех уровней затрат ограниченного ресурса;
- возможностью решения многокритериальных задач (на основе принципа: если задача оптимальна по одному критерию и допустима по остальным - она оптимальна);
- предоставлением в процессе диалога дополнительной информации о структуре логической сети, в частности выделением связных подсетей и допустимых выборок;
- гибкостью форм учета логических связей и удобством ведения диалога.
Время, затрачиваемое на выполнение оптимизационных расчетов, зависит от количества мероприятий, количества логических связей, объема ограниченного ресурса, конкретных особенностей логической сети и численных значений показателей. АДПБЗ предоставляет хорошие возможности для организации разнообразных итерационных процедур решения большеразмерных задач. Например, при наличии “сверхбольшой” связной подсети можно исключить несколько ЛС таким образом, чтобы разбить эту подсеть на части, найти оптимальные решения для разных уровней затрат ограниченного ресурса и исключить из них те, которые нарушают ранее исключенные ЛС. Повышению скорости счета может способствовать сокращение количества знаков у параметров мероприятий (округление).
Следует отметить, что равновесные случайные процессы в экономике обычно тесно связаны с комбинаторными процессами, в частности при:
- разработке инвестиционных проектов;
- управлении работами;
- управлении портфелем ценных бумаг;
- разработке больших систем;
- решении инженерно-экономических задач (компоновка оптимальных по надежности систем).
Промышленная применимость
Способ регулировки интегральных характеристик равновесного случайного процесса по настоящему изобретению может применяться как в технике, так и в других областях.
Хотя настоящее изобретение описано с использованием примера конкретной реализации, его объем определяется исключительно прилагаемой формулой изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВЫБОРА ЗНАЧЕНИЙ ПАРАМЕТРОВ ВНЕШНЕЙ СРЕДЫ, СОГЛАСОВАННЫХ С ОПТИМАЛЬНЫМ УПРАВЛЕНИЕМ РАВНОВЕСНЫМ СЛУЧАЙНЫМ ПРОЦЕССОМ | 2014 |
|
RU2558251C1 |
| СПОСОБ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ РАВНОВЕСНЫМ СЛУЧАЙНЫМ ПРОЦЕССОМ | 2014 |
|
RU2557483C1 |
| Способ оптимизации расходов сточных вод общесплавных систем водоотведения | 2018 |
|
RU2685897C1 |
| СИСТЕМА И СПОСОБ ДЛЯ АВТОМАТИЧЕСКОГО ПЛАНИРОВАНИЯ ЛЕЧЕНИЯ | 2015 |
|
RU2684173C2 |
| Способ определения индекса сейсмомиграционной активности в эпицентральном поле сейсмичности | 2018 |
|
RU2698559C1 |
| ГОРЕЛКА ДЛЯ ПЛАЗМЕННО-ДУГОВОЙ ОБРАБОТКИ (ВАРИАНТЫ) И СПОСОБ ЕЕ ИСПЫТАНИЙ ПЕРЕД ЕЕ ВКЛЮЧЕНИЕМ | 1996 |
|
RU2119852C1 |
| ИМИТАЦИОННАЯ МОДЕЛЬ СИСТЕМЫ УПРАВЛЕНИЯ ВОЗДУШНОЙ МИШЕНЬЮ НА ОСНОВЕ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА ИЗ СОСТАВА МИШЕННОГО КОМПЛЕКСА | 2020 |
|
RU2782035C2 |
| Электронная система медицинских осмотров (ЭСМО), способ прохождения осмотра в системе ЭСМО и программно-аппаратный комплекс Терминал в составе системы ЭСМО | 2019 |
|
RU2743088C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ МОНИТОРИНГА РИСКОВ ДЛЯ ИНФОРМАЦИОННО-УПРАВЛЯЮЩЕЙ СИСТЕМЫ В УСЛОВИЯХ ИНФОРМАЦИОННО-ТЕХНИЧЕСКИХ ВОЗДЕЙСТВИЙ | 2016 |
|
RU2634169C1 |
| Способ управления памятью компьютерной системы | 2016 |
|
RU2647627C1 |
Изобретение относится к области вычислительной техники и может быть использовано для регулировки интегральных характеристик равновесного случайного процесса. Техническим результатом является расширение функциональных возможностей. Способ заключается в том, что измеряют независимые случайные величины, характеризующие исследуемый процесс, и исходные параметры, именуемые показателями этого случайного процесса, затем в соответствии с априорной информацией о нем строят имитационные модели и вводят измеренные факторы и исходные параметры в память процессорного устройства в качестве входных сигналов для имитационных моделей. 6 з.п. ф-лы, 4 ил.
minPL{maxi{M{ϕi(Fai, PL)}}}.
minPL M{Ф(Fa1, Fa2, PL)},
где 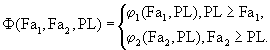
(PL≥Fa1)=Рзав.
(Fa2 ≥ PL)=Рзан.
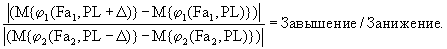
| US 6216083 А, 10.04.2001 | |||
| RU 2059975 C1, 10.05.1996 | |||
| СПОСОБ ДИАГНОСТИКИ ПО СТАТИЧЕСКОМУ НИЗКОЧАСТОТНОМУ СИГНАЛУ | 1997 |
|
RU2129301C1 |
| ВЕРОЯТНОСТНЫЙ АВТОМАТ | 2000 |
|
RU2169944C1 |
| DE 19506109 C1, 05.06.1996 | |||
| Кипятильник для воды | 1921 |
|
SU5A1 |
Авторы
Даты
2004-05-27—Публикация
2002-09-30—Подача