СПОСОБ ВЫБОРА ЗНАЧЕНИЙ ПАРАМЕТРОВ ВНЕШНЕЙ СРЕДЫ, СОГЛАСОВАННЫХ С ОПТИМАЛЬНЫМ УПРАВЛЕНИЕМ РАВНОВЕСНЫМ СЛУЧАЙНЫМ ПРОЦЕССОМ Российский патент 2015 года по МПК G06F17/00 

Область техники, к которой относится изобретение

Данное изобретение относится к вычислительной технике, а конкретнее - к способу выбора значений параметров внешней среды, согласованных с оптимальным управлением равновесным случайным процессом.

Уровень техники

В настоящее время процедура выбора значений параметров внешней среды для управления равновесным случайным процессом достаточно известна (см., к примеру, патент США №6216083, опубл. 10.04.2001, патент РФ №2059975, опубл. 10.05.1996, и патент РФ №2229741, опубл. 27.05.2004).

Однако ни в одном из этих или других известных документов не говорится о том, как осуществлять выбор значений параметров внешней среды, согласованных с оптимальным управлением равновесным случайным процессом.

Раскрытие изобретения

Целью настоящего изобретения является разработка такого технического решения, которое расширяло бы функциональные возможности известных способов управления равновесными случайными процессами, обеспечивая в автоматизированном режиме выбор значений параметров внешней среды, согласованных с оптимальным управлением равновесным случайным процессом.

Эта цель достигается благодаря тому, что в настоящем изобретении предложен способ выбора значений параметров внешней среды, согласованных с оптимальным управлением равновесным случайным процессом (РСП), заключающийся в том, что: выделяют для РСП его характеристики в виде независимых случайных величин, именуемых далее факторами, и условно постоянных величин, именуемых далее показателями, и рассматривают эти показатели и параметры законов распределения вероятностей факторов в качестве координат фазового пространства, в котором протекает РСП; строят для исследуемого РСП в соответствии с априорной информацией о нем эволюционно-симулятивную модель (ЭСМ), взаимно увязывающую координаты фазового пространства и разделяющую эти координаты на исходные показатели, управляющие параметры и расчетные показатели; выделяют среди факторов внешние факторы, параметры законов распределения вероятностей которых не являются управляющими параметрами; загружают ЭСМ в память процессорного устройства без выделенных внешних факторов; измеряют с помощью соответствующих датчиков исходные показатели исследуемого РСП и вводят измеренные исходные показатели в память процессорного устройства в качестве входных сигналов для ЭСМ; рассчитывают интегральную характеристику РСП и ее интервал изменений; выделяют в интервале изменений равноотстоящие точки и с применением ЭСМ для каждого из внешних факторов выполняют в процессорном устройстве в автоматизированном режиме в каждой из выделенных точек расчет совместных с интегральной характеристикой реализаций значений данного фактора и соответствующих значений этого же фактора на сглаживающей полиномиальной кривой и рассчитывают тесноту связи фактора и интегральной характеристики, а также устанавливают физически допустимые в данных условиях пределы изменения фактора; применяют процедуру сужения пределов изменения внешних факторов, переходя от внешнего фактора с большим значением тесноты к внешнему фактору с ее меньшим значением и принимают внешние факторы с суженными пределами в качестве значений параметров внешней среды, согласованных с оптимальным управлением РСП.

Особенность способа по настоящему изобретению состоит в том, что в интервале изменений интегральной характеристики РСП могут выделять десять равноотстоящих точек, а в качестве сглаживающей полиномиальной кривой могут использовать кубический полином.

Еще одна особенность способа по настоящему изобретению состоит в том, что если в составе ЭСМ имитационная модель условий завышения и имитационная модель условий занижения совпадают, то процедуру сужения предела могут осуществлять за один этап, в котором: рассчитывают в автоматизированном режиме в процессорном устройстве несколько совместных с рассчитанной с помощью ЭСМ оптимальной интегральной характеристикой реализаций данного фактора, находят их среднее и погрешность измерения; и устанавливают суженный предел равным погрешности измерения значения данного фактора; если же в составе ЭСМ имитационная модель условий завышения и имитационная модель условий занижения не совпадают, то процедуру сужения предела могут осуществлять за несколько этапов, в которых: на первом этапе рассчитывают в автоматизированном режиме в процессорном устройстве на каждом шаге несколько совместных с оптимальной при данных исходных показателях интегральной характеристикой реализаций данного фактора, находят их среднее и погрешность измерения и устанавливают суженный предел равным погрешности измерения значения данного фактора, на втором и последующих этапах повторяют те же действия, что и на первом этапе, до тех пор, пока предел изменения значения данного фактора не станет меньше или равным погрешности измерения этого фактора, либо пока не возникнет несовместность ЭСМ.

Наконец, еще одна особенность способа по настоящему изобретению состоит в том, что могут рассчитывать пятнадцать совместных реализаций данного фактора.

Краткое описание чертежей

Настоящее изобретение иллюстрируется приложенными чертежами.

На Фиг. 1 приведена экранная форма модуля Equilibrium с загруженной Эволюционно-симулятивной моделью (1)-(5), с исходными данными из таблицы 2 и результатами прямого оптимизационного расчета.

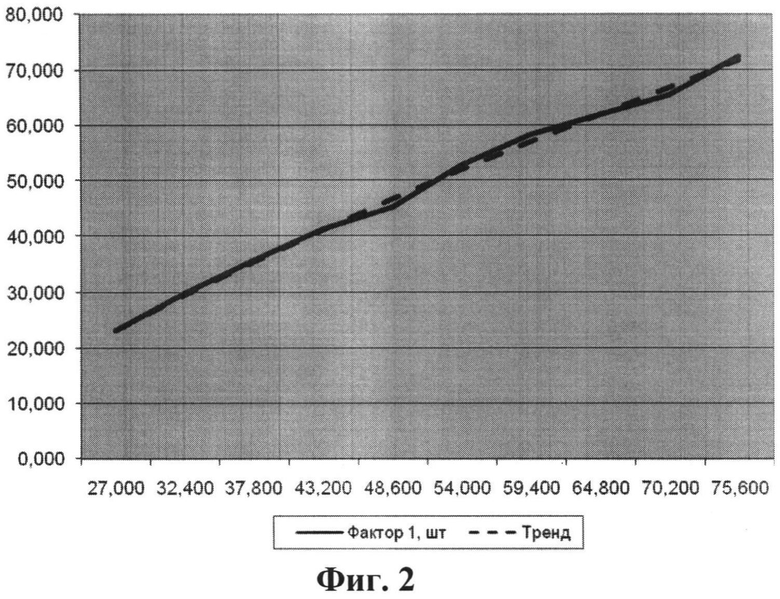
На Фиг. 2 показана зависимость совместной с PL реализации фактора f₁ от оптимальной реализации PL.

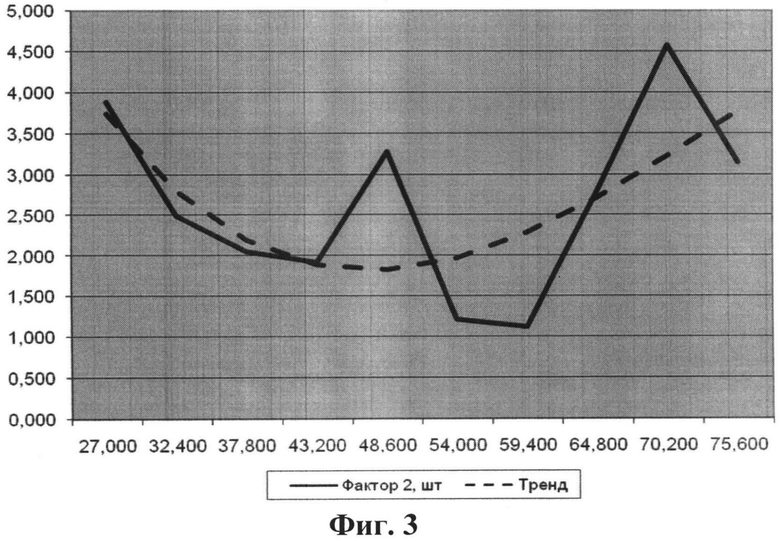
На Фиг. 3 показана зависимость совместной с PL реализации фактора f₂ от оптимальной реализации PL.

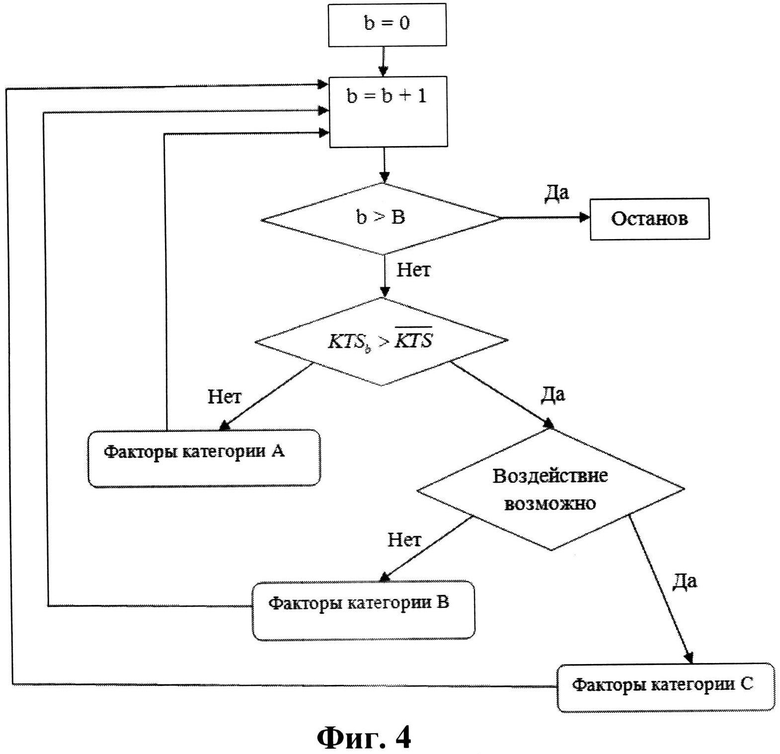
На Фиг. 4 показана блок-схема алгоритма разделения внешних факторов на категории.

Подробное описание

Равновесным случайным процессом (далее - РСП) называется процесс, траектория которого в фазовом пространстве определяется сочетанием случайных факторов и управляющих воздействий, направление и сила которых определяются размером и направлением отклонения фактической траектории процесса от сглаженной. В этом случае регулирование, целью которого является поддержание равновесия, должно учитывать суммарный результат случайных воздействий за конечный промежуток времени.

Примерами равновесных случайных процессов могут служить: удержание в состоянии равновесия тела, масса и плотность которого изменяются под воздействием случайных факторов (например, поддержание на заданной траектории космического корабля, внутри которого происходит перемещение масс; удержание мишени под жестким излучением в магнитном поле); удержание траектории движения объекта при сильных отклоняющих воздействиях (удержание курса морского судна во время шторма); поддержание постоянного давления в сосуде с упругими стенками, поступление и истечение текучей среды из которого подвержено случайным воздействиям (давление в газо- или нефтепроводах).

Кроме того, равновесные случайные процессы известны и в других областях. В биологии их примерами могут быть поддержание кровяного давления, либо равновесие в биологических популяциях. В теории больших систем равновесными случайными процессами описывается управление потоками запросов, очередями; в психологии - поведение, основанное на соизмерении рисков; в социологии - формирование коллективных решений и предпочтений. В экономике примерами равновесных случайных процессов являются ситуации на локальных, региональных и глобальных рынках товаров, услуг, ценных бумаг, а кроме того, управление, основанное на нормах и нормативах.

Как уже отмечено в разделе «Уровень техники», определение и регулирование характеристик РСП подробно описано в патенте РФ №2229741. В частности, в этом документе раскрыт метод построения эволюционно-симулятивной модели (ЭСМ) исследуемого РСП. ЭСМ представляет собой строгую структурную формулировку задачи, а ее название получено путем объединения двух терминов «эволюционный» и «симулятивный». Термин «эволюционный» указывает на то, что в ЭСМ применяется оптимизация, использующая некоторые принципы естественной эволюции, которая, в свою очередь, представляет собой направленный случайный поиск. Термин «симулятивный» указывает на то, что ЭСМ допускает использование принципов диалогового (симулятивного) моделирования как при разработке имитационных моделей, так и непосредственно в процессе расчетов, в случае, если в течение моделируемого РСП информация о процессе может экспертно пополняться или видоизменяться.

Внешние условия протекания РСП, а также каналы, посредством которых можно воздействовать на этот РСП, характеризуются законами распределения вероятностей некоторых независимых случайных величин (факторов), и некоторыми условно постоянными величинами (исходными показателями). Параметры этих законов распределения вероятностей значений факторов, а также эти исходные показатели далее именуются характеристиками РСП. Основными характеристиками РСП являются PL, Р⁰ и З/З, поясняемые далее и определяемые структурной формулировкой эволюционно-симулятивной модели (ЭСМ). Показатели, зависящие хотя бы от одной из основных характеристик РСП, именуются далее расчетными показателями.

В данном описании отмеченные выше условно постоянные величины и параметры законов распределения вероятностей упомянутых факторов (т.е. характеристики РСП) рассматриваются в качестве координат фазового пространства, в котором протекает данный РСП.

Как уже отмечено выше, в способе по настоящему изобретению для исследуемого РСП в соответствии с априорной информацией о нем строят эволюционно-симулятивную модель (ЭСМ), взаимно увязывающую координаты упомянутого фазового пространства и разделяющую эти координаты на исходные показатели, управляющие параметры и расчетные показатели. Следует специально отметить, что исходными показателями могут быть как условно-постоянные величины, так и параметры законов распределения вероятностей факторов.

Управляющим параметром является тот параметр, воздействие которого направленно изменяет режим протекания РСП. Среди указанных факторов выделяют внешние факторы, параметры законов распределения вероятностей которых не являются управляющими параметрами. Поэтому построенную ЭСМ загружают без указанных (выделенных) внешних факторов в память процессорного устройства, в котором эта ЭСМ будет функционировать. В качестве такого процессорного устройства может быть выбран персональный компьютер, сервер либо несколько подобных устройств, объединенных сетью. Конкретный вид процессорного устройства не входит в объем притязаний данного изобретения.

Далее в процессе протекания исследуемого РСП с помощью соответствующих датчиков измеряют исходные показатели этого РСП и вводят измеренные исходные показатели в память процессорного устройства в качестве входных сигналов для разработанной ЭСМ. В процессе функционирования этой ЭСМ находят оптимальную траекторию РСП и соответствующее управление РСП так, как это описано в патенте тех же авторов по заявке №2014140060, поданной 03.10.2014, все содержание которой включено сюда посредством ссылки.

Введем теперь некоторые обозначения в дополнение к тем, которые были введены в указанной заявке.

Как уже отмечено, внешним фактором назовем фактор, параметры закона распределения вероятностей значений которого не являются управляющими параметрами. Пусть:

- $$f_b^{env},b=\mathrm{1,}\dots ,B$$ - внешний фактор (b - номер внешнего фактора, В - количество внешних факторов);

- $$f_b^{env}(t_n),b=\mathrm{1,}\dots ,B$$ - значения параметров закона распределения вероятностей внешнего фактора $$f_b^{env}$$ в момент t_n;

- $$\overline{f^{env}}(t_n)$$ - значение параметров законов распределения вероятностей всех внешних факторов в момент t_n.

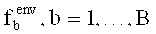
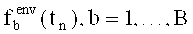
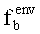
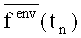
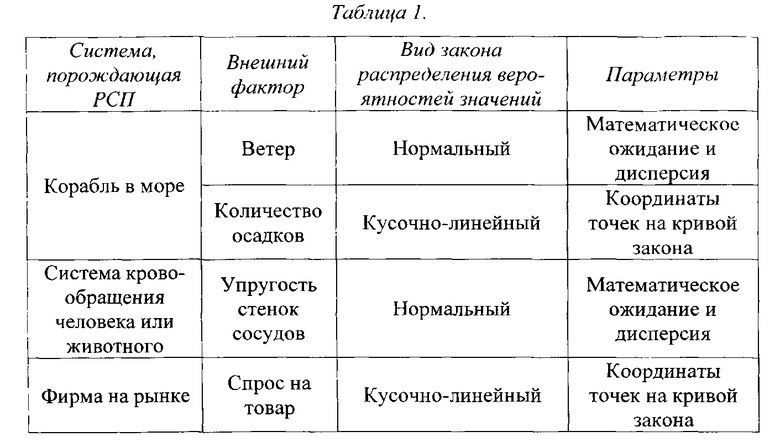
Параметры факторов 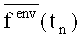$$\overline{f^{env}}(t_n)$$ характеризуют состояние внешней среды для протекания РСП в момент t_n. Иллюстративные примеры некоторых систем, порождающих РСП, и некоторых внешних факторов, действующих на эти системы:

Предполагается, что мы имеем некоторые возможности влиять на состояние внешней среды (вызвать или предотвратить осадки в том или ином районе путем распыления с самолета реагентов; улучшить упругость сосудов путем приема лекарств; повышать спрос на товар с помощью рекламы и т.п.).

Пусть U^env(t_n) - область допустимых значений параметров законов распределения вероятностей внешних факторов в момент t_n.

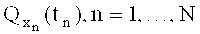
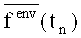
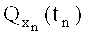
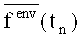
Оптимальная траектория $$Q_{x_n}(t_n),n=\mathrm{1,}\dots ,N$$ может быть осуществлена при разных значениях параметров законов распределения вероятностей внешних факторов $$\overline{f^{env}}(t_n)$$ , но вероятность того, что в момент t_n траектория пройдет через оптимальную точку $$Q_{x_n}(t_n)$$ в момент t_n, зависит от параметров $$\overline{f^{env}}(t_n)$$ .

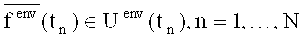
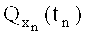
Задача состоит в том, чтобы найти такие значения для параметров законов распределения вероятностей внешних факторов $$\overline{f^{env}}(t_n)\in U^{env}(t_n),n=\mathrm{1,}\dots ,N$$ , при которых вероятность прохождения оптимальной точки $$Q_{x_n}(t_n)$$ траекторией РСП была бы максимальна.

Будем предполагать, что параметры законов распределения вероятностей внешних факторов 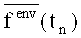$$\overline{f^{env}}(t_n)$$ в момент t_n слабо зависят или вовсе не зависят от значений этих параметров в любой иной момент t_n′. При этом предположении очевидно, что если существует способ, который позволяет решить задачу для момента t_n, то этот способ может быть итерационно применен для любой совокупности моментов t_n, n=1,…,N. С учетом этого аргумент t_n далее опускается.

Обратимся теперь к трем экспериментальным фактам, установленным с помощью вычислительных экспериментов с Эволюционно-симулятивными моделями (ЭСМ) равновесных случайных процессов (РСП).

Факт 1 выражается в следующем утверждении:

между фактором f (не обязательно внешним) и основными характеристиками РСП: PL, Р⁰, З/З - существует корреляционная зависимость.

При этом, поскольку между основными характеристиками существует взаимно однозначное соответствие (оно непосредственно вытекает из структурной формулировки эволюционно-симулятивной модели), то корреляция между f и PL равна корреляции между f и Р⁰, а также корреляции между f и З/З. Все сказанное в полной мере относится и к любому внешнему фактору 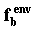$$f_b^{env}$$ .

Теснота корреляционной связи может быть как пренебрежимо малой, так и почти детерминированной. Это зависит как от особенностей имитационных моделей ρ₁, ρ₂, ρ₃, ρ₄ в составе ЭСМ, так и от особенностей исходных данных.

Для иллюстрации сделанных утверждений рассмотрим следующую простейшую Эволюционно-симулятивную модель:

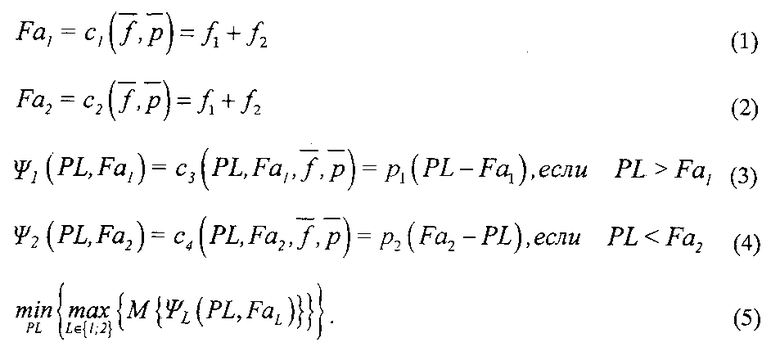
Будем считать, что факторы имеют равномерное распределение на конечном интервале. Исходные данные о факторах и исходных показателях приведены в таблице 2.

На Фиг. 1 показана Форма 1 модуля Equilibrium, в который загружена Эволюционно-симулятивная модель (1)-(5), введены исходные данные из Таблицы 2 и представлены результаты расчета, полученные в автоматизированном режиме при осуществлении диалоговой процедуры:

Расчет→Прямой/Обратный→Прямой расчет→…

В правом нижнем углу на Фиг. 1 в качестве расчетных показателей указаны:

- План - значение PL, оптимальное по критерию (5);

- Фактор 1 - совместная с PL реализация фактора 1 (то есть ƒ₁);

- Фактор 2 - совместная с PL реализация фактора 2 (то есть f₂).

Выполним диалоговую процедуру:

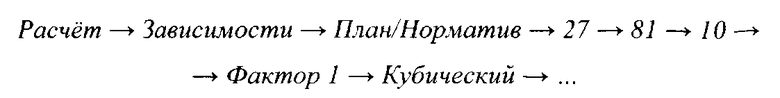
Результат показан на Фиг. 2, где в общей системе координат показаны зависимость совместных с PL реализаций f₁ от PL и сглаживающий эту зависимость тренд (кубический полином).

Из Фиг. 2 очевидно, что корреляционная зависимость f₁ от PL очень тесная и почти линейная. Это является прямым экспериментальным подтверждением сделанного утверждения по факту 1.

Вместе с тем, корреляционная зависимость может быть и пренебрежимо малой. Выполним диалоговую процедуру:

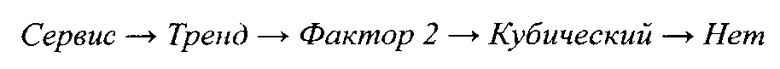
На Фиг. 3 показана зависимость совместной с PL реализации фактора f₂ от PL. Из Фиг. 3 очевидно, что корреляционная зависимость f₂ от PL пренебрежимо мала (случайные колебания значений фактора перекрывают изменения фактора в результате какой-либо тенденции).

Предельно высокая корреляционная зависимость фактора f₁ от PL и предельно низкая корреляционная зависимость фактора f₂ от PL объясняется конкретными особенностями простейшей модели (1)-(5) и особенностями исходных данных. В частности, из (1) и (2) видно, что Fa ₁ и Fa ₂ линейно и одинаково зависят от факторов f₁ и f₂. При этом нижняя граница интервала изменения значений первого фактора [23, 75] существенно больше верхней границы изменения значений второго фактора [1, 5].

В общем случае, при достаточно сложных имитационных моделях ρ₁, ρ₂, ρ₃, ρ₄ и разнообразных видах законов распределения вероятностей значений факторов установить тесноту связи фактора и основных характеристик РСП можно только экспериментально.

Факт 2 выражается утверждением:

если имитационные модели ρ₁ (для расчета Fa1) и ρ₂ (для расчета Fa2) совпадают, то области значений всех факторов (в том числе внешних) могут быть неограниченно сужены.

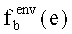
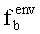
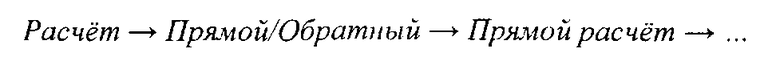
Пусть $$f_b^{env}(e)$$ совместная с PL реализация фактора $$f_b^{env}$$ , полученная в результате осуществления одной из следующих диалоговых процедур:

или

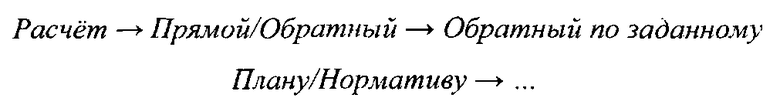
или

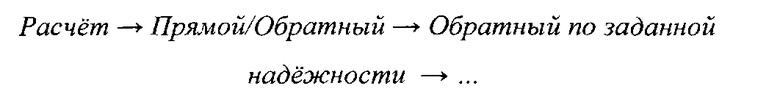
или

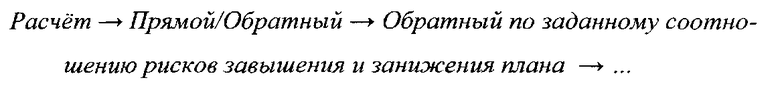
Пусть:

- $$[\underset{\_}{f_b^{env}(e)},\overline{f_b^{env}(e)}]$$ интервал, являющийся окрестностью $$f_b^{env}(e)$$ ;

- $${\Delta }_b=\overline{f_b^{env}(e)}-\underset{\_}{f_b^{env}(e)}$$ - длина этого интервала.

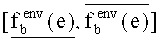
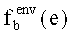
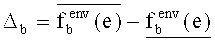
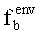
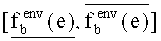
Замену исходного закона распределения вероятностей значений фактора $$f_b^{env}$$ равномерным распределением в пределах $$$$ $$[\underset{\_}{f_b^{env}(e)},\overline{f_b^{env}(e)}]$$ назовем сужением области определения фактора, а сам интервал назовем суженным. При этом предполагается, что Δ_b не больше исходной области определения и что Δ_b>0.

В дополнение к этому факт 3 выражается утверждением:

если имитационные модели ρ₁ (для расчета Fa1) и ρ₂ (для расчета Fa2) не совпадают, то при сужении областей определения значений факторов может возникнуть несовместность условий задачи. Этим ограничиваются возможности сужения областей определения значений факторов.

Способ по настоящему изобретению основан на использовании описанных выше экспериментально установленных фактов и направлен на приближенное решение сформулированной выше задачи путем сужения пределов (областей определения) внешних факторов. Способ предполагает последовательное осуществление следующих трех этапов:

- Этап 1 - оценка тесноты связи внешних факторов и основных характеристик РСП;

- Этап 2 - разделение внешних факторов на категории;

- Этап 3 - сужение областей значений внешних факторов.

Этап 1. Оценка тесноты связи внешних факторов и основных характеристик РСП

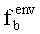
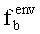
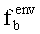
Формально, чтобы установить тесноту связи между PL и каким-либо из внешних факторов $$f_b^{env}$$ , можно многократно выполнить диалоговую процедуру: Расчет→Прямой/Обратный→Прямой расчет… и таким образом сформировать массивы реализаций фактора $$f_b^{env}$$ и PL. Это позволит рассчитать коэффициент корреляции между $$f_b^{env}$$ и PL. Этот способ установления тесноты связи, с одной стороны, весьма трудоемкий, а с другой стороны, не учитывает, что при разных значениях PL коэффициент корреляции также может иметь разные значения. Нас же интересует, прежде всего, именно степень влияния изменения PL на изменение параметров закона распределения вероятностей значений $$f_b^{env}$$ : наличие этого влияния и его зашумленность. Ниже предлагается более экономный способ оценки тесноты связи, не имеющий отмеченных недостатков, который может выполняться в автоматизированном режиме.

Для внешнего фактора 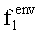$$f_1^{env}$$ выполняем диалоговую процедуру

При этом в автоматизированном режиме в общей системе координат строятся график зависимости совместных с PL реализаций фактора $$f_1^{env}$$ от PL и график сглаживающего эту зависимость тренда (подобно тем, что показаны на Фиг. 2 и 3). Одновременно, дается табличное представление этих графиков (графики и таблица автоматически распечатываются на листе «Графики» модуля Equilibrium). В качестве примера график зависимости совместных с PL реализаций фактора $$f_1^{env}$$ от PL и график сглаживающего эту зависимость тренда, показанные на Фиг. 2, в табличной форме представлены в таблице 3.

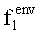
Критерий тесноты связи любого фактора (не только внешнего) $$f_b^{env}$$ и PL будем выражать коэффициентом KTS_b, который рассчитывается по формуле

где KTS_b - критерий тесноты связи внешнего фактора b и PL;

$$f_{b,l}^{env}$$ - фактическая координата точки l фактора b;

$$f_{b,l}^{tr}$$ - координата точки l на линии тренда.

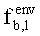
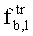
Коэффициент KTS_b показывает среднее отклонение фактических точек от соответствующих точек сглаживающего тренда, выраженное в процентах.

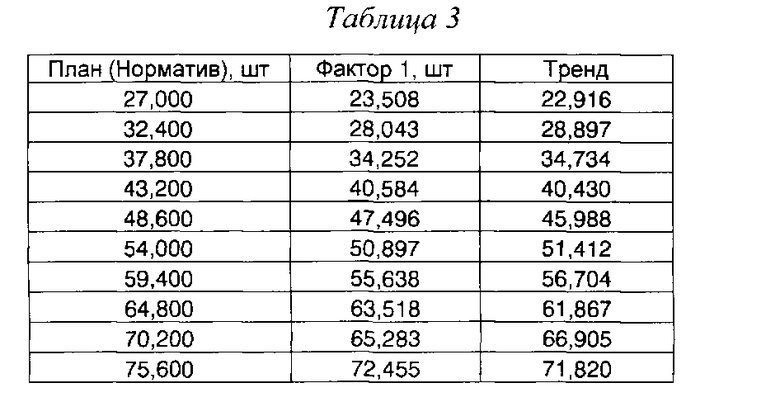
Способ расчета KTS_b на примере KTS₁ на основе данных таблицы 3 показан в таблице 4.

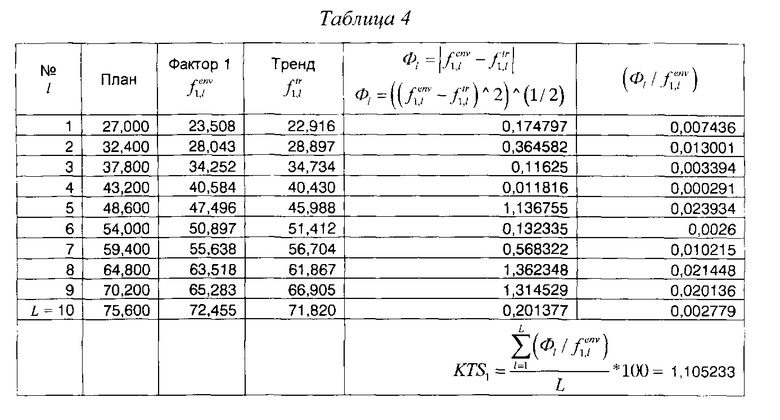
После того как выполнен расчет KTS₁, для расчета остальных коэффициентов необходимо выполнить диалоговую процедуру

где b пробегает значения от 2 до В. В результате мы получим значения KTS_b, b=1,…,В.

Внешний фактор b будем считать достаточно коррелированным с основными характеристиками РСП, если 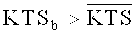$$KT{S}_b>\overline{KTS}$$ .

Как показывает опыт, часто можно положить, что 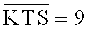$$\overline{KTS}=9$$ . Эта рекомендация не является обязательной. С учетом конкретных особенностей РСП значение $$\overline{KTS}$$ может быть изменено.

Расчет KTS₂ дан в таблице 5.

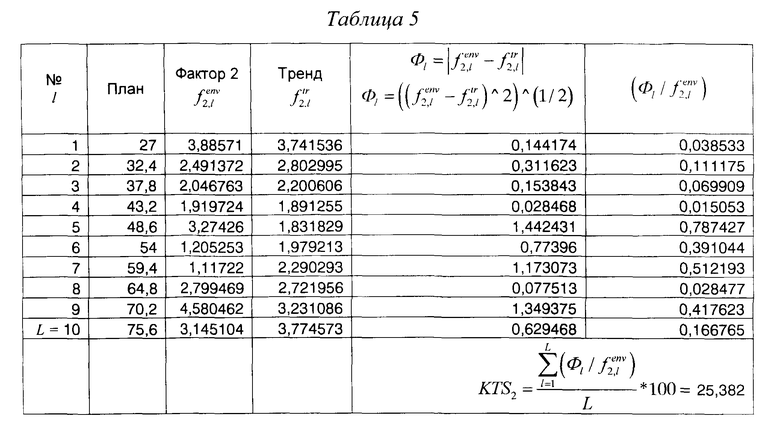
Сравнение графиков на Фиг. 2 и 3 и значений KTS₁=1,105233 и KTS₂=25,382 наглядно иллюстрирует то, как показатель KTS_b выражает тесноту связи фактора и основных характеристик РСП.

Этап 2. Разделение внешних факторов на категории.

Поскольку внешние факторы характеризуют среду, то возможности воздействия на параметры законов распределения вероятностей этих факторов обычно ограничены. Эти ограничения определяется конкретными физическими (или химическими, биологическими, техническими, организационными и экономическими и иными) особенностями РСП. С учетом этого, все внешние факторы могут быть разделены на 3 основные категории:

- Категория А включает те внешние факторы, которые мало влияют на основные характеристики РСП;

- Категория В включает те внешние факторы, которые сильно влияют на основные характеристики РСП, но воздействие на параметры законов распределения вероятностей значений которых либо вовсе невозможно или заведомо нецелесообразно по какой-либо причине или совокупности причин (физических, химических, биологических, технических, организационных, экономических или иных);

- Категория C включает те внешние факторы, которые сильно влияют на основные характеристики РСП, и воздействие на параметры законов распределения вероятностей которых возможны и целесообразны с учетом всей совокупности условий (физических и др.).

Блок-схема алгоритма разделения внешних факторов на категории показана на Фиг. 4.

Этап 3. Сужение областей значений внешних факторов.

Пусть М_А, М_B и М_C - множества факторов категории A, B и C соответственно. Будем считать, что:

- х_А=1,…,Х_А - индекс по порядку и без повторений нумерует факторы из множества М_А по мере убывания KTS, так что 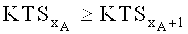$$KT{S}_{x_A}\ge KT{S}_{x_A+1}$$ ;

- х_B=1,…,Х_В - индекс по порядку и без повторений нумерует факторы из множества М_B по мере убывания KTS, так что 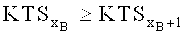$$KT{S}_{x_B}\ge KT{S}_{x_B+1}$$ ;

- х_C=1,…,X_C - индекс по порядку и без повторений нумерует факторы из множества М_С по мере убывания KTS, так что 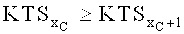$$KT{S}_{x_C}\ge KT{S}_{x_C+1}$$ .

Сужение пределов областей значений для факторов категории А не требуется.

Вначале осуществляем сужение пределов областей значений для факторов категории B, а затем для факторов категории C.

Пусть 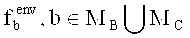$$f_b^{env},b\in M_B{\displaystyle \cup M_C}$$ - фактор категории B или C. Для любого b процедура сужения состоит в том, что:

- во-первых, Nr раз повторяется диалоговая процедура:

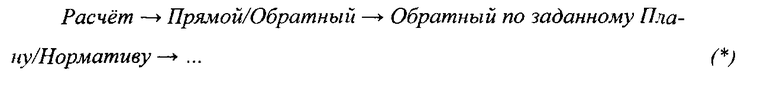
и формируется массив реализаций 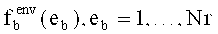$$f_b^{env}(e_b),e_b=\mathrm{1,}\dots ,Nr$$ ;

- во-вторых, устанавливаются правила выбора среди этих реализаций конкретной реализации с номером 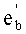$$e_b^{\text{'}}$$ ;

- в-третьих, устанавливается длина Δ_b интервала сужения.

Границы суженного интервала:

- нижняя граница 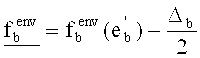$$\underset{\_}{f_b^{env}}=f_b^{env}(e_b^{\text{'}})-\frac{{\Delta }_b}{2}$$ ;

- верхняя граница - 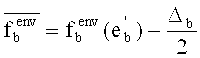$$\overline{f_b^{env}}=f_b^{env}(e_b^{\text{'}})-\frac{{\Delta }_b}{2}$$ .

Таким образом, суженный интервал (пределы): 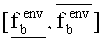$$[\underset{\_}{f_b^{env}},\overline{f_b^{env}}]$$ .

При этом

где

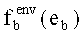
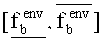
- Р^Δ - вероятность, что при однократном применении диалоговой процедуры (*) реализация фактора $$f_b^{env}(e_b)$$ попадет в пределы $$[\underset{\_}{f_b^{env}},\overline{f_b^{env}}]$$ ;

- Р* - вероятность, что, осуществив Nr раз диалоговую процедуру (*) среди реализаций 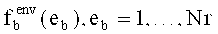$$f_b^{env}(e_b),e_b=\mathrm{1,}\dots ,Nr$$ , хотя бы одна из них попадет в этот интервал.

При этом:

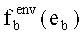
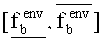
- (1-Р^Δ) - вероятность того, что в одном испытании $$f_b^{env}(e_b)$$ не попадет в пределы $$[\underset{\_}{f_b^{env}},\overline{f_b^{env}}]$$ ;

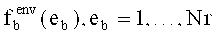
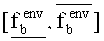
- (1-P^Δ)^Nr - вероятность того, что за Nr испытаний ни одна реализация $$f_b^{env}(e_b),e_b=\mathrm{1,}\dots ,Nr$$ не попадет в пределы $$[\underset{\_}{f_b^{env}},\overline{f_b^{env}}]$$ ;

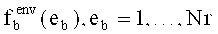
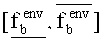
- 1-(1-P^Δ)^Nr - вероятность того, что за Nr испытаний хотя бы одна реализация $$f_b^{env}(e_b),e_b=\mathrm{1,}\dots ,Nr$$ попадет в пределы $$[\underset{\_}{f_b^{env}},\overline{f_b^{env}}]$$ .

Иначе говоря Р*=1-(1-P^Δ)^Nr. Отсюда возникает формула (7) для расчета Nr.

Чаще всего суженный интервал 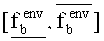$$[\underset{\_}{f_b^{env}},\overline{f_b^{env}}]$$ составляет от 0,1 до 0,3 от исходного (доверительного) интервала. Если фактор имеет равномерное распределение, то это означает, что 0,1≤P^Δ≤0,3. При других законах распределения вероятностей эта величина интервала в принципе может быть и меньше 0,1, но скорее всего она больше. Вероятность Р*, как правило, принимается равной 0,95 или, реже, 0,99. Соответствующие значения Nr представлены в таблице 6.

Для исчерпывающей конкретизации процедуры сужения необходимо сформулировать алгоритм выбора $$e_b^{\text{'}}$$ из реализаций $$f_b^{env}(e_b),e_b=\mathrm{1,}\dots ,Nr$$ и установления длины Δ_b интервала сужения. Этот алгоритм имеет разные варианты для факторов категории B и категории C при условиях, когда имеет место факт 2 и факт 3.

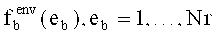
Алгоритм сужения интервалов областей значений для факторов категории B при соблюдении условий, когда имеет место факт 2.

1. х_B=0

2. x_B=x_B+1

3. Если х_B>x_B - останов.

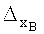
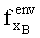
4. Полагаем $${\Delta }_{x_B}$$ равной погрешности, в пределах которой мы способны прогнозировать значение фактора $$f_{x_B}^{env}$$ на момент t_n, исходя из физической природы этого фактора.

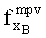
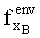
5. Пусть $$f_{x_B}^{mpv}$$ - наиболее вероятное значение фактора $$f_{x_B}^{env}$$ , найденное с помощью методов прогнозирования, соответствующих физической (или иной) природе этого фактора.

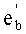
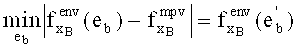
6. Находим $$e_b^{\text{'}}$$ такое, что $$\underset{e_b}{\min }\left|f_{x_B}^{env}(e_b)-f_{x_B}^{mpv}\right|=f_{x_B}^{env}(e_b^{\text{'}})$$

7. Переходим к 2.

Алгоритм сужения интервалов областей значений для факторов категории В при соблюдении условий, когда имеет место факт 3.

1. х_B=0

2. х_B=х_B+1

3. Если х_B>Х_B - останов.

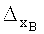
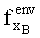
4. Полагаем $${\Delta }_{x_B}$$ равным доверительному интервалу для прогнозируемого значения фактора $$f_{x_B}^{env}$$ на момент t_n.

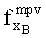
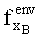
5. Пусть $$f_{x_B}^{mpv}$$ - наиболее вероятное значение фактора $$f_{x_B}^{env}$$ , найденное с помощью методов прогнозирования, соответствующих физической (или иной) природе данного фактора.

6. d=0

7. d=d+1: Если d>10 то переход к 2.

8. Осуществляем диалоговую процедуру (*). Если появляется сообщение: «Условия задачи несовместны» - останов.

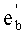
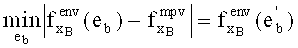
9. Находим $$e_b^{\text{'}}$$ такое, что $$\underset{e_b}{\min }\left|f_{x_B}^{env}(e_b)-f_{x_B}^{mpv}\right|=f_{x_B}^{env}(e_b^{\text{'}})$$ .

10. Осуществляем сужение интервала $${\Delta }_{x_B}$$ на 5%.

11. Переходим к 7.

Алгоритм сужения интервалов областей значений для факторов категории C при соблюдении условий, когда имеет место факт 2.

1. х_C=0

2. х_C=х_C+1

3. Если х_C>Х_C - останов.

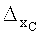
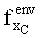
4. Полагаем $${\Delta }_{x_C}$$ равной погрешности, в пределах которой мы способны регулировать значение фактора $$f_{x_C}^{env}$$ на момент t_n.

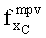
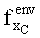
5. Пусть $$f_{x_C}^{mpv}$$ - наиболее предпочтительное значение фактора $$f_{x_C}^{env}$$ , установленное исходя из физической (или иной) природы фактора, либо исходя из соображений минимума затрат, необходимых, чтобы достичь это значение.

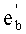
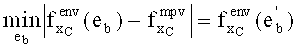
6. Находим $$e_b^{\text{'}}$$ такое, что $$\underset{e_b}{\min }\left|f_{x_C}^{env}(e_b)-f_{x_C}^{mpv}\right|=f_{x_C}^{env}(e_b^{\text{'}})$$

7. Переходим к 2.

Алгоритм сужения интервалов областей значений для факторов категории C при соблюдении условий, когда имеет место факт 3.

1.х_C=0

2. х_C=х_C+1

3. Если х_C>Х_C - останов.

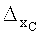
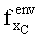
4. Полагаем $${\Delta }_{x_C}$$ равной погрешности, в пределах которой мы способны регулировать значение фактора $$f_{x_C}^{env}$$ на момент t_n.

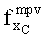
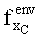
5. Пусть $$f_{x_C}^{mpv}$$ - наиболее предпочтительное значение фактора $$f_{x_C}^{env}$$ , установленное исходя из физической (или иной) природы фактора, либо исходя из соображений минимума затрат, необходимых, чтобы достичь это значение.

6. d=0

7. d=d+1: Если d>10 то переход к 2.

8. Осуществляем диалоговую процедуру (*). Если появляется сообщение: «Условия задачи несовместны» - останов.

9. Находим 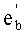$$e_b^{\text{'}}$$ такое, что $$\underset{e_b}{\min }\left|f_{x_C}^{env}(e_b)-f_{x_C}^{mpv}\right|=f_{x_C}^{env}(e_b^{\text{'}})$$ .

10. Осуществляем сужение интервала 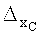$${\Delta }_{x_C}$$ на 5%

11. Переходим к 7.

Пример 1

Рассмотрим электростанцию, в которой установлено несколько силовых установок. Каждая установка представляет собой дизельный двигатель, вращающий динамо-машину. При этом:

- Fa - общая нагрузка (суммарный спрос на электроэнергию со стороны потребителей);

- PL - мощность электростанции;

- Ψ₁(PL,Fa), PL>Fa - сокращение подачи топлива при избытке мощности (сумма уменьшения подачи на работающие двигатели и прекращения подачи на выключаемые двигатели);

- Ψ₂(PL,Fa), PL>Fa - увеличение подачи топлива при недостатке мощности (сумма увеличения подачи на работающие двигатели и дополнительную подачу на включаемые двигатели).

Предположим, что мы имеем некоторую возможность влиять на параметры спроса на электроэнергию Fa (например, уменьшить амплитуду суточных колебаний спроса с помощью аккумуляторов).

Способ обеспечивает поддержание такого интервала колебаний спроса Fa, при котором достижение минимального расхода топлива r будет наиболее вероятно.

Пример 2

Рассмотрим газопровод, в который под давлением подается газ из двух основных источников (две компрессорные станции, приближенные к соответствующим местам добычи) и у которого имеется несколько категорий потребителей газа. При этом:

- Fa - фактическое давление в газопроводе;

- PL - нормативное давление;

- Ψ₁(PL,Fa), PL>Fa - сокращение подачи газа, когда фактическое давление больше нормативного;

- Ψ₂(PL,Fa), PL>Fa - увеличение подачи газа, когда фактическое давление меньше нормативного.

Предположим, что мы имеем некоторую возможность влиять на параметры спроса на газ со стороны разных категорий потребителей.

Способ обеспечивает поддержание такого интервала колебаний распределения спроса между потребителями, при котором минимизация расхода энергии r будет наиболее вероятна.

Пример 3.

Рассмотрим корабль в море. От проложенного курса корабль отклоняется под действием подводных течений и ветра. При этом:

- Fa - фактическое положение корабля;

- PL - положение корабля, которое он должен занимать согласно заданному курсу;

- Ψ₁(PL,Fa), PL>Fa - угол поворота штурвала, при отклонении от курса в одну сторону;

- Ψ₂(PL,Fa), PL>Fa - угол поворота штурвала, при отклонении от курса в другую сторону.

Предположим, что мы имеем некоторую возможность влиять на параметры случайных воздействий. Например, путем установки различных обтекателей можно снизить влияние течений и ветра.

Способ обеспечивает подбор такого интервала колебаний внешних воздействий, при котором достижение минимума расхода топлива r будет наиболее вероятно.

Таким образом, настоящее изобретение расширяет функциональные возможности известных способов управления равновесными случайными процессами, обеспечивая в автоматизированном режиме выбор значений параметров внешней среды, согласованных с оптимальным управлением равновесным случайным процессом.

Данное изобретение относится к вычислительной технике. Технический результат - обеспечение в автоматизированном режиме выбора значений параметров внешней среды, согласованных с оптимальным управлением равновесным случайным процессом (РСП). Для этого предложен способ, в котором: выделяют для РСП его характеристики и рассматривают их в качестве координат фазового пространства, в котором протекает РСП; строят для исследуемого РСП в соответствии с априорной информацией о нем эволюционно-симулятивную модель (ЭСМ), взаимно увязывающую координаты упомянутого фазового пространства; загружают ЭСМ в память процессорного устройства без выделенных внешних факторов; измеряют с помощью соответствующих датчиков исходные показатели исследуемого РСП и вводят их в память процессорного устройства в качестве входных сигналов для ЭСМ; рассчитывают интегральную характеристику РСП и ее интервал изменений; выделяют в этом интервале изменений равноотстоящие точки и выполняют в автоматизированном режиме в каждой из выделенных точек расчет совместных с интегральной характеристикой реализаций значений данного фактора и соответствующих значений этого же фактора на сглаживающей полиномиальной кривой и рассчитывают тесноту связи фактора и интегральной характеристики, а также устанавливают физически допустимые в данных условиях пределы изменения фактора; применяют процедуру сужения пределов изменения внешних факторов, переходя от внешнего фактора с большим значением тесноты к внешнему фактору с ее меньшим значением и принимают внешние факторы с суженными пределами в качестве значений параметров внешней среды, согласованных с оптимальным управлением РСП. 3 з.п. ф-лы, 4 ил., 6 табл., 3 пр.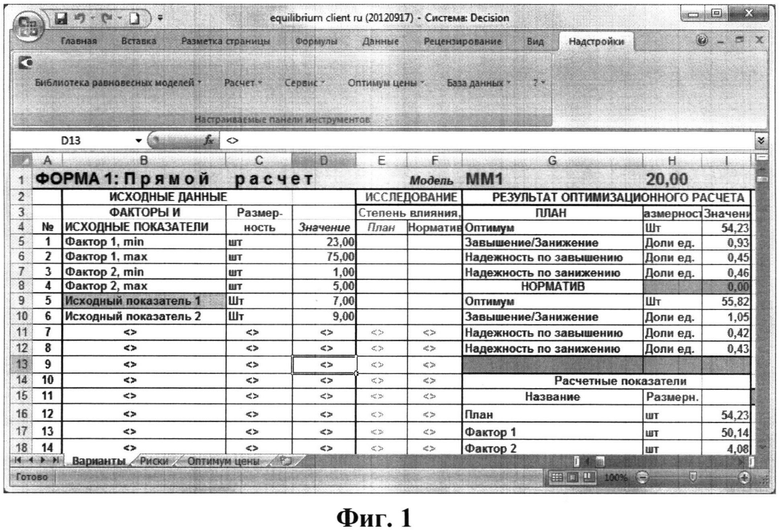

1. Способ выбора значений параметров внешней среды, согласованных с оптимальным управлением равновесным случайным процессом (РСП), заключающийся в том, что:
- выделяют для упомянутого РСП его характеристики в виде независимых случайных величин, именуемых далее факторами, и условно постоянных величин, именуемых далее показателями, и рассматривают эти показатели и параметры законов распределения вероятностей упомянутых факторов в качестве координат фазового пространства, в котором протекает РСП;
- строят для исследуемого РСП в соответствии с априорной информацией о нем эволюционно-симулятивную модель (ЭСМ), взаимно увязывающую координаты упомянутого фазового пространства и разделяющую эти координаты на исходные показатели, управляющие параметры и расчетные показатели;
- выделяют среди упомянутых факторов внешние факторы, параметры законов распределения вероятностей которых не являются управляющими параметрами;
- загружают упомянутую ЭСМ в память процессорного устройства без выделенных внешних факторов;
- измеряют с помощью соответствующих датчиков упомянутые исходные показатели исследуемого РСП и вводят измеренные исходные показатели в упомянутую память процессорного устройства в качестве входных сигналов для упомянутой ЭСМ;
- рассчитывают интегральную характеристику РСП и ее интервал изменений;
- выделяют в упомянутом интервале изменений равноотстоящие точки и с применением упомянутой ЭСМ для каждого из упомянутых внешних факторов выполняют в упомянутом процессорном устройстве в автоматизированном режиме в каждой из упомянутых выделенных точек расчет совместных с упомянутой интегральной характеристикой реализаций значений данного фактора и соответствующих значений этого же фактора на сглаживающей полиномиальной кривой и рассчитывают тесноту связи упомянутого фактора и упомянутой интегральной характеристики, а также устанавливают физически допустимые в данных условиях пределы изменения упомянутого фактора;
- применяют процедуру сужения упомянутых пределов изменения внешних факторов, переходя от внешнего фактора с большим значением упомянутой тесноты к внешнему фактору с ее меньшим значением и принимают внешние факторы с суженными пределами в качестве упомянутых значений параметров внешней среды, согласованных с оптимальным управлением РСП.

2. Способ по п. 1, в котором в упомянутом интервале изменений интегральной характеристики РСП выделяют десять упомянутых равноотстоящих точек, а в качестве упомянутой сглаживающей полиномиальной кривой используют кубический полином.

3. Способ по п. 1 или 2, в котором:
- если в составе упомянутой ЭСМ имитационная модель условий завышения и имитационная модель условий занижения совпадают, то упомянутую процедуру сужения предела осуществляют за один этап: рассчитывают в автоматизированном режиме в упомянутом процессорном устройстве несколько совместных с рассчитанной с помощью упомянутой ЭСМ оптимальной интегральной характеристикой реализаций данного фактора, находят их среднее и погрешность измерения; и устанавливают суженный предел равным упомянутой погрешности измерения значения данного фактора;
- если в составе упомянутой ЭСМ имитационная модель условий завышения и имитационная модель условий занижения не совпадают, то упомянутую процедуру сужения предела осуществляют за несколько этапов: на первом этапе рассчитывают в автоматизированном режиме в упомянутом процессорном устройстве на каждом шаге несколько совместных с оптимальной при данных исходных показателях интегральной характеристикой реализаций данного фактора, находят их среднее и погрешность измерения и устанавливают суженный предел равным упомянутой погрешности измерения значения данного фактора, на втором и последующих этапах повторяют те же действия, что и на первом этапе, до тех пор, пока упомянутый предел изменения значения данного фактора не станет меньше или равным погрешности измерения этого фактора, либо пока не возникнет несовместность условий упомянутой ЭСМ.

4. Способ по п. 3, в котором рассчитывают пятнадцать упомянутых совместных реализаций данного фактора.