Изобретение относится к области вооружения, а именно к системам управления воздушными мишенями на основе беспилотных летательных аппаратов (далее - БПЛА) с неизменяемой формой крыла, и может быть использована при разработке систем управления воздушных мишеней на основе БПЛА из состава перспективного мишенного комплекса. Воздушные мишени на основе БПЛА в составе перспективного мишенного комплекса применяются при проверке и испытаниях систем и комплексов противовоздушной обороны ближнего действия, малой, средней дальности и дальнего действия, в том числе зенитных и зенитных ракетно-пушечных комплексов.
Технический результат использования изобретения заключается в возможности проверки технических решений системы управления воздушной мишенью с помощью имитационной модели, что позволяет использовать полученные результаты при проектировании и натурных испытаниях мишенного комплекса.
Кроме этого, на полезной модели могут быть определены возможности использования в системе управления БПЛА законов управления группой мишеней при создании мишенным комплексом сложной воздушной обстановки.
Известно, что основой системы управления воздушной мишенью на основе БПЛА во время всех фаз полета является ее автопилот.
Автопилот - это, как правило, электромеханическое управляющее устройство, которое обеспечивает движение БПЛА по заранее заданному пути [1, 2, 3]. В общем, работа имитационных моделей (далее - ИМ) систем управления воздушными мишенями на основе БПЛА обеспечивается формируемым полетным заданием, автопилотом, состоящим из двух основных контуров управления (контур управления продольным движением и контур управления боковым движением) и самим летательным аппаратом, построенным по конкретной аэродинамической схеме.
В известной патентной и научной литературе, соответствующей современному уровню развития техники представлены описания систем управления беспилотными летательными аппаратами [4, 5], раскрывающие только поэлементный конструктив автопилота и предлагаемые изменения, в части касающейся введения дополнительных блоков и систем, обеспечивающих выполнение разных целевых установок (например, дополнительное введение системы автоматического распознавания и автосопровождения объектов наблюдения).
Известные имитационные модели обладают рядом недостатков, а именно:
не позволяют формировать полетное задание для воздушной мишени непосредственно в имитационной модели системы управления с последующей возможностью графического отображения как требуемых, так и реально отрабатываемых траекторий воздушной мишенью в соответствии с заданным полетным заданием;
отсутствует возможность формирования полетного задания различной степени сложности;
отсутствует визуализация поведения планера воздушной мишени на всем этапе полета;
отсутствует возможность наблюдения за изменением соответствующих параметров системы управления воздушной мишенью, вызванных изменением направления полета мишени в пространстве;
применяемый математический аппарат для формирования полетного задания воздушной мишени, как правило, позволяет формировать в основном прямолинейные участки траектории движения воздушной мишени лишь с небольшим изменением направления движения, вызванного необходимостью движения в следующую точку («путевую точку») пространства, в связи с чем воздушная мишень не способна с высокой степенью достоверности воспроизводить траектории движения отдельных реальных летательных аппаратов, совершающих соответствующие маневры.
Кроме этого, известные ИМ не позволяют отражать траекторию полета воздушной мишени в трехмерном пространстве, имеющую важную роль при совершении воздушной мишенью пространственных маневров типа «раскручивающаяся спираль», «неправильная бочка» и других.
Наиболее близкими к предлагаемой ИМ являются следующие две модели.
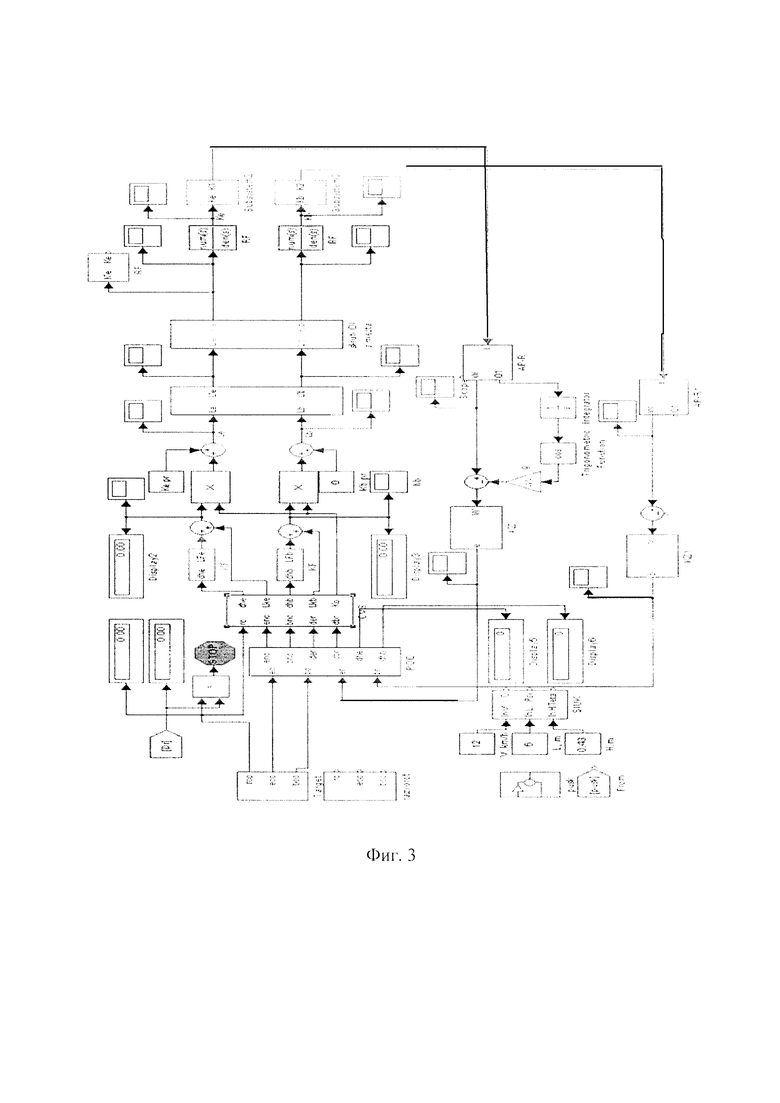
Первая - это цифровая имитационная модель системы управления маневренным летательным аппаратом (далее - ЛА) малой дальности [6], структура которой представлена на фиг. 3. Имитационная модель содержит: программу движения цели относительно точки пуска ЛА в плоскости угла места и азимута, алгоритм программного вывода, алгоритм работы компенсатора динамической ошибки наведения.
Алгоритм программного вывода представляет собой программу обхода дыма, обеспечивающую быстрый захват ЛА на сопровождение оптико-электронной системой в зависимости от направления вектора скорости ветра. Запуск алгоритма компенсации динамической ошибки наведения производится сразу после захвата ЛА на сопровождение по угловым координатам.
Вычисление команд управления ЛА производится как на начальном участке, так и на участке наведения.
В формировании суммарных команд управления ЛА на участке наведения участвуют сигналы с выходов корректирующих фильтров, сигналы компенсации динамической ошибки, команды вывода ЛА на кинематическую траекторию. Выработанные таким образом команды управления передаются на борт ЛА, где исполняются путем изменения положения органов управления в соответствующих плоскостях. Команды управления при этом преобразуются из измерительной в исполнительную систему координат, с учетом угла скручивания.
Недостатком данной ИМ, дополнительно к вышеперечисленным, можно отнести то, что параметры и конфигурация траектории движения ЛА малой дальности определяются не заданным заранее полетным заданием, а необходимостью обеспечения максимально быстрой встречи ЛА малой дальности с целью.
Непосредственное использование такой системы управления и ее ИМ не позволяет достоверно воспроизводить траектории движения отдельных ЛА, имитирующих атаку наземных целей с выполнением, соответствующих маневров.
Следовательно, применять цифровую имитационную модель системы управления маневренным ЛА малой дальности в качестве имитационной модели системы управления воздушными мишенями на основе беспилотных летательных аппаратов в составе перспективного мишенного комплекса не представляется возможным.
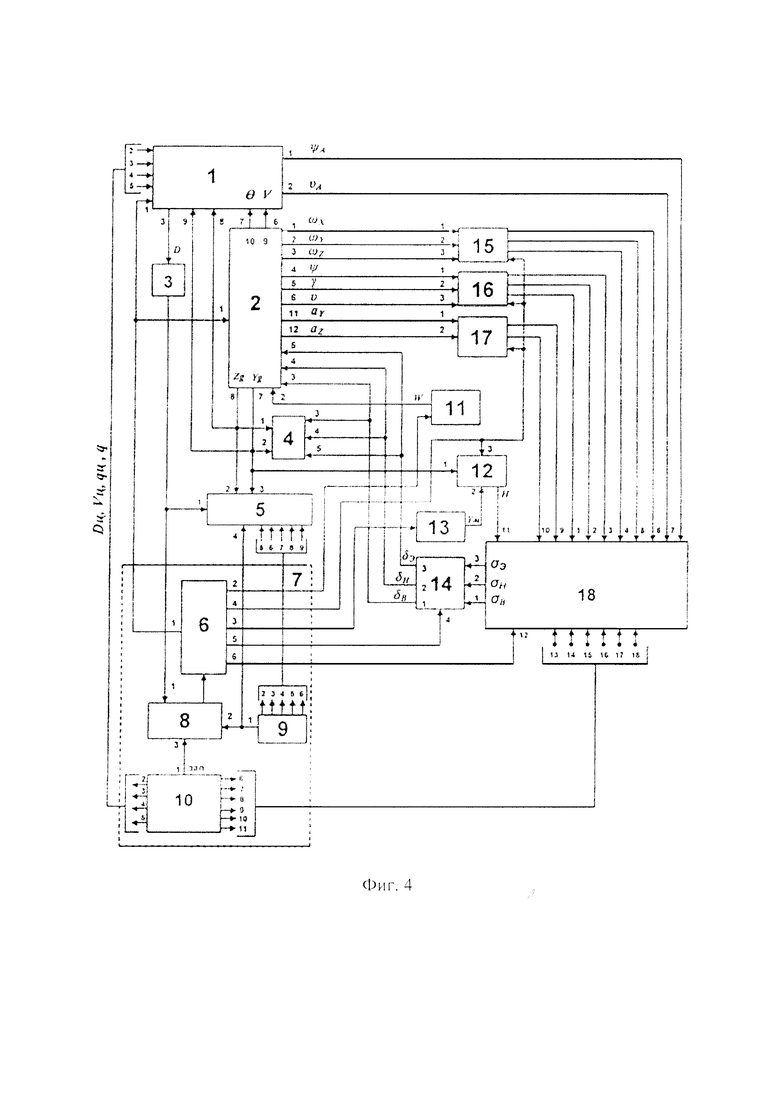
Вторая - это моделирующий комплекс для проверки системы управления беспилотного летательного аппарата [7], структура которого представлена на фиг. 4.
Моделирующий комплекс для проверки системы управления БПЛА содержит: устройство моделирования бокового движения БПЛА и устройство моделирования продольного движения БПЛА, входящие в состав имитатора БПЛА, имитатор рулевых механизмов, имитатор измерителя координат объекта наблюдения, имитатор датчиков угловых скоростей, имитатор измерителей углов, имитатор измерителей линейных ускорений, имитатор ветровых порывов, имитатор подстилающей поверхности, имитатор радиовысотомера, устройство выработки сигналов управления, блок контроля пролета, устройство обработки результатов испытаний и устройство управления испытаниями, в состав которого входят пульт управления, задатчик параметров объекта наблюдения и блок формирования серии пусков.
Основное назначение моделирующего комплекса - это оценка точности системы управления БПЛА по величине промаха (пролета ЛА мимо объекта наблюдения) при многократном задании начальных условий и исходных данных с непрерывной пошаговой проверкой правильности выполнения операций.
Работа моделирующего комплекса построена следующим образом.
Вначале в соответствии с программой проведения моделирования осуществляется настройка комплекса.
Выбирается тип решаемой задачи, после чего в соответствии с выбранной задачей происходит начальная установка дальности до объекта наблюдения и параметров относительного движения объекта наблюдения и БПЛА в соответствующих алгоритмах.
Далее в устройство обработки результатов испытаний вводятся параметры объекта наблюдения - длина, высота и высота радиолокационного центра отражения объекта наблюдения, а также количество пусков в серии испытаний, достаточных для получения достоверных оценок в алгоритмах.
После чего выбирается и устанавливается режим проведения моделирования.
В результате многократного повторения вышеописанных операций в любом из режимов работы, моделирующим комплексом вырабатываются сигналы о положении ЛА в пространстве и его относительной скорости движения, о текущей дальности до объекта наблюдения, а также об углах визирования объекта наблюдения, которые далее поступают в устройство выработки сигналов управления.
Работа моделирующего комплекса заканчивается по достижении встречи летательного аппарата с объектом наблюдения, когда текущая дальность будет равна нулю, а также если количество произведенных пусков равно количеству заданных пусков. После чего комплекс переходит в режим обработки результатов с дальнейшим отображением заданных величин на экран соответствующего индикатора.
Таким образом, моделирующий комплекс для проверки системы управления БПЛА выполняет прежде всего функцию оценки качества системы управления БПЛА на основании полунатурных испытаний, требующих специализированной стендовой аппаратуры.
К недостаткам моделирующего комплекса для проверки системы управления БПЛА, с точки зрения, анализа возможностей имитации им полетов воздушных мишеней на основе БПЛА в составе мишенного комплекса можно отнести следующие:
избыточную сложность при проверке и отработке законов управления, реализуемых в алгоритмах работы системы управления БПЛА;
необходимость в проведении полунатурных испытаний каждый раз после внесения изменений в структуру автопилота или в полетное задание, что экономически не всегда целесообразно;
необходимость в проведении периодической метрологической поверки стендовой аппаратуры, что также требует дополнительных ресурсных затрат.
Задачей изобретения является проведение исследования по возможности реализации различных законов управления на основе формируемых полетных заданий для воздушных мишеней на основе БПЛА при имитации типовых маневров средств воздушного нападения, в том числе пространственных маневров, а также проведение анализа процессов, протекающих в контурах автопилота воздушной мишени, с возможностью коррекции параметров системы управления воздушной мишени для определения возможностей по повышению достоверности имитации типовых маневров реальных ЛА.
Для решения задачи изобретения предлагается использовать в качестве ее основы элементы системы управления воздушными мишенями на основе БПЛА мишенного комплекса, изображенные на фиг. 5, 6, 7, 8.
Как правило, динамика продольных движений (скорость перемещения вперед, маневр по тангажу, набор высоты, снижение) развязаны от динамики боковых скольжений (рыскания, движения по крену), что позволило упростить модель автопилота, а также использовать методику последовательного замыкания контура обратной связью.
Основная идея, лежащая в основе последовательного замыкания контура обратной связью, состоит в замыкании нескольких простых контуров обратной связью последовательно вокруг динамического объекта с разомкнутым контуром. Это позволяет избежать необходимость разработки одной (более сложной) системы управления.
Таким образом, в целом система управления воздушной мишенью на основе БПЛА состоит из двух автопилотных контуров.
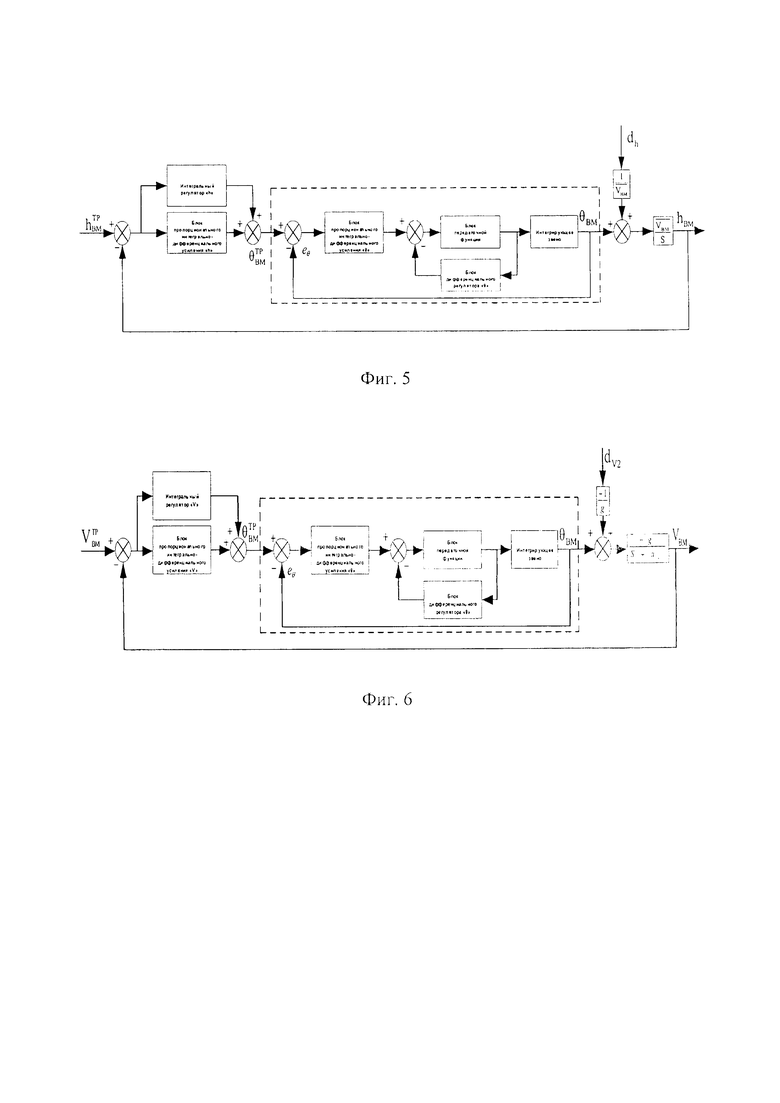
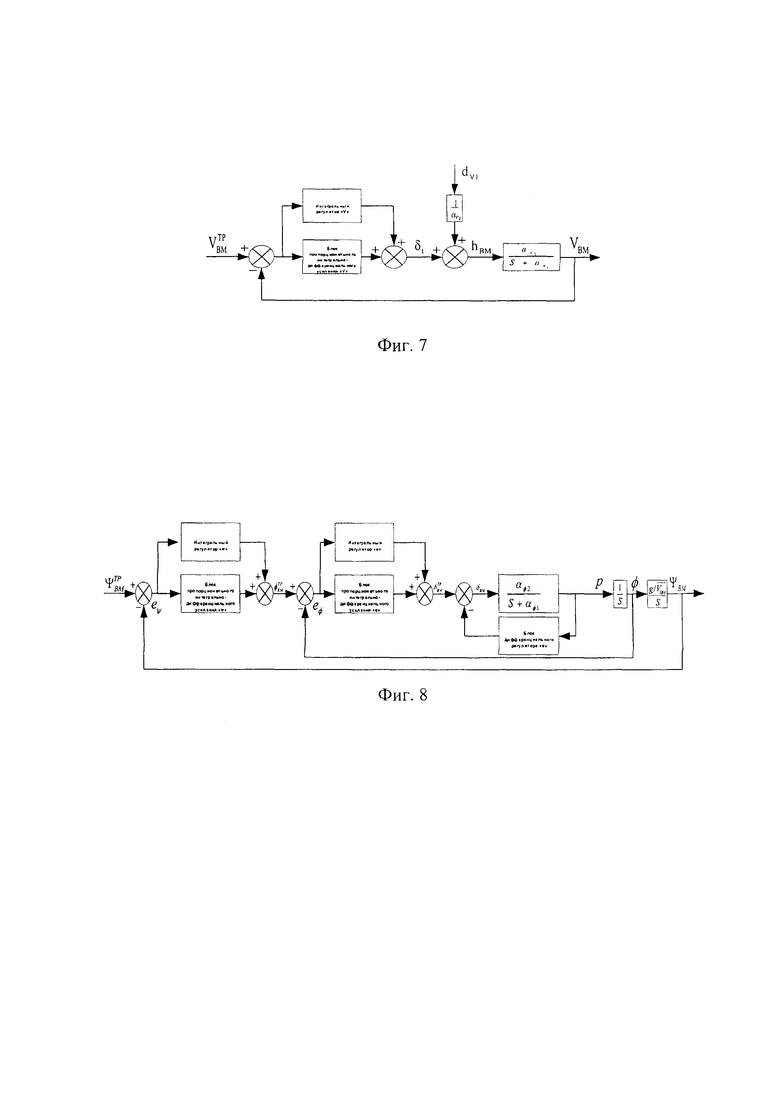
Первым является контур автопилота для управления продольным движением воздушной мишени на основе БПЛА, который использует в своем составе подконтуры обратной связи: подконтур выдерживания высоты полета воздушной мишени на основе БПЛА с помощью управляющих сигналов по тангажу с последовательным замыканием с подконтуром автопилота стабилизации по углу тангажа, используемого в качестве внутреннего подконтура (фиг. 5), подконтур выдерживания скорости воздушной мишени на основе БПЛА с помощью регулирования тангажа (фиг. 6), подконтур стабилизации скорости воздушной мишени на основе БПЛА с помощью дроссельной заслонки (фиг. 7), которые в своем составе также имеют блоки реализующие соответствующие коэффициенты усиления, которые участвуют в формировании необходимого уровня значений сигналов, в дальнейшем поступающих на блоки контуров, реализующие передаточные функции как для боковой динамики, которые выражают связь между отклонением элерона и углом крена и связь между углом крена и курсовым углом соответственно, так и для динамики продольных движений, которые моделируют связь между отклонением руля высоты и углом тангажа, углом тангажа и высотой, воздушной скоростью и высотой, а также положением дроссельной заслонки и углом тангажа с воздушной скоростью соответственно.
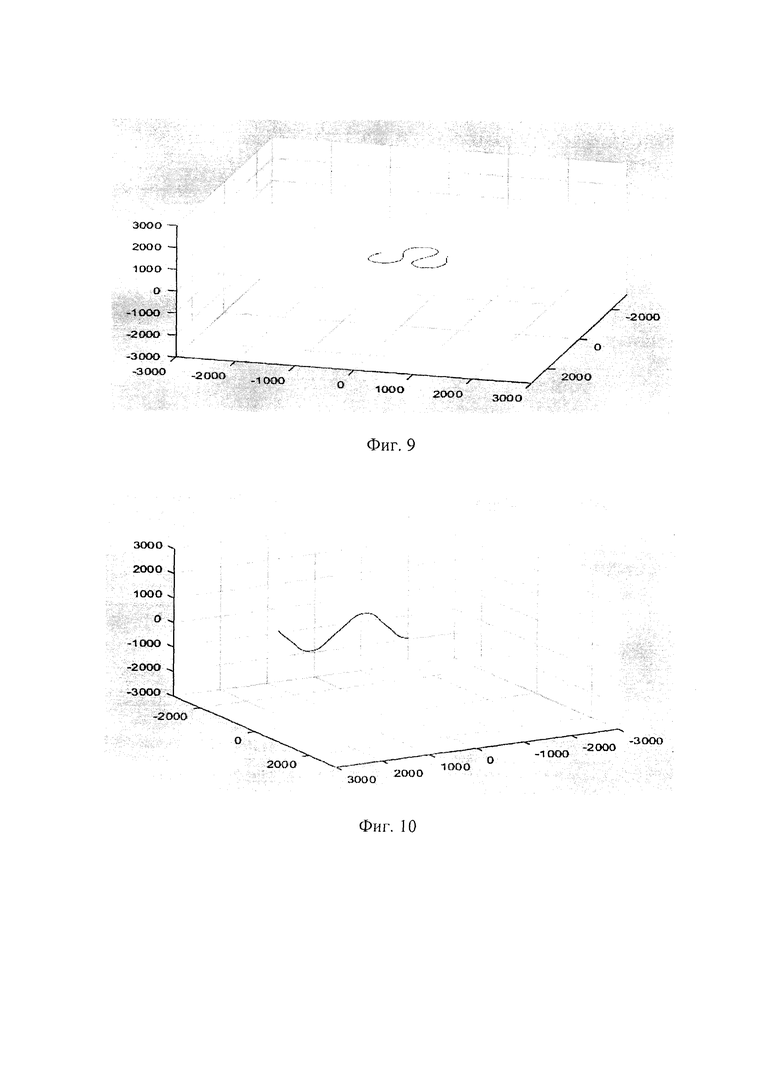
Вторым является контур автопилота для управления боковым движением воздушной мишени на основе БПЛА, который включает в себя подконтур управления курсовым углом воздушной мишени с последовательным замыканием с подконтуром управления креном воздушной мишени (фиг. 8) и имеет коэффициент усиления дифференциального регулятора демпфирования скорости крена для внутреннего контура, коэффициенты усиления пропорционального и интегральных звеньев регулирования угла крена, коэффициенты усиления пропорционального и интегральных звеньев регулирования курсового угла, связанных с автопилотом бокового движения.
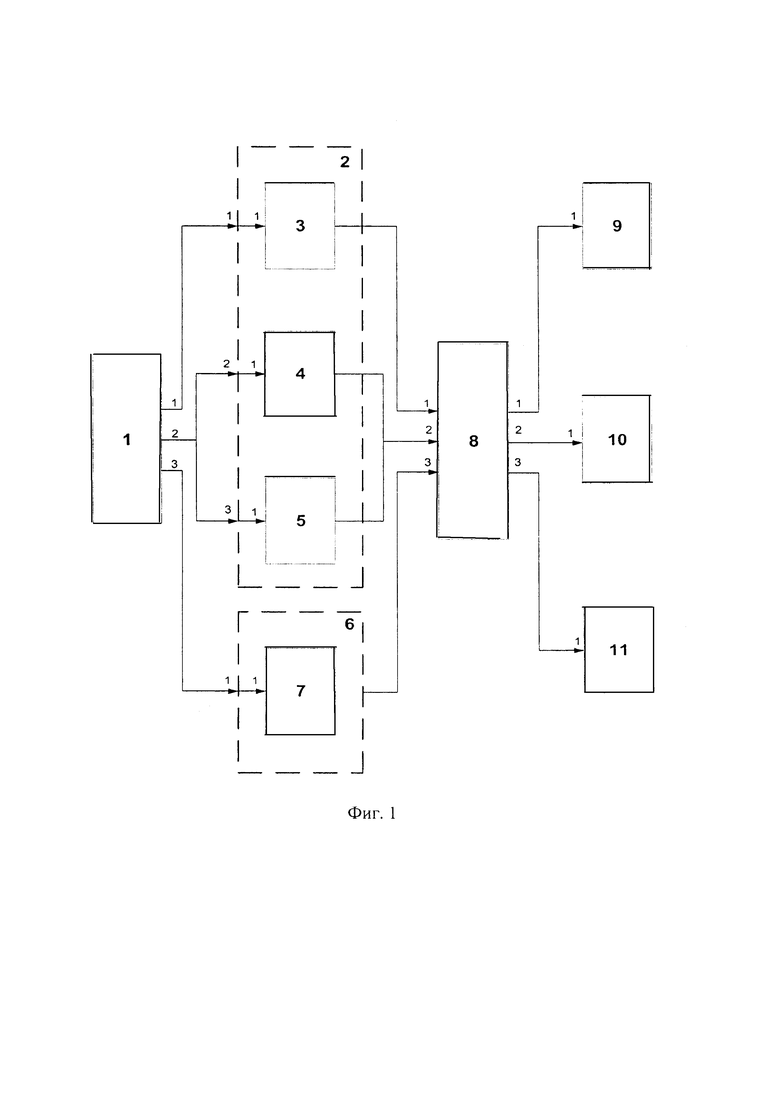
Сущность системы управления воздушной мишенью на основе БПЛА поясняется структурной схемой, представленной на фиг. 1.
На схеме обозначены:
1 - блок исходных данных;
2 - контур автопилота для управления продольным движением воздушной мишени;
3 - подконтур выдерживания высоты полета воздушной мишени на основе БПЛА с помощью управляющих сигналов по тангажу с последовательным замыканием с подконтуром автопилота стабилизации по углу тангажа;
4 - подконтур выдерживания скорости воздушной мишени на основе БПЛА с помощью регулирования тангажа;
5 - подконтур стабилизации скорости воздушной мишени на основе БПЛА с помощью дроссельной заслонки;
6 - контур автопилота для управления боковым движением воздушной мишени на основе БПЛА;
7 - подконтур управления курсовым углом воздушной мишени с последовательным замыканием с подконтуром управления креном воздушной мишени;
8 - блок воздушной мишени на основе БПЛА;
9 - блок графического отображения траектории полета воздушной мишени на основе БПЛА;
10 - блок визуализации полета воздушной мишени на основе БПЛА;
11 - блок вывода параметров полета воздушной мишени на основе БПЛА. В соответствии с фиг.1 в блоке исходных данных 1 формируется система
координат, в которой осуществляется полет воздушной мишени, начальные параметры движения воздушной мишени, а также полетное задание для формирования требуемой траектории пространственного движения воздушной мишени.
Первый выход блока 1, на котором формируется требуемое значение высоты полета воздушной мишени, соединен с первым входом контура 2 и далее поступает на первый вход подконтура 3, с выхода которого снимается текущее значение высоты полета воздушной мишени, которое поступает на первый вход блока 8.
Второй выход блока 1, на котором формируется требуемое значение скорости полета воздушной мишени, соединен со вторым и третьим входом контура 2 и далее поступает на первый вход подконтуров 4 и 5, с выходов которых снимается текущее значение скорости полета воздушной мишени, которое поступает на второй вход блока 8.
Третий выход блока 1, на котором формируется требуемое значение курсового угла полета воздушной мишени, соединен с первым входом контура 6 и далее поступает на первый вход подконтура 7, с выхода которого снимается текущее значение курсового угла полета воздушной мишени, которое поступает на третий вход блока 8.
Блок 8 представляет из себя имитацию воздушной мишени на основе БПЛА, реализованную с помощью пакета визуального моделирования Simulink матричной математической системы MATLAB, с учетом ее геометрических размеров и присущих ей аэродинамических коэффициентов.
Сигналы с контуров 2 и 6 поступив в блок 8, в соответствии с загруженным в блоке исходных данных 1 полетным заданием, приводят в движение воздушную мишень на основе БПЛА.
В соответствии с установленным в блоке исходных данных 1 временем дискретизации с выхода 1 блока 8 на вход 1 блока 9 поступают соответствующие сигналы, характеризующие изменение траектории движения воздушной мишени на основе БПЛА, после чего на рабочий стол пользователя выводится программное окно с отображением реально отрабатываемой траекторией воздушной мишенью на основе БПЛА в трехмерном пространстве.
Одновременно с вышеприведенной операцией с выхода 2 блока 8 на вход 1 блока 10 поступают соответствующие сигналы, описывающие поведение ВМ на основе БПЛА в воздушном пространстве, после чего на рабочий стол пользователя одновременно с предыдущим окном, выводится программное окно с отображением реакции аэродинамической схемы воздушной мишени на основе БПЛА на полетное задание, отображаемое в трехмерном пространстве.
Синхронно с вышеперечисленными операциями с выхода 3 блока 8 на вход 1 блока 11 поступают сигналы, соответствующие значениям параметров полета воздушной мишени на основе БПЛА, после чего на рабочий стол пользователя одновременно с предыдущими окнами, выводится программное окно с графическим отображением изменения соответствующих параметров во времени.
Изобретение в виде имитационной модели системы управления воздушной мишенью на основе БПЛА из состава мишенного комплекса разработана с помощью пакета визуального моделирования Simulink матричной математической системы MATLAB и показана на фиг. 2.
Сущность изобретения заключается в том, что в отличие от известных моделей, для выполнения задачи изобретения на входных элементах имитационной модели формируется ряд математических зависимостей, определяющих требуемые параметры движения воздушной мишени на основе БПЛА в пространстве (далее - полетное задание).
Полетное задание определяется заранее с учетом требуемых значений перегрузок, ускорений и выбранной траектории движения воздушной мишени на основе БПЛА.
Для этого, в отличие от известных способов [8], предлагается рассматривать требуемое движение воздушной мишени на основе БПЛА в прямоугольной системе координат OXYZ, начало отсчета которой находится в точке стояния наземного пункта управления воздушными мишенями, и использовать систему, состоящую из следующих уравнений:
VBM=aV+bV⋅t - закон изменения скорости воздушной мишени, где:
aV - коэффициент, определяющий начальное значение скорости воздушной мишени, который имеет размерность - м/с;
bV - коэффициент, определяющий с каким ускорением воздушная мишень будет совершать полет, который имеет размерность - м/с2;
t - текущее время моделирования полета воздушной мишени.
θВМ=aθ+bθ⋅t+cθ⋅t2+dθ⋅sin(mθ⋅t) - закон изменения угла наклона вектора скорости воздушной мишени относительно направления параллельного оси X для вертикальной плоскости управления (угол тангажа), где:
aθ - коэффициент, определяющий начальное значение угла тангажа в радианах, при котором воздушная мишень начинает совершать маневр в вертикальной плоскости;
bθ - коэффициент, определяющий значение скорости изменения угла θВМ при совершении мишенью маневра в вертикальной плоскости, который имеет размерность - 1/сек;
cθ - коэффициент, определяющий значение ускорения изменения угла θВМ при совершении мишенью маневра в вертикальной плоскости, который имеет размерность - 1/сек2;
dθ - коэффициент, определяющий значение амплитуды угла θВМ в радианах при моделировании маневра гармонического типа;
mθ - коэффициент, определяющий значение частоты, совершаемого воздушной мишенью маневра гармонического типа в вертикальной плоскости, который имеет размерность - 1/сек.
ΨВМ =aΨ+bΨ⋅t+cΨ⋅t2+dΨ ⋅sin(mΨ⋅t) - закон изменения угла наклона вектора скорости воздушной мишени относительно направления параллельного оси X для горизонтальной плоскости управления (курсовой угол), где:
aΨ - коэффициент, определяющий начальное значение курсового угла в радианах, при котором воздушная мишень начинает совершать маневр в горизонтальной плоскости;
bΨ - коэффициент, определяющий значение скорости изменения угла ΨВМ при совершении мишенью маневра в горизонтальной плоскости, который имеет размерность - 1/сек;
cΨ - коэффициент, определяющий значение ускорения изменения угла ΨВМ при совершении мишенью маневра в горизонтальной плоскости, который имеет размерность - 1/сек2;
dΨ - коэффициент, определяющий значение амплитуды угла ΨВМ в радианах при моделировании маневра гармонического типа;
mΨ - коэффициент, определяющий значение частоты, совершаемого воздушной мишенью маневра гармонического типа в горизонтальной плоскости, который имеет размерность - 1/сек.
Коэффициенты aθ,Ψ, bθ,Ψ, сθ,Ψ, используются для моделирования движения ВМ по дуге параболы, в этом случае коэффициент dθ,Ψ принимается равным 0.
При изменении значений коэффициентов bθ,Ψ, сθ,Ψ в качестве нового значения аθ,Ψ, принимается текущее на данный момент времени t значение угла θВМ (ΨВМ).
При необходимости моделирования движения цели по гармоническому закону значения коэффициентов bθ,Ψ, сθ,Ψ принимаются равными нулю, значение коэффициента аθ,Ψ, соответствует текущему θВМ (ΨВМ) на момент начала маневра гармонического типа.
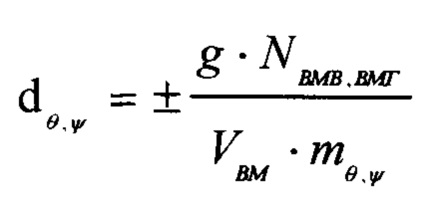 - коэффициент, определяющий значение амплитуды изменения угла тангажа и курсового угла воздушной мишени в радианах при моделировании маневра гармонического типа, где:
- коэффициент, определяющий значение амплитуды изменения угла тангажа и курсового угла воздушной мишени в радианах при моделировании маневра гармонического типа, где:
± - знак выбирается в зависимости от требуемого направления движения воздушной мишени в момент начала маневра;
g=9,8 м/с2 - ускорение свободного падения;
NВМВ,ВМГ - коэффициент, определяющий значение перегрузки, которая характеризует интенсивность маневра как в вертикальной, так и в горизонтальной плоскостях, которая является безразмерной величиной;
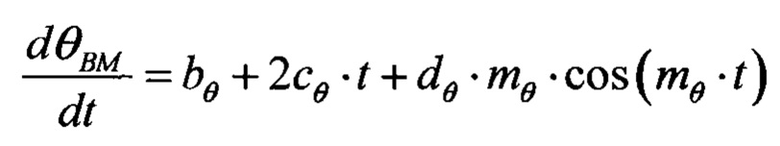 - закон изменения угловой скорости угла тангажа воздушной мишени;
- закон изменения угловой скорости угла тангажа воздушной мишени;
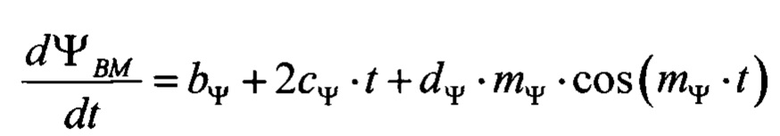 - закон изменения угловой скорости курса воздушной мишени;
- закон изменения угловой скорости курса воздушной мишени;
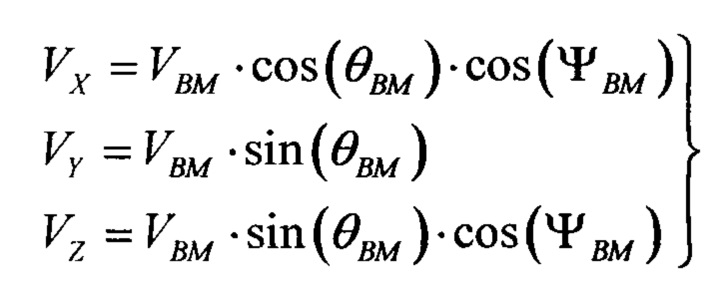 - законы изменения составляющих вектора скорости воздушной мишени по соответствующим осям прямоугольной системы координат OXYZ, которые получены в результате преобразования сферической системы координат в прямоугольную, при этом составляющие VX, VY, VZ отличаются друг от друга соответствующими тригонометрическими функциями углов θВМ, ΨВМ.
- законы изменения составляющих вектора скорости воздушной мишени по соответствующим осям прямоугольной системы координат OXYZ, которые получены в результате преобразования сферической системы координат в прямоугольную, при этом составляющие VX, VY, VZ отличаются друг от друга соответствующими тригонометрическими функциями углов θВМ, ΨВМ.
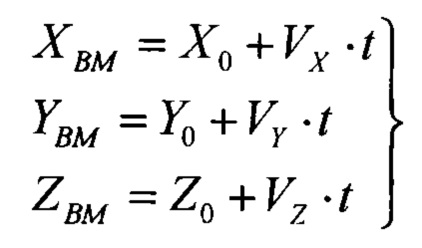 - законы изменения текущих координат воздушной мишени;
- законы изменения текущих координат воздушной мишени;
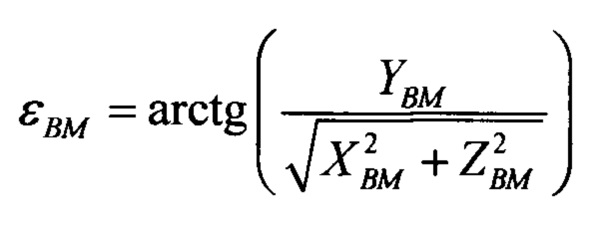 - закон изменения текущего угла места воздушной мишени;
- закон изменения текущего угла места воздушной мишени;
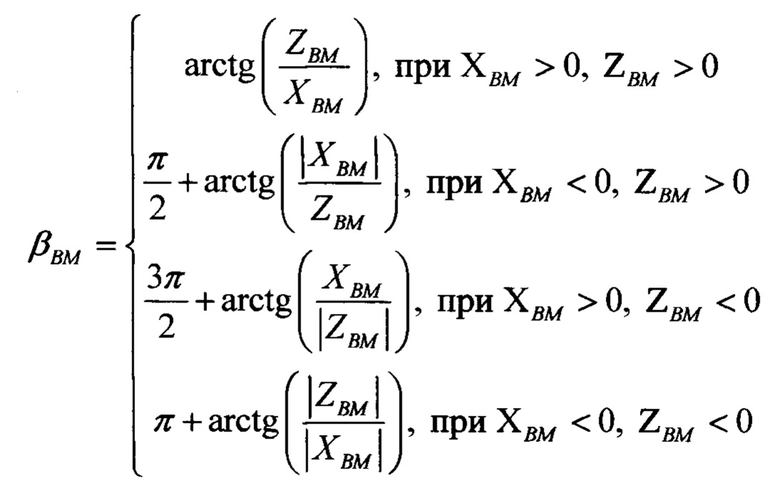 - закон изменения текущего азимута воздушной мишени.
- закон изменения текущего азимута воздушной мишени.
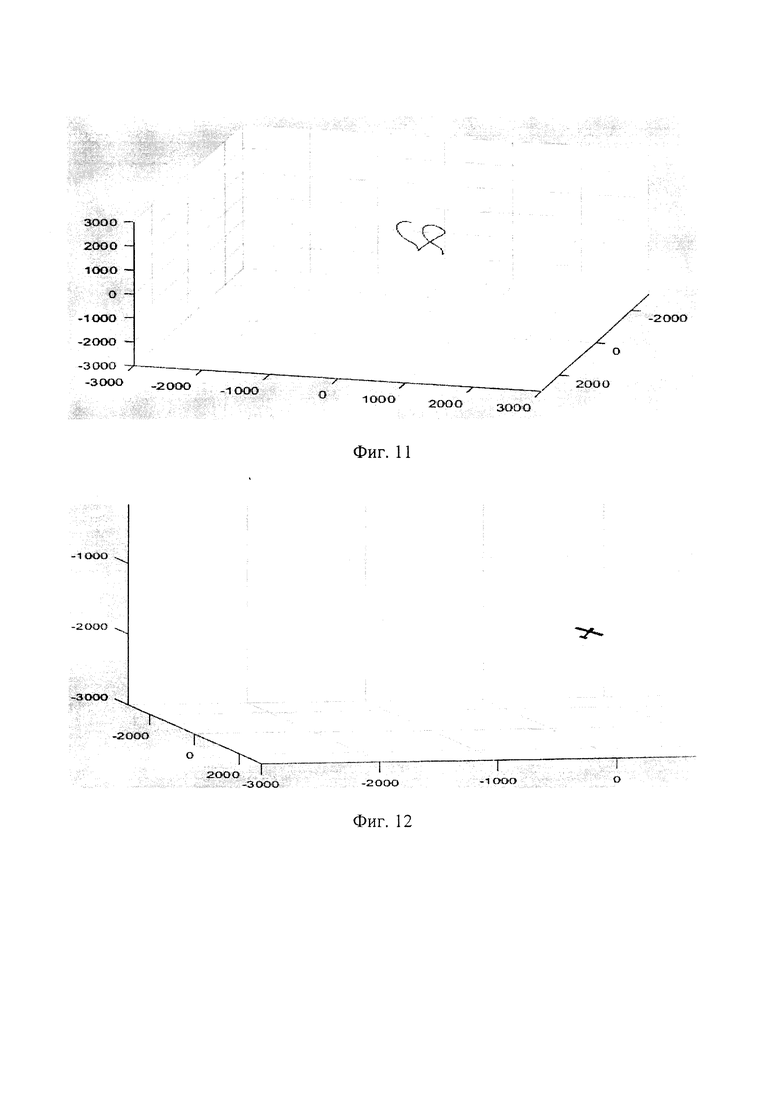
Используя предложенные зависимости возможно формировать различные полетные задания для воздушной мишени на основе БПЛА, которые в свою очередь позволят ей совершать различного рода маневры, в том числе пространственные (фиг. 9, 10, 11).
Вышеприведенная математическая модель полетного задания, а также операторная схема автопилота воздушных мишеней на основе БПЛА являются базовыми структурными элементами имитационной модели системы управления воздушной мишенью на основе БПЛА из состава мишенного комплекса.
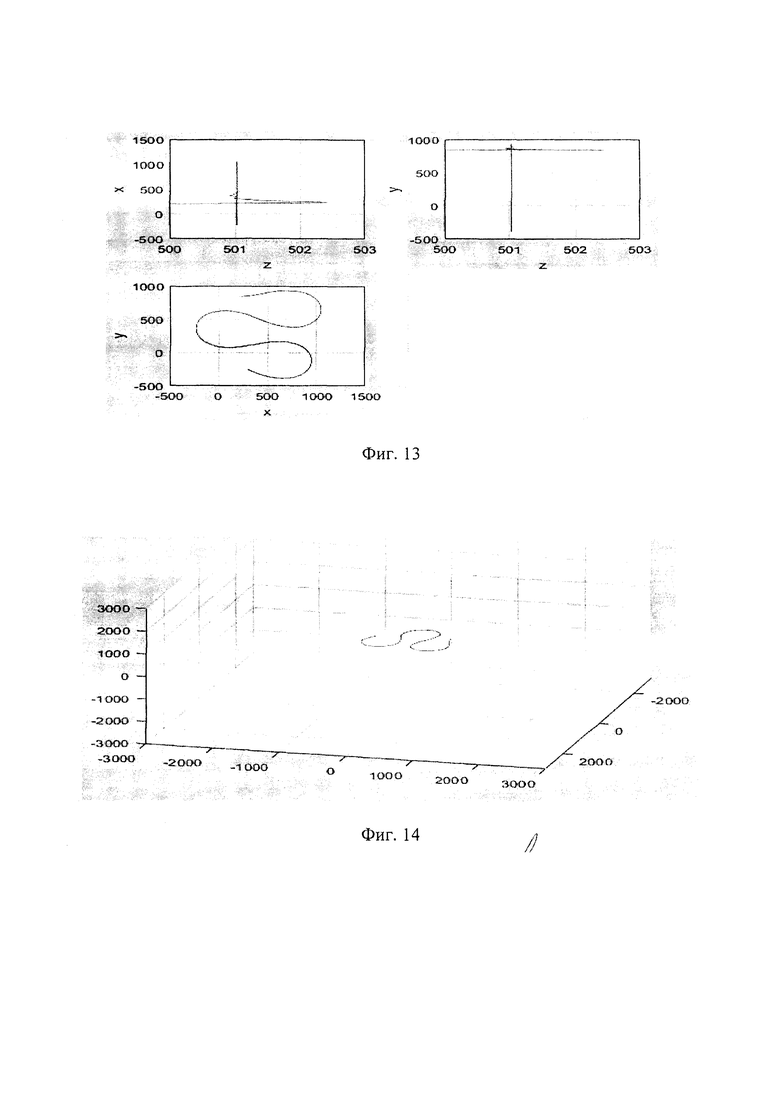
Возможности системы MATLAB позволяют визуализировать движение планера воздушной мишени, что в итоге позволяет исследовать динамику полета воздушной мишени на основе БПЛА (фиг. 12).
Кроме того, зная геометрические размеры воздушной мишени и аэродинамические коэффициенты ее планера, имитационная модель системы управления воздушной мишенью на основе БПЛА позволяет имитировать полет практически любой воздушной мишени на основе БПЛА за счет внесения соответствующих изменений в структурные блоки контуров автопилота и блок графической прорисовки планера воздушной мишени в системе MATLAB.
Дополнительно имитационная модель системы управления воздушной мишенью на основе БПЛА, за счет введения в ее состав блоков отображения траекторий движения воздушной мишени в каждой из плоскостей, позволяет проводить анализ и давать качественную оценку точности работы автопилота воздушной мишени на основе БПЛА по результатам сравнения графиков траекторий требуемого движения и реально отрабатываемого автопилотом воздушной мишени (фиг. 13, 14).
Фигуры 9-14 получены путем использования приведенных выше математических зависимостей полетного задания при моделировании в среде программирования Matlab и позволяют оценить только конечный результат управления воздушной мишенью ввиде траектории ее полета относительно наземного пункта управления. В данной среде моделирования не предусматривается графическое отображение текущих углов и проекций векторов в рассматриваемой системе координат.
Таким образом, разработанная имитационная модель системы управления воздушной мишенью на основе БПЛА позволяет проводить исследования по возможности реализации различных законов управления на основе формируемых полетных заданий для воздушных мишеней на основе БПЛА при имитации типовых маневров средств воздушного нападения, в том числе пространственных маневров, а также осуществлять анализ процессов, протекающих в контурах автопилота воздушной мишени, с возможностью коррекции параметров системы управления воздушной мишени для определения возможностей повышения достоверности имитации типовых маневров реальных ЛА без проведения натурных и полунатурных экспериментов.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Верба B.C., Татарский Б.Г. Принципы построения и особенности применения комплексов с БЛА. М.: Радиотехника, 2016. 505 с.
2. Моисеев B.C. Групповое применение беспилотных летательных аппаратов. - Казань: Редакционно-издательский центр «Школа», 2017. 572 с. (Серия «Современная прикладная математика и информатика»).
3. Рэндал У. Биард, Тимоти У. МакЛэйн. Малые беспилотные летательные аппараты: теория и практика. Перевод с английского. - Москва: МИР-радиоэлектроники, Техносфера. 2015. 312 с.
4. Изобретения к патенту RU 2 189 625 С1. «Система управления беспилотным летательным аппаратом».
5. Изобретение к патенту RU 155 323 U1. «Система управления беспилотным летательным аппаратом».
6. Математическая морфология. Электронный математический и медико-биологический журнал - Т. 10 Вып. 2. - 2011. УДК 623.451 Пространственная имитационная модель контура теленаведения ЗУР для исследования стрельбы в движении. Желнин А.А.
7. Описание полезной модели к патенту RU 103 215 U1. «Моделирующий комплекс для проверки системы управления беспилотного летательного аппарата».
8. Романова И.К. Траектории полета летательных аппаратов. Учебное пособие. М.: Издательство МГТУ им. Н.Э. Баумана, 2017.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ ГРУППОЙ МАНЕВРЕННЫХ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2022 |
|
RU2818981C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы беспилотного летательного аппарата малой дальности с использованием интеллектуальной системы геопространственной информации | 2019 |
|
RU2722599C1 |
| СПОСОБ КОМБИНИРОВАННОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2014 |
|
RU2586399C2 |
| Пространственная имитационная модель системы управления автоматическим маневренным летательным аппаратом | 2019 |
|
RU2735418C2 |
| СПОСОБ ДИСТАНЦИОННОЙ КОРРЕКЦИИ ПОЛЕТНОГО ЗАДАНИЯ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2020 |
|
RU2755411C1 |
| МОДЕЛИРУЮЩИЙ КОМПЛЕКС ДЛЯ ПРОВЕРКИ СИСТЕМЫ УПРАВЛЕНИЯ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2010 |
|
RU2432592C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК СИСТЕМЫ САМОНАВЕДЕНИЯ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2024 |
|
RU2830544C1 |
| БЕСПИЛОТНЫЙ КОМПЛЕКС ДЛЯ АВИАЦИОННО-ХИМИЧЕСКИХ РАБОТ | 2023 |
|
RU2817270C1 |
| Способы формирования данных об ориентации объекта и навигационный комплекс летательного аппарата для их реализации | 2020 |
|
RU2745083C1 |
| КОМПЛЕКС УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ | 2004 |
|
RU2270471C1 |
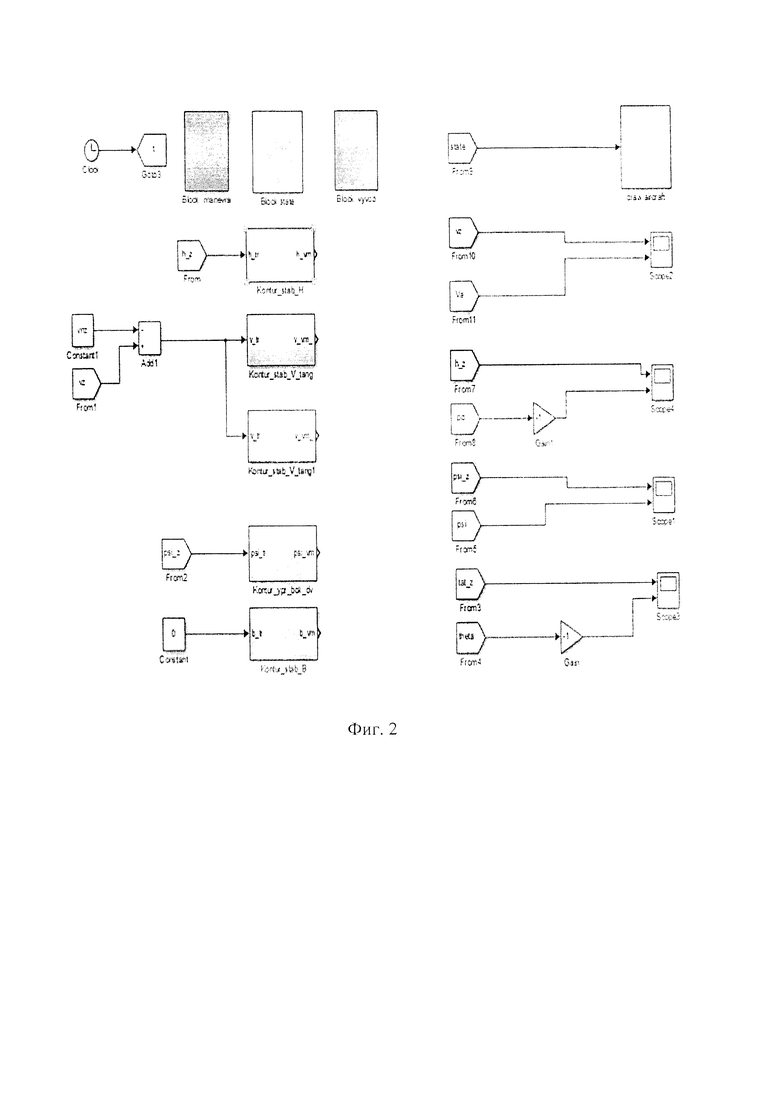
Имитационная модель системы управления воздушной мишенью на основе беспилотного летательного аппарата из состава мишенного комплекса содержит контуры автопилота для управления боковым и продольным движениями воздушной мишени на основе БПЛА. Контур управления боковым движением автопилота содержит подконтур управления курсовым углом воздушной мишени с последовательным замыканием с подконтуром управления креном воздушной мишени и имеет коэффициент усиления дифференциального регулятора демпфирования скорости крена для внутреннего контура. Контур управления продольным движением содержит подконтуры обратной связи: подконтур выдерживания высоты полета воздушной мишени на основе БПЛА с помощью управляющих сигналов по тангажу с последовательным замыканием с подконтуром автопилота стабилизации по углу тангажа, используемого в качестве внутреннего подконтура, подконтур выдерживания скорости воздушной мишени на основе БПЛА с помощью регулирования тангажа, подконтур стабилизации скорости воздушной мишени на основе БПЛА с помощью дроссельной заслонки, которые в своем составе также имеют блоки, реализующие соответствующие коэффициенты усиления. Технический результат – обеспечение проверок технических решений системы управления воздушной мишенью с помощью имитационной модели. 14 ил.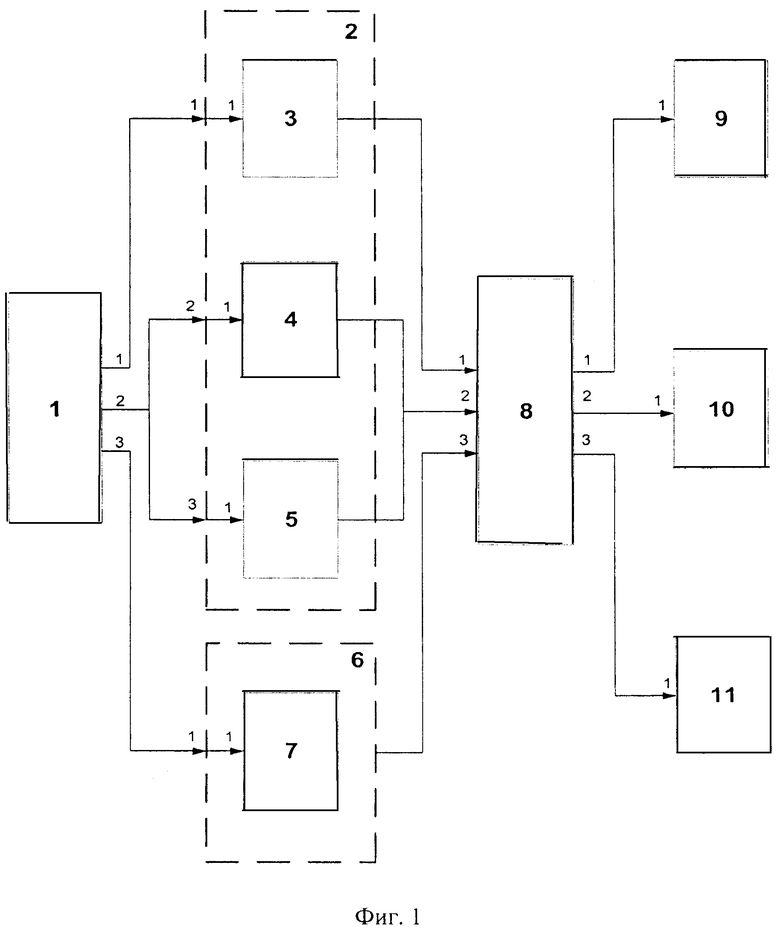
Имитационная модель системы управления воздушной мишенью на основе беспилотного летательного аппарата из состава мишенного комплекса, включающая в себя операторную схему автопилота воздушной мишени на основе БПЛА, на входе элементов которого формируется ряд математических зависимостей, определяющих требуемые параметры движения воздушной мишени на основе БПЛА в пространстве, отличающаяся от известных тем, что контур автопилота для управления боковым движением воздушной мишени на основе БПЛА включает в себя подконтур управления курсовым углом воздушной мишени с последовательным замыканием с подконтуром управления креном воздушной мишени и имеет коэффициент усиления дифференциального регулятора демпфирования скорости крена для внутреннего контура, коэффициенты усиления пропорционального и интегральных звеньев регулирования угла крена, коэффициенты усиления пропорционального и интегральных звеньев регулирования курсового угла, связанных с автопилотом бокового движения, а контур автопилота для управления продольным движением воздушной мишени на основе БПЛА использует в своем составе подконтуры обратной связи: подконтур выдерживания высоты полета воздушной мишени на основе БПЛА с помощью управляющих сигналов по тангажу с последовательным замыканием с подконтуром автопилота стабилизации по углу тангажа, используемого в качестве внутреннего подконтура, подконтур выдерживания скорости воздушной мишени на основе БПЛА с помощью регулирования тангажа, подконтур стабилизации скорости воздушной мишени на основе БПЛА с помощью дроссельной заслонки, которые в своем составе также имеют блоки, реализующие соответствующие коэффициенты усиления, которые участвуют в формировании необходимого уровня значений сигналов, в дальнейшем поступающих на блоки контуров, реализующие передаточные функции как для боковой динамики, которые выражают связь между отклонением элерона и углом крена и связь между углом крена и курсовым углом соответственно, так и для динамики продольных движений, которые моделируют связь между отклонением руля высоты и углом тангажа, углом тангажа и высотой, воздушной скоростью и высотой, а также положением дроссельной заслонки и углом тангажа с воздушной скоростью соответственно с возможностью имитации управляемого полета воздушной мишени на основе БПЛА в соответствии с заданным полетным заданием.
| Комплекс бортового оборудования вертолетов и самолетов авиации общего назначения | 2016 |
|
RU2640076C2 |
| Устройство для загрузки в газогенератор дров и других кусковых топлив | 1946 |
|
SU68145A1 |
| СПОСОБ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СУДНОМ ПО КУРСУ И ИНТЕЛЛЕКТУАЛЬНАЯ СИСТЕМА ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2012 |
|
RU2519315C2 |
| KR 1915860 B1, 06.11.2018 | |||
| EP 719429 B1, 10.06.1998. | |||
Авторы
Даты
2022-10-21—Публикация
2020-05-25—Подача