Изобретение относится к связи, а именно к передаче дискретной информации аналоговыми сигналами по каналам с ограниченной полосой пропускания. Предлагаемый способ может быть использован в системах радиосвязи, в которых применяется амплитудная модуляция с подавленной несущей (АМ-ПН), а цифровые данные представлены в виде взаимно ортогональных фазоманипулированных синусоидальных сигналов (ОФМ) или наборов таких сигналов.
Известен способ передачи данных с многими поднесущими, описанный в книге Прокис Джон. Цифровая связь. Пер. с англ. / Под ред. Д.Д.Кловского. - М.: Радио и связь. 2000. - 800 с., стр.593-595. Последовательность действий в аналоге следующая:
на передающей стороне информационную последовательность разбивают на блоки по r бит;
каждые r бит преобразуют в сигналы с квадратурной амплитудной модуляцией (КАМ), или сигналы с ОФМ на каждой из N несущих и получают комплексные точки сигнала, соответствующие информационным символам на поднесущих Xn, n=0,1, …N-1;
производят N-точечное обратное дискретное преобразование Фурье последовательности символов 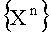 ;
;
преобразуют полученную комплексную последовательность в вещественную последовательность;
вводят защитный интервал между смежными сигнальными блоками для устранения межсимвольной интерференции;
демодулируют сигнал путем вычисления дискретного преобразования Фурье после аналого-цифрового преобразования.
Недостатком известного способа является относительно низкая помехоустойчивость (Помехоустойчивость - способность системы передачи и приема информации противостоять помехам (см. В.А.Васин, В.В.Калмыков, Ю.Н.Себекин, А.И.Сенин, И.Б.Федоров - Горячая линия - Телеком, 2005. 472 с.)), если не учитывается канальный коэффициент передачи.
Известен способ приема двоичных фазоманипулированных на 180 градусов сигналов с фазоразностной модуляцией (Патент РФ №2146078, МПК Н04L 27/22, 2000 г.).
Способ заключается в следующей последовательности действий:
спектр принятого радиосигнала переносится в низкочастотную область, определяются низкочастотные отфильтрованные сигналы в обоих квадратурных ортогональных (cos, sin) каналах, бинарно {0,1} квантуются, по значениям этих бинарно квантованных сигналов обоих каналов {00, 01, 10, 11} в текущем и предшествующем битах принимается решение об изменении или не изменении фазы принимаемого сигнала на 180°.
Так как центральная частота гетеродина в приемнике не равна частоте гетеродина передатчика, то вектор принимаемого сигнала на координатной плоскости (X, Y) медленно поворачивается относительно вектора гетеродина приемника. В моменты времени, соответствующие переходу через ноль проекции вектора принимаемого сигнала на ортогональные оси координат, для устранения прохождения на выход приемного устройства несанкционированного срабатывания (из-за шумов) компаратора вблизи нуля, в каждом квадратурном канале величина отфильтрованного низкочастотного сигнала сравнивается с заданным пороговым значением (Uпор) по абсолютной величине. Если величины низкочастотных отфильтрованных сигналов обоих каналов больше Uпор по абсолютной величине, то результаты анализа текущего и задержанного на один бит бинарно квантованных сигналов обоих каналов суммируются и поступают на выход приемного устройства, если величина низкочастотного отфильтрованного сигнала одного из каналов меньше Uпор. по абсолютной величине, то на выход приемного устройства поступают только результаты анализа текущего и задержанного на один бит бинарно квантованных сигналов другого канала. Причем в данном квадратурном канале в этот момент времени отфильтрованный низкочастотный сигнал, вследствие свойства ортогональности, близок к максимальному (по абсолютной величине) значению.
Недостатком данного способа является относительно низкая помехоустойчивость, обусловленная необходимостью жесткого выбора порогового значения, зависящего от условий приема, и уменьшения отношения сигнал/шум из-за не учета одной из квадратурных компонент при идентификации символов.
Наиболее близким по своей сущности к предлагаемому способу и достигаемому результату является способ, реализованный в «Демодуляторе взаимно ортогональных синусоидальных сигналов с фазоразностной модуляцией» (Авторское свидетельство SU 1277423 А1, МПК Н04L 27/22, 1986 г.), который заключается в следующем: что для сигнала, с N≥2 поднесущими fn, где n=1,2 …N, с К посылками длительностью Т с защитным интервалом длительностью, τ, где k=1,2, …K, вычисляют М≥2 раз квадратурные компоненты (проекции) 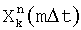 и
и 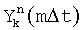 , m=1,2, …M, Δt=τ/M. Для каждой k-й посылки на fn поднесущей частоте, в моменты времени mΔt вычисляют и запоминают фазы
, m=1,2, …M, Δt=τ/M. Для каждой k-й посылки на fn поднесущей частоте, в моменты времени mΔt вычисляют и запоминают фазы 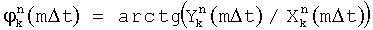 , разности фаз смежных посылок
, разности фаз смежных посылок 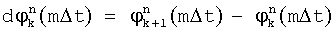 , набег фаз
, набег фаз 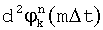 - угловое отклонение разности фаз от ближайшей эталонной точки, обусловленное помехами. Вычисляют математические ожидания и дисперсии набега фаз
- угловое отклонение разности фаз от ближайшей эталонной точки, обусловленное помехами. Вычисляют математические ожидания и дисперсии набега фаз 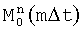 и
и 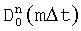 . По вычисленным величинам дисперсий определяют весовые коэффициенты kj, с которыми берутся для частотных поднесущих fn в моменты времени mΔt значения уточненных квадратурных компонент
. По вычисленным величинам дисперсий определяют весовые коэффициенты kj, с которыми берутся для частотных поднесущих fn в моменты времени mΔt значения уточненных квадратурных компонент 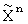 ,
, 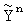 . По уточненным проекциям
. По уточненным проекциям 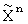 ,
, 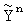 вычисляют фазы посылок, разности фаз между соседними посылками
вычисляют фазы посылок, разности фаз между соседними посылками 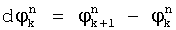 и по разностям фаз идентифицируют принятые информационные символы посредством выбора ближайшей эталонной точки.
и по разностям фаз идентифицируют принятые информационные символы посредством выбора ближайшей эталонной точки.
Недостатком прототипа является относительно низкая помехоустойчивость, обусловленная тем, что отсутствует учет погрешности переноса спектра принимаемого радиосигнала с ФРМ в низкочастотную область.
Целью заявляемого технического решения является разработка способа демодуляции радиосигнала с ФРМ, обеспечивающего повышение помехоустойчивости за счет учета частотных и фазовых ошибок формирования опорного колебания в приемнике и статистической обработки принимаемых сигналов.
Заявленный способ расширяет арсенал средств данного назначения.
Поставленная цель в заявляемом техническом решении достигается тем, что в известном способе демодуляции радиосигналов с ФРМ, заключающемся в том, что для сигнала, с N≥2 поднесущими fn, где n=1,2 …N, с К посылками длительностью посылки Т, с защитным интервалом длительностью τ, где k=1,2, …K, вычисляют квадратурные компоненты 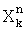 ,
, 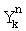 , для каждой k-й посылки на fn поднесущей частоте, вычисляют и запоминают фазы
, для каждой k-й посылки на fn поднесущей частоте, вычисляют и запоминают фазы 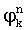 , разности фаз смежных посылок
, разности фаз смежных посылок 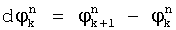 , набеги фаз
, набеги фаз 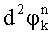 , после чего идентифицируют принятый информационный символ, содержащийся в k-й посылке. В заявляемом способе предварительно принимают радиосигнал с ФРМ на несущей частоте f0, переносят его спектр на величину, равную значению fo в низкочастотную область частот, затем перемещенный радиосигнал дискретизируют, вычисляют квадратурные компоненты перемещенного дискретизированного радиосигнала
, после чего идентифицируют принятый информационный символ, содержащийся в k-й посылке. В заявляемом способе предварительно принимают радиосигнал с ФРМ на несущей частоте f0, переносят его спектр на величину, равную значению fo в низкочастотную область частот, затем перемещенный радиосигнал дискретизируют, вычисляют квадратурные компоненты перемещенного дискретизированного радиосигнала 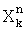 ,
, 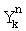 посредством выполнения над ним операции комплексного преобразования Фурье, далее, полученные значения комплексных коэффициентов Фурье преобразуют в тригонометрическую форму, определяют погрешность переноса
посредством выполнения над ним операции комплексного преобразования Фурье, далее, полученные значения комплексных коэффициентов Фурье преобразуют в тригонометрическую форму, определяют погрешность переноса 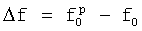 , где
, где 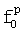 - реальная частота переноса спектра радиосигнала априори неизвестная, для этого, для каждой разности фаз
- реальная частота переноса спектра радиосигнала априори неизвестная, для этого, для каждой разности фаз 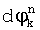 вычисляют по два ее новых значения
вычисляют по два ее новых значения 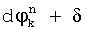 и
и 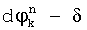 , где δ - предварительно заданная поправка значений фазы, после чего с учетом новых значений разностей фаз вычисляют по два новых значений набега фазы
, где δ - предварительно заданная поправка значений фазы, после чего с учетом новых значений разностей фаз вычисляют по два новых значений набега фазы 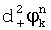 и
и 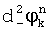 , где индексы «+» и «-» соответствуют сложению и вычитанию δ при вычислении разности фаз. Затем вычисляют математические ожидания
, где индексы «+» и «-» соответствуют сложению и вычитанию δ при вычислении разности фаз. Затем вычисляют математические ожидания 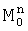 ,
, 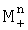 ,
, 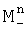 и дисперсии
и дисперсии 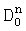 ,
, 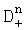 ,
, 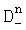 набегов фазы по множеству N несущих частот, где индексы «о», «+», «-» определяют значения математических ожиданий и дисперсий, соответственно без учета поправки, с учетом +δ и -δ. Вычисляют с учетом каждого из математических ожиданий
набегов фазы по множеству N несущих частот, где индексы «о», «+», «-» определяют значения математических ожиданий и дисперсий, соответственно без учета поправки, с учетом +δ и -δ. Вычисляют с учетом каждого из математических ожиданий 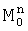 ,
, 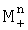 ,
, 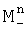 уточненные набеги фаз
уточненные набеги фаз 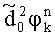 ,
, 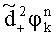 ,
, 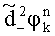 по их значениям вычисляют дисперсии уточненных набегов фаз
по их значениям вычисляют дисперсии уточненных набегов фаз 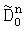 ,
, 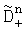 ,
, 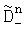 . Выбирают из полученных дисперсий
. Выбирают из полученных дисперсий 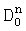 ,
, 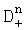 ,
, 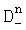 и
и 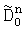 ,
, 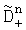 ,
, 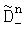 наименьшую и соответствующее ей по индексу математическое ожидание. Вычисляют математическое ожидание по множеству К посылок M0. Погрешность переноса спектра радиосигнала вычисляют по формуле Δf=М0/2πT, запоминают ее и компенсируют сдвиг при приеме очередного сигнала из К посылок, а идентификацию информационных символов выполняют с учетом значения М0, причем действия по определению математического ожидания М0 и Δf повторяются при поступлении очередного сигнала из К посылок.
наименьшую и соответствующее ей по индексу математическое ожидание. Вычисляют математическое ожидание по множеству К посылок M0. Погрешность переноса спектра радиосигнала вычисляют по формуле Δf=М0/2πT, запоминают ее и компенсируют сдвиг при приеме очередного сигнала из К посылок, а идентификацию информационных символов выполняют с учетом значения М0, причем действия по определению математического ожидания М0 и Δf повторяются при поступлении очередного сигнала из К посылок.
Новая совокупность существенных признаков позволяет достичь указанного технического результата за счет учета частотных и фазовых ошибок формирования опорного колебания в приемнике и статистической обработки принимаемых сигналов.
Заявляемый способ поясняется чертежами, на которых:
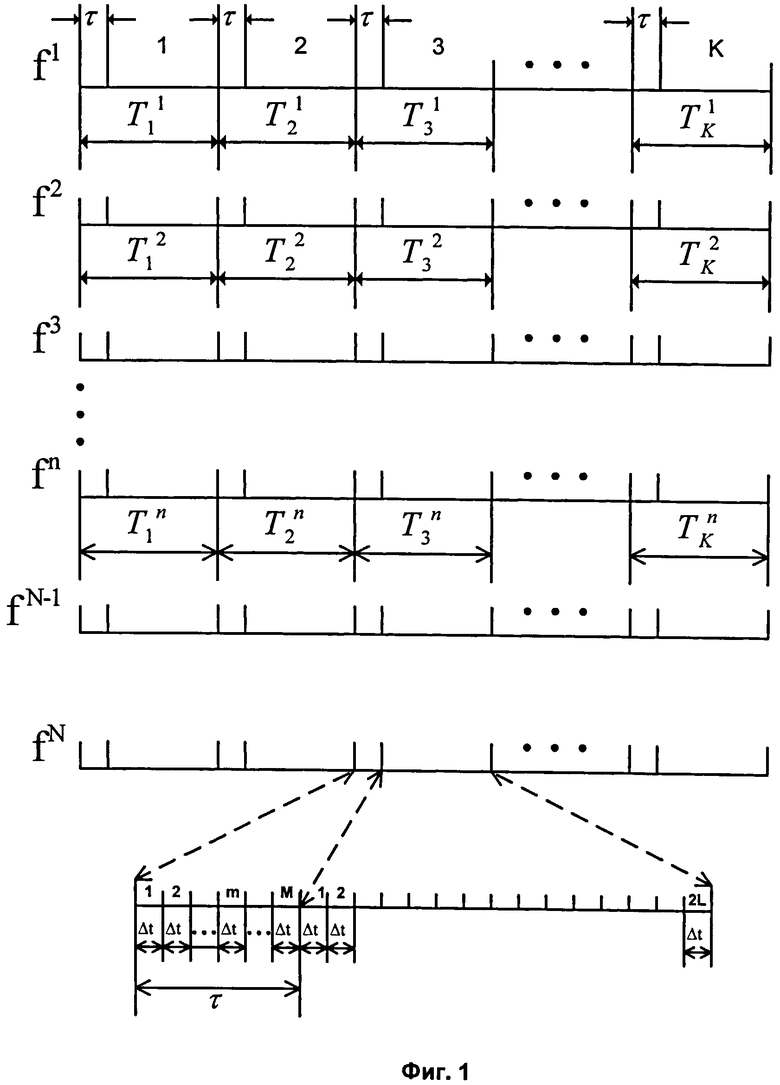
на Фиг.1 показана структура принимаемого многочастотного сигнала;
на Фиг.2 показана последовательность преобразований спектра радиосигнала, обеспечивающая компенсацию погрешности начального переноса спектра;
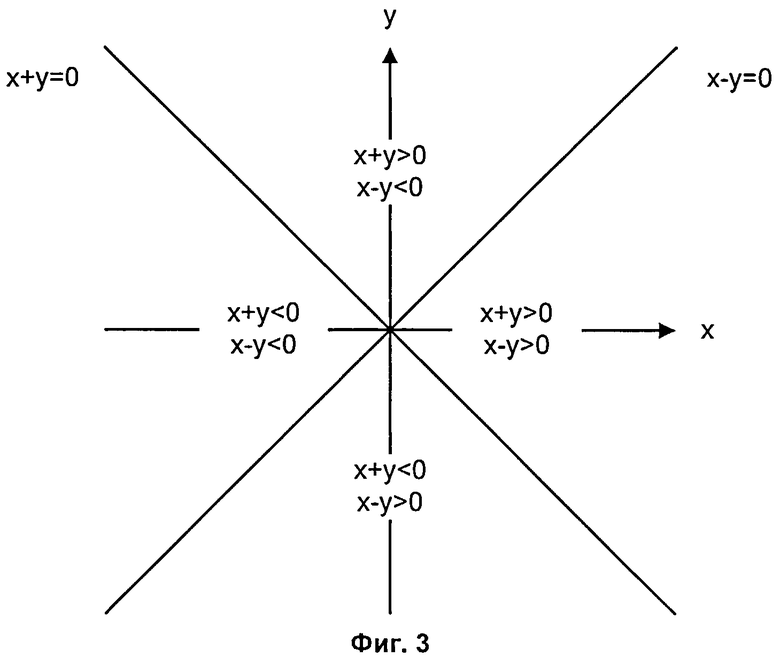
на Фиг.3 приведены четыре области комплексной плоскости, для каждой из которых указывается правило вычисления фазы φ;
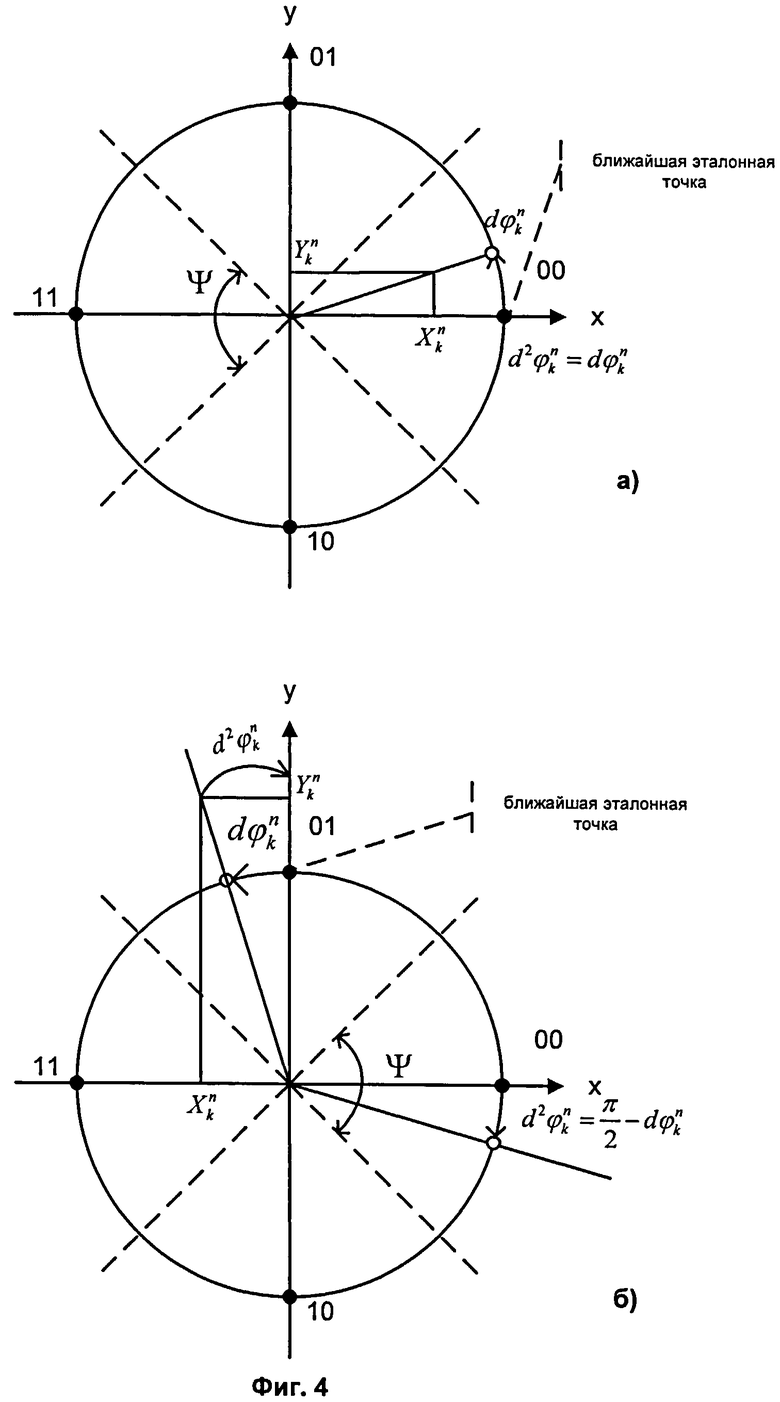
на Фиг.4 иллюстрируется правило вычисления набега фазы и идентификации информационных символов.
Реализация заявляемого способа поясняется следующим образом. Структурно сигнал состоит из К посылок, каждая посылка - цифровой символ в зависимости от кратности модуляции - это один или несколько бит, длительность посылки равна τ, множество посылок по частоте равно N. Любая посылка начинается с защитного интервала длительностью τ, на посылке имеются дискретные отсчеты сигнала с интервалом дискретизации Δt=τ/М=(T-τ)/2L (см. фиг.1). Принимаемый радиосигнал - это амплитудно-модулированный, с подавленной несущей многочастотный сигнал, с относительной фазовой модуляцией цифровой информации на каждой поднесущей. Переносят спектр этого сигнала в область низких частот на величину, равную значению fо. Если прием на данной радиочастоте уже был, при переносе учитывают вычисленную на предыдущем интервале из К посылок погрешность частотного сдвига Δf. Алгоритм компенсации частотного сдвига известен (Прокис Джон. Цифровая связь. Пер. с англ. / Под ред. Д.Д.Кловского. - М.: Радио и связь. 2000. - 800 с., стр.131-134).
Из сигнала xs(t) (см. фиг.2) формируют аналитический сигнал 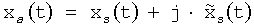 , где
, где 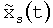 - сигнал, сопряженный по Гильберту с xs(t), получают посредством фазовращателя на 90° всех частот исходного сигнала xs(t). Сигнал хa(t) умножают на комплексную экспоненту
- сигнал, сопряженный по Гильберту с xs(t), получают посредством фазовращателя на 90° всех частот исходного сигнала xs(t). Сигнал хa(t) умножают на комплексную экспоненту 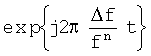 . Берут реальную часть комплексного сигнала
. Берут реальную часть комплексного сигнала 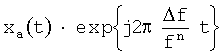 . При этом получают действительный сигнал, у которого скомпенсирован частотный сдвиг
. При этом получают действительный сигнал, у которого скомпенсирован частотный сдвиг 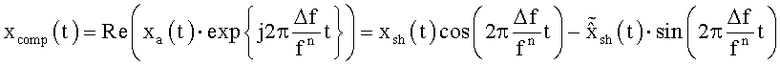 (см. фиг.2).
(см. фиг.2).
Получают дискретизацией этого сигнала вещественную последовательность из М отсчетов на защитном интервале длительностью τ и 2L отсчетов на интервале длительностью Т-τ, вычисляют по ним дискретное L точечное комплексное преобразование Фурье 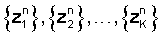 сигнала на интервалах [τ,T],[T+τ,2Т],…[(K-1)Т,КТ] всех К посылок. Границы посылок известны по тактовому синхронизму. Алгоритмы вычисления дискретного преобразования Фурье известны, например А.Оппенгейм, Р.Шафер. Цифровая обработка сигналов. Москва: Техносфера, 2006. - 856 с. Преобразуют полученные комплексные числа
сигнала на интервалах [τ,T],[T+τ,2Т],…[(K-1)Т,КТ] всех К посылок. Границы посылок известны по тактовому синхронизму. Алгоритмы вычисления дискретного преобразования Фурье известны, например А.Оппенгейм, Р.Шафер. Цифровая обработка сигналов. Москва: Техносфера, 2006. - 856 с. Преобразуют полученные комплексные числа 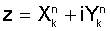 из декартовой формы в тригонометрическую форму. Для преобразования комплексных чисел из декартовой формы в тригонометрическую форму необходимо производить вычисления квадратов амплитуды комплексных чисел
из декартовой формы в тригонометрическую форму. Для преобразования комплексных чисел из декартовой формы в тригонометрическую форму необходимо производить вычисления квадратов амплитуды комплексных чисел 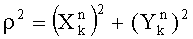 и фазы комплексных чисел φ=arctg(y/x) (см. фиг.4). Для вычисления фазы произвольного комплексного числа необходимо разделить комплексную плоскость на четыре части при помощи прямых x-у=0, х+у=0 (см. фиг.3).
и фазы комплексных чисел φ=arctg(y/x) (см. фиг.4). Для вычисления фазы произвольного комплексного числа необходимо разделить комплексную плоскость на четыре части при помощи прямых x-у=0, х+у=0 (см. фиг.3).
Для каждой четверти комплексной плоскости фазу вычисляют по следующему правилу:
Вычисляют последовательно на интервале, равном длине посылки координаты 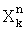 ,
, 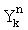 , где n=1,2, …N, k=1,2, …K. По их значениям вычисляют фазы
, где n=1,2, …N, k=1,2, …K. По их значениям вычисляют фазы 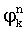 , разности фаз между соседними посылками
, разности фаз между соседними посылками 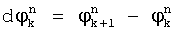 , набеги фазы
, набеги фазы 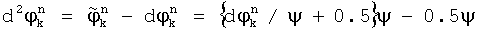 , где
, где 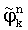 - ближайшая к
- ближайшая к 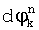 эталонная точка, {} - дробная часть вещественного числа, ψ - размер сектора модуляции (определяется видом модуляции, для ООФМ ψ=180°, для ДОФМ ψ=90°, для ТОФМ ψ=45°. Вариант нахождения набега фазы для двукратной относительной фазовой модуляции иллюстрируется на фиг. 4.
эталонная точка, {} - дробная часть вещественного числа, ψ - размер сектора модуляции (определяется видом модуляции, для ООФМ ψ=180°, для ДОФМ ψ=90°, для ТОФМ ψ=45°. Вариант нахождения набега фазы для двукратной относительной фазовой модуляции иллюстрируется на фиг. 4.
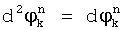 , если
, если 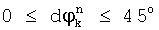 ;
;
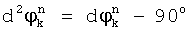 , если
, если 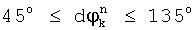 ;
;
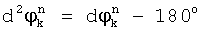 , если
, если 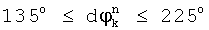 ;
;
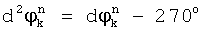 , если
, если 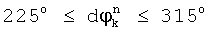 ;
;
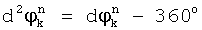 , если
, если 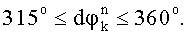
Набег фазы - это отклонение фазы принимаемых сигналов от номинальных фаз передаваемых сигналов, которое вызвано помехой и несоответствием частот гетеродинов передатчика и приемника, то есть погрешностью переноса спектра Δf. Сдвиг частоты может быть таким, что разности фаз (точки dφ) будут расположены близко к границам секторов модуляции. В этом случае даже небольшой шум будет приводить к неверному определению правильной эталонной точки и ошибочному определению набега фаз. Для борьбы с данным эффектом производят дополнительные вычисления набегов фаз со сдвигом ±δ.
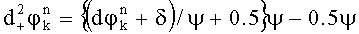 и
и 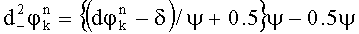 .
.
Составляющая набега фазы из-за шума есть случайная величина. Мерой разброса набега фазы по причине шума является дисперсия. Чем больше величина дисперсии, тем больше вероятность ошибочного приема информации. Для повышения точности определения частотного сдвига из-за шума производится набор статистики по всем поднесущим и посылкам принятого сигнала, причем из множества вариантов демодуляции со сдвигом по времени для дальнейшей обработки выбирается посылка, для которой установлен тактовый синхронизм.
По набегам фазы 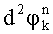 ,
, 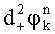 ,
, 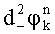 вычисляют математические ожидания и дисперсии набегов фазы:
вычисляют математические ожидания и дисперсии набегов фазы:
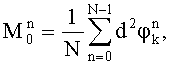
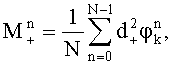
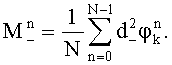
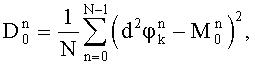
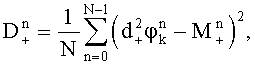
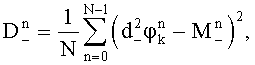
вычисляют три варианта уточненных набегов фазы
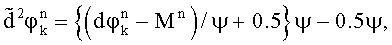
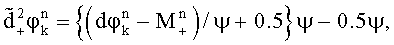
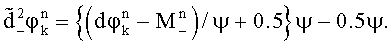
Для случайных величин 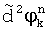 ,
, 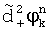 ,
, 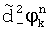 с нулевыми средними значениями вычисляют дисперсии
с нулевыми средними значениями вычисляют дисперсии
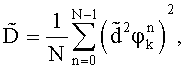
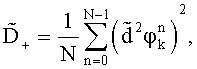
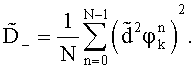
Выбирают среди всех полученных дисперсий D0, D+, D-, 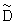 ,
, 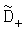 ,
, 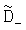 наименьшую и соответствующее ей по индексу математическое ожидание, затем вычисляют математическое ожидание по множеству К посылок M0.
наименьшую и соответствующее ей по индексу математическое ожидание, затем вычисляют математическое ожидание по множеству К посылок M0.
Вычисляют погрешность переноса спектра радиосигнала по формуле Δf=M0/2πТ и сохраняют её для приема очередного сигнала из К посылок.
По вычисленным и накопленным значениям разницы фаз между двумя соседними посылками с учетом полученного значения М0 идентифицируют принятые информационные символы, для этого из разностей между соседними посылками 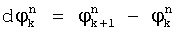 дополнительно вычитают математическое ожидание набега фазы М0, после чего определяют ближайшую к
дополнительно вычитают математическое ожидание набега фазы М0, после чего определяют ближайшую к 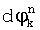 эталонную точку. Эталонным точкам соответствуют передаваемые символы. Например, при ДОФМ (см. фиг.4), если
эталонную точку. Эталонным точкам соответствуют передаваемые символы. Например, при ДОФМ (см. фиг.4), если 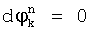 , то принята двоичная последовательность 00; если
, то принята двоичная последовательность 00; если 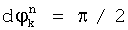 , то принята двоичная последовательность 01; если
, то принята двоичная последовательность 01; если 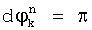 , то принята двоичная последовательность 11; если
, то принята двоичная последовательность 11; если 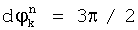 , то принята двоичная последовательность 10. Достигаемым техническим результатом предлагаемого способа демодуляции радиосигналов с фазоразностной модуляцией является повышение помехоустойчивости приема и расширение арсенала средств данного назначения.
, то принята двоичная последовательность 10. Достигаемым техническим результатом предлагаемого способа демодуляции радиосигналов с фазоразностной модуляцией является повышение помехоустойчивости приема и расширение арсенала средств данного назначения.
| название | год | авторы | номер документа |
|---|---|---|---|
| МНОГОКОДОВЫЙ СИГНАЛ С УМЕНЬШЕННЫМ ОТНОШЕНИЕМ ПИКОВОГО ЗНАЧЕНИЯ К СРЕДНЕКВАДРАТИЧЕСКОМУ ЗНАЧЕНИЮ | 2009 |
|
RU2490812C2 |
| СПОСОБ ПЕЛЕНГАЦИИ РАДИОСИГНАЛОВ И ПЕЛЕНГАТОР ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2419805C1 |
| СПОСОБ ПЕРЕДАЧИ И ПРИЕМА РЕФЛЕКСНО-МОДУЛИРОВАННЫХ СИГНАЛОВ | 1990 |
|
RU2007877C1 |
| Способ пеленгации телефонных радиосигналов с амплитудной модуляцией | 2023 |
|
RU2798775C1 |
| СПОСОБ ДЕМОДУЛЯЦИИ КРАТКОВРЕМЕННЫХ СИГНАЛОВ С МНОГОУРОВНЕВОЙ АБСОЛЮТНОЙ ФАЗОВОЙ МОДУЛЯЦИЕЙ В УСЛОВИЯХ ЗАМИРАНИЙ | 2018 |
|
RU2684605C1 |
| ДЕМОДУЛЯТОР ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2008 |
|
RU2393641C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТНОГО СДВИГА МЕЖДУ РАДИОСИГНАЛАМИ | 2017 |
|
RU2668342C2 |
| РАДИОМОДЕМ | 2010 |
|
RU2460215C1 |
| КОГЕРЕНТНЫЙ ДЕМОДУЛЯТОР AM-СИГНАЛА С ИСПОЛЬЗОВАНИЕМ ВЗВЕШЕННОЙ СУММЫ НИЖНЕЙ БОКОВОЙ ПОЛОСЫ/ВЕРХНЕЙ БОКОВОЙ ПОЛОСЫ ДЛЯ ПОДАВЛЕНИЯ ПОМЕХ | 2004 |
|
RU2342772C2 |
| СПОСОБ ПЕЛЕНГАЦИИ РАДИОСИГНАЛОВ И ПЕЛЕНГАТОР ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2341811C1 |
Изобретение относится к технике связи и может быть использовано при передаче дискретной информации аналоговыми сигналами по каналам, в которых применяется амплитудная модуляция с подавленной несущей, а данные представлены в виде взаимно ортогональных фазоманипулированных синусоидальных сигналов или наборов таких сигналов. В способе демодуляции принимают радиосигнал на несущей частоте f0, переносят его спектр его на величину, равную значению f0 в низкочастотную область, затем перемещенный радиосигнал дискретизируют, вычисляют квадратурные компоненты перемещенного дискретизированного радиосигнала 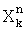 ,
, 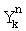 . Вычисление погрешности переноса спектра радиосигнала осуществляют по формуле Δf=М0/2πT, где М0 - математическое ожидание по множеству К посылок. Вычисленную погрешность запоминают и компенсируют сдвиг при приеме очередного радиосигнала, состоящего из К посылок на N частотах, а идентификацию информационного символа выполняют с учетом значения М0, причем действия по определению математического ожидания М0 и Δf повторяются при поступлении очередного сигнала из К посылок. Технический результат - повышение помехоустойчивости за счет учета частотных и фазовых ошибок формирования опорного колебания в приемнике и статистической обработки принимаемых сигналов. 1 з.п. ф-лы, 5 ил.
. Вычисление погрешности переноса спектра радиосигнала осуществляют по формуле Δf=М0/2πT, где М0 - математическое ожидание по множеству К посылок. Вычисленную погрешность запоминают и компенсируют сдвиг при приеме очередного радиосигнала, состоящего из К посылок на N частотах, а идентификацию информационного символа выполняют с учетом значения М0, причем действия по определению математического ожидания М0 и Δf повторяются при поступлении очередного сигнала из К посылок. Технический результат - повышение помехоустойчивости за счет учета частотных и фазовых ошибок формирования опорного колебания в приемнике и статистической обработки принимаемых сигналов. 1 з.п. ф-лы, 5 ил.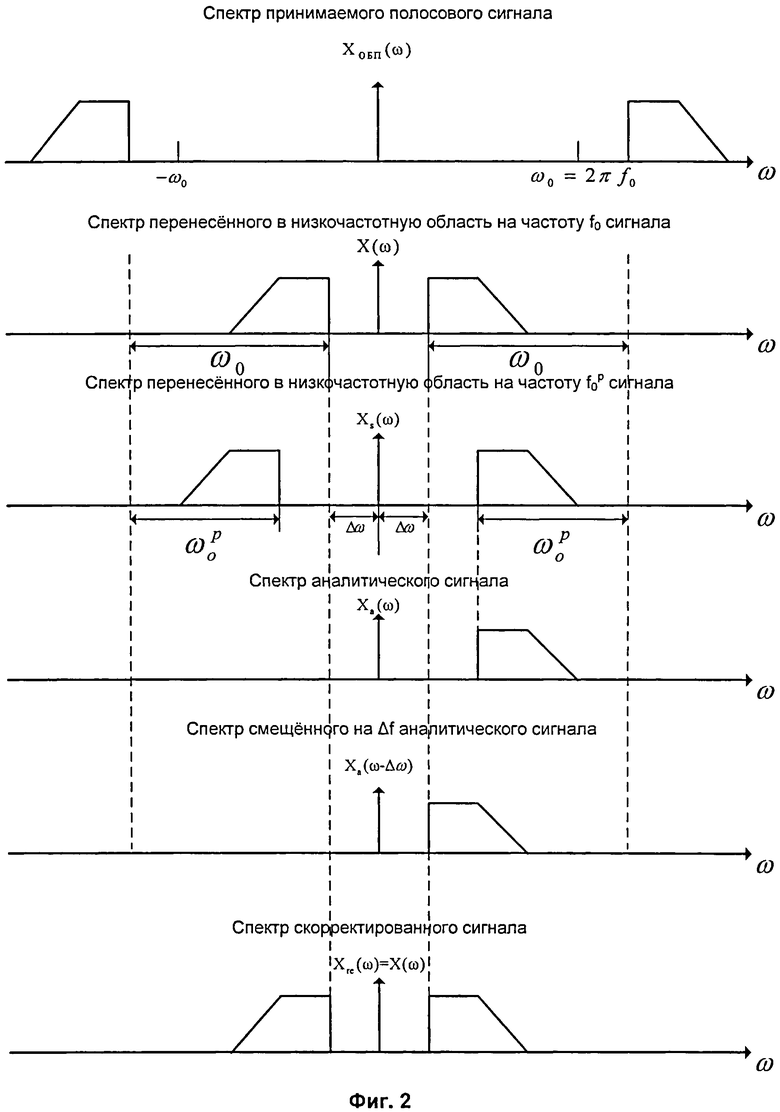
1. Способ демодуляции радиосигналов с фазоразностной модуляцией (ФРМ), заключающийся в том, что для сигнала с N≥2 поднесущими fn, где n=1, 2…N, с K посылками длительностью посылки Т, с защитным интервалом длительностью τ, вычисляют квадратурные компоненты 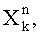
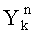 для каждой k-й посылки, где k=1, 2, …K, на fn поднесущей частоте, вычисляют и запоминают фазы
для каждой k-й посылки, где k=1, 2, …K, на fn поднесущей частоте, вычисляют и запоминают фазы 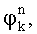 разности фаз смежных посылок
разности фаз смежных посылок  набеги фаз
набеги фаз 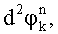 после чего идентифицируют принятый информационный символ, содержащийся в k-й посылке, отличающийся тем, что предварительно принимают радиосигнал на несущей частоте f0, переносят его спектр на величину, равную значению f0, в низкочастотную область, затем перемещенный радиосигнал дискретизируют, вычисляют квадратурные компоненты перемещенного дискретизированного радиосигнала
после чего идентифицируют принятый информационный символ, содержащийся в k-й посылке, отличающийся тем, что предварительно принимают радиосигнал на несущей частоте f0, переносят его спектр на величину, равную значению f0, в низкочастотную область, затем перемещенный радиосигнал дискретизируют, вычисляют квадратурные компоненты перемещенного дискретизированного радиосигнала 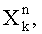
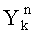 посредством выполнения над ним операции комплексного преобразования Фурье, далее полученные значения комплексных коэффициентов Фурье преобразуют в тригонометрическую форму, определяют погрешность переноса
посредством выполнения над ним операции комплексного преобразования Фурье, далее полученные значения комплексных коэффициентов Фурье преобразуют в тригонометрическую форму, определяют погрешность переноса 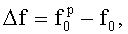 где
где 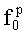 - реальная частота переноса спектра радиосигнала, априори неизвестная, для этого для каждой разности фаз
- реальная частота переноса спектра радиосигнала, априори неизвестная, для этого для каждой разности фаз 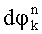 вычисляют по два ее новых значения
вычисляют по два ее новых значения 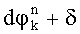 и
и 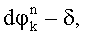 где δ - предварительно заданная поправка значений фазы, после чего с учетом новых значений разностей фаз вычисляют по два новых значений набега фазы
где δ - предварительно заданная поправка значений фазы, после чего с учетом новых значений разностей фаз вычисляют по два новых значений набега фазы 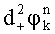 и
и  где индексы «+» и «-» соответствуют сложению и вычитанию δ при вычислении разности фаз, затем вычисляют математические ожидания
где индексы «+» и «-» соответствуют сложению и вычитанию δ при вычислении разности фаз, затем вычисляют математические ожидания 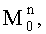
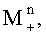
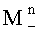 и дисперсии
и дисперсии 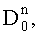
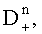
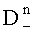 набегов фазы по множеству N поднесущих частот, где индексы «0», «+», «-» определяют значения математических ожиданий и дисперсий соответственно без учета поправки, с учетом +δ и -δ, вычисляют с учетом каждого из математических ожиданий
набегов фазы по множеству N поднесущих частот, где индексы «0», «+», «-» определяют значения математических ожиданий и дисперсий соответственно без учета поправки, с учетом +δ и -δ, вычисляют с учетом каждого из математических ожиданий 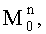
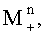
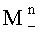 уточненные набеги фаз
уточненные набеги фаз 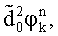 ,
, 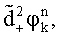
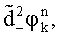 по значениям которых вычисляют дисперсии уточненных набегов фаз
по значениям которых вычисляют дисперсии уточненных набегов фаз 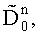
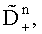
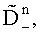 выбирают из полученных дисперсий
выбирают из полученных дисперсий 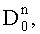
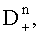
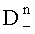 и
и 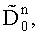
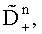
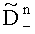 наименьшую и соответствующее ей по индексу математическое ожидание, затем вычисляют математическое ожидание по множеству K посылок М0, вычисляют погрешность переноса спектра радиосигнала по формуле
наименьшую и соответствующее ей по индексу математическое ожидание, затем вычисляют математическое ожидание по множеству K посылок М0, вычисляют погрешность переноса спектра радиосигнала по формуле 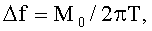 запоминают ее и компенсируют сдвиг при приеме очередного радиосигнала, состоящего из K посылок на N частотах, а идентификацию информационного символа выполняют с учетом значения М0, причем действия по определению математического ожидания М0 и Δf повторяются при поступлении очередного сигнала из K посылок.
запоминают ее и компенсируют сдвиг при приеме очередного радиосигнала, состоящего из K посылок на N частотах, а идентификацию информационного символа выполняют с учетом значения М0, причем действия по определению математического ожидания М0 и Δf повторяются при поступлении очередного сигнала из K посылок.
2. Способ по п.1, отличающийся тем, что для идентификации информационных символов из разностей фаз между соседними посылками 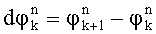 дополнительно вычитают математическое ожидание набега фазы М0, вычисленное по K принятым посылкам, после чего определяют ближайшую к
дополнительно вычитают математическое ожидание набега фазы М0, вычисленное по K принятым посылкам, после чего определяют ближайшую к 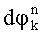 эталонную фазу, соответствующую заданному виду модуляции, которая идентифицирует принятый символ.
эталонную фазу, соответствующую заданному виду модуляции, которая идентифицирует принятый символ.
| US 2004008618 A1, 15.01.2004 | |||
| US 2005089108 A1, 28.04.2005 | |||
| RU 2005138861 A, 10.06.2006 | |||
| Демодулятор взаимоортогональных синусоидальных сигналов с фазоразностной модуляцией | 1985 |
|
SU1277423A1 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ СИНХРОНИЗАЦИИ ЧАСТОТЫ В СИСТЕМЕ OFDM | 2005 |
|
RU2338325C1 |
| ДЕМОДУЛЯЦИЯ ПОДДИАПАЗОНОВ ДЛЯ ОСНОВАННЫХ НА OFDM СИСТЕМ СВЯЗИ | 2005 |
|
RU2353065C2 |
| JP 11266223 A, 28.09.1999 | |||
| WO 2001026264 A1, 12.04.2001. | |||
Авторы
Даты
2012-12-10—Публикация
2011-06-08—Подача