Изобретение относится к способу криптографической обработки с использованием эллиптической кривой с помощью вычислительного устройства и к устройству для осуществления способа.
Конечный объект называется полем Галуа. Свойства и определение поля Галуа описаны в работе [3].
С широким распространением компьютерных сетей и соответствующих приложений, реализуемых с помощью электронных систем связи (сетей связи), возрастающие требования предъявляются к надежности передачи данных. Аспект надежности передачи данных учитывает в том числе
- возможность отказа передачи данных,
- возможность искажения данных,
- аутентификацию данных, то есть, возможность определения и идентификации отправителя,
- защиту конфиденциальности данных.
Под термином "код" понимают данные, применяемые при криптографической обработке. Из способа, основанного на использовании открытого ключа [4], известно применение секретного и общедоступного кода.
Нарушителем считается несанкционированное лицо, пытающееся получить доступ к коду.
В частности в компьютерной сети, в возрастающей степени в портативных носителях информации, например в мобильном телефоне или карточке со встроенной микросхемой, необходимо обеспечить предотвращение доступа к хранящемуся в памяти коду даже тогда, когда нарушитель завладевает вычислительным устройством, мобильным телефоном или карточкой со встроенной микросхемой.
Для обеспечения достаточной надежности криптографического способа коды, в частности при асимметричном способе, определяются длиной, равной нескольким сотням битов. Область памяти вычислительного устройства или портативного носителя информации в большинстве случаев ограничена. Длина введенного в такую область памяти кода в несколько сотен битов уменьшает свободное место для памяти в компьютере или носителе информации, так что одновременно может храниться лишь небольшое количество таких кодов.
Из [1] и [2] известна эллиптическая кривая и ее применение при криптографической обработке.
Задача изобретения заключается в том, чтобы создать способ криптографической обработки с помощью вычислительного устройства с использованием по меньшей мере одной эллиптической кривой, требующий меньшего объема памяти.
Данная задача решается согласно признакам независимых пунктов формулы изобретения.
Предложен способ криптографической обработки по меньшей мере с использованием одной эллиптической кривой с помощью вычислительного устройства, при этом эллиптическая кривая задана в первой форме, причем несколько первых параметров определяют эллиптическую кривую первой формы. Эллиптическая кривая преобразуется во вторую форму путем определения нескольких вторых параметров, причем по меньшей мере один из вторых параметров уменьшается по длине по сравнению с одним из первых параметров. Эллиптическая кривая после преобразования, то есть во второй форме, применяется для криптографической обработки.
За счет значительного сокращения одного из первых параметров обеспечивается экономия области памяти, предоставляемой для этого параметра. Так как область памяти, например на карточке со встроенной микросхемой, ограничена, то за счет экономии нескольких сотен битов для каждого сокращенного параметра получают свободное место в памяти, например, для записи следующего секретного кода. Несмотря на сокращение соответствующего параметра надежность криптографического способа гарантируется.
При применении эллиптической кривой в криптографическом способе затраты нарушителя на приобретение кода возрастают экспоненциально его длине.
В одном из вариантов выполнения изобретения первая форма эллиптической кривой определяется следующим образом:
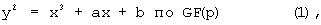
где GF(p) - поле Галуа с р элементами и
х, y, a, b - элементы объекта GF(p),
Используемое ниже обозначение "mod p" обозначает специальный случай для поля Галуа, а именно натуральные числа меньше р, "mod" обозначает оператор MODULO и соответствует операции деления на целое число с остатком.
В другом варианте выполнения изобретения вторая форма эллиптической кривой определяется следующим образом:
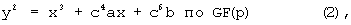
где с обозначает константу.
Для экономии объема памяти уравнение (1) преобразуют в уравнение (2) и параметр, определяющий эллиптическую кривую, согласно уравнению (2) сокращают.
Еще один вариант осуществления изобретения заключается в том, что сокращают параметр а тем, что константу с выбирают таким образом, что выражение

становится значительно меньше других параметров, описывающих эллиптическую кривую по уравнению (2). За счет такого сокращения параметр требует соответственно меньше места для памяти.
Согласно дальнейшему развитию изобретения заявленный способ находит применение в следующих случаях:
- кодирование и декодирование:
Данные кодируются отправителем с использованием симметричного или асимметричного способа и на противоположной стороне декодируются получателем.
- предоставление кода службой сертификации:
Доверительное учреждение (служба сертификации) предоставляет код, причем должно гарантироваться, что код принадлежит этой службе сертификации.
- цифровая подпись или проверка цифровой подписи:
Электронный документ подписывают, и подпись прилагают к документу. Получатель на основании подписки может установить, действительно ли документ подписал соответствующий отправитель.
- асимметричная аутентификация:
На основании асимметричного способа пользователь может обеспечить свою идентификацию. Предпочтительно это осуществляется путем кодирования соответствующим секретным (личным) кодом. С помощью соответствующего общедоступного кода данного пользователя каждый может определить, что кодирование принадлежит действительно данному пользователю.
- сокращение кодов:
Вариант криптографической обработки включает в себя сокращение кода, который может предпочтительно применяться для последующего способа криптографии.
Кроме того, заявлено устройство, которое содержит процессор, выполненный таким образом, что эллиптическая кривая задается в первой форме, причем эллиптическую кривую определяют несколько первых параметров, и эллиптическая кривая преобразуется во вторую форму тем, что определяют несколько вторых параметров, причем по меньшей мере один из вторых параметров сокращают по его длине относительно первого параметра. Наконец, для криптографической обработки определяют эллиптическую кривую второй формы.
Данное устройство может представлять собой карточку со встроенной микросхемой, имеющей защищенную и незащищенную области памяти, причем как в защищенной, так и в незащищенной области памяти можно хранить код, то есть параметры, характеризующие эллиптическую кривую.
Данное устройство особенно пригодно для осуществления способа согласно изобретению или одного из поясненных выше вариантов его осуществления.
Усовершенствованные варианты осуществления изобретения очевидны из зависимых пунктов.
Изобретение поясняется ниже на примерах, иллюстрируемых чертежами, на которых показано следующее:
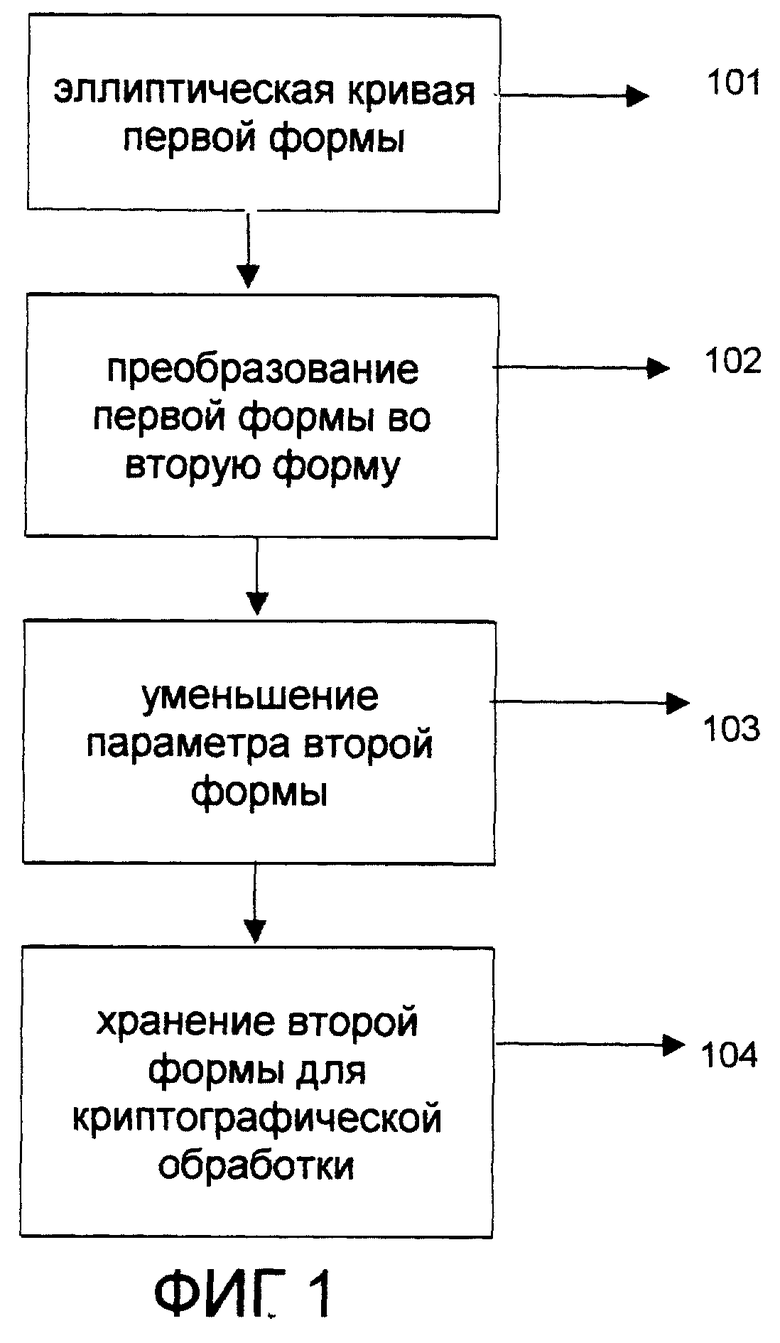
Фиг.1 - Способ криптографической обработки с помощью эллиптической кривой, причем по меньшей мере один параметр эллиптической кривой сокращен, и тем самым создается экономия части области памяти, необходимой для параметров эллиптической кривой;
Фиг.2 - Выбор возможностей для простого числа р, так что параметр а эллиптической кривой сокращается;
Фиг.3 - Способ определения эллиптической кривой и последующее преобразование во вторую форму;
Фиг.4 - Схема криптографической обработки;
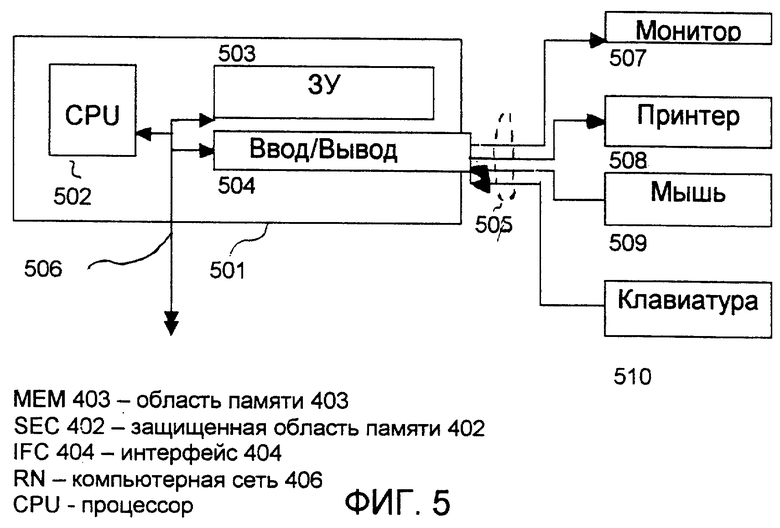
Фиг.5 - Процессорный блок.
Фиг.1 показывает способ обработки с помощью эллиптической кривой. Эллиптическая кривая (блок 101) преобразуется для этого из первой формы во вторую форму (блок 102), один параметр второй формы сокращается (блок 103), и вторая форма записывается в память для криптографической обработки (блок 104). Нижеуказанные операции поясняются, причем некоторые возможности сокращения пояснены на примере.
Приводится описание, каким способом достигается сокращение длины параметра а в уравнении эллиптической кривой (эллиптическая кривая первой формы, см. блок 101)
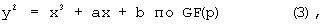
причем р является простым числом больше 3 и GF(p) представляет собой поле Галуа с р элементами.
Эллиптическая кривая
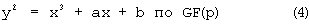
может быть путем преобразования переведена в бирационально изоморфную эллиптическую кривую
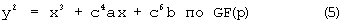
(эллиптическая кривая во второй форме, см. блок 102). Путем надлежащего выбора констант с можно сократить коэффициент


(см. блок 103), в результате чего объем памяти, необходимый для хранения этого коэффициента, может быть незначительным по сравнению с объемом памяти для параметра а.
В соответствии с уравнением (5) затем определяются числа
с4а (или -с4а) или с2
1. Определение числа "с4а"
Для определения числа с4а (или -с4а) различают предпочтительно следующие случаи:
1.1. р≡ 3 mod 4
В этих записях действительно следующее:
- все квадраты являются также четвертой степенью,
- ‘-1’ не является квадратом.
Пусть p=4k+3 и s - четвертая степень, образующая мультипликативную подгруппу четвертой степени (например, квадратов) в GF(p).
Дано
V={1,s,s2,s3,... ,s2k} количество четвертых степеней в GF(p) и
NQ=={-1, -s,-s2, -s3,... ,-s2k} количество не квадратов в GF(p)
1. К каждому элементу а=st из V
имеется элемент с4=s2k+1-t из V,
причем с4а=s2k+1=1 в GF(p)
2. К каждому элементу а=-st из V
имеется элемент с4=s2k+1-t из V
причем с4а=-s2k+1=-1 в GF(p).
При этом s, t и k обозначают элементы объекта из GF(p).
Для р≡ 3 mod 4 параметр а можно перевести посредством надлежащего выбора констант с в число с4а=1 в GF(p) или c4a=-1 в GF(p).
1.2. р≡ 1 mod 4
Для такого объекта действительно следующее:
- (р-1)/4 элементов мультипликативной группы объекта являются четвертыми степенями;
- (р-1)/4 элементов мультипликативной группы объекта являются квадратами, но не четвертыми степенями;
- (р-1)/2 элементов мультипликативной группы объекта не являются квадратами;
- ‘-1’ не является не квадратом,
А) р≡ 5 mod 8
Для такого объекта дополнительно действительно следующее:
- ‘-1’ квадрат, но не четвертая степень,
- ‘+2’, ‘-2’ не квадраты.
Пусть р=8k+5 и s четвертая степень, которая образует мультипликативную подгруппу четвертой степени в GF(p).
Имеется
V={1, s, s2, s3,... ,s2k} количество четвертых степеней в GF(p) и
Q={-1,-s,-s2,-s3,... ,-s2k} количество квадратов, не являющихся четвертыми степенями в GF(p)
NQ={2,2s,2s2,2s3,... ,2s2k-2,-2s,-2s2,-2s3,... ,-2s2k} количество не квадратов в GF(p)
1. К каждому элементу а=st из V имеется элемент с4=s2k+1-t из V причем с4a=s2k+1=1 в GF(p)
2. К каждому элементу а=-st из Q имеется элемент с4=s2k+1-t из V причем с4а=-s2k+1=-1 в GF(p).
3. К каждому элементу а=2st из NQ имеется элемент с4=s2k+1-t из V причем с4а=2s2k+1=2 в GF(p).
4. К каждому элементу а=-2st из NQ имеется элемент с4=s2k+1-t из V причем c4a=-2s2k+1=-2 в GF(p).
Для р≡ 5 mod 8 параметр а можно перевести посредством надлежащего выбора констант с в число
с4a=1 или -1 или 2 или -2 в GF(p).
В) р≡ 1 mod 8
Число с4a можно определить по следующей схеме:
Для r=1, -1, 2, -2, 3, -3, 4, -4,...
- образовать z≡ ra-1 mod p;
- вычислить u≡ z(p-1)/4 mod p;
- прекратить, если u=1;
- сохранить в памяти z=с4 и r=с4а.
2. Определение числа "с2 в GF(p)"
Для определения числа с2 mod p вначале в соответствующем объекта GF(p) определяют, является ли а четвертой степенью, квадратом или не четвертой степенью или не квадратом.
2.1. p=4k+3
Для данных объектов вычисляется u=а(p-1)/2 в GF(p).
- Если u=1 в GF(p), то а является четвертой степенью (или квадратом). В этом случае с4=а-1 в GF(p).
- Если u=-1 в GF(p), то а не является квадратом. В этом случае с4=-а-1 в GF(p).
2.2. p=8k+5
Для этих объектов выполняется: u=a(p-1)/4 в GF(p).
- Если u=1 в GF(P), то а является четвертой степенью. В этом случае с4=а-1 в GF(p).
- Если u=-1 в GF(p), то а является квадратом, но не четвертой степенью. В этом случае с4=-а-1 в GF(p).
- Если u не 1 и не -1 в GF(p), то а не квадрат. В этом случае вычисляется v=(2a)(p-l)/4 в GF(p). Если v=1 в GF(p), то с4=2а-1 в GF(p), в противном случае с4=-2а-1 в GF(p).
2.2. p=8k+1
Для этих объектов согласно 1.2, описан случай В.
Во всех трех случаях можно рассчитать с затратами O(log р) оба корня (с2 и -с2) из с4. Для случая р=4k+3 допустимо только одно из двух указанных решений, а именно то решение, которое является квадратом в GF(p). В других случаях допустимы оба решения. Тем самым можно рассчитать коэффициент с6b эллиптической кривой.
На основании замкнутых формул для случаев p=4k+3 и p=8k+5 на практике предпочтительны простые числа.
Пример 1.
Пусть простое число р=11⇒ случая 1.1: р≡ 3 mod 4
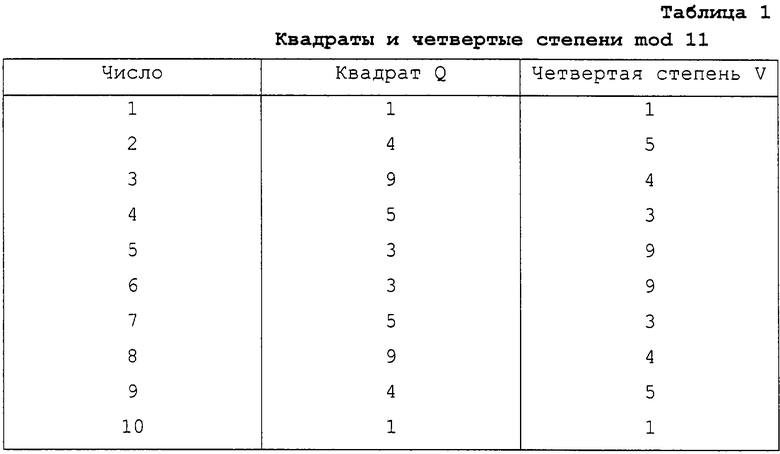
Тем самым выявляется количество квадратов Q, количество четвертых степеней V и количество не квадратов NQ относительно
Q=V={1, 3, 4, 5, 9};
NQ={2, 6, 7, 8, 10}.
a ∈ V=Q⇒ ас4=1
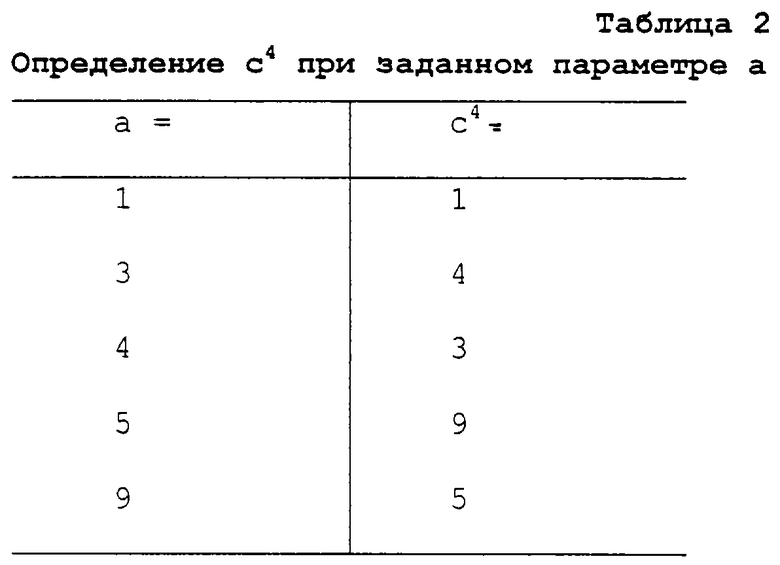
а ∈ NQ⇒ ас4=-1
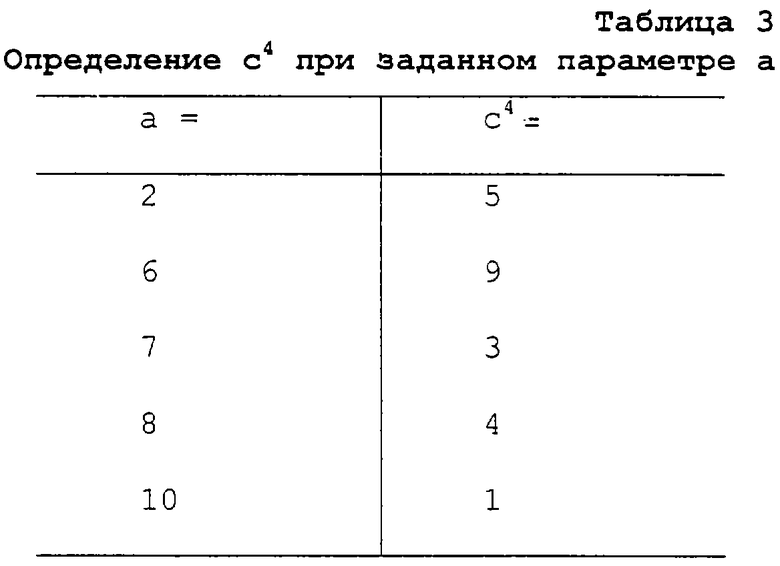
Таблица 2 показывает различные возможности распределения значении а и с4, которые в выражении ас4 постоянно дают 1, а таблица 3 показывает различные возможности распределения значении а и с4, которые в выражении ас4 постоянно дают -1. Это действительно в GF (11).
Пример 2.
Пусть простое число р=13⇒ случая 1.2 А): р≡ 1 mod 4 и одновременно р≡ 5 mod 8.
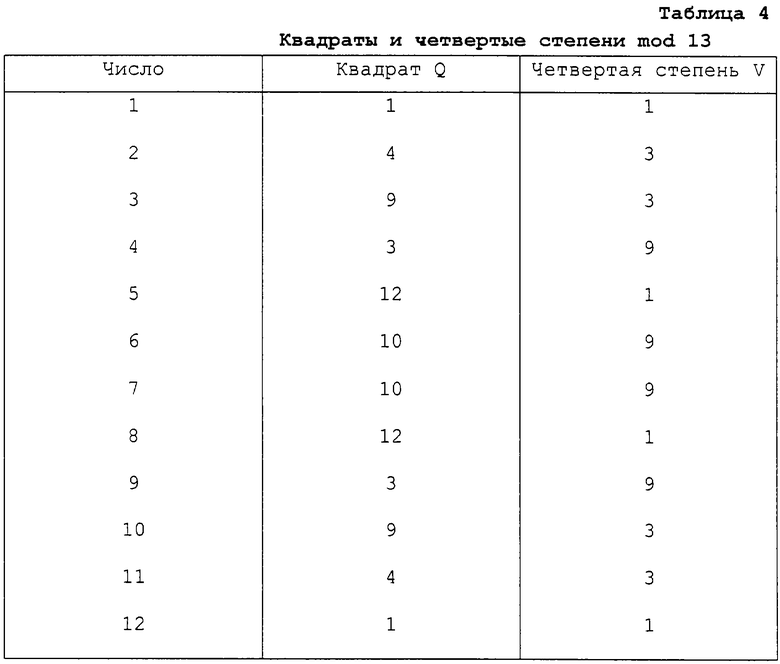
Тем самым определяется количество квадратов Q (которые не являются четвертыми степенями), количество четвертых степеней V и количество не квадратов NQ;
Q={4, 10, 12};
V={1, 3, 9};
NQ=(2, 5, 6, 7, 8, 11}.
а ∈ V⇒ с4 ∈ V

⇒ ac4≡1 mod 13
a ∈ Q

⇒ ac4≡-1 mod 13
a ∈ NQ
NQ={2, 5, 6, 7, 8, 11}, с
2· V={1, 5, 6} и
2· Q={7, 8, 11}
Случай: a ∈ NQ и a ∈ (2· V)
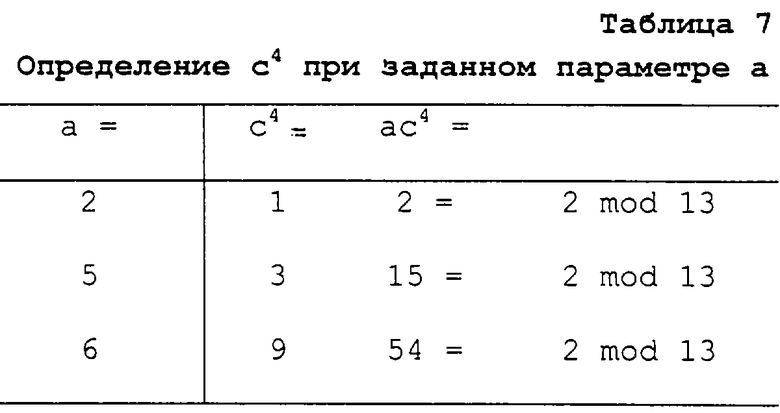
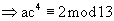
Случай b: a ∈ NQ и a ∈ (2· Q)
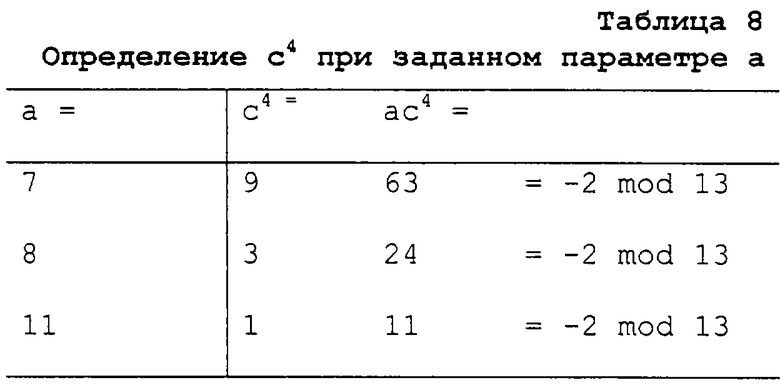
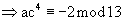
Полученная описанным способом эллиптическая кривая второй формы (блок 103) применяется для криптографической обработки.
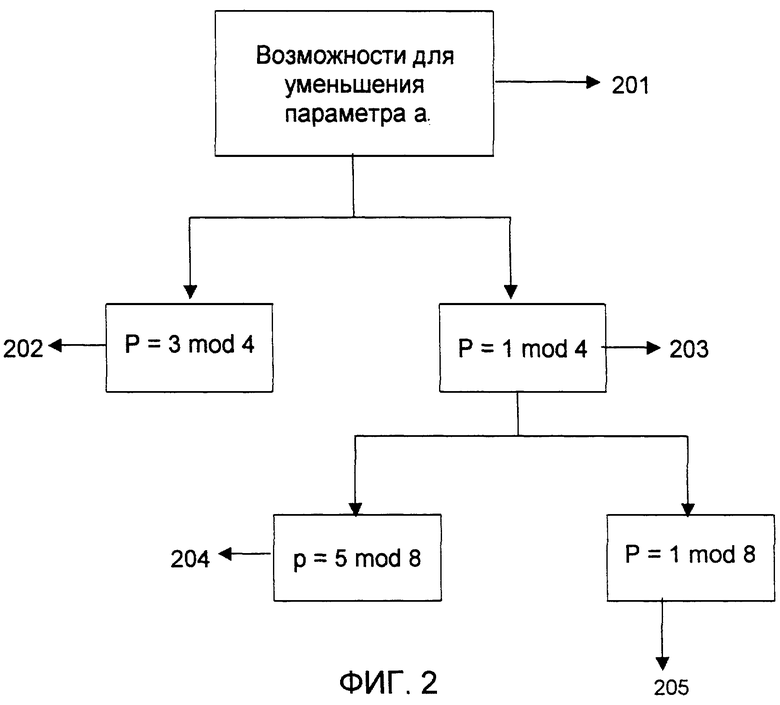
Фиг.2 показывает выбор возможностей для выбора простого числа с целью сокращения параметров а (блок 201), как описано выше. Возможный вариант 202 определяет р таким образом, что действительно выражение р=3 mod 4. В этом случае можно сократить параметр а с помощью вышеописанного способа. То же самое справедливо для р=1 mod 4 (блок 203), причем различие приводится раздельно для обоих случаев р=5 mod 8 (блок 204) и р=1 mod 8 (блок 205). Замкнутые формулировки для определения сокращенного параметра а приведены выше. Фиг.2 показывает наглядно выбор возможностей, не претендуя на полный выбор.
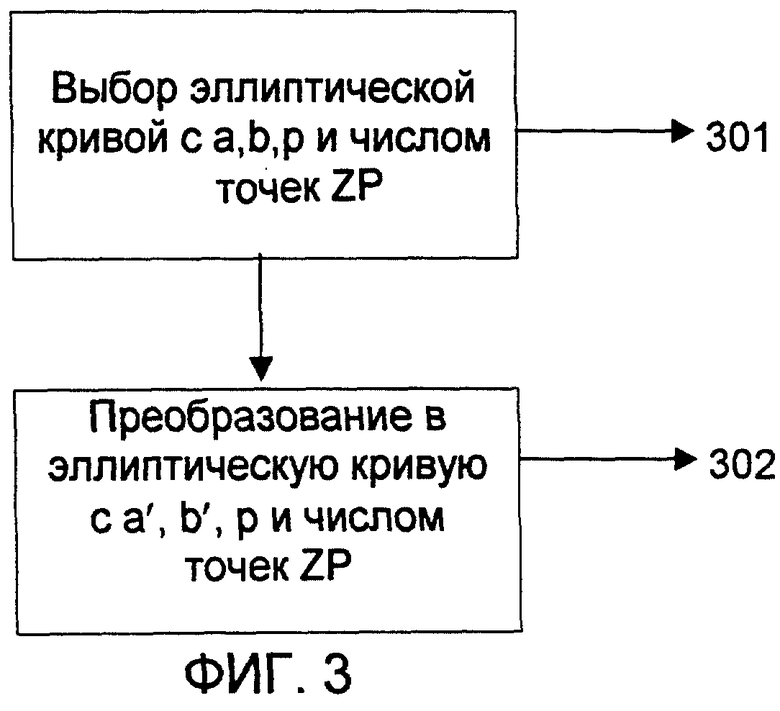
Согласно фиг.3, на первом этапе 301 определяется эллиптическая кривая с параметрами a, b, p и числом точек ZP по уравнению (1). На этапе 302 эллиптическая кривая преобразуется (ср. уравнение (2)). После преобразования эллиптическая кривая имеет параметры а’, b’, р и ZP. Параметры а’ и b’ указывают на то, что параметры а и b были изменены, причем параметр, предпочтительно параметр а’, имеет небольшую длину по сравнению с параметром а, так что за счет ввода в память параметра а’, вместо параметра а в качестве идентификатора эллиптической кривой, обеспечивается экономия объема памяти.
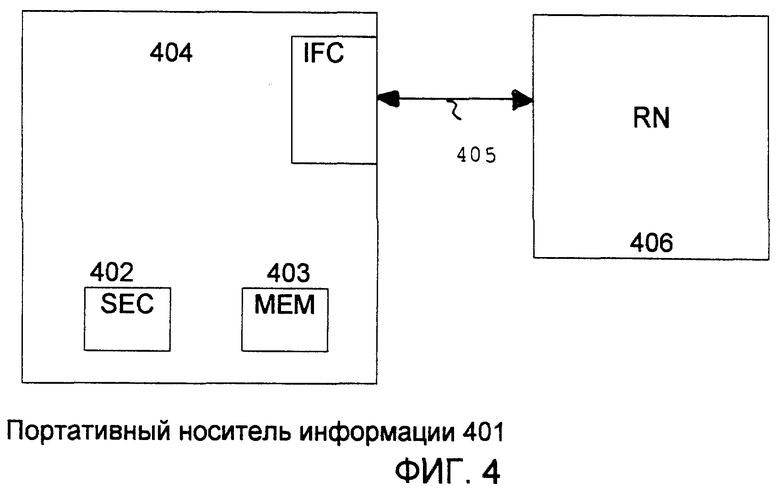
На фиг.4 показана последовательность криптографической обработки.
Портативный носитель информации 401, предпочтительно карточка со встроенной памятью, содержит незащищенную область памяти MEM 403 и защищенную (надежную) область памяти SEC 402. С помощью интерфейса IFC 404 по каналу 405 осуществляется обмен данными между носителем информации 401 и компьютерной сетью 406. Компьютерная сеть 406 включает в себя несколько компьютеров, соединенных между собой и осуществляющих информационный обмен друг с другом. Данные для работы портативного носителя информации имеются в распоряжении в распределенном виде предпочтительно в компьютерной сети RN 406.
Защищенная область памяти 402 выполнена нечитабельной.
Данные защищенной области памяти 4D2 используются с помощью процессора в портативном носителе информации 401 или в компьютерной сети 406. Например, операция сравнения в качестве результата может указать, было ли успешным или нет сравнение введенных данных с кодом в защищенной области памяти.
Параметры эллиптической кривой введены в защищенную область памяти 402 или в незащищенную область памяти 403. В частности, секретный или личный код хранится в защищенной области памяти и общедоступный код - в незащищенной области памяти.
На фиг.5 показан процессорный блок 501. Процессорный блок 501 включает в себя процессор CPU 502, ЗУ 503 и интерфейс 504 ввода-вывода, используемый различными способами через выведенный из процессорного блока 501 интерфейс 505: через графический интерфейс выходные данные выводятся на монитор 507 для визуального представления и/или на принтер 508. Ввод осуществляется с помощью манипулятора "мышь" 509 или клавиатуры 510. Процессорный блок 501 содержит также шину 506, которая обеспечивает соединение ЗУ 503, процессора 502 и интерфейса 504 ввода-вывода. Кроме того, к шине 506 можно присоединить дополнительные компоненты: дополнительное ЗУ, жесткий диск и т.д.
Источники информации:
1. Neal Koblitz: A Course in Number Theory and Cryptography, Springer Verlag New York, 1987, ISBN 0-387-96576-9, Seiten 150-179.
2. Alfred J. Menezes: Elliptic Curve Public Key Cryptosystems, Kluwer Academic Publishers, Massachusetts 1993, ISBN 0-7923-9368-6, Seiten 83-116.
3. Rudolf Lidi, Harald Niederreiter: Introduction to finite fields and their applications, Cambridge University Press, Cambridge 1986, ISBN 0-521-30706-6, Seiten 15, 45.
4. Christoph Ruland: Informationssicherheit in Datennetzen, DATACOM-Verlang, Bergheim 1993, ISBN 3-89238-081-3, Seiten 73-85.
Изобретение относится к криптографии. Технический результат заключается в уменьшении длины по меньшей мере одного параметра эллиптической кривой и обеспечения высокой надежности. Для этого параметры эллиптической кривой хранят в запоминающем устройстве вычислительного устройства. Эти параметры имеют значительную длину. С помощью определенного алгоритма параметр сокращают, тогда как другие параметры составляют длину, равную нескольким сотням битов. 2 н. и 8 з.п. ф-лы, 5 ил., 8 табл.
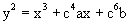
путем определения нескольких вторых параметров, причем по меньшей мере один из вторых параметров сокращен по своей длине по сравнению с первым параметром, где х, у - переменные; а, b - первые параметры; с - константа, в) причем по меньшей мере сокращают параметр а путем выбора константы с так, что выражение с4 a mod p определяется с существенно меньшей длиной по сравнению с длиной параметра b и длиной заданной величины p, г) и при этом эллиптическую кривую второй формы сохраняют на носителе информации и используют в криптографической обработке.
| US 5497423 А, 05.03.1996 | |||
| US 5442707 A, 15.08.1995 | |||
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2007884C1 |
Авторы
Даты
2004-07-10—Публикация
1999-02-02—Подача