Настоящее изобретение касается шифрования сообщений на основе использования точек на эллиптической кривой и более конкретно упомянутого шифрования детерминированной природы.
Для применения криптографического преобразования к сообщению, для вставления произвольных чисел в математические структуры применяют обычные алгоритмы. Для этой цели эллиптические кривые являются математическими структурами, которые способны упростить применение таких криптографических преобразований и одновременно уменьшить потребности в памяти по сравнению со случаем использования других криптографических преобразований.
Тем не менее, эффективные алгоритмы, предназначенные для вставки произвольных чисел с использованием эллиптических кривых, являются вероятностными. Следовательно, время выполнения таких алгоритмов не является постоянным, оно зависит от шифруемого сообщений. Таким образом, если нарушитель определит, что при применении алгоритма время его работы было различным, он может получить информацию о зашифрованном сообщении.
Для маскировки времени, нужного для вероятностного алгоритма вставки, возможно обеспечить добавление ненужных этапов в этот алгоритм, чтобы его применение всегда занимало одинаковый период времени, независимо от обрабатываемого сообщения.
Точка Р эллиптической кривой определяется ее абсциссой Х и ординатой Y, при этом Х и Y удовлетворяют следующему выражению:
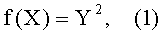
где f(X) - это многочлен f(X)=Х3+аХ+b.
Известно семейство многочленов, которое удовлетворяют равенству Скальба и которое дает возможность определить такую точку на эллиптической кривой, как описано в документе «Construction of Rational Points on Elliptic curves over finite fields» (Построение рациональных точек эллиптических кривых над конечными полями), авторы Эндрю Шаллуе (Andrew Shallue) и Кристиан ван де Вустейне (Christiaan van de Woestijne).
Многочлены X1(t), X2(t), X3(t) и U(t) удовлетворяют равенству Скальба, если они удовлетворяют следующему выражению:
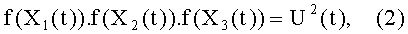
где f - это функция, которая определяет рассматриваемую эллиптическую кривую, а t - параметр.
Многочлены, которые удовлетворяют равенству Скальба, могут иметь два параметра u и t. В этом случае равенство Скальба записывается следующим образом:
f(X1(t,u)).f(X2(t,u)).f(X3(t,u))=U2(t,u).
Выражения такого типа могут использовать два параметра u и t. Тем не менее, в рассматриваемых приложениях целесообразно предусмотреть присвоение любого значения параметру u или в качестве альтернативы параметру t. Таким образом, остается выбрать значение единственного параметра.
При выбранных параметрах t и u заметим, что X1=X1(t,u), X2=X2(t,u), Х3=X3(t,u), U=U(t,u), при этом X1, X2, Х3 и U являются элементами Fq. Это выражение (2) означает, что, по меньшей мере, одно из чисел f(X1), f(X2) и f(X3) соответствует квадрату элемента в конечном поле Fq.
Тогда, когда определен квадрат элемента, f(Xi), в поле Fq, мы можем получить точку на эллиптической кривой 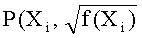
Вычисление 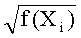
q=3 mod 4.
В этом случае известно, что
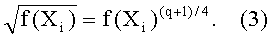
Следовательно, для определения точки на эллиптической кривой (1) необходимо определить, какое число среди трех чисел f(X1), f(X2) и f(Х3) соответствует квадрату элемента в конечном поле Fq. Для этой цели мы можем предусмотреть сначала проверку того, является ли элемент f(X1) квадратом элемента в конечном поле Fq, далее, если это не так, применить ту же проверку для элемента f(X2) и, наконец, если это тоже не правильно, аналогично проверить элемент f(Х3). Тем не менее, при такой процедуре определение точки на эллиптической кривой не всегда занимает одинаковое время, так как это определение выполняется быстрее, если квадратом является первый элемент, по сравнению со случаем, когда только третий элемент является квадратом.
Потенциальный нарушитель может использовать эту разницу в затраченном времени для определения точки на эллиптической кривой для взлома секретности, связанной с параметром, который позволит сгенерировать эту точку. А в области криптографии эти параметры должны оставаться секретными.
Эти параметры могут, в частности, соответствовать паролям. Таким образом, важно, чтобы определение этих точек не давало информации, предоставляющей возможность взлома секретности параметра, и, соответственно, должны быть исключены атаки на основе анализа времени, затраченного на определение точки на кривой.
Для преодоления этого недостатка возможно методично проверять три элемента f(Xi) для всех i от 1 до 3. Таким образом, время определения точки на кривой не будет зависеть от определенной точки.
Тем не менее, проверка, является ли элемент выражения (2) квадратом в конечном поле Fq, является сложной операцией, в частности, предполагающей возведение в степень, реализация которого затратна с точки зрения времени. В случае, когда мы хотим определить точку на эллиптической кривой на основе равенств Скальба и осуществлять эти определения за постоянное время, в описанном выше случае требуется четыре операции возведения в степень, одно возведение в степень для проверки каждого из членов в выражении (2) Скальба и одно возведение в степень для вычисления квадратного корня, как описано в выражении (3).
Цель настоящего изобретения состоит в улучшении этой ситуации.
Согласно первому аспекту настоящего изобретения предложен способ выполнения криптографического преобразования в электронном компоненте, включающий в себя этап получения точки P(X,Y), исходя, по меньшей мере, из одного параметра t, на эллиптической кривой, удовлетворяющей выражению:
Y2=f(Х); и
исходя из многочленов X1(t), X2(t), X3(t) и U(t), удовлетворяющих следующему равенству:
f(X1(t)).f(X2(t)).f(X3(t))=U(t)2
в конечном поле Fq, независимо от параметра t, при этом q удовлетворяет равенству q=3 mod 4;
упомянутый способ включает в себя следующие этапы:
/1/ получают значение параметра t;
/2/ определяют точку Р путем выполнения следующих подэтапов:
/i/ вычисляют X1=X1(t), Х2=X2(t), Х3=X3(t) и U=U(t);
/ii/ если элемент f(X1).f(X2) является квадратом в конечном поле Fq, то проверяют, является ли элемент f(X3) квадратом в конечном поле Fq, и вычисляют квадратный корень из элемента f(Х3), абсциссой точки Р является Х3, а квадратный корень f(Х3) является ординатой точки Р;
/iii/ иначе проверяют, является ли элемент f(X1) квадратом в конечном поле Fq, и если является, вычисляют квадратный корень из элемента f(X1), абсциссой точки Р является X1, а квадратный корень f(X1) является ординатой точки Р;
/iv/ иначе вычисляют квадратный корень элемента f(X2), абсциссой точки Р является Х2, а квадратный корень из f(X2) является ординатой точки Р;
/3/ используют упомянутую точку Р в следующих криптографических приложениях: при шифровании, или хешировании, или подписывании, или аутентификации, или идентификации.
Благодаря этим конструкциям возможно определить точку на эллиптической кривой образом, подходящим для использования в области криптографии, так как, с одной стороны, это определение требует одного и того же времени независимо от входного параметра t и, с другой стороны, эффективно, так как уменьшается количество требуемых операций.
Это определение занимает постоянное время, которое не зависит от входного параметра или параметров. Фактически, даже если этот способ подразумевает различные варианты обработки в зависимости от элемента, который соответствует квадрату в равенстве Скальба, независимо от определяемой точки на кривой осуществляют одинаковое количество операций одинакового типа. Более конкретно, независимо от определяемой точки на кривой, выполняют следующий список операций:
- проверка на то, что элемент является квадратом в Fq;
- определение квадратного корня.
Следовательно, невозможно осуществить атаку, основанную на затратах времени.
Более того, это определение эффективно, так как ограничено количество выполняемых затратных операций. Фактически возможно проверить, является ли один из трех элементов выражения (2) Скальба квадратом в конечном поле Fq, с использованием самое большее двух операций типа возведения в степень. Более точно, заметим, что в одном варианте осуществления настоящего изобретения проверка, является ли элемент квадратом, соответствует возведению в степень, которое является наиболее затратной операцией, применяемой в настоящем контексте.
На этапе /2/-/ii/ необходимо решить, является ли элемент R0:
R0=f(X1).f(X2)
квадратом.
Этот этап может соответствовать проверке, является ли элемент квадратом, при этом применяется дополнительное возведение в степень, или этот этап может быть основан на заранее вычисленном значении, полученном при более ранних вычислениях в случае, когда многочлен, удовлетворяющий равенству Скальба, соответствует элементу, который не может быть квадратом. В последнем случае, который показан в следующих разделах, применение способа предпочтительно требует только одного возведения в степень. Но в наихудшем случае применение способа, соответствующего одному варианту осуществления настоящего изобретения, соответствует двум возведениям в степень, одно - для проверки, является ли R0 квадратом, и другое возведение в степень - для проверки, является ли некоторый элемент квадратом, применяемой или к f(X3), или к f(X1).
При выполнении таких вычислений в соответствии с одним вариантом осуществления настоящего изобретения время, затрачиваемое на выполнение операций, отличающихся от возведения в степень, пренебрежимо мало по сравнению со временем выполнения возведения в степень. Далее, благодаря характеристикам настоящего изобретения, вместо четырех возведений в степень, как описано выше в обычном случае, самое большее нужно выполнить два возведения в степень. Такое уменьшение количества возведений в степень очень полезно.
В одном варианте осуществления настоящего изобретения на этапе /2/-/ii/ выполняют следующие этапы:
- вычисляют такой R1, что:
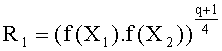
- если 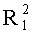
На этапе /2/-/iii/ проверяют, является ли элемент f(X1) квадратом в конечном поле Fq, в соответствии со следующими этапами:
- вычисляют такой 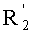
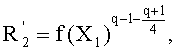
- вычисляют такой 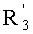
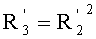
- вычисляют такой 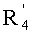
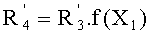
Если 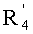
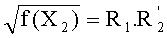
Этот вариант осуществления изобретения является общим и может быть легко применен к любому семейству многочленов, которые удовлетворяют равенству Скальба. Заметим, что в случае, когда в равенстве (2) Скальба f(X2) является квадратом, то есть последний проверяемый элемент из трех элементов в равенстве Скальба, не нужно осуществлять новое возведение в степень типа 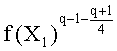
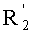
В одном варианте осуществления настоящего изобретения многочлены, удовлетворяющие равенству Скальба, выражаются в координатах Якоби в X', Y' и Z следующим образом:
X'=X.Z2,
Y'=Y.Z3,
и операции нахождения обратного элемента преобразуются в операции умножения.
Преобразование в координаты Якоби позволяет преобразовать операции нахождение обратного элемента в умножения при надлежащем выборе элемента Z.
В одном варианте осуществления настоящего изобретения многочлены, удовлетворяющие равенству Скальба, выражены в координатах Якоби, в соответствии с чем точка P(X,Y) записывается как P(X',Y',Z), при этом:
X'=X.Z2,
Y'=Y.Z3,
где функция f записана как fZ(X') и удовлетворяет следующему равенству:
fZ(X')=X'3+a.X'.Z4+b.Z6,
а эллиптическая кривая удовлетворяет выражению:
Y'2=fZ(X'),
и многочлены, удовлетворяющие равенству Скальба и выраженные в координатах Якоби, представляют собой 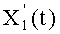
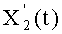
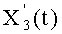
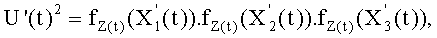
где Z(t) определен таким образом, что операции нахождения обратного элемента преобразованы в операции умножения.
Здесь встает вопрос преобразования в координаты Якоби многочленов Уласа, удовлетворяющих равенству Скальба, как сказано ранее. В этом случае возможно ограничить количество возведений в степень двумя и одновременно исключить любое вычисление обратных элементов при обеспечении выполнения за постоянное время определения точки Р на эллиптической кривой.
В одном варианте осуществления изобретения многочлены, удовлетворяющие равенству Скальба, таковы, что возможно установить значение Х3(t) для любого возможного t, чтобы f(X3(t)) никогда не был квадратом элемента в Fq,
при этом на этапе /2/-/ii/ элемент f(X1).f(X2) не является квадратом в конечном поле Fq,
при этом на этапе /2/-/iii/ проверяют, является ли элемент f(X1) квадратом в конечном поле Fq, в соответствии со следующими этапами:
- вычисляют такой 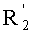
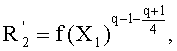
- вычисляют такой 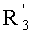
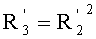
- вычисляют такой 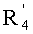
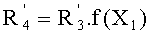
при этом, если 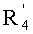
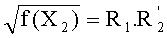
где 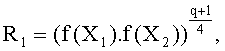
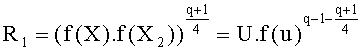
Таким образом, в конкретном случае, возможно дополнительно ограничить количество выполняемых возведений в степень путем использования конкретного семейства многочленов, так что возможно установить значение X3(t) для любого возможного t, чтобы f(X3(t)) никогда не был квадратом элемента в Fq. Здесь предпочтительно может быть использовано семейство многочленов Уласа, которое определено в документе «Рациональные точки на определенных гиперэллиптических кривых над конечными полями» («Rational points on certain hyperelliptic curves over finite fields»), автор Масие Улас (Macie Ulas), 11 июня 2007 года.
Для такого семейства многочленов, которые удовлетворяют равенству Скальба, можно записать следующее:
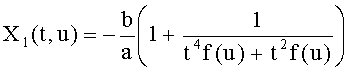
X2(t,u)=t2f(u)X1(t,u),
X3(t,u)=u,
U(t,u)=t3f(u)4f(X1(t,u)),
где f(u)=u3+au+b, а и b - такие элементы Fq, что их произведение не равно нулю.
Эти многочлены могут быть предпочтительно использованы при определении множества значений параметра u, при которых f(X3)=f(u) не является квадратом элемента в Fq.
Таким образом, на этапе /2/-/ii/ элемент f(X1).f(X2) не является квадратом в конечном поле Fq, тогда на этапе /2/-/iii/ проверяют, является ли элемент f(X1) квадратом в конечном поле Fq, в соответствии со следующими этапами:
- вычисляют такой 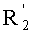
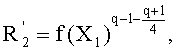
- вычисляют такой 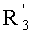
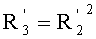
- вычисляют такой 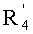
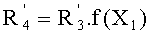
Далее, если 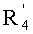
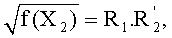
где 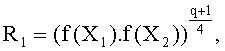
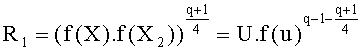
В частности, элемент 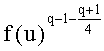
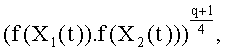
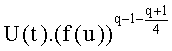
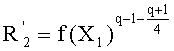
В этом случае эти конкретные многочлены выражают в координатах Якоби, в соответствии с чем точка P(X,Y) записывается как P(X',Y',Z), где:
X'=X.Z2,
Y'=Y.Z3,
при этом функция f записана как fZ(X') и удовлетворяет следующему равенству:
fZ(X')=X'3+a.X'Z4+b.Z6,
а эллиптическая кривая удовлетворяет выражению:
Y'2=fZ(Х'),
в котором многочлены, удовлетворяющие равенству Скальба и выраженные в координатах Якоби, представляют собой 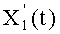
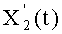
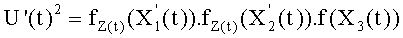
и где Z(t) определен таким образом, что операции нахождения обратного элемента преобразованы в операции умножения.
На этапе /1/ значение параметра t может быть получено как функция пароля или идентификатора. Таким образом, возможно предусмотреть использование в качестве параметра непосредственно пароля или производной от пароля.
В одном варианте осуществления настоящего изобретения криптографическое приложение представляет собой аутентификацию или идентификацию путем проверки целостности, и на этапе /1/ осуществляют следующие этапы:
/а/ генерируют случайное число;
/б/ получают зашифрованное число путем шифрования упомянутого случайного числа на основе функции шифрования с использованием ключа шифрования, определенного из пароля или идентификатора, соответствующего параметру; и
/в/ передают зашифрованное число для проверки целостности.
С помощью этой процедуры при проверке целостности возможно получить случайное число, являющееся функцией зашифрованного числа, полученного из пароля. Далее осуществляют восстановление значения параметра t путем применения подходящей функции.
Согласно второму аспекту настоящего изобретения предложено электронное устройство, содержащее подходящее средство применения способа выполнения криптографического преобразования в соответствии с первым аспектом настоящего изобретения.
Другие аспекты и достоинства изобретения будут ясны после прочтения описания одного из вариантов осуществления изобретения.
Также изобретение будет лучше понятно из следующих фиг.:
фиг.1 - вид, показывающий основные этапы способа выполнения криптографического преобразования в соответствии с одним вариантом осуществления настоящего изобретения;
фиг.2 - вид, подробно показывающий способ выполнения криптографического преобразования в соответствии с одним вариантом осуществления настоящего изобретения; и
фиг.3 - вид, подробно показывающий способ выполнения криптографического преобразования в соответствии с одним вариантом осуществления настоящего изобретения в конкретном случае многочленов Уласа.
На фиг.1 показаны основные этапы способа выполнения криптографического преобразования в соответствии с одним вариантом осуществления настоящего изобретения.
Эти основные этапы подходят для определения точки на эллиптической кривой, причем упомянутая точка предназначена для использования в криптографическом приложении. Криптографическое преобразование такого типа может быть выполнено электронным компонентом безопасным образом, то есть без определения этой точки, что не дает никакой информации об определенной точке.
Это преобразование содержит, в конечном поле Fq, где характеристика q равна 3 mod 4, этап получения точки P(X,Y) на эллиптической кривой, удовлетворяющей выражению:
Y2=f(X).
Абсцисса Х точки P(X,Y) соответствует одному из элементов X1(t), X2(t) и X3(t) для полученного значения t, так что
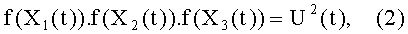
где X1(t), X2(t), Х3(t) и U(t) - многочлены, удовлетворяющие равенству Скальба в конечном поле Fq.
Более конкретно, многочлены, которые удовлетворяют равенству Скальба и которые определены в документе «Рациональные точки на определенных гиперэллиптических кривых над конечными полями» («Rational points on certain hyperelliptic curves over finite fields»), автор Масие Улас (Macie Ulas), 11 июня 2007 года, представляют собой функции двух параметров u и t. В контексте настоящего изобретения одному из параметров может быть предпочтительно присвоено значение и, следовательно, многочлены, удовлетворяющие равенству Скальба, являются функциями одного параметра t.
Для определения точки на кривой при входных параметрах u и t мы попытаемся определить те числа из X1=X1(t,u), Х2=X2(t,u), Х3=Х3(t,u), которые соответствуют квадрату элемента в конечном поле Fq. Для этой цели предпочтительно предусмотреть применение двух различных вариантов обработки в зависимости от того, является ли элемент f(X1).f(X2) квадратом в конечном поле Fq.
На начальном этапе 100 с учетом параметра t вычисляют:
Xi=Xi(t) для i, равного от 1 до 3,
и
U=U(t).
На этапе 11 мы определяем, является ли элемент f(X1).f(X2) квадратом элемента. Это решение может быть основано на предыдущих вычислениях или может быть основано на проверке в ходе применения этого способа. Если элемент f(X1).f(X2) является квадратом, то элемент f(X3) также является квадратом. В этом случае на этапе 12 предусматривают вычисление квадратного корня элемента f(X3). Таким образом, на этапе 16 определяют точку Р, абсцисса Х3 и ордината Y3 которой удовлетворяют следующему выражению:
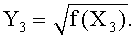
Заметим, что если произведение f(X1).f(X2) является квадратом элемента, то из этого следует, что f(Х3) также является квадратом. Тем не менее, чтобы определение точки на эллиптической кривой требовало постоянного времени, предусматривают применение проверки 10, в ходе которой проверяют, что элемент f(X3) действительно является квадратом. Эта проверка 10 позволяет обеспечить постоянное время при применении способа, соответствующего одному варианту осуществления настоящего изобретения.
В противном случае, то есть когда элемент f(X1).f(X2) не является квадратом элемента, можно сказать, что или f(X1) или f(X2) является квадратом. Следовательно, мы можем сначала предусмотреть проверку на этапе 13, является ли квадратом элемент f(X1). Если проверка завершилась положительно, то на этапе 14 вычисляют квадратный корень упомянутого элемента с целью получения ординаты точки Р:
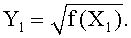
Таким образом, на этапе 17 мы получаем точку Р с абсциссой X1 и ординатой Y1.
Если проверка на этапе 13 выдает отрицательный ответ, то можно заключить, что элемент f(X2) является квадратом. Следовательно, на этапе 15 мы получаем ординату Y2 точки Р на эллиптической кривой в соответствии с выражением:
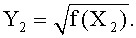
Тогда точку P(X2, Y2) кривой можно получить на этапе 18.
Заметим, что достижение этапов 16, 17 или 18 с целью получения точки на эллиптической кривой в соответствии с одним вариантом осуществления настоящего изобретения требует аналогичных операций. Таким образом, независимо от входных параметров t и u, невозможно осуществить атаку на основе затраченного времени.
Тогда точку P(Xi, Yi), для i, равного от 1 до 3, можно целесообразно использовать в следующих криптографических приложениях: при шифровании, или хешировании, или подписывании, или аутентификации, или идентификации, так как определение этой точки не предоставляет никаких элементов, которые могут помочь взломать секретность этой точки.
В поле Fq, в котором q соответствует 3 mod 4, возможно различными путями проверить, является ли элемент квадратом. Проверки того, является ли элемент квадратом, такие как проверки 10 и 13 с фиг.1, могут быть осуществлены следующим образом.
В одном варианте осуществления настоящего изобретения, когда пытаются определить, является ли элемент А квадратом в Fq, могут выполнить следующие этапы:
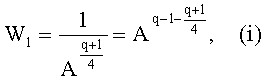
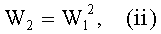
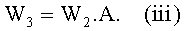
Наконец, если элемент А является квадратом, то:
- W1 соответствует обратному элементу для квадратного корня из А, то есть 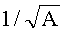
- W2 соответствует обратному элементу А; и
- W3 соответствует значению 1.
Таким образом, когда W3 равен 1, из этого следует, что элемент А является квадратом в конечном поле Fq. Если А не является квадратом, то W3 не равен 1.
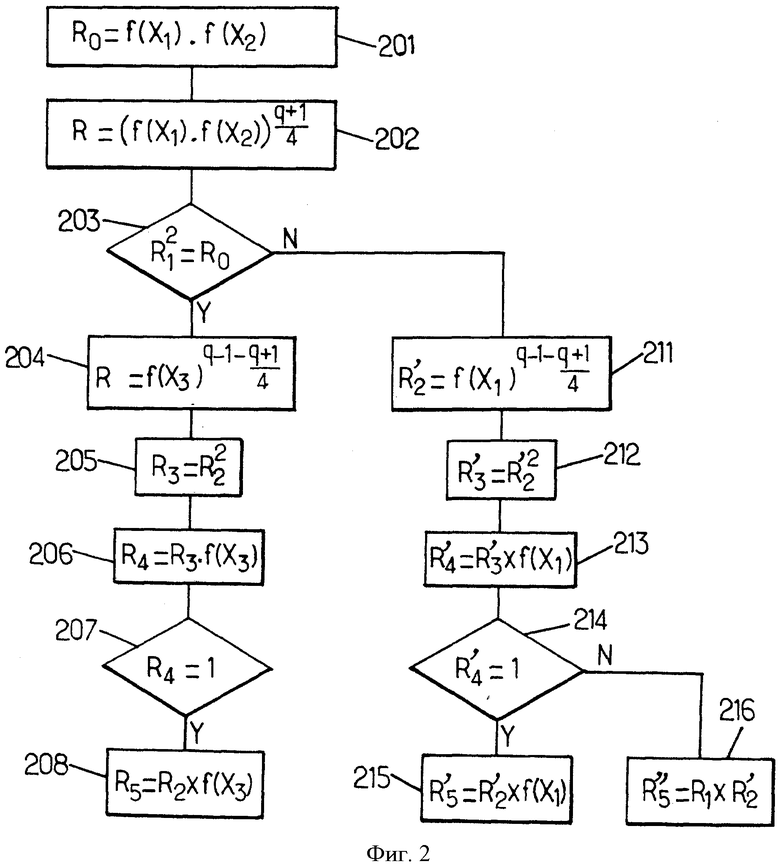
На фиг.2 показана реализация способа выполнения вычисления в соответствии с одним вариантом осуществления настоящего изобретения.
В одном варианте осуществления настоящего изобретения на этапе 201 осуществляют следующее умножение:
R0=f(X1).f(X2).
Далее проверяют, является ли элемент R0 квадратом, что делают путем применения этапов (iv) и (v). Таким образом, на этапе 202 мы вычисляем:
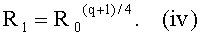
Далее на этапе 203 мы определяем, выполняется ли следующее равенство:
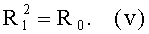
Решают, является ли элемент R0, равный f(X1).f(X2), квадратом или не является. В случае, когда элемент R0 является квадратом, применяют проверку с целью определения, является ли квадратом элемент f(X3). Результат последней проверки известен заранее, так как R0 является квадратом, так что результат этой проверки является положительным. Тем не менее, с целью обеспечения постоянного времени желательно применять его в соответствии с этапами от /i/ до /iii/.
Таким образом, на этапе 204 осуществляют следующее вычисление:
R2=f(X3)(q-1-(q-1)/4).
Здесь R2 соответствует вычислению обратного элемента для квадратного корня из элемента f(X3) в случае, когда f(X3) является квадратом.
Далее на этапе 205 вычисляют следующее:
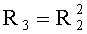
Здесь R3 соответствует обратному элементу для f(Х3).
Далее на этапе 206 R3 умножают на элемент f(Х3), тем самым получая элемент R4. Как мы знаем, f(X3) является квадратом, так что мы также знаем, что элемент R4 равен 1. Эти этапы 205 и 206 выполняют с целью обеспечения постоянного времени определения точки Р на эллиптической кривой.
Следовательно, на этапе 207 проверяют, соответствует ли 1 элемент R4. В этом случае результат упомянутой проверки является положительным, так как он следует из проверки 203.
Далее на этапе 208 осуществляют следующее вычисление:
R5=R2.f(X3).
Здесь получают значение точки Р на кривой, абсцисса которой равна Х3, а ординатой является квадратный корень из f(X3), то есть значение R5.
В случае, когда на этапе 11 решают, что элемент f(X1).f(X2) не является квадратным корнем, то или элемент f(X1), или элемент f(X2) является квадратным корнем.
Далее необходимо определить, какой из этих двух элементов f(X1) и f(X2) соответствует квадрату.
Для этого выполняют операции, аналогичные описанным ранее, за исключением случая, когда элемент f(X1) не является квадратом.
На этапе 211 выполняют следующее вычисление:
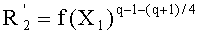
В случае, когда f(X1) является квадратом, 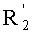
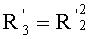
чтобы получить обратный элемент для f(X1) в случае, когда f(X1) будет квадратом.
Таким образом, умножая 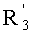
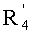
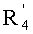
Далее на этапе 215 выполняют следующее вычисление:
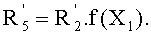
Таким образом, элемент 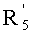
Получают точку Р с абсциссой X1 и ординатой - 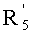
В случае, когда результат проверки 214 отрицательный, элемент f(X1) не является квадратом. Из этого следует, что квадратом в равенстве (2) Скальба является элемент f(X2). В этом случае на этапе 216 выполняют следующее вычисление:
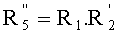
Заметим, что приведенное выше выражение дает возможность получать квадратный корень f(X2), не выполняя операцию возведения в степень, такую как операция, выполняемая на этапе 204 или также на этапе 211. Фактически здесь остроумно осуществляют умножение вместо возведения в степень.
Далее мы получаем 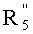
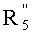
В варианте осуществления изобретения, описанном ранее со ссылкой на фиг.2, независимо от определения точки Р, то есть независимо от того, основано ли это определение на значении X1, или X2, или Х3, выполняют аналогичные вычисления, таким образом обеспечивается постоянное время определения точки на эллиптической кривой.
Более конкретно, выполняют две операции возведения в степень, одно возведение в степень на этапе 202 и другое возведение в степень на этапе 204 или 211, в зависимости от результата проверки 203. Таким образом, больше не нужно осуществлять четыре возведения в степень для определения точки на кривой в контексте многочленов Скальба за постоянное время.
В одном варианте осуществления настоящего изобретения возможно выбрать многочлены, которые удовлетворяют равенству Скальба, таким образом, чтобы многочлен f(X3(t)) никогда не соответствовал квадрату, при любом значении t. В этом случае равенство Скальба:
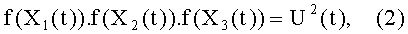
может быть записано в следующем виде:
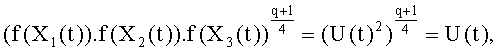
а также в следующем виде:
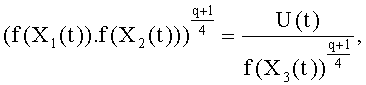
а также:
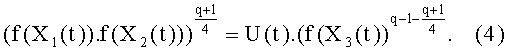
Все эти выражения справедливы, только если выполняется условие q=3 mod 4. Далее, если элемент 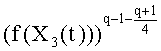
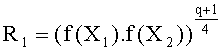
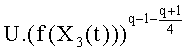
Эти условия могут быть выполнены с использованием примера набора многочленов, удовлетворяющих равенству Скальба и описанных в документе «Рациональные точки на определенных гиперэллиптических кривых над конечными полями» («Rational points on certain hyperelliptic curves over finite fields»), автор Масие Улас (Macie Ulas), 11 июня 2007 года. В этом документе описаны следующие многочлены, которые удовлетворяют равенству (2) Скальба:
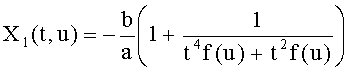
X2(t,u)=t2f(u)X1(t,u),
X3(t,u)=u,
U(t,u)=t3f(u)4f(X1(t,u)),
где f(u)=u3+au+b, а и b - такие элементы Fq, что их произведение не равно нулю.
Таким образом, путем определения значения u, которое установлено и не соответствует квадрату в Fq, значение R1 представляет собой установленное значение, которое может быть заранее вычислено в соответствии с равенством (4) для любого определения точки Р в соответствии с одним вариантом осуществления настоящего изобретения.
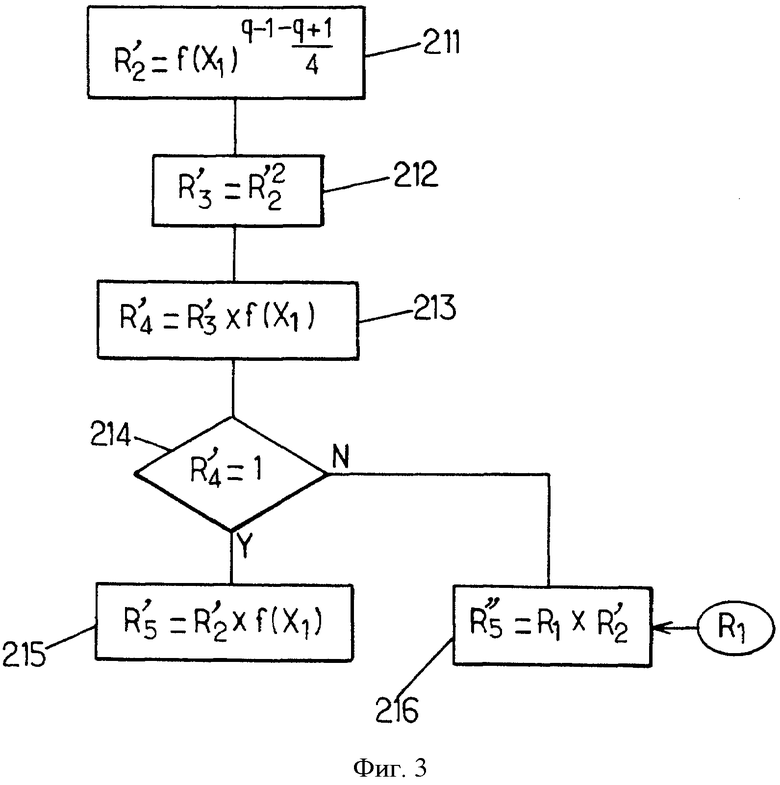
На фиг.3 подробно показан способ выполнения криптографического преобразования в соответствии с одним вариантом осуществления настоящего изобретения в частном случае многочленов Уласа для установленного многочлена Х3(t,u) в соответствии с одним вариантом осуществления настоящего изобретения. В этом случае могут быть применены одни этапы 211-216. Если выполняют этап 216, то значение R1 может быть восстановлено из области памяти, так как оно было вычислено ранее.
Соответственно, количество возведений в степень, требуемое для определения точки на кривой, может быть дополнительно уменьшено до одного возведения в степень, которое соответствует проверке 10 или проверке 13.
В одном варианте осуществления настоящего изобретения предпочтительно предусматривают использование координат Якоби. Это преобразование в координаты Якоби дает возможность преобразовать операции нахождения обратного элемента в операции умножения, которые быстрее и легче применяются. Заметим, что такой вариант осуществления изобретения не может быть применен для всех кривых типа Скальба, в том числе для конкретного случая кривых Уласа.
Выражение эллиптической кривой:
X3+aX+b=Y2
может быть записано в координатах Якоби следующим образом:
X'3+aX'Z4+bZ6=Y'2.
Заметим, что координаты точки (X,Y) могут быть записаны в координатах (X',Y',Z') Якоби следующим образом:
X'=X.Z2 и
Y'=Y.Z3.
Следовательно, мы должны определить многочлен Z(t,u) таким образом, чтобы координаты X', Y' и Z Якоби могли быть записаны без обратного элемента.
В следующих разделах это преобразование в координаты Якоби применяют в конкретном случае кривых Уласа, как указано выше.
В этом контексте любую операцию нахождения обратного элемента исключают с учетом следующего выражения:
Z(t,u)=a(t4f(u)2+t2f(u)),
в котором установлено значение u.
Фактически многочлены Уласа могут быть записаны в следующей форме в координатах Якоби:
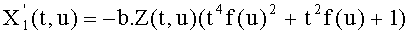
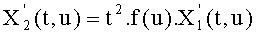
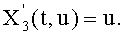
Следовательно, заметим, что не существует никаких нахождений обратных элементов в координатах Якоби. Так как эта операция может быть такой же затратной, как и возведение в степень, эти координаты дают возможность значительно улучшить время вычисления.
Далее для получения координаты Y' Якоби желательно вычислить U'(t,u), эквивалент U(t,u) в координатах Якоби.
В этом случае в классических координатах имеем:
U(t,u)2=f(X1(t,u)).(f(X2(t,u)).f(X3(t,u)).
Далее мы можем записать в координатах Якоби:
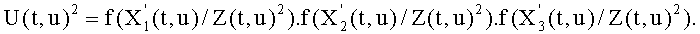
Написав
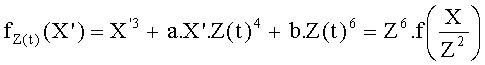
мы получим следующее выражение:
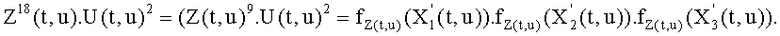
Тогда:
U'(t,u)=Z(t,u)9.U(t,u),
где U'(t,u) - это выражение U(t,u) в координатах Якоби.
В этом случае, когда считается, что U(t,u) удовлетворяет выражению:
U(t,u)=t3.f(u)2.f(Х2(t,u)),
мы можем записать:
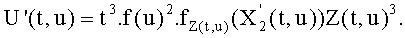
Равенство Скальба в координатах Якоби:
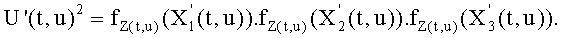
Тем не менее, как в случае многочленов Уласа, возможно требовать, чтобы 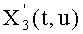
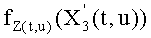
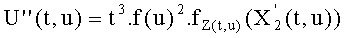
и соответствующее равенство Скальба представляет собой следующее:
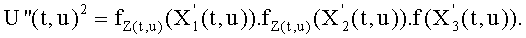
Целесообразно, что настоящее изобретение может быть реализовано в криптографическом преобразовании любого типа, в котором используют эллиптические кривые. Оно может быть особенно полезно в протоколах аутентификации пароля, таких как «Установка соединения с аутентификацией пароля». В этом случае оно позволяет улучшить эффективность вычисления, не давая возможности проводить атаку, связанную со временем выполнения криптографического преобразования.
Также настоящее изобретение может быть применено для протоколов сохранения конфиденциальности, таких как протоколы, используемые для проверки электронных документов удостоверения личности, таких как электронные паспорта.
Изобретение относится к способу и устройству выполнения криптографического преобразования в электронном компоненте. Технический результат заключается в повышении безопасности установки соединений с аутентификацией пароля за счет повышения эффективности выполнения криптографического преобразования. В способе выполняют получение точки P(X,Y) исходя из параметра t на эллиптической кривой, удовлетворяющей выражению Y2=f(X), и исходя из многочленов X1(t), X2(t), Х3(t) и U(t), удовлетворяющих равенству f(X1(t)).f(X2(t)).f(X3(t))=U(t)2 в Fq, при этом q=3 mod 4, далее получают значение параметра t и определяют точку Р путем выполнения подэтапов, на которых (i) вычисляют Х1=X1(t), X2=X2(t), Х3=Х3(t) и U=U(t), (ii) если элемент f(X1).f(X2) является квадратом, то проверяют, является ли элемент f(X3) квадратом в Fq, и если является, то вычисляют квадратный корень из элемента f(X3), чтобы получить точку Р(Х3), (iii) иначе проверяют, является ли элемент f(X1) квадратом, и если является, вычисляют квадратный корень из f(X1), чтобы получить точку P(X1), (iv) иначе вычисляют квадратный корень элемента f(X2), чтобы получить точку P(X2), и далее эту точку Р используют в криптографическом приложении. 2 н. и 6 з.п. ф-лы, 3 ил.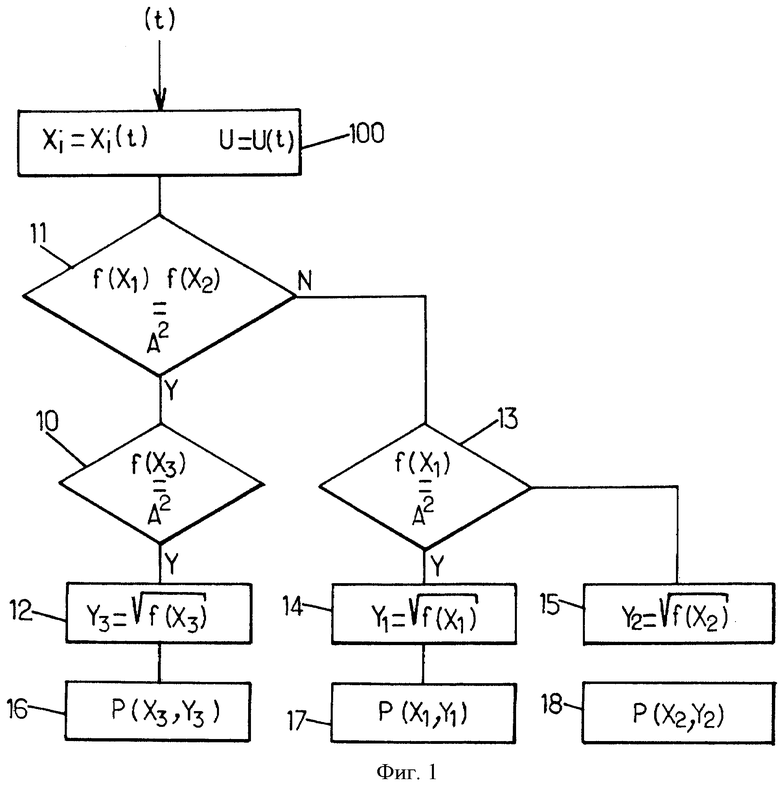
1. Способ выполнения криптографического преобразования в электронном компоненте, включающий в себя этап получения точки P(X,Y), исходя по меньшей мере из одного параметра t, на эллиптической кривой, удовлетворяющей выражению:
Y2=f(Х); и
исходя из многочленов X1(t), X2(t), X3(t) и U(t), удовлетворяющих следующему равенству Скальба:
f(X1(t)).f(X2(t)).f(X3(t))=U(t)2
в конечном поле Fq, независимо от параметра t, при этом q удовлетворяет равенству q=3 mod 4;
при этом выполняют следующие этапы:
/1/ получают значение параметра t;
/2/ определяют точку Р путем выполнения следующих подэтапов:
/i/ вычисляют X1=X1(t), X2=X2(t), Х3=X3(t) и U=U(t),
/ii/ если элемент f(X1).f(X2) является квадратом в конечном поле Fq, то проверяют, является ли элемент f(X3) квадратом в конечном поле Fq, и вычисляют квадратный корень из элемента f(X3), при этом абсциссой точки Р является Х3, а квадратный корень из f(X3) является ординатой точки Р;
/iii/ в противном случае проверяют, является ли элемент f(X1) квадратом в конечном поле Fq, и если является, вычисляют квадратный корень из элемента f(X1), при этом абсциссой точки Р является X1, а квадратный корень из f(X1) является ординатой точки Р;
/iv/ в противном случае вычисляют квадратный корень из элемента f(X2), при этом абсциссой точки Р является Х2, а квадратный корень из f(X2) является ординатой точки Р;
/3/ используют упомянутую точку Р в следующих криптографических приложениях: при шифровании, или хешировании, или подписывании, или аутентификации, или идентификации.
2. Способ выполнения криптографического преобразования по п.1, в котором на этапе /2/-/ii/ выполняют следующие этапы:
- вычисляют такой R1, что:
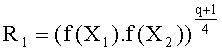 ,
,
- если 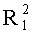 равен f(X1).f(X2), то решают, что элемент f(X1).f(X2) является квадратом в поле Fq;
равен f(X1).f(X2), то решают, что элемент f(X1).f(X2) является квадратом в поле Fq;
при этом на этапе /2/-/iii/ проверяют, является ли элемент f(Х1) квадратом в конечном поле Fq, в соответствии со следующими этапами:
- вычисляют такой 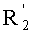 , что:
, что:
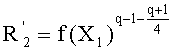 ,
,
- вычисляют такой 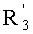 , что:
, что:
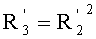 ,
,
- вычисляют такой 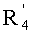 , что:
, что:
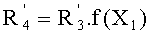 ,
,
причем если 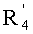 не равен 1, то на этапе /2/-/iv/ квадратный корень из f(X2) получают в соответствии со следующим выражением:
не равен 1, то на этапе /2/-/iv/ квадратный корень из f(X2) получают в соответствии со следующим выражением:
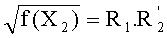 .
.
3. Способ выполнения криптографического преобразования по п.1 или 2, в котором многочлены, удовлетворяющие равенству Скальба, выражают в координатах Якоби, при этом точку P(X,Y) записывают как P(X',Y',Z), так что:
X'=X.Z2,
Y'=Y.Z3,
причем функция f записана как fZ(X') и удовлетворяет следующему равенству:
fZ(X')=X'3+a.X'.Z4+b.Z6,
а эллиптическая кривая удовлетворяет выражению:
Y'2=fZ(X'),
при этом многочлены, удовлетворяющие равенству Скальба и выраженные в координатах Якоби, представляют собой 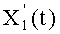 ,
, 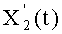 ,
, 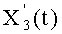 , Z(t) и U'(t) и удовлетворяют равенству Скальба в координатах Якоби:
, Z(t) и U'(t) и удовлетворяют равенству Скальба в координатах Якоби:
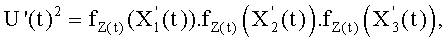
где Z(t) определен таким образом, что операции обращения преобразуются в операции умножения.
4. Способ выполнения криптографического преобразования по п.1 или 2, в котором многочлены, удовлетворяющие равенству Скальба, позволяют установить значение Х3(t) для любого возможного t таким, чтобы f(X3(t)) никогда не являлся квадратом элемента в Fq,
при этом на этапе /2/-/ii/ элемент f(X1).f(X2) не является квадратом в конечном поле Fq,
на этапе /2/-/iii/ проверяют, является ли элемент f(X1) квадратом в конечном поле Fq, в соответствии со следующими этапами:
- вычисляют такой 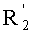 , что:
, что:
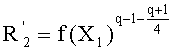 ,
,
- вычисляют такой 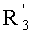 , что:
, что:
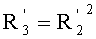 ,
,
- вычисляют такой 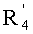 , что:
, что:
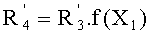 ,
,
причем, если 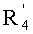 не равен 1, то на этапе /2/-/iv/ получают квадратный корень из f(X2) в соответствии со следующим выражением:
не равен 1, то на этапе /2/-/iv/ получают квадратный корень из f(X2) в соответствии со следующим выражением:
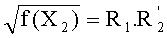 ,
,
где 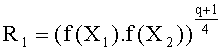 ,
,
причем R1 получают заранее из следующего выражения:
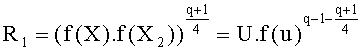 .
.
5. Способ выполнения криптографического преобразования по п.4, в котором многочлены, которые удовлетворяют равенству Скальба, выражают в координатах Якоби, при этом точку P(X,Y) записывают как Р (X', Y', Z), причем
X'=X.Z2,
Y'=Y.Z3,
где функция f записана как fZ(X') и удовлетворяет следующему выражению:
fZ(X')=X'3+a.X'.Z4+b.Z6,
а эллиптическая кривая удовлетворяет выражению:
Y'2=fZ(X'),
при этом многочлены, удовлетворяющие равенству Скальба и выраженные в координатах Якоби, представляют собой 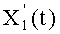 ,
, 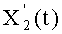 , Z(t) и U'(t) и удовлетворяют равенству Скальба в координатах Якоби:
, Z(t) и U'(t) и удовлетворяют равенству Скальба в координатах Якоби:
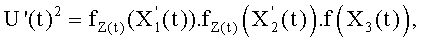
причем Z(t) определен таким образом, что операции обращения преобразуются в операции умножения.
6. Способ выполнения криптографического преобразования по п.1, в котором на этапе /1/ значение параметра t получают как функцию пароля или идентификатора.
7. Способ выполнения криптографического преобразования по п.1, в котором криптографическое приложение представляет собой аутентификацию или идентификацию путем проверки целостности, и
на этапе /1/ осуществляют следующие этапы:
/а/ генерируют случайное число;
/б/ получают зашифрованное число путем шифрования упомянутого случайного числа на основе функции шифрования с использованием ключа шифрования, определенного из пароля или идентификатора, соответствующего параметру; и
/в/ передают зашифрованное число для проверки целостности.
8. Электронное устройство, содержащее средство, выполненное с возможностью реализации способа выполнения криптографического преобразования по п.1.
| Ролик рольганга преимущественно прокатного стана | 1980 |
|
SU1014617A1 |
| WO 2000005837 A1, 03.02.2000 | |||
| СПОСОБ КРИПТОГРАФИЧЕСКОЙ ОБРАБОТКИ С ИСПОЛЬЗОВАНИЕМ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ С ПОМОЩЬЮ ВЫЧИСЛИТЕЛЬНОГО УСТРОЙСТВА И УСТРОЙСТВО ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 1999 |
|
RU2232476C2 |
| Способ удаления сурьмы из чернового олова | 1939 |
|
SU57827A1 |
Авторы
Даты
2014-06-27—Публикация
2010-06-15—Подача