Изобретение относится к области железнодорожной автоматики и может быть использовано для контроля состояния рельсовых линий, входящих в состав рельсовых цепей синусоидального тока.
Известны способы определения фазового сдвига между двумя синусоидальными напряжениями, т.е. способы определения начальной фазы второго напряжения относительно начальной фазы первого, соответствующей моменту перехода напряжения через нуль от отрицательных значений к положительным, на основе непосредственного измерения их действующих значений [1, стр.230] и формирования ширины импульсов одинаковой амплитуды и среднего их значения, прямо пропорционального фазовому сдвигу [1, стр.231]. Эти способы не могут быть использованы для определения начальной фазы напряжения на приемном конце рельсовой линии, отсчитываемой от начальной фазы напряжения на ее питающем конце, так как в рельсовых цепях на перегонах эти напряжения удалены друг от друга на большие расстояния.
Известен способ определения фазового сдвига (между двумя синусоидальными напряжениями на основе преобразования фазового сдвига во временной интервал Δ t между переходами через нуль этих напряжений, который пропорционален фазовому сдвигу: ϕ =360° · Δ t/T [1, стр.235].
Данный способ можно использовать для определения начальной фазы напряжения U2 на выходе рельсовой линии относительно начальной фазы напряжения U1, на ее входе при их большом удалении друг от друга, если имеется третье напряжение - напряжение синхронизации, начальные фазы которого на питающем (с территориальной точки зрения) и приемном концах рельсовой линии либо равны либо стабильно сдвинуты на определенный угол.
В качестве напряжения синхронизации на перегонах можно использовать пониженное напряжение линии автоблокировки при условии стабильности фаз на приемном и питающем концах.
Данный способ выбран авторами в качестве прототипа.
Целью изобретения является способ определения начальной фазы напряжения на приемном конце рельсовой линии, входящей в состав рельсовой цепи синусоидального тока при отсутствии напряжения синхронизации. Указанная цель достигается тем, что в рельсовой линии, входящей в состав рельсовой цепи синусоидального тока и нагруженной на номинальное сопротивление ZH, равное номинальному волновому сопротивлению ZBH рельсовой линии, соответствующему номинальным значениям комплексного сопротивления Z0H Ом/км рельсовой нити и комплексной проводимости Y0H Ом/км изоляции, в нормальном режиме измеряются действующие значения напряжений и токов (U1, U2, I1, I2) на ее питающем и приемном концах, сдвиг по фазе Δ ϕ 2, между напряжением U2 и током I2; по известным длине 1 км рельсовой линии, номинальному сопротивлению Z0H рельсовой нити, номинальной проводимости Y0H изоляции рассчитываются номинальное волновое сопротивление ZBH, номинальный коэффициент распространения волны γ H=α H+jbH, номинальный коэффициент КH=U1H/U2H в нормальном режиме и при нагрузке ZH=ZBH; по измеренным U1, U2, I1, I2 и Δ ϕ 2 вычисляются реальная нагрузка ZH=(U2/I2)• 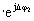
 рельсовой линии и коэффициент К=(U2·I1)/(U1·I2); при выполнении условия ZH=ZBH вычисляется фаза напряжения U2 по соотношению
рельсовой линии и коэффициент К=(U2·I1)/(U1·I2); при выполнении условия ZH=ZBH вычисляется фаза напряжения U2 по соотношению
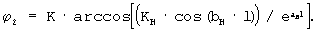
Справедливость соотношений для определения ϕ 2 следует из следующих рассуждении применительно к частоте 50 Гц питающего напряжения рельсовой цепи.
Сопротивление рельсовой нити длиной 1 км равно Z0=0.8· ej65° =0.3381+j0.72505 [2, стр.43]. Отклонение в процессе эксплуатации его вещественной части принимаем равным ±10.
Z0max=0.3381+(0.3381· 0.1)+j0.72505=0.81487· еj62.845° . За номинальное сопротивление рельсовой нити принимаем
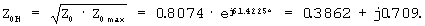
Проводимость балласта Y0 изменяется в процессе эксплуатации от Y0min=G0min+jQ0min до Y0max=G0max+jQ0max При этом за номинальную проводимость Y0H принимаем значение 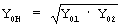 , где Y01=1, Y02=1+jQ02, где Q02 изменяется в пределах arctg(Q02/1)≤ 10° [2, стр.43]. В этом случае Y02=1+j0.17633=1.015· ej10° . За номинальную проводимость принимаем
, где Y01=1, Y02=1+jQ02, где Q02 изменяется в пределах arctg(Q02/1)≤ 10° [2, стр.43]. В этом случае Y02=1+j0.17633=1.015· ej10° . За номинальную проводимость принимаем 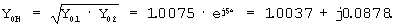 Номинальное волновое сопротивление
Номинальное волновое сопротивление
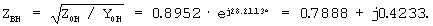
Номинальный коэффициент распространения волны
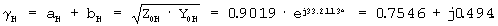
Номинальная нагрузка
ZH=ZBH=0.8952· ej28.2113° =0.7888+j0.4233
Если Z0=Z0H=R0H+jX0H, Y0=Y0H=G0H+jQ0H γ =γ H=aH+jbH, ZB=ZBH и рельсовая линия нагружена на ZH=ZBH, то ее уравнения состояния
имеют
вид [3]
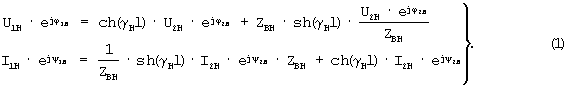
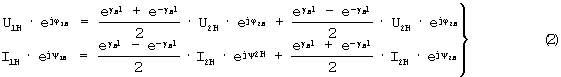
Из(2)

Так как γ H=α H+jbH, то:
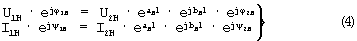
Из первого уравнения системы (4)
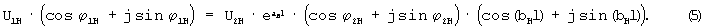
Из (5) следует
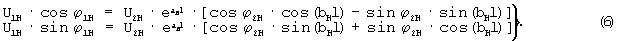
Принимая ϕ 1=0
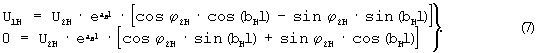
Из 2-го уравнения системы (7)
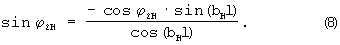
После подстановки (8) в первое уравнение (7)
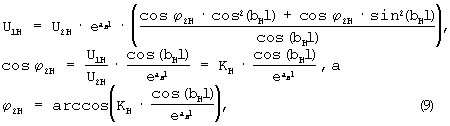
где КH=U1H/U2H. При этом КH не зависит от величины U1H, т.е. от величины напряжения питания рельсовой линии в нормальном режиме.
При работе рельсовой цепи в номинальном, т.е. согласованном режиме, входное сопротивление нагруженной рельсовой линии будет равно сопротивлению ее номинальной нагрузки и, следовательно
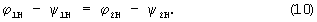
Если разделить первое уравнение (4) на второе, то с учетом (10) получим, что
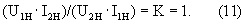
При "нарушении" номинального согласованного режима работы рельсовой цепи, вызванного изменением вещественной части проводимости изоляции, будет изменяться значение коэффициента К (оно не будет равно I)
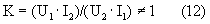
Будет изменяться также и фаза напряжения U2. При этом ее текущее значение будет очень близко к величине
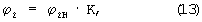
где ϕ 2H вычисляется по (9), а коэффициент К - по (12), в котором U1, U2, I1, I2 - измеряемые текущие действующие значения напряжения и тока на входе и выходе рельсовой линии.
В таблице 1 представлены действительные значения начальной фазы ϕ 2Д напряжения U2 при изменении вещественной части проводимости изоляции от 0.01 до 5 См/км при ϕ 1=0, Z0=Z0H=0.3862 + j0.709 Ом/км и ZH=ZBH=0.7888+j0.4233, полученные на основе математического моделирования работы рельсовой цепи с использованием известных соотношений
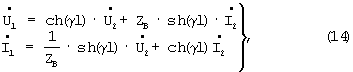
а также значения ϕ 2P, полученные на основе моделирования ее работы с использованием соотношений (9), (12) и (13).
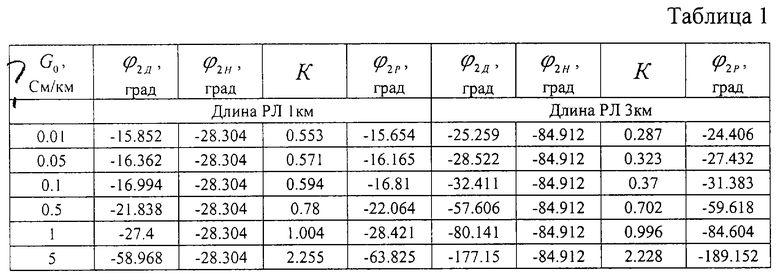
Из таблицы (1) видно, что ϕ 2Р, отличается от ϕ 2Д не более чем на 8.2%, что подтверждает возможность использования полученных соотношений для определения ϕ 2 при отсутствии напряжения синхронизации.
С практической точки зрения за номинальные значения параметров рельсовых линий при работе их на частоте 50 Гц можно принять: Z0Н=0.8· еj65° Ом/км, Y0H=1 См/км. Однако в этом случае, как показали исследования, погрешность определения ϕ 2, при изменении мнимых частей сопротивления рельсовой нити и проводимости изоляции возрастает, но не превышает 9%. В таблице 2 представлены (для этого случая) результаты анализа изменения фазы напряжения U2 на основе точного моделирования работы РЛ с использованием (14), а также с использованием (13).
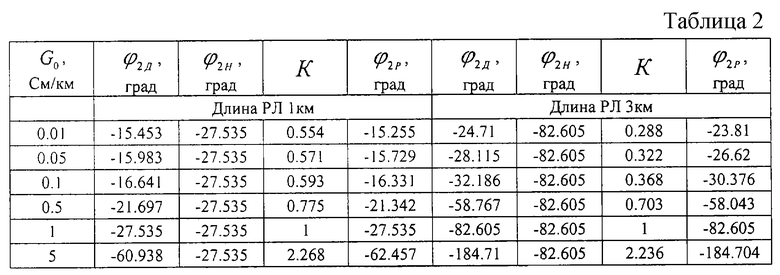
Номинальные параметры эксплуатируемой на частоте 50 Гц рельсовой линии, нагруженной на приведенное к ее выходу сопротивление ZH, выбирается так.
Известное сопротивление нагрузки ZH принимается равным номинальному волновому сопротивлению ZBH рельсовой линии при номинальном сопротивлении рельсовой нити Z0H=0.8· еj65° Ом/км.
Номинальная проводимость при этом вычисляется по известному соотношению Y0H=Z0H/Z
Сравнительный анализ с прототипом показывает, что предлагаемый способ отличается тем, что предварительно по известным длине l км рельсовой линии, номинальному сопротивлению Z0H, рельсовой нити, номинальной проводимости Y0H, изоляции рассчитывается номинальное волновое сопротивления ZBH, номинальный коэффициент распространения волны γ H=α H+jbH, номинальный коэффициент КH=U1H/U2H в нормальном режиме и при нагрузке ZH=ZBH; по измеренным в нормальном режиме U1, U2, I1, I2 и Δ ϕ 2 вычисляются реальная нагрузка ZH=(U2/I2)· ejΔ ϕ 2 рельсовой линии и коэффициент К=(U2·I1)/(U1·I2); при выполнении условия ZH≈ZBH вычисляется фаза напряжения U2, по соотношению 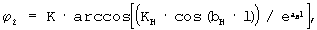 , которое не известно, как не известна и последовательность выполнения предлагаемых процедур, обеспечивающих определение начальной фазы U, при отсутствии напряжения синхронизации.
, которое не известно, как не известна и последовательность выполнения предлагаемых процедур, обеспечивающих определение начальной фазы U, при отсутствии напряжения синхронизации.
Предлагаемый способ соответствует критериям изобретения "новизна", "существенные отличия", "изобретательский уровень".
Использование данного способа обеспечивает возможность определения начальной фазы напряжения U2 на выходе рельсовой линии и, тем самым, контроля состояния сопротивлений рельсовой нити и балласта по способу [4] при отсутствии напряжения синхронизации с целью повышения безопасности движения поездов.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Кушнир Ф.В. и др. Измерения в технике и связи. Учебник для вузов. Изд. 2-е, доп. и перераб. М.: Связь, 1976, - 432с.
2. Дмитренко И.Е., Сапожников В.В., Дьяков Д.В. Измерения и диагностирование в системах железнодорожной автоматики, телемеханики и связи. Учебник для вузов ж.-д. Трансп./Под ред. И.Е.Дмитренко. М.: Транспорт, 1994, - 263с.
3. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Том первый. Л.: Энергоиздат, 1981, - 495с.
4. Пиманов А.Е. Определение первичных параметров рельсовой линии по измеренным в нормальном режиме комплексным амплитудам токов и напряжений на ее входе и выходе. "Безопасность движения поездов"// Труды научно-практической конференции. - М.: МИИТ, 2002, - 290с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ СОПРОТИВЛЕНИЙ РЕЛЬСОВОЙ НИТИ И БАЛЛАСТА РЕЛЬСОВОЙ ЛИНИИ | 2001 |
|
RU2222452C2 |
| Способ определения сопротивления рельсовой линии | 2019 |
|
RU2711548C1 |
| УСТРОЙСТВО ИЗМЕРЕНИЯ СОПРОТИВЛЕНИЯ ИЗОЛЯЦИИ РЕЛЬСОВОЙ ЛИНИИ | 2007 |
|
RU2349924C1 |
| СПОСОБ ИЗМЕРЕНИЯ СОПРОТИВЛЕНИЯ ИЗОЛЯЦИИ РЕЛЬСОВОЙ ЛИНИИ | 2011 |
|
RU2484485C1 |
| СПОСОБ КОНТРОЛЯ ПРОВОДИМОСТИ ИЗОЛЯЦИИ ОТНОСИТЕЛЬНО ЗЕМЛИ УЧАСТКА СЕТИ С ИЗОЛИРОВАННОЙ НЕЙТРАЛЬЮ | 2003 |
|
RU2242015C1 |
| Рельсовая цепь | 1989 |
|
SU1794752A1 |
| УСТРОЙСТВО ВОЗБУЖДЕНИЯ ГАЗОВОГО ЛАЗЕРА | 1990 |
|
RU2008752C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УДАЛЕННОСТИ ОДНОФАЗНОГО ЗАМЫКАНИЯ В ТРЕХФАЗНОЙ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ | 2003 |
|
RU2249226C2 |
| Способ измерения сопротивления изоляции с экстраполяцией тока абсорбции | 2022 |
|
RU2795369C1 |
| УСТРОЙСТВО АВТОМАТИЧЕСКОГО СОГЛАСОВАНИЯ ИМПЕДАНСА АНТЕННО-ФИДЕРНОГО ТРАКТА С КОМПЛЕКСНОЙ НАГРУЗКОЙ | 2021 |
|
RU2775607C1 |
Изобретение относится к области железнодорожной автоматики и предназначено для использования при осуществлении контроля состояния рельсовых линий, входящих в состав рельсовых цепей синусоидального тока. На питающем и приемном концах рельсовой линии имеются действующие значения напряжений и токов U1, U2, I1, I2, сдвиг по фазе между напряжением U2 и током I2 составляет Δϕ2. Предварительно по известной длине l км рельсовой линии, номинальному значению комплексного сопротивления Z0Н рельсовой нити, номинальной проводимости YOH изоляции рассчитывают номинальное волновое сопротивление ZВН рельсовой линии, номинальный коэффициент распространения волны γ H=aН+jbH, номинальный коэффициент КН=U1Н/U2Н в нормальном режиме и при нагрузке ZH=ZBH. По измеренным U1, U2, I1, I2 и Δϕ2 вычисляют реальную нагрузку ZH=(U2/I2)· еjΔϕ2 рельсовой линии и коэффициент К=(U2·I1)/(U1·I2), при выполнении условия ZН≈ZВН вычисляют фазу напряжения U2 по соотношению ϕ2=К· arccos[(Кн·cos(bн·l))/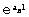 ]. Данный способ характеризуется упрощенной совокупностью составных операций и, в частности, не требует напряжения синхронизации. 2 табл.
]. Данный способ характеризуется упрощенной совокупностью составных операций и, в частности, не требует напряжения синхронизации. 2 табл.
Способ определения начальной фазы напряжения на приемном конце рельсовой линии, входящей в состав рельсовой цепи синусоидального тока и нагруженной на номинальное сопротивление ZH, равное номинальному волновому сопротивлению ZBH рельсовой линии, соответствующему номинальным значениям комплексного сопротивления ZOH Ом/км рельсовой нити и комплексной проводимости YOH См/км изоляции, согласно которому в нормальном режиме измеряют действующие значения напряжений и токов U1, U2, I1, I2 на ее питающем и приемном концах, сдвиг по фазе Δ ϕ 2 между напряжением U2 и током I2, отличающийся тем, что предварительно по известной длине l км рельсовой линии, номинальному значению комплексного сопротивления ZOH рельсовой нити, номинальной проводимости YOH изоляции рассчитывают номинальное волновое сопротивление ZBH рельсовой линии, номинальный коэффициент распространения волны γ H=α H+jbH, номинальный коэффициент КH=U1H/U2H в нормальном режиме и при нагрузке ZH=ZBH, по измеренным U1, U2, I1, I2 и Δ ϕ 2 вычисляют реальную нагрузку ZH=(U2/I2)/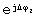 рельсовой линии и коэффициент К=(U2·I1)/(U1·I2), при выполнении условия ZH≈ZBH вычисляют фазу напряжения U2 по соотношению
рельсовой линии и коэффициент К=(U2·I1)/(U1·I2), при выполнении условия ZH≈ZBH вычисляют фазу напряжения U2 по соотношению
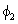 =К· arccos[(КH·cos(bH·l))/
=К· arccos[(КH·cos(bH·l))/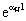 ].
].
| КУШНИР Ф.В | |||
| и др | |||
| Измерения в технике связи | |||
| Учебник для вузов | |||
| - М.: Связь, 1976, с.235 | |||
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ СВОБОДНОСТИ ПЕРЕГОНА | 1992 |
|
RU2082642C1 |
| УСТРОЙСТВО ДЛЯ ФАЗИРОВАНИЯ ПРЕОБРАЗОВАТЕЛЕЙ ЧАСТОТЫ РЕЛЬСОВЫХ ЦЕПЕЙ | 1992 |
|
RU2070125C1 |
| RU 94015042 A1, 27.12.1995. | |||
Авторы
Даты
2004-09-27—Публикация
2003-02-04—Подача