Предлагаемый способ относится к электрическим измерениям, а именно к измерениям сопротивления изоляции. Он особенно актуален в тех случаях, когда контролируемый объект имеет большую электрическую емкость относительно "земли" и большие токи абсорбции, которые мешают измерению сопротивления изоляции.
Известен способ [Пат. 2522177 РФ, МПК G01R 31/06. Способ определения качества компаундирования обмоток электрических машин / Наконечный А.И., Калан В.А., Науменко А.Г. и др. - Опубл. 31.10.2012, Бюл. №13]. Один из ключевых моментов данного способа заключается в том, что на объект измерений подают постоянное напряжение U и измеряют сопротивление R(t) объекта в течении времени, достаточного для достижения величины сопротивления практически установившегося значения.
Недостатком данного способа является большое время измерения. В большинстве случаев контролируемый объект имеет емкость относительно "земли", а также ток абсорбции, который мешает измерению сопротивления изоляции. Наличие тока заряда емкости и наличие тока абсорбции искажают результат измерения. Поэтому для правильного измерения сопротивления изоляции в известном способе дожидаются, когда станут практически равными нулю ток заряда и ток абсорбции. Если заряд емкости ускорить можно, то ускорить прекращение тока абсорбции практически невозможно. Во многих случаях ток абсорбции соизмерим с током утечки (который также называют током сквозной проводимости) длительное время, десятки и даже сотни секунд после прикладывания измерительного напряжения.
Наиболее близким по технической сущности к предлагаемому способу (прототипом) является способ измерения установившегося значения сопротивления изоляции [Пат. РФ № 2101716, МПК G01R 27/02, 1998]. Способ измерения заключается в том, что измеряют величину сопротивления, его первую и вторую производные по времени и за установившееся значение сопротивления изоляции принимают удвоенное значение сопротивления изоляции в тот момент, когда первая производная имеет максимум, а вторая производная равна нулю.
Недостатком прототипа является большая погрешность. Во-первых, такой способ применим только в том случае, когда ток в измерительной цепи имеет чисто экспоненциальный закон, то есть не учитывается ток абсорбции. Во-вторых, для расчетов используется одна единственная характерная точка, когда первая производная имеет максимум, а вторая производная равна нулю. При этом любой шум, который может возникнуть в этот момент времени, существенно повлияет на результат измерений.
Задачей предлагаемого способа является снижение времени измерения и снижение погрешности измерения сопротивления изоляции.
Технический результат заключается в том, что за счет большого количества результатов измерения тока, участвующих при расчетах, усредняется шум, в результате снижается погрешность. Кроме этого, за счет использования для аппроксимации аналитической формулы, которая лучшим образом описывает изменение тока во времени, удается на небольшом временном интервале осуществить аппроксимацию с высокой точностью, с последующей экстраполяцией. Это приводит к снижению времени измерения.
Поставленная задача достигается способом измерения сопротивления изоляции, в котором выполняют два измерительных полуцикла с разными прикладываемыми измерительными напряжениями U1 и U2. В каждом полуцикле вычисляют оценку (прогноз) установившегося значения тока iоц1 и iоц2. Вычисляют сопротивление изоляции по формуле Rиз=(U1-U2)/(iоц1-iоц2). Для вычисления оценки (прогноза) установившегося значения тока после прикладывания измерительного напряжения, в моменты времени t0, t1, t2, … tN-1 выполняют N измерений тока i0, i1, i2,…iN-1 и выполняют аппроксимацию этих значений тока первой функцией вида
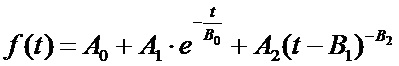 ,
,
то есть вычисляют численные значения A0, A1, A2, B0, B1, B2, в качестве оценки (прогноза) установившегося значения тока iоц1 или iоц2 используют значение A0. Для выполнения аппроксимации значений тока i0, i1, i2,…iN-1 первой функцией задают начальное приближение 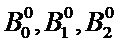 , выполняют шаги итерационной последовательности для значений
, выполняют шаги итерационной последовательности для значений 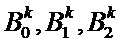 в соответствии с одним из известных итерационных методов оптимизации до достижения минимума целевой (второй) функции
в соответствии с одним из известных итерационных методов оптимизации до достижения минимума целевой (второй) функции 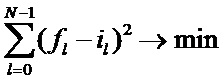 , где il - измеренные значения тока i0, i1, i2,…iN-1, ряд значений первой функции fl - вычисляются подстановкой в первую функцию ряда значений времени t0, t1, t2, … tN-1. Как для начального приближения, так и для последующих итераций вычисление целевой (второй) функции осуществляется в следующей последовательности а, б, в.
, где il - измеренные значения тока i0, i1, i2,…iN-1, ряд значений первой функции fl - вычисляются подстановкой в первую функцию ряда значений времени t0, t1, t2, … tN-1. Как для начального приближения, так и для последующих итераций вычисление целевой (второй) функции осуществляется в следующей последовательности а, б, в.
а - Считая 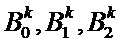 константами, вычисляются значения
константами, вычисляются значения 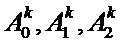 методом наименьших квадратов, реализуемом прямым (не итерационным) способом.
методом наименьших квадратов, реализуемом прямым (не итерационным) способом.
б - Затем в первую функцию подставляются значения 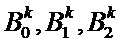 , полученные в соответствии с известным итерационным методом оптимизации и подставляются значения
, полученные в соответствии с известным итерационным методом оптимизации и подставляются значения 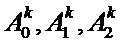 , полученные методом наименьших квадратов, реализуемом прямым (не итерационным) способом.
, полученные методом наименьших квадратов, реализуемом прямым (не итерационным) способом.
в - Затем в первую функцию подставляется ряд значений времени t0, t1, t2, … tN-1 и тем самым получается новый ряд значений первой функции fl, который подставляется в целевую (вторую) функцию и вычисляется значение целевой (второй) функции.
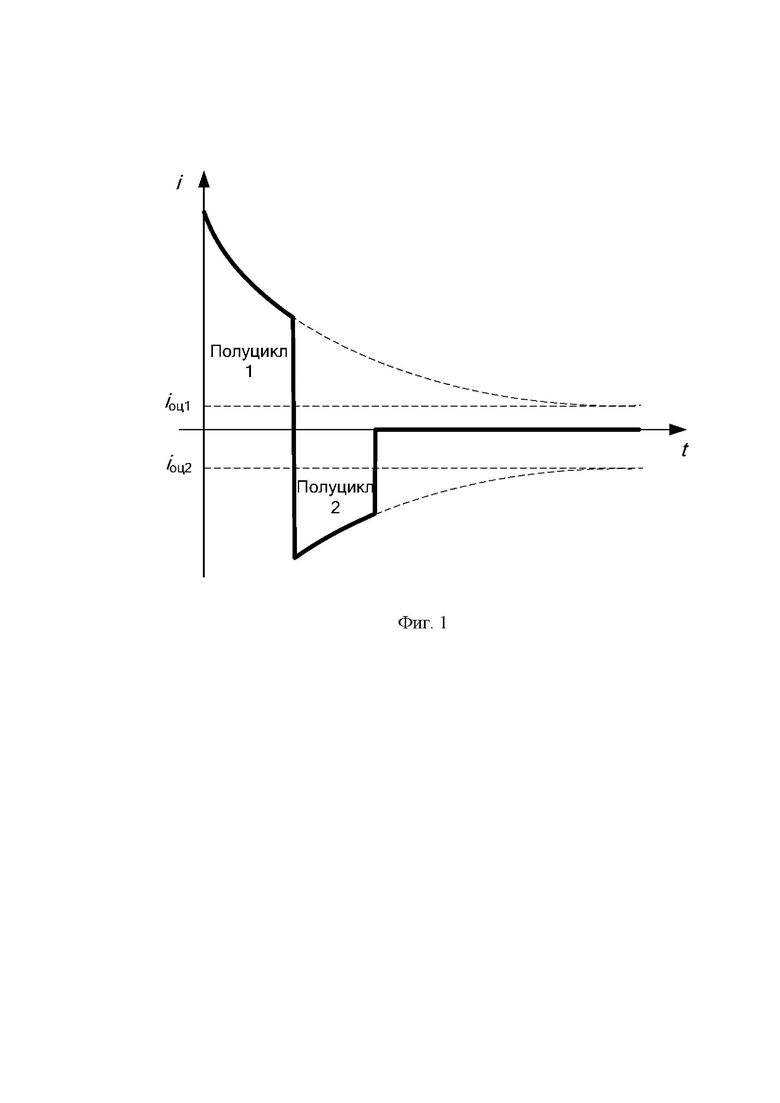
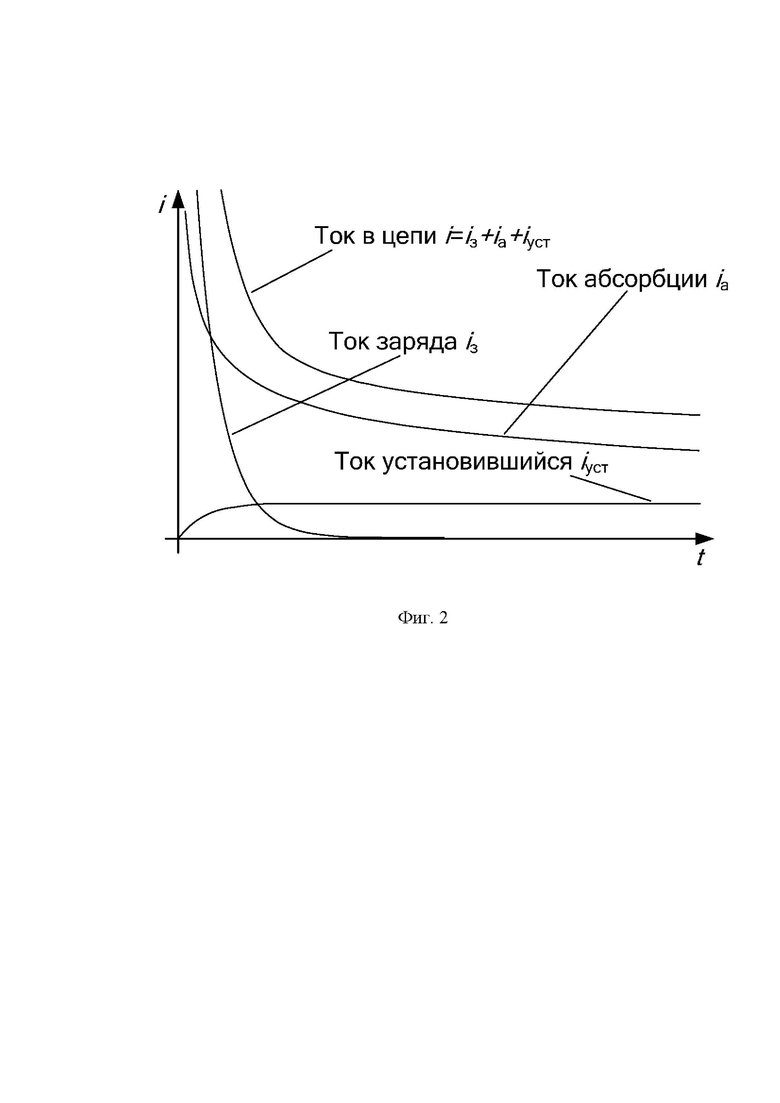
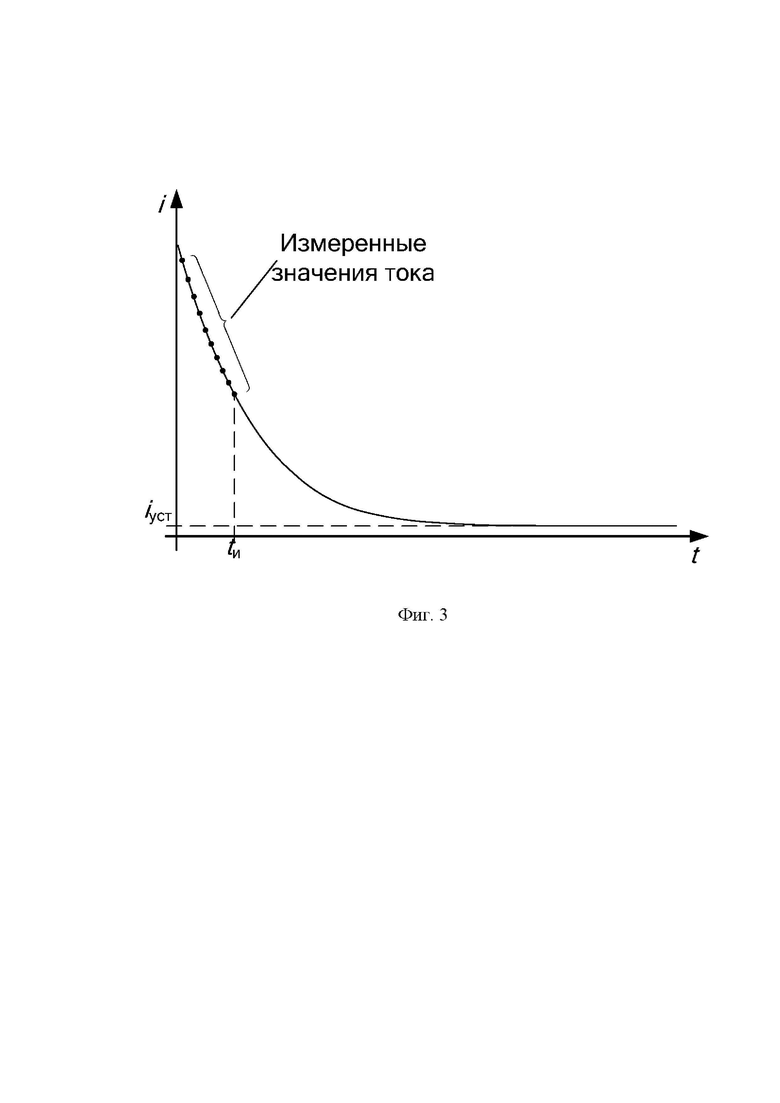
На фиг. 1 приведен график изменения тока в обоих полуциклах, на фиг. 2 приведен график изменения тока в измерительной цепи, состоящий из трех составляющих, на фиг. 3 приведен график, поясняющий экстраполяцию.
Для описания предлагаемого способа введем следующие обозначения.
iуст - установившееся значение тока, которое будет действовать в измерительной цепи через продолжительное время;
iоц - оценка (прогноз) установившегося значения тока, которая вычисляется до окончания тока абсорбции;
l - номер измеренного тока il, (то есть индекс для i0, i1, i2,…iN-1);
t0, t1, t2, … tN-1 - моменты времени, в которые измеряются токи;
N - количество измеренных значений тока
k - номер шага итерационного метода оптимизации для варьирования значений 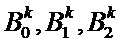 , то есть верхний индекс для
, то есть верхний индекс для 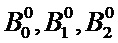 ;
; 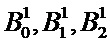 ;
; 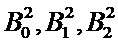 …
…
Как и в некоторых известных способах измерения сопротивления изоляции в процессе измерения реализуются два полуцикла с различными измерительными напряжениями, например, U1=+50 В и U2= -50 В. При этом используется формула Rиз=(U1-U2)/(iуст1-iуст2), где iуст1, iуст2 - измеренные установившиеся значения тока. Два полуцикла необходимы для устранения влияния постоянной составляющей напряжения сети относительно земли. В предлагаемом способе используются не измеренные установившиеся значения тока, а оценки (прогнозы) установившихся значений iоц1 и iоц2, которые вычисляются с помощью экстраполяции. На фиг. 1 приведен график тока в обоих полуциклах, который поясняет процесс измерения сопротивления изоляции. Как видно из графика, в обоих полуциклах ток не доходит до установившегося значения. Для вычисления сопротивления изоляции используется формула Rиз=(U1-U2)/(iоц1-iоц2).
При измерении сопротивления изоляции на длительность измерения влияет ёмкость, а также ток абсорбции. На фиг. 2 приведен график изменения тока в измерительной цепи, состоящий из трех составляющих, при прикладывании постоянного напряжения. Это ток заряда ёмкости, ток абсорбции и ток утечки.
Время заряда ёмкости уменьшить можно, например, увеличив ток заряда. Однако после заряда ёмкости, когда напряжение на ёмкости уже не меняется, остаётся ток абсорбции, который не позволяет быстро произвести измерение сопротивление изоляции. И при этом никакие ускоренные методы заряда ёмкости не помогут уменьшить время измерения в случае большого тока абсорбции. Если выждать достаточно большое время, то в измерительной цепи останется только установившееся значение тока iуст, который протекает через сопротивление изоляции.
В предлагаемом способе уменьшение времени измерения сопротивления изоляции достигается за счет экстраполяции тока абсорбции. То есть в каждом полуцикле вычисляется оценка (прогноз) установившегося значения тока iоц в измерительной цепи, не дожидаясь окончания тока абсорбции, это поясняется на фиг. 3. В начале измерительного цикла, в интервале от нулевого момента времени до момента, обозначенного tи, производится несколько (N) измерений тока в измерительной цепи. В измерительной цепи невозможно по-отдельности измерять зарядный ток, ток абсорбции и ток утечки, в измерительной цепи действует сумма этих токов. По измеренным значениям можно определить численные значения функции, в соответствии с которой изменяется ток во времени, в том числе и оценку (прогноз) установившегося значения iоц. Если точность прогнозирования достаточно высокая, то после момента времени tи нет необходимости продолжать измерительный цикл (полуцикл), прогнозируемое значение тока iоц можно использовать для вычисления сопротивления изоляции.
Проведенные многочисленные эксперименты показали, что ток в измерительной цепи изменяется во времени в соответствии с первой функцией:
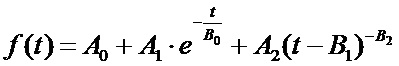
Для определения численных значений A0, A1, A2, B0, B1, B2 первой функции, которые соответствуют закономерности изменения тока в текущем полуцикле наиболее целесообразно применять метод наименьших квадратов. Существует много вариантов реализации метода наименьших квадратов. Один из них заключается в том, что варьируя значения A0, A1, A2, B0, B1, B2, добиваются того, что измеренные значения тока i0, i1, i2,…iN-1 становятся очень близки к значениям первой функции fl, вычисленным подставляя в неё значения времени t0, t1, t2, … tN-1. То есть требуется выполнить один из методов оптимизации, минимизируя эту разницу:
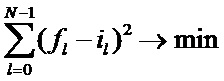
Следует учитывать, что аппроксимацию и экстраполяцию будет выполнять микроконтроллер, встроенный в измеритель сопротивления изоляции, причем прямо в процессе измерительного цикла. Причем время, затрачиваемое на вычисления, увеличивает время цикла измерения. То есть после момента tи пройдет время вычислений, после чего цикл (полуцикл) измерения заканчивается. Как показали эксперименты, процедура оптимизации с шестью варьируемыми переменными требует больших вычислительных затрат. При этом время измерения существенно увеличивается.
В предлагаемом способе переменные A0, A1, A2 вычисляются прямым методом, а переменные B0, B1, B2 - итерационным. Благодаря этому существенно снижаются вычислительные затраты.
Суть предлагаемого метода состоит в следующем. В самом начале измерительного цикла в моменты времени t0, t1, t2, … tN-1 сделано N измерений тока i0, i1, i2,…iN-1. Рассмотрим переопределенную систему уравнений:
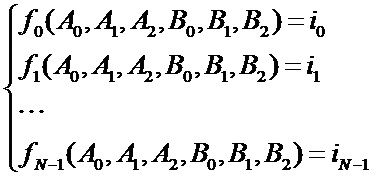
Более подробно:
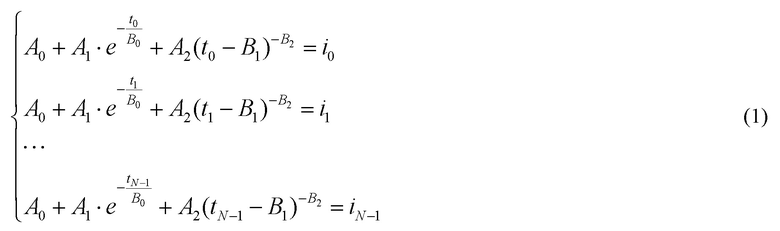
Речь идет о «решении» этой системы в смысле максимальной близости левой и правой частей системы уравнений. Следует обратить внимание, что число уравнений N значительно больше числа неизвестных, то есть больше шести. Поэтому система является переопределенной.
Суть метода наименьших квадратов заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей el=fl-il. Тогда метод наименьших квадратов можно записать следующим образом:
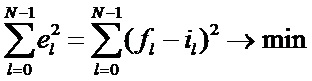
Существует известный способ реализации метода наименьших квадратов, с использованием домножения на транспонированную матрицу A, которая обозначается AT. Этот способ работоспособен только для нахождения коэффициентов при базисных функциях, которыми в нашем случае являются 1, 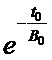 и
и 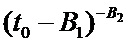 . Если неизвестные входят в состав базисных функций, то этот способ не работает. То есть значения B0, B1 и B2 необходимо находить другим способом.
. Если неизвестные входят в состав базисных функций, то этот способ не работает. То есть значения B0, B1 и B2 необходимо находить другим способом.
Рассмотрим случай, когда значения B0, B1, B2 в выражении (1) известны (константы) и методом наименьших квадратов нужно найти значения A0, A1, A2. В системе уравнений (1) при этом все уравнения линейные, так как только A0, A1, A2 - неизвестные, а все остальные символы - это константы, то есть известные числа.
Запишем эту СЛАУ в матричном виде:
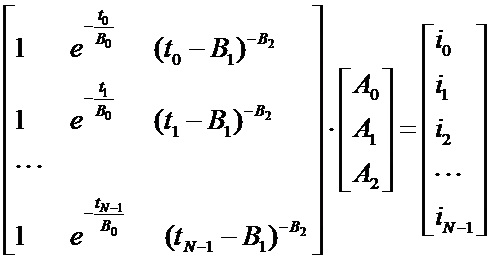
В левой части - прямоугольная матрица размерностью Nx3, обозначим её A. Затем следует столбец неизвестных, обозначим его x. В правой части - столбец свободных членов размерностью Nx1, обозначим его b. Тогда получим СЛАУ в привычном виде:
A·x=b
Однако, это переопределенная СЛАУ, в которой N уравнений и 3 неизвестных. В общем случае такая СЛАУ не имеет решения, её можно «решить» в смысле выбора такого вектора x, при котором минимизируется «расстояние» между векторами A·x и b. В соответствии с МНК применяется критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы. То есть:
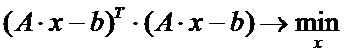
Один из самых распространенных способов реализации МНК заключается в умножении левой и правой частей СЛАУ на AT:

Матрица AT имеет размерность 3хN, поэтому матрица (AT·A) имеет размерность 3х3. По этой же причине столбец (AT·b) имеет размерность 3х1. В результате получаем три уравнения с тремя неизвестными. Эта СЛАУ имеет единственное решение. Причем это решение гарантирует минимизацию суммы квадратов разниц левой и правой частей уравнений СЛАУ вида (1). Затем СЛАУ вида (2) решается одним из известных методов решения, например, методом исключения Гаусса или методом Жордана. То есть будут найдены значения A0, A1, A2 при заданных константах B0, B1, B2.
Описанная реализация МНК не позволяет находить значения B0, B1, B2.
Предполагаемый комбинированный метод заключается в следующем. Значения В0, В1 и В2 отыскиваются известным итерационным методом, например, методом Левенберга - Марквардта. То есть задается начальное приближение 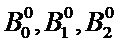 и производят действия, соответствующие методу Левенберга-Марквардта над значениями
и производят действия, соответствующие методу Левенберга-Марквардта над значениями 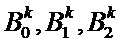 . Но, каждый раз, перед вычислением значения целевой (второй) функции
. Но, каждый раз, перед вычислением значения целевой (второй) функции 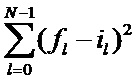 , происходит обращение к процедуре нахождения значений А0, А1 и А2 прямым методом. То есть для каждых значений
, происходит обращение к процедуре нахождения значений А0, А1 и А2 прямым методом. То есть для каждых значений 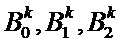 будут найдены наилучшие значения А0, А1 и А2. В результате, по окончании алгоритма определения значений В0, В1 и В2 будут так же определены значения А0, А1 и А2. Таким образом, производя аппроксимацию кривой тока на начальном участке, получим численные значения всех переменных в первой функции.
будут найдены наилучшие значения А0, А1 и А2. В результате, по окончании алгоритма определения значений В0, В1 и В2 будут так же определены значения А0, А1 и А2. Таким образом, производя аппроксимацию кривой тока на начальном участке, получим численные значения всех переменных в первой функции.
Экстраполяция производится следующим образом. При 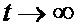 экспоненциальная и степенная функции стремятся к нулю:
экспоненциальная и степенная функции стремятся к нулю:
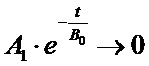 ;
;
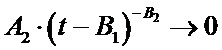 .
.
Поэтому остается значение А0, оно то и является оценкой (прогнозом) установившегося значения тока.
Для достижения поставленной задачи изобретения главным образом влияют три фактора. Во-первых, при осуществлении большого количества (N) измерений тока усредняется случайная помеха. Поэтому предлагаемый способ обеспечивает снижение погрешности измерения сопротивления изоляции. Во-вторых, за счет аппроксимации и экстраполяции тока в измерительной цепи существенно снижается время измерения. В третьих, за счет применения комбинированного метода наименьших квадратов, то есть применение прямого и итерационного способа реализации метода наименьших квадратов, удается существенно снизить вычислительные затраты, что делает предлагаемый способ реализуемым при использовании микроконтроллеров.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения вещественной и мнимой составляющих переменного напряжения | 2021 |
|
RU2780348C1 |
| Устройство измерения сопротивления изоляции с ускоренным зарядом емкости сети | 2022 |
|
RU2792304C1 |
| СПОСОБ ИЗМЕРЕНИЯ СОПРОТИВЛЕНИЯ ИЗОЛЯЦИИ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ | 2014 |
|
RU2585930C1 |
| СПОСОБ ИЗМЕРЕНИЯ СОПРОТИВЛЕНИЯ ИЗОЛЯЦИИ И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2014 |
|
RU2585965C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОВОГО СОПРОТИВЛЕНИЯ ПЕРЕХОД - КОРПУС СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ В КОРПУСНОМ ИСПОЛНЕНИИ | 2006 |
|
RU2300115C1 |
| СПОСОБ КОНТРОЛЯ СОПРОТИВЛЕНИЯ ИЗОЛЯЦИИ В ЭЛЕКТРИЧЕСКОЙ СЕТИ С ИЗОЛИРОВАННОЙ НЕЙТРАЛЬЮ | 2020 |
|
RU2725898C1 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ ИЗОЛЯЦИИ ФИДЕРОВ ТРЕХФАЗНОЙ СЕТИ | 2009 |
|
RU2400764C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ПАРАМЕТРОВ АСИНХРОННЫХ ЭЛЕКТРОДВИГАТЕЛЕЙ | 2016 |
|
RU2623834C1 |
| СПОСОБ КОСВЕННОГО КОНТРОЛЯ ТЕМПЕРАТУРЫ ПРОВОДА ВОЗДУШНОЙ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ | 1999 |
|
RU2157040C1 |
| СПОСОБ ИЗМЕРЕНИЯ МЕХАНИЧЕСКИХ ВЕЛИЧИН | 2001 |
|
RU2210744C1 |
Изобретение относится к электрическим измерениям, а именно к измерениям сопротивления изоляции, особенно в тех случаях, когда контролируемый объект имеет большую электрическую емкость относительно "земли" и большие токи абсорбции. Сущность: выполняют два измерительных полуцикла с разными прикладываемыми измерительными напряжениями U1 и U2. В каждом полуцикле вычисляют оценку (прогноз) установившегося значения тока iоц1 и iоц2 и вычисляют сопротивление изоляции по формуле Rиз=(U1-U2)/(iоц1-iоц2). Для вычисления оценки установившегося значения тока после прикладывания измерительного напряжения в моменты времени t0, t1, t2, … tN-1 выполняют N измерений тока i0, i1, i2,…iN-1 и выполняют аппроксимацию этих значений тока функцией вида
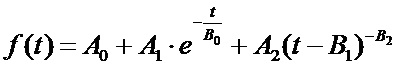
с помощью комбинации прямого и итерационного способов реализации метода наименьших квадратов. В качестве оценки установившегося значения тока используют значение A0.Технический результат: снижение времени и погрешности измерения сопротивления изоляции. 3 ил.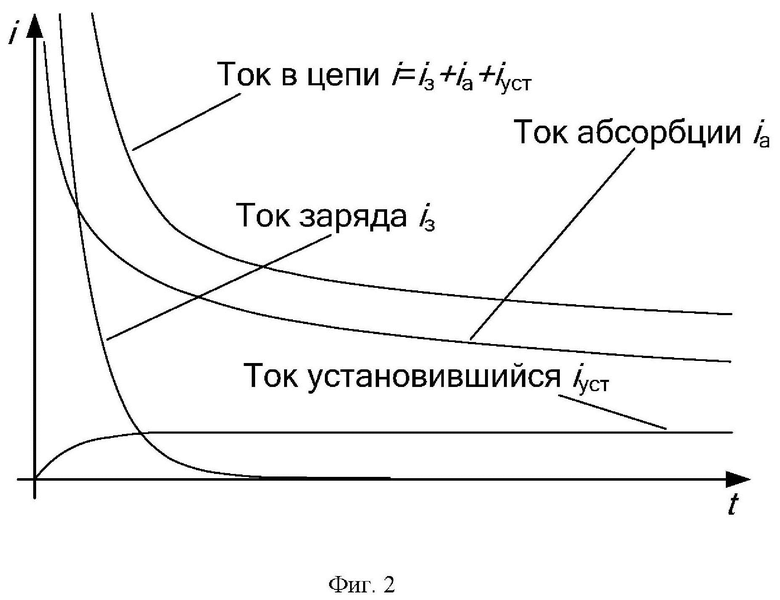
Способ измерения сопротивления изоляции, в котором выполняют два измерительных полуцикла с разными прикладываемыми измерительными напряжениями U1 и U2, в каждом полуцикле вычисляют оценку - прогноз установившегося значения тока iоц1 и iоц2, вычисляют сопротивление изоляции по формуле Rиз=(U1-U2)/(iоц1-iоц2), для вычисления оценки – прогноза установившегося значения тока после прикладывания измерительного напряжения в моменты времени t0, t1, t2, … tN-1 выполняют N измерений тока i0, i1, i2,…iN-1 и выполняют аппроксимацию этих значений тока первой функцией вида
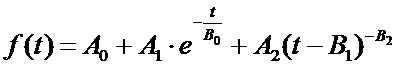
то есть вычисляют численные значения A0, A1, A2, B0, B1, B2, в качестве оценки - прогноза установившегося значения тока iоц1 или iоц2 - используют значение A0, для выполнения аппроксимации значений тока i0, i1, i2,…iN-1 первой функцией задают начальное приближение 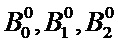
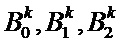
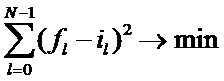
а - считая 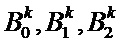
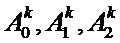
б - затем в первую функцию подставляются значения 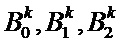
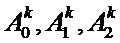
в - затем в первую функцию подставляется ряд значений времени t0, t1, t2, … tN-1 и тем самым получается новый ряд значений первой функции fl, который подставляется во вторую - целевую - функцию и вычисляется значение второй - целевой - функции.
| СПОСОБ ИЗМЕРЕНИЯ СОПРОТИВЛЕНИЯ ИЗОЛЯЦИИ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ | 2014 |
|
RU2585930C1 |
| Способ измерения сопротивления изоляции электрических сетей с контролем точности измерения посредством использования методов математической статистики | 2019 |
|
RU2705231C1 |
| US 20200256905 A1, 13.08.2020 | |||
| DE 102019214532 A1, 25.03.2021 | |||
| JP 60131476 A, 13.07.1985 | |||
| JP 60155983 A, 16.08.1985. | |||
Авторы
Даты
2023-05-03—Публикация
2022-10-24—Подача