СПОСОБ МОДЕЛИРОВАНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ АВИАЦИОННОЙ ПАНЕЛИ Российский патент 2004 года по МПК G01M5/00 

Решение относится к испытаниям на прочность конструктивных элементов летательных аппаратов, в частности панелей с использованием метода моделирования.

Исследования статической прочности летательных аппаратов подразделяются на три этапа (Статические испытания на прочность сверхзвуковых самолетов/ Рец. акад. А.И.Макаревский. - М.: Машиностроение, 1974. - С.9).

1-й этап: выбор конструктивного материала;

2-й этап: опытные экспериментальные исследования прочности конструктивных образцов, панелей, отсеков; исследования на масштабных моделях и т.д., целью которых являются:

а) выбор рациональных силовых схем;

б) проверка методики расчета;

в) получение экспериментальных зависимостей;

г) исследование новых явлений;

д) оценка влияния технологических процессов;

е) отработка методики и техники исследований.

3-й этап: статические испытания, при которых воспроизводятся величина и распределение нагрузки, действующей на летательный аппарат.

Объем исследований по каждому этапу зависит от степени изученности решаемых задач. Так, на ранней стадии проектирования находят применение масштабные модели типа панелей (рис. 1.17 и 1.21, соответственно с.24 и 26 вышеуказанного источника).

Первая представляет собой монолитную прямоугольную панель, асимметричо подкрепленную относительно ее срединной поверхности прямоугольным ребром (стрингером) вдоль продольной оси симметрии.

Вторая - панель, состоящая из прямоугольной обшивки, имеющей заклепочное соединение с продольным набором (стрингерами) и поперечным (шпангоутами) и нагруженной по кромкам нормальными распределенными сжимающими усилиями (прототип).

Обе модели представляют собой элементы натурной конструкции, чем достигается наибольшее соответствие их трехмерных напряженно-деформированных состояний. Как показано в работе (Бабурченков М.Ф., Бородачев Н.М. Напряженно-деформированное состояние прямоугольной подкрепленной пластины //Известия АН СССР. Механика твердого тела. - М.: Наука, 1979, №4. - С.162-169), в случае тонких ребер напряженно-деформированное состояние пластины является обобщенно плоским (Там же, с.163).

Основой моделирования являются методы подобия и размерностей, поэтому моделирование осуществляется в соответствии с системой критериев подобия. Для подобия явлений необходимо обеспечить равенство в модели и натуре численных значений каждого из критериев подобия, входящих в критериальное решение объемной статической задачи (Прошко В.М., Славин O.K. Вопросы статического и динамического подобия при моделировании напряженно-деформированного состояния конструкций // Экспериментальные исследования инженерных сооружений. - М.: Наука, 1973. - С.99-101). Из критериального решения следует, в частности, формула перехода от напряжений, измеренных в модели σ _м, к напряжениям в натуре σ _н, а именно:

σ _н=σ _мК_р/(К_IКδ ),

где К_р=Р_н/Р_м - масштаб силового подобия;

К_I=I_н/I_м - общий масштаб геометрического подобия;

Кδ =δ _н/δ _м - масштаб толщин.

Здесь индексы "н" и "м" относятся к натуре и модели соответственно.

При моделировании первой краевой задачи механики деформируемого твердого тела масштабы геометрического К_I и силового K_р подобий выбираются произвольно. Однако для тонкостенных моделей обычно K_I≠_{Kδ .}

Поэтому необходимо для конкретных задач оценить влияние последнего неравенства на реализацию подобия (Славин O.K. и др. Моделирование при расчетах на прочность тонкостенных машиностроительных конструкций методом фотомеханики // Расчеты на прочность. - М.: Машиностроение, 1980. - Вып.21. - С.53-68). Там же дан обзор работ по вопросам двухмасштабного подобия,т.е. при K_I≠_{Kδ . К конструктивным элементам, допускающим двухмасштабное моделирование, относятся тонкостенные стержни открытого профиля, а также стержни закрытых (коробчатых) профилей постоянного сечения.}

Для стержней выполняется принцип Сен-Венана, т.е. особенности приложения внешних сил к растянутому стержню проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня. Исключение могут составлять тонкостенные стержни (Феодосьев В.И. Сопротивление материалов. Изд. 9-е, перераб. - М.: Наука, 1986. - С.35) и безусловно панели, так как их длина и ширина соизмеримы. По этой причине для таких объектов при моделировании необходимо воспроизводить не только нагрузки, но и их распределение.

Вторая особенность. Элементы, находящиеся в сложнонапряженном состоянии, требуют для определения компонентов напряжений (σ _x, σ _y, τ _xy) измерений относительных деформаций по крайней мере в трех направлениях в каждой расчетной точке. Для тонкостенных элементов это количество удваивается, так как рекомендуется устанавливать измерители деформаций симметрично относительно срединной поверхности для исключения влияния местного изгиба. Поэтому схема измерения должна прорабатываться на основании расчетных данных и анализа напряженного состояния конструкции. (Статические испытания на прочность сверхзвуковых самолетов... - С.273). Обе особенности связаны с необходимостью анализа решений задач о напряженно-деформированном состоянии подкрепленной прямоугольной пластины при точном удовлетворении граничных условий.

Задача. Расширение возможностей оптимизации силовой схемы авиационной панели на основе методических положений способа моделирования с использованием новых свойств поля напряжений.

Технический результат достигается тем, что применен способ моделирования напряженно-деформированного состояния авиационной панели, включающий нагружение масштабной модели в виде прямоугольной обшивки (пластины), соединенной дискретно, на отдельных участках или непрерывно с продольным и поперечным силовыми наборами. Отличительные признаки: напряжения в панели в натуре σ _н определяют по вышеприведенной формуле перехода от напряжений, измеренных в модели σ _м, к напряжениям в натуре:

σ _н=σ _мК_р/(К_IКδ )

с учетом масштаба толщин kδ , причем

Kδ =K_h=K_t,

где K_h=h_н/h_м - масштаб толщин обшивки;

2h_н - толщина обшивки натуры;

2h_м - толщина обшивки модели;

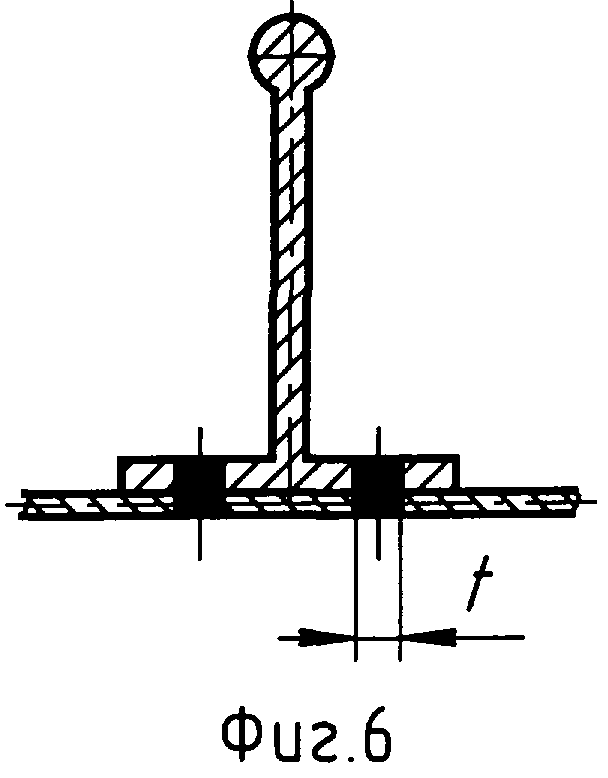
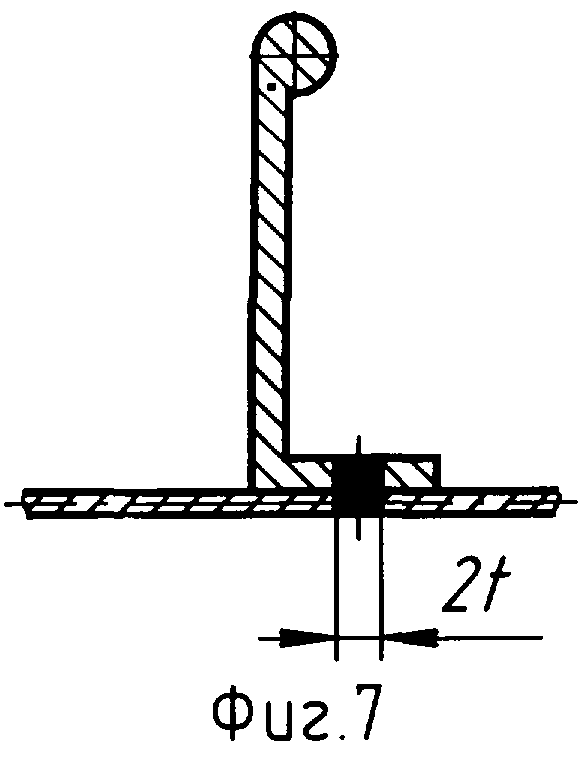
K_t=tsн

/tsм - масштаб толщин силового набора;

2tsн

- ширина контактной зоны элемента подкрепления в его поперечном сечении у натуры;

2tsм

- ширина контактной зоны того же элемента у модели, а для идентичного напряженно-деформированного состояния натуры и модели принимают K_h=K_t, одинаковые граничные условия, произвольный общий масштаб геометрического подобия и равные относительные модули продольной упругости.

При этом нагружение модели осуществляют растягивающими или сжимающими усилиями по торцам силового набора, либо по кромкам обшивки с сохранением подобия распределения усилий по натуре.

Ограничимся рассмотрением панелей с пересекающимися профилями (Гиммельфарб А.Л. Основы конструирования в самолетостроении: Учеб. пособие - 2-е изд., перераб. и доп. - М.: Машиностроение, 1980. - С.71-73), которые не соединены между собой и имеют компенсацию разреза при помощи косынки (рис. 7.50) или не требуют ее из-за различной высоты профилей (рис. 7.51). С другой стороны, создать конструкцию, обшивка которой имела бы высокие критические напряжения при двухосном сжатии, трудно. Обшивка обычных авиационных конструкций, подкрепляемая продольным набором (стрингерами), имеет низкие критические напряжения σ _укр при сжатии в поперечном направлении (Статические испытания сверхзвуковых самолетов... - С. 24-26). Как правило, величина σ _{у кр} в три-четыре раза меньше σ _{х кр}. Это позволяет воспользоваться методом суперпозиции двух решений для случаев подкрепления пластины силовым набором в направлении осей x и y.

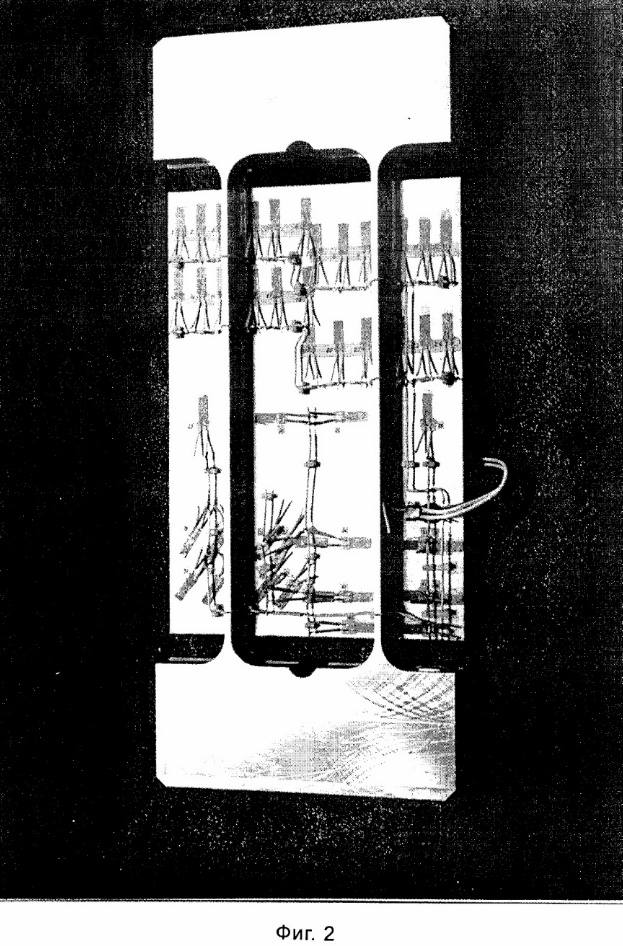
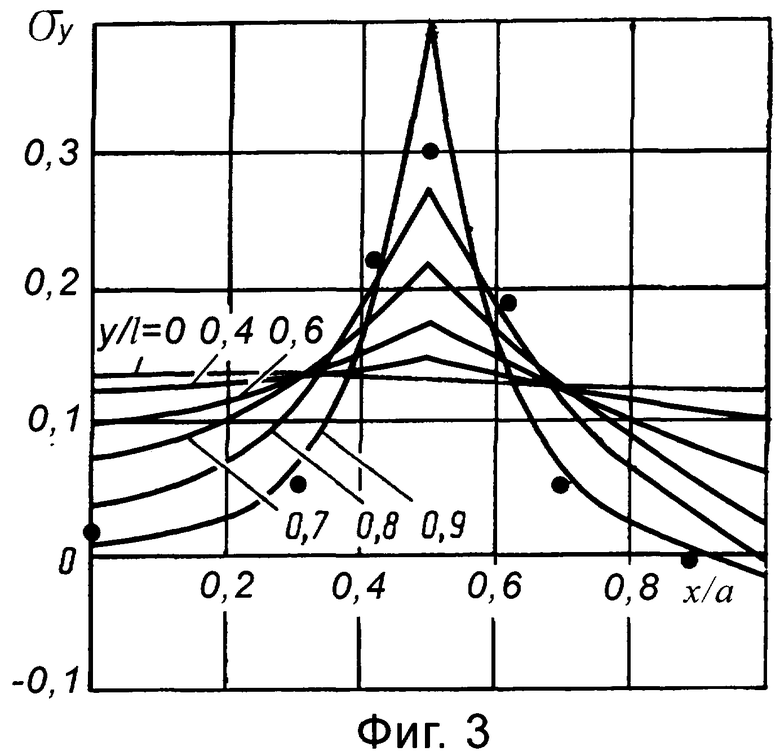
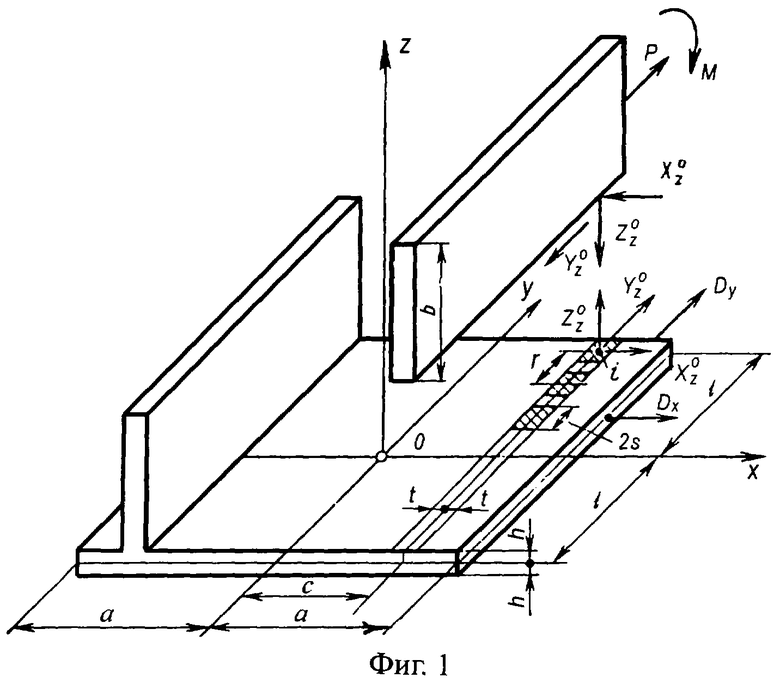
Фиг.1 изображает конструктивный элемент панели; фиг.2 - модель монолитной панели; фиг.3 - график зависимости компоненты напряжений σ _y; фиг.4, 5, 6, 7 - поперечные сечения профилей.

Конструктивный элемент (фиг.1) состоит из прямоугольной пластины шириной 2a, длиной 2I, толщиной 2h и подкрепляющих ребер толщиной 2t и высотой b. Ребра соединены с пластиной на произвольном количестве участков шириной 2t, длиной 2s с шагом r. Оси х, y (прямоугольной системы координат Ox,y,z) совпадают с осями симметрии срединной плоскости пластины, а ось z нормальна к ней. Кромки пластины нагружены распределенными нормальными усилиями D_x и D_y, торцы ребер - продольными силами Р и моментами М в плоскости наибольшей жесткости.

Для авиационных панелей характерны малая толщина (t<<а) и большая высота (b>>2h) ребер, но в этом случае конструктивный элемент идентичен расчетной модели, исследованной в работе (Бабурченков М.Ф., Бородачев Н.М. Подход к решению плоских контактных задач для прямоугольной области// Современные проблемы механики и авиации=Modern problems of mechanics and aviation: [Сб. статей] АН СССР, MB и ССО СССР, Нац. ком. СССР по теорет. и прикл. механике, МАИ. Редкол.: М. А. Лаврентьев и др. - М.: Машиностроение, 1982. - С.55-64). При этом вследствие принятых размеров ребра, в точках i зоны контактного взаимодействия компоненты напряжения Z_z°_{=Xz°=0. Касательные усилия Yz°переносятся в срединную плоскость пластины и рассматриваются как объемные силы, а напряженно-деформированное состояние пластины как обобщенно плоское. Ребро моделируется стержнем, воспринимающим изгиб и растяжение. Взаимодействие ребра и пластины сведено к равенству перемещений в точках i по линии х=с. Граничные условия для пластины выполняются точно. Рассмотрены следующие случаи:}

а) дискретное взаимодействие по точкам i=1, 2,... , N;

б) взаимодействие на участках длиной 2s при i=1, 2,... , N;

в) непрерывное соединение ребра.

Анализ решения показывает, что упругое состояние подкрепленной прямоугольной пластины зависит от безразмерных параметров, в частности от γ =t/h, Е⁰=Е/Е^r (с≤ а). Здесь Е, E^r - модули продольной упругости материалов пластины и ребра соответственно. Отсюда следует вывод: напряженно-деформированные состояния у подкрепленных пластин с одинаковым отношением толщины ребра 2t к толщине пластины 2h при прочих равных условиях идентичны. Применительно к натуре и модели это означает необходимость равенства отношений толщин

t_м/h_м=t_н/h_н или h_н/h_м=t_н/t_м.

Последние представляют собой масштаб толщин Кδ , причем

Кδ =K_h=K_t,

где K_h=h_н/h_м - масштаб толщин обшивки (пластины);

K_t=t_н/t_м - масштаб толщин силового набора.

При этом должны выполняться одинаковые граничные условия (например, одинаковые напряжения по торцам ребер и кромкам пластины), произвольный общий масштаб геометрического подобия (равные относительные размеры), равные относительные модули продольной упругости

Е0м

=Е0н,

т.е. Е_м/Еrм

=Е_н/Еrн.

Кроме того, если ребра расположены вне кромок пластины (с<а), то упругое состояние зависит от коэффициента Пуассона σ . Однако для металлов изменение σ от 0,25 до 0,35 практически не влияет на распределение напряжений (Пономарев С.Д., Бидерман В.Л., Лихарев К.К. и др. Расчеты на прочность в машиностроении. - М.: Машгиз, 1956. - Т.1. - С.169).

Указанные особенности упругого состояния сохраняются при симметричном подкреплении пластины относительное срединной плоскости и в более простом случае при периодическом подкреплении несколькими ребрами.

Экспериментальное исследование проводилось на монолитных образцах - моделях (фиг.2), изготовленных из алюминиевого сплава АК4 - 1 Т1 ГОСТ 17232-99 (предел прочности σ _B=396 МПа, условный предел текучести σ ₀₂=302 МПа) на фрезерном станке с ЧПУ. Это обеспечило качество поверхностного слоя и стабильность размеров. Полудлина l принята такой, чтобы имелась зона упругого состояния, для которой справедлива теория бруса:

Тензодатчики устанавливались с двух сторон пластины, всего 46 штук. В эксперименте реализовано нагружение торцев ребер равномерно распределеными усилиями интенсивностью 200 МПа с помощью шарнирных захватов испытательной машины.

Экспериментальные данные сравнивались с результатами численной реализации соответствующего аналитического решения. На фиг.3 приведены графики компоненты σ _y для второго варианта исполнения при Е⁰=1 и σ =0,33. Точками обозначены значения σ _y при y/I=0.9, полученные по результатам тензометрирования образцов того же типоразмера. Изучался случай нагружения торцев ребер равномерно распределенной нагрузкой равной единице. Поля напряжений для образцов первого и второго вариантов исполнения (γ =2) отличались между собой не более чем на 10%; при сравнении с результатами численной реализации - не более чем на 15% по отношению к величине исходного нагружения. Однако уменьшение высоты ребра до b/2h≤ 10 приводит к увеличению погрешности из-за влияния изгиба пластины. Она становится при этом свыше 20%.

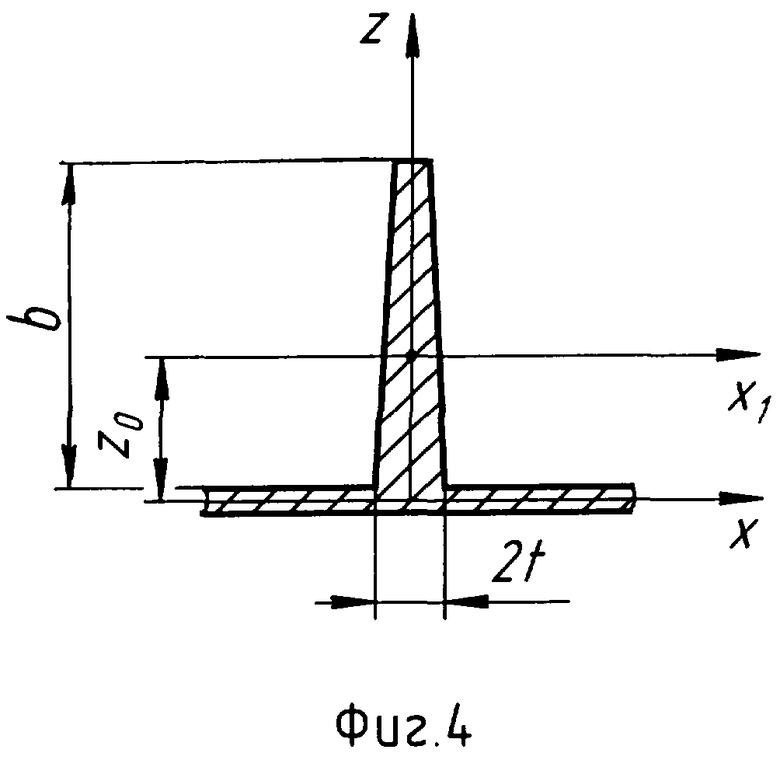
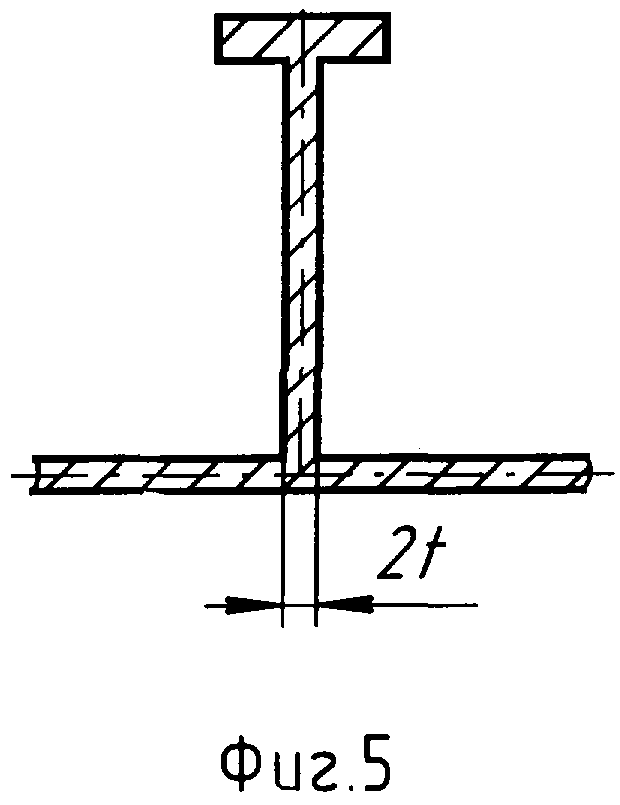
Обобщим полученные результаты на случай высоких профилированных ребер высотой b и толщиной в месте перехода к пластине (фиг.4 и 5), равной ширине зоны контактного взаимодействия 2t^s. Определим параметр 2t^s как ширину контактной зоны элемента подкрепления в его поперечном сечении. Из условия равенства перемещений точек нижней грани следует, что профилированное ребро можно заменить ребром с прямоугольным поперечным сечением толщиной, равной ширине контактной зоны 2t^s, и эквивалентной высотой b⁰=2/t^sω^{. При этом параметр}

ω =(1/S^r)+(z2n

/Jrx1),

где S - площадь поперечного сечения профилированного ребра;

z₀ - координата центра масс этого сечения;

Jrx1

- главный момент инерции сечения относительно центральной оси x₁.

Очевидно, что для прямоугольного ребра эта ширина совпадает с его толщиной, т.е. 2t^s=2t.

Аналогичным образом для сборных панелей, сварных или клепаных ширина контактной зоны 2t^s=d соответствует однорядному соединению шириной (диаметром) d (фиг.6) или 2t^s=2d для двухрядного соединения (фиг.7). Поэтому для решения вопроса оптимального распределения массы силового набора достаточно иметь в распоряжении расчетные или опытные данные для пластины, подкрепленной прямоугольным ребром. Такой способ можно применять для определения упругого состояния пластины в зависимости от конструктивного исполнения ребра, если напряженное состояние последнего не изменяется по толщине и допустима гипотеза плоских сечений.

Таким образом, связь между напряжениями σ нij

в натуре (в панели) и в модели σ мij определяется соотношением

σ нij

=σ мijK_p/(K_IKδ ), (i.j=1, 2),

где σ ₁₁=σ _х, σ ₁₂=σ ₂₁=τ _xy, σ ₂₂=σ _y - компоненты напряжения;

к_р=Р_н/Р_м - масштаб силового подобия;

k_I=I_н/I_м - общий масштаб геометрического подобия;

кδ -масштаб толщин, который определяется формулой изобретения.

Изобретение относится к испытательной технике. Сущность: нагружают масштабную модель в виде прямоугольной обшивки, соединенную дискретно на отдельных участках или непрерывно с продольными и поперечными силовыми наборами. Напряжение в панели в натуре определяют по заданной формуле перехода от напряжений, измеренных в модели, к напряжениям в натуре. Для идентичного напряженно-деформированного состояния натуры и модели принимают равными масштаб толщин обшивки и масштаб толщин силового набора, одинаковые граничные условия, произвольный общий масштаб геометрического подобия и равные относительные модули продольной упругости. Нагружение модели осуществляют растягивающими или сжимающими усилиями по торцам силового набора, либо по кромкам обшивки с сохранением подобия распределения усилий по натуре. Технический результат: повышение достоверности испытаний. 1 з.п. ф-лы, 7 ил.

1. Способ моделирования напряженно-деформированного состояния авиационной панели, включающий нагружение масштабной модели в виде прямоугольной обшивки, соединенной дискретно на отдельных участках или непрерывно с продольными и поперечными силовыми наборами, отличающийся тем, что напряжение в панели в натуре σ_н определяют по формуле перехода от напряжений, измеренных в модели σ_м, к напряжениям в натуре: σ_н=σ_мк_р/(к_Iкδ), с учетом масштаба толщин кδ, причем кδ=к_h=к_t, где к_р=p_н/р_м - масштаб силового подобия; к_I=I_н/I_м - общий масштаб геометрического подобия; кδ=δ_н/δ_м - масштаб толщин; к_h=h_н/h_м - масштаб толщин обшивки; 2h_н - толщина обшивки натуры; 2h_м - толщина обшивки модели; K_t=tsн

/tsм - масштаб толщин силового набора; 2ts н- шиpинa контактной зоны элемента подкрепления в его поперечном сечении; 2tsм - шиpинa контактной зоны того же элемента у модели, а для идентичного напряженно-деформированного состояния натуры и модели принимают равными масштаб толщин обшивки и масштаб толщин силового набора, одинаковые граничные условия, произвольный общий масштаб геометрического подобия и равные относительные модули продольной упругости.2. Способ по п.1, отличающийся тем, что нагружение модели осуществляют растягивающими или сжимающими усилиями по торцам силового набора либо по кромкам обшивки с сохранением подобия распределения усилий по натуре.