Настоящее изобретение относится к области конструкций. Оно, в частности, касается конструкций типа усиленной панели и, более конкретно, таких панелей, которые армированы элементами жесткости. Изобретение относится к расчету сопротивления таких конструкций, подвергающихся комбинированным нагрузкам.
УРОВЕНЬ ТЕХНИКИ
Тонкие усиленные конструкции составляют подавляющую часть первичных конструкций выпускаемых самолетов.
Панели, в общем случае, армируются элементами жесткости, которые перпендикулярны друг другу и образуют прямоугольные зоны на обшивке панели, ограниченные элементами жесткости и именуемые карманами.
Таким образом, конструкция самолета рассматривается как скелет из элементов жесткости, снабженный обшивкой:
- продольные элементы жесткости (в общем случае, именуемые лонжеронами): они обеспечивают опору конструкции в главном направлении нагрузок,
- поперечные элементы жесткости (в общем случае, именуемые «рама» или "ребро"): их основной задачей является обеспечение поддержки лонжеронов,
- панель (в общем случае, именуемая обшивкой): как правило, она принимает нагрузку в плоскости (мембрана).
Лонжероны и стрингеры установлены под углом 90° друг другу и образуют прямоугольные карманы на обшивке.
Однако в течение 1950-х и 60-х годов, для конструкций космических кораблей, NASA разработало новый принцип усиленных конструкций под названием "изосетка" (см. фиг. 1).
Такая усиленная конструкция, таким образом, состоящая из армированной обшивки с сетью элементов жесткости, установленных под углом θ° (θ=60°, в конструкциях, рассматриваемых NASA) между ними. Элементы жесткости выполнены в форме пластин и встроены в панель. Вследствие своей геометрии, эта конфигурация обладает ортотропными свойствами (изотропными при θ=60°), и карманы, сформированные на обшивке, имеют треугольную форму.
В нижеследующем описании, термины «конструкция, усиленная треугольными карманами» или «панель, усиленная треугольными карманами» используются для определения конструкций или панелей, армированных пересекающимися элементами жесткости, образующими треугольные карманы.
В литературе имеются скудные данные для расчета сопротивления и устойчивости такой конструкции, усиленной треугольными карманами.
Традиционные способы расчета для панелей, усиленных треугольными карманами
Способ для аналитического расчета панелей, усиленных карманами в виде равносторонних треугольников, описан в «NASA Contract Report "Isogrid" design handbook» (NASA-CR-124075, 02/1973).
Этот способ тщательно задокументирован, но представляет ряд серьезных ограничений: использование только равносторонних треугольников: угол =60°, расчет прилагаемых напряжений, но без расчета допустимого напряжения, коэффициент Пуассона материала, равный только 1/3.
Традиционный способ представляет много ограничений и не позволяет учитывать все проблемы, с которыми приходится сталкиваться при проектировании самолета, в частности, касающиеся граничных условий и пластичности. Это не позволяет уверенно использовать его для аналитического расчета конструкции панелей, усиленных треугольными карманами.
ЗАДАЧИ ИЗОБРЕТЕНИЯ
Для осуществления структурного анализа панелей, усиленных треугольными карманами, разработан способ структурного анализа, основанный на теории композитной пластины и учитывающий ее конкретные разновидности разрушения. Этот способ применим к плоским панелям, выполненным из материала с изотропными свойствами.
Описанный здесь способ предусматривает изменение угла при основании между элементами жесткости (который равен 60° в “изосеточных” конструкциях). Это означает, что свойство изотропии панели уже не гарантируется.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Изобретение относится, в этом смысле, к способу задания размеров аналитическим методом, по существу, плоской панели, состоящей из однородного и изотропного материала, причем панель состоит из обшивки, армированной набором (именуемым “сеткой”) из трех параллельных пучков элементов жесткости, встроенных в панель, причем карманы, образованные на обшивке группами элементов жесткости, имеют треугольную форму, элементы жесткости выполнены в форме пластин, и усиленная панель должна соответствовать техническим условиям на механическое сопротивление заранее определенным внешним нагрузкам, углы между пучками элементов жесткости таковы, что треугольные карманы имеют форму любого равнобедренного треугольника.
Согласно одной преимущественной реализации, способ включает в себя этапы:
Этап 2 - расчета напряжений, прилагаемых в обшивке и элементах жесткости, а также потока в обшивке и нагрузок в элементах жесткости, на основании геометрии усиленной панели, и внешних нагрузок, предположительно находящихся в плоскости панели и приложенных в центре тяжести секции (панели), причем усиленная панель представляет собой сборку из двух ортотропных пластин, сетка элементов жесткости представляет собой эквивалентную панель.
Этап 3 - расчета внутренних нагрузок усиленной панели,
Этап 4 - анализа сопротивления, включающего в себя расчет коэффициентов запаса прочности материала при допустимой и предельной нагрузке,
Этап 5 - расчета допустимого локального напряжения,
Предпочтительно, способ предусматривает учет перераспределения прилагаемых напряжений между панелью и сеткой элементов жесткости вследствие:
остаточного коробления элементов жесткости, согласно определению эффективного прямого сечения для каждого типа элемента жесткости (0°, +θ или -θ), A0° st, A+θ st и A-θ st,
остаточного коробления кармана путем расчета эффективной толщины панели: ts_eff,
пластичности внешних нагрузок, посредством итерационного процесса над различными свойствами материала, в частности, модулем Юнга и коэффициентами Пуассона: E0° st, E+θ st, E-θ st для элементов жесткости и Ex s, Ey s и νep st для обшивки, с помощью закона Рамберга-Осгуда.
Согласно предпочтительной реализации способа, отвечающего изобретению, он включает в себя этап коррекции прилагаемых нагрузок для учета пластичности, с использованием итерационного метода для расчета пластических напряжений, осуществляемого, пока пять параметров материала (E0° st, E+θ st, E-θ st, Eskin, νep), введенные в начале процесса, по существу, не сравняются с соответствующими параметрами, полученными в результате расчета пластического напряжения.
Согласно преимущественной реализации, способ включает в себя этап 4, анализа сопротивления, содержащий расчет коэффициентов запаса прочности материала при допустимой и предельной нагрузке, выполняемый путем сравнения приложенных нагрузок, вычисленных в компонентах усиленной панели, с максимально допустимыми напряжениями материала, причем приложенные нагрузки корректируются с учетом пластичности усиленной панели.
Согласно преимущественной реализации, способ включает в себя этап 5 для расчета допустимого локального напряжения, который включает в себя подэтап 5A расчета допустимого потока коробления и коэффициента запаса прочности для карманов в виде равнобедренного треугольника, причем прилагаемые напряжения, подлежащие учету для расчета коэффициента запаса прочности, являются, только напряжениями, действующими на обшивку, причем используемые внешние потоки, будучи потоками, прилагаемыми к обшивке, не соответствуют усиленной панели, испытывающей полную нагрузку.
В этом случае, этап 5A расчета допустимого потока коробления и коэффициента запаса прочности для карманов в виде равнобедренного треугольника, предпочтительно, включает в себя два подэтапа: сначала, расчета допустимых значений для пластин, подвергающихся вариантам чистой нагрузки (сжатию в двух направлениях в плоскости, сдвиговой нагрузке), с использованием метода конечных элементов, затем вычисления кривых взаимодействия между этими вариантами чистой нагрузки.
В частности, расчет допустимых значений включает в себя следующие подэтапы, на которых:
- создают параметрическую модель FEM треугольной пластины,
- испытывают различные комбинации для получения результатов коробления,
- получают параметры, согласующиеся с аналитической полиномиальной формулой
В конкретном варианте реализации, в случае чистой нагрузки, кривые взаимодействия задаются на следующих подэтапах:
- создания моделей конечных элементов нескольких треугольных пластин с разными углами равнобедренного треугольника, причем угол (θ) равнобедренного треугольника определяется как угол при основании равнобедренного треугольника,
- для каждого угла равнобедренного треугольника:
1/ расчета посредством модели конечных элементов для определения допустимого потока складкообразования (без поправки на пластичность) для различных значений толщины пластины.
2/отслеживания кривой допустимого потока коробления согласно отношению 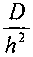 (D- жесткость пластины, h- высота треугольника), причем эта кривая определяется для малых значений
(D- жесткость пластины, h- высота треугольника), причем эта кривая определяется для малых значений 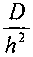 , уравнением второй степени согласно этому отношению, коэффициенты K1 и K2 которого зависят от угла и рассматриваемого варианта нагрузки,
, уравнением второй степени согласно этому отношению, коэффициенты K1 и K2 которого зависят от угла и рассматриваемого варианта нагрузки,
3/отслеживания постепенного изменения коэффициентов K1 и K2 полиномиального уравнения в соответствии с углом при основании равнобедренного треугольника, причем эти коэффициенты отслеживаются в соответствии с углом рассматриваемых треугольных пластин, и интерполяции для определения полиномиального уравнения, что позволяет вычислять константы при любом угле равнобедренного треугольника.
Опять же, в случае расчета допустимого потока коробления и коэффициента запаса прочности карманов в виде равнобедренного треугольника, согласно преимущественной реализации, в случае комбинированной нагрузки, используется следующая гипотеза: если некоторые компоненты комбинированной нагрузки напряжены, эти компоненты не учитываются при расчете, и кривые взаимодействия задаются на следующих подэтапах:
- создания моделей конечных элементов нескольких треугольных пластин с разными углами равнобедренного треугольника, причем угол (θ) равнобедренного треугольника определяется как угол при основании равнобедренного треугольника,
- для каждого угла,
1/ расчета посредством модели конечных элементов (FEM) для определения собственного значения коробления, соответствующего разным распределениям внешних нагрузок.
2/ отслеживания кривых взаимодействия, для каждого угла и каждой комбинации нагрузок и аппроксимации этих кривых с помощью одного уравнения, описывающего все эти комбинации:
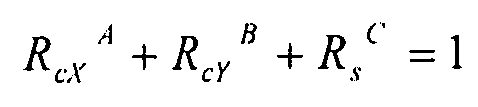 (или
(или 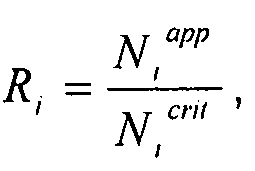 уравнения, в которых R
i представляет величину нагрузки, и N
i app и N
i crit - прилагаемые потоки и критические потоки для i=cX, cY или s, соответствующие вариантам сжатия по осям X и Y и согласно варианту сдвиговой нагрузки), где A, B, C - эмпирические коэффициенты.
уравнения, в которых R
i представляет величину нагрузки, и N
i app и N
i crit - прилагаемые потоки и критические потоки для i=cX, cY или s, соответствующие вариантам сжатия по осям X и Y и согласно варианту сдвиговой нагрузки), где A, B, C - эмпирические коэффициенты.
Преимущественно, способ также содержит подэтап расчета коэффициентов запаса прочности, путем решения следующего уравнения:
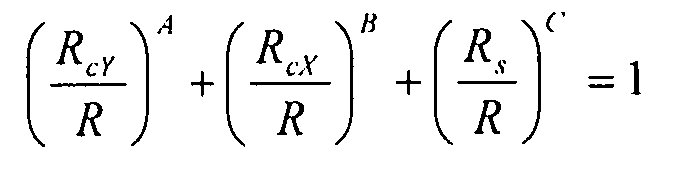 ,
,
где 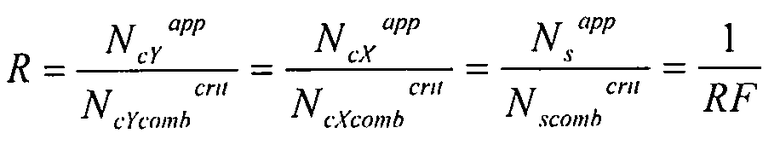 .
.
Согласно преимущественной реализации, способ использует, для расчета допустимого напряжения с поправкой на пластичность, коэффициент поправки на пластичность η, заданный следующим образом:
- для всех вариантов нагрузки (чистой и комбинированной) за исключением сдвиговой нагрузки,
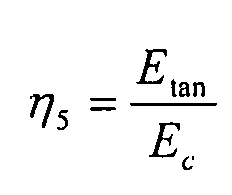
- для вариантов чисто сдвиговой нагрузки:
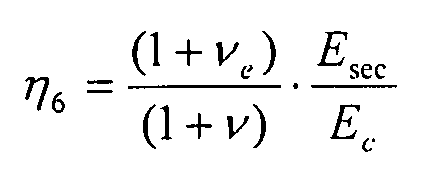
причем поправка на пластичность вычисляется с использованием эквивалентного упругого напряжения фон Мизеса.
Согласно преимущественной реализации, в случае свободно опирающихся или фиксированных пластин в виде равнобедренного треугольника, в случае комбинированной нагрузки, используется кривая взаимодействия: 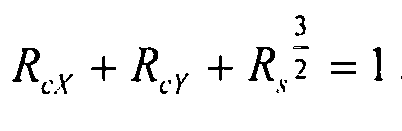 , для всех вариантов нагрузки.
, для всех вариантов нагрузки.
Согласно преимущественной реализации, способ включает в себя этап 5 для расчета допустимого локального напряжения, который включает в себя подэтап 5B расчета допустимого напряжения коробления и коэффициента запаса прочности для ребра элемента жесткости, рассматриваемого как прямоугольная панель, причем напряжения, прилагаемые для расчетов коэффициента запаса прочности, являются напряжениями, только в ребрах элементов жесткости.
Согласно преимущественной реализации способа, он включает в себя этап 6, расчета общей потери устойчивости, дающий данные по допустимому потоку коробления, и коэффициентов запаса прочности, для плоской усиленной панели, в условиях чистой или комбинированной нагрузки, причем прилагаемые потоки, подлежащие учету для расчета коэффициента запаса прочности, являются внешними потоками усиленной панели.
В этом случае, в частности, способ преимущественно включает в себя следующие подэтапы:
- использования общего закона поведения (уравнение 6-8), задающего соотношения потоков и моментов между потоком и моментами с одной стороны и деформациями с другой, причем рассматривается состояние напряжений в плоскости,
- использования общих уравнений баланса (уравнений 6-9 и 6-10) элемента усиленной панели, связывающих потоки, моменты и плотность поверхностной прочности,
- решения дифференциального уравнения общего вида (уравнения 6-17), связывающего потоки напряжения, плотность поверхностной прочности, деформации и изгиб элементов жесткости.
Согласно предпочтительной реализации, способ включает в себя этап итерации, позволяющий изменять значения прилагаемых напряжений или значения размеров панелей, согласно результатам, по меньшей мере, одного из этапов 3-6.
С другой стороны, изобретение относится к компьютерному программному продукту, включающему в себя ряд инструкций, предназначенных для реализации вышеописанного способа, причем этот набор инструкций выполняется на компьютере.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Нижеследующее описание, приведенное исключительно в порядке примера варианта осуществления изобретения, пользуется ссылками на прилагаемые чертежи, в которых:
фиг. 1 - пример плоской панели, усиленной треугольными карманами,
фиг. 2 - определение нагрузки и системы координат,
фиг. 3 - геометрическое определение панели
фиг. 4 - соединение в конструкции, усиленной треугольными карманами,
фиг. 5 - пример общей потери устойчивости панели, усиленной треугольными карманами,
фиг. 6 - теория эффективной ширины,
фиг. 7 - общая блок схема способа согласно изобретению,
фиг. 8 - разложение сетки на элементарные треугольники,
фиг. 9 - элементарный равнобедренный треугольник, используемый при расчете массы панели,
фиг. 10 - элементарный прямоугольный треугольник, используемый при расчете массы панели,
фиг. 11 - элементарная форма сетки элементов жесткости в панели, усиленной треугольными карманами,
фиг. 12 - случай чистых нагрузок усиленной пластины,
фиг. 13 - схема нагрузок на элемент жесткости,
фиг. 14 - выражение коэффициентов Kc в зависимости от вариантов граничных условий,
фиг. 15 - панель элементов жесткости, рассматриваемая как сборка из двух ортотропных пластин,
фиг. 16 - нагрузки на элементарную форму сетки элементов жесткости для панели, усиленной треугольными карманами,
фиг. 17 - способ расчета приложенных нагрузок с поправкой на пластичность,
фиг. 18 - соглашения по системе обозначений элементарного равнобедренного треугольника,
фиг. 19 - A линейная или квадратичная интерполяция коэффициента K,
фиг. 20 - случай комбинированной нагрузки,
фиг. 21 - соглашения по потоку и моментам,
фиг. 22 - значение 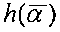 согласно различным граничным условиям, в случае сжатия,
согласно различным граничным условиям, в случае сжатия,
фиг. 23 - коэффициент коробления при сдвиге для четырехсторонней свободно опирающейся конфигурации,
фиг. 24 - таблица значений коэффициента коробления при сдвиге,
фиг. 25 -коэффициент коробления при сдвиге для фиксированной с четырех сторон конфигурации,
фиг. 26 - постепенное изменение константы K1 в зависимости от угла равнобедренного треугольника для свободно опирающейся треугольной пластины,
фиг. 27 - постепенное изменение константы K2 в зависимости от угла равнобедренного треугольника для свободно опирающейся треугольной пластины,
фиг. 28 - постепенное изменение константы K1 в зависимости от угла равнобедренного треугольника для фиксированной треугольной пластины,
фиг. 29 - постепенное изменение константы K2 в зависимости от угла равнобедренного треугольника для фиксированной треугольной пластины,
ПОДРОБНОЕ ОПИСАНИЕ ВАРИАНТА ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Описанный способ анализа сопротивления, в основном, плоской, металлической панели, усиленной треугольными карманами, подлежит реализации в форме программы на компьютере известного типа.
Способ подлежит реализации для, в основном, плоской конструкции (элементы жесткости и обшивка). Описанный здесь способ применяется исключительно для расчета типичных структурных параметров со следующими ограничениями:
Края исследуемой зоны не граничат с отверстием.
Ни один из элементов жесткости не выходит за пределы исследуемой зоны.
Каждое сечение должно быть ограничено элементами жесткости.
Предполагается, что все треугольные карманы в обшивке имеют одинаковую толщину.
Предполагается, что все элементы жесткости имеют одинаковые размеры.
Этот способ используется для расчета панелей, построенных из однородного и изотропного материала (например, но без ограничения, металла), для которого описательные монотонно возрастающие кривые (σ, ε) можно идеализировать согласно таким формулам, как R&O (см. ниже).
На фиг. 7 изображена упрощенная блок схема способа, отвечающего изобретению.
В конструкции, усиленной треугольными карманами, может происходить два типа разрушения (возникновение которого оценивается на этапах 4 и 6 способа): дефект материала (который является объектом этапа 4): прилагаемые напряжения достигли максимально допустимого напряжения материала (Ftu или Fsu), общее разрушение: общее коробление (в том числе, сетки элементов жесткости) происходит на всей панели (эта верификация является объектом этапа 6).
Кроме того, два типа потери устойчивости (объект этапа 5) снижают общую жесткость конструкции, усиленной треугольными карманами, но не приводят к общему разрушению конструкции в целом:
потеря устойчивости панели: коробление треугольных карманов
потеря устойчивости элементов жесткости: коробление ребер элементов жесткости
Покоробленные секции могут выдерживать только часть нагрузки, которую они выдерживали до коробления. Таким образом, в конструкции происходит перераспределение приложенных нагрузок.
Заметим, что, согласно настоящему изобретению, расчет остаточного коробления не рассматривается. Таким образом, вышеописанные два типа коробления рассматриваются как разновидности разрушения.
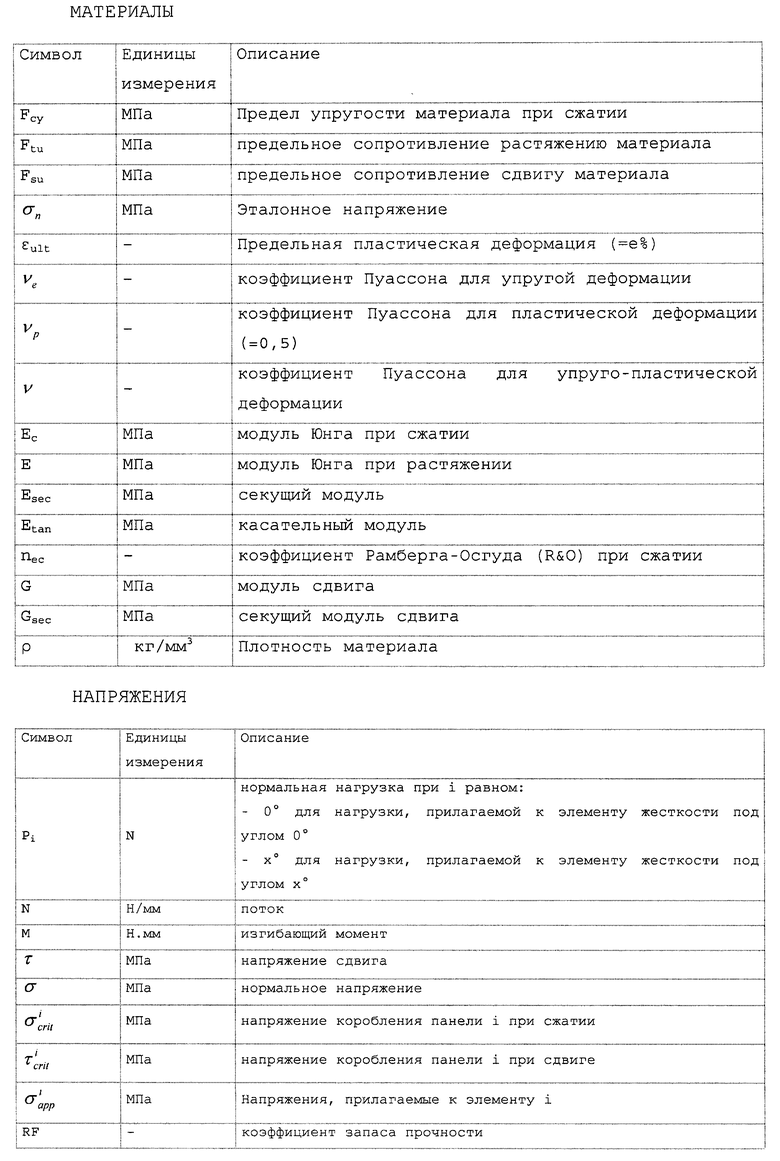
СИСТЕМА ОБОЗНАЧЕНИЙ И ЕДИНИЦЫ ИЗМЕРЕНИЯ
На фиг. 2 поясняются соглашения по условным обозначениям и системам координат.
Для каждого элемента жесткости задана локальная система координат. Ось x задана в плоскости прямого сечения элемента жесткости, это ось выхода, в направлении главного размера элемента жесткости. Ось z задана как ось, нормальная к плоскости обшивки, в направлении элемента жесткости. Наконец, ось y является третьей осью в прямолинейной системе координат.
Для сил и нагрузок, отрицательный знак силы по оси x означает сжатие элемента жесткости, положительный знак означает растяжение.
Положительный изгибающий момент вызывает сжатие в обшивке и растяжение в элементах жесткости.
Общие условные обозначения, используемые в данной заявке, приведены в следующей таблице.
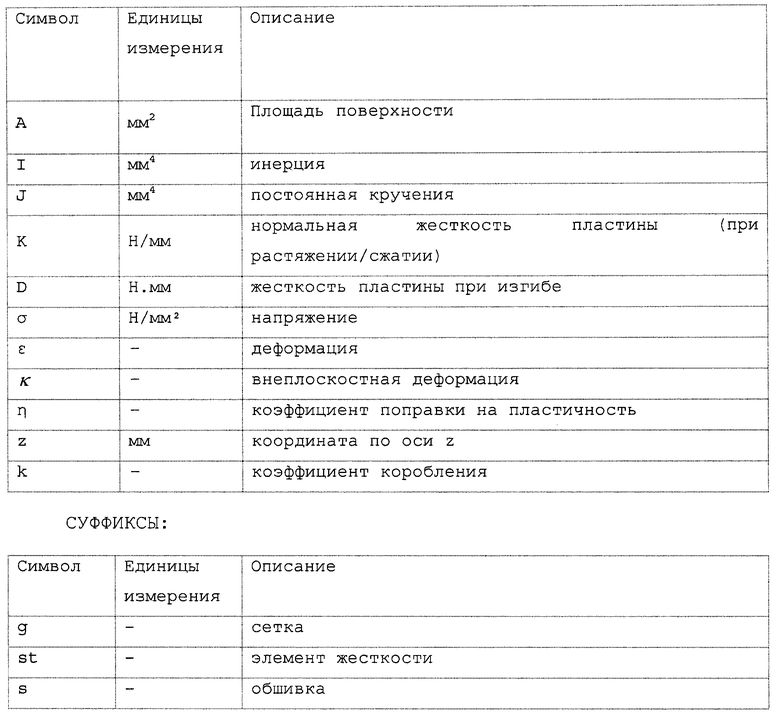
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Геометрические характеристики панели, рассмотренной здесь в порядке неограничительного примера, представлены на фиг. 3.
Для остального описания используется несколько гипотез. Предполагается, что ось z является плоскостью симметрии для прямого сечения элемента жесткости. Кроме того, размеры a и h заданы согласно нейтральному волокну элемента жесткости. Кроме того, рассматриваемая панель, усиленная треугольными карманами, не имеет элементов жесткости на двух сторонах, заданных уравнениями: X=0 и X=Lx
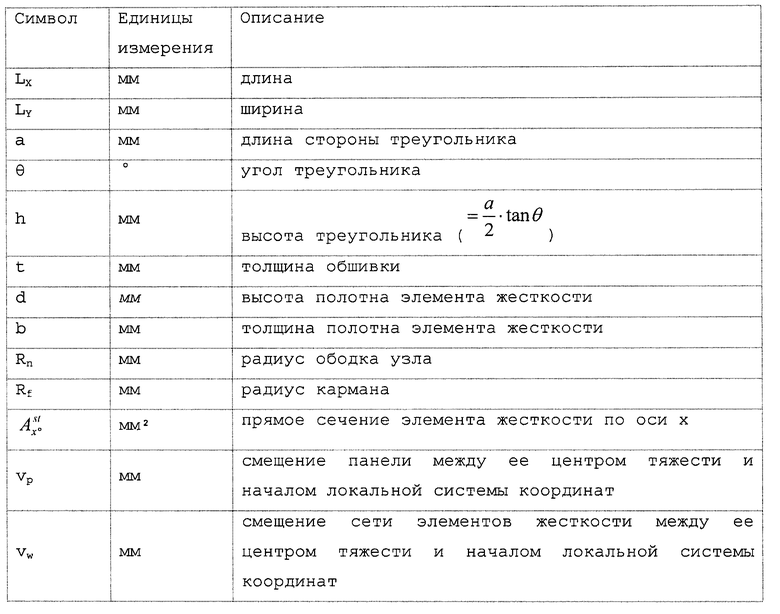

ОПРЕДЕЛЕНИЯ
Для остального описания заданы следующие термины.
В конструкции, усиленной треугольными карманами, сеткой называется полная сеть отдельных элементов жесткости.
Термин «узел» используется для описания пересечения нескольких элементов жесткости в конструкции, усиленной треугольными карманами (см. фиг. 4). На практике, это элемент сложной конструкции, имеющий радиусы кривизны в двух направлениях.
Когда конструкция (испытывающая нагрузки только в своей плоскости) проявляет значительные, видимые поперечные смещения нагрузок в плоскости, это называется короблением. На фиг. 5a показан такой случай локальной потери устойчивости панели, усиленной треугольными карманами.
Явление коробление можно продемонстрировать, нажимая на противоположные стороны плоского листа картона, с целью приблизить их друг к другу. Для малых нагрузок, коробление является упругим (обратимым), поскольку оно исчезает при устранении нагрузки.
Локальное коробление (или локальная потеря устойчивости) пластин или обшивок проявляется в возникновении выпуклостей, или волн и типично для пластин, составляющих тонкие конструкции. При рассмотрении усиленных панелей, локальное коробление, в отличие от общего коробления, описывает потерю устойчивости, при которой панель между лонжеронами (элементами жесткости) коробится, но элементы жесткости продолжают поддерживать панели и не демонстрируют сколько-нибудь значительных внеплоскостных деформаций.
Таким образом, конструкция может представлять два состояния равновесия:
устойчивое: в этом случае, смещения увеличиваются контролируемым образом с ростом нагрузок, т.е. можно говорить о том, что способность конструкции выдерживать дополнительные нагрузки сохраняется, или
неустойчивое: в этом случае, деформации мгновенно возрастают, и способность выдерживать нагрузки резко снижается
Теоретически, при короблении возможно также нейтральное равновесие, это состояние характеризуется увеличением деформации в отсутствие изменения нагрузки.
При слишком больших деформациях коробления конструкция разрушается. Если велика вероятность того, что компонент или часть компонента испытывает коробление, то ее концепция должна согласовываться с напряжениями, связанными как с сопротивлением, так и короблением.
Общая потеря устойчивости это явление, которое имеет место, когда элементы жесткости больше не способны противодействовать внеплоскостным смещениям панели при короблении.
На фиг. 5b показан пример общего коробления при сжатии конструкции, усиленной треугольными карманами, когда панель входит в первый режим общего коробления.
Таким образом, необходимо определить, действуют ли элементы жесткости как простые опоры панели (при сжатии, сдвиговой нагрузке и комбинированной нагрузке). Если это условие не выполняется, разумно предположить, что сборка панели и элементы жесткости испытывают общее коробление в режиме потери устойчивости, чего следует избегать при проектировании конструкций, используемых в авиации.
Общее (или глобальное) разрушение происходит, когда конструкция больше не способна выдерживать дополнительные нагрузки. В этом случае, можно сказать, что конструкция достигла разрушающей нагрузки или предельной нагрузки.
Общее разрушение охватывает все типы разрушений:
- разрушение вследствие потери устойчивости (общей потери устойчивости, остаточного коробления)
- разрушение, вызванное превышением максимальной нагрузки, выдерживаемой материалом (например, после локального коробления).
Эффективная ширина (или рабочая ширина) обшивки панели определяется как участок обшивки, который поддерживается лонжероном в конструкции усиленной панели, которая не испытывает коробления под действием осевой сжимающей нагрузки.
Само по себе коробление обшивки не означает разрушение панели; фактически панель будет выдерживать дополнительные нагрузки, пока напряжение не достигнет величины, при которой стойка, образованная элементом жесткости и эффективной панелью, начнет разрушаться. Когда напряжение в элементе жесткости превышает напряжение коробления обшивки, обшивка рядом с элементом жесткости выдерживает дополнительное напряжение благодаря опоре, обеспеченной элементами жесткости. Однако напряжение в центре панели не превышает начальное напряжение коробления, при любом напряжении на уровне элемента жесткости.
Обшивка более эффективна вокруг положения элементов жесткости благодаря наличию локальной опоры, препятствующей короблению. При данном уровне напряжения, более низком, чем напряжение локального коробления обшивки, эффективная ширина равна ширине панели. Теория эффективной ширины изображена на фиг. 6.
ИДЕАЛИЗАЦИЯ МАТЕРИАЛА
Здесь следует заметить, что вплоть до достижения предела текучести (Fcy), кривая напряжение-деформация материала идеализируется известным законом Рамберга-Осгуда (именуемым в остальном описании формулой R&O):
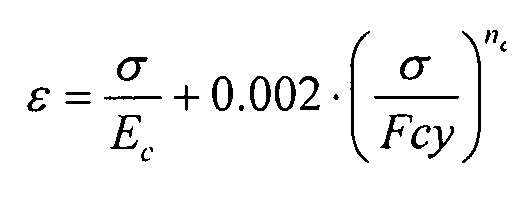 уравнение 0-1
уравнение 0-1
Можно вывести следующие выражения:
секущий модуль:
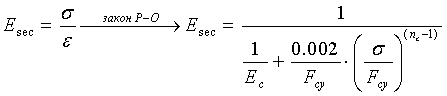
уравнение 0-2
касательный модуль

уравнение 0-3
коэффициент Пуассона:
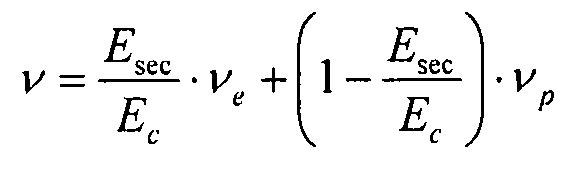 , где
, где 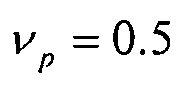
уравнение 0-4
Заметим, что, для отношения R&O (параметра n или скорректированного n), известного специалистам в данной области техники, эти уравнения корректируются только в зоне [0; Fcy]. Для следующей части этого исследования, эту зону нужно продлить с Fcy до Ftu. Сверх Fcy, можно использовать разные кривые вплоть до предельного напряжения, в частности: формулу R&O с использованием модифицированного коэффициента n, или эллиптический метод.
В дальнейшем, формула R&O использует измененный коэффициент. Поддерживается неразрывность между двумя кривыми. Измененный коэффициент n в формуле R&O вычисляется следующим образом:
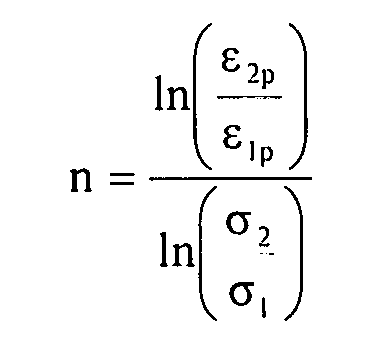 уравнение 0-5,
уравнение 0-5,
где:
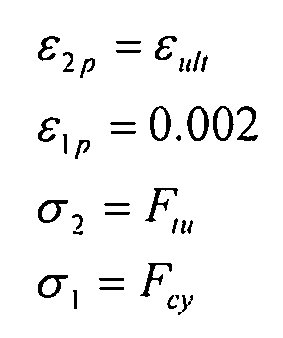
заметим, что для использования этой формулы, должно выполняться следующее условие: Ftu>Fcy и εult >0,002
Согласно эллиптическому методу, в случае превышения Fcy, используется другая кривая вплоть до предельного напряжения: кривая эллиптического удлинения. Естественно, гарантируется неразрывность между кривой R&O и кривой эллиптического удлинения.
Отношения напряжение/деформация эллиптического удлинения таковы:
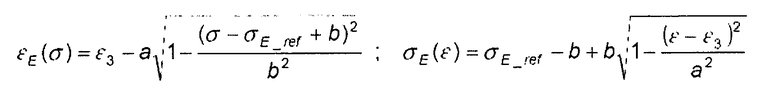
уравнение 0-6,
где:
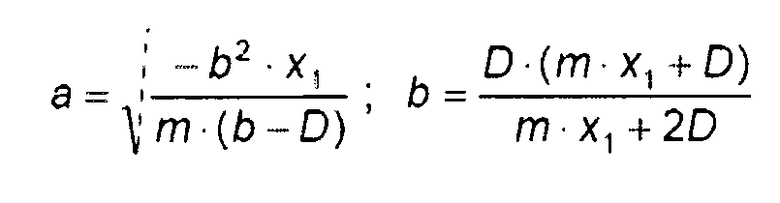 - параметры эллипса
- параметры эллипса
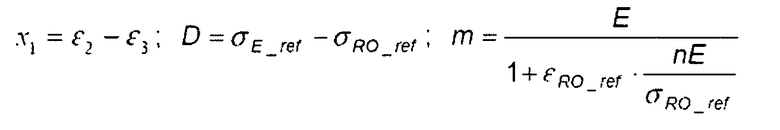
ПЛАСТИЧНОСТЬ
Снова заметим, что известно, что коэффициенты поправки на пластичность зависят от типа нагрузки и граничных условий.
Коэффициенты поправки на пластичность для плоских прямоугольных панелей представлены в нижеследующей таблице 1.
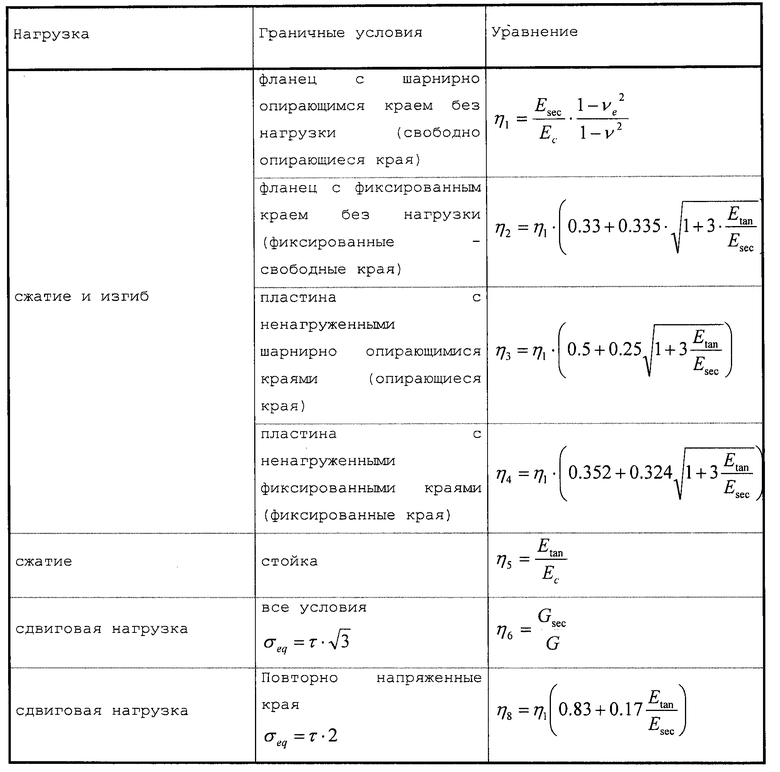
В конкретном случае сдвиговой нагрузки, кривая напряжение - деформация при сжатии материала также используется для:
расчета эквивалентного нормального напряжения: 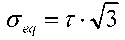
расчет соответствующих значений Es и ν на основании этого напряжения: 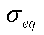
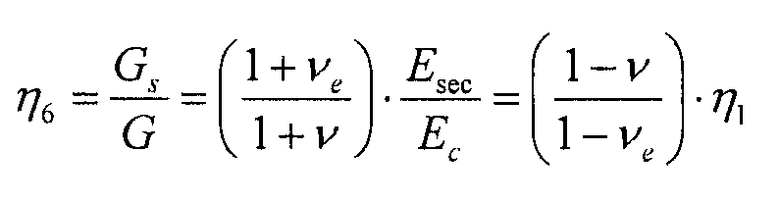
Этап 1 - модуль ввода данных: геометрия, материал, нагрузка
Способ включает в себя первую фазу ввода данных, относящихся к рассматриваемой панели, усиленной треугольными карманами, и к нагрузке, прилагаемой к этой панели. Эти данные вводятся с использованием известных средств и сохраняются в базе данных, также известного типа.
Входные параметры для аналитического расчета панелей, усиленных треугольными карманами, в частности, включают в себя:
Общие размеры: прямоугольная панель (размеры: Lx, Ly)
прямое сечение элементов жесткости: размеры ребра: b, d
постоянная толщина панели (t)
границы нагрузки панели Nx, Ny, Nxy
расчет массы
Эта часть предназначена для полного расчета массы панели, усиленной треугольными карманами, в том числе, с учетом радиусов ободка и узла. Этот этап расчета массы не зависит от остального описанного здесь способа. Масса вычисляется известным способом с использованием геометрического определения панели.
Данные, вводимые для этого процесса, представляют собой геометрию панели, включая радиусы карманов и узлов (Rn и Rf). Выходными данными является масса панели.
Масса вычисляется суммированием массы обшивки и лонжеронов. Также учитываются радиусы гребней между двумя лонжеронами и между обшивкой и лонжеронами. Расчет массы основан на двух элементарных треугольниках: равнобедренном треугольнике и прямоугольном треугольнике (см. фиг. 8, 9 и 10).
Этап 2 - расчет приложенных нагрузок
Этот этап позволяет вычислять напряжения, прилагаемые в обшивке и элементах жесткости, на основании геометрии панели, усиленной треугольными карманами, и внешних нагрузок. Способ предусматривает учет поправки на пластичность приложенных нагрузок, произведенной с использованием итерационного процесса. Это позволяет учитывать остаточное коробление элементов жесткости и карманов.
Это представляет существенный прогресс по отношению к «NASA "Isogrid" design handbook» (NASA-CR-124075, 02/1973), поскольку, в частности, принимает во внимание следующие моменты: сетка элементов жесткости с θ≠60, панель, усиленная треугольными карманами, рассматриваемая как сборка из двух ортотропных пластин.
Входные данные на этом этапе представляют собой:
Геометрические данные:
θ: угол при основании треугольника,
a: основание треугольника,
Ai st: прямое сечение элемента жесткости, i=0°, θ или -θ.
ts: толщина обшивки,
tg: толщина панели, эквивалентной сетке
Данные по материалу:
Ex s , Ey s: модуль Юнга обшивки,
Gxy s: модуль сдвига обшивки,
νxy s, νyx s: коэффициент Пуассона обшивки,
Est : модуль Юнга элементов жесткости,
νst : коэффициент Пуассона элементов жесткости
данные материала (n: коэффициент Рамберга-Осгуда, Fcy, Ftu, νplast =0,5)
нагрузки, прилагаемые к конструкции (Nx 0, Ny 0, Nxy 0)
Данные, получаемые в результате выполнения этого этапа, представляют собой:
Nx s, Ny s, Nxy s: поток в обшивке,
σx s, σy s, σxy s: напряжения в обшивке,
σ0°, σθ, σ-θ: напряжения в элементах жесткости,
F0°, Fθ, F-θ: нагрузки в элементах жесткости.
В следующей части описания предполагается, что обшивка выполнена из изотропного материала.
Способ предусматривает входные данные для:
анализа сопротивления (этап 4): напряжений в обшивке и в элементах жесткости
анализа коробления карманов (этап 5.1): напряжений в обшивке
анализа коробления элементов жесткости (этап 5.2): напряжения в элементах жесткости
анализа общей потери устойчивости (этап 6): напряжений в обшивке и в элементах жесткости для расчета жесткости при изгибе панели, усиленной треугольными карманами.
Способ расчета требует входных данных по остаточному короблению элементов жесткости: A0° st, A+θ st и A-θ st и по остаточному короблению карманов: ts_eff
способ учитывает перераспределения прилагаемых напряжений между панелью и сеткой элементов жесткости вследствие в первом случае, остаточного коробления элементов жесткости, согласно определению эффективного прямого сечения для каждого типа элемента жесткости (0°, +θ или -θ): A0° st , A+θ st и A-θ st, и, во втором случае, остаточного коробления кармана через эффективную толщину панели: ts_eff, наконец, пластических деформаций, вызванных приложением внешних нагрузок, с использованием итерационного процесса над разными свойствами материала: E0° st, E+θ st, E-θ st для элементов жесткости и Ex s, Ey s и νep st для обшивки.
Внешняя нагрузка, предположительно, лежит в плоскости панели и прилагается в центре тяжести сечения:
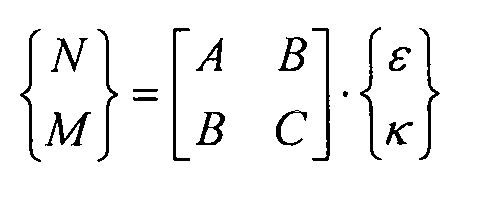
поэтому: ε≠0 и κ=0 →, где 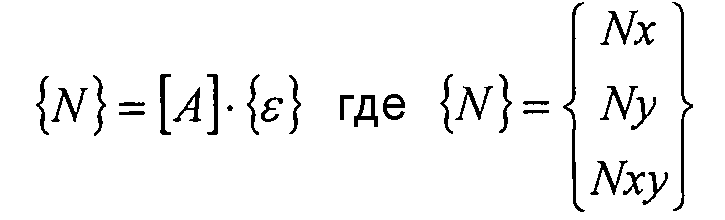
Таким образом, напряжения в обшивке не зависят от толщины обшивки и положения в плоскости. Кроме того, напряжения в элементах жесткости не зависят от положения на сечении элемента жесткости, но только от угла элемента жесткости.
Геометрическое определение сетки элементов жесткости, используемое для производства вычислений, приведено на фиг. 11:
для получения панели, усиленной треугольными карманами, эта элементарная форма связывается с обшивкой, и повторяется необходимое число раз. Таким образом, этот способ не позволяет учитывать принцип геометрии краев.
Для каждого элемента жесткости, реальное сечение (Ai st при i: 0°, +θ или -θ) задано коэффициентом: 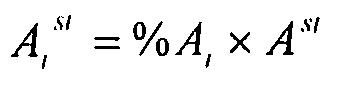 (в данном неограничительном примере рассматривается только случай
(в данном неограничительном примере рассматривается только случай 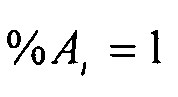 .
.
Прямое сечение элементов жесткости включает в себя сечение радиуса кармана 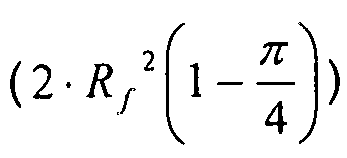 .
.
Независимо от их положения на сетке, напряжения и деформации одинаковы для каждого типа элемента жесткости (0°, +θ, -θ).
Для учета пластической деформации, которая может происходить в каждом элементе жесткости, существует отдельный модуль Юнга для каждого типа элемента жесткости (0°, +θ, -θ): 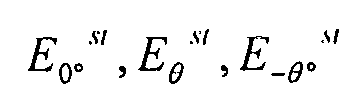 .
.
“Материальная” матрица E задана в виде:
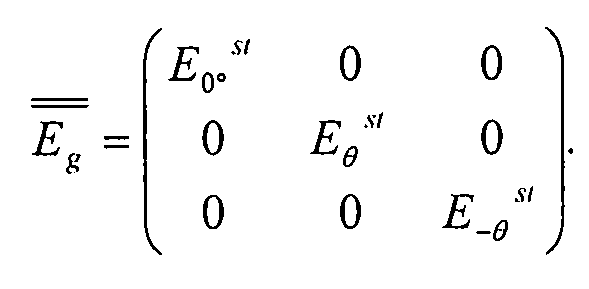
Этап 3 - расчет внутренних нагрузок
3.1 Пластина, эквивалентная элементам жесткости
3.1.1 Соотношение между глобальными деформациями и деформациями элементов жесткости
Геометрические условные обозначения и соглашения проиллюстрированы на фиг. 16. Мы ищем соотношение между (εx, εy, εxy) и (ε0°, εθ, ε-θ). Общие деформации заданы следующими формулами:
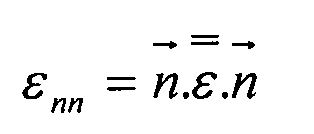
Поэтому деформации таковы:
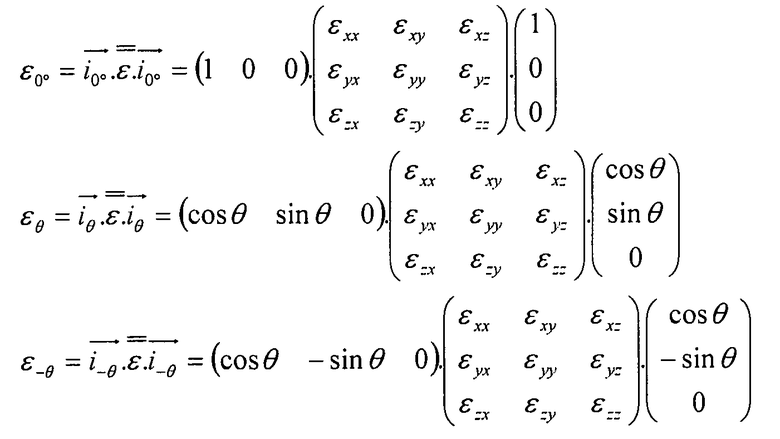
И наконец:
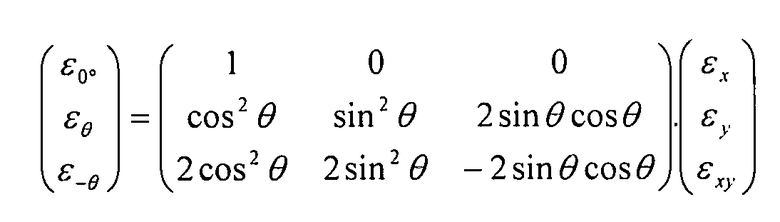
Уравнение 3-1
Вышеприведенная матрица обозначается Z:
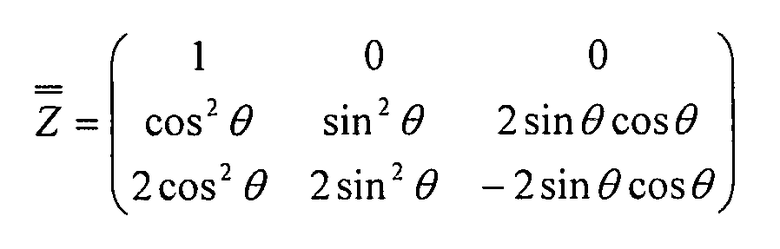
3.1.2 Соотношение между напряжениями и деформациями
Как было сказано, геометрические условные обозначения и соглашения проиллюстрированы на фиг. 16. Нагрузки в элементах жесткости заданы следующими выражениями:
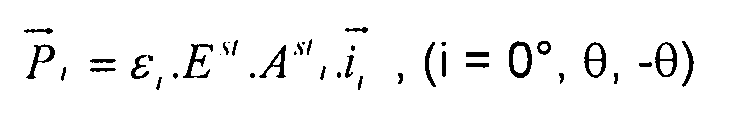 ,
,
Уравнение 3-2
Таким образом, базовый элемент подвергается следующим нагрузкам: 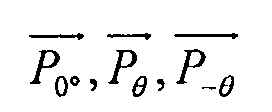 (
(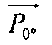 учитывается два раза, поскольку размер базового элемента по оси Y равен 2h, поэтому элемент жесткости, соответствующий углу 0°, также следует учитывать).
учитывается два раза, поскольку размер базового элемента по оси Y равен 2h, поэтому элемент жесткости, соответствующий углу 0°, также следует учитывать).
По оси x:
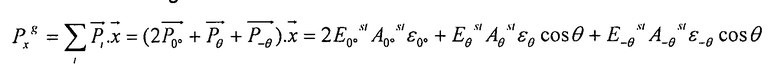
По оси y:
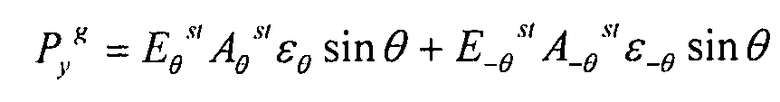
Сдвиговая нагрузка в плоскости 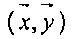 :
:
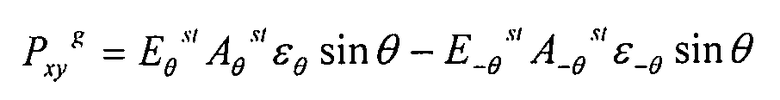
Уравнение 3-3
Для получения напряжений, нагрузка делится на площадь поверхности базового элемента. Сечение базового элемента на нормальной поверхности по оси X равно 2htg=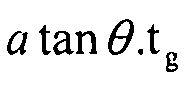 . Сечение базового элемента на нормальной поверхности по оси Y равно atg.
. Сечение базового элемента на нормальной поверхности по оси Y равно atg.
В отношении напряжений, имеем:
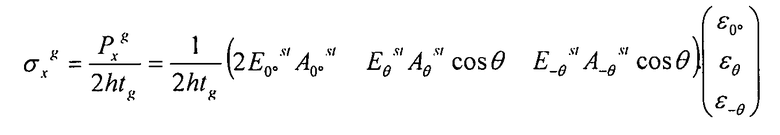
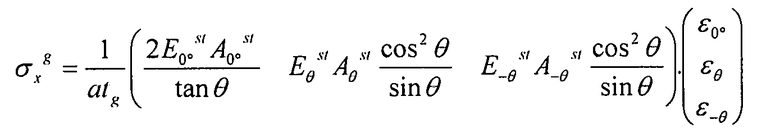
Для σy и νxy, получаем тем же способом:
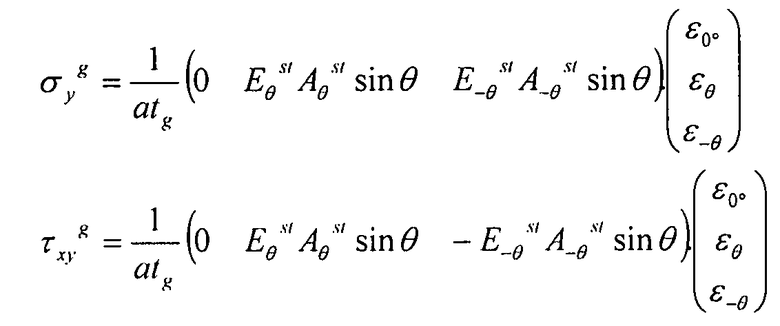
Те же результаты можно представить в матричной форме:
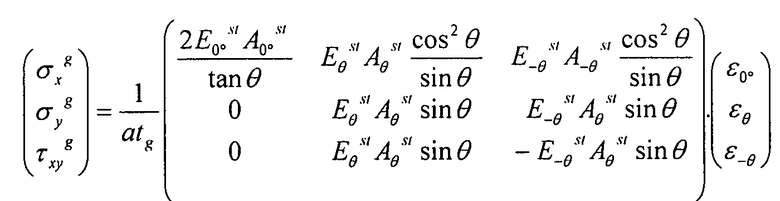
Уравнение 3-4
Вышеприведенная матрица обозначается T:
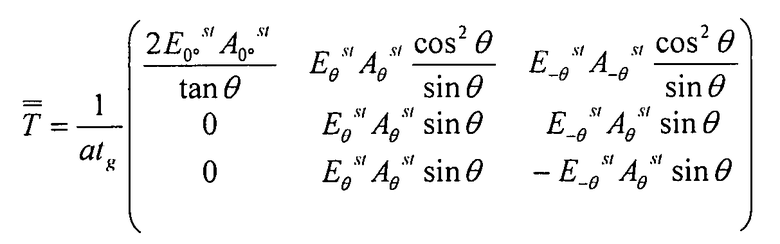
Таким образом, используя уравнение 3-1 и обозначение матрицы Z, получаем:
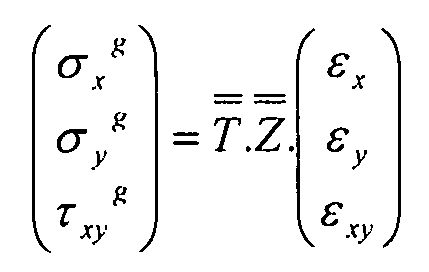
Уравнение 3-5
Вышеприведенная матрица обозначается W: 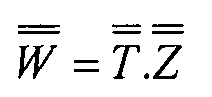
Это соотношение (уравнение 3-5) означает, что панель, эквивалентная элементам жесткости ведет себя аналогично анизотропному материалу (матрица W может быть заполнены: все ее элементы имеют ненулевые значения).
3.2 Усиленные панели
Мы используем гипотезу Кирхгофа: плоские сечения остаются плоскими после деформации. Сеть элементов жесткости моделируется эквивалентной панелью, ведущей себя согласно матрице W (см. уравнение 3-5). Этот подход моделирования панели, усиленной треугольными карманами, двумя ортотропными пластинами представлен на фиг. 15.
Для расчета νyx, имеем: 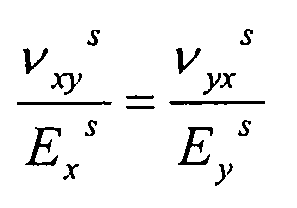
3.2.1. Напряжения и нагрузки элементов жесткости
Поток в панели, эквивалентной элементам жесткости
Общее выражение потоков таково:
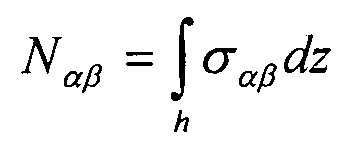
Уравнение 3-6
Поток по оси X выражается следующим образом:
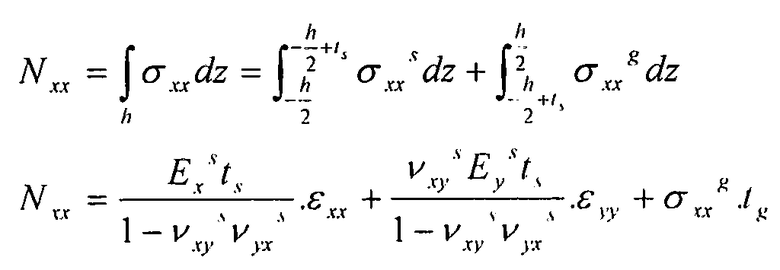
с использованием уравнения 3-5:
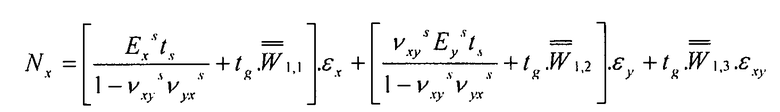
и, с использованием того же способа для потоков Ny и Nxy.
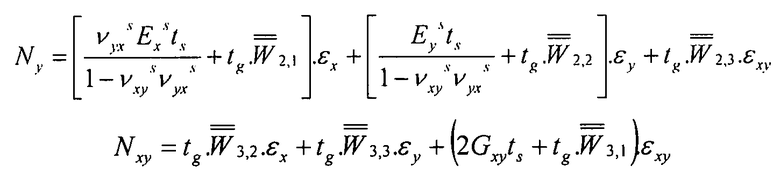
Уравнение 3-7
Эти выражения отчетливо демонстрируют распределение потока между обшивкой и панелью, эквивалентной элементам жесткости. В обшивке, соотношение между потоками и деформациями таково:
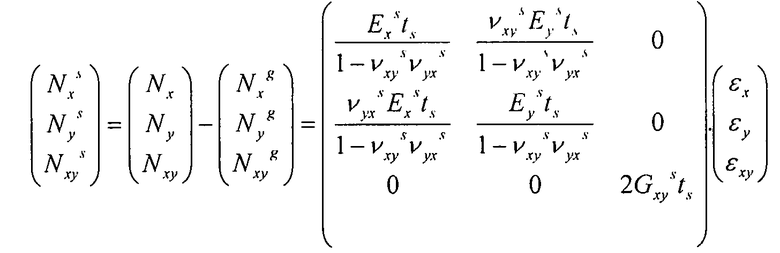
Уравнение 3-8
Обозначим X вышеприведенную матрицу:
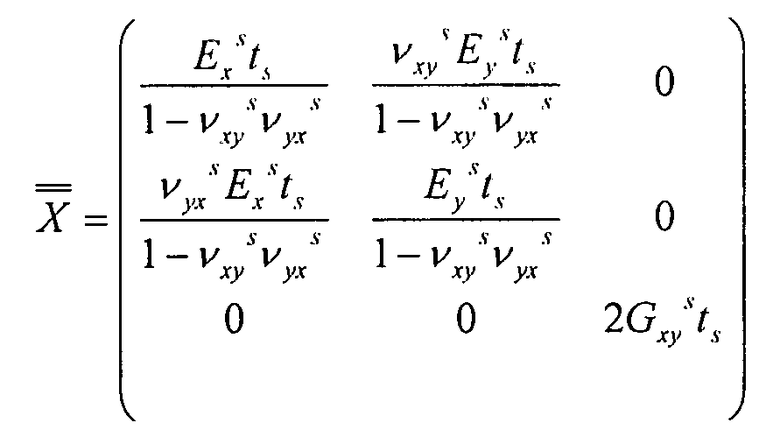
Таким образом:

Уравнение 3-9
Обратив это соотношение, потоки в сетке можно выразить согласно общим прилагаемым потокам:
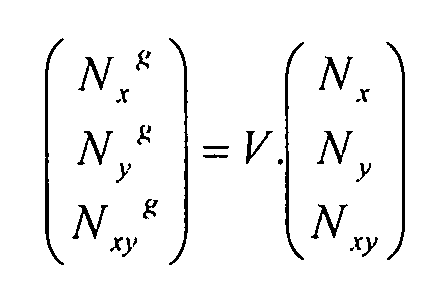
Уравнение 3-10,
где: 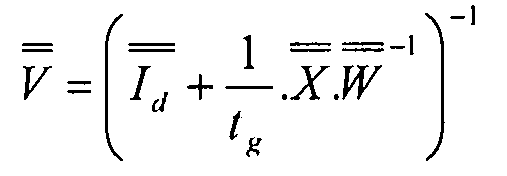 (
(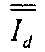 - единичная матрица)
- единичная матрица)
Напряжения и нагрузки в элементах жесткости
Поток в панели, эквивалентной элементам жесткости можно выразить в виде:
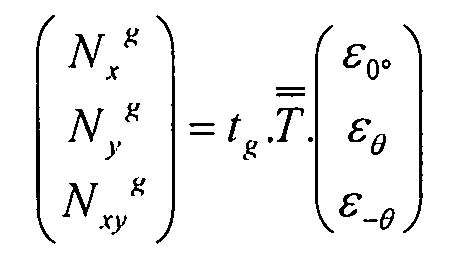
Уравнение 3-11
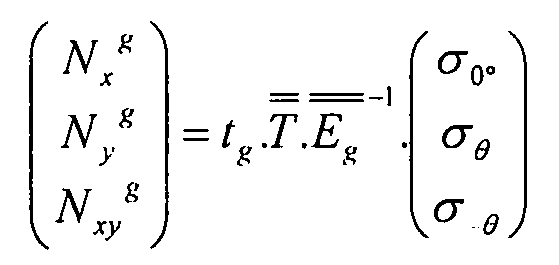
Уравнение 3-12
Используя следующую систему обозначений: 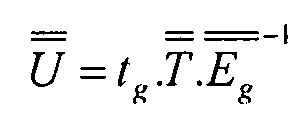 , имеем:
, имеем:
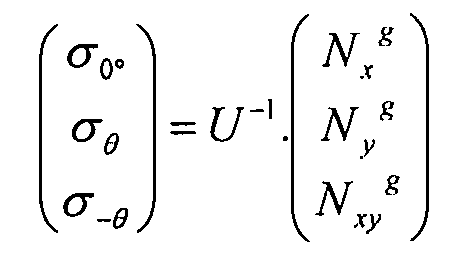
Уравнение 3-13
Наконец, нагрузки и напряжения в элементах жесткости выражаются согласно потокам внешних нагрузок:
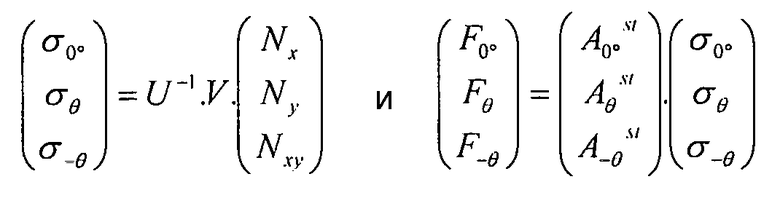
Уравнение 3-14
3.2.2 Потоки и напряжения в обшивке
Согласно уравнению 3-8, потоки в обшивке выражаются следующим образом:
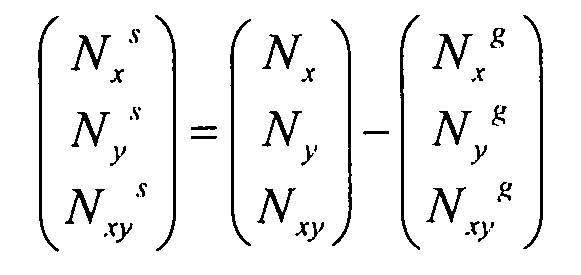
Уравнение 3-15
Таким образом, напряжения в обшивке выражаются в виде:
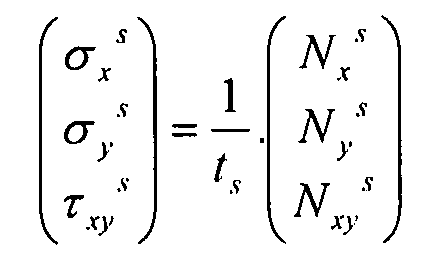
Уравнение 3-16
3.3 Способ расчета приложенных нагрузок с поправкой на пластичность представлен здесь со ссылкой на матрицы, введенные в описании (фиг. 17).
Заметим, что теория, используемая для расчета пластичности, предполагает свойство изотропии обшивки, которая образует обшивку. Решение для приложенных нагрузок с поправкой на пластичность обеспечивается методом итераций.
Процесс схождения должен осуществляться, пока пять параметров материала (E0° st, E+θ st, E-θ st, Eskin, νep), введенные в начале итерационного процесса, не сравняются с соответствующими параметрами, вычисленными на выходе (после расчета пластического напряжения). На упомянутой фиг. 17 параметры схождения указаны серым фоном.
В частности, в этом итерационном процессе, первоначально вводятся нагрузки, прилагаемые к сетке элементов жесткости и к обшивке.
Для сетки элементов жесткости, данные i-й итерации модуля Юнга элементов жесткости E0° st, E+θ st, E-θ st в 3 направлениях: 0°, +θ, -θ, позволяют, совместно со значением угла θ и геометрией, вычислить матрицу [T] (уравнение 3-4). Значения угла θ и геометрия, дают матрицу [Z] (уравнение 3-1). Матрицы [T] и [Z] задают матрицу [W] (уравнение 3-5).
Для обшивки, данные материала изотропной обшивки Eskin, νep) позволяют вычислить матрицу [X] (уравнение 3-8).
Матрицы [W] и [X] позволяют вычислить матрицы [U] (уравнение 3-13) и [V] (уравнение 3-10).
Результаты, полученные из этих матриц, включают в себя: потоки, упругие напряжения, поправки на пластичность для напряжений, значения (i+1)-й итерации модуля Юнга скорректированных элементов жесткости и обшивки, и коэффициента Пуассона скорректированной обшивки, и нагрузки в элементах жесткости.
Очевидно, что расчет повторяется, пока значение изменения модуля Юнга и коэффициентов Пуассона в ходе итерации не станет меньше заранее определенного порога.
Влияние поправки на пластичность на расчет общего коробления
Естественно, поправка на пластичность вносит изменение в матрицу закона поведения, вычисленную в модуле общей потери устойчивости через 5 параметров материала (см. раздел, посвященный общей потере устойчивости).
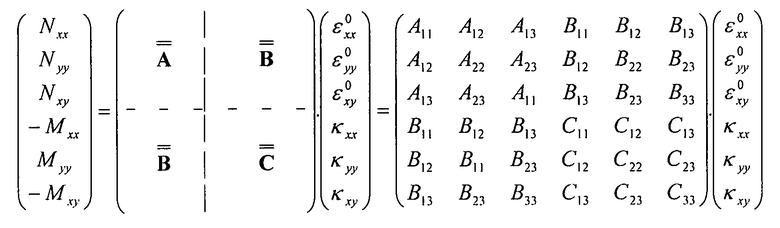
Уравнение 3-17
Таким образом, поправка на пластичность также изменяет коэффициенты Ωi (i=1, 3), используемые для расчета общего коробления. Поправка на пластичность в анализе общего коробления обеспечивается этими измененными коэффициентами Ωi.
3.4 Пример: распределение нагрузок в условиях двухосной сжимающей нагрузки и сдвиговой нагрузки
На этапе расчета прилагаемых напряжений учитывается радиус гребня кармана для расчета сечения элемента жесткости. Кроме того, остаточное коробление отсутствует, что позволяет записать:
%A0° st=%A+ө st=%A-ө st =100%
ts_eff=ts
В описанном здесь неограничительном примере, геометрия панели, усиленной треугольными карманами, задана как:
Lx=1400,45 мм a=198 мм радиус узла: Rn=9 мм
Ly=685,8 мм t=3,64 мм радиус кармана: Rf =4 мм
θ=58° b=2,5 мм d=37,36 мм
Рассмотрим изотропный материал. В качестве упруго-пластического закона используется закон Рамберга-Осгуда.
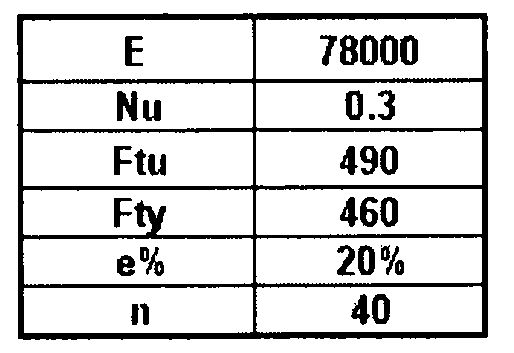
Nx=-524,65 Н/мм
Ny=-253,87 Н/мм
Nxy=327,44 Н/мм
Способ расчета внутренних нагрузок и приложенных нагрузок с учетом поправки на пластичность записывается в матричной форме:
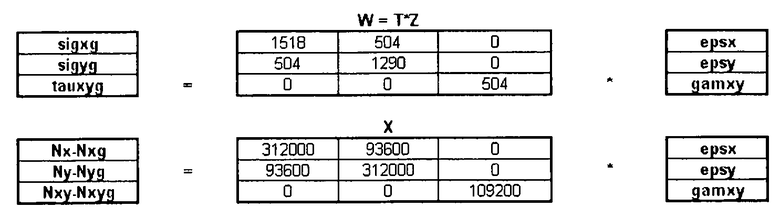
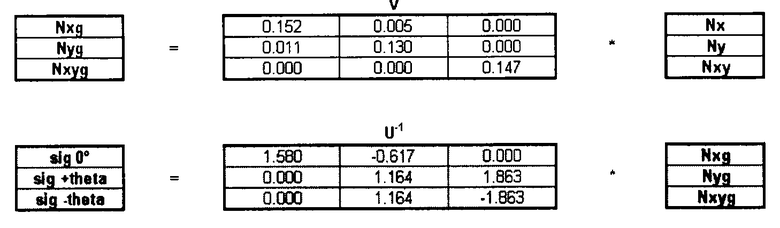
Полученные результаты представляют собой потоки, напряжения и нагрузки в элементах жесткости:
Nxg=-81,1 Н/мм σ0°=-101,14 МПа F0°=-10441 Н
Nyg=-39 Н/мм σ+θ=44,25 МПа F+θ=4437 Н
Nxyg=48,1 Н/мм σ-θ=-137,07 МПа F-θ=-13537 Н
А также потоки и напряжения в обшивке:
Nxs=-443,5 Н/мм σxs=-121,85 МПа
Nys=-214,87 Н/мм σys=-59,03 МПа
Nxys=279,3 Н/мм τxys=76,76 МПа
В этом примере, прилагаемые напряжения находятся в упругом домене.
Распределение потока между обшивкой и сеткой элементов жесткости сведено в следующую таблицу:
(Н/мм)
Этап 4 - модуль анализа сопротивления:
Эта фаза имеет своей задачей вычисление коэффициентов запаса прочности (RF) путем сравнения с приложенными нагрузками, вычисленными в компонентах панели, усиленных треугольными карманами, и максимально допустимого напряжения материала.
Допустимые напряжения в предельно нагруженном материале определяются посредством: Ftu (предельного сопротивления растяжению материала) в сравнении с напряжениями, прилагаемыми к ребрам элементов жесткости, Ftu в сравнении с главными напряжениями, прилагаемыми к обшивке, Fsu (предельного сопротивления сдвигу материала) в сравнении с максимально допустимым сдвигом в обшивке.
Анализ сопротивления состоит в расчете коэффициентов запаса прочности максимально нагруженного и предельно нагруженного материала. Прилагаемые напряжения получаются из нагрузок в плоскости (сжатия, сдвиговой нагрузки) или вне плоскости (давления).
Входными данными для этого расчета являются:
допустимые значения для материала: Fty, Fcy, Fsy, Ftu, Fsu
напряжения, прилагаемые к конструкции:
напряжения на обшивке (σxs, σys и σxys)
нормальные напряжения в элементах жесткости
Примечание: прилагаемые напряжения корректируются для пластичности согласно способу расчета прилагаемых напряжений, как указано выше.
Выходными данными являются коэффициенты запаса прочности.
Анализ сопротивления в плоскости панели основан на следующих гипотезах. Напряжения в обшивке не зависят от толщины обшивки и положения в плоскости. Напряжения в элементе жесткости не зависят от положения на сечении элемента жесткости, но только от угла элемента жесткости.
Эти гипотезы неприемлемы при учете остаточного коробления и внеплоскостного поведения. В этих случаях функции max/min известных типов нужно реализовать с учетом этих явлений.
Расчет главных напряжений:
Для расчета коэффициента запаса прочности обшивки используются главные напряжения (σmax, σmin и τmax):
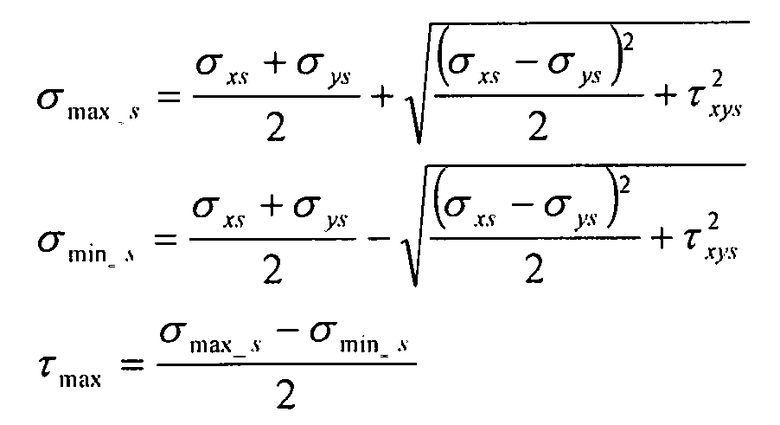
Уравнение 4-1
Значение σmax, используемое при расчете коэффициента запаса прочности задано как абсолютный максимум между σmax_s и σmin_s, вычисленными в уравнении 4-1.
Коэффициент запаса прочности при предельной нагрузке (LL):
коэффициент запаса прочности ребер элементов жесткости:

коэффициент запаса прочности обшивки:
максимальный сдвиг: 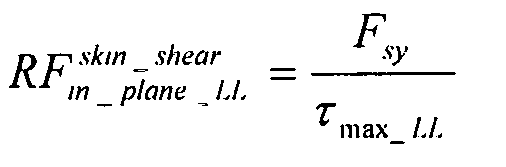
В этой формуле, если Fsy не известно, можно использовать Fsu/√3
Главное напряжение: 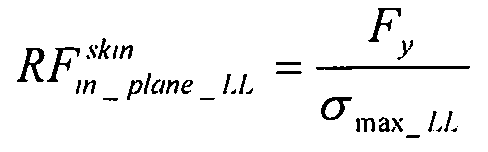
коэффициент запаса прочности обшивки вычисляется при предельной нагрузке:
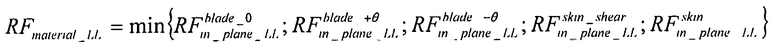
Уравнение 4-2
Коэффициент запаса прочности при предельно допустимой нагрузке UL:
коэффициент запаса прочности ребер элементов жесткости:
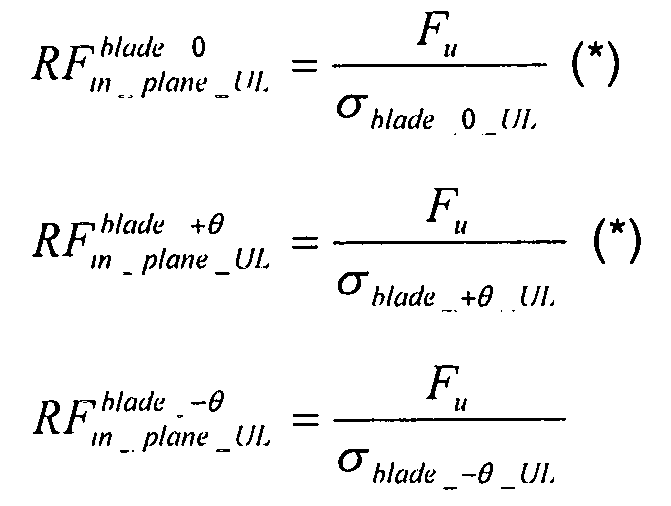
Примечание: если Fcu не известно, можно использовать Fcy или Ftu
коэффициент запаса прочности обшивки:
максимальный сдвиг: 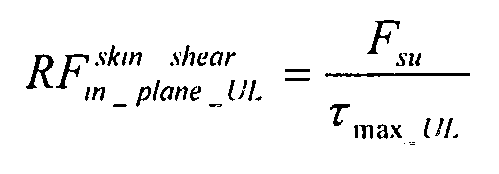
главное напряжение: 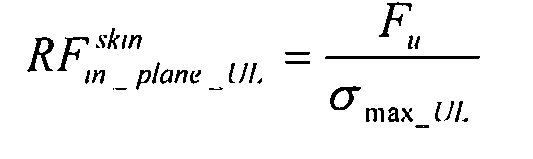
коэффициент запаса прочности обшивка вычисляется при предельно допустимой нагрузке:
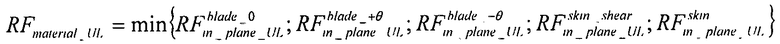
Анализ внеплоскостного сопротивления панели не входит в объем настоящего изобретения.
Согласно примеру реализации этой части способа для анализа сопротивления в плоскости, исследуется та же геометрия и тот же вариант нагрузок, что и в предыдущих разделах. В первом случае, предполагается, что отношение нагрузок равно 1.
Коэффициент запаса прочности ребер элементов жесткости:
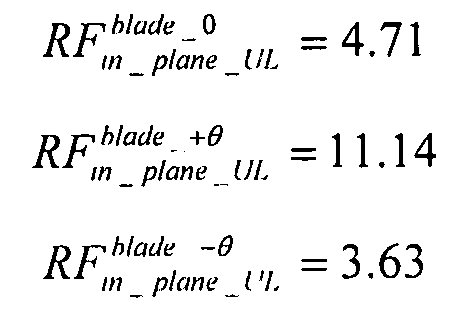
коэффициент запаса прочности обшивки:
расчет главных напряжений:
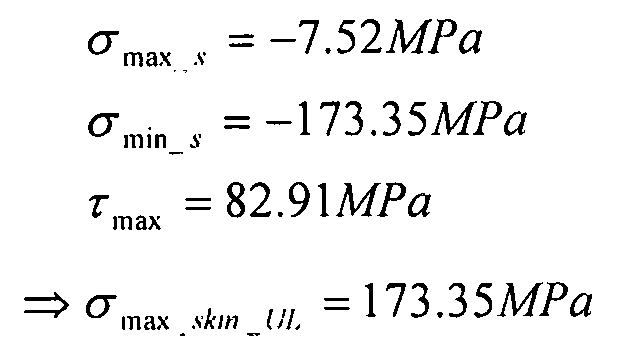
допустимый сдвиг: 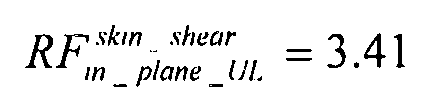
главное напряжение: 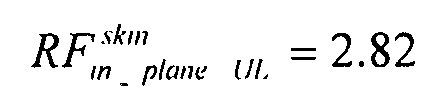
коэффициент запаса прочности охватывает RF при предельно допустимой нагрузке (UL)
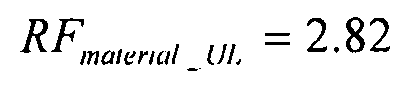
При расчете пластических деформаций применяется метод итераций, пока приложенные нагрузки не достигнут нагрузки потери сопротивления (для внесения поправок на пластичность). В каждом цикле итерации применяются те же вычисления, что описаны выше.
Этап 5 - Расчет допустимого локального напряжения
Два типа потери устойчивости снижают общую жесткость конструкции, усиленной треугольными карманами, но не приводят к общему разрушению конструкции в целом
потеря устойчивости панели: коробление треугольных карманов
потеря устойчивости элементов жесткости: коробление ребер элементов жесткости
Покоробленные секции могут выдерживать только часть нагрузки, которую они выдерживали до коробления. Таким образом, в конструкции происходит перераспределение приложенных нагрузок.
Заметим, что, согласно настоящему изобретению, расчеты остаточного коробления не производятся. Таким образом, вышеописанные два типа коробления рассматриваются как разновидности разрушения.
5A - расчет локального коробления панели:
в панелях, усиленных треугольными карманами, карманы представляют собой пластины треугольной формы, подвергающиеся комбинированным нагрузкам в плоскости. Для вычисления допустимого потока коробления и коэффициентов запаса прочности в условиях чистой нагрузки полной усиленной панели, используется способ на основании модели конечных элементов (FEM).
В этом разделе описан расчет допустимого потока коробления кармана для карманов в виде равнобедренного треугольника: угол при основании треугольника может принимать любые значения, и, в данном неограничительном примере, от 45° до 70°. Расчет потока выполняется с граничными условиями двух типов: свободно опирающийся и фиксированный
Прилагаемые напряжения, подлежащие учету для расчета коэффициента запаса прочности, представляют собой исключительно напряжения, действующие на обшивку, и определены в предыдущем разделе, посвященном расчету прилагаемых напряжений.
Входными данными для этого раздела являются:
геометрические данные (основание треугольника, угол равнобедренного треугольника, толщина обшивки)
данные материала (линейные (E, ν) и нелинейные (Fcy, Ftu, e%, nc))
только изотропный материал
значения допустимого потока пластического коробления относятся только к Fcy
граничные условия: свободно опирающийся или фиксированный
нагрузки, прилагаемые к обшивке.
Заметим, что все внешние потоки, используемые в этом разделе, являются потоками, прилагаемыми к обшивке, и не соответствуют полной нагрузке усиленной панели. Кроме того, высота треугольника (h), используемая как эталонная длина для расчета коробления, уменьшается до половины толщины ребер элементов жесткости.
В этом разделе формула, используемая для высоты треугольника, имеет вид: h=h_red
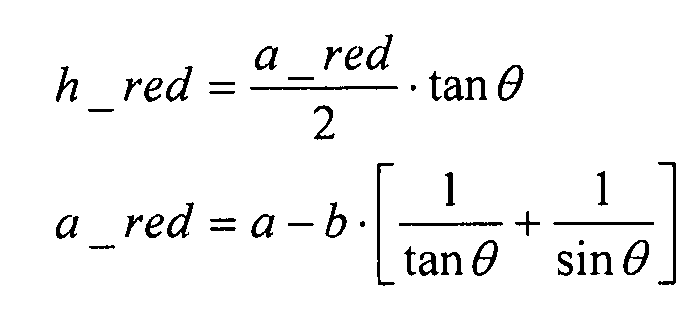
Выходными данными являются:
допустимое коробление кармана.
коэффициент запаса прочности
Этот раздел имеет своей задачей вычисление допустимых потоков для пластин в виде равнобедренного треугольника.
Оно включает в себя две части: 1/ расчет допустимых значений для свободно опирающихся треугольных пластин (часть 5A.5), 2/расчет допустимых значений для фиксированных треугольных пластин (часть 5A.6).
Две следующие части следуют тому же подходу: сначала расчет допустимых значений для треугольных пластин, подвергающихся вариантам чистой нагрузки (сжатие по X, сжатие по Y и сдвиговая нагрузка), затем расчет кривых взаимодействия между тремя вариантами чистой нагрузки.
5A.1 Принцип расчета
Рассматриваемые варианты чистой нагрузки представлены на фиг. 12.
В письменной документации описано несколько аналитических методов расчета локального коробления треугольников. Сравнение этих методов показывает большое различие между ранее упомянутыми напряжениями коробления. Кроме того, некоторые параметры, используемые в этих методах, получены вычислением методом конечных элементов, тесты часто являются эмпирическими, и некоторые способы не обеспечивают абсолютно никаких данных для углов, отличных от 60°.
Не приводя полного теоретического обоснования решения этой проблемы, которое заняло бы слишком много места, можно кратко сказать, что способ наподобие описанного здесь, который не является ограничительным, реализует способ, полностью основанный на модели конечных элементов (FEM):
создают параметрическую модель FEM треугольной пластины (параметры: угол при основании, толщина, высота треугольника, граничные условия),
применяют множество различных комбинаций для получения линейных результатов коробления,
получают параметры, используемые в аналитической формуле (коэффициенты K).
При расчете допустимых значений также следует учитывать эффекты индуцированной пластичности. Приложенные нагрузки являются либо простыми нагрузками, либо комбинациями этих простых нагрузок.
5A.2 Случай чистой нагрузки
Кривые взаимодействия заданы следующим образом. Было создано шесть моделей конечных элементов треугольных пластин с углами от 45° до 70° в данном неограничительном примере, который относится к углам треугольника. В этом разделе угол равнобедренного треугольника (θ) определяется как угол при основании равнобедренного треугольника (см. фиг. 18). Для каждого угла равнобедренного треугольника и для каждого варианта чистой нагрузки, исследование организовано в три этапа:
1/расчет с помощью модели конечных элементов (FEM)
Линейные вычисления локального коробления треугольников с помощью модели конечных элементов (FEM) известного типа производились для определения допустимого потока складкообразования (без поправки на пластичность) для различных значений толщины и, таким образом, различных значений жесткости пластины. Заметим, что первый наблюдаемый режим всегда представляет единичное коробление (единичную выпуклость).
2/отслеживание кривой допустимого потока коробления согласно 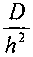 . В целом, в письменной документации, допустимый поток коробления выражается следующим образом:
. В целом, в письменной документации, допустимый поток коробления выражается следующим образом:
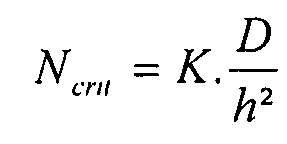
K- константа,
D- жесткость пластины: 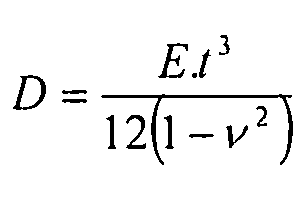 ,
,
h- высота треугольника: 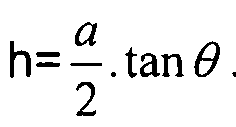 .
.
Однако это исследование показывает, что, в случае треугольных пластин, и для всех малых значений отношения 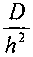 , выражение допустимого потока коробления, использующее уравнение первой степени относительно
, выражение допустимого потока коробления, использующее уравнение первой степени относительно 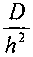 , не пригодно. Более качественные результаты достигаются с помощью уравнения второй степени в следующем виде:
, не пригодно. Более качественные результаты достигаются с помощью уравнения второй степени в следующем виде:
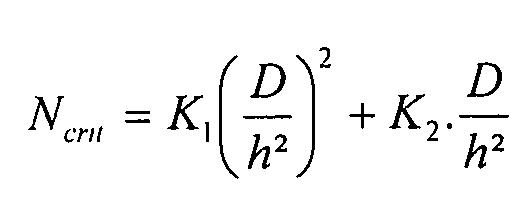 (значение упругости)
(значение упругости)
Уравнение 5-1
Константы K1 и K2 зависят от угла и рассматриваемого варианта нагрузки. Таким образом, для каждого случая и каждого угла, получается значение констант K1 и K2.
3/отслеживание постепенного изменения K1 и K2 в зависимости от угла при основании равнобедренного треугольника
K1 и K2 отслеживаются в соответствии с углом, и осуществляется интерполяция для определения полиномиального уравнения, позволяющего вычислить эти константы при любом угле от 45° до 70°. На фиг. 19 показаны линейная и квадратичная интерполяция для коэффициентов K. Очевидно, что эта функция также позволяет экстраполировать значения за пределы, но вблизи домена в пределах от 45° до 70°. Таким образом, зная угол равнобедренного треугольника и граничные условия, можно напрямую вычислить допустимый поток коробления исследуемой треугольной пластины.
5A.3 Случай комбинированной нагрузки
В этом случае используется следующая гипотеза: если некоторые компоненты комбинированной нагрузки подвергаются растяжению, эти компоненты уменьшаются до нуля (не учитываются при расчете). На самом деле, консервативно считать, что компоненты, испытывающие растяжение, не оказывают влияние на исследуемый поток коробления и не увеличивают напряжение коробления на пластине. Например, если Nx app =+200 Н/мм (что указывает на растяжение) и Ns app =300 Н/мм, то допустимая комбинированная нагрузка снижается до допустимой чистой сдвиговой нагрузки.
Рассматриваемые варианты нагрузки представлены на фиг. 21. В этом разделе, использовали три модели конечных элементов: три пластины в виде равнобедренного треугольника с углами равными 45°, 60° и 70°. Для каждого угла, исследование организовано в два этапа:
1/ расчет с помощью модели конечных элементов (FEM)
Для всех представленных ниже комбинаций, линейные вычисления методом конечных элементов производились для определения собственного значения коробления, соответствующего разным распределениям внешних нагрузок.
Можно видеть, что первый наблюдаемый режим всегда представляет единичное вздутие.
Создается впечатление, что кривая взаимодействия слабо зависит от значения 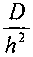 .
.
2/ отслеживание кривых взаимодействия
Кривая взаимодействия отслеживается для каждого угла и каждой комбинации нагрузок. Затем различные кривые аппроксимируются классическими кривыми, расчет которых принимает следующую форму:
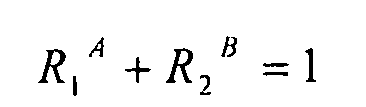 ,
,
где 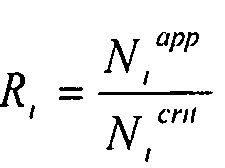 , i=cX, cY или s.
, i=cX, cY или s.
Результаты и сделанные выборы показывают, что уравнения кривых взаимодействия не зависят от угла при основании равнобедренного треугольника и поэтому совместимы и могут быть унифицированы единым уравнением, охватывающим все комбинации, в следующем виде:
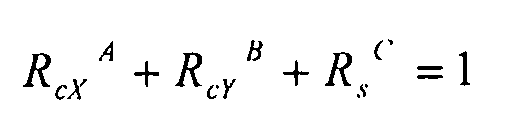
На основании этого уравнения, для определения коэффициентов запаса прочности, можно решить следующее уравнение:
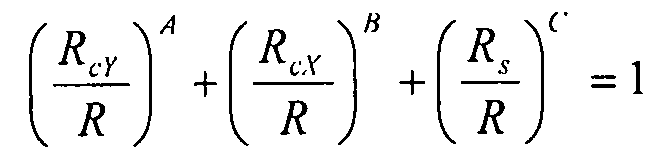 ,
,
где 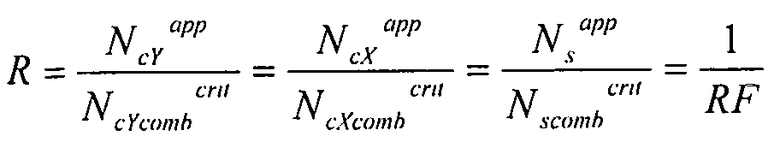
5A.4 Коэффициент поправки на пластичность
Получить поправку на пластичность для вариантов чистой нагрузки, в соответствии с углом равнобедренного треугольника и граничными условиями очень сложно. Фактически, для треугольных пластин, функции отклонения сложны и порождают многочисленные проблемы цифрового интегрирования.
В результате, было решено использовать консервативный коэффициент η, на основании NACA Report 898 ("A Unified Theory of Plastic Buckling of Columns and Plates", июль 1947).
Этот коэффициент задан для всех вариантов нагрузки (чистой и комбинированной) за исключением сдвиговой нагрузки как:
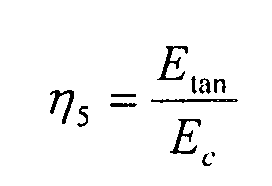
и для вариантов чистой сдвиговой нагрузки как:
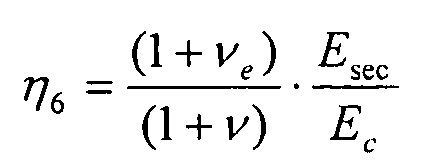
Поправка вычисляется с использованием эквивалентного упругого напряжения фон Мизеса:
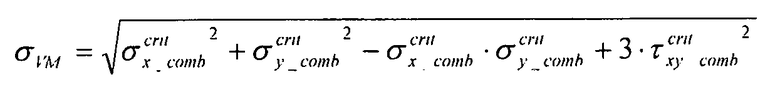
Таким образом, можно вычислить допустимые скорректированные напряжения:
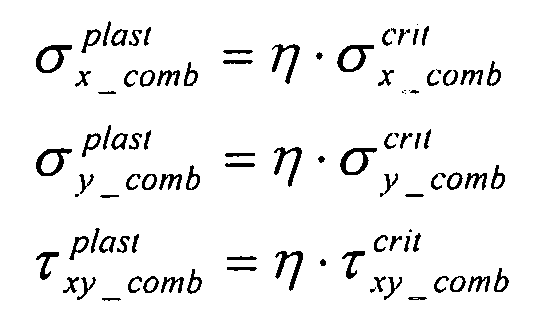
Для вариантов чистой нагрузки (сжатие по X, сжатие по Y или сдвиговая нагрузка), поправка на пластичность также вносится в напряжение фон Мизеса, поэтому для вариантов чисто сдвиговой нагрузки скорректированное напряжение равно: 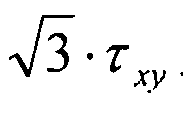 .
.
5A.5 свободно опирающиеся пластины в форме равнобедренного треугольника
Случай чистой нагрузки
На фиг. 26 и 27 показано постепенное изменение констант K1 и K2 в зависимости от угла равнобедренного треугольника. Уравнения этих кривых (где θ измеряется в градусах):

Значения K1 и K2, в условиях сжатия только по X и сжатия только по Y равны, когда угол равнобедренного треугольника равен 60°. Точка пересечения при 60° гарантирует изотропное поведение конструкции, усиленной треугольными карманами при 60°, в отношении локального коробления в обшивке.
Случай комбинированной нагрузки
В случае комбинированной нагрузки, анализ осуществляется с помощью модели конечных элементов для линейного расчета коробления для свободно опирающихся треугольных пластин. Поэтому мы выбираем консервативную кривую взаимодействия, близкую к расчетным кривым взаимодействия, но в простой формуле, которая становится кривой, используемой согласно описанному здесь способу. Ее уравнение имеет вид: 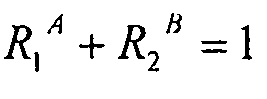 , где
, где 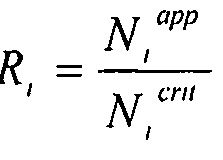 , i=cX, cY или s.
, i=cX, cY или s.
Взаимодействие: сжатие по X + сжатие по Y (вариант 1)
В этом случае нагрузки, для углов от 45° до 70°, мы выбираем консервативную кривую взаимодействия. Иначе говоря, кривую, которая обозначает взаимодействие до значения, меньшего, чем сумма сжатий RcX по X и RcY по Y, в отношении всех кривых взаимодействия, вычисленных для значений угла от 45° до 70°. Эта кривая задана следующим уравнением: 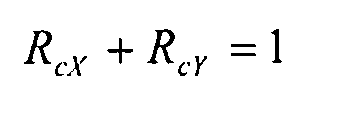
Взаимодействие: сжатие по X + сдвиговая нагрузка (вариант 2)
В этом случае нагрузки, для углов от 45° до 70°, мы выбираем консервативную кривую взаимодействия, в отношении разных кривых взаимодействия согласно углам от 45° до 70°, заданную следующим уравнением: 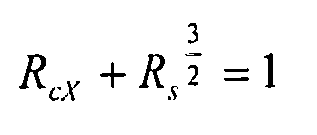
Взаимодействие: сжатие по Y + сдвиговая нагрузка (вариант 3)
для углов от 45° до 70°, для определения коэффициента запаса прочности в случае комбинированной сжимающей нагрузки по Y и сдвиговой нагрузки, мы выбираем консервативное уравнение, выраженное следующей формулой: 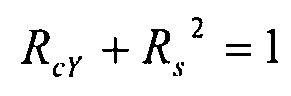 . Чтобы придти к единому уравнению, охватывающему все варианты нагрузки, мы предлагаем использовать другую, еще более консервативную кривую
. Чтобы придти к единому уравнению, охватывающему все варианты нагрузки, мы предлагаем использовать другую, еще более консервативную кривую 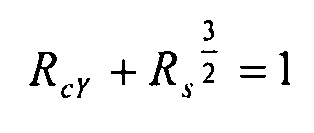 .
.
Взаимодействие: сжатие по X + сжатие по Y + сдвиговая нагрузка (вариант 4)
Уравнение, используемое для этого варианта нагрузки, имеет вид 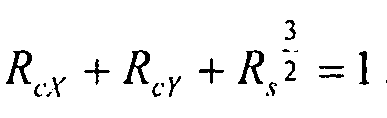 . Это уникальное уравнение используется для всех вариантов комбинированной нагрузки.
. Это уникальное уравнение используется для всех вариантов комбинированной нагрузки.
5A.6 Фиксированные пластины в виде равнобедренного треугольника
Случай чистой нагрузки
На фиг. 28 и 29 показано постепенное изменение констант K1 и K2 в зависимости от равнобедренного треугольника. Уравнения этих кривых (где θ измеряется в градусах):

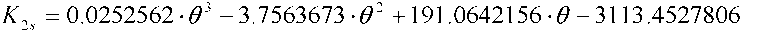
Случай комбинированной нагрузки
В случае комбинированной нагрузки, анализ осуществляется с помощью модели конечных элементов для линейного расчета коробления для фиксированных треугольных пластин. Поэтому мы выбираем консервативную кривую взаимодействия, близкую к расчетным кривым взаимодействия, но в простой формуле, которая становится кривой, используемой согласно описанному здесь способу. Ее уравнение имеет вид: 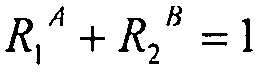 , где
, где 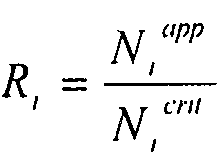 , i=cX, cY или s.
, i=cX, cY или s.
Взаимодействие: сжатие по X+сжатие по Y (вариант 1)
В этом случае нагрузки, для углов от 45° до 70°, мы выбираем консервативную кривую взаимодействия, в отношении разных кривых взаимодействия согласно углам от 45° до 70°, заданную следующим уравнением: 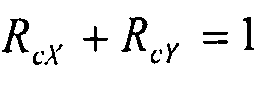 .
.
Взаимодействие: сжатие по X + сдвиговая нагрузка (вариант 2)
В этом случае нагрузки, для углов от 45° до 70°, мы выбираем консервативную кривую взаимодействия, в отношении разных кривых взаимодействия согласно углам от 45° до 70°, заданную следующим уравнением:  .
.
Взаимодействие: сжатие по Y + сдвиговая нагрузка (вариант 3)
Для углов от 45° до 70°, для определения коэффициента запаса прочности в случае комбинированной сжимающей нагрузки по Y и сдвиговой нагрузки, мы выбираем консервативное уравнение, выраженное следующей формулой: 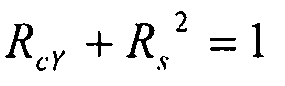 . Чтобы придти к единому уравнению, охватывающему все варианты нагрузки, мы предлагаем использовать другую, еще более консервативную кривую
. Чтобы придти к единому уравнению, охватывающему все варианты нагрузки, мы предлагаем использовать другую, еще более консервативную кривую 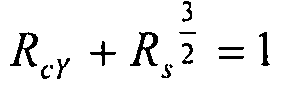 .
.
Взаимодействие: сжатие по X+сжатие по Y+сдвиговая нагрузка (вариант 4)
Уравнение, используемое для этого варианта нагрузки, имеет вид 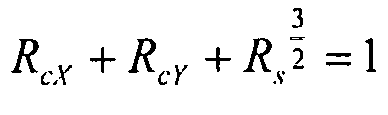 . Это единое уравнение используется для всех вариантов комбинированной нагрузки.
. Это единое уравнение используется для всех вариантов комбинированной нагрузки.
5B Расчет локального коробления элемента жесткости:
Этот модуль вычисляет напряжение коробления и коэффициент запаса прочности ребра элемента жесткости, рассматриваемого как прямоугольная панель с разнообразными граничными условиями, задаваемыми пользователем.
Прилагаемые напряжения, подлежащие учету для расчета коэффициента запаса прочности, однозначно являются напряжениями в ребрах элементов жесткости, полученными из модуля расчета прилагаемых напряжений.
На сетке элементов жесткости, один или несколько типов ребер элементов жесткости подвергаются сжимающей нагрузке. Таким образом, нужно вычислять допустимое напряжение сжатия.
Входными данными этого модуля являются:
геометрические данные: размеры ребер элементов жесткости (длина, высота, толщина),
данные материала (линейные (E, ν) и нелинейные (Fcy, Ftu, εult, nc)). В данном примере рассматривается только изотропный материал,
граничные условия (имеется четыре),
нагрузки, прилагаемые к ребрам элементов жесткости.
Выходными данными являются допустимый поток коробления ребра элемента жесткости и коэффициент запаса прочности. Допустимое напряжение коробления ребра элемента жесткости выражается в виде (см. фиг. 13 касательно соглашений по системе обозначений):
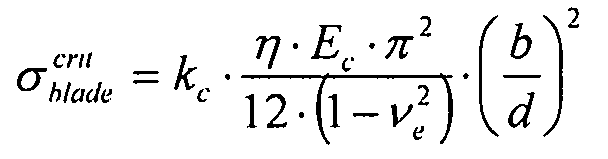
Уравнение 5-2
где:
b: толщина ребра элемента жесткости
d: высота ребра элемента жесткости
Lb: длина ребра элемента жесткости
Ec: модуль Юнга при сжатии
νe: коэффициент Пуассона в области упругих деформаций
kc: коэффициент локального коробления (зависящий от граничных условий и геометрии)
η: коэффициент поправки на пластичность
Примечание: длина ребра элемента жесткости задана как
(Lb)=a (для ребер элементов жесткости в направлении X)
(Lb)=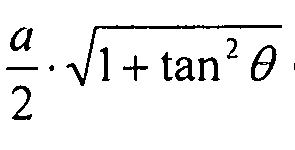 (для ребер элементов жесткости в поперечных направлениях)
(для ребер элементов жесткости в поперечных направлениях)
На ребро элемента жесткости можно налагать многочисленные граничные условия согласно окружающей конструкции, (см. фиг. 14). Заметим, что, если Lb/d превышает значение Lim, то kc становится равным kc на бесконечности. Рекомендуемый консервативный коэффициент коробления для расчетов на основании многочисленных анализов конечных элементов согласно варианту 2 (2 фиксированных края - один свободно опирающийся край - один свободный край).
Согласно вышеупомянутым граничным условиям и согласно таблице 1, где приведены коэффициенты поправки на пластичность для прямоугольных пластин, коэффициент поправки на пластичность, используемый в этом случае, имеет вид:
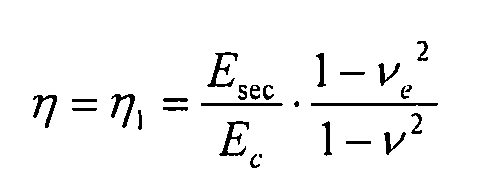
Формула для расчета коэффициента запаса прочности ребра элемента жесткости в отношении коробления пригодна для всех типов ребер элементов жесткости, используемых, в данной панели, усиленной треугольными карманами (0°, +θ, -θ):
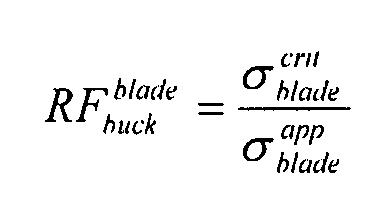
Следующий пример основан на той же геометрии, которая использовалась в предыдущих разделах. Геометрия элементов жесткости такова: b=2,5 мм, и d=37,36 мм. Длина ребер элементов жесткости обозначена (Lb): Lb=a=198 мм для ребер элементов жесткости в направлении X, и Lb=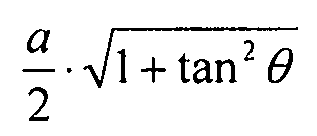 =186,82 мм для ребер поперечных элементов жесткости. Используются следующие граничные условия: 2 стороны являются фиксированными - 1 сторона является свободно опирающейся - 1 сторона является свободной.
=186,82 мм для ребер поперечных элементов жесткости. Используются следующие граничные условия: 2 стороны являются фиксированными - 1 сторона является свободно опирающейся - 1 сторона является свободной.
Таким образом: 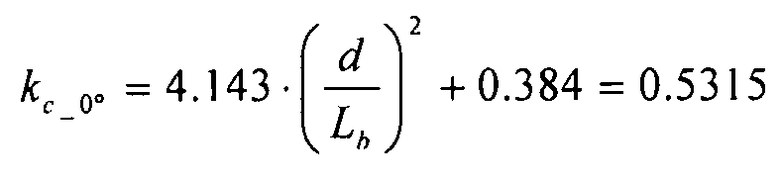 для ребер элементов жесткости в направлении X, и
для ребер элементов жесткости в направлении X, и 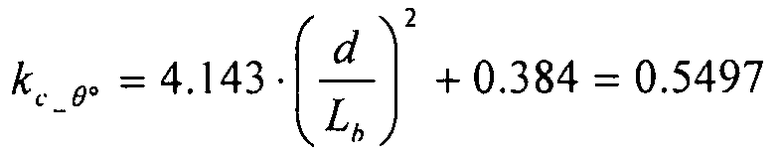 для ребер поперечных элементов жесткости.
для ребер поперечных элементов жесткости.
При этом нагрузка коробления для каждого элемента жесткости такова:
Коэффициент поправки на пластичность при короблении ребра элемента жесткости имеет вид:
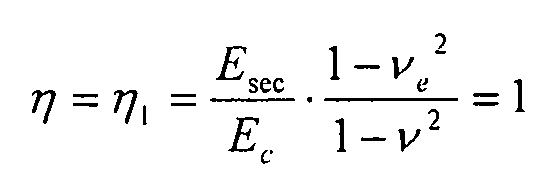 (упругая деформация)
(упругая деформация)
Нагрузки, прилагаемые к элементам жесткости, таковы:
σ0°=-101,14 МПа
σ+θ=44,25 МПа
σ-θ=-135,07 МПа
Ниже приведены результаты расчета коэффициента запаса прочности:
Этап 6 - расчет общей потери устойчивости:
Этот этап обеспечивает данные по допустимому потоку коробления для плоской панели, усиленной треугольными карманами, в условиях чистой или комбинированной нагрузки.
Формулы основаны на короблении ортотропных пластин. Возможны два или четыре граничных условия согласно варианту нагрузки (4 свободно опирающихся края, 4 фиксированных края, 2 нагруженных свободно опирающихся края и 2 фиксированных поперечных края, 2 нагруженных фиксированных края и 2 свободно опирающихся поперечных края). Прилагаемые потоки, подлежащие учету для расчета коэффициента запаса прочности, являются внешними потоками панели, усиленной треугольными карманами, которые являются входными данными.
Имеются следующие входные данные:
Геометрические данные:
Lx: длина панели, эквивалентной сетке
Ly: ширина панели, эквивалентной сетке,
ts: толщина обшивки,
tg: толщина панели, эквивалентной сетке,
Данные по материалу:
Ex s, Ey s: модуль Юнга обшивки,
Gxy s: модуль сдвига обшивки,
νxy s, νyx s: коэффициент Пуассона обшивки,
Ex g , Ey g: модуль Юнга сетки,
Gxy g: модуль сдвига сетки,
νxy g, νyx g: коэффициент Пуассона сетки,
Нагрузки, прилагаемые к конструкции (Nx 0, Ny 0, Nxy 0, pz)
граничные условия (возможны 2 или 4 согласно типу нагрузки)
Выходными данными являются:
Nx c, Ny c, Nxy c: допустимые потоки коробления,
Nx c comb, Ny c comb, Nxy c comb: допустимые комбинированные потоки коробления,
коэффициенты запаса прочности.
Мы используем гипотезу Кирхгофа: плоские сечения остаются, в основном, плоскими после деформации. Сетка (элементов жесткости) моделируется в данном случае эквивалентной панелью. Обшивка и панель, эквивалентная сетке, рассматриваются как пластины ортотропной природы.
Параметры материала подчиняются следующему соотношению: 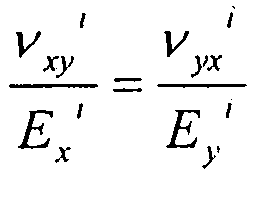 .
.
Соглашения по потоку и моментам проиллюстрированы на фиг. 21.
6.1.1 Смещения
Вектор 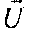 представляет смещение точки M(x,y) средней поверхности:
представляет смещение точки M(x,y) средней поверхности: 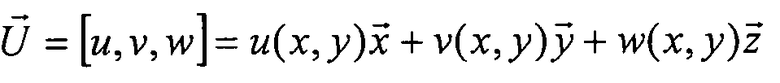
Различные переменные не зависят от z, поскольку рассматривается плоское напряженное состояние 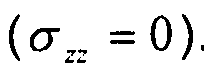 .
.
6.1.2 Деформации
Общее выражение деформаций в сечении пластины, находящемся на расстоянии z от средней оси, имеет вид:
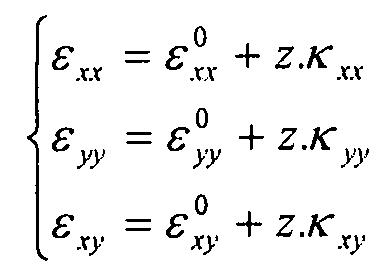
Уравнение 6-1,
где:
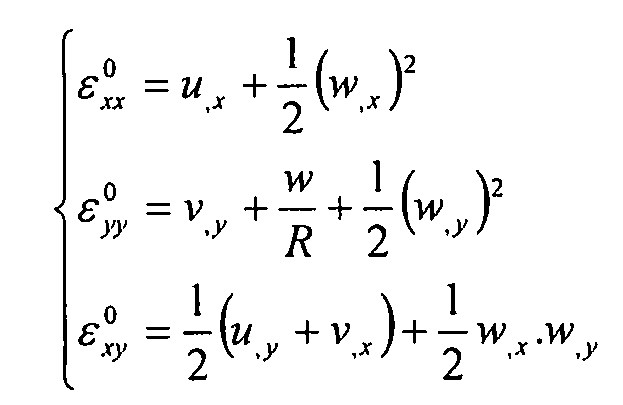
Уравнение 6-2
Члены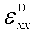 ,
, 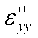 и
и 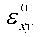 выражают вклад в деформацию в плоскости пластины. Члены,
выражают вклад в деформацию в плоскости пластины. Члены, 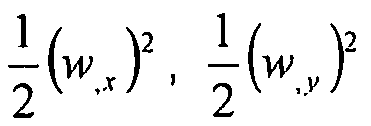 и
и 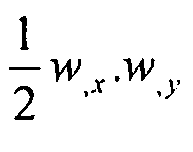 выражают нелинейный вклад в деформацию в плоскости пластины. Член R представляет радиус обшивки, но здесь мы рассматриваем плоскую пластину, поэтому
выражают нелинейный вклад в деформацию в плоскости пластины. Член R представляет радиус обшивки, но здесь мы рассматриваем плоскую пластину, поэтому 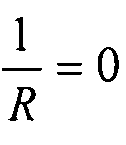 .
.
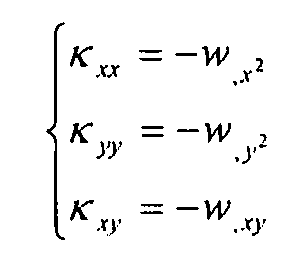
Уравнение 6-3
Члены 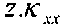 ,
, 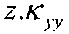 и
и 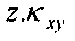 выражают вклад в деформацию, обусловленный изменением кривой пластины (z- расстояние от средней оси пластины).
выражают вклад в деформацию, обусловленный изменением кривой пластины (z- расстояние от средней оси пластины).
6.1.3 Законы поведения
Обшивка и панель, эквивалентная элементам жесткости, рассматриваются как ортотропные пластины. Таким образом, существуют следующие соотношения между напряжениями и деформациями:
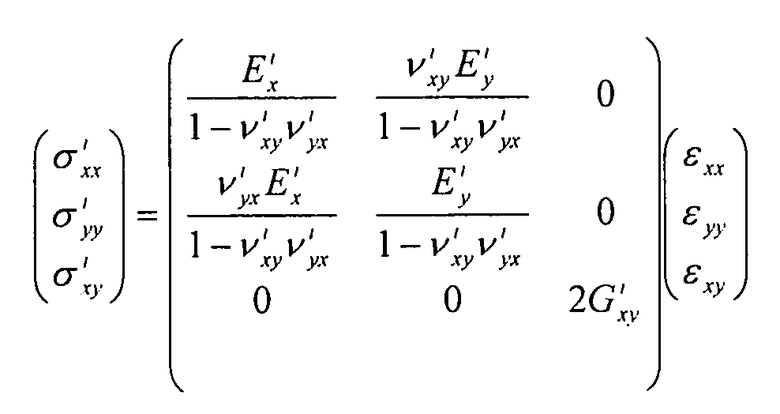
Уравнение 6-4,
где i=(s, g) (индексы s для значений, относящихся к обшивке, и индексы g для значений, относящихся к сетке элементов жесткости).
6.1.4 Поток и моменты
Ниже приведены выражения потока и моментов в расчете на единицу длины:
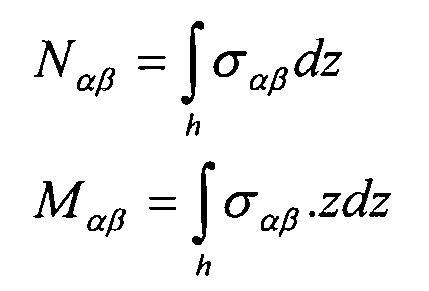
Уравнение 6-5,
где (α,β)=(x,y).
- поток:
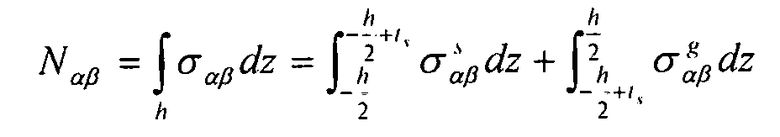
Используя уравнение 6-5 и соотношение 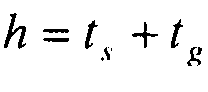 , находим:
, находим:
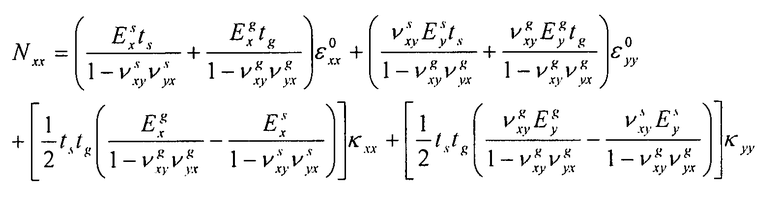
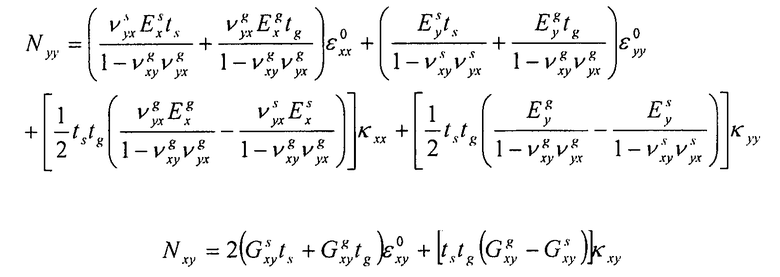
Уравнение 6-6
- моменты в расчете на единицу длины:
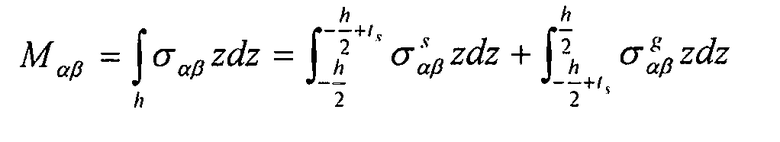
Используя уравнение 6-5 и соотношение 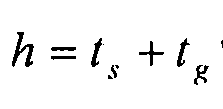 , находим:
, находим:
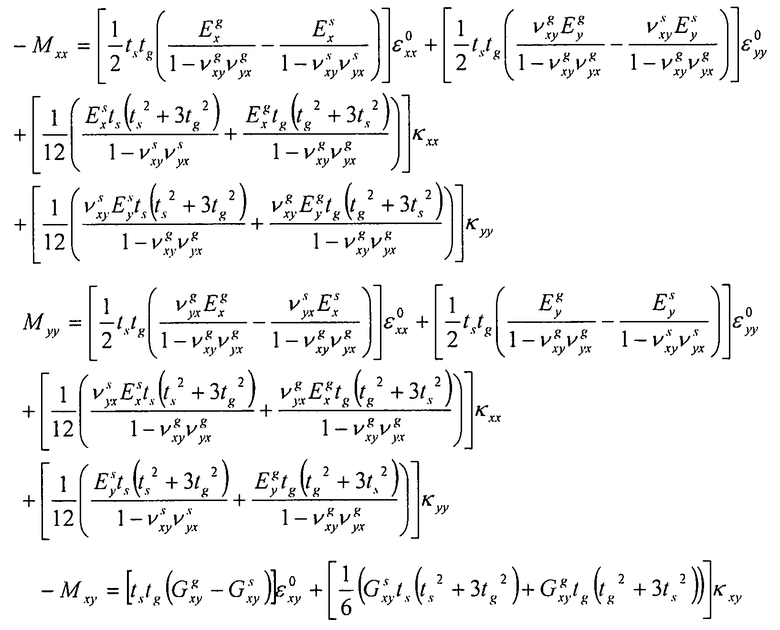
Уравнение 6-7
Исходя из вышесказанного, получаем общий закон поведения (между потоком и моментами с одной стороны и деформациями с другой):
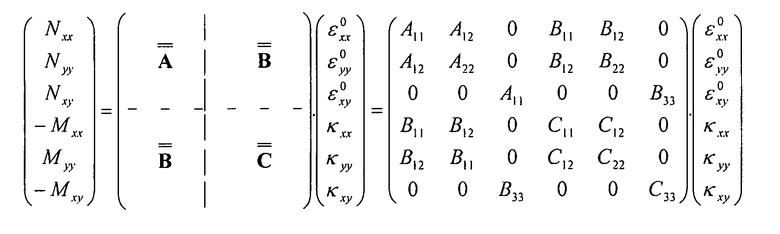
Уравнение 6-8
- Матрицы A, B и C являются симметричными.
6.2 Уравнения баланса
Общие уравнения баланса элемента панели (или обшивки) заданы следующими выражениями, связывающих потоки, моменты и плотность поверхностной прочности:
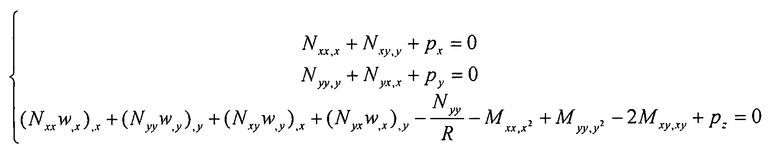
Уравнение 6-9,
где 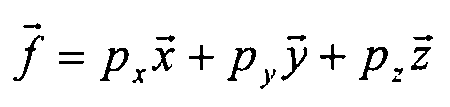 - плотность поверхностной силы, действующей на элемент обшивки. Плотность поверхностной силы действует только в радиальном направлении Z, но не в других направлениях. Поэтому
- плотность поверхностной силы, действующей на элемент обшивки. Плотность поверхностной силы действует только в радиальном направлении Z, но не в других направлениях. Поэтому 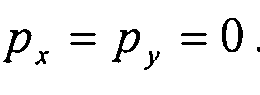 . Кроме того, в данном примере мы рассматриваем случай плоской пластины, поэтому
. Кроме того, в данном примере мы рассматриваем случай плоской пластины, поэтому 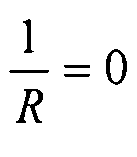 . Таким образом, получаем упрощенные уравнения баланса:
. Таким образом, получаем упрощенные уравнения баланса:
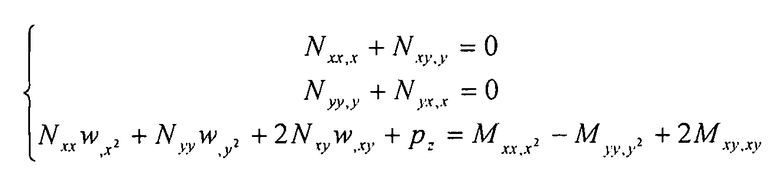
Уравнение 6-10
6.3 Для общего решения этих уравнений, зададим следующие векторы

Уравнение 6-11
К пластине обычно прилагаются следующие нагрузки:
поток однородного сжатия по
оси
x: 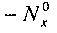
поток однородного сжатия по
оси
y: 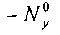
поток однородного сдвига в плоскости x-y: 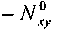
однородное давление по
оси
z: 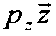
Таким образом, поскольку приложенные нагрузки, заданные ниже, являются однородными, можно сделать вывод о том, что первые два уравнения системы уравнений 6-10 верны. 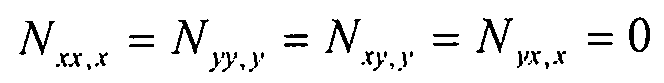 .
.
Выражение моментов:
Используя уравнение 6-8 и уравнение 6-11, получаем следующие соотношения:
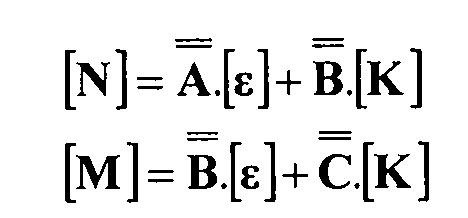
Уравнение 6-12
Поскольку прилагаемые потоки являются однородными, получаются следующие соотношения:
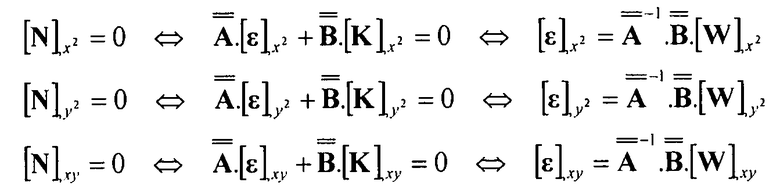
Уравнение 6-13
при том, что: 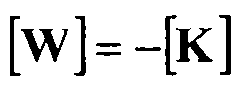 .
.
Отсюда, для моментов:
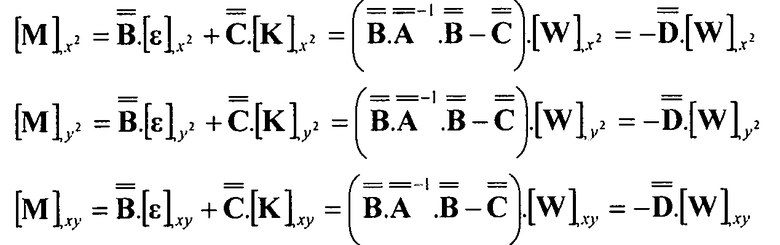
Уравнение 6-14,
где
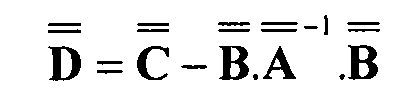
Уравнение 6-15
D это матрица глобальной жесткости, которая является симметричной.
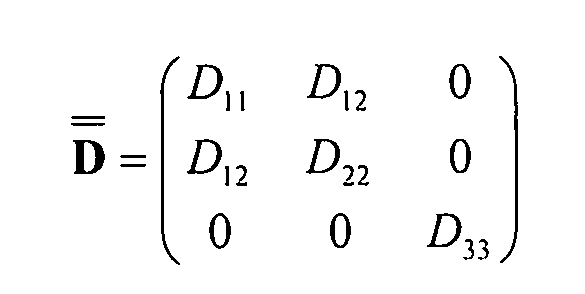
Таким образом, из уравнения 6-10 можно вывести моменты:
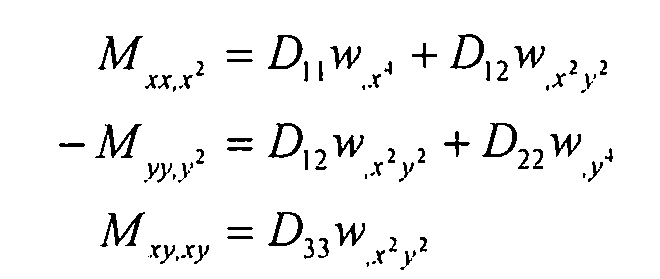
Уравнение 6-16
Выражая уравнение 6-10 через смещения, получаем дифференциальное уравнение общего вида:
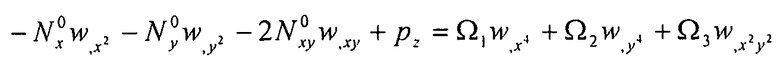
Уравнение 6-17,
где:
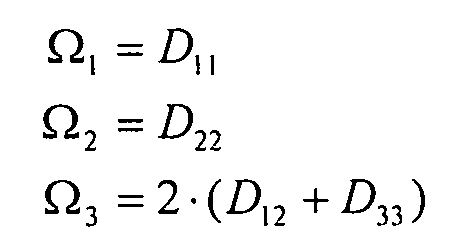
Уравнение 6-18
в следующем разделе, панель, усиленная треугольными карманами, моделируется ее тремя изгибами элементов жесткости (Ω1, Ω2 и Ω3) для вычисления потоков коробления в ортотропной пластине.
В этом случае вновь используется следующая гипотеза: если некоторые компоненты комбинированной нагрузки находятся в состоянии натяжения, эти компоненты не учитываются при расчете. На самом деле, консервативно считать, что компоненты, испытывающие растяжение, не оказывают влияние на исследуемый поток коробления и не увеличивают напряжение коробления на пластине.
6.4 Допустимый поток коробления
6.4.1 Поток продольного сжатия (сжатие по X)
Пластина подвергается воздействию потока однородного продольного сжатия (по оси x): 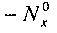 . Таким образом:
. Таким образом: 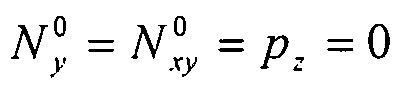 . В результате, дифференциальное уравнение общего вида (уравнение 6-17) приобретает вид:
. В результате, дифференциальное уравнение общего вида (уравнение 6-17) приобретает вид:
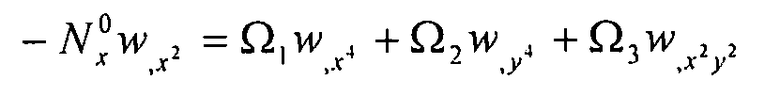
Уравнение 6-19
Сначала рассмотрим свободно опирающуюся пластину (граничные условия описаны далее):
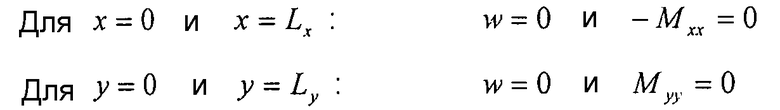
Следующее выражение для смещения w удовлетворяет всем вышеуказанным граничным условиям:
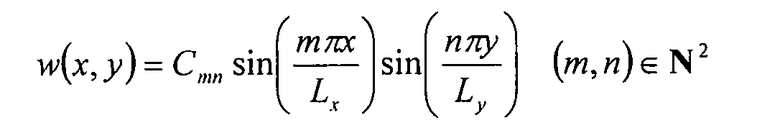
Уравнение 6-20
Предыдущее выражение для w должно удовлетворять дифференциальному уравнению общего вида (уравнение 6-19), откуда получаем:
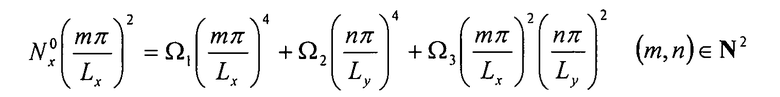
Минимальное значение 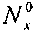 соответствует значению допустимого потока общего коробления
соответствует значению допустимого потока общего коробления 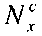 . Мы показываем, что это значение равно:
. Мы показываем, что это значение равно:
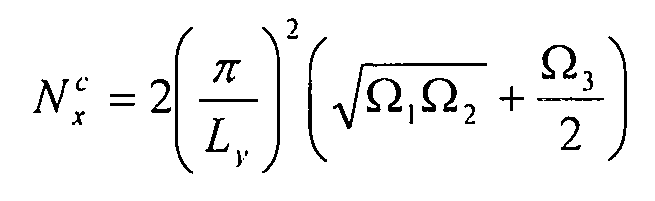
Уравнение 6-21
Эту формулу можно обобщить для различных граничных условий (нагруженных краев и свободно опирающихся или фиксированных поперечных краев):
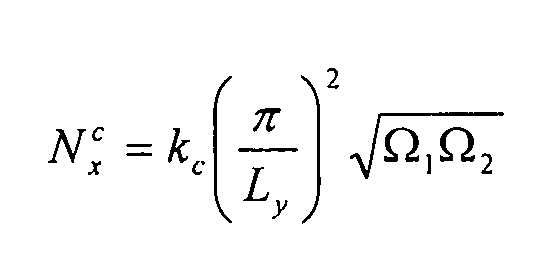
Уравнение 6-22,
где
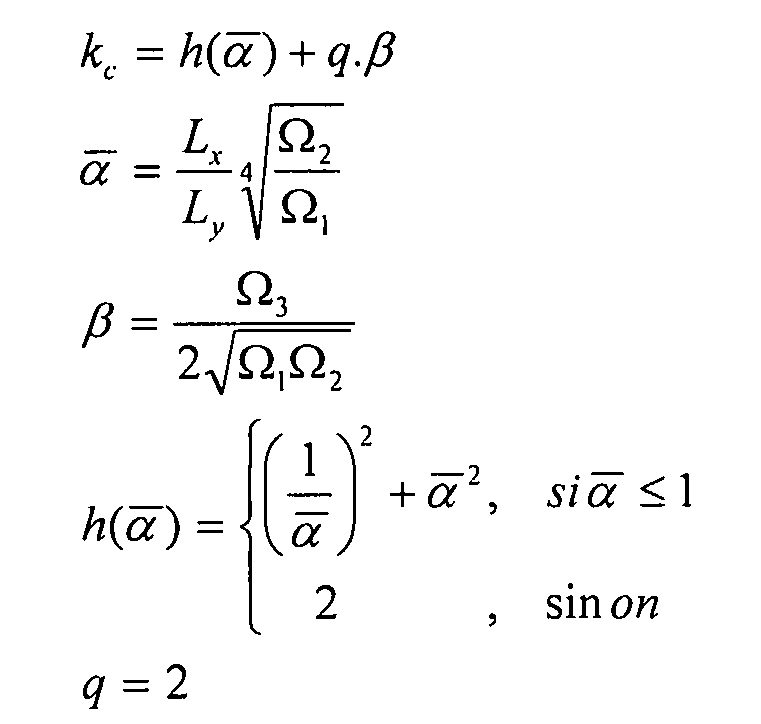
На фиг. 22 показано значение 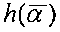 согласно различным граничным условиям (случай четырех свободно опирающихся краев является базовой кривой).
согласно различным граничным условиям (случай четырех свободно опирающихся краев является базовой кривой).
6.4.2 Поток поперечного сжатия (сжатие по Y)
Пластина подвергается воздействию потока однородного поперечного сжатия (по оси y): 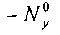 . Таким образом:
. Таким образом: 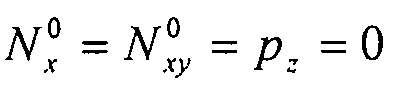 . Решение такое же, как описано в предыдущем разделе.
. Решение такое же, как описано в предыдущем разделе.
Допустимый поток коробления 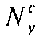 выражается в виде:
выражается в виде:
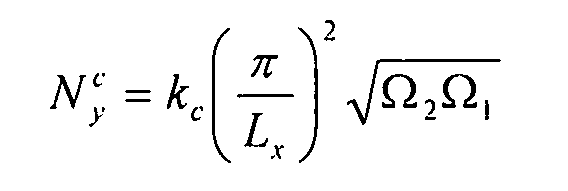
Уравнение 6-23,
где
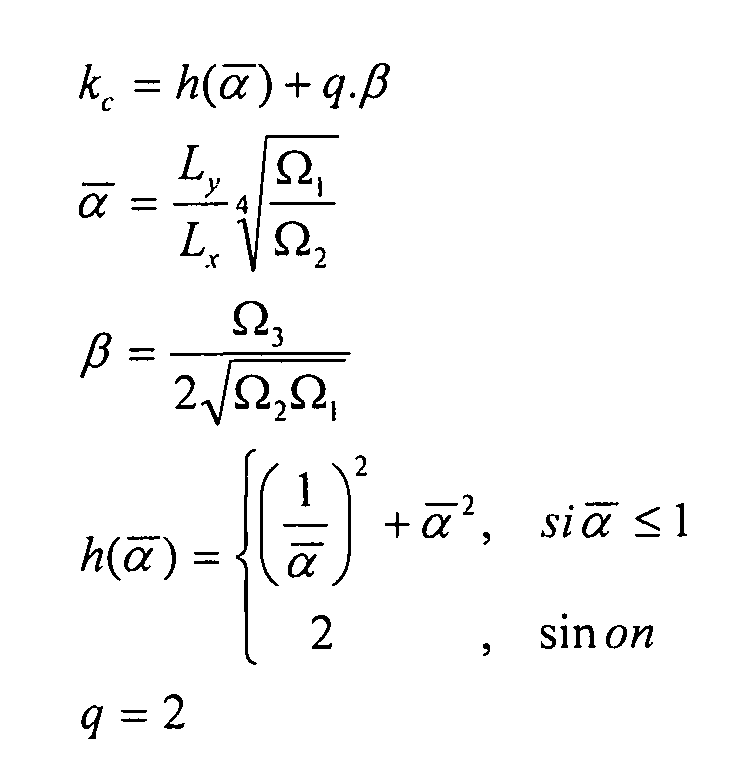
6.4.3 Сдвиговый поток
Пластина подвергается воздействию потока однородного сдвига: 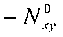 . Таким образом:
. Таким образом: 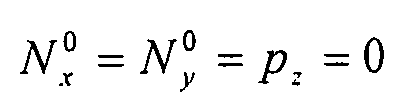 . Заметим, что в этом абзаце, следующие формулы справедливы только для Ly<Lx. В противном случае, некоторые члены нужно заменить: Lx ←→ Ly и Ω1 ←→ Ω2. Допустимый поток коробления
. Заметим, что в этом абзаце, следующие формулы справедливы только для Ly<Lx. В противном случае, некоторые члены нужно заменить: Lx ←→ Ly и Ω1 ←→ Ω2. Допустимый поток коробления 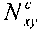 выражается в виде:
выражается в виде:
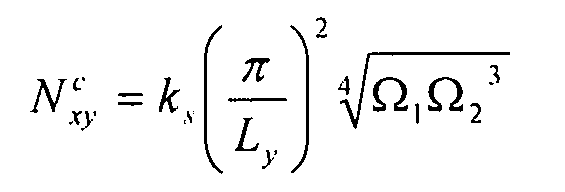
Уравнение 6-24,
где 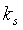
Входные данные таблицы и графика заданы в виде:
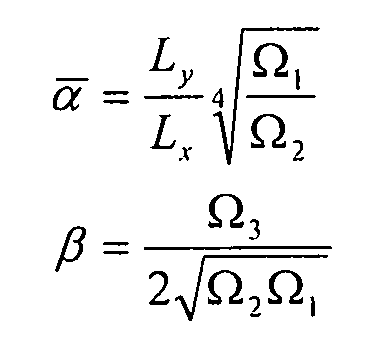
6.4.4 Поток двухосного сжатия
Пластина подвергается воздействию комбинированной нагрузки: поток однородного продольного сжатия (по оси x) и поток однородного поперечного сжатия (по оси
y): 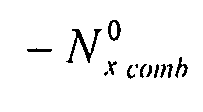 и
и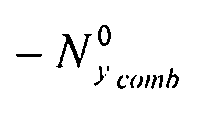 . Таким образом:
. Таким образом: 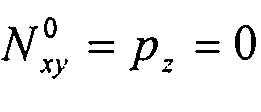 . Определим λ из:
. Определим λ из: 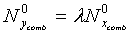
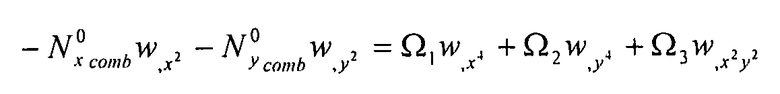
Уравнение 6-25
Граничные условия четырех свободно опирающихся краев:
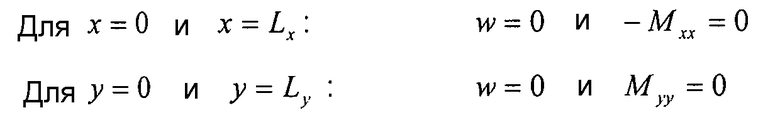
Выражение смещения:
Следующее выражение для смещения w удовлетворяет всем вышеуказанным граничным условиям:
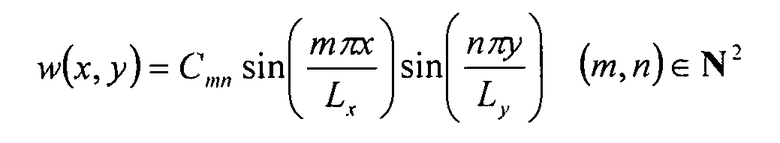
Уравнение 6-26
Допустимый поток коробления (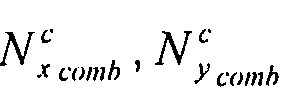 )
)
Предыдущее выражение для w должно удовлетворять дифференциальному уравнению общего вида (уравнение 6-25), откуда получаем:
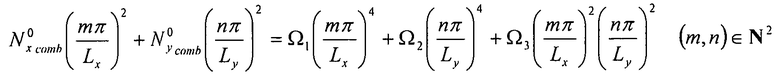
Выражение  через λ должно удовлетворять условию:
через λ должно удовлетворять условию:
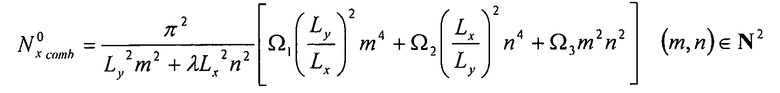
Таким образом, получаем допустимые потоки коробления:
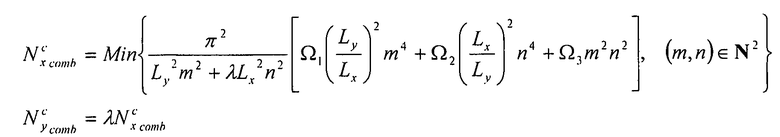
Уравнение 6-27
Граничные условия: четыре фиксированных края:
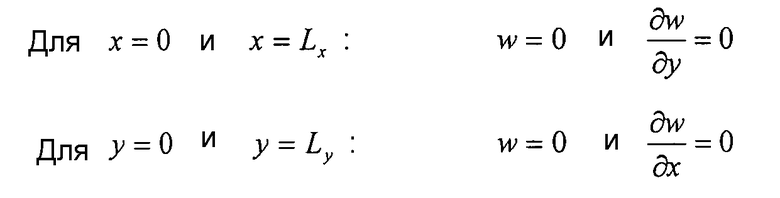
Выражение смещения:
Следующее выражение смещения w удовлетворяет всем вышеуказанным граничным условиям:
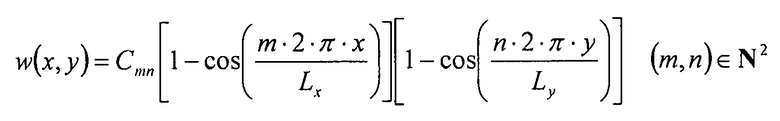
Уравнение 6-28
Допустимый поток коробления (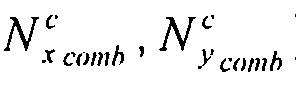 ):
):
Выражение 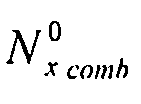 зависит от λ и должно удовлетворять условию:
зависит от λ и должно удовлетворять условию:
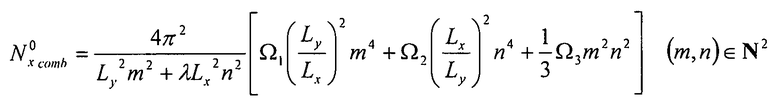
Таким образом, получаем допустимые значения потока коробления:
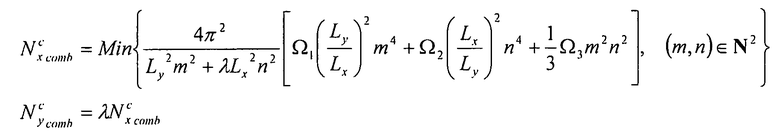
Уравнение 6-29
6.4.5 Поток продольного сжатия и поток сжатия со сдвигом
Пластина подвергается воздействию комбинированной нагрузки: однородного продольного сжатия (по оси X) и потока сжатия со сдвигом: 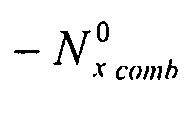 и
и 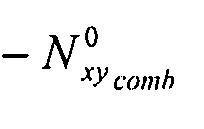
Таким образом: 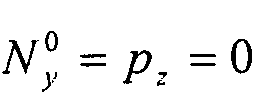 .
.
Уравнение взаимодействия:
уравнение взаимодействия для комбинированных потоков продольного сжатия и сжатия со сдвигом имеет вид:
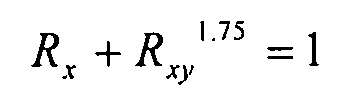
Уравнение 6-30,
где
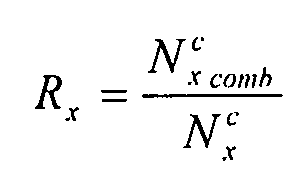 - коэффициент потока продольного сжатия
- коэффициент потока продольного сжатия
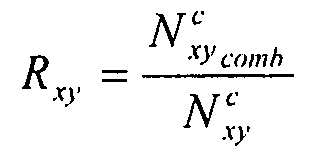 - коэффициент сдвигового потока,
- коэффициент сдвигового потока,
где 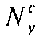 и
и 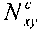 - допустимые значения потока коробления, вычисленные выше для одноосной нагрузки.
- допустимые значения потока коробления, вычисленные выше для одноосной нагрузки.
6.4.6 Поток поперечного сжатия и поток сжатия со сдвигом
Пластина подвергается воздействию потока однородного поперечного сжатия (по оси
y) и сдвигового потока: 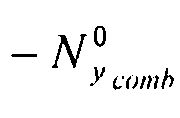 и
и 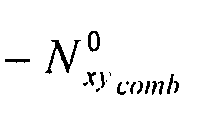
Таким образом: 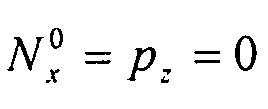 .
.
Уравнение взаимодействия для комбинированных потоков поперечного сжатия и сжатия со сдвигом имеет вид:
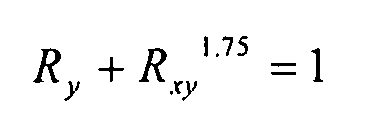
Уравнение 6-31,
где:
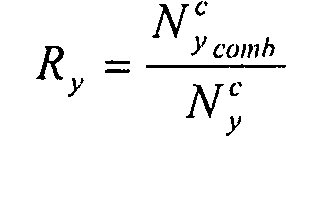 - коэффициент потока поперечного сжатия
- коэффициент потока поперечного сжатия
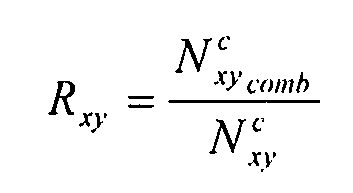 - коэффициент сдвигового потока,
- коэффициент сдвигового потока,
где 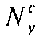 и
и 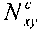 - допустимые значения потока коробления, вычисленные выше для одноосной нагрузки.
- допустимые значения потока коробления, вычисленные выше для одноосной нагрузки.
6.4.7 Поток двухосного сжатия и поток сжатия со сдвигом
Пластина подвергается воздействию комбинированных нагрузок: потоку однородного продольного сжатия (по оси
x) и потоку однородного поперечного сжатия (по оси
y), а также потоку коробления: 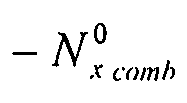 ,
, 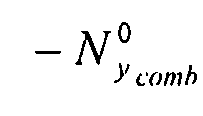 и
и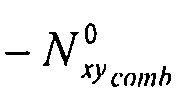 .
.
Таким образом: 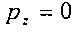 .
.
Уравнение взаимодействия получается в два этапа. Сначала определяется коэффициент запаса прочности RFbi, соответствующий потоку двухосного сжатия:
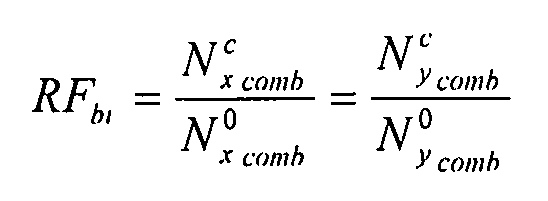
Уравнение 6-32
Затем это значение используется в уравнении взаимодействия для комбинированных потоков двухосного сжатия и сжатия со сдвигом:
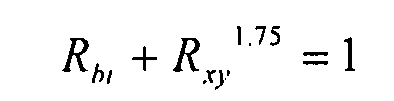
Уравнение 6-33,
где:
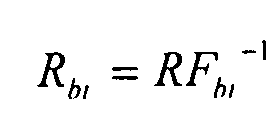 - коэффициент потока двухосного сжатия
- коэффициент потока двухосного сжатия
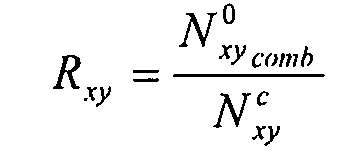 - коэффициент сдвигового потока,
- коэффициент сдвигового потока,
где  - допустимый поток коробления, вычисленный при чистой сдвиговой нагрузке.
- допустимый поток коробления, вычисленный при чистой сдвиговой нагрузке.
Способ, отвечающий изобретению, также включает в себя цикл итерации (см. фиг. 7). Этот цикл позволяет изменять значение приложенных нагрузок или значения размеров рассматриваемых панелей, усиленных треугольными карманами, согласно результатам, по меньшей мере, одного из этапов 3-6.
Способ наподобие описанного выше, можно реализовать, по меньшей мере, частично, в виде макроса в программе типа электронной таблицы.
Такая программа, использует, таким образом, например, в качестве входных данных данные о материале и геометрии, хранящихся в специально предназначенной для этого зоне, а также различные варианты рассматриваемых нагрузок и граничных условий, и выдает в качестве выходных значений массу панели, коэффициент запаса прочности при предельно допустимой нагрузке, относящихся, в частности, к треугольным карманам, элементам жесткости и общему разрушению. Эти выходные данные, таким образом, отражают варианты нагрузок или задание размеров, которые несовместимы с желаемыми коэффициентами запаса прочности.
ПРЕИМУЩЕСТВА ИЗОБРЕТЕНИЯ
Очевидно, что ранее известный процесс, предложенный NASA, получил существенное развитие в рамках настоящего изобретения с учетом особенностей авиастроения:
- локальные допустимые значения для элементов жесткости (разрушение, потеря поперечной устойчивости и т.д.) для сжимающей нагрузки в направлении X или Y и сдвиговой нагрузки,
- локальные допустимые значения треугольной обшивки для сжимающей нагрузки в направлении X или Y и сдвиговой нагрузки,
- поправка на пластичность,
- предварительный расчет массы,
- расчет общего коробления для сжимающей нагрузки в направлении X или Y и сдвиговой нагрузки.
Основными усовершенствованиями являются расчет допустимых напряжений для разных типов коробления и расчет адаптированных коэффициентов запаса прочности.
Расширения: вариант нагрузки
- двойное сжатие (для локального и общего коробления)
- комбинированная нагрузка: сжимающая и сдвиговая нагрузка
Расширения: улучшение параметров способа
- отсутствие ограничений на коэффициент Пуассона материала
- изменение угла сетки (отличного от 60°)
- пластичность, когда конструкция, усиленная треугольными карманами, рассматривается как эквивалентная усиленная панель
- граничные условия (присоединение или промежуточные граничные условия) для локального или общего коробления
Одним из наиболее значительных преимуществ способа задания размеров, отвечающего изобретению, является возможность установки панелей, усиленных треугольными карманами, вместо и взамен панелей, которые раньше создавали с помощью двух перпендикулярных наборов элементов жесткости (лонжеронов и продольных балок), расположенных под ними, что дает, при равном механическом сопротивлении, выигрыш в массе, достигающий в отдельных случаях 30%.
РАЗНОВИДНОСТИ ИЗОБРЕТЕНИЯ
Объем настоящего изобретения не ограничивается конкретными типами варианта осуществления, рассмотренного выше в порядке примера, но, напротив, позволяет специалистам в данной области техники предлагать изменения, не выходящие за рамки объема.
В данном описании изобретения упомянуты углы при основании равнобедренного треугольника от 45° до 70°, которые соответствуют современным требованиям к авиационным конструкциям. Однако очевидно, что аналогичный способ можно реализовать для всех значений угла равнобедренного треугольника в панелях, усиленных треугольными карманами.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПТИМИЗАЦИИ ПРОЦЕССА ПРОЕКТИРОВАНИЯ КОНСТРУКЦИИ КОМПОЗИЦИОННОЙ ПАНЕЛИ, УСИЛЕННОЙ ЭЛЕМЕНТАМИ ЖЕСТКОСТИ | 2006 |
|
RU2431189C2 |
| Слоистая панель | 1979 |
|
SU806833A1 |
| ИНТЕГРАЛЬНАЯ ПАНЕЛЬ МИНИМАЛЬНОЙ МАССЫ ИЗ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ ДЛЯ ОБВОДООБРАЗУЮЩИХ АГРЕГАТОВ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2013 |
|
RU2542801C2 |
| ПОДРЕЛЬСОВАЯ ПРОКЛАДКА | 2005 |
|
RU2288314C1 |
| КРЫЛО С УПРАВЛЯЕМОЙ ЗАКРУТКОЙ | 2018 |
|
RU2696138C1 |
| ПРОКЛАДКА-АМОРТИЗАТОР ДЛЯ РЕЛЬСОВОГО СКРЕПЛЕНИЯ | 2010 |
|
RU2451123C2 |
| Слоистая панель | 1982 |
|
SU1048075A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИНТЕГРАЛЬНЫХ ХАРАКТЕРИСТИК ДЛЯ КОНСТРУКЦИЙ В ВИДЕ УПРУГИХ ПЛАСТИНОК И ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ, СООТВЕТСТВЕННО ФОРМА И ПОПЕРЕЧНОЕ СЕЧЕНИЕ КОТОРЫХ ИМЕЮТ ВИД ПРОИЗВОЛЬНОГО ТРЕУГОЛЬНИКА И ПАРАЛЛЕЛОГРАММА | 2002 |
|
RU2223475C1 |
| СПОСОБ ПОВЫШЕНИЯ ДИНАМИЧЕСКОЙ ЖЕСТКОСТИ ФУНДАМЕНТА ПРИ ВИБРАЦИОННОЙ НАГРУЗКЕ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2018 |
|
RU2687211C1 |
| КРОВЕЛЬНАЯ СЭНДВИЧ-ПАНЕЛЬ | 2024 |
|
RU2837209C1 |
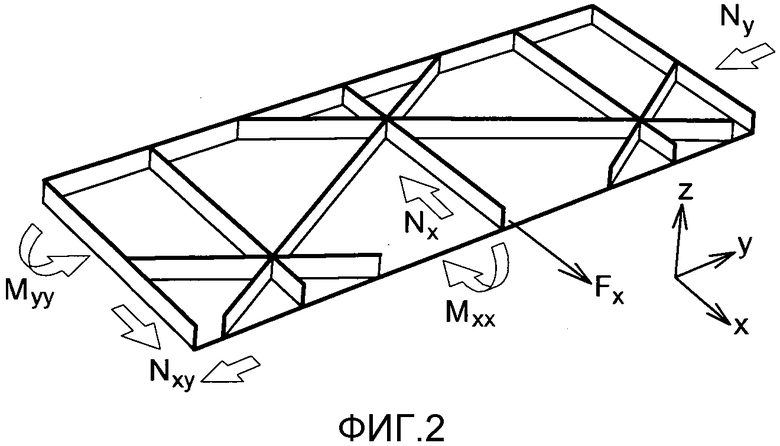
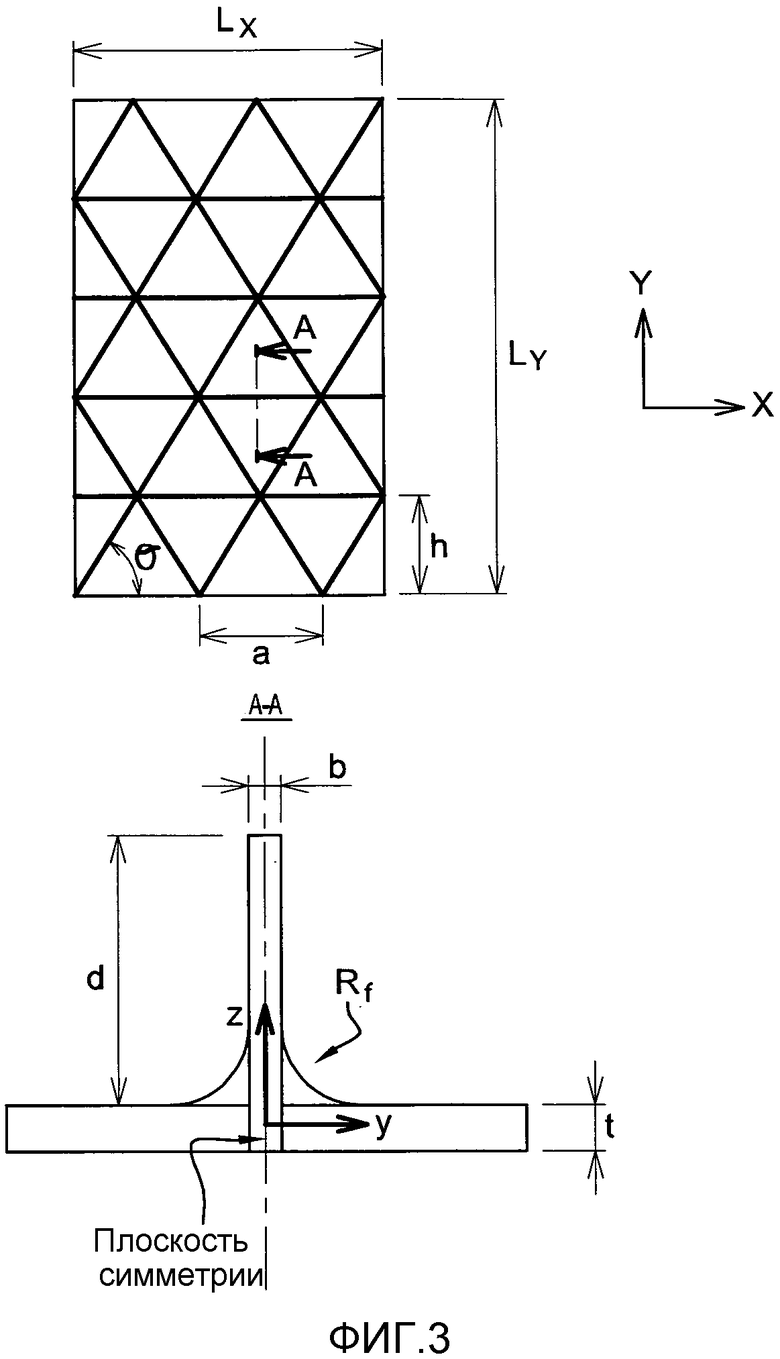
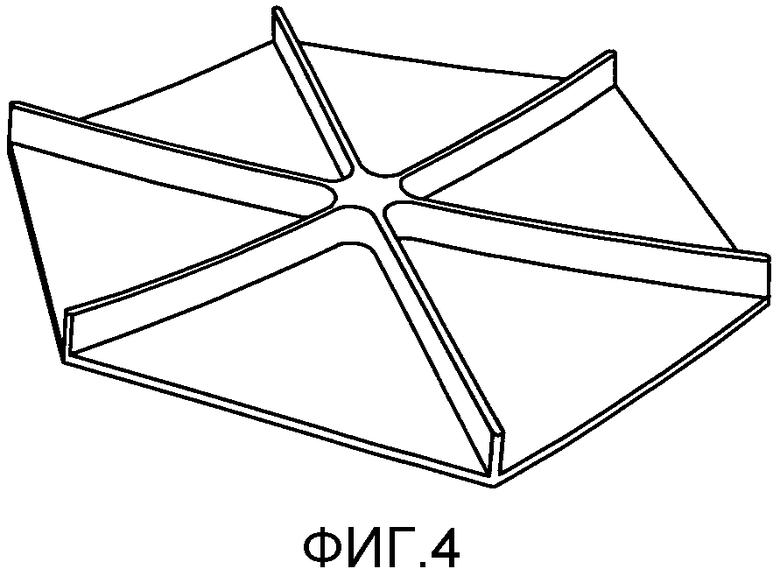
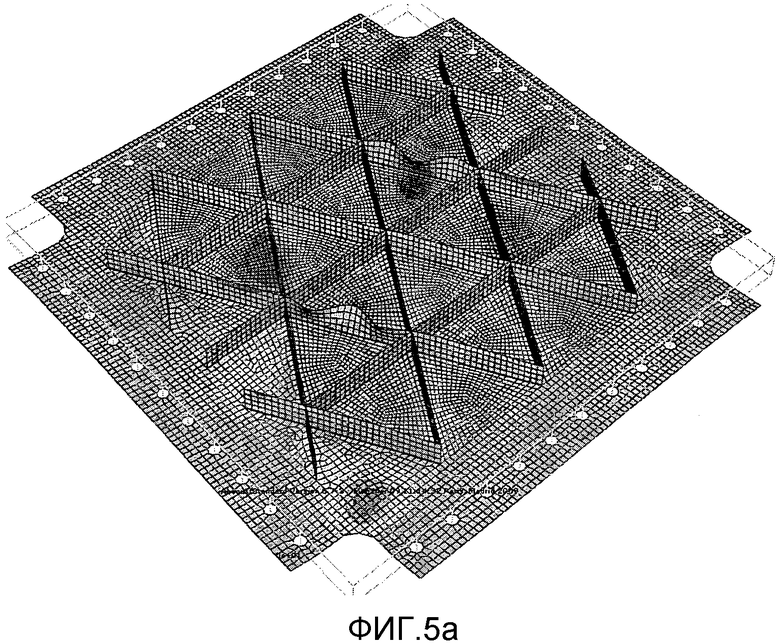
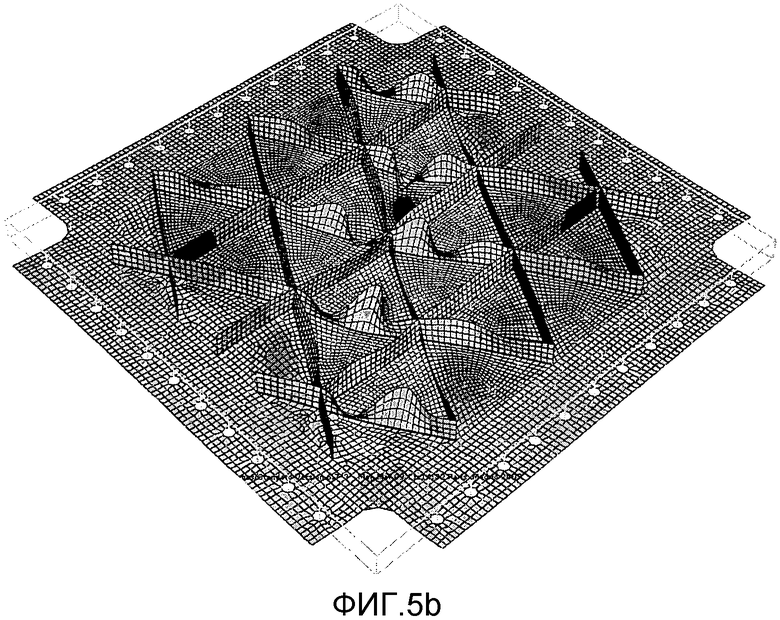
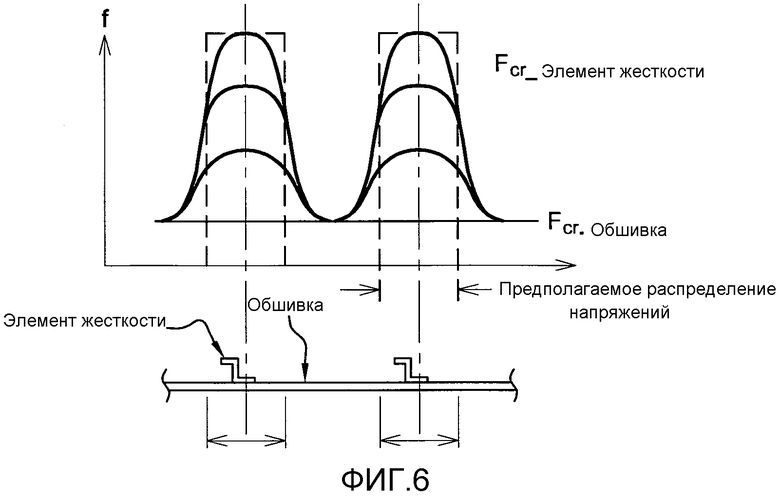
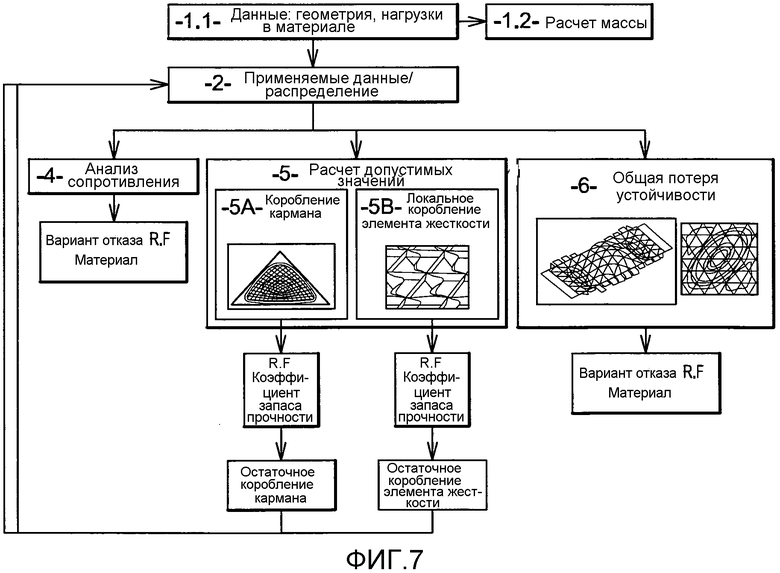
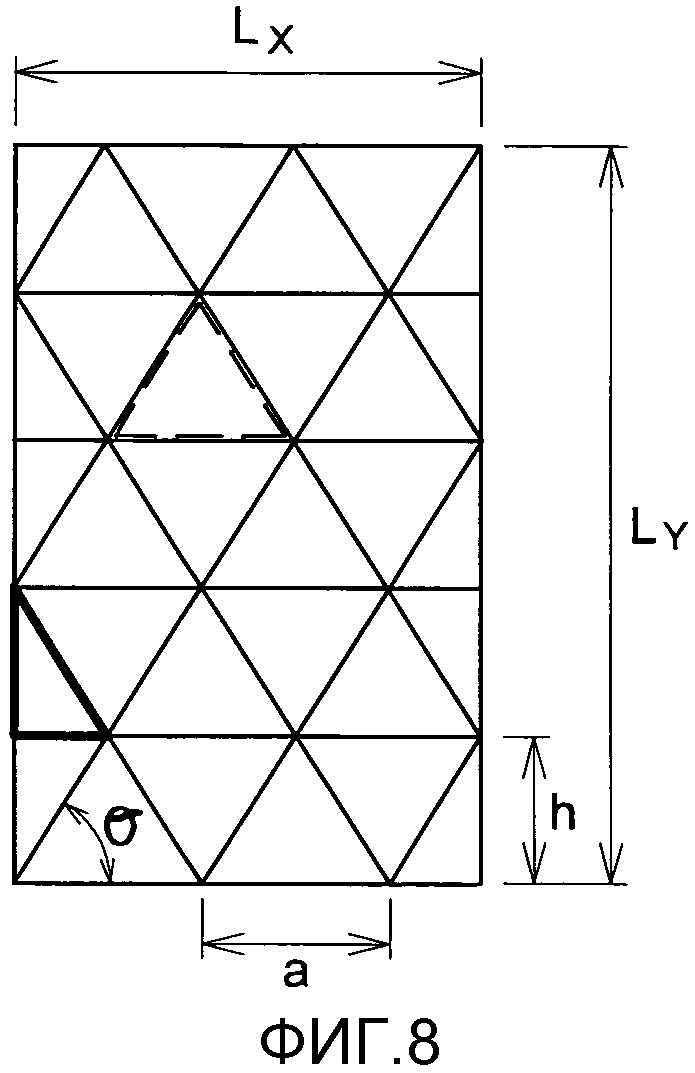
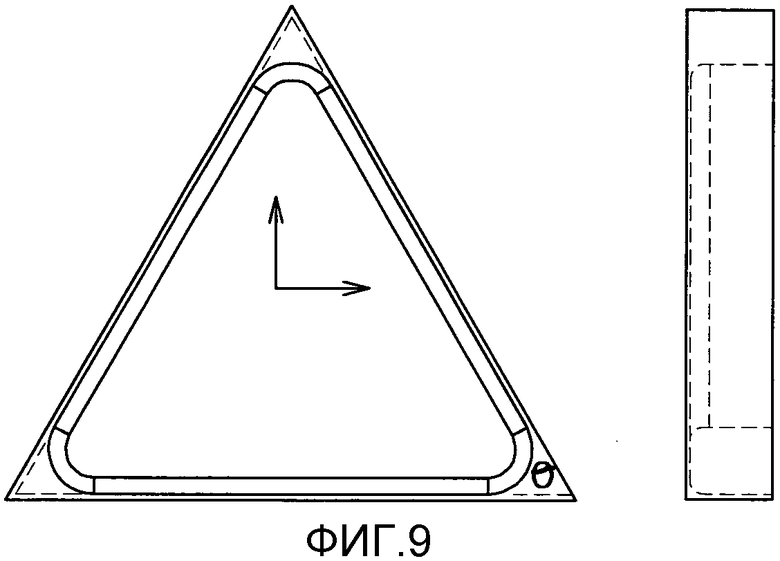
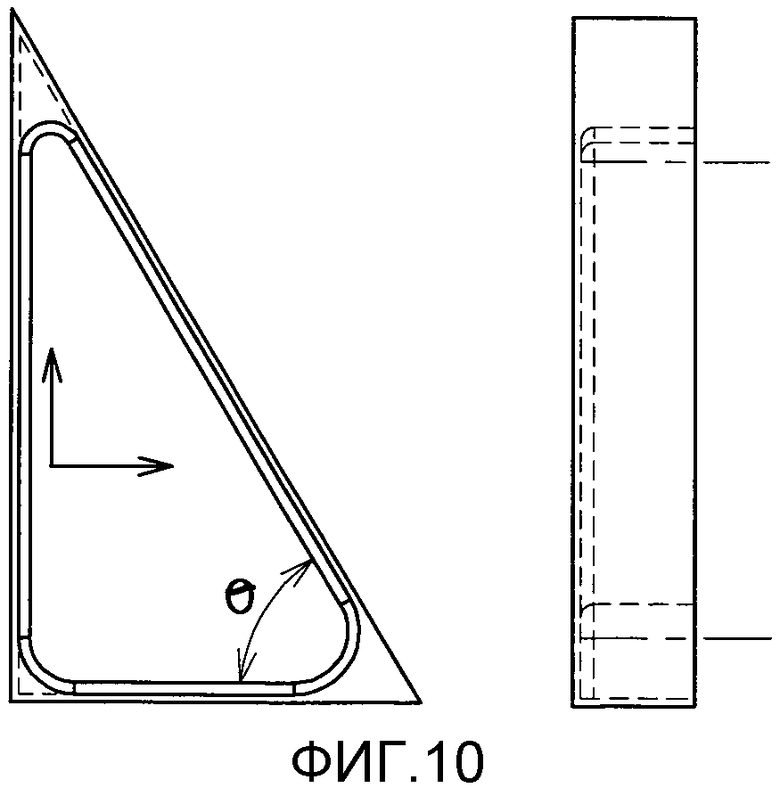
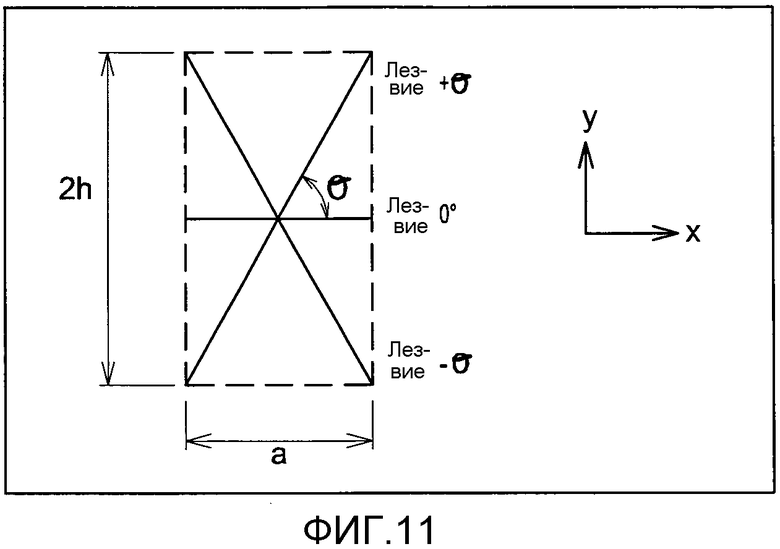
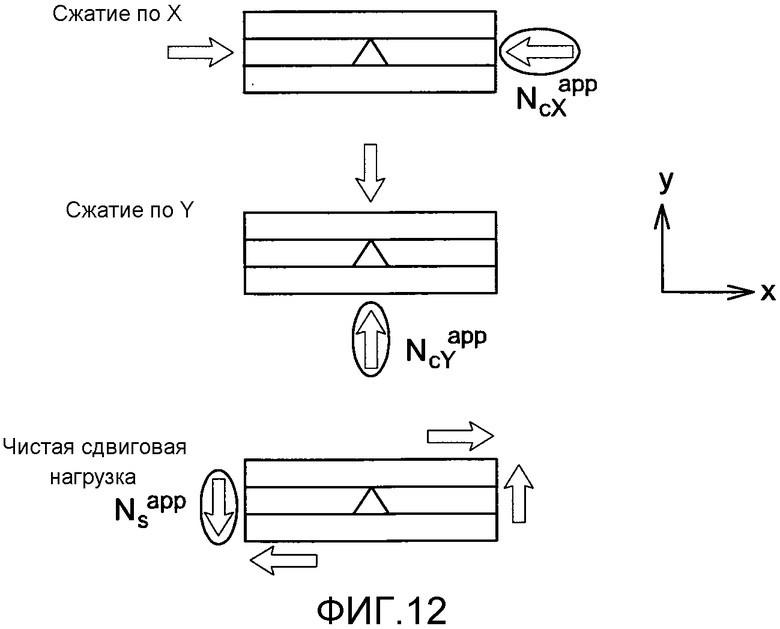
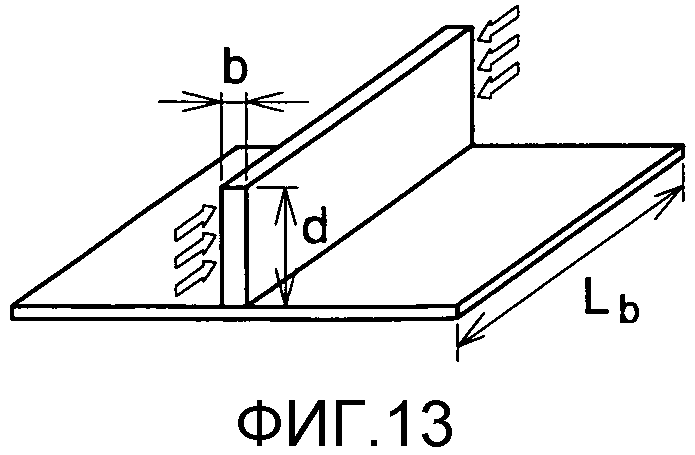
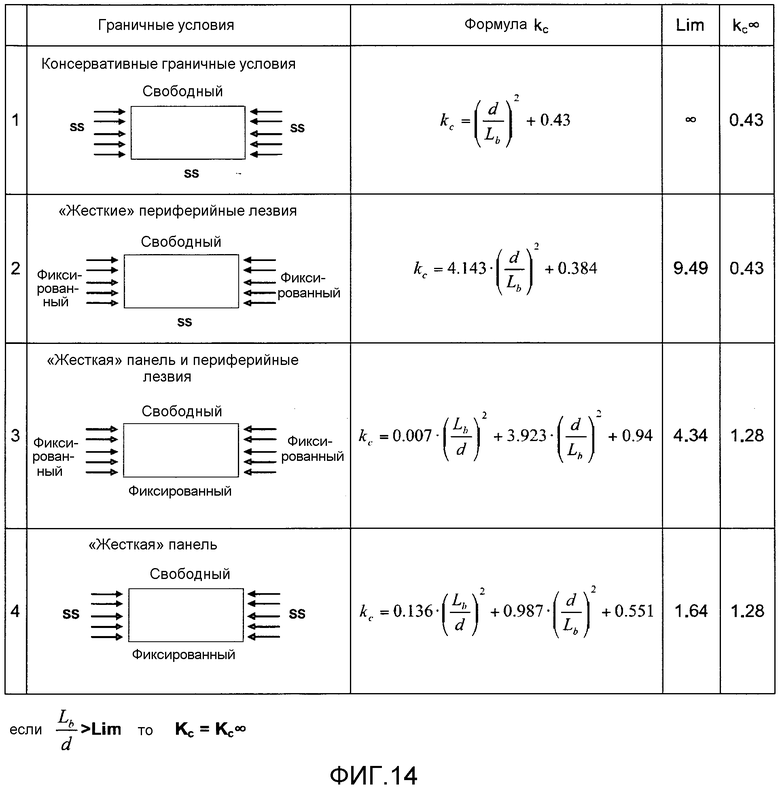
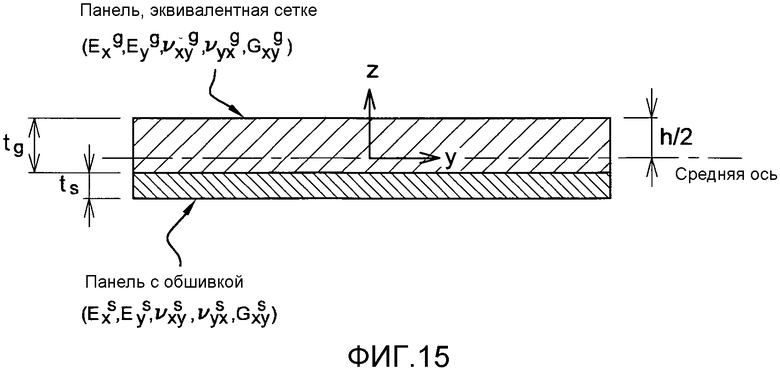
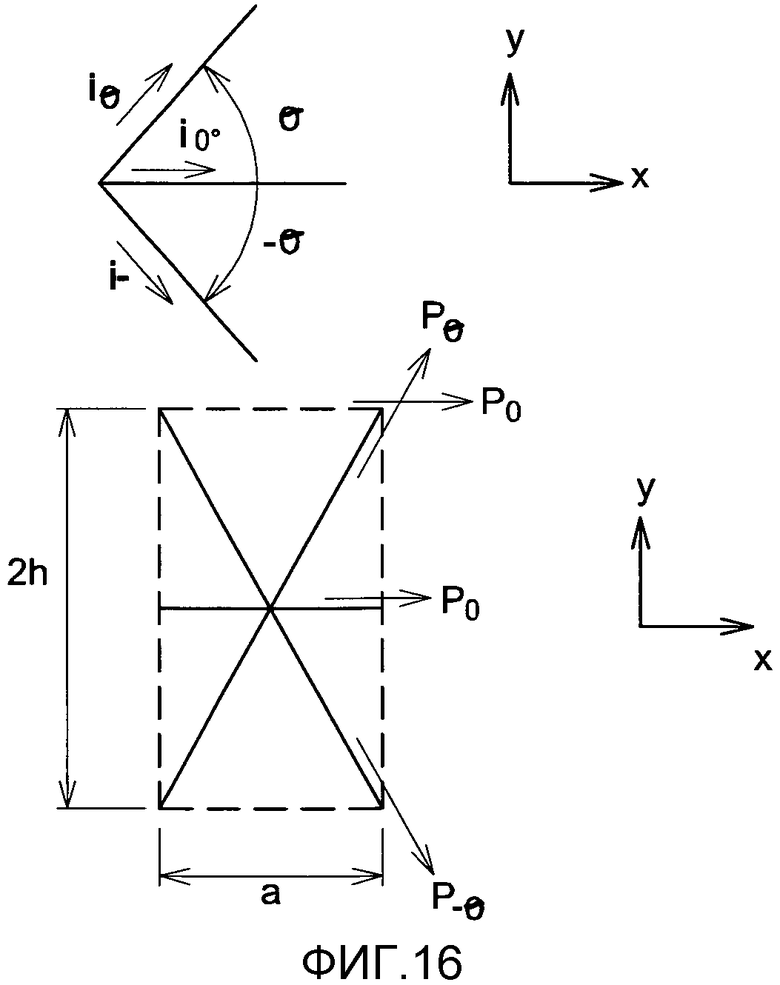
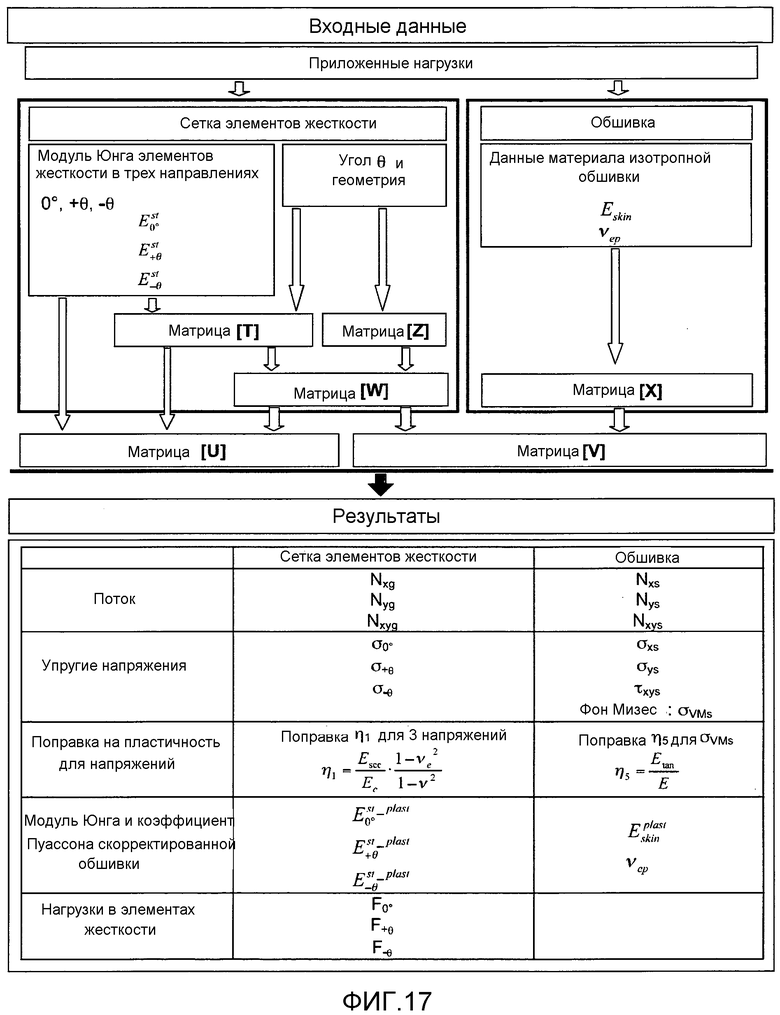
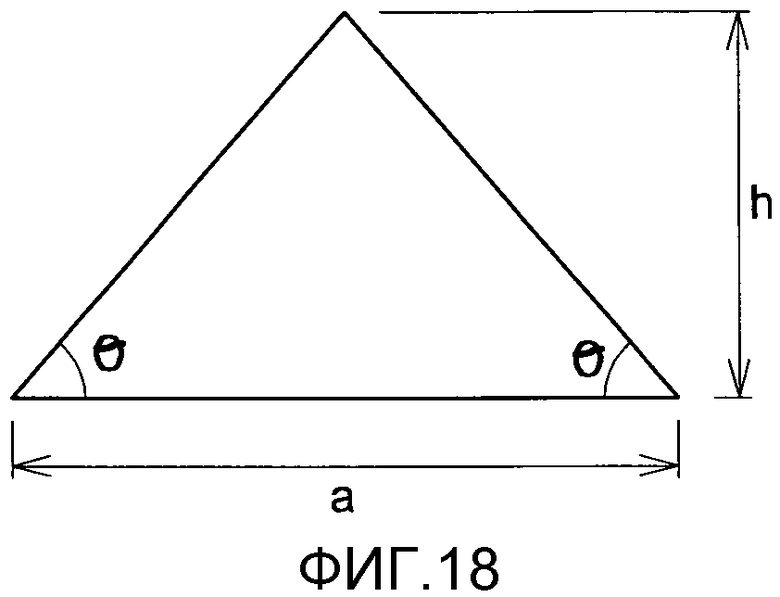
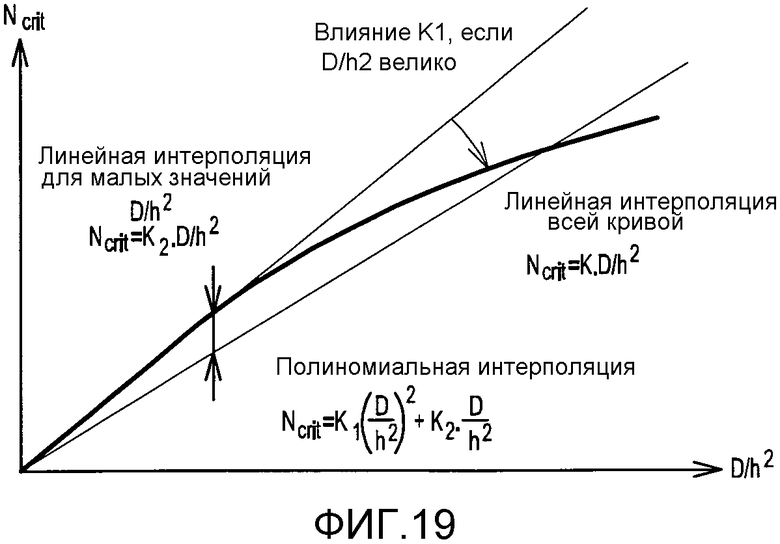
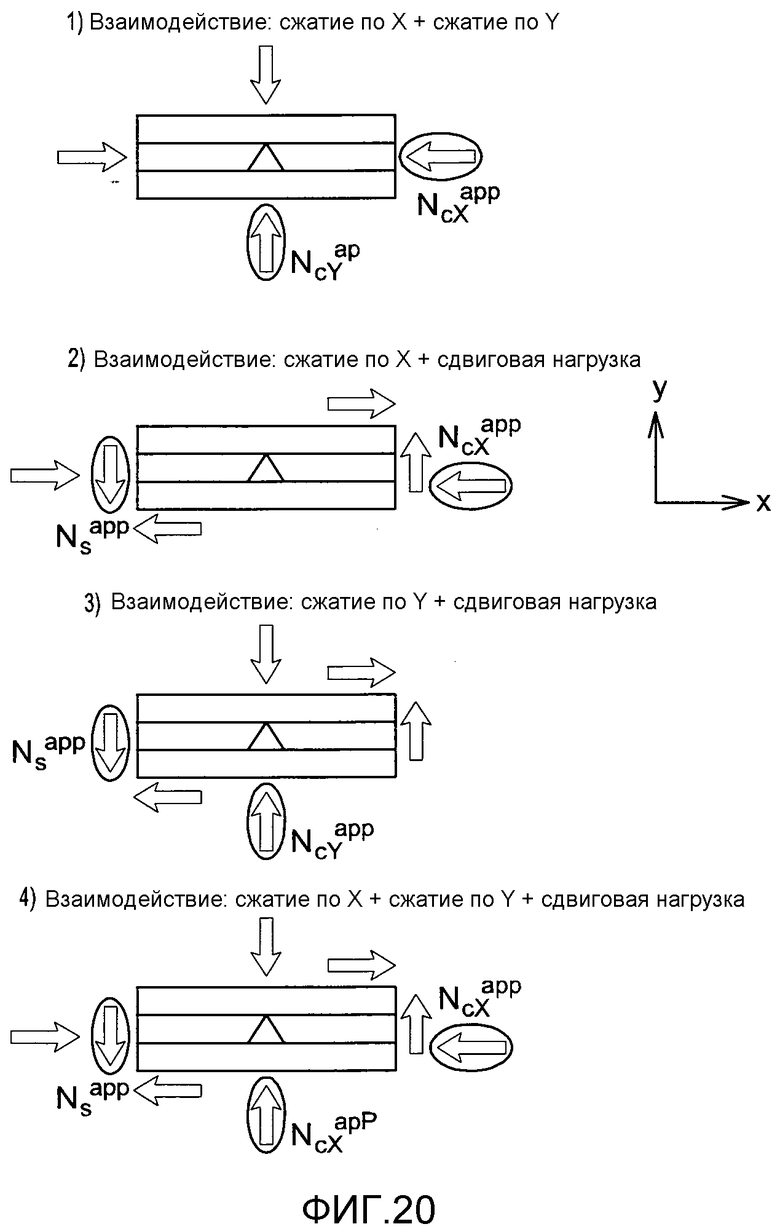
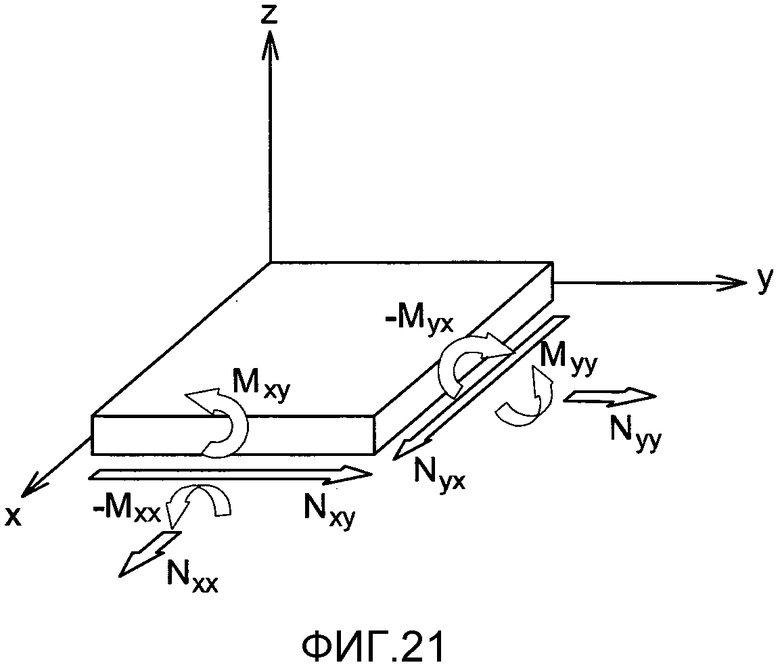
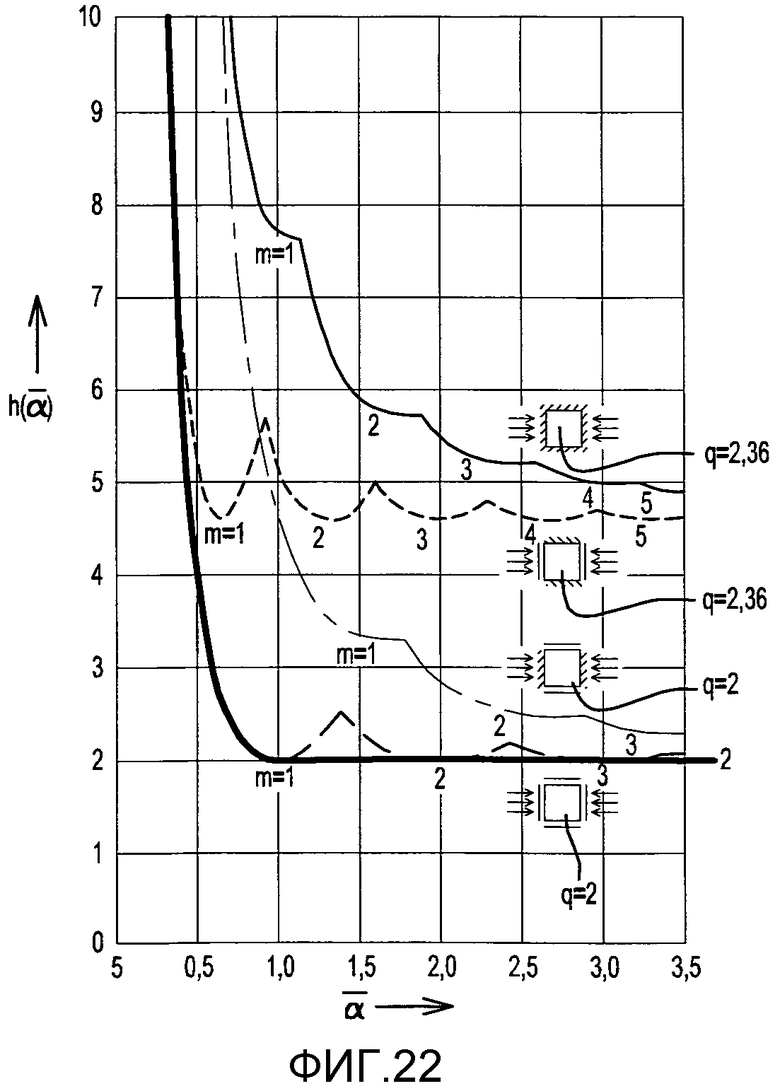
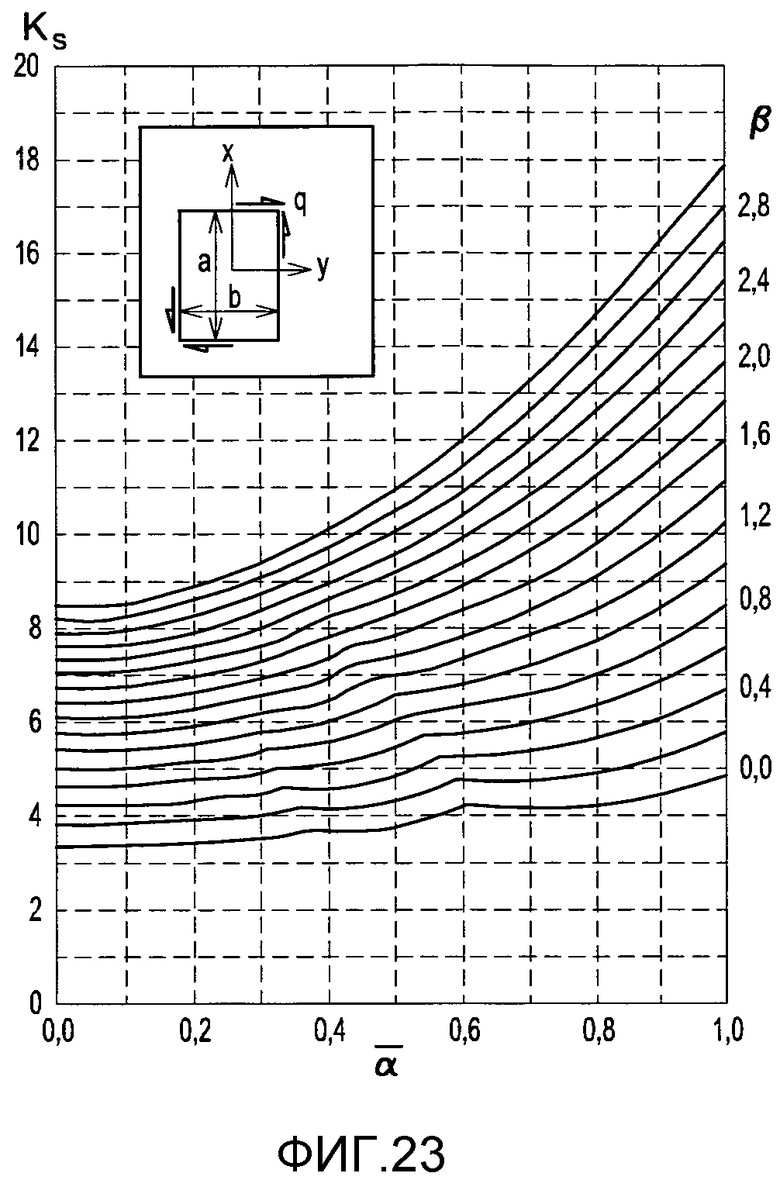
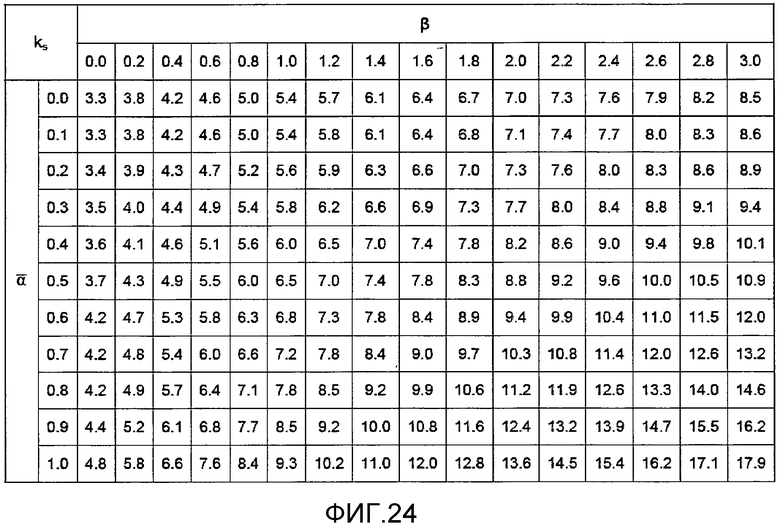
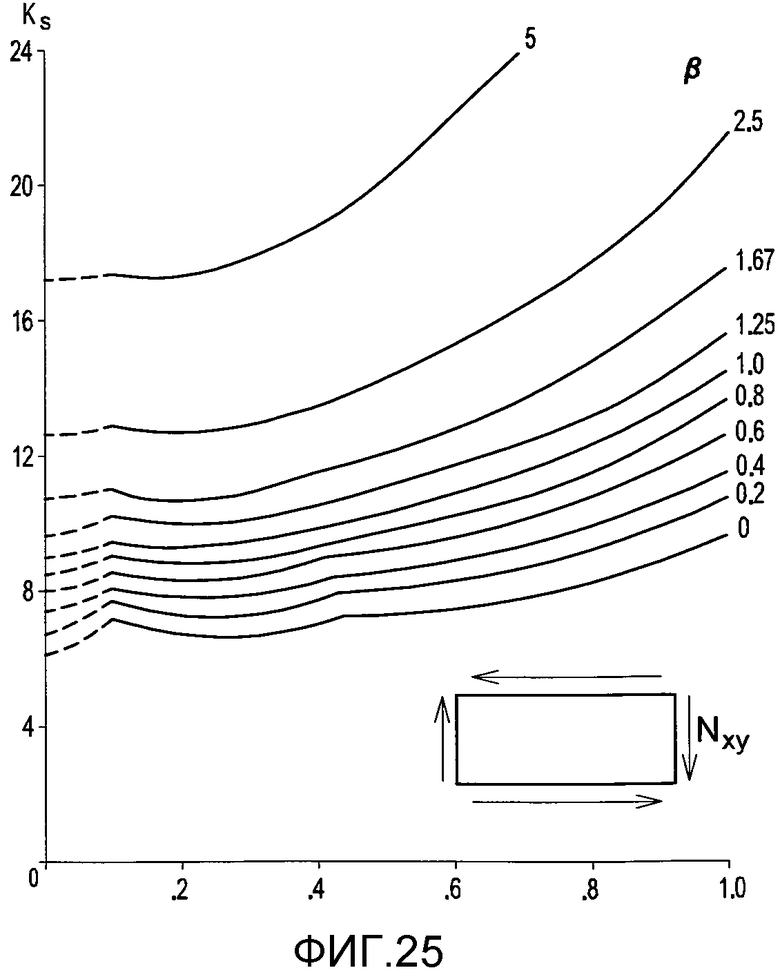
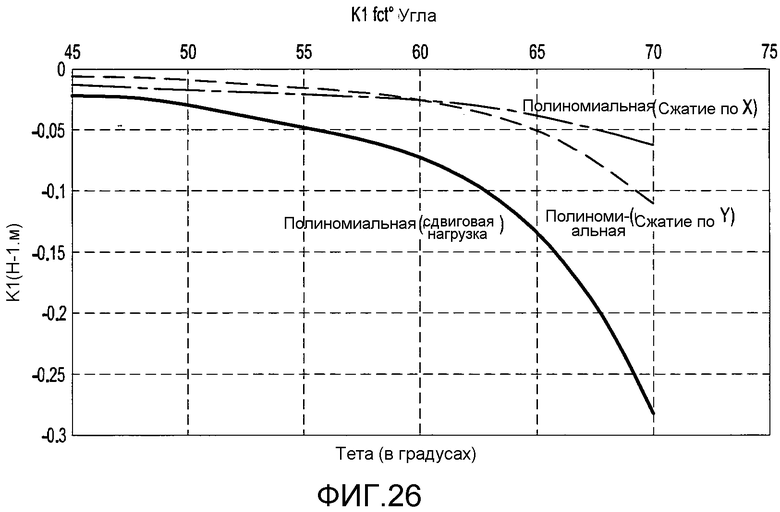
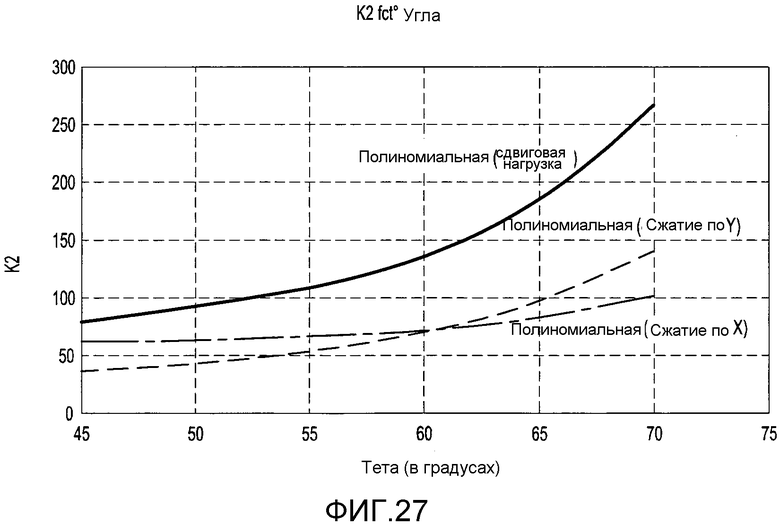
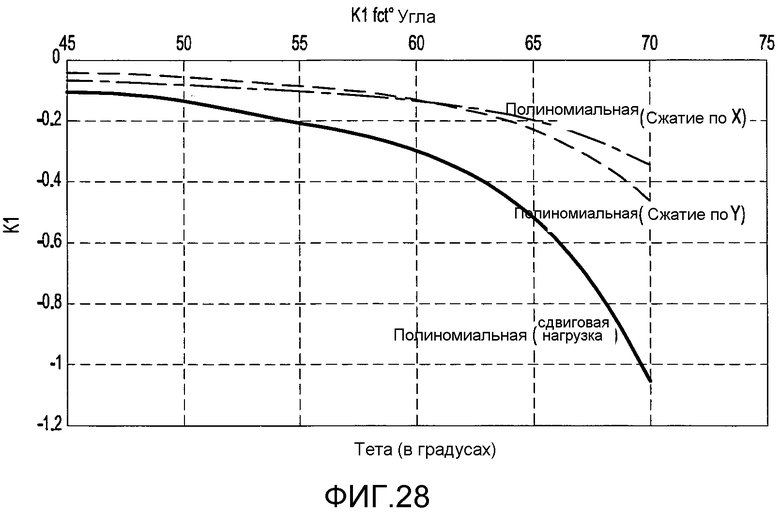
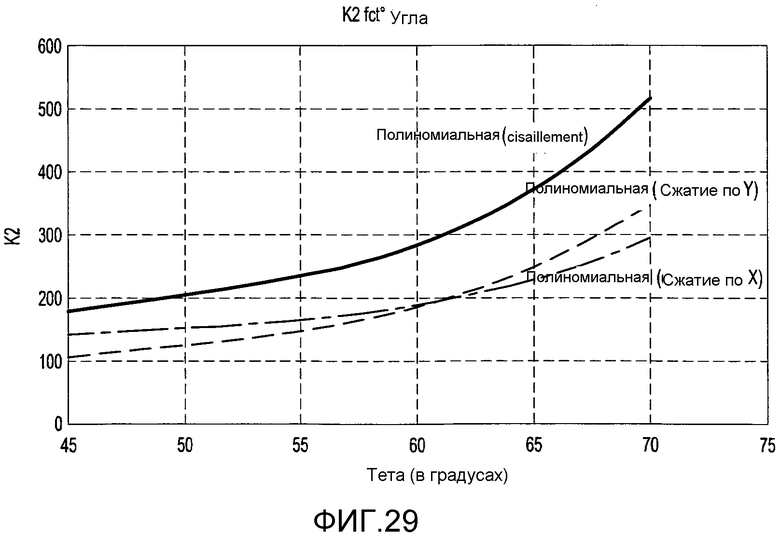
Изобретение относится к конструкциям усиленных панелей и касается расчета сопротивления таких конструкций, подвергшихся комбинированным нагрузкам. Панель выполнена из однородного и изотропного материала. Панель состоит из обшивки, армированной (сеткой) из трех параллельных пучков элементов жесткости, встроенных в панель. При этом карманы, определенные на обшивке группами элементов жесткости, имеют треугольную форму. Углы между пучками элементов жесткости таковы, что треугольные карманы имеют форму равнобедренного треугольника. При задании размеров аналитическим методом плоской панели учитывается перераспределение прилагаемых напряжений между панелью и сеткой элементов жесткости вследствие остаточного коробления элементов жесткости на этапе задания эффективного прямого сечения для каждого типа элемента жесткости; остаточного коробления кармана на этапе расчета эффективной толщины панели; пластичности прилагаемых внешних нагрузок на этапе реализации итерационного процесса над различными свойствами материала, в частности, модулем Юнга и коэффициентами Пуассона, и с помощью закона Рамберга-Осгуда. Достигается расчет допустимых напряжений для разных типов коробления и адаптированных коэффициентов запаса прочности, возможность установки панелей, усиленных треугольными карманами, минимизация массы конструкции. 8 з.п. ф-лы, 1 табл., 30 ил.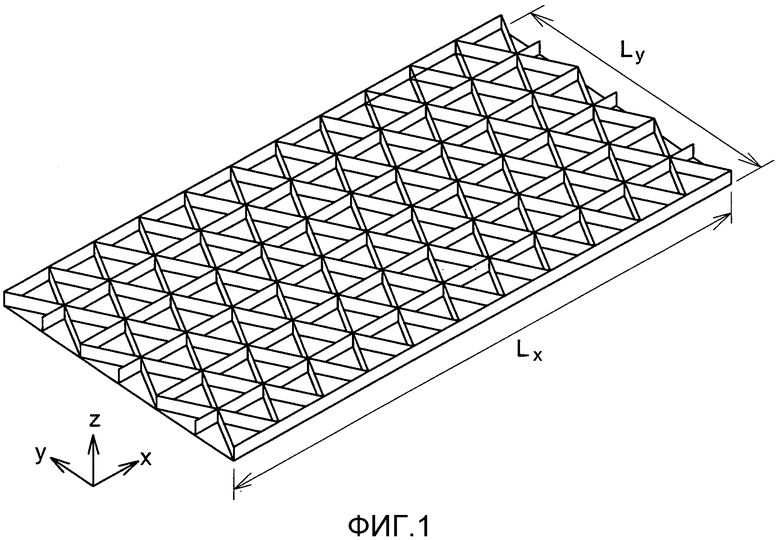
1. Способ задания размеров аналитическим методом, по существу, плоской панели, состоящей из однородного и изотропного материала, причем панель состоит из обшивки, армированной набором (именуемым “сеткой”) из трех параллельных пучков элементов жесткости, встроенных в панель, причем карманы, определенные на обшивке группами элементов жесткости, имеют треугольную форму, при этом элементы жесткости выполнены в форме пластин, причем усиленная панель должна соответствовать техническим условиям на механическое сопротивление заранее определенным внешним нагрузкам,отличающийся тем, что углы между пучками элементов жесткости таковы, что треугольные карманы имеют форму равнобедренного треугольника любого вида, причем способ учитывает перераспределение прилагаемых напряжений между панелью и сеткой элементов жесткости вследствие:
- остаточного коробления элементов жесткости, на этапе задания эффективного прямого сечения для каждого типа элемента жесткости, обозначаемого A0° st, A+θ st и A-θ st, для углов 0°, +θ или -θ соответственно,
- остаточного коробления кармана на этапе расчета эффективной толщины панели, обозначаемой ts_eff,
- пластичности прилагаемых внешних нагрузок, на этапе реализации итерационного процесса над различными свойствами материала, в частности, модулем Юнга и коэффициентами Пуассона: E0° st, E+θ st, E-θ st для элементов жесткости и Ex s, Ey s и νep st для обшивки, и с помощью закона Рамберга-Осгуда.
2. Способ по п.1, отличающийся тем, что он включает в себя этап, на котором корректируют прилагаемые нагрузки с учетом пластичности, с использованием итерационного метода для расчета пластических напряжений, осуществляемого, пока пять параметров материала (E0° st, E+θ st, E-θ st, Eskin, νep), введенные в начале процесса, по существу, не сравняются с соответствующими параметрами, полученными в результате расчета пластического напряжения.
3. Способ по п.1, отличающийся тем, что он включает в себя этап, на котором рассчитывают допустимый поток коробления и коэффициент запаса прочности для карманов в виде равнобедренного треугольника, причем прилагаемые напряжения, подлежащие учету для расчета коэффициента запаса прочности, являются напряжениями, действующими только на обшивку, причем используемые внешние потоки будучи потоками, прилагаемыми к обшивке, не соответствуют усиленной панели, испытывающей полную нагрузку.
4. Способ по п.3, отличающийся тем, что он включает в себя два подэтапа, на которых рассчитывают допустимые значения для пластин, подвергающихся вариантам чистой нагрузки (сжатию в двух направлениях в плоскости, сдвиговой нагрузке), с использованием метода конечных элементов, после чего вычисляют кривые взаимодействия между этими вариантами чистой нагрузки.
5. Способ по п.4, отличающийся тем, что расчет допустимых значений включает в себя подэтапы, на которых:
- создают параметрическую модель FEM треугольной пластины,
- испытывают различные комбинации для получения результатов коробления,
- получают параметры, согласующиеся с аналитической полиномиальной формулой.
6. Способ по п.4, отличающийся тем, что в случае чистой нагрузки кривые взаимодействия задают на подэтапах, на которых
- создают модели конечных элементов нескольких треугольных пластин с разными углами равнобедренного треугольника, причем угол (θ) равнобедренного треугольника определяется как угол при основании равнобедренного треугольника, при этом
- для каждого угла равнобедренного треугольника:
1/ производят расчет посредством модели конечных элементов для определения допустимого потока складкообразования (без поправки на пластичность) для различных значений толщины пластины,
2/ отслеживают кривую допустимого потока коробления согласно отношению 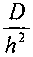 (D - жесткость пластины, h - высота треугольника), причем эта кривая определяется для малых значений отношения
(D - жесткость пластины, h - высота треугольника), причем эта кривая определяется для малых значений отношения 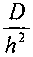 , уравнением второй степени согласно этому отношению, коэффициенты K1 и K2 которого зависят от угла и рассматриваемого варианта нагрузки,
, уравнением второй степени согласно этому отношению, коэффициенты K1 и K2 которого зависят от угла и рассматриваемого варианта нагрузки,
3/ отслеживают постепенное изменение коэффициентов K1 и K2 полиномиального уравнения в соответствии с углом при основании равнобедренного треугольника, причем эти коэффициенты отслеживаются в соответствии с углом рассматриваемых треугольных пластин, и интерполируют для определения полиномиального уравнения, что позволяет вычислять константы при любом угле равнобедренного треугольника.
7. Способ по п.4, отличающийся тем, что в случае комбинированной нагрузки используют гипотезу, согласно которой, если некоторые компоненты комбинированной нагрузки находятся в состоянии натяжения, эти компоненты не учитываются при расчете, и тем, что кривые взаимодействия задают на подэтапах, на которых
- создают модели конечных элементов нескольких треугольных пластин с разными углами равнобедренного треугольника, причем угол (θ) равнобедренного треугольника определяется как угол при основании равнобедренного треугольника,
- для каждого угла,
1/ производят расчет посредством модели конечных элементов (FEM) для определения собственного значения коробления, соответствующего разным распределениям внешних нагрузок,
2/ отслеживают кривые взаимодействия для каждого угла и каждой комбинации нагрузок, и аппроксимируют эти кривые с помощью одного уравнения, описывающего все эти комбинации,
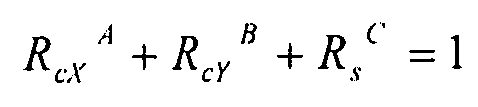 (или
(или 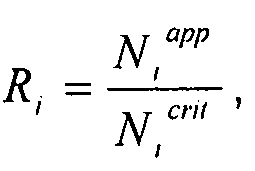 , уравнения, в которых R
i представляет величину нагрузки, и Ni app и Ni crit - прилагаемые потоки и критические потоки для i=cX, cY или s, в соответствии с вариантами сжатия по осям X и Y и согласно варианту сдвиговой нагрузки), где A, B, C - эмпирические коэффициенты.
, уравнения, в которых R
i представляет величину нагрузки, и Ni app и Ni crit - прилагаемые потоки и критические потоки для i=cX, cY или s, в соответствии с вариантами сжатия по осям X и Y и согласно варианту сдвиговой нагрузки), где A, B, C - эмпирические коэффициенты.
8. Способ по п.7, отличающийся тем, что в случае свободно опирающихся или фиксированных пластин в виде равнобедренного треугольника, в случае комбинированной нагрузки, используют кривую взаимодействия 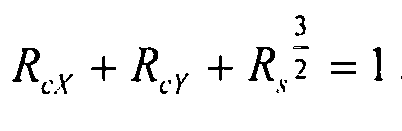 , для всех вариантов нагрузки.
, для всех вариантов нагрузки.
9. Способ по любому из предыдущих пунктов, отличающийся тем, что он включает в себя этап, на котором рассчитывают общую потерю устойчивости, дающую данные по допустимому потоку коробления, и коэффициенты запаса прочности для плоской усиленной панели в условиях чистой или комбинированной нагрузки, причем прилагаемые потоки, подлежащие учету для расчета коэффициента запаса прочности, являются внешними потоками усиленной панели.
| Craig Collier, Phil Yarrington, Barry van West: "Composite, Grid-Stiffened Panel Design for Posts Buckling Using Hypersizer" Collection of Technical Papers - AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Material Conference, vol | |||
| Топчак-трактор для канатной вспашки | 1923 |
|
SU2002A1 |
| JP 2000193536 A, 14.07.2000 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ГРАНИЧНЫХ УСЛОВИЙ И КРИТЕРИЕВ ФОРМООБРАЗОВАНИЯ МЕТАЛЛИЧЕСКИХ ДЕТАЛЕЙ | 2006 |
|
RU2336135C2 |
| Кипятильник для воды | 1921 |
|
SU5A1 |
| US 2004055349 A1, 25.03.2004 | |||
Авторы
Даты
2015-09-20—Публикация
2010-09-13—Подача