Область техники, к которой относится изобретение
Настоящее изобретение относится, по существу, к перемежению в системе связи, а более конкретно к способу оптимизации параметров в соответствии с размером перемежителя для перемежения с частичным обратным порядком битов (Ч-ОПБ) и использующему его перемежителю.
Уровень техники
Хотя субблочный канальный перемежитель, разработанный согласно спецификации IS-2000, выпуск C(1×EV-DV) F/L, выполняет Ч-ОПБ операцию для перестановки строк так же, как существующий канальный перемежитель, разработанный согласно спецификации IS-2000, выпуск А/В, субблочный канальный перемежитель отличается от канального перемежителя тем, что формирователь иначе формирует адреса считывания и требует полного учета влияния выбранных параметров перемежителя на выбор символов квазидополнительного турбокода (КДТК, QCTC).
Следовательно, существует потребность в анализе принципов функционирования субблочного канального перемежителя и канального перемежителя и в создании критерия формирования оптимальных параметров для канальных перемежителей. Оптимальные параметры будут обеспечивать наилучшую эффективность в канальных перемежителях, скомпонованных в соответствии с IS-2000, выпуск А/В, и IS-2000, выпуск С.
Сущность изобретения
Задачей настоящего изобретения является, по существу, устранение по меньшей мере указанных выше проблем и/или недостатков и обеспечение по меньшей мере преимуществ, описанных ниже. Соответственно задачей настоящего изобретения является создание способа оптимизации параметров для Ч-ОПБ перемежения и перемежителя, использующего оптимизированные параметры.
Другой задачей настоящего изобретения является создание способа оптимизации параметров m и J в соответствии с размером перемежителя для Ч-ОПБ перемежения и перемежителя, использующего их.
Для решения указанных выше и других задач предложены Ч-ОПБ перемежитель и способ оптимизации параметров в соответствии с размером перемежителя для Ч-ОПБ перемежителя. Ч-ОПБ перемежитель последовательно, по столбцам, конфигурирует поток входных данных размера N в матрицу, имеющую 2m строк и (J-1) столбцов и R строк в J-ом столбце. Ч-ОПБ перемежитель перемежает конфигурированные данные и построчно считывает перемеженные данные. Здесь, N, m, J и R заданы следующим образом:
Краткое описание чертежей
Указанные выше задачи, признаки и преимущества настоящего изобретения станут более очевидны из последующего подробного описания предпочтительных вариантов осуществления изобретения с учетом приложенных чертежей.
Фиг.1 иллюстрирует Ч-ОПБ перемежение при N=384, m=7 и J=3 согласно варианту осуществления настоящего изобретения.
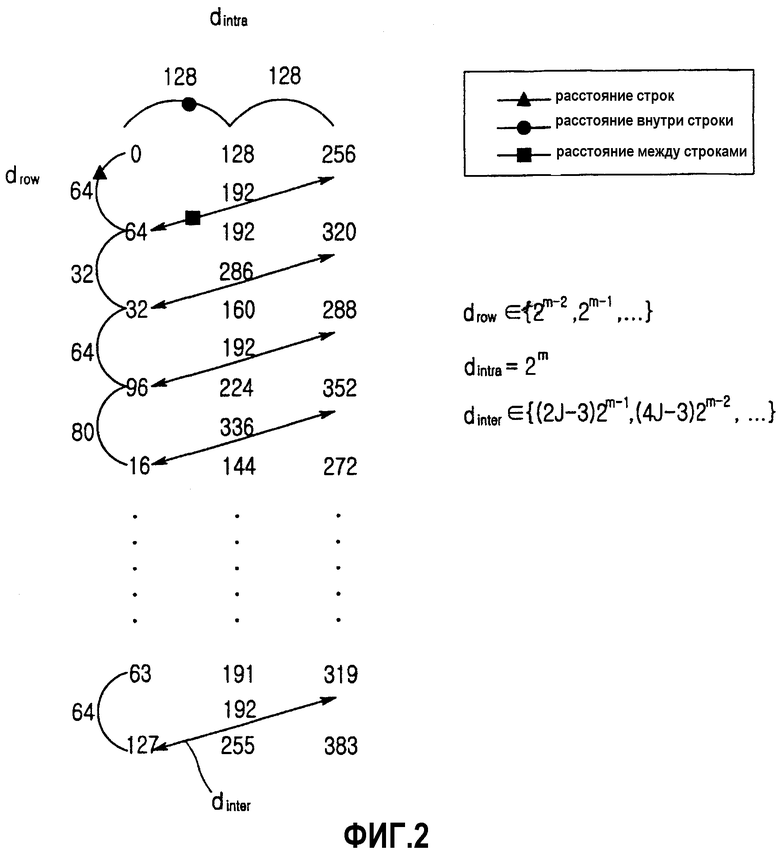
Фиг.2 иллюстрирует расстояния между адресами считывания после Ч-ОПБ перемежения при N=384, m=7 и J=3 согласно варианту осуществления настоящего изобретения.
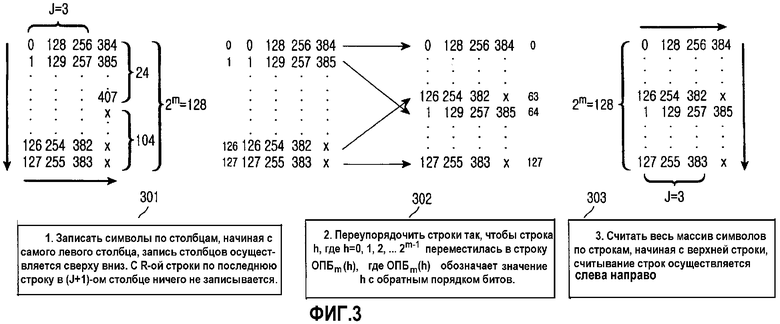
Фиг.3 иллюстрирует Ч-ОПБ перемежение при N=408, m=7, J=3 и R=24 согласно варианту осуществления настоящего изобретения.
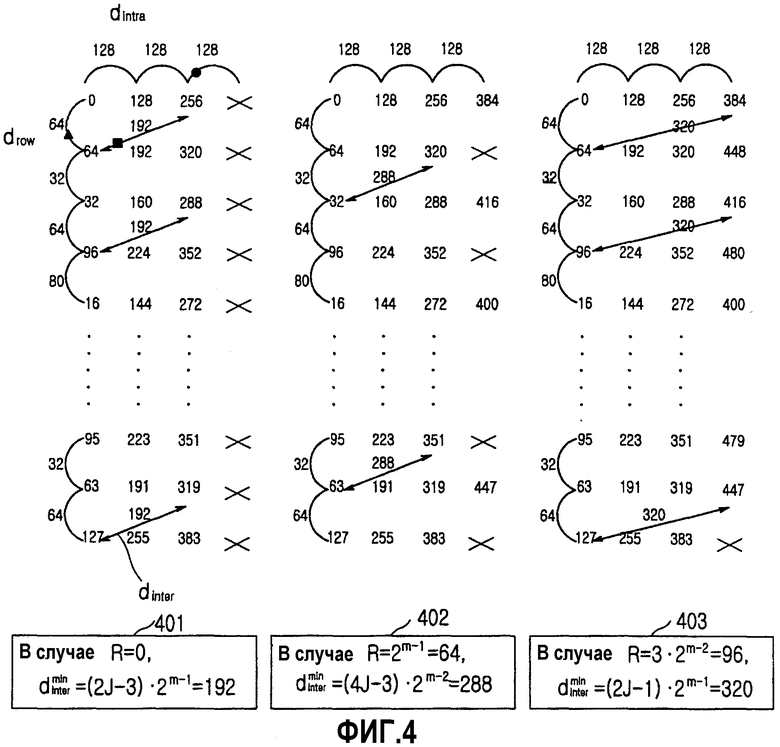
Фиг.4 иллюстрирует минимальное расстояние внутри строки после Ч-ОПБ перемежения при N=408, m=7 и J=3 согласно варианту осуществления настоящего изобретения.
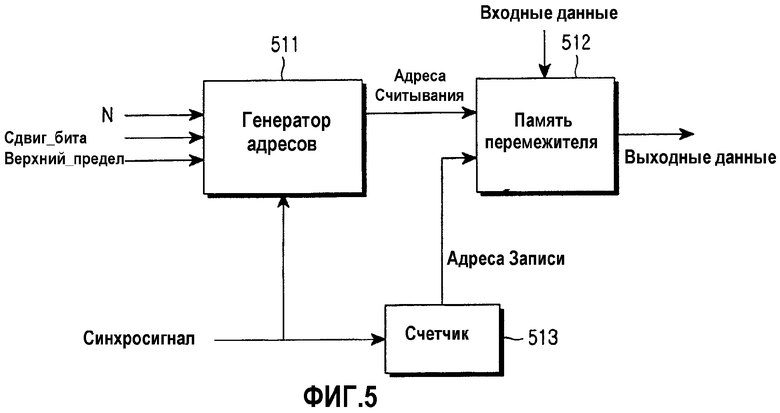
Фиг.5 является функциональной схемой перемежителя, в котором использован вариант осуществления настоящего изобретения.
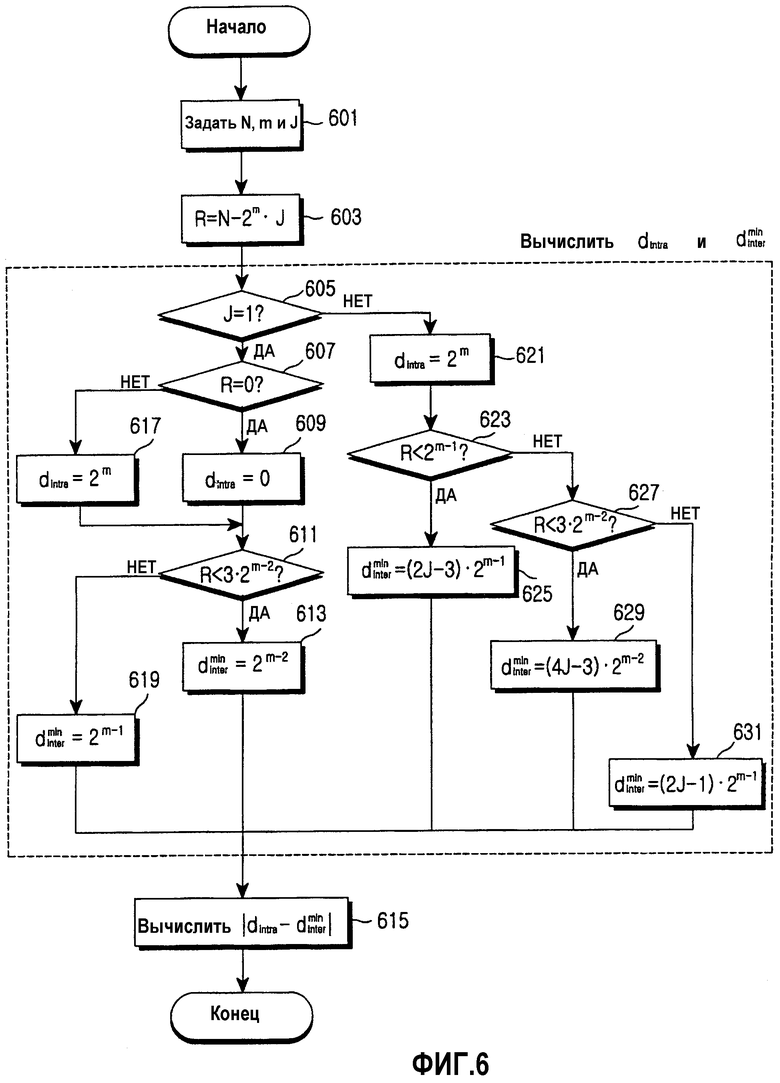
Фиг.6 является блок-схемой, поясняющей первый пример операции определения оптимальных параметров перемежителя согласно варианту осуществления настоящего изобретения.
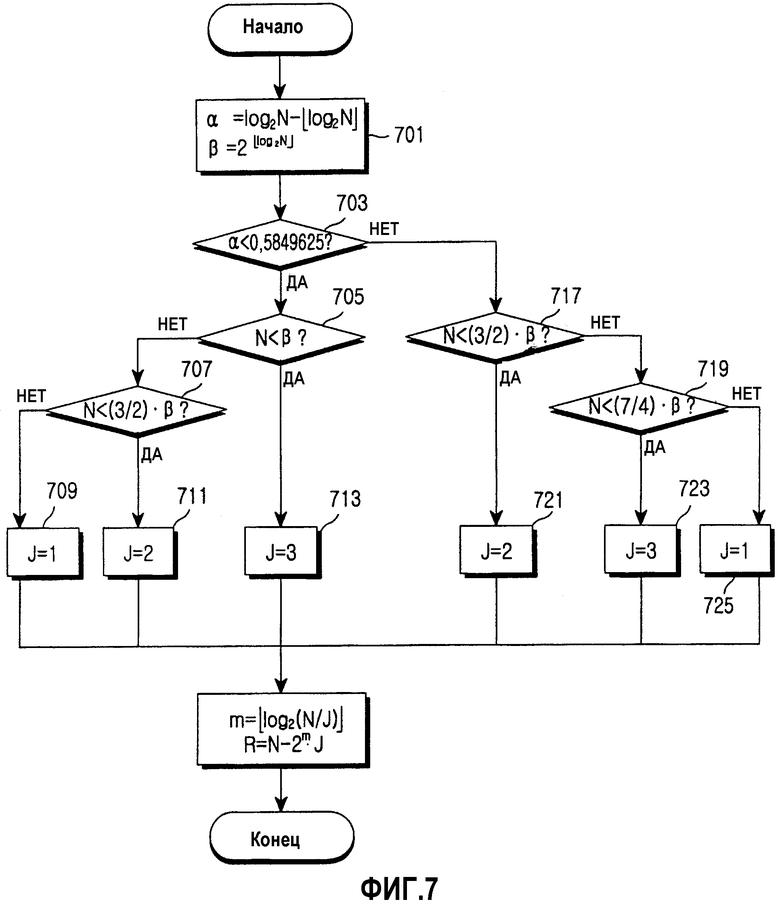
Фиг.7 является блок-схемой, поясняющей другой пример операции определения оптимальных параметров перемежителя согласно варианту осуществления настоящего изобретения.
Подробное описание предпочтительных вариантов осуществления
Ниже, со ссылкой на приложенные чертежи, подробно описано несколько предпочтительных вариантов осуществления настоящего изобретения. В чертежах использована сквозная нумерация. В последующем описании, для ясности, опущено подробное описание известных функций или конфигураций.
Ниже будет описано Ч-ОПБ перемежение, к которому применяются разные варианты осуществления настоящего изобретения, и принципы определения параметров для оптимального Ч-ОПБ перемежения согласно вариантам осуществления настоящего изобретения.
Фиг.5 является функциональной схемой Ч-ОПБ перемежителя, в котором использован вариант осуществления настоящего изобретения. Согласно фиг.5 генератор 511 адресов принимает размер N перемежителя, первый параметр m (то есть Сдвиг_Бита), второй параметр J (то есть Верхний_Предел) и сигнал синхронизации Синхросигнал, и формирует адреса считывания для считывания символов битов из памяти 512 перемежителя. Параметры m и J определяются в контроллере более высокого уровня (не изображен) и подаются на генератор 511 адресов или определяются в соответствии с размером N перемежителя в генераторе 511 адресов. Память 512 перемежителя в режиме записи последовательно сохраняет символы битов входных данных в адресах записи, соответствующих значениям счетчика 513, и в режиме считывания выводит символы битов из адресов считывания, принятых от генератора 511 адресов. Счетчик 513 принимает сигнал синхронизации. Синхросигнал, формирует значение счетчика и подает его в качестве адреса записи АДР Записи в память 512 перемежителя.
Как описано выше, Ч-ОПБ перемежитель последовательно записывает входные данные в память 512 перемежителя в режиме записи и считывает данные из памяти 512 перемежителя в соответствии с адресами считывания, сформированными генератором 511 адресов. Более подробно Ч-ОПБ перемежитель описан в заявке на патент Кореи № 1998-54131, зарегистрированной 10 декабря 1998 года.
При функционировании генератор 511 адресов формирует адрес считывания Ai для перестановки символа посредством формулы
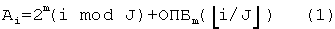
где i=0, 1,..., N-1 и N=2m×J.
В уравнении (1) N обозначает размер последовательности входных данных перемежителя, а m и J являются параметрами перемежителя, называемыми Сдвиг_Бита и Верхний_Предел соответственно.
Фиг.1 иллюстрирует Ч-ОПБ перемежение при N=384, m=7 и J=3. Согласно фиг.1 матрица перемежения имеет 2m строки, начинающиеся индексом 0 и J столбцов, начинающихся индексом 0. После этапа 101 индекс строки и индекс столбца символа в результирующей матрице выражаются как 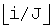 и (i mod J), соответственно. Следовательно, после
и (i mod J), соответственно. Следовательно, после 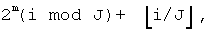 i-ый символ последовательности входных данных имеет в качестве адреса считывания номер, соответствующий
i-ый символ последовательности входных данных имеет в качестве адреса считывания номер, соответствующий 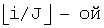 строке и (i mod J)-му столбцу. В каждой строке имеется J символов, и расстояние между символами в строке составляет 2m.
строке и (i mod J)-му столбцу. В каждой строке имеется J символов, и расстояние между символами в строке составляет 2m.
На этапе 102 над индексом строки 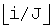 производится операция ОПБ. Если расстояние между символами в соседних строках одного столбца является расстоянием строк drow, то операция ОПБ над индексами строк приводит к такой перестановке строк, чтобы два минимальных расстояния строк drow составляли 2m-2 и 2m-1, как иллюстрируется фиг.2. Следовательно, после
производится операция ОПБ. Если расстояние между символами в соседних строках одного столбца является расстоянием строк drow, то операция ОПБ над индексами строк приводит к такой перестановке строк, чтобы два минимальных расстояния строк drow составляли 2m-2 и 2m-1, как иллюстрируется фиг.2. Следовательно, после 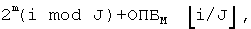 i-й символ последовательности входных данных имеет в качестве адреса считывания номер, соответствующий ОПБm
i-й символ последовательности входных данных имеет в качестве адреса считывания номер, соответствующий ОПБm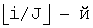 строке и (i mod J)-му столбцу в третьей матрице слева. В итоге последовательность адресов считывания формируется посредством перестановок строк матрицы 2m×J в Ч-ОПБ перемежителе. Матрица с переставленными строками считывается сначала по строкам сверху вниз с последующим считыванием каждой строки слева направо.
строке и (i mod J)-му столбцу в третьей матрице слева. В итоге последовательность адресов считывания формируется посредством перестановок строк матрицы 2m×J в Ч-ОПБ перемежителе. Матрица с переставленными строками считывается сначала по строкам сверху вниз с последующим считыванием каждой строки слева направо.
Для ясности описания расстояние между соседними адресами в одной строке определено как «расстояние внутри строки dintra». Если J≠1, то dintra=2m. Если J=1, то расстояние внутри строки отсутствует (не определено).
Расстояние между соседними адресами в разных строках, а именно расстояние между последним адресом в строке и первым адресом в следующей строке, определено как «расстояние между строками dinter». Расстояние dinter является одной из нескольких величин, вычисляемых как функция параметров m и J. Когда m и J определены, результирующее минимальное расстояние между строками
dinter определено как  .
.
Так как два минимальных расстояния строк drow составляют 2m-2 и 2m-1, то
Если J=1, 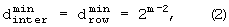
Иначе 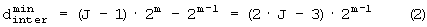
Почему  вычисляется посредством уравнения (2) при J≠1, ясно из фиг.2. Если J=1, что подразумевает, что матрица перемежения имеет только один столбец, то
вычисляется посредством уравнения (2) при J≠1, ясно из фиг.2. Если J=1, что подразумевает, что матрица перемежения имеет только один столбец, то  равно
равно 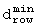 , то есть 2m-2 .
, то есть 2m-2 .
Как описано выше, параметры перемежителя m и J используются как номера строк и столбцов в матрице последовательности адресов считывания и как параметры функции, определяющей расстояния между адресами считывания. Следовательно, характеристики Ч-ОПБ канального перемежителя зависят от параметров перемежителя m и J.
До описания способа определения параметров субблочного канального перемежителя, обеспечивающих наилучшую эффективность перемежения, согласно варианту осуществления настоящего изобретения будут описаны задачи канальных перемежителей в соответствии со спецификацией IS-2000, выпуски А/В и С. Затем будет описано определение параметров перемежителя отдельно в двух случаях: N=2m×J и N=2m×J+R.
Согласно спецификации IS-2000, выпуск А/В, задачей канального перемежителя является повышение эффективности декодирования, которая ухудшается при неблагоприятном воздействии затухания на последовательные символы кода, посредством рассеивания ошибки, которое происходит в результате перестановки символов. Для повышения эффективности декодирования перемежение должно быть выполнено так, чтобы расстояние между соседними адресами (расстояние между адресами) было максимальным.
Между тем, задачей субблочного канального перемежения, как описано в спецификации IS-2000, выпуск С, является обеспечение возможности селектору символов КДТК «на выходе» перемежителя выбрать подходящие символы кода, соответствующие скорости кодирования, и, следовательно, обеспечить наилучшую эффективность на этой скорости кодирования, а также рассеять ошибки посредством перестановки символов. Для достижения этой цели перемежение должно быть выполнено так, чтобы расстояния между адресами были максимальными и унифицированными.
Соответственно, чтобы удовлетворить требованиям на канальный перемежитель спецификации IS-2000, выпуск А/В, и субблочный канальный перемежитель спецификации IS-2000, выпуск С, перемежитель должен быть разработан так, чтобы перестановка последовательности адресов считывания при перемежении осуществлялась унифицированно. Это можно сделать, определив параметры перемежителя m и J, максимизирующие минимальное расстояние между адресами и минимизирующие разность между расстояниями между адресами.
Как указано выше, расстояния между адресами распределены по категориям на расстояние внутри строки dintra и расстояние между строками dinter. Расстояние внутри строки является функцией от m, а расстояние между строками является функцией от m и J. Так как существует несколько расстояний между строками, то вычисляется минимальное расстояние между строками  . Минимальное расстояние между адресами при J равном 1 всегда равно 2m-2, а при J не равном 1 является меньшим значением из минимального расстояния между строками
. Минимальное расстояние между адресами при J равном 1 всегда равно 2m-2, а при J не равном 1 является меньшим значением из минимального расстояния между строками  и минимального расстояния внутри строки
и минимального расстояния внутри строки  . Разность между расстояниями между адресами при J равном 1 равна 2m-2, так какрасстояние внутри строки dintra равно 0, а при J не равном 1 равно разности между расстоянием внутри строки dintra и минимальным расстоянием между строками
. Разность между расстояниями между адресами при J равном 1 равна 2m-2, так какрасстояние внутри строки dintra равно 0, а при J не равном 1 равно разности между расстоянием внутри строки dintra и минимальным расстоянием между строками  .
.
Это можно выразить следующим образом:
Если J=1, |0-2m-2|=2m-2,
Иначе 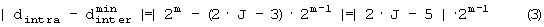
Так как N=2m×J, то 2m в уравнении (3) заменяется на N/J, из чего следует:
Если 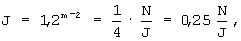
Иначе 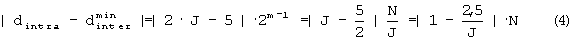
При J=3 в уравнении (4) разность между расстояниями между адресами минимизируется. Следовательно, 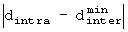 =0,166667N.
=0,166667N.
Таблица 1, приведенная ниже, иллюстрирует изменения расстояний между адресами считывания с увеличением m при N=384. При J=3 максимальная разность между расстояниями между адресами минимизируется, 64, а минимальное расстояние между адресами dmin максимизируется, 128.

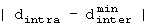
Выше описан способ определения оптимальных параметров перемежителя при N=2m×J. Ниже описан способ определения оптимальных параметров перемежителя при N=2m×J+R. Здесь R является остатком от деления N на 2m. Следовательно, R является положительным целым числом, меньшим 2m.
Фиг.3 иллюстрирует Ч-ОПБ перемежение при N=408, m=7, J=3 и R≠0. Согласно фиг.3, аналогично случаю, где R=0, номера в матрице с переставленными строками после этапа 302 считываются в качестве адресов считывания по строкам сверху вниз, при этом каждая строка считывается слева направо, как описано на этапе 303. Так как R≠0, то количество столбцов равно J+1, и номера внесены только в R строк (J+1)-го столбца, в остальных (2m-R) строках номера отсутствуют.
В сущности, при R≠0, последовательность адресов считывания формируется перестановкой строк матрицы 2m×J, каждая строка которой содержит J или J+1 элементов в Ч-ОПБ перемежителе. Матрица с переставленными строками считывается по строкам сверху вниз, при этом каждая строка считывается слева направо.
Дополнительно при R≠0 параметры перемежителя m и J определены так, чтобы минимальное расстояние между адресами считывания было максимизировано, а разность между расстояниями между адресами считывания была минимизирована.
Расстояние между строками dinter является функцией m, 2m, вне зависимости от того R=0 или R≠0. Однако, хотя при R=0 минимальное расстояние между строками  является функцией от m и J, при R≠0 оно является функцией от m, J и R.
является функцией от m и J, при R≠0 оно является функцией от m, J и R.
Минимальное расстояние между строками определяется в соответствии с J посредством уравнения (5) и уравнения (6).
При J=1
Для 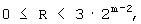
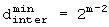
Для 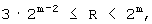
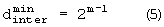
При J≠1,
Для 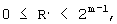
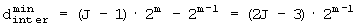
Для 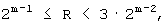
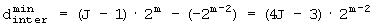
Для 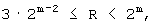
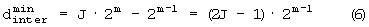
Фиг.4 иллюстрирует вывод уравнения (6) при m=7 и J=3. Согласно фиг.4 при 0≤R<2m-1, расстояние между строками между двумя соседними строками, имеющими расстояние строк drow, равное 2m-l, при этом последний столбец верхней строки является пустым, является минимальным расстоянием между строками ( (2J-3)·2m-1). При 2m-1≤R<3·2m-2, расстояние между строками между двумя соседними строками, имеющими расстояние строк drow, равное 2m-2,при этом последний столбец верхней строки является пустым, является минимальным расстоянием между строками
(2J-3)·2m-1). При 2m-1≤R<3·2m-2, расстояние между строками между двумя соседними строками, имеющими расстояние строк drow, равное 2m-2,при этом последний столбец верхней строки является пустым, является минимальным расстоянием между строками 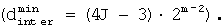
При 3·2m-2≤R<2m расстояние между строками между двумя соседними строками, имеющими расстояние строк drow, равное 2m-2,и элементы в последних столбцах, является минимальным расстоянием между строками ( =(2J-1)·2m-1). Например, если R=0, минимальное расстояние между строками равно 192, как указано ссылочной позицией 401. Если R=64(2m-1), то минимальное расстояние между строками равно 288, как указано ссылочной позицией 402. Если R=96(3·2m-2), то минимальное расстояние между строками равно 320, как указано ссылочной позицией 403. Уравнение (5) может быть выведено аналогичным образом для J=1.
=(2J-1)·2m-1). Например, если R=0, минимальное расстояние между строками равно 192, как указано ссылочной позицией 401. Если R=64(2m-1), то минимальное расстояние между строками равно 288, как указано ссылочной позицией 402. Если R=96(3·2m-2), то минимальное расстояние между строками равно 320, как указано ссылочной позицией 403. Уравнение (5) может быть выведено аналогичным образом для J=1.
Приведенная ниже таблица 2 иллюстрирует изменения в параметрах перемежителя J и R в расстоянии внутри строки dintra, минимальном расстоянии между строками  и минимальном расстоянии между адресами считывания dmin, в отношении шести размеров пакетов кодера (ПК), в соответствии со спецификацией IS-2000, выпуск С.
и минимальном расстоянии между адресами считывания dmin, в отношении шести размеров пакетов кодера (ПК), в соответствии со спецификацией IS-2000, выпуск С.
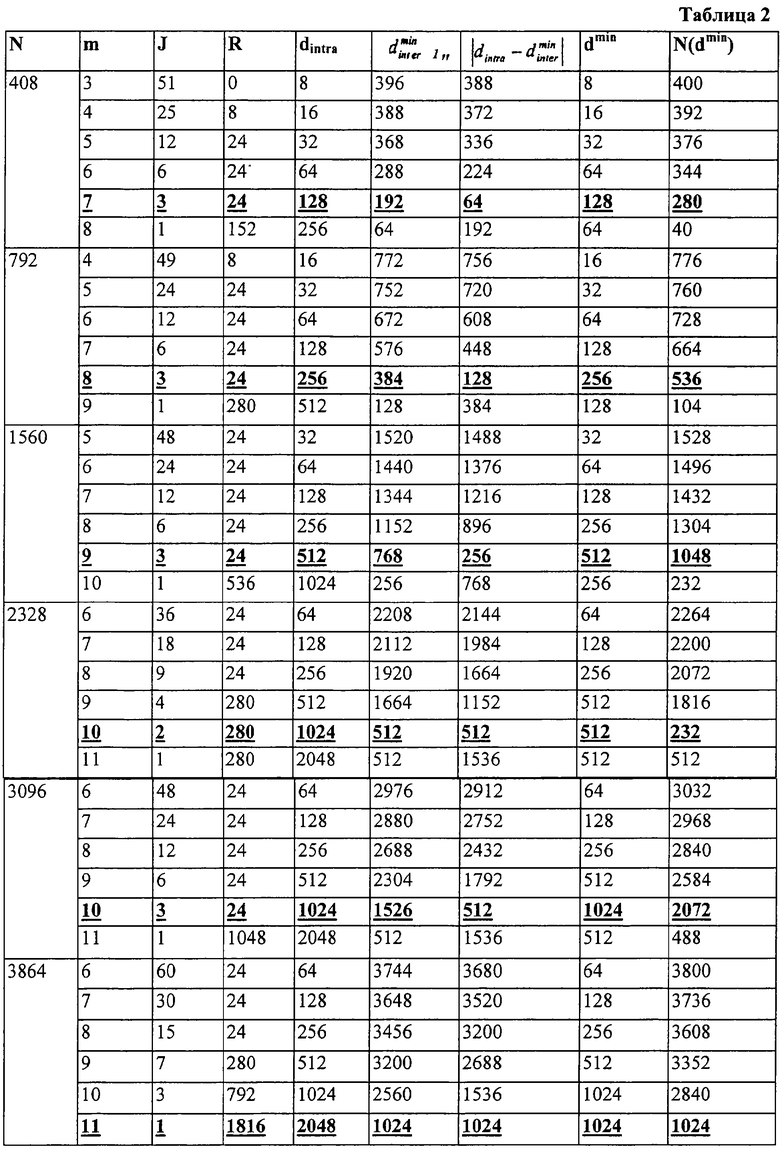
Как описано выше, аналогично случаю, где R=0, выбираются оптимальные параметры перемежения, которые максимизируют минимальное расстояние между адресами и минимизируют разность между расстояниями между адресами.
В таблице 2 минимальное расстояние между адресами считывания dmin в восьмом столбце является меньшим из расстояния внутри строки dintra и минимального расстояния между строками  . Следовательно, параметры, максимизирующие минимальное расстояние между адресами считывания dmin могут быть получены посредством выбора строки, имеющей максимальное значение в восьмом столбце. Для размеров ПК в 2328 и 3864 три строки и две строки удовлетворяют этому условию. В этом случае должны быть выбраны строки, удовлетворяющие другому условию минимизации разности между адресами считывания
. Следовательно, параметры, максимизирующие минимальное расстояние между адресами считывания dmin могут быть получены посредством выбора строки, имеющей максимальное значение в восьмом столбце. Для размеров ПК в 2328 и 3864 три строки и две строки удовлетворяют этому условию. В этом случае должны быть выбраны строки, удовлетворяющие другому условию минимизации разности между адресами считывания 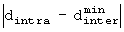 . Они выделены полужирным и подчеркнутым шрифтом в таблице 2. Валидность (истинность) этого условия очевидна при сравнении строк, имеющих максимальное dmin в функции n(dmin) в последнем столбце. Здесь, n(dmin) указывает количество пар адресов, имеющих минимальное расстояние между адресами dmin.
. Они выделены полужирным и подчеркнутым шрифтом в таблице 2. Валидность (истинность) этого условия очевидна при сравнении строк, имеющих максимальное dmin в функции n(dmin) в последнем столбце. Здесь, n(dmin) указывает количество пар адресов, имеющих минимальное расстояние между адресами dmin.
Строки, выделенные полужирным и подчеркнутым шрифтом в таблице 2, удовлетворяют двум условиям для выбора оптимальных параметров перемежителя, указанным выше. Как отмечено, если удовлетворяется второе условие, то первое условие удовлетворяется заведомо. Для сведения, ясно, что расстояния внутри строки dintra и минимальные расстояния между строками  , перечисленные в таблице 2, равны вычисленным по Ч-ОПБ перемеженным адресам считывания. Таблица 2 охватывает случай деления N на 2m или J без остатка и случай деления N на 2m или J с остатком R (то есть N=2m×J+R(0≤R<2m)). Здесь параметры перемежителя, выделенные полужирным и подчеркнутым шрифтом, являются оптимальными для каждого размера ПК.
, перечисленные в таблице 2, равны вычисленным по Ч-ОПБ перемеженным адресам считывания. Таблица 2 охватывает случай деления N на 2m или J без остатка и случай деления N на 2m или J с остатком R (то есть N=2m×J+R(0≤R<2m)). Здесь параметры перемежителя, выделенные полужирным и подчеркнутым шрифтом, являются оптимальными для каждого размера ПК.
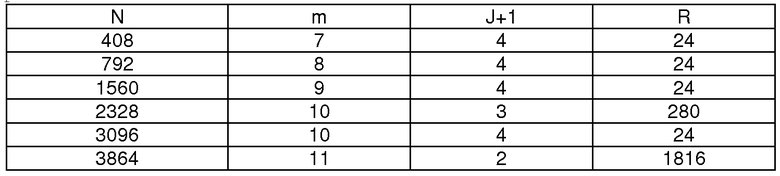
В таблице 3 перечислены оптимальные параметры перемежителя для каждого размера перемежителя N, при N=2m×(J-1)+R(0≤R<2m), то есть N делится на 2m или J либо без остатка, либо с остатком R. Описание, сделанное в контексте J, также может быть использовано при замене J на (J-1).
Описание, приведенное выше, предлагает способ выбора параметров перемежителя, которые, предполагается, обеспечивают наилучшую эффективность при использовании, например, канального перемежителя, скомпонованного в соответствии со спецификацией IS-2000, выпуск А/В, и субблочного канального перемежителя, скомпонованного в соответствии со спецификацией IS-2000, выпуск С.
Как описано выше, при формировании адресов считывания в канальном перемежителе оптимальными параметрами перемежителя являются параметры, максимизирующие расстояние между адресами и одновременно минимизирующие разность между расстояниями между адресами. Следовательно, параметрами перемежителя для субблочного канального перемежения при компоновке субблочного канального перемежителя в соответствии со спецификацией IS-2000, выпуск С, являются значения в строках с полужирным и подчеркнутым шрифтом таблицы 2. Хотя выбор параметров перемежителя был описан для субблочного канального перемежителя, скомпонованного в соответствии со спецификацией IS-2000, выпуск С, очевидно, что та же самая идея может быть использована также в отношении систем других стандартов.
Фиг.6 является блок-схемой, поясняющей операцию определения оптимальных параметров перемежителя согласно варианту осуществления настоящего изобретения. В частности, эта операция связана с вычислением 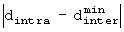 . Вычисляя
. Вычисляя 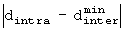 с изменяющимися параметрами (m, J), выбираются оптимальные параметры (m, J), минимизирующие параметры
с изменяющимися параметрами (m, J), выбираются оптимальные параметры (m, J), минимизирующие параметры 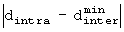 .
.
Согласно фиг.6, когда на этапе 601 заданы размер перемежителя N и параметры m и J, на этапе 603 вычисляется параметр R посредством вычитания 2m×J из N. На этапе 605 определяется, равен ли J единице (1). Вследствие этого определяется, имеет ли матрица перемежения единственный столбец. Если J равен 1, то процедура переходит к этапу 607 (ветвь «Да» из этапа 605 принятия решения) и если J не равен 1, то процедура переходит к этапу 621 (ветвь «Нет» из этапа 605 принятия решения). На этапе 607 определяется, равен ли R нулю (0) (то есть является ли N целочисленным множителем 2m). Напротив, если R равен 0 (ветвь «Да» из этапа 607 принятия решения), то на этапе 609 расстояние внутри строки dintra устанавливается в 0. Если R не равен 0 (ветвь «Нет» из этапа 607 принятия решения), то на этапе 617 dintra устанавливается в 2m.
После определения dintra на этапе 611 определяется, меньше ли R, чем 3×2m-2. Если R меньше 3×2m-2 (ветвь «Да» из этапа 611 принятия решения), то на этапе 613 минимальное расстояние между строками  устанавливается в 2m-2. Если R равен или больше 3×2m-2 (ветвь «Нет» из этапа 611 принятия решения), то на этапе 619
устанавливается в 2m-2. Если R равен или больше 3×2m-2 (ветвь «Нет» из этапа 611 принятия решения), то на этапе 619  устанавливается в 2m-1.После определения
устанавливается в 2m-1.После определения , на этапе 615 вычисляется
, на этапе 615 вычисляется 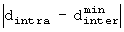 .
.
Между тем, если на этапе 605 определяется, что J не равен 1, то на этапе 621 dintra устанавливается в 2m, и на этапе 623 определяется, меньше ли R, чем 2m-l. Если R меньше 2m-1 (ветвь «Да» из этапа 623 принятия решения), то на этапе 625  устанавливается в (2J-3)×2m-1 и затем процедура переходит к этапу 615. Если R равен или больше 2m-1 (ветвь «Нет» из этапа 623 принятия решения), то на этапе 627 определяется, меньше ли R, чем 3×2m-2. Если R меньше 3×2m-2 (ветвь «Да» из этапа 627 принятия решения), то на этапе 629
устанавливается в (2J-3)×2m-1 и затем процедура переходит к этапу 615. Если R равен или больше 2m-1 (ветвь «Нет» из этапа 623 принятия решения), то на этапе 627 определяется, меньше ли R, чем 3×2m-2. Если R меньше 3×2m-2 (ветвь «Да» из этапа 627 принятия решения), то на этапе 629  устанавливается в (4J-3)×2m-2. Если R равен или больше 3×2m-2 (ветвь «Нет» из этапа 627 принятия решения), то на этапе 631
устанавливается в (4J-3)×2m-2. Если R равен или больше 3×2m-2 (ветвь «Нет» из этапа 627 принятия решения), то на этапе 631  устанавливается в (2J-1)×2m-1 и затем процедура переходит к этапу 615.
устанавливается в (2J-1)×2m-1 и затем процедура переходит к этапу 615.
Оптимальные параметры перемежителя m и J получаются для заданного N посредством вычисления 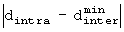 при изменении (m, J). Если J является одним из значений 1, 2 и 3, то может быть выведена логическая формула, обеспечивающая выбор J без многократного вычисления.
при изменении (m, J). Если J является одним из значений 1, 2 и 3, то может быть выведена логическая формула, обеспечивающая выбор J без многократного вычисления.
Опуская процедуру вывода логического уравнения, ниже приведено это логическое уравнение.
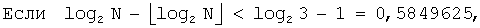
Для 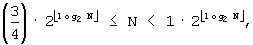 J=3,
J=3,
Для 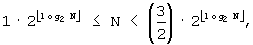 J=2,
J=2,
Для 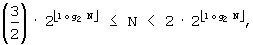 J=1.
J=1.
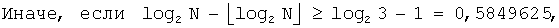
Для 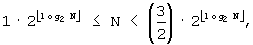 J=2,
J=2,
Для 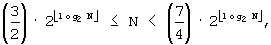 J=3, (7)
J=3, (7)
Для 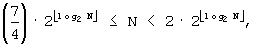 J=1.
J=1.
Оптимальный параметр m вычисляется из оптимального параметра J, полученного из уравнения (7), следующим образом:
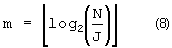
Согласно фиг.7 ниже кратко описывается выбор оптимальных параметров перемежителя посредством указанного простого логического уравнения.
1. Для заданного N оптимальный параметр J получен посредством уравнения (7).
2. Параметр m вычислен посредством уравнения (8) с использованием N и J.
Фиг.7 является блок-схемой, поясняющей операцию определения оптимальных параметров перемежителя согласно другому варианту осуществления настоящего изобретения.
Согласно фиг.7, когда задан N, на этапе 701 вычисляются переменная α посредством 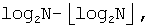 и переменная β посредством
и переменная β посредством 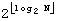 . На этапе 703 принятия решения определяется, меньше ли α первого порогового значения, 0,5849625. Если α меньше первого порогового значения (ветвь «Да» из этапа 703 принятия решения), то на этапе 705 принятия решения осуществляется принятие другого решения, меньше ли N, чем β. Если N равен или больше β (ветвь «Нет» из этапа 705 принятия решения), то процедура переходит к этапу 707. Напротив, если N меньше β (ветвь «Да» из этапа 705 принятия решения), то на этапе 713 J определяется равным 3.
. На этапе 703 принятия решения определяется, меньше ли α первого порогового значения, 0,5849625. Если α меньше первого порогового значения (ветвь «Да» из этапа 703 принятия решения), то на этапе 705 принятия решения осуществляется принятие другого решения, меньше ли N, чем β. Если N равен или больше β (ветвь «Нет» из этапа 705 принятия решения), то процедура переходит к этапу 707. Напротив, если N меньше β (ветвь «Да» из этапа 705 принятия решения), то на этапе 713 J определяется равным 3.
Между тем, на этапе 707 принятия решения определяется, меньше ли N, чем (3/2)×β. Если N меньше (3/2)×β (ветвь «Да» из этапа 707 принятия решения), то на этапе 711 J определяется равным 2. Иначе, на этапе 709 J определяется равным 1 (ветвь «Нет» из этапа 707 принятия решения).
Если на этапе 703 определяется, что α равен или больше первого порогового значения (ветвь «Нет» из этапа 703 принятия решения), то на этапе 717 принятия решения осуществляется принятие решения, меньше ли N, чем (3/2)×β. Если N меньше (3/2)×β (ветвь «Да» из этапа 717 принятия решения), то на этапе 721 J определяется равным 2. Иначе, на этапе 719 принятия решения определяется, меньше ли N, чем (7/4)×β. Если N меньше (7/4)×β (ветвь «Да» из этапа 719 принятия решения), то на этапе 723 J определяется равным 3. Иначе, на этапе 725 J определяется равным 1 (ветвь «Нет» из этапа 719 принятия решения).
Как описано выше, оптимальные параметры m и J могут быть вычислены просто посредством логических уравнений, использующих N. Оптимальные m и J равны m и J, получаемым в результате многократного вычисления с использованием различных значений (m, J), как поясняется таблицей 2. Это устраняет необходимость в хранении оптимальных значений m и J, соответствующих значениям N.
Например, при N=2328 оптимальные значения m и J вычисляются посредством процедуры, поясняемой фиг.7, или посредством уравнений с (8) по (10), следующим образом:
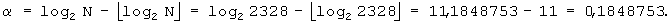
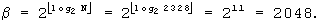
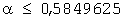 и
и 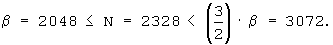 Следовательно J=2
Следовательно J=2
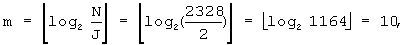
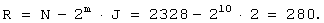
Для сведения, уравнение (7) выводится следующим образом.
В каждом случае, при описании фиг.6, уравнения (5) и уравнения (6), 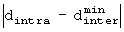 определяется следующим образом.
определяется следующим образом.
А. При J=1,
А-1. Если R=0, 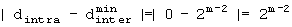
А-2. Если 0<R<3·2m-2, 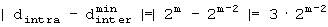
A-3. Если 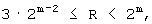
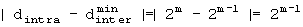
В. При J≠1,
В-1. Если 0≤R<2m-1, 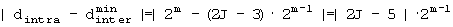
В-2. Если 2m-1≤R<3·2m-2, 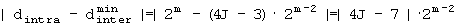
В-3. Если 3·2m-2≤R<2m, 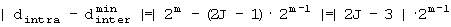
Так как N=2m·J+R и 0≤R<2m, то J·2m≤N<(J+1)·2m. После деления этого выражения на J и взятия от полученного выражения логарифма по основанию 2
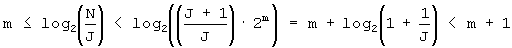
Следовательно, 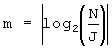 . Используя
. Используя 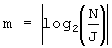 , J может быть выражен как функция от N для всех случаев А и В.
, J может быть выражен как функция от N для всех случаев А и В.
А'. При J=1, так как  то R=N-2m=N-2
то R=N-2m=N-2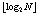 . Следовательно, случаи А-1, А-2 и А-3 могут быть выражены как функции от N. Из этого следует:
. Следовательно, случаи А-1, А-2 и А-3 могут быть выражены как функции от N. Из этого следует:
A'-1: Если 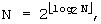
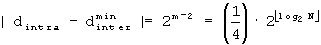
A'-2: Если 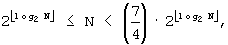
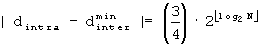
A'-3: Если 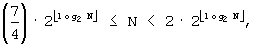
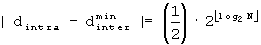
B'. При J≠1, так как 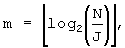
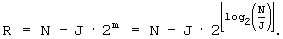
Затем случаи В-1, В-2 и В-3 могут быть выражены как функции N вместо R. Следовательно,
B'-1: Если 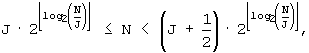
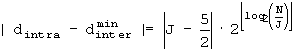
B'-2: Если 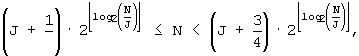
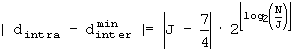
B'-3: Если 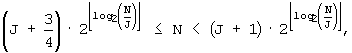
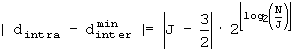
B''. При J=2, так как 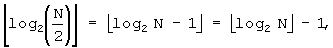
B''-1: Если 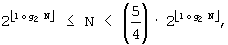

B''-2: Если 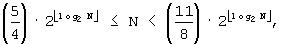

B''-3: Если 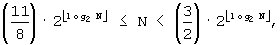

B'''. При J=3,
так как 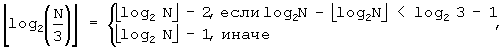
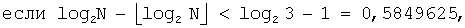
B'''-1': Если 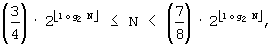

B'''-2': Если 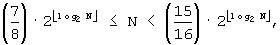
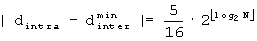
B'''-3': Если 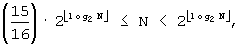
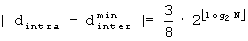
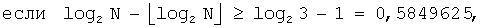
B'''-1'': Если 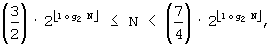
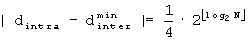
B'''-2'': Если 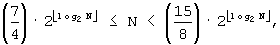
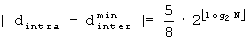
B'''-3'': Если 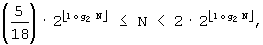
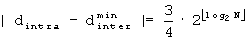
Если J равен 4 или больше, то этот случай не рассматривается, так как в любом из случаев, где J=1, 2 и 3 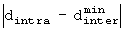 не может быть меньше чем
не может быть меньше чем 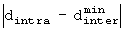 .
.
Уравнение (7) получается посредством выбора из случаев А'-1, А'-2, А'-3, B"-1, B"-2, B"-3, B"'-1', B"'-2' и B"'-3' случая, в котором выражение 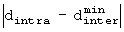 является минимальным.
является минимальным.
Аналогично, уравнение (8) получается посредством выбора из случаев А'-1, А'-2, А'-3, B"-1, B"-2, B"-3, B"'-1", B"'-2" и B"'-3" случая, в котором выражение 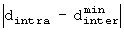 является минимальным.
является минимальным.
Согласно вариантам осуществления настоящего изобретения, как описано выше, параметры перемежителя m и J просто оптимизируются в соответствии с размером N перемежителя для Ч-ОПБ перемежения.
Хотя изобретение было проиллюстрировано и описано в отношении некоторых предпочтительных вариантов осуществления, для специалистов в данной области техники очевидно, что не удаляясь от сущности и объема изобретения, могут быть сделаны разные изменения в форме и в деталях, как определено согласно приложенной формуле изобретения.
Изобретение относится к перемежению в системе связи, а именно к способу оптимизации параметров перемежителя Ч-ОПБ (с частичным обратным порядком битов) в соответствии с его размером. Ч-ОПБ перемежитель последовательно, по столбцам, конфигурирует поток входных данных размера N в матрицу, имеющую 2m строк и (J-1) столбцов и R строк в J-ом столбце, Ч-ОПБ перемежает сконфигурированные данные и считывает перемеженные данные по строкам. 2 н. и 3 з.п. ф-лы, 7 ил.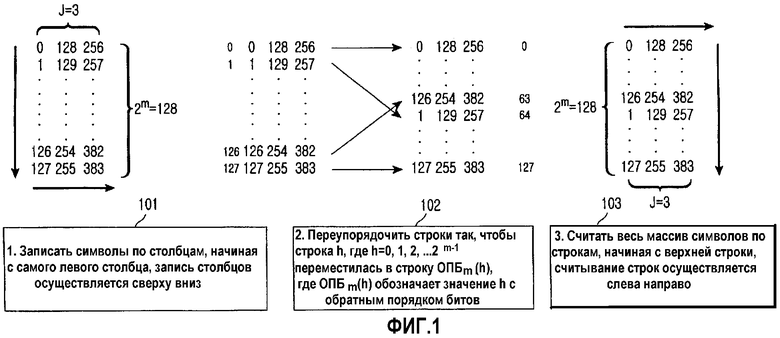
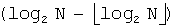 и вторую переменную посредством
и вторую переменную посредством 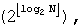 сравнивают значение первой переменной с выбранным первым пороговым значением, сравнивают размер N перемежителя по меньшей мере с одним заданным вторым пороговым значением, определенным по коэффициенту второй переменной, определяют первый параметр J в соответствии с результатами сравнения и определяют второй параметр m посредством
сравнивают значение первой переменной с выбранным первым пороговым значением, сравнивают размер N перемежителя по меньшей мере с одним заданным вторым пороговым значением, определенным по коэффициенту второй переменной, определяют первый параметр J в соответствии с результатами сравнения и определяют второй параметр m посредством
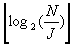
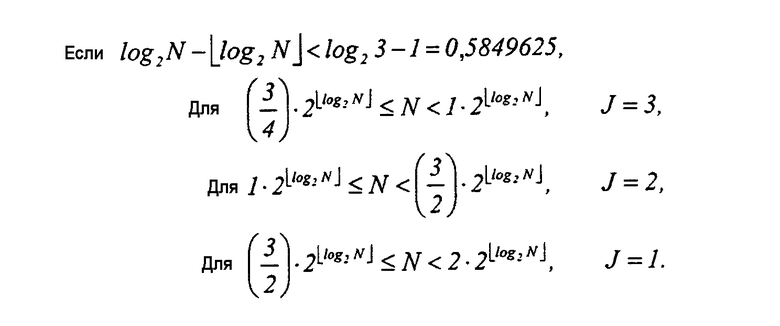
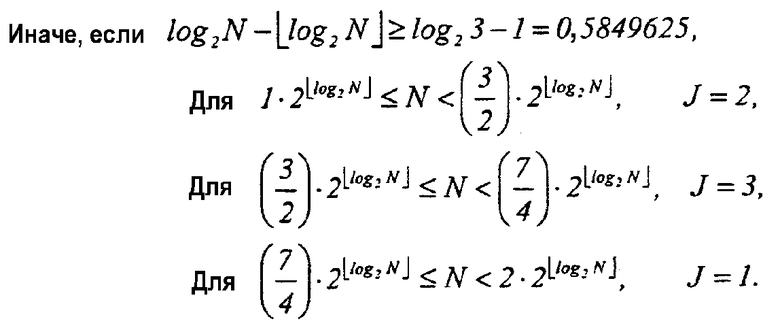
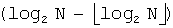 с использованием заданного размера N перемежителя и второй переменной посредством
с использованием заданного размера N перемежителя и второй переменной посредством  сравнения значения первой переменной с заданным первым пороговым значением, сравнения размера N перемежителя по меньшей мере с одним заданным вторым пороговым значением, определеннным по коэффициенту второй переменной, определения первого параметра J в соответствии с результатами сравнения, вычисления второго параметра m посредством
сравнения значения первой переменной с заданным первым пороговым значением, сравнения размера N перемежителя по меньшей мере с одним заданным вторым пороговым значением, определеннным по коэффициенту второй переменной, определения первого параметра J в соответствии с результатами сравнения, вычисления второго параметра m посредством 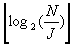 , вычисления третьего параметра R посредством N=2m·J+R, последовательного конфигурирования по столбцам входного потока данных размера N в матрицу, имеющую 2m строк и (J-1) столбцов и R строк в J-ом столбце, причем 0≤R<2m, Ч-ОПБ перемежения сконфигурированных данных и формирования адресов считывания для считывания перемеженных данных по строкам.
, вычисления третьего параметра R посредством N=2m·J+R, последовательного конфигурирования по столбцам входного потока данных размера N в матрицу, имеющую 2m строк и (J-1) столбцов и R строк в J-ом столбце, причем 0≤R<2m, Ч-ОПБ перемежения сконфигурированных данных и формирования адресов считывания для считывания перемеженных данных по строкам.
| US 6304991 B1, 16.10.2001.RU 2108667 C1, 10.04.1998.RU 2110148 C1, 27.04.1998.WO 00/35102 A1, 15.06.2000.WO 99/07076 A2, 11.02.1999.WO 00/70771 A1, 23.11.2000.US 5446747 A, 29.08.1995. |
Авторы
Даты
2005-09-27—Публикация
2003-02-06—Подача