Изобретение относится к области строительства, в частности к графоаналитическим способам определения контактных напряжений на границе взаимодействия конструкций сооружений с плоскодеформируемыми грунтовыми основаниями, необходимыми для расчета конструкций и самих оснований и определения в них сложного напряженно-деформированного состояния (НДС) для прогноза поведения под нагрузкой.
Известен способ определения напряжений в зоне силового контакта штампа с грунтовым основанием и торфяной залежью в условиях плоской деформации, заключающийся в установке датчиков напряжений в плоскости контакта заподлицо с поверхностью подошвы штампа и замере величины контактных напряжений в точках плоскости контакта под возрастающими ступенями внешнего давления на штамп [1, 2].
Недостаток известного способа прямого определения контактных напряжений заключается в отсутствии конструкций датчиков точечного определения напряжений. Так, измерительная мембрана датчика занимает часть площади контакта, а величину среднего напряжения приводят расчетным путем к точке контакта, поэтому условия, а следовательно, и измерение контактных напряжений становится невозможным в таких точках, как под кромками по периметру подошвы штампа. Низка и точность измерения, связанная с изменениями НДС грунта под прогибающейся в процессе измерений мембраной датчика. Прямое измерение контактных напряжений не позволяет прогнозировать, а следовательно, рассчитывать эпюры контактных напряжений в зависимости от физико-механических характеристик основания, от размера, формы, жесткости и шероховатости подошвы штампа, глубины его бокового пригруза и величины заглубления и др., а только констатируют результаты частного опыта.
Известен способ определения контактных напряжений, заключающийся в графоаналитическом построении составных эпюр напряжений под площадью контакта жесткого штампа с плоскодеформируемым основанием, исходя из сочетания упругого состояния материала основания по Буссинеску с пластическим состоянием по Прандтлю в плоскости контакта, и определении закона перемещения границ этих состояний под подошвой штампа с ростом внешнего давления, отличающийся тем, что для зоны упругих деформаций расчет контактных напряжений ведут по зависимости (Буссинеска) 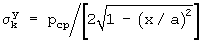 - для круглого жесткого штампа радиусом r=а или по зависимости (М.Садовского)
- для круглого жесткого штампа радиусом r=а или по зависимости (М.Садовского) 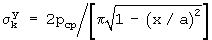 - для полосового жесткого штампа шириной в=2а, где х - расстояние от центральной оси симметрии подошвы штампа, строят эпюру упругих контактных напряжений для заданного значения внешнего давления рср в виде вогнутой параболы σz=f(рср) от краев до центра подошвы штампа, а также прямоугольник эпюры среднего давления рср, а контактные напряжения в зонах сдвигов, развивающихся от края штампа к центру с ростом давления рср определяют по уравнению линии, срезающей пики эпюры бесконечных упругих контактных напряжений под краями штампа в точке границы раздела зон упругих и сдвиговых (пластических) деформаций, где предельное по прочности давление σz п=cNc+γ|DNq+4aγ2Nγ(1-х/а) приравнивается к σz y, получаемому на основании равенства суммы площадей эпюр σz y=f(pcp), σz п=f(pcp) и площади прямоугольной эпюры среднего давления по всей ширине (диаметру) подошвы штампа [3].
- для полосового жесткого штампа шириной в=2а, где х - расстояние от центральной оси симметрии подошвы штампа, строят эпюру упругих контактных напряжений для заданного значения внешнего давления рср в виде вогнутой параболы σz=f(рср) от краев до центра подошвы штампа, а также прямоугольник эпюры среднего давления рср, а контактные напряжения в зонах сдвигов, развивающихся от края штампа к центру с ростом давления рср определяют по уравнению линии, срезающей пики эпюры бесконечных упругих контактных напряжений под краями штампа в точке границы раздела зон упругих и сдвиговых (пластических) деформаций, где предельное по прочности давление σz п=cNc+γ|DNq+4aγ2Nγ(1-х/а) приравнивается к σz y, получаемому на основании равенства суммы площадей эпюр σz y=f(pcp), σz п=f(pcp) и площади прямоугольной эпюры среднего давления по всей ширине (диаметру) подошвы штампа [3].
Несмотря на получение общей картины распределения контактных напряжений в зонах упругих и сдвиговых (пластических) деформаций и общей закономерности их развития с ростом зон сдвигов при росте внешнего давления (рср), сходимость рассчитываемых контактных напряжений с замеряемыми «in situ» мала, что связано, с одной стороны, с неучетом в формулах зависимости σz y и σz п от формы, жесткости и размеров штампа, шероховатости его подошвы и др., а с другой стороны, неучетом площади закраевых эпюр напряжений поверхностного растяжения-сжатия грунта (торфа) в основание штампа и на поверхности трещин, развивающихся за края штампа в воронке сжатия из-за нарушения структурной прочности грунта (торфа).
Наиболее близким по технической сущности к предлагаемому является способ определения контактных напряжений, заключающийся в графоаналитическом построении составных эпюр напряжений под площадью контакта жесткого штампа с плоскодеформируемым основанием, исходя из сочетания в плоскости контакта упругого состояния грунта (торфа) основания с пластическим состоянием, и определении закона перемещения границ этих состояний под подошвой штампа с ростом внешнего давления, отличающийся тем, что для зоны упругих деформаций контактные напряжения определяют по зависимости (Буссинеска) 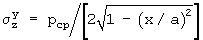 для круглого штампа радиусом г=а или зависимости (М.Садовского)
для круглого штампа радиусом г=а или зависимости (М.Садовского) 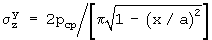 для полосового штампа шириной в=2а, где х - расстояние от центральной оси симметрии подошвы штампа, строят по ширине подошвы штампа эпюру упругих контактных напряжений σz y=f(pcp) в виде вогнутой параболы с бесконечными значениями напряжений под краями штампа, а также прямоугольную эпюру среднего контактного напряжения σср=-pср, а контактные напряжения в зонах сдвига, развивающихся с ростом внешнего давления рср от краев подошвы штампа к его центру, определяют по уравнению линии, срезающей пики эпюры бесконечных упругих контактных напряжений под краями штампа в точке границы раздела зон упругих и сдвиговых (пластических) деформаций, в виде σz п=pпр+А(а-х), где х - расстояние от цента штампа до искомой точки, в которой определяется предельное давление рпр, согласно решению В.В.Соколовского с учетом угла ϕ внутреннего трения грунта, по которому рпр=CN'c+γNγ'a+qNq', где N'c, Nγ' и Nq' - коэффициенты несущей способности основания, С - удельное сцепление грунта, q - величина бокового пригруза, при этом учитывается равенство площади эпюры среднего контактного давления и суммы площадей эпюр упругих и сдвиговых контактных напряжений [4].
для полосового штампа шириной в=2а, где х - расстояние от центральной оси симметрии подошвы штампа, строят по ширине подошвы штампа эпюру упругих контактных напряжений σz y=f(pcp) в виде вогнутой параболы с бесконечными значениями напряжений под краями штампа, а также прямоугольную эпюру среднего контактного напряжения σср=-pср, а контактные напряжения в зонах сдвига, развивающихся с ростом внешнего давления рср от краев подошвы штампа к его центру, определяют по уравнению линии, срезающей пики эпюры бесконечных упругих контактных напряжений под краями штампа в точке границы раздела зон упругих и сдвиговых (пластических) деформаций, в виде σz п=pпр+А(а-х), где х - расстояние от цента штампа до искомой точки, в которой определяется предельное давление рпр, согласно решению В.В.Соколовского с учетом угла ϕ внутреннего трения грунта, по которому рпр=CN'c+γNγ'a+qNq', где N'c, Nγ' и Nq' - коэффициенты несущей способности основания, С - удельное сцепление грунта, q - величина бокового пригруза, при этом учитывается равенство площади эпюры среднего контактного давления и суммы площадей эпюр упругих и сдвиговых контактных напряжений [4].
Существенным недостатком известного способа являются большие неточности в определении контактных напряжений из-за неверного определения закономерностей развития под штампом зон упругих и сдвиговых (пластических) деформаций, зависящих от жесткости, формы и размеров штампа, шероховатости его подошвы, возможности прилипания грунта к подошве штампа и др., а также из-за недоучета площадей эпюр закраевых поверхностных напряжений, обусловленных структурной прочностью грунта и определяющих воронку сжатия и степень развития закраевых трещин в воронке сжатия под краями штампа.
Практические исследования контактных напряжений датчиками напряжений нового типа, компенсирующими прогибы измерительных мембран в момент замера напряжений, позволили установить не только разницу с теоретическими современными расчетами контактных напряжений в зонах сдвига, но и в известных зонах упругих деформаций, что позволило усомниться в правомерности использования формул Буссинеска и М.Садовского в расчетах упругих контактных напряжений.
Технический результат по предлагаемому способу определения контактных напряжений в грунте, заключающемуся в графоаналитическом построении составных эпюр напряжений в плоскости контакта жесткого штампа с плоскодеформируемым основанием, исходя из сочетания упругого состояния основания с пластическим, определении закона перемещения границ этих состояний в плоскости контакта с ростом внешнего среднего давления (рср) с учетом распределения упругих контактных напряжений по закону вогнутой параболы и распределения контактных напряжений сдвига σz п под гладкой подошвой штампа по закону прямой линии, пересекающейся с вогнутой параболой упругих напряжений на границе раздела зон упругих и сдвиговых деформаций, достигается тем, что по данным испытания грунта рассчитывают в зависимости от угла ϕ внутреннего трения, с - сцепления, γ - объемного веса параметры несущей способности основания под штампом известной формы, размеров, жесткости и степени шероховатости его подошвы: величину среднего (рср (пр,кр,кпр)), краевого (p2 (пр,кр,крп)) и максимального (р1 (пр,кр,крп)) значения давления под центром подошвы штампа в предельном, критическом и предельно-критическом состоянии основания по формулам р2 кпр=[πcCtgϕ)/(Ctgϕ+ϕ-π/2)]+[cCosϕ/(1+Sinϕ)], p2 кр=c[Sinϕ·(π-2ϕ)+2(π-Cosϕ)]/{(1+Sinϕ)[2-tgϕ·(π-2ϕ)]}, р2 пр=(1/2)(р2 кр-|ркр2 раст|), где |ркр2 раст|=[4Cosϕ-p2 кр(1-Sinϕ)2/(1+Sinϕ)2 - давление растяжения под центром штампа в критическом для основания состоянии, р1 (пр, кр, крп)=[р2 (пр, кр, крп))(1-Sinϕ)2+4сCosϕ]/(1-Sin ϕ)2, рср=(пр, кр, крп)=р2 (пр, кр, крп)х(1+Sin2ϕ)+2cCosϕ]/(1-Sinϕ)2, соответствующую зонам развития сдвига от краев штампа до его центра по схеме Хилла, до противоположных сторон штампа с формированием грунтового ядра до краев штампа - по схеме Прандтля и за противоположные стороны штампа с увеличением грунтового ядра за края штампа с временным повышением несущей способности основания, а затем с проявлением провальных осадок основания; величину давления потери структурной прочности материала основания при растяжении (pстр раст) и сжатии (pстр сж):|pстр раст|=2Cosϕ/(1+Sinϕ),|pстр сж|=2Cosϕ/(1-Sinϕ) и расчетным путем устанавливают расстояние d=в(1-Sinϕ)2/4Sinϕ от края в сторону от штампа, соответствующее влиянию давлению связности грунта ре=-cCtgϕ; расстояние от края в сторону от штампа
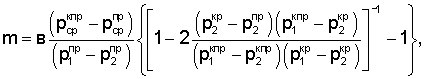
соответствующее величине удаления центра зон сдвигов за края штампа с давлением рц=-[р2 крп(в+2m)-2p2 пр(в+m+tо)]/(в+2tо), где to=в(р1 крп-р1 кр)/(р1 кр-p2 кр) - величина зоны развития сдвигов за краями штампа в предельно-критическом состоянии основания; ширину эквивалентного штампа во=в +2 m, под которым рассматривают контактное взаимодействие с основанием; далее от правого края штампа в масштабе наносят вправо от начала координат в центре симметрии штампа точки Ц[(а+m), (-рц)] и D[(a+d), (-ре)], от левого края влево на расстоянии [-(tо+а)] проводят вертикаль, на которой откладывают точки А[-(а+tо),р1 крп], В[-(а+tо),рср крп], С[-(а+tо),р2 крп], а на расстоянии [±(m+а)] и [±а] проводят дополнительные вертикали, точки А и С соединяют прямыми линиями L1 и L2 с точкой Ц, а точку А и В соединяют прямыми линиями M1 и Мср с точкой D, точку пересечения прямой Мср с вертикалью [-(m+а)] с координатами G[-(m+a), рG], где рG=[(pcp пр+cCtgϕ)2(в+m+d)/(в+2d)]-cCtgϕ, соединяют с точкой Ц прямой линией N, определяющей с ростом рср сужение асимптот (аас) ветвей вогнутой параболы эпюры упругих контактных напряжений 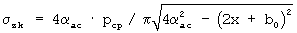 под полосовым и
под полосовым и 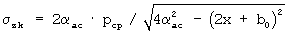 под круглым штампом, а также точку G соединяют с точкой S[fкр I, 0], где fкр I=(а+d)[p2 пр-0,5|pстр раст|/(p2 пр+cCtgϕ) - расстояние от центра штампа до точки штампа с давлением, соответствующим значению «первой критической нагрузки» Рср.кр I=рср пр-[(р2 пр-0,5|рстр раст|)(pср пр+cCtgϕ)/(р2 пр+cCtgϕ)] на прямой Мср, прямой линией Р перемещения полюса вогнутой параболы эпюры упругих контактных напряжений с ростом рср, а контактные напряжения определяют по ординатам эпюр, которые строят из точки F пересечения прямой M1 с вертикалью, проходящей через точку К пересечения прямой Мср с горизонталью эпюры рср, путем проведения ветви вогнутой параболы σzк через точку F и полюс П до ∞ у вертикали асимптоты аас и до точки Т [-(а+m); 2рср/π] для полосового или Т[-(а+m):2pcp/π] - для круглого штампа, с одной стороны, и, с другой стороны, путем проведения прямой линии J из точки F в точку Ф[+а; рф], где рф=2рср-рF=рF-2R, a R=τmax пр=(1/2)(рF-рБ) - радиус круга Мора предельно-максимального по прочности состояния грунта под штампом на вертикали, проходящей через точки F, К и Б, причем отрезки FK=КБ=R, а линия J - есть эпюра развития при рср сдвиговых (пластических) деформаций под краем штампа, далее построенные эпюры зеркально отображают относительно оси ординат и получают эпюры упругих и сдвиговых контактных напряжений под плоскостью штампа, а из точки Ф проводят кривую линию эпюры закраевых поверхностных напряжений на поверхности воронки сжатия грунта за краями штампа с уравнением σпов=[2π/|рф|]arcSin(а/r), где r - расстояние от края за пределы штампа.
под круглым штампом, а также точку G соединяют с точкой S[fкр I, 0], где fкр I=(а+d)[p2 пр-0,5|pстр раст|/(p2 пр+cCtgϕ) - расстояние от центра штампа до точки штампа с давлением, соответствующим значению «первой критической нагрузки» Рср.кр I=рср пр-[(р2 пр-0,5|рстр раст|)(pср пр+cCtgϕ)/(р2 пр+cCtgϕ)] на прямой Мср, прямой линией Р перемещения полюса вогнутой параболы эпюры упругих контактных напряжений с ростом рср, а контактные напряжения определяют по ординатам эпюр, которые строят из точки F пересечения прямой M1 с вертикалью, проходящей через точку К пересечения прямой Мср с горизонталью эпюры рср, путем проведения ветви вогнутой параболы σzк через точку F и полюс П до ∞ у вертикали асимптоты аас и до точки Т [-(а+m); 2рср/π] для полосового или Т[-(а+m):2pcp/π] - для круглого штампа, с одной стороны, и, с другой стороны, путем проведения прямой линии J из точки F в точку Ф[+а; рф], где рф=2рср-рF=рF-2R, a R=τmax пр=(1/2)(рF-рБ) - радиус круга Мора предельно-максимального по прочности состояния грунта под штампом на вертикали, проходящей через точки F, К и Б, причем отрезки FK=КБ=R, а линия J - есть эпюра развития при рср сдвиговых (пластических) деформаций под краем штампа, далее построенные эпюры зеркально отображают относительно оси ординат и получают эпюры упругих и сдвиговых контактных напряжений под плоскостью штампа, а из точки Ф проводят кривую линию эпюры закраевых поверхностных напряжений на поверхности воронки сжатия грунта за краями штампа с уравнением σпов=[2π/|рф|]arcSin(а/r), где r - расстояние от края за пределы штампа.
Предложенный графоаналитический способ определения контактных напряжений под полосовым и круглым штампом средних размеров позволяет с большой точностью, подтвержденными практическими исследованиями получить значение реактивных давлений под конструкциями, работающими на грунтовом основании в любом диапазоне действующих на них нагрузок. Впервые способ позволил обосновать возможность проявления под краями штампов отрицательных значений контактных напряжений в диапазоне действия малых внешних нагрузок, учесть закраевое поверхностное натяжение грунта за краями штампа, вызванное структурной прочностью грунта на растяжение. Впервые устанавливаются точные определяющие зависимости для значений предельных, критических и предельно-критических по прочности и устойчивости для основания нагрузок, существенно уточняется значение «первой критической нагрузки ркр I», появляется возможность определения давления «условно-мгновенной деформации грунта».
Основной технический результат по предложенному способу заключается в возможности установления границ развития с ростом среднего давления зон сдвигов и упругих деформаций, что по сути является решением смешанной упругопластической контактной задачи, выраженным единым уравнением прямой Мср, соответствующей закономерности развития пиков максимальных контактных напряжений с ростом среднего давления (на прямой M1) под подошвой штампа, устанавливающих эту границу раздела зон. Впервые появляется возможность обосновать на разных этапах нагружения величину несущей способности грунтового основания и получить четкие границы фазовых переходов состояния грунта под штампом. Так, впервые были установлены границы «условно мгновенного упругого» деформирования грунта под нагрузкой рмгн, «первой критической нагрузки» ркр I, предельной, критической и предельно-критической нагрузки, отражающие ранее не установленные запредельные фазовые состояния грунтовых оснований.
Предложенный способ впервые позволил установить закономерности развития контактных напряжений в торфяных залежах и в идеально связных и сыпучих средах, а также выяснить возможность перехода грунтовых сред из предельного состояния сразу в предельно-критическое состояние.
Следует отметить, что, зная влияние на краевые давления жесткости, формы, размеров и шероховатости материала штампа, можно по предложенному способу определить их влияние на закономерность развития как контактных напряжений, так фазовых переходов состояния грунта основания.
Знание истинности эпюр контактных напряжений под штампом и за его краями впервые позволяет с большой точностью и достоверностью рассчитывать по глубине деформируемого основания его напряженно-деформированное состояние. Ранее при расчете НДС основания σх, σz, τzx исходили из наперед заданного треугольного, прямоугольного, стреловидного распределения напряжений под штампом от действия внешней нагрузки, действующей на штамп по этому же закону, что является обоснованным только для абсолютно гибких штампов. В зависимости от жесткости эти закономерности резко меняются, как отмечено практическими исследованиями и в предложенном способе.
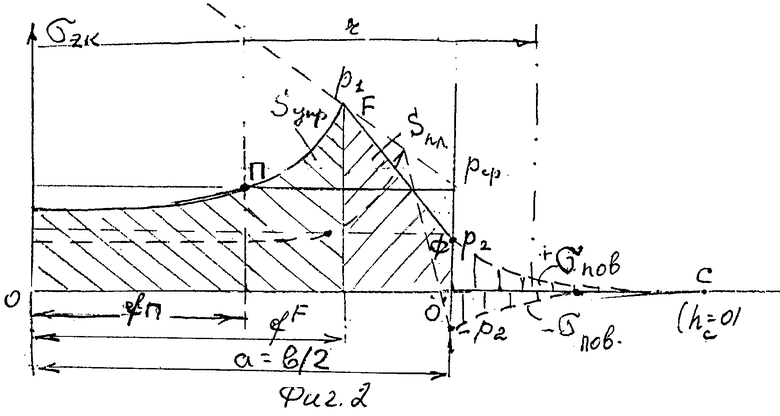
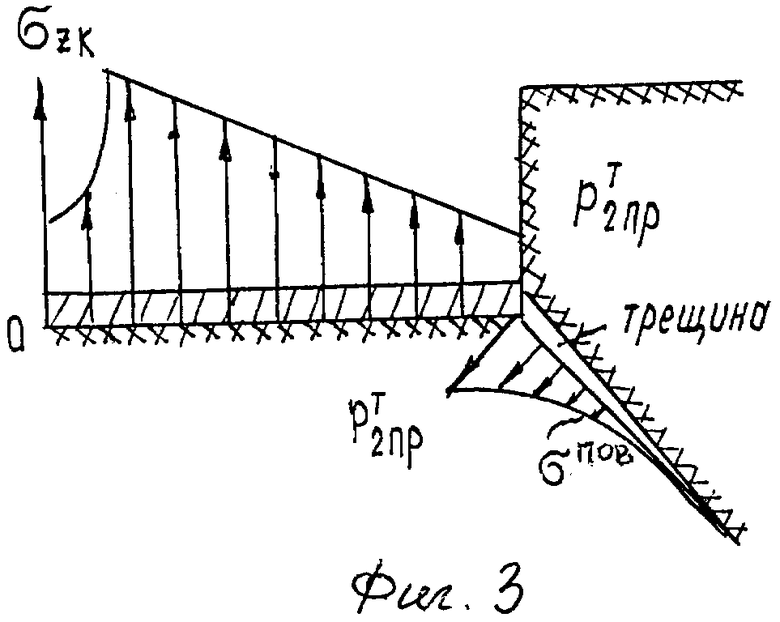
Предлагаемое изобретение поясняется чертежами, где на фиг.1 представлена схема построения определяющих прямых и графиков эпюр упругих и сдвиговых контактных напряжений, совмещенная с диаграммой Мора максимально-предельного по прочности состояния грунта под плоскостью штампа, на фиг.2 - эпюра закраевых напряжений поверхностного натяжения грунта в воронке сжатия за периметром штампа, фиг.3 - эпюра закраевых напряжений в трещине торфяного основания.
Пример реализации способа. Для супеси по результатам инженерных изысканий (или по нормативным данным) получают значения физико-механических характеристик деформируемого плоским жестким полосовым штампом грунтового основания:ϕ=36° - угол внутреннего трения, с=0,02 МПа - удельное сцепление, γ=20 кН/м3 - плотность грунта. По расчетным зависимостям определяют значения: p2 крп=0,2095 МПа, p1 крп=3,395 МПа, рср крп=1,802 МПа, ркрп2 раст=0,012 МПа, р2 кр=0,1153 МПа, рср кр=1,1037 МПа, p1 кр=2,092 МПа, p2 пр=0,0487 МПа, рср пр=0,5762 МПа, р1 пр=1,1037 МПа=рср кр; строят определяющие прямые с учетом значений m=0,1237в, d=0,0723в, to=0,659в, где в=2а, а во=в+2m=1,2474в (фиг.1) в прямоугольной системе с началом координат на оси симметрии под подошвой штампа. Для давления рср=ркр I=0,2711 МПа находим точку S полюса вогнутых парабол на расстоянии от центра штампа fs о=0,59a, что соответствует ≈½ полуширины штампа. Из точки S проводят прямую в точку G (фиг.1), где рG=1,1916 МПа и при рср=ркр I проводят горизонталь эпюры средних контактных напряжений, отсекающей по линии M1 точку развития асимптоты аас и на линии Р точку П полюса вогнутой параболы, ветвь которой проводят через точки F, П до ∞ у вертикали асимптот и до точки Т, где давление рт=(2π)ркр I=0,1726 МПа. Точку F соединяют с точкой Ф с рассчитанными координатами линией J эпюры сдвиговых контактных напряжений под гладким штампом, а эпюру упругих и сдвиговых контактных напряжений зеркально отображают относительно оси ординат. Дополнительное построение кругов Мора (фиг.1) на диаграмме максимально предельного по прочности состояния грунта под штампом позволяет быстро и точно определить в заданной системе координат при заданном среднем давлении значения максимальных (пики) и минимальных контактных напряжений на границе зон упругих и сдвиговых деформаций и по краям зоны сдвиговых (пластических) деформаций.
Предложенный способ определения контактных напряжений открывает новое научное направление в механике контактного взаимодействия в геомеханике, позволяющее теоретически расширить знания в области линейной механики грунтов, расчете конструкций на линейно-деформируемом полупространстве, теории резания и экскавации грунтов, теории трещин, проходимости техники и т.д. С практической стороны уже на первом этапе развития нового направления получены четкие и точные зависимости, определяющие несущую способность грунтовых оснований и торфяных залежей без введения коэффициентов запаса прочности, что дает сотни миллионов рублей в год экономии при проектировании и строительстве зданий и сооружений.
Источники информации
1. Винокуров Ф.П., Тетеркин А.Е. и др. Строительные свойства торфяных грунтов. - Минск: изд-во АН БССР, 1962. - с.145-147 (аналог).
2. Абелев М.Ю. Слабые водонасыщенные глинистые грунты как основания сооружений. - М.: Стройиздат, 1973. - с.12-124 (аналог).
3. Механика грунтов и фундаментостроение (Труды 5-го Международного конгресса)/ Перевод с англ. А.В.Юфина под ред. Н.А.Цытовича. - М.: изд-во лит-ры по строительству, 1966. - С.224-228 (аналог).
4. Горбунов-Пасадов М.И., Маликова Т.А., Соломин В.И. Расчет конструкций на упругом основании. - М.: Стройиздат, 3-е изд., перераб. и доп., 1984. - с.63-66 (прототип).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ ГРУНТОВОГО ОСНОВАНИЯ И ТОРФЯНОЙ ЗАЛЕЖИ | 2004 |
|
RU2270990C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНО МАКСИМАЛЬНОЙ КОНТАКТНОЙ ПРОЧНОСТИ ГРУНТОВОГО ОСНОВАНИЯ В УСЛОВИЯХ ПЛОСКОЙ ДЕФОРМАЦИИ | 2004 |
|
RU2265824C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ И ОСАДОК ГРУНТОВОГО ОСНОВАНИЯ И ТОРФЯНОЙ ЗАЛЕЖИ | 2007 |
|
RU2343448C2 |
| СПОСОБ ХРУСТАЛЕВА Е.Н. ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ ПАРАМЕТРОВ ПРОЧНОСТИ МАТЕРИАЛЬНОЙ СРЕДЫ | 2015 |
|
RU2615598C1 |
| СПОСОБ ПОВЫШЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ ОСНОВАНИЯ СООРУЖЕНИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2376417C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ГРУНТОВОГО, ТОРФЯНОГО И МЕРЗЛОГО ОСНОВАНИЙ | 2007 |
|
RU2345360C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНОГО СОСТОЯНИЯ МАТЕРИАЛЬНОЙ СРЕДЫ В РАЗЛИЧНЫХ УСЛОВИЯХ ЕЕ НАГРУЖЕНИЯ | 2014 |
|
RU2559043C1 |
| СПОСОБ ХРУСТАЛЕВА Е.Н. ОПРЕДЕЛЕНИЯ СРЕДНЕГО ПРЕДЕЛЬНОГО ДАВЛЕНИЯ ДЛЯ СЖИМАЕМОЙ ШТАМПОМ МАТЕРИАЛЬНОЙ СРЕДЫ | 2015 |
|
RU2624592C2 |
| СПОСОБ СООРУЖЕНИЯ ЖЕЛЕЗНОДОРОЖНОГО ПУТИ И УСТРОЙСТВО ЖЕЛЕЗНОДОРОЖНОГО ПУТИ | 2008 |
|
RU2365697C1 |
| УСТРОЙСТВО ОПОРЫ ДОМКРАТА ПОДЪЕМНИКА | 2008 |
|
RU2378481C1 |
Изобретение относится к области строительства, в частности к графо способам определения контактных напряжений грунтов. Способ заключается в графоаналитическом построении составных эпюр напряжений в плоскости контакта жесткого штампа с плоскодеформируемым основанием, исходя из сочетания упругого состояния основания с пластическим, определении закона перемещения границы этих состояний в плоскости контакта с ростом внешнего среднего давления (pcp) с учетом распределения упругих контактных напряжений σzк y по закону вогнутой параболы и распределения контактных напряжений сдвига σz п под гладкой подошвой штампа по закону прямой линии, пересекающейся с вогнутой параболой упругих напряжений на границе раздела зоны упругих и сдвиговых деформаций, при этом по данным испытания грунта рассчитывают в зависимости от угла ϕ внутреннего трения, с - сцепления, γ - объемного веса параметры несущей способности основания по штампам известной формы, размеров, жесткости и степени шероховатости его подошвы, контактные напряжения определяют по ординатам эпюр, далее построенные эпюры зеркально отображают относительно оси ординат и получают эпюры упругих и сдвиговых контактных напряжений под плоскостью штампа. Технический результат - решение смешанной упруго-пластической контактной задачи. 3 ил.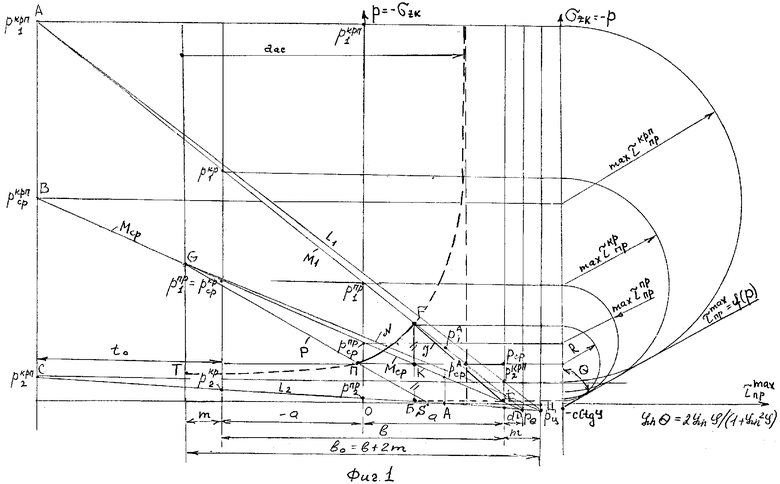
Способ определения контактных напряжений в грунте, заключающийся в графо-аналитическом построении составных эпюр напряжений в плоскости контакта жесткого штампа с плоскодеформируемым основанием, исходя из сочетания упругого состояния основания с пластическим, определении закона перемещения границы этих состояний в плоскости контакта с ростом внешнего среднего давления (рср) с учетом распределения упругих контактных напряжений σzк y по закону вогнутой параболы и распределения контактных напряжений сдвига σz п под гладкой подошвой штампа по закону прямой линии, пересекающейся с вогнутой параболой упругих напряжений на границе раздела зоны упругих и сдвиговых деформаций, отличающийся тем, что по данным испытания грунта (торфа) рассчитывают в зависимости от угла ϕ внутреннего трения, с - сцепления, γ - объемного веса параметры несущей способности основания под штампом известной формы, размеров, жесткости и степени шероховатости его подошвы: величину среднего (рср (пр,кр,крп)), краевого (р2 (пр,кр,крп)) и максимального (p1 (пр,кр,крп)) значения давления под центром подошвы штампа в предельном, критическом и предельно-критическом состоянии основания по формулам р2 крп=[πcCtgϕ/(Ctgϕ+ϕ-π/2)]+[cCosϕ/(1+Sinϕ)], p2 кр=c[Sinϕ·(π-2ϕ)+2(π-Cosϕ)]/{(1+Sinϕ)[2-tgϕ·(π-2ϕ)]}, p2 пр=(1/2)(p2 кр-|pкр2 раст|), где |pкр2 раст|=[4Cosϕ-p2 кр(1-Sinϕ)2]/(1+Sinϕ)2 - давление растяжения под центром штампа в критическом для основания состоянии, p1 (пр,кр,крп)=[p2 (пр,кр,крп)(1+Sinϕ)2+4cCosϕ]/(1-Sinϕ)2, рср (пр,кр,крп)=[р2 (пр,кр,крп)(1+Sin2ϕ)+2cCosϕ]/(1-Sinϕ)2, соответствующую зонам развития сдвига от краев штампа до его центра по схеме Хилла, далее до противоположных сторон штампа с формированием грунтового ядра до краев штампа - по схеме Прандтля и за противоположные стороны штампа с увеличением грунтового ядра за края штампа с временным повышением несущей способности основания, а затем с проявлением провальных осадок основания; величину давления потери структурной прочности материала основания при растяжении (рстр раст) и сжатии (рстр сж):|рстр раст|=2Соsϕ/(1+Sinϕ), (рстр сж=2Сosϕ/(1-Sinϕ) и расчетным путем устанавливают расстояние d=в(1-Sinϕ)2/4Sinϕ от края в сторону от штампа, соответствующее влиянию давлению связности грунта ре=-cCtgϕ; расстояние от края в сторону от штампа 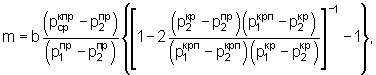 соответствующее величине удаления центра зон сдвигов за края штампа с давлением рц=-[p2 крп(в+2m)-2p2 пр(в+m+t0)]/(в+2t0), где t0=в(p1 крп-p1 кр)/(pi крп-p2 кр) - величина зоны развития сдвигов за краями штампа в предельно-критическом состоянии основания; ширину эквивалентного штампа во=в+2m, под которым рассматривают контактное взаимодействие с основанием; далее от правого края штампа в масштабе наносят вправо от начала координат в центре симметрии штампа точки Ц[(а+m), (-рц)] и D[(a+d), (-ре)], от левого края влево на расстоянии [-(t0+a)] проводят вертикаль, на которой откладывают точки А[-(а+t0),р1 крп], BK[-(a+t0),pcp крп], C[-(a+t0), p2 крп], а на расстоянии [±(m+а)] и [±а] проводят дополнительные вертикали, точки А и С соединяют прямыми линиями L1 и L2 с точкой Ц, а точку А и В соединяют прямыми линиями M1 и Мср с точкой D, точку пересечения прямой Мср с вертикалью [-(m+а)] с координатами G[-(m+а),рG], где pG=[(pcp пр+cCtgϕ)2(в+m+d)/(в+2d)]-cCtgϕ, соединяют с точкой Ц прямой линией N, определяющей с ростом рср сужение асимптот (аас) ветвей вогнутой параболы эпюры упругих контактных напряжений
соответствующее величине удаления центра зон сдвигов за края штампа с давлением рц=-[p2 крп(в+2m)-2p2 пр(в+m+t0)]/(в+2t0), где t0=в(p1 крп-p1 кр)/(pi крп-p2 кр) - величина зоны развития сдвигов за краями штампа в предельно-критическом состоянии основания; ширину эквивалентного штампа во=в+2m, под которым рассматривают контактное взаимодействие с основанием; далее от правого края штампа в масштабе наносят вправо от начала координат в центре симметрии штампа точки Ц[(а+m), (-рц)] и D[(a+d), (-ре)], от левого края влево на расстоянии [-(t0+a)] проводят вертикаль, на которой откладывают точки А[-(а+t0),р1 крп], BK[-(a+t0),pcp крп], C[-(a+t0), p2 крп], а на расстоянии [±(m+а)] и [±а] проводят дополнительные вертикали, точки А и С соединяют прямыми линиями L1 и L2 с точкой Ц, а точку А и В соединяют прямыми линиями M1 и Мср с точкой D, точку пересечения прямой Мср с вертикалью [-(m+а)] с координатами G[-(m+а),рG], где pG=[(pcp пр+cCtgϕ)2(в+m+d)/(в+2d)]-cCtgϕ, соединяют с точкой Ц прямой линией N, определяющей с ростом рср сужение асимптот (аас) ветвей вогнутой параболы эпюры упругих контактных напряжений 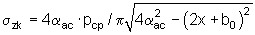 под полосовым и
под полосовым и 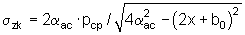 под круглым штампом, а также точку G соединяют с точкой S[fкр I, 0], где fкр I=(а+d)[р2 пр-0,5|рстр раст|)/(p2 пр+cCtgϕ) - расстояние от центра штампа до точки штампа с давлением, соответствующим значению «первой критической нагрузки» рср.кр I=Pcp пр-[(р2 пр-0,5|рстр раст|)(рср пр+cCtgϕ)(р2 пр+cCtgϕ)] на прямой Мср, прямой линией Р перемещения полюса вогнутой параболы эпюры упругих контактных напряжений с ростом рср, а контактные напряжения определяют по ординатам эпюр, которые строят из точки F пересечения прямой M1 с вертикалью, проходящей через точку К пересечения прямой Мср с горизонталью эпюры рср, путем проведения ветви вогнутой параболы σzк через точку F и полюс П до ∞ у вертикали асимптоты aас и до точки Т[-(а+m); 2рср/π] для полосового или Т[-(а+m); рср/2] - для круглого штампа с одной стороны и с другой стороны - путем проведения прямой линии J из точки F в точку Ф[+а; рф], где рф=2рср-рF=рF-2R, a R=τmax пр=(1/2) (рF-рБ)-радиус круга Мора предельно-максимального по прочности состояния грунта под штампом на вертикали, проходящей через точки F, К и Б, причем отрезки FK=КБ=R, а линия J - есть эпюра развития при рср сдвиговых (пластических) деформаций под краем штампа, далее построенные эпюры зеркально отображают относительно оси ординат и получают эпюры упругих и сдвиговых контактных напряжений под плоскостью штампа, а из точки Ф проводят кривую линию эпюры закраевых поверхностных напряжений на поверхности воронки сжатия грунта за краями штампа с уравнением σпов=[2π/|рф|]arcSin (а/r), где r - расстояние от края за пределы штампа.
под круглым штампом, а также точку G соединяют с точкой S[fкр I, 0], где fкр I=(а+d)[р2 пр-0,5|рстр раст|)/(p2 пр+cCtgϕ) - расстояние от центра штампа до точки штампа с давлением, соответствующим значению «первой критической нагрузки» рср.кр I=Pcp пр-[(р2 пр-0,5|рстр раст|)(рср пр+cCtgϕ)(р2 пр+cCtgϕ)] на прямой Мср, прямой линией Р перемещения полюса вогнутой параболы эпюры упругих контактных напряжений с ростом рср, а контактные напряжения определяют по ординатам эпюр, которые строят из точки F пересечения прямой M1 с вертикалью, проходящей через точку К пересечения прямой Мср с горизонталью эпюры рср, путем проведения ветви вогнутой параболы σzк через точку F и полюс П до ∞ у вертикали асимптоты aас и до точки Т[-(а+m); 2рср/π] для полосового или Т[-(а+m); рср/2] - для круглого штампа с одной стороны и с другой стороны - путем проведения прямой линии J из точки F в точку Ф[+а; рф], где рф=2рср-рF=рF-2R, a R=τmax пр=(1/2) (рF-рБ)-радиус круга Мора предельно-максимального по прочности состояния грунта под штампом на вертикали, проходящей через точки F, К и Б, причем отрезки FK=КБ=R, а линия J - есть эпюра развития при рср сдвиговых (пластических) деформаций под краем штампа, далее построенные эпюры зеркально отображают относительно оси ординат и получают эпюры упругих и сдвиговых контактных напряжений под плоскостью штампа, а из точки Ф проводят кривую линию эпюры закраевых поверхностных напряжений на поверхности воронки сжатия грунта за краями штампа с уравнением σпов=[2π/|рф|]arcSin (а/r), где r - расстояние от края за пределы штампа.
| Горбунов-Пасадов М.И | |||
| и др | |||
| Расчет конструкций на упругом основании | |||
| М.: Стройиздат., 3-е изд., перераб | |||
| и доп., 1984, с.63-66 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ ДЕФОРМАЦИИ | 1998 |
|
RU2145655C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК СЛОЯ ПОЧВОГРУНТА, ПРЕИМУЩЕСТВЕННО ИМЕЮЩЕГО НИЗКУЮ И СРЕДНЮЮ ПЛОТНОСТЬ, И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2192006C2 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ КОНТАКТНОГО НАПРЯЖЕНИЯ | 1991 |
|
RU2023995C1 |
| RU 93043439 А, 20.12.1995 | |||
| Способ испытания образцов грунта | 1987 |
|
SU1578653A1 |
Авторы
Даты
2005-12-10—Публикация
2004-04-26—Подача