Изобретение относится к фундаментальной астрометрии и может быть использовано для абсолютных определений экваториальных координат светил и астрономических координат места наблюдения.
Считается, что абсолютность определений соблюдается при том условии, что в качестве известных величин принимают гринвичское истинное звездное время на 0 часов всемирного времени и момент кульминации Солнца на меридиане Гринвича в дату наблюдений.
Существуют методы абсолютных определений склонения и прямого восхождения, при которых из точки с известной широтой места измеряют зенитные расстояния звезд в моменты их верхнего или нижнего кульминаций и получают поправку часов к местному времени точки с известной долготой. Для наблюдений используют меридианный круг. (В.В.Подобед, В.В.Нестеров. Общая астрометрия. - М.: Наука. Гл. ред. физ-мат. лит. 1982. 114-120 с.).
Такие наблюдения не обеспечивают достаточную точность и производительность, а участие широты места и местного времени в определениях нарушает принцип абсолютности.
Призменный пассажный инструмент служит для абсолютного определения склонений светил по их наблюдению в двух плоскостях, параллельных плоскости меридиана, расположенных по обе стороны от последней на равных и известных угловых расстояниях. При этом не требуется знания широты места. (Доклад Магомедова Р.М. на научном собрании астрометрических отделов ГАО АН СССР. 5.10.1988 г.).
Однако призменный пассажный инструмент не может наблюдать светила в моменты их прохождения через меридиан и не обеспечивает достаточной точности наблюдений. Он не имеет разделенного круга и поэтому не может определить широту места.
С целью абсолютного определения экваториальных координат светила и астрономических координат места наблюдения предлагаются зеркальный меридианный круг и способ наблюдений с его помощью.
Зеркальный меридианный круг - это телескопическое устройство, имеющее объектив 1 и окуляр 2 (см. фиг.1), составляющие зрительную трубу. В общей фокальной плоскости объектива и окуляра установлена сетка нитей 3 в виде взаимно перпендикулярных вертикальных и горизонтальных боковых и средних нитей, пересекающихся на оптической оси инструмента и освещаемых лампочкой 4. Он имеет горизонтальную ось вращения 5, на которой смонтирован разделенный круг 6, который требуется для получения широты места. Перед объективом установлены три плоскопараллельных зеркала 7, 8 и 9. Зеркало 7 закреплено справа от визирной плоскости под известным углом G к ней так, чтобы луч света от светила до кульминации проходил в правую половину объектива. Зеркало 8 закреплено слева под тем же углом G к плоскости визирования так, чтобы луч света от того же светила, отраженный от зеркала 9, закрепленного справа, параллельно плоскости визирования, направлялся в левую половину объектива.
Такая установка зеркал создает боковую плоскость визирования, удаленная от визирной плоскости трубы инструмента на угловое расстояние, заданное углом G наклона зеркал 7 и 8 к этой плоскости. При этом формируются два изображения наблюдаемого светила.
Вначале инструмент устанавливают в меридиане в положении «круг влево». При этом зеркала 7 и 9 рабочей поверхностью направлены влево.
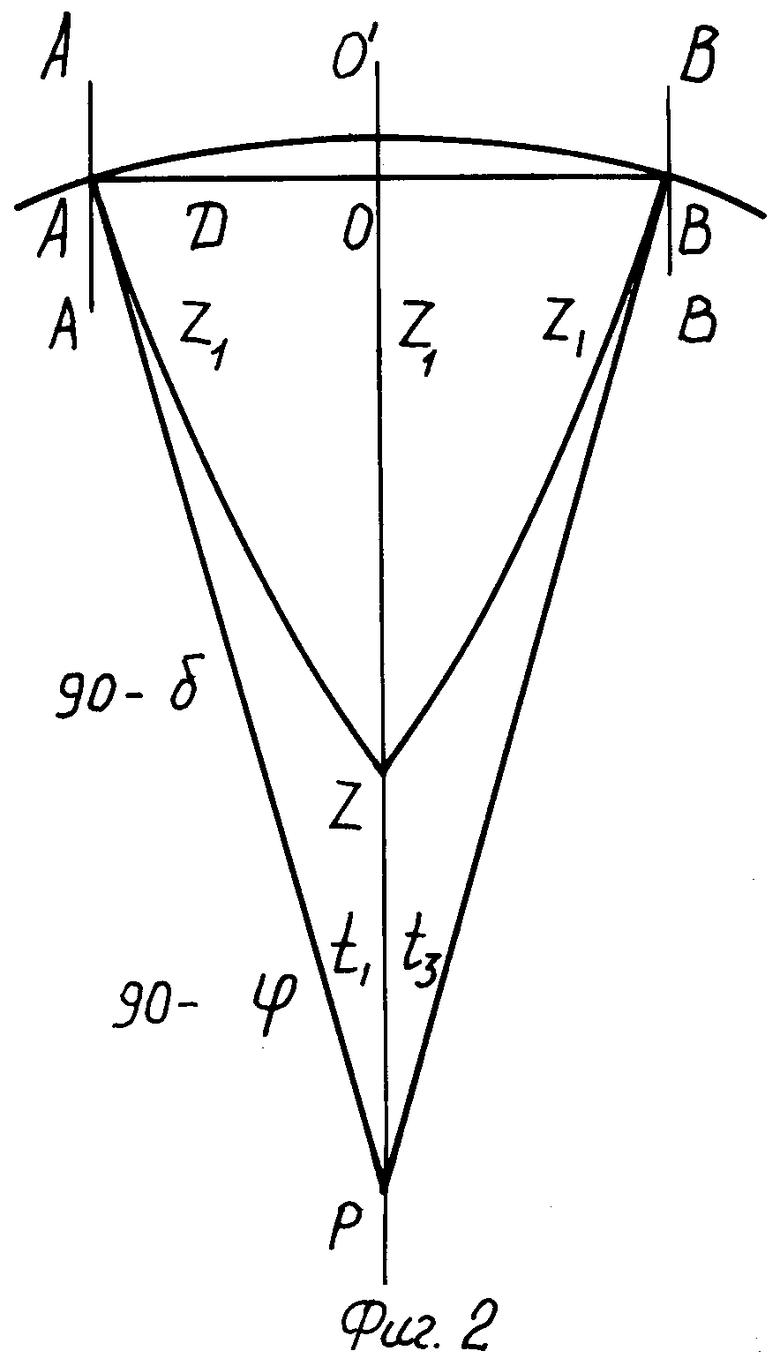
При достижении светилом плоскости визирования А-А на угловом расстоянии D=90-G от плоскости меридиана (см. фиг.2), два изображения светила сливаются в одну в точке пересечения центральных нитей сетки. В этот момент выполняют отсчеты часов и разделенного круга и получают момент T1 гриничского времени и зенитное расстояние светила в этот момент z1.
По ходу суточного движения одинарное изображение светила, минуя зеркала, пересекает плоскость меридиана, и в этот момент снимают показания часов Т2 и разделенного круга z2.
При этом образуется прямоугольный сферический треугольник АОР с углом у полюса мира Δt=Т2-T1=t1 и известным катетом D, противолежащим углу t1 и параллактический угол APZ с измеренным зенитным расстоянием z1.
Из треугольника АОР определяется склонение δ светила по формуле cosδ=sinD/sinΔt;
местный часовой угол светила равен разности моментов звездного времени прохождения светила между визирными плоскостями А-А и О-Р, то есть tм=Δt.
Широта места ϕ определяется из параллактического треугольника APZ по формуле
sinz1=sinδsinϕ+cosδcosϕcostм
и из соотношения ϕ=δ-z2.
Долгота места выводится согласно концепции Магомедова по наблюдению Солнца из разности моментов всемирного времени его кульминаций на местном Т2 и гринвичском МK меридианах:
λ=Т2-МK.
(Концепция гласит: Долгота места определяется из разности моментов всемирного или гринвичского звездного времени между одним и тем же астрономическим явлением, который происходит на разных меридианах в разные физические моменты времени).
Имея долготу места, получают прямое восхождение светила α из соотношения α=S2+λ, где
S2=S0+Т2+μТ2; (μ=0.0027379093...)
S0 - истинное звездное время на 0 часов всемирного времени.
Для обнаружения ошибок инструмента и наблюдателя, а также вывода окончательных результатов наблюдений производят перекладку инструмента в положение «круг право» и выполняют идентичные наблюдения на третьей визирной плоскости, справа от плоскости меридиана.
Изобретение относится к области астрометрии. Способ заключается в том, что наблюдают светила с регистрацией моментов гринвичского времени прохождения светила через боковую визирную плоскость, параллельную плоскости меридиана и удаленную от него на известное угловое расстояние, а также через плоскость меридиана и измеряют соответствующие зенитные расстояния. При этом образуются сферические треугольники, из решения которых определяются искомые величины. Для реализации способа используют меридианный круг, перед объективом которого установлены три зеркала для создания двух изображений светила и создания боковой визирной плоскости, параллельной плоскости меридиана. Техническим результатом изобретения является обеспечение абсолютности астрономических определений. 2 з.п. ф-лы, 2 ил.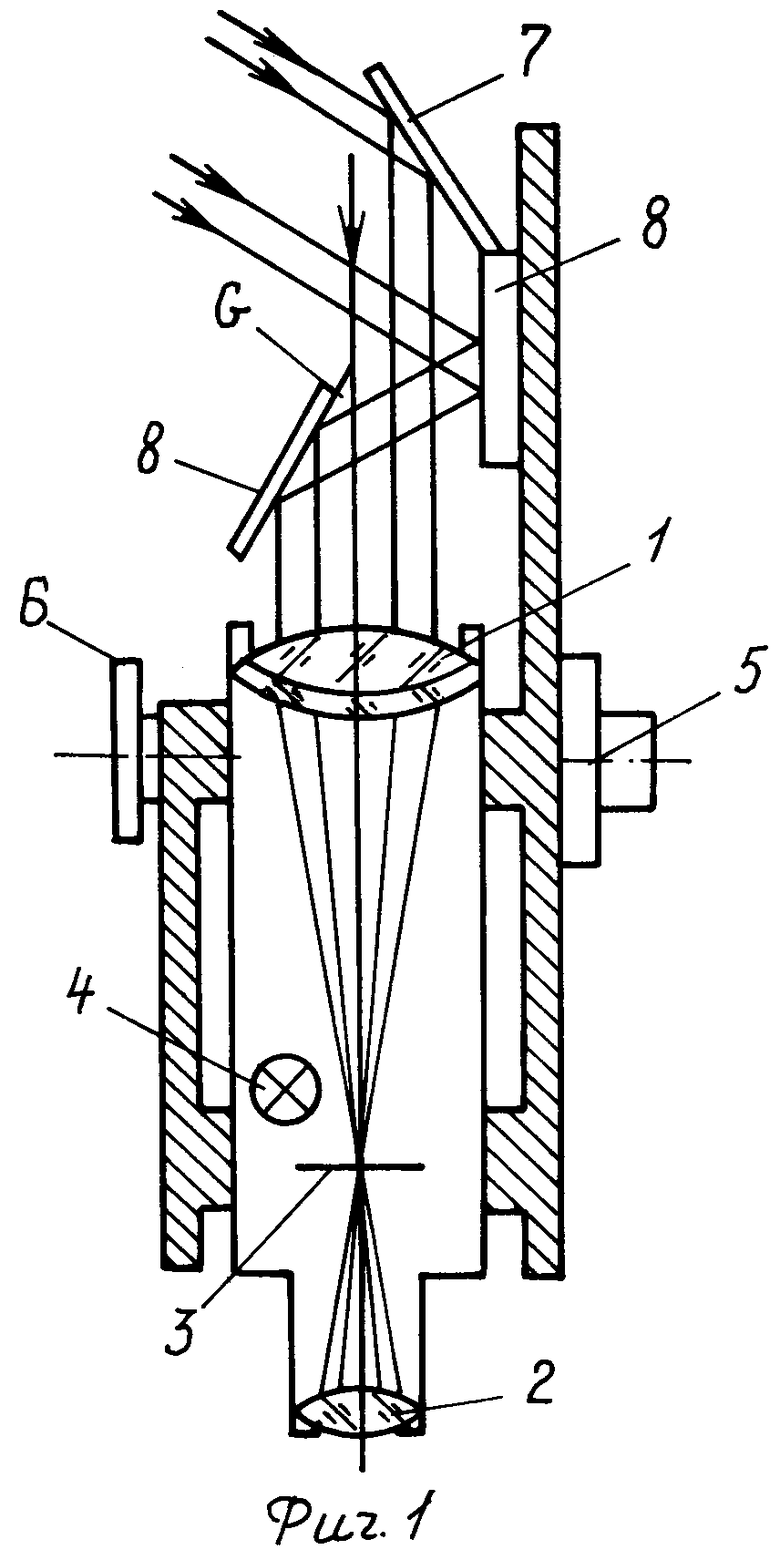
| В.В.ПОДОБЕД и др | |||
| Общая астрометрия | |||
| - М.: Наука, 1982, с.114-120 | |||
| RU 96105046 А, 27.06.1998 | |||
| RU 98120675 A, 27.08.2000 | |||
| US 5995280 A, 30.11.1999. |
Авторы
Даты
2005-12-27—Публикация
2003-07-15—Подача