Изобретение относится к навигации и управлению угловой ориентацией и орбитальным местоположением космического аппарата (КА) и предназначено для использования на автономно функционирующем КА.
В качестве средств навигации широко известны и традиционно используются радиотехнические наземные измерительные пункты (НИП). НИПы территориально разнесены по долготе-широте таким образом, чтобы перекрыть как можно большее пространство. Такое размещение НИПов обусловлено тем, что сеансы измерений дальностей до КА, азимута и угла места реализуются лишь на тех участках, где выполняются условия радиовидимости между НИП и КА. И, тем не менее, при периоде обращения КА, например около полутора часов из 15-16 суточных витков, не менее 6 проходят вне зон радиовидимости с территории бывшего СССР. К тому же имеется ограничение, обусловленное тем, что каждому НИПу требуется некоторое время для приготовления к дальнейшей работе. На навигационные измерения могут быть наложены также ограничения, связанные с невозможностью одновременной работы двух различных НИПов.
Таким образом имеет место несоответствие между потребностью в глобальном масштабе при проведении измерений и существующими возможностями. К тому же требования к точности измерения параметров движения КА сочетаются со стоимостью аппаратуры НИПа и со стоимостью обслуживания задействованного количества измерительных пунктов.
Другим известным навигационным средством является космическая система, которая состоит из совокупности навигационных спутников и наземного измерительного комплекса. Возможность воспользоваться измерениями относительно данной системы зависит от взаимного расположения навигационных спутников и КА. Существует неопределенность реализации навигационных измерений в заданных или любых районах пространства, так как их возможность связана со временем ожидания момента появления хотя бы одного навигационного спутника и длительность ожидания для разных КА различна. Другими словами, в различных подпространствах сферы действия спутниковой системы навигации вероятность навигационных определений различна. Говорить в этом случае о глобальности как о максимальном значении отношения обслуживаемого системой подпространства ко всему предназначенному для навигации околоземному пространству можно лишь условно. В том же ограничительном смысле следует говорить о непрерывности навигационных определений, так как непрерывность обусловлена одновременной геометрической видимостью нескольких спутников, что не всегда последовательно доступно. Также не следует говорить в абсолютном смысле и об оперативности.
А между тем, как в случае использования НИПов, так и при использовании космической системы навигации непрерывность измерений является тем средством, которое обеспечивает необходимые точностные показатели навигационных определений.
В то же время точные последовательные данные о местоположении КА в пространстве являются тем исходным материалом, который служит для расчета последовательной угловой ориентации КА, например, относительно Земли. Заметим, что среди измерений рассмотренными средствами параметров отсутствует определение пространственного положения направления «КА - центр Земли», относительно которого производится по существу угловое управление КА при любом его целевом функционировании. В общем, целью навигационных определений должен бы быть именно этот параметр. Однако при принятом подходе он непосредственно ненаблюдаем. Поэтому для его определения привлекаются дополнительные навигационные средства, в частности небесные ориентиры. По сути это означает, что в дополнение к искусственной навигационной системе используется еще вторая навигационная система - система естественных опорных астроориентиров. Разные системы с разными системами отсчета расщепляют единое движение КА на два движения - пространственное и угловое. Необходимо признать, что такая опосредствованная методика, призванная не изначально, а в самом конце навигационного процесса охарактеризовать движение КА как угловое, порождает не только дополнительные объемы работ, но и точностные погрешности ориентации.
Таким образом, задача навигации КА традиционно решается независимо от задачи углового управления КА и на практике алгоритмы навигации и управления угловой ориентацией КА изначально не зависят друг от друга.
В итоге рассмотрения уровня традиционно используемой техники следует признать, что существует проблема обеспечения в реальном времени и в глобальном масштабе максимально точных, непрерывных и прямых измерений таких навигационных переменных, которые могли бы непосредственно соответствовать переменным управления и способствовали бы синтезу алгоритмов управления и навигации в одной автономной бортовой системе управления КА.
Характерной чертой данной проблемы является то, что для ее решения необходимо выйти за рамки известных методов. Решать ее следует с тех точек зрения, которые позволяют рассматривать навигационно-управленческий процесс как нечто единое и целое.
Известна «Автономная бортовая система управления космического аппарата «ГАСАД» [заявка 93007754 (патент 2033949), 1993], которая не претендует на решение указанной проблемы, однако обозначает некоторые способы получения и обработки астрономических измерений. Данная система содержит: датчик Земли, датчик Полярной звезды и навигационной звезды (звездный датчик), вычислитель, устройство запоминания, временное устройство и исполнительные органы. При этом:
- выходы датчика Земли, звездного датчика, устройства запоминания связаны со входами вычислителя по соответствующим сигналам; с временным входом вычислителя соединен также выход временного устройства, а вход исполнительных органов соединен с выходом вычислителя;
- устройство запоминания содержит параметры базы отсчета инерциальной долготы, причем этими параметрами являются прямое восхождение Полярной звезды и угол относительно общей плоскости чувствительности датчика Земли и звездного датчика, равный углу между плоскостью, содержащей направления «центр Земли - Полярная звезда» и «центр Земли - полюс мира», и плоскостью, содержащей направления «центр Земли - Полярная звезда» и «центр Земли - навигационная звезда»;
- вычислитель выполнен с возможностью определения широты КА по углу «центр Земли - КА - Полярная звезда»;
- вычислитель выполнен с возможностью выработки управляющего сигнала для угловой ориентации КА по каналу рысканья на основе измеренных соответствующих угловых рассогласований для совмещения общей плоскости чувствительности датчика Земли и звездного датчика, содержащей продольную ось КА, с плоскостью, содержащей центр Земли, КА и Полярную звезду;
- вычислитель выполнен с возможностью определения инерциальной долготы местоположения КА по азимутальному углу поворота навигационной звезды вокруг направления «КА - Полярная звезда», отсчитываемому в соответствующем поле зрения от базового углового положения плоскости, содержащей направления «КА - навигационная звезда» и «КА - Полярная звезда».
Рассмотрим, может ли данная система по совокупности своих признаков служить прототипом изобретения. Но вначале отметим следующее. Странно, конечно, говорить о том, что само собой разумеется. Так, выбор наземного измерительного пункта или выбор навигационного спутника в качестве искусственного опорного ориентира не являются равнозначными. Такой выбор обычно обосновывается своеобразием конкретного случая. Например, особенностями решаемой задачи, используемой орбиты и т.д.
Аналогичное значение имеет выбор той или иной приполюсной звезды в качестве естественного опорного ориентира.
Для обеспечения глобальности пространства навигационных определений, непрерывности и точности астрономических измерений опорная звезда должна быть:
1) наблюдаема с любой точки используемой орбиты;
2) относительно неподвижна (изменение прямого восхождения звезды должно быть по возможности минимальным за срок активного существования КА).
Заметим здесь, что приполюсная зона звезд в силу прецессии земной оси вообще является зоной особых прямых восхождений.
В этом случае становится очевидным, что при обеспечении глобальности пространства и непрерывности навигационных измерений особенности той или иной используемой орбиты накладывают свои ограничения на свободу выбора той или иной звезды из зоны северного полюса мира или из зоны южного полюса мира. Так, при движении КА в перигейной зоне орбиты типа «Молния» Полярная звезда затеняется Землей. В то же время опорная звезда из области южного полюса наблюдаема из любых точек этой же орбиты. К тому же изменение прямого восхождения Полярной звезды за 10 лет составляет 4,3 минуты, что в градусном исчислении равно 1°4,5' (4,3мин×15'/мин). Говорить в этом случае о высоких точностных показателях не приходится. Следует отметить, что Полярная звезда по «неустойчивости» своего относительного местоположения в пространстве превосходит все звезды как северной так и южной приполюсной зоны.
Правда, координатные изменения Полярной звезды могут периодически уточняться в бортовых вычислительных алгоритмах посредством коррекции их текущих фактических координат. Учитывая, что изменение координат по времени известно, реализовать такую коррекцию возможно за счет значительного усложнения бортового программного обеспечения. Разумеется, при наличии других вариантов усложнять программное обеспечение нерационально.
Необходимо признать, что глобальность, непрерывность и точность навигационных измерений при использовании Полярной звезды в этом случае не обеспечивается. Рассматриваемая система изначально предназначена работать совместно с традиционными средствами навигации и призвана решать ограниченную узкую задачу. Это следует также из того обстоятельства, что в ней не предусматривалось местоопределение КА относительно географической широтно-долготной сетки Земли. Более того, система не предназначена обеспечивать соответствие параметров реальной орбиты параметрам заданной и не содержит средств обработки измеренных угловых данных с целью получения их высокоточных значений.
По существу все признаки рассматриваемой системы основаны на использовании Полярной звезды как основополагающего навигационного ориентира. Помимо этого, эти признаки содержат также следующие неопределенности и недостатки:
1) Заявленная задача - определять широту местоположения КА по углу «центр Земли - КА - Полярная звезда» не решается ввиду того обстоятельства, что не учитывается поправка, которая обусловлена полярным расстоянием Полярной звезды и значение которой зависит от инерциальной долготы.
2) Не определена нулевая приборная база отсчета инерциальной долготы, соответствующая внешней нулевой базе отсчета, относительно которой происходит и отсчет времени.
3) Не определен момент обнуления бортового времени.
4) В общей плоскости чувствительности данной системы содержится продольная ось КА, что не позволяет переориентировать ось на заданные целевые точки Земли, не прервав тем самым сеанс навигации.
Таким образом, признаки рассмотренной системы не являются наиболее близкими к признакам изобретения, а потому данная система не может быть признана прототипом изобретения.
Аналогом изобретения может служить также типичная система управления ориентацией и стабилизации КА, включающая в основном традиционные компьютер, датчик Земли, звездный датчик, инерционные маховики.
Такая система предназначена решать задачи угловой ориентации и стабилизации.
В этих режимах идентифицируются и отслеживаются звезды, попадающие в поле зрения датчика, а также осуществляется стабилизация, что может быть также отнесено к общим с изобретением признакам.
В основу изобретения положена техническая задача - создать бортовую систему управления космического аппарата, которая позволила бы с высокой точностью обеспечить автономный контроль угловой ориентации, автономное определение углового и местоположения аппарата относительно широтно-долготной сетки Земли, автономное определение рассогласований реальной орбиты от заданной и автономное их устранение.
Технический результат сводится к:
- исключению использования наземной инфраструктуры навигации и управления КА;
- обеспечению глобальности пространства навигационных измерений, осуществляемых бортовыми средствами КА;
- осуществлению синтеза алгоритмов управления и навигации;
- реализации прямых и непрерывных измерений параметров орбитального движения при соответствии друг другу углов ориентации и навигации;
- определению в реальном масштабе времени углового и местоположения аппарата как в инерциальном пространстве, так и относительно широтно-долготной сетки Земли;
- обеспечению высоких точностей параметров углового и местоположения КА на текущий и прогнозируемый интервал;
- выявлению эволюционных изменений орбитальных параметров относительно заданной орбиты и осуществлению их автоматического устранения.
Технический результат, который сводится к нескольким результатам, на уровне функционального обобщения можно представить как автономность, независимость КА от комплексов наземного и космического базирования, т.е. от внешних искусственных средств навигации и управления.
В структурный состав предлагаемой системы управления входят, помимо управляющего компьютера, несколько процессоров, предназначенных параллельно осуществлять каждый свою функцию, а также в качестве исполнительных органов инерционные маховики и двигатели импульсной коррекции.
Все устройства системы, в том числе датчик Земли, звездный датчик, запоминающее устройство и временное устройство соответствующим образом и по соответствующим сигналам соединены линиями связи.
Технический результат достигается за счет:
I. АВТОНОМНОЙ УГЛОВОЙ ОРИЕНТАЦИИ:
(задействованы: процессор управления положением, датчик Земли, звездный датчик, инерционные маховики и соответствующие алгоритмы)
1). Система астроориентиров формируется из двух звезд приполюсной зоны: опорной и навигационной и (центра) Земли.
2). Плоскость, содержащая направление центральной оси датчика Земли на центр Земли и направление с КА на опорную звезду, совмещается постоянно в процессе орбитального движения с жесткой плоскостью, образованной центральными осями датчиков и закоординированной в системе координат звездного датчика.
II. АВТОНОМНОГО ОПРЕДЕЛЕНИЯ ИНЕРЦИАЛЬНОЙ ДОЛГОТЫ:
(задействованы: звездный датчик, процессор обработки угловых данных и соответствующие алгоритмы)
3). Поворот навигационной звезды (обусловленный орбитальным движением КА) вокруг опорной звезды в поле зрения звездного датчика фиксируется в координатах звездного датчика как инерциально-долготное изменение орбитального положения КА.
III. ФИКСАЦИИ БОРТОВОЙ ТОЧКИ ОТСЧЕТА ИНЕРЦИАЛЬНОЙ ДОЛГОТЫ:
(задействованы: проектные расчеты, процессор обработки угловых данных и соответствующие алгоритмы)
4). При проектных расчетах базовая инерциальная долгота КА определяется прямым восхождением опорной звезды в градусном исчислении на тот момент орбитального движения, когда базовый угол между жесткой плоскостью датчиков и плоскостью направлений с КА на обе звезды в поле зрения звездного датчика соответствует моменту кульминации опорной звезды.
5). Бортовая нулевая точка отсчета инерциальной долготы координируется в координатах звездного датчика как положение плоскости направлений с КА на обе звезды на момент, когда проектная инерциальная долгота обнуляется, а диапазон изменения базового угла достигает значения базовой инерциальной долготы.
IV. ФИКСАЦИИ ВНЕШНЕЙ ТОЧКИ ОТСЧЕТА ИНЕРЦИАЛЬНОЙ ДОЛГОТЫ И ВРЕМЕНИ:
(задействовано временное устройство)
6). В качестве внешней точки отсчета инерциальной долготы становится (см. п. 4, 5) точка весеннего равноденствия.
7). Бортовое время КА синхронизируется с часовым углом точки весеннего равноденствия относительно гринвичского меридиана и обнуляется по истечении времени полного поворота Земли.
V. АВТОНОМНОГО ОПРЕДЕЛЕНИЯ ГЕОГРАФИЧЕСКОЙ ДОЛГОТЫ:
(задействованы: звездный датчик, процессор обработки угловых данных, временное устройство и соответствующие алгоритмы)
8). Географическая долгота КА определяется по соответствующим математическим зависимостям, учитывающим скорость вращения Земли, текущее время и измеренную инерциальную долготу.
VI. АВТОНОМНОГО ОПРЕДЕЛЕНИЯ ШИРОТНОГО МЕСТОПОЛОЖЕНИЯ:
(задействованы: проектные расчеты, датчик Земли, звездный датчик, процессор обработки угловых данных, запоминающее устройство и соответствующие алгоритмы)
9). При проектных расчетах угол между направлением с КА на опорную звезду и осью Земли определяется полярным расстоянием опорной звезды на момент, когда базовая инерциальная долгота КА соответствует прямому восхождению опорной звезды в градусном исчислении. Значения указанного угла при иных значениях инерциальной долготы определяются по известной математической зависимости и представляются в постоянном запоминающем устройстве (ПЗУ).
10) Географическая широта КА определяется посредством преобразования измеренного угла между центральной осью датчика Земли, направленной на центр Земли, и направлением с КА на опорную звезду (координируемым звездным датчиком) и с учетом угла между направлением с КА на опорную звезду и осью Земли, представленного в запоминающем устройстве значением, соответствующим тому значению инерциальной долготы, при котором определяется широта.
VII. АВТОНОМНОГО ОПРЕДЕЛЕНИЯ РЕАЛЬНОЙ ОРБИТЫ И ТОЧНОЙ УГЛОВОЙ ОРИЕНТАЦИИ:
(задействованы: процессор обработки угловых данных, процессор управления положением, запоминающее устройство, временное устройство, инерционные маховики и соответствующие алгоритмы)
11). Орбита в инерциальном пространстве определяется совокупностью точек, образуемых на каждый временной такт инерциально-долготными и инерциально-широтными измерениями.
12). Уровень точности звездного датчика (в свете несопоставимости значений ошибок обоих датчиков) трактуется как базовый уровень и потому погрешность угловых измерений отнесена к погрешности датчика Земли.
13). Погрешность измерений интерпретируется в форму мнимой погрешности характера орбитального движения.
14). Параметры реального и по сути «гладкого» движения КА определяются статистической обработкой стохастических инерциально-долготных и инерциально-широтных измерений с помощью соответствующего программного модуля (нейронной сети) и по мере обработки представляются посредством записи в оперативном запоминающем устройстве (ОЗУ).
15). При указанной обработке устраняются ошибки в измерениях и на несколько тактовых шагов вперед прогнозируются значения инерциально-долготных и инерциально-широтных углов для реализации последующей уточненной угловой ориентации КА.
VIII. АВТОНОМНОГО ОПРЕДЕЛЕНИЯ НЕСООТВЕТСТВИЙ ПАРАМЕТРОВ РЕАЛЬНОЙ ОРБИТЫ ПАРАМЕТРАМ ЗАДАННОЙ ОРБИТЫ.
(задействованы: проектный расчет, запоминающее устройство (ПЗУ и ОЗУ), процессор обработки орбитальных данных и соответствующие алгоритмы)
16). На борту КА посредством записи в постоянное запоминающее устройство (ПЗУ) представляется (соответствующий требованиям целевой функции КА) заданный орбитальный виток своими традиционными параметрами и в форме инерциально-долготных и инерциально-широтных углов на каждый временной такт.
17). По соответствующим математическим зависимостям и непосредственно по имеющимся данным определяются период, большая полуось, эксцентриситет, аргумент перигея, наклонение и прямое восхождение восходящего узла реального, представленного в ОЗУ орбитального витка.
18). По результатам сопоставления параметров реальной орбиты и представленных в ПЗУ параметров заданной орбиты определяются искомые отклонения.
19). По известным зависимостям и по выявленным отклонениям определяются: последовательность корректирующих воздействий, тип корректирующего импульса, точка его приложения, значение импульса скорости, значение энергозатрат и времени работы двигательной установки (ДУ).
IX. АВТОНОМНОЙ РЕАЛИЗАЦИИ КОРРЕКЦИИ.
(задействованы: процессор управления положением, временное устройство, инерционные маховики, двигатели коррекции и соответствующие алгоритмы)
20). По точке и направлению приложения импульса определяются и реализуются угловые развороты КА относительно моделируемой на борту системы координат, обеспечивающие необходимое направление вектора корректирующего импульса, а по продолжительности импульса - время работы ДУ.
X. АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕХНИЧЕСКИМ ПРОЦЕССОМ.
(задействованы: управляющий компьютер и периферийные устройства)
21) В условиях многозадачного режима работы управляющим компьютером циклически опрашивается и оценивается текущее состояние периферийных устройств, обновляются данные внутренней базы данных и принимаются необходимые команды воздействия с целью должного протекания процесса.
Следует отметить, что совокупность вышепредставленных признаков относится к группе изобретений, связанных между собой единым замыслом - единой синтезированной по части навигации и управления автономной бортовой системой КА.
На фиг.1 представлена иерархическая структурная схема автономной бортовой системы управления; на фиг.2 - схематическое изображение астрономических пространственных и временных соотношений как основы навигационных определений; на фиг.3 - космический аппарат на околоземной орбите со схемой измеряемых углов, стабилизированный относительно направления на центр Земли и направления на опорную звезду; на фиг.4 - таблица звезд из окрестности северного полюса мира; на Фиг.5 - таблица звезд из окрестности южного полюса мира; на фиг.6 - космический аппарат с расширенным полем зрения звездного датчика и возможностью ориентировать продольную ось в любую точку Земли; на фиг.7 - схема затенения Землей звездных ориентиров на различных орбитах; на фиг.8 - сферический треугольник, предназначенный для определения угла между плоскостью, содержащей направления на опорную и навигационную звезды, и плоскостью, содержащей направления на опорную звезду и полюс мира; на фиг.9 - схема определения бортовой точки отсчета инерциальной долготы; на фиг.10 - схема определения угла между направлением с КА на опорную звезду и осью Земли; на фиг.11 - орбита, формируемая точками, которые координируются инерциально-долготными и инерциально-широтными углами; на фиг.12 - схема, иллюстрирующая взаимное положение значений географической долготы и инерциальной долготы; на фиг.13 - схема построения геоцентрической вертикали с помощью 4-х сканирующих датчиков; на Фиг.14 - схема геометрии измерений при определении геоцентрической вертикали; на фиг.15 - моноблок астродатчиков КА, его «жесткая» плоскость и координация осей датчиков в моноблоке; на фиг.16 - схема различий систематических и случайных ошибок; на фиг.17 и 18 представлены схемы, иллюстрирующие ошибки углового пространственного положения КА в плоскости долготного канала и в плоскости широтного канала соответственно; на фиг.19 - схемы, иллюстрирующие реальную и мнимую орбиты в моменты измерения широтного угла; на фиг.20 - схема, иллюстрирующая реальное и мнимое положение КА в моменты измерения широтного угла; на фиг.21 - блок-схема статистической обработки измеренных данных; на фиг.22 - зависимость от времени стохастических широтных и долготных данных, предназначенных для обучения нейронной сети - программного модуля обработки; на фиг.23 - таблица результатов обработки измерительной информации на орбитальном участке с 500 по 559 сек; на фиг.24 - графическая зависимость от времени реальной, измеренной и спрогнозированной нейронной сетью инерциальной долготы на орбитальном участке с 500 по 559 сек; на фиг.25 - графическая зависимость от времени реального, измеренного и спрогнозированного нейронной сетью широтного эквивалента на орбитальном участке с 500 по 559 сек; на фиг.26 - таблица результатов обработки измерительной информации на орбитальном участке с 2999 по 3058 сек; на фиг.27 - графическая зависимость от времени реальной, измеренной и спрогнозированной нейронной сетью инерциальной долготы на орбитальном участке с 2999 по 3058 сек; на фиг.28 - графическая зависимость от времени реального, измеренного и спрогнозированного нейронной сетью широтного эквивалента на орбитальном участке с 2999 по 3058 сек; на фиг.29 - графическая зависимость от времени реальной и спрогнозированной нейронной сетью инерциальной долготы на интервале полного витка с 0 по 5402 сек; на фиг.30 - графическая зависимость от времени реального и спрогнозированного нейронной сетью широтного эквивалента на интервале полного витка с 0 по 5402 сек; на фиг.31 - сравнительная таблица параметров, обработанных различными методами - линейным трендом и нейронной сетью на орбитальном участке с 3049 по 3058 сек; на фиг.32 - график сравнений долготных параметров, спрогнозированных линейным трендом и нейронной сетью на орбитальном участке с 3049 по 3058 сек; на фиг.33 - график сравнений широтных параметров, спрогнозированных линейным трендом и нейронной сетью на орбитальном участке с 3049 по 3058 сек; на фиг.34 - заданная орбита и реальная орбита и элементы, характеризующие каждую из орбит; не фиг.35 - таблица параметров трех орбит, поясняющая определение апогея и перигея; на фиг.36 - годографы скоростей двух орбит с зонами и точками апогея и перигея; на фиг.37 - орбита и соответствующие оси изменения наклонения, аргумента перигея и прямого восхождения восходящего узла под действием боковой корректирующей силы; на фиг.38 - орбита и боковой импульс, который в общем случае изменяет все три элемента, определяющие ориентацию орбиты; на фиг.39 - схема, поясняющая зависимости от угла разворота плоскости орбиты величины бокового импульса и величины угла, характеризующего направление импульса; на фиг.40 - схема непосредственного разворота плоскости орбиты для изменения ее наклонения; на фиг.41 - схема, поясняющая изменение внутриплоскостных элементов орбиты под действием тангенциальной силы; на фиг.42 - схема, иллюстрирующая коррекцию положения перигея (аргумента перигея) под действием тангенциального импульса; на фиг.43 - орбита и ее точки, в которых изменения большой полуоси, эксцентриситета и аргумента перигея под действием тангенциальной силы имеют экстремальные значения; на фиг.44 - таблица, в которой приведены уравнения приращений орбитальных элементов при действии тангенциальной или боковой силы.
На представленных фигурах обозначены: 1 - Земля, 2 - небесная сфера, 3 - направление на полюс мира, 4 - направление на опорную звезду, 5 - направление на навигационную звезду, 6 - экватор, 7 - небесный экватор, 8 - меридиан Гринвича, 9 - небесный меридиан абсолютной точки отсчета 0,γ, 10 - плоскость Гринвичского меридиана, 11 - меридиан опорной звезды, 12 - первая плоскость, 13 - вторая плоскость, 14 - космический аппарат, 15 - звездный датчик, 16 - датчик Земли, 17 - плоскость чувствительности, 18 - геоцентрическая вертикаль, 19 - орбита, 20 - раствор поля зрения звездных датчиков, 21 - моноблок астроприборов, 22 - двухстепенной привод моноблока астроприборов, 23 - продольная ось КА, 24 - двигательная установка, 25 - центр Земли, 26 - точка касания горизонта линией визирования датчика Земли, 27 - горизонт, 28 - мгновенное поле зрения, 29 - область сканирования мгновенным полем зрения, 30 - бортовая система отсчета измерений датчика Земли, 31 - слой СО2, 32 - теневой участок орбиты, 33 - первая касательная в вершине угла λ, 34 - вторая касательная в вершине угла λ, 35 - шкала инерциальной долготы.
На представленных фигурах также обозначены: γ - точка весеннего равноденствия, «0» - приборная база отсчета, 0 - абсолютное направление на внешнюю точку отсчета при t=0, образованное пересечением плоскости небесного экватора плоскостью Гринвичского меридиана, α - прямое восхождение опорной звезды, μ - полярное расстояние опорной звезды, t - часовой угол точки весеннего равноденствия относительно Гринвичского меридиана, tм - шкала времени полного поворота Земли, шкала бортового времени, σ - угол треугольника, вершиной которого является полюс мира, ρ - угол треугольника, вершиной которого является навигационная звезда, β - полярное расстояние навигационной звезды, ε - угловое расстояние между звездами, x, у, z - координатные оси датчика Земли, x0, y0, z0 - координатные оси звездного датчика, ω - угол между центральной осью датчика Земли и направлением «КА - опорная звезда», ω0 - угловая связь между системами координат звездного датчика и датчика Земли, λ - угол между первой и второй плоскостями, ψ - угол, фиксирующий приборную базу отсчета относительно жесткой плоскости датчиков, ϕ - угол между первой плоскостью и абсолютным опорным направлением, угол между жесткой плоскостью датчиков и абсолютным опорным направлением, угол между жесткой плоскостью датчиков и плоскостью Гринвичского меридиана, который при t=0 совпадает с прямым восхождением опорной звезды, А - апогей орбиты, П - перигей, В - восходящий узел, Н - нисходящий узел, Ω - прямое восхождение восходящего узла, i - наклонение орбиты, ∈ совпадает с прямым восхождением опорной звезды, А - апогей орбиты, П - перигей, В - восходящий узел, Н - нисходящий узел, Ω - прямое восхождение восходящего узла, i - наклонение орбиты, ∈ - аргумент перигея, u - аргумент КА, ϑ - истинная аномалия КА, 2α - расстояние между перигеем и апогеем орбиты, е - эксцентриситет, F - фокус орбиты, Д и Д1 - точки пересечения орбиты с малой полуосью, ι - инерциальная долгота, ∂ - географическая долгота, η - широта, ζ - долготная ошибка, ξ - широтная ошибка, Z - измеряемый датчиком угол между бортовой системой отсчета и направлением на видимый горизонт Земли, ∑ - измеряемый датчиком угол до направления на горизонт в противоположную сторону, ΔV - импульс скорости, Vη - трансверсальная скорость, Δχ - угол разворота плоскости орбиты, j - угол, характеризующий направление импульса ΔV.
Внутренние бортовые средства КА, которые схематично изображены на фиг.1, структурно и функционально подразделяются на три уровня:
- на уровне локального управления посредством звездного датчика и датчика Земли измеряются параметры внешнего процесса орбитального движения, который протекает в форме угловых изменений, а посредством инерционных маховиков и двигателей коррекции осуществляются воздействия на данный процесс с целью изменения его параметров;
- на уровне управления угловым и местоположением КА посредством процессора управления положением вырабатываются законы управления угловым положением КА, его орбитальным местоположением по результатам сопоставления (в процессоре обработки орбитальных данных) параметров реальной орбиты с параметрами заданной (представленной в запоминающем устройстве) и по результатам статистической обработки измеренных данных (в процессоре обработки угловых данных, в котором производится также преобразование инерциальных параметров в географические);
- на уровне стратегического управления в условиях реального времени и многозадачного последовательно-параллельного режима работы управляющий компьютер циклически (используя сетку частот временного устройства) опрашивает и оценивает текущее состояние периферийных устройств, обновляет данные внутренней базы данных и принимает необходимые команды воздействия с целью должного протекания общего процесса.
Рассмотрим астрономическую основу процесса навигации и управления и для этого обратимся к фиг.2, на которой представлено схематическое изображение астрономических пространственных и временных соотношений.
Обратим внимание на следующие обстоятельства:
1) точка весеннего равноденствия и полюсы мира на небе ничем не отмечены, это абстрактные точки;
2) углы α, μ, t подвержены в той или иной мере изменению.
Причина изменения α состоит в том, что точка весеннего равноденствия (точка пересечения небесного экватора с эклиптикой) смещается относительно неподвижных звезд вследствие прецессии.
Причина изменения μ состоит в том, что полюс мира (ось вращения Земли) движется вследствие прецессий вокруг полюса эклиптики, непрерывно изменяя экваториальные координаты звезд.
Отметим, что влияние прецессии сказывается гораздо сильнее для звезд, близких к полюсу мира.
Причина изменения t состоит в том, что за начало отсчета часовых углов принята точка (точка пересечения небесного экватора с небесным меридианом), не принимающая участия в суточном вращении небесной сферы.
Ситуация, схваченная определенными угловыми соотношениями в момент весеннего равноденствия, в следующий момент "разморозится".
Зададимся, тем не менее, целью связать ситуацию (систему ориентиров) новыми угловыми отношениями таким образом, чтобы указанные абстрактные точки (точка γ и полюс мира) содержались бы уже в плоскостях, то есть конкретизируем ситуацию.
Вообще-то, если мы на какую-либо систему смотрим изолированно, то это еще не значит, что она существует изолированно и дело здесь сводится к тому, чтобы определить связи системы. Обратим внимание на то, что направление 3 и направление 4 содержатся в плоскости 12, в которой опорная звезда находится на момент 0h гринвичского Всемирного времени в своей верхней кульминации, а направления 4 и 5 содержатся во второй плоскости 13, которая неизменна в инерциальном пространстве. Эти плоскости пересекаются под углом λ.
Подчеркнем следующее обстоятельство - вторая плоскость 13 посредством угла λ фиксирует в пространстве первую плоскость 12, которая содержит направление «центр Земли - северный полюс мира». При этом полюс мира фиксируется в пространстве не только этой плоскостью, но и полярным расстоянием μ.
В свою очередь, зафиксированная таким образом в инерциальном пространстве первая плоскость 12 посредством угла, отсчитываемого от нее и равного в градусном исчислении прямому восхождению опорной звезды 4, фиксирует в пространстве положение меридиана точки весеннего равноденствия γ, которая тоже ничем не отмечена на небе.
Дальнейшее определение внешних связей системы ориентиров связано с проявлением угловых отношений первой плоскости 12 к плоскости Гринвичского меридиана.
Гринвичское звездное время есть часовой угол точки весеннего равноденствия относительно Гринвичского меридиана, то есть t в градусном измерении. Положение точки весеннего равноденствия γ относительно первой плоскости 12 определено выше прямым восхождением опорной звезды, то есть углом α. Очевидно, что первая плоскость 12 и плоскость Гринвичского меридиана 10 пересекаются под углом, равным α-t. При t=0 плоскость Гринвичского меридиана совпадает с направлением на точку весеннего равноденствия γ, т.е. в этот момент плоскость 12 и плоскость Гринвичского меридиана 10 пересекаются под углом, равным прямому восхождению α опорной звезды.
Напомним, что в астрономических ежегодниках определены Гринвичские часовые углы точки весеннего равноденствия γ, а соответственно, и промежутки времени.
Данная пространственная ситуация, включающая в себя такие геометрические элементы, как направления 0, 3, 4, 5 и плоскости 12, 13 и 10, характеризуется снижением уровня абстрагирования и определенными угловыми соотношениями.
Особое значение здесь приобретает точка 0, совпадающая в представленный момент с точкой γ. Особое значение данной точки обусловлено тем, что ей предназначено быть нулевой базой отсчета времени и долготы.
При t=0 точка 0 становится нулевой базой отсчета временной меры часового угла.
Что же касается нулевой базы отсчета значений долготы, то дело здесь несколько сложнее.
Вопрос в следующем. Точка γ смещается вдоль эклиптики к западу со скоростью 50,3'' в год, поэтому ее необходимо соотносить к тому моменту, к равноденствию которого относятся координаты звезд.
Разумеется, координаты звезд в нашем случае должны быть отнесены к определенной эпохе.
Здесь следует отметить, что только у экваториальных звезд годовое приращение их прямых восхождений равно годовому смещению точки весеннего равноденствия γ. Годовые же приращения прямых восхождений приполюсных звезд не подчиняются такому соответствию.
Приполюсная зона звезд является зоной особых прямых восхождений, где годовые приращения прямых восхождений могут быть положительными, отрицательными и даже очень близкими к нулевым значениям.
Так как звездные сутки - это промежуток времени между двумя последовательными одноименными кульминациями точки γ, то очевидно, что смещение точки γ на 0'',133=0s,0084 в сутки приводит к рассогласованию между продолжительностью звездных суток и периодом полного поворота Земли и, таким образом, звездные сутки становятся короче.
Если же координаты звезд отнесены к определенной эпохе (заморожены) и при этом их годовые (суточные) приращения прямых восхождений соответствуют годовому (суточному) смещению точки γ, то проблемы здесь нет и звездные сутки окажутся равными периоду полного поворота Земли.
В связи с этим предпочтительными для использования в качестве ориентиров являются те приполюсные звезды, годовые приращения прямых восхождений которых равны (или близки) годовому смещению точки γ.
При t=0 точка 0 через каждый полный поворот Земли будет фиксироваться в пространстве плоскостью Гринвичского меридиана и, таким образом, последующая ситуация повторит предшествующую.
В этом случае значения географических долгот будут совпадать со значениями прямых восхождений звезд (например, экваториальных).
Таким образом, точка 0, направление на которую образовано пересечением плоскости небесного экватора плоскостью Гринвичского меридиана, становится абсолютной нулевой точкой отсчета не только времени, но и долготы.
В общем-то прецессия изменяет не только значения прямых восхождений звезд, но и их полярные расстояния.
Для инженерных приложений предпочтительной является такая пространственная система ориентиров, в которой координатные изменения незначительны.
На фиг.3 схематически представлен космический аппарат на околоземной орбите со схемой измеряемых углов, стабилизированный относительно направления на центр Земли и направления на опорную звезду.
Возникает вопрос: каким образом выявленные астрометрические основы могут стать полезными для нашей цели?
Известно, что полезность означает отношение предмета, рассматриваемого как часть, к некоей взаимосвязи предметов, рассматриваемой как целое.
Целое, в нашем случае, это взаимосвязь бортовых устройств КА с пространственной структурой внешней среды.
Общей характерной особенностью каждой астрометрической основы, то есть каждого частного предмета, будь-то система ориентиров, абсолютная точка отсчета, инерциальная долгота или взаимосвязь долгот, является угловая мера, исчисляемая в зависимости от необходимости и во временной мере.
Следовательно, польза может заключаться в выявленных угловых отношениях.
В качестве материальных точек-ориентиров используем опорную звезду 4, навигационную звезду 5 и центр Земли.
Отметим, что опорная и навигационная звезды отображаются в звездном датчике с соответствующей координацией их относительно приборных осей.
Центр Земли реализуется датчиком Земли как расчетное местоположение некоторой точки относительно бортовой базы отсчета. Направление на эту точку трактуется как геоцентрическая вертикаль.
Плоскость, которая содержит центральные оси звездного датчика и датчика Земли, а также отображения опорной звезды и центра Земли, назовем плоскостью чувствительности 17.
Чтобы воспользоваться координатными соотношениями астрономической основы, «заморозим» местоположение КА в орбитальной точке, принадлежащей первой плоскости 12, таким образом, чтобы плоскость чувствительности 17 совместилась с первой плоскостью 12, в которой опорная звезда находится в своей верхней кульминации, а геоцентрическая вертикаль совпала с направлением «КА - центр Земли».
Очевидно, что в этом случае плоскость чувствительности 17 станет первой плоскостью 12, а плоскость, образованная направлениями «КА - опорная звезда» и «КА - навигационная звезда» - второй плоскостью 13 и эти плоскости пересекутся под углом λ.
В этот момент КА аналогично опорной звезде 4 кульминирует в первой плоскости 12 и его прямое восхождение равно прямому восхождению опорной звезды или, в градусном исчислении, равно углу ϕ, то есть равно инерциальной долготе, которая при нулевом часовом угле точки γ относительно гринвичского меридиана соответствует географической долготе.
Зная координацию плоскости чувствительности 17 в осях звездного прибора и значение угла ϕ, не составляет труда рассчитать в осях звездного датчика положение нулевой приборной базы отсчета инерциальной долготы, соответствующей абсолютной точке отсчета 0.
По значению же часового угла точки γ относительно гринвичского меридиана шкалируется бортовое звездное время, обнуляемое через каждые 24 часа.
Помимо углов ϕ и λ, для координации Земли в пространстве используется также полярное расстояние опорной звезды μ. Этот угол служит для координирования Земли в первой плоскости. Очевидно, что угол «центр Земли - КА - опорная звезда», обозначенный ω, служит аналогичной цели - он координирует положение КА в плоскости чувствительности 17.
Обратим внимание, что первая плоскость 12, которая содержит центр Земли, полюс мира и опорную звезду, в рассмотренном зафиксированном моменте совмещена с плоскостью чувствительности 17, образованной центральной осью земного датчика и центральной осью звездного датчика и в которой координируются направления на центр Земли и опорную звезду.
Если «разморозить» ситуацию и удерживать при орбитальном движении положение плоскости чувствительности совмещенным с плоскостью, содержащей направления «КА - опорная звезда» и «КА - центр Земли», то возникнет эффект вращения плоскости чувствительности КА вокруг направления на опорную звезду 4.
Данный эффект обусловлен орбитальным движением КА и поддерживается соответствующим угловым управлением КА в пространстве.
Как приведение КА к указанному угловому положению, так и поддержание этого положения во времени невозможно без осуществления управляемого движения КА.
Рассмотрим данный вопрос детальнее.
Управляемым называется такое движение, в процессе которого под действием управляющей силы КА переходит из некоторого начального состояния в заданное конечное состояние.
Характер управляемого движения обуславливается таким образом особенностями начального и конечного состояний.
В общем случае угловое положение КА может быть задано взаимным расположением двух систем координат, направление осей одной из которых устанавливает требуемую, а другой - жестко связанную с аппаратом действительную ориентацию аппарата.
Первую из этих систем координат принято называть базовой системой отсчета, вторую - связанной системой координат.
Поскольку в общем случае оси связанной и базовой систем не совпадают, задачу ориентации КА можно определить как задачу совмещения осей связанной системы координат с осями базовой.
Понятно, что для решения данной задачи движение аппарата вокруг собственного центра масс должно быть управляемым. Такое управление позволяет придать КА любое требуемое положение в пространстве и поддерживать это положение при действии на аппарат различных возмущающих моментов. При этом можно выделить два характерных режима управления. Первый соответствует процессу приведения осей связанной системы координат к осям базовой системы отсчета. Если рассматривать этот режим с момента отделения КА от ракеты-носителя, то он включает в себя:
- торможение (гашение) начальной угловой скорости;
- поиск физических ориентиров, используемых для технического воспроизведения базовой системы отсчета;
- поворотный маневр с целью совмещения осей базовой и связанной систем координат.
Второй режим, называемый обычно режимом стабилизации, предназначен для поддержания требуемой ориентации КА с заданной точностью.
Положение координатных осей связанной системы в базисной системе координат определяется углами крена, рыскания и тангажа.
В нашем случае за базовую систему координат принята система двух направлений «КА - центр Земли» 28 и «КА - опорная звезда» 4, взаимное угловое положение которых изменяется в зависимости от местоположения КА в пространстве. В качестве третьего используется направление, соединяющее изображения в звездном датчике опорной и навигационной звезд, то есть используется проекция плоскости 13, которая образована направлениями «КА - опорная звезда» 4 и «КА - навигационная звезда» 5. Угловое положение данного направления относительно базовой плоскости, образованной первыми двумя направлениями, тоже изменяется в зависимости от местоположения КА в пространстве.
Для проведения операций ориентации с целью обеспечения рассмотренного совмещения вначале необходимо погасить угловые скорости вращения КА.
При отделении от ракеты-носителя КА приобретает значительный кинетический момент, произвольно расположенный в пространстве.
Режим гашения начальных угловых скоростей реализуется известным алгоритмом управления по сигналам измерителя угловой скорости КА и с помощью соответствующего управляющего момента исполнительных органов.
Затем производится ориентация КА на Солнце. Этот режим необходим для обеспечения служебных систем КА энергией и получения определенной пространственной ориентации связанных осей КА. Захват Солнца, приведение и удержание его в поле зрения солнечного датчика осуществляется традиционным методом с помощью сигналов солнечного датчика, измерителя угловых скоростей и управляющих моментов исполнительных органов по каналам крена, рыскания и тангажа.
По известным алгоритмам реализуются также поиск Земли 1 с использованием направления «КА - Солнце», последующий захват ориентира земным датчиком 16 и построение геоцентрической вертикали.
Соответствующими поворотными маневрами КА с изменением координации Солнца в солнечном датчике осуществляется ориентация поля зрения звездного датчика 15 на ту область небесной сферы, в которой находится опорная звезда 4.
Следует заметить, что ориентация поля зрения звездного датчика на окрестность опорной звезды может быть осуществлена до режима поиска и захвата Земли поворотом КА вокруг направления «КА - Солнце».
По завершении этого режима телевизионная камера звездного датчика регистрирует на ПЗС-матрице изображения звезд, попадающих в ее поле зрения. В результате обработки полученных видеоданных определяется положение звезд в приборной системе координат. В памяти звездного датчика (в бортовом звездном каталоге) хранятся данные о положении звезд в звездной системе координат.
Сопоставление приборных и каталожных координат одних и тех же звезд позволяет определить взаимную ориентацию приборной и звездной систем координат. Опознавание зарегистрированных на ПЗС-матрице звезд осуществляется по критерию одинаковости угловых расстояний между ними в обеих упомянутых системах координат.
Таким образом опознается опорная звезда 4, направление на которую затем совмещается с плоскостью, образованной центральными осями звездного датчика и датчика Земли.
При движении КА по орбите 19 процессор управления положением по непрерывным показаниям звездного датчика 15 вырабатывает уставки, предназначенные устранить возникшее угловое рассогласование между указанной плоскостью и направлением на опорную звезду. Для устранения рассогласования задействованы исполнительные органы и канал управления по крену.
Управление по каналам тангажа и рыскания осуществляется с помощью датчика Земли, предназначенного реализовать геоцентрическую вертикаль.
Динамические процессы при осуществлении указанных режимов теоретически хорошо проработаны и на практике не вызывают непреодолимых проблем.
Напомним, что состояние КА как динамической системы в общем определяется как набор переменных состояний в момент времени t0, по которым можно предсказать поведение динамической системы в любой другой момент времени t>t0.
Совокупность таких переменных представляется в виде вектора состояния.
Известно, что не только традиционные наклонная дальность, азимут, угол места и их производные, но и эквивалентные им параметры могут формировать вектор состояния, более того, недостающие параметры можно восполнить математическими зависимостями, позволяющими получить значения неизмеряемых параметров.
Рассмотрим вектор состояния КА, формируемый эквивалентными параметрами.
Как уже было сказано, в процессе функционирования космический аппарат непрерывно ориентируется таким образом, чтобы в плоскости чувствительности, материализованной чувствительными элементами звездного датчика, всегда оказывались бы два направления: направление на центр Земли центральной оси датчика Земли и направление «КА - опорная звезда».
Заметим, что координатная фиксация на каждый временной такт положения в звездном датчике плоскости, содержащей направления на звезды, производится относительно приборной базы отсчета «0», которая рассматривается в последующем материале. Здесь же скажем лишь о том, что относительно приборной базы отсчета «0» бортовым процессором рассчитывается инерциальная долгота КА.
Положение же направления «КА - опорная звезда» относительно центральной оси датчика Земли также рассчитывается бортовым процессором, а при учете поправки, зависимой от значений инерциальной долготы, определяется инерциальная широта КА.
По результатам этих измерений определяются не только пройденные по широте и долготе угловые расстояния, но и соответствующие скорости, которые могут быть разложены по осям управления КА, а также при векторном сложении - орбитальная скорость.
Таким образом становятся известными угловое и местоположение КА в инерциальном пространстве, а при преобразовании, учитывающем скорость вращения Земли и текущее бортовое время, - проекция местоположение КА относительно широтно-долготной сетки Земли, то есть трасса КА.
Вообще для реализации пространственного и углового движения КА из состояния в момент t0 в состояние на момент времени t>t0 необходим такой набор переменных состояния, который характеризовал бы не только начальное угловое и местоположение КА относительно широтно-долготной сетки Земли, но также и последующее угловое и местоположение КА.
При этом состояние в момент времени t>t0 должно соответствовать требуемому состоянию с достоверной точностью.
В связи с этим следует отметить следующее обстоятельство: измерения инерциально-широтных и инерциально-долготных углов обрабатываются на борту КА специальным программным модулем статистической обработки.
Цель статистической обработки данных - выявить трендовую компоненту в стохастическом массиве входных данных и получить прогнозируемые значения инерциально-широтных и инерциально-долготных углов на некоторое число тактовых шагов после входных значений.
В результате осуществления указанной процедуры углы, определяющие положение осей КА относительно направления на центр Земли, а также относительно широтно-долготной сетки Земли, приобретают значения повышенной точности.
Более того, высокоточные значения указанных углов прогнозируются от последних измерений на несколько шагов вперед, что позволяет осуществить управление угловым и местоположением КА в пространстве с повышенной точностью.
Здесь следует заметить, что определение углового положения КА и определение местоположения КА в пространстве не являются двумя раздельными режимами.
Высокоточный режим определения углового положения осей КА относительно направления на центр Земли и относительно широтной плоскости Земли, содержащей подспутниковую точку, одновременно является высокоточным режимом местоопределения КА в пространстве.
Из вышеизложенного следует, что набор переменных состояния КА в момент времени t0 достаточен, чтобы предсказать поведение динамической системы на момент времени t>t0.
Следует также заметить, что параметры, потребные для формирования вектора состояния КА, определяются на борту КА автономно. При необходимости традиционно используемые параметры могут быть рассчитаны на борту КА по соответствующим математическим соотношениям, о чем пойдет речь в последующих материалах.
В вышеприведенных материалах отмечено, что особо важное значение имеет правильный выбор опорных звезд.
На фиг.4 и 5 представлены таблицы звезд из окрестностей северного и южного полюсов мира соответственно. Ранее уже отмечалось, что приполюсная зона звезд является зоной особых прямых восхождений, где годовые приращения прямых восхождений могут быть положительными, отрицательными и даже очень близкими к нулевым значениям.
Отнесем координаты звезд в нашем случае к эпохе 2000, а для сравнения координатных приращений представим данные эпохи 1950.
Для указанных эпох данные, включающие, помимо координат, также обозначения звезд и звездные величины, сведем в две таблицы: в таблице 4 представим координаты звезд из окрестности северного полюса, в таблице 5 - координаты звезд из окрестности южного полюса.
Выбор звезды в качестве опорной или навигационной обусловлен допустимым значением ее координатного изменения, а также возможностями обнаружительной способности звездного датчика и размерами его поля зрения.
Звездные величины должны соответствовать обнаружительной способности датчика. Освоенные промышленностью датчики способны обнаруживать звезды до 7-8 звездной величины. Представленные в таблицах звезды удовлетворяют этому условию.
Что же касается вопроса координатных изменений звезд, то этот вопрос необходимо рассмотреть детальнее.
Если исходить из того, что точка γ смещается со скоростью 50'',24 в год и за 50 лет ее смещение составит 2512'' или 168s (2m48s), то за те же 50 лет прямое восхождение неподвижной звезды должно увеличиться на те же 2m48s. Однако, как уже говорилось, приполюсная зона является зоной особых прямых восхождений звезд и их приращения за 50 лет, как об этом свидетельствуют представленные в таблицах координаты, изменяются в довольно широком диапазоне.
При приращении прямого восхождения звезды в 2m48s, равного смещению точки γ, справедливо считать, что звезда неподвижна, а при приращении в 00m00s звезда за 50 лет условно смещается на 2m48s.
Для нашего случая из северной приполюсной зоны мы выбираем в качестве опорной звезду 1642, а в качестве навигационной - 454, из южной приполюсной зоны в качестве опорной - звезду 3983, а в качестве навигационной - 459. Приращения прямых восхождений этих звезд близки к указанному значению в 2m48s.
Такой выбор обусловлен следующим соображением.
Звездными сутками принято считать промежуток времени между первой кульминацией точки γ и последующей одноименной кульминацией этой же точки, которая смещается в течение этого промежутка. Поэтому звездные сутки короче (на величину смещения) периода вращения Земли. Чтобы промежуток времени между первой кульминацией звезды и последующей одноименной кульминацией той же звезды стал равным полному периоду вращения Земли, выбранная звезда в отличие от точки γ должна быть неподвижна, то есть приращение ее прямого восхождения должно быть, по меньшей мере, близким к значению в 2m48s.
Здесь уместно отметить, что и приращения склонений звезд из северной зоны (-16 37.56 и -16 40.01) должны быть близки друг другу, как и приращения звезд из южной зоны (+16 42.22 и +16 38.67).
Целесообразно также, чтобы полярные расстояния опорных звезд (1642 и 3983) были, по возможности, минимальными, а угловое расстояние между опорной и навигационной звездами вписывалось в половину наименьшего размера поля зрения звездного датчика (поля зрения современных датчиков лежат в диапазоне от 8°×8° до 13°×13°, а астросистема распознавания созвездия разработки МББ и СИРА имеет поле зрения трех оптических головок - 30°×40°).
В некоторых конкретных случаях выбор звезд может быть произведен и по более мягкому критерию относительно координатных приращений.
Также в некоторых конкретных случаях могут быть разные требования к размеру поля зрения звездного датчика.
Очевидно, что (кроме стационарной орбиты) потребный диапазон широтного углового раствора поля зрения звездного датчика необходимо увеличивать в зависимости от значений широтных местоположений КА на орбите.
Освоенные промышленностью звездные датчики не обладают достаточным для наших целей полем зрения в широтной плоскости.
Необходимый угловой широтный раствор поля зрения звездного датчика может быть обеспечен соответствующим набором нескольких оптических головок и/или использованием привода, реализующего два фиксированных позиционных положения.
При использовании двухпозиционного привода для его управления потребуется определенная логика переключения фиксированных положений оптической головки. Например, команда на переключение из первого положения во второе может быть сформирована по факту попадания изображения опорной звезды в некоторую предельную координатную зону поля зрения датчика.
Вариант наращивания поля зрения посредством набора оптических головок может быть реализован в единый моноблок совместно с датчиком Земли.
По сравнению с двухпозиционным вариантом вариант моноблока является более предпочтительным ввиду отсутствия логики позиционирования и исключения возможных люфтовых погрешностей фиксации позиции оптической головки.
Тот или иной вариант расширения поля зрения звездного датчика, тот или иной размер его широтного раствора зависит от наклонения используемой орбиты (на которой планируется обеспечить широтные измерения в полном объеме) и определяется требованиями каждого конкретного проекта.
Правда, возможен и общий вариант, обеспечивающий максимальный размер широтного поля зрения путем набора оптических головок датчика, как и общий вариант одной оптической головки датчика, который «удерживает» опорную звезду в центре своего поля зрения, отслеживая посредством внешнего привода изменяемые угловые положения КА относительно направления на опорную звезду. Эти варианты удовлетворяют любому наклонению используемой орбиты конкретного случая, правда, с неравными точностными характеристиками.
Заметим, что на выбор значения угла широтного раствора может повлиять и реализация целевой функции КА, которая в некоторых случаях может потребовать угловой переориентации целевой аппаратуры.
При активном функционировании КА часто для выполнения целевой функции существует необходимость увода центральной оси целевой аппаратуры с направления на центр Земли и переориентации ее на тот или иной район земной поверхности.
При отсутствии у целевой аппаратуры соответствующего привода реализация указанной ориентации ведет к рассогласованию материализованной плоскости чувствительности астродатчиков с направлением «КА - центр Земли» и к передислокации в бортовых алгоритмах баз отсчета инерциальных долгот и широт местоположения КА.
Использование для этой цели специального мат. обеспечения представляется нецелесообразным.
Потребную угловую ориентацию КА с жестко установленной на нем целевой аппаратурой можно обеспечить, если использовать двухстепенной привод моноблока астроприборов.
На фиг.6 представлен космический аппарат с расширенным полем зрения звездного датчика и возможностью ориентировать продольную ось в любую точку Земли посредством двухстепенного привода 22.
Моноблок 21 с расширенным полем зрения 20 в этом случае состоит из двух звездных датчиков 15 и датчика Земли 16.
При продолжительном по времени отслеживании одного и того же района земной поверхности - это оптимальный вариант.
Правда, на прогнозируемых участках полета при относительно минимальных по времени перенацеливаниях можно обойтись и без специального привода.
Если же целевая аппаратура обладает возможностью различно ориентировать относительно продольной оси КА свою центральную ось, то в приводе тоже нет необходимости.
Очевидно, что в некоторых ситуациях выбранные звезды могут быть затенены Землей и потому могут быть недоступны астродатчикам КА на некоторых участках орбитального движения.
На фиг.7 представлены: слева - вариант, при котором задействованы звезды из окрестности северного полюса мира, справа - звезды южного полюса.
Слева представлены низкая приэкваториальная круговая орбита 19, средняя круговая орбита с некоторым «оптимальным» наклонением и орбита с «неоптимальным» наклонением.
Ясно, что, если наклонение круговой низкой или круговой средней орбиты не превышает некоторого порогового значения, то все точки орбиты обладают видимостью задействованных звезд 4 и 5 северной приполюсной зоны. Точки орбиты не видимы задействованными звездами тогда, когда они затенены Землей 1, как на теневом участке 32 орбиты с «неоптимальным» наклонением.
В общем следует отметить, что продолжительность теневого участка (как и его наличие) обусловлены диаметром Земли, значением наклонения орбиты и высотой орбиты.
У геостационарной орбиты в этом случае особое положение - ее точки наблюдаются задействованными как северными, так и южными звездами.
На изображении справа задействованы звезды из окрестности южного полюса мира и представлены: низкая круговая орбита, средняя круговая орбита и орбита типа «Молния», наклонение которой около 65°.
То, что было сказано для варианта с задействованными северными звездами, справедливо и для варианта с задействованными южными звездами.
Особо следует подчеркнуть следующее: у высокоэллиптической орбиты типа «Молния» перигейный участок ненаблюдаем северными звездами, апогейный же участок, который является обычно участком целевого функционирования КА, расположен в северном полушарии на значительной высоте и потому наблюдаем и северными, и южными звездами.
Круговые полярные орбиты в отличие от рассмотренных имеют следующие особенности: из-за недопустимости так называемого «складывания» осей управления они обладают в приполюсных зонах участками, на которых реализуется пассивный режим КА - режим постоянной солнечной ориентации (ПСО).
Как уже было отмечено, первая плоскость 12 и вторая плоскость 13 астрономической основы совмещаются соответственно в некоторый момент орбитального движения КА с его плоскостью чувствительности 17 и его плоскостью, образованной направлениями «КА - опорная звезда» и «КА - навигационная звезда».
Угол λ между указанными плоскостями определяется заранее при проектировании из треугольника, вершинами которого на небесной сфере являются: полюс мира, опорная звезда и навигационная звезда.
На фиг.8 данный треугольник с искомым углом изображен на сфере. В связи с этим показаны касательные 22 и 23 к его сторонам в вершине искомого угла. Но так как радиус небесной сферы бесконечного размера, для расчета искомого угла используются следующие формулы плоской тригонометрии, которые связывают между собой стороны и углы треугольника:
1) cos ε=cos β cos μ+sin β sin μ cos σ;
2) cos β=cos μ cos ε+sin μ sin ε cos λ.
Определенный таким образом угол λ соответствует моменту, когда КА находится в плоскости кульминации опорной звезды. В другие моменты времени плоскость чувствительности, содержащая центральные оси датчиков, благодаря эффекту вращения ометает за орбитальный виток небесную сферу, а навигационная звезда 5 (ее отображение) двигается в звездном датчике 15 по «замкнутой» кривой.
Обратимся к фиг.9, на которой изображены два характерных положения КА на орбите: правое, совпадающее с плоскостью, в которой кульминирует опорная звезда, и левое, совпадающее с абсолютным опорным направлением 0.
Положение на орбите 19 космического аппарата 14, изображенного на фигуре справа, характеризуется углом λ, при котором инерциальная долгота КА равна прямому восхождению опорной звезды.
Очевидно, что в некоторый момент орбитального движения инерциальная долгота КА станет равной 0°. Так как плоскость 13, содержащая направления на звезды, неизменна в пространстве, то любой угловой поворот КА вследствие орбитального движения повлечет за собой изменение угла между этой плоскостью и плоскостью чувствительности 12. Это происходит непрерывно при движении КА по орбите, когда центр Земли 25 и опорная звезда 4 (их отображения) удерживаются в плоскости чувствительности.
При переходе КА из правого орбитального положения в левое плоскость чувствительности совмещается с абсолютным опорным направлением. Угол между плоскостью чувствительности и отображением в звездном датчике плоскости 13 (второй плоскости астрономической основы) принимает при этом значение, которое фиксирует приборную базу отсчета инерциальной долготы и которое соответствует нулевому значению инерциальной долготы.
Подчеркнем, что угол ψ, фиксирующий в звездном датчике приборную базу отсчета «0» относительно плоскости чувствительности, определяется заранее расчетным путем при обнулении инерциальной долготы КА, равной прямому восхождению опорной звезды. Данный угол при любом местоположении опорной звезды в плоскости чувствительности имеет одно и то же значение, которое учитывается затем в бортовых алгоритмах расчета инерциальной долготы.
Инерциальная широта местоположения КА определяется как разница измеренного угла «центр Земли - КА - опорная звезда» и 90°, однако при этом необходимо учесть и поправку, которая обусловлена полярным расстоянием опорной звезды μ. См. фиг.10.
Учет этой поправки обеспечивает по существу определение угла «центр Земли - КА - полюс мира» в любых орбитальных точках, в которых, разумеется, она имеет то или иное значение.
Обратим внимание, что пространственные положения КА характерны тем, что плоскость чувствительности совпадает с направлением «центр Земли - полюс мира» в моменты совмещения с плоскостью угла μ, то есть в моменты прохождения плоскости, в которой опорная звезда находится в верхней или нижней кульминации.
Очевидно, что в эти моменты измеренный угол «центр Земли - КА - опорная звезда» необходимо при определении широты уменьшить на величину полярного расстояния μ при верхней кульминации звезды и увеличить на ту же величину при нижней кульминации.
В орбитальных позициях, в которых плоскость чувствительности КА перпендикулярна той же плоскости чувствительности КА, размещенного в поз.1, поправка, обусловленная полярным расстоянием опорной звезды, принимает нулевые значения.
В общем, текущее значение поправки зависит от значения текущей инерциальной долготы.
Каждому значению инерциальной долготы строго соответствует определенное значение поправки, которая может быть заранее рассчитана и представлена в бортовом запоминающем устройстве.
Текущая поправка определяется произведением полярного расстояния опорной звезды на косинус угла, значение которого равно разнице значений текущей инерциальной долготы и угла между первой плоскостью и абсолютным опорным направлением.
Для определения широты местоположения КА, таким образом, следует воспользоваться соотношением:
η=(ω-90°)-μ cos(ι-ϕ),
где η - широта, ω - угол «центр Земли - КА - опорная звезда», μ - полярное расстояние опорной звезды, ι - инерциальная долгота, ϕ - угол между первой плоскостью 12 и абсолютным опорным направлением.
Полярное расстояние опорной звезды обуславливает также колебания КА по крену.
Удержание направлений на опорную звезду и на центр Земли в плоскости чувствительности бортовых датчиков приводит при орбитальном движении КА к колебаниям этой плоскости по каналу крена с амплитудой, равной полярному расстоянию опорной звезды.
Угловое положение КА относительно северо-южной оси зависит от инерциальной долготы КА.
Очевидно, что в орбитальных положениях КА, когда ι=ϕ и когда ι=ϕ+180°, плоскость чувствительности КА совмещается с плоскостью угла μ и с северо-южной осью.
В орбитальных положениях КА, когда ι=ϕ+90° и когда ι=ϕ+270°, плоскость чувствительности отклоняется от северо-южной оси на угол, равный полярному расстоянию опорной звезды.
Каждому значению инерциальной долготы строго соответствует определенное угловое положение КА относительно северо-южной оси, которое может быть заранее рассчитано и представлено в бортовом запоминающем устройстве.
Текущее угловое положение КА определяется произведением полярного расстояния опорной звезды на синус угла, значение которого равно разнице значений текущей инерциальной долготы и угла между первой плоскостью 12 и абсолютным опорным направлением.
Схема измерений инерциальной долготы и широты орбитального местоположения КА представлена на фиг.11, где обозначено: 1 - Земля, 14 - КА, 19 - орбита, 25 - центр Земли, ι - инерциальная долгота, η- широта.
Инерциальной долготой является угол абсолютного пространства в диапазоне изменения от 0 до 360°, отсчитываемый в направлении вращения Земли на плоскости небесного экватора от абсолютной точки отсчета 0 и совпадающий с географической долготой через каждый период полного поворота Земли.
Здесь следует пояснить, что прямое восхождение координирует неподвижные звезды относительно точки γ, а инерциальная долгота координирует движущийся на фоне неподвижных звезд космический аппарат относительно абсолютной точки отсчета 0.
Для перевода инерциальной долготы в географическую используется процессор обработки угловых данных.
Перевод осуществляется следующим образом. Взаимные соотношения географической долготы и инерциальной долготы в различные моменты 24-часового цикла (периода полного поворота Земли) представлены в вариантах а) и б) на фиг.12 (вид со стороны Северного полюса мира).
На данном рисунке приняты следующие обозначения: 0 - абсолютное опорное направление, 1 - Земля, 2 - небесная сфера, 8 - меридиан Гринвича, ι - инерциальная долгота, ∂ - географическая долгота, t - время на Гринвиче. В варианте а) проиллюстрировано взаимное положение значений географической долготы и инерциальной долготы на 0h на меридиане Гринвича. На данный момент значения географической долготы совпадают со значениями инерциальной долготы. Так, значению инерциальной долготы в 30° (обозначенному на рисунке стрелкой) соответствует географическая долгота в 30°. В варианте б) проиллюстрировано взаимное положение географической долготы и инерциальной долготы на момент t=10h. На данный момент, как и на другие отличные от нуля моменты времени, значения географической долготы не совпадают со значениями инерциальной долготы.
Рассмотрим два возможных варианта, при которых различно определяются отношения между долготами.
1) Определим на данный момент времени значение географической долготы, которое должно соответствовать, например, 240° инерциальной долготы (обозначено на рисунке стрелкой).
На момент времени t=10h Земля повернется на угол, равный 150°. Этот угол меньше инерциальной долготы в 240°, их разница составит 90°. В данном случае инерциальной долготе в 240° соответствует географическая долгота в 90°.
2) Определим на тот же момент времени t=10h значение географической долготы, которое должно соответствовать, например, инерциальной долготе в 90°.
Угол поворота Земли в 150° при этом не меньше, а больше значения инерциальной долготы и разница между ними составит 60°. В этом случае географическая долгота будет равняться разнице 360° и 60°, то есть 300°.
Таким образом, географическая долгота и инерциальная долгота связаны следующими зависимостями:
1) λг=λи-(ω.t) при ω.t<λи;
2) λг=360°-[(ω.t) -λи] при ω.t>λи,
где скорость поворота Земли ω=15°/час; λг - географическая долгота; λи - инерциальная долгота; t - время.
Что же касается ориентации оси КА относительно центра Земли, то такая ориентация обеспечивается посредством датчика Земли.
Схема построения геоцентрической вертикали с помощью четырех сканирующих датчиков представлена на фиг.13.
Принцип определения геоцентрической вертикали 18 базируется на измерении угла между направлением на горизонт Земли 27, определяемый как граница космос-Земля, и осями КА в различных точках горизонта.
Направление геоцентрической вертикали - это биссектриса угла между двумя диаметрально противоположными точками визируемого горизонта 27.
Принцип основан на использовании температурного контраста, существующего между земной поверхностью и космическим пространством. Используемые для этого датчики должны обладать чувствительностью к излучениям в диапазоне от 11 до 20 мкм.
Поля зрения датчиков располагаются попарно в двух взаимно перпендикулярных плоскостях, при этом угол зрения каждого датчика посредством сканирования мгновенным полем зрения 28 охватывает зону с границей Земля-космос.
Приемник лучистой энергии фиксирует угловое положение горизонта Земли как резкий перепад энергетической яркости (оптического контраста) между краем диска Земли и окружающим ее космическим пространством.
Датчик Земли измеряет положение горизонта в бортовой системе координат КА.
Известны два типа ошибок измерений:
1)инструментальные ошибки;
2)ошибки, вызванные непостоянством явления видимого горизонта (ошибки «феномена).
Инструментальные ошибки самого датчика - это электронный шум, ошибки квантования и другие.
Инструментальные ошибки представляются в виде суммы гауссова случайного процесса и ошибки типа смещения. Случайные ошибки - не коррелированы (белый шум), постоянные ошибки измерений (смещение) допустимо считать ошибками с бесконечным временем корреляции.
Ошибки «феномена» вызываются неопределенностью слоя СО2 в атмосфере Земли. Вследствие временных и пространственных флуктуаций атмосферы определение горизонта по положению слоя СО2 производится с большей ошибкой, чем в случае определения горизонта непосредственно по краю земного диска (земному лимбу).
Ошибки «феномена» наиболее сильно выражены на малых высотах полета КА и быстро уменьшаются с увеличением высоты.
На больших высотах преобладают инструментальные ошибки. В нашем случае используется датчик, состоящий из четырех сканирующих устройств: два из них производят измерение в плоскости чувствительности и два в ортогональной плоскости.
На фиг.14 представлена схема геометрии измерений при определении геоцентрической вертикали, которая «ортогональна» плоскости чувствительности.
После измерения датчиком 16 угла Z между бортовой системой отсчета 30 и направлением на видимый горизонт Земли и угла ∑ до направления на горизонт в противоположную сторону определяется геоцентрическая вертикаль 18, которая должна быть в плоскости чувствительности 17 и строго ориентироваться на центр Земли 25.
Обратим внимание, что ошибка ζ, вызываемая неопределенностью горизонта, электронным шумом и смещением, как и ошибка ξ при измерении в плоскости чувствительности, вообще говоря, затрудняет строгую ориентацию на центр Земли.
Измеряемые углы определяются следующими соотношениями:
Z=Zном-ζ;
∑=∑ном+ζ,
где Zном, ∑ном - номинальные значения углов.
Аналогично определяются углы в плоскости чувствительности. Угол между бортовой системой отсчета 30 и направлением на центр Земли определяется как половина суммы измеренных углов.
Отметим, что точности используемых датчиков несоизмеримы по своим значениям друг с другом. Высокая точность звездного датчика в 2-3 угловые секунды приобретает чрезвычайно важное значение ввиду того обстоятельства, что угол между центральной осью датчика Земли и направлением «КА - опорная звезда» может быть измерен с почти эквивалентной точностью, если изначально на Земле осуществить и паспортизировать связь между системами координат звездного датчика и датчика Земли.
В частности, эту угловую связь между центральной осью х датчика Земли 16 и визирной осью y0 звездного датчика 15 необходимо осуществить и отъюстировать по возможности в одном блоке и таким образом, чтобы плоскость двух осей x0, y0 звездного датчика и плоскость двух осей x, y датчика Земли образовали одну плоскость чувствительности 17. См. фиг.15.
Значение измеренного при этом угла ω0 между центральной осью датчика Земли и визирной осью звездного датчика должно быть представлено в соответствующих бортовых алгоритмах.
Очевидно, что в этом случае угол в поле зрения звездного датчика между визирной осью и направлением «КА - опорная звезда» должен суммироваться с углом ω0, представляющим вышеуказанную связь.
Таким образом становится возможным высокоточное измерение положения в пространстве центральной оси x датчика Земли относительно направления «КА - опорная звезда». Совпадает ли в этом случае центральная ось датчика с направлением на центр Земли, - это другой вопрос. Здесь важно только само высокоточное знание этого положения.
Это высокоточное знание относится к широтной угловой связи в плоскости чувствительности, в которой уровень точности звездного датчика является по существу базовым уровнем.
Долготное же измерение реализуется в плоскости, перпендикулярной плоскости чувствительности. Но так как приборная база отсчета инерциальной долготы фиксируется относительно плоскости чувствительности с высокой расчетной точностью, то очевидно, что реальное измерение долготного угла может также осуществляться с точностью, эквивалентной точности звездного датчика.
Таким образом, при обеспечении высокоточной угловой связи между координатными системами датчиков точностной уровень звездного датчика является базовым уровнем как при широтном измерении, так и при измерении долготного угла.
На фиг.16 представлена схема различий систематических и случайных ошибок датчика Земли.
Центр каждой мишени представляет собой истинное значение измеряемой величины, а каждая точка - это измерение. Сумма измерений характеризуется смещением и разбросом. На рисунке первом и третьем сверху представлены смещенные результаты. Стандартное отклонение или разброс результатов отдельных измерений является мерой погрешности. Датчик с хорошей повторяемостью результата (или малой случайной ошибкой) имеет, очевидно, хорошую случайную погрешность, но не обязательно дает правильную выходную величину, поскольку сдвиг может существенно исказить результат, т.е. точность датчика невелика. Результаты измерений на рисунке втором и четвертом имеют малую погрешность, но только результат, показанный на рисунке четвертом является точным. На диаграммах справа истинная величина представлена прямой линией, на которую наложены результаты измерений.
Точность измерения зависит как от смещения, так и от разброса:
- большое смещение + большой разброс = низкая точность;
- малое смещение + большой разброс = низкая точность;
- большое смещение + малый разброс = низкая точность;
- малое смещение + малый разброс = высокая точность.
В условиях орбитального движения координатная система датчиков преобразовывается в навигационную координатную систему, связанную с долготным и широтным местоположением КА. Существует и ряд других преобразований бортовых систем координат, порождающих ошибки. Таким образом, к инструментальным ошибкам датчика и к ошибкам, вызванным непостоянством явления видимого горизонта Земли, добавляются ошибки преобразований. При построении геоцентрической вертикали измерения производятся по двум каналам: в широтной, т.е. в плоскости чувствительности, и в долготной - ортогональной плоскости.
По результатам произведенных измерений и последующих преобразований координатных систем центральная ось датчика посредством соответствующего вращения КА ориентируется на центр Земли с указанными ошибками.
Все ошибки безотносительно к природе их происхождения условимся рассматривать в долготном канале как одну долготную ошибку, а все ошибки в широтном канале - как одну широтную ошибку.
Угловое пространственное положение КА в плоскости, ортогональной плоскости чувствительности, то есть в плоскости долготного канала, представлено на фиг.17.
Обратим внимание, что в обозначении под цифрой 18 значится геоцентрическая вертикаль, хотя направление от датчика 16 до центра Земли 25 отклонено на значение долготной ошибки ζ. Под цифрой 18 скорее следовало бы представлять центральную ось датчика Земли.
Очевидно, что если бы центральная ось датчика была строго ориентирована на центр Земли 25, то инерциальная долгота ι имела бы другое значение, а именно ее значение для ситуации, изображенной на данной фигуре, было бы меньше на величину долготной ошибки ζ.
Данные рассуждения справедливы и для углового положения КА, изображенного на фиг.18 в плоскости широтного канала.
На данной фигуре под цифрой 18 аналогично обозначению на предшествующей фигуре значится фиктивная геоцентрическая вертикаль, отличие которой от истинной вертикали обусловлено наличием ошибки ξ. Очевидно, что при устранении широтной ошибки ξ угловые положения КА, изображенные на фигуре в пространстве северного и южного полушарий Земли, станут соответствовать истинной широте своего местоположения.
Широтная и долготная ошибки уводят центральную ось датчика в сторону от направления на притягивающий центр Земли. Однако присутствуют ли эти ошибки при очередном измерении, неизвестно. Но вне зависимости от этой неопределенности можно с уверенностью утверждать, что КА в каждый момент измерения широты и долготы находится в действительной точке орбиты.
Допустимо, тем не менее, вообразить, что центральная ось датчика всегда строго ориентирована на центр Земли. Правда, при таком допущении КА в каждый момент измерения должен находиться не в реальной орбитальной точке, а в некоторой мнимой точке.
Обратимся к фиг.19, на которой представлены два вида а) и Б), иллюстрирующие реальное и мнимое положение КА в моменты измерения широтного угла соответственно.
На данном рисунке обозначены: 1 - Земля, 14 - КА, 4 - направление на опорную звезду, 6 - экватор, 18 - геоцентрическая вертикаль, 19 - орбита, 19ф - мнимая орбита, 25 - притягивающий центр Земли, η - широта, ξ - широтная ошибка.
На рисунке слева (вид А) космический аппарат 14 находится в действительной орбитальной точке. Изображены также и другие реальные точки, в которых КА находится в моменты измерений широтного угла.
Широтный угол η измеряется с ошибкой ξ и поэтому центральная ось датчика ориентируется в сторону от центра Земли.
На рисунке справа (вид Б) изображено воображаемое положение, когда центральная ось датчика при тех же ошибках ξ в широтных углах η совпадает с геоцентрической вертикалью 18, но при этом КА находится в мнимых точках, образующих мнимую орбиту 19ф.
Следует отметить, что все относящееся при широтном измерении к мнимым точкам, справедливо и для мнимых точек при долготном измерении.
Таким воображаемым образом можно представить погрешность датчика Земли в форме погрешности характера движения КА.
Очевидно, что широтные и долготные углы, если бы они не содержали ошибок, характеризовали бы движение КА, его орбиту с высокой точностью. Можно сказать и по другому - характер движения КА, то есть его местоположение в пространстве, в разные моменты времени обуславливает те или иные значения широтных и долготных углов в те же моменты времени.
Таким образом, значения широтных и долготных углов зависят, с одной стороны, от местоположения КА в пространстве, с другой, - от измерительных ошибок.
Обратимся к фиг.20, на которой проиллюстрирована эта зависимость.
На данной фигуре обозначены: 14о - КА в реальной точке орбиты на нулевой момент времени, 14о м - КА в мнимой точке на тот же момент времени, 144 - КА в реальной точке на момент в 4 минуты, 144 м - КА в мнимой точке на четвертой минуте, 3 - направление на полюс мира, 18 - геоцентрическая вертикаль, 19 - орбита, 25 - центр Земли, η0 - широтный угол на нулевой момент времени, η4 - широтный угол на момент в четыре минуты, ξ0 - широтная ошибка на нулевой момент времени.
Мнимые точки, расположенные на рисунке вдоль плоскости орбиты, образуют облако измеренных широтных данных.
При достаточном количестве таких точек в облаке данных возможна их статистическая обработка.
Очевидно, что в нашем случае статистическая обработка широтных и долготных данных может быть использована для выявления характера движения КА, т.е. для точного выявления линии, по которой происходит движение КА.
Очевидно также, что по результатам такой обработки центральная ось датчика должна ориентироваться на центр Земли с высокой точностью.
Со статистической точки зрения, измеренные данные следует отнести к временному ряду, который может быть обработан тем или иным способом погашения несистематических составляющих.
Проведенное сравнение способов решения задачи аппроксимации кривой, по которой движется КА, выявило преимущество нейронной сети, в частности RBF-сети (сеть с радиальными базисными функциями).
Таким образом, для бортовой статистической обработки лучше использовать именно такой программный модуль. На фиг.21 представлена блок-схема обработки.
Обратим внимание, что вследствие возмущений орбитальных параметров КА движется по замысловатой линии, не расположенной по существу в одной плоскости и вовсе не являющейся замкнутой.
В этой связи обучение сети (ее программирование) сильно зависит от предъявляемого ей в процессе обучения набора учебных данных. Учебные данные должны быть типичными для задачи, решению которой обучается сеть. Такое программирование сети может быть осуществлено еще до запуска КА, но возможно обучение сети произвести и в реальных условиях.
Для подтверждения обоснованности использования нейронной сети в качестве бортового программного модуля обработки произведено моделирование движения КА.
Моделирование производилось на персональном компьютере с использованием нейронной сети системы STATISTICA.
Такой выбор продиктован задачей временных рядов, в которых связи между данными в нашем случае близки к линейным на ограниченном участке орбиты и заведомо нелинейны - на относительно протяженных участках, например на полном витке.
При моделировании в качестве опорных параметров для оценки служили расчетные инерциальные широта и долгота, в качестве измеренных углов - инерциально-долготные и инерциально-широтные измерения стохастической природы и в качестве отфильтрованных параметров - параметры, обработанные нейронной сетью.
Оценкой на соответствующем временном интервале служили значения рассогласований между расчетными инерциальными, так называемыми реальными, параметрами и обработанными, отфильтрованными параметрами.
На вход нейронной сети для обучения подавались широтные и долготные наборы данных стохастической природы. Следует подчеркнуть, что обучающие данные и измеренные данные (инерциальные долгота и широта) имеют различные флюктуации, о чем свидетельствуют графические зависимости, представленные на фиг.22. Обработка информации преследовала цель - выявить трендовую компоненту в условно измеренных данных.
На фиг.23 представлена таблица результатов обработки нейронной сетью условно измеренной информации на орбитальном участке с 500 по 559 сек.
В качестве входных данных нейронной сети использовались измерения инерциальной широты (столбец 2), измерения инерциальной долготы (столбец 6) и соответствующее им время (столбец 1).
Результирующие данные обработки представлены соответствующими значениями на каждый такт времени в столбцах 3 и 7 таблицы.
Так, в столбце 3 представлены обработанные, то есть спрогнозированные нейронной сетью, значения инерциальной широты, а в столбце 7 - спрогнозированные значения инерциальной долготы.
В столбце 4 и 8 приведены опорные значения реальной инерциальной широты и реальной инерциальной долготы соответственно, которые служат, как было условлено, для сравнения с ними спрогнозированных значений и определения эффективности модуля обработки.
Анализируя ошибки, представленные в угловых секундах в столбцах 5 и 9, можно признать, что обработанные нейронной сетью данные как по инерциальной широте, так и по инерциальной долготе обладают хорошей сходимостью с опорными значениями.
На фиг.24 и 25 представлены результаты обработки в графической форме. Представлены графические зависимости от времени реальной, измеренной и спрогнозированной информации на участке с 500 по 559 сек (с 0 по 60 сек). Из графика видно, что пилообразная линия (измерения) преобразована обработкой в гладкую пунктирную линию (прогноз), которая совпадает с линией сплошной, с реальной линией движения КА.
На фиг.26, 27 и 28 представлены таблица и графические зависимости результатов обработки нейронной сетью условно измеренной информации на другом орбитальном участке с 2999 по 3058 сек.
Трактовка данных и выводы по результатам данной обработки аналогичны предыдущим.
На фиг.29 и 30 представлены графические зависимости от времени результатов обработки условно измеренной информации на полном витке. Графики свидетельствуют о хорошей сходимости обработанных данных с опорными значениями (с пунктирной линией).
На фиг.31 представлена сравнительная таблица параметров, обработанных линейным трендом и нейронной сетью на орбитальном участке с 3049 по 3058 сек.
В данной таблице в столбцах 2 и 5 приведены опорные значения реальной инерциальной широты и реальной инерциальной долготы, предназначенные для сравнения с ними обработанных спрогнозированных значений.
Обработанные линейным трендом и нейронной сетью значения инерциальной широты представлены в столбцах 3 и 4 соответственно.
Обработанные линейным трендом и нейронной сетью значения инерциальной долготы представлены в столбцах 6 и 7 соответственно.
Сравнительному анализу, таким образом, подлежат параметры столбцов 3 и 4 и параметры столбцов 6 и 7.
Результатом сравнения служит степень их приближения к параметрам, представленным в столбцах 2 и 5.
Очевидно, что наиболее предпочтительным методом обработки измерительных данных является метод, основанный на использовании нейронной сети.
На фиг.32 и 33 представлены графики сравнения параметров, обработанных различными методами на участке с 3049 по 3058 сек. Очевидно, что наибольшей сходимостью с критерием обладают параметры, обработанные нейронной сетью.
Таким образом, моделирование показало, что наиболее предпочтительным методом обработки измерительных данных является метод, основанный на использовании нейронной сети.
Для той или иной целевой функции КА всегда осуществляется выбор соответствующей орбиты.
Ее пространственно-временные характеристики должны удовлетворять всем условиям для решения стоящей перед КА задачи, будь-то обзорное наблюдение определенного района земной поверхности, будь-то съемка конкретного наземного объекта, зондирование Земли в интересах хозяйственной деятельности или обеспечение связи между районами.
Конкретная, оптимальная для целевой задачи орбита является базовой средой, в которой сложнейшие взаимодействия различных средств космической системы осуществляются в пространстве, соответствующем определенному времени, и во времени, соответствующем определенному пространству.
Вот почему так важно поддержание параметров расчетной орбиты в приемлемых диапазонах.
Удовлетворяющий предъявляемым требованиям орбитальный виток, заданный своими традиционными параметрами и в форме инерциально-долготных и инерциально-широтных значений с тактовым временным шагом, равным такту бортовых измерений, представляется на борту КА посредством его записи в постоянное запоминающее устройство.
На орбите по мере статистической обработки измерительной информации очередной реальный виток записывается в оперативное запоминающее устройство для последующего сравнения его с заданным.
Любая орбита однозначно определяется шестью независимыми параметрами Кеплерова движения, четыре из которых характеризуют движение КА внутри плоскости орбиты и два - ориентацию плоскости орбиты в пространстве. Элементами орбиты называются параметры, определяющие ее положение в пространстве, размеры и форму. Обратимся к фиг.34, на которой представлены: заданная орбита, реальная орбита и все элементы, характеризующие каждую из орбит.
На данной фигуре обозначены: 1 - Земля, 6 - плоскость экватора, 191, 192 - реальная орбита и заданная соответственно, 0, γ - направление на точку весеннего равноденствия, B1 (B2) и H1 (Н2) - восходящий и нисходящий узлы реальной (заданной) орбиты, Ω1 ( Ω2) - прямое восхождение восходящего узла реальной (заданной) орбиты, П1 (П2) и A1 (A2) - перигей и апогей реальной (заданной) орбиты, i1 (i2) - наклонение реальной (заданной) орбиты, ∈1 (∈2) - аргумент перигея реальной (заданной) орбиты, 2α1 (2α2) - расстояние между перигеем и апогеем реальной (заданной) орбиты, ϑ - истинная аномалия КА (аргумент КА u=ϑ+∈).
Параметры, а также характерные орбитальные точки реальной орбиты определяются на борту КА следующим образом.
Период обращения T1 измеряется как промежуток времени между последовательными прохождениями КА двух точек, в которых значение широты одно и то же (например, точек восходящего или нисходящего узла орбиты).
При наклонении, равном 0°, период T1 - это промежуток времени между последовательными прохождениями КА двух точек, в которых значение инерциальной долготы одно и то же.
Большая полуось α1 определяется по формуле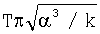 
, где k - гравитационный параметр, равный 3,986·105 км3/с2.
Угловые скорости в перигее и апогее реальной орбиты известны по результатам измерений.
Точка с максимальной угловой скоростью становится точкой перигея и координируется углами широты и инерциальной долготы. Аналогично определяется и координируется и точка апогея.
Отношение скоростей полета КА в перигее и апогее обратно пропорционально отношению величин радиусов-векторов этих точек орбиты, т.е. Vп/Va=rа/rп, где rа, rп - расстояния от центра Земли до апогея и перигея соответственно. В связи с тем, что 2α=(rа+rп), отношения скоростей можно представить в следующем виде Vп/Va=(2α-rп)/rп, откуда определяется радиус-вектор перигея. А затем из формулы 2α=(rа+rп) при подстановке в нее rп определяется rа.
Эксцентриситет орбиты становится известным из следующей формулы e1=(rа1-rп1)/(ra1+rп1).
Восходящий B1 (и нисходящий H1) узел орбиты определяется непосредственно как точка с некоторым значением инерциальной долготы и с нулевым значением широты.
Зная координаты точки перигея П1 и восходящего узла В1, определяется в плоскости орбиты угол, соответствующий аргументу перигея ∈1.
Аналогично рассчитывается аргумент КА u или истинная аномалия КА ϑ.
Наклонение i1 реальной орбиты определяется как максимальное значение широтного угла.
Таким образом становятся известными следующие параметры реальной орбиты: α1, е1, ∈1, Ω1, i1 и u (или ϑ).
По результатам сопоставления параметров реальной орбиты и представленных в ЗУ параметров заданной орбиты определяются искомые отклонения.
Так, сопоставив значения инерциальных долгот в момент прохождения КА восходящих узлов каждой из орбит (т.е. в момент, когда оба значения широты равны нулю), получим рассогласование Δ Ω как разницу указанных долгот.
Аналогично, достаточно сопоставить значения наклонений i1 и i2 и их разница выявит величину их рассогласований Δi.
В результате осуществления коррекций реальной орбиты по устранению рассогласований Δ Ω и Δi плоскость реальной орбиты совместится с плоскостью заданной орбиты.
Здесь следует отметить, что при одном и том же значении Ω и при одном и том же значении i размеры и формы двух орбит, лежащих в одной плоскости, могут не совпадать.
Различная ориентация перигеев двух орбит свидетельствует, что значения их аргументов разные, а потому Δ∈ количественно характеризует указанную ориентацию, а соответствующие Δα и Δe количественно характеризуют различие в размерах и форме.
Следует также отметить и различие в форме измерений орбитальных скоростей: скорость реальной орбиты представлена в град/сек, а скорость заданной орбиты - в км/сек (и в град/сек).
Известны следующие формулы, позволяющие определить скорость в км/сек реальной орбиты в перигее и апогее:
V2 п=(k/α)[(1+e)/(1-е)] и V2 a=(k/α)[(1-е)/(1+e)].
Сопоставление этих скоростей с угловыми скоростями позволяет обеспечить их взаимную конвертируемость на любом орбитальном участке.
Таким образом обеспечивается определение отклонений реальной орбиты от заданной: Δα, Δe, Δ∈, Δi, Δ Ω, а также конвертируемость скоростей.
Измеренные на орбитальном витке данные, как показано выше, сглаживаются нейронной сетью на каждый временной такт с секундными погрешностями. Обработанные таким образом данные записываются в бортовое ЗУ для использования при определении параметров орбиты. Временной такт для той или иной конкретной орбиты выбирается оптимальным. В отличие от рассматриваемых ниже трех типов орбит (см. фиг.35) условимся, что в нашем случае при определении перигея и апогея временной шаг будет равен 10 сек. На фиг.35 представлена сводная таблица расчетных параметров трех орбит (три подтаблицы). Высокая эллиптическая орбита со значениями периода, высот перигея и апогея и эксцентриситета задана и с временным шагом 1000 сек, измеренным углом в градусах и скоростью V''/сек на каждый момент после истечения каждого шага. С соответствующими параметрами заданы "квазистационарная" и низкая эллиптическая орбита. Отметим, что по данным, представленным в ЗУ, выявляются угловые расстояния, пройденные КА за каждые 10 секунд. Определим для каждой из трех орбит угловые расстояния, пройденные за временные шаги, и проставим полученные значения в пустых третьих столбцах каждой подтаблицы (пустые четвертые столбцы каждой из подтаблиц служат для фиксации зоны нахождения точек перигея и апогея). Легко убедиться из подтаблиц, что наименьшие значения угловых расстояний, такие как 1,86°, 8,16° и 10,05° соответствуют зонам нахождения точек апогея, а наибольшие значения угловых расстояний - зонам нахождения точек перигея. В четвертых столбцах каждой подтаблицы эти зоны отмечены буквами А (апогей) и П (перигей). Диапазон зон ограничивается такими равными (или близкими) значениями угловых расстояний за 10-ти секундный шаг (V''/c×10 с), которые достоверно отличаются своими значениями от внутризонных значений при располагаемых точностях. Диапазоны перигейной зоны (ПЗ) и апогейной зоны (АЗ) для (табличных) орбит будут такими:
- высокой ПЗ: ˜1530'',4→˜2991'',6←˜1640'',16 (1530''); АЗ: ˜80'',028→˜66'',96←˜79'',92;
- стационарной ПЗ: -150'',84→˜154'',08←˜150'',84; АЗ: ˜150'',12→˜146'',88←˜150'',12;
- низкой ПЗ: ˜2309'',4→˜2325'',9←˜2301'',8; АЗ: ˜1814'',4→˜1804'',3←˜1819''.
Заметим, что для квазистационарной орбиты требуется шаг больше 10 сек. Срединные угловые значения диапазонов зон определяют точки перигея и апогея. Следует иметь в виду, что точки А и П разнесены угловым расстоянием на 180°. На фиг.36 проиллюстрировано вышеизложенное и представлены годографы угловых скоростей круговой и высокоэллиптической орбит. Векторы OR равны здесь угловой скорости в последовательные моменты времени.
При фиксации восходящего узла орбиты и перигея по сглаженным данным аргумент перигея определяется как угол между долготами восходящего узла и перигея (по направлению движения КА).
Таким образом определяются апогей, перигей и его аргумент, а из следующих формул - все необходимые параметры: T=2π√α3/k, откуда α; 2α=(ra+rп), но так как Vп/Va=ra/rп, то Vп/Va=(2α-rп)/rп, откуда rп;
ra=(2α-rп);
e=(ra-rп)/(ra+rп);
r=α(1-е2)/1-е cosϕ, где ϕ - здесь угол, отсчитываемый от оси эллипса, соединяющий апогей с перигеем.
Коррекция параметров реальной орбиты с целью обеспечения их соответствия параметрам заданной орбиты зависит от величины, точки приложения и направления корректирующего импульса.
По направлению действия известны боковой и тангенциальный импульсы, под действием которых осуществляется устранение отклонений реальной орбиты от заданной.
Следует отметить, что в нашем случае корректирующие маневры необходимо осуществлять под действием импульсной тяги.
Рассмотрим, какие последствия возникают при приложении бокового импульса.
Обратимся к фиг.37, на которой обозначено: 1 - Земля, 10 - плоскость экватора, 30 - орбита, линия узлов ВН - ось изменения наклонения орбиты i, ось мира F1P - ось изменения прямого восхождения восходящего узла Ω, ось F1Q - ось изменения аргумента перигея ∈ (эта ось перпендикулярна плоскости орбиты и также проходит через центр Земли), γ - направление на точку весеннего равноденствия, А - точка апогея, П - точка перигея.
Очевидно, что боковая сила изменяет i, Ω, ∈, т.е. ориентацию плоскости орбиты в пространстве, но не изменяет ни формы орбиты, ни ее размеров.
Точкой приложения боковой силы при маневре для совмещения плоскостей орбит служит одна из двух точек на линии пересечения плоскостей орбиты (точка, ближайшая к апогею).
Такая точка определяется при сопоставлении реальной и заданной орбит как точка с общими координатами, т.е. как точка, принадлежащая обеим орбитам.
Рассмотрим фиг.38, на которой представлена реальная орбита 301 с восходящим узлом B1, с наклонением i1 и аргументом перигея ∈1. Перечисленные параметры реальной орбиты не соответствуют аналогичным параметрам В2, i2, ∈2 заданной орбиты 302. После приложения в соответствующей точке бокового соответствующего импульса ΔVв параметры реальной орбиты приобретут значения параметров заданной орбиты.
Под действием бокового импульса будет происходить разворот вектора скорости относительно оси, проходящей через точку приложения боковой силы (точка М, фиг.37) и центр Земли (точка F1).
При полете КА по эллиптической орбите вектор скорости в любой точке, кроме перигея и апогея, не совпадает с линией местного горизонта. Проекцию вектора скорости на линию местного горизонта называют трансверсальной скоростью Vη и она определяется из соотношения: Vη=VcosΘ, где угол Θ=arctg[(1+ecosϑ)/esinϑ]. Здесь е, ϑ и V известны.
При боковом маневре в точке М осью разворота орбиты является ось М'M, проходящая через точку приложения боковой силы и центр Земли. По этой оси и направлен вектор разворота орбиты Δχ, т.е. ось разворота орбиты не совпадает ни с одной из осей изменения i, Ω и ∈. В этом случае приращения всех трех элементов (Δiв, Δ Ωв, Δ∈в) определяются проекциями вектора разворота плоскости орбиты Δχ на соответствующие оси их изменения.
Изменения наклонения орбиты, прямого восхождения восходящего узла и аргумента перигея под действием бокового импульса зависят от аргумента КА u в точке маневра (u=ϑ+∈).
Для изменения прямого восхождения восходящего узла импульс боковой силы нужно прикладывать в точках с аргументом, равным 90° или 270°. Однако при наклонениях орбиты i, не равных 90°, приложение бокового импульса в точках исходной орбиты с u0=90° или u0=270° вызовет изменение аргумента перигея. Поскольку u=∈+ϑ, то изменение аргумента перигея ∈ приведет и к изменению аргумента КА u в точке маневра. Поэтому аргумент КА на орбите после маневра уже не будет равен 90° или 270°. В результате боковой импульс изменит не только прямое восхождение восходящего узла, но и наклонение орбиты.
Обратимся к фиг.39, на которой обозначено: 301 - плоскость исходной орбиты (плоскость реальной орбиты), 302 - плоскость орбиты после маневра (плоскость заданной орбиты), Δχ - угол разворота плоскости орбиты, ΔVв - боковой импульс, Vη - трансверсальная скорость, j - угол, характеризующий направление вектора ΔVв.
Угол Δχ, плоскость которого перпендикулярна линии пересечения плоскостей реальной и заданной орбит, определяется как максимальная разница значений координат орбитальных точек, лежащих в плоскости угла.
При известном Δχ потребная величина импульса ΔVв может быть определена из соотношения: ΔVв=2Vηsin0,5Δχ. В этом случае направление вектора ΔVв относительно плоскости исходной орбиты будет характеризоваться углом j=90°+0,5Δχ. Для круговых орбит, как известно, вектор скорости в любой точке орбиты перпендикулярен радиусу-вектору. Следовательно, для круговых орбит Vη=Vкр.
Для эллиптических орбит трансверсальная скорость полета является величиной переменной.
Максимальное значение она имеет в перигее, минимальное - в апогее. Поэтому и величина импульса ΔVв при развороте плоскости данной орбиты в перигее будет максимальной, а в апогее - минимальной.
Если боковая сила будет приложена в одном из узлов орбиты, ось разворота будет совпадать с осью изменения наклонения орбиты. Следовательно, боковая сила, приложенная в узлах орбиты, вызовет изменение лишь наклонения орбиты.
Схема непосредственного разворота плоскости исходной орбиты для изменения ее наклонения приведена на фиг.40. В одном из узлов орбиты 301 прикладывается импульс скорости ΔVв, под действием которого происходит разворот плоскости орбиты на угол Δχ. В результате наклонение орбиты 302 будет отличаться на угол Δi=Δχ.
Рассмотрим, какие последствия возникают при приложении тангенциального импульса.
Направление действия тангенциальной силы или совпадает с направлением вектора скорости полета, или противоположно ему.
Поэтому тангенциальная сила может изменять только величину скорости полета. Направление скорости при действии тангенциальной силы не изменяется. Тангенциальная сила не вызывает изменения наклонения орбиты и прямого восхождения восходящего узла. Чтобы определить, какие изменения орбиты вызовет тангенциальная сила, рассмотрим уравнение V=√k[(2/r)-(1/α)]. Так как k - величина постоянная, а r в точке маневра не изменяется, то при маневре увеличение (уменьшение) величины скорости вызовет изменение α.
Рассмотрим фиг.41. На ней показана эллиптическая орбита 301 с фокусами F1 и F2 до маневра.
Пусть в момент выполнения импульсного маневра КА находился в точке М с истинной аномалией ϑ. Расстояние от этой точки до первого фокуса равно r, а расстояние до второго фокуса - r'.
Как известно, эллипсом называется геометрическое место точек, для которых справедливо равенство r+r1=2a. Если скорость полета в точке М увеличить на ΔVт, это вызовет увеличение большой полуоси на Δαт.
Очевидно, что увеличится расстояние до второго фокуса и он из точки F2 переместится в точку F2'. Величина этого перемещения Δr'=2Δαт. Известно также, что касательная в любой точке эллипса является биссектрисой внешнего угла, образованного радиусами-векторами этой точки. Вектор скорости направлен по касательной к траектории (к эллипсу в точке М). Поэтому угол τ=τ'. Поскольку после маневра направления вектора скорости и радиуса-вектора КА не изменяются, то не изменяются и углы τ и τ'. Это означает, что направление на второй фокус сохранится и он переместится вдоль радиуса-вектора r' на величину 2Δαт, в точку F2'. Перемещение второго фокуса из точки F2 в точку F2' приводит к изменению межфокусного расстояния на величину 2Δст, а это означает, что изменится и эксцентриситет орбиты e (e=с/α). Перемещение второго фокуса приводит также к повороту линии апсид на угол Δ∈т, т.е. тангенциальная сила, изменяя большую полуось орбиты, изменяет и аргумент перигея.
Обратимся к фиг.42. Если коррекцию положения перигея осуществить за счет тангенциального импульса, приложенного в одной из точек пересечения орбиты с малой полуосью (точка Д), то в результате изменится и величина большой полуоси.
Последнее вызывает также изменение периода обращения. В результате после такой одноимпульсной коррекции нужно будет проводить еще коррекцию величины большой полуоси. Поэтому в тех случаях, когда при коррекции положения перигея изменение большой полуоси недопустимо, такую коррекцию целесообразно выполнять, используя два тангенциальных импульса, прикладываемых в точках Д и Д' (фиг.42). Величины этих импульсов должны быть одинаковыми, а знаки разными. При двухимпульсном маневре под действием положительного импульса ΔVт1, приложенного в точке Д, аргумент перигея изменится на Δ∈т1 и большая полуось увеличится на Δαт1. Под действием отрицательного импульса ΔVт2, прикладываемого в точке Д' промежуточной орбиты, большая полуось уменьшится на Δαт2, а аргумент перигея ∈ изменится так же, как и при первом импульсе.
Отметим, что энергетические затраты на выполнение маневра определяются не только выбранной ориентацией управляющего импульса (например, тангенциального или бокового), но и точкой его приложения на орбите.
На орбите имеются не только точки, в которых тот или иной импульс силы не вызывает изменений отдельных элементов орбиты, но и точки, в которых данная сила обеспечивает наибольшее изменение заданного элемента орбиты.
Обратимся к фиг.43.
На данном рисунке указаны точки, в которых изменения α, е и ∈ под действием приложенной тангенциальной силы имеют экстремальные значения. В уравнении Δαт=(2Δα2V/k)ΔVт большая полуось α - величина постоянная для любой точки данной орбиты. Переменной величиной в этом уравнении является только скорость полета, максимальное значение которой в перигее, а минимальное - в апогее. Следовательно, один и тот же по величине и направлению действия импульс скорости ΔVт в перигее будет вызывать максимальные изменения большой полуоси, а в апогее - минимальные.
Максимальные же изменения эксцентриситета орбиты под действием тангенциальной силы происходит в перигее и апогее орбиты. Однако нужно иметь в виду, что для увеличения эксцентриситета орбиты тангенциальный импульс в перигее должен быть положительным, а в апогее - отрицательным.
Тангенциальная сила, приложенная в точках перигея и апогея, не вызывает поворота линии апсид. В этих случаях направления r и r' совпадают с линией апсид и второй фокус будет перемещаться вдоль этой линии. Для коррекции положения перигея (апогея) орбиты, когда величина большой полуоси должна быть сохранена, целесообразно применять два тангенциальных импульса, прикладываемых в точках (Д, Д') пересечения орбиты с малой полуосью. При этом величины обоих импульсов должны быть одинаковыми, а их знаки разными.
Необходимые изменения ориентации плоскости орбиты выполняются только под действием боковой силы. Для совмещения двух орбитальных плоскостей боковой управляющий импульс прикладывается в той из двух точек на линии пересечения плоскостей, которая ближе к апогею. При изменении прямого восхождения восходящего узла приложение боковой силы в точках с аргументом, равным 90° и 270°, приводит и к изменению наклонения орбиты.
Для изменения наклонения орбиты управляющий импульс прикладывается в одном из узлов орбиты.
При сопоставлении параметров реальной орбиты с параметрами заданной орбиты определяются следующие рассогласования: Δ Ω, Δi, Δ∈, Δα и Δе. Для устранения каждого из указанных рассогласований в вышеизложенных материалах выявлен вид корректирующего импульса, его направление и точка его приложения. Очевидно, что прежде всего плоскость реальной орбиты должна быть совмещена с плоскостью заданной орбиты. Учитывая, что коррекция долготы восходящего узла исходной орбиты приводит к изменению наклонения i и аргумента перигея ∈, результатом первого корректирующего воздействия должно быть устранение рассогласования Δ Ω. Поэтому истинное рассогласование Δ∈ может быть выявлено только после устранения Δ Ω. Второй импульс должен быть направлен на устранение Δi, то есть на окончательное совмещение плоскостей орбит. Два указанных импульса являются боковыми. Устранение Δα и Δе производится приложениями тангенциальных импульсов. Коррекция положения перигея, т.е. коррекция ∈, в том случае, когда величина α должна быть сохранена, производится двумя тангенциальными импульсами, прикладываемыми в точках пересечения орбиты с малой полуосью.
Уравнения приращений элементов орбиты при том или ином корректирующем импульсе представлены на фиг.44.
Входящие в уравнения такие элементы реальной орбиты, как α, е, i, u, а также Vη, как показано выше, определяются. Значения каждого из приращений выявляются при сопоставлении заданной и реальной орбит. Значение приращения скорости ΔV, потребного для осуществления каждого вида маневра, определяется из представленных формул.
Затраты скорости связаны с затратами топлива двигателя формулой К.Э.Циолковского ΔV=ωэIn(m0/m0-mт), где ωэ - эффективная скорость истечения газов из сопла двигателя, m0 - масса КА до маневра, mт - масса топлива, расходуемого на маневр. Решая ее относительно массы топлива, получаем
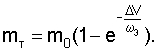
Все рассмотренные действия являются детерминированными, а потому при соответствующем бортовом программном обеспечении могут быть реализованы в автономном режиме.
| название | год | авторы | номер документа |
|---|---|---|---|
| АВТОНОМНАЯ БОРТОВАЯ СИСТЕМА УПРАВЛЕНИЯ КОСМИЧЕСКОГО АППАРАТА "ГАСАД" | 1993 |
|
RU2033949C1 |
| СПОСОБ УДЕРЖАНИЯ ГЕОСТАЦИОНАРНОГО КОСМИЧЕСКОГО АППАРАТА НА ЗАДАННОЙ ОРБИТАЛЬНОЙ ПОЗИЦИИ | 2011 |
|
RU2481249C2 |
| СПОСОБ БАЛЛИСТИЧЕСКОГО ОБЕСПЕЧЕНИЯ МОНИТОРИНГА КОСМИЧЕСКОГО АППАРАТА НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2022 |
|
RU2787796C1 |
| СПОСОБ МОНИТОРИНГОВОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2019 |
|
RU2721812C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ОКОЛОСТАЦИОНАРНОЙ ОРБИТЕ | 2019 |
|
RU2716394C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ОКОЛОСТАЦИОНАРНОЙ ОРБИТЕ | 2018 |
|
RU2703696C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2013 |
|
RU2559371C2 |
| СПОСОБ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2020 |
|
RU2729347C1 |
| СПОСОБ АВТОНОМНОЙ КОЛЛОКАЦИИ НА ОКОЛОСТАЦИОНАРНОЙ ОРБИТЕ | 2021 |
|
RU2768994C1 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ЦЕНТРА МАСС КОСМИЧЕСКОГО АППАРАТА | 2011 |
|
RU2487823C1 |
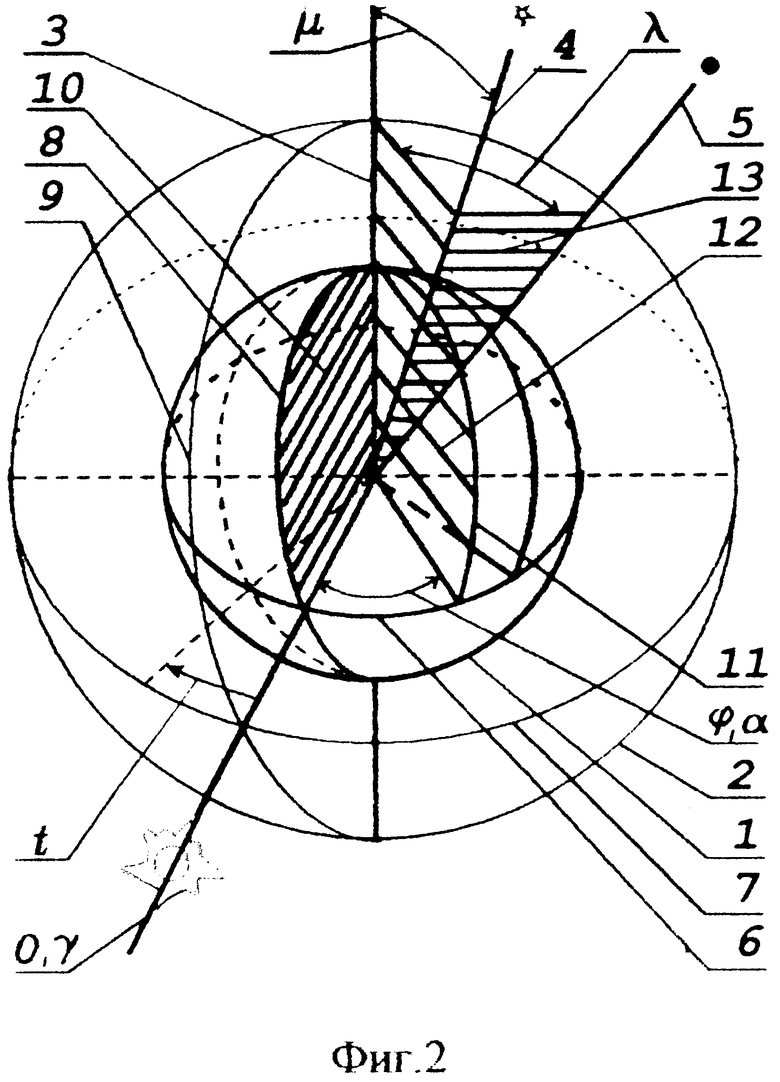
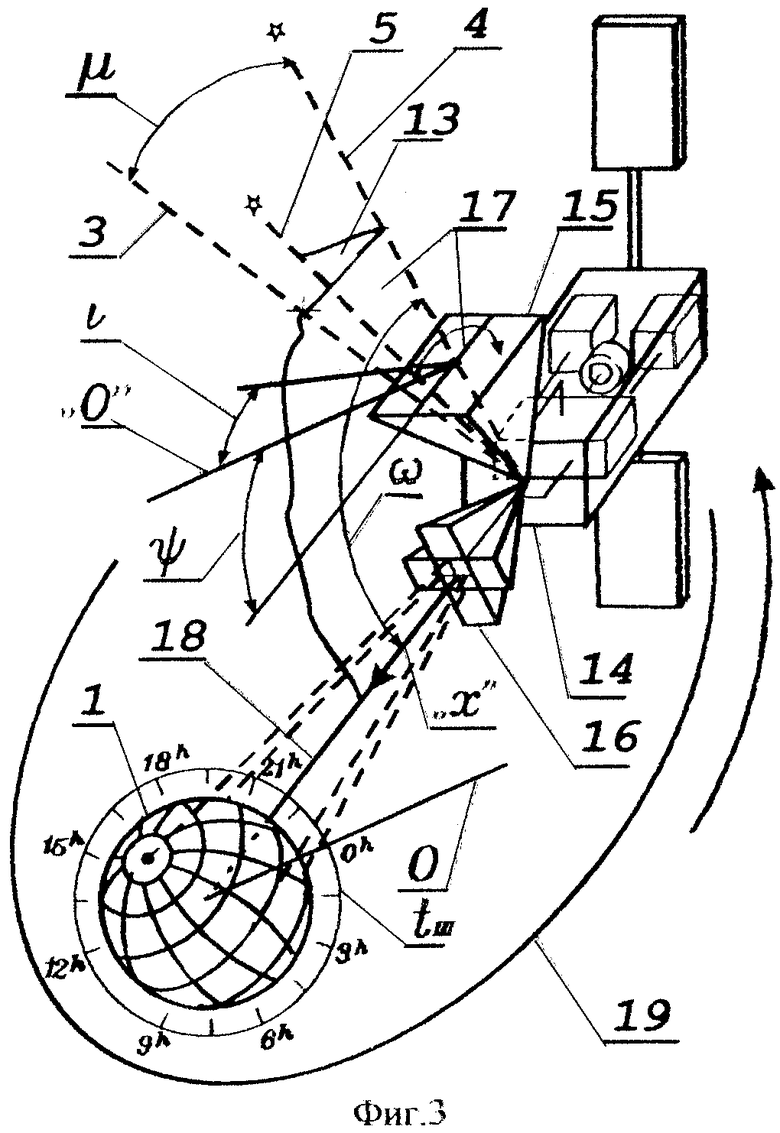
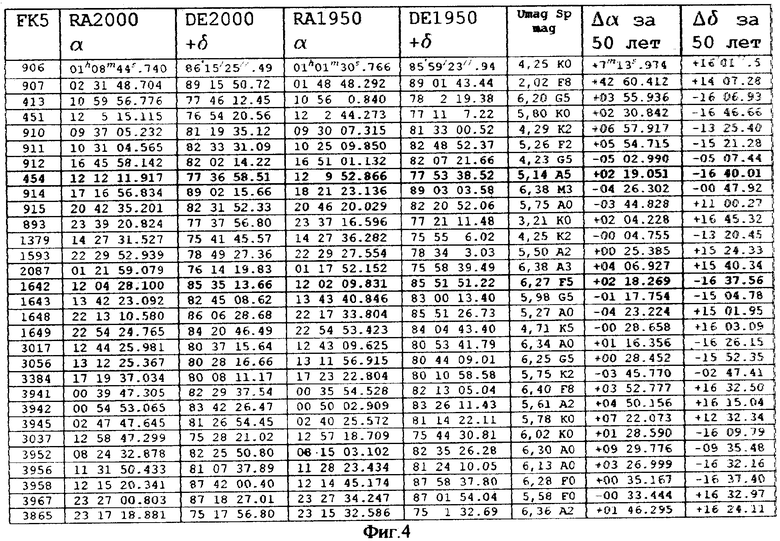
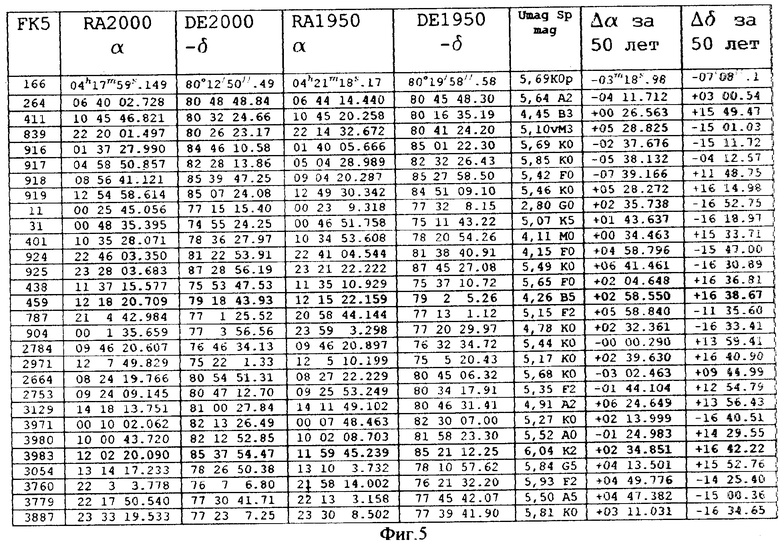
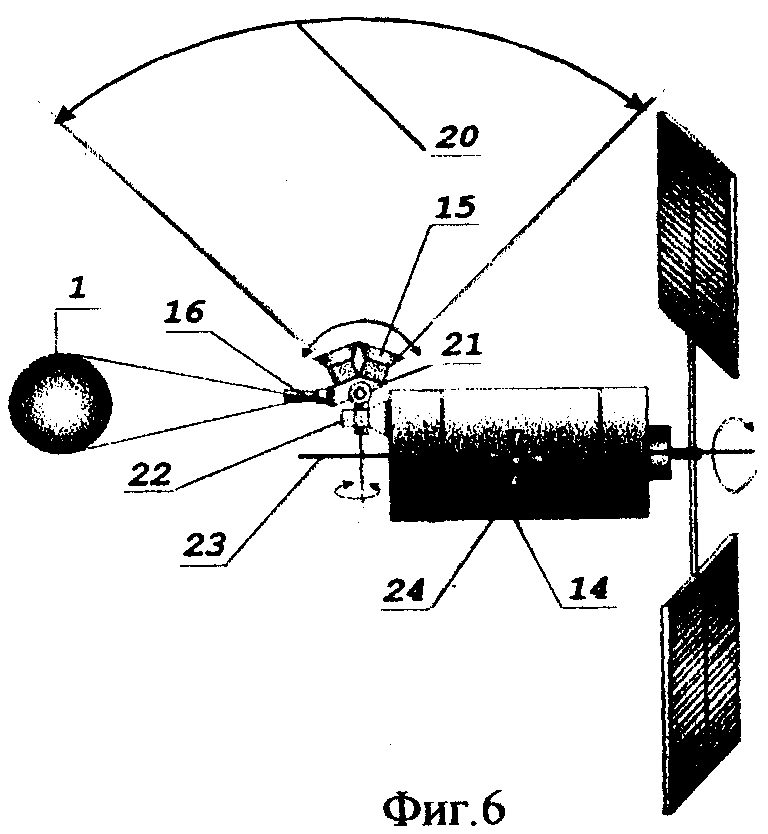
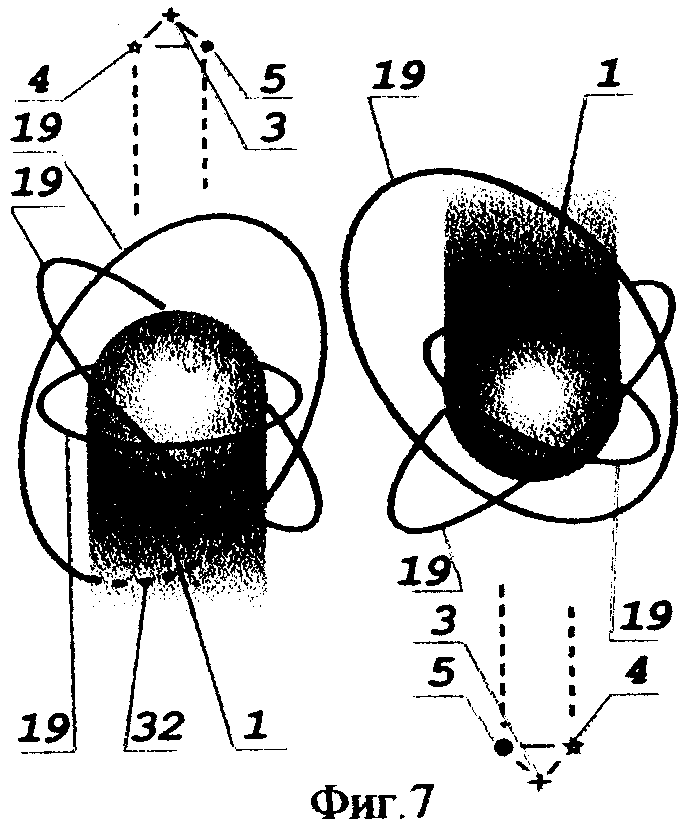
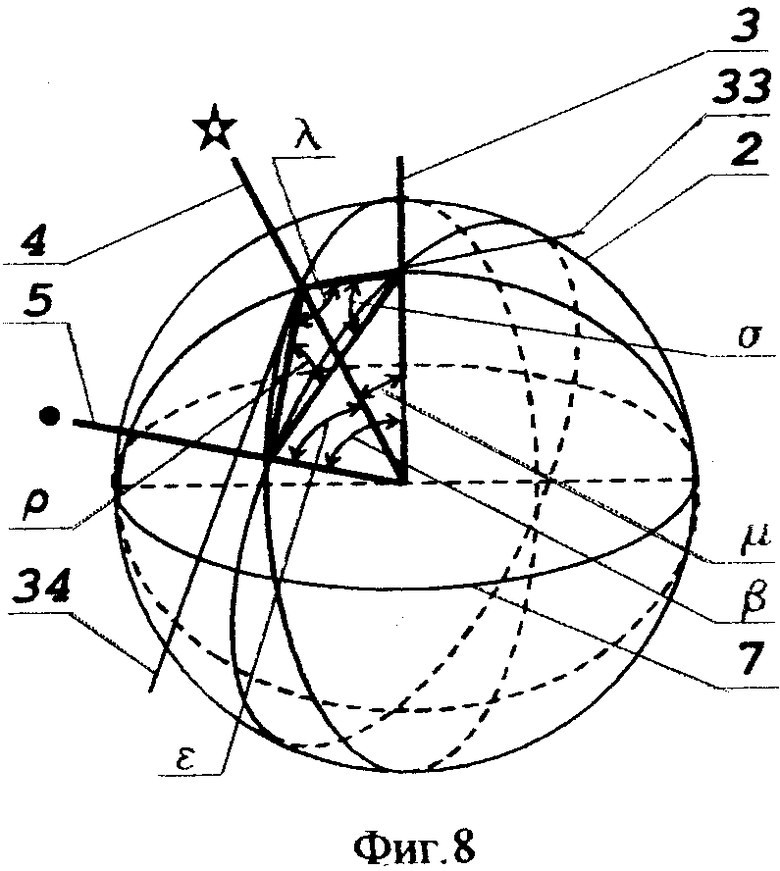
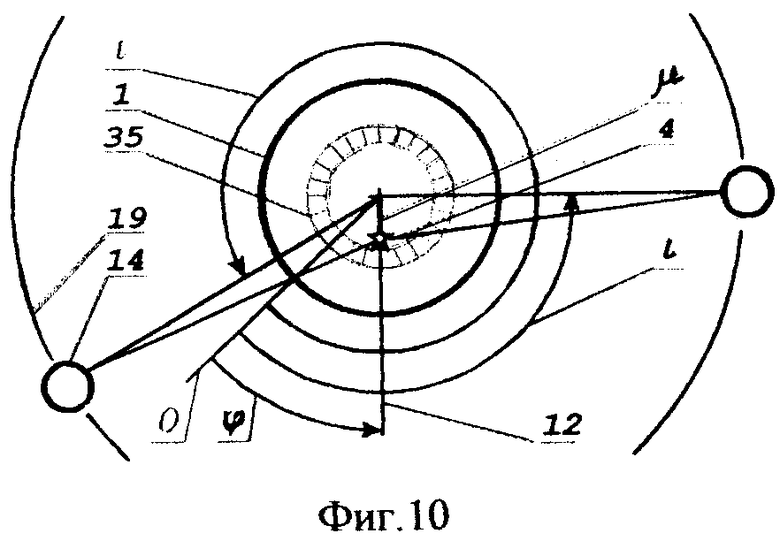
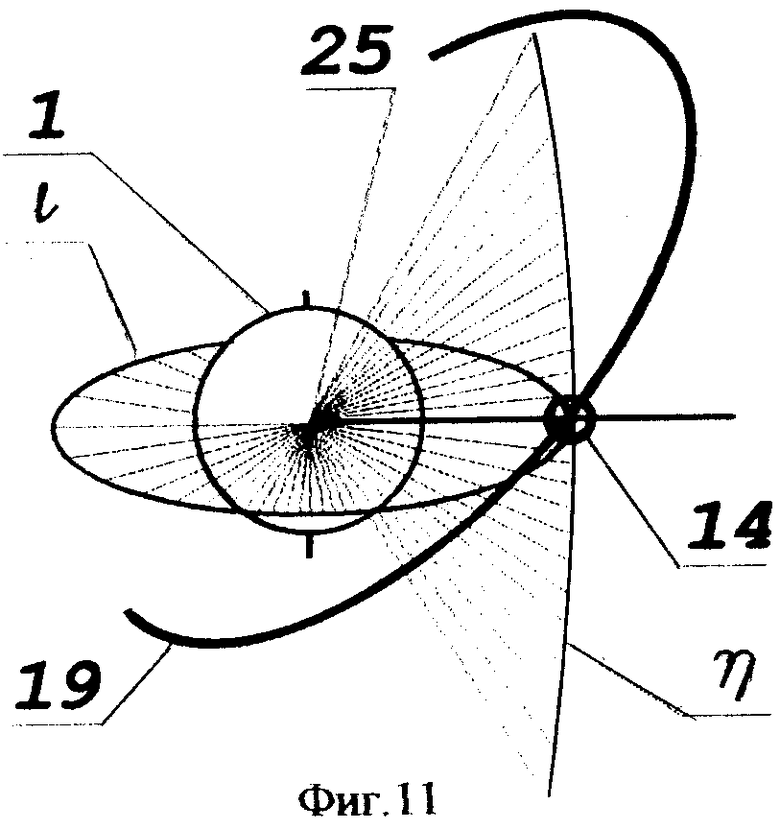
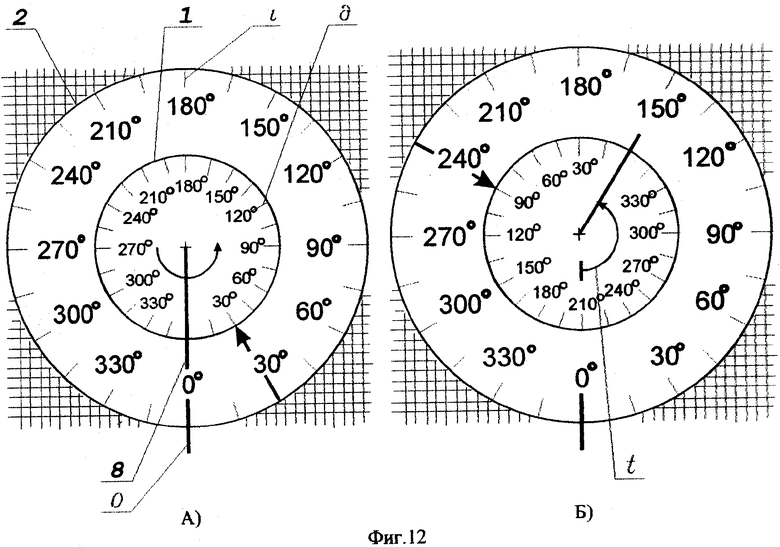
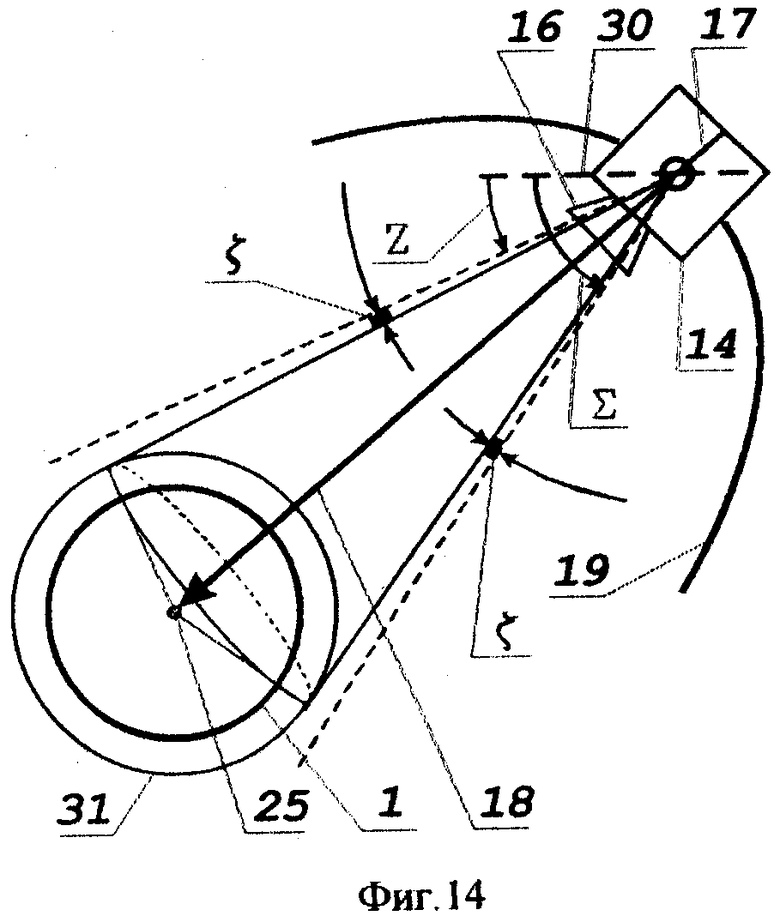
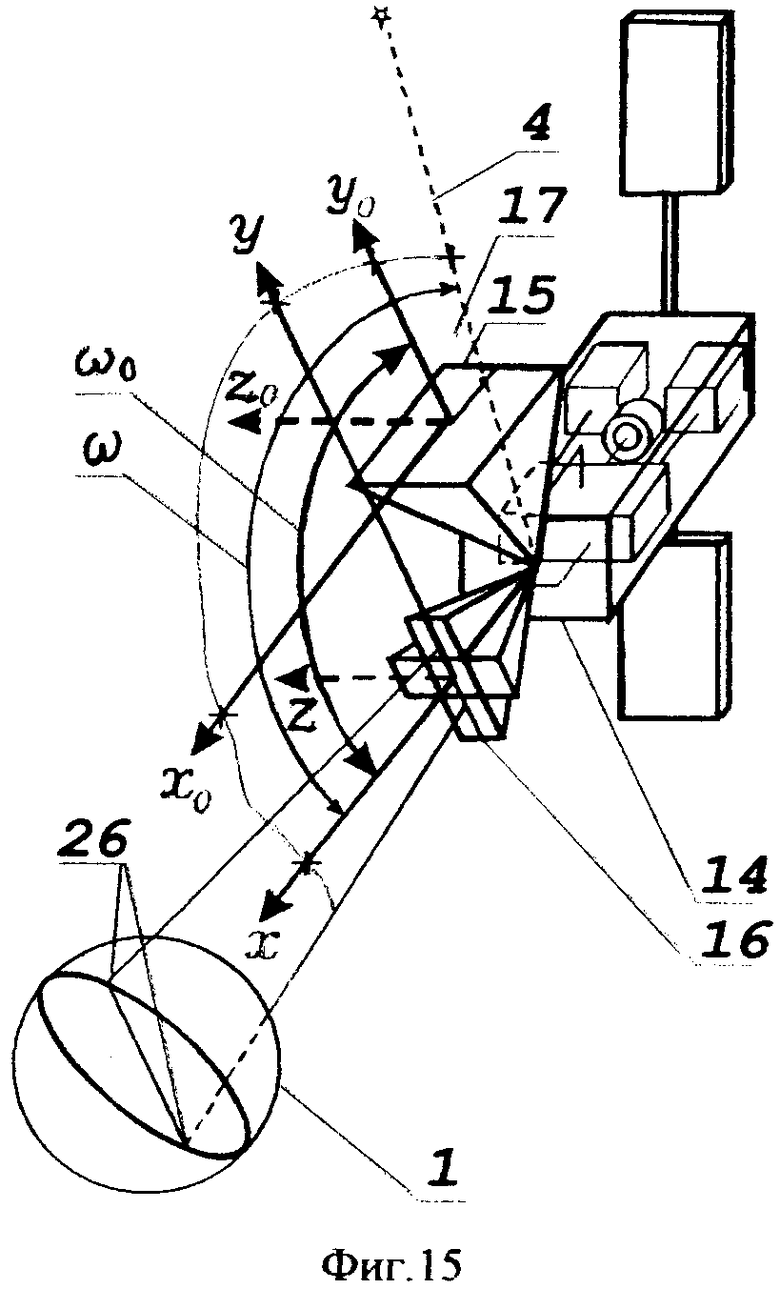
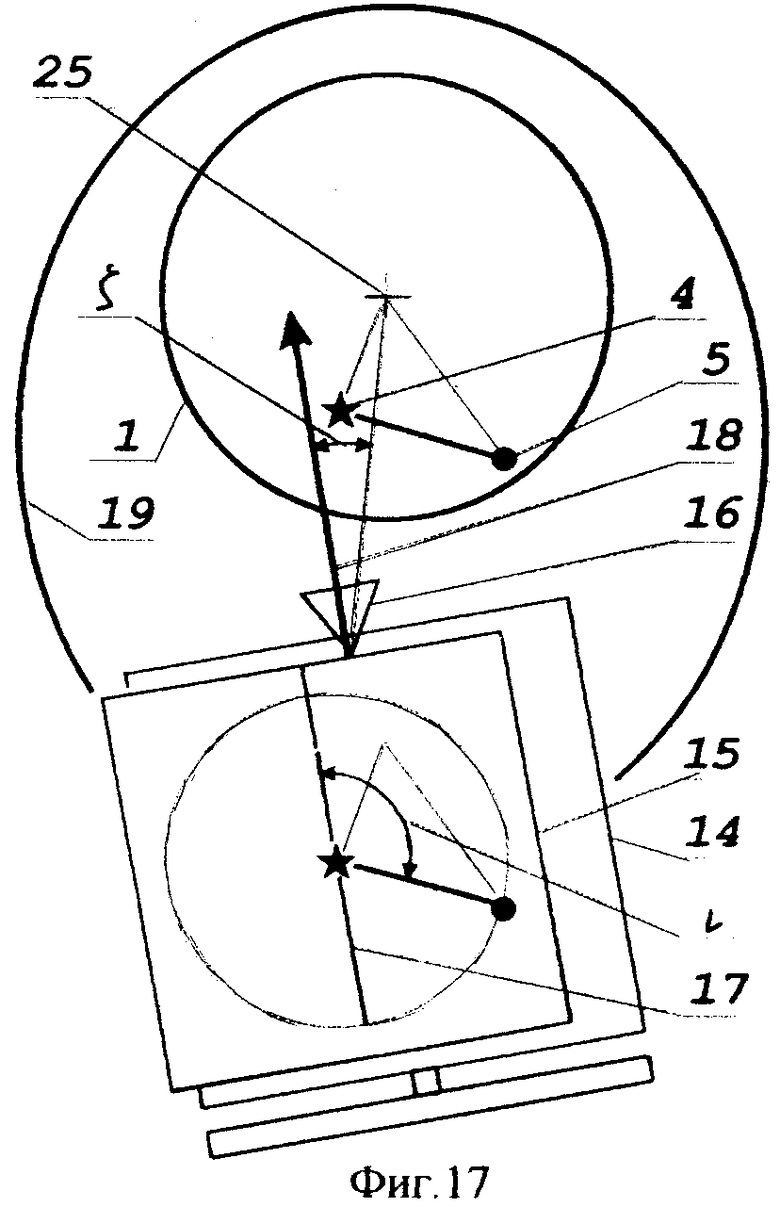
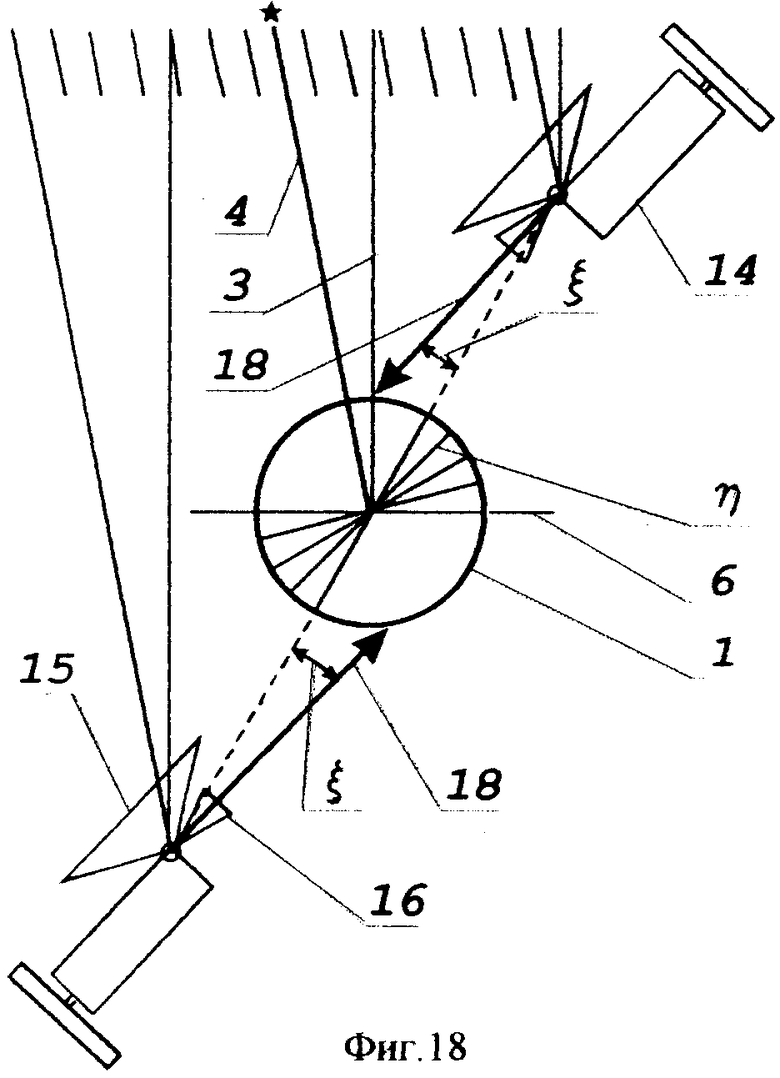
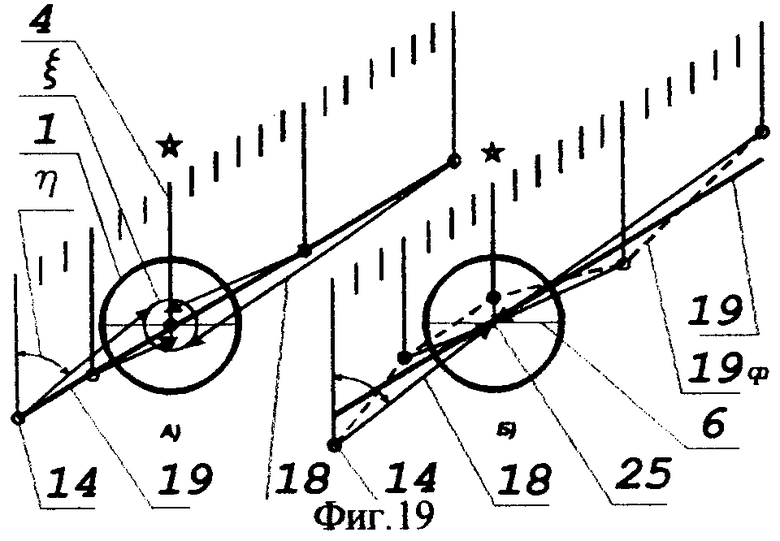
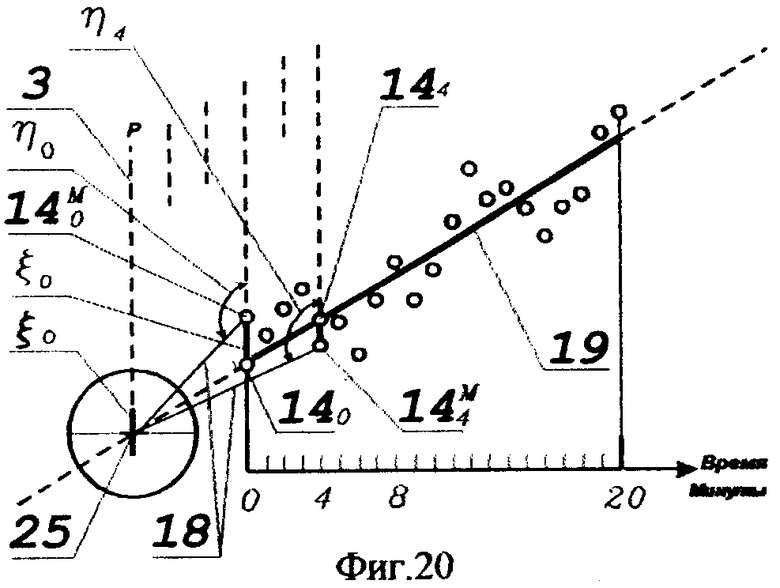
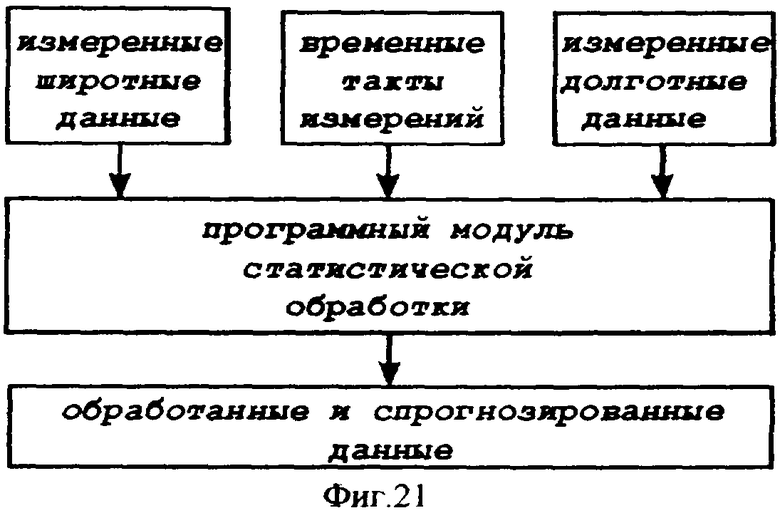
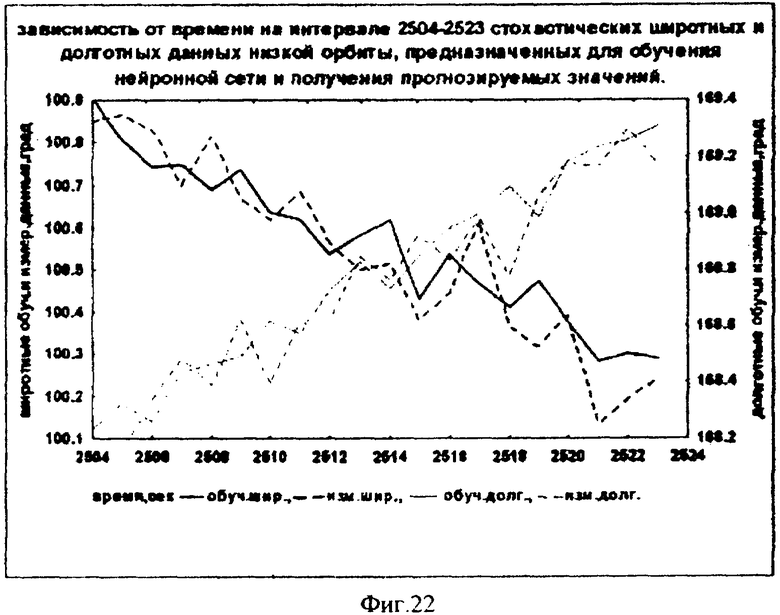
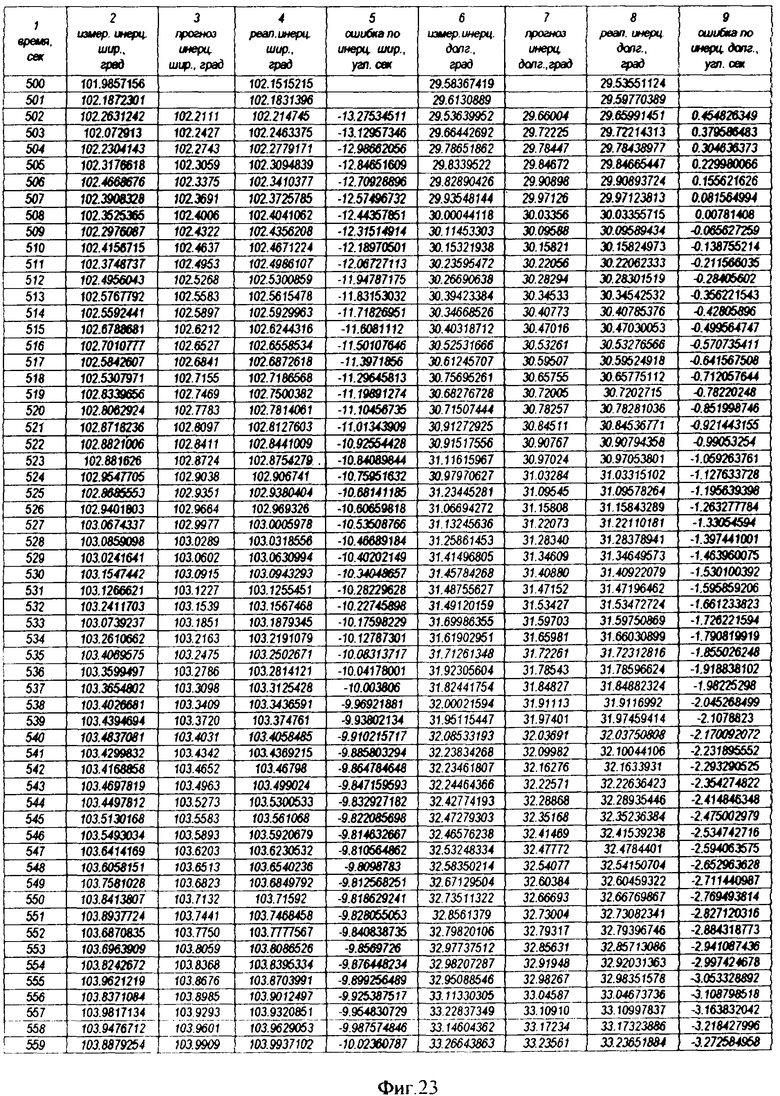
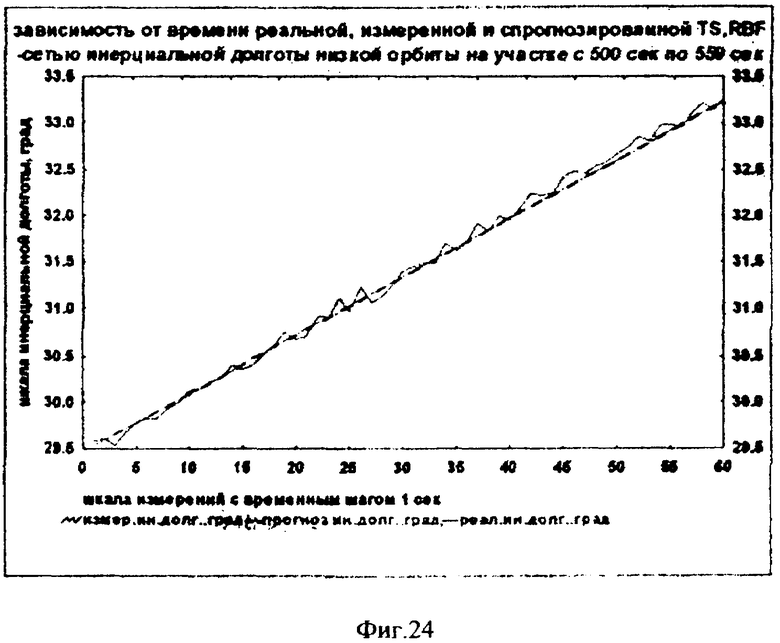
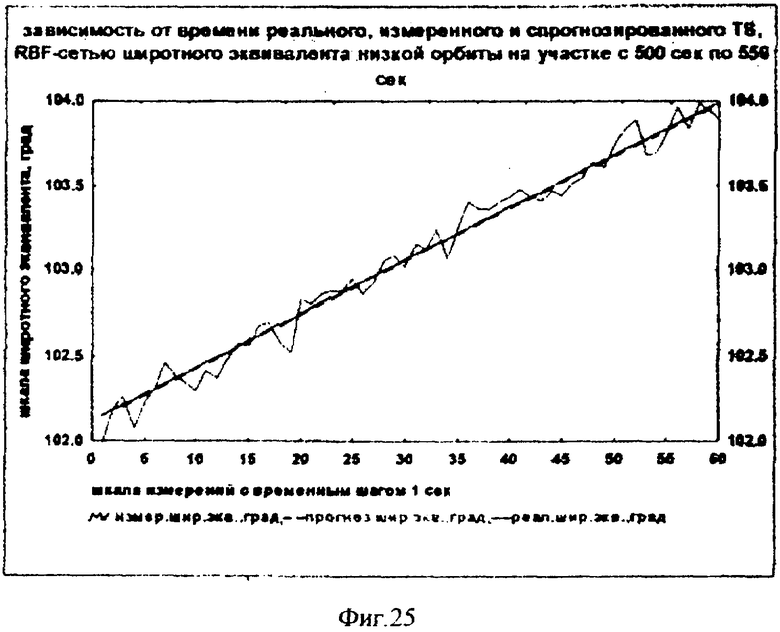
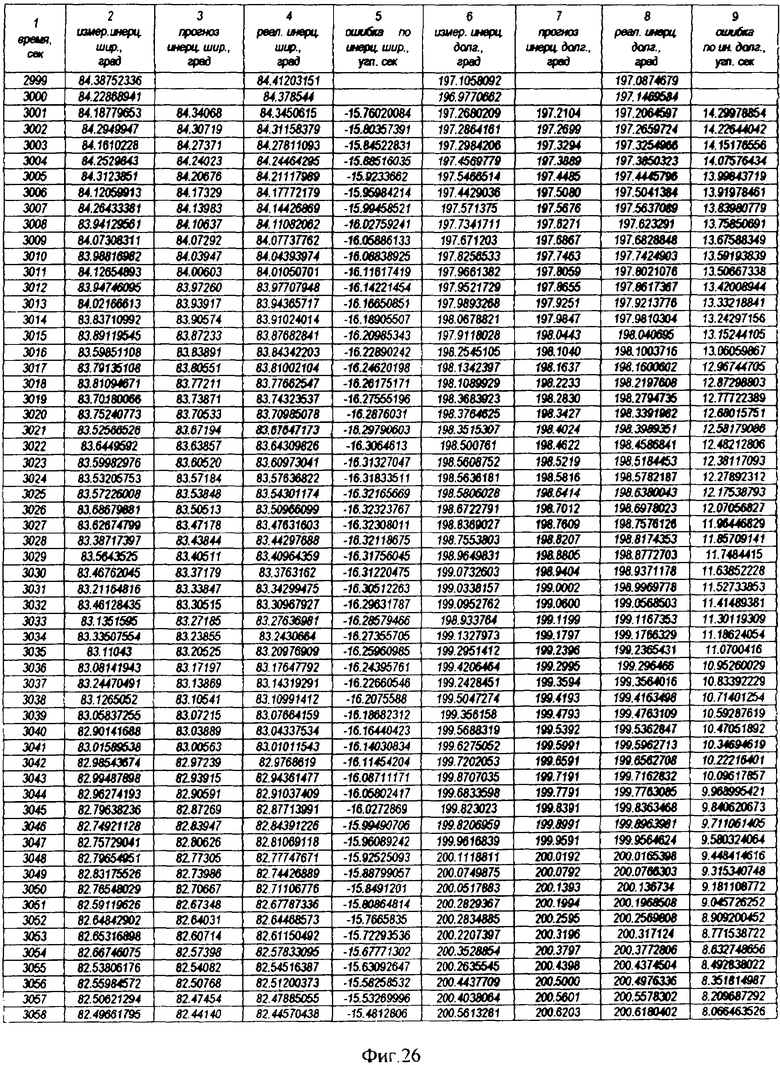
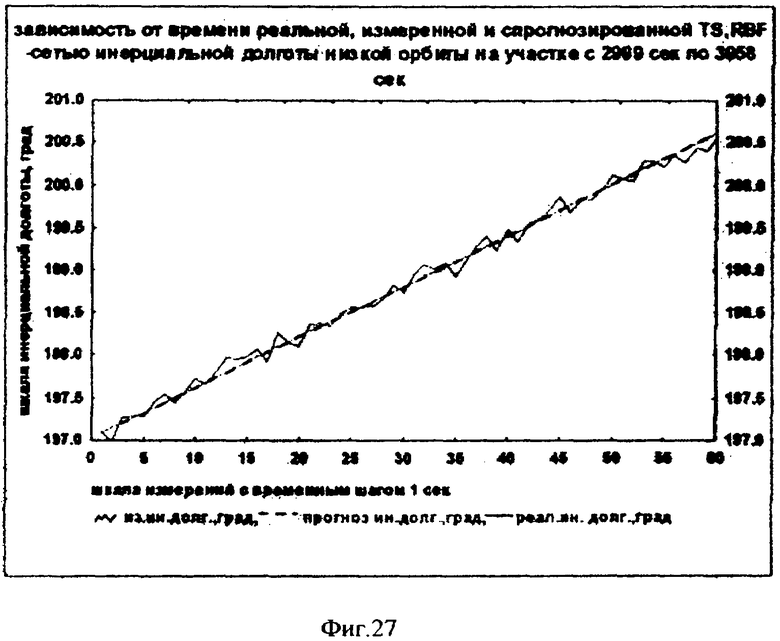
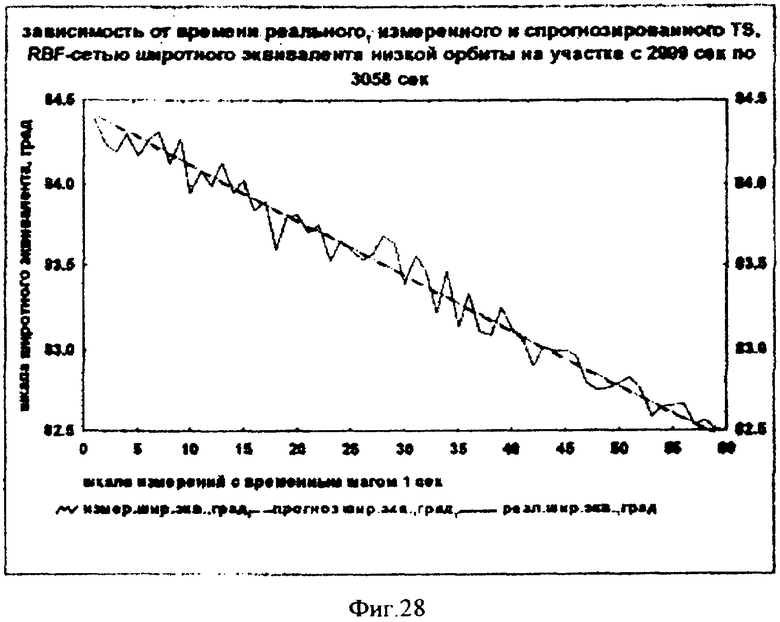
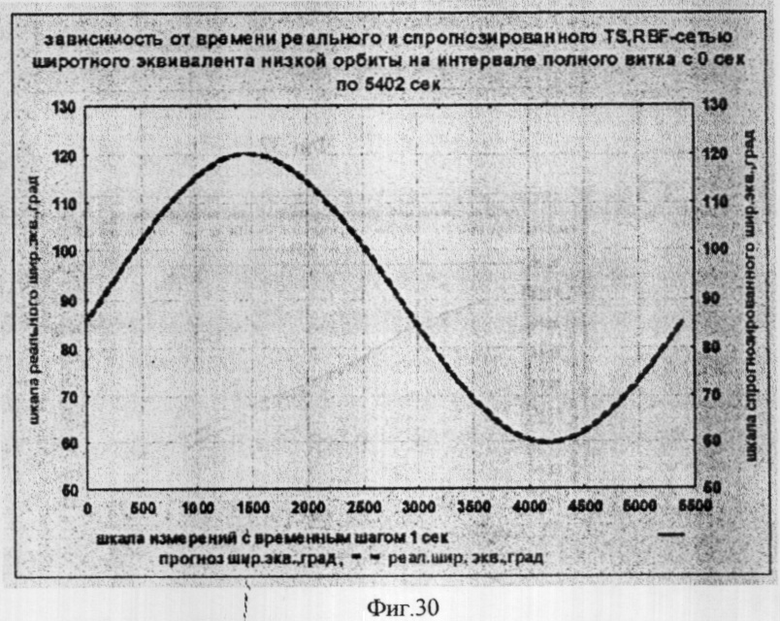
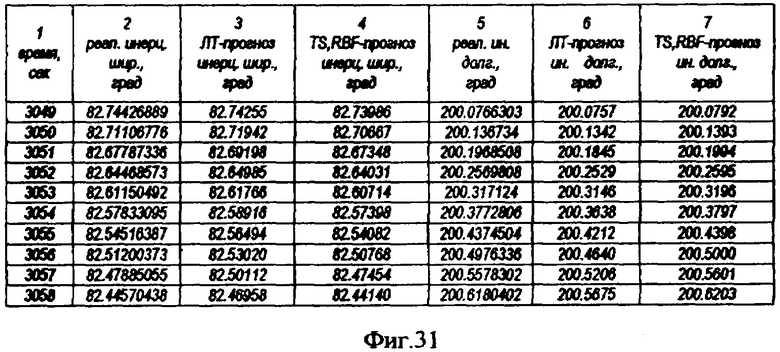
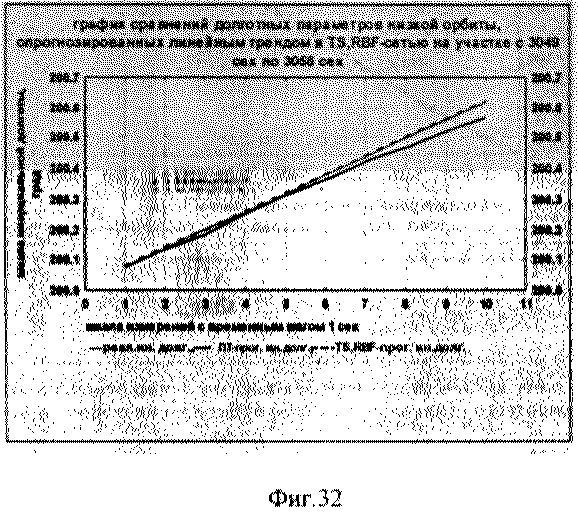
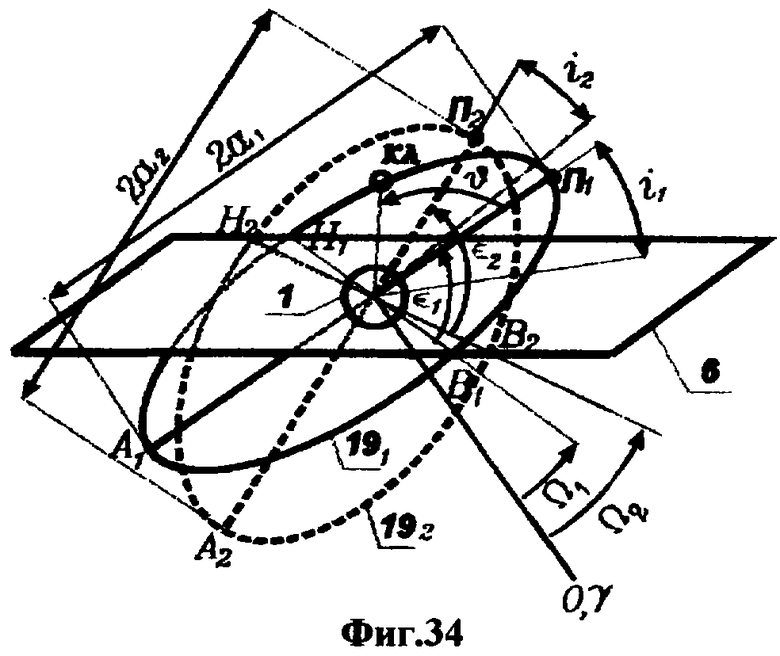
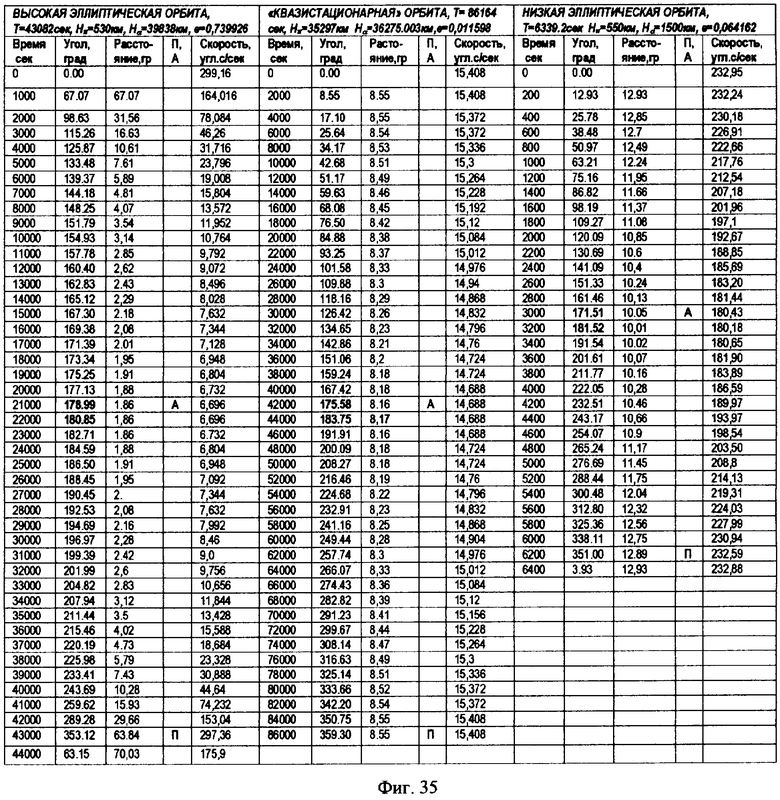
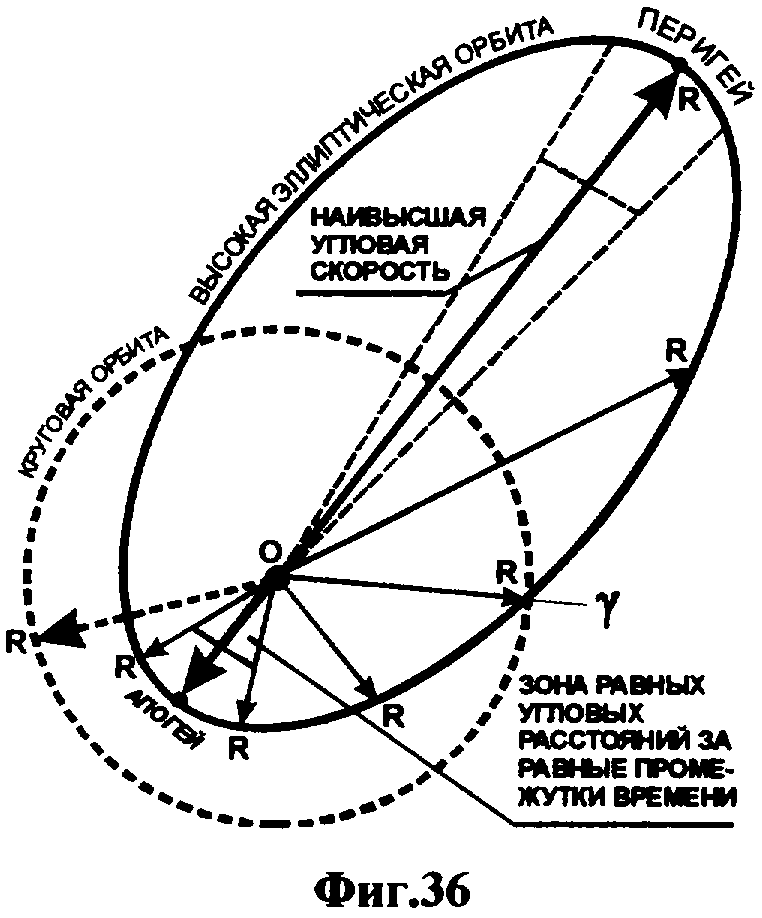
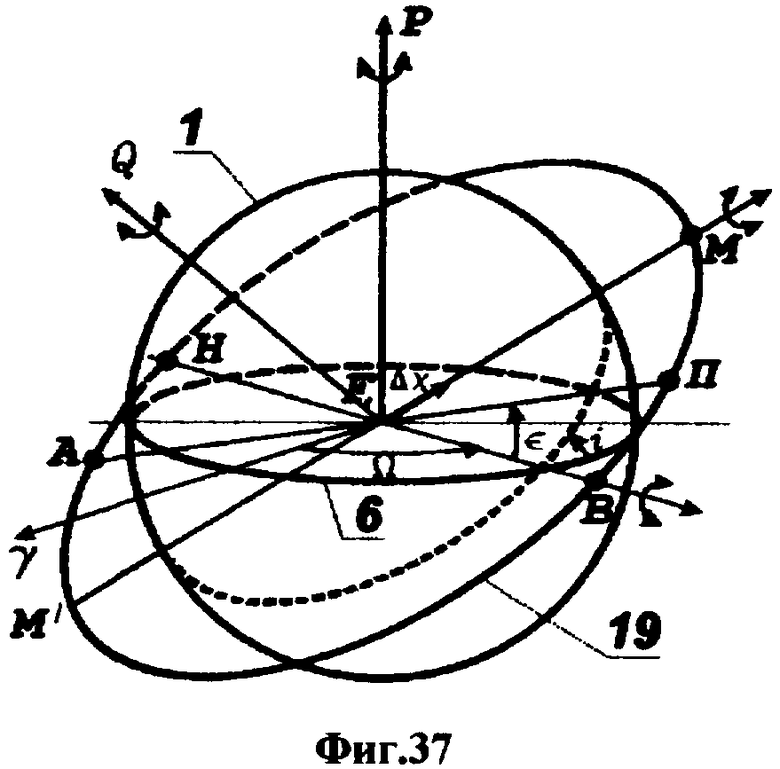
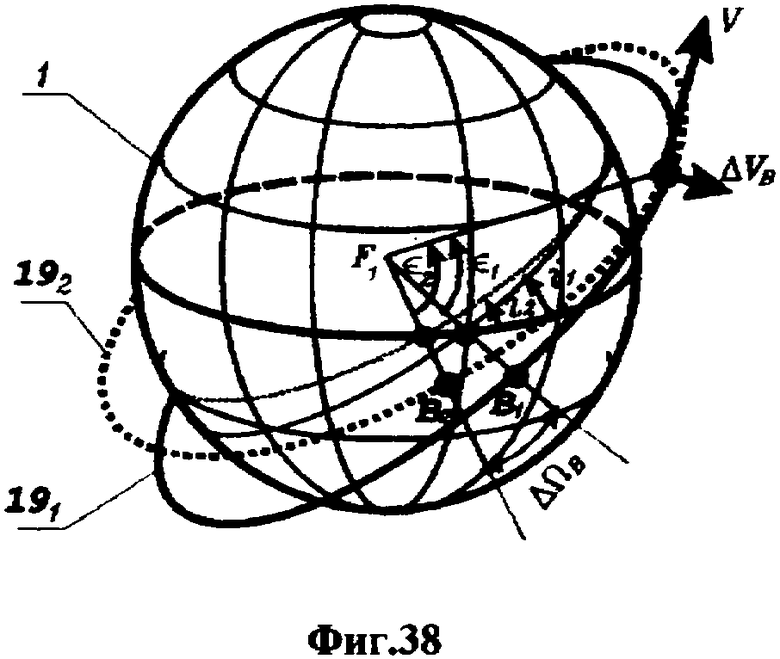
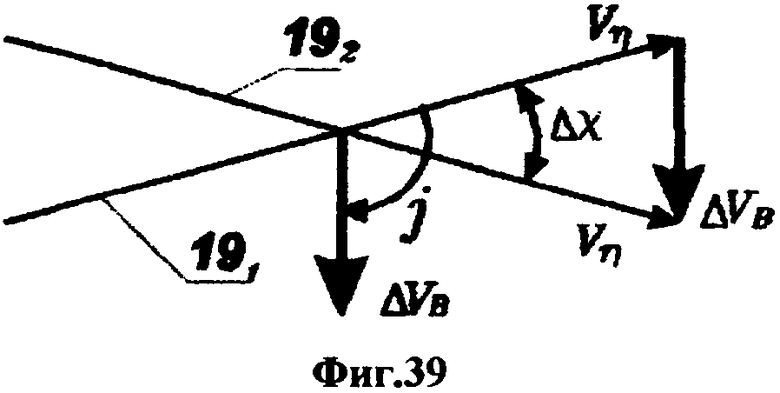
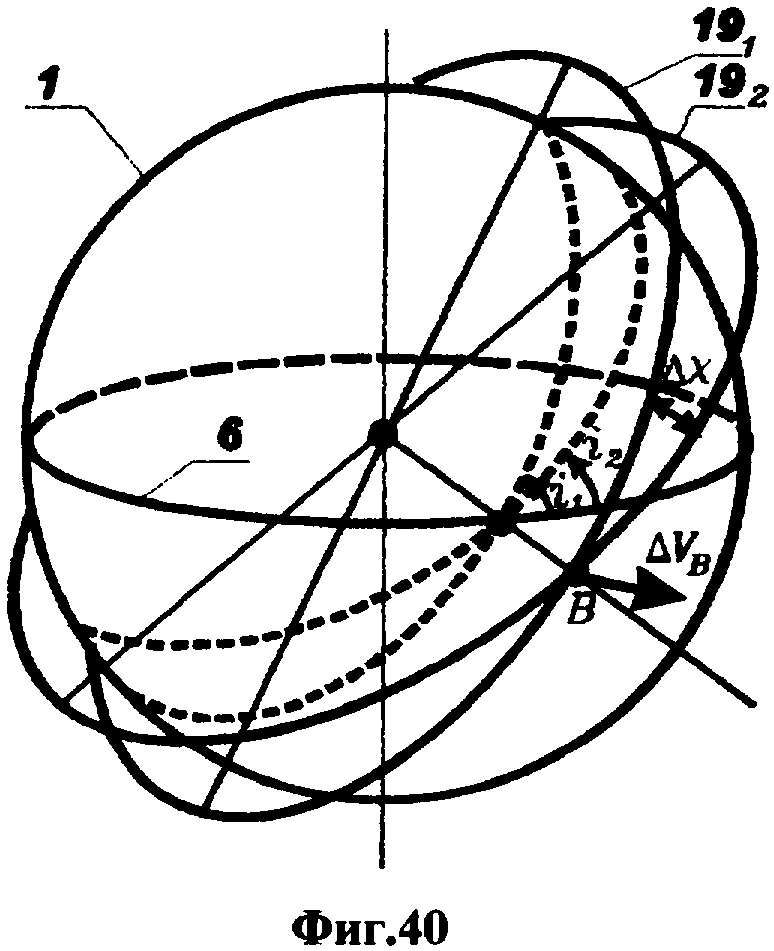
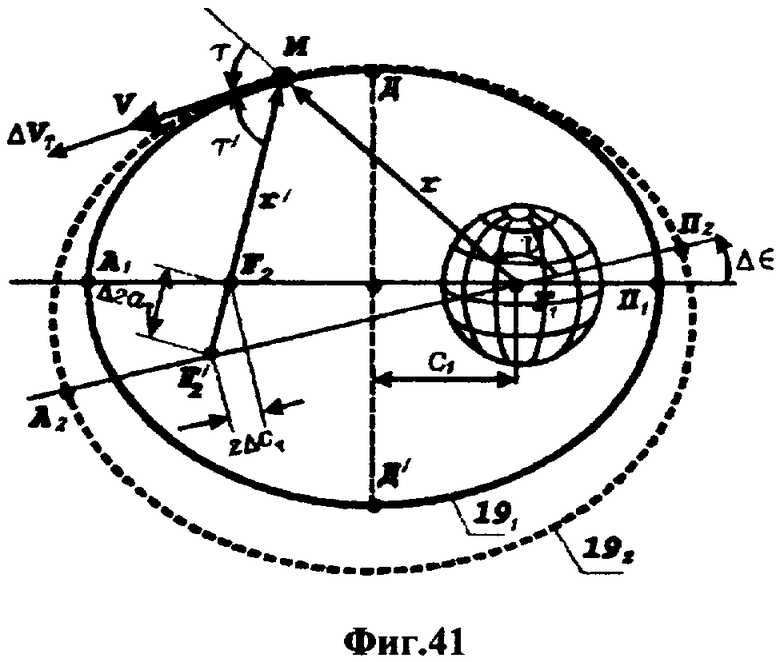
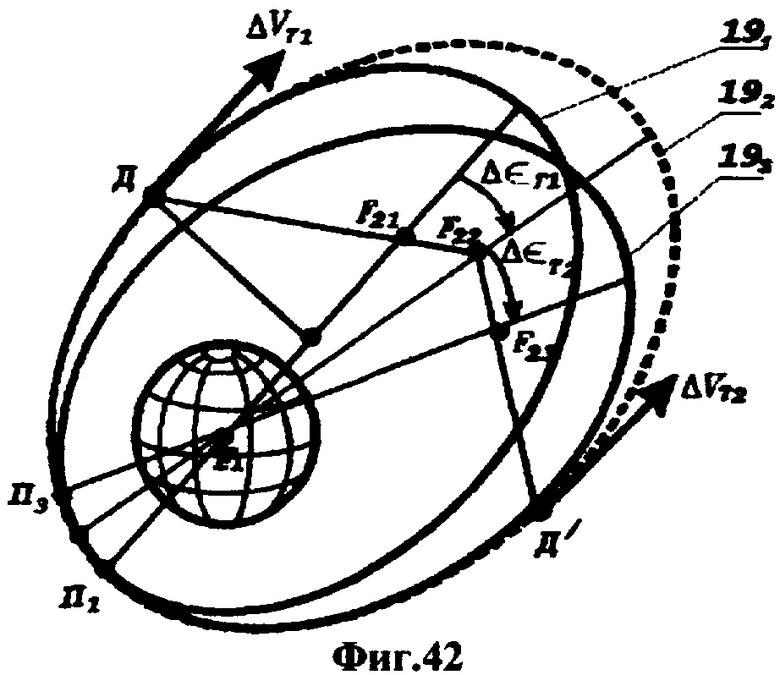
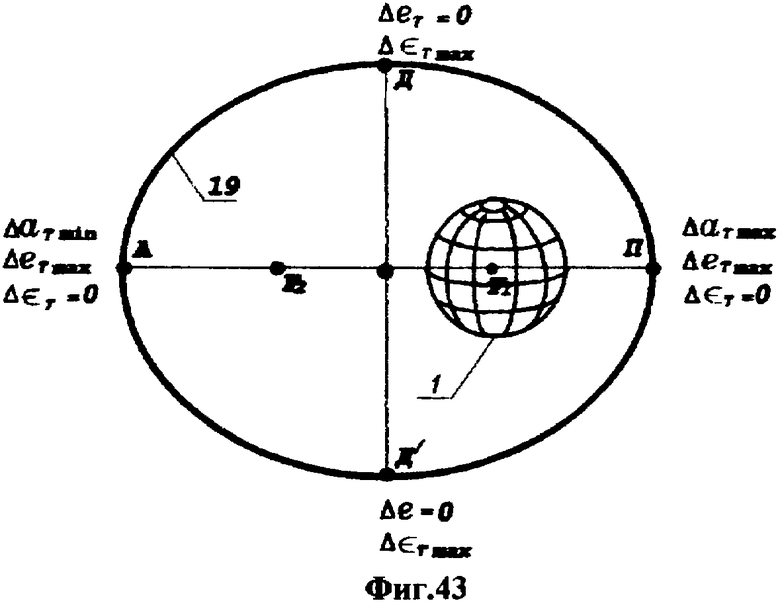
Изобретение относится к астронавигации, управлению угловым и орбитальным положением космического аппарата (КА). Предлагаемая система содержит управляющий компьютер, звездный датчик, датчик Земли, запоминающее и временное устройства, процессоры управления положением, обработки угловых и орбитальных данных, инерционные маховики и двигательную установку коррекции орбиты КА. В качестве астроориентиров используются опорная и навигационная звезды из зоны полюса мира. С помощью бортовых средств направление с КА на опорную звезду и направление центральной оси датчика Земли на центр Земли совмещаются с плоскостью, образованной центральными осями датчиков. Смещение направления на опорную звезду относительно центральной оси датчика Земли трактуется как широтное изменение орбитального положения КА. Отсчитываемый от базы датчика поворот навигационной звезды вокруг опорной звезды принимается за инерциально-долготное изменение. Точкой отсчета долготы служит точка весеннего равноденствия, с часовым углом которой синхронизировано бортовое время. Это время обнуляется по завершении полного поворота Земли. Стохастические измерения посредством статистической обработки сглаживаются и преобразовываются в географические широтные и долготные параметры. Сглаженные инерциальные параметры сравниваются с представленными в запоминающем устройстве параметрами заданного витка орбиты КА. Выявленные отклонения орбиты устраняются посредством двигательной установки коррекции. Технический результат изобретения состоит в повышении точности автономного определения параметров углового и местоположения КА при выявлении эволюционных изменений орбитальных параметров КА относительно заданной орбиты и их автоматическом устранении. 44 ил.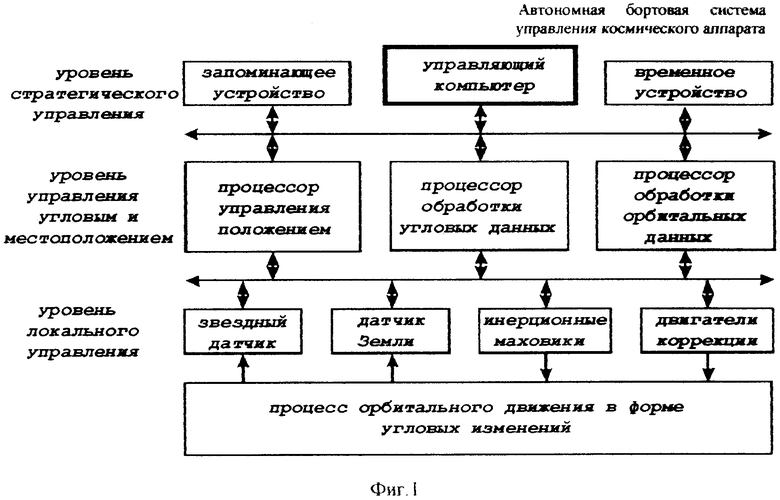
Автономная бортовая система управления космического аппарата (КА), содержащая соединенные линиями связи датчик Земли, по меньшей мере один звездный датчик, временное устройство, устройство запоминания, исполнительные органы и процессор управления положением, определяющий угловые рассогласования между осями КА и осями внешней системы координат и формирующий управляющие сигналы на указанные исполнительные органы для обеспечения заданного относительного положения этих систем координат, отличающаяся тем, что указанные процессор и исполнительные органы в виде инерциальных маховиков обеспечивают при орбитальном движении КА совмещение направления на опорную звезду, выбранную из зоны полюса мира, с визирной плоскостью, содержащей центральную ось звездного датчика, а центральной оси датчика Земли - с направлением на центр Земли, причем в плоскости чувствительности, заданной данными осями, определяемое указанным процессором смещение опорной звезды характеризует изменение широтного угла орбитального положения КА, а поворот в звездном датчике навигационной звезды вокруг опорной звезды - инерциально-долготное изменение орбитального положения КА, причем инерциальная долгота отсчитывается от бортовой нулевой точки отсчета, которая координируется углом между плоскостью, заданной направлениями с КА на обе указанные звезды, и плоскостью чувствительности на момент обнуления измеряемого на борту КА прямого восхождения опорной звезды, зависимый от инерциальной долготы угол между направлением с КА на опорную звезду и осью Земли записывается в запоминающем устройстве, а бортовое время КА синхронизировано с часовым утлом точки весеннего равноденствия и обнуляется во временном устройстве по истечении времени полного поворота Земли, при этом в систему введен процессор обработки угловых данных с программой статистической обработки стохастических инерциально-долготных и инерциально-широтных измерений, который выполнен с возможностью определения трендовых компонентов на каждый такт измерений, трансляции их для записи в запоминающее устройство, прогноза угловых данных на несколько тактовых шагов вперед для реализации последующей уточненной угловой ориентации КА и обеспечения, при учете скорости вращения Земли и текущего времени, преобразования уточненной инерциальной долготы в географическую долготу и преобразования уточненного широтного угла в географическую широту с учетом угла между направлением с КА на опорную звезду и осью Земли, при этом в систему также введен процессор обработки орбитальных данных, определяющий период, большую полуось, эксцентриситет, аргумент перигея, наклонение и прямое восхождение восходящего узла реального орбитального витка с учетом результатов статистического сглаживания, записанных в запоминающем устройстве, и выявляющий посредством сравнения указанных параметров с параметрами, записанными в запоминающем устройстве, отклонения реальных параметров орбиты от заданных и по выявленным отклонениям определяющий вид, точку приложения, значение импульса и последовательность реализации корректирующих воздействий посредством двигательной установки КА, при этом в систему также введен управляющий компьютер.
| АВТОНОМНАЯ БОРТОВАЯ СИСТЕМА УПРАВЛЕНИЯ КОСМИЧЕСКОГО АППАРАТА "ГАСАД" | 1993 |
|
RU2033949C1 |
| СПОСОБ СМАЗЫВАНИЯ ЗУБЧАТОЙ ПЕРЕДАЧИ | 2016 |
|
RU2637565C1 |
| DE 3417661 A1, 15.11.1984 | |||
| US 4294420 А, 13.11.1981. | |||
