Изобретение относится к радиосвязи и может быть использовано для выделения сигналов при наличии узкополосных помех. Кроме того, возможно его применение в измерительной технике, когда имеет место преобразование неэлектрических величин в электрические с последующим их измерением на фоне помех. Все способы компенсации помех используют информацию о помехе.
Известен метод компенсации помех (Ю.Д.Иванов, Н.А.Минченко. Увеличение коэффициента подавления помехи компенсатором без уменьшения быстродействия. Радиотехнические системы и устройства. Сб. научных трудов учебных институтов связи. - Л.: изд. ЛЭИС, 1985, с.16-18.), в котором помеха принимается отдельным компенсационным приемным устройством и используется в компенсаторе для выделения сигнала в нулевых точках несущего колебания помехи. Недостатком этого способа является его неосуществимость при приеме только аддитивной смеси сигнала.
Известен способ компенсации внутриканальных аддитивных радиопомех в приемниках амплитудно-модулированных, частотно фазоманипулированных радиосигналов и устройство для его осуществления (№ публикации 96101435 от 1998.02.10, МПК 6 Н 04 В 1/10), в котором производят выделение компенсирующего сигнала помехи из принимаемой смеси полезного сигнала и сигнала помехи путем формирования отсчетов сигнала помехи в моменты нулевых значений полезного сигнала в принимаемой аддитивной смеси. Недостатком этого способа является необходимость синхронизации, т.е. знания реальной фазы сигнала. Схемы синхронизации усложняют достижение цели и неработоспособны в условиях дрейфа фазы сигнала.
В качестве прототипа выбран способ компенсации помех (Семенов Б.А. "Алгоритм компенсации помех, отличающихся от полезного сигнала симметрией спектров", в сборнике трудов VI Международной конференции "Радиолокация, навигация, связь". Воронеж, 25-27 апреля 2000, т.2. - С.996-1002), в котором проводят дискретизацию смеси сигнала и помехи в нулевых и экстремальных точках несущего колебания сигнала и вычитают модули суммарных спектров дискретизированных сигнала и помехи, соответственно построенных по временным отсчетам в точках экстремумов сигнала и по временным отсчетам в нулевых точках сигнала:
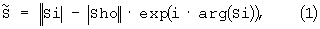

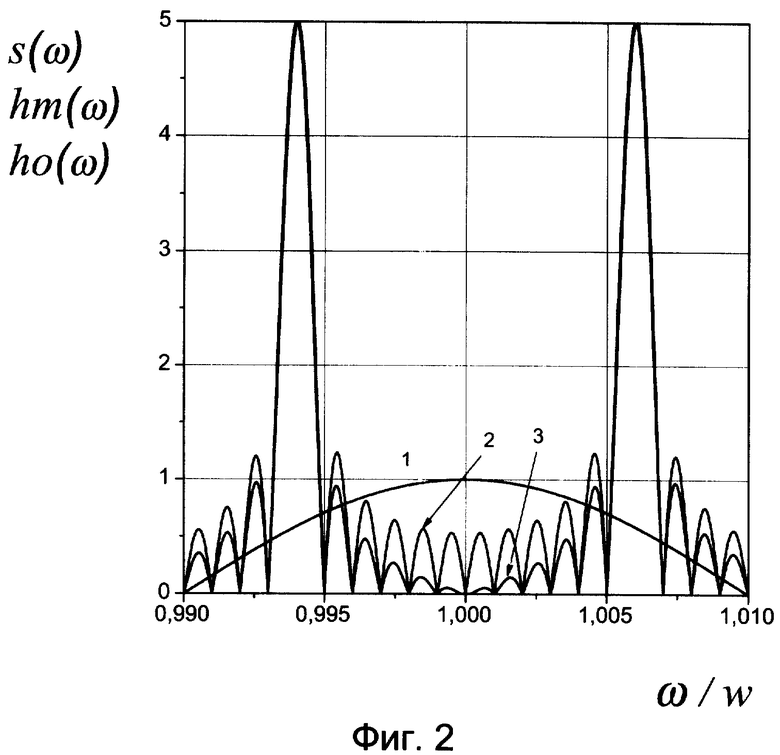
где 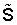 - восстановленный комплексный спектр копии сигнала, Si - комплексный спектр суммы сигнала и помехи, построенный по временным отсчетам в точках экстремума сигнала, Sho - комплексный спектр помехи, построенный по временным отсчетам в нулевых точках сигнала. Недостаток прототипа - необходимость синхронизации, т.е. знания моментов нулевых значений несущей сигнала. Схемы синхронизации усложняют практическую реализацию способа и делают его практически неосуществимым в условиях нестационарного по фазе канала. Второй недостаток - фиксированный интервал дискретизации, равный половине периода несущего колебания сигнала, что приводит к увеличению ошибки восстановления спектра при расширении спектра сигнала. Сущность (1) заключается в следующем. Предположим, что правильные спектры сигнала и помехи имеют вид, представленный на фиг.1, где кривая 1 - модуль спектра сигнала s(ω), кривая 2 - модуль спектра помехи h(ω). После дискретизации сигнала и помехи, заключающейся во взятии отсчетов через полпериода сигнала в ненулевых и нулевых точках несущей сигнала, модули спектров помехи содержат ложные спектральные пики на зеркальной частоте 2·w-wh (фиг.2), где w и wh круговые частоты сигнала и помехи. Причем hm(ω) (кривая 2), ho(ω) (кривая 3) могут и не совпадать, что и вызывает ошибку компенсации. Спектр же дискретизированного сигнала (кривая 1) накладывается на исходный спектр. Здесь следует обратить внимание на еще один недостаток прототипа - необходимость использования преобразования Фурье (ПФ) в комплексной области. Обычное ПФ дает только левую половину спектров, изображенных на фиг.2, и вовсе не применимо, если помеха окажется правее сигнала по частоте. Дискретизация входного процесса в нулевых точках несущей сигнала оставляет только спектр помехи. Поэтому при вычитании |Si|-|Sho| должен получиться приблизительно модуль спектра сигнала sm, если hm(ω)=ho(ω). Для восстановления сигнала необходимо иметь комплексный спектр. Поскольку в нашем распоряжении имеется лишь спектральная функция суммарного процесса, то полученный модуль спектра сигнала необходимо умножить на фазовый множитель, содержащий аргумент спектра входного процесса arg(Si).
- восстановленный комплексный спектр копии сигнала, Si - комплексный спектр суммы сигнала и помехи, построенный по временным отсчетам в точках экстремума сигнала, Sho - комплексный спектр помехи, построенный по временным отсчетам в нулевых точках сигнала. Недостаток прототипа - необходимость синхронизации, т.е. знания моментов нулевых значений несущей сигнала. Схемы синхронизации усложняют практическую реализацию способа и делают его практически неосуществимым в условиях нестационарного по фазе канала. Второй недостаток - фиксированный интервал дискретизации, равный половине периода несущего колебания сигнала, что приводит к увеличению ошибки восстановления спектра при расширении спектра сигнала. Сущность (1) заключается в следующем. Предположим, что правильные спектры сигнала и помехи имеют вид, представленный на фиг.1, где кривая 1 - модуль спектра сигнала s(ω), кривая 2 - модуль спектра помехи h(ω). После дискретизации сигнала и помехи, заключающейся во взятии отсчетов через полпериода сигнала в ненулевых и нулевых точках несущей сигнала, модули спектров помехи содержат ложные спектральные пики на зеркальной частоте 2·w-wh (фиг.2), где w и wh круговые частоты сигнала и помехи. Причем hm(ω) (кривая 2), ho(ω) (кривая 3) могут и не совпадать, что и вызывает ошибку компенсации. Спектр же дискретизированного сигнала (кривая 1) накладывается на исходный спектр. Здесь следует обратить внимание на еще один недостаток прототипа - необходимость использования преобразования Фурье (ПФ) в комплексной области. Обычное ПФ дает только левую половину спектров, изображенных на фиг.2, и вовсе не применимо, если помеха окажется правее сигнала по частоте. Дискретизация входного процесса в нулевых точках несущей сигнала оставляет только спектр помехи. Поэтому при вычитании |Si|-|Sho| должен получиться приблизительно модуль спектра сигнала sm, если hm(ω)=ho(ω). Для восстановления сигнала необходимо иметь комплексный спектр. Поскольку в нашем распоряжении имеется лишь спектральная функция суммарного процесса, то полученный модуль спектра сигнала необходимо умножить на фазовый множитель, содержащий аргумент спектра входного процесса arg(Si).
Итак, в прототипе два основных недостатка: неосуществимость в условиях нестационарного по фазе канала; снижение эффективности при расширении спектра сигнала.
Целью предлагаемого способа является обеспечение возможности компенсации помех в условиях нестационарного по фазе канала и расширения полосы частот сигнала за счет изменения интервала дискретизации.
Как было показано, способ компенсации помех (1) основан на большом сходстве спектров отсчетов помехи, взятых в нулевых и ненулевых точках несущей сигнала. Тот факт, что эти спектры имеют зеркальную симметрию - просто свойство преобразования Фурье процесса, дискретизированного с невыполнением теоремы отсчетов. Тем не менее, он наводит на мысль как в отсутствии информации о положении нулевых точек сигнала, сделать сигнал, равным нулю в компенсационном канале. Для этого сформируем зеркальный спектр. Это можно сделать разными способами. Можно, например, использовать свойство эрмитовости спектров и сместить спектр из отрицательной области частот, однако это возможно лишь при интервале дискретизации, равной четверти периода несущей сигнала. Более общим является следующий метод. Пусть имеется спектр Si. Для формирования его зеркального спектра Sz, реальную часть Re(Sz) на частоте ω заменим Re(Si) на частоте 2·w-ω и мнимую часть Im(Sz) на частоте ω заменим - Im(Si) на частоте 2·w-ω. После дискретизации во временной области, временным отсчетам соответствуют отсчеты по частоте. Пронумеруем отсчеты по частоте так, что текущей частоте ω соответствует номер j, а частоте сигнала w соответствует номер jo. Для сигнала его частота будет равна зеркальной частоте, поэтому модули спектра сигнала s и его зеркального спектра sz будут равны: s=sz. Поскольку мнимые части этих спектров противоположны по знаку, то при их алгебраическом суммировании получится удвоенный спектр сигнала, а при вычитании - нуль (с точностью до фазы сигнала). Так как мы имеем дело с суммой помехи и сигнала, то необходимо сформировать зеркальный по отношению к частоте сигнала w комплексный спектр временных отсчетов входной суммы Sz. Для получения суммы спектров сигнала сформируем сумму Si+Sz, где Si - комплексный спектр входной смеси. Для получения разности спектров сигнала сформируем разность Si-Sz. Спектр помехи и ее зеркальный спектр являются сопряженными на зеркальных частотах, поэтому их сумма и разность приблизительно равны по модулю, что и дает возможность скомпенсировать помеху путем формирования разностного спектра |Sr|, равного модулю разности модулей суммы и разности полученных спектров |Sr|=||Si+Sz|-|Si-Sz||. Полученный спектр содержит удвоенный модуль сигнала, поэтому его следует разделить на 2. Для получения комплексного спектра копии сигнала |Sr| нужно умножить на фазовую функцию. С целью исключения необходимости выделения отдельно мнимой и действительной частей спектра входной смеси, как это сделано в прототипе, и сохранения однотипности операций, предлагается сформировать фазовый множитель в форме отношения спектра входной смеси к ее модулю, т.е. сформировать единичный направляющий вектор спектра 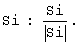 Как известно, период дискретизации Δt должен быть равен или меньше половины периода наивысшей гармоники в спектре для формирования неискаженных спектров. Возможность уменьшения Δt позволяет расширять спектр сигнала при фиксированной несущей частоте. Если Fm - наибольшая частота в спектре сигнала, то ошибка восстановления будет квадратично расти с увеличением Fm: ε≈(2,2·Fm·Δt)2 (Ж.Макс. Методы и техника обработки сигналов при физических измерениях. Том 1, стр.81. Москва, "Мир", 1983 г.). В предлагаемом способе компенсация этой ошибки происходит как бы автоматически, поскольку при увеличении Fm в соответствии с теоремой отсчетов необходимо пропорционально уменьшать Δt.
Как известно, период дискретизации Δt должен быть равен или меньше половины периода наивысшей гармоники в спектре для формирования неискаженных спектров. Возможность уменьшения Δt позволяет расширять спектр сигнала при фиксированной несущей частоте. Если Fm - наибольшая частота в спектре сигнала, то ошибка восстановления будет квадратично расти с увеличением Fm: ε≈(2,2·Fm·Δt)2 (Ж.Макс. Методы и техника обработки сигналов при физических измерениях. Том 1, стр.81. Москва, "Мир", 1983 г.). В предлагаемом способе компенсация этой ошибки происходит как бы автоматически, поскольку при увеличении Fm в соответствии с теоремой отсчетов необходимо пропорционально уменьшать Δt.
Перечень графических материалов.
Фиг.1. Спектры сигнала и помехи.
Фиг.2. Спектры дискретизированных сигнала и помехи. Интервал дискретизации равен половине периода несущей сигнала.
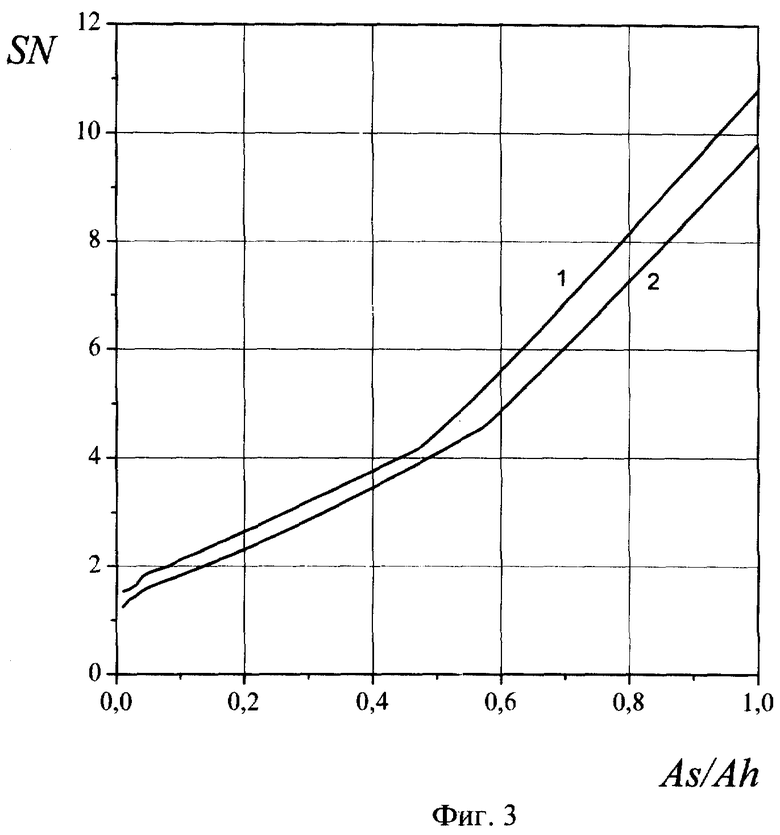
Фиг.3. Теоретическая зависимость отношения энергии восстановленного сигнала к энергии ошибки SN от отношения амплитуды сигнала As к амплитуде помехи Ah на входе.
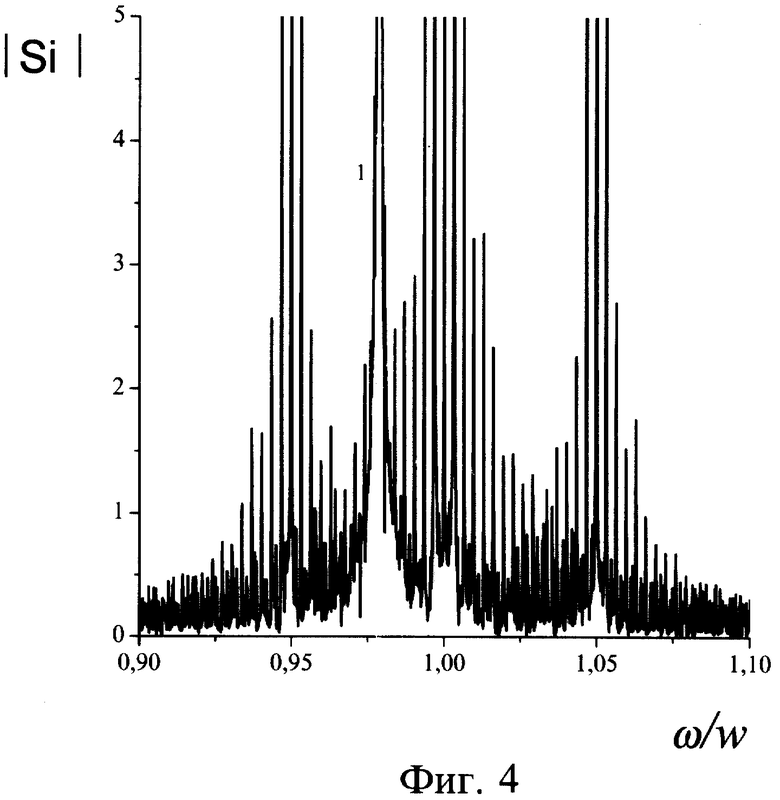
Фиг.4. Спектр суммы пачек AM сигнала с синусоидальной огибающей Ω при 100% глубине модуляции и гармонической помехи.
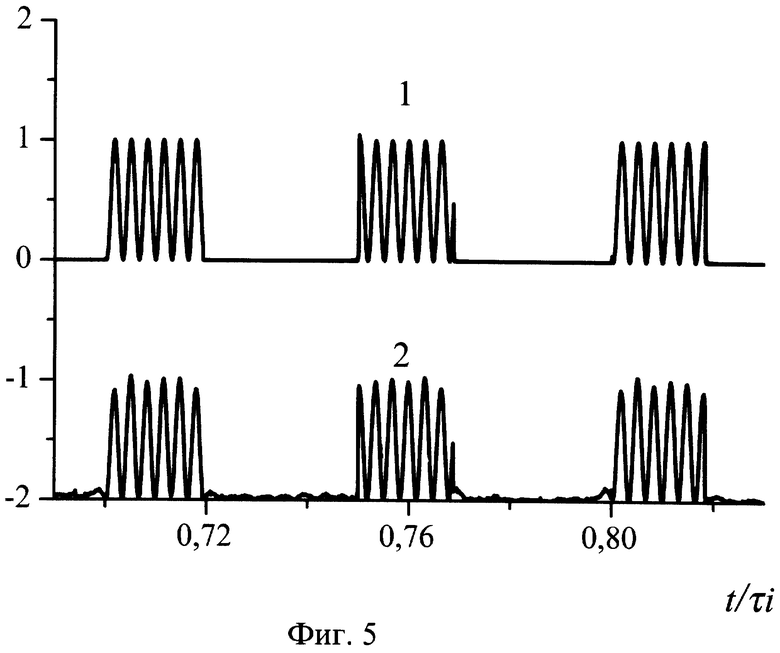
Фиг.5. Восстановленная копия AM сигнала, спектр которого изображен на фиг.4.
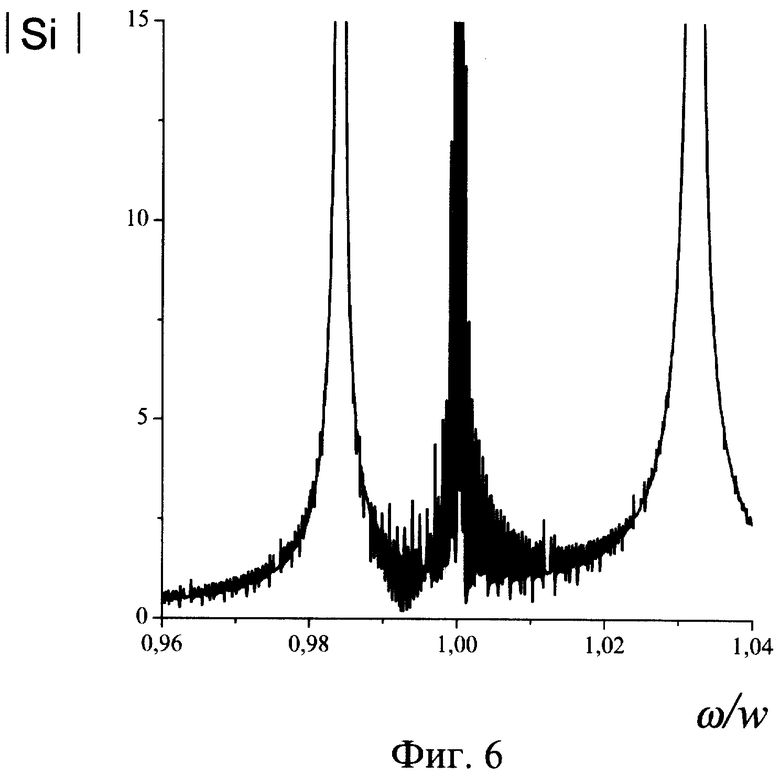
Фиг.6. Спектр входного процесса, состоящий из сигнала и двух узкополосных помех. Сигнал представляет собой последовательность пачек отрезков синусоид с постепенно уменьшающейся длительностью.
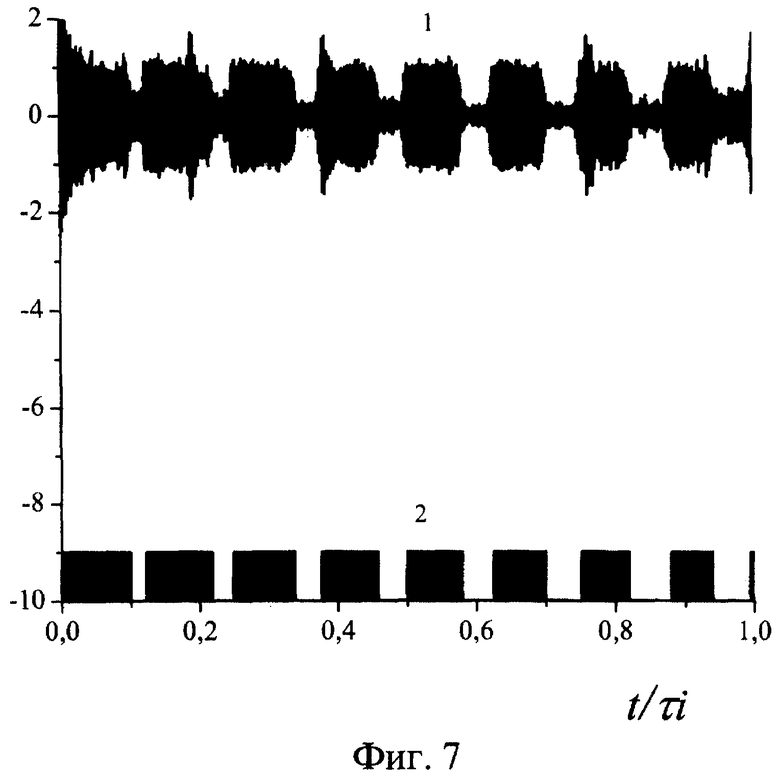
Фиг.7. Восстановленная копия сигнала, спектр которого изображен на фиг.6.
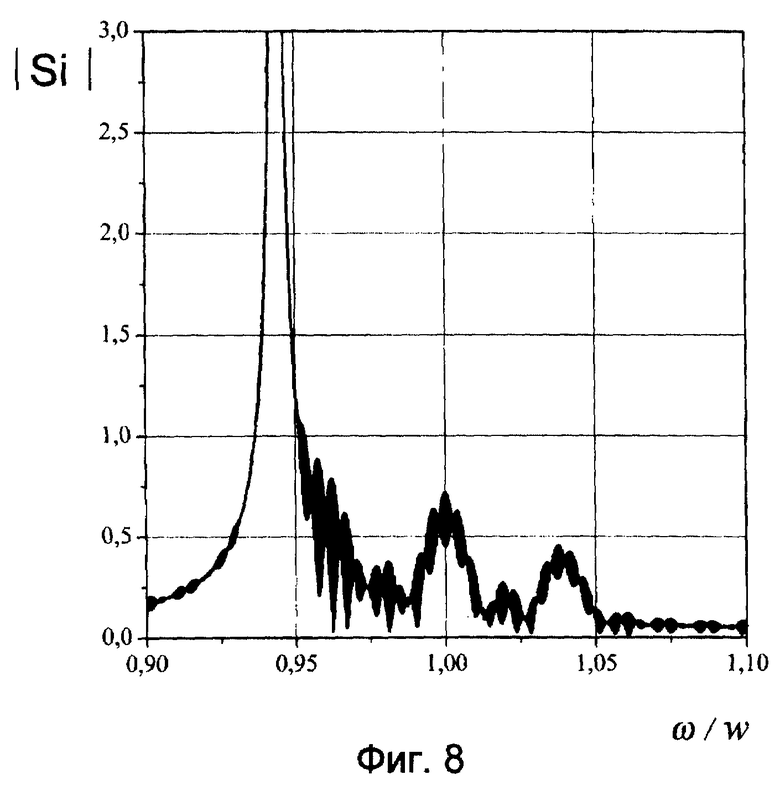
Фиг.8. Спектр входного процесса, состоящий из ФМ сигнала и узкополосной помехи.
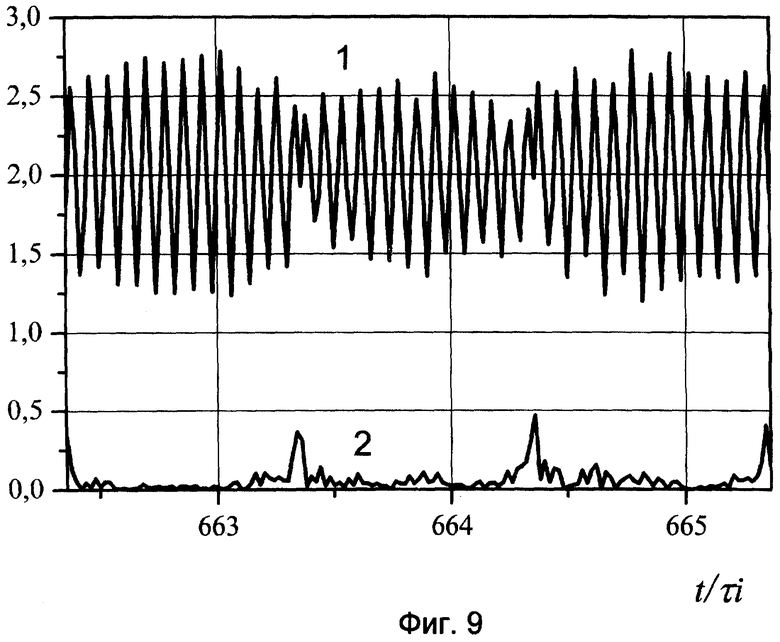
Фиг.9. Восстановленная копия ФМ сигнала, спектр которого изображен на фиг.8.
Для проверки работоспособности предлагаемого способа были проведены теоретические исследования и компьютерное моделирование с использованием сигналов амплитудной и фазовой модуляции. На фиг.3 представлена теоретическая зависимость отношения энергии восстановленного сигнала к энергии ошибки SN от отношения амплитуды сигнала As к амплитуде помехи Ah на входе. Кривая 1 - прототип, кривая 2 - предлагаемый способ. В качестве сигнала и помехи взяты отрезки синусоиды. Графики построены для Δt=π/2w, Ah=1 В, w=12500·2π Гц, wh=13000·2π Гц, N2=40, N1=384, df=9 Гц, ΔF=1254 Гц, где N2, N1 - число отсчетов сигнала и помехи соответственно, df- разрешение по частоте, ΔF - полоса сигнала.
Фиг.3 иллюстрирует потенциальные свойства предлагаемого способа и свидетельствует о практически одинаковой эффективности сравниваемых способов. Спектр суммы пачек сигнала с синусоидальной огибающей Ω при 100% глубине модуляции и гармонической помехи (кривая 1) представлены на фиг.4. Амплитуда помехи в 15 раз превышает амплитуду сигнала, w=12500·2π Гц, Ω=w/20, Δt=π/4w, Ah=1 В, wh=12233·2π; Гц, df=1,5 Гц, ΔF=2500 Гц, N1=N2= 216. Результат восстановления изображен на фиг.5, где 1 - входной сигнал, 2 - восстановленная копия сигнала, t - время, τi - длительность сигнала. На фиг.6 показан спектр входного процесса, состоящий из сигнала и двух узкополосных помех. Сигнал представляет собой последовательность пачек отрезков синусоид с постепенно уменьшающейся длительностью. Амплитуды и фазы помех одинаковы, причем Ah/As=10, Ah=1 В, w=12500·2π Гц, wh1=12300·2π Гц, wh2=12900·2π Гц, Δt=π/2w, df=0,76 Гц, ΔF=2000 Гц, N1=N2 =216.
Восстановленный сигнал представлен на фиг.7, где 1 - реальное напряжение копии сигнала, а 2 - тоже напряжение на выходе аналога пороговой схемы. На фиг.8 изображен спектр входного процесса, состоящий из сигнала и узкополосной помехи. Сигнал представляет собой несколько отрезков синусоид, отличающихся поворотом фазы на π (ФМ сигнал). Здесь длительность элементарной посылки τi=100 мкс, Ah/As=3, Ah=1 В, w= 25000·2π Гц, wh=118000·2π Гц, Δt=π/2w, df= 7,6 Гц, ΔF=20000 Гц, N1=216. Фрагмент восстановленного сигнала показан на фиг.9, где 1 - реальное напряжение копии сигнала, а 2 - напряжение на выходе дифференцирующей схемы. Хорошо видны моменты поворота фазы. Представленные данные свидетельствуют о работоспособности предлагаемого способа в условиях несинхронной дискретизации и с различными интервалами дискретизации (Δt=π/2w, π/4w). В зависимости от канала связи (измерения) способ можно реализовать как непосредственно на входе приемного устройства, так и в тракте промежуточной частоты. Все операции с электрическими напряжениями, перечисленные в формуле изобретения по отдельности хорошо известны в радиотехнике и существуют устройства для их выполнения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОМПЕНСАЦИИ УЗКОПОЛОСНЫХ ПОМЕХ | 2015 |
|
RU2584003C1 |
| СПОСОБ АДАПТИВНОГО ПОДАВЛЕНИЯ ПОМЕХ | 2011 |
|
RU2456743C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ШИРОКОПОЛОСНОГО СИГНАЛА | 2012 |
|
RU2517799C1 |
| СПОСОБ ДОПЛЕРОВСКОЙ ФИЛЬТРАЦИИ ИОНОСФЕРНЫХ СИГНАЛОВ | 2012 |
|
RU2516589C1 |
| СПОСОБ ОБРАБОТКИ ШИРОКОПОЛОСНЫХ СИГНАЛОВ С ОРТОГОНАЛЬНЫМ СДВИГОМ С КОМПЕНСАЦИЕЙ СТРУКТУРНЫХ И ИНТЕРМОДУЛЯЦИОННЫХ ПОМЕХ | 2005 |
|
RU2288537C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2483319C2 |
| Способ спектрального анализа многочастотных периодических сигналов с использованием компенсации комбинационных составляющих | 2019 |
|
RU2730043C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2476986C1 |
| СПОСОБ РАДИОПРИЕМА ВЫСОКОСКОРОСТНОЙ ИНФОРМАЦИИ КОСМИЧЕСКОЙ РАДИОЛИНИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2013 |
|
RU2530322C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВРЕМЕНИ ПРИХОДА СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2524843C2 |
Изобретение относится к радиосвязи и может быть использовано для выделения сигналов при наличии узкополосных помех. Способ компенсации узкополосных помех основан на формировании комплексного спектра Фурье, полученных в результате дискретизации входного процесса временных отсчетов, а также формировании из комплексного спектра Фурье зеркального по отношению к частоте несущего колебания полезного сигнала комплексного спектра временных отсчетов и последующем формировании суммы и разности этих спектров. После формирования модуля разностного спектра, деления его на два, умножении на сформированный фазовый множитель и обратного преобразования Фурье полученного произведения восстанавливают копию полезного сигнала. Технический результат - компенсация узкополосных помех в условиях нестационарного по фазе канала и расширение полосы частот сигнала. 1 з.п. ф-лы, 9 ил.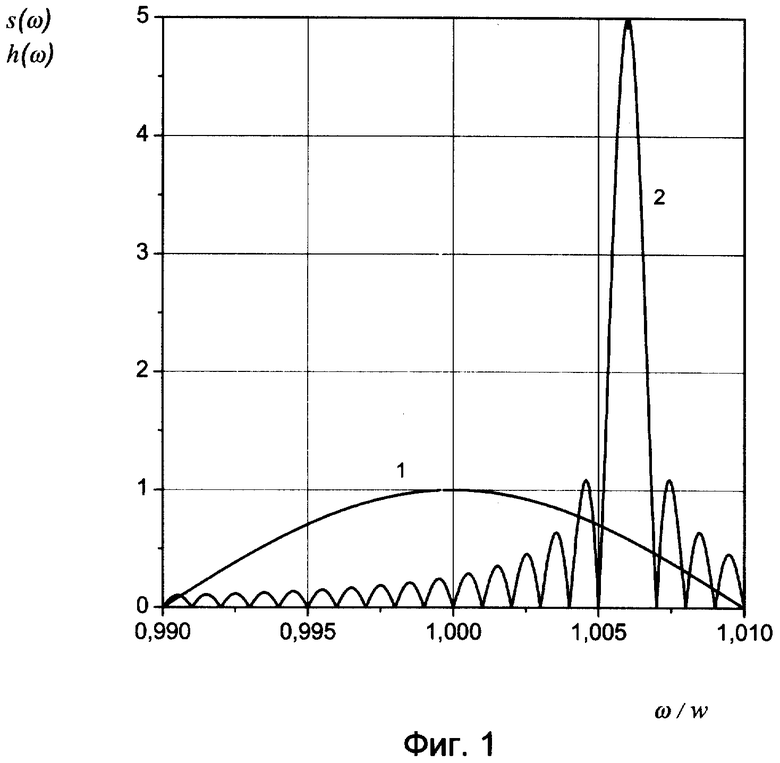
| СЕМЕНОВ Б.А | |||
| Алгоритм компенсации помех, отличающихся от полезного сигнала симметрией спектра | |||
| Сб | |||
| трудов VI Международной конференции "Радиолокация, навигация, связь" | |||
| Воронеж, 2000, т.2, с.996-1002 | |||
| СПОСОБ КОМПЕНСАЦИИ ВНУТРИКАНАЛЬНЫХ АДДИТИВНЫХ РАДИОПОМЕХ В ПРИЕМНИКАХ АМПЛИТУДНО-МОДУЛИРОВАННЫХ, ЧАСТОТНО- И ФАЗОМАНИПУЛИРОВАННЫХ РАДИОСИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1996 |
|
RU2100903C1 |
| Устройство подавления узкополосной помехи для радиоприемника двухполосного сигнала | 1986 |
|
SU1378067A1 |
| СПОСОБ ИНВЕРСНО-КВАДРАТУРНОГО ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ ЧАСТОТЫ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2001 |
|
RU2187901C1 |
| Устройство для контактной стыковой сварки оплавлением | 1988 |
|
SU1593834A1 |
Авторы
Даты
2006-01-27—Публикация
2004-02-12—Подача