Заявленное изобретение относятся к автоматическому управлению и может использоваться при регулировании не только величины выходного параметра объекта, но и при регулировании скорости изменения этого параметра, его ускорения и производных более высокого порядка.
Известны системы автоматического регулирования САР [1], у которых управляющее воздействие с выхода регулятора, поступающее на вход объекта, однозначно может сформировать желаемое значение (величину) скорости изменения регулируемого параметра. Недостаток этих систем в том, что объектами регулирования могут быть только те объекты, инерционностью (внутренним запаздыванием) которых можно пренебречь. Примером таких CAP могут быть системы, включающие пропорциональные или идеально интегрирующие объекты регулирования (механический редуктор, безынерционный усилитель, делитель напряжения, датчики сигналов и т.д., а также гироскоп, интегрирующий привод, гидравлический демпфер и т.д.).
Известны CAP [2], включающие объекты с емкостной структурой, инерционностью которых пренебречь нельзя. Эти CAP обеспечивают с определенным запаздыванием достаточную точность регулирования желаемого значения выходного параметра объекта. При этом качество (точность) регулирования достигается своевременной идентификацией параметров объекта (его внутреннего запаздывания Т1,... и коэффициента усиления К), а также соответствующей подстройкой параметров регулятора. Недостаток этих устройств в том, что они не позволяют сформировать желаемую точность значений совокупности самой величины и ее динамической характеристики регулируемого параметра в задаваемый момент времени (т.е. позволяя добиться желаемого значения величины, они не позволяют получить соответствующих производных по времени: скорости изменения, ускорения и производных более высокого порядка). Быстродействия компенсации внутренней инерционности объекта (в этих CAP) возможно при повышении коэффициента усиления регулятора. Используемое в регуляторе интегрирующее звено (ПИ-, ПИД-регуляторы) [2] сглаживает создаваемое перерегулирование при компенсации статической ошибки. Но при этом создается внутренняя инерционность в самом регуляторе (ПИ-, ПИД-регуляторы), снижается быстродействие регулятора, недостатком является также то, что дополнительная инерционность не позволяет осуществить задачу регулирования скоростными данными выходного регулируемого параметра.
Задача заявляемого изобретения заключается в том, чтобы обеспечить не только заданную величину выходного параметра объекта любой структуры (и с любой инерционностью), но и желаемую динамическую характеристику (скорость, ускорение и производные более высоких порядков) за минимальный (физически реализуемый) интервал времени или в желаемый момент времени.
Сущность заявленного изобретения в том, что в систему автоматического регулирования, включающую последовательно соединенные задатчик, блок контроля, объект, идентификатор и формирователь текущего воздействия, выходом подсоединенный ко второму входу блока контроля, на третий вход которого подсоединены выходы идентификатора, а на четвертый - выход объекта, выходы задатчика и блока контроля также подсоединены на входы идентификатора, при этом идентификатор включает в себя блок управления, определители объекта и регулятора, вычислитель корней, включающий блок памяти и стандартный вычислитель; входы блока управления подсоединены на входы идентификатора, а выходы вычислителей корней подсоединены на входы идентификатора и входы определителей объекта и регулятора, выходы которых подсоединены на выходы идентификатора, выход определителя объекта также подсоединен на вход определителя регулятора; дополнительно введены формирователь показательной функции, на третий вход которого подсоединены выходы идентификатора; выход формирователя показательной функции подсоединен на вход формирователя текущего воздействия; формирователь показательной функции включает в себя последовательно соединенные блок управления, блок заданного состояния, блок текущего состояния и блок коррекции коэффициентов; третьи входы формирователя показательной функции подсоединены к входу блока управления, а через первый и второй входы формирователя показательной функции подсоединены выходы соответственно задатчика и объекта на вторые входы блока заданного состояния и блока текущего состояния соответственно, блок управления также подсоединен ко второму входу блока коррекции коэффициентов и к третьему входу блока текущего состояния, на второй вход которого подсоединен выход блока коррекции коэффициентов, а выход блока текущего состояния подсоединен на выход формирователя показательной функции; в идентификатор введен формирователь степенной функции, включающий последовательно соединенные дифференциатор, формирователь, системы, вычислитель неизвестных, на второй вход которого подсоединен выход дифференциатора, а выход которого подсоединен на выход формирователя степенной функции; в вычислитель корней дополнительно введены последовательно соединенные преобразователь, дифференциатор, определитель приближения, вход вычислителя корней подсоединен на вход преобразователя, выход дифференциатора подсоединен на вход стандартного вычислителя, выход которого подсоединен на первый вход блока памяти, на второй вход которого подсоединен выход определителя приближения, первый выход блока памяти подсоединен на второй вход определителя приближения, а второй выход блока памяти подсоединен на выход вычислителя корней.
Введенные элементы в совокупности позволяют осуществить поставленную задачу благодаря выполнению ими ряда функций.
Функция 1. Ускоренной идентификации параметров объекта и регулятора (постоянных времени, коэффициента усиления и корней характеристического уравнения), а также текущего значения переменной времени t для заданной характеристики выходного параметра yз, yз'... и текущей yт, yт', yт''....
1.1 Введение формирователя степенной функции выходного параметра от времени позволяет найти зависимость между производными выходной функции и внутренним запаздыванием Т1, Т2... в текущий момент времени. Вводится новая переменная ″а″ (ф.1), применение которой возможно при t≠0

где а(t)= получена из равенства 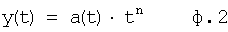
y, y', y''... - выходной параметр и его производные
t - переменная времени
n - наибольший порядок производных от переменной, входящих в диф. уравнение ф.3
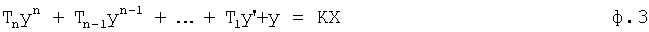
Новую переменную ф.1 подставляют в производные выходного параметра ф.4:
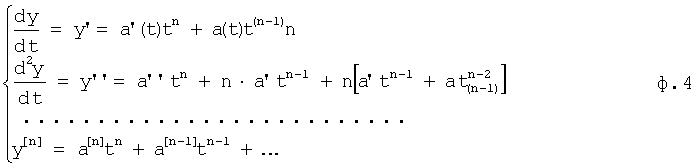
Формулы 2 и 4 подставляются в дифуравнение исследуемой CAP (или объекта) ф.3.
Пример: если максимальная производная дифуравнения имеет второй порядок, т.е. n=2, то после подстановки дифуравнение имеет вид
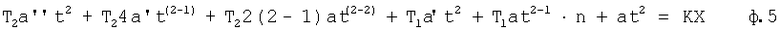
приравниваются подобные слагаемые
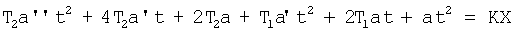
Приравниваются коэффициенты при переменных с одинаковыми степенями. В результате получается система уравнений ф.6 и ф.7 при n=2, x'=0


где Т1, Т2... - постоянные времени внутреннего запаздывания
К - коэффициент усиления
а) Определение постоянных времени внутреннего запаздывания Т1... осуществляется в следующей последовательности:
- по характеристики выходного параметра y, y',... (заданной или текущей) определяется характеристика вновь введенной переменной а(ti), a'(ti),... по формулам 1 и 4
- полученные значения характеристики новой переменной а(ti) подставляются в формулы 6 и находятся постоянные внутреннего запаздывания T1, Т2,...
Если система (объект) находится в вынужденном состоянии и на вход поступает сигнал отличный от нуля, то новую переменную а(t) подставляют в формулу 7 и находят коэффициент усиления К и другие соответствующие характеристики, зависящие от входного сигнала
б) Определение текущего иди заданного момента времени осуществляется в следующей последовательности:
- текущая характеристика а'(t), a''(t)... новой переменной a(t) определяется из системы уравнений ф.1 и 4 по известным y, y',... или из ф.6 по известным Т1, Т2... при этом производные введенной величины а(t) зависят не только от постоянных внутреннего запаздывания, но и от значения самой величины а(t):
- если входной сигнал системы (или объекта) Х(t) отличен от нуля, и характер, его изменения зарание известен, то новая переменная а(t) находится по ф.7, найденное значение а(t) подставляется в ф.1 и 4; нахождение корней ф.1 и 4 позволяет найти значение искомого момента времени (tз или tт). Если система находится в свободном состоянии, то новая переменная а(t) может определятся из ф.1.
При выполнении математических действий (ф.3 и 4) в пунктах а) и б) возникает необходимость нахождения корней степенного многочлена (для нахождения корней характеристического уравнения передаточной функции, для нахождения корней и математических выражениях в текущих значениях производных высоких порядков). Введенный в вычислитель корней преобразователь позволяет сформировать систему двух степенных уравнений: одно уравнение определяет действительную часть исследуемого многочлена, а другое уравнение определяет мнимую часть исследуемого многочлена. В эти два уравнения входят два неизвестных: одно из которых определяет действительную часть корней исследуемого многочлена, а другое неизвестное определяет мнимую часть, но при этом выражается через действительное число (для удобства вычислений). При этом действительные корни этих двух степенных уравнений однозначно определяют мнимую и действительные части комплексных корней исследуемого степенного многочлена. Совместное решение полученной системы двух степенных уравнений (с двумя неизвестными) становится возможным благодаря понижению степени дифференцированием (дифференциатором), нахождением промежуточных корней (поэтапным определением приближения) и последующему поэтапному повышению степени исследуемого многочлена до заданного значения (благодаря блоку памяти). Преимущество этого вычислителя заключается в том, что после "разделения" поиск мнимой и действительной части комплексного корня упрощается до области действительных значений, т.е. мнимая рассматривается как действительная, и только после нахождения действительного выражения мнимой части, это значение переводится в область комплексных значений.
Функция 2. Эффективная адаптация динамической характеристика входного регулирующего воздействия на объект по динамической характеристики объекта.
Введенный формирователь показательной функции определяет показательное решение дифуравнения системы (объекта и регулятора), которое могло бы обеспечить, желаемую совокупность характеристик выходного параметра в заданном и текущем состоянии, т.е. в заданном и текущем моменте времени.
Сущность и последовательность операций а) и б), выполняемых для каждого этапа, обеспечивающего рассматриваемую функцию:
1-ый этап - определение необходимого показательного решения (т.е. значение коэффициентов, входящих в показательное решение), обеспечивающего заданную характеристику выходного параметра yз, yз',..., с учетом известных корней передаточной функции объекта и регулятора. Блок заданного состояния включает в себя вычислитель слагаемых и вычислитель коэффициентов; а) вычисление слагаемых А1, А2,..., входящих в показательное решение системы (или объекта) осуществляется из формулы 8 по ф.9. По найденным и вычисленным ранее корням (объекта и необходимого регулятора) составляется система уравнений ф.8,
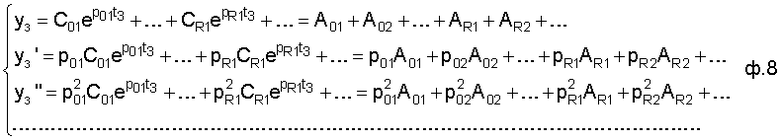
где yз, yз', yз'', ... - характеристика (заданная) регулируемого параметра
р01, р02,... рR1, рR2,... - найденные идентификатором корни передаточной функции объекта р и вычисленные необходимые корни регулятора р,
с01, с02,... сR1, сR2,... - постоянные интегрирования (свободные искомые с0 и вынужденные сR)
t - переменная времени
A01, A02,... AR1, AR2,... - искомые слагаемые Aji=CjiePjit
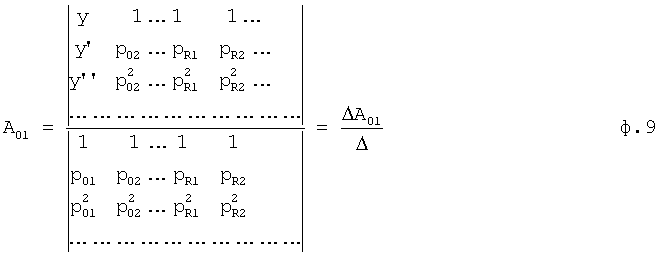
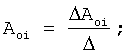
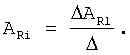
б) вычисление постоянных интегрирования (вычислителем коэффициентов интегрирования) Сji по найденным слагаемым Аji... и по найденному ″заданному″ моменту tз (при которых выполняется заданная характеристика выходного параметра) из формулы 10
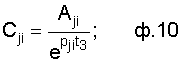
где j - составляющая выходного параметра (свободная ″О″, вынужденная ″R″)
i=1, 2...
2-ой этап - нахождение выходного показательного решения для системы, существующей в текущий момент времени, (ее идентификация) осуществляется блоком текущего состояния, который включает идентификатор свободного состояния (выполняющий группу операций "А") и формирователь нового текущего состояния (выполняющий группу операций "Б").
"А" группа операций позволяет определить свободное состояние объекта в текущий момент времени (находятся коэффициенты интегрирования свободного состояния Со в реальной системе регулирования, а также независимый коэффициент усиления для каждого исследуемого слагаемого свободного состояния К)
а) определение коэффициентов интегрирования Сoi свободной составляющей выходного параметра для реальной в текущий момент времени CAP, т.е. находится "относительное" свободное состояние (с учетом вынужденного, формируемого характером изменения входного регулирующего воздействия). При этом:
- по формулам 9 (аналогично нахождению показательного решения для заданных параметров yз, yз',...) определяются слагаемые А01,... АR1,... для текущей характеристики выходного параметра yт, yт',... ф.11

- по найденным слагаемым Аji..., текущему моменту tт времени и известным корням pji... вычисляются постоянные интегрирования Сji... .
б) нахождение независимого коэффициента усиления К для каждого исследуемого слагаемого Аoi свободной составляющей (А01+А02+...) позволяет найти изменение "абсолютного" (независимого от других слагаемых) 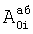 в каждый момент времени для данной реальной системы, таким образом "абсолютное" свободное состояние
в каждый момент времени для данной реальной системы, таким образом "абсолютное" свободное состояние 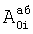 определяется по найденным слагаемым Аoi (относительным) и коэффициентам "относительного" свободного состояния Сoi с учетом дифференциальной формы уравнения всей системы CAP и текущего момента времени tт. Для этого каждое исследуемое слагаемое (свободной составляющей) Аoi переносится в правую часть дифуравнения поэтапно, а слагаемые вынужденного состояния ARi (задаваемые) и не исследуемые на данном этапе слагаемые свободного состояния
определяется по найденным слагаемым Аoi (относительным) и коэффициентам "относительного" свободного состояния Сoi с учетом дифференциальной формы уравнения всей системы CAP и текущего момента времени tт. Для этого каждое исследуемое слагаемое (свободной составляющей) Аoi переносится в правую часть дифуравнения поэтапно, а слагаемые вынужденного состояния ARi (задаваемые) и не исследуемые на данном этапе слагаемые свободного состояния 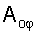 переносятся в левую. Формируется система с "новыми" внутренними постоянными запаздывания
переносятся в левую. Формируется система с "новыми" внутренними постоянными запаздывания 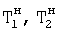 ... .
... .
Подробный ход вычислений (с соответствующими пояснениями) рассматривается ниже, на примере стандартной CAP.
Для определения ″абсолютного″ значения исследуемого слагаемого (не зависящего от значений других слагаемых), его выделяют как частное y* решение, а все остальные слагаемые относят к общему решению без правой части 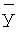 . Тогда коэффициенты внутреннего запаздывания "нового" дифуравнения
. Тогда коэффициенты внутреннего запаздывания "нового" дифуравнения 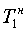 ... находят по корням нового общего решения дифуравнения без правой части. Если новое дифуравнение представить ф.12
... находят по корням нового общего решения дифуравнения без правой части. Если новое дифуравнение представить ф.12
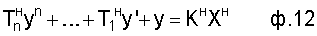
где 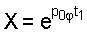
то общее решение этого дифуравнения ф.13

где 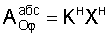 - искомое слагаемое
- искомое слагаемое
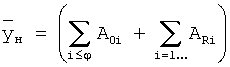 - общее решение нового дифуравнения без правой части
- общее решение нового дифуравнения без правой части
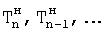 - новые коэффициенты внутреннего запаздывания находят по корням нового характеристического уравнения ф.14 после раскрытия скобок ф.15
- новые коэффициенты внутреннего запаздывания находят по корням нового характеристического уравнения ф.14 после раскрытия скобок ф.15

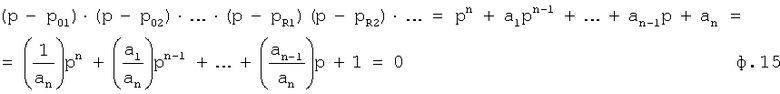
Для нахождения коэффициента усиления (т.е. коэффициента, стоящего в правой части) нового дифуравнения, т.е. "абсолютного" коэффициента Кн рассматриваемого слагаемого свободного состояния, подставляется частное решение 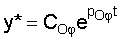 в формулу "нового" дифуравнения ф.12 [3]. Получили ф.16
в формулу "нового" дифуравнения ф.12 [3]. Получили ф.16
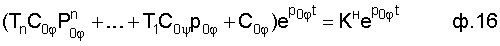
Приравнивая коэф. при 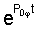 в ф.16 вычисляют Кн
в ф.16 вычисляют Кн
Поэтапно находятся абсолютные значения коэффициентов К1 н... для каждого слагаемого свободного состояния Aoi.
Нахождение "абсолютного" значения слагаемых свободного состояния выходного параметра объекта необходимо в разные моменты времени для решения ряда возникающих (на практике) задач (основных и сопутствующих):
- проверки области допустимых значений (ОДЗ) соответствующих физических и технических характеристик;
- формирование САР (новой), у которой корни вынужденного состояния отличны от существующих на данный момент времени (реальных);
- корректировки относительных коэффициентов свободной составляющей выходного параметра объекта (для CAP, у которой корни показательного решения имеют заданные значения), если эти коэффициенты отличаются от заданных;
- корректировки идентифицируемого текущего момента времени, если он больше заданного tт>tз, или если полученный момент времени создает интервал времени регулирования Δ=(tз-tт) слишком большой, не обеспечивающий достаточного быстродействия; эта задача становится возможной при помощи соответствующей коррекции коэффициентов свободного состояния объекта.
"Б" группа операций выполняется формирователем нового текущего состояния. При этом проверяется совпадение реальных параметров регулируемой величины CAP в текущий момент времени с заданными. Если в текущий момент времени параметры CAP (р01..., pR1..., C01..., CR1...) равны заданным и заданный момент времени tз больше текущего tт, то эти параметры передаются на выход формирователя текущего воздействия без изменений. Если идентифицируемые текущие параметры не совпадают с заданными, то операции группы "Б" обеспечивают необходимую корректировку.
а) если коэффициенты интегрирования 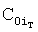 в текущий момент времени не совпадают с заданными
в текущий момент времени не совпадают с заданными 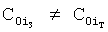 , корни характеристического уравнения CAP равны заданным, и текущий момент времени tт меньше заданного tз>tт то необходимая информация о коэффициентах интегрирования и корнях дифуравнения передается на вход блока коррекции коэффициентов, который создает дополнительное вынужденное состояние (воздействие) с корнями характеристического уравнения pдi, равными корням =poi корректируемого слагаемого свободного состояния (т.е. вводится дополнительное частное решение
, корни характеристического уравнения CAP равны заданным, и текущий момент времени tт меньше заданного tз>tт то необходимая информация о коэффициентах интегрирования и корнях дифуравнения передается на вход блока коррекции коэффициентов, который создает дополнительное вынужденное состояние (воздействие) с корнями характеристического уравнения pдi, равными корням =poi корректируемого слагаемого свободного состояния (т.е. вводится дополнительное частное решение 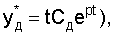 коэффициенты которых корректируются
коэффициенты которых корректируются 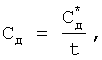 тем самым позволяя получить в сумме необходимые значения коэффициентов. В конце соответствующего интервала времени коррекции "абсолютное" значение корректируемого слагаемого системы с введенной коррекцией и заданной CAP совпадают по величине, что дает возможность перейти к заданной CAP. Результат скорректированного показательного решения (в течение корректировки и после корректировки) передается на вход формирователя текущего воздействия;
тем самым позволяя получить в сумме необходимые значения коэффициентов. В конце соответствующего интервала времени коррекции "абсолютное" значение корректируемого слагаемого системы с введенной коррекцией и заданной CAP совпадают по величине, что дает возможность перейти к заданной CAP. Результат скорректированного показательного решения (в течение корректировки и после корректировки) передается на вход формирователя текущего воздействия;
б) если корни регулятора 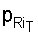 в текущий момент tт не совпадают с заданными
в текущий момент tт не совпадают с заданными 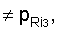 то для формирования текущего момента нового регулятора
то для формирования текущего момента нового регулятора 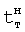 (у которого корни совпадают с заданными), находят новое текущее "относительное" свободное состояние объекта
(у которого корни совпадают с заданными), находят новое текущее "относительное" свободное состояние объекта 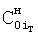 по "абсолютно" свободному
по "абсолютно" свободному 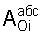 состоянию на текущий момент tт, по заданным корням регулятора рRiз и известным корням объекта рoi, а также по заданным коэффициентам интегрирования
состоянию на текущий момент tт, по заданным корням регулятора рRiз и известным корням объекта рoi, а также по заданным коэффициентам интегрирования 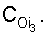 Значение текущего момента реальной (старой) CAP подставляется в ф.17 (под текущим моментом подразумевается момент перехода системы в новый режим) для вычисления абсолютного значения каждого слагаемого свободной составляющей выходного параметра
Значение текущего момента реальной (старой) CAP подставляется в ф.17 (под текущим моментом подразумевается момент перехода системы в новый режим) для вычисления абсолютного значения каждого слагаемого свободной составляющей выходного параметра
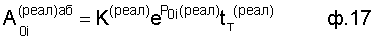
где 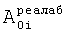 - "абсолютное" значение слагаемого свободной составляющей в реальной CAP. После чего в это слагаемое подставляются новые параметры, например новый момент времени t=0 (или какой-либо другой желаемый момент времени, позволяющий повысить быстродействие или избежать каких-либо критических состояний оговоренных ОДЗ). Подстановка нового текущего момента времени позволяет вычислить новый абсолютный коэффициент ф.18
- "абсолютное" значение слагаемого свободной составляющей в реальной CAP. После чего в это слагаемое подставляются новые параметры, например новый момент времени t=0 (или какой-либо другой желаемый момент времени, позволяющий повысить быстродействие или избежать каких-либо критических состояний оговоренных ОДЗ). Подстановка нового текущего момента времени позволяет вычислить новый абсолютный коэффициент ф.18
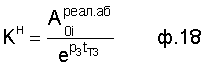
В дальнейших вычислениях для нахождения постоянных интегрирования слагаемых "относительного" свободного состояния используется ф.16, в которой постоянные COi вычисляются по известным Kн, Тn, 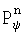 и ф.19
и ф.19
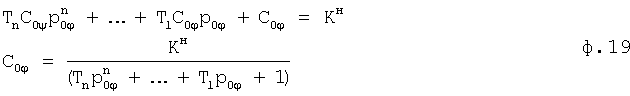
После того как все постоянные интегрирования (относительные коэффициенты) будут найдены, их значения сравниваются с заданными и при необходимости выполняется корректировка дополнительным вынужденным состоянием п. а). После чего полученные значения параметров новой скорректированной CAP передаются в формирователь текущего воздействия; в) если в силу действий возмущений (внешних или внутренних) или при повторении уже пройденного режима регулирования, идентифицированный текущий момент времени регулирования превышает заданный, то переход к новому моменту времени осуществляется аналогично пунктам а) и б). При этом посыпается сигнал в блок коррекции, который создает дополнительное вынужденное состояние, позволяющее подучить промежуточное заданное состояние, обеспечивающее необходимое конечное.
3-ий этап, для того чтобы некорректируемые постоянные интегрирования оставить без изменения, необходимо, чтобы корень вводимого дополнительного вынужденного состояния был равен корню корректируемого слагаемого, тогда дополнительное вынужденное состояние будет иметь частное решение ф.20
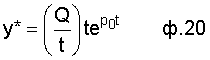
Пример объекта, описываемого дифуравнением 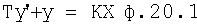
Общее решение с правой частью без коррекции
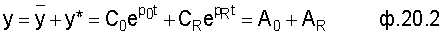
Общее решение при воздействии коррекции
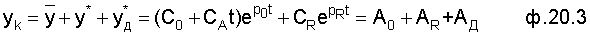
Находится абсолютное значение корректируемого слагаемого до коррекции и после:
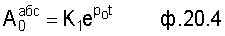
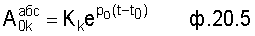
После приравнивания этих слагаемых находят математическое выражение для коэффициента усиления коэффициента Кк (т.е. для "абсолютного" значения корректируемого слагаемого) ф.20.6
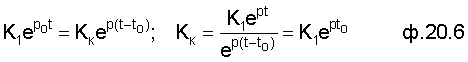
где tо - момент времени, необходимый для согласования заданного момента tтз
(используемого при описании CAP с заданными параметрами) и реальной системы у которой корректируется постоянная интегрирования в период введенного дополнительного вынужденного состояния t-tо. Если под моментом времени (t-to) задать момент времени, когда абсолютное значение корректируемого слагаемого достигнет желаемого значения и дополнительное вынужденное состояние необходимо отключить, то момент времени to будет обозначать начальный момент времени коррекции. Задав моменты времени to и (t-to) в ф.20.6 определяется Kк, которое необходимо для нахождения Cд относительной постоянной интегрирования дополнительного вынужденного состояния 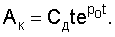
Для нахождения момента времени t (при котором необходимо начинать коррекцию) приравнивают абсолютное значение корректируемого слагаемого в действительной (реальной) САР до коррекции и абсолютное значение корректируемого слагаемого в CAP с введенной коррекцией. ф.20.7
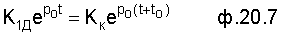
получили: 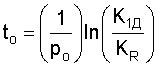
Функция 3-тщательяого контроля за ошибкой регулирования обеспечивает повышение надежности CAP. Если CAP подвержена очень частым возмущающим воздействиям, то надежность обеспечивается блоком контроля, который проверяет текущее значение ошибок Δy=(yз-yт), Δy'=(y'з-y'т) с учетом внутренних параметров объекта (Т1, Т2,... К) по ф.21
Xp≤S1+S2
где 

В тех случаях, когда результат вычислений (производимых формирователем показательной функции и другими элементами) не обеспечивает требований соответствующего контроля (т.е. он превышал необходимый ″интеграл″ компенсации), блок контроля прекращает передачу регулирующего воздействия с выхода формирователя текущего воздействия и продолжает регулирование по интегралу компенсации ф.22, величина которого вычислена самим блоком контроля

где F - обеспечивает плавность и надежность технической реализации регулирующего воздействия
В течение этого времени система, формируя показательное решение по новым вычислениям, полученным идентификатором, адаптируется к возмущениям или вызывает оператора для устранения непредвиденных ситуаций. После прекращения возмущений или после соответствующей адаптации к этим возмущения блок контроля, получив подтверждение правильности используемых параметров ф.21, переключает на свой выход сигнал с выхода формирователя текущего воздействия для динамической настройки выходного параметра объекта.
Экономический эффект достигается благодаря точности и надежности регулирования, что создает более эффективный технологический режим в технических (физических иди других) процессах. Открываются возможности по уменьшению затрат энергии, износа оборудования.
На фиг.1 изображена структурная схема заявленной системы автоматического регулирования динамической характеристика выходного параметра.
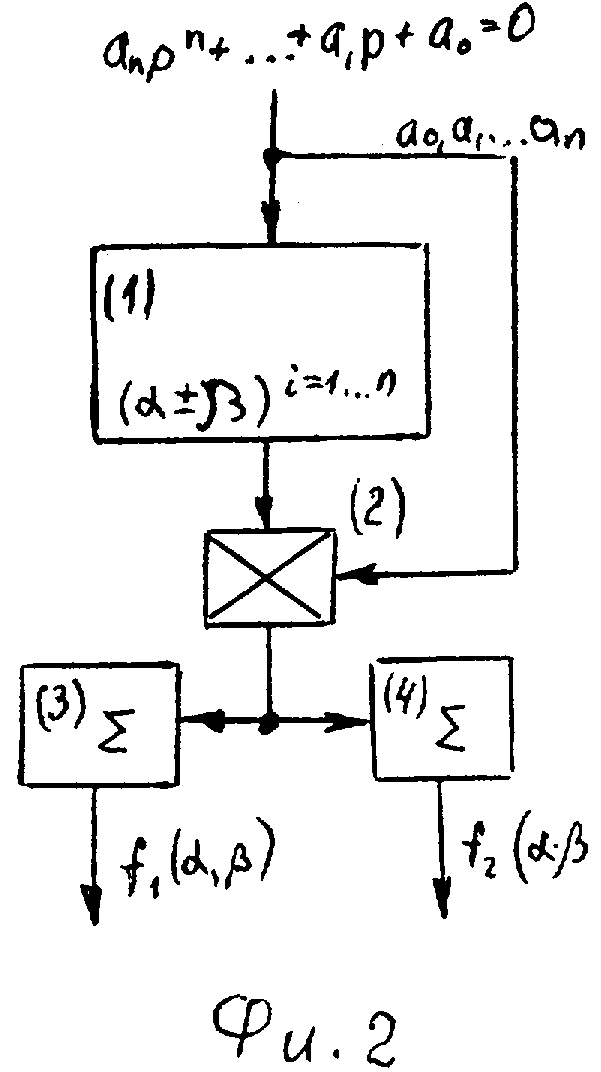
На фиг.2 изображена структурная схема преобразователя 4.3.1, входящего в вычислитель корней 4.3.
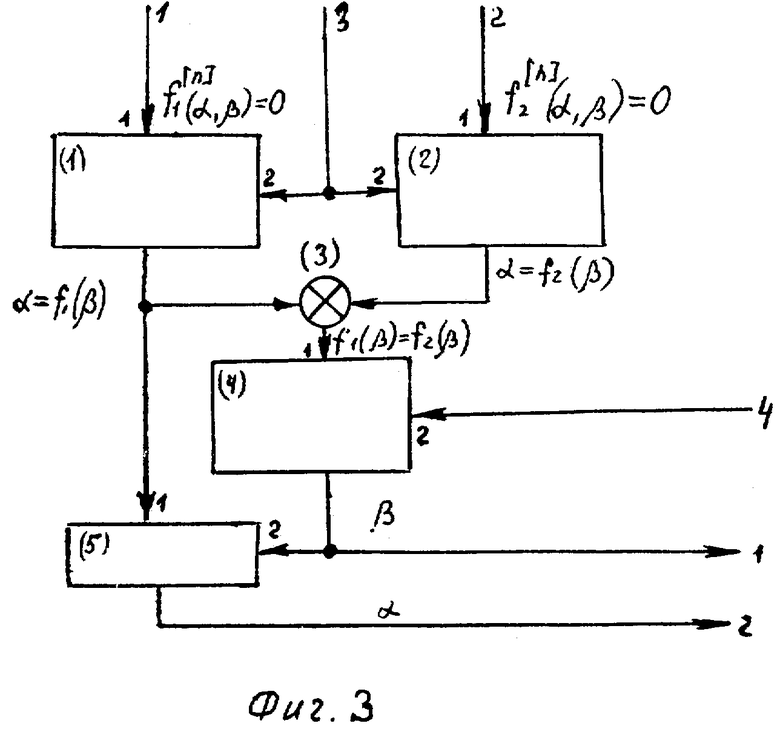
На фиг.3 изображена структурная схема определителя приближения 4.3.2, входящего в вычислитель корней 4.3.
Выход задатчика 1 подсоединен на первые входы идентификатора 4, блока контроля 2 и формирователя показательной функции 5. Выход блока контроля 2 подсоединен ко второму входу идентификатора 4 и к входу объекта 3. Выход объекта 3 подсоединен к третьему входу идентификатора 4, к четвертому входу блока контроля 2 и к второму входу формирователя показательной функции 5. Три выхода идентификатора 4 подсоединены на третьи входы формирователя показательной функции 5 и (на третий вход) блока контроля 2. Выход формирователя показательной функции 5 подсоединен на вход формирователя текущего воздействия 6, выход которого подсоединен на второй вход блока контроля 2.
Идентификатор 4 включает в себя последовательно соединенные блок управления 4.1, формирователь степенной функции 4.2, вычислитель корней 4.3, определитель объекта 4.4 и определитель регулятора 4.5. Входы идентификатора 4 подсоединены на входы блока управления 4.1; а первый выход идентификатора 4 подсоединен на выход вычислителя корней 4.3 и на вход определителя регулятора 4.5. Выход определителя регулятора 4.5 подсоединен на второй вход идентификатора 4, а выход определителя объекта 4.4 подсоединен на третий выход идентификатора 4.
Формирователь показательной функции 5 включает в себя последовательно соединенные блок управления 5.4, блок заданного состояния 5.1, блок текущего состояния 5.2 и блок коррекции 5.3, второй вход которого подсоединен на выход блока управления 5.4, а второй выход - на второй вход блока текущего состояния 5.2. Второй выход блока текущего состояния 5.2 подсоединен на выход формирователя показательной функции 5. Входы блока управления 5.4 подсоединены на третьи входы формирователя показательной функции 5.
Блок заданного состояния 5.1 включает в себя последовательно соединенные вычислитель слагаемых 5.1.1 и вычислитель коэффициентов 5.1.2.
Блок текущего состояния 5.2 включает в себя последовательно соединенные идентификатор свободного состояния 5.2.1, формирователь нового текущего состояния 5.2.2.
Формирователь степенной функции 4.2 включает в себя последовательно соединенные дифференциатор 4.2.1, формирователь системы уравнений 4.2.2, вычислитель неизвестных 4.2.3. Выход дифференциатора 4.2.1 подсоединен на второй вход вычислителя неизвестных 4.2.3. Вычислитель корней 4.3 включает в себя последовательно соединенные преобразователь 4.3.1, дифференциатор 4.3.3, стандартный вычислитель 4.3.4, блок памяти 4.3.5 и определитель приближения 4.3.2. Дифференциатор вторым выходом подсоединен на первый вход определителя приближения 4.3.2, выход которого подсоединен на второй вход блока памяти 4.3.5, второй выход которого подсоединен на выход вычислителя корней 4.3.
Преобразователь 4.3.1 фиг.2 включает в себя последовательно соединенные формирователь степеней (1), умножитель (2) и параллельно два сумматора (3) и (4), на входы которых подсоединен выход умножителя (2), а выходы которых подсоединены на два выхода преобразователя 4.3.1.
Определитель приближения 4.3.2 фиг.3 включает определители неизвестной по производной (1), (2), (4), сумматор (3), элемент подстановки (5). Первый и второй входы преобразователя 4.3.1 подсоединены к первым входам определителей неизвестных по производным (1) и (2), на вторые входы которых подсоединены третьи входы преобразователя 4.3.1. Выход определителей неизвестных (1), (2) подсоединены на входы сумматора (3). Выход сумматора (3) подсоединен на первый вход определителя неизвестной по производной (4), выход которого подсоединен на второй вход элемента подстановки (5) и первый выход определителя приближения 4.3.2. Выход определителя неизвестной по производной (1) также подключен на первый вход элемента подстановки (5), выход которого подсоединен на второй выход определителя приближения 4.3.2.
Примером технической реализации задатчика 1 может быть программируемое устройство, в память которого занесены задаваемые значения характеристики выходного параметра yзi (ti), y'зi (ti).... При задании нескольких совокупностей (определяющих значения производных для ряда значений выходного параметра) их последовательность (т.е. последовательность выполнения ряда значений выходного параметра) может задаваться параметром времени ti=1,2,3..., либо значением основной величины выходного параметра (например, ее возрастанием yз1<yз2<yз3... и т.д.)
Если регулируемый параметр задается непрерывной функцией от времени, то задатчик вычисляет значения y(tj), y'(tj)... момента времени tj, найденного из формулы 23

где tт - текущий момент времени
Δt - определяется в зависимости от параметров объекта, его внутреннего запаздывания Т1, Т2,... и внешнего τ1...τi.
Блок контроля 2 позволяет непрерывно контролировать динамическое состояние процесса регулирования, т.е. находить не только текущее значение ошибки регулирования (yз-yт), (y'з-yт)..., но и по значениям внутренних постоянных запаздывания Т1, Т2,... контролирует динамическую составляющую совокупности выходного параметра и при появлении перерегулирования (внутренней кинетической или потенциальной энергии) динамической составляющей (приводящей к перерегулированию выходного параметра) с учетом постоянных дифференцирования (в CAP, включающих дифференцирующие звенья) Т1*, Т2*,..., при не выполнении ф.24, обеспечивает своевременную корректировку регулирующего воздействия
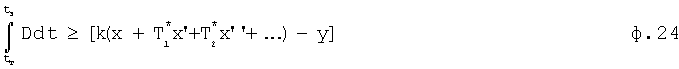
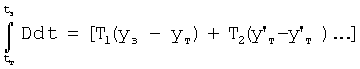 - интеграл необходимого регулирующего воздействия, (необходимого для преодоления внутреннего запаздывания объекта)
- интеграл необходимого регулирующего воздействия, (необходимого для преодоления внутреннего запаздывания объекта)
X, X'... - входное (регулирующее) воздействие и его производные (учет которых необходим в дифференцирующих звеньях)
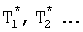 - постоянные дифференцирования или интегрирования в реально дифференцирующих, интегродифференцирующих или изодромных звеньях
- постоянные дифференцирования или интегрирования в реально дифференцирующих, интегродифференцирующих или изодромных звеньях
D=(T1y'+T2y''+...)
Для формирования адекватного к новым возмущающим воздействиям сигнала регулирующего воздействия за минимально короткое время, блок контроля 2 производит вычисление регулирующего воздействия на объект по ф.25
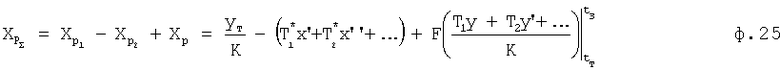
где 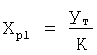 - составляющая, обеспечивающая "пассивное" поддержание уже существующего значения регулируемого параметра;
- составляющая, обеспечивающая "пассивное" поддержание уже существующего значения регулируемого параметра;
Xp2=(T1 *x'+T2 *x''+...) составляющая, учитывающая дифференцирующие и интегрирующие свойства объекта;
F - функция, задаваемая с учетом необходимого интеграла компенсации, а также с учетом технической и физической реализуемости исполнительных устройств.
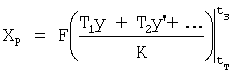 - составляющая, определяемая внутренним запаздыванием объекта и F-функцией от этого запаздывания.
- составляющая, определяемая внутренним запаздыванием объекта и F-функцией от этого запаздывания.
Блок контроля 2 обеспечивает надежность CAP, осуществляя текший контроль за сформированным регулирующим входным воздействием на объект. При этом учитывается необходимое ″пассивное″ регулирующее воздействие 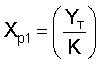 и необходимое текущее значение "активного" регулирующего воздействия
и необходимое текущее значение "активного" регулирующего воздействия 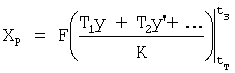 (создающее необходимое изменение выходного параметра).
(создающее необходимое изменение выходного параметра).
Если поступающее на вход блока контроля, сформированное регулирующее воздействие имеет "активную" часть меньше интеграла необходимой компенсации, то оно без изменения передается на выход блока контроля и параллельно проверяется точность вычислений внутренней динамической характеристика Т1, Т2,... и текущего значения переменной времени tт по динамической характеристики выходного параметра ф.26-30.
Подстановка найденных идентификатором величин tз, tт, Aoi, ARi, Poi, PRi в математические выражения ф.26-30 позволяет постоянно контролировать их справедливость (точность идентификации).
1) переменные времени(заданная и текущая) определяют (значение необходимого времени регулирования) интервал, величина которого определяется по ф.26

Справедливость этой формулы получена следующим образом из ф.27
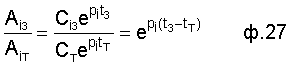
где Ai - слагаемые показательного решения дифуравнения системы 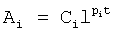 ;
;
pi - корни характеристического уравнения;
tз, tт - значения моментов времени заданного и текущего
2) постоянные интегрирования показательного решения
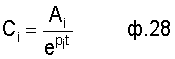
3) постоянные времени внутреннего запаздывания Тn, Тn-1,... Т1 исследуемой CAP подставляются в дифуравнение ф.29 и др.

4) для каждого из корней характеристического уравнения проверяется справедливость ф.30
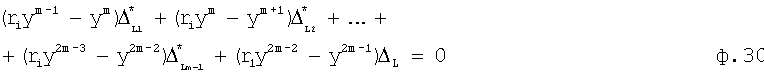
где ri - проверяемый корень;
y, y', y''... - значения выходного параметра и его производные разных порядков в исследуемый момент времени t
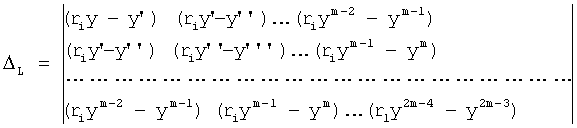
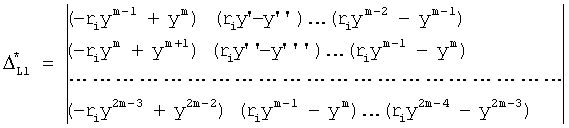
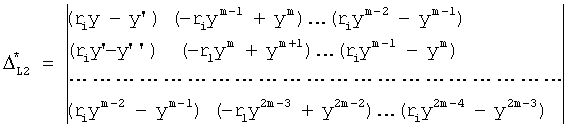
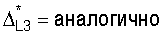 и т.д.
и т.д.
Пояснения к математическому выражению ф.30 (порядок его получения - доказательство его справедливости):
- из системы уравнений (для характеристики выходного параметра)
y=, y'=, y''=... (ф.8) можно получить математическое выражение ф.30б
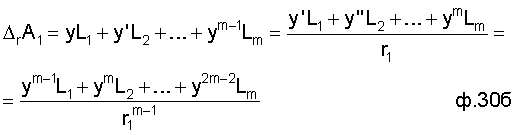
где Δr - основной определитель
L1, L2... - алгебраические дополнения к элементам определителя Δ1,2... искомого слагаемого A1,2
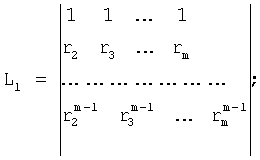
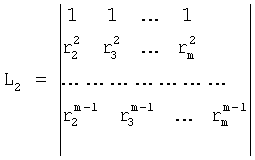 и т.д.
и т.д.
Из математических равенств ф.30б можно составить систему уравнений ф.30а, в которой одно из уравнений можно использовать для формирования формулы 30, например, последнее уравнение [...]*, а другие для формирования системы, которая бы позволяла найти определители L1, L2... Lm к формуле 30
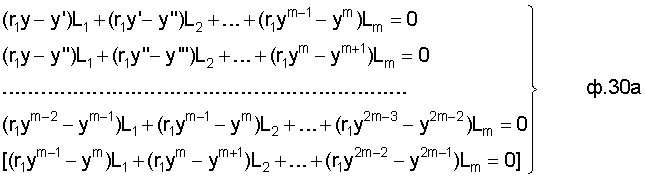
Если точная идентификация внутренних параметров CAP (Т1, Т2,... К) вследствие возмущений (непредсказуемых и стремительных) невозможна, то равенства формула 26-30 не выполняются, и после достижения текущего "активного" регулирующего воздействия необходимого (максимально допустимого) значения, регулятор блока контроля начинает формировать чисто "пассивное" регулирующее воздействие, поддерживающее текущее значение регулируемого параметра не выше заданного, при этом внутренняя динамическая составляющая (выражаемая через производные выходного параметра) доводит до полного исчезновения ошибки регулирования. Другими словами ″пассивное" регулирующее воздействие на позиционный объект будет равнотекущему значению регулируемого параметра деленному на коэффициент усиления объекта К (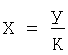 ). Входного "активного" регулирующего воздействия не будет, а в роли "активного" воздействия (изменяющего выходной параметр) будет внутреннее текущее "активное динамическое" свободное состояние.
). Входного "активного" регулирующего воздействия не будет, а в роли "активного" воздействия (изменяющего выходной параметр) будет внутреннее текущее "активное динамическое" свободное состояние.
Таким образом, основной сигнал регулирующего воздействия, полученный с выхода формирователя текущего воздействия 6, пропускается блоком контроля 2 без изменения, если подтверждается правильность расчетов ф.24, и точность идентификации параметров ф.26-30.
Если правильность какого-то параметра не подтверждается, то блок контроля 2 подает соответствующую команду на вход идентификатора 4 о необходимости учета новых возмущений для более точной идентификации свободного состояния, т.е. более точного нахождения производных разных порядков выходного параметра с учетом нестабильности возмущений и т.п., о чем информируется оператор.
Если внутренние и внешние сбои нарушают точность вычислений текущего свободного состояния объекта и т.п.; то вводимое при этом блоком 2 регулирование по интегралу необходимого активного воздействия позволяет предотвратить перерегулирование и добиться желаемой точности регулирования по основному параметру y, без учета заданных производных yз', yз'',...), что как правило достаточно для предотвращения аварийных режимов.
Объектом 3 может быть любой технологический процесс или физический (технический) объект независимо от его внутренней структуры. К выходному регулируемому параметру могут предъявляться любые физически реализуемые требования по поддержанию постоянного или переменного значения не только величины регулируемого параметра, но и его производных.
Если инерционность исполнительных устройств требует дополнительного их учета, то для упрощения расчетов, при составлении показательного решения дифуравнения CAP дополнительно учитывают свободную составляющую исполнительного устройства наравне со свободной составляющей объекта.
Идентификатор 4 включат в себя блоки, которые выполняют следующие функции:
- блок управления 4.1 позволяет фиксировать измеренные величины выходного регулируемого параметра, входного регулирующего воздействия и принимать заданные значения регулируемого параметра, передавая их на вход формирователя степенной функции 4.2, управляя при этом режимами его вычислений,
- формирователь степенной функции 4.2 благодаря действию управляющего воздействия с выхода блока управления 4.1 позволяет определить следующие параметры: А) постоянные времени внутреннего запаздывания (регулятора или системы; заданные и реальные) T1, Т2...,
Б) коэффициент усиления исследуемой структуры К; В) момент времени, являющейся переменной, входящей в математическое описание исследуемого выходного параметра,
- вычислитель корней 4.3 позволяет найти корни характеристического уравнения (их действительные и мнимые составляющие) и корни для переменной времени t степенных многочленов любой степени (Г),
- определитель объекта 4.4 определяет (Д) передаточную функцию объекта,
- определитель регулятора 4.5 определяет (Е) передаточную функцию регулятора.
А) Определение постоянных времени внутреннего запаздывания Т1, Т2,... осуществляется для
- регулятора по текущим значениям X, Х',...
- системы по заданным значениям yз, yз',...
- системы по текущим значениям yт, yт',...
Порядок вычислений:
- по ф.1 и ф.4 вычисляются а, а', а'',... (значение а из формулы 1 подставляется в ф.4 и выводятся математические выражения для а', a'',... ф.31
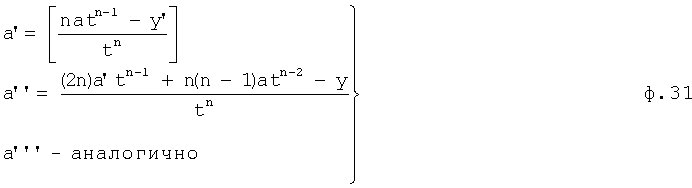
- по найденным математическим выражения для а, а',... определяются Т1...Тn по формуле 32; математические выражения для Т1... найдены из системы уравнений, полученных приравниванием коэффициентов аналогично примеру, приведенному в формулах 5, 6, 7.

и т.д.
Б) коэффициент усиления К находится из формулы 7, подстановкой в формулу 32б найденных значений а и Тn.

В) определение текущего (или заданного) момента переменной времени tт до найденной переменной величине а(to), а(to),... и внутренним постоянным запаздывания Т1, Т2.
Порядок вычислений: переменной tт зависящей от значения to:
- по известным (найденным ранее) значениям внутреннего запаздывания Т1..., коэффициента усиления К и величины входного сигнала (воздействия) Х из математических выражений в ф.6 и 7 определяют математические выражения для переменной а, а',... приведенных в ф.33 и 34


и т.д.
Если входное воздействие является переменной во времени величиной, то в формулы 35 и 34 вносятся соответствующие коррективы, обусловленные необходимостью учитывать дополнительное математическое выражение функциональной зависимости Х=fx(t).
- после чего по найденным а, а', а'',... находят tт, совместно решая ф.33 и ф.2; в зависимости от характера изменения входного воздействия Х используют следующие варианты решения:
1) если Х(≠0)=const, то математическое выражение, определяющее переменную времени примет вид ф.35

2) если Х=fx(t), то после подстановки этой зависимости в ф.5 и последующего составления системы уравнений из коэффициентов (аналогично ф.6 и 7), определяющих значения математических зависимостей для а, а',... аналогично ф.33, 34 и получается математическое выражение аналогичное ф.35
3) если объект (или система) находится в свободном состоянии, т.е. Х=0, тогда в формулу 34 (или аналогичную ей) подставляют 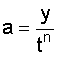
После чего, из выражения ф.4 получают ф.35б, в которой произведена соответствующая подстановка а и а'
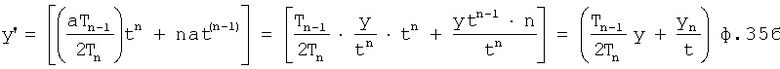
Полученное выражение 35б используется для нахождения текущей переменной tт в ф.36

4) Если значение входного воздействия Х не известно (или по какой-либо причине установить структуру исследуемого объекта невозможно) и невозможно сформировать уравнение аналогичное математическому выражению ф.5, то поиск переменной времени производят используя ф.1 и ф.4. Для этого находят производную ф.1, получают выражение в ф.35в

Формула 35в используется для подстановки в ф.35г
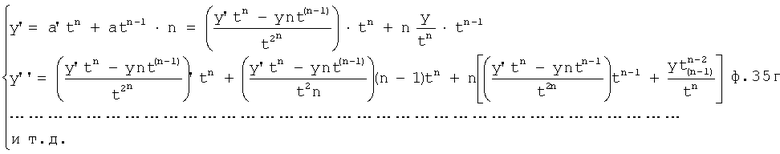
Для полученной системы уравнений ф.35г находятся значения корней переменной времени t в вычислителе корней 4.3, полученные значения корней должны быть справедливы для всех уравнений ф.4 (или ф.35г). Если корень не справедлив для всех уравнений, то он не является искомым моментом времени. Для ф.35г принято y=0 при t=0 из ф.2.
Для проведение уточняющей проверки найденного значения момента времени t при всех из четырех 1)...4) вариантах и найденных значений внутренних постоянных запаздывания текущего значения переменной а(t), а'(t), ..., эти значения подставляют в ф.2, 4, 6, 7.
Если подстановка подтверждает правильность, то окончательные результаты передаются на выход формирователя степенной функции.
Г) Вычисление корней степенного многочлена при определении текущего момента переменной времени tт из ф.35г и при нахождении корней характеристического уравнения осуществляется вычислителем корней 4.3, который позволяет найти действительную α и мнимую β части комплексных корней р.
Преобразователь 4.3.1 отделяет вещественную часть (действительную) L исследуемого степенного многочлена M=L+B=a0+a1p+a2p2+... от мнимой β фиг.2. Формирователь степени (I) возводит переменную р в соответствующую степень ф.37.
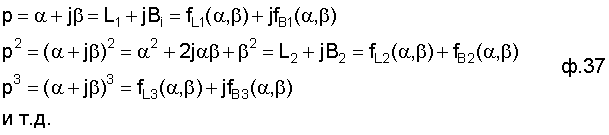
где р=рi=1,2... корни характеристического уравнения (степенного многочлена);
α - действительная часть корня р;
β - мнимая часть корня р;
L - действительная часть исследуемого многочлена M;
В - мнимая часть исследуемого (степенного) многочлена М;
Li - действительная часть переменной Р после возведения переменной в степень;
Вi - мнимая часть выражения, полученного после возведения переменной в степень.
Умножитель (2) находит произведение соответствующего коэффициента а1, а2, ..., на соответствующее выражение, полученное после возведения переменной в степень ф.38

Сумматор (3) и (4) отделяют действительную часть L=L1+L2+... от мнимой В=В1+В2+...
Таким образом, преобразователь позволяет определить зависимости действительной части L степенного многочлена М от действительной α мнимой β частей переменной Р, аналогично определяется зависимость мнимой части В степенного многочлена М от действительной α мнимой β частей переменной р. Полученные выражения приведены в ф.39.

Дифференциатор 4.3.3 определяет производные разных порядков L', L''... B', B''... по двум переменным α и β ф.40а
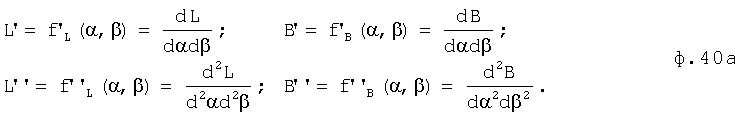
На выходе 2 дифференциатора формируется производная (n-1)го порядка, где - максимальная степень многочлена L или В.
При этом получается система двух уравнений с двумя неизвестными первой степени ф.40б:
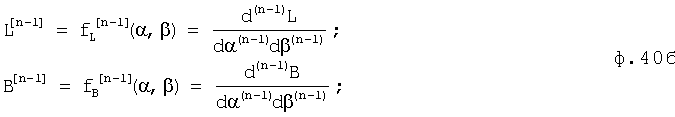
На первом выходе дифференциатора формируются системы равенств, полученные дифференцированием по двум переменным ф.41, порядок дифференцирования для каждой из систем определяется соответственно последовательный i=2, 3,...

Стандартный вычислитель 4.3.4 находит корни α и β системы двух равенств ф.40б первой степени (т.е. переменная имеет первую степень).
Блок памяти 4.3.5, после поступления синхроимпульса с выхода стандартного вычислителя 4.3.4, заносит в свою память найденные вычислителем 4.3.4 значения двух неизвестных, входящих в систему уравнений, полученной дифференцированием (n-1)ой степени по двум переменным каждой из исследуемых равенств. Эти значения α, β через первый выход блока памяти 4.3.5 передаются на второй вход определителя приближения 4.3.2, где используются для нахождения корней производных меньшего порядка (имеющих показатель степени больший). С выхода определителя приближения 4.3.2 найденные корни первого приближения (... потом второго и последующих) поступают на второй вход блока памяти, где заносятся в оперативную память (если это первое приближение или если подученные значения последующих приближений намного отличаются от предыдущих). Если отличие не существенно, то полученное последнее приближение заносится в основную память, после чего поиск последующих приближений данного корня прекращается.
Поэтапное уменьшение порядка производной рассматриваемого многочлена и нахождение корней каждой из производных (т.е. с уменьшением производной степень исследуемого равенства будет увеличиваться) по корням предыдущей производной позволяет перейти к поиску корней исследуемой системы.
Подробно изображенный на фиг.3 определитель приближения 4.3.2 находит корни двух неизвестных для системы из двух степенных равенств, используя при этом корни (ранее найденные), хранящиеся в основной памяти или оперативной (блока памяти 4.3.5) и являющиеся корнями степенных равенств с меньшей степенью или корнями предыдущих приближений.
Определители неизвестных по производным (1), (2) и (4) формируют на своих выходах значения корней (соответствующих приближений для соответствующих систем равенств) по следующим формулам 42-45 [3 стр.390, 391].
Блоком памяти 4.3.5 обеспечивается формирование в определителях неизвестных по производным (1), (2), (4) (входящих в определитель приближений 4.3.2) следующие режимы работы:
1) нахождение первого приближения
1.1 для первого и последнего корня по ф.42:
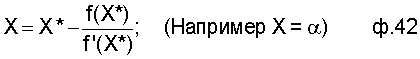
где 
- формула 43 получена из уравнения для зависимости 2-го порядка, т.е. если 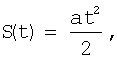
тогда 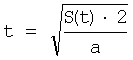 (где а=S''(t), t - явл. переменной)
(где а=S''(t), t - явл. переменной)
α', β' - корни от системы двух равенств (степенных многочленов) производной f' большего порядка, чем исследуемая f (у которой показатель степени равенств, входящих в систему, больше, чем показатель степени многочлена производной)
"-" - при поиске первого корня;
"+" - при поиске последнего корня.
1.2 для второго и последующих корней, кроме последнего (п.1.1) формула 44 получена из подобия треугольника [Л.3, стр.388]

где 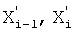 - корни производной большего порядка (меньшей степени равенств), которые расположены последовательно и между которыми должен располагаться искомый корень Xi:
- корни производной большего порядка (меньшей степени равенств), которые расположены последовательно и между которыми должен располагаться искомый корень Xi:
2) нахождение второго и последующих приближений

где 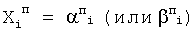 - значения корней предыдущего приближения;
- значения корней предыдущего приближения;
i - номер корня.
Общая формула, по которой определители неизвестных по производная (1) и (2) формируют выходной сигнал примет вид ф.46

где N - базовая величина α (действительное число), не включающая второй неизвестной (например β) и равная а), б), в):
а) результатам вычислений по ф.43 (для первого и последнего корня) согласно п.1.1, т.е. =X*;
б) одному (например, первому) из используемых корней производной (от исследуемого равенства), между которыми ищется корень согласно п.1.2, т.е. X'i-1;
в) корню предыдущего приближения (если оно уже найдено) согласно п.2.1, т.e. 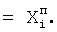 .
.
f(N,β) - функция, в которую подставляется базовая величина N и которая включает второе неизвестное β.
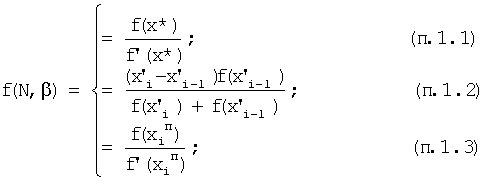
В результате выходной сигнал определителя неизвестных (1) равен ф.46.1

выходной сигнал определителя неизвестных по производным (2) равен ф.46.2

Сумматор 3 приравнивает два математических выражения ф.46.1 и ф.46.2, позволяя исключить одну из неизвестных (например α) и сформировать многочлен с одной неизвестной ф.47

Определитель неизвестных по производным (4), используя равенство с одним неизвестным ф.47 и ранее найденные корни производных от исследуемого равенства (т.е. производного более высокого порядка), производит вычисления согласно формулам 42-45. Вычисления производятся сначала для первого приближения, результаты которых фиксируются блоком памяти 4.3.5, результаты первого приближения используются для нахождения второго приближения и т.д.
Элемент подстановки (5) найденное значение корня β подставляет в выражение для нахождения второго корня α. Полученные значения неизвестных α, β соответствующего приближения искомого корня подставляется на выход определителя приближения.
В совокупности, входящие в вычислитель корней 4.3 элементы, работают следующим образом. Преобразователь 4.3.1 формирует систему двух уравнений с двумя неизвестными. Дифференциатор 4.3.3 находит производные разных порядков для каждого из двух уравнений.
После нахождения корней (n-1) производной стандартным вычислителем 4.3.4 определитель приближения корней 4.3.2 по формулам 42-45 определяет два независимых решения относительно одного из переменных (например α). Приравнивая эти два решения сумматором 3, получают степенной многочлен с одним неизвестным (в рассматриваемом примере β), используемый определителем неизвестных по производным (4) для нахождения этого неизвестного (в рассматриваемом примере β).
После нахождения приближения этого неизвестного и использования его в элементе подстановки (5) для нахождения второго неизвестного (в рассматриваемом примере α), полученные значения α, β записываются блоком памяти 4.3.5 в оперативную память и сравниваются с предыдущими значениями. Если эти значения существенно отличаются, то начинается следующий этап уточнения нового приближения по результатам расчетов предыдущего приближения. Когда результаты текущего приближения станут практически совпадать с предыдущими, полученные значения корней pi=α±jβ заносятся в основную память и переходят к поиску значений α и β следующего корня pi+1 этого же порядка производной. Если все корни этого (рассматриваемого) порядка производной уже найдены, то переходят к поиску корней меньшего порядка производной (имеющего большую степень при неизвестном). Блок памяти 4.3.5 запоминает окончательные результаты вычисления корней, занося их в основную память и формируя на выходе соответствующий сигнал.
Д) Определитель объекта 4.4 по корням характеристического уравнения, полученного с выхода вычислителя коней 4.3 для входа и выхода объекта с учетом общей структуры CAP, определяет передаточную функцию объекта ф.48

где Wсис передаточная функция системы (по характеристики выходного параметра объекта)
Wрег - передаточная функция регулятора, заранее известная или идентифицированная в текущем времени с учетом происходящих в нем помех (возмущений)
Wоб - передаточная функция объекта.
Е) Определитель регулятора 4.5 по заданной передаточной функции системы и идентифицированной передаточной функции объекта (параметры которых поступают с выхода вычислителя корней 4.3 и с выхода определителя объекта 4.4) определяет передаточную функцию регулятора, которая обеспечивала бы заданные изменения выходного параметра объекта по ф.49

Формирователь показательной функции 5 по корням характеристического уравнения р... и текущему значению момента времени tт определяет коэффициенты интегрирования С1, С2,... показательного решения дифуравнения системы автоматического регулирования заданной (по заданному выходному параметру) и реальной - по текущей характеристики выходного параметра реальной y, y', .... При несоответствии коэффициентов интегрирования заданным значениям коэффициентов, формирователь 5 находит вынужденную составляющую дифуравнения CAP, позволяющую в совокупности со свободной составляющей добиться желаемых значений коэффициентов интегрирования.
Идентификация свободной и вынужденной составляющей для заданной CAP осуществляется блоком заданного состояния 5.1 по формулам 8-10.
Идентификация свободной и вынужденной составляющей для реальной CAP осуществляется по ф.8-11. Нахождение ″абсолютных″ (независящих от текущего вынужденного состояния) значений свободной составляющей объекта в текущий момент времени позволяет при необходимости осуществить корректировку постоянных интегрирования для заданного состояния CAP.
Для этого блок коррекции 5.3 вводит дополнительное вынужденное состояние согласно ф.20 и аналогично ф.20.1-20.7.
Формирователь текущего воздействия 6 до показательному решению дифуравнения системы, определяющему вынужденное состояние объекта, находит математическую зависимость необходимого входного воздействия на объект, создающего на его выходе это показательное решение выходного регулируемого параметра. При этом можно использовать математические выражения, полученные аналогично ф.19 /согласно Л.3 стр.741 ф.(9), (10)/. В полученное окончательное математическое выражения входного регулирующего воздействия подставляется необходимый текущий момент времени, тем самым подготавливая исполнительные устройства для формирования этого текущего момента времени (его физических или технических параметров).
Работа CAP осуществляется следующим образом.
Статический режим возможен лишь только при условии, если сигнал задания yз, y'з... заранее согласован с внутренними параметрами объекта и поэтому его можно считать осуществимым при соответствующей адаптации не только алгоритма регулирующего воздействия, но и самого алгоритма задания. Информация, хранящаяся в памяти идентификатора, полученная (от оператора) или идентифицированная ранее, сравнивается с текущей идентифицированной информацией. При этом ошибка регулирования сведена до нуля.
При появлении ощутимой ошибки регулирования, обусловленной изменением сигнала задания или появлением новых возмущающих воздействий, CAP начинает поиск нового алгоритма регулирования. При этом идентификатор 4 с достаточной точностью и быстродействием обеспечивает нахождение параметров объекта и всей CAP в целом. Определитель регулятора, входящий в идентификатор, учитывая внутренние параметры объекта и внутренние параметры необходимой системы, определяет структуру регулятора. По этой структуре формирователь показательной ф. 5 корректирует постоянные интегрирования и при необходимости вводит дополнительное вынужденное состояние (корни которого равны корням слагаемых свободного состояния объекта), позволяющее скорректировать текущее значение коэффициентов свободного состояния объекта.
Формирователь текущего воздействия по показательному решению (его вынужденному, с учетом коррекции, состоянию) определяет необходимое входное воздействие с учетом принятого текущего момента времени.
Экономический эффект достигается усовершенствованием технологического процесса, повышением точности выполнения делаемого технического задания, уменьшением энергозатрат и износа оборудования.
Источники информации
1. Кулаков Г.Т. Инженерные экспресс-методы расчета промышленных систем регулирования: Спр., 1984, с.40-43.
2. Ротач В.Я. Теория автоматического управления теплоэнергетическими процессами: Учебник для вузов. - М.: Энергоатомиздат, 1985, с.87-90.
3. Выгодский М.Я. Справочник по высшей математике. М.: Гос. изд. технико-теоретической литературы, 1967, с.741.
Система автоматического регулирования динамической характеристикой выходного параметра. Использование: для управления технологическими процессами в энергетике и др. отраслях. Технический результат заключается в положении динамической точности регулируемого параметра. В заявленной системе регулятор настраивается не только по параметрам внутреннего запаздывания объекта, но и по коэффициентам интегрирования показательного решения дифуравнения системы, при этом могут корректироваться коэффициенты свободного состояния объекта дополнительным вынужденным состоянием. В CAP введен формирователь показательного решения, включающий блок заданного состояния, блок текущего состояния и блок коррекции, кроме этого в идентификатор введен формирователь степенной функции, позволяющий сделать возможным идентификацию внутренних постоянных времени и текущего момента времени; в вычислитель корней введен преобразователь и вычислитель неизвестных по производным, что необходимо для нахождения корней характеристического уравнения. 3 ил.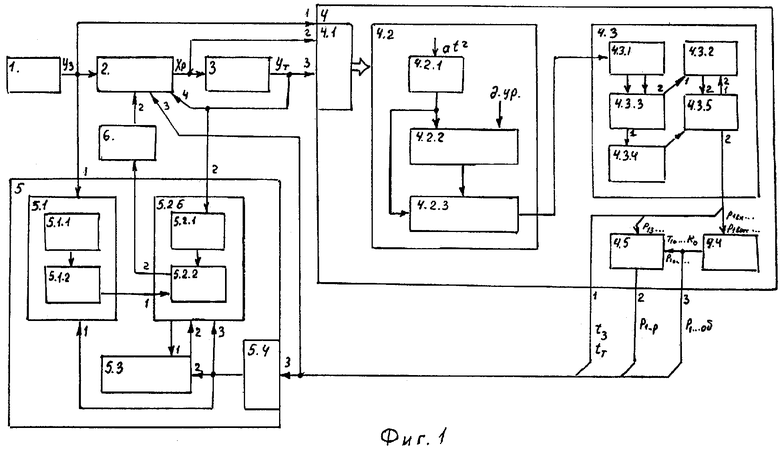
Система автоматического регулирования динамической характеристикой выходного параметра, включающая последовательно соединенные задатчик, блок контроля, объект и идентификатор; формирователь текущего воздействия, выходом подсоединенный ко второму входу блока контроля, на третий вход которого подсоединены выходы идентификатора, а на четвертый - выход объекта; выходы задатчика и блока контроля также подсоединены на выходы идентификатора, при этом идентификатор включает в себя блок управления, определители объекта и регулятора, вычислитель корней, включающий блок памяти и стандартный вычислитель, входы блока управления идентификатора подсоединены на входы идентификатора, а выход вычислителя корней подсоединен на входы определителей объекта и регулятора, выходами идентификатора являются выходы вычислителя корней, определители объекта и определители регулятора, отличающаяся тем, что введены формирователь показательной функции, на третий вход которого подсоединены выходы идентификатора; выход формирователя показательной функции подсоединен на вход формирователя текущего воздействия; формирователь показательной функции включает в себя последовательно соединенные блок управления формирователя, блок заданного состояния, блок текущего состояния и блок коррекции коэффициентов; третьи входы формирователя показательной функции подсоединены к входу блока управления формирователя, а через первый и второй входы формирователя показательной функции подсоединены выходы соответственно задатчика и объекта на вторые входы блока заданного состояния и блока текущего состояния соответственно, блок управления формирователя также подсоединен ко второму входу блока коррекции коэффициента и к третьему входу блока текущего состояния, на второй вход которого подсоединен выход бока коррекции коэффициентов, а выход блока текущего состояния подсоединен на выход формирователя показательной функции; в идентификатор введен формирователь степенной функции, причем блок управления идентификатора, формирователь степенной функции и вычислитель корней соединены последовательно, формирователь степенной функции включает в себя последовательно соединенные дифференциатор, формирователь системы уравнений, вычислитель неизвестных, на второй вход которого подсоединен выход указанного дифференциатора, выход которого подсоединен на выход формирователя степенной функции; в вычислитель корней дополнительно введены последовательно соединенные преобразователь, дифференциатор вычислителя, определитель приближения, вход вычислителя корней подсоединен на вход преобразователя, выход дифференциатора вычислителя подсоединен на вход стандартного вычислителя, выход которого подсоединен на первый вход блока памяти, на второй вход которого подсоединен выход определителя приближения, первый выход блока памяти подсоединен на второй вход определителя приближения, а второй выход блока памяти подсоединен на выход вычислителя корней.
| РОТАЧ В.Я | |||
| Теория автоматического управления теплоэнергетическими процессами | |||
| Учебник для ВУЗов, Москва, Энергоатомиздат, 1985, с.87-90 | |||
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА УПРАВЛЕНИЯ | 1992 |
|
RU2068196C1 |
| СИСТЕМА АВТОМАТИЗАЦИИ | 1998 |
|
RU2213365C2 |
| Система автоматического регулирования | 1988 |
|
SU1569802A1 |
| US 5513097 A, 30.04.1996. | |||
Авторы
Даты
2007-01-27—Публикация
2005-02-09—Подача