Изобретение относится к автоматическому управлению и может использоваться для регулирования динамического состояния выходного параметра объекта в задаваемый момент времени при разной степени устойчивости емкостных составляющих объекта.
Известен П-регулятор по ошибке ф.1 (пропорциональный)
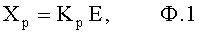
где Kp - коэффициент;
E - ошибка регулирования.
Пропорциональный (П) закон регулирования равномерно пропускает все частоты регулирования, а быстродействие ограничивается только физической реализуемостью исполнительных органов. При этом он включает в себя усилитель ошибки регулирования. Недостаток этого регулирования в том, что статическая ошибка объекта с пограничными состояниями устойчивости не всегда позволяет добиться желаемой точности.
Известен ПИ-регулятор [л.2] (ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНЫЙ), поддерживающий значение необходимого параметра на заданном уровне без статической ошибки. При этом он включает в себя идентификатор параметров объекта, вычитатель текущего значения регулируемого параметра от заданного (т.е. определитель ошибки регулирования). Недостаток этого устройства в том, что объектами регулирования могут быть только инерционные объекты с достаточной степенью устойчивости.
Известна система автоматического регулирования (CAP) [Л.3, стр.9], в которой регулирующее воздействие задается устройством с программным алгоритмом управления. При этом она включает в себя программируемое командное устройство, формирующее регулирующее воздействие по сигналу задания и по текущему значению выходного параметра.
Недостаток этой системы автоматического регулирования в том, что уменьшение ошибки (до требуемой точности для заданных моментов времени) невозможно при сильных возмущающих воздействиях и сложной внутренней структуре объекта - внутреннее запаздывание объекта может создать большое перерегулирование, технологически недопустимое.
Известны комбинированные системы автоматического управления САУ (л.4), которые обеспечивают оптимальное по быстродействию и устойчивости регулирование. САУ построена таким образом, чтобы по задающему воздействию система была разомкнута, а по возмущающему воздействию была замкнута. Устройство, формирующее регулирующее воздействие, включает специальные сумматоры и подсоединенные на их входы блоки:
- блок, отрабатывающий задающее воздействие a(t), звено W1м(p),
- блок, формирующий воздействие по ошибке Θ(t), звено W1p,
- блок, формирующий корректирующее воздействие, звено Wкp.
Недостаток известных САУ в том, что управление значением регулируемого параметра возможно только по величине. При этом величины производных от заданного значения выходного параметра в заданные моменты времени (их скорость и ускорение) несут случайный характер.
Задача заявленного изобретения заключается в том, чтобы обеспечить необходимую точность и заданную область допустимых значений для каждой из емкостных составляющих, образующих в сумме значение выходного параметра объекта.
Сущность заявленного изобретения заключается в том, что в систему автоматического регулирования емкостными составляющими объекта, включающую блок задания, регулятор с постоянными параметрами, регулятора с переменными параметрами, регулятора по текущей ошибке и последовательно соединенные блок проверки ОДЗ планируемой CAP, блок сравнения моделей, формирователь регулирующего воздействия, объект, идентификатор и блок контроля ОДЗ действующей CAP, выход которого подсоединен ко второму входу формирователя регулирующего воздействия и к третьему входу блока задания, к первому и второму входам которого подсоединены входы заявленной CAP, выход идентификатора также подсоединен на входы каждый из входящих в заявленную систему блоков, выходы которых подсоединены на второй вход блок проверки ОДЗ планируемой CAP, на первый вход которого и входы всех остальных блоков подсоединен выходы блока задания; блок задания включает блок динамических характеристик выходного параметра, подсоединенный к входу и выходу блока задания, регулятор с постоянными параметрами включает регулятор по заданию, вход и выход которого подсоединен к соответствующим входам и выходам регулятора с постоянными параметрами, блок проверки ОДЗ планируемой CAP включает соединенные последовательно формирователь алгоритма и вычислитель, формирователь алгоритма включает в себя последовательно соединенные формирователь системы уравнений дифференцированием полного решения и первый вычислитель определителей системы; блок контроля ОДЗ действующей CAP включает в себя последовательно соединенные формирователь модели объекта и второй вычислитель; формирователь модели объекта включает подсоединенную к выходу схему сравнения; формирователь регулятора по заданию включает в себя подсоединенные к выходам два вычислителя постоянных входного воздействия, идентификатор включает в себя определитель внешнего запаздывания и индикатор, выходы которых подсоединены на выход идентификатора, дополнительно введены корректирующий регулятор, включающий последовательно соединенные компенсатор системной ошибки, компенсатор случайной ошибки и подсоединенный к их выходам сумматор, в блок задания введены блок внутренних отдельных составляющих, блок дополнительных вспомогательных составляющих, входы и выходы которых подсоединены к входам и выходам блока задания; в регулятор с постоянными параметрами введены регулятор по начальной ошибке, регулятор по заданному моменту времени, входы и выходы которых подсоединены к соответствующим входам и выходам регулятора с постоянными параметрами, а в регулятор по заданию введены последовательно соединенные определитель корней математической модели регулятора, определитель запаздывания и параллельно соединенные формирователь регулятора при инерционности первого порядка и формирователя регулятора при инерционности второго порядка, выходы которых подсоединены на входы вычислителей постоянных входного воздействия; в регулятор с переменными параметрами введены последовательно соединенные регулятор переменных коэффициентов, регулятор переменных корней, регулятор переменного запаздывания и регулятор переменной структуры, выходы и входы которых подсоединены к соответствующим входам и выходам регулятора с переменными параметрами; в регулятор по текущей ошибке введены последовательно соединенные дифмодель параметров регулятора, определитель запаздывания регулятора по начальной ошибке, регулятор по текущей характеристике ошибки; в формирователь алгоритма (входящий в блок проверки ОДЗ планируемой CAP) введены последовательно соединенные «формирователь системы логарифмический уравнений из определителей» (подсоединенный к выходу вычислителя определителя системы), «формирователь логарифмический зависимостей между определителями» и «элемент подстановки зависимостей между определителями», выход которого подсоединен на вход первого вычислителя, а также введен «формирователь системы уравнений из алгебраических дополнений», вход которого подсоединен к выходу «формирователя системы уравнений дифференцированием полного решения», а выход - на второй вход «элемента подстановки зависимостей между определителями»; в идентификатор введены быстродействующий вычислитель, фильтрующий вычислитель, подсоединенный к его выходу «вычислитель модели с переменными корнями», «определитель последовательности взаимодействия звеньев математической модели» и подсоединенный к нему «определитель ОДЗ выходных параметров каждого звена», все они входами подсоединены к входу идентификатора, а выходами - к выходу идентификатора и входу индикатора; «определитель внешнего запаздывания» подсоединен входом к второму выходу «вычислителя модели с переменными корнями», а выходом к входу «определителя последовательности взаимодействия звеньев математической модели», в «определитель внешнего запаздывания» введены подсоединенные ко входу «быстродействующий канал» и «фильтрующий канал», выходы которого подсоединены к введенной «схеме сравнения», выход которой подсоединен на выход «определителя внешнего запаздывания»; в «формирователь модели объекта» (входящий в «блок контроля ОДЗ действующей CAP») введены подсоединенные ко входу «первый канал реакции» и «второй канал емкостных составляющих», выходы которых подсоединены на входы схемы сравнения.
Введенные устройства в совокупности позволяют идентифицировать характеристики внутренних состояний отдельных составляющих объекта, выражая эти состояние через математические модели их выходных параметров. При этом рассматривается влияние этих параметров на текущие изменения тех звеньев, которые попадают под влияние этих выходных параметров. Параллельные каналы идентификации дополняют друг друга и позволяют получить всеобъемлющую информацию об объекте, которая необходима для создания адекватного регулирующего воздействия. Заявленное изобретение позволяет добиться не только заданных значений выходных параметров в необходимые моменты времени, но в то же время получить желаемую скорость и ускорение регулируемого параметра не только на выходе объекта, но и на выходе каждого из отдельных звеньев, входящих во внутреннюю структуру объекта.
Помимо качественных характеристик процесса регулирования заявленная CAP позволяет контролировать ОДЗ не только выходного параметра самого объекта на протяжении всего времени регулирования, но и внутренние значения ОДЗ каждого из внутренних звеньев объекта на протяжении всего времени регулирования. Полученный положительный результат заявленной CAP позволяет избежать неблагоприятных технологических режимов, создающих нежелательный износ оборудования, и предотвратить аварии, к которым эти режимы могут привести.
Регулирование составляющих выходных характеристик внутренних звеньев объекта предъявляет к CAP повышенные требования и приводит к неизбежной необходимости осуществления идентификации параметров объекта на разных качественных уровнях процесса обработки данных о текущем состоянии составляющих CAP и процесса отработки (и проектирования) регулирующего воздействия для того, чтобы компенсировать любые возмущающие воздействия, от которых зависят регулируемые величины, входящие в регулируемые параметры.
Введенный в блок задания 1 (фиг.1) блок внутренних отдельных составляющих 1.2 позволяет по совокупности заданных динамических характеристик y, y', y”,… объекта определить, какие (для этой совокупности) при этом будут выходные параметры y(1), y(2), y(3)… каждого из звеньев W(1), W(2), W(3)…, из которых состоит математическая модель объекта WO, при условии, что их подсоединение носит последовательный характер. Если разделить математическую модель объекта WO на отдельные звенья W(1), W(2), W(3)…W(n) фиг.2, то для выходных параметров y(1), y(2), y(3),…y(n) каждого из звеньев можно составить по две системы уравнений ф.2
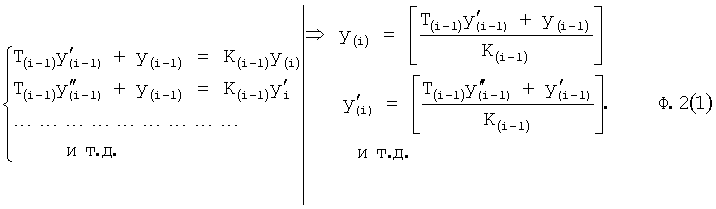
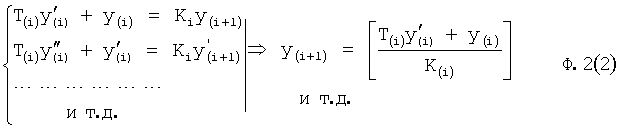
где y(i), 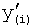 ,
, 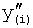 … - выходной параметр и его производные i-го звена; для примера рассмотрено позиционное звено с передаточной функцией
… - выходной параметр и его производные i-го звена; для примера рассмотрено позиционное звено с передаточной функцией 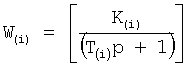
T(i) - постоянная внутреннего запаздывания i-го звена, 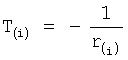
r(i) - корень математической модели i-го звена, значение которого определяется идентификатором (входящим в CAP) или задается оператором.
Первая из этих систем уравнений ф.2(1) отражает зависимость выходного параметра звена y(i) (и его производных 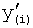 …) от выходного параметра (задаваемого или необходимого) последующего звена y(i-1),
…) от выходного параметра (задаваемого или необходимого) последующего звена y(i-1), 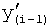 ,
, 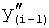 …
…
Вторая из этих систем уравнений ф.2(2) отражает, как по найденным необходимым значениям i-го звена y(i), 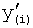 ,
, 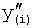 можно найти необходимые значения выходного параметра y(i+1),
можно найти необходимые значения выходного параметра y(i+1), 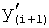 и его производных
и его производных 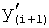 ,
, 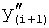 ,
, 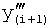 … предыдущего звена (i+1)-го.
… предыдущего звена (i+1)-го.
Таким образом, по заданной динамической характеристике 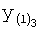 ,
, 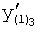 ,
, 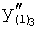 … последнего звена W1 (выход которого является выходом объекта W) из системы уравнений ф.2(2) можно определить выходной параметр второго звена (предпоследнего) W2 по ф.3
… последнего звена W1 (выход которого является выходом объекта W) из системы уравнений ф.2(2) можно определить выходной параметр второго звена (предпоследнего) W2 по ф.3

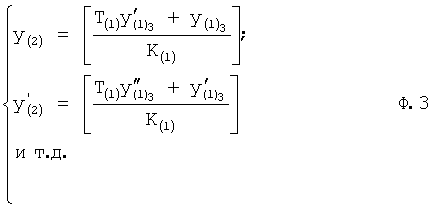
где 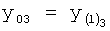 ,
, 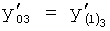 и т.д.
и т.д.
Найденные значения в ф.3 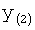 ,
, 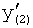 ,
, 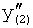 … подставляются в ф.2(2) для вычисления выходного параметра
… подставляются в ф.2(2) для вычисления выходного параметра 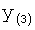 ,
, 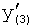 ,
, 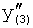 третьего звена, выход которого подсоединен на вход второго звена W2 и т.д.
третьего звена, выход которого подсоединен на вход второго звена W2 и т.д.
Из системы уравнений ф.2 видно, что для обеспечения заданной совокупности динамической характеристики y, y', y”… необходимо обеспечить соответствующую совокупность выходных параметров y(1)… каждого из звена W(1)… Значения y(1)…, входящие в эту совокупность, можно найти по корням r1, r2, r3… и коэффициентам С1, С2… дифференциальной математической модели объекта и входному воздействию на объект Xp. Последовательность соединения звеньев W(1)… может задаваться оператором по результатам предыдущих вычислений либо определяться «Формирователем последовательности взаимодействия внутренних составляющих объекта сравнением постоянных коэффициентов частного и полного решения вынужденного состояния объекта» 16, фиг.1.
Таким образом, введенный «Блок внутренних отдельных составляющих» 1.2 (фиг.1) при помощи дополнительных вычислений ф.3 по заданной текущей динамической характеристике y, y', y”… и параметрам характеристического уравнения математической модели объекта r1… позволяет определить соответствующие текущие выходные параметры y(1) отдельных звеньев W(1)… При этом вычисляются необходимые коэффициенты С1… свободного Cсв1… и вынужденного Св1… состояния полного решения дифуравнения полной математической модели объекта Wo и математической модели каждого из звеньев W(1)…(Ссв1…)Cв1…).
Введенный «Блок дополнительных вспомогательных состояний 1.3», фиг.1, формирует новую совокупность заданных параметров («дополнительную») 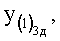
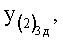
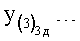 (или
(или 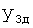 ,
, 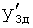 ,
, 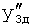 ), необходимую для осуществления плавного регулирования Xp, при котором регулирующее воздействие не будет превышать ОДЗ для регулирующих исполнительных механизмов и для ОДЗ амплитудо-частотной характеристики АЧХ регулирующего входного канала объекта.
), необходимую для осуществления плавного регулирования Xp, при котором регулирующее воздействие не будет превышать ОДЗ для регулирующих исполнительных механизмов и для ОДЗ амплитудо-частотной характеристики АЧХ регулирующего входного канала объекта.
Для получения оптимального регулирующего воздействия, не выходящего за рамки ОДЗ (при котором входное воздействие X,∈ОДЗ), используют систему уравнений ф.4.
Если в «Блоке контроля ОДЗ действующей CAP 18» (фиг.1) математическая модель регулирующего воздействия Xp в какой-либо момент времени превышает допустимые значения, то на соответствующем выходе «Блока…18» появится сигнал коррекции регулирующего воздействия Xp и введения дополнительных промежуточных значений заданного параметра 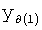 ,
, 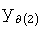 ,
, 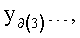 идущий в «Блок дополнительных вспомогательных состояний 1.3». При этом в «Звене вычисления новых промежуточных…6» (фиг.3) подставляются известные внутренние и внешние параметры и по ф.4 определяются значения неизвестных параметров.
идущий в «Блок дополнительных вспомогательных состояний 1.3». При этом в «Звене вычисления новых промежуточных…6» (фиг.3) подставляются известные внутренние и внешние параметры и по ф.4 определяются значения неизвестных параметров.

где r1…rn - корни математической модели объекта;
r1p, r2p, rnp - корни слагаемых математической модели регулирующего воздействия;
n - количество слагаемых математической модели регулирующего воздействия равно количеству заданных значений выходных параметров 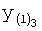 ,
, 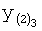 ,
,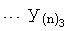 (или их производных
(или их производных 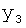 ,
, 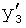 ,
, 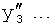 ).
).
Если оператору необходимо выбрать совокупность значений заданных параметров, решая вопрос о физической (или технической) реализуемости этой совокупности значений, то эта задача разделяется на шесть этапов:
- на первом этапе в систему уравнений ф.4 подставляются заданные выходные 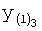 ,
, 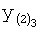 ,
, 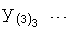 (или
(или 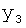 ,
, 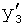 ,
, 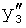 ) и внутренние r1 r2 r3 параметры объекта; после этого по ф.4 вычисляются корни rp1, rp2… слагаемых математической модели регулирующего воздействия (в звене 1), фиг.3;
) и внутренние r1 r2 r3 параметры объекта; после этого по ф.4 вычисляются корни rp1, rp2… слагаемых математической модели регулирующего воздействия (в звене 1), фиг.3;
- на втором этапе в систему уравнений ф.4 подставляют начальные значения выходных параметров 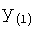 ,
, 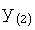 ,
, 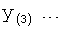 каждого из звеньев W1… объекта W0; после чего вычисляются значения постоянных коэффициентов С1p, С2p,… слагаемых входного регулирующего воздействия Xp (в звене 2), фиг.3;
каждого из звеньев W1… объекта W0; после чего вычисляются значения постоянных коэффициентов С1p, С2p,… слагаемых входного регулирующего воздействия Xp (в звене 2), фиг.3;
- на третьем этапе определяется диапазон изменения входного регулирующего воздействия по математической модели.
При этом полное решение дифуравнения CAP преобразуют в степенной многочлен с общим основанием. Общее основание формируется по ф.5. Вводится новая единица измерений 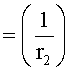 ф.6. Отрицательные показатели степеней при основании преобразуют в положительные, переводя основания в знаменатель ф.7. Математическое выражение приводится к общему знаменателю ф.8. Текущее значение решения дифуравнения умножается на приведенный общий знаменатель (т.е. знаменатель правой части степенного многочлена переносится в числитель левой ф.8).
ф.6. Отрицательные показатели степеней при основании преобразуют в положительные, переводя основания в знаменатель ф.7. Математическое выражение приводится к общему знаменателю ф.8. Текущее значение решения дифуравнения умножается на приведенный общий знаменатель (т.е. знаменатель правой части степенного многочлена переносится в числитель левой ф.8).
На четвертом этапе в математическое выражение ф.8, полученное на третьем этапе, вместо текущих значений подставляются граничные значения ОДЗ (для входного параметра и отдельно для его производной). После приведения к удобному виду полученное математическое выражение рассматривается как степенной многочлен и находятся его корни. Натуральный логарифм от каждого из полученных корней степенного многочлена делится на соответствующий корень (т.е. корень, используемый в основании степенного многочлена). Ф.5.2.
В полученные моменты времени значение исследуемого параметра пересекает границу ОДЗ (если в данном промежутке модель объекта можно считать линейной). После этого определяются значения исследуемого параметра, в моменты до граничного момента времени и после, что позволяет судить о характере изменения исследуемого параметра.
В ф.5.1 и 5.5 определяется общее основание Zi для преобразования решения дифуравнения в степенной многочлен azn…+…
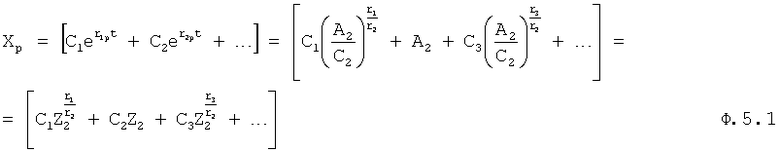
где 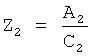 (или
(или 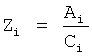 ) основание степенного многочлена (i=2)
) основание степенного многочлена (i=2)
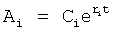

ф.5.2 получена следующим образом:
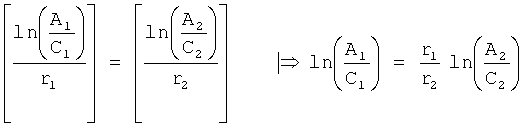
тогда
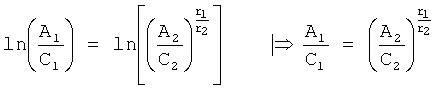
Для любого слагаемого 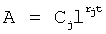 получают
получают
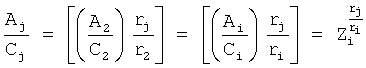
Для избавления от дробных степеней вводится новая единица изменения (для корней полного решения дифуравнения)

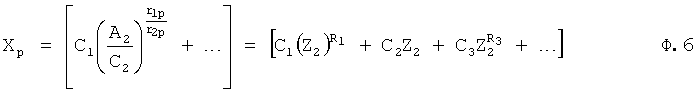
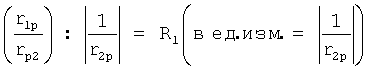 ; т.е.
; т.е. 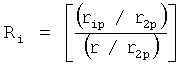
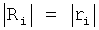 (т.е. равны по модулю)
(т.е. равны по модулю)
Для перехода отрицательных степеней к положительным переносят «основание» в знаменатель: если 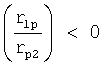 (т.е. отрицательно), то (R1)<0.
(т.е. отрицательно), то (R1)<0.
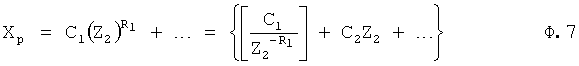
где (-R1)>0.
После приведения всех слагаемых к общему знаменателю, его переносят в числитель, домножая на Xp (стоящий в левой части равенства)
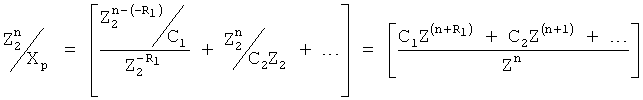
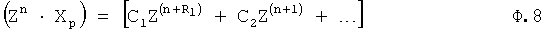
где Xp - входное регулирующее воздействие.
Ф.5…8 могут использоваться для исследования любых параметров, изменяющихся во времени.
На пятом этапе (звено 5) математическую модель входного регулирующего воздействия Xp изменяют таким образом, чтобы параметр, вышедший за пределы ОДЗ, уменьшить до допустимых значений (при этом используют математическую модель, полученную на третьем этапе).
На шестом этапе (звено 6) математическую модель входного регулирующего воздействия, полученную после пятого этапа, подставляют в систему уравнений ф.4 и вычисляют новые (дополнительные) промежуточные (задаваемые) выходные параметры звеньев математической модели объекта.
Введенные в быстродействующий вычислитель 11 (идентификатора 99) фиг.4. (фиг.4.1) дифференциаторы, делители, схема сравнения… позволяют моделировать исследуемый параметр (входной Xp и выходной Y) на ближайший интервал времени Δt. “Схема сравнения частных от деления производных 11.5” (Фиг.4) определяет параметры и структуру дифференциальной модели, интегральной модели и позиционного звена первого порядка ф.9. Если алгоритм “схемы сравнения…11.5.” фиксирует структуру модели позиционного звена 2-го порядка, то “вычислитель внутренних параметров… 11.6” определяет параметры позиционного звена по ф.10. По модели входного воздействия Xp и выходного параметра yo “вычислитель передаточной функции делением 11.8” переходит к модели объекта 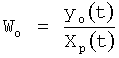 .
.
Вышеперечисленные формулы получены из математических выражений ф.11
Корни характеристических уравнений моделей с инерционностью 1-го порядка находят по следующим формулам ф.9
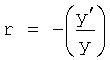 - для
- для дифференцирующей модели с запаздыванием,
дифференцирующей модели с запаздыванием,
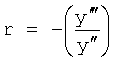 - для интегрирующей модели с запаздыванием ф.9,
- для интегрирующей модели с запаздыванием ф.9,
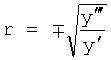 - для модели с незатухающими колебаниями,
- для модели с незатухающими колебаниями,
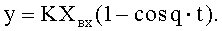
Корни характеристического уравнения позиционной модели с инерционностью 2-го порядка находят по ф.10
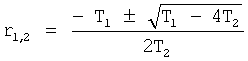
где 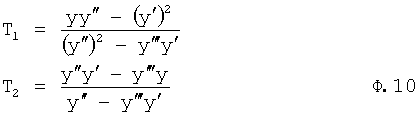
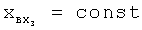 постоянно условно выходной параметр звеньев ф.11.1, где
постоянно условно выходной параметр звеньев ф.11.1, где 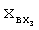 принято постоянным для данного промежутка времени идентификации
принято постоянным для данного промежутка времени идентификации
- инфференцирующего
- интегрирующего
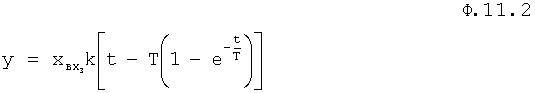

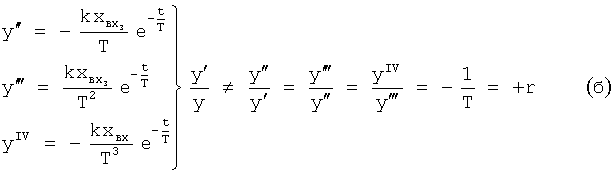
- инерционного 1-го порядка
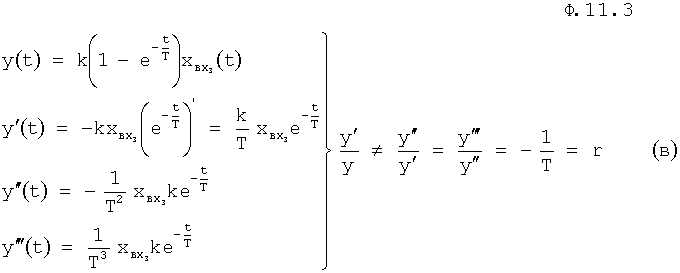
- консервативного колебательного
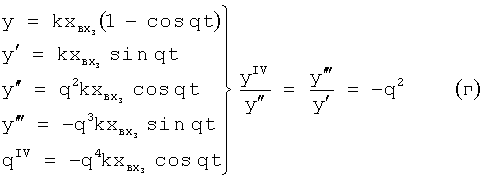
- позиционного второго порядка: 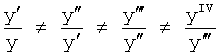

При этом выполняется одна из совокупностей (а), (б), (в), (г), (д) равенств, позволяющих отнести структуру звена к дифференциальной, интегральной и т.д.
Если необходимо идентифицировать состояние CAP и объекта на более длительный период времени, «Уточняющий вычислитель 12 (фиг.4)» формирует дифференциальную модель с производными 3-го и более высоких порядков. При этом задача идентификации усложняется и требует рассмотрения четырех моделей, которые, взаимно дополняя друг друга, создают взаимосвязанную всеобъемлющую модель (т.е. модель 7.1 обеспечивает быстродействие, модель 7.2 обеспечивает максимальное приближение к реальному объекту, модель 7.3 позволяет обеспечить совокупность достаточного быстродействия и достаточной точности, модель 7.4 обеспечивает максимальную чувствительность при идентификации кратковременных возмущений). У оператора появляется возможность учесть все возможные версии дальнейшего прогноза изменения выходного параметра объекта.
Если все четыре модели совпадают, то достоверность модели реальному объекту (и реальной CAP) равна 80%. Если какие-либо модели отличаются, то необходимо рассматривать совокупность всех моделей как единое целое и быть готовым к любому из четырех прогнозов.
Определитель характеристического уравнения 7.1 позволяет определить внутренние запаздывания в «первом» приближении, т.к. при этом производные высоких порядков (выше тех, которые входят в дифуравнение) не учитываются. Идентификация этой модели требует минимального времени для вычислений и не требует дополнительных измерений (т.е. точность этой модели является достаточной для «первого приближения»).
Определитель характеристического уравнения 7.2 формирует модель, максимально приближенную к достоверным параметрам объекта, т.к. все используемые для ее вычисления, производные высоких порядков получены непосредственным вычитанием параметров, измеренных в разные моменты времени. Чем больше дополнительных моментов времени, при котором производились измерения, тем выше степень производных, используемых в дифуравнении объекта (или САР). Недостаток этой модели в том, что взаимосвязь дополнительных измерений не позволяет идентифицировать кратковременные возмущения.
Определитель характеристического уравнения 7.3 позволяет получить производные высоких порядков по производным более низкого порядка, что уменьшает время, необходимое на идентификацию (и позволяет идентифицировать возмещения средней длительности). Но при этом появляются дополнительные лишние корни характеристического уравнения, для исключения которых необходимо хотя бы одно дополнительное измерение исследуемого параметра. Параметры, идентифицированные во второй (дополнительный) момент времени, сравниваются с параметрами, идентифицированные, в первом моменте времени, и выбираются те, которые совпадают.
Определитель характеристического уравнения 7.4 определяет модель по параметрам ряда Тейлора и позволяет формировать модель без дополнительных повторных измерений. Производные высоких порядков при этом получены из стенной модели, в которой используются коэффициенты, полученные из коэффициентов ряда Тейлора. Данная модель максимально точно отражает кратковременные возмущения. Недостаток этой модели в том, что ее точность уменьшается при увеличении интервала времени, на протяжении которого можно использовать эту модель (этот недостаток характерен для всех степенных рядов).
Таким образом, если производные высоких порядков настолько малы, что ими можно пренебречь, то параметры характеристического уравнения находят из системы уравнений ф.12.2 (фиг.4, «определитель характеристического уравнения 12.7.1»)
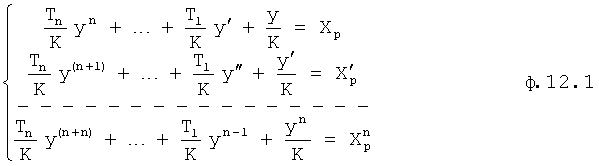
где K - коэффициент усиления объекта,
y(n+1)…y(n+n) - производные высоких порядков, которыми можно пренебречь,
где 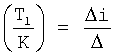 - постоянные внутреннего запаздывания
- постоянные внутреннего запаздывания
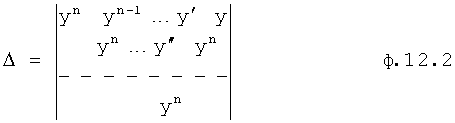
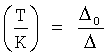
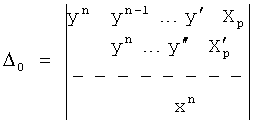
Для того чтобы компенсировать неточность математической модели «первого приближения» с выхода определителя характеристического уравнения 7.1, в определителе характеристического уравнения 7.2 (при использовании ф.12.1) производные высоких порядков определяются по измерениям в дополнительные моменты времени t1, t2, t3, фиг.12.3
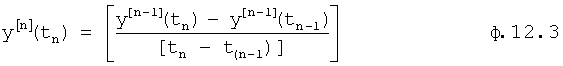
Для проверки найденных производных используют ряд Тейлора
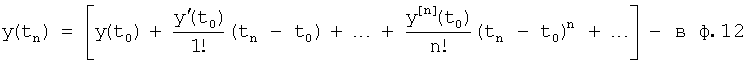
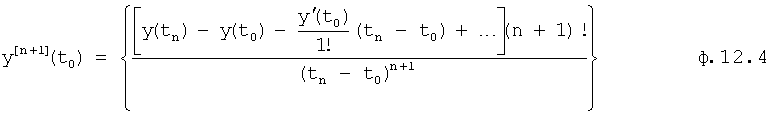
Так как для формирования математической модели определителем характеристического уравнения 7.2 требуется достаточно большой промежуток времени, причины неточности этой модели будут заключаться в том, что те параметры, которые вычисляются при этом, не отражают кратковременных возмущений, действующих на объект.
Для того чтобы производные высоких порядков определить по производным более низкого порядка, измерение которых не связано с соответствующими трудностями, прибегают к модели производных высокого порядка в виде степенной функции ф.13 с неизвестным корнем h переменной времени в показателе степеней. По известным производным определяют возможные корни модели производных высоких порядков по ф.14.
Если есть возможность, полученные корни производных высокого порядка проверяются хотя бы еще одним дополнительным измерением производных низкого порядка и соответствующими вычислениями ф.14. Если при повторном измерении корни производных высокого порядка совпадают с корнями, полученными после первого измерения, то эти корни являются доминирующими и подтверждают их достоверность. Бином Ньютона, используемый в ф.15, позволяет судить о допустимости использования ф.13 в приближенной математической модели исследуемого объекта ф.14.
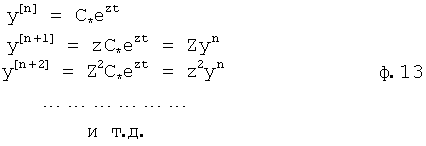
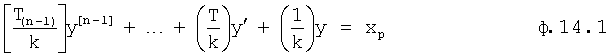
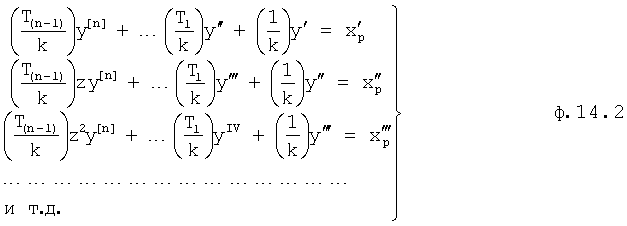
где 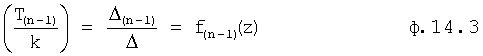
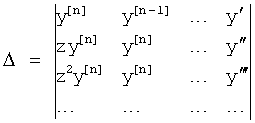
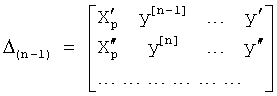
и т.д.
Z - неизвестное (значение введенного корня в ф.13)
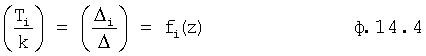
i=1…(n-1);

Значения f1…(n-1)(z), fk(z) подставляются в ф.14.1 и после раскрытия скобок определяют постоянные  альтернативной модели дифференциального уравнения объекта, у которой степень производных, как правило, выше чем, у первоначальной модели. В определителе 12.8.3 (фиг.2) вычисляются корни Z*… альтернативной модели с постоянными
альтернативной модели дифференциального уравнения объекта, у которой степень производных, как правило, выше чем, у первоначальной модели. В определителе 12.8.3 (фиг.2) вычисляются корни Z*… альтернативной модели с постоянными 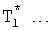
Найденные значения 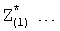 подставляют в ф.14.3…14.5 и вычисляют возможные совокупности
подставляют в ф.14.3…14.5 и вычисляют возможные совокупности 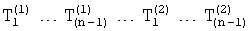 и т.д. для первоначальной модели дифуравнения. Для каждой из совокупностей
и т.д. для первоначальной модели дифуравнения. Для каждой из совокупностей 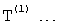 ,
, 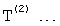 и т.д. вычисляют возможные совокупности корней в определителе корней 12.8.2.
и т.д. вычисляют возможные совокупности корней в определителе корней 12.8.2.
Для того чтобы оценить, насколько правомерно использование формулы ф.13, производят соответствующие преобразования математического выражения полного решения дифуравнения ф.14
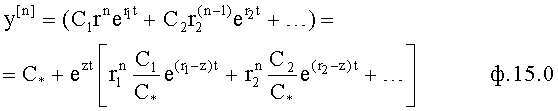
При соответствующих значениях C* и z значение в квадратных скобках можно приблизить к единице
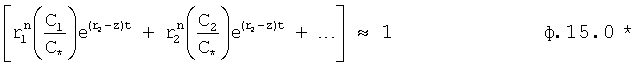
тогда y[n]=C*ezt
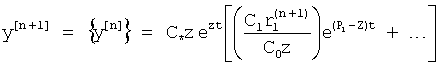
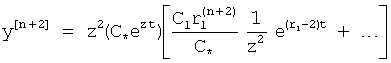
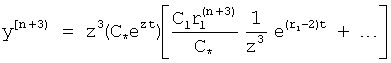
Если подставить 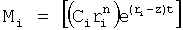 выражение в скобках ф.15.0*, то получится ф.15.1
выражение в скобках ф.15.0*, то получится ф.15.1
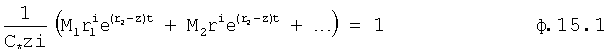
Если знаменатель левой части перенести в числитель правой, то получится ф.15.2
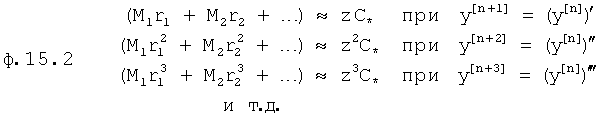
На характер изменения выходного параметра объекта основное влияние оказывает доминирующий корень rд, т.е. корень, который ближе всего расположен к границе устойчивости при отрицательных корнях (r<0) или имеющий большую неустойчивость при наличии положительных корней (r>0). Из вышесказанного и ф.15.2 видно, что если учитываются только доминирующие корни rд, то при рассмотрении производных высокого порядка можно использовать ф.12. Тогда значение “z” находится из системы уравнений ф.13.
Таким образом, определитель характеристического уравнения 12.7.3 позволяет вычислить несколько вариантов математической модели характеристического уравнения (постоянные внутреннего запаздывания которых 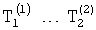 , а корни
, а корни 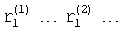 ), максимальная степень которых равна максимальной степени известных производных выходного параметра. Помимо этого, определяется одна модель, степень характеристического уравнения которой значительно выше максимальной степени известных производных выходного параметра (постоянные внутреннего запаздывания которой
), максимальная степень которых равна максимальной степени известных производных выходного параметра. Помимо этого, определяется одна модель, степень характеристического уравнения которой значительно выше максимальной степени известных производных выходного параметра (постоянные внутреннего запаздывания которой 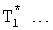 и корни
и корни 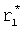 ).
).
Для того чтобы по однократным измерениям можно было с минимальной точностью судить о кратковременных возмущениях, в «Определителе характеристического уравнения 7.4» используются производные высоких порядков, полученные из степенного многочлена, коэффициенты которого найдены из ряда Тейлора по ф.16. Дифференцирование соответствующего степенного ряда и подстановка его и его производных в дифуравнение исследуемого объекта ф.17 позволяет определить постоянные внутреннего запаздывания.
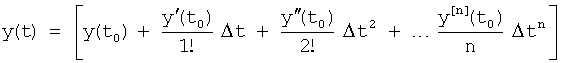
где y(t0), y'(t0)… - значение выходного параметра и его производные Δt=(t-t0), при t0=0, Δt=t;
t - текущий момент времени
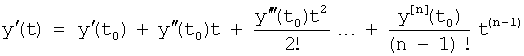
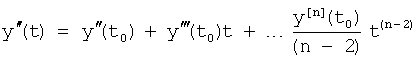
………………………………………………………
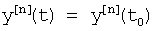
Полученные y(t), y'(t) подставляют в дифуравнение объекта ф.17
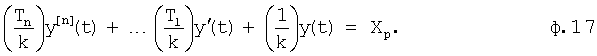
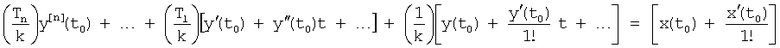
После раскрытия скобок находятся коэффициенты при одинаковых степенях.
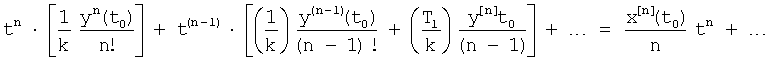
Коэффициенты перед одинаковыми степенями входного и выходного воздействия приравнивают, получая систему уравнений ф.18

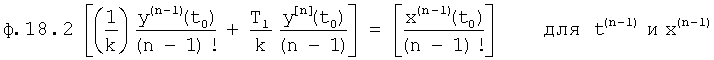
…………………………………………………
и т.д.
Из системы уравнений ф.18

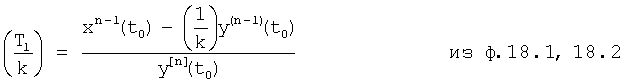
…………………………………………………
и т.д.
Определитель корней характеристического уравнения 12.8 сводит задачу нахождения у комплексных корней к определению точек пересечения между действительными и мнимыми кривыми. Для того чтобы построить действительные и мнимые кривые, введенный «отделитель действительной части 12.9» (фиг.4) подставляет модель комплексного корня r=α±iβ в характеристическое уравнение ф.19. После возведения комплексного корня в соответствующие степени (2-ю, 3-ю…), используя при этом бином Ньютона (л.6, стр.25) ф.20, полученные члены разложения М1, М2… умножаются на стоящий перед скобкой соответствующий коэффициент внутреннего запаздывания T1, T2…
Из полученного многочлена выделяют слагаемые с комплексной единицей и приравнивают эту часть нулю. Аналогично приравнивают нулю ту часть, которая включает слагаемые с действительными числами. Каждая из частей включает по две переменные координаты (α, β), которые между собой связаны неявной функцией, поэтому образуют совокупность кривых (пересекающих в точках с координатами комплексных корней). Построение кривых удобно начинать по точкам пересечения этих кривых с осями координат (с осью α, при β=0, и с осью, β при α≠0). В «определителях корней на осях 12.10.(1…4)» нулевые значения переменных α=0, β=0 поочередно подставляются отдельно в равенство для действительной части L=f1(αβ) характеристического уравнения и в равенство, образующее мнимую часть характеристического уравнения B=f2(αβ) ф.21. В результате получаются четыре степенных многочлена, каждый из которых включает по одному переменному (т.е. является степенным многочленом с одним неизвестным, действительные корни которых являются точками пересечений «кривых» с осями координат) ф.22
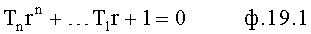
где T1…n - коэффициенты внутреннего запаздывания характеристического уравнения, найденные в определителях 12.7 фиг.4.
r=(α±jβ) - корни, которые подставляют
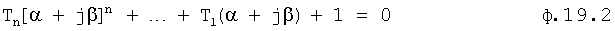
из Бинома Ньютона (a+b)n=[an+nan-1b+…]=[M1+M2+…]
где 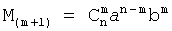

Характеристическое уравнение примет вид ф.20
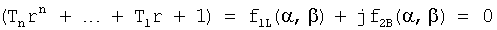


В равенство (ф.20.1) подставляют нулевое значение одной из переменных
- β=0, тогда 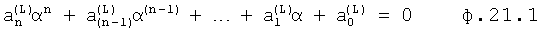
где  получаются после подстановки β=0
получаются после подстановки β=0
- α=0, тогда 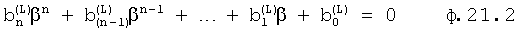
где  получаются после подстановки α=0.
получаются после подстановки α=0.
В равенство «B» (ф.20.2) подставляют
- β=0, тогда 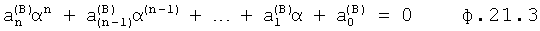
где  получаются после подстановки β=0
получаются после подстановки β=0
- α=0, тогда 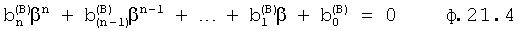
где  получаются после подстановки α=0
получаются после подстановки α=0
Определители корней на осях 12.10.1… находят действительные значения корней степенных многочленов ф.21.1…4 поэтапным дифференцированием степенного многочлена характеристического уравнения. Производная максимальной степени характеристического уравнения состоит из многочлена с минимальной степенью, поэтому решается стандартными формулами ф.22 или формулой Кардано. Полученные корни максимальной производной используются для задания областей формирования рядов Тейлора по ф.23. Количество рядов Тейлора равно количеству искомых корней соответствующей производной от одного из четырех степенных многочленов соответствующего характеристического уравнения (т.е. равно максимальной степени исследуемого на данном этапе многочлена). Для сформированных рядов Тейлора вычисляются корни, из которых оставляют те корни, которые распложены между соответствующими двумя корнями (между которыми сформирован рассматриваемый ряд Тейлора) производной меньшей степени. Ф.24. Уточнение найденных корней производится способом касательных ф.25 в «вычислителе … 12.36».
По найденным корням первого этапа вычисляются корни второго этапа: при этом рассматривается производная математической модели степенного многочлена, 1 меньшего порядка, но большей степени в «вычислителе корней 12.13.2» аналогично предыдущему этапу [л.6, стр.15]
a 1r2+a 2r+c=0
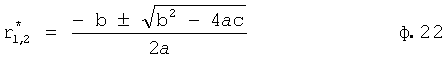
где 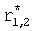 - корни максимальной производной одного из четырех степенных многочленов характеристического уравнения (находятся в стандартном…12.12 на предварительном этапе).
- корни максимальной производной одного из четырех степенных многочленов характеристического уравнения (находятся в стандартном…12.12 на предварительном этапе).
На первом этапе формируются ряды Тейлора второй степени ф.23
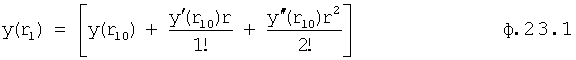
где 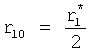
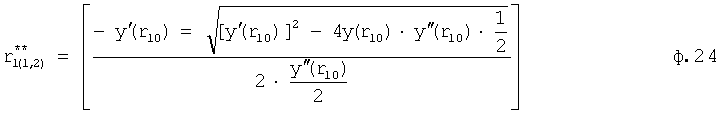
получены по ф.22, из двух корней выбирают тот, который расположен левее 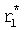
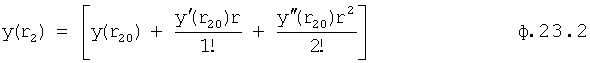
где 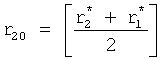
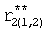 находят по формуле 22 и оставляют тот корень, который расположен левее
находят по формуле 22 и оставляют тот корень, который расположен левее 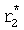 .
.
Найденные значения 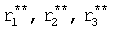 уточняются способом касательных по ф.25, Л.7, стр.390. ф.(3)
уточняются способом касательных по ф.25, Л.7, стр.390. ф.(3)
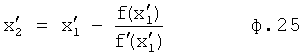 ,
,
где 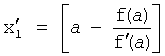
f(a) - функция [и касательная f'(a)] в точке 
Искомые корни исследуемых четырех степенных многочленов ф.21.1… получаются на последних этапах. Поиск областей расположения искомых корней проводится между корнями соответствующих производных, которые найдены на предыдущих этапах.
Найденные корни на последних этапах соответствуют точкам пересечения кривых с осями α и β неявных функций ф.20.1 (фиг.6.1) и ф.20.2 (фиг.6.2).
Если кривые действительной части L и кривые мнимой части В поместить на одну плоскость осей, то точки пересечения этих кривых будут иметь координаты, значения которых соответствуют значениям мнимой β и действительной α части корней исследуемого характеристического уравнения ri=αi+jβ.
Для того чтобы решить систему двух уравнений с двумя неявными функциями (с двумя неизвестными α и β) ф.26, переходят к решению системы уравнений, составленных для прямых, проходящих через точки пересечения кривых с осями ф.8. По координатам точки пересечения этих прямых задают соотношение переменных α=f/β, которое подставляется в уравнения системы неявных функций ф.26.
Если формулы 20 представить более подробно, то поиск кривых двух неявных функций αB=fB(β) αL=fL(β) системы уравнений L=0 и В=0 можно показать графически фиг.6… После подстановки α=0 и β=0 в соответствующие равенства L=0 и В=0 получаются четыре частных случая 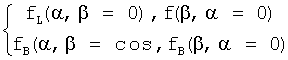
Из ф.26 видно, что для нахождения корней βi удобно осуществлять подстановку 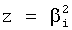 , которая позволяет получить формулы [более удобные] для вычисления корней ф.22, 23. Ф.27.
, которая позволяет получить формулы [более удобные] для вычисления корней ф.22, 23. Ф.27.
Если анализировать характер изменения исследуемых кривых αL=f(β), αB=f(β) в интервалах между ближайшими корнями (от βi до +βi), то учитывают, что эти кривые 1) непрерывны и 2) не имеют комплексных корней (т.е. количество точек перегиба равно количеству корней). Исходя из вышесказанного, исследуемые кривые в интервале от βi до β=0 будут плавно изменяться: увеличиваться, если действительный корень αi на оси α положителен (или отрицательный, если корень на действительной оси α отрицательный αi<0), фиг.64.
Формируются системы из двух уравнений для каждого из интервалов ф.29. Точки пересечения двух кривых второй степени являются приближенными значениями искомых корней характеристического уравнения ф.26.1.1. Если максимальная степень «n» характеристического уравнения четная (т.е. если n - четное число), то
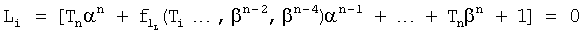
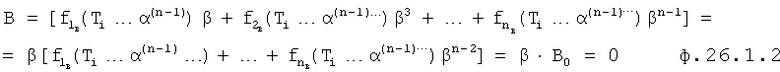
не четная, то
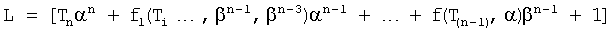
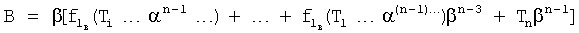
После подстановки α=0 и β=0 в L=0 и B=0 получены ф.26.2 (где z=β2)
при n - четной

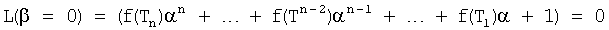
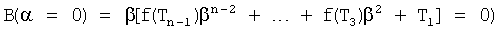
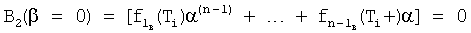
при n - нечетной
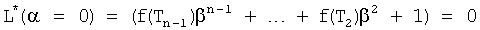
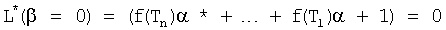
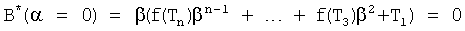
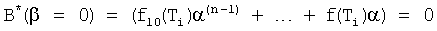
Развернутое нахождение функций T1… для ф.26 приведены в ф.27 для характеристического уравнения пятого порядка производных
T5r5+Tyr4+T3r3+T2r2+T1r+1=0
Подставляется r=α+jβ ф.27.1
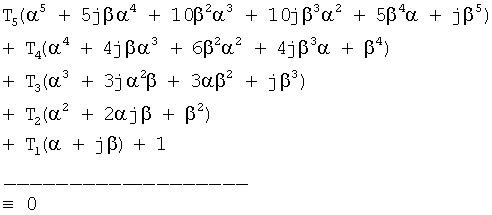
Из ф.27.1 находят «L» и «B» ф.27.2
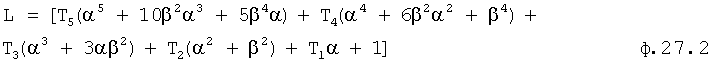
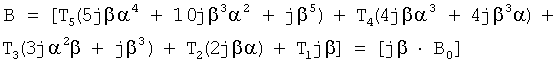
Их ф.27.2 находят L(α=0), L(β=0), B(α=0), B(β=0) ф.27.3
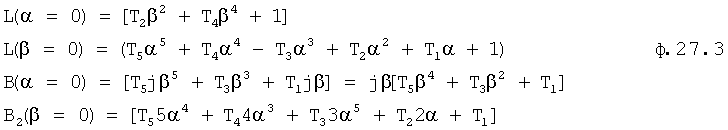
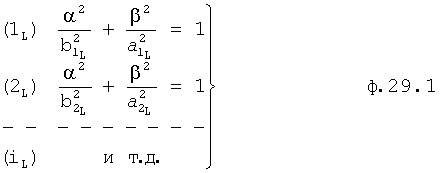
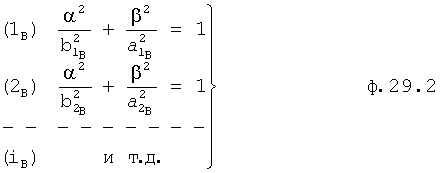
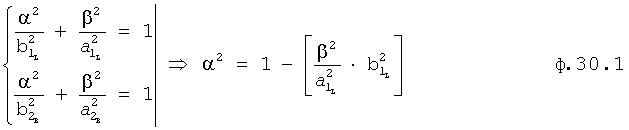
после подстановки
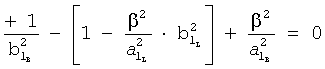
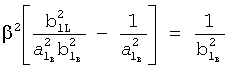
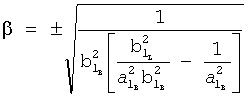
Найденное значение β подставляют в одну из формул 30.1
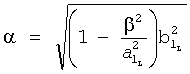
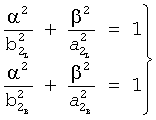
Мнимую β и действительную α части корня r2=α2±jβ2 находят аналогично ф.30.1 и т.д.
Таким образом, определитель точки пересечения двух кривых 12.57 (фиг.4), используя ф.30.1…, определяет приближенные значения действительных αi и мнимых βi составляющих корня ri=αi±jβi.
Уточняющий вычислитель комплексных корней 12.18 (фиг.4). используя численные преобразования, позволяет повысить точность нахождения комплексных корней.
Исходное характеристическое уравнение ф.19.1 делится на значение явных действительных корней
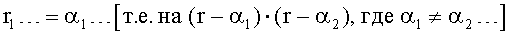
найденных по ф.21.1 (или ф.21.3). Явные действительные корни, имеют действительные значения, неравные между собой, т.е. α1≠α2 и т.д.
Если αi=αj…, то эти значения однозначно нельзя отнести ни к действительным корням ri=αi, ни к комплексным ri=αi+jβi.
После деления получается степенной многочлен с четным максимальным значением степени ф.31*
M=Tn+rn*+T(n*-1)r(n*-1)+…+T1r+1=0.
Сущность «численного» нахождения комплексных коней неявной функции заключается в том, что действительную L=0 и мнимую B=0 части приводят к виду степенного многочлена ф.31.0 [л.8, стр.404] относительно мнимой части корня
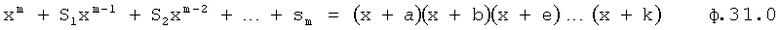
где 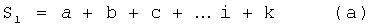
S2=ab+ac+…+ik
S3=abc+abd+…
………………
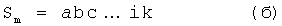
Максимальная степень n* исходного исследуемого характеристического уравнения, полученного после деления, четная. Для приведения уравнения к виду ф.31.0 используют ф.31.1… из ф.26.1.1
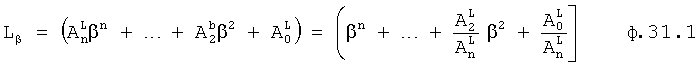
где
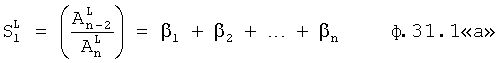
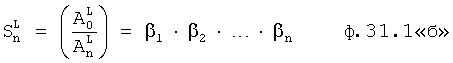
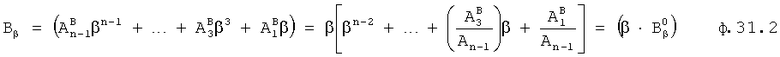
где
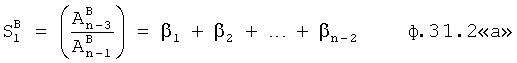
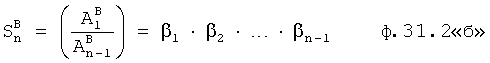
Формируется степенной многочлен с одним неизвестным α по ф.32.0, которая получена из ф.31.1 «а», «б» и ф.31.2 «а», «б» (которые в свою очередь получены из ф.30.0 а, б)
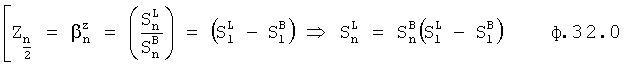
Из степенного многочлена 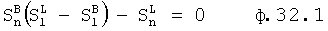
определяется и подставляется в ф.32.2

rn=αn±βn.
Найденные α и β ф.32.2 корня r1,2=α+jβ подставляют в ф.33, в которой степенной многочлен «М» (ф.31.*) делится на произведение биномов [(r-r1)(r-r2)] найденных корней
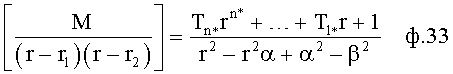
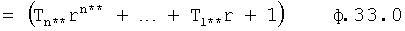
В степенной многочлен ф.33.0 подставляют (r=α+jβ) и разделяют на действительную L**=0 и мнимую В**=0 части
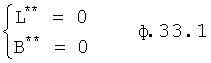
Максимальная степень n** также четная, а ф.33.1 приводится к виду ф.31.0 по ф.31.1…
Из ф.31.0 «б» и «а» видно, что если разделить коэффициент Sm одного многочлена на коэффициент степенного многочлена SmД, корни которого включают корни предыдущего многочлена, за исключением одного rД, то результат от деления будет равен этому корню ф.34
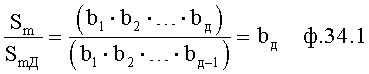
Для проверки найденных значений α и β, входящих в искомые r1, r2
Делитель многочленов фиг.7 делит исходный многочлен Lβ (ф.31.1) на бином, двучлен 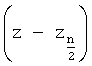 с найденным корнем
с найденным корнем 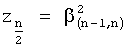 . В результате ф.33.2 получается степенной многочлен
. В результате ф.33.2 получается степенной многочлен 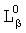 со степенями, равными степеням многочлена
со степенями, равными степеням многочлена 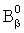 (в скобках) ф.31.2
(в скобках) ф.31.2
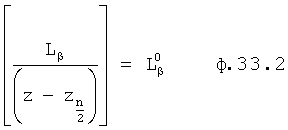
Приравнивание коэффициентов в многочленах  и
и  при членах β с одинаковыми степенями позволяет получить равенства с одним неизвестным α1, имеющих разные степени. Из полученного равенства вычисляются α11… По найденным значениям α1… формируют степенные многочлены с неизвестным β. Для этого найденные значения α1… подставляют в
при членах β с одинаковыми степенями позволяет получить равенства с одним неизвестным α1, имеющих разные степени. Из полученного равенства вычисляются α11… По найденным значениям α1… формируют степенные многочлены с неизвестным β. Для этого найденные значения α1… подставляют в  (или
(или 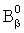 ) и вычисляются β1.
) и вычисляются β1.
Если n - нечетная, то
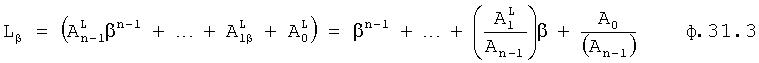
где 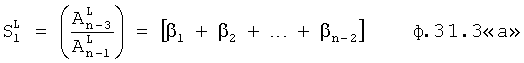
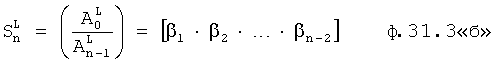
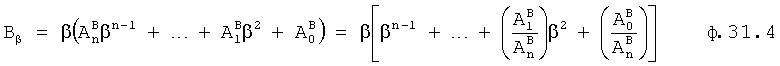
где 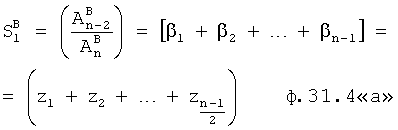
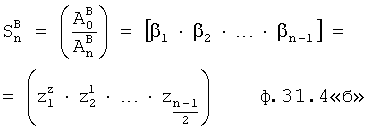
И если от S1 отнять коэффициент S1Д (другого многочлена), то в результате тоже получится корень rД, отсутствующий в многочлене с меньшей максимальной степенью ф.34.2
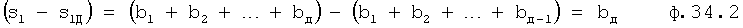
Прировняв ф.34.1 к ф.34.2, получают ф.35
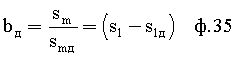
Показатель максимальной степени В** при z=β2 меньше, чем у многочлена L**.
После приведения многочленов L** и В** к виду 31.0 находится значение αn-1 из ф.36
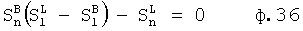
Найденное значение αn-1 подставляется в ф.35 и определяется значение корня 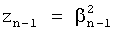 по ф.32.2
по ф.32.2
rn-1=αn-1±jβn-1.
Таким образом, каждый найденный корень rn, r(n-1)… позволяет понизить степень исходного многочлена делением на бином [(r-ri,1)·(r-ri,2)] и идентифицировать все входящие в него корни.
Используемые в быстродействующем 11 и уточняющем 12 вычислителях (фиг.4) производные выходного параметра отражают влияние на объект возмущающих воздействий, действующих на высоких частотах, - это позволяет вовремя предотвратить последствия внутренних изменений, к которым могут привести внезапные возмущения.
Параллельно этим идентифицирующим исследованиям высоких частот внезапных возмущающих воздействий и независимо от них фильтрующий вычислитель 13 исследует характеристики возмущений непосредственно средних и низких частот. При этом процесс идентификации не требуют «статистической» обработки высоких частот и позволяет максимально быстро отделить влияние высоких частот от влияния средних и низких частот, отделив их от суммарного наложения вычитанием «статистической обработки» высоких частот (тем самым отразив их внутреннюю сущность и характер переходных процессов объекта, влияющих на выходной параметр).
Выполняемые преобразования введенным фильтрующим вычислителем 13 заключаются в том, что введенные в него элементы, фиг.7 и фиг.8 (вычислитель корней условной модели 1, определитель структуры 2 и вычислитель производных 3), позволяют определить постоянные внутреннего запаздывания (Т1, Т2,…), не прибегая к измерению реальных производных выходного параметра для заданного момента времени. При этом для нахождения постоянных внутреннего запаздывания исследуется текущее значение выходного параметра и значение текущего момента времени в вычислителе корней условной модели 1 ф.37 (для уточнения вычислений в определителе структуры текущее значение выходного параметра измеряется для двух моментов времени ф.38). При этом выходной параметр и текущий момент времени относительно начального значения выходного параметра и начального момента времени изменяется медленно, что обеспечивает фильтрацию высоких частот (изменения) возмущающего (внутреннего и внешнего) воздействия на выходной параметр. Для повышения точности идентификации на низких частотах используется определитель структуры 2, фиг.7 и фиг.8. При этом производится измерение выходного параметра в дополнительные моменты времени ф.38.
При стабильной структуре передаточной функции W исследуемого объекта, определитель структуры 2 выбирает ту структуру (интегральную, дифференциальную или позиционную), которая наиболее близко отражает параметр внутреннего запаздывания структуры реального объекта, не прибегая при этом к параметрам производных от выходною параметра и передавая на свой выход найденный доминирующий корень в доминирующей структуре
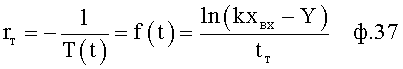
где tт - текущий момент времени,
r - корень дифференциальной модели, получен из y (t)
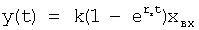
Корень дифуравнения в зависимости от структуры, фиг.8, определяется по-разному (л.3, стр.57-101):
- интегральная структура с замедлением
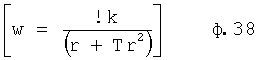
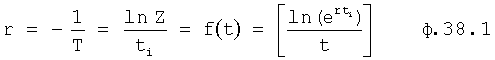
где находится из ф.38.1.1
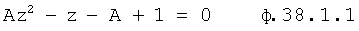
где 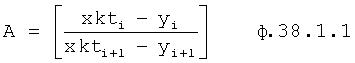
ti+1=2ti
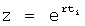
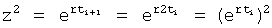
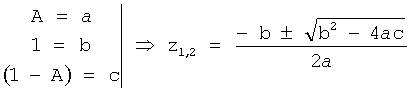
Формула 38.1.1.1 получена из системы уравнений ф.38.1.2. При этом выходной параметр у(t) измеряется через интервал времени Δt, равный моменту времени ti, в который производились предыдущие измерения, т.е. Δt=(ti+1-ti)=ti, t(i-1)=2ti
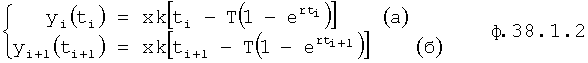
Скобки квадратные раскрываются и (xkti) и (xkti+1) переносятся в левую часть равенств. После этого равенство (а) делится на равенство (б) ф.38.1.2
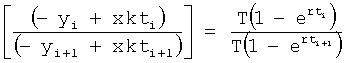
После подстановки А получается:
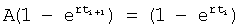
После раскрытия скобок
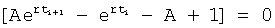
После подставки 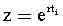 получается ф.38.1.1, дифференциальная структура включает корень r (постоянной T) внутреннего запаздывания
получается ф.38.1.1, дифференциальная структура включает корень r (постоянной T) внутреннего запаздывания
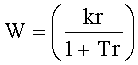
который находится по ф.38.2
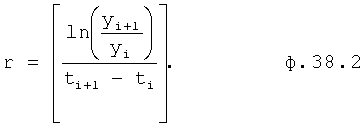
ф.38.2 найдена из системы уравнений ф.38.2.1
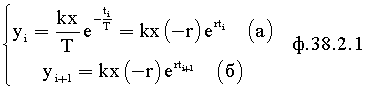
Равенство ф.38.2.1 «б» делится на ф.38.2.1 «а» ф.38.2.2
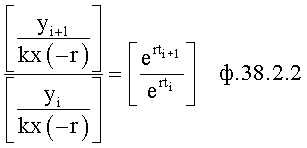
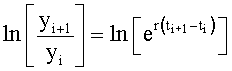
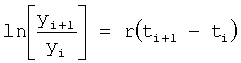
позиционная структура  описываемая дифуравнением (т.е. разностным) с двумя корнями (запаздывания и производными 1-го и 2-го порядка), является более точной моделью позиционного звена (чем условная модель с одним корнем). Для нахождения корней r1, r2 используются измеренные значения выходного параметра, которые получены через заданные промежутки времени Δt=t1 (равные первому моменту времени). Тогда t2=2t1, t3=3t1, t4=4t1 общая формула для выходного параметра позиционного звена ф.38.3.0
описываемая дифуравнением (т.е. разностным) с двумя корнями (запаздывания и производными 1-го и 2-го порядка), является более точной моделью позиционного звена (чем условная модель с одним корнем). Для нахождения корней r1, r2 используются измеренные значения выходного параметра, которые получены через заданные промежутки времени Δt=t1 (равные первому моменту времени). Тогда t2=2t1, t3=3t1, t4=4t1 общая формула для выходного параметра позиционного звена ф.38.3.0
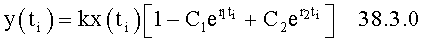
Для нахождения корней r1, r2 по ф.38.3.0 составляются четыре равенства ф.38.3.1
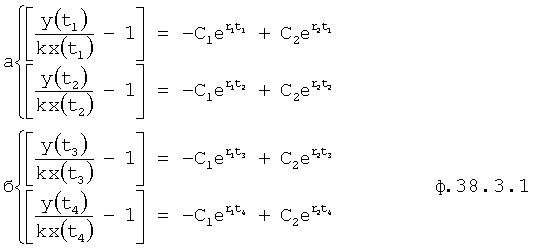
В ф.38.3.1 подставляют L1…4 и R1, R2… по ф.38.3.2
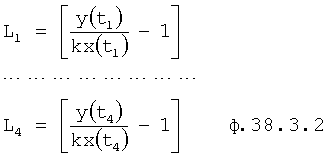
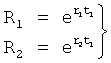 тогда
тогда
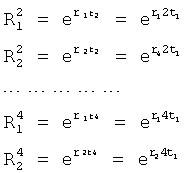
Получаются две системы уравнений ф.38.3.3 «а» и «б»
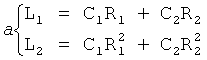
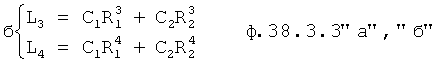
Из каждой системы уравнений «а» и «б» определяются С1 и С2 ф.38.3.4
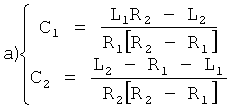
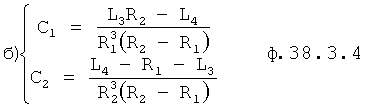
Приравнивая С1 а=С1 б и С2 а=С2 б, получают систему двух уравнений с двумя неизвестными R1 и R2 ф.38.3.5
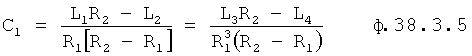
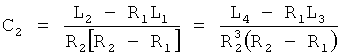
После сокращения на (R2-R1) и избавления от знаменателя получается ф.38.3.6
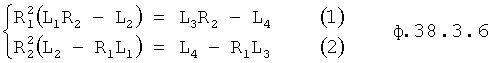
Из ф.38.3.6(1) получают 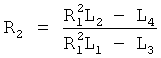
Значение R2 подставяяют в ф.38.3.6(2)
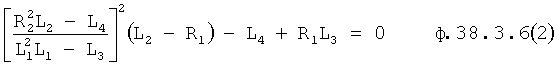
Выражение в скобках возводят во 2-ю степень, получается ф.38.3.7
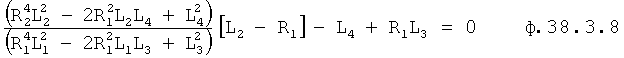
После приведения к общему знаменателю получится ф.38.3.9 для R1
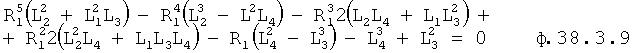
Полученный степенной многочлен ф.38.3.9 решается относительно 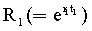 и подставляется в ф.38.3.10 для вычисления
и подставляется в ф.38.3.10 для вычисления 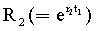
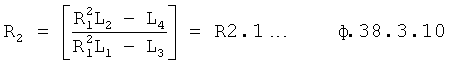
где R1=R1.1… найдены по ф.38.3.9.
По найденным R1i и R2i вычисляются r1i и r2i: по ф.38.3.11
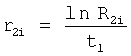
Если найден корень r для каждого текущего момента времени, то можно определить производные изменения корня r'… во времени. Т.к. значение корней, найденных по ф.38, не зависит напрямую от влияния текущих кратковременных возмущений (внутренних или внешних), использование этих корней для вычисления текущих производных выходного параметра приводит к тому, что полученные значения производных 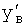 ,
, 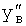 , … не зависят от кратковременных возмущений, поэтому отличаются от реально измеренных
, … не зависят от кратковременных возмущений, поэтому отличаются от реально измеренных 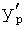 ,
, 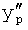 , … Следовательно, при переходе к модели с постоянными корнями (дифуравнения), но при большем их количестве, получаются параметры, значения которых зависят от длительных возмущений или функции от интеграла высокочастотных возмущений (задача интеграла высокочастотных возмущений - фильтровать и суммировать, а задача функции от интеграла - находить усредненную функцию делением интеграла на интервал времени, в течение которого определялся интеграл). Формулы ф.39 позволяют найти производные выходного параметра по вычисленным корням r и его производным r' - эти найденные производные
, … Следовательно, при переходе к модели с постоянными корнями (дифуравнения), но при большем их количестве, получаются параметры, значения которых зависят от длительных возмущений или функции от интеграла высокочастотных возмущений (задача интеграла высокочастотных возмущений - фильтровать и суммировать, а задача функции от интеграла - находить усредненную функцию делением интеграла на интервал времени, в течение которого определялся интеграл). Формулы ф.39 позволяют найти производные выходного параметра по вычисленным корням r и его производным r' - эти найденные производные 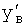 ,
, 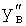 отличаются от реальных, но получаемые по ним корни ф.40 более стабильны и позволяют приблизить модель к реальному объекту.
отличаются от реальных, но получаемые по ним корни ф.40 более стабильны и позволяют приблизить модель к реальному объекту.
Для того чтобы максимально избавиться от погрешности (вносимой вычислителем корней условной модели 1 и определителя структуры 2 фиг.8), используется вычислитель постоянных внутреннего запаздывания 4.3 и вычислитель корней 5.1.3, в которых корни математической модели вычисляются по ф.40.3.1… При этом требуется больше времени для идентификации и увеличивается количество измерений выходного параметра в заданные моменты времени.
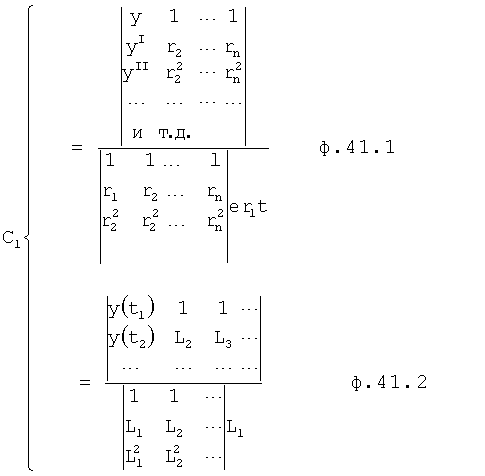
По найденным значениям корней r1, r2… по ф.41 определяются постоянные коэффициенты С1,… полного решения дифуравнения.
В зависимости от структуры модели производные выходного параметра условных моделей приведены в ф.39.1:
- позиционная структура звена 1-го порядка
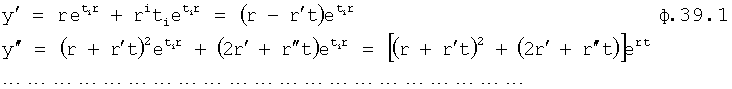
и т.д.,
где
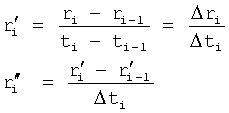
и т.д.
- интегрирующая структура звена
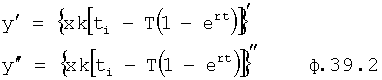
и т.д.
- дифференцирующая структура звена
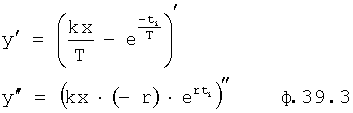
и т.д.
- позиционная структура звена 2-го порядка (инерционного или колебательного)
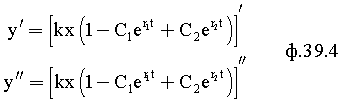
и т.д.
- по вычисленным производным ф.39… вычисляют постоянные внутреннего запаздывания Т1, Т2… по ф.40
Если необходимо обеспечить быстродействие, то используют ф.40.1
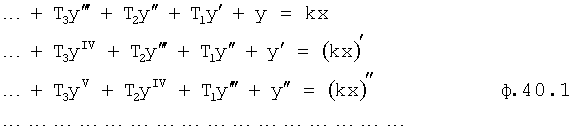
и т.д.,
где 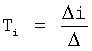
y', y''… вычисляются по ф.39.
Достоинство ф.39.1 в том, что легко находятся производные высоких порядков. Если необходимо обеспечить сочетание быстродействия и качества, то используют ф.4.2, для которой требуются дополнительные измерения выходного параметра в моменты времени t1…m (что снижает быстродействие, но приближает математическую модель к параметрам реального объекта)
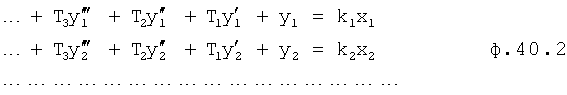
и т.д.,
где 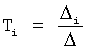
yi=y(ti); 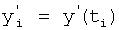
i=1,2.
Если необходимо обеспечить максимальную точность математической модели объекта (включающую параметры коэффициентов внутреннего запаздывания Т), то используют ф.40.3, в которой обеспечивают результаты измерения выходного параметра через заданные промежутки времени Δt=t1; т.е. t2=2t1, t3=3t1….
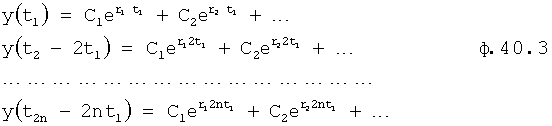
 После подстановки
После подстановки
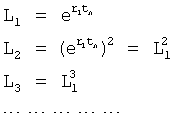
и т.д.
Из ф.40.3 получают ф.40.3.1
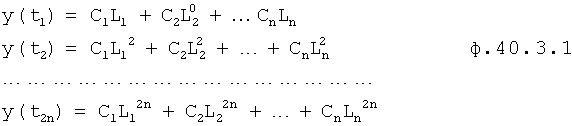
Из ф.40.31 формируют «n» систем уравнений, в каждую из которых входят по «n» равенств, определяющих С1 ф.40.3.2
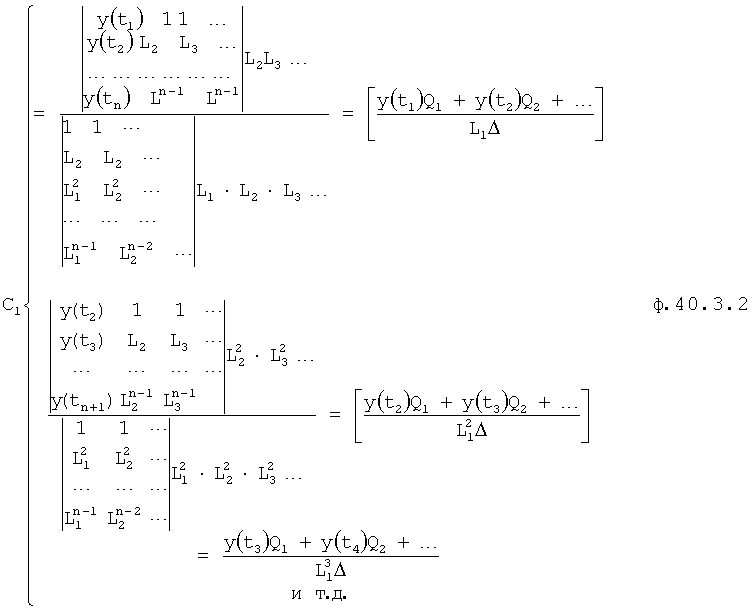
где Q1 - алгебраические дополнения.
Если приравнивать между собой равенства, входящие в ф.40.3.2, то получится новая система уравнений ф.40.3.3
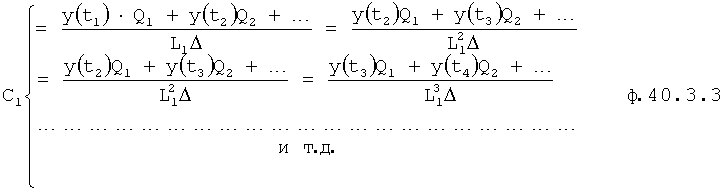
После сокращения на L1 и Δ1 получится уравнение ф.40.3.4 и система уравнений ф.40.3.5
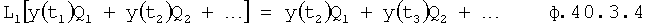
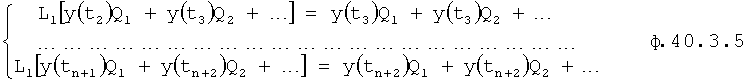
Систему уравнений ф.40.3.5 решают относительно (Q2, Q3…) при помощи алгебраических дополнений ф.40.3.6
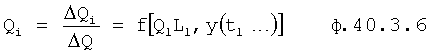
Найденные Q2… подставляют в ф.40.3.4 и сокращают на Q1, получается ф.40.3.7, в которой L является неизвестным.
По найденным значениям L1… вычисляют r1… по ф.40.3.8
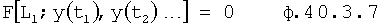

Найденные значения r1… позволяют вычислить коэффициенты решения дифуравнения по ф.41.
Где у', y'' - вычисленные производные по модели с переменными корнями r=f(t) ф.39
Где L - вычислены из ф.40.3.7
C2 = … Аналогично
…………………
Сущность введенных изменений в фильтрующий вычислитель 13 (фиг.4) заключается в том, что они позволяют фильтровать помехи, приводящие к погрешности идентификации. При этом
1) канал идентификации, включающий вычислитель корней условной модели 1 (фиг.8), имеет максимальное быстродействие и упрощает процесс формирования дифуравнений, описывающего состояние объекта, включающего высокие степени производных;
2) канал идентификации, включающий определитель структуры 2, уменьшает затраты времени, необходимые для идентификации структуры передаточной функции (дифференциальной, интегральной или позиционной), что в свою очередь характеризует устойчивость и уменьшает соответствующую, связанную со структурой погрешность идентификации;
3) канал идентификации определяет модель объекта по значениям выходного параметра, измерение которого проводилось соответствующее количество раз через определенный интервал времени, без учета производных (вычисленных или измеренных), что позволяет полностью избавится от помех.
Сравнение трех моделей идентификации (1, 2, 3) между собой позволяет судить не только о внутренних состояниях объекта, но и о характере помех, возникающих в процессе регулирования, что очень важно в сложных технологических процессах.
Основным параметром устойчивости является действительная часть корня. В то же время мнимая часть корня однозначно влияет на колебательность. Поэтому удобно переходить к модели объекта с переменными корнями во времени (действительными или комплексными). Переменные корни позволяют определять промежутки времени, для которых модель принимает неустойчивый характер.
Введенные в канал действительных переменных корней (фиг.4 п.14.1) элементы позволяют определить значения корней в любой интервал времени Δt и для дифуравнения с любой степенью производных по ф.42 за минимально короткое время.
Введенные в канал «переменных комплексных корней 14.2 фиг.4» изменения позволяют найти переменные комплексные корни для дифуравнения с производными любой степени. При этом вычисления сводятся к нахождению приведенных переменных коэффициентов ф.45 дифуравнения по формулам 43 и 44 и определению функции времени для найденных коэффициентов по формулам 40.3…и 41, используемых в фильтрующем вычислителе 13 п.4.3 и п.5.1.3, фиг.8. Формула 40.3 примет вид ф.46. Соответствующим образом изменятся и все последующие формулы 40.3.1 и т.д., принимая вид ф.47. Введенные изменения позволяют использовать формулы [л.9, стр.198] для нахождения комплексных переменных корней п.11, фиг.10, ф.48. Блок проверки корней 13, используя соответствующие переменные коэффициенты  проверяет точность найденных переменных корней по формулам 49. Блок определения ОДЗ п.12, используя ф.50 определяет зоны устойчивых значений корней tну<tуст<tkу и зоны неустойчивых tнн<tнус<tkн,
проверяет точность найденных переменных корней по формулам 49. Блок определения ОДЗ п.12, используя ф.50 определяет зоны устойчивых значений корней tну<tуст<tkу и зоны неустойчивых tнн<tнус<tkн,
Канал действительных переменных корней п.14.1 производит вычисления по ф.42
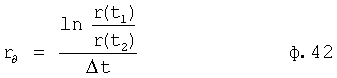
Где r∂ - действительное значение переменного корня исследуемой составляющей выходного параметра
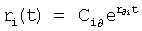
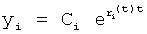
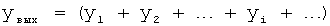
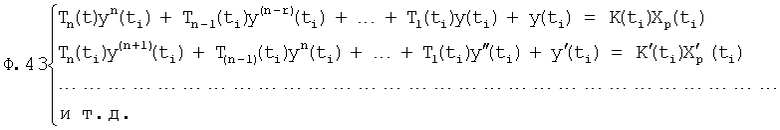
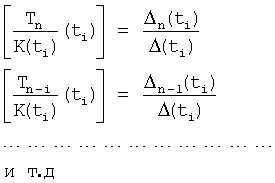
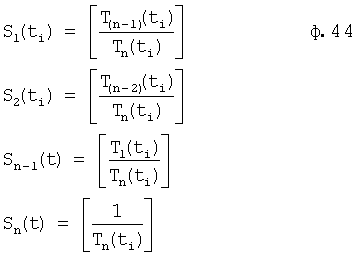
Характеристическое уравнение рассматриваемого дифуравнения ф.43 можно привести к виду ф.45
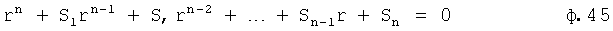
где
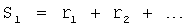
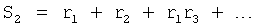
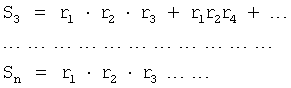
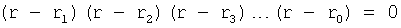
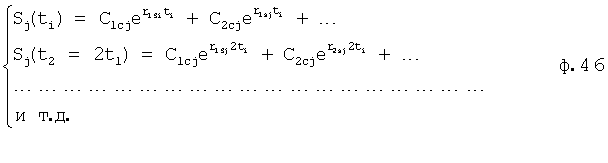
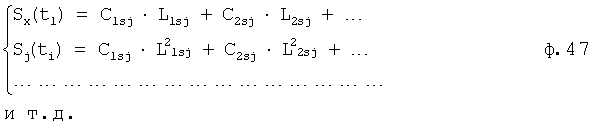
где r(1…)(s) - корень математического выражения, отражающий переменный характер исследуемой составляющей 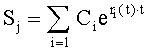
После того как по ф.46 и ф.47 будут определены математические модели для изменения во времени коэффициентов S1…, формулы ф.48 позволяют определить изменение во времени каждого из корней r1…(t) выходного параметра
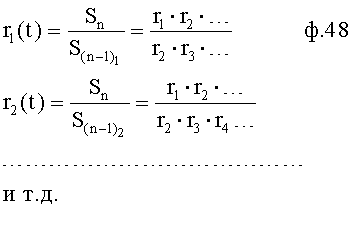
Полученные значения r1…(t) (для их проверки) подставляют в ф.49 и проверяют с полученными ранее значениями S1 и S2 из ф.45…47
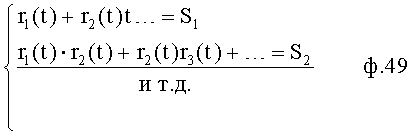
Полученные модели ф.48 подставляют в ф.50 для области определения ОДЗ.
Вычисляются tгр граница устойчивости для каждой из ф.(1), (2),…ф.50.1

Выбирается устойчивая область, справедливая для каждого равенства (1), (2).
и т.д.
Если корень R=ert (решения y=eRt) изменяется быстро и в «малом» (и в «большом»), что не позволяет пренебречь этим изменением, то дифуравнение примет вид ф.49.1 (п.15 фиг.10)
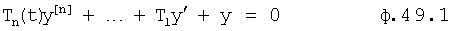
где подставляется решение 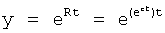
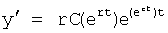
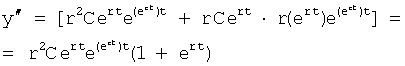
Получается ф.49.2 после сокращений на 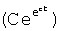
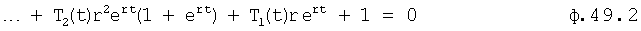
После дифференцирования (п.16 фиг.10) уравнение ф.49.2 получается ф.49.3
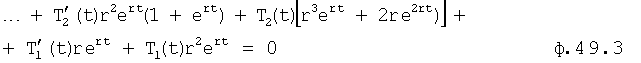
После сокращения на rert получается ф.49.4
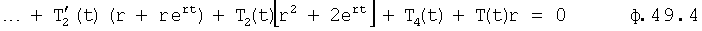
Уравнение ф.49.4 решается относительно ert ф.49.5 (п.18 фиг.10)
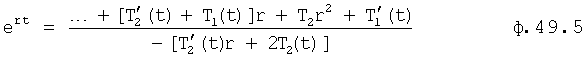
После повторного дифференцирования (п.17 фиг.10) ф.49.2 примет вид ф.49.6
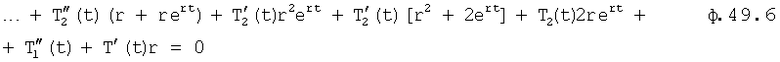 Ф.49.6 решается относительно R=ert (п.18 фиг.10) ф.49.7
Ф.49.6 решается относительно R=ert (п.18 фиг.10) ф.49.7
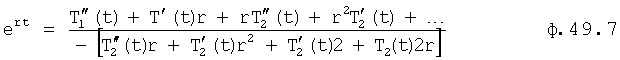
Определить степени «r» переменного корня «R» (п.19 фиг.10) приравнивает ф.49.5 и ф.49.7, и исключает ert и находит значение корней r степенного многочлена ф.49.8
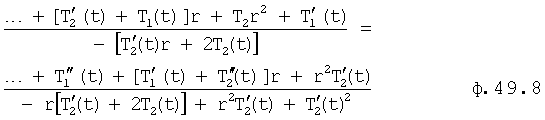
Определитель постоянных полного решения дифуравнения (п.20 фиг.10) формирует система уравнений из полного решения дифуравнения и его производных ф.49.9
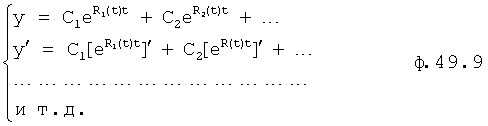
После подстановки в ф.49.9 значения текущего момента времени tT определяются постоянные полного решения ф.49.10
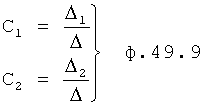
где Δ,Δ1… - определители системы уравнений ф.49.9.
Введенные изменения в определитель внешнего запаздывания 15, фиг.4, позволяют обеспечить непрерывный контроль (в текущем режиме регулирования) за параметром внешнего запаздывания, при этом не требуется использования дополнительного калиброванного входного воздействия. Так как при этом иногда требуется обеспечить быстродействие, а иногда возникает необходимость фильтрации помех, создаваемых неучтенными возмущениями на объект, используют два параллельных канала 1-й и 2-й.
Введенные изменения в быстродействующий канал 1-й, фиг.11, позволяют найти взаимозависимость между постоянными коэффициентами С1, …, входящими в соответствующие слагаемые выходного параметра y1, …, ф.51, что в свою очередь позволяет сформировать уравнение с неизвестным Сi ф.52.
Для того чтобы выразить соотношение между коэффициентами С1…, из ф.51.1 находят t по ф.51.2
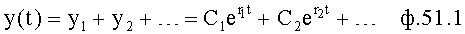
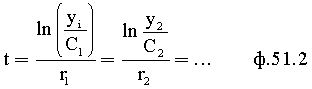
Из ф.51.2 можно сформировать систему уравнений ф.51.3
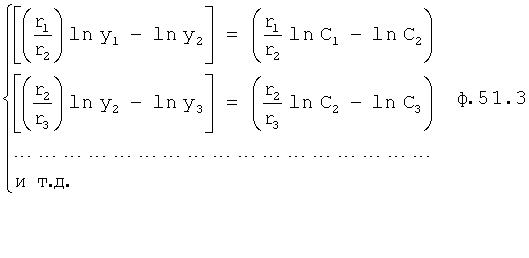
После преобразований ф.51.3 примет вид ф.51.4
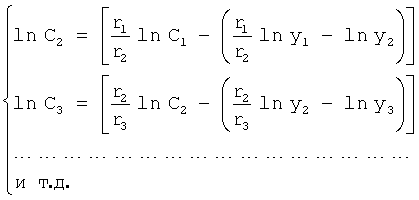
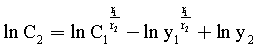
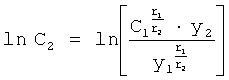
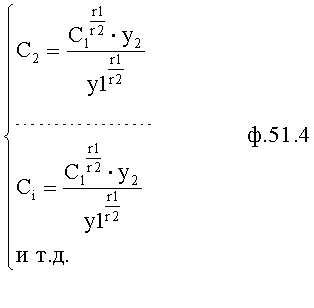
где значения r1 находят из ф.51.5 по коэффициенту T1…
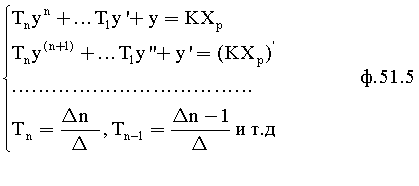
 а значения у1 … находят из системы уравнений ф51.6 после подстановки r1
а значения у1 … находят из системы уравнений ф51.6 после подстановки r1
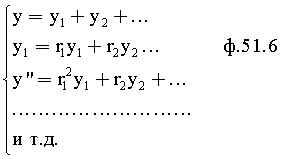
Найденные соотношения 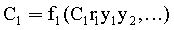 подставляются в решение дифуравнения yиз для известного момента времени tизв
подставляются в решение дифуравнения yиз для известного момента времени tизв

показатели степеней при С приводят к общему знаменателю
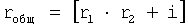
И вводится новая переменная 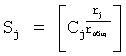 , тогда
, тогда 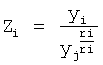
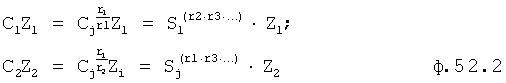
Формула 52 примет вид степенного многочлена с одним неизвестным Sj ф.53
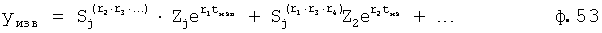
Нахождение корней Sj1… в ф.53 позволяет определить возможные совокупности значения коэффициентов С1, С2… по ф.5.2.2 и ф.5.1.4.
Найденные значения С1, С2… подставляются в ф.51.2 и подбирается соответствующая совокупность коэффициентов, определяется текущий момент времени tт.
Введенные в фильтрующий канал (фиг.12) изменения позволяют контролировать изменения «внешнего» запаздывания, не прибегая к дополнительным калиброванным входным воздействиям, при этом воздействие высокочастотных помех не влияет на точность идентификации. Введенный формирователь системы уравнений выходных параметров через известный интервал времени 6.1 (фиг.12) позволяет по значениям исследуемого параметра y, величина которого y(ti), y(ti+Δt)… измерена через заданные постоянные промежутки времени Δt, и по постоянным коэффициентам полного решения дифуравнения С1… (полученным относительно заданного момента времени rзад) определить текущее значение момента времени tт. При этом используется система уравнений ф.54, которая получена из математического выражения для полного решения дифуравнения. Если выходной параметр измерялся через одинаковые промежутки времени, то слагаемые полного решения дифуравнения, характеризующие относительно независимость каждой из емкостной составляющей исследуемого (входного или выходного) параметра, разделяются на постоянную М1… и переменную Мn1… составляющие. В то же время переменная составляющая Мn, представляет собой степенную функцию 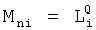 , а систему уравнений ф.54 можно представить в виде совокупности степенных уравнений. Для нахождений оснований L этих степенных функций можно использовать ф.40.3 7, для нахождения коэффициентов, стоящих перед основанием степенной функции, можно использовать ф.40.3.1…6. По найденным коэффициентам ф.40.3.7 определяются корни степенного многочлена, значения которых совпадают со значениями Li основания степенных функций Li Q переменных (Мn) cоставляющих.
, а систему уравнений ф.54 можно представить в виде совокупности степенных уравнений. Для нахождений оснований L этих степенных функций можно использовать ф.40.3 7, для нахождения коэффициентов, стоящих перед основанием степенной функции, можно использовать ф.40.3.1…6. По найденным коэффициентам ф.40.3.7 определяются корни степенного многочлена, значения которых совпадают со значениями Li основания степенных функций Li Q переменных (Мn) cоставляющих.
Сущность членений заключается в том, что подстановка коэффициентов С1…, корней r1… в постоянные составляющие М1 (соответствующих слагаемых выходного (входного) параметра) позволяет определить момент времени t1, при котором производилось первое измерение (используемое в системе уравнений параметров у)
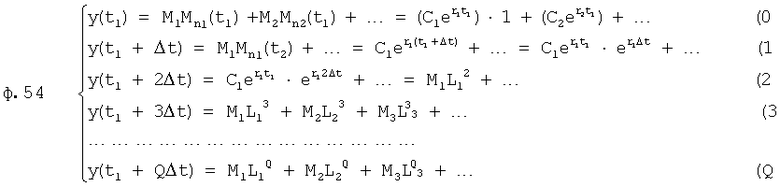
где 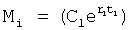 - постоянная составляющая слагаемого
- постоянная составляющая слагаемого
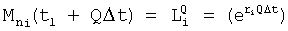 - переменная составляющая
- переменная составляющая

L1,2,… - находят по ф.40.3.7, полученной по ф.40.3.1…6
Найденные значения L1,2… подставляются в ф.54 и вычисляются постоянные составляющие 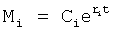 (i=1,2) по ф.55.
(i=1,2) по ф.55.

где Δi, Δ - определители системы уравнений ф.54.
Найденные значения М1…, С1… r1… подставляются в ф.56 и вычисляется момент времени t1, с которого начаты измерения выходного параметра y(t1) при формировании ф.54
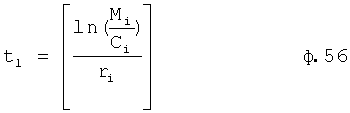
где 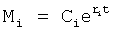 найдены из ф.55
найдены из ф.55
Ci найдены из ф.41.2 для известного заданного tзад момента времени п.4, п.5 фиг.12
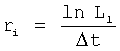 найдены из ф. 40.3.8, п.3 фиг.12,
найдены из ф. 40.3.8, п.3 фиг.12,
Δt - интервал времени, через который проводились измерения у(t1), y(t1+Δt)…
Каждый из каналов определения внешнего запаздывания, фиг.13 (быстродействующий 1 и фильтрующий 3), помимо определителя момента времени входного и выходного параметра объекта включает в себя соответствующий (5.1 и 5.2) блок вычитателей, структурная схема которого приведена на фиг.14. Введенные изменения в блок вычитателей позволяют сравнивать текущий момент времени входного и выходного параметра и определять внешнее запаздывание в более жестких условиях, чем обычные:
1) при действии возмущающих помех (таймер 3 измеряет временную задержку внешнего запаздывания независимо от помех);
2) при изменяющихся входных воздействиях (схема сравнения 7 открывает ключ 6 при изменении входного сигнала, изменяя схему вычитания, позволяя хранить предыдущий сигнал в памяти и использовать его для сравнения).
Введенная схема сравнения 6 фиг.13 позволяет сравнить идентификацию внешнего запаздывания «в малом», т.е. при небольших кратковременных воздействиях (полученную в быстродействующем канале), с идентификацией внешнего запаздывания «в большом» (полученную в фильтрующем канале). Получение исчерпывающей информации об объекте позволяет предотвратить неблагоприятные режимы.
Для математического моделирования выходного параметра при изменившихся входных воздействиях необходимо учитывать изменившиеся значение постоянных C1… полного решения дифуравнения. Значения коэффициентов С1… зависят от последовательности взаимодействия внутренних составляющих математической модели ф.57 (W1, W2…) Стандартные полные решения дифуравнения не позволяют увидеть последовательности взаимодействия отдельных составляющих. Для составления такой математической модели используют, определитель последовательности взаимодействия звеньев математической модели 16» и фиг.4 (и фиг.15). Введенный элемент сравнения «5» сравнивает выходной параметр исследуемого звена Wj в конечный момент i-го воздействия и в начальный (i+1)-го воздействия (фиг.16), позволяя проверить правильность выбранной позиции для данного звена ф.58 в элементе подстановки звена 4.1 (фиг.1.5).
Таким образом, вычислитель частных постоянных при i-м воздействии по постоянным общего решения 1 использует ф.59. Подключенный к его выходу вычислитель значений выходного параметра звена при конечном моменте входного I-го воздействия использует ф.60. Вычислитель частных постоянных при i+1-м воздействии использует ф.61. Вычислитель значения выходных параметров звена в начальный момент (i+1) воздействия использует ф.62.
Введенные определители выбранной позиции 3 фиг.15 подставляют в соответствующую позицию каждое из звеньев и выбирают то звено, у которого параметры совпадают при изменении входного воздействия ф.57. После найденного звена в первой позиции переключается поиск звена во второй позиции и т.д.
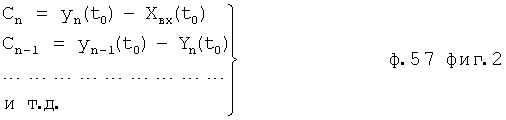
где - yn=(XвхW1) - выходной параметр звена Wn.
Tny′n+yn=Xp - Дифуравнение звена Wn
- yn-1=(yn·Wn-1) - выходной параметр звена Wn-1
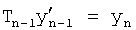 - Дифуравнение звена Wn-1
- Дифуравнение звена Wn-1
и т.д. (фиг.2)
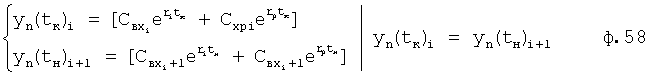
Где yn(tк)i - выходной параметр Wn в конечный момент воздействия i-го
y(tн)i+1 выходной параметр Wn звена в начальный момент (i+1)-го воздействия
Свхi - находят по постоянным Cni полного решения дифуравнения с выхода определителя, фиг.15 при Xp i-м по ф.59
Cвхi+1 - находят по постоянным С полного решения дифуравнения Cn(i+1) при Хр(i+1)-м по ф.59.
При известном входном воздействии математическую модель Тiy'i+yi=Xвx исследуемого звена Wi переносят в правую часть дифуравнения и рассматривают его выходной параметр yi, в виде частного решения 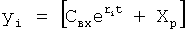 у которого коэффициент отличается от коэффициента полного решения
у которого коэффициент отличается от коэффициента полного решения 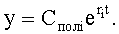 При этом постоянные частного решения Свx находятся по постоянным полного решения Сn, найденным определителем динамических характеристик 1 фиг.15. ф.59
При этом постоянные частного решения Свx находятся по постоянным полного решения Сn, найденным определителем динамических характеристик 1 фиг.15. ф.59
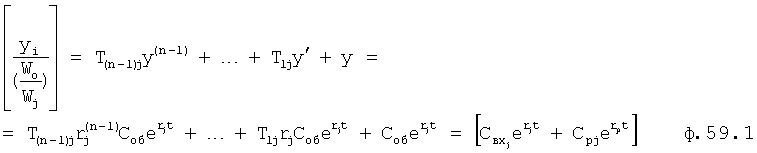
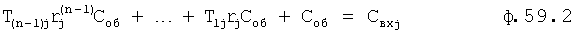
После приравнивания коэффициентов при одинаковых степенях 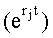 получается ф.59.2. Из ф.59.2 вычисляется коэффициент Свxj при i-м входном воздействии. Найденные значения подставляют в ф.58.
получается ф.59.2. Из ф.59.2 вычисляется коэффициент Свxj при i-м входном воздействии. Найденные значения подставляют в ф.58.
Для того чтобы обеспечить контроль за значениями ОДЗ выходных параметров звеньев W1… (на которые условно разделена математическая модель объекта), находят полные решения дифуравнений каждого звена ywi. При составлении дифуравнений учитывается положение звена Wi, фиг.2, относительно других звеньев (для нахождения входного воздействия на исследуемое звено) и значение корня ri дифуравнения, формирующего внутреннюю постоянную запаздывания Тi этого звена ф.60 фиг.17. Замена показательной функции etr степенной Zr с переменным основанием Z=et ф.61 позволяет упростить поиск области изменения исследуемого параметра. Отрицательные значения степененей ri<0 переносятся в знаменатель. Для избавления от дробных значений степеней вводится новая единица измерений, величина которой равна дробному значению 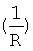 , в знаменателе которой стоит значение общего знаменателя, к которому приводятся все значения степеней ф.62. В результате получается математическое выражение, позволяющее стандартными методами решить неравенства относительно ОДЗ [л.7, стр.356…386]
, в знаменателе которой стоит значение общего знаменателя, к которому приводятся все значения степеней ф.62. В результате получается математическое выражение, позволяющее стандартными методами решить неравенства относительно ОДЗ [л.7, стр.356…386]
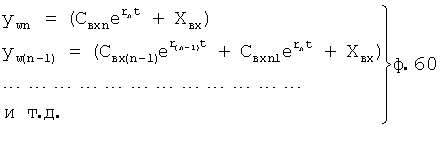
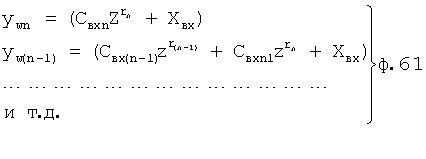
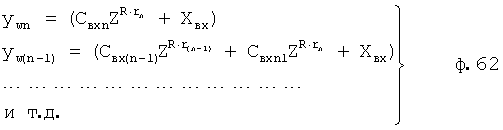
Уравнения ф.62 приравнивают границам ОДЗ ф.63
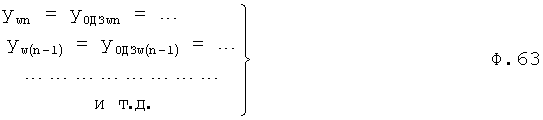
Нахождение корней Z1… ф.63 для каждого из уравнений позволяет найти моменты времени, при которых происходит пересечение значения исследуемого параметра УWn… и значения границ ОДЗ, по которой определяют интервалы времени между ними.
Формула 64 позволяет перейти от основания степенной функции к переменной времени
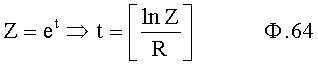 .
.
Формулы 63 и 64 можно использовать для задания ”желаемых” значений ywn… и проверки полученной модели САР (возможности достижения заданных значений ywзодn…).
Для более детального получения информации об объекте и САР в «блок контроля ОДЗ действительной САР в 18» (фиг.1) введены два канала 18.1 и 18.3 (фиг.18). Канал 18.1 разделяет реакцию объекта на текущее воздействие и предыдущее.
Канал 18.3 определяет интегральную постоянную для каждой емкостной составляющей объекта.
Введенный вычислитель реакции на текущее воздействие 3 фиг.18 в ф.65.1 подставляет коэффициенты, найденные по ф.65.6
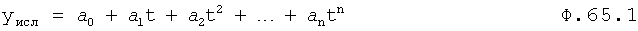
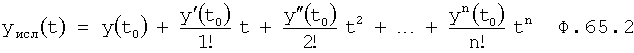
где a0=y(t0)
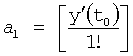
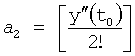 ;
;
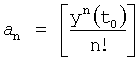
t - «малое»
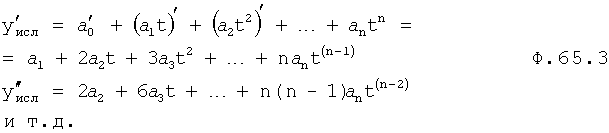
где а 0, а 1, а 2… - приняты «постоянными» в «малом» ф.65.3 (но «переменными» в «большом», т.е.
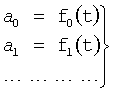 находят по ф.65.5 из системы уравнений
находят по ф.65.5 из системы уравнений
Следовательно, коэффициенты из ряда ф.65.1 a 0, a 1… в ф.65.3 можно считать постоянными (аналогично ряду Тейлора ф.65.2), т.е. момент времени (t0) выбран близким к исследуемому моменту (tисл) ф.65.2. ф.65.3 справедлива, т.к. дифуравнение описывает состояние объекта (изменение Δy=(yнач-yтек) выходного параметра и его производных), на какой-то малый момент времени (tн) при нахождении производных можно считать, что переменная времени t изменялась в ”малом”
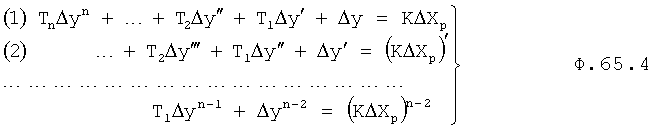
После подстановки ф.65.1, ф.65.3 в формулу 65.4 получится ф.65.5
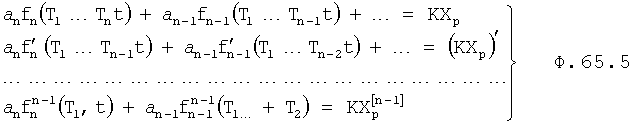
где 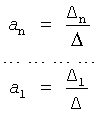
Δn…1 - определители соответствующего столбца,
Δ - главный определитель,
Δy, Δy'… - изменение текущего значения исследуемого параметра «у» и его производных ”y'” …
Из ф.65.4(1) видно, что дифуравнение описывает реакцию Δу на текущее входное воздействие Хр(t).
Введенный «вычислитель реакции объекта на предыдущие воздействия 4» от текущих значений исследуемого параметра yт, y'т… отнимает «реакцию объекта на текущее» Δyт воздействие ф.66
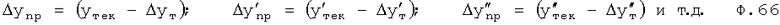
Формирователь эквивалентного суммарного входного воздействия 5 включает вычислитель корней входного воздействия, который производит вычисления по ф.67
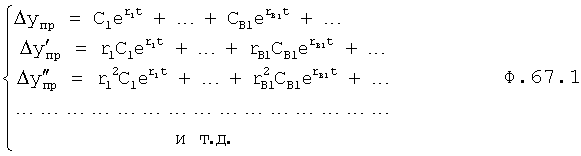
где r1… - корни дифмодели объекта (известны),
rB1… - корни математической модели «условного» входного воздействия, реакция на которое эквивалентна «результирующей реакции», вызванной всеми предыдущими воздействиями (значения которых необходимо найти).
Из уравнений ф.67.1 формируют 2п2 систем уравнений. Характеристическое уравнение для «n» систем ф.67.1 находится из уравнения ф.67.2
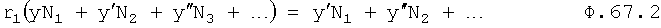
где y=Δyпр; y'=Δy'пр и т.д.,
N1 - алгебраическое дополнение к элементу у,
N2=N1f2(r, y', y”…) - алгебраическое дополнение к элементу y в определители Δ,
N3=N1f3(r, у', у”…);
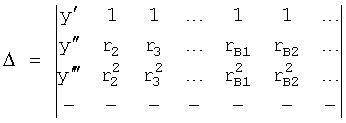
и т.д.
После сокращения на ф.67.2 примет вид ф.67.3
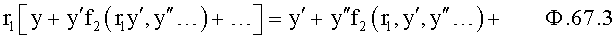
Полученный степенной многочлен ф.67.3 делят на характеристическое уравнение объекта (или передаточную функцию объекта) ф.67.4

Корни полученного степенного многочлена соответствуют корням дифуравнения входного воздействия.
Вычислитель постоянных полного решения производит вычисления по ф.68.1
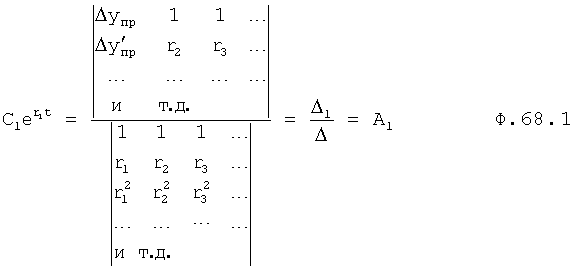
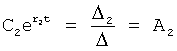
и т.д.
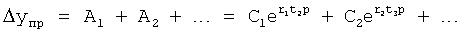

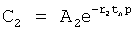
и т.д.
Найдены постоянные С1… подставляют в ф.69 для нулевого начального параметра ΔУн=0
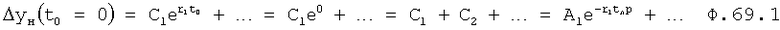
В ф.69.1 подставляют 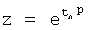 и вычисляется z из ф.69.2
и вычисляется z из ф.69.2

Найденные значения z1… подставляют в ф.69.3 для t′1… (при которых ΔYпр равно заданному значению)
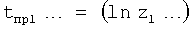
Найденные значения подставляют в ф.68.2 для вычисления С… постоянных полного решения дифуравнения, которые используют для вычисления постоянных входного воздействия С по ф.70
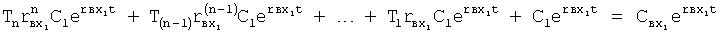
тогда
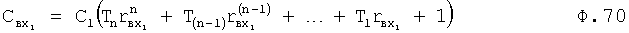
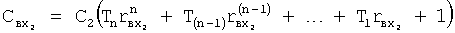
и т.д.
Найденные значения корней (из ф.67.3…4) и постоянных (ф.70) подставляют в математическую модель эквивалентного суммарного входного воздействия ф.71
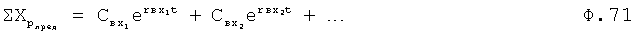
Формирователь степенной модели …9 (фиг.18) формирует реакцию объекта на суммарную модель предыдущих входных воздействий по ф.65.1…
Сумматор реакции объекта 10 на текущее и предыдущие воздействия позволяет моделировать исследуемый параметр в текущем времени.
Если производную максимальной степени yn задать функцией от времени yn=fn(t), то при нахождении производных меньшей степени y[n-1] по ф.72 (и входящих в них постоянных ф.73), изменением значения производной максимальной степени для данного момента времени идентификации можно пренебречь, что видно из ф.75.
Дифуравнение объекта, после подстановки в него (ф.74.2) математических выражений производных меньшей степени (найденных по ф.73), можно использовать для нахождения производной максимальной степени ф.74.3.
Введенный определитель емкостных составляющих п.12 фиг.18 позволяет (по постоянным интегрирования) ф.73 определить емкостные составляющие, влияющие на исследуемый выходной параметр.
Для этого используется математическая модель ее производной. Степень производной выбирается максимальной из входящих в дифуравнение.
Производные меньшей степени находят поэтапным интегрированием максимальной производной. При вычислении постоянных интегрирования используют текущие значения измеренных производных меньших порядков ф.73. Измеренное значение производной максимальной степени для текущего момента считается «постоянным» в «малом», что допустимо при нахождении производных меньшего порядка.
Элемент, понижающий производную 11.1 (фиг.18), находит производную степени по ф.72
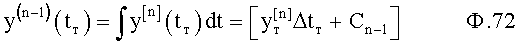
где y[n](tт) - производная «n» степени, измеренная в момент времени tт, и считается постоянной в ф.72, т.к. используется для определения y(n-1) при изменении Δt в «малом» = yт [n].
Cn-1 - постоянная интегрирования вычисляется по ф.73
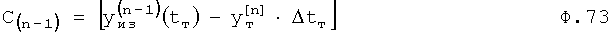
где 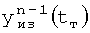 - производная (n-1) степени, измеренная в момент tт
- производная (n-1) степени, измеренная в момент tт
Аналогично находится y(n-2)(tт), C(n-2) и т.д.
Для определения измерения y[n] при «большом» измерении Δt введенный «определитель максимальной производной п.14» (фиг.18) подставляет найденные производные y(n-1)… и постоянные C(n-1)… из ф.73 в ф.74.1.
В отличие от известных математических моделей объекта ф.75 (1 и 2), введенная математическая модель определяется по ф.75.3
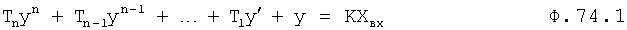
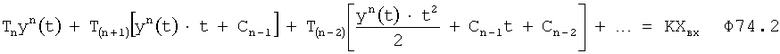
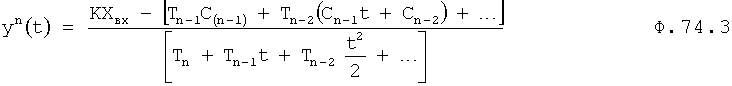



где
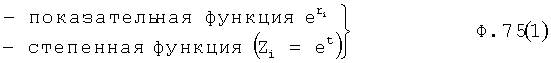
где
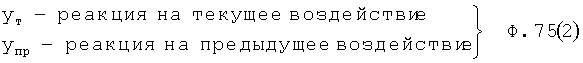
- интегральная функция ф.75.(3),
где С1… постоянные интегрирования, находят по ф.73.
На фиг.19 приведена зависимость производной y[n] максимального порядка в «малом» и «большом» от текущего момента времени.
Если t1 далеко от t0, то для определения постоянных интегрирования С1… фиг.19, ф.73 используют измеренные производные y(n+m), степень которых выше yn (степени входящей в дифуравнение), тогда для нахождения производной ”n” степени используют ф.76
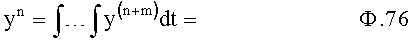
где y(n+m) - const.
По постоянным внутреннего запаздывания Т1, Т2 (полученные с выхода идентификатора 19) блок контроля 19 отделяет текущею реакцию yт (на текущие входные воздействие xp) от реакции на предыдущие воздействия ynp (в 1-м канале модели ф.75.2) и определяет емкостные составляющие С… (постоянные интегрирования ф.73) в модели объекта ф.75.3.
Полученные математические модели ф.75.1…3 используются для окончательного определения характеристик измерения исследуемого параметра (выходных параметров какого-либо из звеньев W1…Wn входящего в математическую модель объекта ф.77).
Определитель интегралов времени с недопустимыми параметрами 18.2 использует ф.77.1
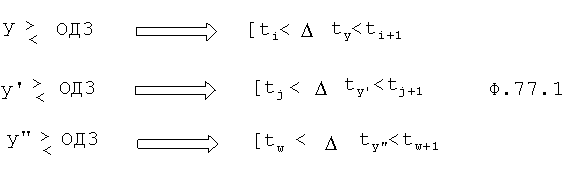
где ti, ti+1 - вычисляется из y=ОДЗy
tj, tj+1 - вычисляется из y'=ОДЗy'
tw,tw+1 -”- из y″=ОДЗy″
Определитель установившихся параметров п.18.3 (фиг.1) использует ф.77.2
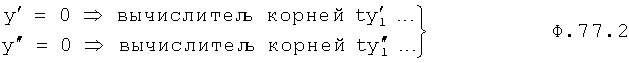
Вычислитель элементарных значений (ymax1, ymin1…) п.18.4 по ф.77.3/л.7 стр.383, 386, §287/

где экстремальные значения (вершины) находят по корням tсер из y'(t)=0
- точки перегиба tпер из y''(t)=0,
- нулевые значения y0 из fчис(t)=0; f'чис(t)=0,
- неустойчивость y(t)→∞ из fзн=0, f'зн=0,
Вычислитель параметров в ближайшем интеграле времени Δtбл п.18.5 фиг.1 уточняет момент времени, при котором исследуемый параметр примет заданные значения y(t)=yзад⇒вых.
Введенные в блок контроля 18 и идентификатор 19 измерения позволяет определить последовательность и величину взаимодействия составляющих математической модели объекта (и САР в целом).
Найденные значения параметров используются в блоках формирования регулирующего воздействия п.6…10 фиг.1:
- регулятор с постоянными параметрами 6,
- регулятор с переменными коэффициентами 7.1,
- регулятор с переменными корнями 7.2,
- регулятор по ошибке 8,
- корректирующий регулятор 9.
Введенные изменения в регулятор с постоянными параметрами 6 (фиг.10) обеспечивают плавность при переходе от одной заданной совокупности yi, y'i, y''i… к другой y(i+1), y'(i+1), y''(i+2)…
Плавность алгоритма регулирования достигается за счет формирования системы уравнений ф.79 поэтапной подстановкой известных корней дифуравнения объекта r01 в уравнение ф.78.2, полученной из системы уравнений динамической характеристики объекта ф.78.1.
Динамическая характеристика (y, y'…) выходного параметра описывается системой уравнений ф.78.1
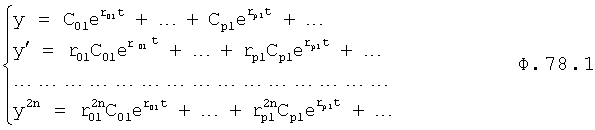
Из системы уравнений ф.78.1 находят равенство 78.2, включающее из корней и совокупности динамической характеристики y, y'…y2n(tj) для какого-то момента времени
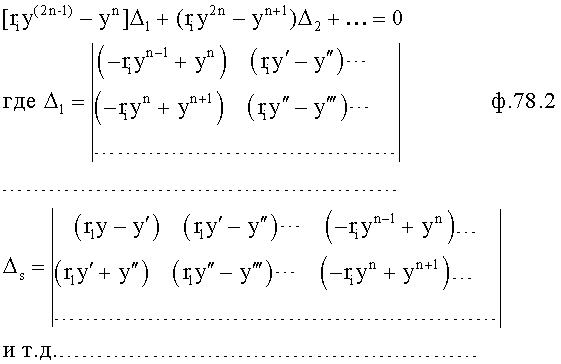
 S=1, 2 - номер столбца, в который подставляют значения коэффициентов, стоящих в правой части от равенства, условно принятых известными.
S=1, 2 - номер столбца, в который подставляют значения коэффициентов, стоящих в правой части от равенства, условно принятых известными.
После поэтапной подстановки известных корней объекта r01… получается система уравнений ф.79
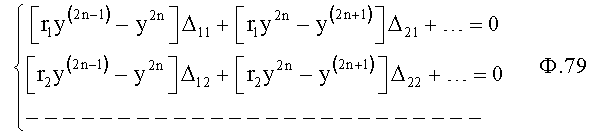
где y, y'… - заданные параметры = yз, y'з…,
yN, yN+1… - производные высоких порядков, которые неизвестны и которые находят из системы уравнений ф.79, после раскрытия квадратных скобок […].
Найденные значения yN, yN+1 (производных высокого порядка), значения которых задаются yз, yз', … подставляются в ф.78.2. После раскрытия скобок в ф.78.2 получается ф.80.1 и характеристическое уравнение САР ф.80.2
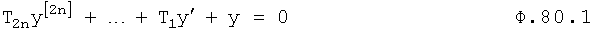

где T2n, T(2n-1)… - постоянные внутреннего запаздывания САР.
Полученное характеристическое уравнение САР ф.80.2 делится на степенной многочлен характеристического уравнения объекта ф.80.3, и вычисляется степенной многочлен характеристического уравнения регулятора ф.80.4
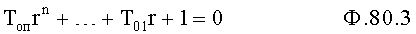
где Toп… - постоянные внутреннего запаздывания объекта.

Из ф.80.4 определяются корни математической модели регулятора rp1…, являющиеся корнями степенного многочлена.
Найденные корни позволяют определить постоянные полного решения дифуравнения объекта п.9 фиг.20 (фиг.22) Из системы уравнений ф.81 вычисляются составляющие А заданного значения регулируемого параметра yз (п.9(1) фиг.22)
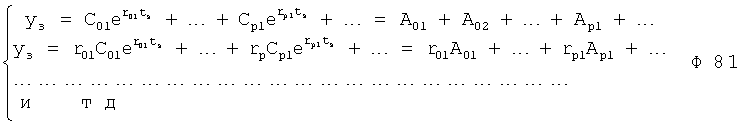
где 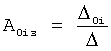
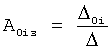
Найденные значения составляющих А… позволяют определить зависимость постоянных С времени tз, необходимого для получения заданных параметров y3, y'3…
Найденные зависимости С…=f(t) ф.82 подставляются в ф.83 для начального момента заданного цикла регулирования
И т.д.

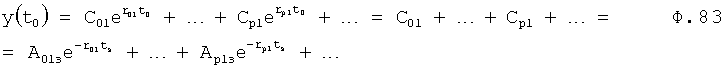
где 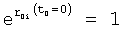
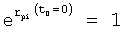
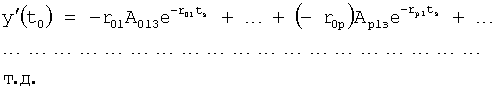
Если объект имеет инерционность 1-го порядка фиг.21, то для нахождения необходимого времени регулирования tз используется ф.84.1, в которую входит начальное значение выходного параметра yн(t0)n, известное заранее
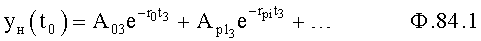
где r0i найден идентификатором (п.19 фиг.1),
rp1 - вычислены по ф.80.4,
А0з, Ар1з… - вычислены по ф.81.
Если необходимо обеспечить быстродействие, то из найденных tз выбирают «желаемый» (как правило, «минимальный и технически реализуемый») и подставляют его в ф.84.2 для нахождения постоянных С01, Ср1… полного решения
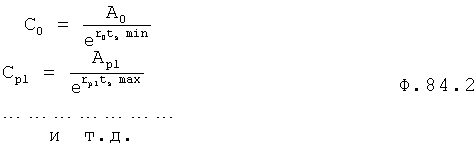
Если объект имеет инерционность 2-го порядка (если заданные параметры включают заданное значение y и ее производную 1-го порядка y), то формируется система уравнений ф.85.1, в которой неизвестными являются tк* и t0

После подстановки соответствующих значений ф.85.1 примет вид ф.85.2
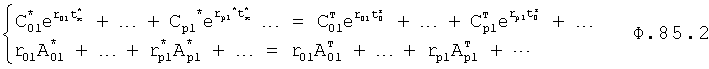
Где ”*” состоит после параметра, описывающего режим при предыдущем входном воздействии,
”т” стоит после параметра, описывающего необходимый заданный режим,
tк * - конечный момент времени предыдущего входного воздействия,
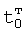 - начальный момент времени заданного режима, после подстановки в ф.85.2 известных значений
- начальный момент времени заданного режима, после подстановки в ф.85.2 известных значений 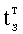 и A01з… Ар1з… получится ф.85.3
и A01з… Ар1з… получится ф.85.3
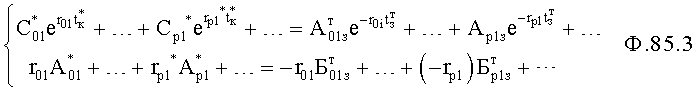
Подстановка 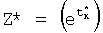 и
и 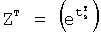 позволяет ф.85.3 преобразовать в систему степенных многочленов, в которой Z* и Zт неизвестны
позволяет ф.85.3 преобразовать в систему степенных многочленов, в которой Z* и Zт неизвестны
Найденные из системы уравнений ф.85.3 значение (tк *) - позволяет определить в какой момент необходимо прекратить предыдущее воздействие и начать заданный режим регулирования.
Найденное из системы уравнений ф.85.3 значение tз т позволяет вычислить по ф.86 постоянные 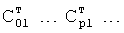 полного решения дифуравнения заданного режима
полного решения дифуравнения заданного режима

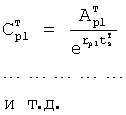
Если задаются внутренние составляющие объекта yw1, yw2, фиг.2, инерционностью выше 2-го порядка, то регулирование по «начальной ошибке (6.2 фиг.1) позволяет упростить расчеты фиг.20, определить рассогласования п.3 (фиг.20) по заданным параметрам составляющих y3w1, y3w2, … вычисляет значения «вынужденной» (т.е. определяемой инерционностью стоящих впереди звеньев wi+1, wi+2… объекта yзw1) динамической характеристике объекта ф.87.
Из ф.87.1 получают ф.87.2
из 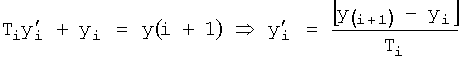


из 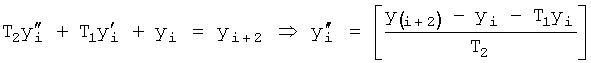
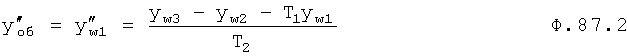
где Тi получены из передаточных функций w1 и w2 (после объединения).
Если в ф.87. подставить значения yзw1…, то будут получены вынужденные значения yв', yв''…
С выхода идентификатора п.19 поступает текущее значение yтw1… (и текущее значение yоб, yоб', y”об…).
По ф.88 вычисляется «начальная ошибка»
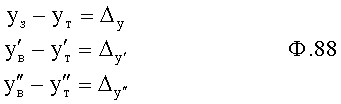
Определитель корней математичкой модели регулятора 4.2 использует ф.78.1…2 и ф.79.
При этом заданным параметром будет начальное рассогласование, полученное с вывода подстановки видна из ф.89 [л.10. стр.52-55].
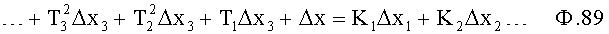
где Δxi=Δ”yi
Δxз=Δyзi
------------------
Таким образом, ф.78.2 примет вид ф.90
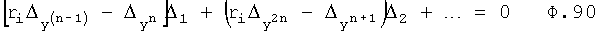
т.е. y=Δy,
y'=Δy'
и т.д.
Определитель зависимости п.9.2 использует ф.81 и ф.82, подставляя в них
yз=Δyз
y'з=Δy'з
-----------
и т.д.
Из которых вычисляются Ai0Δyз…ApiΔyз…
Вычислитель постоянных полного решения дифуравнения п.5 фиг.20 использует найденные зависимости формулы 82 в формуле 83, но при этом t0 поставляется tз. Из ф.81 вычисляется tз
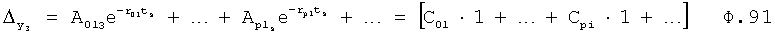
где 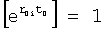 и т.д.
и т.д.
Полученное значение tз подставляется в ф.82 и вычисляются постоянные C0з…Cp1
Вычислитель постоянных входного воздействия п.6.1…3 (фиг.20) найденные значения постоянных Ср… подставляет в левую часть дифуравнения объекта ф.92 и приравниваются коэффициенты при одинаковых степенях ф.92.2, чтобы найти постоянные входного воздействия Cвхp1
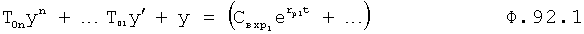
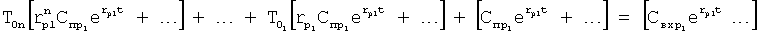
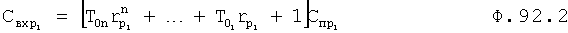 Если заданные параметры y, … необходимо обеспечить в заданный момент времени, то параметры регулятора находятся из ф.93 (п.1 фиг.23)
Если заданные параметры y, … необходимо обеспечить в заданный момент времени, то параметры регулятора находятся из ф.93 (п.1 фиг.23)
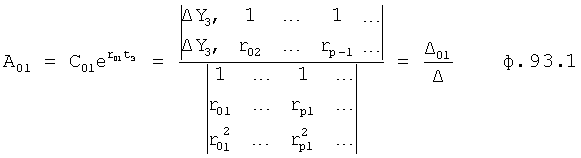
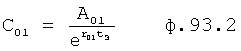
Где 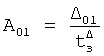 вычисляется
вычисляется
Задано
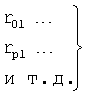 Корни математической модели объекта r0 и регулятора rp вычислены по предыдущим формулам
Корни математической модели объекта r0 и регулятора rp вычислены по предыдущим формулам
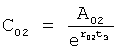 и т.д.
и т.д.
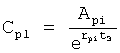
Если заданы параметры y, y' … для нескольких моментов времени tз1, tз2, (yз(t),  … yз(t2),
… yз(t2),  …), то после нахождения рассогласования (п.2 фиг.23) ф.94
…), то после нахождения рассогласования (п.2 фиг.23) ф.94

где yзi - заданное значение для момента tзi;
yнi - значение в начальный момент t0i.
Формируется совокупность I, II… систем управления п.3 ф.95.1…
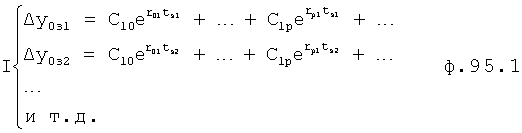
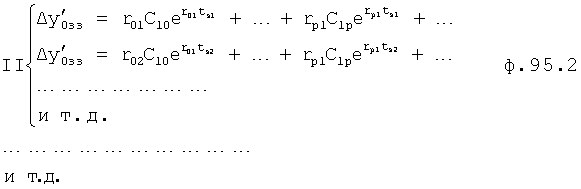
и т.д.
Из системы управления I ф.95.1 получены формулы для определения постоянных ф.96.1 … (п.4 фиг.23)
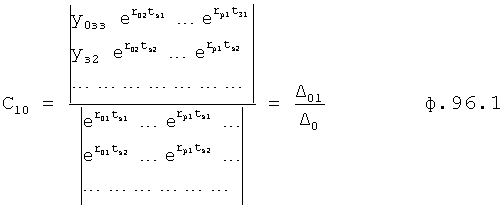

Аналогично находятся из системы уравнения II ф.52.2 формулы 97.1…
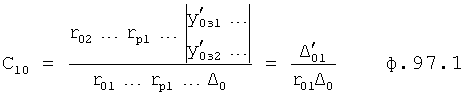
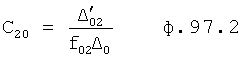
и т.д.
Для нахождения математической модели п.5 фиг.23 приравнивают равенства для i-го постоянного C0i, которые позволяют из модели исключить значение постоянной ф.98 (т.е. ф.96.1 приравнивается формуле 97.1)
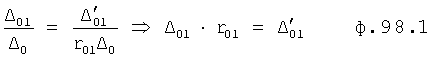
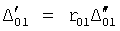
и т.д.
Совокупность равенства в ф.98.1… позволяет формировать систему уравнений, в которую включены алгебраические дополнения Д1, Д2… к замечаниям столбца y0з1, y0з2,  … и т.д. ф.99 (п.6 фиг.23)
… и т.д. ф.99 (п.6 фиг.23)
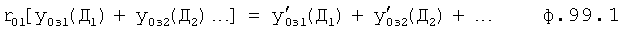
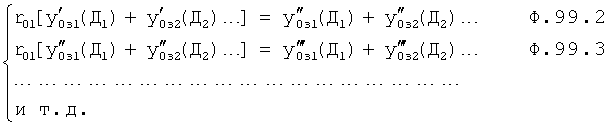
Система уравнений ф.99.2… позволяет вычислить зависимость ф.100 для алгебраических дополнений Д2…
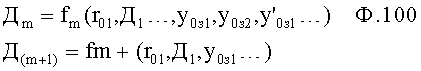
и т.д.,
где Д1… «условно» приняты известными (перенесены в правую часть равенства),
r01 - «условно» принято известным.
Найденные функции ф.100 подставляются в ф.99.1 и получается модель объекта. Количество найденных функций fm… равно количеству задаваемых выходных параметров входящих в объект звеньев y3w1, yзw2…
Для того, чтобы найти значения дополнений Д1…(m-1) условно принятых известными (п.7 фиг.23), в ф.99.1 (после подстановки в нее функции ф.100, поэтапно подставляются значения корней объекта r01… (которые определены идентификатором 19). В результате получается система уравнений ф.101.
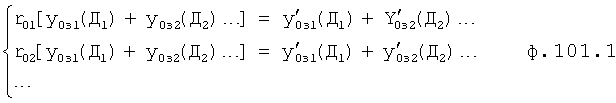
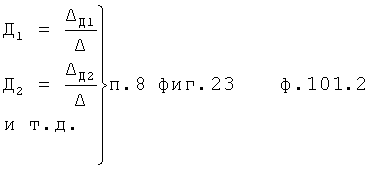
Значения Д1… ф.101.2 подставляются в ф.100 для вычисления Дm, Дm+1….
Найденные значения всех последних Д1… подставляются в ф.102 (полученную из ф.99.1)
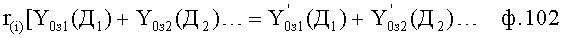
где ri являются одним из корней математической модели САР.
Позиция 9 фиг.23 раскрывает скобки ф.102 и вычисляет постоянные внутреннего запаздывания Т1, по которым находят все необходимые корни r… математической модели САР.
По ф.103.1… определяются необходимые постоянные полного решения
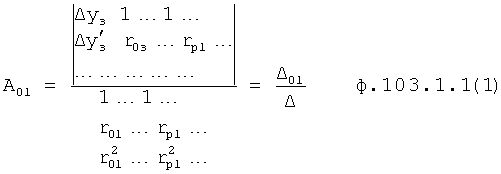
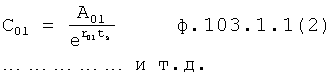
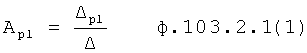
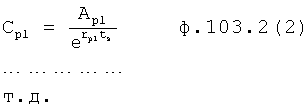
Если в регуляторе 6.1…3 формируется модель с большой «неустойчивостью» (r>0 положителен) или с большей колебательностью (r=α±jω, где ω - большая), что создает превышение ОДЗ, то для формирования регулятора используется регулятор с переменным коэффициентом постоянных п.7.1 фиг.1. Задатчик корней регулятора п.1 фиг.24 для регулирующего воздействия использует математическую модель, которая включает корни с допустимой устойчивостью α∈ОДЗ и колебательностью ω∈ОДЗ.
После этого задатчик момента времени п.2 выбирает момент времени tз, позволяющий обеспечить необходимые интервалы времени Δt для регулирования. Вычислитель рассогласования п.3 вычисляет Δyз=y(tз)-y(t0), Δy'з=y'(tз)-y'(t0)… рассогласование относительно начального момента времени.
Вычислитель постоянных п.4 производит вычисление постоянных С по ф.104.2, полученной из системы уравнений ф.104.1
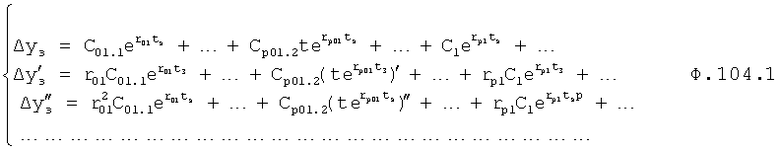
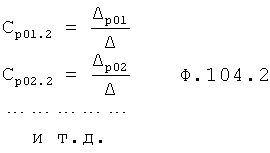
По постоянным Ср01,2… определяются соответствующие постоянные Свхр01.2…
входного воздействия.
Если необходимо обеспечить плавность регулирования (при задании динамической характеристики y, y'… в соответствующие моменты времени tз1…, то наиболее эффективным является регулятор с «переменными корнями» математической модели, п.7.2 фиг.1 и фиг.24.
Формирователь структуры модели п.5 фиг.24 использует ф.105.3, полученные из ф.105.1

где χ - сигнал задания на входе регулятора,
y - выходной регулируемый параметр объекта.
Из ф.105.1 получены ф.105.2
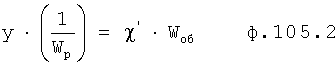
где 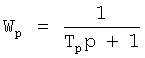
Из 105.2 вычисляются математические выражения, стоящие в левой части 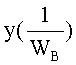 и правой части равенства χ(Wф), и получается ф.105.3
и правой части равенства χ(Wф), и получается ф.105.3
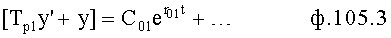
Формирователь совокупности систем дифуравнений п.6 (фиг.24) для каждого момента t1… формирует соответствующую систему уравнений. Для момента t1 формируется ф.106.1, для момента t2 формируется ф.196.2 и т.д.
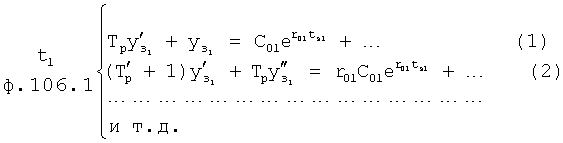
где 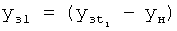 ;
; 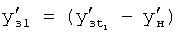
yн, 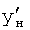 - начальные значения регулируемого параметра и т.д.
- начальные значения регулируемого параметра и т.д.
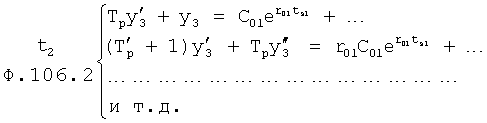
t3
и т.д.
Вычислитель текущего значения внутреннего запаздывания T(tз1…) и производных от его значения Т(tз1…), T′′(tз1…)… в заданные моменты времени tз1, tз2… п.7
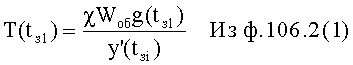
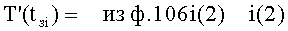
и т.д.,
где i=1…
Формирователь совокупности систем уравнений, включающих производные от запаздывания Тр регулятора (п.8), значения которых вычислены для заданных моментов времени из ф.106.1…, получает ф.107.1…
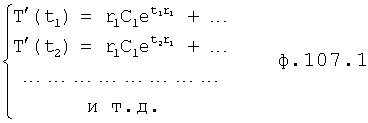
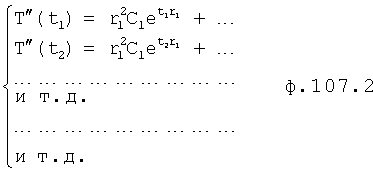
Объединитель систем уравнения п.9 решает системы уравнений ф.107.1… относительно одной из постоянных полного решения Сi ф.108.1…
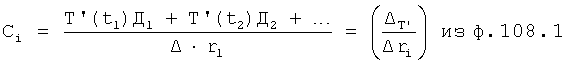
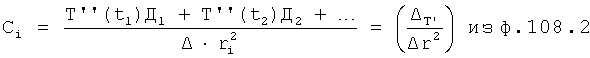
и т.д.
После приравнивания ф.108.1 и ф.108.2 получится ф.109.1
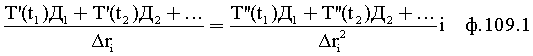
где Д1… - алгебраические дополнения к Т', T''… определителей систем уравнений ф.107.1… После приравнивания ф.108.2 и ф.108.3 получится ф.109.2
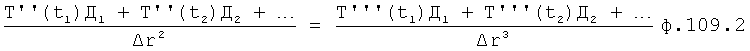
… и т.д.
После объединения ф.109.1… получается система уравнений ф.110 и т.д.

Определитель дополнений п.10 определяет зависимость каждого дополнения Д1… относительно одного из них Д1 и относительно соответствующего корня из системы уравнений с ф.110 по ф.111
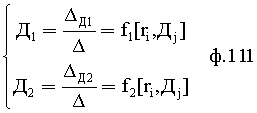
и т.д.
Определитель корней характеристического уравнения модели запаздывания Тр регулятора п.11 (фиг.24),
Найденные значения Д1… из ф.111 подставляются в ф.112
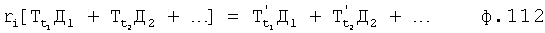
После раскрытия скобок ф.112 будет соответствовать характеристическому уравнению математической модели внутреннего запаздывания регулятора Тр ф.113, по найденным Ттn… из ф.112 вычисляются корни степенного многочлена ф.113 (rт1…), которые подставляются в математическую модель запаздывания регулятора ф.107.
Из одной из систем уравнений ф.107.1… определитель постоянных (полного решения модели дифуравнения) запаздывания регулятора Тр (п.12 фиг.24) определяет соответствующие значения постоянных Ст1… ф.114
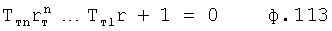
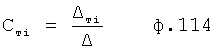
где 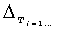 - определители системы уравнений ф.107.1.
- определители системы уравнений ф.107.1.
Таким образом, корень математической модели регулятора примет вид ф.115
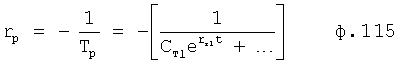
После подстановки корня регулятора в дифуравнение объекта получится ф.116
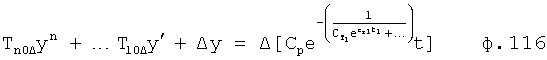
Определитель постоянной регулятора п.13 (фиг.24) подставляет значения рассогласования для заданного момента Δyзt1, 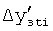 …, в ф.116 и вычисляется Срвх по ф.117
…, в ф.116 и вычисляется Срвх по ф.117
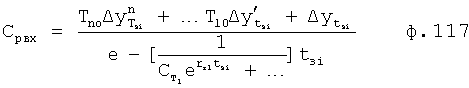
Если объект имеет сложную математическую модель, то используется регулятор с переменными коэффициентами запаздывания Т1… п.7.3.
Формирователь совокупности систем уравнений п.14 определяет значения коэффициентов запаздывания Тр1 и производные от 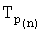 и
и 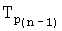 коэффициента запаздывания
коэффициента запаздывания 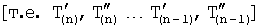 в заданные моменты времени
в заданные моменты времени 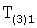 … ф.118.1… (из ф.105.2) так же и т.д.
… ф.118.1… (из ф.105.2) так же и т.д.
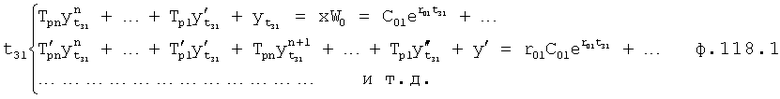
и т.д.…
где r01… - найдены идентификатором п.19 фиг.1,
C01… найдены по «Х» ф.105.2,
t31… - заданные моменты времени,
y31…, 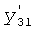 - заданные значения выходного параметра.
- заданные значения выходного параметра.
- коэффициенты внутреннего запаздывания регулятора, которые необходимо обеспечить из условия допустимости rp1(t31), rp1…(t32)
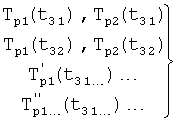
Формирователь модели постоянных п.15 определяет постоянные С1 относительно искомых коэффициентов внутреннего запаздывания регулятора (переменного) Т1р, Т2р … в заданные моменты времени t1(3) по ф.119.1…
Где Tnp - приведенное Tn-1, т.е. деленное на Т
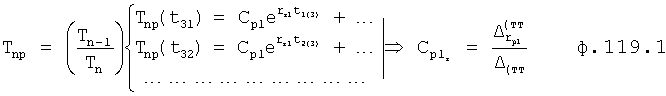
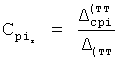
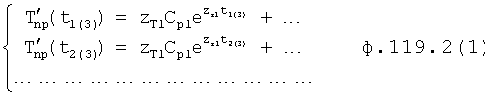
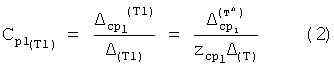

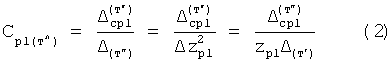
и т.д.
«Формирователь системы уравнений приравниванием коэффициентов п.16 использует ф.120 (ф.119.1(2) приравнивается с ф.119.2(2) и т.д.
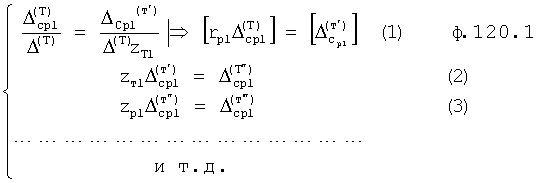
Где 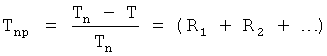 ; r1 - корни характеристического уравнения модели коэффициентов
; r1 - корни характеристического уравнения модели коэффициентов 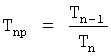
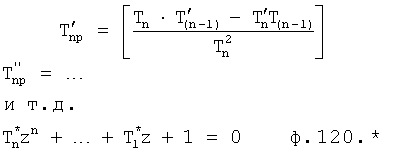
После подстановки алгебраических дополнений Д в систему уравнений ф.120, система уравнений примет вид ф.121
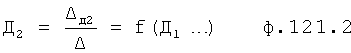
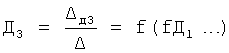
Найденные формулы для дополнений Д1… ф.121.1 подставляют в ф.122
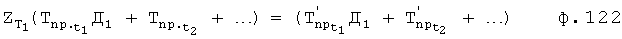
После раскрытия скобок в ф.122 получается степенной многочлен ф.120*.
Определитель корней z1… математической модели [коэффициента 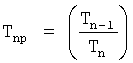 запаздывания] п.17 по коэффициентам
запаздывания] п.17 по коэффициентам 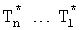 ф.120*, полученным из ф.122, определяет корни степенного многочлена Z1,2…
ф.120*, полученным из ф.122, определяет корни степенного многочлена Z1,2…
Определитель постоянных п.18 находит Ср1 из любой ф.119.1…(2).
Определитель слагаемых приведенного коэффициента запаздывания п.19 использует ф.123
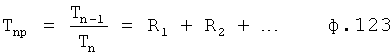
где 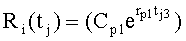 - слагаемые математической модели,
- слагаемые математической модели,
tj - заданные моменты времени.
Элементы проверки коэффициентов запаздывания п.20 найденные слагаемые R1… подставляют в модель характеристического уравнения регулятора ф.124
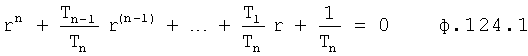
где
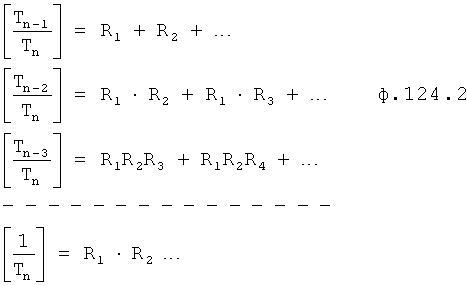
В ф.124.2 подставляют поэтапно значения слагаемых: сначала для первого заданного момента R1…(t31), полученные значения коэффициентов запаздывания проверяются с заданными значениями коэффициентов запаздывания в первый момент времени. Затем во второй заданный момент времени и т.д.
Если значения совпадают, то модель САР найдена правильно. В противном случае возникает необходимость использовать другой алгоритм регулятора: используется регулятор с переменной структурой п.7.4 фиг.1 (фиг.24) - пошаговый.
Если найденные переменные корни R1…=f1…(t) правильны, то определитель постоянных полного решения САР п.23 находит Ср1…С01 из системы уравнений ф.125
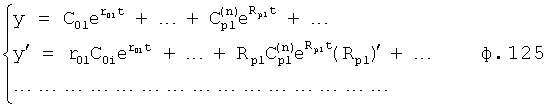
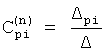
Определитель постоянных входного регулирующего воздействия п.24 по ф.126 приравнивает коэффициенты при одинаковых степенях ф.126
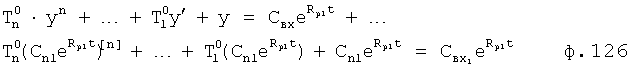
где 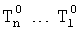 - постоянные запаздывания объекта.
- постоянные запаздывания объекта.
Если элемент проверки коэффициентов запаздывания п.22 подтвердит, что найденные переменные корни R1… не смогут обеспечить коэффициенты запаздывания регулятора Tp1… в заданные моменты времени T3…, то регулятор с переменной структурой («пошаговый» п.7.4) поэтапно идентифицирует значения переменных корней R1… для каждого пошагового интервала времени Δt.
Формирователь (математической) модели (для коэффициентов) запаздывания п.21 фиг.24 (Tp(n-2), Tp(n-3)…Tp1…) Tp1=f1(t1), Tp2=f2 использует ф.118…ф.120.
Задатчик интервалов времени п.22 весь процесс регулирования делит на интервалы времени, через которые структура регулятора меняется по возможности плавно.
Вычислитель (коэффициентов) запаздывания для заданного интервала п.23 в исследуемые моменты времени (входящие в интервал соответствующего «шага») вычисляет значения коэффициентов запаздывания и их производные. Для этого в ф.120.2 и ф.120.3 подставляются исследуемые моменты tис1.
Вычислитель (текущих значений корней характеристического управления) п.24 находит корни степенного многочлена, коэффициенты которого образованы коэффициентами запаздывания в исследуемый момент времени tис1.
Вычислитель производных текущих значений корней регулятора п.25 определяет разницу между значениями корней в текущий момент времени и предыдущий момент времени фиг.5.
Аналогично находятся производные 2-й и 3-й степени и т.д.
По найденным корням r1…(t) и производным от этих значений формируется математическая модель каждого из корней, входящих в характеристическое уравнение регулятора «определителем математической модели корней» п.26 по ф.127
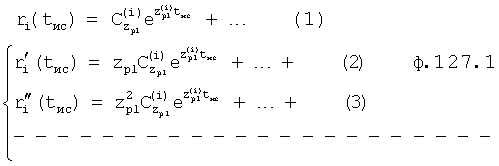
Из совокупности систем уравнений ф.127.1 формируется система уравнений ф.127.2 из
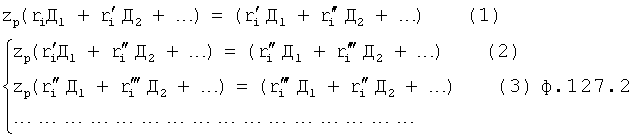
которой находятся алгебраические дополнения Д2, … как функции одного из дополнений Д1 ф.127.3
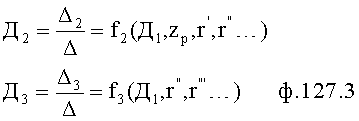
и т.д.
Найденные значения ф.127.3 подставляются в ф.127.2(1) и получается степенной многочлен ф.127.4, корни которого zp1, zp2… позволяют сформировать математическую модель переменного корня регулятора ri, справедливого для заданного интервала времени Δt
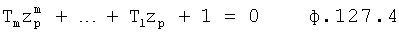
По данным корням модели zp1… из ф.127.1 определяются постоянные Сz1…, стоящие перед ними, в «определителе постоянных для заданного интервала» п.27.
Если объект подвержен частным возмущениям, то наиболее эффективным является «регулятор по текущей ошибке» п.8 фиг.1. При этом неточность идентификации параметров объекта (связанная с их переменным характером) не оказывает существенного влияния, т.к. доминирующим при формировании регулирующего воздействия является ошибка и производные от ее значения. Алгоритм формирования регулирующего воздействия получен из ф.128
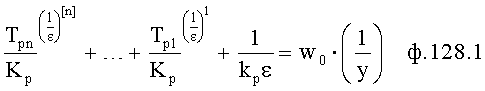
Ф.128.1 получена из ф.128.2
где Δxвх=ε(tr),
Tpn - коэффициенты запаздывания регулятора,
Kp - коэффициент усиления регулятора,
ε - ошибки регулирования,
Y - выходной параметр регулятора.
Для того чтобы получить параметры регулятора, используют ф.129
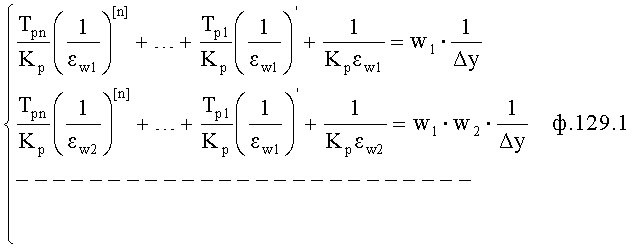
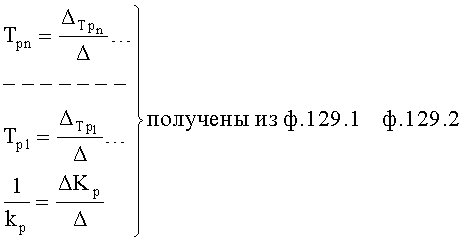
ф.129.2 получены из ф.129.1
 - определители системы уравнений ф.129.1.
- определители системы уравнений ф.129.1.
εw1… - ошибки регулирования отдельных звеньев регулятора в начальный момент регулирования.
 вычисляются по известной последовательности звеньев w1…
вычисляются по известной последовательности звеньев w1…
Из ф.128.1 получены ф.130, позволяющие определитель текущее значение регулирующего воздействия
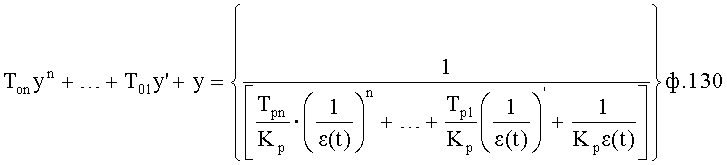
где 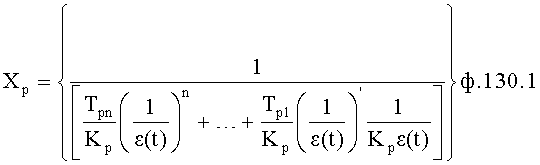
где Xp=ф.130.1… входное регулирующее воздействие,
ε(t), ε'(t)… - текущее значение ошибки выходного параметра фиг.25.
Для обеспечения задачи заявленного изобретения (контроль и регулирование состояния каждого из звеньев объекта W1…) необходимо максимально точно реализовать заданную модель переходного процесса каждого из звеньев объекта.
Компенсация непредвиденных помех осуществляется введенным корректирующим регулятором 9, выходной регулирующий сигнал 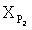 которого прибавляется к регулирующему сигналу, сформированному одним из основных регуляторов (п.6, п.7 задания или ошибки п.8).
которого прибавляется к регулирующему сигналу, сформированному одним из основных регуляторов (п.6, п.7 задания или ошибки п.8).
Непредвиденная ошибка εн разделяется на системную ошибку εст и случайную εсл
(εн=εст+εсл).
Для нахождения непредвиденной ошибки из текущего значения выходного сигнала заданной математической модели CAP вычитается сигнал с выхода объекта
(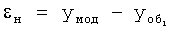 ,
, 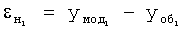 ,
, 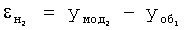 ,…),
,…),
п.9.1 фиг.26.
Определитель математической модели п.10 позволяет получить систему уравнений по дифференциальной характеристике ошибки ε'… (объединяемой коэффициентами запаздывания Т1 ф.131 (1) и интегральной характеристики ф.131(2)…), в которой происходит накопление ошибки 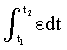 и усреднение ее текущего значения, т.е. полученные в результате постоянные
и усреднение ее текущего значения, т.е. полученные в результате постоянные  характеризуют системную ошибку εст. Найденные коэффициенты запаздывания Тε1 системной ошибки ф.132 позволяют сформировать регулирующее воздействие п.5 фиг.26, компенсирующее системную ошибку
характеризуют системную ошибку εст. Найденные коэффициенты запаздывания Тε1 системной ошибки ф.132 позволяют сформировать регулирующее воздействие п.5 фиг.26, компенсирующее системную ошибку
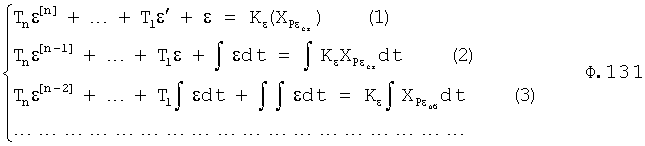
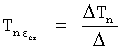
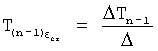
------------
где 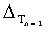 …, Δ - определители, найденные из ф.132.
…, Δ - определители, найденные из ф.132.
Со второго выхода формирователя регулирующего воздействия поступает сигнал, характеризующий переходной период компенсации системной ошибки εст, позволяющий вычитанием от нее текущего значения ошибки εт получить значение случайной ошибки εсл

Формирователь интеграла компенсации п.7 предназначен максимально сгладить случайную ошибку εсл (п.7 фиг.26). Для этого используется ф.133(1), интегрирование которой по ф.133(2) позволяет добиться максимального эффекта при компенсации внезапных возмущений
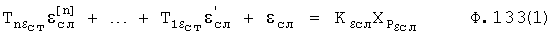
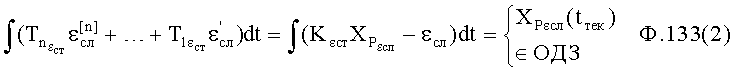
«Блок проверки ОДЗ планируемой CAP» п.5 фиг.1 включает в себя «формирователь логарифмических зависимостей» п.5-4 фиг.1, позволяющий получить систему уравнений с математическими зависимостями ф.134 (п.5.6 фиг.1) для определения характеристик (быстродействия и качества.) каждой из сформированных алгоритмов регулирующего воздействия п.6, п.7, п.8 фиг.1
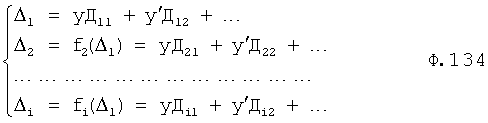
и т.д.
где f2(Δ1), f3(Δ1) - находят из системы уравнений ф.135 поэтапно
где Δ1… найдены из ф. 136.2
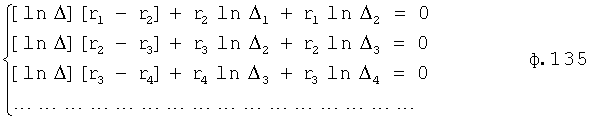
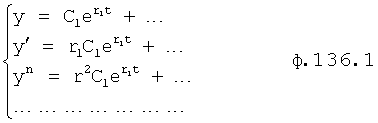
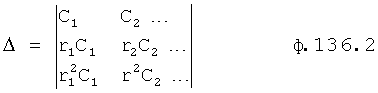
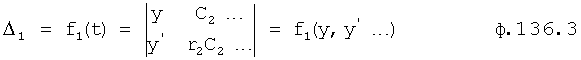
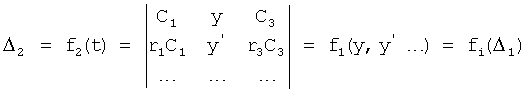
и т.д.,
где 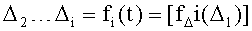 определяют из ф.135 и подставляют в ф.
определяют из ф.135 и подставляют в ф.
Д1.1… - алгебраические дополнения к y, y ',… в ф.136,
Д2.1… - алгебраические дополнения к y, y,'… в ф.136.4
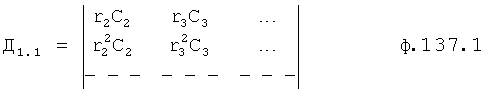
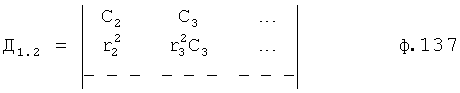
и т.д.
Для нахождения ∈ ОДЗ выходного параметра "y" приравнивают значению границы устойчивости y=yгр.уст и подставляют в ф.134, из которой вычисляются y,' y'…
Δ1, tу.гр из ф.138.1…,
где Δy'…Δф.134 находят из ф.134,
Δ1…Δi находят из ф.136
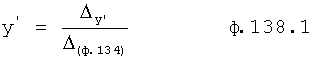
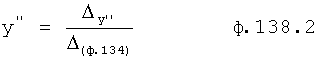
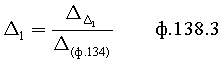
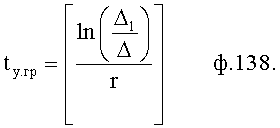
Экстремальные значения (максимальные или минимальные) находят подстановкой нулевой производной y'=0 в ф.134 и последующим нахождением: y', y''…
Δ1, ty'=0 по ф.138.1…
и т.д.
Таким образом, вышеприведенные блоки, используя формулы 2…138, позволяют осуществить те задачи, которые стоят перед заявленной автоматической системой регулирования. Возможность регулирования не только величиной выходного параметра объекта, но и отдельными внутренними емкостными составляющими объекта позволяет предотвратить аварийные режимы, уменьшить износ объекта (оборудования, используемого в регулируемом техпроцессе) и продлить его срок службы, что приносит экономический эффект. Заявленная CAP повышает качество регулирования и открывает новый круг задач (стоящий перед CAP).
На фигуре 1 изображена структурная схема системы автоматического регулирования емкостными составляющими объекта.
На фигуре 2 изображена структурная схема объекта.
На фигуре 3 изображена структурная схема блока дополнительных вспомогательных состояний (п.1.3 фиг.1).
На фигуре 4 изображена структурная схема идентификатора (п.19 фиг.1).
На фигуре 4.1 изображена структурная схема быстродействующего вычислителя поз.11.
На фигуре 4.2 изображена техническая реализация быстродействующего вычислителя п.11 фиг.4.
На фигуре 5 изображена последовательность вычисления производных исследуемого параметра (п.12.7.2 фиг.4).
На фигуре 6.1… изображены графики, отражающие исследуемые зависимости, используемые для нахождения корней характеристического уравнения (п.12.8.1…фиг.4).
На фигуре 6.1.1.1…2 изображены графики влияния чисто мнимых корней (r=±jβ) на действительные L=f1(z, α=0)=f2(β, α=0) составляющие характеристического уравнения.
(Tnrn+…+T1r+1)=L+jB=0.
На фигуре 6.1.1.1 изображен график функции от новой переменной z=β2 для частного случая α=0 неявной функции f(β,α)=0, полученной из мнимой части "L" характеристического уравнения (Tnrn+…+T1r+1)=(L+β)=0 подстановкой r=(α±jβ).
На фигуре 6.1.1.2 изображен график функции fL=(β,α) для частного значения α=0, которое определяет зависимость действительной части характеристического уравнения от чисто мнимых корней r=jβ.
На фигуре 6.1.2 изображен график функции зависимости мнимой составляющей «В» характеристического уравнения от чисто мнимых корней 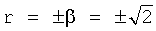 .
.
На фигуре 6.2 изображены графики зависимостей (действительной L и мнимой B составляющих характеристического уравнения) от мнимой составляющей корня r=α±jβ.
На фигуре 6-3 изображены графики построения неявных функций α=f(β).
На фигуре 6.3.1 приведен график неявных функций для действительной части L, последовательность построения которой предлагается следующая:
- построение значений α1, α2… при β=0 по функции fL(α, β=0).
- построение значений β1, β2… при α=0 по функции fL(α, β=0).
- построение эллипсов по вершинам α1,2, α3,4, α12=b1, α34=b2 и координатам β1=α1; β2=α2 по формулам 29.1, которые приближенно отражают исследуемые кривые.
Построение совокупности эллипсов ф.29.2 (фигура 6.3.2) осуществляют аналогично фиг.6.3.1, поэтому график для этой фигуры не приводят. Таким образом, фигура 6.3.2 должна изображать построение графика α=f(β) по fВД(β,α)=0, входящей в мнимую часть B=[β·fвд].
На фигуре 6.4 изображен график нахождения корней ri системы двух уравнений по графикам пересечения двух неявных функций αL=fL(β); αB=fB(β) ф.30.
На фигуре 6.5.1 изображено графическое нахождение корней.
На фигуре 6.5.2 изображен алгоритм вычисления действительных корней по корням производной.
На фигуре 6.5.3 - расположение действительных корней по корням производной.
На фигуре 7 изображена структурная схема уточняющего вычислителя (п.12 фиг.4).
На фигуре 7.1 изображена структурная схема уточняющего вычислителя комплексных корней (п.12.18 фиг.4).
На фигуре 8 изображена структурная схема фильтрующего вычислителя «В».
На фигуре 9 изображена структурная схема определителя структуры дифуравнения.
На фигуре 10 изображена структурная схема канала переменных комплексных корней (п.14.2).
На фигуре 11 изображена структурная схема определителя момента времени в быстродействующем канале.
На фигуре 12 изображена структурная схема определителя момента времени фильтрующего канала.
На фигуре 13 изображен определитель внешнего запаздывания (п.15 фиг.14).
На фигуре 14 изображена структурная схема блока вычитателей.
На фигуре 15 изображена структурная схема определителя последовательности взаимодействия звеньев математической модели (п.16 фиг.4).
На фигуре 16 изображена структурная схема элемента подстановки звена (п.4.1…фиг.15).
На фигуре 17 изображена структурная схема определителя ОДЗ выходных параметров каждого звена (п.17 фиг.4).
На фигуре 18 изображена структурная схема формирователя модели объекта.
На фигуре 19 изображена диаграмма нахождения производной «n»-й степени исследуемого параметра у.
На фигуре 20 изображена структурная схема регулятора с постоянными параметрами (п.6 фиг.1).
На фигуре 21 изображена структурная схема формирователя регулирования по заданию (п.6.1 фиг.1 и фиг.20).
На фигуре 22 изображена структурная схема определителя зависимостей.
На фигуре 23 изображена структурная схема регулятора для заданных моментов времени (п.6.3 фиг.1).
На фигуре 24 изображена структурная схема регулятора с переменными параметрами.
На фигуре 25 изображена структурная схема регулятора по текущей ошибке (п.8 фиг.1).
На фигуре 26 изображена структурная схема корректирующего регулятора (п.9 фиг.1).
На фигуре 27 изображена структурная схема блока проверки ОДЗ планируемой CAP.
Система автоматического регулирования емкостными составляющими объекта фиг.1 включает в себя следующие составляющие:
1. блок задания, у которого первый и второй вход подсоединен к входам заявленной CAP, третий вход подсоединен к выходу идентификатора п.19, а выходами - к входу блока проверки ОДЗ планируемой CAP п.5 и к входам регуляторов п.6…9; в состав блока задания п.1 входят последовательно соединенные блоки 1.1, 1.2, 1.3 и подсоединенные к ходам и выходам блока задания:
1.1 блок динамических характеристик выходного параметра,
1.2 блок внутренних отдельных составляющих,
1.3 блок дополнительных отдельных составляющих, который включает в себя последовательно соединенные устройства:
1) звено вычисления корней регулирующего воздействия,
2) звено вычисления коэффициентов регулирующего воздействия,
3) преобразователь дифуравнения в степенной многочлен, включающий последовательно соединенные элементы:
(1) - определитель основания степенного многочлена,
(2) - элемент ввода новой единицы измерения корней,
(3) - преобразователь отрицательных степеней в положительные,
(4) - определитель общего знаменателя;
4) звено проверки ОДЗ, включающий последовательно соединенные элементы:
(1) - элемент подстановки пограничных значений,
(2) - вычислитель корней степенного многочлена,
(3) - определитель момента времени с пограничными параметрами,
(4) - определитель исследуемого параметра между пограничными состояниями;
5) звено коррекции экстремальных недопустимых значений входного воздействия;
6) звено вычисления новых промежуточных значений выходного параметра;
2. Объект, у которого вход и выход подсоединены к входу идентификатора п.19, а вход также подсоединен к выходу формирователя регулирующего воздействия п.3.
3. Формирователь регулирующего воздействия, у которого первый вход подсоединен к выходу блока сравнения модели п.4, а второй вход подсоединен к выходу блока контроля ОДЗ действительной CAP п.18,
4. Блок сравнения модели своим входом подсоединен к выходу блока проверки ОДЗ планируемой CAP п.5,
5. Блок проверки ОДЗ планируемой CAP фиг.1 и фиг.27, на второй вход которого подсоединены выходы п.6.9 и который включает в себя следующие устройства:
5.1 формирователь системы уравнения дифференцированием полное решение, входом подсоединенный к входу блока проверки ОДЗ планируемой CAP, а выходом - на входы вычислителя определителей системы 5.2 и формирователя системы уравнений из алгебраических дополнений 5.5,
5.2 вычислитель определителя системы, выход которого подсоединен на вход последовательно соединенных п.5.3, 5.4, 5.6, 5.7, 5.11.1, 5.12.1,
5.3 формирователь системы логарифмических уравнений из определителей,
5.4 формирователь логарифмических зависимостей между определителями,
5.5 формирователь системы уравнений из алгебраических дополнений, выход которого подсоединен ко второму входу п.5.6,
5.6 элемент подстановки зависимостей между определителями, выход которого также подсоединен к входу последовательно соединенных элемента подстановки нулевых производных выходного параметра п.5.8, вычислителя i-го определителя п.5.11.2, вычислителя момента времени п.5.12.2,
5.7 элемент подстановки ОДЗ выходного параметра, который также подсоединен на вход вычислителя производных на границе ОДЗ выходного параметра п.5.9,
5.8 элемент подстановки нулевых производных выходного параметра, который также подсоединен выходом на вход вычислителя экстремальных выходных параметров п.5.10,
5.9 вычислитель производных на границе ОДЗ выходного параметра, выход которого подсоединен на выход п.5,
5.10 вычислитель экстремальных выходных параметров, выход которого подсоединен на выход п.5,
5.11 (1), 5.11 (2) вычислители i-го определителя,
5.12 (1), 5.12 (2) вычислители момента времени, выходы которых подсоединены на выходы п.5;
6. Регулятор с постоянными параметрами, включающий параллельно соединенные три блока регулирования;
6.1 регулятор по заданию (фиг.21, фиг.20), включающий (последовательно соединенные п.«4» и «9.1», на выход которого параллельно подсоединены п.«7» и «8», выходы которых подсоединены на входы п.«6.1» и соответственно п.« 6.2») следующие устройства:
- «4» определитель корней математической модели, включающий последовательно соединенные
1) формирователь зависимости выходного параметра от корней дифуравнения,
2) элемент подстановки заданных динамических характеристик выходного параметра, выход которого также подсоединен на вход п.5,
3) формирователь системы уравнений поочередной подстановкой корней объекта,
4) вычислитель производных высокого порядка,
5) вычислитель характеристического уравнения,
6) вычислитель корней характеристического уравнения,
- «9.1» определитель зависимостей (фиг.22), который (так же как п.9.2) включат в себя последовательно соединенные элементы:
1) вычислитель составляющих заданного параметра,
2) определитель постоянных по функции времени,
3) определитель начальных параметров;
- «7» формирователь регулятора при инерционности 1-го порядка,
- «8» формирователь регулятора при инерционности 2-го порядка,
- «6.1», «6.2» вычислитель постоянных входного воздействия,
- 6.2 регулятор по начальной ошибке (фиг.20), включающий последовательно соединенные устройства:
- «3» определитель рассогласования,
- «4.2» определитель корней математической модели регулятора,
- «9.2» определитель зависимостей,
- «5» определитель постоянных полного решения,
- «6.3» вычислитель постоянных входного воздействия,
6.3 регулятор по заданному моменту времени (фиг.23), включающий параллельно соединенные:
- «1» регулятор для одиночных моментов времени,
- «11» регулятор для совокупности заданных моментов времени, в который входят последовательно соединенные:
2.1…) вычитатели параметров 1-го… момента времени,
3.1…) определители решения дифуравнения для рассогласования,
4.1…) определители математической модели для вычисления постоянных по величине параметра,
5) формирователь системы равенств для 1-го постоянного,
6) формирователь системы уравнений для алгебраических дополнений,
7) элемент подстановки корней модели объекта,
8) вычислитель дополнений,
9) вычислитель корней,
10) вычислитель постоянных;
7. Регулятор с переменными параметрами, включающий параллельно соединенные четыре блока регулирования (фиг.24):
7.1 регулятор с переменными коэффициентами, в который входят последовательно соединенные устройства:
1) задатчик корней регулятора,
2) задатчик момента времени,
3) вычислитель рассогласования,
4) вычислитель постоянных;
7.2 регулятор с переменными корнями, включающий последовательно соединенные устройства:
5) формирователь структуры,
6) формирователь совокупности систем дифуравнений,
7) вычислитель текущих значений внутреннего запаздывания,
8) формирователь совокупности систем уравнений запаздывания,
9) объединитель систем уравнений,
10) определитель дополнения,
11) определитель корней характеристического уравнения,
12) определитель постоянных полного решения,
13) определитель постоянных входного воздействия;
7.3 регулятор с переменным запаздыванием, в который входят последовательно соединенные устройства:
14) формирователь совокупности дифуравнений,
15) формирователь модели постоянных,
16) формирователь системы уравнений приравниванием коэффициентов,
17) определитель корней модели запаздывания,
18) определитель постоянных,
19) определитель слагаемых приведенных коэффициентов,
20) элемент проверки коэффициентов запаздывания;
7.4 регулятор с переменной структурой, в который входят последовательно соединенные устройства:
21) формирователь модели запаздывания,
22) задатчик интервала времени,
23) вычислитель запаздывания для заданного интервала,
24) вычислитель корней,
25) вычислитель производных от значения корней.
26) определитель математической модели корней,
27) определитель постоянных модели;
8. Регулятор по текущей ошибке, включающий последовательно соединенные (фиг.25) устройства:
1) дифференциальная модель параметров регулятора,
2) определитель запаздывания регулятора по начальной ошибке,
3) регулятор по текущей характеристике ошибки;
9. Корректирующий регулятор (фиг.26), включающий последовательно соединенные блоки:
«9.1» компенсатор системной ошибки, включающий последовательно соединенные устройства:
1) определитель неучтенной ошибки вычитанием, который также подсоединен на вход п.9.2 (6),
10) определитель математической модели, который включает последовательно соединенные элементы:
(2) определитель текущей динамической характеристики неучтенной ошибки дифференцированием,
(3) фильтрация неучтенной ошибки интегрированием,
(4) вычислитель математической модели неучтенной ошибки из системы уравнений дифференциальной и интегральной характеристики, выход которого также подсоединен на вход п.«9.2(7)»,
5) формирователь регулирующего воздействия, первый выход которого подсоединен на вход сумматора «8»,
«9.2» компенсатор случайной ошибки, включающий последовательно соединенные устройства:
6) определитель случайной ошибки вычитанием,
7) формирователь интеграла компенсации;
«9.3» сумматор;
10. Формирователь регулирующего воздействия включает п.6…9 фиг.1;
18. Блок контроля ОДЗ действительной CAP, включающий последовательно соединенные блоки:
"18.1" формирователь модели объекта (фиг.18), который включает 1-й и 2-й каналы, подсоединенные входами к входу п.18.1, а выходами к входам п.17,
1-й канал определителя реакции на входное и предыдущие воздействия, включающий последовательно соединенные устройства:
3) вычислитель реакции на текущее воздействие по степенной модели, выход которого также подсоединен на второй вход сумматора п.10),
4) вычислитель реакции объекта на предыдущие воздействия,
5) формирователь эквивалентной сумы воздействия, включающий последовательно соединенные элементы:
(6) - вычислитель корней входного воздействия,
(7) - вычислитель постоянных полного решения по моменту времени,
(8) - вычислитель постоянных входного воздействия;
9) формирователь степенной модели реакции на сумму предыдущих воздействий;
10) сумматор;
2-й канал определения емкостных составляющих и максимальной производной, включающий последовательно соединенные блоки:
15) определитель производных меньшей степени (выходы которого также подсоединены на входы п.16), в которые входят последовательно соединенные
11.1… элементы, понижающие производную, каждая из которых включает в себя последовательно соединенные элементы:
(12) интегратор, соединенный со всеми входами других интеграторов и со входом п.15,
(13) вычислитель постоянных интегрирования, выход которого подсоединен к входу п.3;
12.3…5 формирователи структуры характеристического уравнения, выходы которых подсоединены к соответствующим входам п.7.1…4:
(3) блок приравнивания коэффициентов слагаемых с одинаковыми степенями,
(4) формирователь приближенной степенной функции для производных высокого порядка,
(5) вычислитель производных высокого порядка вычитанием;
12.7.1…4 определители характеристического уравнения, выходы которых подсоединены на входы п.12.8.1…4:
(7.1) определитель характеристического уравнения при нулевых производных высокого порядка,
(7.2) определитель характеристического уравнения по дополнительным измерениям выходного параметра,
(7.3) определитель характеристического уравнения исключением дополнительных корней,
(7.4) определитель характеристического уравнения по параметрам ряда Тейлора;
12.8.1…4 определители корней характеристического уравнения (выходы которых подсоединены на выходы п.12), при этом каждый из которых включает в себя последовательно соединенные блоки:
«12.9» - отделитель действительной части от мнимой,
«12.10.1…4» - определители корней на осях, каждый из которых включает в себя последовательно соединенные элементы:
(11) - поэтапный дифференциатор,
(12), (13.1…) - вычислители корней, подсоединенные последовательно:
(12) - стандартный вычислитель,
14) определитель модели максимальной производной,
16) формирователь модели выходного параметра;
18.2 определитель интервала превышения ОДЗ,
18.3 определитель установившихся значений,
18.4 определитель максимумов и минимумов,
18.5 вычислитель ближайших значений;
19. Идентификатор, выходы которого подсоединены на соответствующие входы составляющих CAP и на выходы внутренних блоков идентификатора п.11…17 (входы которых подсоединены на входы идентификатора п.19):
«11» - быстродействующий вычислитель, входы которого также подсоединены ко входам входящих в него п.7.1…2 (фиг.4.1):
7.1, 7.2 определители внутреннего запаздывания, в которые входят последовательно соединенные элементы п.1…4, п.6:
1) дифференциатор исследуемого параметра,
2) делитель производных большей степени на меньшую,
3) дифференциатор частного от деления,
4) элемент равенства,
5) схема сравнения частных от деления производных, вход которой подсоединен к выходу п.2, а выход - к входу п.6 и выходу п.7;
6) вычислитель параметров позиционного звена второго порядка;
8. Вычислитель передаточной функции делением модели входных и выходных параметров;
«12» - уточняющий вычислитель (фиг.7), включающий последовательно соединенные блоки:
12.1…2 дифференциаторы модели, подсоединенные входами ко входам п.12:
(1) дифференциатор дифмодели CAP, подсоединенный выходам к входам п.4…5 и п.7.1,
(2) дифференциатор модели после подстановки ряда Тейлора,
(13.1…) - вычислитель корней соответствующего этапа, каждый из которых в свою очередь включает в себя последовательно соединенные п.14…16:
- 14* - формирователь многочлена 2-ой степени,
- 15* - стандартный вычислитель,
- 16* - вычислитель корней методом касательных;
«12.17» - определитель точки пересечения двух кривых.
«12.18» - уточняющий вычислитель комплексных корней, включающий последовательно соединенные блоки (фиг.7.1):
9.1… блоки вычисления одного из корней, выходы которых также подсоединены к входам п.16 и п.«12», в который входят последовательно соединенные элементы п.1…4, 6…8, а элемент п.5 входами подсоединен - к выходам п.3, а выходами - к входам п.6 и п.8:
1) делитель на известные корни, выход которого также подсоединен на выход п.9,
2) отделитель действительной и мнимой части,
3.1.) 3.2) делители на коэффициенты слагаемых с максимальной степенью,
4) делитель свободного члена действительной части на свободный член мнимой части,
6) вычитатель первого коэффициента мнимой части от первого коэффициента действительной части,
7) элемент приравнивания частного от деления и остатка от вычитания,
8) вычислитель действительной части корня, выход которого также подсоединен на выход п.9,
9) вычислитель мнимой части корня,
10. Блок проверки найденных корней,
16. Схема сравнения;
«13» - фильтрующий вычислитель, выходы которого подсоединены также к входам п.14 (фиг.8 и фиг.9), а входы - к входам внутренних блоков п.1. п.2, п.4.3 и п.6, при этом выходы п.1 и п.2 подсоединены к последовательно соединенным п.3.1…2, п.4.1…3, п.5.1.1…3, п.5.2.1…3, п.5.3, п.5.4:
1. Вычислитель корней условной модели, на один из входов которого дополнительно подсоединен выход п.6,
2. Определитель структуры, в который входят последовательно соединенные п.1…3, п.2.1…3 и п.3:
1.1) вычислитель корней интегрального звена,
1.2) вычислитель корней дифзвена,
1.3) вычислитель корней позиционного звена,
2.1…3) схема сравнения,
3) центральная схема сравнения;
3. Вычислители производных,
4. Вычислители постоянных внутреннего запаздывания,
5.1 вычислители корней,
5.2 схема сравнения, выходной параметр которой подсоединен к выходу п.5,
5.3 вычислитель коэффициентов решения,
5.4 вычислитель текущих значений выходного параметра,
«14» вычислитель модели с переменными корнями, включающий каналы п.14.1 и п.14.2, подсоединенные параллельно (входами к входам п.14, а выходами к входам п.15 фиг.4):
14.1 канал действительных переменных корней, включающий последовательно блоки:
1) вычислитель натурального логарифма отношения значений изменившегося корня,
2) делитель на интервал времени между измерениями,
3) фильтрующий вычислитель (п.13 фиг.4);
14.2 канал комплексных переменных корней (фиг.10) разделяется на подканалы +1 и +2, входы которых подсоединены к выходу п.1.2, а выходы - к входу п.12:
1.2) вычислитель внутреннего запаздывания для текущего момента времени по производным,
12) блок определения ОДЗ;
+1 медленно меняющихся корней п.1.3, п.4, п.11, п.13 (постоянных в «малом»),
1.3) делитель на текущие коэффициент усиления и коэффициент внутреннего запаздывания при производной максимальной степени,
4) определитель функции времени для приведенных коэффициентов, включающий параллельно соединенные п.5, п.8…9 (каждый из п.5, п.8…9 включает последовательно соединенные п.*6…7*):
(5) определитель суммы произведений (n-1) корней,
*6* формирователь системы уравнений для текущих моментов,
*7* фильтрующий вычислитель (п.13 фиг.4),
(8) определитель произведения (n) корней,
(9) определитель суммы корней,
(10) определитель суммы произведения двух корней;
11) вычислитель корней делением функции коэффициентов, выход которого подсоединен на вход п.12,
13) блок проверки корней,
+2 определитель быстроменяющихся корней п.14, включающий последовательно соединенные п.15…20:
15) элемент подстановки переменного корня,
16) дифференциатор, выход которого также подсоединен на вход п.18,
17) дифференциатор,
18) формирователь двух уравнений относительно переменного корня,
19) определитель степени переменного корня,
20) определитель постоянных полного решения дифуравнения;
"15". Определитель внешнего запаздывания (п.15 фиг.4, фиг.13 выход которого также подсоединен к входу определителя последовательности взаимодействия звеньев математической модели), включающий в себя подсоединенные ко входу каналы п.1 и п.3, а выходы к входам схемы п.6:
=1) быстродействующий канал, включающий п.2.1, п.2.2, входами подсоединенные к соответствующим входам п.15, а выходами - на входы входящей п.5.1:
- 2.1, 2.2 определители момента времени быстродействующие фиг.11, включающие последовательно соединенные элементы:
*1* вычислитель корней полного решения дифуранения по производным выходного параметра,
*2* вычислитель слагаемых выходного сигнала,
*3* вычислитель соотношения между коэффициентами полного решения дифуравнения,
*4* формирователь степенного многочлена для известного выходного параметра в известный момент времени,
*5* определитель корней степенного многочлена,
*6* определитель постоянных коэффициентов для каждого из корней,
*7* определитель текущего момента времени по слагаемым,
- 5.1 и 5.2 блоки вычитаний фиг.14, у которых вход регулируемого параметра «Y» подсоединен на отрицательные входы вычитателей п.5.1…3, а вход сигнала регулирующего воздействия «X» подсоединен на положительный вход вычитателя п.5.1 и на вход идентификатора изменения (1), включающего последовательно соединенные
дифференциатор 1.1 и схему сравнения 1.2; выход идентификатора изменения подсоединен на входы таймера 3, элемента памяти 4, идентификатора помех 2,
на второй вход которого подсоединен выход сумматора 5.1, а выход которого подсоединен на второй выход блока вычитателей (п.5.1, 5.2 фиг.13), первый выход таймера подсоединен на второй вход элемента памяти 4, выход которого и второй выход таймера подсоединен па положительный вход вычитателя 5.2, второй выход таймера 3 также подсоединен на положительный вход вычитателя 5.3, выход которого подсоединен на вход схемы сравнения 7, первый выход которого подсоединен на второй вход элемента ключа 6, на основной вход которого подсоединен выход вычитателя 5.2, а выходы схемы сравнения 7 и ключа 6 подсоединены на входы сумматора 5.4, выход которого подсоединен на соответствующий выход блока вычитателей (п.5.1…2 фиг.14);
=3) фильтрующий канал (фиг.13), включающий подсоединенные к соответствующим входам п.4.1 и п.4.2, выходы которых подсоединены на входы п.5.2:
- 4.1 и 4.2 определители моментов времени фильтрующего канала фиг.12, включающие последовательно соединенные блоки п.4, п.5 и п.6, при этом выход п.4 подсоединен на вход п.6:
4) блок исходных настроек, включающий последовательно соединенные п.1…3,
(1) формирователь системы уравнений по выходному параметру через равные промежутки времени,
(2) определитель общих степенных составляющих, выход которого также подсоединен на дополнительный выход п.4,
(3) определитель корней,
5) определитель решения дифуравнения, включающий последовательно соединенные п.5.1…2:
(5.1) задатчик начального момента времени,
(5.2) вычислитель постоянных коэффициентов полного решения,
6) определитель текущего момента, включающий в себя последовательно соединенные
(6.1) формирователь системы уравнения выходного параметра через известные интервалы времени,
(6.2) вычислитель переменных составляющих для данной системы,
(6.3) вычислитель постоянных составляющих слагаемых выходного параметра первого момента,
(6.4) вычислитель первого момента времени,
=6) схема сравнения
«16». Определитель последовательности взаимодействия звеньев математической модели Фиг.15, подсоединенный выходам также на вход п.17 фиг.4 и включающий последовательно соединенные п.1. п.2, п.3.1… и т.д., п.5.1… и т.д.:
1) определитель динамических характеристик и коэффициента полного решения дифуравнения, подсоединенный также на входы п.3.1… и т.д.,
2) идентификатор изменения,
3) 3.1… определители позиции 1-й… и т.д., каждый из которых включает, параллельно соединенные, п.4.1…:
4) 4.1… элементы подстановки звена, каждый из которых в свою очередь включает п.(1)…(5), при этом входы п.(1) и п.(3) подсоединены к входу соответствующего элемента п.4.1…(фиг.16):
(1) вычислитель частных постоянных при (+1)-м воздействии, выход которого подсоединен к входу п.(2),
(2) вычислитель значений выходного параметра звена в конечный момент (+1)-го воздействия, выход которого подсоединен к входу п.5,
(3) вычислитель частных постоянных при (+1)-м воздействии, выход которого подсоединен на вход п.(4),
(4) вычислитель значений выходного параметра звена в начальный момент (+1)-го воздействия,
(5) схема сравнения, выход которой подсоединен на выход соответствующего элемента п.4.1…;
5) 5.1… окончательные модели звеньев, выходы каждого из которых подсоединены на входы определителя последующей позиции (3.+1) и окончательной модели последующего звена (5.+1);
«17». Определитель ОДЗ выходного параметра, включающий последовательно соединенные п.(1)…(7) (фиг.16):
(1) формирователь решения дифуравнения для выходного параметра каждой внутренней составляющей,
(2) элемент подстановки переменного основания степенной функции,
(3) формирователь положительных степеней,
(4) делитель единицы измерения корней на общий знаменатель степеней,
(5) элемент подстановки новой единицы измерения корней,
(6) вычислитель неравенств ОДЗ;
«20». Индикатор, на входы которого подсоединены выходы п.«11»…«17».
Входящий в блок задания п.1 (фиг.1) блок динамических характеристик п.1.1. принимает от оператора совокупность заданной характеристики выходного параметра и его производных: y, y', y”, …
Если дифференциальная модель объекта имеет производные выходного параметра выше второй степени, то блок 1.1 осуществляет проверку технической реализуемости заданной совокупности регулируемого параметра по ф.139,
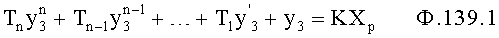
где T1… - коэффициенты внутреннего запаздывания выходного параметра объекта, как правило, полученные после соответствующей линеаризации для исследуемого интервала времени:
K - Коэффициент усиления объекта.
Из Ф.139.1 вычисляется требуемое значение регулирующего воздействия Xp, позволяющее обеспечить заданную совокупность параметров y, y', по ф.139.2
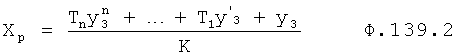
Полученное значение Xp сравнивается с технически реализуемым значением регулирующего воздействия. Если полученное значение технически не реализуется, то выходной сигнал блока задания 1 (полученный результат ф.139.2) передается на вход блока индикации 20, входящий в идентификатор 19, который оповещает об этом оператора их отдельных составляющих п.1.2 фиг.1 принимает от оператора заданные параметры каждого из внутренних звеньев W01, W02, … модели объекта фиг.2 «y1, y2, y3, …». Если заданные параметры имеют характеристики выходного параметра y0, y'0, y”, …, то эти значения в ф.2…3, и вычисляются значения выходного параметра каждого из звеньев дополнительных вспомогательных состояний 1.3 для предварительной оценки (и технической) реализуемости регулирующего воздействия Xp и для оценки параметров при переходном процессе. Решаются следующие задачи фиг.3:
имеется математическая модель CAP, параметры которой определяются в первом положении (т.е. параметры регулятора принимаются постоянными - линеаризованными при приближении);
- для этого звено вычисления корней регулирующего воздействия системы уравнений ф.4 определяет корни дифуравнения регулятора ф.140.1;
- после чего в звенья вычисления коэффициентов регулирующего воздействия п.2 в уравнении ф.4 подставляются начальные значения выходного параметра каждого из математической модели объекта и вычисляются постоянные полного решения дифуравнения ф.140.2
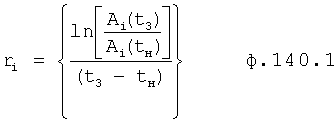
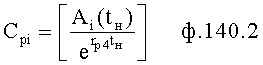
- полученная математическая модель регулятора и системы в целом CAP проверяется на допустимость переходных характеристик;
- математическая модель регулятора и CAP в целом преобразуется в степенной многочлен по ф.5.1… и по ф.6…8 преобразователем дифуравнения в степенной многочлен п.3 фиг.3,
- звено проверки ОДЗ п.4.1 фиг.3 подставляет в полученный степенной многочлен пограничные значения ОДЗ,
- вычисление корней степного многочлена п.4.2 позволяет определить моменты времени, при которых регулирующее воздействие или регулируемый параметр выходит за рамки ОДЗ п.4.3,
- определитель исследуемого параметра между пограничными состояниями п.4.4 приравнивает нулю полученные производные степенного многочлена, после чего находит корни полученных степенных равенств, что позволяет найти моменты времени, при которых параметр принимает максимальные - экстремальные значения (точки перегиба) исследуемого параметра (Xp или Y) и сравнить их с допустимыми значениями;
- приравнивание модели к допустимым значениям позволяет вычислить физически реализуемые параметры регулятора и задания новых промежуточных значений;
- звено коррекции экстремальных недопустимых значений входного воздействия п.4.5 позволяет по задаваемой допустимой переходной характеристике определить математическую модель физически реализуемого регулятора,
- звено вычисления новых промежуточных значений выходного параметра объекта п.4.6 по физически реализуемой модели регулятора определяет «промежуточные значения» задаваемой совокупности выходного параметра, которые тоже нуждаются в проверке технической реализуемости, аналогично «исходным заданным параметрам».
Пояснения к ф.140.1 и ф.140.2
Из ф.4.1… получается система уравнений ф.140.1.1
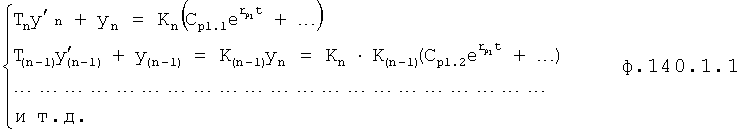
Из ф.140.1.1 определяется зависимости ф.140.1.2
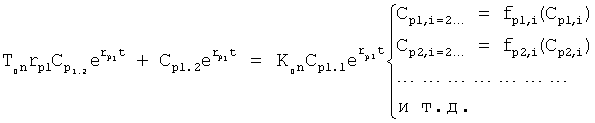
Приравниваются коэффициенты при одинаковых степенях
- 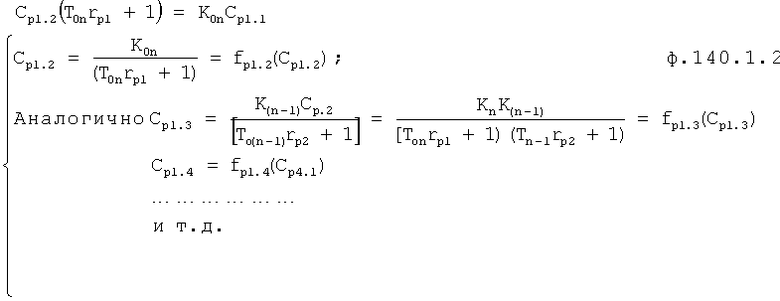
- 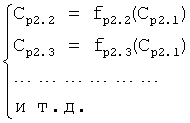
и т.д.
- 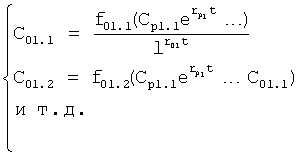
- 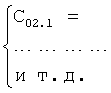
и т.д.
По ф.140.2 формируется система уравнений ф.140.1.3 подстановкой найденных fji… из ф.140.1.1
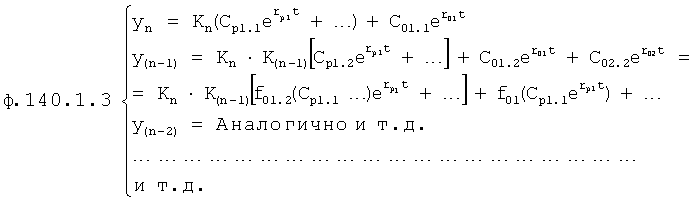
Из системы уравнений ф.140.3 определяются слагаемые Ap1.1 по ф.140.1.4.
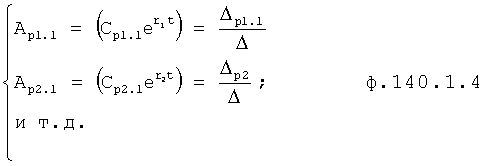
В ф.140.1.4 подставляются выходные параметры y1… звеньев W1… математической модели объекта и вычисляются Ap1.1, Ap2.1… А01…

Вычисленные параметры ф.140.1.5 подставляются в систему уравнений ф.140.1.6
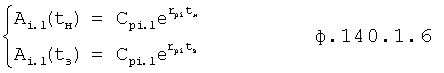
Система уравнений ф.140.1.6 решается относительно неизвестного корня r0i…. По ф.140.1.7
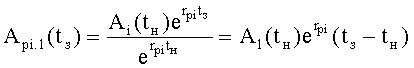
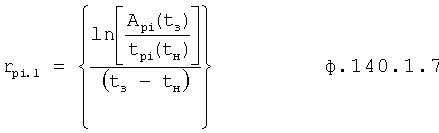
r0i=……Аналогично.
Найденные значения корней rpi…r0i… (по ф.140.1.7) подставляются в ф.140.1.4 и вычисляются Cpi…C0i с ф.140.2.1
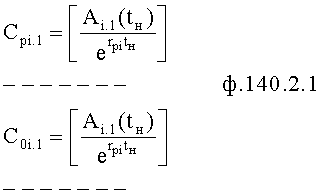
Полученные значения корней и постоянных (частных решений) подставляются в зависимости ф.140.1.2 и вычисляются постоянные полного решения дифуравнения CAP Cp1n…C01n.
Формирователь регулирующего воздействия п.10 фиг.1 включает в себя блоки регулирования п.6…9, формирующие алгоритмы регулирования, дополняющие друг друга, каждый из которых при определенных условиях имеет свое преимущество (см. таблицу).
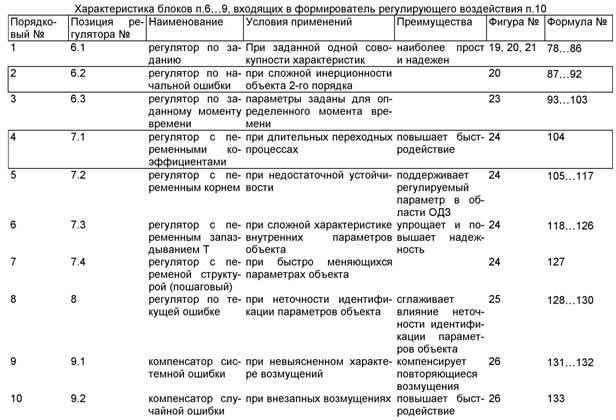
Регулятор с постоянными параметрами п.6 обеспечивает плавность при переходе от начальной совокупности параметров y, y, … к заданной совокупности y, y, …
Регулятор по заданию п.6.1 фиг.21 формирует параметры алгоритма в звеньях:
1) «формирователь зависимости выходных параметров от корней дифуравнения» использует решение дифуравнения в виде математического описания CAP, при этом для составления системы уравнений дифференцируется сумма слагаемых из показательной функции ф.141
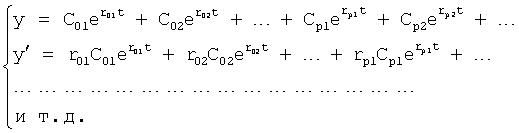
где
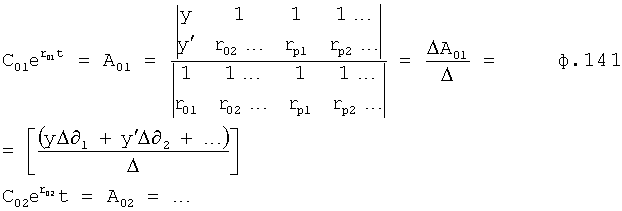
и т.д.
После соответствующих подстановок получается совокупность систем уравнений (1), (2), … ф.142:
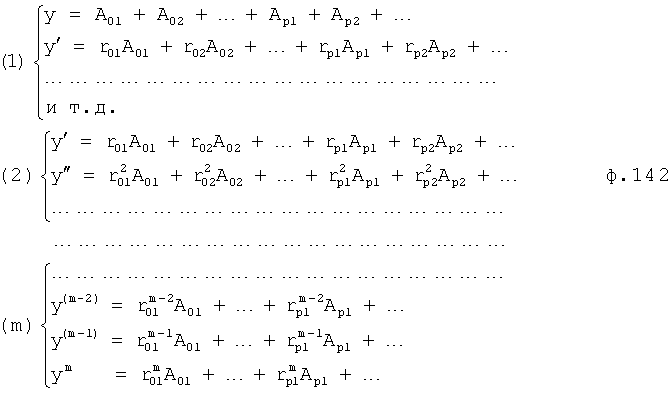
После использования алгебраических дополнений ф.143 для произвольно взятого исследуемого параметра A можно найти совокупность решений
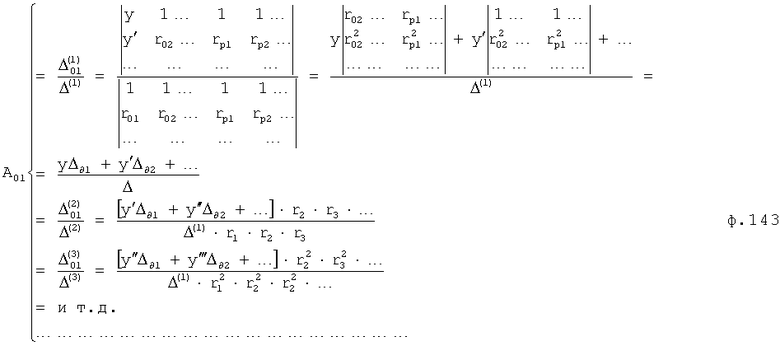
Приравниванием каждого решения, входящего в совокупность ф.143, составляется система уравнений ф.144
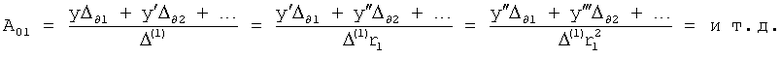
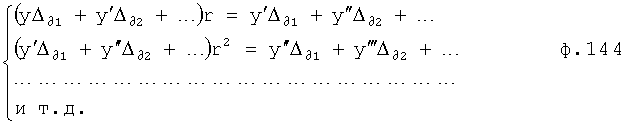 После раскрытия скобок и переноса слагаемых, кроме одного, в левую часть получается система уравнений ф.145
После раскрытия скобок и переноса слагаемых, кроме одного, в левую часть получается система уравнений ф.145
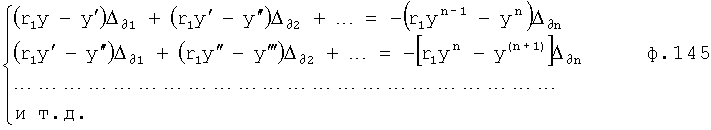
Из системы уравнений ф.145 получаются математические выражения для определения алгебраических дополнений по ф.146, при этом одно из алгебраических дополнений «условно принято за известное» и оставляется в правой части каждого из уравнений, входящих в систему.
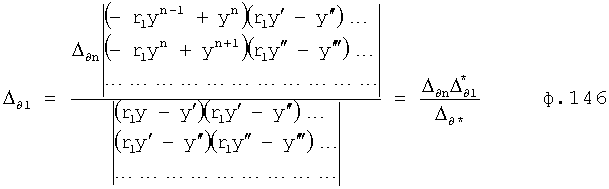
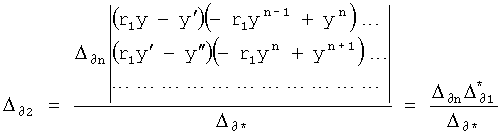
Полученные из ф.146 значения алгебраических дополнений подставляются в ф.147.1, в результате получается ф.147.2.
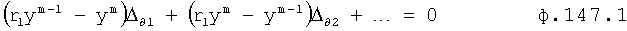
ф.147.1 не входит в ф.145
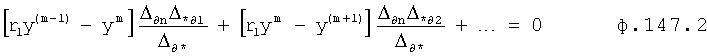
После сокращения на  получается ф.148
получается ф.148
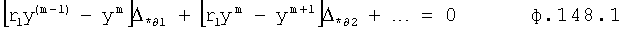
где
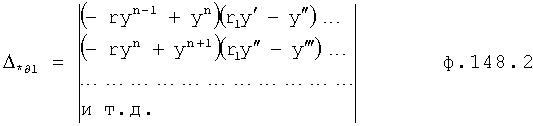
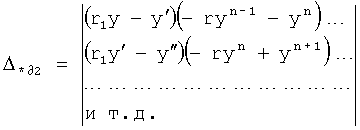
…………………
и т.д.
y, y' … - производные высоких порядков являются неизвестными.
Элемент подстановки заданных динамических характеристик выходного параметра п.2) подставляет заданные параметры yз, y'з, … (полученные по y1, y2….) в ф.148.
Формирователь системы уравнений поочередной подстановкой корней объекта “п.3)”: подставляет по одному из корней r01… дифуравнения объекта в ф.148: в ф.149(1), ф.149(2)…
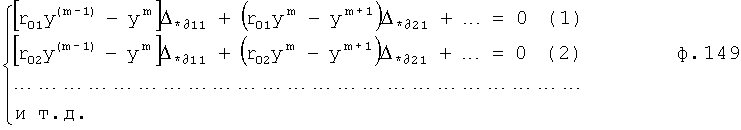
где Δ*∂ij - алгебраическое дополнение ф.148.2 корня модели объекта r0j….
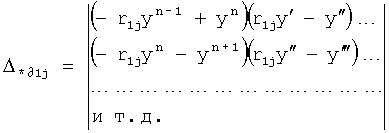
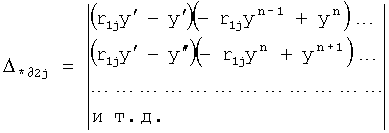
……………………………………
и т.д.
В полученной системе уравнений неизвестными будут производные высоких порядков (степень которых выше степени заданных производных). Количество неизвестных производных должно быть равным количеству уравнений, а следовательно, количеству корней дифуравнения объекта. Вычислитель производных высокого порядка п.4) из системы уравнений ф.149 определяет неизвестные производные. Для этого в ф.149 открываются скобки и формируются уравнения относительно неизвестных производных высокого порядка yn, yn+1, … Количество неизвестных равно количеству корней объекта ф.150
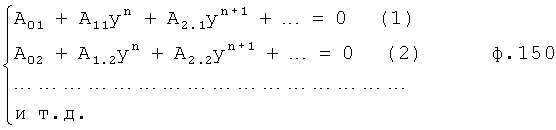
где A0i=1… - свободные члены () уравнения,
A1i=1… - коэффициенты. Стоящие при неизвестной производной y,
A2i=1 - коэффициенты, стоящие при неизвестной производной y и т.д.
Axi - находятся после раскрытия скобок ф.149

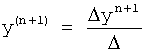
и т.д.
Вычислитель корней характеристического уравнения п.5, полученные производные высокого порядка, а также заданные выходные параметры y, y', … подставляются в ф.148.1…, при этом значение корней САР считается неизвестным. После раскрытия скобок уравнения ф.148 оно преобразуется в степенной многочлен, который совпадает с характеристическим уравнением CAP.
Вычислитель корней характеристического уравнения п.6) определяет корни степенного многочлена, полученного на выходе п.5). После этого полученный многочлен делится на степенной многочлен характеристического уравнения объекта регулирования и получается характеристическое уравнение регулятора, включающего корни модели регулятора.
Подстановка найденных корней характеристического уравнения в полное решение дифуравнения CAP и приравнивание его и его производных заданным параметрам yз, y'з, … в вычислителе составляющих заданного параметра п.9.1) фиг.22 (входящего в определитель зависимостей п.9.1…2 фиг.20 регуляторов п.6.1…2) позволяет найти составляющие в виде показательных функций Ap, A, A, …, сумма которых равна задаваемым значениям ф.151:
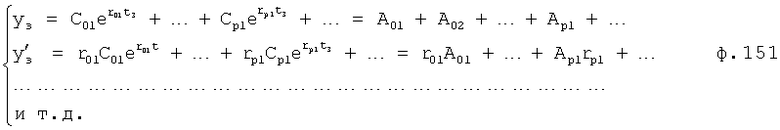
где
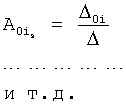 ;
;
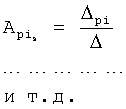 .
.
Определитель постоянных по функции времени п.9.2 позволяет определить зависимость постоянных С, С, … полного решения дифуравнения от показательных составляющих заданного значения регулируемого параметра и необходимого интервала времени регулирования ф.152
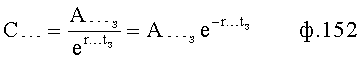
Найденные зависимости (С…=f(tз) ф.152) постоянных от заданной совокупности параметров yз…, формирующих степенные функции Ajiз…Cjiеr, подставляются в ф.153 для начального момента заданного цикла регулирования. Определитель начальных параметров по функции времени (т.е. по необходимому интервалу времени регулирования) п.9.3 определяет зависимость математической модели состояния объекта в начальный момент времени через степенные функции, определенные по заданным параметрам
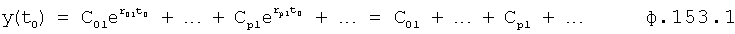
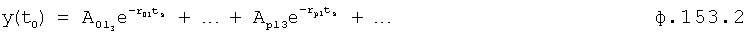
где
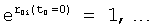
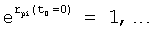
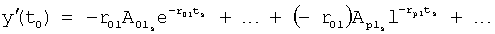
………………………………………………………
и т.д.
Если интервал переходного процесса непродолжительный и если модель объекта можно упростить до инерционной 1-го порядка, то формирователь регулирования при инерционности 1-го порядка п.7 фиг.21 в полученные (с выхода определителя зависимостей п.9.1) ф.153 зависимости подставляет начальные значения регулируемого параметра в элементе подстановки начальных значений п.7.1).
Вычислитель интервала регулирования п.7.2) по ранее приведенным формулам из ф.153 определяет момент времени, при котором выходной регулируемый параметр примет заданное значение.
Для этого после приведения степеней в ф.153.2 к общему знаменателю q и вводов условной единицы измерения 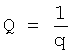 (где q - общий знаменатель степеней) слагаемые с отрицательными степенями (r - отрицательные) преобразуются к дробным выражением с положительными степенями и приводятся к одному общему знаменателю, который переносится в левую часть равенства: ф.153.2 примет вид ф.154
(где q - общий знаменатель степеней) слагаемые с отрицательными степенями (r - отрицательные) преобразуются к дробным выражением с положительными степенями и приводятся к одному общему знаменателю, который переносится в левую часть равенства: ф.153.2 примет вид ф.154
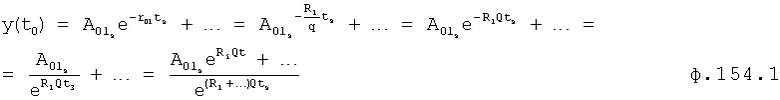
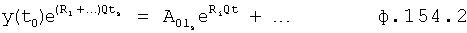 ,
,
где R1… получены после приведения степеней к общему знаменателю.
Нахождение корней этого степенного многочлена ф.154.2 позволяет выбрать соответствующий интервал времени, т.е. Δt=tз, равный одному из корней.
Найденное значение интервала времени подставляется в формулы 152 для определения постоянных C… полного решения дифуравнения "вычислителем постоянных полного решения дифуравнения CAP" п.7.3).
Вычислитель постоянных входного воздействия п.6.1…2 фиг.21 каждое из слагаемых 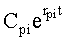 вынужденного состояния
вынужденного состояния 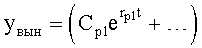 подставляет в дифуравнение объекта ф.155
подставляет в дифуравнение объекта ф.155
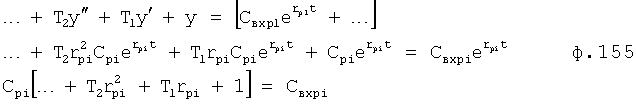
После этого приравниваются коэффициенты при одинаковых степенях
…………………………
и т.д.
Таким образом, регуляторы п.6…9 формируют алгоритмы по ф.78-133, при этом взаимодействие входящих в него устройств осуществляется по структурным схемам фиг.19…26.
Формирователь регулирующего воздействия п.10 принимает сигнал заданных параметров на входы регуляторов п.6…8 для осуществления поиска алгоритма, формирующего наиболее оптимальный переходной процесс, при этом учитываются выходные параметры объекта (п.2) и параметры внутренних его емкостных составляющих объекта, полученных с выхода идентификатора п.19. Полученные алгоритмы формирования регулирующего воздействия (п.6…8) позволяют получить математические модели переходного процесса регулируемых параметров для каждого из алгоритмов в блоке проверки ОДЗ планируемой CAP ф.134…138.
После того как блок сравнения моделей п.4 фиг.1 выбрал алгоритм, формирующий переходной процесс с желаемой переходной характеристикой, формирователь регулирующего воздействия п.4 формирует текущее значение входного воздействия Хр, а компенсирующий регулятор п.9 контролирует рассогласование между выходным параметром объекта и моделью, сформированной блоком проверки ОДЗ планируемой CAP п.5, для последующей корректировки рассогласования выходного параметра объекта или выходных параметров внутренних звеньев объекта, вызванных неучтенными возмущающими воздействиями. Компенсатор системной ошибки п.9.1 позволяет сформировать дополнительное регулирующее воздействие для компенсации ошибки, которая не поддается корректировке алгоритмами основных регуляторов п.6…8. Компенсатор случайной ошибки п.9.2 формирует дополнительное регулирующее воздействие, компенсирующее внезапное текущее возмущение.
Совокупность основных регуляторов п.6…8 и дополнительных п.9.1…2 позволяет создать максимально возможное физически (и технически) реализуемое регулирующее воздействие.
Блок проверки ОДЗ планируемой CAP п.5 исследует характер изменения выходного параметра объекта y, y′, y′′, … (и его внутренних звеньев y1, y2 …) и регулирующею воздействия Хр, находя максимальные и минимальные значения (для разных интервалов времени), точки перегиба и фиксируя интервалы времени, при которых исследуемый параметр достигает границу ОДЗ или превышает допустимые значения (ОДЗ) ф.134…138.
Блок сравнения моделей п.4 анализирует полученную информацию по заданным критериям качества, и если ни одна из моделей п.6…8 не отвечает заданным требованиям, формирует на своем выходе команду задания дополнительной совокупности выходных характеристик yд, y'д, …, которая является промежуточной между текущим состоянием объекта и заданным состоянием. Значение, характеризующее дополнительное промежуточное состояние, формируется задатчиком вспомогательных совокупностей выходных параметров п.1.3.
После этого формируется промежуточный этап регулирования, при котором формирователь регулирующего воздействия п.10 повторяет цикл поиска алгоритма регулирующего воздействия. Если найденный алгоритм регулирования обеспечивает CAP, параметры которого не превышают ОДЗ в блоке проверке ОДЗ планируемой CAP ф.134…138, то формирователь регулирующего воздействия п.3 обеспечивает текущее значение регулирующего воздействия на входе объекта регулирования п.2.
Идентификатор 19 с первого момента регулирования начинает идентификацию динамической характеристики регулируемого параметра в "вычислителе быстродействующем" п.11 фиг.4, с последующим уточнением: т.е. увеличением производной дифуравнения объекта, в "вычислителе уточняющем" п.12. Полученные результаты сравниваются с параметрами, полученными на выходе "вычислителя фильтрующего" п.13.
Быстродействующий вычислитель А включает в себя (фиг.4.2) два независимых канала к1, к2 и делатель "д". При этом вход канала к1 подсоединен к входу объекта Xp, а вход канала к2 подсоединен к выходу объекта Y. Выходы обоих каналов подсоединены к входам делителя "д" и к выходам быстродействующего вычислителя А. Канал к1 позволяет с максимальным быстродействием получить динамическую характеристику параметра, поступающего на вход объекта и являющегося результатом управляющего воздействия регулятора. Канал к2 исследует динамическую характеристику выходного параметра объекта и является результатом воздействия системы регулирования на объект, делитель "д" делит динамическую характеристику выходного параметра объекта на динамическую характеристику входного параметра объекта, что позволяет в результате получить переходную характеристику объекта ф.1 Wоб. Выход делителя "д" подсоединен на соответствующий выход быстродействующего вычислителя A.
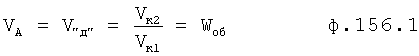
где VA - первый выходной сигнал быстродействующего вычислителя A,
V"д" - выходной сигнал делителя "д".
Vк1, Vк2 - выходные сигналы первого и второго каналов к1 и к2.
Каждый из каналов к1, к2 включают в себя (фиг.4.2) последовательно соединенные дифференциаторы 1.1, …, 1.4, делители 3.1, …, 3.4, входы которых подсоединены на выходы дифференциаторов, элементы сравнения 2.1, … 2.3, соединенные входами на соответствующие выходы делителей, логические элементы "И" 4.1, …, 4.4, входами подключенные к выходам элементов сравнения, и вычислитель динамических характеристик 5, на вход которого подсоединены выходы элементов "И" и выходы дифференциаторов 1.1, …, 1.4. Выход делителя 3.2 также подсоединен на вход дифференциатора 1.5, выход которого подсоединен на вход элемента сравнения 2.4, который в свою очередь подсоединен выходом на входы элементов "И".
Дифференциаторы 1.1, …, 1.5 передают на свои выходы результаты дифференцирования входных сигналов. Элементы сравнения 2.1, …, 2.4 формируют на своих выходах командные сигналы, например "I", при равенстве входных сигналов, сигналов с первого и второго входа.
Делители 3.1…3.4 формируют на своих выходах сигналы, по величине равные частным от деления сигналов первых входов на соответствующие сигналы со вторых входов.
Элементы "И" 4.1…4.4 формируют на своих выходах командные сигналы при определенной совокупности входных сигналов.
Соответствующая совокупность входных сигналов для каждого элемента "И" определяется ф.2…ф.6.
Совокупность входных сигналов для элемента "И" 4.1 получена из математического выражения ф.2
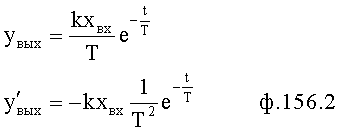
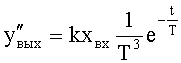
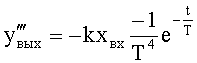
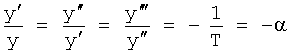
где xвх=const.
Выходной сигнал первого элемента сравнения 2.1 станет соответствовать команде "I" при выполнении равенства из ф.3


где y, y′, y′′, … - значение исследуемого параметра и его производные.
Командный сигнал на входе элемента "И" 4.1 свидетельствует о том, что динамическая характеристика исследуемого параметра (Xp или y) соответствует динамической характеристике дифференцирующего звена, и при вычислении внутренних параметров выбирается дифференцирующая структура.
При этом команда с выхода элемента "И" 4.1 будет задавать на входе вычислителя 5 структуру для вычислений, соответствующую дифференцирующему звену ф.2.
Совокупность входных сигналов для элемента "И" 4.2 получена из математического выражения ф.4
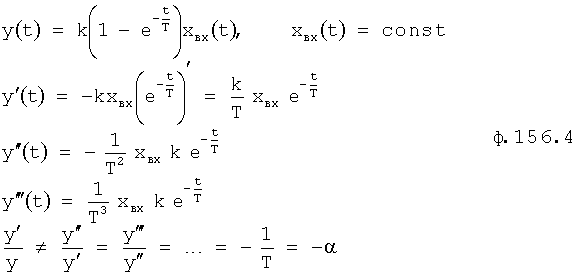
Единичный выходной сигнал элемента "И" ф.2 задает структуру звена с инерционностью 1-го порядка, позволяющего моделировать исследуемый параметр.
Элемент "И" 4.3 формирует единичный выходной командный сигнал при совокупности входных сигналов, полученных из ф.5, которая обусловлена ф.6. Структура ф.6 описывает интегрирующее звено с запаздыванием.
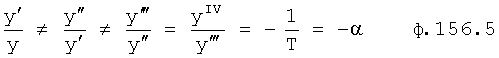
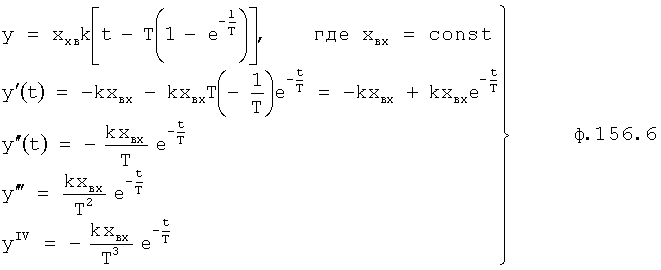
Единичный выходной сигнал на выходе элемента "И" 4.3 задает интегральную структуру на входе вычислителя динамических характеристик 5.
Элемент "И" 4.4 формирует единичный командный выходной сигнал при выполнении неравенств ф.7, полученный дифференцированием математических выражений, описывающих изменение выходного параметра позиционного звена с дифуравнением второго порядка. ф.8.
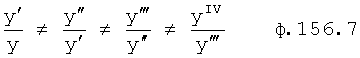
ф.156.8: где Xвх=const, см. ниже при инерционности 2-го порядка
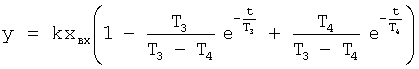
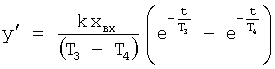
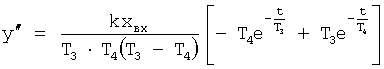
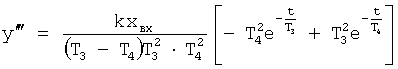
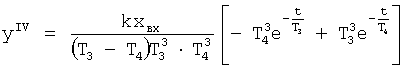
- при колебательной характеристики
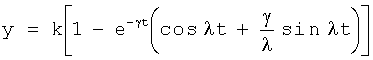
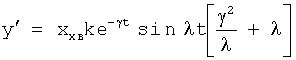
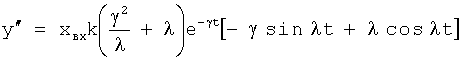
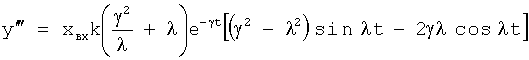
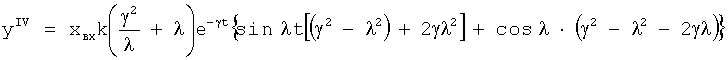
- при консервативности (колебаниях с одинаковой амплитудой)
y=kxвх=(1-cosgt); где Xхв=cosgt.
y′=g kxвхsingt.
y′′=g2kxвхcosgt.
y′′′=-g3 kxвхsingt.
yIV=-g4kxвхcosgt.
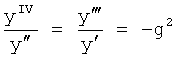 .
.
Вычислитель динамических характеристик 5 принимает на своих входах командный сигнал: со 2-го входа - дифференцирующего звена, с 3-го входа - инерционного звена 1-го порядка, с 4-го входа - интегрирующего звена, с пятого входа - позиционного звена второго порядка. После поступления командного сигнала на один из соответствующих входов 2…5 вычислитель 5 использует нижеприведенные формулы:
ф156.9 - для дифференцирующего звена: 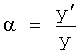
ф.156.10 - для инерционного звена 1-го порядка: 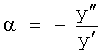
ф.156.11 - для интегрирущего звена: 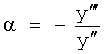
ф.156.12 - для позиционного звена 2-го порядка
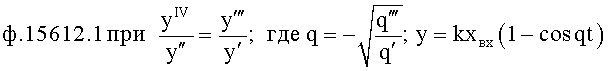
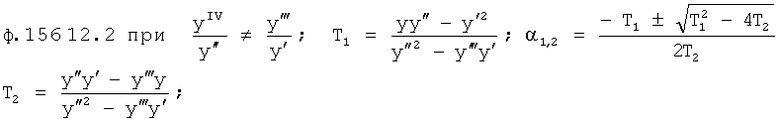
ф.156 12. 2 получены из системы уравнений ф.13
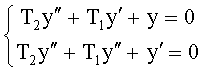
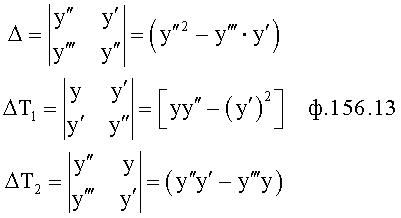
 ;
; 
Уточняющий вычислитель п.12 фиг.4 включает определители характеристических уравнений п.7.1… (фиг.7) которые выполняют функцию
Формирователя степенного многочлена и вычисляют коэффициенты при степенном многочлене первого приближения, имеющего количество корней больше, чем количества корней у исследуемого характеристического уравнения 1.
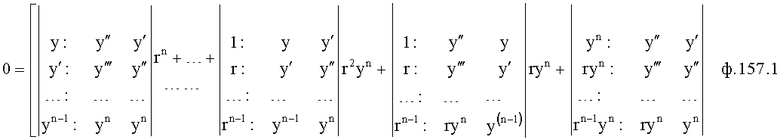
где y, y′, y′ … - величина исследуемого параметра и ее производные (по времени),
n - максимальная степень исследуемого характеристического уравнения,
m - максимальная степень многочлена, полученного при первом приближении в поиске возможных корней при измеренных y, y′, … yn,
r - переменная степенного многочлена.
Формула 157.1 получена из системы математических выражений ф.157.2
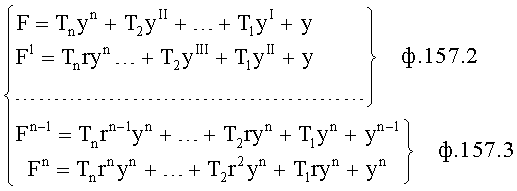
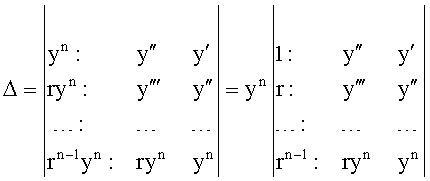
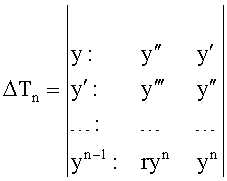
……………………………
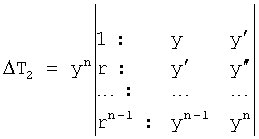

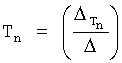
………………
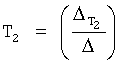
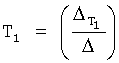
Значения T1…Tn подставляют в ф.157.3 и получают ф.157.4
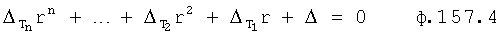
На выход формирователя степенного многочлена поступают коэффициенты, найденные и используемые при "первом приближении". Общее количество корней многочлена"первого приближения" равно ф.157.5
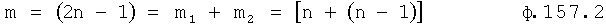
где m1 - количество корней, значения которых равны значениям корней, входящих в характеристическое уравнение исследуемого параметра m1=n,
m2 - количество корней, не равных корням характеристического уравнения m2=n-1.
Вычислитель мнимой и действительной части подставляет значение аргумента p=α+jβ в степенной многочлен, коэффициенты которого задаются сигналом со входа, после приведения подобных членов и объединения слагаемых с мнимой единицей, результат можно представить в виде суммы двух функций ф.157.6
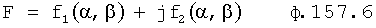
Сигнал с синхровыхода свидетельствует о том, что вычисления завершены, и, попадая на вход задатчика аргументов 2, включает его в режим работы. Найденные значения действительных и мнимых частей f1, f2 степенного многочлена F с информационных выходов вычислителя действительной и мнимой части на информационные входы вычислителя действительных корней 8.1… фиг.7.
После поступления синхроимпульса задает нулевые значения аргументов α=0, β=0 которые поочередно подставляются в функции f1, f2.
По найденным мнимым корням с выхода вычислителя действительных корней 3 (после подстановки в f1; α=0) β1, β2 задатчик постоянных аргументов формирует эти значения на своих выходах фиг.7. Утоняющий вычислитель аргумента находит среднее арифметическое между двумя последовательно расположенными значениями постоянных аргументов фиг.6.5.
Таким образом, для поиска комплексных корней задаются оси с постоянным мнимым аргументов β1=const, β2=… На первом предварительном этапе задаются оси проведенные через значения мнимых аргументов при α=0 (для нахождения действительных корней α1-n, на каждой из этих осей и для каждой из функций f1 и f2).
На втором этапе сравниваются действительные α корни двух функций f1, f2, расположенных на одной мнимой оси βi. Результат сравнения сравнивается с результатом сравнения на близлежащих осях βi-1, βi+1=const. Если последовательность расположения корней на ближайших осях разная, то поиск корней производится на оси, задаваемой из ф.158 (βy=…) фиг.7.
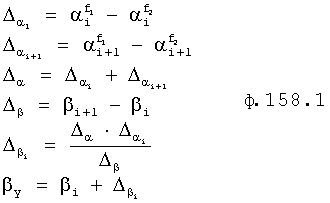
Выход формирователя ряда Тейлора подсоединен на вход стандартного вычислителя корней, выход которого подсоединен на вход второй схемы сравнения. Выход второй схемы сравнения подсоединен через выход вычислителя корней по корням производной Ф.
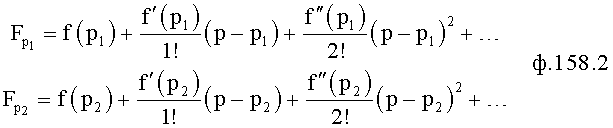
где P1, P2, … - корни производной
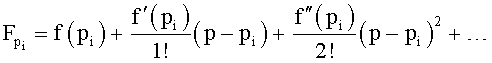
Первая схема сравнения из четырех найденных корней для каждого ряда Тейлора оставляет по одному ближнему справа (большему) и слева (меньшему) к используемому корню производной. Из оставленных корней оставляют только действительные. После этого, фиг.6.5…, оставляют без изменения максимальный (крайний справа) и минимальный (крайний слева), остальные оставленные группируют парами (близлежащие) и находят среднее арифметическое между ними. Максимальный, минимальный и среднеарифметические передают на выход первой схемы сравнения.
Схема сравнения из четырех найденных корней (для каждого ряда Тейлора) оставляет ближайший к соответствующему корню производной в окрестности которого составлялся ряд Тейлора.
Таким образом, определитель корней фиг.7 вычисляет стандартными способами корни степенного многочлена четвертой степени, полученного дифференцированием (многократным) исследуемого многочлена F(p)=аnpn+…+аΔp+а0. Из полученных корней оставляются действительные, для каждого из которых формируется ряд Тейлора четвертой степени и т.д. Вычислитель корней по производным определяет действительные корни для степенного многочлена пятой степени…, потом шестой степени и т.д.
Определитель корней (после разделения мнимой и действительной частей) фиг.6… подставляет в степенной многочлен значение аргумента (α или β) постоянным на данным этапе поиска. После этого вычислитель корней находит действительные корни второго аргумента. Выч. корней соотв. этапа п.13.1… определяет дальнейшую область поиска и уточняет задаваемый и вычисляемый аргументы, что позволяет найти значение искомых комплексных корней.
Уточняющий вычислитель фиг.7 определяет комплексные корни исследуемого многочлена для двух моментов времени. После сравнения их оставляют те корни, которые одинаковые для двух моментов времени.
Используемые для идентификации объекта вычислители быстродействующий и уточняющий позволяют по текущим значениям производных пар найти математическую модель объекта для текущего момента времени. Быстродействующий вычислитель находит модель в виде дифуравнения первой или второй стены. Уточняющий вычислитель позволяет уточнить модель в виде дифуравнения с постоянными коэффициентами, степень которого увеличивается до желаемой точности. Недостаток этих вычислителей в том, что быстрое получение параметра внутреннего запаздывания отражает действие возмущений, поэтому требует дополнительной систематизации и исследования характера изменения возмущений. Параллельно фильтрующий идентификатор позволяет получить внутренние параметры объекта, избежав влияния на них возмущений. Для этого производные (разной степени) выходного параметра вычисляются по математической модели в виде дифуравнения первой степени позиционного звена с переменным коэффициентом (переменным корнем характеристического уравнения).
На фиг.8 изображена структурная схема фильтрующего вычислителя 13. Информационный вход и синхровход фильтрующего вычислителя подсоединены к информационным входам и синхровходам вычислителя корня x условной модели 1 и определителя структуры 2, выход которого подсоединен на вход вычислителя коэффициентов дифуравнения 4. Выход вычислителя корня характеристического уравнения подсоединен на вход вычислителя производных 3, выход которого подсоединен на вход вычислителя коэффициентов дифуравнеиия 4. Информационный выход вычислителя коэффициентов 4 подсоединен на вход математической модели 5 и на выход фильтрующего вычислителя. Синхровыход вычислителя коэффициентов дифуравнения подсоединен на второй синхровход С2 вычислителя корня условной модели 1 и на синхровыход фильтрующего вычислителя. Выход математической модели 5 подсоединен на второй вход схемы сравнения 6, на первый вход которой подсоединен вход ”И” фильтрующего вычислителя, а выход которого подсоединен на третий сннхровход С3.
Вычислитель корня условной модели 1 моделирует объект в виде позиционного звена, описываемого дифуравнением первой степени с переменный корнем характеристического уравнения ф.159.1
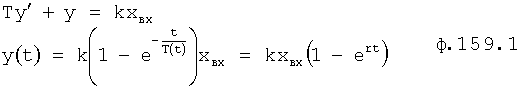
где 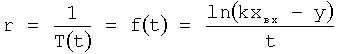
Характер изменения корня r зависят от структуры объекта (интегральной, дифференциальной и т.д.). Определитель структуры 2 (фиг.9) подробно изображен на структурной схеме фиг.12. Входящие в него вычислители корней интегрирующей структуры 1.1, дифференцирующей 1.2 и позиционной 1.3 определяют текущие значения корней моделируемых структур. Схемы сравнения 2.1, 2.2. 2.3 позволяют сравнивать вычисленные значения корней в текущий момент времени с вычисленными значениями в предыдущий момент этой же структуры, центральная схема сравнения 3 выбирает ту структуру, у которой скорость изменения корня характеристического уравнения минимальна, т.е. разница между текущим значением и значением в предыдущий момент минимальна. Выбранная структура используется для вычисления постоянных внутреннего запаздывания (постоянных коэффициентов дифуравнения) модели объекта вычислителем коэффициентов дифуравнений 4. Определитель структуры 2 включает в себя фиг.9 синхровход и информационный вход, подсоединенные на входы вычислителя корней интегрирующей структуры 1.1, дифференцирующей структуры 1.2 и позиционной структуры 1.3, подсоединенные выходами на входы соответствующих схем сравнения 2.1, 2.2, и 2.3. Выходы схем сравнения 2.1, 2.2 и 2.3 подсоединены на первый, второй и третий вход центральной схемы сравнения, выход которой подсоединен на выход определителя структуры. Формулы, используемые вычислителями корней, получены следующим образом:
для интегрирующей модели ф.160.1
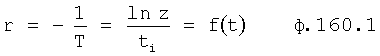
получена из
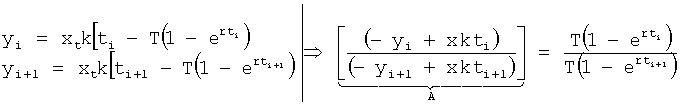
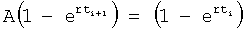
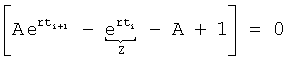
Az2-z-A+1=0
где 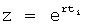
t(i+2)=2t;
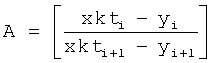
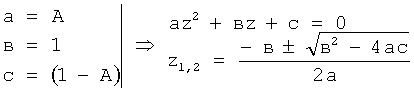
- для диффернцирующей модели ф.160.2
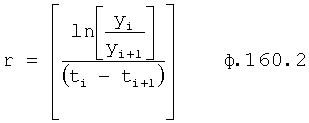
Получена из
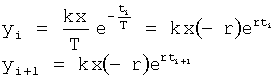
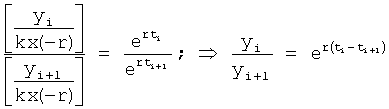
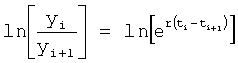
- для позиционной модели ф.160.3 «а», «б», «в»

Ф.160.3, где R1 - неизвестное значение, находится определителем корней фиг.6, входящим также в «определитель корней позиционного звена п.1.3.
По найденным совокупностям R1,i, R2,i находятся возможные значения r1,1…1,5, r2,1…2,5 по ф.160.3.1
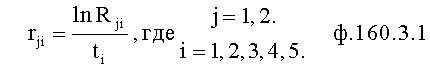
После этого выбирается совокупность r1, r2, которая в течение времени изменяется минимально, т.е. 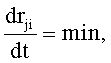 и передаются выбранные значения на выход вычислителя корней позиционного звена. Формулы 160… получены следующим образом:
и передаются выбранные значения на выход вычислителя корней позиционного звена. Формулы 160… получены следующим образом:
1) находятся решения дифуравнения в виде ф.160.3.2 для моментов времени t1, t2, t3, t4 (где t2=2t1, t3=3t1, t4=4t1)
формируются две системы уравнений ф.160.3.3 и ф.160.3.4
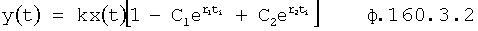
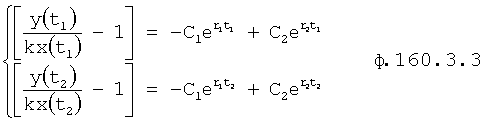
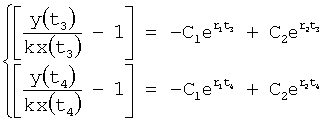
3) в уравнение п.2 подставляются значения ф.160.4
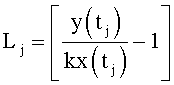
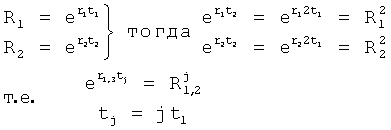
Получили 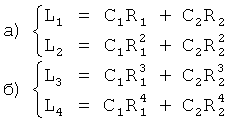
4) в каждой системе определяют С1, С2 ф.160.5
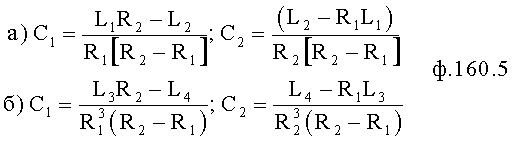
Приравниванием найденных математических выражений а и б для каждого коэффициента С1 и С2 получена система из двух уравнений с двумя неизвестными R1 и R2 ф.160.6
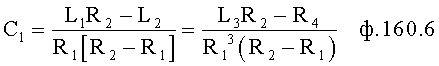
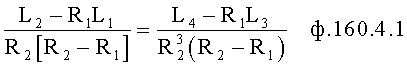
После упрощений ф.160.4.2
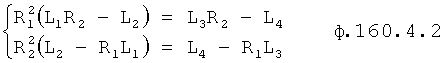
Для перехода к одному неизвестному преобразуют к виду ф.160.4.3
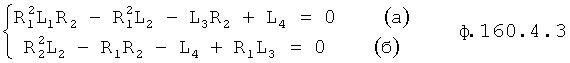
из 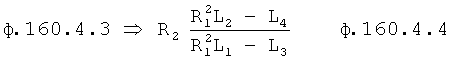
получится ”a” ф.160.4.4.
После подстановки R2 в ф.160.4.3 ”б” получится ф.160.4.5
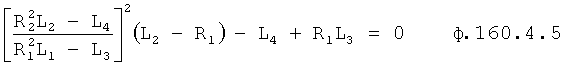
После возведения скобок во вторую степень […]2 ф.160.4.6
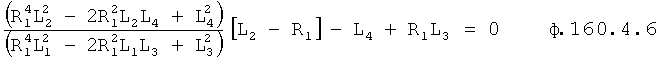
После приведения к общему знаменателю ф.160.4.6 получена ф.160.3.
Схемы сравнения 2.1, 2.2, 2.3 включают в себя элементы запаздывания τ и элементы вычитания ”b”. Центральная схема сравнения определяет, на каком из трех входов минимальный сигнал, и выбирает с соответствующую ей по структуре модель. Схема сравнения 2.1, 2.2, 2.3 сравнивают текущие значения корней характеристического уравнения с ранее найденными значениями корней. Разница между текущими и ранее найденными значениями корней характеристического уравнения передается с выхода схем сравнения 2.1… 2.3 на центральную схему сравнения 3, которая выбирает минимальную и определяет, какая из структур дифуравнения наиболее точно моделирует объект. Выходной сигнал центральной схемы сравнения 3 задает структуру математической модели объекта, которая используется 1. Вычислитель корней 1 отличается от вычислителей корней 1.1, 1.2, 1.3 повышенной надежностью и точностью, необходимой для качественной идентификации параметров объекта. Найденные значения корней используются для численного определения производных выходного параметра объекта более высокого порядка. Вычислитель производных 3 подставляет найденные значения корней и скорость их изменения в ф.161, которые получены для модели объекта с переменными корнями характеристического уравнения
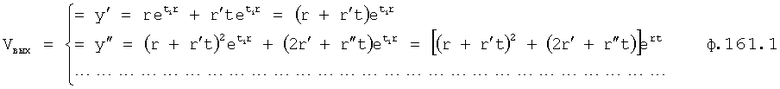
где Vвых - сигнал на первом выходе вычислителя производных
ti=f(ti) - корни дифуравнения сигнала, поступающего на первый вход Vвх1
Vвх1=y=yrt
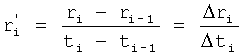
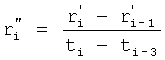
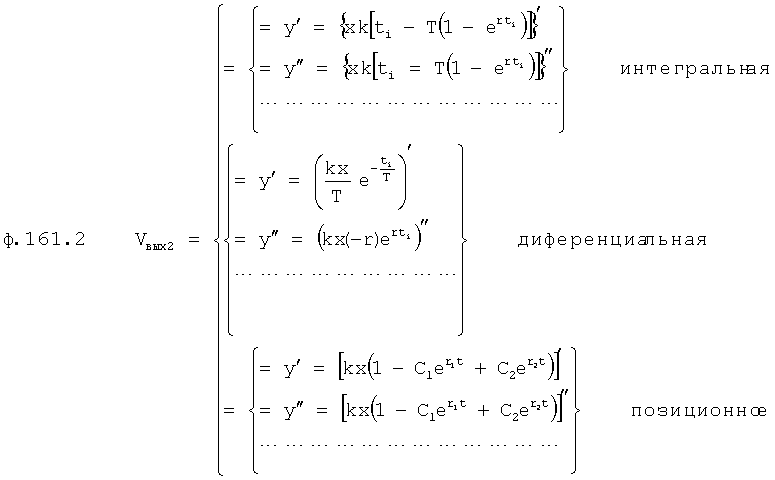
где 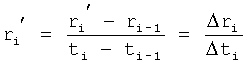

………………………………и т.д.
r=f(t).
Вычислитель коэффициентов дифуравнения 4 по производным высоких порядков, найденным вычислителем производных 3, определяет коэффициенты модели объекта в виде дифуравнения с производными высокого порядка и постоянными коэффициентами (внутреннего запаздывания Т…, т.е. с постоянными корнями характеристического уравнения) ф.162. При этом в вычислителе коэффициентов 4.2 структура дифуравнения получена определителем структуры 2. Пример позиционного звена ф.162
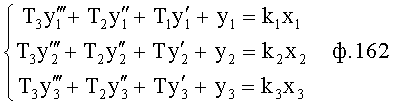
где 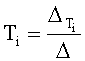 - постоянные коэффициенты,
- постоянные коэффициенты,
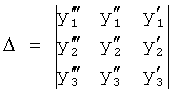 - главный определитель,
- главный определитель,
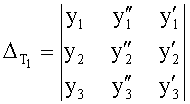 ;
; 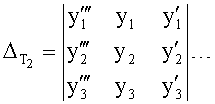
В общем виде
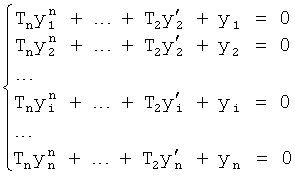
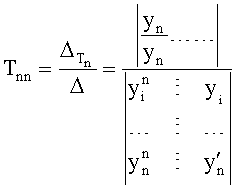
где Тi - икомые внутренние постоянные времени (коэффициенты степенного многочлена),
yi - измеренные значения выходного параметра,
y'i, y”i - вычисленные производные для моментов времени ti (i=1…n),
1) в вычислителе коэффициентов п.4.1 коэффициенты дифуравнения определяются по формуле ф.163
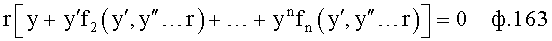
где r - искомый корень,
f2…fn - функции от производных выходного параметра, которые находятся из уравнения ф.164
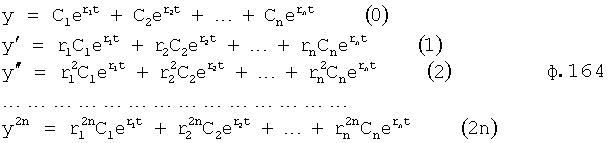
А) формируются системы, включающие равенства 1…2п
1-я система включает (1)…(n) равенства,
2-я система включает (2)…(n+1) равенства,
3-я система включает (3)…(n+2). равенства,
Б) из каждой системы находится решение для одного из корней ri ф.165

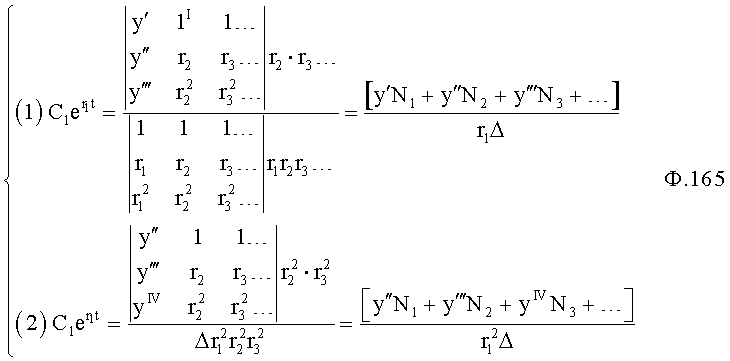
и т.д.,
где N1… - алгебраические дополнения к элементам,
В) приравниванием двух последовательно полученных решений формируют новую систему уравнений ф.166
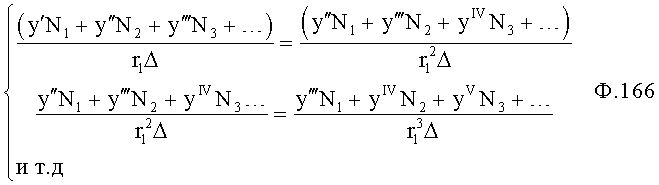
Г) поле приведения к общему знаменателю каждого из равенств находится решение системы ф.166 в виде ф.167
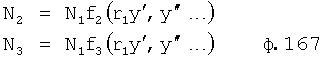
Д) полученные решения ф.167 подставляются в равенство ф.168, которое получено приравниванием системы «0» (включающей 0…(n-1) равенство) и «1» (включающей 1…(n) равенство) ф.168
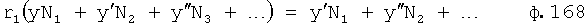
Е) после сокращения N1 в ф.167 получена степенная функция ф.169
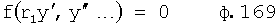
где r1… - корни степенной функции соответствуют корням дифуравнения. Далее подстановкой найденных r1… … в ф.170, полученную из системы ф.164, находятся коэффициенты решения в виде функции времени С1…
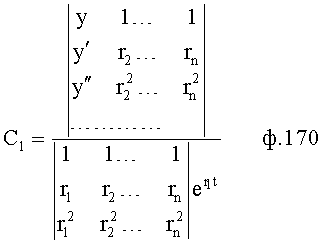
С2=
и т.д.
В вычислителе коэффициентов 4.3 определяются коэффициенты дифуравнения из системы уравнений
а) - (1), (2)…(n),
б) - (2), (3)…(n+1),
в) - (3), (4)…(n+2),
где (1), (2)…(n+…) в ф.171

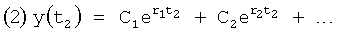
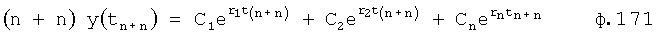
Формируется система измеренных в дополнительные моменты времени, кратные первому моменту ф.171.1/
После подстановки кратных моментов времени t2=2t1…/
Получены
при 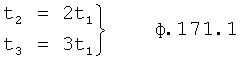
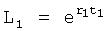 , L2=L1 2
, L2=L1 2
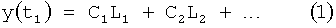
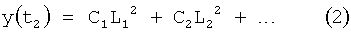
Для каждой из систем а), б), в)… находятся решения в виде ф.171.2 и т.д.
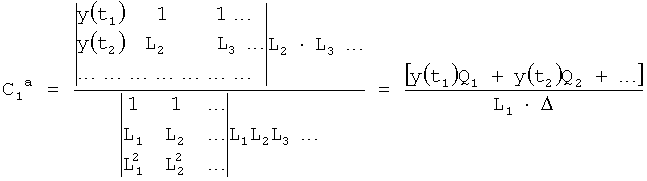
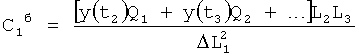
и т.д.
После приравнивания двух последовательно найденных решений получены новые уравнения ф.172.
После подстановки и сокращения L1 ф.172.1.
Уравнения … (аб), (бв)… и т.д. объединяются в систему, из которой находится решение ф.174 для Q2, Q3… (алгебраических дополнений), при этом алгебраическое дополнение ф.174
Q1 - условно считается известным
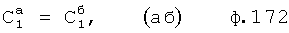
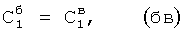
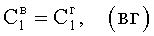
…………………………
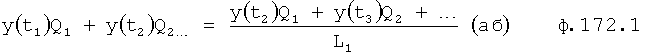
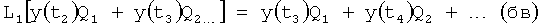
…………………………
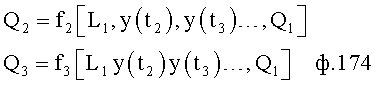
…………………………
и т.д.
Решение Q2=f2(…); Q3=f3… ф.174 подставляются в сравнение (aб) ф.172 и сокращается алгебраическое дополнение (условно принятое известным).
Получается уравнение степенного многочлена ф.175
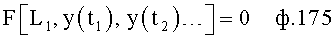
В отличие от “характеристического уравнения” этот степенной многочлен “F” имеет корни L1… в виде независимых решений L1… для каждого отдельного звена W1, W2… ф.2.
Или каждой внутренней независимой постоянной Т1… (запаздывания) времени при позиционном звене, т.е. решении в виде ф.176
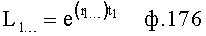
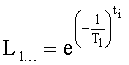 - при позиционном звене.
- при позиционном звене.
При этом структурная схема передаточной функции объекта разбивается на звенья.
Для осуществления обратной связи по проверке точности идентификации параметров объекта используется математическая модель 5 с постоянными коэффициентами п.5 фиг.8, корни которой определяет вычислитель корней п.5.1.
Вычислитель корней 5.1 включает в себя три независимых 5.1.1…3 (фиг.11) вычислителя корней степенных многочленов, примеры технической реализации которых приведены в уточняющем вычислителе п.12 фиг.4.
Техническая реализация вычислителя корней 5.1.3 отличается тем, что после нахождения корней L1… степенного многочлена F (коэффициенты которого поступают на вход вычислителя корней 5.1.3) найденные значения корней L1… принимаются за независимые решения для условных передаточных функций W1, W2…, на которые разбивается передаточная функция объекта, в связи с чем корни характеристического уравнения находятся по формулам ф.177
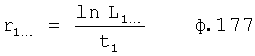
где 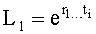 - корни степенного многочлена f, коэффициенты которого поступают на вход п.5.1.3
- корни степенного многочлена f, коэффициенты которого поступают на вход п.5.1.3
t1 - момент времени, который принят в системе уравнений ф.171 за t1.
(lnL1…)=r1…t1 - получена из L1…=er1…ti логарифмированием.
Схема сравнения 5.2 фиг.8 позволяет хранить в памяти информацию:
1) с выхода вычислителя 5.1.2 об устойчивости «в малом» выходного параметра объекта (по структуре дифуравнения: интегральной, дифференциальной или позиционной), полученной для каждого текущего интервала времени (длительность этого интервала зависит от степени производных дифуравнения модели объекта и является минимально короткой); эту информацию удобно использовать в «оперативном регулировании», обеспечивающем гарантированную надежность САР (качество и устойчивость регулирования) при внезапных возмущающих воздействиях; преимущество этого скоростного идентификатора в том, что на него не действуют кратковременные высокочастотные возмущения, воздействие которых хорошо идентифицируется в быстродействующем вычислителе;
2) с выхода вычислителя 5.1.1 фиг.8 об устойчивости и качестве не только “в малом”, но и в “большом” (при больших изменениях координат САР) параметры определяются за минимально короткое время, меньше чем п.3, но больше чем пункт “1”), при этом для снятия текущих координат (определения исследуемого переменного корня дифуравнения для разных моментов времени) используется позиционное звено как удобная условная модель, не влияющая на результат идентификации структуры, а используемая только для нахождения производных разных порядков от выходного параметра в каждый из текущих моментов времени, т.е. скорость изменения корня позиционного звена в текущий момент времени является параметром при нахождении производных высоких порядков. Найденные производные в разные моменты времени позволяют перейти к решению вопроса (задачи) нахождения дифуравнения с постоянными коэффициентами и постоянными корнями, по которым судят об устойчивости объекта. Недостаток этого способа в том, что условная модель при идентификации не позволяет избавиться от “шумов”, т.е. от “помех” средних частот (обусловленных остаточной ошибкой идентификации производных высоких порядков, преодолеть которую не позволяет позиционная структура условной модели);
3) с выхода вычислителя корней 5.1.3 о текущих значениях (внутренних параметров объекта) без "помех" (создаваемых методами ускоренной идентификации п.п.1), 2)). Чтобы избавиться от недостатков предыдущих способов используют более длительную технологию идентификации, которая не оперирует производными, а учитывает только позиционные значения выходного параметра.
Вычислитель коэффициентов 5.3 фиг.11 определяет постоянные коэффициенты полного решения дифуравнения математической модели объекта для каждого из трех способов нахождения корней 5.1.1, 5.1.2. 5.1.3;
Вычислитель текущих значений выходного параметра 5.4 в ожидаемый момент времени для каждой из трех совокупностей коэффициентов, полученных соответствующими тремя способами 5.1.1, 5.1.2, 5.1.3.
Полученная характеристика выходного параметра математической модели 5 при точной идентификации параметров объекта должна по величине совпадать характеристикам выходного параметра реального объекта.
Схема сравнения 6 сравнивает текущее значение реального объекта и текущее значение математической модели. При существенном их отличии на выходе схемы сравнения 6 формируется синхроимпульс, который перезапускает вычислитель корней 1, т.е. перезадает новый начальный момент времени, отсчет от которого используется при вычислении параметров математической модели в вычислителе корней 1.
Сравнение текущего значения выходного параметра с каждым из трех ожидаемых значений выходного параметра позволяет судить о том, какой из способов наиболее точно для данного момента времени определяет параметры объекта, и о причинах, которые не позволяют другим способам приблизиться к реальным значениям выходного параметра. Сравнение результатов, полученных тремя способами, дает наиболее полное представление об объекте.
Кроме того, решены основные задачи в регулировании и достигнуты следующие положительные результаты:
1) повышение порядка дифуравнения модели позволяет приблизить ее характеристики к характеристикам выходного параметра реального объекта;
2) а переход к постоянным коэффициентам делает дифуравнение удобным в вычислительных операциях при определении переходных характеристик, "запаса устойчивости", "показателя качества" и т.д., входящие в блок линеаризации п.11…13 фиг.4 вычислители имеют следующие особенности:
- быстродействующий вычислитель определяет параметры CAP (устойчивость и качество регулирования) независимо для каждого момента времени, фиксируя малейшие возмущения и оценивая возможность этих возмущений вывести объект из равновесия;
- уточняющий вычислитель позволяет уточнить параметры объекта повышением степени дифуравнения математической модели; при этом необходимое время идентификации удваивается до двух моментов;
- фильтрующий вычислитель позволяет определить длительные переходные процессы внутреннего состояния объекта, характер которых невозможно соединять с кратковременными переходными изменениями, которые фиксируются вычислителями п.11…12.
В совокупности входящие в "Блок линеаризации" п.11…13 вычислители позволяют получить модель объекта в виде дифуравнения с достаточно высокой степенью производных и с постоянными коэффициентами. При этом вычислители п.11…12 позволяют учитывать действие кратковременных помех, а фильтрующий вычислитель п.13 позволяет формировать модель без учета кратковременных возмущений. Блок линеаризации п.11…13 фиг.4 позволяет решить две задачи I и II:
I - определяется структура дифуравнения, которая используется при моделировании исследуемого объекта;
- позиционная структура,
- интегрирующая структура,
- дифференцирующая структура,
1) быстродействующий вычислитель п.11 определяет для каждого момента времени производные выходного параметра y, y', y”, y”'… и подставляет их в формулы, позволяющие определить структуру объекта;
2) входящий в фильтрующий вычислитель п.13 определитель структуры 2 фиг.8 и фиг.9 фиксирует текущие значения выходного параметра четырех последовательных моментов времени y(t1), y(t2), y(t3), y(t4), подбирает структуру дифуравнения, коэффициенты (корни характеристического уравнения) которого требуют минимальной корректировки при приближении его характеристики к характеристикам выходного параметра реального объекта в определителе структуры.
В вычислителе корней 5.1.1 и 5.1.3 идентификация структуры и устойчивости системы осуществляется по корням полного решения дифуравнения, которое используется для математического моделирования "объекта" (или CAP).
II-я задача - повышение точности найденной структуры дифуравнения подстановкой производных более высоких порядков от выходного параметра (и от входного при дифференциальной структуре). Для осуществления этой задачи с минимальной затратой времени используется уточняющий вычислитель п.12), но при этом неизбежно приходится сталкиваться с влиянием кратковременных возмущений. Для того чтобы их влияние било минимальным, используются вычислители коней 1, производных 3, коэффициентов 4 фиг.8, входящие в "фильтрующий вычислитель п.13.
Сравнения данных, полученных на выходе уточняющего вычислителя п.12, с данными, полученными на выходе фильтрующего вычислителя п.13 (и экспресс-данными на выходе быстродействующего вычислителя п.11), позволяют выделить наличие кратковременных возмущений для их дальнейшего изучения и устранения причин их возникновения, а также для своевременной идентификации аварийного режима, что одновременно обеспечивает повышение точности (качества) и надежность (безаварийности) регулирования.
Таким образом, при «статическом» регулировании, когда заданная величина задается в виде статического значения (т.е. постоянной величиной на данном этапе регулирования величиной), блок линеаризации дает исчерпывающую информацию об объекте, но эта информация недостаточна, если регулируемая величина управляется не только по величине, но и по скорости, что неизбежно в технологических процессах и в системах робототехники на сборочных линиях и других системах.
Математическая модель системы автоматического регулирования (CAP) дифуравнением позволяет разбить модель на отдельные составляющие в виде полного решения дифуравнения ф.178
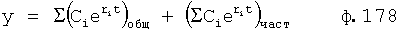
где 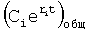 - составляющие общей модели,
- составляющие общей модели,
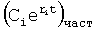 - составляющие частной модели.
- составляющие частной модели.
Состояние этих составляющих определяется параметрами.
Для удобства идентификации значение ri считается постоянным в течение времени идентификации Δt, а значение t1 принимается средним ф.179
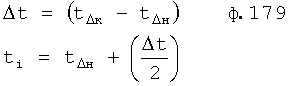
где tΔн - начальный момент идентификации,
tΔк - конечный момент идентификации.
Задача определителя изменения параметров во времени п.14 фиг.4 (входящий в идентификатор п.19) фиг.10 состоит в том, чтобы уточнить модель CAP, полученную на выходе блока линеаризации п.11…13, за счет перехода от постоянных во времени параметров (r1…) к переменным (ri…=f(t)…).
При переменных параметрах объекта "вычислитель модели с переменными корнями" п.14 использует "канал действительных переменных корней " п.14.1, если переходной процесс не имеет колебательности, и "канал комплексных переменных корней" п.14.2, если модель с действительными корнями не совпадает с реальным характером изменения исследуемого параметра объекта. При этом если корни меняются медленно, то их считают «условно постоянными», или постоянными "малом", и используется блок определения функции времени для приведенных коэффициентов" п.4.
Если пренебречь изменением корней в «малом» нельзя, то динамическую модель объекта получают на выходе «определителя быстроменяющихся корней» п.14 фиг.10 по ф.49.1…
Для этого модель решения дифуравнения п.2 с переменным корнем 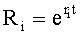 п.15
п.15 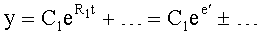 дифференцируется дважды п.16 и п.17. Полученные два уравнения решаются относительно
дифференцируется дважды п.16 и п.17. Полученные два уравнения решаются относительно 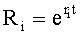 и приравниваются между собой п.18. Получается степенной многочлен, основанием которого является постоянная степени r переменного корня
и приравниваются между собой п.18. Получается степенной многочлен, основанием которого является постоянная степени r переменного корня 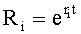 п.19.
п.19.
Подстановка найденных функций времени переменных корней R1… в систему уравнений ф.49.9 (п. 30 фиг.10) позволяет вычислить постоянные С…
Введенные переменные параметры ri=f(t)… усложняют модель и делают ее неудобной в вычислениях, но она необходима для изучения процессов, влияющих на CAP, учет которых необходим для формирования регулирующего воздействия (математическое выражение которого имеет частное решение дифуравнения).
Вход определителя изменения параметра (ri) во времени п.14.1 подсоединен на вход определителя текущих значений корня 1, выход которого подсоединен на вход фиксатора изменений 2, выход которого подсоединен на вход фильтрующего вычислителя 3, выход которого подсоединен на выход определителя изменения параметра во времени.
Определитель текущих значений корня 1 производит вычисления по ф.180
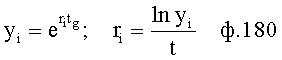
Фиксатор изменения 2 производит вычисления до формуле 181
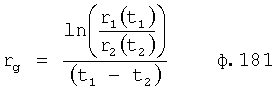
где

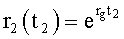
Фильтрующий вычислитель 3 имеет структуру, фиг.8, и использует те же формулы.
Таким образом, изменение корня r математически моделируется в виде полного решения дополнительного дифуравнения. При этом сначала находится корень дополнительного дифуравнения (максимальная производная которого имеет первую степень) с выхода фиксатора изменений 2. Потом при необходимости степень дополнительного дифуравнения увеличивается, для чего используется фильтрующий вычислитель фиг.8.
Решение общего дифуравнения примет вид ф.182
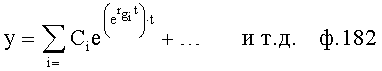
Если объект имеет кроме внутреннего запаздывания (Т…) еще и «внешнее», то определитель внешнего запаздывания п.14 фиг.4, фиг.11…14 использует быстродействующий и фильтрующий каналы
В САР существует запаздывание, не влияющее на форму выходного параметра. Структурная схема (определителя внешнего запаздывания фиг.13.
Канал быстродействующих характеристик 1 и фильтрующий канал 2 подключены на вход блока внешних характеристик. п.14, фиг.4, а выходы их подключены к входам схемы сравнения 6. Выход схемы сравнения 6 подсоединен к выходу блока внешних характеристик
Входы каждого из каналов (канала 1 и канала 2 фиг.13) подсоединены на соответствующие определители моментов времени ti для входных параметров (Xp - 2.1 первый канал и ч.1 второй канал) и выходных параметров (у - 2.1 первый канал и ч.2 второй канал)
Выходы определителей ч.1 и ч.2 (фиг.13) подсоединены на соответствующие входы блока вычитателя 52, выход которого подсоединен на 2-й вход схемы сравнения 6. Выходы определителей моментов времени 2.1 и 2.2 (фиг.13) подсоединены на соответствующие входы вычитателя 5.1, выход которого через выход второго канала (фильтрующего) подсоединен на первый вход схемы сравнения 6.
Канал быстродействующих характеристик 1 включает в себя последовательно подсоединенные вычислители фиг.11;
входящие в определитель момента времени п.2.1 (и п.2.2):
1. Вычислитель отдельных составляющих полного решения дифуравнения,
1.1 вычислитель корней полного решения дифуравнения по производным выходного параметра по ф.183
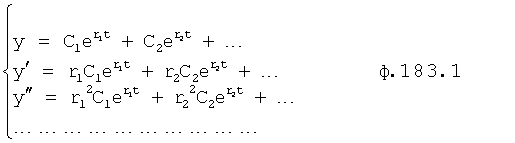
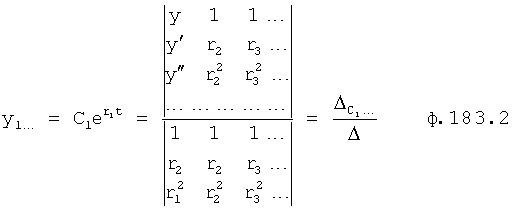
1.2 вычислитель слагаемых y1… выходного сигнала ф.183.2,
2. Вычислитель коэффициента 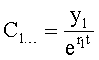 момента t ф.184.
момента t ф.184.
Для этого находится соотношение между коэффициентами C2…=f2…(C1)… по ф.184.0
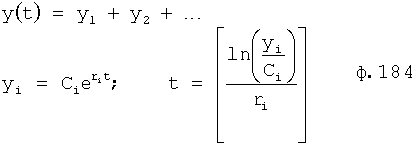
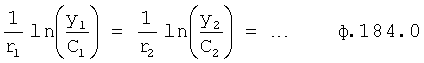
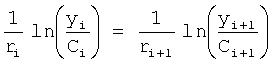 ;
; 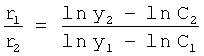
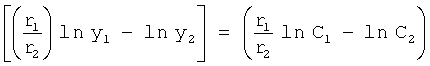
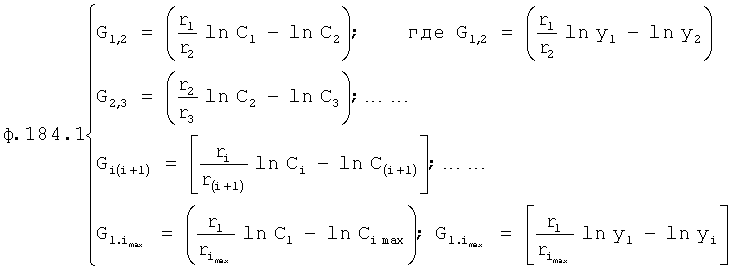
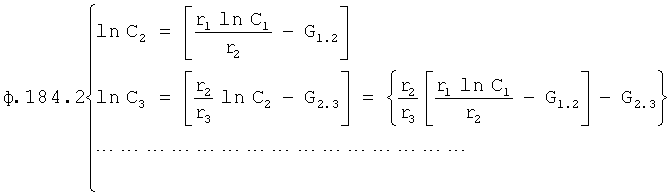
Формулы подстановки поэтапной ф.184.1 позволяют получить уравнение с одним неизвестным (например, С1).
После нахождения этого неизвестного можно перейти к нахождению всех других неизвестных из ф.184.2 (С2…).
3. Вычислитель соотношения между коэффициентами полного решения дифуравнения ф.185
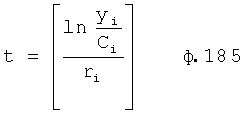
Приравниваются равенства ф.185 для разных значений корней ri=1.
4. Формирователь степенного многочлена для известного выходного параметра в известный момент времени вычисляет степенные функции (erit1), входящие в полное решение дифуравнения САР ф.186, где
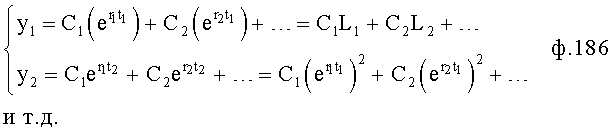
где t2=2t1,
t3=3t1,
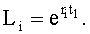
Степенные функции L1… находят из степенного уравнения ф.175, полученного по ф.171-174.
5. Определитель корней степенного многочлена вычисляет корни дифуравнения r1… из системы логарифмических уравнений ф.187
ln Li=ri·t; 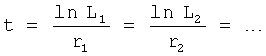
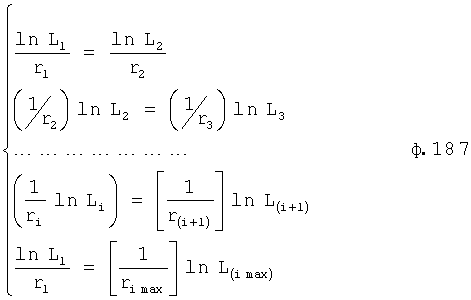 .
.
6. Определитель постоянных коэффициентов для каждого из корней по системе уравнений ф.186 после подстановки найденных Li ф.188
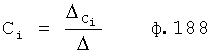
7. Определитель текущего момента времени по слагаемым ф.189
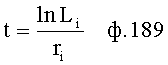
Блоки вычитателей 5.1 (канал быстродействующих характеристик 1) и 5.2 (канал фильтрующий 3) определяют внешнее запаздывание выходного параметра.
Вход блока вычитателей (I.3 и 2.3) фиг.14 подсоединен на выход дифференциатора 1, выход которого подсоединен на вход схемы сравнения 1.
Выход схемы сравнения 2 подсоединен на вход таймера 3 и элемент памяти 4, выход которого подсоединен на положительный вход первого вычитателя 5. Первый таймер 3 подсоединен на второй вход элемента памяти 4, а второй выход таймера 3 подсоединен на положительные входы первого 5 и второго 6 вычитателей. Второй вход блока вычитателей подсоединен на отрицательные входы первого (5) и второго (6) вычитателей. Выход первого вычитателя 5 подсоединен на информационный вход ключа 8, на управляющий вход которого подсоединен первый выход второй схемы сравнения 7.
Выход второго вычитателя 6 подсоединен на вход второй схемы сравнения 7, выход которой подсоединен на первый вход сумматора 9. Информационный выход ключа 8 подсоединен на второй вход сумматора 9, выход которого подсоединен на выход блока вычитателей.
Дифференциатор 1 находит производную от входного сигнала
Схема сравнения 1 формирует на своем выходе синхроимпульс при входном сигнале, не равном единице. Таймер 3 формирует сигнал на 2 выходе, равный интервалу времени, измеренному с момента поступления синхроимпульса. На втором выходе таймера фиксируется измеренный интервал времени, полученный перед поступлением синхроимпульса на вход запуска таймера.
Элемент памяти 4 после поступления на первый вход синхроимпульса фиксирует сигнал, поступающий на второй вход. Вычитатели 5 и 6 складывают сигналы, поступающие на положительные входы, и отнимают сигналы, поступающие на отрицательные входы. Вторая схема сравнения отрицательный входной сигнал пропускает на первый выход, а положительный - на свой второй выход. Ключ 8 пропускает сигнал с информационного входа на свой выход при отрицательном сигнале на его управляющем сигнале. Сумматор 9 складывает входные сигналы.
Блок вычитателей (входящий в первый 1.3 и второй 2.3 каналы) позволяет судить о внешнем запаздывании по идентифицированным моментам времени ti входного воздействия Хр и выходного параметра у. Если входное воздействие Хр не меняет своей динамической характеристики, то идентифицированный момент времени 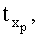 поступая на вход дифференциатора 1 формирует на его выходе единичный сигнал. При этом выходной сигнал таймера 1 будет равен сигналу
поступая на вход дифференциатора 1 формирует на его выходе единичный сигнал. При этом выходной сигнал таймера 1 будет равен сигналу 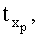 если регулирующий сигнал (воздействие) поступает на вход объекта с начального момента. В противном случае таймер 1 измеряет текущий момент времени с того момента, когда изменение динамических характеристик входного воздействия прекратилось, т.е. с того момента, когда производная от текущего момена времени стада равна единице.
если регулирующий сигнал (воздействие) поступает на вход объекта с начального момента. В противном случае таймер 1 измеряет текущий момент времени с того момента, когда изменение динамических характеристик входного воздействия прекратилось, т.е. с того момента, когда производная от текущего момена времени стада равна единице.
B момент, когда изменится динамическая характеристика входного регулирующего воздействия, сигнал с выхода дифференциатора станет отличным от единицы ≠1. При этом синхроимпульс с выхода схемы сравнения 2, поступая на вход таймера 3, перезапускает отсчет переменной времени, величина которой передается на второй выход, на первом выходе таймера сохраняется момент времени предыдущего отсчета, приостановленный импульсом перезапуска. Синхроимпульс с выхода первой схемы сравнения 2, поступая в элемент памяти 4, дает команду о сохранении в памяти значения момента времени (предыдущего отсчета) с первого выхода таймера 3.
Сигнал с выхода первого вычитателя 5 равен запаздыванию предыдущей входной динамической характеристики после поступления на таймер синхроимпульса и при отрицательном выходном сигнале второго вычитателя 6.
При положительном выходном сигнале второго вычитателя 6 ключ 6 закрывается и вторая схема сравнения пропускает через себя сигнал c выхода второго вычитателя 6, величина которого равна внешнему запаздыванию новой совокупности динамических характеристик входного воздействия. Таким образом, на выходе сумматора 9 (после синхроимпульса первой схемы сравнения 2) поступает сигнал, равный внешнему запаздыванию предыдущего регулирующего воздействия. После того как появляется возможность фиксировать внешнее запаздывание с выхода объекта, ключ 8 закрывается и на выход сумматора 9 поступит сигнал с выхода второго вычитателя 6 через схему (вторую) сравнения 7, величина этого сигнала равна внешнему запаздыванию новой входной динамической характеристики.
Схема сравнения 3 фиг.15 позволяет сравнить идентификацию характеристик в ″малом″ (полученную в быстродействующем канале от характеристик, справедливых при исследовании в ″большом″ (т.е. полученных в ″фильтрующем канале)).
Определитель последовательности взаимодействия звеньев математической модели п.16 фиг.4, фиг.15…16 позволяет определить выходной параметр каждого звена п.17 (фиг.4 и 17).
Определение отдельных составляющих позволяет уточнить параметры отдельных внутренних переходных процессов между структурными единицами, на которые ″условно″ разбит объект.
Известные идентификаторы внутреннего запаздывания объекта позволяют получить математическое описание в виде дифуравнения с постоянными коэффициентами Т1, Т2 … Но этого недостаточно при выполнении следующих задач:
1) при регулировании объекта со сложной структурой, у которого регулируется не только позиционное значение выходного параметра, но и скорость (ускорение) его изменения, т.е. не только y, но и y', y'' … Так как на значение производных y', y''… влияют не только постоянные внутреннего запаздывания Т1… (корни r1…), входящие в дифуравнение, но и постоянные коэффициенты решения этого дифуравнения С1… ф.190.1
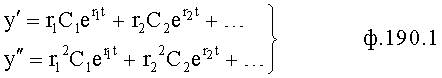
2) при необходимости обеспечения требуемого качества и устойчивости (ОДЗ - области допустимых значений) не только выходного параметра yвых, но и внутренних составляющих yв1, yв2…, на которые можно ″условно″ разделить математическую модель объекта. Это необходимо для обеспечения благоприятного режима эксплуатации объекта, сохранения его внутренних физических и технологических свойств. Это обеспечат увеличение срока эксплуатации и предотвратит аварийные ситуации.
Значение коэффициентов С1… зависит от последовательности взаимодействия внутренних составляющих W1… ф.190.2
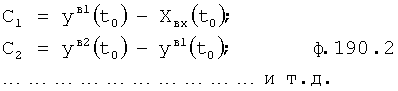
где 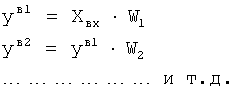
Стандартное дифуравнение и его решение не позволяет увидеть последовательность взаимодействия отдельных составляющих в их математической модели. Для составления такой математической модели используют "определитель последовательности п.16 фиг.4, выходной сигнал которой позволяет разбить математическую модель на структурные составляющие фиг.15.
На первый вход формирователя последовательности поступает сигнал, включающий информацию о дифуравнении объекта и системы о полном решении дифуравнения ф.191
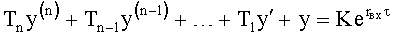
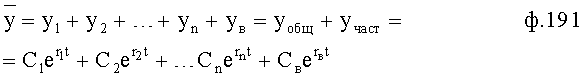
где yчаст=yв - частное решение yчаст дифуравнения равно вынужденной yв,
yобщ=yс - общее решение yобщ дифуравнение равно свободному yс;
 - полное решение равно сумме частного и общего, а следовательно, сумме свободной составляющей и вынужденной.
- полное решение равно сумме частного и общего, а следовательно, сумме свободной составляющей и вынужденной.
После поступления сигнала на первый вход формирователь последовательности п.3.1… перемещает одно из общих решений дифуравнения в правую часть дифуравнения, тем самым преобразуя его в одно из частных решений (фиг.15) и присваивая ему позицию W1 фиг.2. Это перемещение позволяет найти yв1=f(t) из ф.192.
Ф.192.1 - дифуравнение, поступающее на первый вход формирователя последовательности п.1.1
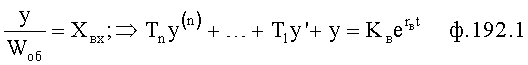
Перенос одного из звеньев (например) на первую позицию ф.192.2
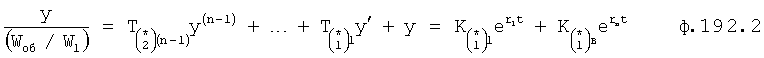
Где решение 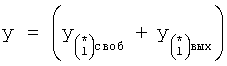
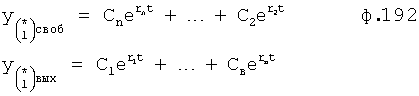
y - выходной параметр объекта;
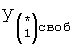 - свободная составляющая ф(*);
- свободная составляющая ф(*);
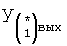 - вынужденная составляющая ф(*).
- вынужденная составляющая ф(*).
Вычислитель коэффициентов п.1.2 определяет 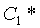 ф.193.1.
ф.193.1.
В левую часть дифуравнения ф. 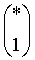 подставляют
подставляют 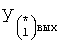

По известным С1, Св …, Tn-1, T1[=f(r1…)] вычисляют 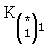 ,
, 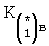 приравниванием коэффициентов в слагаемых с одинаковыми степенями правой и левой части дифуравнения ф.193.2. Тогда
приравниванием коэффициентов в слагаемых с одинаковыми степенями правой и левой части дифуравнения ф.193.2. Тогда 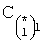 ф.193.2
ф.193.2
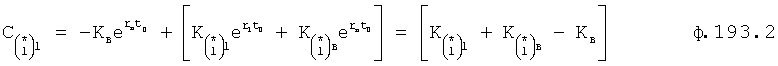
где t0=0.
Это значение С1* сравнивается со значением С1 ф.57…59.
Если С1* совпадает с С1, то положение W1 выбрано правильно и схема сравнения 5 фиг.16 формирует на своем выходе команду перехода к поиску положения составляющей W2.
И входной сигнал элемента подстановки параметров звена п.4.1… (входящие в определитель соответствующей позиции п.3.1) поступает на вход «окончательной модели звена» п.5.1…
Эта команда поступает на вход следующего определителя позиции и задает режим перемещения W2 в левую часть дифуравнения, т.е. рассматривает его решение не свободным (общим), а вынужденным (частным).
Если 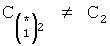 , то W1 возвращают в общее решение, а составляющую W2 перемещают в вынужденное решение. Формирователь последовательности п.3.1… формирует дифуравнение согласно новому общему и частному решению. Это дифуравнение используется в вычислителе коэффициентов для нахождения
, то W1 возвращают в общее решение, а составляющую W2 перемещают в вынужденное решение. Формирователь последовательности п.3.1… формирует дифуравнение согласно новому общему и частному решению. Это дифуравнение используется в вычислителе коэффициентов для нахождения 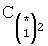 . В схеме сравнения п.5 сравнивается, фиг.16, найденное значение
. В схеме сравнения п.5 сравнивается, фиг.16, найденное значение 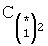 с найденными ранее С2.
с найденными ранее С2.
Аналогично определяется положение всех остальных математических составляющих W1… Найденный порядок математического взаимодействия этих составляющих передается на вход элемента памяти 5, первый выход которого подсоединен на второй вход блока определения последующей позиции п.3 (i+1).
В формуле 194 приведена система уравнений, из которой, используя метод определителей, можно найти yв1, … Для примера, формулы 194 составлены для внутренних составляющих W1, W2 …, последовательность расположения которых приведена на фиг.2, формулы 194 получены из системы уравнений ф.195.
Элемент памяти S позволяет фиксировать найденные правильные координаты yв1, … и соответствующую найденную последовательность W1…
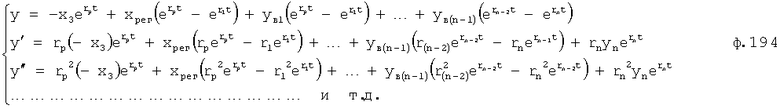
где
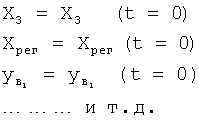
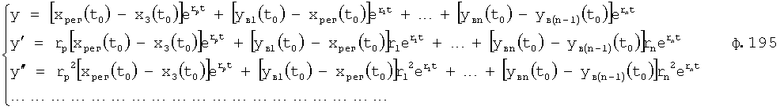
Процесс идентификации происходит в два этапа: на этапе первого приближения вычисления производятся определителем последовательности (″определителями позиций″ п.3.1… фиг.15), второго приближения - полученные значения уточняются в блоке контроля переходных внутренних параметров (окончательной модели звена п.5.1…).
Схема сравнения, входящая в п.5, проверяет правильность первого и второго этапа при допустимой точности, схема сравнения в п.5 формирует сигнал, позволяющий передать найденные проверенные правильные значения параметров на выход определителя отдельных составляющих.
Таким образом, контроль (идентификация) отдельных внутренних составляющих (их влияние друг на друга через переменные внутренние параметры yВ1, …) позволяет обеспечить желаемые значения:
1) надежности - запаса внутренней устойчивости каждой переменной внутренней составляющей yВ1, …;
2) качества - минимум ошибки:
а) - позиционной yвых;
б) - динамической - производных y', y''.
При регулировании сложного объекта, у которого область допустимых значений (ОДЗ) (показателей качества и запаса устойчивости) имеет относительно узкую полосу, приходится прибегать к моделированию выходного (иди любого другого) параметра для каждого текущего момента времени. Исследование выходного параметра для нахождения его критических значений при помощи временной модели осуществляется «Определителем временных интервалов с критическими параметрами объема» - «определитель ОДЗ выходных параметров каждого звена» п.17, фиг.17. По формулам 60-64 математическая модель каждого из звеньев объекта преобразуется к форме, удобной для анализа. После подстановки пограничных значений ОДЗ  ,
,  … корни полученных равенств позволяют найти моменты времени …, в которые исследуемый параметр достигает yт=yгр границ области ОДЗ.
… корни полученных равенств позволяют найти моменты времени …, в которые исследуемый параметр достигает yт=yгр границ области ОДЗ.
Так как математическая модель объекта, используемая в п.17 (фиг.4) для нахождения границ ОДЗ, недостаточна для решения более сложных поставленных задач:
I - анализ реакции объекта на входное воздействия, т.е. отделение реакции на текущего воздействие от реакции на сумму предыдущих воздействий;
II - анализ текущей величины емкостных составляющих объекта, разделение их по степени инерционности.
Для контроля за текущим значением ожидаемого изменения выходного параметра y(t), чтобы обеспечить заданную область допустимых значений ОДЗ, необходимо формировать модель объекта в виде математической зависимости, включающей переменную времени t1, по внутренним параметрам запаздывания Т1, Т2, текущим и выходным параметрам y(t), y'(t)…. При решении этой задачи стандартным способами (по ″частной и корневым″ характеристикам) невозможно добиться быстрой коррекции модели в текущем времени, когда в силу возмущающих внешних (или внутренних) процессов (возмущений) параметры и структуру САР приходится изменять непредвиденным образом.
1-й канал «реакции» - определитель реакции на входное и предыдущие воздействия п.1 фиг.18, осуществляет ф.196 подстановку ряда Тейлора в дифуравнение, сделав эту задачу возможной.
При этом используется дифуравнение, определяющее состояние выходного параметра объекта в ″малом″ y(t) для разных ti при малом изменении Δt=[ti-t(i+1)] после подстановки в него ряда Тейлора ф.196.
После подстановки ряда Тейлора в дифуравнение ф.196.3,
где «дифуравнение» ф.196.1,
где Δy - изменение выходного параметра;
Δx1, Δx2… - изменение выходного сигнала;
f1(t)… - возмущения;
K1, K2… - коэффициенты передачи, показывают отношение выходной величины звена к входной в установившемся режиме;
T1, T2… - постоянные времени
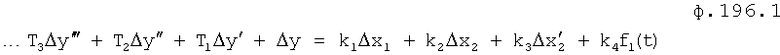
Где «ряд Тейлора» ф.196.2,
где t - текущий момент времени;
t0 - момент времени, для которого известно значение рассматриваемой функции.
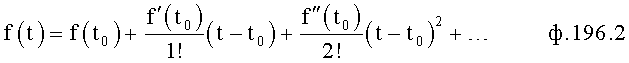
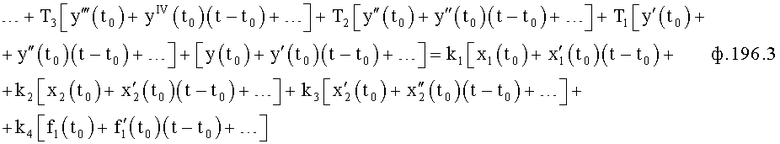 x1=Δx, y=Δy - упрощенная запись.
x1=Δx, y=Δy - упрощенная запись.
Для того чтобы определить изменение выходного параметра в ″большом″, т.е. на большом интервале времени, в заявленном устройстве используются производные от дифуравнения, объединенные в систему уравнений ф.19, и сумма дополнительных вынужденных состояний, отражающая влияние на выходной параметр предыдущих воздействий, отсутствующих на текущий момент: y=yтех.воз+yпред.воз.
Система уравнений, полученная дифуравнением ф.197
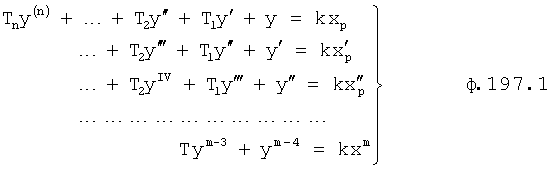
После подстановки ф.198 в ф.197.1 получится ф.198.1

которая составлена из уравнений, полученных дифференцированием ″общего дифуравнения″, характеризующего совокупность внешних (входных xp, x'p… и выходных y, y', …) и внутренних (составляющих внутреннего запаздывания T1, T2, …) параметров объекта (или исследуемой САР). Вместо текущего значения y(t) подставлен степенной ряд ф.198
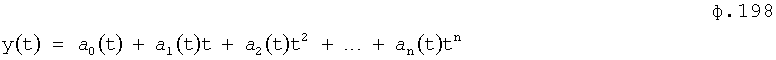 - степенной ряд
- степенной ряд
где  - переменные во времени коэффициенты
- переменные во времени коэффициенты
При t=ti
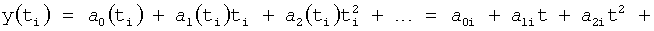
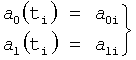
при t=t1; a 0i; a 1i … - коэффициенты, которые можно принять как постоянные во времени Δt - малом.
Т.е. для удобства (идентификации) значения коэффициентов, входящих в степенной ряд (используемый вместо ряда Тейлора) в интервале времени Δt: a 0(ti), a 1(ti) … (в промежутке которого находятся производные разных порядков для момента t1), считаются постоянными.
При t=ti±Δtм производными от коэффициентов можно пренебречь,
т.к. 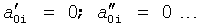
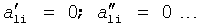
тогда 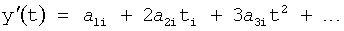
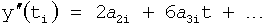
n=(m+ж); ж=1…3 - значения максимальной степени в степенном ряду ф.198.1, выбирается таким, чтобы производная максимального порядка, используемая в ф.198 (полученная из ряда ф.198), приняла вид степенного многочлена 2…4 порядка:
где 2-я степень упрощает нахождение степенного многочлена,
4-ая степень повышает точность расчетов.
Это позволит в дальнейших расчетах (при нахождении исследуемых tu) использовать стандартные методы вычисления корней степенного многочлена, где a i0, a i2 - коэффициенты, являющиеся функцией времени f(t) и полученные для каждого исследуемого момента времени ti
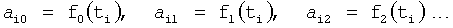
Так как ″общее дифуравнение″ и его производные, входящие в систему уравнений ф.197, характеризуют состояние объекта (САР) для предельно короткого момента времени ti±Δt (необходимого для нахождения y(ti), y'(t), …), получение производных y'(t), y” (t), … не требует нахождения производных от коэффициентов a 0, a 1, … (их значением можно пренебречь (т.е. значения коэффициентов a0, a1, … принимаются постоянными в ″малом″)).
В то же время система уравнений ф.197 может характеризовать изменение выходного параметра y(t) в течение большого промежутка времени Δtбольш., для этого из системы уравнений ф.197 находят входящие в него коэффициенты a 0(t), a 1(t), …. В данном случае значения.
Обеспечение изменения регулируемого параметра в заданных узких пределах регулирования требует моделирования не только на коротком промежутке времени ti±Δt, но и по совокупности 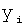 ,
, 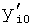 ,
, 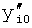 … для ti определять изменение y при большом изменении t (т.е. при большом Δt).
… для ti определять изменение y при большом изменении t (т.е. при большом Δt).
Вычислитель реакции на текущее воздействие производит вычисление по формуле 199, полученной из системы уравнений ф.197
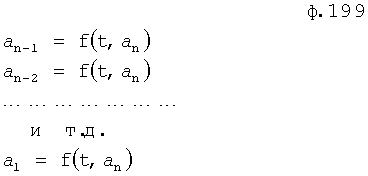
После подстановки найденных зависимостей 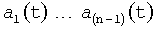 в ф.200 вычисляют
в ф.200 вычисляют 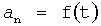 . Найденные a
n…a
0 - подставляют в ф.198.
. Найденные a
n…a
0 - подставляют в ф.198.
Где a n-a n-1 … a 1, a 0 - коэффициенты степенного ряда ф.198
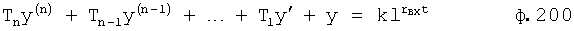
Если значение исследуемого ti известно, то в ф.198 подставляют известное ti и найденные a 0(ti), a 1(ti), …
Если исследуемый момент не известен, то моделируют условно принятое время, значение которого удобно вычислять по измеренному (или вычисленному) значению исследуемого параметра.
Вычислитель найденного состояния a1 вычитает от исследуемых параметров 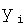 ,
, 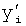 ,
, 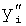 значения параметров уже найденных реакций (на входное воздействие или частное решение), yн, y'н … ф.201
значения параметров уже найденных реакций (на входное воздействие или частное решение), yн, y'н … ф.201
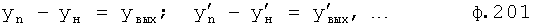
Формирователь частного решения формирует дифуравнение, правая часть которого равна математической модели входного воздействия или математической модели одного из общих решений, условно принятого за ″частное решение″ (после исключения его из левой части дифуравнения).
- для дифуравнения, входящего в вычислитель реакции на текущее воздействие;
- правая часть дифуравнения равна математической модели входного воздействия объекта R(t)=Kert;
- левая часть дифуравнения включает все постоянные внутреннего запаздывания Т1, Т2, … объекта или рассматриваемой САР для того, чтобы выражение 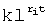 , (стоящее в правой части дифуравнения ф.204) преобразовать в выражение, включающее степенные многочлены, используют пример расчетов ф.205.1
, (стоящее в правой части дифуравнения ф.204) преобразовать в выражение, включающее степенные многочлены, используют пример расчетов ф.205.1
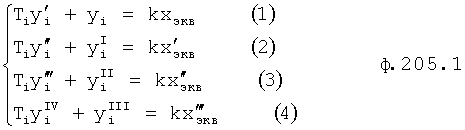

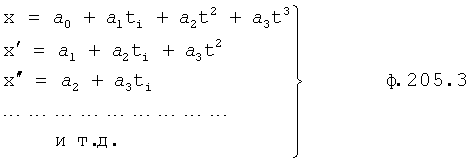
ф.205.3 частная модель предыдущих воздействий, эквивалентная звену W1, перенесенному в правую часть дифуравнения ф.205.1.
И т.д. ф.205.2 подставляют в уравнения ф.205.1.
После подстановки ф.205.2 и ф.205.1 из системы уравнений ф.205.1 (1…3) находят зависимости ф.205
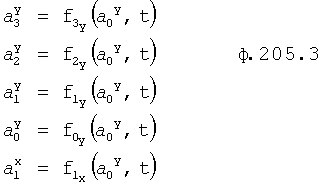
Зависимости 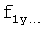 ,
, 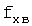 подставляют в ф.205.1(4) и вычисляется зависимость
подставляют в ф.205.1(4) и вычисляется зависимость 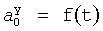 , которая подставляется в формулу для
, которая подставляется в формулу для 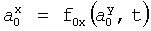 ф.205.3, моделирующее входное эквивалентное воздействие.
ф.205.3, моделирующее входное эквивалентное воздействие.
После того как правая часть дифуравнения примет вид степенного многочлена, а характеристическое уравнение левой части исходного дифуравнения будет разделено на характеристическое уравнение составляющую, перенесенную в правую часть (т.е. выделенную в частное решение), полученное дифуравнение рассматривает реакцию "левой части" на входное воздействие "правой части". Для этого по вышеприведенным формулам находится степенная модель этой реакции.
Для того чтобы проверить полученную модель с реальным объектом, необходимо сравнить выходной параметр объекта y0, y0, … и модели yм, yм, …. Необходимо подставить в полученное математическое выражение 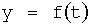 ,
, 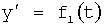 текущей (рассматриваемый) момент времени t. Задатчик значения времени исследуемого состояния определяет интервал времени, на протяжении которого влияло рассматриваемое входное воздействие (или частное решение относительно какого-то из внутренних составляющих емкостных). Интервал времени определяет текущий момент времени ti, что позволит определить параметры реакции yр, yр, … на это воздействие по степенной модели, полученной на выходе определителя в вычислителе.
текущей (рассматриваемый) момент времени t. Задатчик значения времени исследуемого состояния определяет интервал времени, на протяжении которого влияло рассматриваемое входное воздействие (или частное решение относительно какого-то из внутренних составляющих емкостных). Интервал времени определяет текущий момент времени ti, что позволит определить параметры реакции yр, yр, … на это воздействие по степенной модели, полученной на выходе определителя в вычислителе.
Нахождение интервала времени осуществляется таймером, входящим в задатчик (связанный с операторами и пусковыми устройствами). Если измерять таймером невозможно, то значение момента времени (рассматриваемого) находится нахождением корня, общего для каждого из степенных уравнений, входящих в систему. Если общего корня нет, то находят корни для уравнения, выходной параметр объекта у которого представлен производной с большей степенью. К выбранному значению момента времени вычисляют значения выходного параметра и его производных меньшего порядка, для этого используется вычислитель текущих значений - для дифуравнения, входящего в вычислитель реакции на предыдущие воздействия,
- правая часть дифуравнения включает один из корней гi характеристического уравнения левой части дифуравнения ф.202;
- левая часть дифуравнения получается делением характеристического уравнения ф.65а на характеристическое уравнение, составленное с перенесенным корнем ri в правую часть дифуравнения ф.203.
Характеристическое уравнение 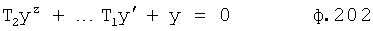
дифуравнения объекта,
где y, y', … yz, T1…T2 - параметры объекта,
ф.203 - деление характеристических уравнений
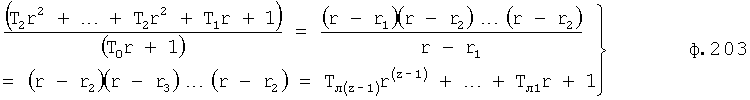
где 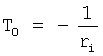 - параметр одного из звеньев объекта.
- параметр одного из звеньев объекта.
Ф.203 - деление характеристических уравнений.
Ф.203 - дифуравнение на выходе формирователя частного решения ф.191 ф.198
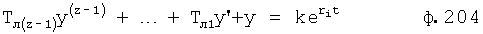
Формирователь составляющей реакции находит ti на текущее входное воздействие, при этом используется степенная модель общего дифуравнения ф.191. Найденный основной момент реакции на текущее входное воздействие ti подставляют в ф.198 и вычисляют y, y', …. Если эти значения не совпадают с текущими значениями, то начальные выходные (и соответственно емкостные внутренние параметры) были не нулевые. Реакция на внутреннюю начальную (емкостную) составляющую определяется формирователями составляющих реакции в вычислителе реакции на предыдущие воздействия.
Если момент времени при, котором измерялись выходные параметры y, y', …, заранее не известен, то в формулу с выходным параметром, имеющую максимальную степень производной, подставляется измеренное значение максимальной производной и вычисляются корни степенного многочлена, из которых выбирается тот корень, который после повторных измерений через интервал времени Δt будет совпадать со значением, равным сумме предыдущего значения ti плюс длительность интервала Δt между измерениями 
При начальных нулевых значениях выходного параметра (и соответственно емкостных нулевых внутренних параметрах) найденный корень текущего момента времени будет справедлив для всех уравнений а, б, …, входящих в систему. Если для других уравнений он не справедлив, то его значения подставляются в эти равенства и находят значения выходных параметров, которые вычисляют от измеренных значений в вычитателе, входящем в формирователь составляющей реакции.
Справедливость вышеприведенных вычислений ti можно увидеть из формулы 205
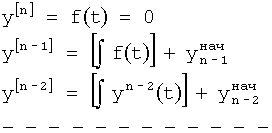
т.е. при 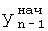 ,
, 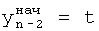 корни f(t) справедливы ф.205 для всех yn-1, yn-2 … y.
корни f(t) справедливы ф.205 для всех yn-1, yn-2 … y.
Таким образом, моделирование начальных (отличных от нуля емкостных) внутренних составляющих (полученных на выходе вычитателя, входящего в формирователь составляющей реакции) осуществляется вычислителем реакции на предыдущие воздействия.
Для этого поочередно каждое из внутренних составляющих (емкостных) переносится в правую часть дифуравнения, выделяя его в частное решение, при этом постоянные времени в левой части дифуравнения вычисляются из корней, оставшихся на данном этапе вычислений в левой части дифуравнения.
Реакцию на текущее входное воздействие можно назвать "вынужденной реакцией", а реакцию объекта (САР) на внутреннее начальное емкостное состояние можно назвать "свободная реакция" на выделенное частное решение. Так как "свободная реакция" является условной по величине, значение которой зависит (не только от входного текущего воздействия, а также других внутренних начальных составляющих) в большой степени от порядка, в котором оно выделялось в частное решение, то и соответственно вычисленный момент времени ty тоже называют условным ф.206.1
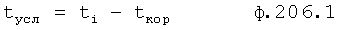
где ti вычисленный момент времени равен моменту реакции на текущее воздействие (в модели ti=t, т.е. явл. переменной);
tкор - момент времени, который используется для коррекции текущего момента в степенной модели с учетом вычисленного (в вычисл. задатчика) условного момента времени ty по ф.206.2

Момент времени (вычисленный в задатчике) "условный" tус используется для нахождения выходных параметров реакции 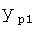 ,
, 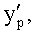 значения которых вычитаются от предыдущих исследуемых параметров y, y …, а также для нахождения момента коррекции.
значения которых вычитаются от предыдущих исследуемых параметров y, y …, а также для нахождения момента коррекции.
Полученные значения "известного" или вычисленного момента времени ti (в формирователе составляющей реакции) и вычисленные "условный" момент времени tус и момент времени "коррекции" 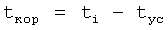 (в формирователях составляющих реакций …) на выходе задатчика значений времени поступают на вход вычислителя текущих значений в степенную модель выходного параметра, сформированную на выходе определяется реакции на частное решение. Степенная модель ″частного решения″ в формирователях … примет вид y=f(t-tкор)… - функции, у которой в степень возводится выражение с скобках (t-tкор), где t - переменная, tкор - вычисленная величина в задатчике… После подстановки ti и tкор в степенную модель вычисляются y(ti), y'(ti)… (а А0) и y (tус=ti-tкор), y'(tус), …
(в формирователях составляющих реакций …) на выходе задатчика значений времени поступают на вход вычислителя текущих значений в степенную модель выходного параметра, сформированную на выходе определяется реакции на частное решение. Степенная модель ″частного решения″ в формирователях … примет вид y=f(t-tкор)… - функции, у которой в степень возводится выражение с скобках (t-tкор), где t - переменная, tкор - вычисленная величина в задатчике… После подстановки ti и tкор в степенную модель вычисляются y(ti), y'(ti)… (а А0) и y (tус=ti-tкор), y'(tус), …
Структурная схема 1-го канала разделителя реакции приведена на фиг.18. Блок (входящий в вычислитель реакции на текущее воздействия 3) отделяет модель реакции объекта на текущее входное воздействие при нулевых начальных условиях.
Блоки … (входящие в вычислитель реакции на предыдущие воздействия 4) разделяют внутренние емкостные составляющие состояния, образующие ненулевые начальные условия.
Сумматор 10 находит сумму всех составляющих степенной модели.
Альтернативной технической реализацией является п.18.1 фиг.18 по ф.196-207. Для решения задачи регулирования отдельными составляющими необходимо повысить точность идентификации.
Т.е. при этом возникает усложнение задачи: обеспечение
- надежности, т.е. точности модели проверкой способом дублирования, т.е. вводом двух параллельных независимых каналов идентификации фиг.18 и последующим сравнением полученных результатов идентификации;
- возможности минимальными вычислениями определить область изменения выходного параметра на разных промежутках времени по характеру изменения производных выходного параметра y', y” …, т.е. необходимо формировать дополнительно модель производной выхода.
Достоинство рассматриваемого способа формирования модели в том, что он позволяет отделить реакцию объекта на текущее входное воздействие от влияния предыдущих воздействий. Таким образом, текущее значение выходного параметра равно сумме реакции на текущее воздействие и остаточного состояния выходного параметра, сформированного предыдущими воздействиями, вычисленными в текущий момент времени. Это открывает возможности определения необходимых, а) предварительных входных воздействий и б) текущего входного воздействия, т.е. разделение реакции объекта, значение его выходного параметра y на yт реакцию на текущее входное воздействие и yпр "остаточных" реакций на предыдущие воздействия (y=yт+yпр).
Недостаток вышерассмотренного способа в том, что математическая модель сложных CAP принимает выражение, неудобное для дифференцирования (со сложным знаменателем). В свою очередь возникают сложные математические вычисления при моделировании производных выходного параметра y', y” …, позволявших судить о характере изменения выходного параметра и обеспечения контроля за ОДЗ.
Для упрощения расчетов при нахождении производных разного порядка и обеспечения надежности (точности модели) ″дублированием″ в заявленном устройстве используется вторая модель (параллельно первой), независимая от первой, сформированная по производной выходного параметра, порядок которой равен максимальному порядку производных, входящих в дифуравнение.
Использование одновременно двух способов объясняется тем, что обеспечение ОДЗ (по параметрам качества и устойчивости) является основной задачей CAP. Каждый способ определения математической модели имеет свои достоинства и недостатки. Поэтому для приближения математической модели к реальному объекту необходимо пользоваться не одним способом, а как минимум двумя.
Первый способ - значение выходного параметра формирует как сумму реакций объекта: на текущее воздействие yт и предыдущие воздействия.
Второй способ позволяет исследовать характер изменения максимальной производной выходного параметра объекта, входящей в дифуравнение, и определить интегральные постоянные, входящие в производные более низкого порядка, которые являются начальными значениями для каждой производной.
Канал моделирования производных высокого порядка 2 фиг.18 включает последовательно соединенные интегратор производных 12.1, вычислитель постоянных интегрирования 13.1.
Для нахождения математического описания объекта рассматривается функция максимальной производной a(t), параметры которой определяются из дифуравнения, включающего постоянные внутреннего запаздывания. В ф.207 приведена функция производной, включающая один переменный коэффициент «a(t)», изменение которого во времени определяется из дифуравнения.
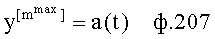
Производные более низкого порядка 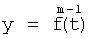 ,
, 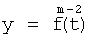 находятся интегрированием производной ф.207 в интеграторе производных 12.1 по ф.208, на второй вход которого с выхода вычислителя постоянных интегрирования 2.2 поступают значения найденных постоянных интегрирования
находятся интегрированием производной ф.207 в интеграторе производных 12.1 по ф.208, на второй вход которого с выхода вычислителя постоянных интегрирования 2.2 поступают значения найденных постоянных интегрирования
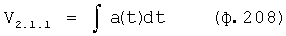
где a(t) можно рассматривать как постоянную в «малом» (т.е. при малом изменении переменной времени, в течение которого определяются производные выходного параметра, входящие в дифуравнение),
тогда 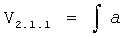 dt=at+Cm-1=y(m-1)
dt=at+Cm-1=y(m-1)
C1 - постоянная интегрирования, значение которой определяется вычислителем постоянных интегрирования 12.2 по ф.209;
m - степень максимальной производной выходного параметра, входящего в дифуравнение
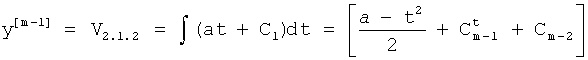 и т.д.
и т.д.
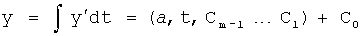
Вычислитель постоянных интегрирования 12.2 производит вычисление коэффициентов C1, C2,… (входящих в ф.209) по формулам
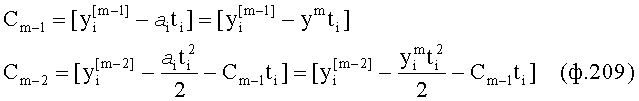 и т.д.
и т.д.
где yi(ti), y'i(ti),… - значения выходных параметров в момент времени, полученные фактически измерением величины выходного параметра, скорости его изменения и ускорения этого значения, а также производных более высоких порядков,
a i=a(ti)=ym(ti) - измеренное значение в момент tэ
Элемент подстановки 2.3 формирует модель дифуравнения объекта (САР), подстановкой в него найденных по ф.208 получили ф.210
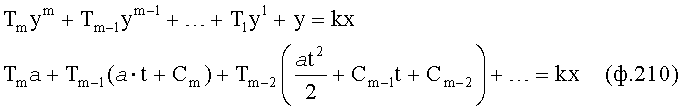
где yi, y', y” находят по ф.208;
C1…Cm вычисляют по ф.209 после подстановки в них измеренных 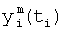 ,
, 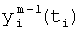 , значение момента времени для которых измерялись
, значение момента времени для которых измерялись 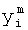 .
.
Из полученного дифуравнения находится зависимость коэффициента «а» от переменной t, при изменении его в «большом».
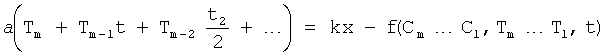
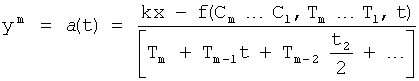
Вычислитель выходного параметра 16 для определения текущего значения выходного параметра y(t)=… использует полученную «m» интегрированием исходной формулы для максимальной производной ym и подстановкой в ней найденных ранее постоянных интегрирования и математической модели максимальной производной.
Назначение схемы сравнения 17 - объединение и совместимое использование данных двух каналов моделирования. Схема сравнения 17 позволяет судить, насколько точны каждый из используемых методов (в первом и втором канале моделирования), и определить причины несовпадений полученных значений параметров. Результаты сравнения позволяют добиться большей достоверности математической модели оператором, осуществляющим текущий анализ и корректировку окончательной модели. Таким образом, оператор имеет информацию:
1) из первого канала - реакцию на текущее воздействие при известном значении текущего момента времени t (при неизвестном t находят условную реакцию - реакцию на предыдущие воздействия в виде реакции на каждую отдельную емкостную составляющую, условно принятую поочередно как частное решение);
2) из второго канала - о влиянии начальных внутренних емкостных составляющих, выраженных в виде постоянных интегрирования C1.
Для нахождения экстремальных (максимальных или минимальных) значений выходного параметра в доступных регулируемых областях или в областях, выходящих за рамки допустимых значений, используется вычислитель экстремальных значений п.18.2(3) фиг.1.
Если модель объекта включает в себя числитель и знаменатель, то дополнительно исследуется числитель и знаменатель самостоятельно. При этом может использоваться стандартный алгоритм, приведенный в

Полученные корни уравнений ф.211
y'(t)=0 - экстр. значений вершин,
y”(t)=0 - точки перегиба
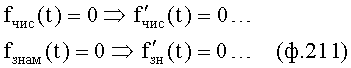
после подстановки в модель уравнения выходного параметра ф.78а позволяют найти исследуемые вершины, точки перегиба и области разрыва непрерывности (неустойчивости).
Для оперативного регулирования помимо перечисленных каналов моделирования (первого и второго) необходим быстродействующий канал моделирования (вычислитель ближайших текущих значений 18.2.4).
Если первый канал моделирования позволяет отделить текущее воздействие (входное) от предыдущих, второй канал моделирования исследует влияние остаточных емкостных составляющих, сформированных предыдущими входными воздействиями, то третий канал моделирования, входящий в выч. ближайших текущих значений 18.2.4, позволяет упростить расчеты по нахождению моментов времени t1=…, в которые регулируемая выходная величина y(t) примет заданное значение yS0 подсоединены на выход вычислителя ближайших значений.
Сокращение времени, необходимого для вычисления значения выходного параметра в заданный момент времени () и для определения момента времени, в котором выходной параметр примет заданное значение (), осуществляется за счет упрощения структуры модели, что осуществляется за счет подстановки нового основания степени ф.212 в решение дифуравнения САР
x=et - выходной сигнал формирователя основания степени
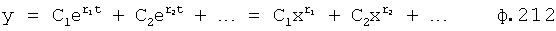
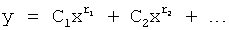 - выходной сигнал элемента подстановки в эл. поэтап. освоб. от радикалов.
- выходной сигнал элемента подстановки в эл. поэтап. освоб. от радикалов.
Если корни r1… имеют дробное значение, то каждое из слагаемых с дробной степенью поэтапно переносится (выделяется) в левую часть решения дифуравнения ф.213
и после возведения в соответствующую степень γ правой и левой части равенства, слагаемое в левой части освобождается от радикала (степени с дробной частью) и переносится в правую часть.
На выходе элемента поэтапного освобождения от радикалов получается степенной многочлен, показатели степени которого имеют целое значение.
Формирователь положительной степени с отрицательной степенью переносит в знаменатель, приводит все слагаемые к общему знаменателю, что позволяет получить модель в виде дроби, в числителе и знаменателе которой - степенные многочлены с целыми положительными степенями, нахождение корней которых возможно стандартными способами.
Вычислитель времени для заданного параметра формирует значение заданного параметра задатчиком выходных параметров (или оператором). Элемент освобождения от знаменателя переносит знаменатель правой части решения дифуравнения в числитель левой части (т.е. заданное значение выходного параметра из левой части переносится в правую и приводится к общему знаменателю). После этого находятся корни числителя и объединяются с правой частью, после чего находятся корни.
Вычислитель установившегося значения (п.18.3) определяет, к чему стремится значение выходного параметра при изменении переменного x=e (момента времени t1) в «большом», для этого находится предел, к которому стремится модель САР со второго выхода при изменении основания степени (x→∞ - стремление к бесконечности ф.214)
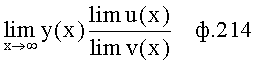
где lim v≠0
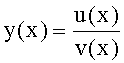
x=et;
г) в малом при X→ai…
если какие-то xi… являются корнями числителя u(x) или знаменателя v(x)
Если 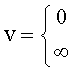 и
и 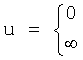 , то необходимо искать обходные пути нахождения предела.
, то необходимо искать обходные пути нахождения предела.
Вычислитель неравенств приравнивает упрощенную модель САР с областью допустимых значений ОДЗ. Упрощенная модель позволяет контролировать ОДЗ в оперативном регулировании, т.е. при определении ближайших выходных регулируемых параметров.
Преобразователь основания степени, найденные значения в вычислителях подставляют в математическое выражение ф.215 для нахождения моментов времени ti, в которых выходной параметр принимает заданное значение, и интервалов времени tj<Δt<tj+1, в которых обеспечивается ОДЗ

Вычислитель выходных параметров для заданного момента времени а6 подставляет текущее значение выходного параметра в модель объекта с выхода формирователя положительных степеней и исключает радикалы по формулам модели с выхода элемента поэтапного освобождения от радикалов. Один из корней этой модели будет равен текущему моменту времени. После этого от исследуемого момента времени tис-tт=Δt отнимается текущий момент времени (если известно, что исследуемый момент времени равен какому-то заданному интервалу времени Δt, наступающему после текущего, то этот интервал прибавляется к идентифицированному текущему ф.216)
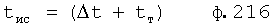
Исследуемый момент времени tис подставляется в модель САР, полученную после освобождения от радикалов и нахождения корней степенного многочлена модели ф.217
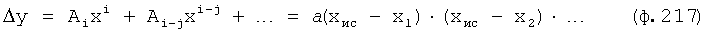
где 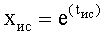
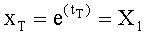 (или одному из х2…i) корней модели,
(или одному из х2…i) корней модели,
xi≠т - принимают за «условные»,
Δy=[y(tис)-y(tт)].
Исследуемое 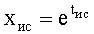 подставляется в ф.217 и вычисляется Δy. Полученное значение Δy прибавляется к текущему значению выходного параметра yт и получается ожидаемое значение выходного параметра y(t) в исследуемый момент времени tис (согласно ф.216, 217 и предыдущим преобразованиям модели ф.212, 213).
подставляется в ф.217 и вычисляется Δy. Полученное значение Δy прибавляется к текущему значению выходного параметра yт и получается ожидаемое значение выходного параметра y(t) в исследуемый момент времени tис (согласно ф.216, 217 и предыдущим преобразованиям модели ф.212, 213).
Таким образом, используемые модели в вычислителе ближайших значений являются оптимальными при оперативном контроле и регулировании выходного параметра.
Совокупность блоков, входящих в идентификатор 19 позволяет (фиг.4) получить исчерпывающую информацию об объекте регулирования, чтобы определить характер дальнейшего изменения регулируемого технологического процесса с учетом всех влияющих на него факторов. Совокупность проведенных в идентификаторе исследований позволяет создать программируемый регулятор с адаптацией (цифровой) входного регулирующего воздействия, максимально приближая выходной (регулируемый) параметр к желаемому значению.
Определитель общих параметров yвых. исследует динамические характеристики выходного параметра объекта как единую сумму всех емкостных звеньев yвых.=XPW1·W2·…
Определитель отдельных составляющих исследует величины внутреннего взаимодействия емкостных звеньев, объекта y(1), y(2)…
Определитель временных интервалов с критическими параметрами контролирует полученные математические модели исследуемых параметров, проверяя выполнение области допустимых значений ОДЗ в ожидаемых разных интервалах времени.
Совокупность п.18 и п.19 позволяет не только с определенной желаемой степенью достоверности идентифицировать характеристики внутренних параметров отдельных, условно разделенных на звенья, составляющих, но и прогнозировать характер изменения этих составляющих для того, чтобы предотвратить неблагоприятные (или аварийные) режимы.
Таким образом, заявленные устройства, входящие в идентификатор, необходимы для осуществления поставленной задачи: «управление каждой из отдельных составляющих объекта».
В начальный момент на входе объекта п.2 фиг.1 формирователь регулирующего воздействия п.3 поддерживает регулирующий параметр Хр, программируемый для предыдущего задания. Идентификатор п.19 хранит информацию об объекте, полученную на предыдущем этапе.
Оператор формирует сигнал задания на входах блока задания п.1 (блока динамической характеристики выходного параметра п.1.1 и блока внутренних отдельных составляющих п.1.2). Если параметры объекта не известны, то регуляторы п.6…7 работают в ждущем режиме, а сигнал задания принимается на входе регулятора по ошибке п.8, который подбирает приближенную характеристику параметров объекта, до уточнения этой характеристики результатами вычислений идентификатора 19.
После того как идентификатор 19 установит исчерпывающую информацию, включаются регуляторы п.6…8, а блок проверки ОДЗ планируемой CAP п.5 моделирует каждый алгоритм регулирования, анализируя ожидаемые значения исследуемых параметров. Схема сравнения п.4 выбирает наиболее оптимальный, передавая его на вход регулирующего воздействия п.3. После того как формирователь регулирующего воздействия п.3 перестроит алгоритм управления и на выходе объекта п.2 появится реакция на новое входное регулирующее воздействие, компенсирующий регулятор п.9 начинает формировать дополнительное входное воздействие, которое корректирует рассогласование между моделью CAP и реальным значением, полученным на выходе идентификатора п.19.
Экономический эффект достигается подстройкой параметров не только текущих выходных объекта п.2, но и текущих внутренних емкостных характеристик, что позволяет предотвратить режимы с неблагоприятными параметрами, приводящие к аварии или износу используемого объекта (при технологических процессах уменьшает поломку и износ используемого в них оборудования), что приводит к экономии металла, необходимого для производства оборудования и т.д.
Источники информации
1. Кулаков Г.Т. Инженерные экспресс-методы расчета промышленных систем регулирования: Справочное пособие. - Мн.: Выш. шк., 1984 г. Стр.40.
2. Кулаков Г.Т. Инженерные экспресс-методы расчета промышленных систем регулирования: Спр. пособие. - Мн.: Выш. шк., 1984 г.
3. Попов Е.П. Теория линейных систем автоматического регулирования и управления: Учеб. Пособие для втузов. - М.: Наука, 1989 г.
4. Справочник по радиоавтоматике / Бурсова Т.В. и др. - К.: Техника, 1992, стр.195-196.
5. Ротач В.Я. Теория автоматического управления теплоэнергетическими процессами: учебник для вузов. - М.: Энергоатомиздат, 1985 г.
6. Цикунов А.Е. Сборник математических формул. / Под. ред. В.И.Довноровича. Изд. 4-е. Мн.: Вышэйш. Школа, 1971, стр.16, 171.
7. Выгодский М.Я. Справочник по высшей математике. - М.: Гос. изд. тех.-теор. лит., 1957.
8. Швецов К.И., Бевз Г.П. Справочник по элементарной математике. - К.: Наукова думка, 1965.
9. Справочник по элементарной математике для поступающих в ВУЗы. - К.: Наукова думка, 1973.
10. Бессекерский Б.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1972.
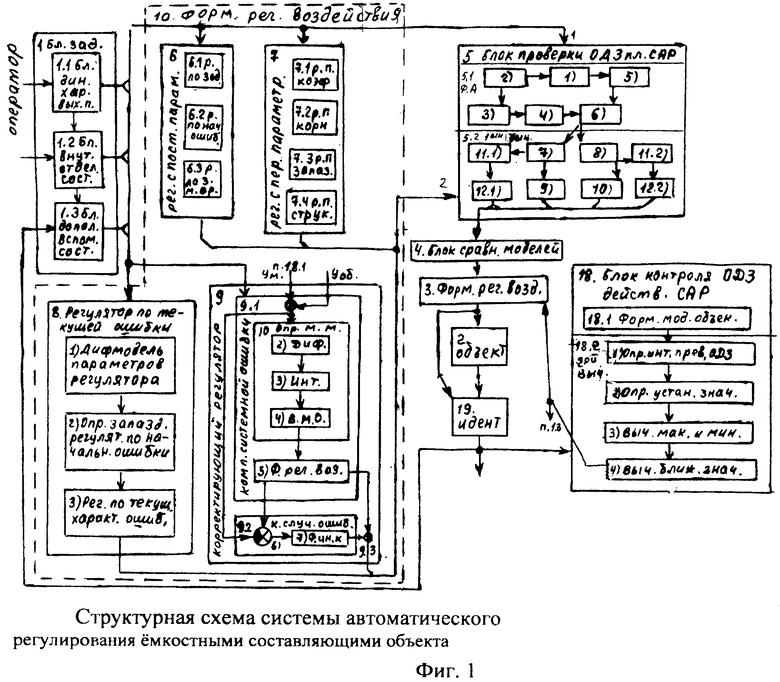

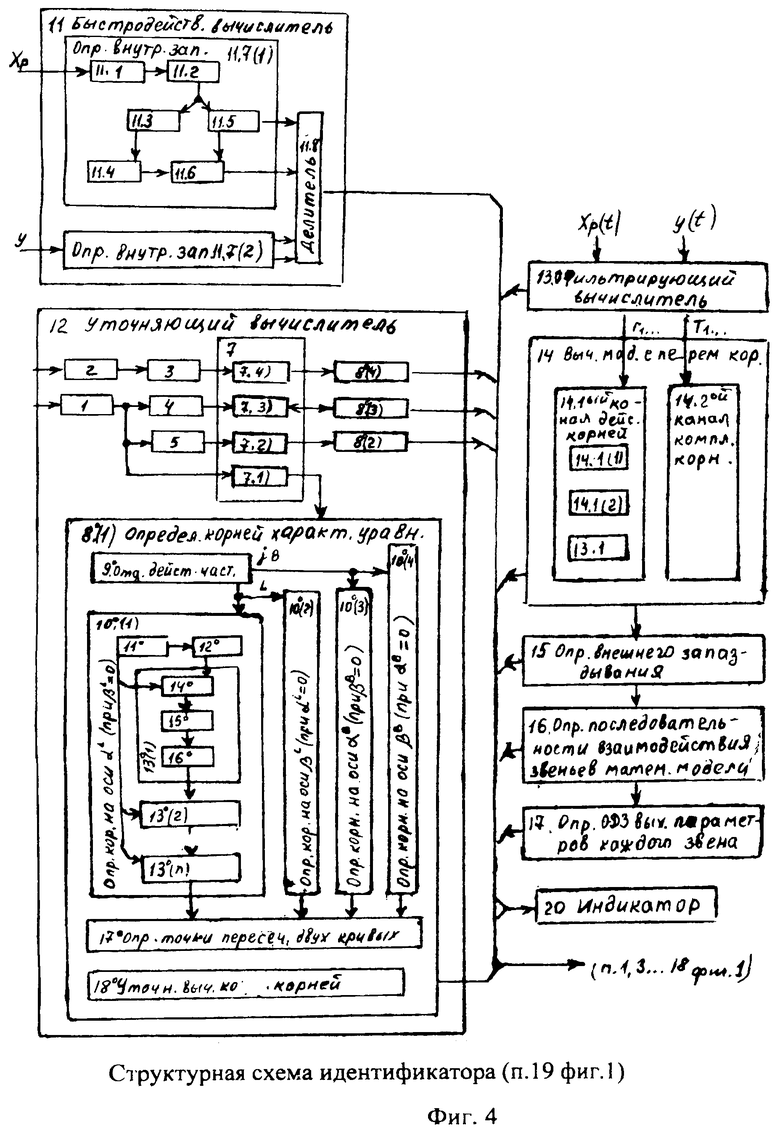
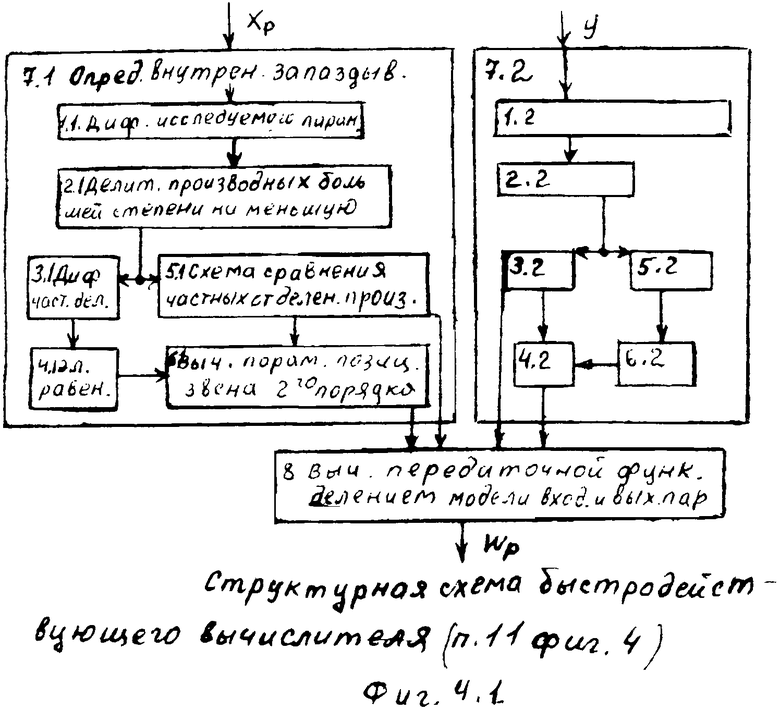
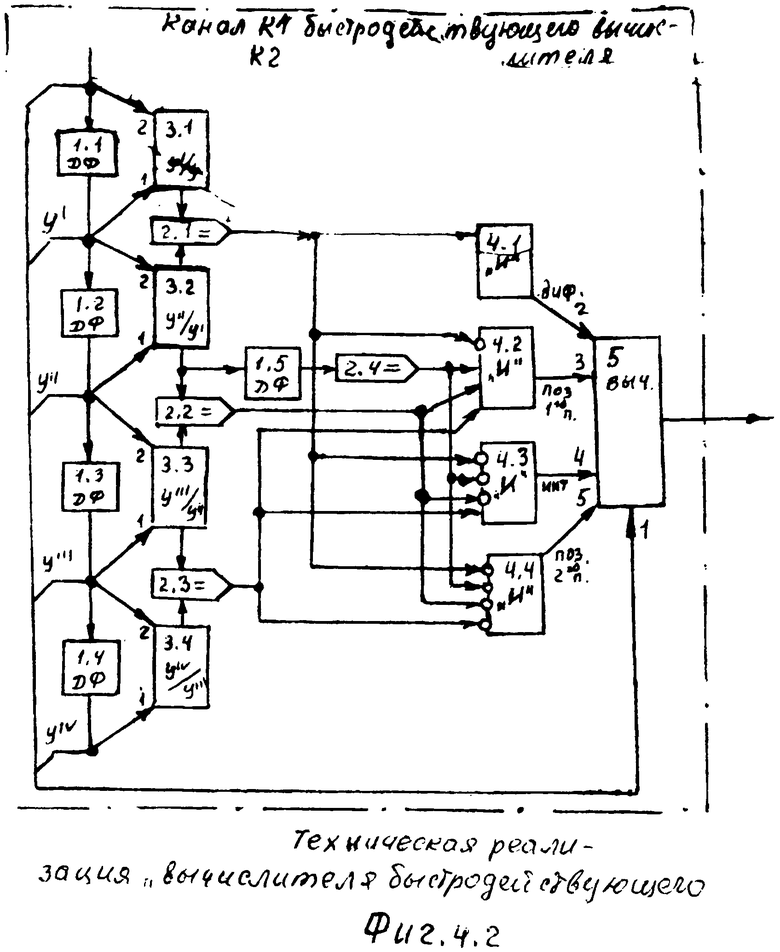

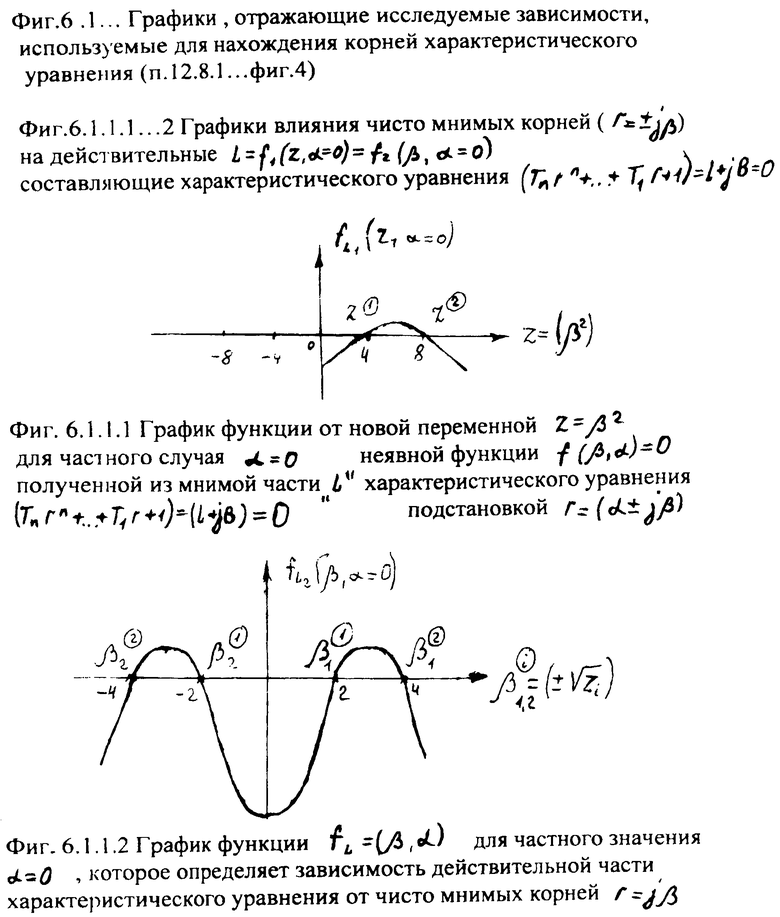
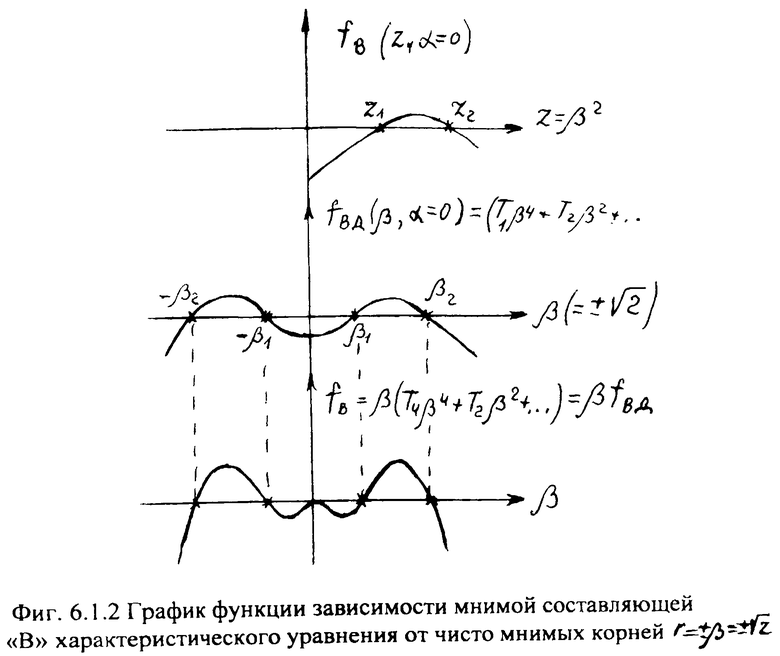
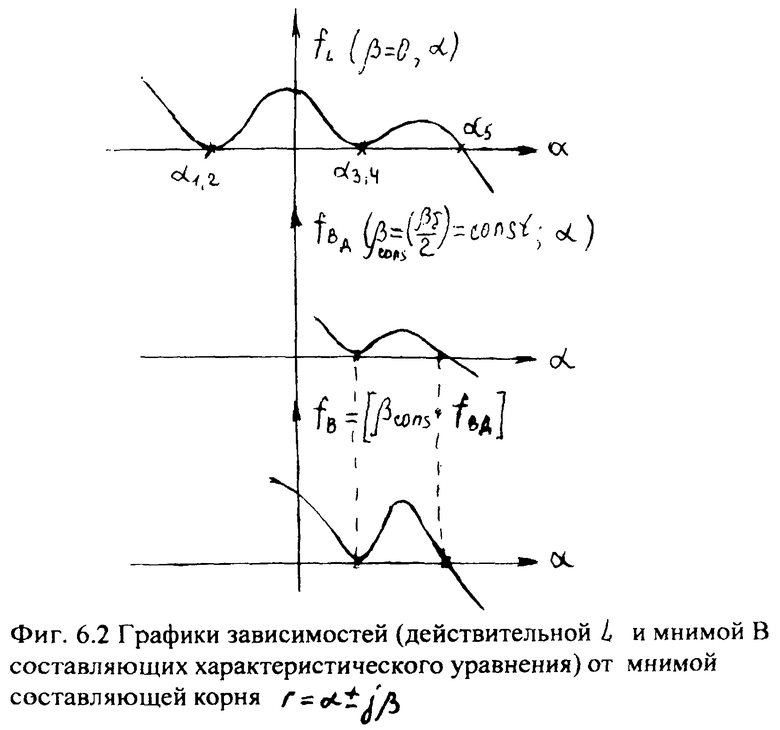

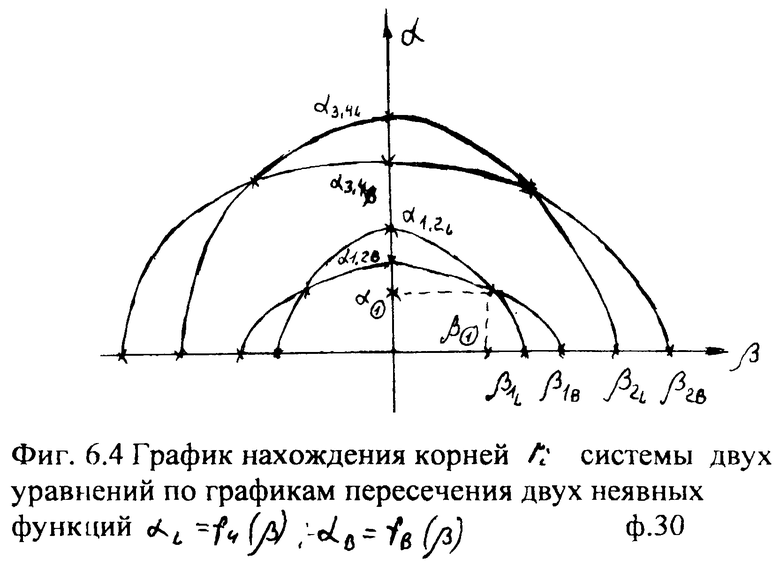
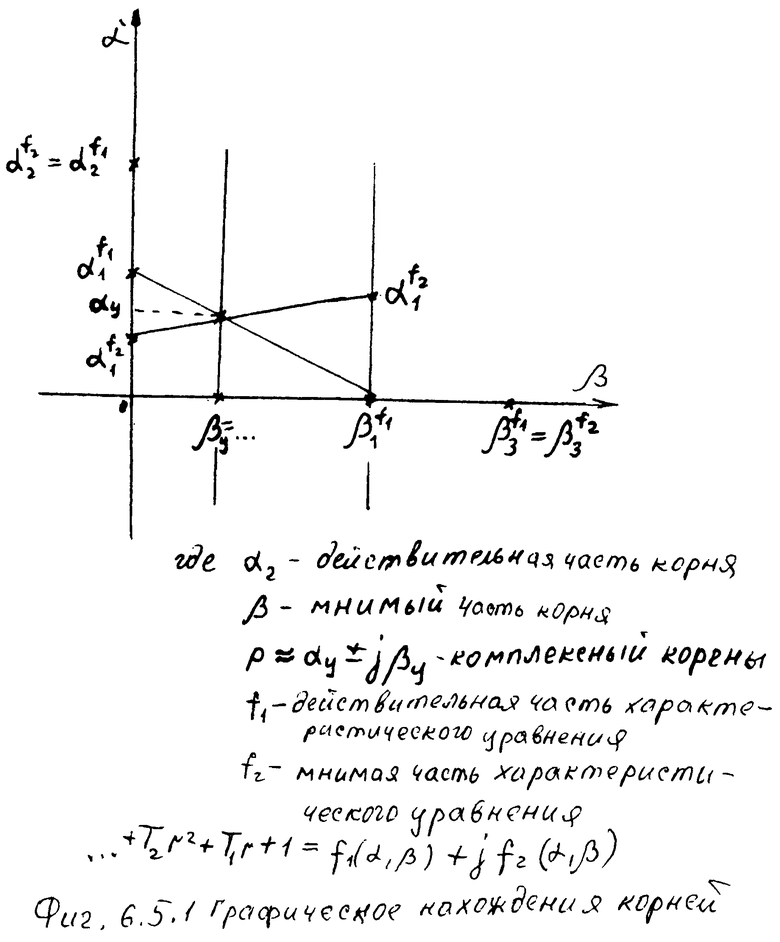
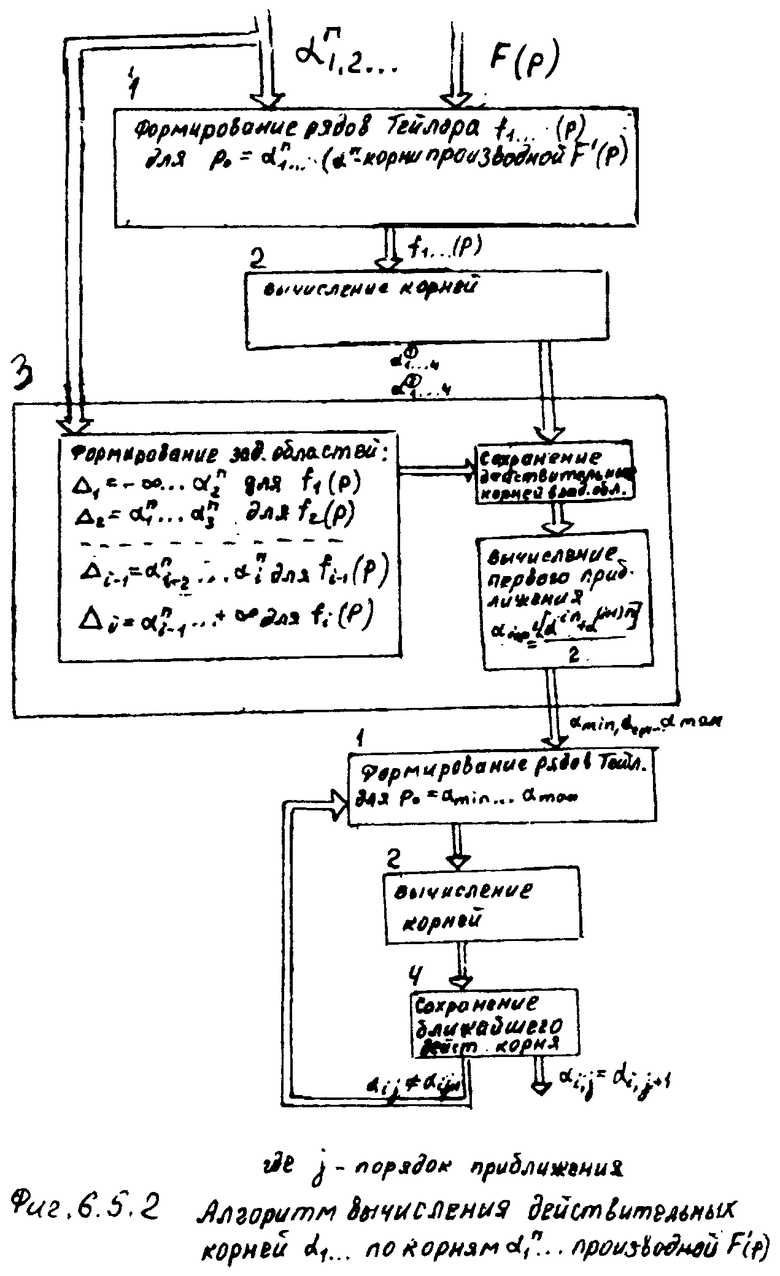
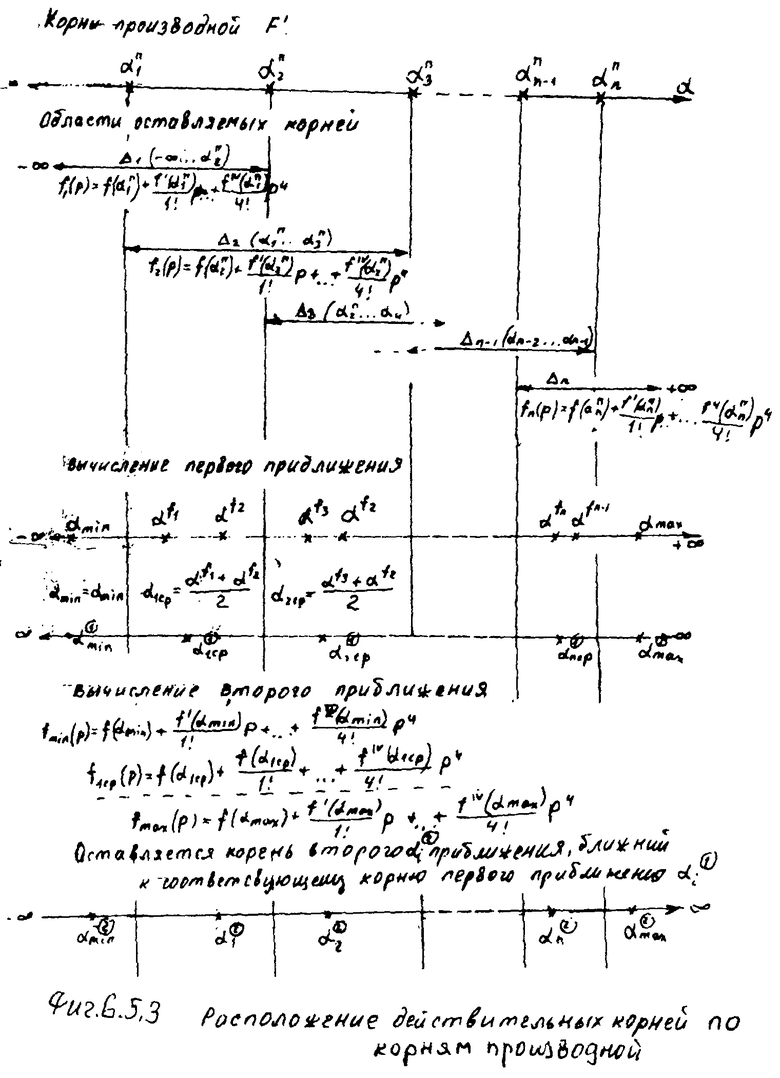
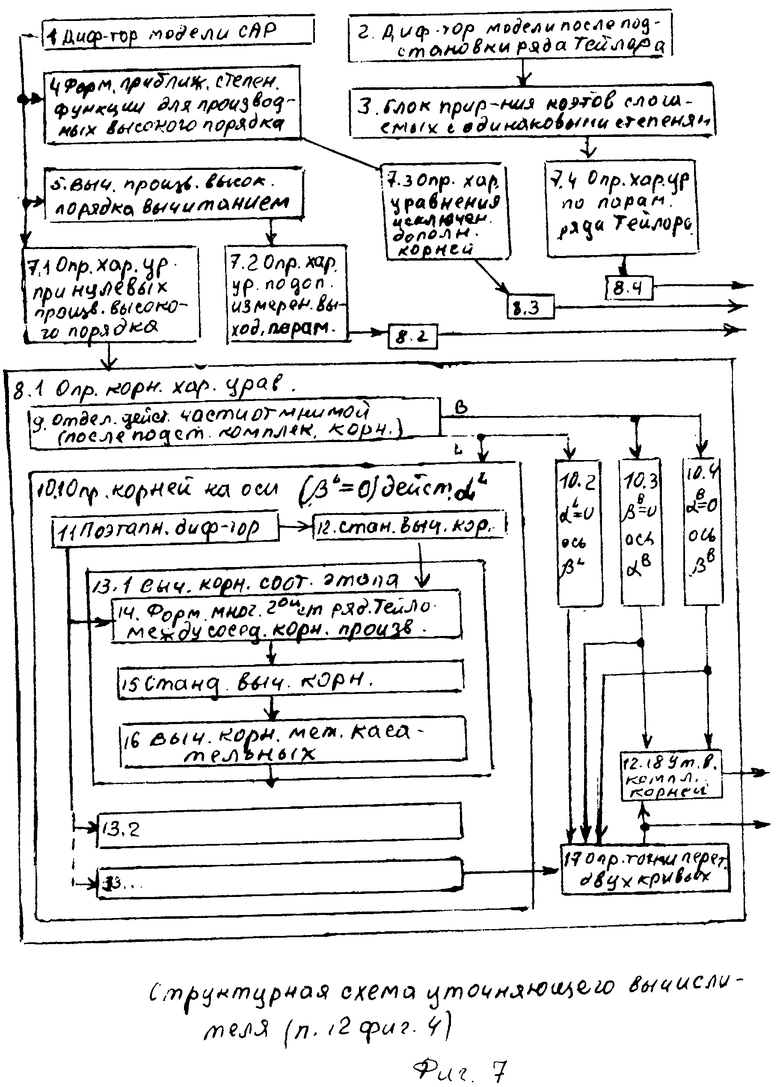
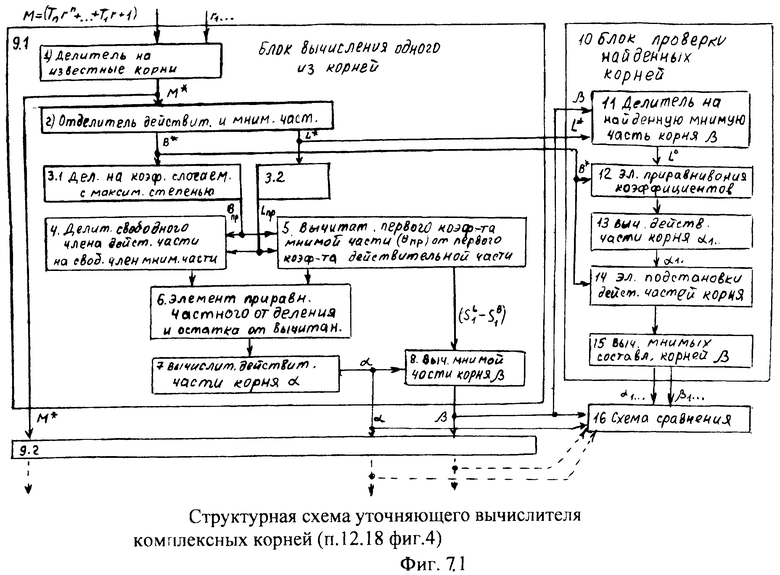
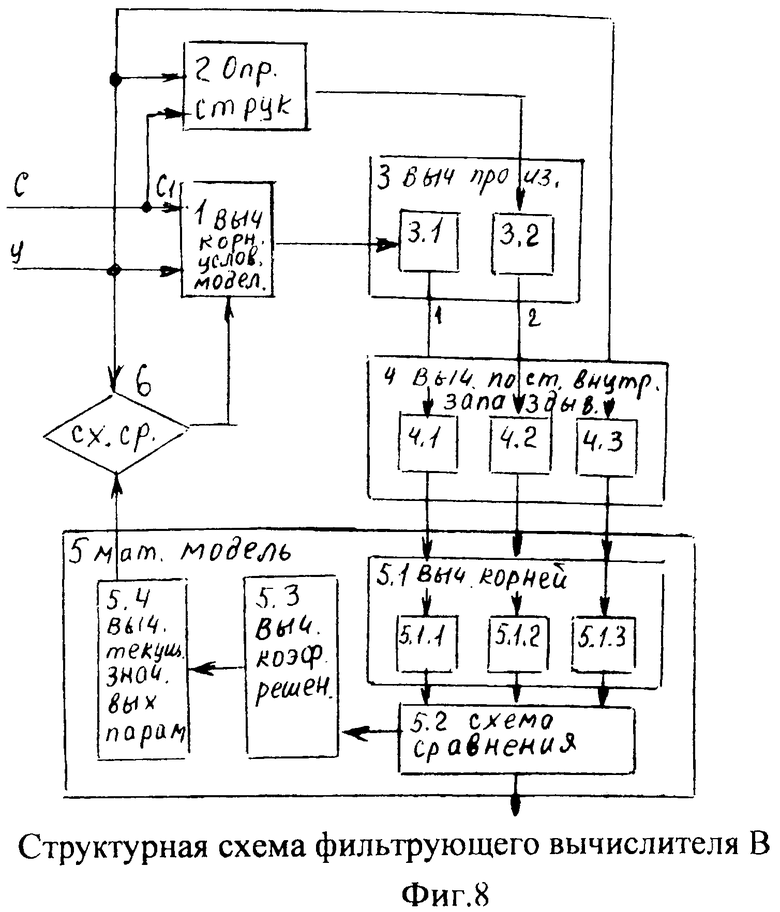
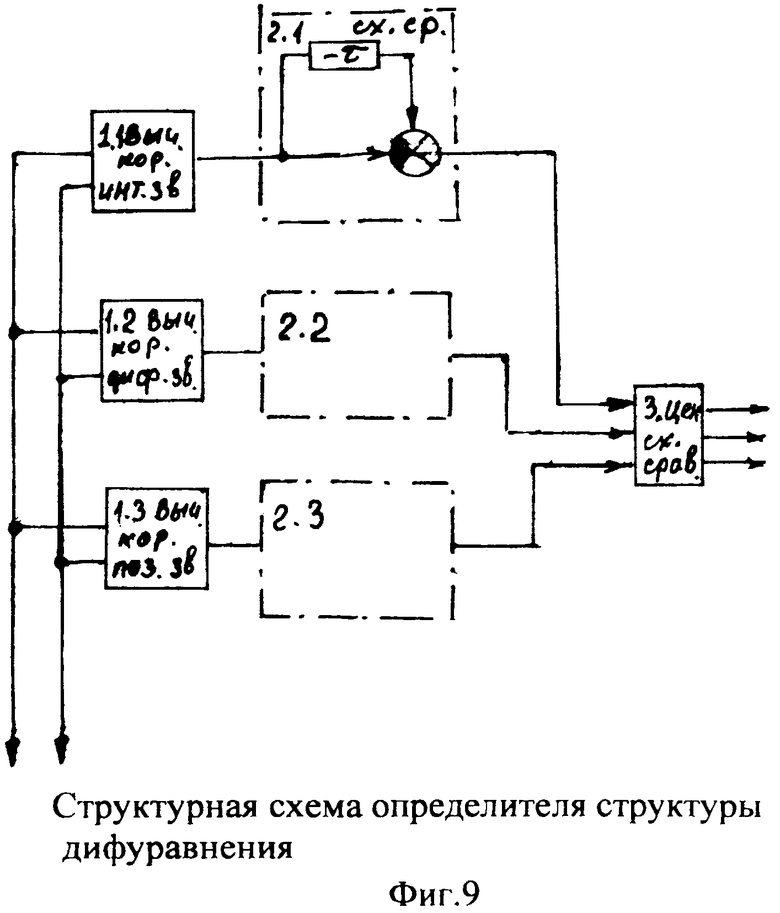
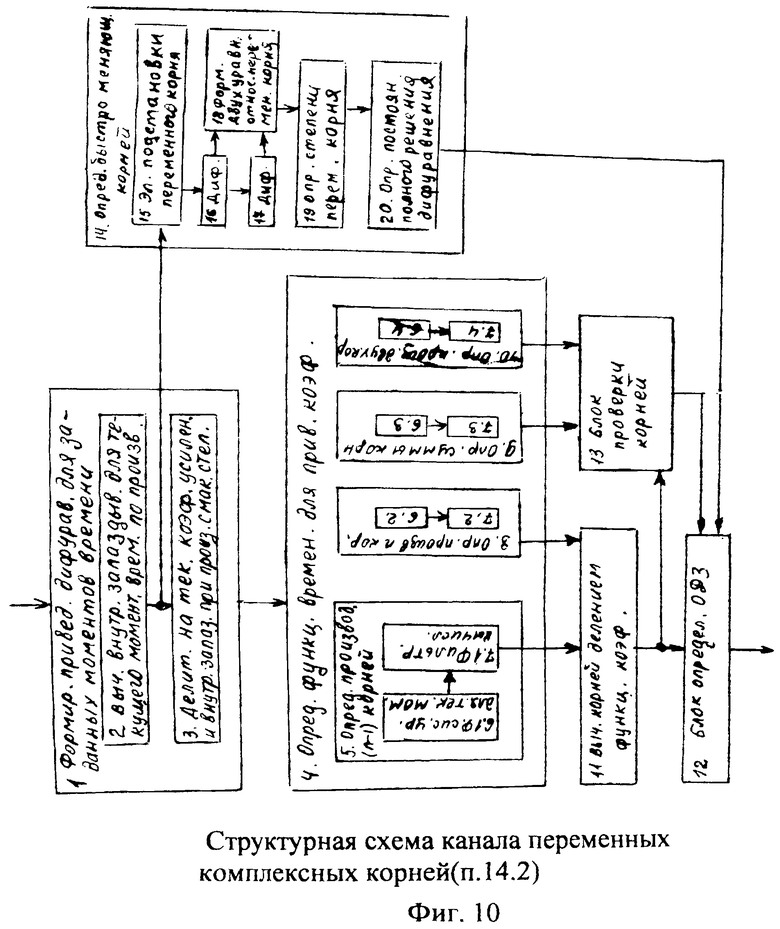

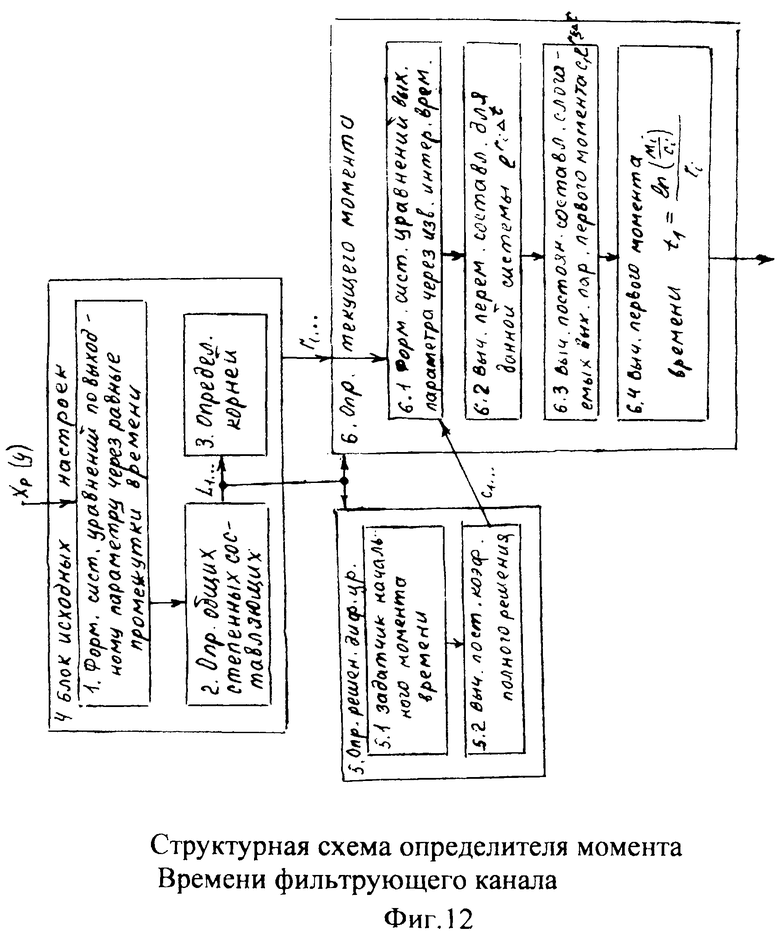
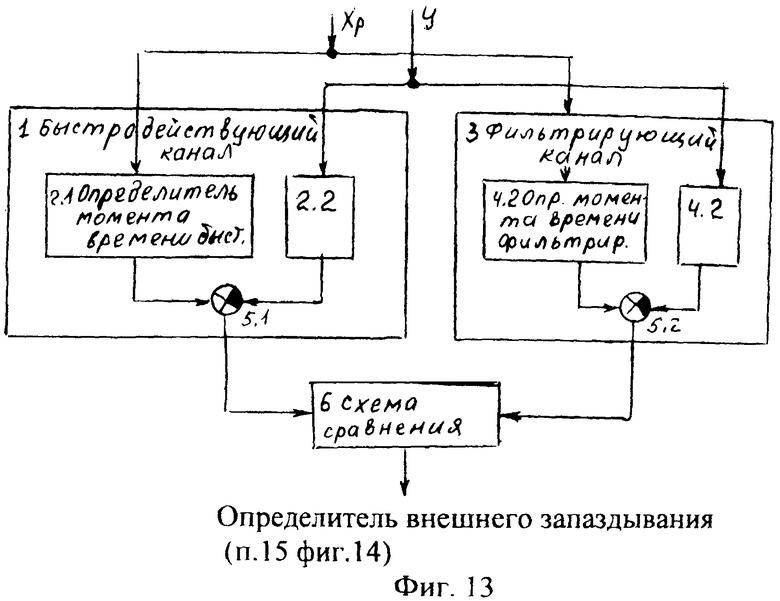
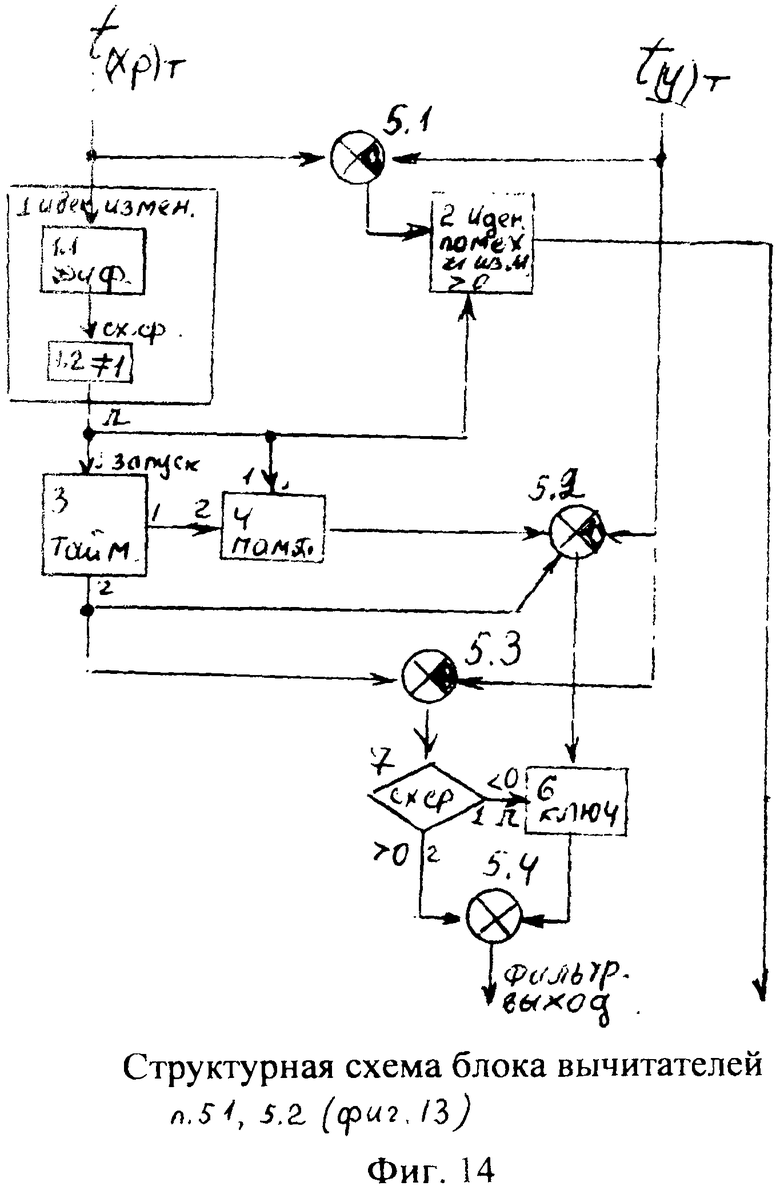
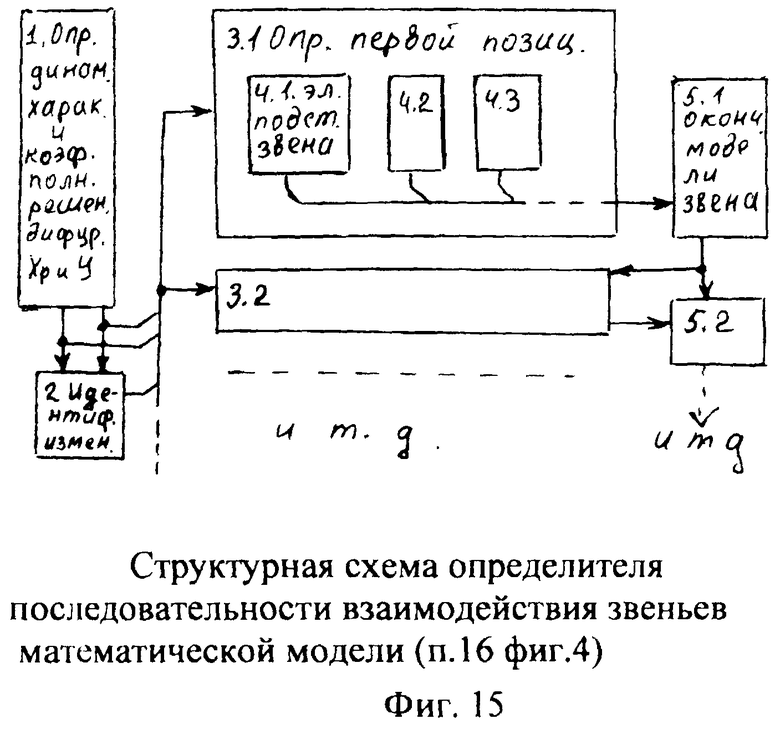
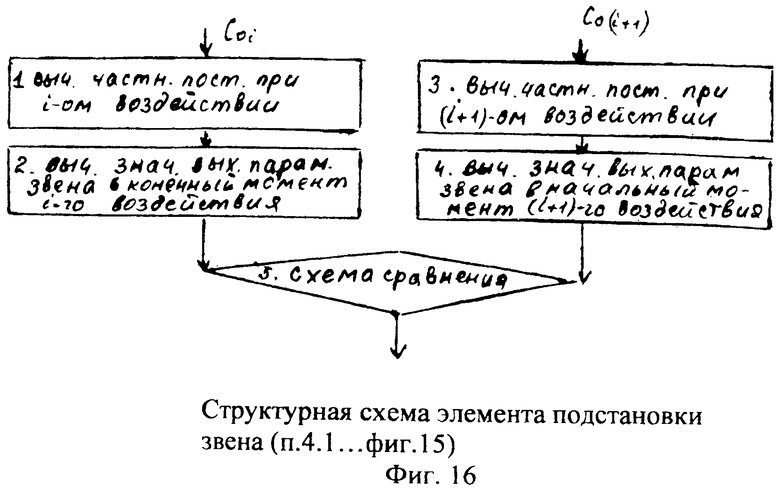

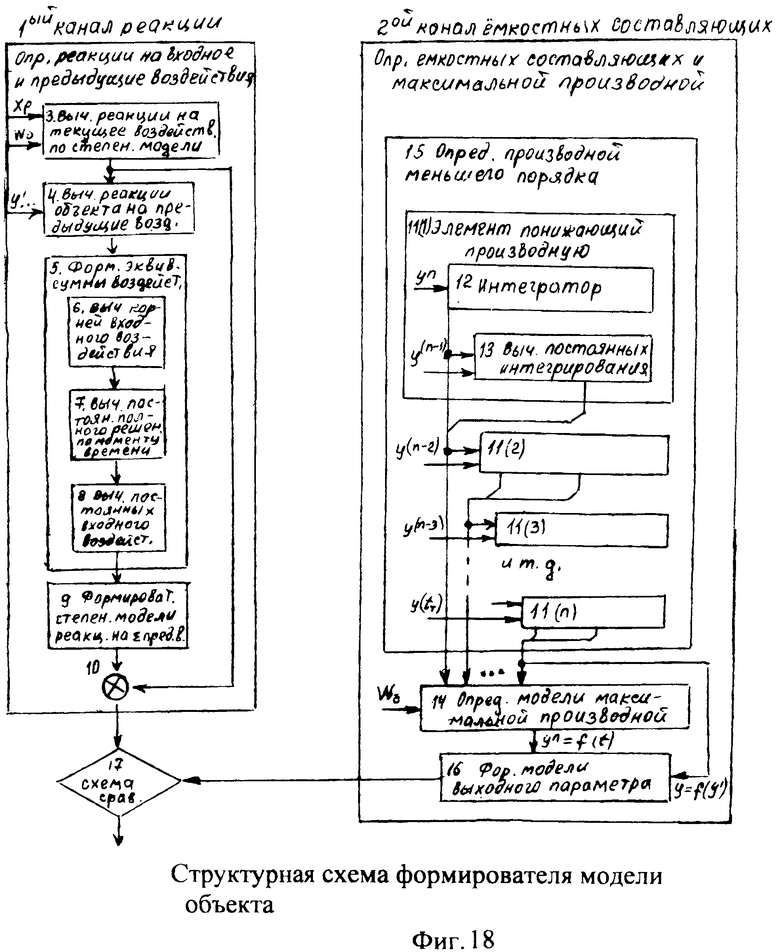
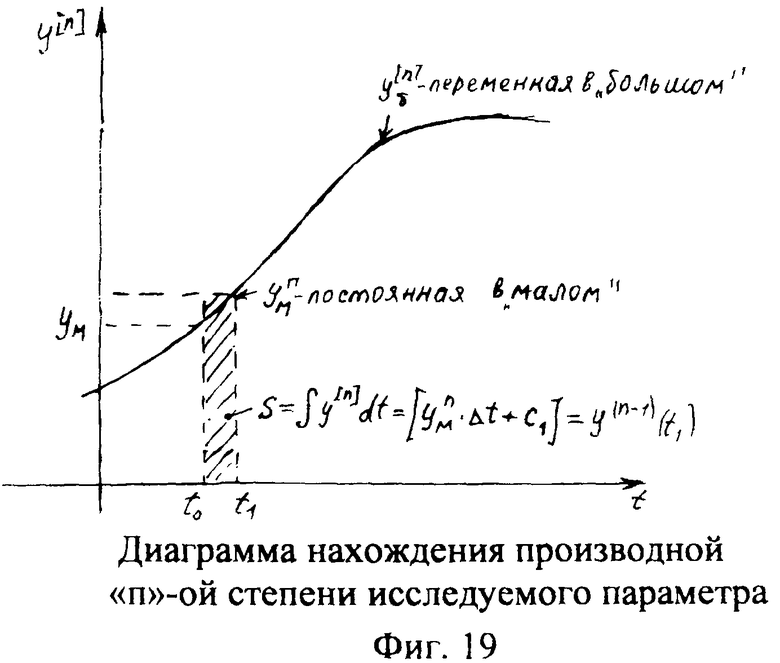
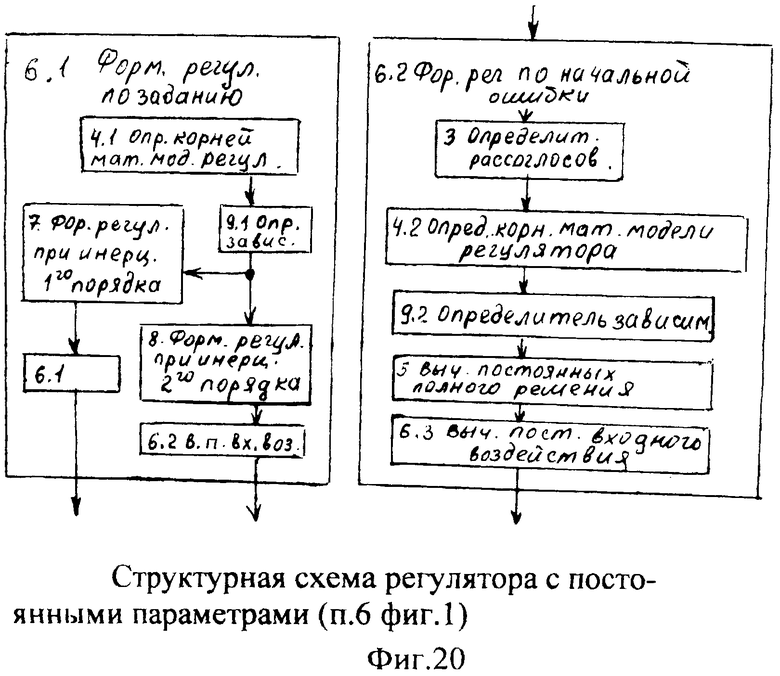
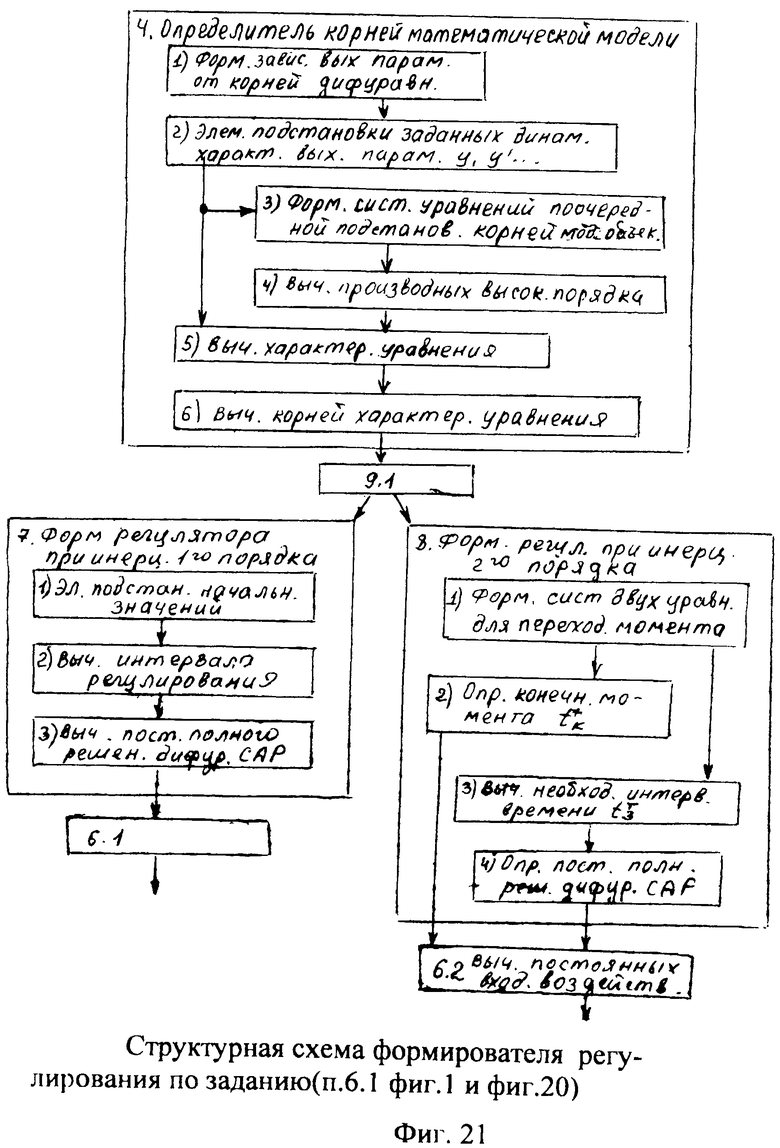
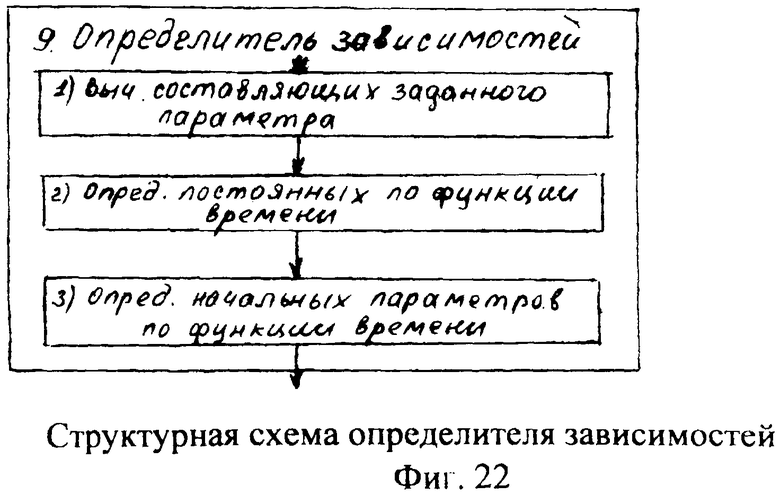

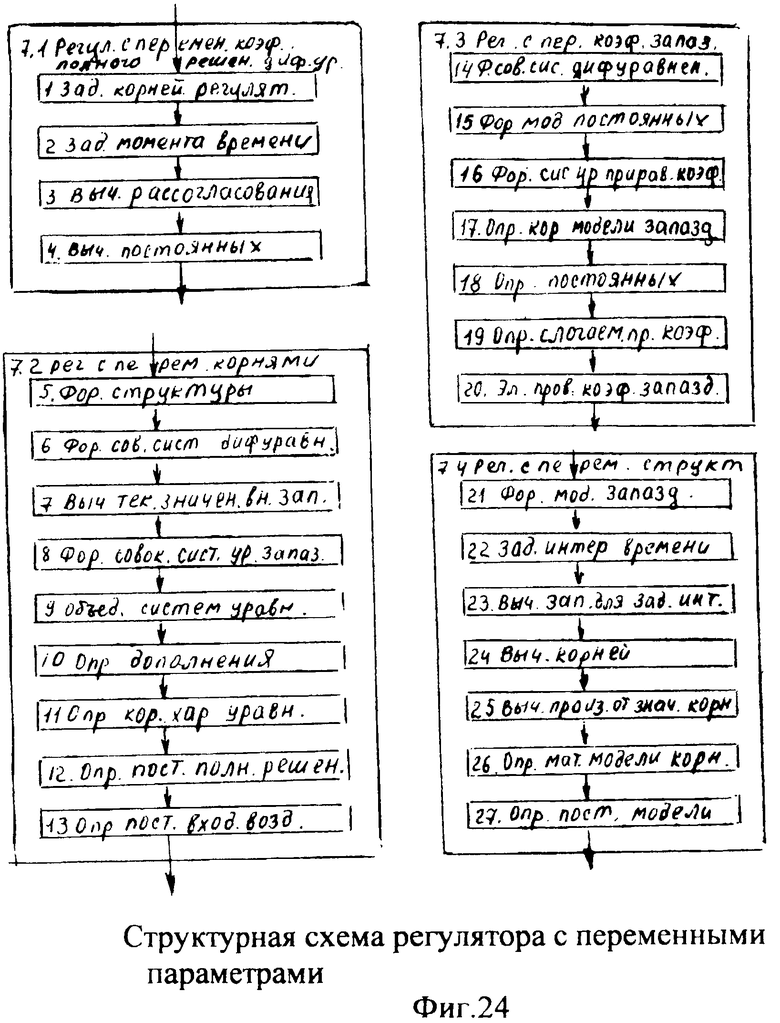
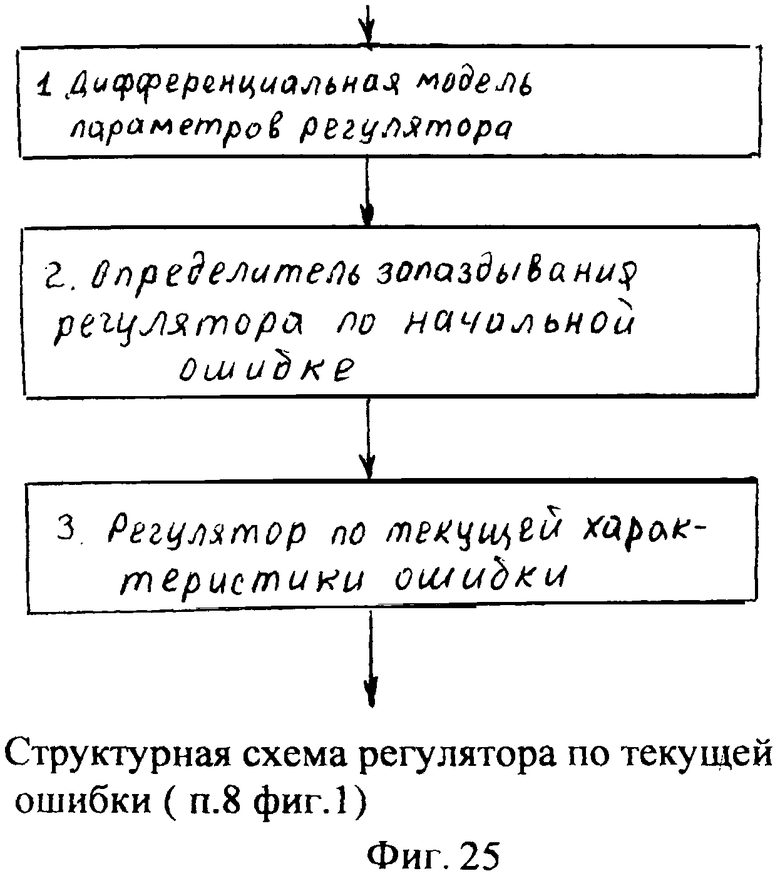
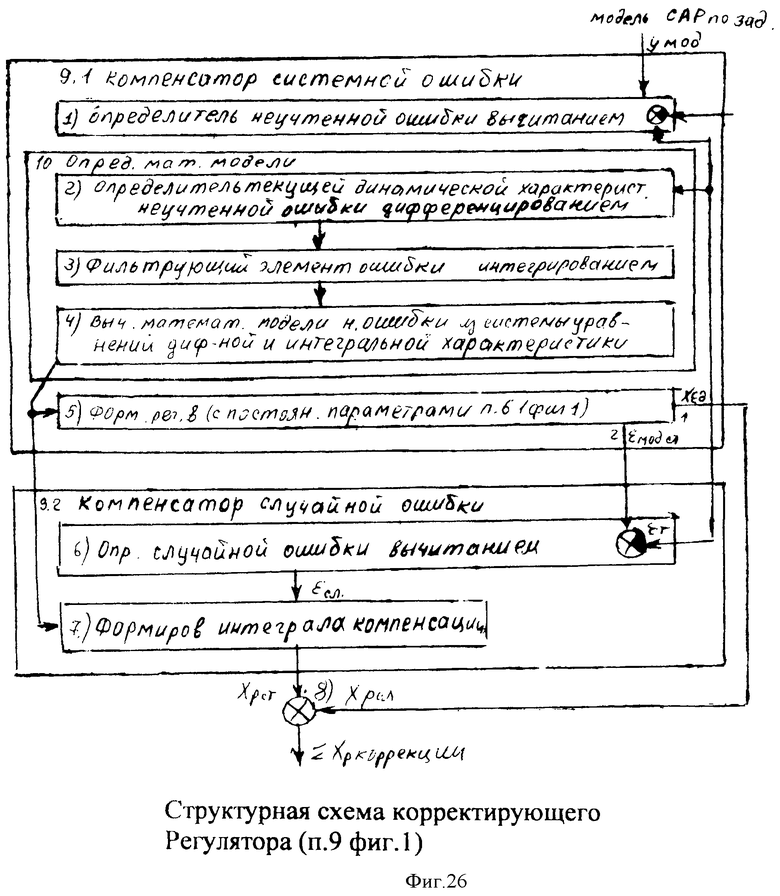
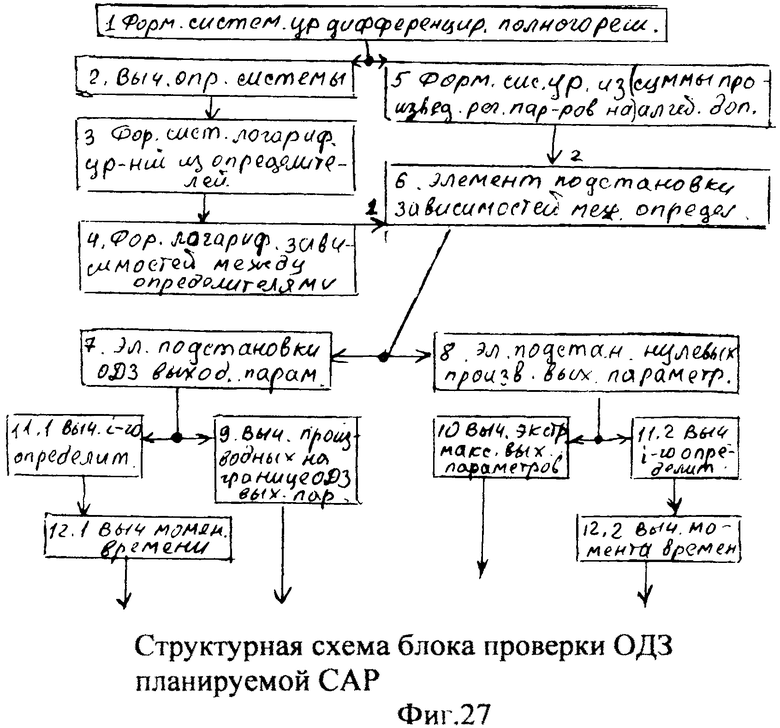
Изобретение относится к автоматическому управлению. Техническим результатом является повышение точности определения области допустимых значений для каждой из емкостных составляющих, образующих в сумме значение выходного параметра объекта за счет определения последовательности отдельных составляющих математической модели объекта и характер взаимодействия между составляющими объекта. Система автоматического регулирования содержит последовательно соединенные блок задания, блоки регулирования с постоянными, переменными параметрами и регулятор по текущей ошибке, блок проверки ОДЗ планируемой CAP, блок сравнения модели, формирователь регулирующего воздействия, объект, идентификатор и блок контроля ОДЗ действующей CAP и введены устройства, которые в совокупности позволяют идентифицировать характеристики внутренних состояний отдельных составляющих объекта, выражая эти состояния через математические модели их выходных параметров. 27 ил., 1 табл.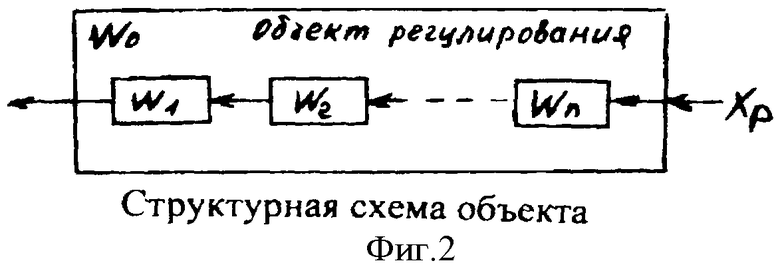
Система автоматического регулирования (САР) емкостными составляющими объекта, включающая блок задания, регулятор с постоянными параметрами, регулятор с переменными параметрами, регулятор по текущей ошибки и последовательно соединенные блок проверки ОДЗ планируемой CAP, блок сравнения моделей, формирователь регулирующего воздействия, объект, идентификатор и блок контроля ОДЗ действующей CAP, выход которого подсоединен ко второму входу формирователя регулирующего воздействия и к третьему входу блока задания, к первому и второму входам которого подсоединены входы заявленной CAP, выход идентификатора также подсоединен на входы каждого из входящих в заявленную систему блоков, выходы которых подсоединены на второй вход блока проверки ОДЗ планируемой CAP, на первый вход которого и входы всех остальных блоков подсоединены выходы блока задания; блок задания включает блок динамических характеристик выходного параметра, подсоединенный к входу и выходу блока задания, регулятор с постоянными параметрами включает регулятор по заданию, вход и выход которого подсоединены к соответствующим входам и выходам регулятора с постоянными параметрами, блок проверки ОДЗ планируемой CAP включает соединенные последовательно формирователь алгоритма и вычислитель, формирователь алгоритма включает в себя последовательно соединенные формирователь системы уравнений дифференцированием полного решения и первый вычислитель определителей системы; блок контроля ОДЗ действующей CAP включает в себя последовательно соединенные формирователь модели объекта и второй вычислитель; формирователь модели объекта включает подсоединенную к выходу схему сравнения; формирователь регулятора по заданию включает в себя подсоединенные к выходам два вычислителя постоянных входного воздействия,
идентификатор включает в себя определитель внешнего запаздывания и индикатор, выходы которых подсоединены на выход идентификатора,
отличающаяся тем, что в нее включены корректирующий регулятор, включающий последовательно соединенные компенсатор системной ошибки, компенсатор случайной ошибки и подсоединенный к их выходам сумматор, в блок задания введены блок внутренних отдельных составляющих, блок дополнительных вспомогательных составляющих, входы и выходы которых подсоединены к входам и выходам блока задания; в регулятор с постоянными параметрами введены регулятор по начальной ошибке, регулятор по заданному моменту времени, входы и выходы которых подсоединены к соответствующим входам и выходам регулятора с постоянными параметрами, а в регулятор по заданию введены последовательно соединенные определитель корней математической модели регулятора, определитель запаздывания и параллельно соединенные формирователь регулятора при инерционности первого порядка и формирователь регулятора при инерционности второго порядка, выходы которых подсоединены на входы вычислителей постоянных входного воздействия; в регулятор с переменными параметрами введены последовательно соединенные регулятор переменных коэффициентов, регулятор переменных корней, регулятор переменного запаздывания и регулятор переменной структуры, выходы и входы которых подсоединены к соответствующим входам и выходам регулятора с переменными параметрами; в регулятор по текущей ошибке введены последовательно соединенные дифмодель параметров регулятора, определитель запаздывания регулятора по начальной ошибке, регулятор по текущей характеристики ошибки; в формирователь алгоритма (входящий в блок проверки ОДЗ планируемой CAP) введены последовательно соединенные формирователь системы логарифмический уравнений из определителей, подсоединенный к выходу вычислителя определителя системы, формирователь логарифмический зависимостей между определителями и элемент подстановки зависимостей между определителями, выход которого подсоединен на вход первого вычислителя, а также введен формирователь системы уравнений из алгебраических дополнений вход которого подсоединен к выходу формирователя системы уравнений дифференцированием полного решения, а выход - на второй вход элемента подстановки зависимостей между определителями; в идентификатор введены быстродействующий вычислитель, фильтрующий вычислитель, подсоединенный к его выходу вычислитель модели с переменными корнями, определитель последовательности взаимодействия звеньев математической модели и подсоединенный к нему определитель ОДЗ выходных параметров каждого звена, все они входами подсоединены к входу идентификатора, а выходами - к выходу идентификатора и входу индикатора; определитель внешнего запаздывания подсоединен входом к второму выходу вычислителя модели с переменными корнями, а выходом к входу определителя последовательности взаимодействия звеньев математической модели, в определитель внешнего запаздывания введены подсоединенные ко входу быстродействующий канал и фильтрующий канал, выходы которого подсоединены к введенной схеме сравнения, выход которой подсоединен на выход определителя внешнего запаздывания; в формирователь модели объекта (входящий в блок контроля ОДЗ действующей CAP) введены подсоединенные ко входу первый канал реакции и второй канал емкостных составляющих, выходы которых подсоединены на входы схемы сравнения.
| ЕР 1780392 А2, 02.05.2007 | |||
| JP 2005202537 A, 28.07.2005 | |||
| АДАПТИВНЫЙ РЕЛЕЙНЫЙ РЕГУЛЯТОР | 2005 |
|
RU2284561C1 |
| RU 2005103338 A, 20.07.2006. | |||
Авторы
Даты
2012-02-10—Публикация
2009-04-03—Подача