Изобретение относится к автоматическому управлению и может использоваться для быстрой идентификации изменившихся параметров внутренней структуры объекта, для постоянного контроля текущего состояния объекта независимо от предыдущей идентификации, что повышает быстродействие формирования текущего регулирующего воздействия независимо от предыдущего. CAP позволяет мгновенно определить последовательность взаимодействия между внутренними составляющими, входящими в передаточную функцию математической модели объекта. Регулятор, входящий в CAP, позволяет формировать регулирующий сигнал, который не требует от регулирующих органов каких-то специальных функциональных возможностей, при этом допустимы возмущающие воздействия как на сам объект, так и на формирователь регулирующего органа. Таким образом, заявленная CAP может использоваться для регулирования внутренней емкостной энергией объекта со сложной, изменяющейся непредвиденно, переменной структурой и переменными параметрами объекта при использовании исполнительных органов, трудно поддающихся регулированию, в связи с возмущениями внутренними или внешними.
Известны системы автоматического регулирования \л.2 стр.40…\, включающие регуляторы по ошибке: П-. ПИ-регуляторы. Они позволяют своевременно реагировать на появления ошибки при регулировании выходного параметра. Недостаток этих систем регулирования в том, что они не позволяют обеспечить необходимое соотношение между внутренними параметрами отдельных составляющих объекта, на которые можно условно разделить объект (или необходимое соотношение между объектами, которые объединены в одну совокупность, входящую в CAP систему автоматического регулирования).
Известны системы автоматического регулирования \л.1, стр.9\, формирующие регулирующее воздействие программируемым устройством по сигналу задания, параметры алгоритма управления у которого зависят от совокупности текущего значения ошибки и известных внутренних параметрах объекта. Недостаток этой CAP в том, что при сложной внутренней структуре объекта и сильних возмущающих воздействиях может возникнуть большое перерегулирование, технологически недопустимое.
Известны многомерные системы регулирования \л.1 стр.189…191\, которые имеют две или несколько входных задающих величин и выходных регулируемых величин. При этом может иметься также любое число возмущающих воздействий. Как правило, регулируемые величины объединены единой внутренней взаимосвязью и системой управления, в которой организуется эта определенная требуемая взаимосвязь. Системы указанного типа часто встречаются в энергетических системах, у которых несколько управляемых составляющих образуют энергетический объект. Управление движением самолета также включает внутренние связи, физически существующие между выходными регулируемыми величинами в самом объекте и требующие организацию специальной программы /л.3 стр.11, 178/.
Недостаток этих систем состоит в том, что при внешних возмущениях к регулирующим органам предъявляются задачи повышенной сложности. Непредвиденность внутренних или внешних возмущений ограничивает возможности регуляторов и может привести к «аварийному режиму», износу оборудования. Таким образом известные уравнения динамики CAP не позволяют компенсировать возмущения связей, заложенных в математическом описании объекта регулирования.
Известны связные CAP \л.2, стр.141\, у которых один регулирующий орган оказывает влияние на несколько регулируемых величин. Регулирующее воздействие формируется из условия автономности расчета каналов регулирования, т.е. соблюдаются следующие условия:
- количество входов равно количеству выходов,
- число прямых каналов равно числу каналов обратной связи.
Для сведения к нулю перекрестного влияния между двумя каналами используют систему уравнений ф.1 и фиг.1. Недостаток этих CAP состоит в том, что при технической реализации абсолютной инвариантности влияние между двумя каналами сложно реализуется особенно при увеличении числа каналов более двух ф.1:


где X1, X2 - регулируемые параметры


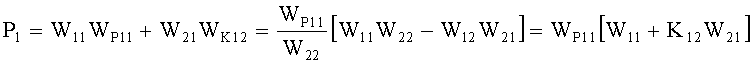

S1=W12WP11+W22WK12=0
S2=W21WP22+W11WK21=0
WBC=[W11W22-W12W21] - предаточная функция взаимосвязи
Известны CAP, включающие трехуровневые контуры регулирования \Л.2, стр.150\:
1-й уровень осуществляет управление исполнительными органами, обеспечивая экстремальную статическую характеристику при ее дрейфе;
2-й уровень осуществляет контроль качества и расчет новых значений динамических настроек, т.е. адаптацию режимов статического (установившегося) и динамического самонастраиванием за счет оптимизации параметров и структуры;
3-й уровень осуществляет две функции:
- коррекцию значений критерия управлений или видоизменения целевых функций;
- самообучающиеся функции накоплением и запоминанием информации своей динамической характеристики и характеристики внешних динамических воздействий.
Третий уровень включат формирователи трех показателей качества: быстродействие, точности либо сведение к нулю перекрестного влияния в комбинированных САР.
Недостаток этих CAP в том, что
- под влиянием внутреннего емкостного состояния объекта очень часто происходит дрейф статической характеристики, которая трудно корректируется;
- при оптимизации параметров и структуры регулятора необходимы повышенные требования идентификации текущего состояния внутренних параметров объекта, которые могут меняться в процессе регулирования;
- при формировании качества:
1) быстродействия возникают режимы, при которых происходит перерегулирование внутренних емкостных параметров объекта;
2) точности показатели колебательности или интегральные от ошибки очень часто бывают недостаточными для надежной работы оборудования;
3) инвариантности в комбинированных CAP используемый математический аппарат, в который входят векторные или относительные скалярные, отражают состояние объекта без учета адаптивного состояния регулирующего водействия, т.к. при его изменении, «адаптации», не позволяют достаточно гибко их менять.
Известны связные CAP \л.2, стр.141\, у которых один регулирующий орган оказывает влияние на несколько регулируемых величин. Регулирующее воздействие формируется из условия автономности расчета каналов регулирования, т.е. соблюдаются следующие условия:
- количество входов равно количеству выходов,
- число прямых каналов равно числу каналов обратной связи
Для сведения к нулю перекрестного влияния между двумя каналами используют систему уравнений ф.1 и фиг.1. Недостаток этих CAP в том, что при техническая реализация абсолютной инвариантности влияния между двумя каналами сложно реализуется особенно при увеличении числа каналов более двух.
Известны многомерные системы регулирования \л.1 стр.189…191\, которые имеют две или несколько входных задающих величин и выходных регулируемых величин. При этом может иметься также любое число возмущающих воздействий. Как правило, регулируемые величины объединены единой внутренней взаимосвязью и системой управления, в которой организуется эта определенная требуемая взаимосвязь. Системы указанного типа часто встречаются в энергетических системах, у которых несколько управляемых составляющих образуют энергетический объект. Управление движением самолета также включает внутренние связи, физически существующие между выходными регулируемыми величинами в самом объекте и требующие организации специальной программы /стр.11, 178, л.3/.
Недостаток этих систем в том, что при внешних возмущениях к регулирующим органам предъявляются задачи повышенной сложности. Непредвиденность внутренних или внешних возмущений ограничивает возможности регуляторов и может привести к «аварийному режиму», износу оборудования. Таким образом известные уравнения динамики CAP не позволяют компенсировать возмущения связей, заложенных в математическом описании объекта регулирования.
Если для математического описания многомерных CAP \Л.3, стр.178\ используется матричная переходная характеристика, при которой каждый элемент представляет временную характеристику процесса по i-му параметру, то в известных CAP для формирования качества переходят к теории автономного регулирования, и матричную переходную характеристику приводят к одномерной, и используют интегральную квадратичную оценку ф.2
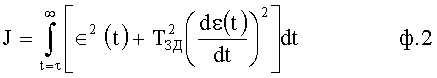
Условие минимума: t≥τ
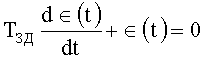
∈(t)=∈(0);
т.е. 

где τ - время запаздывания;
∈ - ошибка;
ТЗД - заданное значение постоянной времени (экстремальное);
НЗД - передаточная функция по заданному воздействию системы.
Используемая при этом интегральная оценка не позволяет оценить качество всех регулируемых параметров во взаимосвязи и выбрать такой режим регулирования, чтобы гарантировал качество всех регулируемых параметров даже в тех случаях, когда какой-либо из параметров имеет малый запас устойчивости или большую инерционность по сравнению с другими параметрами.
Известен П-регулятор \Л.2, стр.40\, перемещающий регулирующий орган пропорционально отклонению регулируемой величины от заданного значения ф.2.1

где Кp - коэффициент усиления регулятора,
e - ошибка регулирования.
Недостаток этого регулятора в том, что если объект имеет сложную инерционность, то добиться желаемой формы переходного процесса (достаточно быстрой и без значительных перерегулирований, приводящих к аварийным режимам) невозможно.
Задача заявленной CAP - обеспечение заданной совокупности внутренних регулируемых параметров объекта. Для решения поставленной задачи возникает необходимость управлять взаимодействием емкостных составляющих внутреннего состояния объекта. Если объект имеет малую устойчивость (или неустойчив), то для решения поставленной задачи возникает необходимость создать такую математическую модель объекта (или CAP), которая обеспечит область допустимых значений (ОДЗ) каждой из составляющих объекта.
Сущность заявленного изобретения заключается в том, что в систему автоматического регулирования, включающую последовательно соединенные вычислитель текущих значений входного воздействия, регулирующий орган, объект регулирования, пропорциональное звено, дополнительно введены последовательно соединенные и подсоединенные к выходу объекта идентификатор емкостного состояния объекта, определитель необходимой емкостной энергии, формирователь инерционных настроек, формирователь емкостной силы (компенсирующий возмущения регулирующего органа), входы введенных устройств также подсоединены к входу САР (через который оператор осуществляет контроль за состоянием CAP),
при этом формирователь инерционных настроек включает последовательно соединенные формирователь динамической структуры, блок проверки ОДЗ и блок поэтапного регулирования,
при этом формирователь динамической структуры включает последовательно соединенные формирователь корней вынужденного состояния, формирователь коэф. свободного состояния, вычислитель корней регулирующего воздействия, вычислитель коэффициентов свободного и вынужденного состояний;
- блок поэтапного регулирования включает в себя последовательно соединенные задатчик технической реализации, формирователь зависимостей математической модели, формирователь системы уравнений зависимостей регулируемого параметра от длительности интервала, формирователь регулирующего воздействия по длительности интервала, определитель математической модели необходимой входной энергии, на второй вход которого подсоединен выход введенного формирователя длительности интервала по регулирующему воздействию, вход которого подсоединен к выходу формирователя системы уравнений зависимостей математической модели;
- формирователь емкостной силы включает последовательно соединенные формирователь системы уравнений емкостных сил, формирователь системы двух уравнений для каждой входной силы, формирователь объединенных уравнений исключением промежуточных входных сил, объединитель уравнений для всех емкостных сил относительно входного воздействия, элемент подстановки математической модели, формирователь зависимостей коэффициентов математической модели выходных сил от коэффициентов входного воздействия, элемент подстановки полученных зависимостей в математическую модель, формирователь системы уравнений относительно коэффициента входного воздействия, вычислитель коэффициентов входного воздействия делением определителей;
при этом вычислитель корней регулирующего воздействия включает в себя последовательно соединенные формирователь модели коэффициентов запаздывания по корням, делитель, формирователь системы уравнений по частным составляющим объекта, задатчик коэффициентов запаздывания регулятора по определителям, формирователь системы подстановкой текущих характеристик, определитель неизвестных системы, элемент подстановки условных коэффициентов, на второй вход которого подсоединен выход формирователя модели коэффициентов запаздывания по корням;
при этом вычислитель коэффициентов свободного и вынужденного состояний включает в себя последовательно соединенные формирователь дифуравнения по коэффициентам запаздывания объекта, формирователь системы уравнений из внутренних составляющих объекта, формирователь определителей системы, формирователь коэффициентов запаздывания объекта через определители, элемент замены коэффициентов запаздывания, формирователь системы уравнений для начальных и заданных значений, элемент приравнивания коэффициентов при одинаковых степенях, вычислитель коэффициентов входной составляющей дифуравнения, вычислитель вынужденного состояния регулируемого параметра, вычислитель коэффициентов свободного состояния регулируемого параметра;
при этом формирователи интервалов, входящие в формирователь регулирующего воздействия по длительности интервала, включают последовательно соединенные задатчик длительности интервала, определитель коэффициентов регулирующего воздействия, звено проверки технической реализации, определитель коэффициентов свободного и вынужденного состояний объекта, звено проверки технической реализации, отрицательный выход которого подсоединен на вход второго корректора длительности интервала, положительный выход которого подсоединен на второй вход определителя дополнительного интервала, первый вход определителя дополнительного интервала подсоединен на выход задатчика длительности, а третий вход подсоединен на положительный выход первого корректора длительности интервала, выход определителя дополнительного интервала подсоединен на второй вход определителя коэффициентов регулирующего воздействия, отрицательный выход звена проверки технической реализации подсоединен на вход первого корректора длительности интервала, отрицательные выходы первого и второго корректоров длительности интервалов подсоединены к второму и третьему выходам формирователя интервала;
- идентификатор емкостного состояния объекта включает последовательно соединенные быстродействующий косвенный определитель емкостной энергии, прямой определитель емкостной энергии на текущем интервале, блок контроля полного переходного периода, блок выходной емкостной энергии, каждые из выходов введенных устройств также подсоединены к входам введенного определителя утечки емкостной энергии;
при этом быстродействующий косвенный определитель емкостной энергии включает последовательно соединенные определитель математической модели для текущего момента времени, определитель текущих выходных параметров для каждой емкостной составляющей, определитель емкостной энергии каждой емкостной составляющей, определитель емкостной энергии объекта в целом;
при этом определитель математической модели для текущего момента времени включает последовательно соединенные определитель корней дифмодели, определитель коэффициентов полного решения дифуравнения по нулевому моменту времени, определитель последовательности звеньев, определитель выходных параметров каждого звена, идентификатор текущего момент времени;
- определитель последовательности звеньев включает в себя последовательно соединенные блоки поиска, каждый из которых включает формирователь выходных параметров и внутреннего запаздывания для исследуемого звена, соответствующие выходы которого подсоединены на входы элемента подстановки текущих выходных параметров в дифуравнения звена и определителя частных коэффициентов, выходы которых подсоединены к соответствующим входам вычислителя входного воздействия звена и вычислителя частного входного воздействия (сумматора), выходы вычислителя входного воздействия и вычислителя частного входного воздействия подсоединены на соответствующие входы схемы сравнения, отрицательный выход которого подсоединен на дополнительный вход формирователя входных параметров и внутреннего запаздывания исследуемого звена, основной вход которого подсоединен к входу блока поиска, положительный выход схемы сравнения подсоединен на выход блока поиска, идущий на вход следующего блока поиска;
при этом идентификатор текущего момента времени включает в себя последовательно соединенные задатчик начальных параметров, вычислитель слагаемых полного решения дифуравнения для начальных параметров, вычислитель слагаемых полного решения для текущих параметров, делитель, определитель логарифма, делитель на корень дифмодели, сумматор, при этом на второй вход вычислитель слагаемых полного решения для текущих параметров подсоединен один из входов идентификатора текущего времени, а на второй вход делителя подсоединен выход вычислителя слагаемых полного решения дифуравнения для начальных параметров;
при этом прямой определитель емкостной энергии на текущем интервале включает последовательно соединенные определитель для отдельных звеньев и определитель для объекта в целом;
блок контроля полного переходного периода включает последовательно соединенные определитель структуры запаздывания, определитель запаздывания каждой составляющей, определитель емкостной энергии по усредненным косвенным параметрам;
при этом определитель структуры запаздывания, входящий в блок контроля полного переходного периода, включает соединенные параллельно
идентификатор плавного процесса и идентификатор процесса с экстремальными точками;
- идентификатор плавного процесса включает последовательно соединенные определитель параметра через заданный интервал времени, преобразователь основания степени, формирователь степенной степени, формирователь системы из уравнений полного решения дифуравнения, формирователь условных дифуравнений, объединитель в систему условных дифуравнений, определитель коэффициентов внутреннего запаздывания условных дифуравнений, определитель основания степени, определитель корней дифуравнения, определитель постоянных коэффициентов полного решения дифуравнения;
идентификатор процесса с экстремальными точками включает последовательно соединенные определитель экстремальных параметров в производных функциях, определитель отдельных производных для вершин переходного процесса, формирователь дифуравнения для вершин переходного процесса, объединитель дифуравнений в систему, вычислитель коэффициентов внутреннего запаздывания, вычислитель корней дифуравнения,
вычислитель коэффициентов полного решения дифуравнения.
Входящие в заявленную CAP устройства позволяют осуществить поставленную задачу, разбивая ее на четыре уровня:
1-й уровень статических характеристик,
2-й уровень динамических характеристик,
3-й уровень качества и самоконтроля,
4-й уровень исполнительный.
1-й уровень статических характеристик позволяет определить необходимую емкостную энергию для каждого звена математической модели объекта, позволяющую обеспечить заданное состояние по ф.2.2…2.13.
Объединенные в формирователь инерционных настроек 2-й и 3-й уровни фиг.3, фиг.4 позволяют учесть свойства, которыми обладают инерционные объекты ф.2.2.
Параметрами безынерционных составляющих объекта могут быть следующие звенья ф.2.2:

Для описания взаимодействия между инерционными составляющими объекта, включающими коэффициенты запаздывания T1…ф.2.3, возникает необходимость использовать законы динамики, ее инерционную систему отсчета, в которой изменение скорости регулируемого параметра у может быть обусловлено только его взаимодействием с другими объектами (их выходными параметрами). Количественной мерой этого взаимодействия является сила (разной физической природы), т.е. входное воздействие «x» создает определенную силу, влияющую на выходное «у». «Чисто» инерционные звенья: ф.2.3

Инерционные с интегрированием
- интегрирующее с замедлением
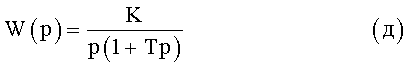
- изодромное

Инерционные при дифференцировании
- дифференциальное с замедлением

При этом остаются справедливы законы Ньютона. Закон сохранения энергии ф.2.4: полная энергия (сумма кинетической, потенциальной…) замкнутой системы объектов, взаимодействующих “силами"(входными и выходными параметрами), остается неизменной

где Епот - потенциальная энергия:
Екин - кинетическая энергия;
Едр - другой вид энергии: тепловая… и т.д. (в некоторых случаях ею можно пренебречь).
При справедливости закона "сохранения энергии", в результате взаимодействия объектов происходит преобразование потенциальной энергии Епо в кинетическую Еки (и наоборот): Епо→Еки и наоборот: Епо→Еки (Еки→Епо).
Для безынерционного звена "закон сохранения энергии" примет вид ф.2.5
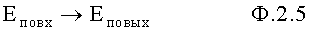
при этом потенциальная энергия на входе преобразуется в потенциальную энергию на выходе.
Для инерционного звена первого порядка ф.2.6: потенциальная энергия преобразуется в кинетическую, после чего полученная кинетическая энергия преобразуется в потенциальную на выходе объекта
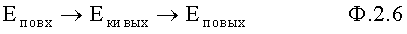
Таким образом, закон «сохранения энергии» в теории автоматического регулирования ТАР при регулировании сложными объектами включает много составляющих и примет вид ф.2.7

Для того чтобы выделить энергию внутренних составляющих Е1… от энергии на выходе объекта удобней ее обозначить как «внутреннюю емкостную», тогда закон сохранения энергии примет вид ф.2.8

Если в выбранной системе отсчета начальное значение входной энергии (энергии входного воздействия), внутренней (емкостной) энергии и выходной (энергии выходного параметра) принять за нулевое, то ф.2.9 объединяет понятие работа А, энергия Е и сила F

При этом входная сила F равна входному параметру Хр, от которого зависит изменение выходного параметра «у» (выходной силы F).
Если звено имеет инерционность 1-го порядка, то потенциальная и кинетическая энергии вычисляются по ф.2.10
Tу'+у=x
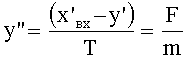
где Т - коэффициент внутреннего запаздывания пропорционален массе m, следовательно, равен ее приведенному значению;
(xвх'-у') - разница входного и выходного параметров пропорциональна силе, следовательно, равна ее приведенному (к соответствующей единице измерения) значению 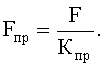
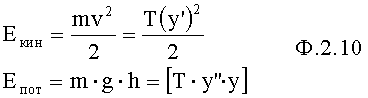
Если объект имеет инерционность второго и более высоких порядков, то закон сохранения энергии имеет более сложную формулу, т.к. кроме изменения энергии выходного параметра «у» необходимо учесть изменения энергии внутренних составляющих объекта (емкостной энергии), что сопряжено со значительными трудностями, поэтому для определения емкостной энергии удобно перейти от ф.2.11 к ф.2.12
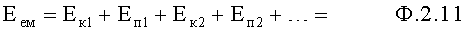
где Eк1…, Eп1… - энергия емкостных составляющих W1… Фиг.1.1
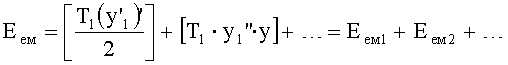
Таким образом, после произведения поэтапных расчетов по ф.2.11 удобно использовать для их проверки ф.2.12

где 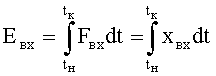

Формулу 2.12 удобно использовать для расчета емкостной энергии при неизвестной структуре объекта, т.к. в нее входят только входной и выходной параметры, но при этом энергией внутренних потерь приходится пренебрегать.
Для того чтобы создать математическую модель CAP, обеспечивающую ОДЗ каждой из составляющих, необходимо обеспечить поддержание емкостной энергии каждой из входящих в объект емкостных составляющих. Энергия, передаваемая на вход, преобразуется в емкостную и в энергию, передаваемую на выход (при условии, что энергией потерь можно пренебречь).
Для регулирования емкостными составляющими каждого устройства, входящего в CAP, используется Первый уровень «статических характеристик», определяющих необходимые емкостные энергии для каждой составляющей, входящей в объект по ф.2.13

Из дифуравнения инерционного звена получают ф.2.13.0
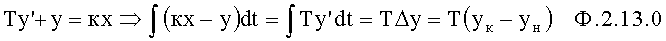
Тогда для заданных у1, у2, … вычисляется необходимая емкостная энергия ф.2.13.1

Второй уровень «динамических характеристик» формирует структуру модели регулирующего и регулируемого параметра, обеспечивающую заданные параметры при заданной устойчивости по ф.3…27.
Третий уровень «качества и самоконтроля» использует модель, полученную с выхода второго уровня, проверяя область допустимых значений ОДЗ, и при необходимости вносит коррекцию в коэффициенты свободного и вынужденного состояний регулируемого параметра и соответствующего регулирующего воздействия. Ф.28. Фиг.5, фиг.6.
Введенный идентификатор емкостного состояния объекта п.7 фиг.2 позволяет получить наиболее полную информацию о внутренних переходных процессах объекта, что открывает возможность управлять ими и улучшить качество технологических процессов.
Идентификатор емкостного состояния объекта п.7 фиг.2 включает (фиг.7.0) быстродействующий косвенный определитель емкостной энергии п.1 (фиг.7.0) и фиг.7.4 (фиг.7.1…3), определяющий емкостную энергию объекта по косвенным показателям (коэффициентам запаздывания Т1…), значение которых определяется для каждого момента ti времени независимо от других моментов времени ti+1…, ti-1… (т.е. значения постоянных T1… справедливы для исследуемого момента времени) по ф.2.13.1А
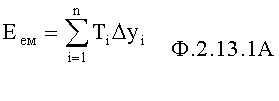
где Т1…n=f(у, у', у"…)
Прямой определитель емкостной энергии на текущем интервале п.2 определяет емкостную энергию объекта по разнице между интервалом входной 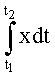 и выходной энергии
и выходной энергии  . При этом точность идентификации увеличивается по сравнению с быстродействующим косвенным определителем емкостной энергии п.1, но требуется определенный интервал времени Δt=t2-t1 для интегрирования исследуемых величин Х и У, ф.2.15. При этом возникает необходимость учитывать (т.е. идентифицировать) энергию потерь, если ею пренебречь нельзя. Например, внутренняя энергия, которая преобразуется в тепловую, не влияющую на исследуемый параметр, можно отнести к энергии потерь, ф.2.13.1Б
. При этом точность идентификации увеличивается по сравнению с быстродействующим косвенным определителем емкостной энергии п.1, но требуется определенный интервал времени Δt=t2-t1 для интегрирования исследуемых величин Х и У, ф.2.15. При этом возникает необходимость учитывать (т.е. идентифицировать) энергию потерь, если ею пренебречь нельзя. Например, внутренняя энергия, которая преобразуется в тепловую, не влияющую на исследуемый параметр, можно отнести к энергии потерь, ф.2.13.1Б
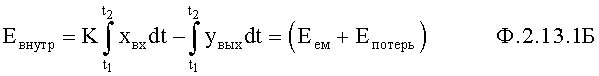
Блок контроля полного переходного периода п.3 фиг.7.0 (фиг.7.6) позволяет определить емкостную энергию объекта по косвенным показателям Тк1…, полученным по конечным параметрам переходного процесса, каждой из составляющих регулируемых параметров объекта у1, у2…
Если математическая модель имеет только действительные корни и переходной исследуемый параметр плавно изменяется, то идентификатор I, входящий в блок контроля полного переходного периода (фиг.7.8), разбивает весь исследуемый участок на равные интервалы времени ф., который принимается за «новую единицу времени». Введенная единица времени позволяет перейти к «частному объединенному уравнению», которое по структуре напоминает дифуравнение, но у которого вместо у1, у2, … подставляются значения исследуемого параметра, зафиксированные через интервалы времени, равные начальному интервалу времени ф.
Если переходной период имеет вершины (максимумы и минимумы), что свидетельствует о комплексных корнях, то идентификатор II (входящий в блок контроля полного переходного периода фиг.7.8) для каждой вершины составляет дифуравнение, значение производных у которых найдены для моментов времени этих вершин.
При этом используется разница между соседними вершинами и интервал времени ф. между этими вершинами. Достоинства блока полного переходного периода в том, что коэффициенты полного запаздывания T1… определяются по форме полной переходной характеристики ф.2.13.1В

где  - определяются из формул ф.2.13.1В, т.е. по форме полной переходной характеристики.
- определяются из формул ф.2.13.1В, т.е. по форме полной переходной характеристики.
Формулы ф.2.13.1В позволяют не учитывать те возмущения, которые не влияют на общую картину переходного периода, т.е. являются экспресс-фильтрами.
Блок выходной емкостной энергии п.4 фиг.7.0 (фиг.7.7, фиг.8) позволяет приблизиться к более точному значению «активной» емкостной энергии, которой обладает объект ф.2.17. При этом объект подвергается дополнительному режиму - «испытательному», у которого входное воздействие определяется по ф.2.13.1Г (не всегда допустимы «рабочий» и «испытательный» режимы, т.к. это может привести к нарушению технологического режима). Полученные при этом результаты справедливы относительно выходного параметра объекта, но при этом не всегда точно отражают все особенности изменений внутренних параметров объекта в процессе регулирования.

к - коэффициент усиления объекта,
x(ti)=0, x'(ti)=0…, т.е. для конечного момента времени условно принято за нулевое значение,
x(ti-1)≷0,
у(ti-1)≷0,
у(ti)=0; у'(ti)=0… и т.д.
Таким образом, быстродействующий косвенный определитель емкостной энергии п.1 (оперативный идентификатор фиг.7.0, фиг.7.1) позволяет идентифицировать коэффициенты запаздывания T1… в каждый текущий момент времени для каждой емкостной составляющей объекта и соответствующие выходные параметры у1… этих составляющих.
Прямой определитель емкостной энергии (блок текущего интервала п.2 фиг.7.0, фиг.7.5) исследует состояние объекта, используя информацию, справедливую для интервала.
Блок контроля полного переходного периода п.3 фиг.7.0, фиг.7.6 рассматривает совокупность характеристик, снятых на протяжении всего интервала переходной характеристики.
Блок выходной емкостной энергии п.4 фиг.7.0, фиг.7.7 создает для объекта дополнительный «пассивный» режим с «нулевым» входным воздействием (х=0), чтобы практически измерить емкостную «активную» энергию объекта, создающую в течение какого-то времени на выходе объекта силу у=0, отличную от нуля при нулевой входной силе.
Совокупность блоков, введенных в идентификатор емкостной энергии, позволяет определить емкостную энергию, используя для этого две приведенные ниже характеристики фиг.7.0:
- коэффициенты внутреннего запаздывания T1… каждой из составляющих объекта:
п.1 - в текущие моменты времени (a),
п.3 - в период полного переходного процесса (в);
- по разнице энергии входа и выхода x-у=…:
п.2 - при «активном» входном воздействии х≠0 (с),
п.4 - при «пассивном» входном воздействии х=0 (д).
Совокупность полученных параметров дает необходимую характеристику, позволяющую следить за состоянием объекта с изменяющимися параметрами (коэффициентом запаздывания Т1… и коэффициентом усиления), характерными для технологических и теплотехнических процессов. При этом возникают нижеприведенные ситуации:
1) если параметр (с) отличен от (д), то в объекте присутствуют неучтенные потери энергии:
- переходящие в тепловую энергию,
- затраченные на преодоление неучтенных сил,
- и т.д.;
2) наблюдение за параметром (а), который определяется в каждый момент времени, независимо от других моментов времени позволяет мгновенно зафиксировать изменение состояния объекта, что позволит своевременно принять определенные меры для исключения нежелательных режимов и их последствий;
3) текущий контроль за параметром (в) позволяет проанализировать значение текущей емкостной энергии независимо от текущих помех (часто влияющих на значение текущих коэффициентов запаздывания T1…, которые в свою очередь влияют на возмущение параметр (а);
4) сравнение параметров (а) и (в) с параметром (с) позволяет в текущем моменте определить неучтенные потери в «активном» режиме;
5) анализ параметров (д) позволяет исследовать «активную» емкостную энергию в «пассивном» режиме и сравнить их с «пассивной» (или «нейтральный») емкостной энергией (в «активном» режиме), т.е. с параметрами (а), (в), (с); задачи, стоящие перед определителем утечки емкостной энергии, зависят от тех задач, которые стоят перед рассматриваемой CAP;
6) сравнение параметра (а) с параметром (в) позволяет определить утечку емкостной энергии в текущем «оперативном» режиме в том случае, если изменением T1… можно пренебречь.
Формулы 2.2…17 позволяют дать общую характеристику особенностей функций каждого из вводимых в CAP блоков.
По найденным необходимым значениям ΔЕемW1, ΔЕемW2… емкостной энергии, на которые должна измениться энергия каждой из емкостных составляющих объекта, определяется емкостная полная энергия Еем. пол=Еем. нач+ΔЕем. изм.
Таким образом, введенный 1-й уровень «статических характеристик» определяет для каждых заданных У1, У2, … фиг.1.1 необходимое количество полной емкостной энергии по ф.2.13.2:

где Еем. нач - емкостная начальная энергия;
Евх=∫xвх(t)dt - входная энергия;
Евых=∫увых(t)dt - выходная энергия;
ΔЕем=∫(xвх-Увых)dt - изменение емкостной энергии.
Поступающая на соответствующие входы (входы Хвх1=Хвхо, Хвх2=Увых1, Увх3=Увых2…) энергия Евх1… определяется поэтапно по ф.2.13.3

При этом функции, формирующие входные воздействия определяются на 1…4 уровне,
где Xвх о (t)=f0(t)
Увых1(t)=f1(t)
… и т.д.
f0(t), f1(t)… зависят от параметров регулирующего органа и объекта регулирования и определяются i-м уровнем регулирования характеристик.
Введенный (в 1-й уровень статических характеристик) формирователь регулятора по статическим характеристикам емкостной энергии (необходимой емкостной энергии с выхода определителя необходимой емкостной энергии) фиг.11 формирует систему уравнений для емкостных составляющих п.1 ф.2.13.2(а б).

Для того чтобы уменьшить количество неизвестных в системе уравнений ф.2.13.2 и учесть начальные значения регулируемых параметров определитель п.2 по ф.2.13.3, определяют зависимость коэффициентов свободных составляющих математической модели выходного параметра объекта от суммы коэффициентов вынужденных составляющих модели выходного параметра
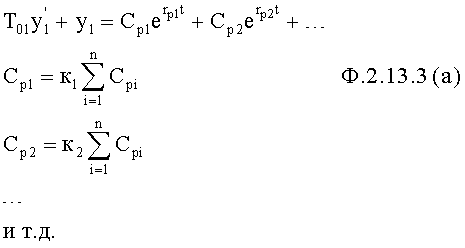
где 
где К1, К2,… задаются из условия технической реализации исполнительного органа и из условия обеспечения совокупности заданных емкостных параметров любой сложности для того, чтобы регулирующее воздействие было достаточно мобильным, используемые коэффициенты К1… должны иметь противоположные знаки.

где Cp1 находят из 2.13.3(а)

После приравнивания коэффициентов при одинаковых степенях получается ф.2.3.3(в)
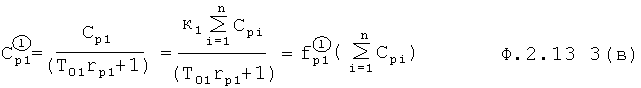
Аналогично находятся 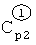 …
…
После подстановки 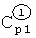 из ф.2.13.3(в) и начальных У1 (t=0)=У1нач в ф.2.13.3(б) вычисляют
из ф.2.13.3(в) и начальных У1 (t=0)=У1нач в ф.2.13.3(б) вычисляют  по ф.2.13.3(г)
по ф.2.13.3(г)

Аналогично находятся все последующие коэффициенты:
 ;
;  ; и т.д.
; и т.д.
В ф.2.13.3(г) подставляют ф.2.13.3(в) и ф.2.13.3(а) и получают ф.2.13.3(д) при t=0

После подстановки зависимостей ф.2.13.3 в систему уравнений ф.2.13.2 определяются интегральные составляющие свободных и вынужденных составляющих полного решения дифуравнения по ф.2.13.4
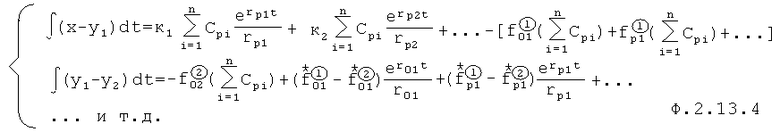
где 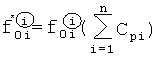


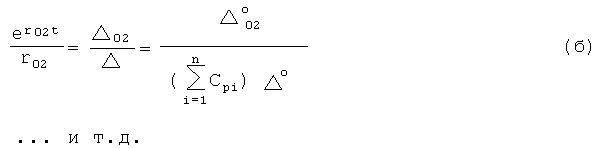

Для нахождения суммы коэффициентов входного воздействия 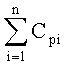 используют ф.2.13.4(а) и (б), получая при этом ф.2.13.5 п.4
используют ф.2.13.4(а) и (б), получая при этом ф.2.13.5 п.4
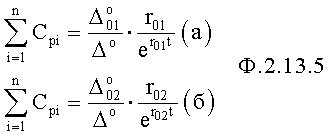
Приравниванием ф.2.13.5(а) и (б) исключают суммарное значение коэффициентов входного воздействия 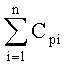 и вычисляют необходимый интервал регулирования Δt по ф.2.13.6
и вычисляют необходимый интервал регулирования Δt по ф.2.13.6
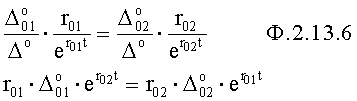

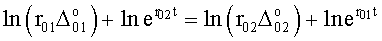

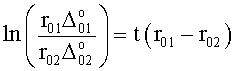
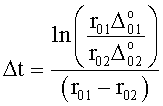
По найденным выше параметрам необходимому интервалу времени т.д., вычисляется сумма коэффициентов входного воздействия п.5 ф.2.13.7
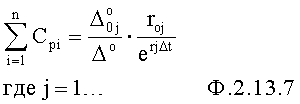
Полученные математические выражения вынужденного состояния ф.2.13.4(в) используются в вычислителе корней вынужденного состояния ф.2.13.8(а) п.6 (фиг.11), в которые подставляются найденные ранее сумма коэффициентов входного воздействия  ф.2.13.7 и интервал времени Δt, необходимый для регулирования ф.2.13.6
ф.2.13.7 и интервал времени Δt, необходимый для регулирования ф.2.13.6


Для вычисления корней вынужденного состояния используется математическая модель двух функций, полученных из интегральной функции слагаемых вынужденного состояния по ф.2.13.8(б) фиг.12.


где 
Входящий в вычислитель корней вынужденного состояния (п.6 фиг.11) вычислитель слагаемых п.2 (фиг.12) определяет коэффициенты Ai по ф.2.13.8(в), которые определяют наклон функции  фиг.13. Схема сравнения п.8 фиг.12 формирует на своем выходе синхросигнал ±1 по алгоритму ф.2.13.9
фиг.13. Схема сравнения п.8 фиг.12 формирует на своем выходе синхросигнал ±1 по алгоритму ф.2.13.9

Формирователь приближения п.1 фиг.12 при поступлении синхросигнала на первый вход начинает поиск значения действительного корня. Начальное значение поиска равно значению синхросигнала ±1 со второго входа ф.2.13.10
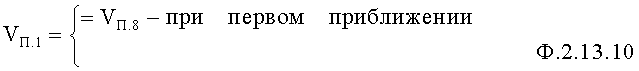
Сигнал с выхода умножителя п.3 равен ф.2.13.11

Сигнал с выхода вычислителя п.4 равен ф.2.13.12

Вычитатель п.5 определяет ошибку поиска текущего приближения по ф.2.13.13

Умножителем п.6 ошибка поиска умножается на синхросигнал с выхода схемы сравнения п.8 по ф.2.13.14
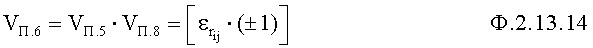
Сумматором п.7 определяется значение приближенного корня на следующем этапе поиска по ф.2.13.15

Если схема сравнения п.9 фиксирует на своем входе сигнал 0<А<1, то его выходной синхросигнал подает команду поиска определителю комплексных корней п.10 фиг.12 на вход формирователя системы уравнений для комплексных корней п.1 фиг.14 по ф.2.13.15
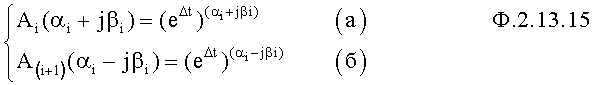
Делитель уравнений п.2 находит отношение уравнений, входящих в систему уравнений с выхода п.1 по ф.2.13.16
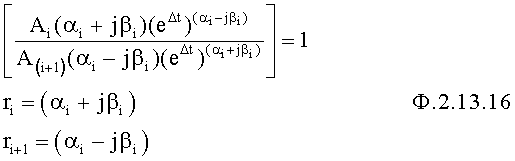
Из полученного отношения находят зависимость значения действительной части корня α от значения мнимой части корня β по ф.2.13.17 в формирователе зависимости… п.3

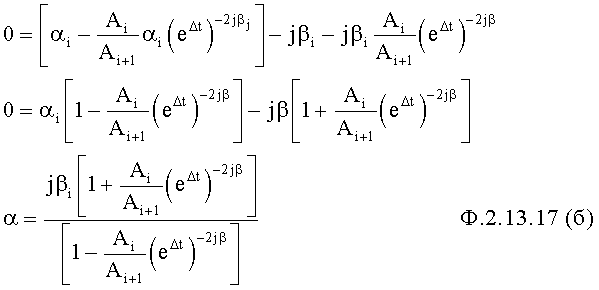
Элемент подстановки зависимости п.4 полученную на первом своем входе функцию ф.2.13.17 подставляет в одно из уравнений, входящих в систему уравнений п.2.13.9. В результате получается ф.2.13.18

Отделитель показат. функции от пропорц. п.5 получает математические выражения, одно из которых содержит показат. функцию, а второе пропорц. ф.2.13.19

где 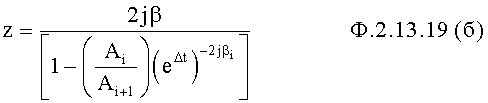

Для того, чтобы построить функции 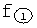 ,
, 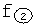 можно использовать поэтапное графическое построение, на первом этапе которого стоят функцию Z ф.2.13.19.(б) фиг.15. При этом в ф.2.13.19(б) подставляется ф.2.13.20 (л.4 стр.602 ф.1)
можно использовать поэтапное графическое построение, на первом этапе которого стоят функцию Z ф.2.13.19.(б) фиг.15. При этом в ф.2.13.19(б) подставляется ф.2.13.20 (л.4 стр.602 ф.1)


На втором этапе полученные на графике фиг.15 значения z(β) подставляются в ф.2.13. 19(а) и строятся графики фиг.16 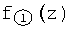 ,
,  , ф.2.13.19(в).
, ф.2.13.19(в).
Первый и второй этапы (фиг.15 и фиг.16) достаточно просты, но довольно громоздки в вычислениях. Чтобы сократить вычисления, используют ф.2.13.21(а), (Л.4 стр.377…382) в определителе асимптот показательной функции п.166

Определитель критических точек по производным от пропор. функции п.7 использует ф.2.13.21(б) л. 4 стр. 356…377:

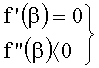 - условие, при котором экстремальное значение β1… является максимумом;
- условие, при котором экстремальное значение β1… является максимумом;
 - условие, при котором экстремальное значение β1… является минимумом.
- условие, при котором экстремальное значение β1… является минимумом.
Определитель точки пересечения графиков линеаризацией п.8 использует в своих вычислениях ф.2.13.22, при этом область поиска определяется по ф.2.13.23


где ti, ti+1, tj, tj+1 - выбираются при соблюдении условий ф.2.13.23(б).
Определитель области линеаризации п.1 фиг.18 (Л.5 стр.49…52), входящий в определитель пересечения графиков линеаризацией п.8 фиг.14, используя найденные ранее асимптоты (горизонтальные, вертикальные, наклонные) и экстремальные точки (максимумы, минимумы, точки перегиба), по условиям, приведенным в ф.2.13.23(б) и ф.2.13.23.(а), определяет моменты времени tлин, для которых находятся линеаризованные математические выражения ф.2.13.22(а) по параметрам ф.2.13.22.(б)
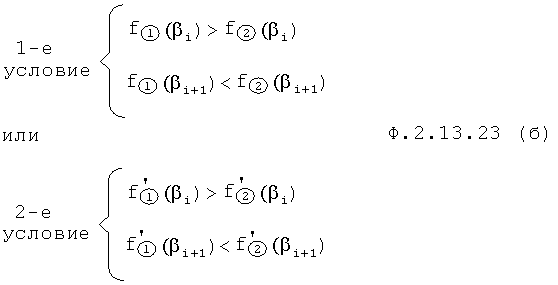

Все последующие устройства п.2…8 фиг.18, входящие в определитель точки пересечения графиков линеаризацией п.8 фиг.14, проводят следующие нижеприведенные математические преобразования.
Вычислитель коэффициентов запаздывания п.2 фиг.18 формирует систему уравнений ф.2.13.24 для каждой из функций, пересечение которых определяется (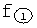 и
и 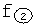 ).
).
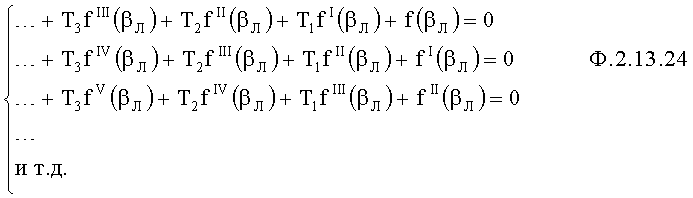
где 
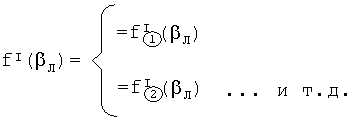

…
и т.д.
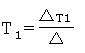 ;
; 
Вычислитель коэффициентов линеаризации дифуравнения полного решения п.3 фиг.18 по коэффициентам запаздывания T1… определяет корни характеристического уравнения (степенного многочлена) ф.2.13.25 и подставляет их систему уравнений ф.2.13.26, составленную для полного решения дифуравнения в точке линеаризации


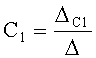 ;
; 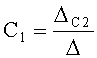 ; …
; …
Формирователь системы уравнений для исследуемых линеаризованных функций п.4 подставляет параметры каждой из функций 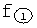 ,
, 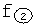 , полученных после преобразований в ф.2.13.24…26, в систему уравнений ф.2.13.27
, полученных после преобразований в ф.2.13.24…26, в систему уравнений ф.2.13.27

Объединитель уравнений п.5 фиг.18 приравнивает дополнительные функции 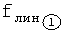 и
и  , находя их пересечение по ф.2.13.28
, находя их пересечение по ф.2.13.28
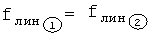
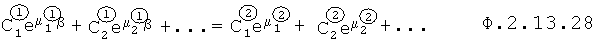
Формирователь степенного многочлена п.7 в ф.2.13.28 вводит новую переменную Z, в результате получается степенной многочлен ф.2.13.29
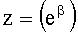

Вычислитель корней степенного многочлена п.7 приводит показатели степеней к общему знаменателю, а приведенные знаменатели слагаемых переводит в числитель ф.27.3, ф.27.4 противоположной части степенного равенства ф.2.13.30, что позволяет отыскать корни степенного многочлена ф.2.13.31

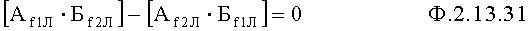
Определитель точек пересечения функции п.8 логарифмирует найденные корни степенного многочлена ф.2.13.32

Найденные значения мнимой части β искомых комплексных корней r=α+jβ вынужденного состояния объекта (равных корням регулирующего воздействия) используются для вычисления действительной части искомых корней по ф.2.13.17(б) в определителях действительной части по мнимой части п.9.1 и п.9.2 фиг.14.
Схема сравнения п.10 фиг.14 позволяет сравнить полученные значения и при их равенстве подтвердить правильность вычислений.
Схема сравнения п.12 фиг.14 позволяет проверить результаты поиска быстродействующего вычислителя п.12 фиг.14, которые включают нижеприведенные устройства п.1…6 фиг.17.
Быстродействующий вычислитель 12 упрощает расчеты, но не позволяет однозначно судить о правильности найденных корней.
Формирователь комплексных корней п.1.1 и п.1.2 подставляет действительные и мнимые части корня в математические выражения дополнительных функций ф.2.13.33
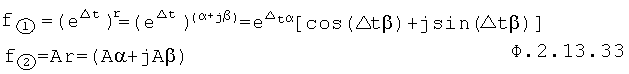
Элементы приравнивания п.2.1 и 2.2 разделяют каждую из дополнительных функций на мнимую Bβ и действительные части Aα и формируют систему уравнений приравниванием между собой мнимой и действительной частей по ф.2.13.34
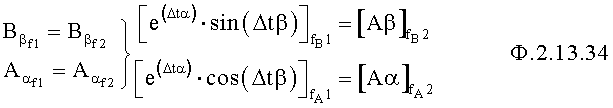
Из системы уравнений ф.2.13.34 определитель зависимости действительной части от мнимой п.3 фиг.17 находит математическое выражение ф.2.13.35
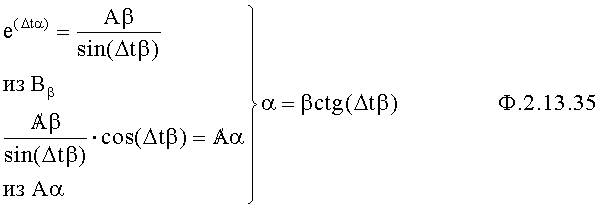
Элемент подстановки п.4 зависимость для действительной части корня α ф.2.13.35 подставляет в математическое выражение для мнимых частей Вβ дополнительных объединенных функций ф.2.13.36. В результате получается уравнение с одним неизвестным.
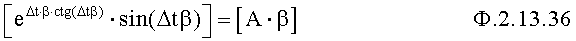
Вычислитель мнимой части п.5 из выражения ф.2.13.36 находит неизвестное значение мнимой части корня β по ф.2.13.37

Найденное значение мнимой части корня β подставляется в зависимость ф.2.13.35 в вычислителе действительной части корня п.6 по ф.2.13.38

Полученные коэффициенты и корни вынужденного состояния проверяются на техническую реализацию исполнительными органами п.1.3 фиг.2. Если техническая реализация возможна, то полученное математическое выражение регулируемого параметра на выходе первого уровня статических характеристик проверяется на ОДЗ в третьем уровне качества и самоконтроля в блоке проверки ОДЗ п.3.1 фиг.2.
Если техническая реализация регулирующего воздействия с выхода первого уровня не возможна, то синхросигнал с выхода определителя технической реализации п.1.3 включает второй уровень динамических характеристик для формирования динамической структуры с переменными корнями (в отличие от первого уровня, в котором корни регулирующего воздействия имели постоянное значение). Структура переменных корней и переменных коэффициентов свободного состояния объекта позволяет обеспечить заданную устойчивость регулирующего воздействия и регулируемого параметра.
Для обеспечения ОДЗ эти параметры корректируются III-м уровнем для компенсации возмущений регулирующего органа, параметры функции входного воздействия корректируются IV-м уровнем.
Для того чтобы решить поставленную задачу, в заявленном изобретении введенный формирователь инерционных настроек разделен на два уровня:
II-й уровень динамических характеристик,
III-й уровень качества и самоконтроля.
Надежность заявленной САР обеспечивается автономностью (независимостью) четырех алгоритмов, для реализации которых используются соответствующие блоки: п.1.2 фиг.11,
- п.2.1…2.3 фиг.2 (фиг.3, фиг.4) формирователь динамической структуры (входящий во II-й уровень) обеспечивает заданный запас устойчивости за счет формирования структуры корней регулирующего воздействия и за счет структуры коэффициентов свободного состояния объекта полного решения дифуравнения (т.е. динамической структуры регулирующего воздействия), но используемый при этом алгоритм не позволяет контролировать ОДЗ (обусловленной технической реализуемостью);
- п.4 фиг.5 (фиг.6) «формирователь регулирующего воздействия по длительности интервала» при узкой области ОДЗ позволяет упростить задачу регулирования, перейти от одного интервала регулирования к «п» независимым интервалам регулирования и задать желаемую длительность каждого из интервалов, после чего определяется «п» независимых структур регулирующего воздействия, но техническая реализуемость регулирующего органа не всегда позволяет осуществить найденную структуру регулирующего воздействия;
- п.5 фиг.5 «формирователь длительности интервала по регулирующему воздействию» позволяет учесть техническую реализуемость исполнительного органа, при этом основной регулируемой величиной выступает не форма регулирующего воздействия, а длительность регулирующего воздействия при чередовании «п» пассивных и активных интервалов, но при этом очень трудно учесть непредвиденные возмущения, действующие не только на параметры объекта, но и на внутренние параметры регулирующего органа;
- п.4.1 фиг.2 (фиг.9) формирователь емкостной силы (входящий в IV-й исполнительный уровень) позволяет учитывать текущее изменение внутренних параметров регулирующего органа (не меняя при этом общую структуру регулирующего воздействия), переходя от нескольких интервалов регулирования (п.4, п.5 фиг.2) к одному.
Известны математические модели объекта (или CAP) в виде дифуравнения ф.3,

где А - левая часть описывает динамическое состояние выходного параметра объекта,
В - правая часть описывает динамическое состояние входного воздействия, создающее соответствующую закономерность динамических характеристик выходного параметра, приведенного в левой части дифуравнения,
yi - выходные регулируемые параметры емкостных составляющих объекта,
xi - входное регулирующее воздействие,
T1… - коэффициенты внутреннего запаздывания.
Существует соответствующая форма решения этого дифуравнения ф.3, приведенная в ф.4 и которая отражает изменение регулируемого параметра «y» в рассматриваемом интервале времени.

где rc1…, rв1… - корни дифуравнения;
Сc1…Св1… - коэффициенты, входящие в соответствующие слагаемые, образующие решение ф.4;
 - совокупность слагаемых, описывающих свободное состояние выходного параметра объекта;
- совокупность слагаемых, описывающих свободное состояние выходного параметра объекта;
 - совокупность слагаемых, описывающих вынужденное состояние, выходного параметра объекта.
- совокупность слагаемых, описывающих вынужденное состояние, выходного параметра объекта.
Таким образом, для того, чтобы перейти к заданной устойчивости и качества CAP (II уровень) от ф.4 переходят к ф.5, в которой (в отличие от ф.4) соответствующий коэффициенты Сс1... и корни rв1… принимают вид (структуру), обеспечивающий желаемую устойчивость при переходном режиме регулирования, необходимом для формирования заданной емкостной характеристики внутреннего состояния объекта, которая позволяет обеспечить заданные значения регулируемого параметра.

Формирователь коэффициентов свободного состояния 21 (2) фиг.2 формирует свободные состояния исследуемых параметров объекта (текущих внутренних выходных или внешних выходных) за счет коэффициентов в виде ф.6

где 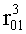 - заданное значение корня емкостной составляющей;
- заданное значение корня емкостной составляющей;
К01…=const;
 - корень коррекции;
- корень коррекции;
Формирователь корней вынужденного состояния 21 (1) фиг.2 формирует корни вынужденного состояния объекта с учетом того, что они равны корням входного воздействия, по ф.7
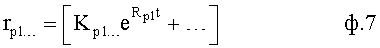
где Kp1 - коэффициент, формирующий «условный» запас устойчивости (при Кpi<0) или неустойчивости (при Кpi>0).
После подстановки необходимых задаваемых коэффициентов свободного состояния объекта Cc1… и корней регулирующего воздействия rp1… ф.7 в дифуравнение ф.3 вычисляются коэффициенты входного воздействия 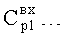 по ф.8 в вычислителе корней регулирующего воздействия п.2.2 фиг.2 (фиг.3) и коэффициентов свободного и вынужденного состояния п.2.3 фиг.2 (фиг.4) с учетом начальных yнi,
по ф.8 в вычислителе корней регулирующего воздействия п.2.2 фиг.2 (фиг.3) и коэффициентов свободного и вынужденного состояния п.2.3 фиг.2 (фиг.4) с учетом начальных yнi, 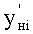 , … и заданных значений y3i,
, … и заданных значений y3i,  , … регулируемого параметра
, … регулируемого параметра

Коэффициенты Kp1… переменных корней регулятора rp1… позволяют задать допустимую устойчивость (или неустойчивость).
Значения показателей степеней 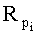 корней регулятора ф.7 позволяют формировать желаемое регулирующее воздействие с учетов внутренних Т01… и текущих параметров у1… объекта.
корней регулятора ф.7 позволяют формировать желаемое регулирующее воздействие с учетов внутренних Т01… и текущих параметров у1… объекта.
Для нахождения корней 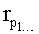 регулирующего воздействие, т.е. показателей степеней
регулирующего воздействие, т.е. показателей степеней  входящих в значение корней ф.7, используются устройства п.1)…7), входящие в вычислитель корней регулирующего воздействия п.2.2 фиг.2. Преобразования, которые при этом используются, приведены ниже фиг.3.
входящих в значение корней ф.7, используются устройства п.1)…7), входящие в вычислитель корней регулирующего воздействия п.2.2 фиг.2. Преобразования, которые при этом используются, приведены ниже фиг.3.
п.1) формирователь коэффициентов запаздывания зависимостей по корням регулятора, т.е. от коэффициентов переменных корней регулятора, включает последовательно соединенные элементы;
п.1.1) «элемент подстановки» значения корней ф.7 подставляется в характеристическое уравнение регулятора ф.9
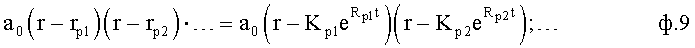
п.1.2) «умножитель», открывая скобки ф.9 и перемножая входящие в них значения, находит зависимость «коэффициентов запаздывания» Тр1… от входящих в корни параметров (коэффициентов кр1… и показателей степеней Rp1… ф.10

где 
Tp1, Tp2 - коэффициенты запаздывания при дифуравнении 2-го порядка;
п.2) «делитель» преобразует формулу переходной характеристики ф.11 WСАР:
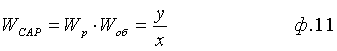
в формулу, объединяющую коэффициенты запаздывания регулятора Tp1… и текущую динамическую характеристику регулируемого параметра y, y1, … ф.12
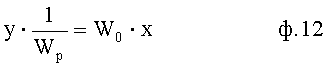
или  - «частное» дифуравнение;
- «частное» дифуравнение;
п.3) «формирователь системы уравнений по частным составляющим объекта» подставляет в дифуравнение ф.12 поочередно каждую из независимых составляющих объекта  образующих «условную частную» модель объекта (т.е. коэффициенты
образующих «условную частную» модель объекта (т.е. коэффициенты 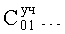 которой допустимы только для «частного дифуравнения» ф.12) по ф.13
которой допустимы только для «частного дифуравнения» ф.12) по ф.13

где  - «условные» коэффициенты «полного» решения «частного» дифуравнения ф.12;
- «условные» коэффициенты «полного» решения «частного» дифуравнения ф.12;
п.4) «задатчик коэффициентов запаздывания регулятора по определителям» формирует зависимость коэффициентов запаздыванием регулятора от определителей системы п.13 по ф.14

где Δ, Δp1… - определители системы уравнений ф.13;
п.5) «формирователь системы подстановкой текущих характеристик» известные начальные ун,  , … и заданные у3,
, … и заданные у3, 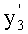 , … характеристики подставляет в ф.14, что позволяет сформировать систему уравнений с двумя неизвестными коэффициентами
, … характеристики подставляет в ф.14, что позволяет сформировать систему уравнений с двумя неизвестными коэффициентами  и
и  по ф.15.
по ф.15.
Приравниванием коэффициентов при одинаковых степенях 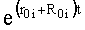 получаем совокупность систем уравнений, в которые входят по два неизвестных
получаем совокупность систем уравнений, в которые входят по два неизвестных 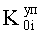 и
и 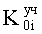 ф.16
ф.16

п.16) «определитель неизвестных системы» находит «условные» коэффициенты 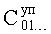 и
и 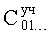 математической модели объекта «частного дифуравнения» ф.12 из системы уравнений ф.15 по ф.16
математической модели объекта «частного дифуравнения» ф.12 из системы уравнений ф.15 по ф.16

где  и
и 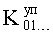 - искомые постоянные из ф.6;
- искомые постоянные из ф.6;
п.7) «элемент подстановки условных коэффициентов» подставляет найденные значения коэффициентов 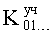 и
и 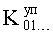 с выхода п.6 из ф.16, справедливых для «частной» формы дифуравнений ф.12 в зависимости, приведенные в ф.14, и находит коэффициент запаздывания регулирующего воздействия по ф.17. Корни регулирующего воздействия позволяют найти коэффициенты запаздывания регулятора.
с выхода п.6 из ф.16, справедливых для «частной» формы дифуравнений ф.12 в зависимости, приведенные в ф.14, и находит коэффициент запаздывания регулирующего воздействия по ф.17. Корни регулирующего воздействия позволяют найти коэффициенты запаздывания регулятора.
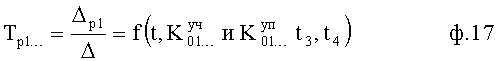
После чего найденные значения коэффициентов запаздывания регулятора Тp1… подставляются в ф.10.1 (полученные с входа п.1) и вычисляются показатели степеней.
Таким образом, входящие в вычислитель корней регулирующего воздействия п.2.2 найденные временные зависимости ф.17 позволяют задать переменные корни ф.7 регулирующего воздействия, обеспечивающие заданную устойчивость регулирующих органов (либо ОДЗ входных принимающих органов объекта).
По найденным значениям корней регулятора (его заданным постоянным коэффициентам Кр1… и переменным показателям степеней Rp1…) формируются коэффициенты регулирующего воздействия в устройствах п.1)…п.8) 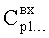 Найденные коэффициенты входного воздействия
Найденные коэффициенты входного воздействия 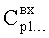 ф.8 позволяют определить коэффициенты вынужденного состояния объекта
ф.8 позволяют определить коэффициенты вынужденного состояния объекта  , входящее в полное решение дифуравнения, устройством п.9 и коэффициенты свободного состояния объекта (регулируемого параметра)
, входящее в полное решение дифуравнения, устройством п.9 и коэффициенты свободного состояния объекта (регулируемого параметра)  устройством п.10) фиг.4. Устройства п.1)…10) входят в вычислитель коэффициентов свободного и вынужденного состояний п.2.3 фиг.2.
устройством п.10) фиг.4. Устройства п.1)…10) входят в вычислитель коэффициентов свободного и вынужденного состояний п.2.3 фиг.2.
Формирователь дифуравнения по коэффициентам запаздывания объекта п.1) по корням объекта r01 находит коэффициенты внутреннего запаздывания Т01… характеристического уравнения объекта ф.18
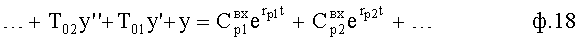
Формирователь системы уравнений из внутренних составляющих регулятора п.2) регулирующее воздействие разделяет на отдельные составляющие (слагаемые) и находит реакцию объекта на каждое из внутренних составляющих регулирующих воздействий. В результате получается система уравнений ф.19

Формирователь определителей системы п.3) находит определители системы уравнений ф.19 по ф.20
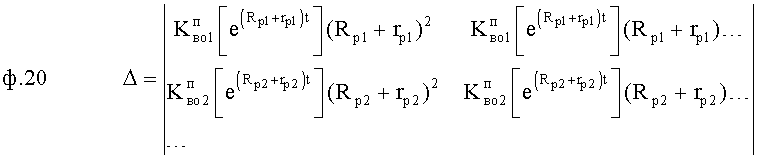

Формирователь коэффициентов запаздывания объекта через определители п.4) позволяет определять как коэффициенты регулятора (коэффициенты входного регулирующего воздействия Cp1 и коэффициенты вынужденного состояния объекта  ) зависят от постоянных запаздывания объекта Т01… из системы уравнений ф.19 по ф.21
) зависят от постоянных запаздывания объекта Т01… из системы уравнений ф.19 по ф.21

где 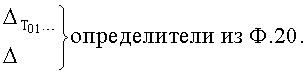
Элемент замены коэффициентов запаздывания п.5) полученные зависимости из ф.21 подставляет в дифуравнение ф.18. После раскрытия определителей получается ф.22

Формирователь системы двух уравнений для начальных и заданных значений п.6) подставляет соответствующие значения регулируемого параметра по ф.23

Элемент приравнивания коэффициентов при одинаковых степенях п.7) формирует систему уравнений, количество которых равно количеству неизвестных  ,
, 

Вычислитель коэффициентов входной составляющей дифуравнения (входного воздействия) п.8) решает системы уравнений ф.24 относительно входящих в них неизвестных по ф.25

Вычислитель вынужденного состояния регулируемого параметра п.9) подставляет найденное значение коэффициентов входных составляющих из ф.25 в дифуравнение по ф.26
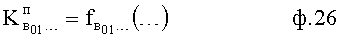
Вычислитель коэффициентов свободного состояния регулируемого параметра п.10) найденные коэффициенты вынужденного состояния 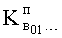 подставляет в полное решение дифуравнения ф.4.4 по ф.27 вычисляются постоянные составляющие
подставляет в полное решение дифуравнения ф.4.4 по ф.27 вычисляются постоянные составляющие  коэффициентов свободного состояния
коэффициентов свободного состояния 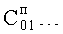 объекта
объекта

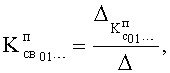
где Ун,  определяются по начальным У1… выходным параметрам емкостных составляющих Wв01… объекта и по
определяются по начальным У1… выходным параметрам емкостных составляющих Wв01… объекта и по  , rp1…
, rp1…
Полученная математическая модель инерционных настроек регулятора с выхода 2-го уровня «динамических характеристик» проверяется «блоком проверки ОДЗ», входящим в 3-й уровень «качества и самоконтроля».
При регулировании параметрами технологических процессов возникает задача контроля ОДЗ емкостной энергией. При этом попутно решаются дополнительные задачи:
1) формирование зависимости коэффициентов запаздывания T1… от текущей емкостной силы F=(Х-У) ф.27.1; п.12 фиг.10
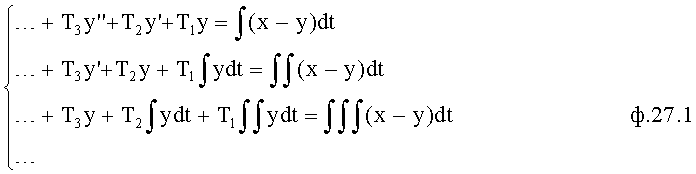
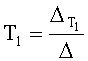 ;
; 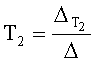 ;
; 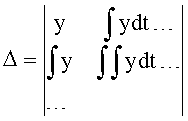 ;
; 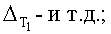
2) определение ОДЗ выходного параметра «Уё» по ОДЗ ёмкостной энергии Еём ф.27.2 п.10 фиг.10
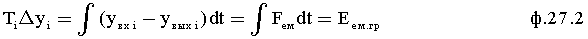
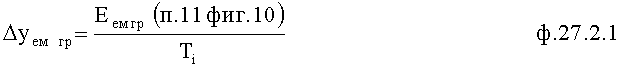
Для того чтобы контролировать ОДЗ емкостной энергии, в формулу 27.2 подставляется значение границы ОДЗ емкостной энергии Еем гр и вычисляется, каким при этом должно быть значение выходного параметра емкостной составляющей «Уе». Полученное значение передается на вход элем. подстан. ОДЗ п.7 фиг.10
В «элементе сокращения корней» п.1 фиг.10, входящем в блок проверки ОДЗ п.3.1 фиг.2, все корни полного решения дифуравнения САР приводят к общему знаменателю ф.27.3, который вводится как новая единица измерения и отбрасывается
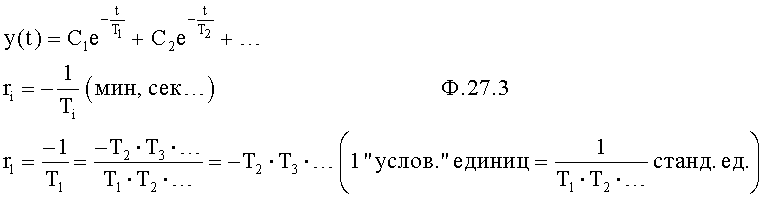
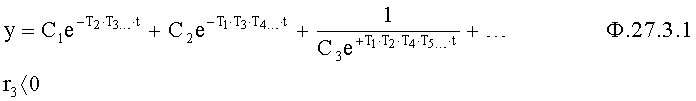
После подстановки нового основания степени, а=еТ ф.27.3 примет вид ф.27.4 п.2 фиг.10

Нахождение корней знаменателя «Б» позволяет проверить математическую модель на устойчивость (непрерывность) на протяжении интервала времени регулирования tнач<t<tкон Ф.27.5. п.4 фиг.10

где Ri=Ri+1=Ri+2=… ф.8 стр.746 л.4
п.3.1 фиг.10.
Найденные корни а1, а2, … степенного многочлена «Б» логарифмируются ф.27.6 для нахождения степенной функции с прежним основанием п.3.2 фиг.10
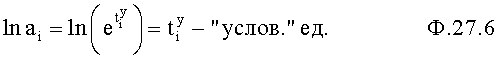
Найденные корни ф.27.5 после логарифмирования ф.27.6 приводят к стандартным единицам измерения по ф.27.7 п.3.3 фиг.10
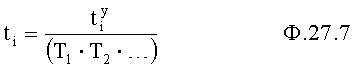
Если полученные значения моментов времени по ф.27.7 на много выходят за рамки времени поддержания заданного значения регулируемого параметра, то можно утверждать о непрерывности (устойчивости) в «малом» п.3.4 фиг.10.
После подтверждения устойчивости в ф.27.3 подставляется один из параметров границы ОДЗ, т.е. переменная y(t) заменяется постоянными границы ОДЗ и переносится в правую часть математической модели ф.27.8 п.7 фиг.10

Таким образом, после приведений к общему знаменателю выражение математической модели и подстановки в нее границы устойчивости п.7.1… фиг.10 идентификатор критических моментов времени п.6.2… (п.6) по ф.27.3…5 определяет моменты времени tгр, при которых регулируемый параметр ф.27.8 принимает значение границы ОДЗ ф.27.9. В отличие от п.6.1 который приравнивает знаменатель к нулю, «идентификатор…» п.2… приравнивает нулю числитель, после подстановки в функцию математической модели границы устойчивости yОДЗ.
Если полученная математическая модель переходных характеристик регулируемых параметров не превышает допустимые значения ОДЗ, то модель регулятора передается на 4-й уровень «исполнительный». Если блок проверки ОДЗ обнаруживает превышение регулируемого параметра допустимый уровень, то его выходной синхронизирующий сигнал «С» поступает на вход «блока поэтапного регулирования» фиг.5.
Для того чтобы найти математическую модель регулятора, которая бы позволила технически реализовать регулирующее воздействие и получить «допустимые» регулируемые параметры, «блок поэтапного регулирования» формирует математические зависимости выходных регулируемых параметров от регулирующего воздействия поэтапным преобразованием математической модели полного решения дифуравнения ф.28.0…, ф.29.0… Полученные в этих формулах зависимости ф.28.0 и 29.0 и т.д. используются в «формирователе системы уравнений» п.3 для описания всей совокупности регулируемых параметров у1… ф.30
В полученную систему уравнений ф.30 подставляются найденные зависимости ф.28.3.4, ф.29.3.
На фиг.1.1 изображен регулируемый параметр У1 (ф.28.0…), У2 (ф.29.0…), …


В ф.28.1 подставляется  и получается ф.28.2
и получается ф.28.2
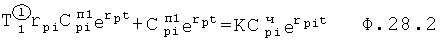
Из ф.28.2 вычисляются Коэф  полного решения по ф.28.3
полного решения по ф.28.3
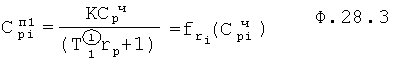
В ф.28.0 подставляется  из ф.28.3 и получают коэффициент свободного состояния регулируемого параметра (полного решения дифуравнения ф.28.0) по формуле 28.4
из ф.28.3 и получают коэффициент свободного состояния регулируемого параметра (полного решения дифуравнения ф.28.0) по формуле 28.4

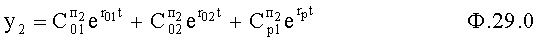

В ф.29.1 подставляют поочередно ф.29.2(а) и (б)
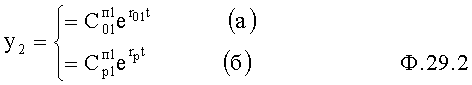
По ф.28.2…4 определяются Сп2 коэффициенты полного решения дифуравнения ф.29.1 по ф.29.3
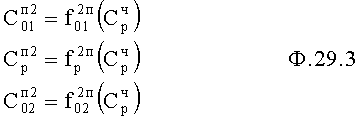
где 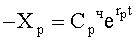 задается из условия допустимой структуры задатчиком технической реализации структуры регулирующего воздействия п.1 фиг.5
задается из условия допустимой структуры задатчиком технической реализации структуры регулирующего воздействия п.1 фиг.5
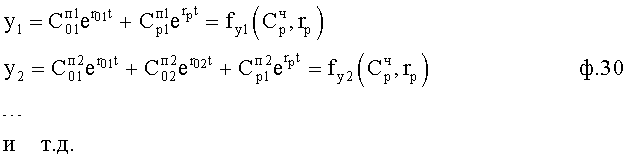
Если регулирующие органы имеют гибкую структуру, то интервалы регулирования формируются «формирователем регулирующего воздействия по заданной длительности интервалов» п.4 ф.31…34.
Если динамическая характеристика используемого регулирующего органа не поддается регулированию (или трудно изменяется), то используется регулирующий сигнал, сформированный «формирователем длительности интервала регулирующего воздействия» п.32 по ф.35.
Формирователь регулирующего воздействия по длительности интервала п.4 фиг.5 включает последовательно соединенные формирователи интервалов п.1, формирователи интервалов п.(1), (2)… и корректоры интервалов п.(1.1), (2.1)…
Каждый из формирователей интервалов п.(1.1…) получает на своем входе информацию о повышении ОДЗ. Задатчик длительности интервал п.1 фиг.6 по заданным критериям (учитывающим особенности объекта) определяет желаемую длительность регулирования каждого их интервалов. Если блок проверки ОДЗ показывает большое перерегулирование, то количество интервалов времени регулирования выбирается равным количеству емкостных составляющих объекта (т.е. ф.31.1), а длительности интервалов выбираются максимально допустимыми Ф.31.2.

где m - количество интервалов регулирования Δt1…m;
n - количество емкостных составляющих 

где Δt Δt1… максимально допустимые.
Определитель коэффициентов запаздывания регулирующего воздействия п.3 фиг.6 формирует систему уравнений ф.32, используя зависимости ф.2.13.1А…ф.2.14.

В ф.32 подставляются ф.2.13.2(а, б) и ф.2.13.4. Получается ф.33, которая (в отличает от ф.2.13.4) при формировании регулирующего воздействия (для упрощения расчетов и для снижения требований к исполнительным органам) на протяжении одного интервала допускает сократить количество корней вынужденного состояния до одного, что делает доступным использовать исполнительные органы с меньшими динамическими возможностями.
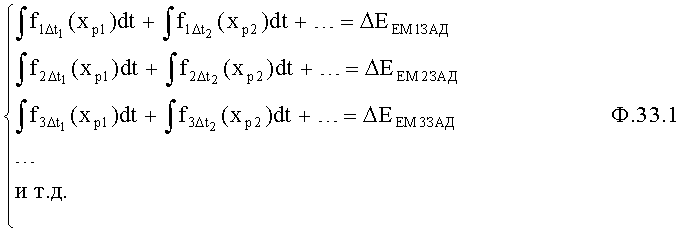
где Δt1=(t1-t0); Δt2=(t2-t1)… и т.д. - интервалы времени регулирования, длительность и последовательность которых задается с учетом технологических и технических характеристик исполнительных органов (или объекта) в п.41 фиг.6.
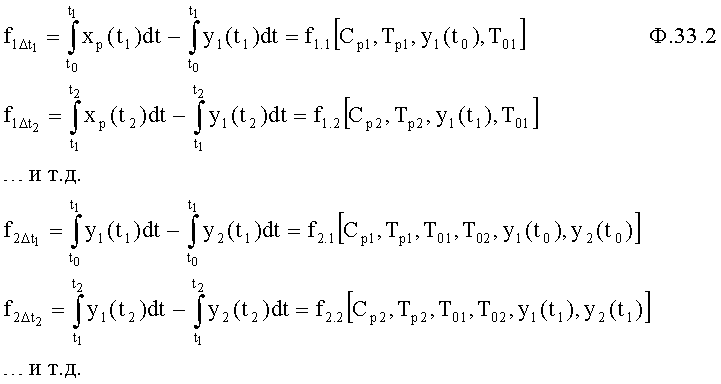
Все параметры, входящие в ф.33, выражают через параметры (коэффициент запаздывания  и коэффициенты решения дифуравнения Ср) математической модели входного регулирующего воздействия Хр(t) для каждого из интервалов регулирования с учетом последовательности этих интервалов, т.е. конечные значения регулируемого параметра предыдущего интервала являются начальными параметрами последующего интервала. При этом количество интервалов должно равняться количеству регулируемых параметров. Формула 34 позволяет получить формулы для вычисления регулирующего воздействия.
и коэффициенты решения дифуравнения Ср) математической модели входного регулирующего воздействия Хр(t) для каждого из интервалов регулирования с учетом последовательности этих интервалов, т.е. конечные значения регулируемого параметра предыдущего интервала являются начальными параметрами последующего интервала. При этом количество интервалов должно равняться количеству регулируемых параметров. Формула 34 позволяет получить формулы для вычисления регулирующего воздействия.

 ;
;  ; и т.д.,
; и т.д.,
где f…(Xp…) определяются по ф.28.0…,
Xp1, Xp2, … определяются из системы уравнений ф.33.1.
Математическая модель регулирующего воздействия Xp проверяется на техническую реализацию в звене п.4 фиг.6. Если возможность реализации не подтверждается, то первый корректор длительности интервала п.5 фиг.6 увеличивает длительность рассматриваемого интервала.
Математическая модель регулируемого параметра также проверяется сравнением с ОДЗ звеном п.7 фиг.6 и при необходимости корректируется вторым корректором длительности интервала п.8.
Если после удлинения времени регулирования исследуемого и предыдущего интервала добиться желаемых характеристик не возможно, то синхросигнал с выхода п.4 фиг.5 подает команду на вход п.5 формирователя длительности интервалов по регулирующему воздействию, который не требует от регулирующего органа высокой динамической точности при измерении регулирующего воздействия.
Для того, чтобы снизить до минимума требования к регулирующим органам в ф.33 подставляют технически реализуемые Хр и Ср в «активном» интервале п.5.2.1 фиг.5 и в «пассивном» режиме. Входное воздействие в пассивном интервале п.5.2.2. должно «контрастировать» с «активным» п.5.2.1, что компенсирует отсутствие динамических настроек и необходимость усреднять регулирующие воздействие в границах интервала при наличии возмущающих воздействий на регулирующее воздействие.
Для преобразования системы уравнений ф.33 используются устройства п.1… фиг.19, входящие в вычислитель длительности интервалов п.5.3 фиг.5. При этом формируется система уравнений таким образом, чтобы неизвестными стали показательные функции, включающие интервалы времени 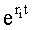 , ф.35.
, ф.35.
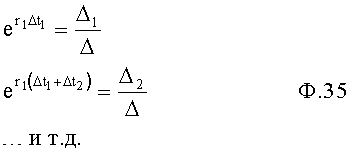
где Δ, Δ1, Δ2… вычисляются из системы уравнений ф.36, которая получена после нижеприведенных преобразований.
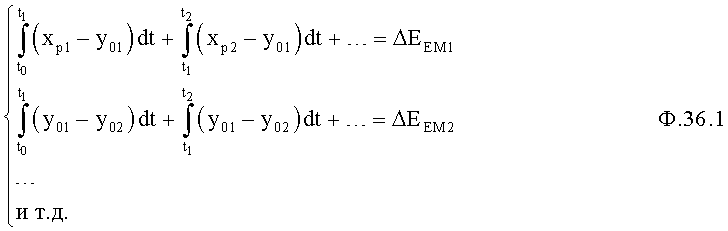
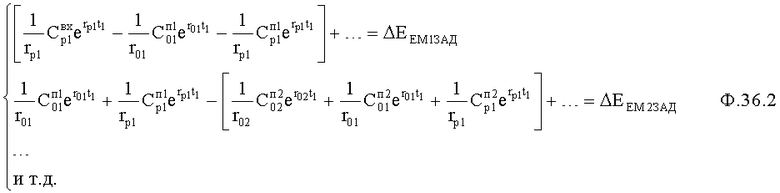

Если корни регулирующего воздействия rpi(Δti) выбираются из условия технической реализации регулирующего воздействия, коэффициенты усиления Cpi (коэффициенты начального значения) регулирующего воздействия (в «активном» или «пассивном» режиме) Cpi выбираются по заданной суммарной емкостной энергии ΔЕём ф.37 задатчиком коэффициентов регулирующего воздействия п.I(1), п.II(1) фиг.19


где rp задается технически реализуемым;
Δt0 - интервал времени, вычисляется из условия технически допустимой скорости изменения регулируемого Уói и регулирующего параметра Хр ф.37.3

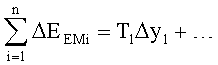 - вычисляемое значение изменения емкостной энергии объекта в целом.
- вычисляемое значение изменения емкостной энергии объекта в целом.
Полученную математическую модель регулирующего воздействия подставляют в математическую модель регулируемого параметра п.I(2), входящего в вычислитель математической модели первого интервала п.I фиг.19.
Определитель математической модели второго интервала п.П.1 по заданным параметрам «пассивного» регулирующего воздействия ф.37.2 вычисляет коэффициенты вынужденного состояния п.II(3).
Полученная математическая модель регулируемого параметра для первого интервала регулирования У1(Δt1) подставляется в формирователь зависимости коэффициентов С01 свободного состояния на втором интервале регулирования для первого параметра регулирования У1 п.П 2.1 «а» ф.38

где 
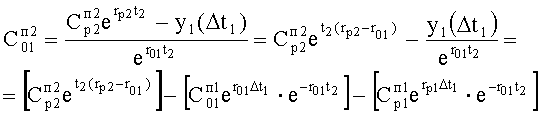
Разделитель известных (r01…, rp1…, Ср1…, C01…) и искомых параметров 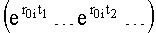 первого регулируемого параметра У1(Δt2) для второго интервала Δt2 раскрывает скобки и, перемножая, группирует известные коэффициенты вокруг неизвестных er…Δt… показательных функций ф.39
первого регулируемого параметра У1(Δt2) для второго интервала Δt2 раскрывает скобки и, перемножая, группирует известные коэффициенты вокруг неизвестных er…Δt… показательных функций ф.39

Аналогично формулам 38 и 39 формируется математическая модель второго регулируемого параметра У2… и т.д.
Результаты расчетов математической модели второго интервала времени подставляются в определитель математической модели 3-го интервала времени для вычисления коэффициентов свободного состояния регулируемого параметра и т.д.
После сложения всех математических моделей У1…(Δt1), У1…(Δt2) для всех интервалов Δt1… времени получится система уравнений ф.40, у которой неизвестными являются показательные функции  ,
, 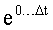 , …
, …

Количество неизвестных равно количеству уравнений, но многие из слагаемых (для второго и последующих интервалов) включают произведения показательных функций ф.39, ф.41

Если каждое из произведений (е…)… рассматривать как независимое неизвестное А1, А2, то количестве неизвестных превышает количество уравнений. Для того чтобы ввести дополнительные уравнения, составляют дополнительные уравнения, составляют дополнительные системы уравнений, у которых заданным параметром есть производные от первоначально заданных параметров. Все последующие расчеты производятся аналогично формирователю систем уравнений фиг.19. При этом формулы принимают вид ф.42 п.III фиг.20 (п.5.3.3, фиг.5)

Вычислитель определителей IV фиг.20 стандартными способами вычисляет определитель системы п.IV.1. Для упрощения расчетов последующие определители находятся только те, которые включают показательную функцию 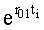 первого регулируемого параметра VI для каждого из интервалов Δti ф.43
первого регулируемого параметра VI для каждого из интервалов Δti ф.43
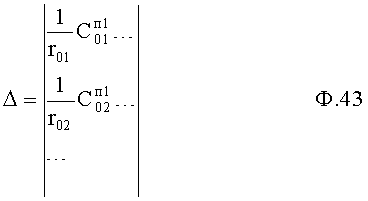
Делением определителей вычисляются первый и последующие неизвестные ф.44 п.V фиг.20

Найденные неизвестные системы позволяют определить длительности интервалов ф.45

Регулирующие воздействия Хр, сформированные 1-м…3-м уровнями, эффективны, если параметры регулирующего органа заранее известны, но если на исполнительный орган действуют непредвиденные возмущения, громоздкие алгоритмы формирования математической модели практически не применимы, поэтому в этом случае прибегают к алгоритму, сформированному 4-м исполнительным уровнем формирователем емкостной силы регулятора п.4.1 фиг.2 (фиг.9).
Если значение входного воздействия Хр (или У0, У1, …) прировнять «силе» и рассматривать как «входную силу» Fвх, то рассмотрение изменения емкостной энергии ΔЕем требует использование «емкостной силы» Fем ф.36.*
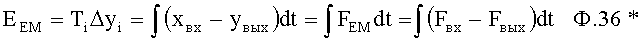
Из ф.36* можно получить понятие «емкостной силы» по ф.37.1* после дифференцирования текущего значения емкостной энергии и подстановки параметров дифуравнения ф.37.2*


Если объект включает несколько звеньев, то изменение энергии объекта в целом равно сумме изменения энергии каждого из звеньев ф.38*
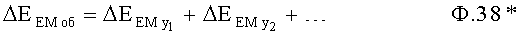
Для нахождения регулирующего воздействия Хр необходимо, чтобы используемая система уравнений ф.39*, содержащая все регулируемы параметры У0, У1…, включала в каждом из уравнений искомую модель регулирующего воздействия (или функцию от нее) Xp(t).

Объединяя попарно уравнения, входящие в ф.39*, формируется новая система уравнений ф.40* (п.2…п.4 фиг.9)
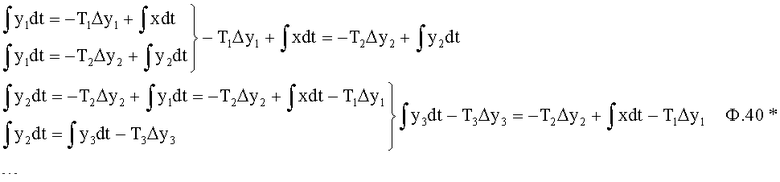
и т.д.
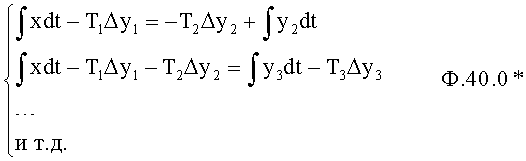
или
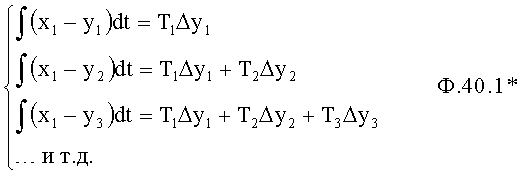
где 
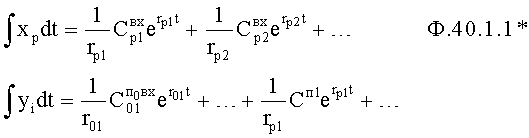

Математические модели полного решения дифуравнения регулируемых параметров у1… ф.40.2* после подстановка их в ф.40* позволяют сформировать систему уравнений относительно коэффициентов входного воздействия ф.41*
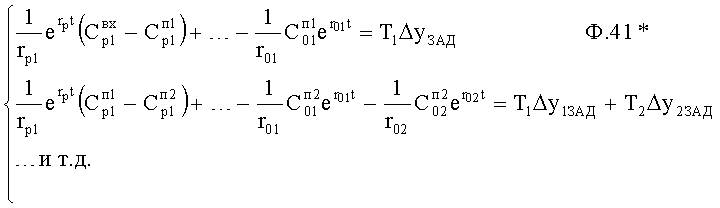
Таким образом, если корни математической модели исполнительного органа 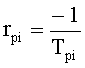 меняются в течение регулирования, а предвидеть это изменение невозможно (следовательно, усреднить их влияние тоже невозможно), то единственная возможность для регулирования - это упрощение алгоритма вычисления, т.е. нахождение коэффициентов дифуравнения по корням, полученным на выходе идентификатора п.7 фиг.2 (п.1 фиг.7) ф.42*
меняются в течение регулирования, а предвидеть это изменение невозможно (следовательно, усреднить их влияние тоже невозможно), то единственная возможность для регулирования - это упрощение алгоритма вычисления, т.е. нахождение коэффициентов дифуравнения по корням, полученным на выходе идентификатора п.7 фиг.2 (п.1 фиг.7) ф.42*

Идентификатор емкостной энергии позволяет определить не только внутренние (Т и К) параметры, но и затраченную энергию, необходимую для изменения регулируемого параметра на заданную величину ΔУ. При этом параллельно (с максимальным быстродействием) определяется непредвиденная утечка энергии E с входа объекта (п.5.3 фиг.7.0), чтобы своевременно предотвратить аварийный режим. Для этого сравнивается емкостная энергия, полученная разными способами идентификации фиг.7.0:
П.1 быстродействующим косвенным определителем… фиг.7.4, позволяющим контролировать и реагировать на любые непредвиденные, даже кратковременные, возмущения;
П.2 прямым определителем… на текущем интервале фиг.7.5, позволяющим пренебрегать (фильтровать) кратковременными возмущениями, если влияние их не существенно;
П.3 блоком контроля полного переходного периода фиг.7.6, позволяющим проанализировать всю совокупность возмущений на протяжении всего периода регулирования, что необходимо при формировании последующих этапов регулирования;
П.4 блоком выходной емкостной энергии фиг.7.7, позволяющим получить «фактическую» информацию о «активной» емкостной энергии, при нулевой входной силе, когда на выходе объекта формируется сила, которая обусловлена только емкостной энергией.
П.1 (фиг.7.0) включает совокупность устройств п.1.1…п.1.4 фиг.4:
П.1.1 определитель математической модели для текущего момента времени фиг.7.1, состоящий из звеньев:
- определитель корней дифференциальной модели п.1), который находит коэффициенты запаздывания  ; … за минимально короткое время (необходимое для определения производных высокого порядка У”, У”', …) по ф.43.1*
; … за минимально короткое время (необходимое для определения производных высокого порядка У”, У”', …) по ф.43.1*

 ;
; 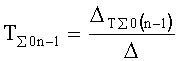 … и т.д.
… и т.д.
 - корни степенного многочлена характеристического уравнения ф.43.2*
- корни степенного многочлена характеристического уравнения ф.43.2*
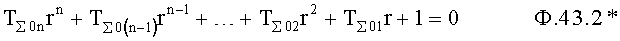
- определитель коэффициентов полного решения дифуравнения п.2) выбирает момент времени, который принят за начало отсчета и подставляет найденные корни в математическую модель регулируемого параметра объекта для вычисления постоянных ф.44*

 ;
; 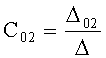 ; …
; …
- определитель последовательности звеньев п.3) составляет для каждой позиции (1-й У01, 2-й У2, … фиг.1.1) отдельную систему уравнений ф.45.1*…, позволяющую определить коэффициент запаздывания исследуемого звена фиг.7.2.
Для звена, подсоединенного к входу объекта, ф.45.1* 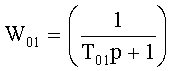
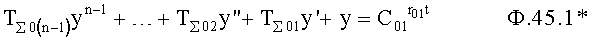
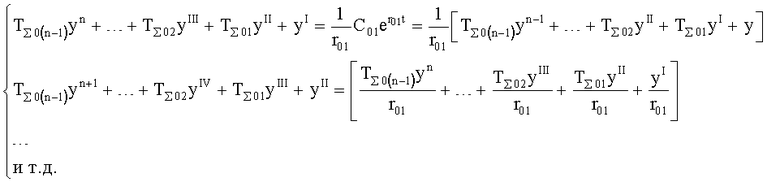
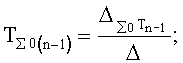
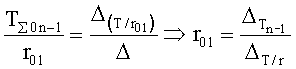
Для звена, подсоединенного к выходу первого звена, ф.45.2* 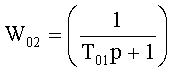
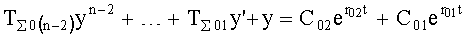

 и т.д.;
и т.д.;
- определитель выходных параметров каждого звена п.4) по выходному параметру последнего звена и его производной определяет из дифуравнения выходной параметр предыдущего звена ф.46.1 и т.д. ф.46.2…

где 
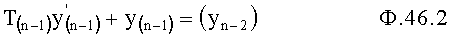
где  из ф.46.1
из ф.46.1

и т.д.;
- идентификатор текущего момента времени п.5) фиг.7.1 (фиг.7.3) позволяет установить интервал времени между двумя моментами времени:
а) при одном из которых известна динамическая характеристика выходного параметра, т.е. известна совокупность у(ti), у'(ti), у”(ti),… уm (полная m=n или не полная m<n);
б) при другом может быть известна одна из трех совокупностей:
1) полного решения дифуравнения математической модели входного регулирующего воздействия 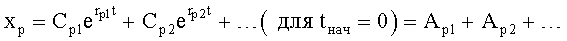
2) динамическая характеристика выходного параметра второго момента времени у(tj), у(tj'), у(tj”), …
3) значение выходного регулируемого параметра во второй момент времени у(tj), для которого справедлива совокупность найденных интервалов времени.
Каждая из совокупностей 1), 2), 3) образует каналы идентификации с выходными параметрами N1, N2, N3, N4 фиг.7.3:
N1 параметры, сформированные II.9.1, п.12.1, п.8.1, п.4.3, п.13.1 ф 50.1…;
N2 параметры, сформированные устройствами II.9.2, п.10, п.5.1, п.4.1, п.5.2, п.1.2, Ф.47.1, …, 49.1;
N3 параметры, сформированные устройствами II.1.1, п.1.1, п.5.3, п.4.2, п.5.4 ф.48.1, …, 49.1;
N4 параметры, сформированные устройствами II.1.2, п.6, п.2, п.7, п.12.2 п.8.2, п.4.4, п.13.2 ф 49.1…
Совокупность «1)» с выходным каналом N1 позволяет определить возможные искомые интервалы времени Δt1, Δt2…, количество которых равно степени дифуравнения входного регулирующего воздействия Хр. При этом динамическая характеристика у', у”… включает производные, степени которых должны равняться (не меньше) количеству корней свободного состояния объекта m=J (r01…J).
Совокупность «1)» с выходными параметрами N2 позволяет получить исчерпывающую информацию о интервале времени Δt=tис-ti между исследуемым tис и любым другим ti при заданном входном воздействии Хр, при этом отсчет времени ведется от начального момента заданного входного воздействии Хр. Информация о текущих значениях tис=tт регулируемого параметра Ут, Ут, Ут, … позволяет определить параметры объекта в начальный момент времени t0 и значение текущего момента времени tт=tт-t0.
Совокупность «2)» с выходным каналом N3 позволяет однозначно судить о величине искомого интервала времени Δtт, благодаря полной динамической характеристике ут, ут', ут”… регулируемого параметра в исследуемый момент времени tт и известный момент времени tиз.
Совокупность «3)» с выходным каналом N4 позволяет определить возможные интервалы времени Δt1, Δt2… для известного значения регулируемого параметра Уиз (tиз) в известный момент времени tиз при неизвестной динамической характеристике.
Совокупность устройств, входящих в канал N1, позволяет использовать математическую модель решения дифуравнения входного воздействия ф.50.1:
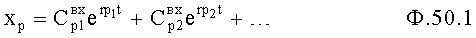
Элемент подстановки в дифуравнение п.9 элементов динамической характеристики п.9.1 (Ут, Ут', …) вычисляет сумму составляющих дифуравнения, стоящих в левой части, включающих текущее значение регулируемого параметра, ее производные и коэффициенты внутреннего запаздывания объекта по ф.50.2

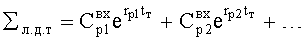
В результате получается показательный многочлен. Преобразователь показательного многочлена в степенной п.12.1 преобразует многочлен в степенной, используя ф.50.3

где a=et.
Вычислитель корней степенного многочлена п.8.1 использует ф.50.4 (1…6).
При наличии дробных корней -1<ri<1 все корни приводятся к общему знаменателю ф.50.4(1) 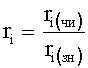

Вводится новая единица измерения времени tусл, позволяющая избавиться от дробных корней по ф.50.4(2):

Отрицательные корни переносятся в знаменатель ф.50.4(3)

После этого все слагаемые степенного многочлена приводятся к общему знаменателю ф.50.4(4)
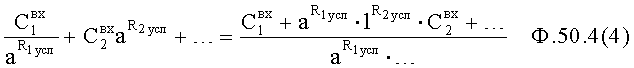
Общий знаменатель степенного многочлена переносится в числитель правой части ф.50.4(5)
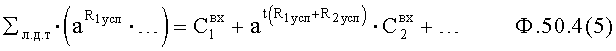
Левая часть дифуравнения переносится в правую часть дифуравнения ф.50.4.(6)

Полученный степенной многочлен решается стандартными способами.
Определитель логарифма п.4.3 преобразует степенной многочлен в показательный ф.50.5

Элемент подстановки стандартных единиц измерения п.73.1 использует ф.50.6

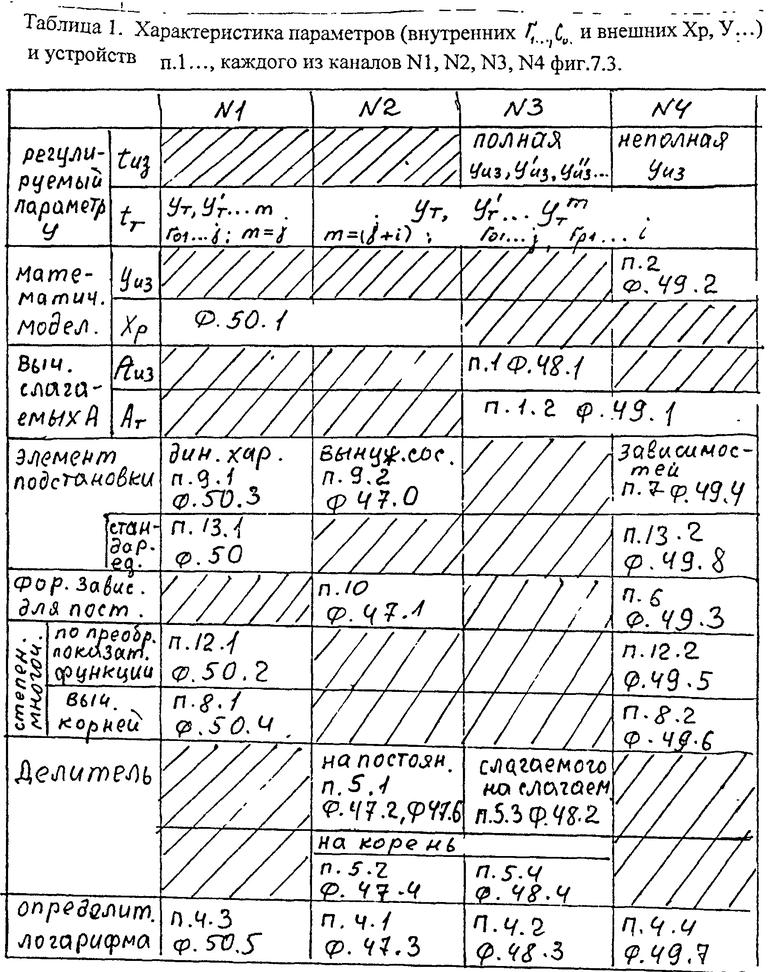
Совокупность устройств, входящих в канал N2, использует модель дифуравнения объекта для подстановки в нее слагаемых вынужденного состояния объекта элементом подстановки п.9 в элементе слагаемых … п.9.2 фиг.7.3 ф.47.0

Полученная формула ф.47.0 позволяет вычислить значения постоянных, входящих в слагаемые вынужденного состояния объекта п.10 фиг.7.3 по ф.47.1
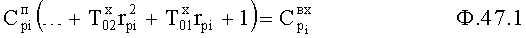

Звено текущих параметров п.1.2, используя ф.49.1, вычисляет текущие значения слагаемых вынужденного состояния объекта.


Делитель на постоянную п.5.1 использует одно из слагаемых вынужденного состояния  объекта, найденное для исследуемого момента времени, и вычисляет переменную
объекта, найденное для исследуемого момента времени, и вычисляет переменную

Определитель логарифма п.4.1 позволяет избавиться от показательной функции по ф.47.3

Делитель п.5.2 позволяет найти однозначное значение текущего tт (исследуемого) момента времени ф.47.4

Совокупность устройств, входящих в канал N3, использует полную динамическую характеристику регулируемого параметра в любой известный момент времени tиз, позволяющую вычислить слагаемое полного решения дифуравнения объекта для известного момента времени по ф.48.1, п.1.1.

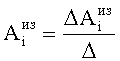
Делитель слагаемых п.5.3 слагаемое, найденное для текущего момента времени, делит на слагаемое, найденное для известного момента времени по ф.48.2, находя показательную функцию без постоянного коэффициента умножения.

Определитель логарифма п.4.2 позволяет исключить показательную функцию ф.48.3, а делитель на корень п.5.4 позволяет найти искомый исследуемый момент времени ф.48.3


Совокупность устройств, входящих в канал N4, не требует динамической характеристики регулируемого параметра для каждого момента времени (совокупности двух моментов времени), между которыми определяется интервал времени. При этом используется полное решение дифуравнения одного момента времени (например, известного) ф.49.2, п.2.
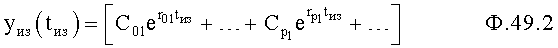
Формирователь зависимости постоянных от величины слагаемых п.6 формирует математическую модель для каждой из постоянных по ф.49.3 


… и т.д.
где i=01, 02, …, p1, p2, …
Элемент подстановки п.7 использует полученные математические модели для постоянных ф.49.3, подставляя их в формулу полного решения дифуравнения для известного момента времени ф.49.2, получая показательный многочлен ф.49.4

Совокупность последовательно соединенных устройств, преобразователя показательного многочлена в степенной п.12.2, вычислителя корней степенного многочлена п.8.2, определителя логарифма п.4.4, элемента подстановки 13.2 используется для нахождения возможных интервалов времени аналогично ф.50.3…ф.50.6.
Схема сравнения п.3 использует полную информацию всех каналов N1…N4 идентификации момента времени. Правильность найденных параметров подтверждается в тех случаях, когда параметры 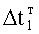 ,
, 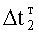 …, полученные каналами N1, равны параметрам с выхода канала N4, а параметр
…, полученные каналами N1, равны параметрам с выхода канала N4, а параметр 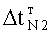 , полученный с выхода канала N2, совпадает с параметром с выхода канала N3
, полученный с выхода канала N2, совпадает с параметром с выхода канала N3 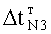 .
.
Схема сравнения п.3 используется для проверки правильности расчетов и поиска причин, не позволяющих добиться точности идентификации. К этим причинам могут относиться возмущения:
- исполнительных регулирующих органов Тр1… (каналы N1, N2);
- внутренних параметров объекта Т01… (каналы N2, N3);
- измерительных устройств;
- вычислительных устройств.
Таким образом, за минимально короткое время «определитель математической модели для текущего момента времени» п.1.1 фиг.7.4 позволяет с максимальным быстродействием контролировать состояние параметров фиг.7.1:
- коэффициент внутреннего запаздывания п.1.1 Т1…,
- последовательность внутренних емкостных звеньев W01… п.3 по условному моменту времени tусл и условной постоянной Cусл… п.2,
- выходные параметры каждого внутреннего звена объекта в первом приближении у01… п.4,
- продолжительность интервала времени регулирования tт.
Измерительные устройства по текущему значению выходного параметра Ут вычисляет динамическую характеристику, т.е. производные ф.51

Определитель текущих выходных параметров п.1.2 фиг.7.4 по текущему моменту времени tт (найденному п.5 фиг.7.1) определяет постоянные С1… ф.52.1 и контролирует выходные y01… параметры внутренних звеньев объекта ф.52.2, проверяя их с полученными в первом приближении (с выхода п.4 фиг.7.1, до нахождения текущего момента времени).
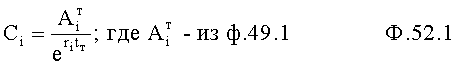
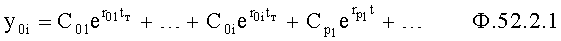

Определитель емкостной энергии каждой емкостной составляющей п.1.3 фиг.7.4 вычисляет емкостную энергию по текущему значению коэффициента запаздывания T1… ф.53

где Δy0i - изменение регулируемого параметра относительно выбранного начала отсчета (t0):
Δy0i=[yi(tт)-yi(t0)]
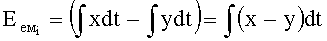
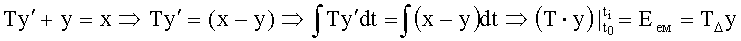
Определитель емкостной энергии объекта в целом п.1.4 фиг.7.4 использует дифуравнения для объекта в целом, дифференцируя разницу входного и выходного параметров ф.54

Таким образом, быстродействующий косвенный определитель емкостной энергии п.1 фиг.7.0 позволяет контролировать состояние всех параметров объекта в каждый момент времени, идентифицируя не только сильнодействующие, но все мельчайшие и самые внезапные возмущения внутренних и внешних параметров объекта.
Прямой определитель емкостной энергии текущего интервала п.2 фиг.7.0 позволяет контролировать текущий исследуемый переходной режим в каждой текущей точке его регулирования относительно заданного начального момента времени фиг.7.5.
Определяется текущее значение емкостной энергии при активном входном воздействии, т.е. при Xв≠0 (при входном воздействии, не равном условно принятому началом отчета, нулевым: как правило, значению входного воздействия до начала действия регулирующего воздействия), вычисляется изменение емкостной энергии с момента начала отсчета t0 до текущего момента tт.
Для отдельных звеньев п.2.1 фиг.7.5 используется ф.55
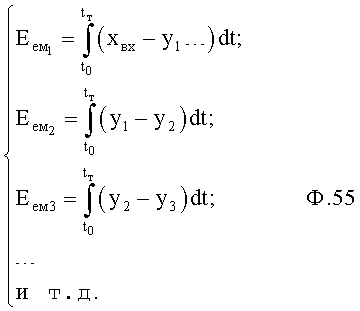
где y01…(tт) определяются с выхода п.1.3 фиг.7.4.
Для объекта в целом п.2.2 фиг.7.5 используют аналогичную формулу ф.56.1

Полученное значение в ф.56.1 проверяется в ф.56.2

где 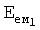 ,
, 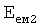 … берутся из ф.55;
… берутся из ф.55;
Еем об берется из ф.56.1.
Таким образом, ф.56.2 использует фактическую емкостную Еем об энергию ф.56.1 для проверки ранее найденных коэффициентов запаздывания Т1…, которые использовались для косвенного определения емкостной энергии ф.53.
Текущее значение емкостной энергии не позволяет учесть действие возмущений в совокупности. Действие возмущений, связанных с нелинейностью параметров объекта, часто имеет свою закономерность, повторяющуюся в каждом периоде регулирования. Для получения исчерпывающей информации о параметрах объекта необходима полная характеристика регулируемого параметра yт на протяжении всего периода регулирования.
Наиболее важными в переходном режиме являются экстремальные точки (максимумы и минимумы), поэтому наиболее точной является идентификация по экстремальным параметрам п.I фиг.78. Но если экстремальные параметры не выражены явно, то прибегают к идентификатору плавного процесса п.II фиг.7.8.
Устойчивость регулируемых параметров y01… является основным параметром при воздействии на объект и разработки САР. Для того чтобы раскрыть устойчивые свойства регулируемого параметра, удобно использовать коэффициенты внутреннего запаздывания Т1… дифуравнения объекта. Величина корней характеристического уравнения  однозначно позволяет определить запас устойчивости.
однозначно позволяет определить запас устойчивости.
Для нахождения коэффициентов запаздывания Т1… составляется система дифуравнений п.4, п.5 для вершин п.I фиг.7.8 ф.57.

где yi,

 определяются п.1, п.2, п.3 фиг.7.8 по графику фиг.7.9 и ф.57.2
определяются п.1, п.2, п.3 фиг.7.8 по графику фиг.7.9 и ф.57.2

где 

где  ;
;
…
и т.д.
Если переходный процесс плавный и найти производные высоких порядков невозможно, то используют идентификатор плавного процесса п.II фиг.7.8. При измерении регулируемого параметра через одинаковые промежутки времени (Δt=t1) t0, t1, t2=(t1+t1), t3=(t2+t1)… и т.д. П.1(II) позволяет сформировать условную форму дифуравнения ф.58
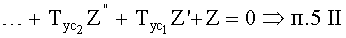
где 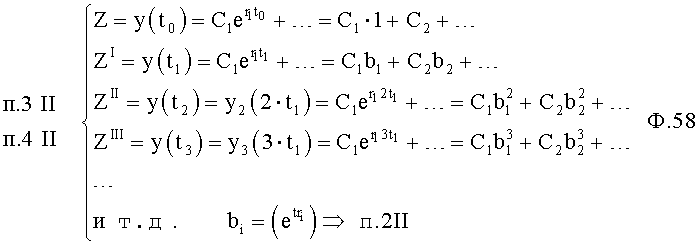
Составляется система условных дифуравнений ф.5.9, которая позволяет вычислить коэффициенты запаздывания Тус… условного дифуравнения ф.59.2
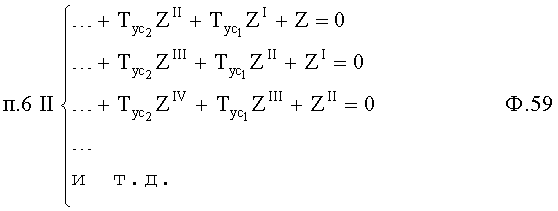
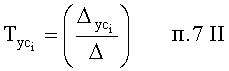
Из характеристического уравнения ф.60.1 условного дифуравнения ф.59 находят условные корни Вус1… ф.60.2 (позволяющие вычислить искомые корни дифуравнения объекта ф.61)
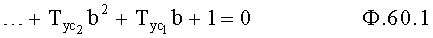
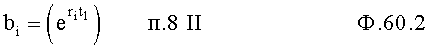
i=1, 2, …
П.9(II) подставляет найденные условные корни в ф.61 для нахождения корней ri характеристического уравнения дифуравнения объекта.
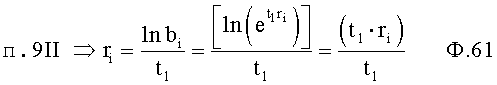
Найденные корни характеристического уравнения подставляются в систему уравнения ф.62 для нахождения постоянных С1… каждого слагаемого А1…, входящего в полное решение дифуравнений п.10 II фиг.7.8

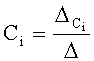
Из-за физических (или технических) особенностей объекта сила, действующая на объект (т.е. входное регулирующее воздействие), затрачивается не только на емкостную энергию Eем и выходную энергию Eвых (обусловленную действием выходной силой Fвых, т.е. выходным регулируемым параметром y), обладает помимо емкостной энергией и энергией потерь Eпот, которая может затрачиваться не только на входе, но и на выходе из объекта. Поэтому так важно определить выходную емкостную энергию Eем вых при пассивном входном воздействии, т.е. при Xр=0 фиг.7.7 (п.4 фиг.7.0).
Блок выходной емкостной энергии п.4 фиг.7.0 формирует нулевое входное воздействие Xр=0 п.4.1 фиг.7.7. При этом определяется выходная энергия объекта, величина которой равна выходной внутренней емкостной энергии объекта п.4.2 фиг.7.7 по ф.63

Текущее значение выходной емкостной энергии Eвых. ем (tт) позволяет в очередной раз проверить коэффициенты внутреннего запаздывания объекта Т1… по ф.64 п.4.3 фиг.7.7, тем самым контролируя утечку энергии на выходе объекта
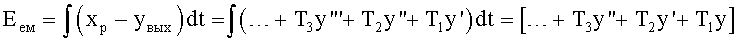
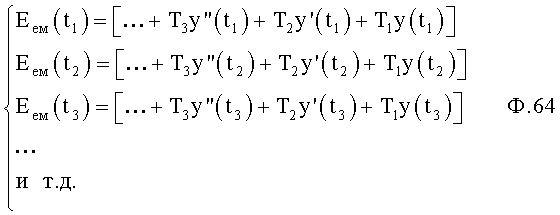


Таким образом, введенные изменения обеспечивают необходимую емкостную энергию каждой из емкостных составляющих объекта.
1-й уровень при формировании регулирующего воздействия исходит из статической заданной характеристики каждой емкостной составляющей:
2-й уровень обеспечивает не только заданную статическую характеристику, но и обеспечивает динамическую характеристику переходного процесса за счет того, что обеспечивается заданный запас устойчивости с помощью структуры переменных корней вынужденного состояния объекта и переменных коэффициентов свободного состояния объекта.
3-й уровень обеспечивает качество, проверяя ОДЗ регулируемых параметров на протяжении всего регулируемого периода и при необходимости разбивая один переходный период на несколько регулируемых периодов.
4-й уровень формирует регулирующее воздействие, исходя из динамической характеристики регулирующих органов, что позволяет своевременно реагировать на возмущения, действующие на исполнительные органы.
Введенный идентификатор емкостной энергии объекта позволяет контролировать потерю энергии на всех этапах, что позволяет скрыть внутреннюю структуру объекта, недоступную для идентификации стандартными способами.
Экономический эффект достигается за счет экономии топлива в теплоэнергетических объектах, за счет уменьшения износа оборудования, связанного с неблагоприятными режимами, и предотвращения аварийных режимов.
Фиг.1.0 - структурная схема многосвязанных САР.
Фиг.1.1 - структурная схема объекта.
Фиг.2 - структурная схема CAP.
Фиг.3 - структурная схема вычислителя корней регулирующего воздействия (п.2.2 фиг.2).
Фиг.4 - структурная схема вычислителя коэффициентов свободного и вынужденного состояний (п.2.3 фиг.2).
Фиг.5 - структурная схема блока поэтапного регулирования (п.3.2 фиг.2).
Фиг.6 - структурная схема формирователя интервала (п.4(1…) фиг.2).
Фиг.7.0 - структурная схема идентификатора емкостного состояния объекта (п.7 фиг.2).
Фиг 7.1 - структурная схема определителя математической модели для текущего момента времени (п.1.1 фиг.7.4).
Фиг.7.2 - структурная схема определителя последовательности звеньев (структуры математической модели) п.3 фиг.7.1.
Фиг 7.3 - структурная схема идентификатора текущего момента времени (п.5 фиг.7.1).
Фиг.7.4 - структурная схема быстродействующего косвенного определителя емкостной энергии (п.1 фиг.7.0).
Фиг.7.5. - структурная схема прямого определителя емкостной энергии текущего интервала (п.2 фиг.7.0).
Фиг.7.6 - структурная схема блока контроля полного переходного периода (п.3 фиг.7.0).
Фиг.7.7 - структурная схема блока выходной емкостной энергии (п.4 фиг.7.0).
Фиг.7.8 - структурная схема определителя структуры запаздывания (п.3.1 фиг.7.6).
Фиг.7.9 - график поэтапного определения экстремальных параметров производных (п.2, п.3 фиг.7.8).
Фиг.8 - графическое нахождение емкостной энергии.
Фиг.9 - структурная схема формирователя емкостной силы по параметрам регулятора (п.4.1 фиг.2).
Фиг.10 - структурная схема блока проверки ОДЗ (п.3.1 фиг.2).
Фиг.11 - структурная схема формирователя регулятора по статической характеристики емкостной энергии (п.1.2 фиг.2).
Фиг.12 - структурная схема вычислителя корней вынужденного состояния (п.6 фиг.11).
Фиг.13 - график дополнительных функций (ф.2.13.8(б)).
Фиг.14 - структурная схема определения комплексных корней (п.10 фиг.12).
Фиг.15 - график зависимости комплексного корня от мнимой части (ф.2.13.20).
Фиг.16 - график зависимости дополнительных функций от комплексного корня (ф.2.13.19(в)).
Фиг.17 - структурная схема быстродействующего вычислителя (п.11 фиг.14).
Фиг.18 - структурная схема определителя точек пересечения графиков линеаризации (п.8 фиг.14).
Фиг.19 - структурная схема формирователя системы уравнений для неизвестных показательной функции (фиг.5 п.5(3.1)).
Фиг.20 - определитель интервалов времени (фиг.5 п.5(3.2)).
Таблица 1. Характеристика параметров (внутренних r1…, С1… и внешних Xp, Y…) и устройств п.1…, каждого из каналов N1, N2, N3, N4 фиг.7.3.
Многосвязная система регулирования фиг.1.1 включает два вычитателя В1, В2, положительными входами подсоединенных к соответствующим входам Хзд1, Хзд2 CAP, a отрицательными к соответствующим выходам соответствующих звеньев W11, W22 объекта. Входы возмущения CAP F1, F2 подсоединены к соответствующим входам соответствующих звеньев объекта W11…, К1…, которые имеют между собой перекрестное соединение.
Для упрощения расчетов в примере технической реализации рассматривается объект, у которого звенья W10, W20… расположены последовательно фиг.1.2.
Фиг.2 - структурная схема заявленной CAP, которая включает в себя последовательно соединенные 1-й уровень статических характеристик, п.5 - формирователь инерционных настроек, 4-й уровень исполнительный, п.6 - объект регулирования, п.8 - пропорциональное звено, п.7 - идентификатор емкостных составляющих, который выходом подсоединен через вторые входы 1-го, 4-го уровня и формирователя инерционных настроек п.3 к входящих в них устройствам.
1-й уровень статических характеристик включает последовательно соединенные определитель необходимой емкостной энергии п.1.1, формирователь регулирования по статической характеристики емкостной энергии п.1.2, определитель технической реализации п.1.3. Выход определителя емкостной энергии п.1.1 подсоединен также на 3-й вход формирователя инерционных настроек п.5, а второй выход определителя технической реализации п.1.3 подсоединен на 4-й вход формирователя инерционных настроек п.5.
Формирователь инерционных настроек п.5 включает в себя последовательно соединенные 2-й уровень динамических характеристик и 3-й уровень качества и самоконтроля:
2-й и 3-й входы формирователя инерционных настроек подсоединены ко 2-му и 3-му уровням,
1-й вход п.5 подсоединен ко второму входу 3-го уровня качества и самоконтроля, 4-й вход п.5 подсоединен на 2-й вход 2-го уровня динамических характеристик.
2-й уровень динамических характеристик включает в себя последовательно соединенные задатчик устойчивости п.2.1, вычислитель корней регулирующего воздействия п.2.2, вычислитель корней свободного и вынужденного состояний п.2.3.
Задатчик устойчивости п.2.1 включает в себя последовательно соединенные формирователь корней вынужденного состояния п.(1) и формирователь свободного состояния п.(2).
3-й уровень качества и самоконтроля включает в себя последовательно соединенные блок проверки ОДЗ п.3.1 и блок поэтапного регулирования п.3.2. Второй выход проверки ОДЗ п.3.1 подсоединен ко второму входу 4-го уровня исполнительного.
4-й исполнительный уровень включает в себя последовательно соединенные вычислитель текущих значений входного воздействия п.4.2, регулирующий орган п.4.3, формирователь емкостных сил п.4.1, выходом подсоединенный на вход вычислителя текущих значений входного воздействия 4.2.
1-й и 2-й входы 4-го исполнительного уровня подсоединены к входам вычислителя текущих значений входного воздействия п.4.2, а выход подсоединен к выходу регулирующего органа п.4.3.
Фиг.3, вычислитель корней регулирующего воздействия включает в себя последовательно соединенные формирователь модели коэффициентов запаздывания п.1, делитель п.2, формирователь системы уравнений по частным составляющим объекта п.3, задатчик коэффициентов запаздывания регулятора по определителям п.4, формирователь системы подстановкой текущих характеристик п.5, определитель неизвестных системы п.6, элемент подстановки условных коэффициентов п.7. Формирователь модели коэффициентов запаздывания п.1 включает в себя последовательно соединенные элемент подстановки п.1.1 и умножитель п.1.2, выход которого также подсоединен ко второму входу элемента подстановки условных коэффициентов п.7. Второй вход вычислителя корней регулирующего воздействия (с выхода идентификатора п.7 фиг.2) подсоединен на второй вход делителя п.2
Вычислитель коэффициентов свободного и вынужденного состояния фиг.4 (п.2.3 фиг.2) включает в себя последовательно соединенные формирователь дифуравнения по коэффициентам запаздывания объекта п.1), формирователь системы уравнений из внутренних составляющих объекта п.2), формирователь определителей системы п.3), формирователь коэффициентов запаздывания объекта через определители 4), элемент замены коэффициентов запаздывания 5), формирователь системы уравнений для начальных и заданных значений 6), элемент приравнивания коэффициентов при одинаковых степенях 7), вычислитель коэффициентов входной составляющей дифуравнения 8), вычислитель вынужденного состояния регулируемого параметра 9), вычислитель коэффициентов свободного состояния регулируемого параметра 10).
Блок поэтапного регулирования фиг.5 (п.3.2 фиг.2) включает в себя последовательно соединенные задатчик технической реализуемости структуры регулирующего воздействия п.1, формирователь зависимостей математической модели п.2, формирователь системы уравнений зависимостей регулируемого параметра от длительности интервала п.3, формирователь регулирующего воздействия по длительности интервала п.4, формирователь длительности интервала по регулирующему воздействию п.5, определитель математической модели необходимой входной энергии п.6. При этом выход формирователя системы уравнений зависимостей регулируемого параметра от длительности интервала п.3 подключен также ко второму входу формирователя длительности интервала по регулирующему воздействию п.5. Второй выход формирователя регулирующего воздействия по длительности интервала п.4 также подсоединен ко второму входу определителя математической модели необходимой входной энергии п.6.
Формирователь регулирующего воздействия по длительности интервала п.4 включает в себя последовательно соединенные формирователи интервалов (1), (2), …, вторые выходы которых подсоединены на входы корректоров интервалов (1.1), (1.2), … Корректор интервалов (i.1) входом подсоединен к формирователю интервалов (i+1.1)-му, а выходом ко второму входу предыдущего формирователя интервала (i.1)-му.
Формирователь длительности интервалов по регулирующему воздействию п.5 включает в себя последовательно соединенные формирователь системы уравнений из суммы интервалов воздействий п.(1), задатчик технической реализации воздействия п.(2), вычислитель длительности интервалов п.(3). При этом задатчик технической характеристики воздействия п.(2) включает параллельно соединенные задатчик активного интервала п.(2.1) и задатчик пассивного интервала п.(2.2). Вычислитель длительности интервалов п.3 включает последовательно соединенные формирователь основной системы уравнений п.(3.1) и уточняющий вычислитель п.(3.2).
Формирователь интервала фиг.6 (п.4(1)…фиг.5) включает последовательно соединенные задатчик длительности интервала п.1, определитель дополнительного интервала п.2, определитель регулирующего воздействия п.3, звено проверки технической реализации п.4, определитель коэффициентов свободного и вынужденного состояний объекта п.6, звено проверки технической реализации п.7. Вторые выходы звеньев проверки технической реализации п.4 и п.7 подсоединены к входам корректоров длительности интервалов п.5 и п.8, первые выходы которых подсоединены ко второму и третьему входам определителя дополнительного интервала п.2, а третьи выходы подсоединены на второй и третьи выходы формирователя интервала. Выход задатчика интервалов п.1 подсоединен также на второй вход определителя коэффициентов регулирующего воздействия п.3.
Идентификатор емкостного состояния объекта фиг.7.0 включает последовательно соединенные быстродействующий косвенный определитель емкостной энергии п.1, прямой определитель емкостной энергии текущего интервала п.2, блок контроля полного переходного периода п.3, блок выходной емкостной энергии п.4, определитель утечки емкостной энергии п.5. При этом вторые и третьи выходы п.1…3 подсоединены к 2…6-му входам определителя утечки емкостной энергии п.5. Определитель возмущений включает в себя схему сравнения п.5.2.3, на входы которого подсоединены вторые выходы п.1 и п.2., а выход которого подсоединен к третьему входу определителя возмущений п.5.3. На входы схемы сравнения п.5.2.4 подсоединены второй выход п.1 и выход сумматора п.5.1.1, выход которого подсоединен на четвертый вход определителя возмущений п.5.3. Третьи выходы п.1 подсоединены на вход сумматора п.5.1.1 и схемы сравнения п.5.2.2, выход которой подсоединен на 6-й вход определителя возмущений п.5.3. Третьи выходы п.2 подсоединены на вход схемы сравнения п.5.2.2 и сумматора п.5.1.2, выход которого подсоединен на вход схемы сравнения п.5.2.4. Второй выход п.2 подсоединен на второй вход схемы сравнения п.5.2.4, выход которой подсоединен на 5-й вход определителя возмущений п.5.3.
Определитель математической модели для текущего момента времени фиг.7.1 (п.1.1 фиг.7.4) включает последовательно соединенные определитель корней дифференциальной модели п.1), определитель коэффициентов полного решения дифуравнения п.2), определитель последовательности звеньев п.3), определитель выходных параметров каждого звена п.4. Выход определителя корней дифференциальной модели п.1) также подсоединен на второй вход определителя последовательности звеньев п.3), выход которого также подсоединен на вход идентификатора текущего момента времени п.5), подсоединенного выходом на второй выход определителя математической модели для текущего момента времени.
Определитель последовательности звеньев фиг.7.2 (п.3 фиг.7.4) включает последовательно соединенные определители позиций А1…, каждый из которых включает последовательно соединенные формирователь переноса звеньев п.1, определитель производной п.2, элемент подстановки исходного уравнения после переноса п.3, формирователь системы уравнений дифференцированием п.4, определитель корней правой части п.5.
Идентификатор текущего момента времени фиг.7.3 (п.5 фиг.7.1) включает четыре канала идентификации, выходы которых N1…4 подсоединены к четырем входам схемы сравнения п.3.
Канал N1 включает в себя последовательно соединенные элемент динамических характеристик п.9.1, преобразователь показательного многочлена в степенной п.12.1, вычислитель корней степенного многочлена п.8.1, определитель логарифма п.4.3, элемент подстановки стандартных единиц п.13.1.
Канал N2 включает в себя последовательно соединенные элемент слагаемых вынужденного состояния п.9.2, вычислитель постоянных вынужденного состояния объекта п.10, делитель на постоянную п.5.1, определитель логарифма п.4.1 и делитель п.5.2. На второй вход делителя на постоянную п.5.1 подсоединен выход звена текущих параметров п.1.2, выход которого также подсоединен на выходы делителя слагаемых п.5.3 (канал N3) и формирователя зависимости постоянных от слагаемых п.6 (канал N4).
Канал N3 включает в себя последовательно соединенные звено начальных параметров п.1.1, делитель слагаемых п.5.3, определитель логарифма п.4.2 и делитель на корень п.5.4.
Канал N4 включает в себя последовательно соединенные формирователь модели известного регулируемого параметра п.2, элемент подстановки п.7, преобразователь показательного многочлена в степенной п.12.2, вычислитель корней степенного многочлена п.8.2, элемент подстановки стандартных единиц п.13.2.
Быстродействующий косвенный определитель емкостной энергии фиг.7.4 (п.1 фиг.7.0) включает в себя последовательно соединенные определитель математической модели для текущего момента времени п.1.1, определитель текущих выходных параметров для каждой емкостной составляющей п.1.2, определитель емкостной энергии каждой емкостной составляющей п.1.3, определитель емкостной энергии в целом п.1.4, вторые выходы п.1.3 и п.1.4 подсоединены ко второму и третьему выходам быстродействующего косвенного определителя емкостной энергии.
Прямой определитель емкостной энергии текущего интервала фиг.7.5 (п.2 фиг.7.0) включает в себя последовательно соединенные определитель для отдельных звеньев п.2.1, определитель для объекта в целом п.2.2, вторые выходы которых подсоединены на второй и третий выходы прямого определителя емкостной энергии текущего интервала.
Блок контроля полного переходного периода фиг.7.6 (п.3 фиг.7.0) включает в себя последовательно соединенные определитель структуры запаздывания п.3.1, определитель запаздывания каждой составляющей п.3.2, определитель емкостной энергии по усредненным косвенным параметрам п.3.3.
Блок выходной емкостной энергии фиг.7.7 (п.4 фиг.7.0) включает в себя последовательно соединенные формирователь нулевых входных воздействий п.4.1, определитель емкостной энергии в текущий момент времени п.4.2, определитель системы дифуравнений для емкостной энергии п.4.3, определитель коэффициентов внутреннего запаздывания из системы уравнений п.4.4.
Определитель структуры запаздывания фиг.7.8 (п.3 фиг.7.6) включает идентификатор по экстремальным точкам п.1 и идентификатор плавного процесса п.II, входы и выходы которых подсоединены к входам и выходам определителя структуры запаздывания. Идентификатор по экстремальным точкам включает в себя последовательно соединенные определитель вершин п.1.1, определитель моментов времени для вершин п.1.2, определитель экстремальных параметров для производных п.2, определитель производных для исследуемых моментов п.3, формирователь дифуравнения для вершин переходного процесса п.4, объединитель дифуравнений в систему п.5, вычислитель коэффициентов внутреннего запаздывания п.6, вычислитель корней дифуравнения п.7, вычислитель коэффициентов полного решения дифуравнений п.8.
Формирователь емкостной силы регулятора фиг.9 (п.4.1 фиг.2) включает в себя последовательно соединенные формирователь системы уравнений емкостных сил п.1, формирователь системы двух уравнений для каждой входной силы п.2, формирователь объединенных уравнений исключением промежуточных входных сил п.3, объединитель уравнений для всех емкостных сил относительно входного воздействия п.4, элемент подстановки полного решения математической модели дифуравнений п.5.1, элемент подстановки заданных параметров п.5.2. элемент подстановки идентифицированных корней регулирующего воздействия п.5.3, формирователь зависимости коэффициентов математической модели выходных сил от коэффициентов входного воздействия п.6, элемент подстановки полученных зависимостей в математическую модель п.7, формирователь системы уравнений относительно входного воздействия п.8, вычислитель коэффициентов входного воздействия п.9.
Блок проверки ОДЗ фиг.10 (п.3.1 фиг.2) включает в себя последовательно соединенные элемент сокращения корней запаздывания на общий знаменатель п.1, формирователь степенного многочлена заменой основания п.2, определитель непрерывности математической модели САР п.4, выход которого подсоединен к входам звена проверки ОДЗ п.5.1. При этом определитель непрерывности математической модели включает последовательно соединенные вычислитель корней степенного многочлена п.3.1, определитель натурального логарифма корней степенного многочлена п.5.2, делитель логарифма на общий знаменатель корней запаздывания п.3.3, элемент сравнения момента времени с заданным временем регулирования п.3.4.
Последовательно соединенные устройства п.3.1, п.3.2, п.3.3, п.3.4 объединены в идентификатор критических моментов времени п.6.1 (в определителе непрерывности математической модели CAP п.4) и п.6.2 (в звеньях проверки ОДЗ п.5.1, п.5.2,…). Второй выход формирователя степенного многочлена заменой основания п.2 подключен к вторым входам звеньям проверки ОДЗ п.5.1…, каждый из которых включает последовательно соединенные элемент подстановки ОДЗ выходных параметров п.7, определитель числителя п.8, идентификатор критических моментов времени п.6.2, схема сравнения п.9. На второй вход схемы сравнения п.9 подсоединен выход определителя емкостной энергии объекта в целом п.1.1 фиг.7.4 (в быстродействующем косвенном определителе емкостной энергии п.1 фиг.7.0). Выход определителя коэффициентов внутреннего запаздывания по емкостной силе п.12 подсоединен не третий вход схемы сравнения п.9 и первый вход определителя ОДЗ выходного параметра п.10, на второй вход которого подсоединен выход задатчика ОДЗ емкостной энергии, а выход которого подсоединен на второй вход элемента подстановки ОДЗ выходного параметра п.7.
Формирователь по статической характеристике емкостной энергии фиг.11 (п.1.2(1) фиг.2) включает последовательно соединенные формирователь системы уравнений для емкостных составляющих п.1, определитель зависимости коэффициентов свободного состояния от коэффициентов входного воздействия п.2, определитель интеграла свободного и вынужденного состояний по сумме коэффициентов входного воздействия п.3, вычислитель интервала времени приравниваем составляющих относительно коэффициентов, вычислитель суммы коэффициентов входного воздействия п.5, вычислитель корней вынужденного состояния пересечением функций п.6.
Вычислитель корней вынужденного состояния фиг.12 (п.6 фиг.11) включает последовательно соединенные формирователь искомого корня п.1, вычислитель показательной функции п.4, вычитатель п.5, умножитель п.6, сумматор п.7, выход которого также подсоединен на третий вход формирователя искомого корня п.1. Выход формирователя искомого корня п.1 подсоединен на второй вход сумматора п.7 и на первый вход умножителя п.3, на второй вход которого подсоединен выход вычислителя слагаемых п.2. Второй вход вычислителя корней вынужденного состояния подсоединен на входы вычислителя слагаемых п.2 и определителя комплексных корней п.10, выход которого также подсоединен на вход вычислителя корней вынужденного состояния. Выход вычислителя слагаемых п.2 подсоединен также к входам двух схем сравнения п.8 и п.9. Выход схемы сравнения п.8 подсоединен ко вторым входам формирователя искомых корней п.1 и умножителя п.6. Выход схемы сравнения п.9 подсоединен на второй вход определителя комплексных корней п.10.
Определитель емкостных корней фиг.14 (п.10 фиг.12) включает последовательно соединенные формирователь системы уравнений для комплексных корней п.1, делитель уравнений п.2, формирователь зависимости действительной составляющей от мнимой п.13, элемент подстановки зависимостей п.4, отделитель показательной функции от пропорциональной п.5, определитель асимптот показательной функции п.6, отделитель мнимой части от действительной п.13.1, определитель точки пересечения графиков линеаризацией п.8.1, определитель мнимой части корня по действительной части функции п.9.1. схему сравнения п.10, схему сравнения п.12. Вход определителя комплексных корней подсоединен также к выходу быстродействующего вычислителя п.11, выход которого также подсоединен на второй вход схемы сравнения п.12. Выход формирователя системы уравнений для комплексных корней п.1 также подсоединен на второй вход элемента подстановки зависимостей п.4. Выход формирователя зависимостей действительной составляющей от мнимой п.13 также подсоединен на вторые входы определителя мнимой части корня по действительной части функции п.9.1 и определителя мнимой части корня по мнимой части функции п.9.2, выход которого подсоединен на второй вход схемы сравнения п.10. Второй выход отделителя показательной функции от пропорциональной п.5 подсоединен на вход определителя критических точек по производной пропорциональной функции п.7, выход которого подсоединен на вход отделителя мнимой части функции от действительной п.13.2. Выход отделителя мнимой части функции от действительной п.13.2 подсоединен на вход определителя точки пересечений графиков п.8.2, выход которого подсоединен на первый вход определителя мнимой части корня по мнимой части функции п.9.2.
Быстродействующий вычислитель фиг.17 (п.11 фиг.14) включает последовательно соединенные формирователь комплексных корней п.1, элемент приравнивания п.2, определитель зависимостей п.2, элемент подстановки п.4, вычислитель мнимой части корня п.5. Второй выход определителя зависимости действительной части от мнимой п.3 подсоединен на вход вычислителя действительной части корня, выход которого подсоединен на второй вход вычислителя мнимой части корня п.5 и на второй выход быстродействующего вычислителя. Формирователь комплексных корней включает звено пропорциональной функции п.1.1 и звено показательной функции п.1.2, выходы которых подсоединены на входы звена действительной части п.2.1 и звена мнимой части п.2.2, входящих в элемент приравнивания п.2. Выход звена действительной части подсоединен на вход определителя действительной части от мнимой п.3, а выход звена мнимой части подсоединен на вторые входы определителя зависимости действительной части от мнимой п.3 и элемента подстановки п.4.
Определитель точек пересечения графиков линеаризации фиг.18 (п.8 фиг.14) включает в себя последовательно соединенные определить области линеаризации п.1, вычислитель коэффициентов запаздывания п.2, вычислитель коэффициентов линеаризации дифуравнения п.3, формирователь системы уравнений для исследуемой функции п.4, объединитель уравнений п.5, формирователь степенного многочлена п.6, вычислитель корней степенного многочлена п.7, определитель точки пересечения функций п.8.
Формирователь системы уравнений для показательной функции фиг.19 (п.5.3.1 фиг.5) включает последовательно соединенные вычислитель математической модели первого интервала п.1 и определители математической модели последующих интервалов п.II.1 и п.II.2,…. Вычислитель математической модели первого интервала включает в себя последовательно соединенные задатчик коэффициентов запаздывания п.(1) и формирователь модели регулируемого параметра п.(2), который в свою очередь включает в себя последовательно соединенные вычислители коэффициентов свободного и вынужденного состояния первого параметра п.(2.1), второго параметра п.(2.2) и т.д. Определители математической модели последующих интервалов п.II.1,… включают в себя последовательно соединенные задатчик регулирующего воздействия п.(3), вычислитель коэффициентов вынужденного состояния п.(4), формирователь математической модели соответствующего параметра п.(5.1), п.(5.2),… Формирователь математической модели соответствующего параметра включает в себя последовательно соединенные формирователь зависимостей коэффициентов свободного состояния п.(а) и разделитель известных коэффициентов и искомых параметров п.(б).
Определитель интервалов времени фиг.20 (п.5.3.2 фиг.5) включает последовательно соединенные формирователь дополнительных уравнений дифференцированием п.III, вычислитель определителей п.IV, вычислитель показательных функций п.V, вычислитель интервалов времени п.VI. Формирователь дополнительных уравнений дифференцированием включает в себя дифференциатор искомых параметров п.1, дифференциатор задаваемых регулируемых параметров п.2. Вычислитель определителей п.IV включает вычислитель определителей системы п.3, вычислитель определителя одного из параметров п.4, который включает в себя последовательно соединенные вычислитель определителя первого п.4.1, второго п.4.2,… и т.д. Вычислитель показательных функций п.V включает в себя последовательно соединенные и подсоединенные к выходу вычислители показательной функции первого интервала п.5.1, второго интервала п.5.2,… и т.д. Вычислитель интервалов времени п.VI включает подсоединенные к входу и выходу вычислители первого интервала времени п.6.1, второго интервала времени п.6.2,… и т.д.
Определитель необходимой емкостной энергии п.1.1 фиг.2, учитывая начальное состояние выходных У01, 02,… и входного параметра Хр, определяет необходимое изменение емкостной энергии Еём, позволяющей обеспечить заданный регулируемый параметр Узад по ф.2.13.2 и ф.2.13.3.
Формирователь регулирования по статической характеристики емкостной энергии п.1.2 фиг.2 (фиг.11) при формировании регулирующего воздействия руководствуется статической характеристикой необходимой емкостной энергии Еём, полученной с выхода «определителя необходимой емкостной энергии» п.1.1 фиг.2 и параметрами внутреннего запаздывания Т01… и усиления K01… объекта, полученными с выхода идентификатора емкостных составляющих объекта п.7 фиг.2. по ф.2.13.2…ф.2.13.38 фиг.11…фиг.18.
Определитель технической реализации п.1.3 фиг.2 математическую модель регулирующего воздействия (Хр1…Кр…), полученную с выхода формирователя регулирования по статическим характеристикам емкостной энергии п.1.2, сравнивает с техническими возможностями реального регулирующего органа. Если техническая характеристика регулирующего органа позволяет осуществить необходимую модель регулирующего воздействия, то выходной синхросигнал посылает команду на вход блока проверки ОДЗ п.3.1, который проверяет математическую модель регулируемого параметра У01… на соответствие задаваемой ОДЗ в течение всего времени регулирования. Если исполнительный орган не способен сформировать математическую модель регулирующего воздействия, то синхросигнал с выхода п.1.3 дает команду запуска II -го уровня динамических характеристик (позволяющего избежать неблагоприятных технических характеристик, формирующих корни математической модели с задаваемым запасом устойчивости вынужденного и свободного состояния регулируемого параметра). В совокупности п.1.1…п.1.3 позволяют проверить возможность формирования математической модели регулирующего воздействия с максимальным быстродействием, проверяя при этом возможность формирования чисто действительных корней, не приводящих к перерегулированию исполнительных органов п.1…п.8. Нахождение комплексных корней регулирующего воздействия п.10 фиг.12 (фиг.14) позволяет сделать решаемой любую совокупность заданных регулируемых параметров. При быстроменяющихся параметрах объекта используется «быстрый вычислитель» п.11 фиг.14 (фиг.17). Если техническая эксплуатация объекта требует повышенной надежности регулирования, то используются п.1…п.10 фиг.14, в которых нахождение комплексных параметров дублируется двумя параллельными каналами, первый из которых включает п.6, п.13.1, п.8.1, п.9.1, а второй включает п.7, п.13.2, п.8.2, 9.2. Полученные данные с выходов каналов сравниваются схемой сравнения п.10, которая позволяет контролировать правильность найденных комплексных корней регулирующего воздействия.
Таким образом, первый уровень статических характеристик обеспечивает решаемость поставленных задач и быстродействия и надежности при нахождении параметров регулирующего воздействия.
Если найденные математические характеристики регулирующего воздействия не осуществимы, то синхросигнал с первого уровня статических характеристик запускает второй уровень динамических характеристик.
Задатчик устойчивости п.2.1 фиг.2 включает в себя формирователь корней вынужденного состояния п.(1) ф.65, формирующий переменный корень rp1… вынужденного состояния ф.5, постоянная составляющая которого Кр1… обеспечивает заданную устойчивость при Кр1…<0 (или неустойчивость при Кр1…>0) ф.7:
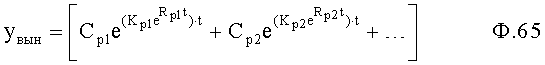
где 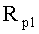 - параметр, который необходимо вычислить в виде постоянной величины для заданной совокупности параметров Т01… объекта, заданной величины регулируемого параметра У01… и заданного значения устойчивости Кр1… вынужденного состояния объекта Увын… и входного регулирующего воздействия Хр…
- параметр, который необходимо вычислить в виде постоянной величины для заданной совокупности параметров Т01… объекта, заданной величины регулируемого параметра У01… и заданного значения устойчивости Кр1… вынужденного состояния объекта Увын… и входного регулирующего воздействия Хр…
Таким образом, формирователь корней вынужденного состояния (1) удобен тем, что однозначно обеспечивает устойчивость составляющих входного (регулирующего) параметра и выходного регулируемого (вынужденного) параметра.
Формирователь коэффициентов свободного состояния п.(2) ф.66, входящий в задатчик устойчивости п.2.1 (ф.4, ф.5, ф.6), задает коэффициент C01…, входящий в свободное состояние регулируемого параметра ф.6. Если объект имеет устойчивые корни r (меньше нуля) математической модели объекта, то для упрощения расчетов C01… выбираются постоянными.
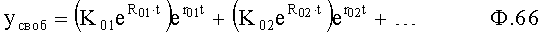
Если одна из свободных составляющих объекта имеет неустойчивую математическую модель, то для коррекции неустойчивости положительных корней r>0 объекта коэффициенты C01… выбираются переменными. Задается желаемое значение устойчивости (r зад 01…) и по ф.67 вычисляется корень коррекции 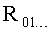 .
.

Таким образом, формирователь коэффициентов свободного состояния п.(2) позволяет компенсировать неустойчивость регулируемого параметра У01…, обусловленную неустойчивостью внутренних параметров объекта r=(-1/T01…)>0.
Совокупность формирователя корней вынужденного состояния п.(1) и формирователя коэффициентов свободного состояния п.(2), входящих в задатчик устойчивости п.2.1 фиг.2, позволяет сформировать исходные данные для расчета регулирующего воздействия с заданным запасом устойчивости регулируемого параметра и регулирующего воздействия даже в том случае, если объект включает в себя звенья с неустойчивой структурой.
Вычислитель корней регулирующего воздействия п.2.2 фиг.2, используя ф.7…ф.17, вычисляет значения постоянных Rp1…, входящих в показание степени переменного корня регулирующего воздействия Хр. Для этого используются устройства показанные на фиг.3. Описание каждого из устройств приведено в разделе «сущность заявленного изобретения».
Вычислитель коэффициентов свободного и вынужденного состояния п.2.3 включает устройства, изображенные на фиг.4. Подробное описание каждого из устройств п.1…п.10 приведено (ранее) в «сущности» заявленного изобретения, при этом используются ф.18…ф.27. Совокупность устройств п.1…п.10 фиг.4 позволяет вычислить коэффициенты математической модели регулирующего воздействия, которая обеспечивает изменение регулируемых устройств от начальных значений Унач 01… до заданных Узад 01…, контролируя на всем протяжении регулирования «запас устойчивости» свободной и вынужденной составляющей. Совокупность всех устройств, входящих во второй уровень «динамических характеристик», позволяет контролировать динамические характеристики (устойчивость) всего переходного регулируемого периода.
Блок проверки ОДЗ п.3.1, входящий в третий уровень «качества и самоконтроля» п.III фиг.2, включает устройства, изображенные на фиг.10.
Элемент сокращения корней п.1 фиг.10 для удобства вычислений корни математической модели регулируемого параметра ф.27.3 приводит к общему знаменателю и вводит новую условную единицу измерения времени, позволяющую избавиться от дробных корней.
Формирователь степенного многочлена п.2 фиг.10 использует ф.27.4 и, подставляя а=(еt), преобразует показательный многочлен в степенной.
Определитель непрерывности математической модели CAP п.4 фиг.10 включает идентификатор критических моментов времени п.6.1, при которых исследуемый многочлен принимает нулевые значения по ф.27.5…ф.27.7. Для этого находятся корни степенного многочлена п.3.1 ф.27.5 (стр.746 л.4) и т.д.
Определитель коэффициентов внутреннего запаздывания п.12, входящий в каждое из звеньев проверки ОДЗ п.5.1…, использует ф.27.1, позволяющую контролировать каждую внутреннюю емкостную составляющую по разнице (входной емкостной силе Fём=х-у) между текущим параметрам входного Хр и выходного параметра У (не прибегая к производным высокого порядка).
Если параметры внутренней емкостной энергии имеют ОДЗ, которая определяется задатчиком ОДЗ п.11 фиг.10 по физическим или техническим характеристикам, то значение ее границ Еём. гр. одз подставляются в определитель ОДЗ выходного параметра Уём. гр. одз п.11 в ф.27.2.1.
Элемент подстановки ОДЗ выходного параметра п.7 в ф.27.8, полученный из полного решения дифуравнения объекта, подставляет границы ОДЗ выходного параметра Угр. одз со второго входа, задаваемые выходным сигналом определителя ОДЭ выходного параметра п.10, или с третьего входа, задаваемого оператором.
Определитель числителя п.8 производит приведение корней r=-1\Т и вводит новую единицу измерения времени (у.е.) ф.27.3.1, преобразуя показательный многочлен в степенной по ф.27.4 и находя корни степенного многочлена ф.27.5. Но при этом вместо исходной формулы ф.27.3 используется ф.27.8. В результате получается ф.68.
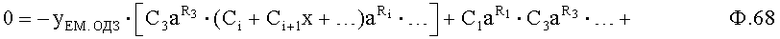
Идентификатор критических моментов времени п.6.2 (в отличие от п.6.1, который исследует только знаменатель «Б» функции) переходит от функции ф.27.3 к уравнению ф.27.8 (которая получена из функции ф.27.3 подстановкой ОДЗ). Используя ф.27.6 и ф.27.7 найденные корни степенного многочлена используют для нахождения моментов времени, при которых емкостная энергия достигает пограничной области ОДЗ ф.68.
Если ОДЗ емкостной энергии задается не для одного звена Wi п.11, а для совокупности звеньев W01…, то ф.27.2.1 п.10 примет вид ф.69

А исследуемая функция с выхода п.7 элемента подстановки ОДЗ выходного параметра примет вид ф.70

Если идентификатор критических моментов времени п.6.1 не смог найти чисто действительных корней, то на его втором выходе формируется синхросигнал, поступающий на второй выход звена проверки ОДЗ п.5.1…, подтверждающий, что выходной регулируемый параметр не превышает ОДЗ емкостной энергии. В противном случае схема сравнения п.9 контролирует, чтобы полученные моменты времени (действительные положительные корни степенного многочлена после подстановки в них стандартных единиц измерения времени) с выхода п.6.2 не попадали в интервал регулирования. Выходной параметр п.9 формирует сигнал о результатах контроля, поступающий на выход блока проверки ОДЗ п.3.1 фиг.2. на вход блока поэтапного регулирования п.3.2.
Таким образом, устройства, входящие в блок проверки ОДЗ фиг.10, позволяют
1) определить неустойчивость и в «малом», и в «большом» п.4 «определителем непрерывности математической модели CAP»;
2) контролировать, чтобы выходной регулируемый параметр У (и емкостная энергия Еём) не выходила за область задаваемой ОДЗ. В противном случае выходной синхросигнал подает команду формирования регулирующего воздействия поэтапно в «блоке поэтапного регулирования» п.3.2. фиг.2.
Если регулируемый параметр не превышает ОДЗ, то на выходе блока проверки ОДЗ п.3.1 фиг.2 формируется команда, которая запускает четвертый «исполнительный уровень».
Блок поэтапного регулирования п.3.2 фиг.2 (фиг.5) начинает поиск регулирующего воздействия по командному сигналу в двух случаях:
1) если регулируемый параметр (емкостная энергия Еём или выходной параметр У) выходит за рамки допустимых значений, то сигнал с выхода блока проверки ОДЗ п.3.1 фиг.2 включает п.3.2;
2) если инерционность регулирующих органов не позволяет осуществить динамические характеристики регулирующего воздействия, сформированного первым «статическим» или вторым «динамическим» уровнем, то сигнал с выхода устройств контроля или с пульта управления оператора начинает работу п.3.2.
Задатчик технически реализуемой структуры регулирующего воздействия п.1 фиг.5 задает функцию регулирующего воздействия (например, в виде показательной функции ф.71).

Формирователь зависимости математической модели регулируемого параметра от регулирующего воздействия п.2 по ф.28.1… и ф.29.1… находит зависимости ф.29.3 постоянных полного решения дифуравнения C01… от параметров входного воздействия (при показательной функции входного воздействия «зависимости» формируются относительно входных Ср и Гр=-1/Тр, входящих в ф.71). Функции ф.29.3, полученные п.1, подставляются в уравнения ф.30 для нахождения зависимостей У01=f01(Ср, Тр), У02=f02(Cp, Тр), …
Формирователь системы уравнений зависимости регулируемого параметра от длительности интервала п.3 подставляет функции ф.30, полученные п.2, в ф.72 (которая используется в формирователе регулирующего воздействия по длительности интервала п.5 и в формирователе длительности интервала по регулирующему воздействию п.5)
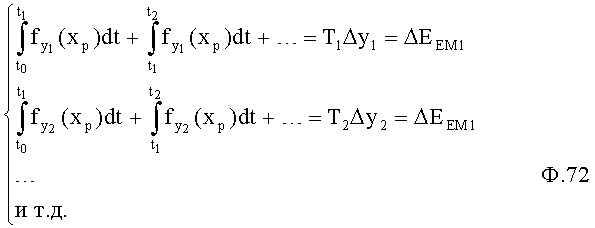
В результате подстановки ф.30 для i-го заданного параметра ΔЕемi=Тi·Δу получается математическое выражение ф.78.1

где 
и т.д.
Преобразование ф.78.1 позволяет получить математическое выражение ф.78.2
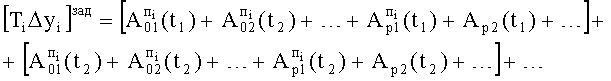
где
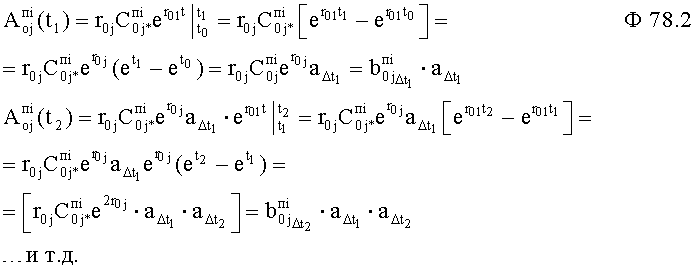

Полученная система уравнений используется для нахождения параметров регулирующего воздействия (Ср1…, rр1…) в формирователе регулирующего воздействия по длительности интервалов п.4. (Фиг.5) в ф.78.3 или для нахождения интервалов регулирования в формирователе длительности интервала по регулирующему воздействию п.5 (фиг.5) в ф.78.4


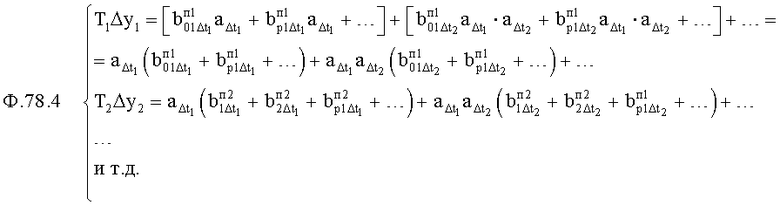
 ;
; 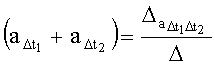 ; и т.д.
; и т.д.
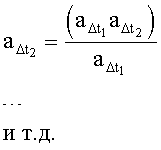
Формирователь интервала п.(1), фиг.6 (входящий в формирователь регулирующего воздействия по длительности интервала п.4 фиг.5) включает задатчик длительности интервала п.1, который задает длительность каждого из интервалов, на которые разделен весь период регулирования, по ф.73.1, составленный относительно входного регулирующего параметра Хр, и по ф.73.2, составленной относительно выходного параметра звена У:

FЕМ=(xp-y)д - допустимое значение емкостной силы

Из результатов вычислений ф.73.1 и ф.73.2 выбирается большее значение и делится на количество интервалов ф.73.3. При вычислении общей продолжительности всех интервалов (ф.73.2) рассматриваются параметры первого (емкостного) звена объекта, вход которого является входом объекта фиг.1.2., т.к. оно участвует в формировании емкостной энергии всех последующих звеньев и к нему предъявляются большие требования.
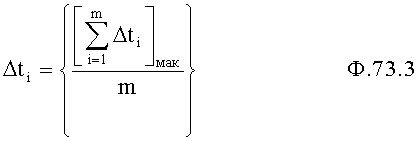
где
y0i - допустимая скорость изменения выходного параметра емкостной составляющей объекта;
Т0i - постоянная внутреннего запаздывания звена Wi фиг.1.2;
ω - степень сложности сочетания заданных внутренних параметров;
m - количество интервалов (как правило, при несложном сочетании регулируемых параметров) равно количеству емкостных составляющих (чем выше степень сложности сочетаний заданных параметров, тем больше интервалов).
Определитель дополнительного интервала п.2 фиг.6, при поступлении на второй и третий входы значения увеличенной длительности интервала с выходов п.5, п.8, вычисляет математические зависимости, приведенные в ф.33, для нахождения параметров регулирующего воздействия Хр (при показательной функции Хр искомыми параметрами являются постоянная Ср и коэффициент внутреннего запаздывания Тр=-1\Гр).
Определитель коэффициентов регулирующего воздействия п.3 использует систему уравнений ф.74.1 для нахождения параметров регулирующего воздействия Хр.
При этом функции f1.1, f1.2, …, f2.1, f2.2, … и т.д. решаются относительно Хр и подставляются в систему уравнений ф.33.1



Например, если регулирующее воздействие имеет показательную функцию, то ф.74.1 примет вид ф.74.2

Если постоянная внутреннего запаздывания Тр регулирующего органа не поддается регулированию, то в ф.74.2 подставляется его значение и вычисляется постоянная Ср1,2… входного воздействия для соответствующего интервала регулирования. Если регулируемым параметром является не только постоянная Ср, но и внутренний коэффициент усиления Тр, то значения этих параметров определяются по ф.74.3, в которые подставляются ОДЗ регулируемого параметра.

Математическое выражение ф.74.3 для постоянной Ср из формулы 2) подставляется в формулу 3) и в формулы ф.74.1.1, ф.74.1.2,… и т.д. для вычислений внутренних запаздываний Тр регулирующего воздействия Хр для каждого интервала времени с учетом границ ОДЗ величины скорости изменения (производной) регулирующего воздействия.
Если постоянная внутреннего запаздывание Тр входного воздействия не регулируется, то звено проверки технической реализации п.4 найденная постоянная Ср для данного интервала времени подставляется в ф.75, которая контролирует соблюдение ОДЗ технической реализуемости исполнительного органа.

Определитель коэффициентов (постоянных) свободного и вынужденного состояний объекта п.6 в дифуравнение объекта подставляет математическую модель входного воздействия, находя коэффициенты вынужденного состояния ф.76.1.

Найденные коэффициенты (постоянные) Св вынужденного состояния подставляются в ф.76.2 для вычисления коэффициентов свободного состояния Ссв1…

где у', у", … - производные регулируемого параметра определяются по начальным параметрам у01, у02,… емкостных составляющих объекта. Для второго интервала и последующих определяют по конечным параметрам предыдущего интервала.
Звено проверки технической реализации п.7 найденную математическую модель регулируемого параметра У=Ссв1е + … подставляет в ф.77 для проверки соблюдения ОДЗ регулируемого параметра.
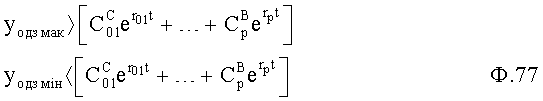
Если звенья проверки технической реализации п.4 и п.8 фиксируют превышения ОДЗ, то корректоры длительности интервала п.5 и п.8 увеличивают соответствующий либо предыдущий (через корректор интервалов п.1.1, п.1.2… и т.д. фиг.5) интервал по ф.78.
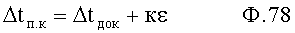
где ε - величина превышения ОДЗ = (ут-уОДЗ);
к - коэффициент коррекции;
Δtдок - интервал времени до коррекции;
Δtп.к - интервал времени после коррекции.
Таким образом, совокупность устройств, входящих в формирователь воздействия по длительности интервала п.4 фиг.5, позволяет задать длительность каждого интервала, в каждом из которых регулирующее воздействие упрощается до желаемого уровня, что упрощает работу исполнительных органов. Для каждого из интервалов находится свой регулируемый параметр (Ср или Гр, при показательной функции регулирующего органа).
Полученные математические модели регулирующего воздействия Хр и регулируемого параметра У проверяются на соблюдение ОДЗ и при их превышении исследуемый интервал увеличивает свою продолжительность. После чего формируется новое регулирующее воздействие.
Если после соответствующих коррекций подобрать параметр регулирующего воздействия невозможно, то синхросигнал с первого выхода п.4 запускает работу формирователя длительности интервала по регулирующему воздействию п.5.
Формирователь длительности интервала по регулирующему воздействию п.5.1 формирует чередование интервалов «активного» и «пассивного» режимов ф.79, используя ф.33.1.

где  ,
,  ,
,  … - интервалы с «активным» режимом
… - интервалы с «активным» режимом 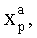
 ,
,  , … - интервалы с «активным» режимом
, … - интервалы с «активным» режимом 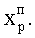
Задатчик «активного» интервала п.5.2.1 фиг.5 (например, показательной функции времени ф.80.1) определяет величину параметров входного регулирующего воздействия  по реально доступному и допустимому значению.
по реально доступному и допустимому значению.

где Тр=(-1\Гр) - постоянная внутреннего запаздывания; если инерционностью исполнительного органа можно пренебречь, т.е Гр=0; то Ф.80.1 примет вид ф.80.2 (например, если исполнительный орган имеет нелинейный ступенчатый характер изменения),
Сра=[(1\Q)Еём зад] - постоянная (или переменный коэффициент), величина которой определяется заданным значением изменения емкостной энергии Еём зад и Q,
Q - коэффициент, величина которого определяет плавность регулирования

Задатчик «пассивного» регулирования п.5.2.2 формирует регулирующее воздействие Хпр ф.81, значение которого должно отличаться от значения активного режима Хар на величину, позволяющую компенсировать отсутствие динамических возможностей регулирующих органов.

где g - коэффициент, величина которого зависит от степени сложности соотношений между значениями заданных параметров У01, У02, … (или Еем1зад. Еем2зад, …), чем сложнее сочетание заданных значений, тем больше g.
Вычислитель длительности интервалов п.5.3 формирует систему уравнений для неизвестных показательной функции п.5.3.1 фиг.5 (фиг.19). П.I фиг.19 формирует математическую модель для первого «активного» интервала. П.II.1 п.II.2, … фиг.19 формируют математическую модель для всех последующих интервалов: второго («пассивного»), третьего («активного»), и т.д.
Вычислитель длительности интервала п.5.3 формирует систему уравнений для неизвестных входного регулирующего воздействия (при математической модели в виде суммы показательных функций неизвестными являются коэффициенты Ср1, Ср2,… Гр1, Гр2,…) формирователем системы уравнений п.5.3.1 фиг.2 (фиг.19).
Задатчик коэффициентов запаздывания и начального значения регулирующего воздействия п.1.1, фиг.19 подставляет заданные параметры регулирующего воздействия (пассивного п.5.2.1 фиг.5 режима) в ф.79.
Формирователь модели регулируемого параметра п.1.2 по параметрам регулирующего воздействия (с выхода п.1.1) и начальным значениям регулируемых параметров формирует параметры регулируемых параметров в вычислителях коэффициентов свободного и вынужденного состояния 1-го параметра п.1.2.1, 2-го параметра п.1.2.2 и т.д. по ф.82.

где Δ, Δ01… находят из системы уравнений при tн

Аналогичные вычисления производятся для второго (пассивного) интервала и всех последующих интервалов, при этом используются ф.37.1…ф.41, ф.80.1,…ф.81.
Задатчики регулирующего воздействия п.П.1.(3), п.П.3.(3), … фиг.19 используют ф.81 для задания «пассивного» регулирующего воздействия. Задатчики регулирующего воздействия п.П.2.(4), п.П.4(4), … для задания активного регулирующего воздействия использует ф.80. Вычислитель коэффициентов вынужденного состояния п.П.1.(4), п.П.2(4), … использует ф.82.1.
Формирователи зависимостей коэффициентов свободного состояния п.П.1.5.1(а), п.П.1.5.2(а), … п.П.2.5.1(а), п.П.2.5.2(а), … и т.д. используют ф.38.1, ф.38.2.
Разделитель на известные коэффициенты и искомые параметры п.П.1.5.1(б), п.П.1.5.2(б), … п.П.2.5.1(б), п.П.2.5.2(б), … и т.д. выделяет искомые (неизвестные значения длительности интервалов регулирования Δt1…) параметры  по ф.39, ф.40.
по ф.39, ф.40.
Определитель интервалов времени п.5.3.2 фиг.5 (фиг.20) использует систему уравнений ф.40, в которую включены не только введенные неизвестные  , но и их произведения А=(аi. aj). Для упрощения расчетов значения произведений А1… ф.41 приняты за отдельные неизвестные, для нахождение которых количество уравнений увеличивают ф.42 дифференцированием исходных уравнений. Дифференциатор искомых параметров п.III.1 использует ф.83.1
, но и их произведения А=(аi. aj). Для упрощения расчетов значения произведений А1… ф.41 приняты за отдельные неизвестные, для нахождение которых количество уравнений увеличивают ф.42 дифференцированием исходных уравнений. Дифференциатор искомых параметров п.III.1 использует ф.83.1

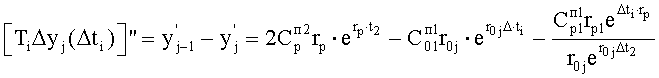 ; и т.д.
; и т.д.
Дифференциатор задаваемых параметров п.III.2 использует ф.83.2

где yi-1, yi, yi+1 - заданные (Фиг.1.1).
Таким образом, полученная математическая модель регулируемого параметра ф.40 дифференцируется ф.83.1: где Уi(t) находят по ф.39; Ср находят по ф.39, - и формируется систем уравнений ф.84 относительно неизвестных а1, а2, …, А1, А2, …

где fa1, fа2, … найдены относительно выбранных показательных функций 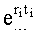 ;
;
fA1, fA2,… найдены относительно выбранных A=ai·aj;
Д1, Д2, … заданные Т1… У1… и их производные, вычисленные по ф.83.2.
Вычислитель определителей 1У использует систему уравнений ф.84 для нахождения определителя системы (основного определителя ф.43 и определителей относительно неизвестных а…, А…).
Неизвестные а…, А… выбираются таким образом, чтобы они (их совокупность) включали все искомые интервалы времени t1, t2,… и позволяли (их совокупность) вычислить каждый из интервалов времени.
Найденные определители (с выхода п.1У) подставляются в ф.44 вычислителем показательной функции У для нахождения выбранных неизвестных а… А…
После того как показательные функции 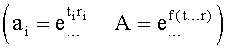 были найдены, вычислитель интервалов 1У логарифмирует найденные функции по ф.45, формирует систему уравнений для нахождения неизвестных интервалов времени t1, t2,… по ф.85.1 и находит эти значения по ф.85.2.
были найдены, вычислитель интервалов 1У логарифмирует найденные функции по ф.45, формирует систему уравнений для нахождения неизвестных интервалов времени t1, t2,… по ф.85.1 и находит эти значения по ф.85.2.


Таким образом, формирователь длительности интервала по регулирующему воздействию п.5 фиг.5 формирует систему уравнений (по заданным значениям регулируемых параметров и технически реализуемому контрасту входных воздействий), позволяющую определить длительность интервалов регулирования «активного» и «пассивного» режимов.
Определитель математической модели необходимого входного воздействия п.6 фиг.5 сравнивает эффективность математических моделей регулирующих воздействий, принятых с выходов п.4 (который позволяет добиться плавности) и п.5 (который позволяет регулировать даже в аварийных режимах, когда износ или поломка рычагов плавного регулирования теряет свои регулирующие свойства) на первом и втором своих входах.
Достоинство блока поэтапного регулирования п.3.2 фиг.2 в том, что требования к исполнительным органам снижаются, но при этом увеличивается полный интервал регулирования. Достоинства формирователя емкостных сил, компенсирующих возмущения регулирующих органов, п.4.1 фиг.2 (фиг.9) позволяет с максимальным быстродействием приспособиться к изменившимся параметрам регулирующего органа и перейти от поэтапного регулирования к регулированию за один период.
Формирователь системы уравнений емкостных сил п.1 фиг.9 формирует систему уравнений по ф.39*.
Формирователь системы двух уравнений для каждой входной силы п.2 фиг.9 используют ф.40*.
Формирователь объединенных уравнений исключением промежуточных входных сил п.3 фиг.9 использует ф.40.0*.
Объединитель уравнений для всех емкостных сил относительного входного воздействия п.4 использует ф.40.1*.
Элемент подстановки п.5 фиг.9 осуществляет следующую подстановку:
1) полное решение математической модели дифуравнения п.5.2 ф.40.1.1* в ф.40.1*;
2) заданные значения параметров У1зад… в ф.40.1*;
3) идентифицированные текущие значения корней регулирующего воздействий Гр1, … и регулируемого параметра Г01, … в ф.40.1.1*.
Формирователь зависимости коэффициентов математической модели выходных сил от коэффициентов входного воздействия п.6 фиг.9 для получения ф.40.2* использует коэффициенты начальных значений С… предыдущих периодов для нахождения коэффициентов начальных значений последующих периодов.
Элемент подстановки полученных значений в математическую модель п.7 фиг.9 ф.40.2* подставляют в ф.40.1.1* и ф.40.1*.
Формирователь системы уравнений относительно коэффициентов входного воздействия п.8 фиг. преобразует систему уравнений ф.40.1* (после подстановок, приведенных в предыдущих устройствах п.5 п.6 п.7) в систему уравнений ф.41*.
Вычислитель коэффициентов входного воздействия делением определителей п.9 использует систему уравнений ф.41* для нахождения коэффициентов входного воздействия Ср1… ф.42.
Таким образом, формирователь емкостной силы п.4.1, входящий в IV-й исполнительный уровень (в отличие от устройств, входящих в 1-й статический уровень и в уровни, формирующие коррекцию инерционных настроек: II-й динамический, III-й качества и самоконтроля, - п.5 фиг.2), позволяет решить задачу регулирования за один временной интервал, непрерывно приспосабливаясь к изменяющимся параметрам (инерционности) регулятора и объекта. Для этого инерционность исполнительного воздействия Хр формируется в виде совокупности корней дифуравнения реального исполнительного органа Гр1, Гр2,…, при этом основными искомыми регулирующими параметрами являются постоянные Ср1, Ср2,… При часто меняющихся параметрах исполнительного органа и достаточно широких областях ОДЗ регулирующего Хр и регулируемого У параметров формирователь емкостных сил п.4.1 является наиболее эффективным задатчиком регулирующего воздействия Хр.
Если параметры регулирующего органа не меняются, то их значение можно включить в математическую модель объекта W0 и использовать III-й уровень, который может компенсировать поэтапным регулированием большую инерционность исполнительного органа или сложность совокупности внутренних задаваемых параметров или объекта.
Если задаваемая совокупность параметров не очень сложная и исполнительные органы свои параметры не меняют часто, то наиболее эффективный II-й динамический уровень, который помимо быстродействия обеспечивает достаточный запас устойчивости, за счет задаваемой устойчивой структуры переменных (динамических) корней регулирующего воздействия и переменных (динамических) коэффициентов свободного состояния объекта. Если ограничения устойчивости не стоят на первом плане, то наиболее эффективным является 1-й статический уровень (со статическими, т.е. постоянными, значениями корней дифуравнения модели регулирующего воздействия).
Вычислитель текущих значений входного воздействия п.4.2 фиг.2 анализирует информацию со всех уровней (1-го…4-го), выбирая наиболее эффективный для данной ситуации, задаваемой оператором и получаемой с выхода идентификатора п.7.
Регулирующий орган п.4.3 принимает сигнал о текущем и последующих значениях регулирующего воздействия и формирует его на входе объекта.
Идентификатор п.7 фиг.2 (фиг.7.0) по текущим значениям входного Хр и выходного параметра объекта У, используя ф.43.1*…ф.64, определяет не только коэффициенты внутреннего запаздывания Т01…, текущие выходные параметры каждой внутренней емкостной составляющей объекта У01,…, но и емкостную энергию Еём:
- по косвенным параметрам Т01, умноженному на изменение выходного параметра,
- по прямому параметру, разнице интеграла входного и выходного параметров.
Так как физическая природа регулируемых параметров объекта изменчива из-за сложности и многогранности физических явлений и их законов, при идентификации параметров объекта используется несколько режимов:
1) для емкостной энергии Еём:
- режим с отличным от нуля входным воздействием (условно принятым «активным»), емкостная энергия при этом пассивно поглощается п.1…п.3 фиг.7.0,
- режим с нулевым входным воздействием (условно принятым «пассивным»), при этом емкостная энергия (накопленная до этого в «пассивном» режиме) активно действует на выходной параметр п.4 фиг.7.0,
2) для внутренних коэффициентов запаздывания Т01, …:
- текущий режим по измеренной динамической характеристике входного и выходного параметров Хр, Хр, …, У01, У02, …, п.1 фиг.7.0 (фиг.7.4),
- режим текущего интервала регулирования, т.е. по совокупности параметров с момента начала регулирования по текущий момент п.2 фиг.7.0 (фиг.7.5),
- полный интервал регулирования, по полной характеристике параметров в течение полного интервала регулирования п.3 (фиг.7.6),
- дополнительный «пассивный» режим, при входном нулевом воздействии (относительно дополнительного все предыдущие режимы считались «активными») п.4 фиг.7.0 (фиг.7.7).
Таким образом, сравнение совокупности выходных, внутренних (запаздывания) и емкостных параметров на разных этапах регулирования активного и пассивного режимов п.5 фиг.7.0 позволяет контролировать достоверность математической модели объекта и характер возмущающих воздействий.
Если параметры исполнительного органа, объекта имеет малую инерционность и требуется повышенная точность, то используются параметры математической модели с выхода п.1 фиг.7.0.
Если возмущения кратковременны, а объект и исполнительный орган имеют большую инерционность, то наиболее эффективны параметры с выхода п.2 фиг.7.0.
Для начального момента регулирования удобно использовать параметры, полученные на протяжении всего предыдущего периода регулирования с выхода п.3 фиг.7.0.
Если найденные параметры с выхода п.1, п.2 и п.3 (полученные с учетом входного активного воздействия) отличны между собой по неизвестной причине, то параметры с выхода п.4 (пассивного режима) позволят окончательно найти реальное значения параметров объекта, без влияния возмущений входного воздействия.
Определитель утечки емкостной энергии п.5 фиг.7.0 позволяет идентифицировать аварийный режим, вызванный утечкой входной энергии. Входящие в него схемы сравнения п.5.2.1… п.5.5.4 используют ф.86.1…ф.86.3, в которых сумма емкостных энергий каждого звена должна равняться емкостной энергии, найденной для объекта в целом ф.86.1 п.5.2.1… п.5.2.4, емкостная энергия каждого звена и всего объекта в целом, полученная с выхода быстродействующего косвенного определителя емкостной энергии п.1, должна равняться емкостной энергии соответствующих звеньев, полученной с выхода прямого определителя емкостной энергии текущего момента п.2 ф.86.2 Ф.86.3 п.5.2.2 и п.5.2.3. Определитель возмущений п.5.3 фиксирует результаты сравнений и сравнивает их с результатами идентификации по переходной характеристике всего интервала регулирования в активном (рабочем) режиме, полученной блоком контроля полного переходного периода п.3 и в пассивном (дополнительном) режиме п.4 полученной блоком выходной емкостной энергии п.4.

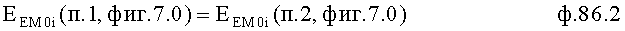

Таким образом, совокупность выходного параметра У01,…, внутреннего запаздывания Т01…, емкостной энергии Еём1… для каждой емкостной составляющей объекта W01… контролирует состояние регулируемого объекта W0 в каждый момент времени п.1, на текущем интервале п.2, на законченном прошедшем интервале (активном рабочем или пассивном дополнительном). Сравнение их значений необходимо для проверки правильности идентификации и для контроля фиксации аварийного режима: большой потерей емкостной энергии, связанной с потерей объектом своих свойств, приводящей к последующей катастрофе.
В начальный момент времени, до поступления команды «пуск», подаваемой оператором, на выход идентификатора п.7 поступает информация о параметрах объекта, задаваемых оператором или полученных в предыдущих периодах регулирования. IV-й исполнительный уровень поддерживает на входе исполнительного органа п.4.3 команду, сформированную в предыдущих периодах регулирования одним из уровней 1-м…4-м, которые в начальный момент регулирования, до поступления команды «пуск», находятся в ждущем режиме.
После того, как заданные значения регулируемых параметров и их область допустимых значений поступят на входы всех уровней регулирования, оператором или автоматическим командным устройством посылается на входы всех устройств сигнал «пуск». Определитель необходимой емкостной энергии п.1.1 фиг.2 находит ее значения и передает на входы формирователя п.1.2 и другие уровни регулирования. Математическая модель регулирующего воздействия, сформированная 1-м уровнем, проверяется на техническую реализацию п.1.3 фиг.2. Если техническая реализация возможна, то математическая модель этого воздействия передается на III-й уровень для проверки ОДЗ п.3.1. Если техническая реализация невозможна, то II-й динамический уровень формирует математическую модель регулирующего воздействия с переменным корнем запаздывания дифуравнения, структура которого обеспечивает заданную устойчивость, а следовательно, и возможность технической реализации. Переменный коэффициент свободной составляющей объекта обеспечивает заданную устойчивость независимо от параметров объекта. Полученная математическая модель регулирующего воздействия на втором динамическом уровне регулирования проверяется третьим уровнем качества и самоконтроля п.3.1.
Если проверяемая математическая модель регулируемого параметра не превышает ОДЗ, то математическая модель соответствующего регулирующего параметра поступает на вход 4-го исполнительного уровня в вычислитель текущих значений входного воздействия.
Параметры исполнительного органа постоянно контролируются четвертым уровнем и при возникновении возмущений или «аварийного» режима четвертый исполнительный уровень п.4.1 начинает подстраиваться к текущему значению параметров исполнительных органов. Если блок проверки ОДЗ п.3.1 фиксирует превышение ОДЗ математической модели регулируемого параметра, то блоком поэтапного регулирования п.3.2 начинает поиск математической модели поэтапного регулирования: при возможности плавного регулирования используется формирователь регулирующего воздействия по длительности интервала п.4 фиг.5. При нелинейности или ограниченности возможностей исполнительного органа используется формирователь длительности интервала по регулирующему воздействию п.5 фиг.5.
Пропорциональное звено с выхода объекта регулирования п.8 идентифицирует коэффициент усиления объекта и при необходимости увеличивает сигнал с выхода объекта для его идентификации. Идентификатор п.7 хранит в своей памяти информацию о предыдущей идентификации и контролирует текущее изменение регулируемых параметров на протяжении всего времени регулирования для предотвращения аварийного регулирования или других неблагоприятных режимов и при необходимости перезапускает поиск новой математической модели регулирующего воздействия.
Экономический эффект достигается благодаря тому, что контроль за внутренней емкостной энергией объекта позволяет повысить срок службы оборудования, входящего в объект регулирования, повысить качество регулирования выходного параметра и предотвратить аварийный режим, связанный с неустойчивой структурой объекта.
Используемая информация
1. Попов Е.П. Теория линейных систем автоматического регулирования и управления: Учеб. Пособие для втузов. - М.: Наука, 1989 г.
2. Кулаков Г.Т. Инженерные экспресс-методы расчетов промышленных систем регулирования: Справочное пособие. - Мн.: Выш. шк., 1984 г.
3. Ротач В.Я. Теория автоматического управления теплоэнергетическими процессами: Учебник для вузов. - Энергоатомиздат, 1985.
4. Выгодский М.Я. Справочник по высшей математике. М.: Гос. изд. «Технико-теоретической лит.», 1957.
5. Бессекерский Б.А., Попов Е.П. Теория систем автоматического регулирования. М.: «Наука», 1972.


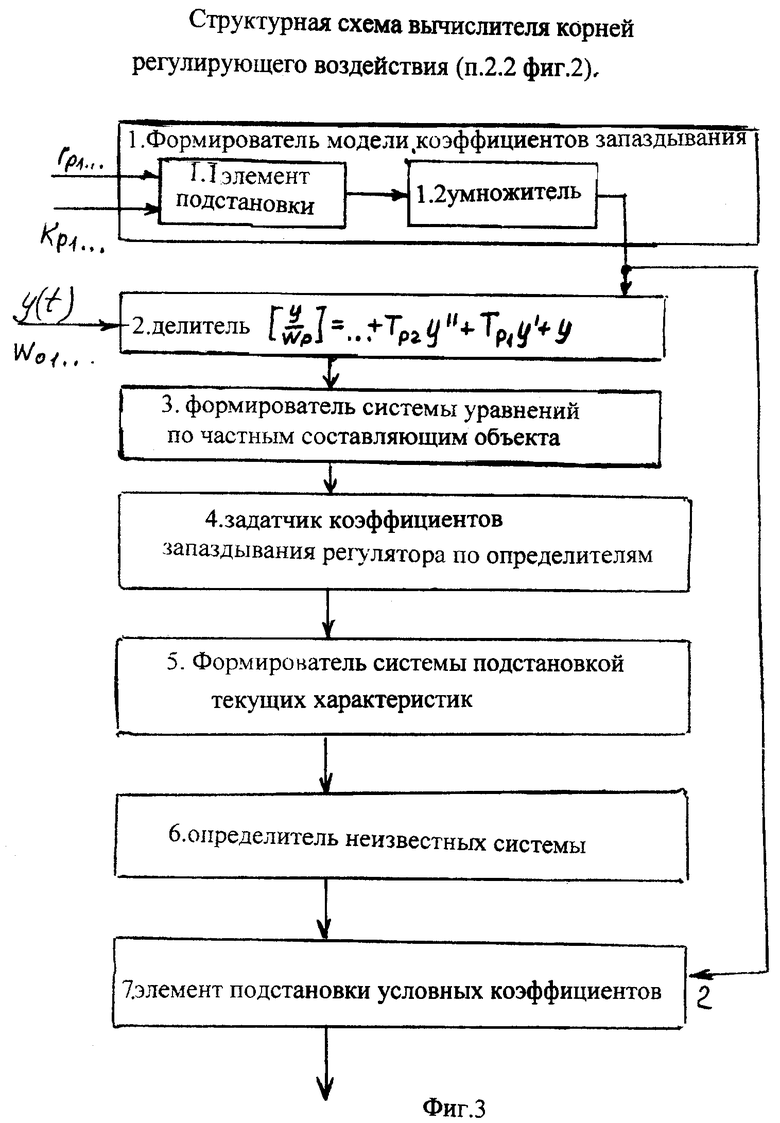

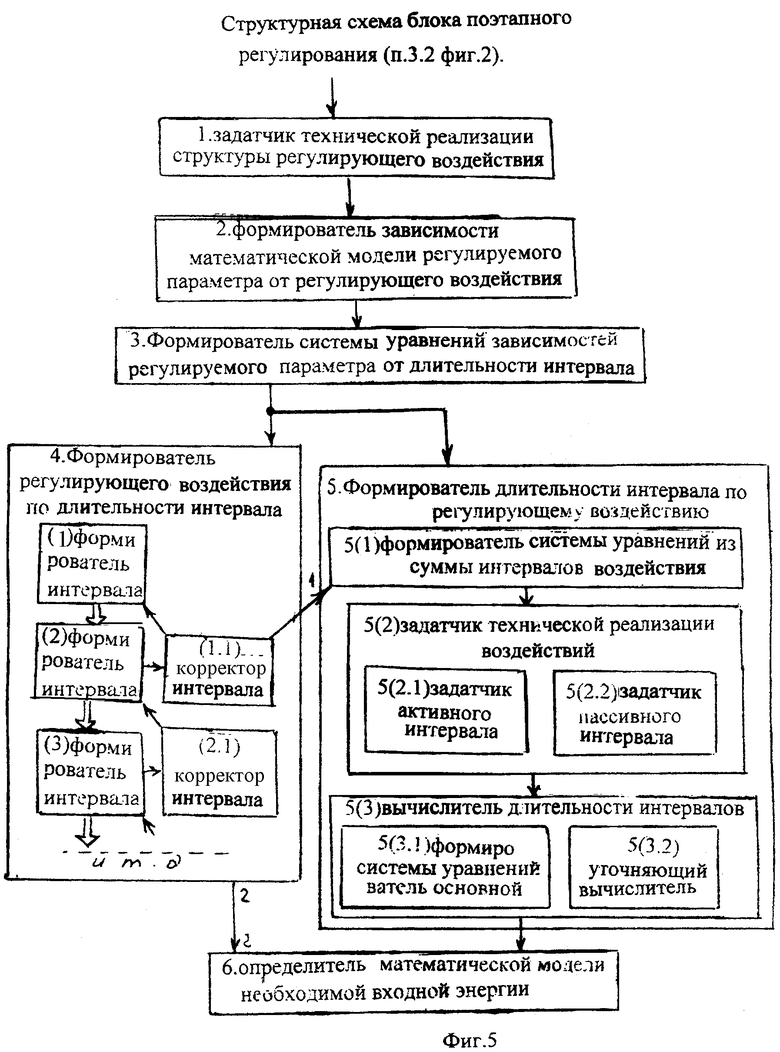
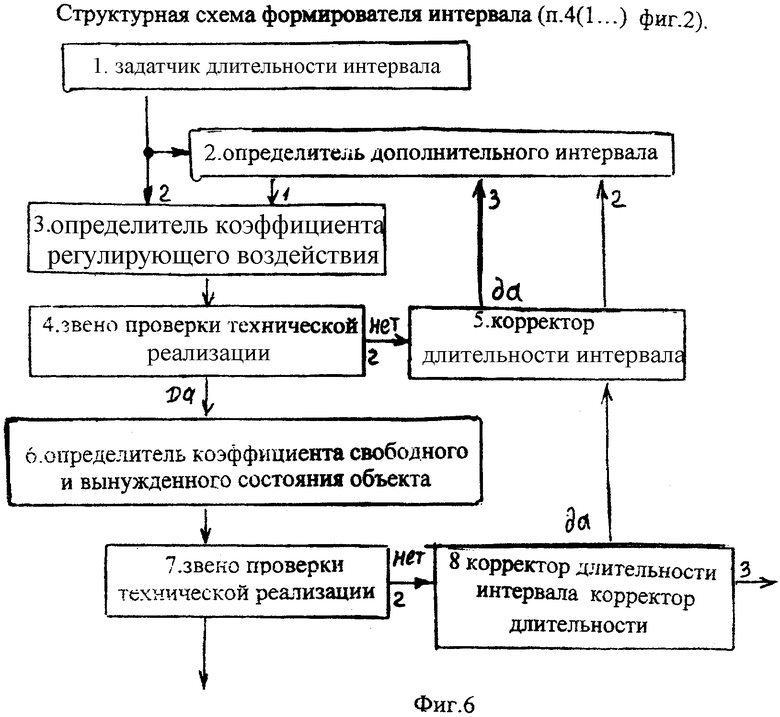

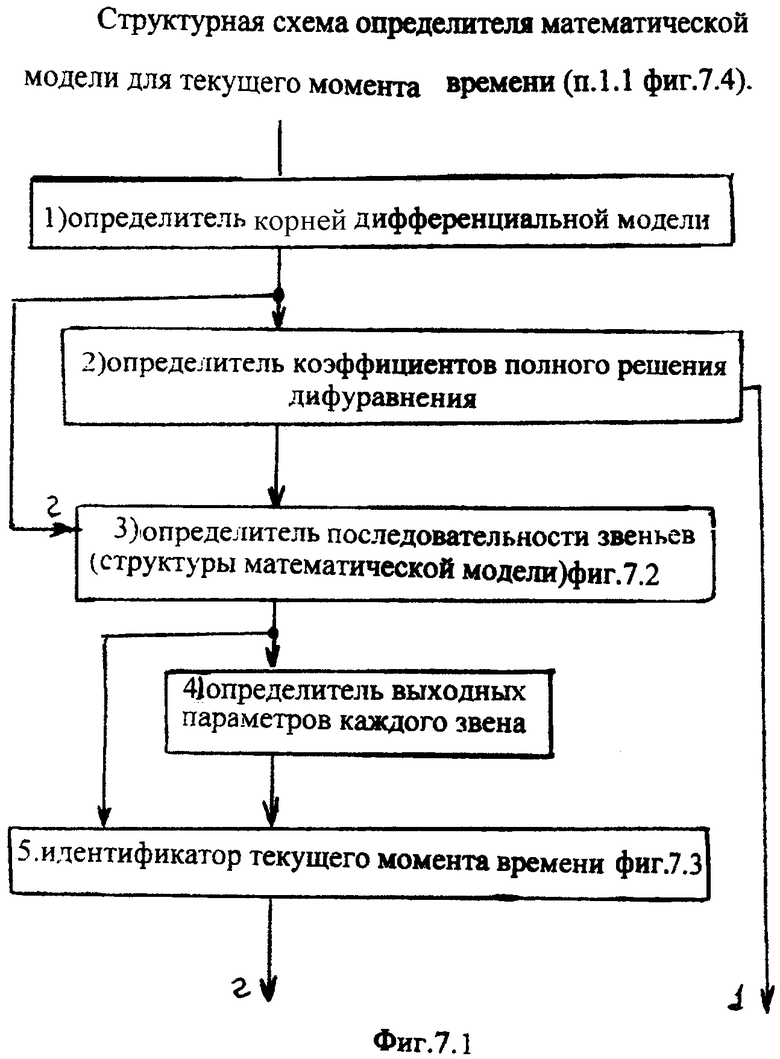
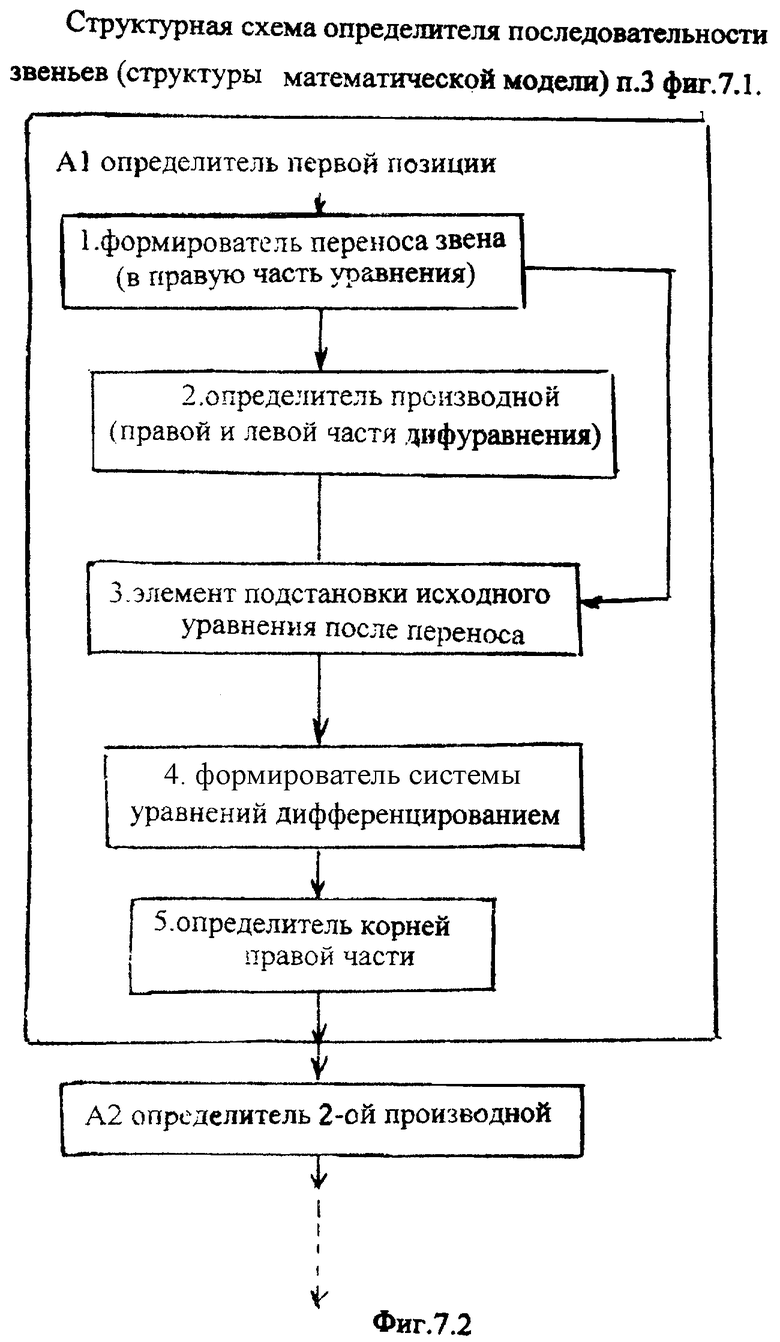

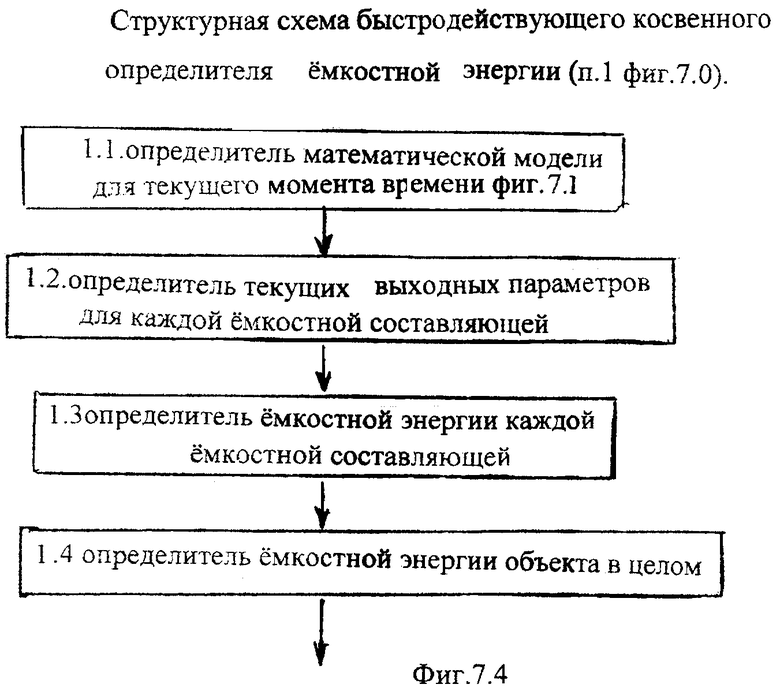
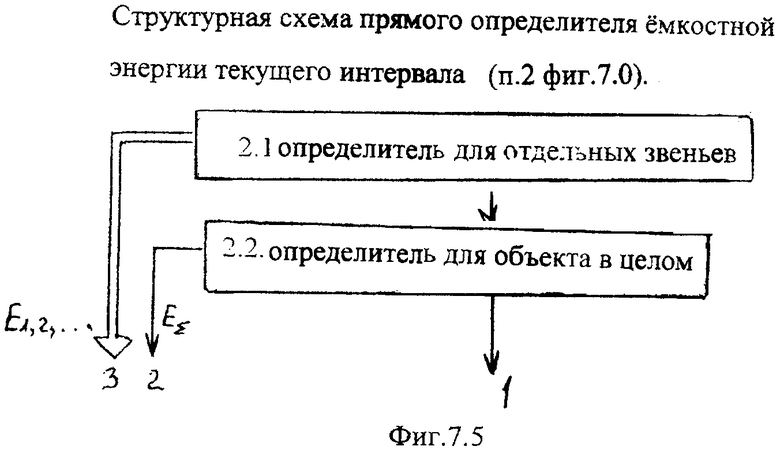


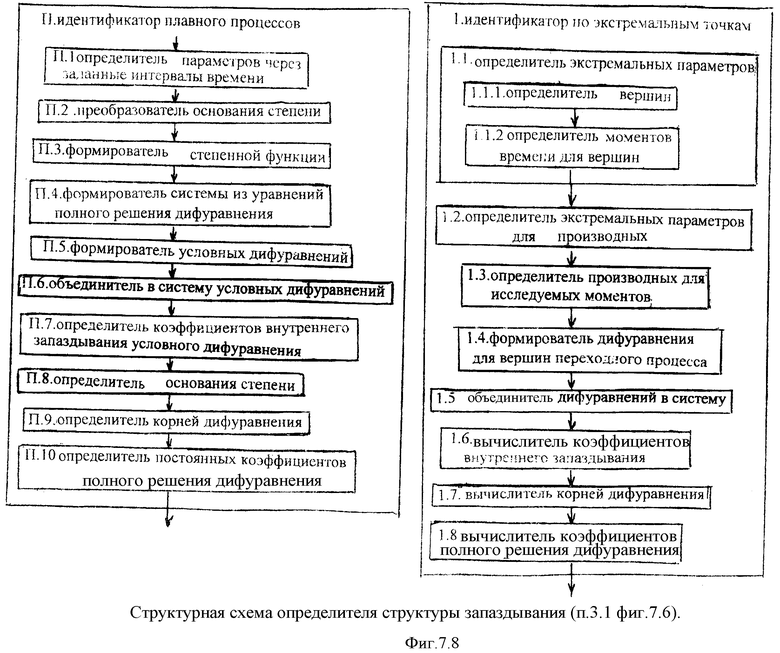
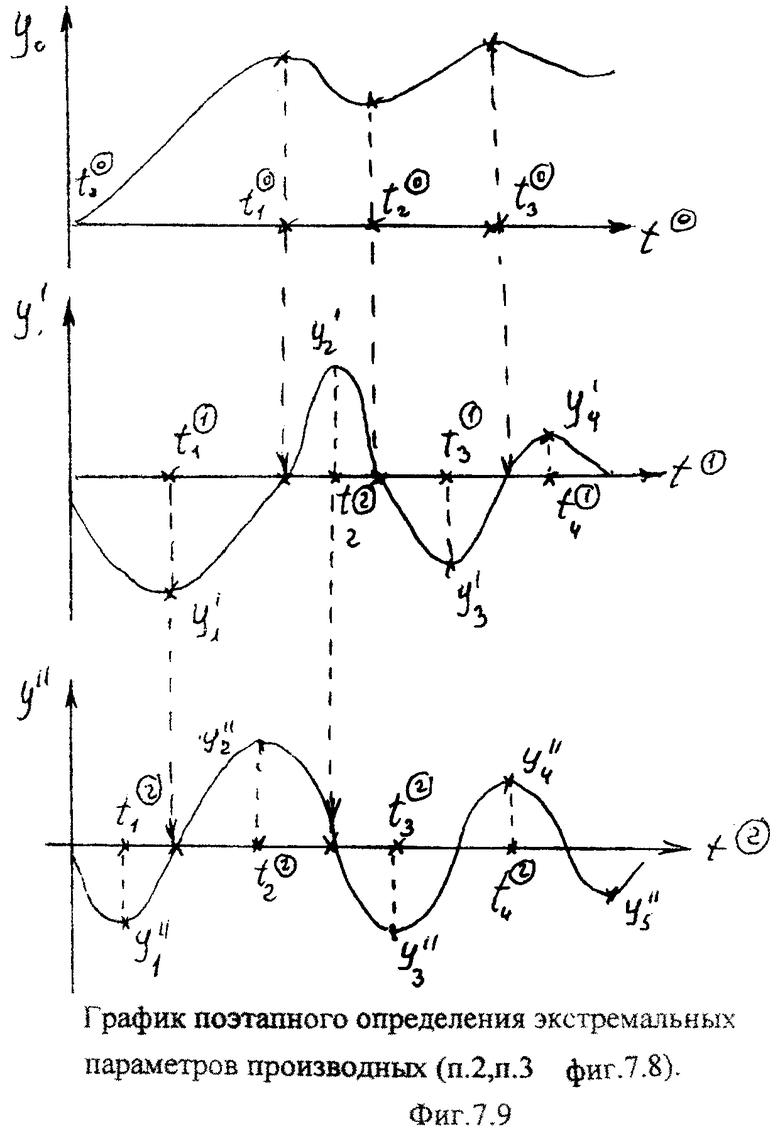
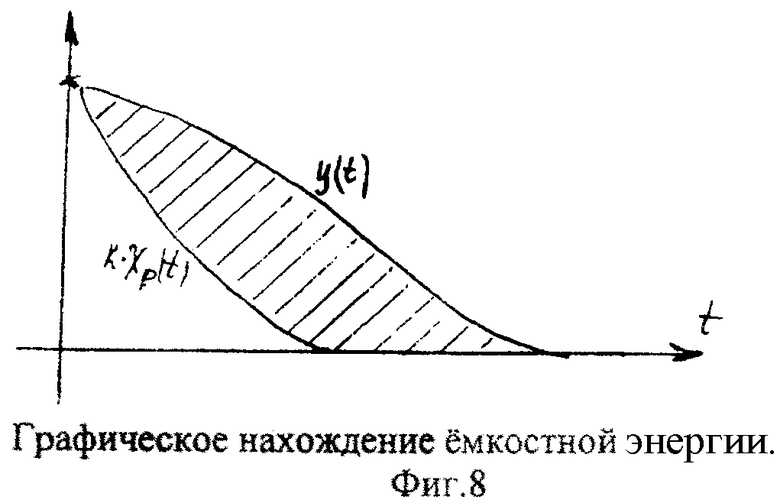


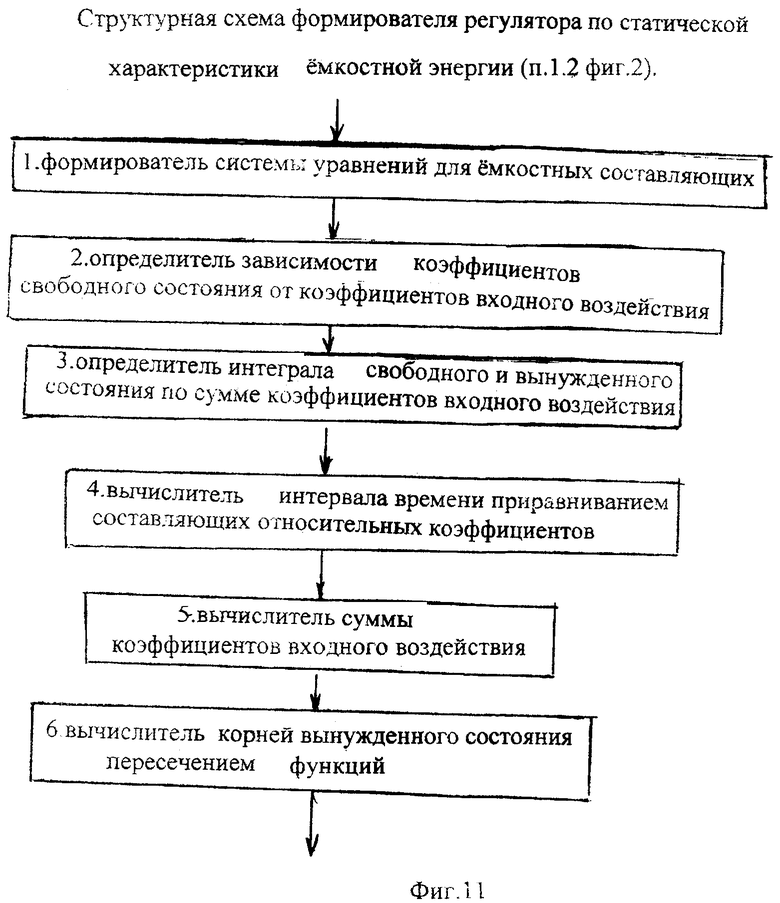

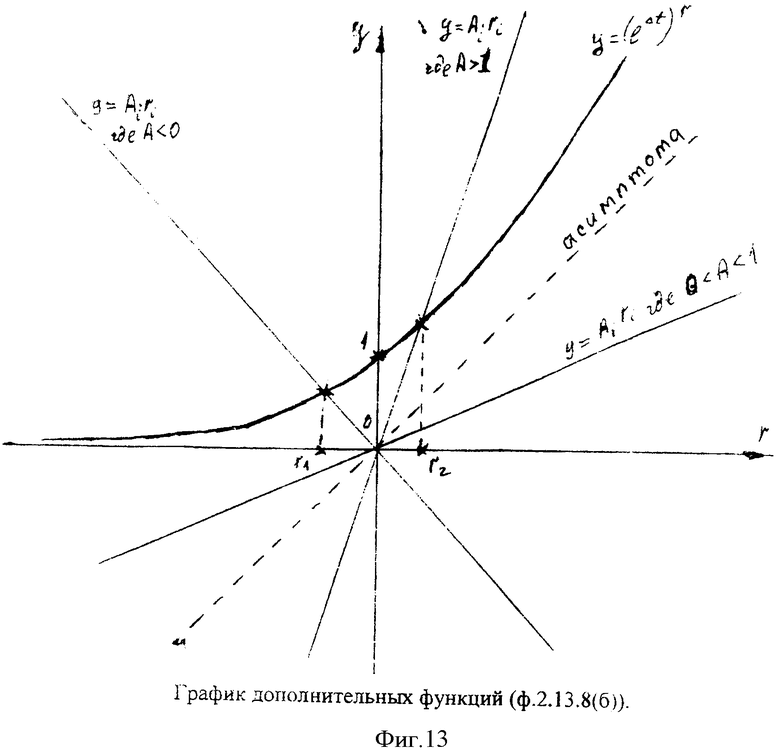
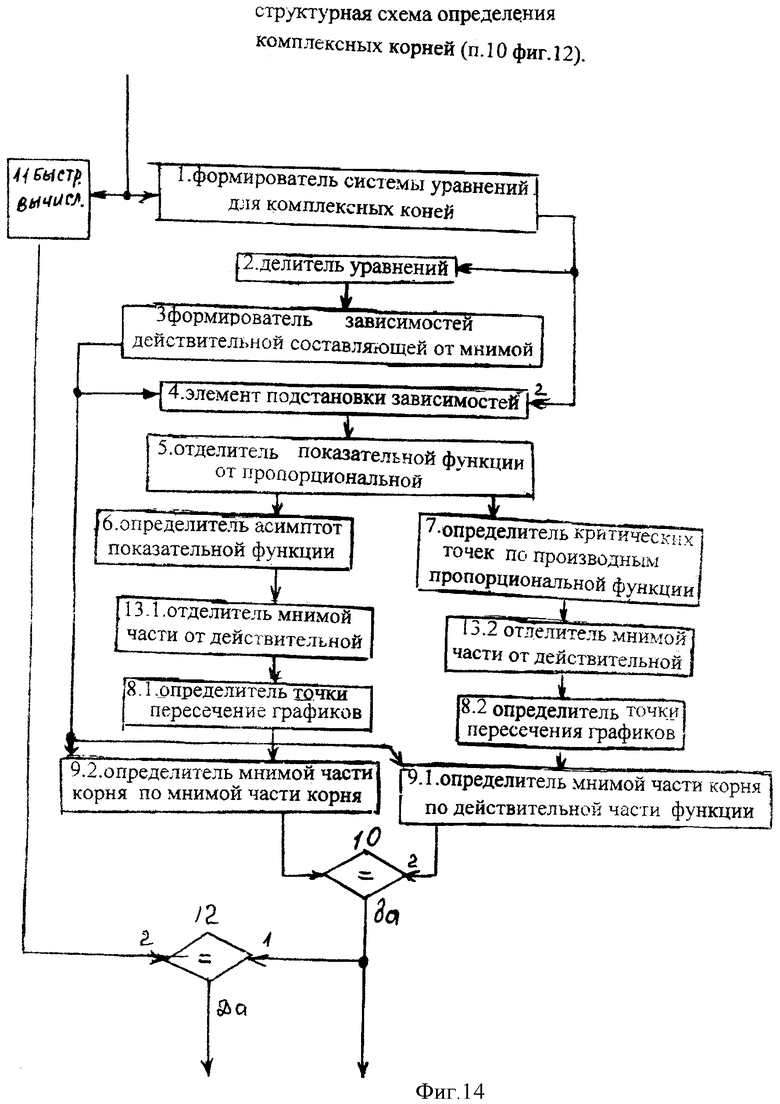
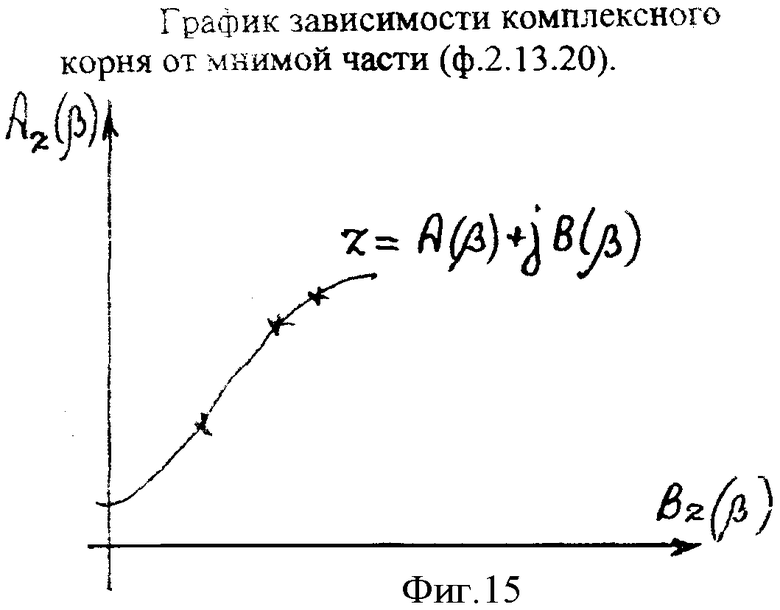
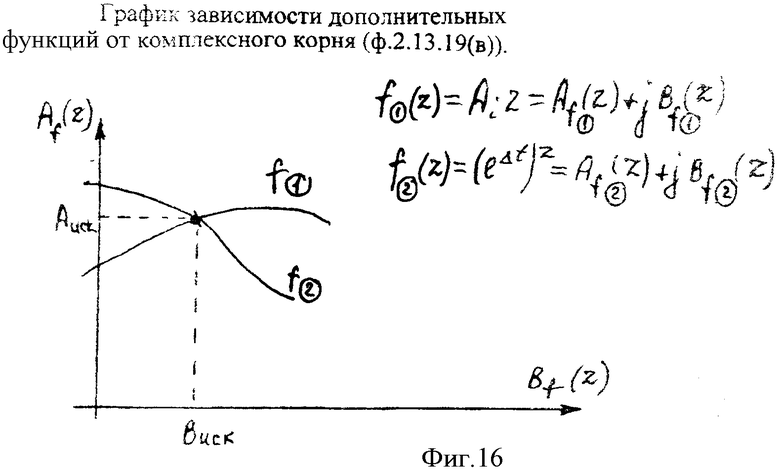
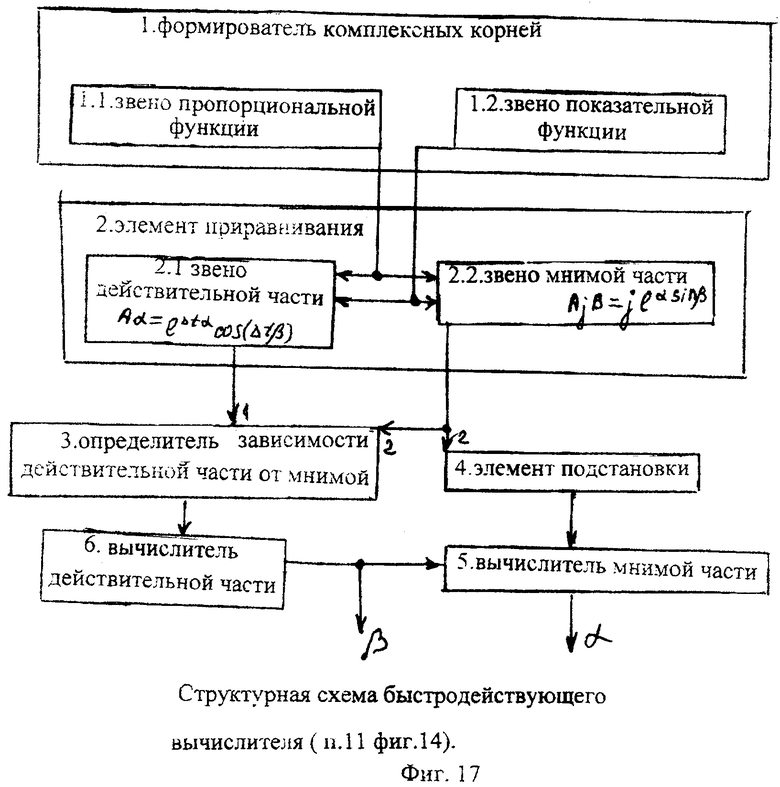


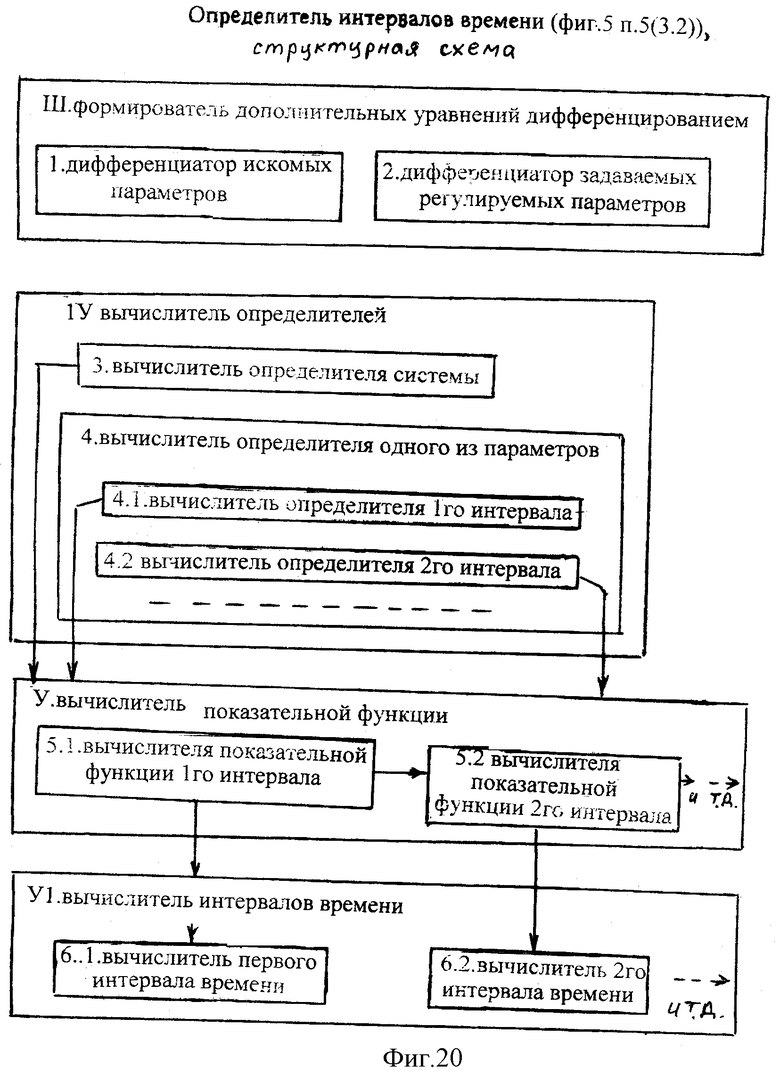
Изобретение относится к области автоматического регулирования. Техническим результатом является повышение эффективности регулирования внутренней емкостной энергии объекта с переменными параметрами. В систему автоматического регулирования, включающую последовательно соединенные объект регулирования, пропорциональное звено, идентификатор, уровень статических характеристик, уровень динамических характеристик, уровень качества и самоконтроля и исполнительный уровень, дополнительно введены в уровень статических характеристик последовательно соединенные определитель необходимой емкостной энергии, формирователь регулирования по статической характеристики емкостной энергии и определитель технической реализации, в уровень динамических характеристик дополнительно введены задатчик устойчивости, вычислитель корней регулирующего воздействия, вычислитель коэффициентов свободного и вынужденного состояния; в третий уровень качества и самоконтроля дополнительно введены последовательно соединенные блок проверки области допустимых значений, блок поэтапного регулирования; в исполнительный уровень введен формирователь емкостных сил, компенсирующий возмущения регулирующего органа; в идентификатор введены последовательно соединенные быстродействующий косвенный определитель емкостной энергии, прямой определитель емкостной энергии текущего интервала, блок контроля полного переходного периода, блок переходной емкостной энергии и определитель емкостной энергии. 29 ил., 1 табл.
Система автоматического регулирования внутренней емкостной энергией объекта с переменными параметрами, включающая последовательно соединенные объект, пропорциональное звено, идентификатор, уровень статических характеристик, уровень динамических характеристик, уровень качества и самоконтроля и исполнительный уровень, отличающаяся тем, что введены последовательно соединенные и подсоединенные к выходу объекта идентификатор емкостного состояния объекта, определитель необходимой емкостной энергии, формирователь инерционных настроек, формирователь емкостной силы (компенсирующий возмущения регулирующего органа), входы введенных устройств также подсоединены к входу CAP (через который оператор осуществляет контроль за состоянием CAP); при этом в уровень статических характеристик введены последовательно соединенные определитель необходимой емкостной энергии, формирователь регулирования по статической характеристике емкостной энергии и определитель технической реализации; в уровень динамических характеристик дополнительно введены задатчик устойчивости (включающий последовательно соединенные формирователь корней вынужденного состояния, формирователь коэффициентов свободного состояния), вычислитель корней регулирующего воздействия, вычислитель коэффициентов свободного и вынужденного состояния; в третий уровень качества и самоконтроля дополнительно введены последовательно соединенные блок проверки ОДЗ, блок поэтапного регулирования; в исполнительный уровень введен формирователь емкостных сил, компенсирующий возмущения регулирующего органа; в идентификатор введены последовательно соединенные быстродействующий косвенный определитель емкостной энергии, прямой определитель емкостной энергии текущего интервала, блок контроля полного переходного периода, блок переходной емкостной энергии и определитель емкостной энергии; формирователь инерционных настроек третьим и четвертым входам подсоединен к входам всех входящих в него устройств, а через выходы уровня статических характеристик к выходам определителя необходимой емкостной энергии и определителя технической реализации; при этом формирователь инерционных настроек включает последовательно соединенные уровень динамических характеристик и уровень качества и самоконтроля, в который входит блок проверки ОДЗ и блок поэтапного регулирования;
выход проверки ОДЗ дополнительно подсоединен на второй вход вычислителя текущих значений входного воздействия;
уровень динамических характеристик включает последовательно соединенные формирователь корней вынужденного состояния, формирователь коэффициентов свободного состояния, вычислитель корней регулирующего воздействия, вычислитель коэффициентов свободного и вынужденного состояния;
блок поэтапного регулирования включает в себя последовательно соединенные задатчик технической реализации, формирователь зависимостей математической модели, формирователь системы уравнений зависимостей регулируемого параметра от длительности интервала, формирователь регулирующего воздействия по длительности интервала, определитель математической модели необходимой входной энергии, на второй вход которого подсоединен выход введенного формирователя длительности интервала по регулирующему воздействию, вход которого подсоединен к выходу формирователя системы уравнений зависимостей математической модели;
формирователь емкостной силы включает последовательно соединенные формирователь системы уравнений емкостных сил, формирователь системы двух уравнений для каждой входной силы, формирователь объединенных уравнений исключением промежуточных входных сил, объединитель уравнений для всех емкостных сил относительно входного воздействия, элемент подстановки математической модели, формирователь зависимостей коэффициентов математической модели выходных сил от коэффициентов входного воздействия, элемент подстановки полученных зависимостей в математическую модель, формирователь системы уравнений относительно коэффициента входного воздействия, вычислитель коэффициентов входного воздействия делением определителей;
при этом вычислитель корней регулирующего воздействия включает в себя последовательно соединенные формирователь модели коэффициентов запаздывания по корням, делитель, формирователь системы уравнений по частным составляющим объекта, задатчик коэффициентов запаздывания регулятора по определителям, формирователь системы подстановкой текущих характеристик, определитель неизвестных системы, элемент подстановки условных коэффициентов, на второй вход которого подсоединен выход формирователя модели коэффициентов запаздывания по корням;
при этом вычислитель коэффициентов свободного и вынужденного состояния включает в себя последовательно соединенные формирователь дифуравнения по коэффициентам запаздывания объекта, формирователь системы уравнений из внутренних составляющих объекта, формирователь определителей системы, формирователь коэффициентов запаздывания объекта через определители, элемент замены коэффициентов запаздывания, формирователь системы уравнений для начальных и заданных значений, элемент приравнивания коэффициентов при одинаковых степенях, вычислитель коэффициентов входной составляющей дифуравнения, вычислитель вынужденного состояния регулируемого параметра, вычислитель коэффициентов свободного состояния регулируемого параметра;
при этом формирователи интервалов, входящие в формирователь регулирующего воздействия по длительности интервала, включают последовательно соединенные задатчик длительности интервала, определитель коэффициентов регулирующего воздействия, звено проверки технической реализации, определитель коэффициентов свободного и вынужденного состояния объекта, звено проверки технической реализации, отрицательный выход которого подсоединен на вход второго корректора длительности интервала, положительный выход которого подсоединен на второй вход определителя дополнительного интервала, первый вход определителя дополнительного интервала подсоединен на выход задатчика длительности, а третий вход подсоединен на положительный выход первого корректора длительности интервала, выход определителя дополнительного интервала подсоединен на второй вход определителя коэффициентов регулирующего воздействия, отрицательный выход звена проверки технической реализации подсоединен на вход первого корректора длительности интервала, отрицательные выходы первого и второго корректоров длительности интервалов подсоединены к второму и третьему выходам формирователя интервала;
идентификатор емкостного состояния объекта включает последовательно соединенные быстродействующий косвенный определитель емкостной энергии, прямой определитель емкостной энергии на текущем интервале, блок контроля полного переходного периода, блок выходной емкостной энергии, каждый из выходов введенных устройств также подсоединены к входам введенного определителя утечки емкостной энергии;
при этом быстродействующий косвенный определитель емкостной энергии включает последовательно соединенные определитель математической модели для текущего момента времени, определитель текущих выходных параметров для каждой емкостной составляющей, определитель емкостной энергии каждой емкостной составляющей, определитель емкостной энергии объекта в целом;
при этом определитель математической модели для текущего момента времени включает последовательно соединенные определитель корней дифмодели, определитель коэффициентов полного решения дифуравнения по нулевому моменту времени, определитель последовательности звеньев, определитель выходных параметров каждого звена, идентификатор текущего момент времени;
определитель последовательности звеньев включает в себя последовательно соединенные блоки поиска, каждый из которых включает формирователь выходных параметров и внутреннего запаздывания для исследуемого звена, соответствующие выходы которого подсоединены на входы элемента подстановки текущих выходных параметров в дифуравнения звена и определителя частных коэффициентов, выходы которых подсоединены к соответствующим входам вычислителя входного воздействия звена и вычислителя частного входного воздействия (сумматора), выходы вычислителя входного воздействия и вычислителя частного входного воздействия подсоединены на соответствующие входы схемы сравнения, отрицательный выход которого подсоединен на дополнительный вход формирователя входных параметров и внутреннего запаздывания исследуемого звена, основной вход которого подсоединен к входу блока поиска, положительный выход схемы сравнения подсоединены на выход блока поиска, идущий на вход следующего блока поиска;
при этом идентификатор текущего момента времени включает в себя последовательно соединенные задатчик начальных параметров, вычислитель слагаемых полного решения дифуравнения для начальных параметров, вычислитель слагаемых полного решения для текущих параметров, делитель, определитель логарифма, делитель на корень дифмодели, сумматор, при этом на второй вход вычислителя слагаемых полного решения для текущих параметров подсоединен один из входов идентификатора текущего времени, а на второй вход делителя подсоединен выход вычислителя слагаемых полного решения дифуравнения для начальных параметров;
при этом прямой определитель емкостной энергии на текущем интервале включает последовательно соединенные определитель для отдельных звеньев и определитель для объекта в целом;
блок контроля полного переходного периода включает последовательно соединенные определитель структуры запаздывания, определитель запаздывания каждой составляющей, определитель емкостной энергии по усредненным косвенным параметрам;
при этом определитель структуры запаздывания, входящий в блок контроля полного переходного периода, включает соединенные параллельно идентификатор плавного процесса и идентификатор процесса с экстремальными точками;
идентификатор плавного процесса включает последовательно соединенные определитель параметра через заданный интервал времени, преобразователь основания степени, формирователь степенной степени, формирователь системы из уравнений полного решения дифуравнения, формирователь условных дифуравнений, объединитель в систему условных дифуравнений, определитель коэффициентов внутреннего запаздывания условных дифуравнений, определитель основания степени, определитель корней дифуравнения, определитель постоянных коэффициентов полного решения дифуравнения;
идентификатор процесса с экстремальными точками включает последовательно соединеные определитель экстремальных параметров в производных функциях, определитель отдельных производных для вершин переходного процесса, формирователь дифуравнения для вершин переходного процесса, объединитель дифуравнений в систему, вычислитель коэффициентов внутреннего запаздывания, вычислитель корней дифуравнения, вычислитель коэффициентов полного решения дифуравнеия.
| RU 2005103338 А, 20.07.2006 | |||
| RU 93029406 А, 10.03.1997 | |||
| RU 93026925 А, 10.03.1997 | |||
| US 7437206 В2, 14.10.2008. |
Авторы
Даты
2013-02-10—Публикация
2010-03-26—Подача