Настоящее изобретение относится к области геофизической разведки, а более конкретно к способу для определения времени пробега и карт времени пробега для осуществления миграции сейсмических данных.
В нефтегазовой промышленности способы геофизической разведки обычно используют для облегчения поиска и оценки подземных углеводородных месторождений. Обычно источник сейсмических волн используют для формирования сейсмического сигнала, который проходит в грунт и по меньшей мере частично отражается подземными сейсмическими отражающими границами (то есть границами раздела между подземными формациями, имеющими различный акустический импеданс). Отраженные волны регистрируют посредством сейсмических датчиков, расположенных на или вблизи поверхности грунта, в толще воды или на известных глубинах в стволах скважин, а получающиеся в результате измерений сейсмические данные могут быть обработаны для получения информации, относящейся к местоположению подземных отражающих границ и к физическим свойствам подземных формаций.
При геофизической разведке природных ресурсов одного вида сейсмическое волновое поле излучают из пункта источника на или вблизи поверхности грунта. Первоначально волновой фронт распространяется как сферически расширяющийся, а излучением охватываются различные слои грунта, которые обычно характеризуются рассогласованием акустического импеданса на границах слоев вследствие изменений свойств породы и скорости распространения акустической волны. Волновое поле отражается от соответствующих границ слоев, для возвращения на поверхность, где механические движения частиц грунта, обусловленные отраженным волновым полем, преобразуются в электрические сигналы посредством преобразователей. Сигналы, которые содержат сейсмические данные, сохраняют в архивном запоминающем устройстве для последующей обработки.
Задача сейсмической разведки заключается в формировании изображения объема подземных формаций в области, представляющей геологический и/или экономический интерес. Для изотропного горизонтального слоя с постоянной скоростью время, прошедшее между излучением волнового поля и приемом волнового поля на приемнике вблизи источника, умноженное на половину средней скорости, характеризует глубину точки падения отраженного волнового поля в слое, который находится сразу же под средней точкой между источником и приемником.
При условии, если отражающая граница наклонена, или скорость переменная по пространству, это простое соотношение более не имеет силы; точка падения смещается вбок относительно средней точки источник/приемник. Для соответствующего картирования наклонных или отклоненных отражающих горизонтов необходима миграция волновых полей, формируемых этими наклонными слоями.
Сложные глубинные условия препятствуют простому суммированию сейсмических записей. Благодаря сложным глубинным условиям происходит рассеяние сейсмических волн по многим направлениям. При простом суммировании местоположение подземных объектов может быть определено ошибочно. Миграция сейсмических записей может обеспечить более точное определение местоположения подземных объектов. Миграция включает в себя геометрический перенос отраженных сигналов для отображения события (границы слоя или другой структуры) на соответствующем месте. Карта времен пробега представляет собой неотъемлемую часть процесса миграции до суммирования. Одним из хорошо известных из уровня техники способов миграции является глубинная миграция Кирхгофа.
В случае глубинной миграции до суммирования часто выбирают миграцию Кирхгофа вследствие низких затрат вычислительных ресурсов по сравнению с другими способами. Для миграции Кирхгофа необходимо использовать генератор времени пробега волнового фронта любого одного из хорошо известных типов, принцип функционирования которого основан на трассировании лучей. Способы трассирования лучей полезны при исследовании сложных геологических структур. При определении времени пробега с трассированием лучей можно использовать как данные первого вступления, так и данные вступлений с максимальной энергией, и эти последние данные обеспечивают построение изображений высокого качества. Однако эти способы относятся к медленным, а при их реализации требуется значительное время для последующей компьютерной обработки.
Вычисление времен пробега волнового поля в выбранных выходных точках - это ключевая составная часть успешной глубинной миграции Кирхгофа сейсмических данных. При наличии сложной геологии времена пробега волнового поля до выходных точек находят путем трассирования лучей от источника. С помощью способов нахождения времен пробегов путем трассирования лучей получают времена пробега для всех вступлений волновых фронтов на выходные точки.
Один из указанных способов изложен в патенте США №5229938 (Shein-Shen Wang et al.), выданном 20 июля 1993 г. В патенте описан способ, предназначенный для получения полных времен пробега для пар, образованных источниками и приемниками, который включает в себя этапы определения набора времен пробега в одном направлении для каждого источника до множества точек изображения и набора времен пробега в одном направлении для каждого приемника до множества точек изображения. Для источников и приемников образуют набор лучей. Времена пробега от места нахождения источника до точек изображения вычисляют с помощью двухточечной интерполяции, используя наборы лучей. Полное время пробега вычисляют путем суммирования двух наборов, по одному набору для каждого положения источника и приемника. Набор полных времен пробега получают для конкретного сочетания источника и приемника для всех изображающих точек.
Эйкональные (конечно-разностные) генераторы времен пробега являются весьма быстродействующими и не формируют зоны геометрической тени. Конечно-разностные генераторы времен пробега всегда обеспечивают возможность выбора времен пробега по первым вступлениям, тогда как при использовании генераторов времен пробега на основе трассирования лучей необходимо конкретно выбирать требуемую часть волнового фронта.
Хорошо известный конечно-разностный генератор времен пробега раскрыт в статье, которую John Vidale опубликовал в Bulletin of the Seismological Society of America, v.78, №6, December 1988, pp.2062-2076. В данном случае времена пробега сейсмических волн первого вступления при любом скоростном строении геологической среды могут быть быстро вычислены на многомерной сетке путем конечно-разностной экстраполяции от точки к точке. Вместо лучей трассируют волновые фронты. Соответствующим образом обрабатывают отраженные волны, а зоны геометрической тени заполняют соответствующими сегментами волновых фронтов. Этот алгоритм является очень быстрым и полезным при томографической инверсии и миграции Кирхгофа в геологическом разрезе, характеризующемся плавными градиентами поперечной скорости.
Времена пробега, на основании которых может быть составлена карта времен пробега или таблица времен пробега, можно вычислить непосредственно путем трассирования лучей на протяжении заданной скоростной модели. Скоростная модель может быть получена хорошо известными из уровня техники способами. Традиционно считается, что скоростная модель характеризует скоростное строение геологической среды для сейсмического волнового поля. Скоростная модель представляет собой двумерную или трехмерную решетку, описывающую распределение скоростей на сетке в пределах области или объема, представляющего интерес. Сетка может быть прямоугольной (x-y-z) сеткой, хотя также можно использовать сферические, многогранные и другие сетки. Задание подходящей скоростной модели для определенного объема сейсмических данных или геологической среды хорошо известно в области техники, к которой относится изобретение, и в настоящей заявке не будет рассматриваться подробно.
Пучок лучей, выходящий из источника, расположенного на поверхности (скоростной модели геологической среды), может проходить вниз в скоростную модель геологической среды и трассироваться на протяжении геологической среды, при этом возникает изменение направления лучей, обусловленное изменениями градиента скорости и преломлением на границах слоев с контрастом скоростей. Точки отражений вдоль каждой из траекторий лучей идентифицируют как точки пересечений лучей с границами слоев. Затем вычисляют время пробега от места расположения источника на поверхности до точки отражения в геологической среде путем интегрирования элементов расстояния вдоль траектории луча при делении каждого элемента на скорость, относящуюся к этому элементу. При использовании принципа взаимности аналогичным образом может быть вычислено время пробега от места расположения приемника на поверхности до точки отражения в геологической среде. Наконец, для определенной пары источник-приемник на поверхности и точки отражения в геологической среде полное время пробега вычисляют путем суммирования времени пробега от источника к точке отражения и времени пробега от точки отражения к приемнику.
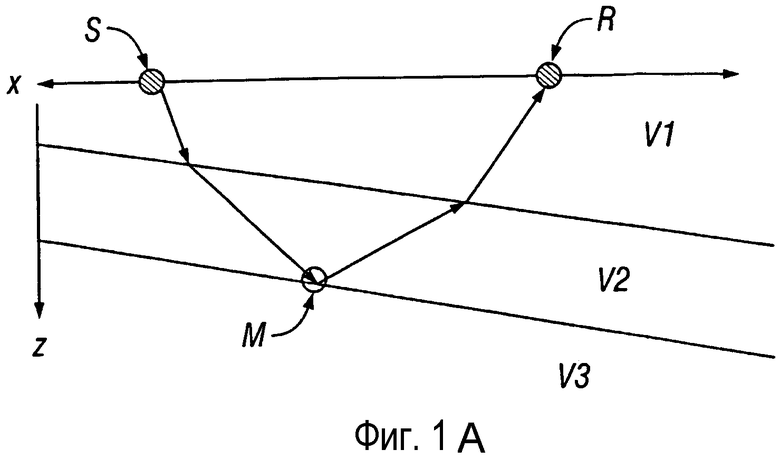
На фигуре 1А представлен пример скоростной модели для случая применения простой трехслойной модели геологической среды с четырьмя сегментами траектории луча. В каждом из трех слоев, V1, V2 и V3, скорость такова, что скорость в слое V1 отличается от скорости в слое V2, а скорость в слое V2 отличается от скорости в слое V3. Источник находится на поверхности геологической среды в местоположении S, из которого сейсмическая волна в виде сегмента луча (показанного стрелкой) проходит через верхний слой V1 модели. Следующий сегмент луча проходит по другому пути с момента, когда он переходит в слой V2. Общее время пробега от источника S до точки М отражения определяется суммой первых двух сегментов луча. На границе раздела второго слоя V2 и третьего слоя V3 луч отражается в точке М отражения обратно к поверхности со скоростью V2 и входит в верхний слой V1, проходит этот верхний слой V1 и затем достигает места R расположения приемника. Для этой конфигурации источника и приемника полное время пробега от источника до приемника вычисляют путем суммирования времен пробега по четырем отдельным сегментированным траекториям.
Вычисленные времена пробега могут быть отображены на сетках, которые имеют узловые структуры, аналогичные структурам скоростных моделей. Эти карты времен пробега представляют собой двумерные или трехмерные решетки, отображающие распределение времен пробега на сетке в пределах области, представляющей интерес. Такие сетки с узловой структурой функционально подобны скоростным моделям тем, что они могут быть прямоугольными (x-y-z) сетками, сферическими, многогранными или другими сетками.
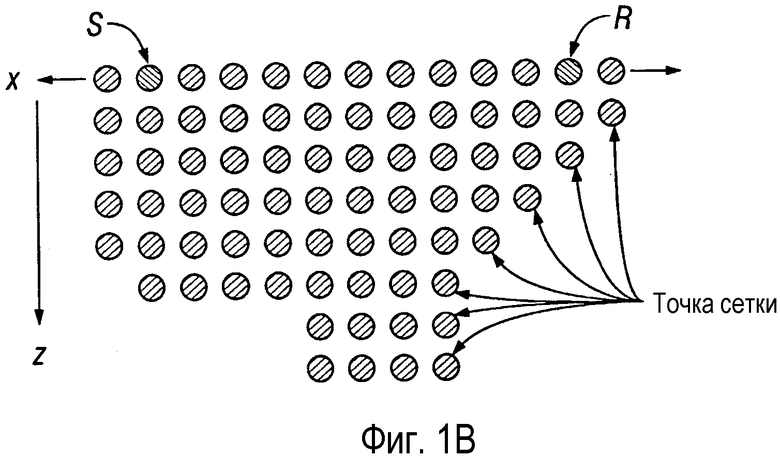
На фигуре 1В представлен пример двумерной вычислительной сетки, которая может быть использована для отображения времен пробега на основании скоростных моделей. Все кружки, включая S и R, на фигуре 1В представляют собой точки сетки, характеризующие узлы, для которых может быть осуществлена оценка времени пробега. Сетка вытянута в поперечном направлении x в обе стороны, что показано стрелками, а также в глубину, что показано стрелкой в направлении z.
Времена пробега можно определить из конечно-разностного решения уравнения эйконала или путем трассирования лучей, как описывалось ранее. Однако согласно обоим способам время пробега определяется асимптотически для высокочастотной волны. Использование этих высокочастотных способов не позволяет точно отображать все конечные частоты, поскольку волны проходят области с зависимой от частоты скоростью, изменяющейся по пространству.
При миграции Кирхгофа изображение формируют путем суммирования зарегистрированных данных метода отраженных волн на пикселах изображения, извлечения выборки данных для суммы на оцениваемом временном интервале, необходимом для прохождения волны от источника до точки изображения на приемнике. Такие времена пробега оценивались в течение десятилетия с помощью решения высокочастотного уравнения эйконала. Первое сообщение об использовании конечно-разностного метода для решения уравнения эйконала сделали Wiggins и другие в 1986 г. Проблемы, которые возникают в случае использования высокочастотных времен пробега при глубинной миграции Кирхгофа, хорошо известны и много обсуждались, начиная с 1990-х годов (Van Trier and Symes, 1991; Vinje et al., 1993; Geoltrain and Brac, 1993; Audebert et al., 1994a). Biondi в 1992 г. сделал попытку усовершенствовать высокочастотные способы путем осуществления зависимого от частоты сглаживания скоростной модели.
Для сохранения амплитуд во время миграции Кирхгофа требуется большая вычислительная мощность. Для сохранения амплитуд необходимо осуществлять взвешивание мигрированных трасс соответствующими амплитудными коэффициентами миграции. Можно сослаться на статью Tygel, опубликованную в Geophysics, vol.59, №12, декабрь 1993, в которой сделан обзор используемых способов. Например, может возникнуть необходимость в вычислении некоторого количества весов, равного количеству выборок, включенных в миграцию, а это требует больших затрат на вычисления.
В 1996 г. Dave Nichols в диссертации, защищенной в Станфорде, в попытке исключить ограничения высокочастотного предположения вчислил монохроматические двумерные функции Грина и осуществил двумерную миграцию. Функция Грина для заданного дифференциального уравнения представляет собой решение неоднородного уравнения с пространственной дельта-функцией в качестве источника. Nichols вычислил монохроматические двумерные функции Грина, использовав конечно-разностный метод в полярных координатах. Nichols обратился ко времени пробега для вычисления приближения функции Грина, то есть дельта-функции во времени. При обработке монохроматической функции Грина как приблизительно синусоидальной волны могут быть вычислены кратные частоты, а получающиеся в результате синусоидальные волны сложены с образованием функции с максимумом. Максимум функции может быть выбран в качестве положения дельта-функции.
В известном уровне техники раскрыты высокочастотные способы и устройства, с помощью которых времена пробега через модели геологической среды с изменяющейся скоростью в структуре вычисляются неточно. В известном уровне техники раскрыты способы и устройства для вычисления амплитудных коэффициентов миграции, для которых требуются большие затраты вычислительной мощности. Поэтому существует необходимость в способе и устройстве для более эффективного и более точного вычисления времен пробега по сравнению со способами из известного уровня техники. Существует необходимость в устройстве и способе для эффективного вычисления амплитудных коэффициентов миграции для точного построения мигрированных изображений и представления структуры геологической среды.
Предложен способ для определения времен пробега сейсмических волн от пункта на поверхности до по меньшей мере одной подземной точки вычислений в пределах множества точек размещения в геологической среде. Задают скоростную модель области. Используя скоростную модель, вычисляют монохроматическое волновое поле для по меньшей мере одной точки вычислений. Определяют развернутую фазу сейсмической волны в соседней точке вычислений, ближайшей к по меньшей мере одной точке вычислений в геологической среде. Используя развернутую фазу соседней точки вычислений, определяют время пробега сейсмической волны до по меньшей мере одной точки вычислений и вычисляют монохроматическое волновое поле для по меньшей мере одной точки вычислений. На основании найденных значений времен пробега могут быть сформированы карты и таблица времен пробега.
Настоящее изобретение и его преимущества будут более понятными при обращении к нижеследующему подробному описанию и сопровождающим чертежам, на которых:
фигура 1А - представляет иллюстрацию скоростной модели геологической среды;
фигура 1В - представляет иллюстрацию примера реализации вычислительной сетки, которая может быть использована для картирования времен пробега, полученных на основании скоростной модели;
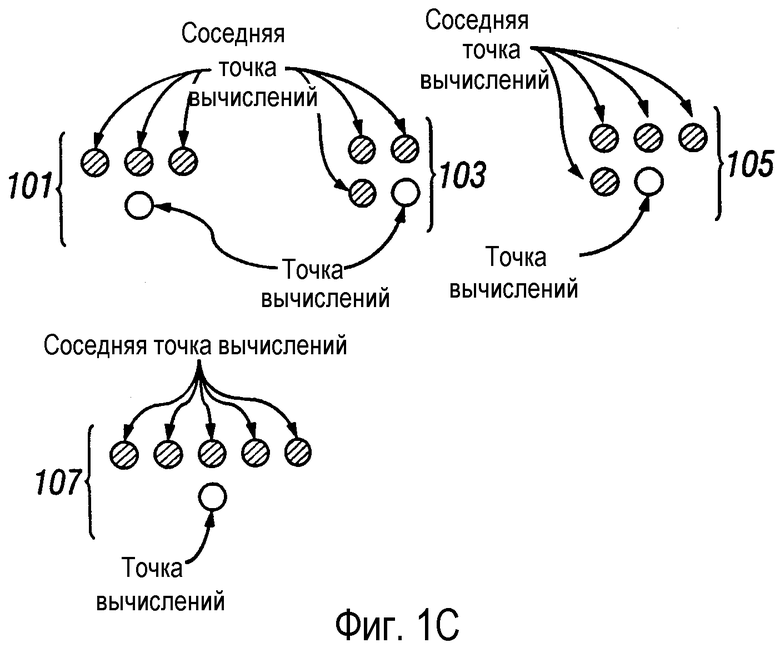
фигура 1С - представляет иллюстрацию отдельных конфигураций соседних точек вычислений относительно точек вычислений сетки из фигуры 1В;
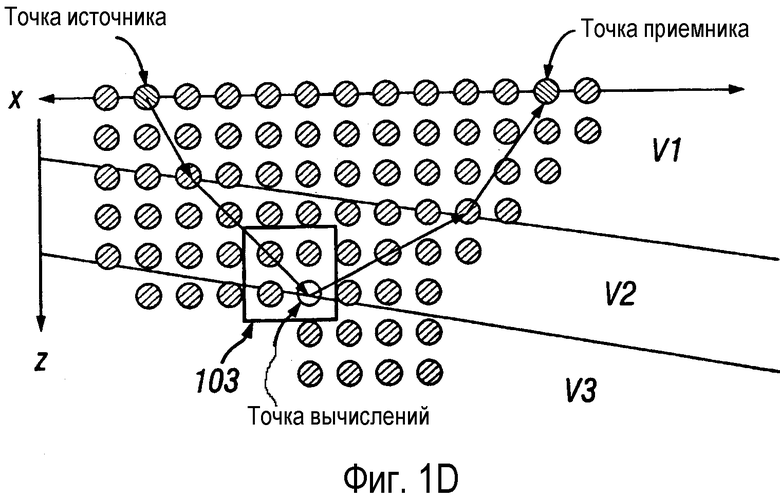
фигура 1D - изображен схематичный пример, иллюстрирующий, каким образом вычислительная сетка для картирования времен пробега из фигуры 1В соотносится с простой скоростной моделью из фигуры 1А при сочетании с развертыванием фазы для точки вычислений согласно настоящему изобретению;
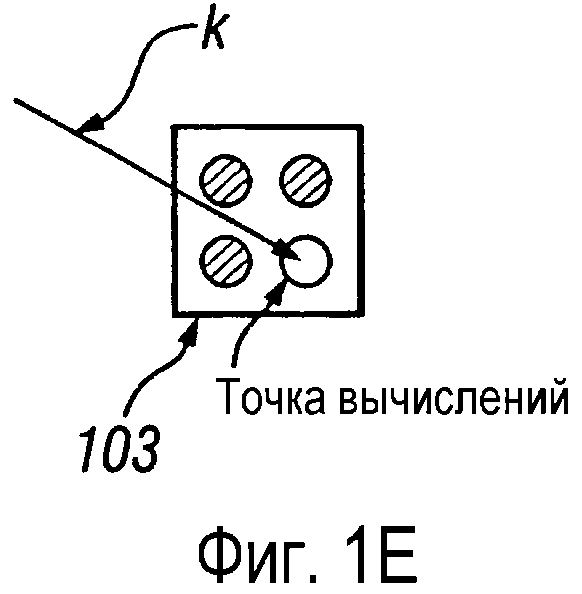
фигура 1Е - представляет пример конфигурации процесса развертывания;
фигура 2 - изображает рабочую диаграмму предпочтительного варианта осуществления настоящего изобретения;
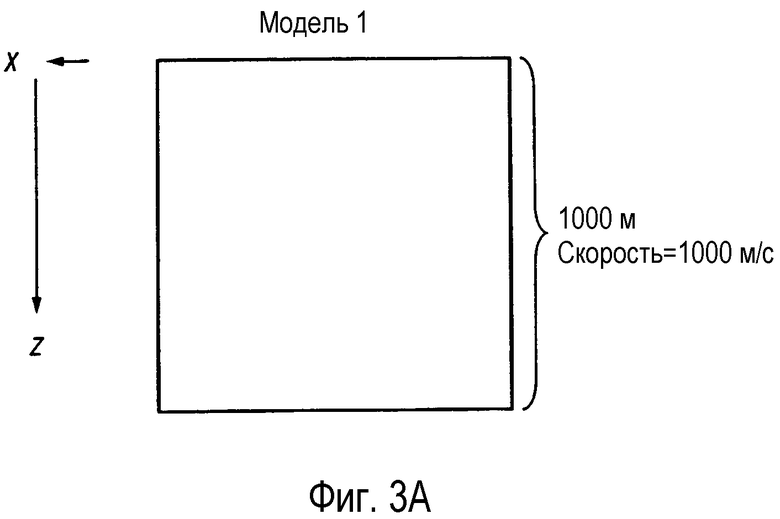
фигура 3А - представляет скоростную модель для модели 1;
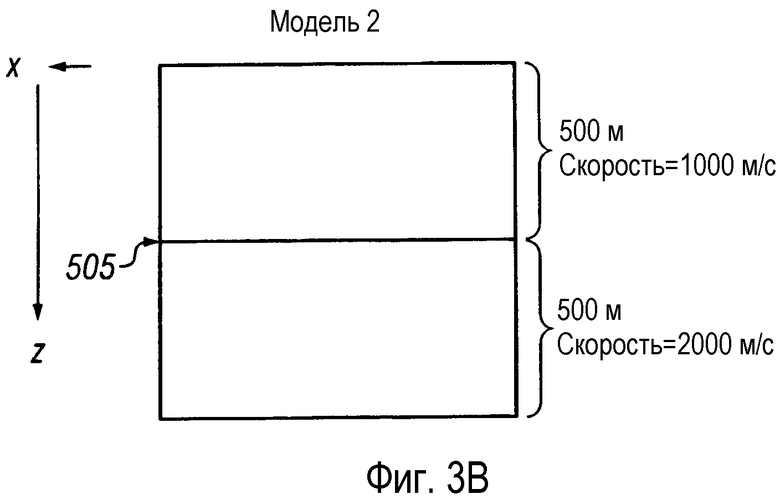
фигура 3В - представляет скоростную модель для модели 2;
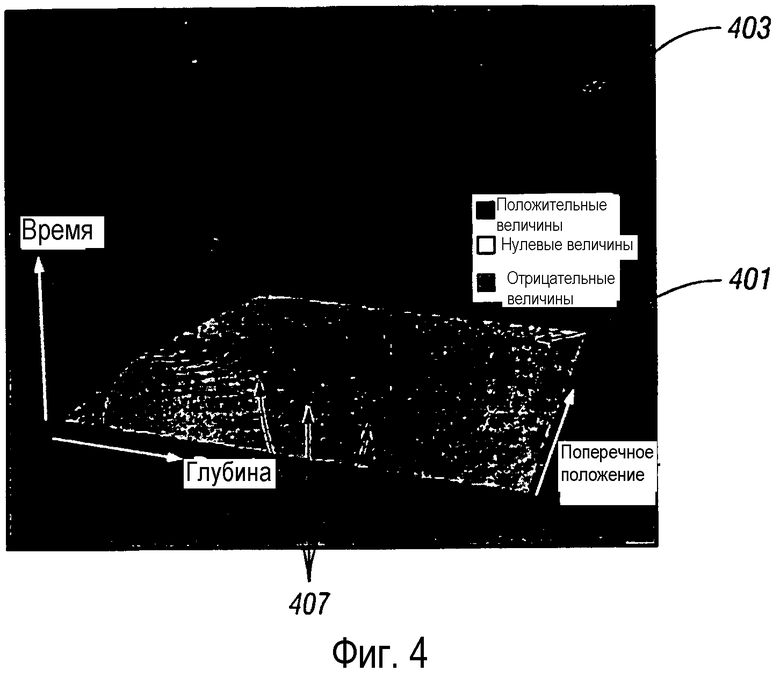
фигура 4 - представляет иллюстрацию волнового поля и полученного времени пробега для модели 1;
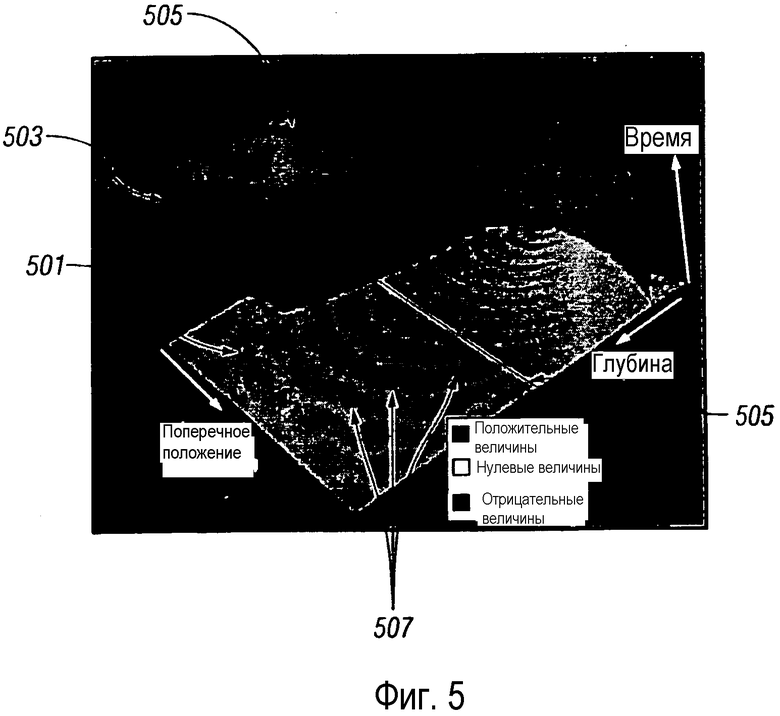
фигура 5 - иллюстрирует волновое поле и время пробега для модели 2;
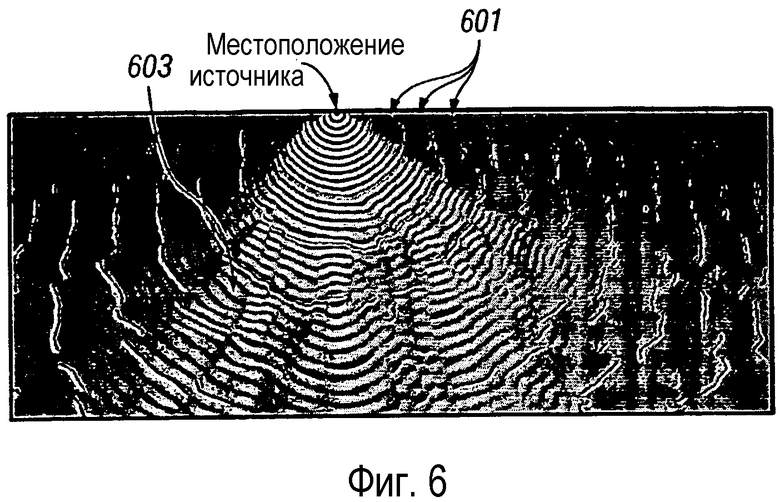
фигура 6 - иллюстрирует действительную часть волнового поля частотой 30 Гц в модели Marmousi с изолиниями времен пробега;
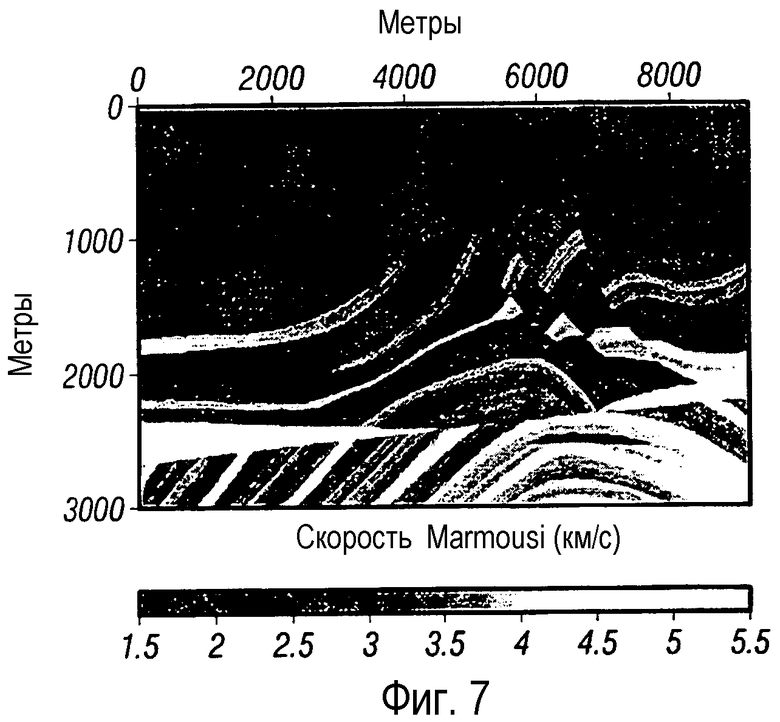
фигура 7 - иллюстрирует скоростную модель для модели Marmousi; и
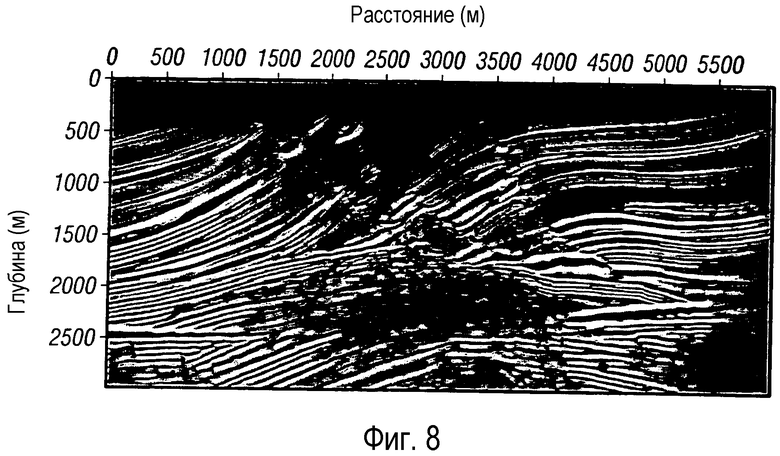
фигура 8 - представляет иллюстрацию мигрированных данных до суммирования по Marmousi при использовании времен пробега, полученных по волновым полям точечного источника частотой 30 Гц.
Хотя изобретение будет описано применительно к предпочтительным вариантам осуществления, должно быть понятно, что изобретение не ограничено ими. Наоборот, оно подразумевается охватывающим все альтернативы, модификации и эквиваленты, которые могут быть включены в рамки сущности и объема изобретения, определенных приложенной формулой изобретения.
Настоящее изобретение относится к способу, предназначенному для определения времен пробега и формирования карт и таблиц времен пробега для осуществления миграции сейсмических данных. Способ согласно изобретению обеспечивает эффективное и точное картирование времен пробега, а также обеспечивает эффективное вычисление амплитудных коэффициентов миграции. Поэтому мигрированные изображения, полученные при использовании картирования времен пробега согласно настоящему изобретению, являются в большей степени непрерывными и точными по положению и амплитуде. Другие преимущества изобретения станут без труда очевидными для специалистов в области техники, к которой относится изобретение, из нижеследующего подробного описания. В том смысле, что нижеследующее подробное описание специально ориентировано на конкретный вариант осуществления или на конкретное использование изобретения, подразумевается, что оно иллюстративное и не должно интерпретироваться как ограничивающее объем изобретения.
Изобретение, описываемое в настоящей заявке, относится к усовершенствованному способу для вычисления времен пробега, в котором исключены недостатки высокочастотных способов из известного уровня техники, таких как обычное трассирование лучей. Время пробега вычисляют на единственной конечной частоте или на нескольких частотах, которые присущи сейсмическим данным. На основании этих времен пробега можно получать сейсмическое изображение более высокого качества, чем при использовании высокочастотных способов. Кроме того, сейсмические данные могут быть разделены на несколько частотных диапазонов, при этом каждый поддиапазон будет уже по сравнению с полным частотным диапазоном данных. Миграцию в каждом поддиапазоне можно осуществлять раздельно, используя карту времен пробега или таблицу времен пробега, вычисленную на центральной частоте поддиапазона, и при этом путем выбора числа частот достичь компромисса между качеством непрерывного изображения и затратами. Способ согласно настоящему изобретению является более эффективным в части требуемой вычислительной мощности, чем другие способы, которые могут быть усовершенствованиями обычного суммирования Кирхгофа, осуществляемого в отношении асимптотических высокочастотных времен пробега.
Преимущество настоящего изобретения заключается в том, что исключается необходимость в функции Грина во временной области, имеющей максимум. Время пробега соотносят с фазой монохроматической функции Грина. Карта или таблица времен пробега может быть получена непосредственно на основании единственной монохроматической функции Грина. Время пробега вычисляют на единственной частоте или на отдельных частотах, получая строгое решение (в пределах точности способа, используемого для вычисления функции Грина) проблемы формирования изображения на этой частоте или на отдельных частотах.
Использование монохроматического волнового поля также позволяет получать амплитуду, которая может быть использована для вычисления амплитудных коэффициентов миграции. Амплитуды, вычисляемые на основании трассирования лучей, обычно имеют разрывы и изменяются беспорядочно. Амплитуды, получаемые на конечной частоте, позволяют иметь более сглаженные мигрированные изображения и более точные изображения отражающих границ.
На фигуре 2 представлена рабочая диаграмма предпочтительного варианта осуществления настоящего изобретения. На этапе 201 формируют скоростную модель в виде решетки, описывающей распределение скоростей на сетке в пределах рассматриваемой области. На этапе 203 выбирают местоположение источника. На этапе 205 вычисляют волновое поле для этого местоположения источника. В предпочтительном варианте осуществления волновое поле вычисляют, используя волновое уравнение акустических волн для пробега в одном направлении. В альтернативных вариантах осуществления предусматриваются решения волновых уравнений акустических и упругих волн как для пробега в одном направлении, так и для полного пробега. Каждое уравнение может быть решено методом конечных элементов или конечных разностей и может быть неявным или явным. Вычисление волнового поля дает неоднозначную неразвернутую фазу и амплитуду в каждой точке вычислений. Начальные времена пробега и начальные значения развернутых фаз могут быть определены и приписаны ко всем узлам решетки. Например, развернутая фаза и время пробега в месте расположения источника равны 0. На этапе 207 выбирают точку вычислений, прилегающую к соседним точкам вычислений, в которых развернутая фаза уже вычислена. Исходно только точка источника пригодна для использования в качестве соседней точки вычислений. Однако по мере увеличения числа вычисленных развернутых фаз появляется возможность выбора точки вычислений на расстоянии от точки источника, и выбранной точке вычислений будут соответствовать несколько возможных ближайших точек. Развернутую фазу сейсмической волны, приходящей в точку вычислений, определяют путем обращения к уже развернутым фазам ближайших соседних точек вычислений. На этапе 209 выбирают соседние точки вычислений для получения опорной развернутой фазы, используемой для получения развернутой фазы точки вычислений. В предпочтительном варианте осуществления на этапе 211 опорную фазу определяют на основании развернутой фазы в одной или в нескольких соседних точках вычислений. Опорную фазу, предназначенную для использования при определении развернутой фазы точки вычислений, получают или выбирают любым соответствующим способом: примеры описаны ниже. На этапе 213 опорную фазу используют для определения развернутой фазы точки вычислений. Развернутую фазу точки вычислений, определенную при использовании опорной фазы соседней точки вычислений, на этапе 215 используют для определения времени пробега в точке вычислений. В альтернативном варианте осуществления настоящего изобретения карты времен пробега и таблицы времен пробега могут быть определены при использовании времен пробега, вычисленных на этапе 215.
В предпочтительном варианте осуществления, показанном на фигуре 2, существенный этап при вычислении времени пробега заключается в определении на этапе 211 развернутой фазы, то есть в преобразовании круговой фазы в диапазоне от -π до π в абсолютную фазу, пропорциональную времени пробега.
В настоящем изобретении времена распространения вычисляют на основании единственной монохроматической функции Грина или для нескольких отдельных, подходящих для этого частот. Время пробега вычисляют на основании единственной монохроматической функции Грина, в которой s(r,t) есть монохроматическое излучение точечного источника в волновом уравнении акустических волн:
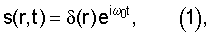
где 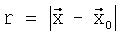 - расстояние между точкой
- расстояние между точкой 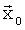 источника и произвольной точкой
источника и произвольной точкой 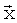 разреза в двух- или трехмерном пространстве;
разреза в двух- или трехмерном пространстве;
ω0 - частота возбуждения;
t - время; и
δ() - дельта-функция Дирака.
Теперь, 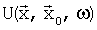 представляет собой решение для акустической волны в случае излучения s(r,ω)=FT(s(r,t)):
представляет собой решение для акустической волны в случае излучения s(r,ω)=FT(s(r,t)):
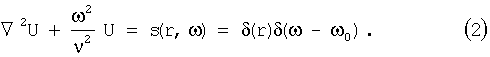
Для заданной скорости 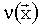 можно вычислить U, используя любой из хорошо известных способов, предназначенных для решения волнового уравнения акустических волн. Такое решение разделяют на амплитуду и фазу:
можно вычислить U, используя любой из хорошо известных способов, предназначенных для решения волнового уравнения акустических волн. Такое решение разделяют на амплитуду и фазу:
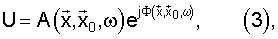
где 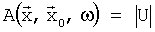 - амплитуда; и
- амплитуда; и
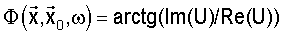 - фаза.
- фаза.
Это разделение U не связано с аппроксимациями: это просто альтернативное представление комплексной функции. Решение во временной области получают с помощью обратного преобразования Фурье U(r,ω). Поскольку U имеет только одну частоту, обратное преобразование Фурье выражается просто как
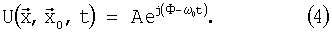
Максимум волнового поля в (4) наблюдается, когда экспонента равна нулю:
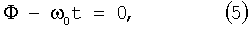
что означает
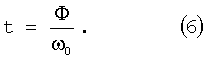
Однако фаза Φ является неоднозначной в том смысле, что при добавлении к ней любого числа, кратного 2π, будет получаться то же самое волновое поле. Прежде чем t=Φ/ω0 станет полезной формулой для вычисления времени пробега, эта неоднозначность должна быть исключена. Если волновое поле вычисляют при шаге сетки, равном половине длины волны или меньшем, то ограниченное изменение фазы от одной точки вычислений до соседней точки может быть использовано для исключения неоднозначности.
Из определения вычисления следует, что в точке источника фаза волнового поля и время пробега: Φисточника=tисточника=0. Далее, поскольку мы знаем, что для волнового поля в точках вычислений, прилегающих к источнику, время пробега должно быть положительным, то на расстоянии от источника, меньшем половины длины волны, мы может выбрать для них абсолютную или развернутую фазу для включения значения 2π, которое перемещает разность Φ-Φисточника в диапазон [0, 2π].
После того как точкам, прилегающим к источнику, задана развернутая фаза, следующим точкам, прилегающим к ним, можно задать развернутую величину. Такое задание продолжают итеративно от точки источника до тех пор, пока всем точкам вычислений не будет задана развернутая фаза. При каждой итерации вычисляют опорную фазу Φоп, на основании предшествующих развернутых фаз точек, соседних с рассматриваемой точкой. Значение, кратное 2π, выбирают для фазы Φ рассматриваемой точки, чтобы обеспечить разность Φ-Φоп находящейся в диапазоне [0, 2π]. В качестве альтернативы прогнозирование развернутой фазы в точке можно представить в виде Φспрогнозированная=Φоп+dΦ, где dΦ вычисляют как локальное время прохождения волны от опорной точки до точки прогнозирования. Затем может выбрано значение, кратное 2π, для размещения разности Φ-Φспрогнозированная в диапазон [-π, π].
Амплитуду 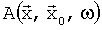 используют для получения амплитудных коэффициентов, необходимых при миграции Кирхгофа. Простым примером вычисления времени пробега на основании монохроматического решения является случай постоянной скорости. Решение получают аналитически в виде
используют для получения амплитудных коэффициентов, необходимых при миграции Кирхгофа. Простым примером вычисления времени пробега на основании монохроматического решения является случай постоянной скорости. Решение получают аналитически в виде
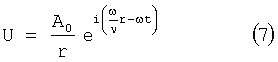
Время пробега имеет простой вид
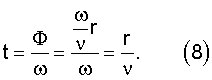 .
.
Это время t представляет собой линейное время пробега.
Разрешение фазовой неоднозначности с помощью развертывания фазы (стадия 211 на фигуре 2) осуществляют путем анализа прилегающих точек вычислений на карте времен пробега путем применения итерационного метода, описанного выше для задания развернутой фазы каждой точке вычислений. Вычисление монохроматического волнового поля дает комплексную волновую функцию для каждой точки вычислений на карте времен пробега. Все точки сетки, показанные на фигуре 1В, могут быть точками вычислений.
Вычисления можно осуществлять, используя действительную и мнимую части комплексной функции. Фаза Φ волновой функции U имеет вид
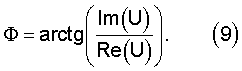 .
.
Эта фаза является неоднозначной в том смысле, что любое добавление значения, кратного 2π, оставляет волновую функцию неизменной. Поэтому для использования фазы в качестве базиса для вычислений времени пробега, используя уравнение (6), эту неоднозначность следует разрешить.
Для разрешения этой неоднозначности требуется дополнительная информация помимо комплексных значений в точке вычислений. Эту дополнительную информацию из соседних точек вычислений получают в результате пространственной эволюции волнового поля и дополнительного отбора соседних точек вычислений, необходимых для определения времени пробега.
Примеры групп соседних точек вычислений для выбора на этапе 209 из фигуры 2, отобранные из неисчерпаемых примеров конфигураций относительно точки вычислений, приведены на фигуре 1С. В конфигурации 101 соседние точки вычислений находятся по глубине выше точки вычислений. В отображениях 101 и 107 показанные узлы вычислительной сетки являются примерами «вертикальной конфигурации». «Угловые конфигурации» 103 и 105 поворачивают влево/вправо при необходимости поместить боковую соседнюю точку вычислений (соседнюю точку вычислений, прилегающую по глубине к точке вычислений) как можно ближе к точке источника. При угловой конфигурации точек вертикальную конфигурацию используют для определения первой точки вычислений на новой глубине ряда точек вычислений. Другие конфигурации должны быть очевидными для специалистов в области техники, к которой относится изобретение. Эти конфигурации являются простыми для экстраполяции двумерного случая к трехмерному.
При дискретных численных вычислениях волновое поле вычисляют в точках вычислений, расположенных достаточно близко для возможности определения абсолютного значения относительного изменения фазы от одной точки вычислений до соседней. При вычислениях методом конечных разностей точки вычислений необходимо разносить на расстояние меньше половины длины волны, чтобы таким образом ограничивать разность фаз величиной, меньшей π. В некоторых методах Фурье точки вычислений могут находиться на расстоянии, превышающем половину длину волны, но тогда при осуществлении способа вычислений предполагается известной функциональная зависимость фазы между точками вычислений. Поэтому, задавая развернутую фазу в ряде соседних точек вычислений, можно определять фазу волны в точке вычислений, задавая требование, заключающееся в том, что ее отклонение от фазы ΦСР, прогнозируемой по соседним точкам вычислений, должно находиться в пределах ±π.
Вторая неоднозначность возникает, когда развернутая фаза, прогнозируемая (на этапе 211 на фигуре 2) по одной соседней точке вычислений, отличается от развернутой фазы, прогнозируемой по другой соседней точке вычислений. Эта неоднозначность может быть разрешена путем осуществления выбора среди ряда возможностей. Развернутая фаза может быть спрогнозирована по соседней точке вычислений с наибольшей амплитудой среди отдельных конфигураций или на основании прогнозирующего параметра со взвешенной амплитудой, полученного на основании соседних точек вычислений. В качестве альтернативы предпочтение может быть отдано соседним точкам вычислений, наиболее близко расположенным к линии, проходящей от точки источника до точки вычислений. Эти способы могут быть полезными, например, в случае использования явной конечно-разностной функции распространения нисходящей волны. Разрешение неоднозначности соседних точек вычислений рассмотрено в приведенных ниже примерах в сочетании с определением фазы точки вычислений.
На фигуре 1D показан схематичный пример связи вычислительной сетки из фигуры 1В для определения карты времен пробега с простой скоростной моделью из фигуры 1А в сочетании с развертыванием фазы для точки вычислений настоящего изобретения. Луч проходит от места расположения источника через слой со скоростью V1 и входит в слой со скоростью V2, в котором он попадает в точку вычислений. Кроме того, в этом примере точка вычислений, показанная на фигуре 1D, совпадает с точкой отражения, но любая точка сетки может быть точкой вычислений. Очерченный прямоугольник 103 охватывает отдельную угловую конфигурацию, включающую в себя точку вычислений и три соседних точки вычислений.
На фигуре 1С показаны несколько конфигураций 101, 103, 105 и 107 соседних точек вычислений. Эти конфигурации полезны при вычислении нисходящего волнового поля по прямоугольной сетке. При развертывании фазы последовательно по горизонтальным рядам возрастающей глубины и последовательном вычислении в пределах ряда в направлении обеих сторон от места расположения источника в конфигурациях, показанных на фигуре 1С, всегда имеются развернутые фазы, применимые во всех соседних точках вычислений, используемых для заданной точки вычислений.
На этапе 213 из фигуры 2 функция прогнозирования максимальной амплитуды может быть использована для разрешения фазовой неоднозначности точки вычислений при использовании выбранного набора соседних точек вычислений, например конфигурации 103 из фигуры 1D. Прогнозируемая фаза в точке вычислений равна
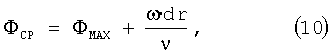
где ΦMAX - опорная фаза, ранее развернутая фаза в соседней точке вычислений с наибольшей амплитудой; и
dr - промежуток, разделяющий точку вычислений и соседнюю точку вычислений с наибольшей амплитудой.
Фаза в точке вычислений представляет собой развернутую фазу, задаваемую уравнением (9), со значением, кратным 2π, добавленным для переноса ее в диапазон ΦСР±π.
В примере конфигурации для выполнения на этапе 211 из фигуры 2 определения развернутых фаз для соседних точек вычислений локальное направление волнового поля характеризуется вектором k волнового числа на фигуре 1Е, где k - волновое число, характеризующее локальную оценку направления волны. В методе прогнозирования максимальной амплитуды для определения фазы ΦСР в узле точки вычислений один из трех узлов соседних точек вычислений должен быть использован в качестве узла опорной фазы ΦMAX, а в предпочтительном варианте осуществления фаза, прогнозируемая на этапе 213 из фигуры 2, равна
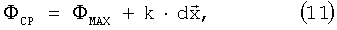 ,
,
где k - величина, оцениваемая на основании соседних точек вычислений; и
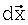 - вектор, направленный от опорной точки к точке вычислений.
- вектор, направленный от опорной точки к точке вычислений.
Альтернативный метод плоской волны должен быть использован для выбора максимальной амплитуды двух левых узлов соседних точек вычислений, где k проходит между ними в конфигурации 103 на фигуре 1Е, вместо всех трех соседних точек вычислений. В этом примере предпочтение отдано соседним точкам вычислений, расположенным наиболее близко к линии, проходящей от точки источника к точке вычислений. Хотя это двумерные примеры, но нетрудно распространить эти случаи на трехмерный случай.
Для разрешения фазовых неоднозначностей может быть выбрана функция прогнозирования плоских волн со взвешенными амплитудами метода наименьших квадратов. Примеры включают в себя набор соседних точек вычислений, например в виде вертикальной конфигурации 107, состоящей из пяти соседних точек вычислений в непосредственной близости над точкой вычислений на фигуре 1С, или в виде угловой конфигурации 105, состоящей из трех соседних точек вычислений, в непосредственно близости над точкой вычислений и одной соседней точки вычислений сбоку от точки вычислений, которая находится ближе всего к точке источника. Фазы и амплитуды для этих соседних точек вычислений могут быть использованы во взвешенном линейном решении методом наименьших квадратов в двумерном случае для следующих параметров: опорной фазы Φ0, как на этапе 211 из фигуры 2, поперечного размера kx, глубины kz. Прогнозируемая фаза имеет вид
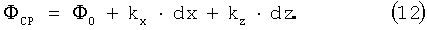
Уравнение может быть распространено на трехмерный случай в виде ΦCP=Φ0+kr·dr, где r может быть использовано в любой выбранной системе координат.
Аналогично, простая функция прогнозирования плоских волн может быть использована для разрешения фазовой неоднозначности при выборе конфигурации из фигуры 1С. Например, конфигурация 103 набора соседних точек вычислений, образованного соседней точкой вычислений непосредственно над точкой вычислений, соседней точкой вычислений сбоку от точки вычислений, ближайшей к точке источника, и соседней точкой вычислений, завершающей прямоугольник, задаваемый точкой вычислений и первыми двумя соседними точками вычислений (например 103 на фигуре 1С и фигуре 1D и фигуре 1Е). Фаза этих трех соседних точек вычислений единственным образом задает функцию прогнозирования плоских волн в виде уравнения (12).
Для выбора любого набора соседних точек вычислений (СТВ) может быть использована функция прогнозирования волнового импульса Гюйгенса. Запишем
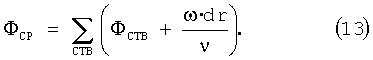
Сумма волновых импульсов также может быть взвешенной, например, с помощью амплитуды:
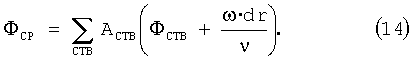
Как видно из этих примеров, имеется возможность выбора при построении функции прогнозирования.
Способ экстраполяции нисходящих непрерывных волн может быть использован для вычисления времен пробега. Сначала вычисляют волновое поле U для одной частоты. Затем для каждого набора глубин вычисляют локальную фазу из уравнения (9) в виде
Φ=tg-1(Im(U)/Re(U)).
Вычисляют угол, например, используя функцию arctg2() на языке Си, с помощью которой значение возвращается в диапазон от -π до +π. Если значение является отрицательным, можно добавить 2π для получения диапазона от 0 до 2π для локальной фазы. Возвращаемое значение можно сравнить с уже определенной фазой в ячейке сетки, наиболее близкой к месту расположения источника на предыдущем этапе вычисления для набора глубин. К локальной фазе может быть добавлено значение, кратное 2π, для получения глобальной фазы, которая больше на величину от 0 до 2π глобальной фазы в сравниваемом месте. В дополнение к этой очень простой функции прогнозирования фазы многие прогнозирующие функции обеспечивают идентичные или аналогичные результаты времен пробега в скоростных моделях.
В показанных на фигурах 3А, 3В, 4 и 5 примерах использованы следующие параметры.
Размеры вычислительной сетки: nx=nz=100.
Шаг вычислительной сетки: dx=dz=10 м.
Частота: 10 Гц.
Скорость:
Модель 1 на фигуре 3А: общий размер по x и y 1000 м. Скорость постоянна на всем протяжении модели, 1000 м/с.
Модель 2 на фигуре 3В: Два слоя толщиной по 500 м, скорость в верхнем слое 1000 м/с и скорость в нижнем слое 2000 м/с.
На фигуре 4 показана действительная часть U, 401, и развернутая фаза для модели постоянной скорости, модели 1 из фигуры 3А. Как и ожидалось, в соответствии с уравнением (8) развернутая фаза возрастает с приблизительно постоянным наклоном. Время пробега, полученное по фазе волнового поля для модели с постоянной скоростью, показано в виде конической поверхности 403. Время отложено вверх от горизонтальной плоскости 401. Изолиниями 407 фазы на карте 401 показаны волны, распространяющиеся стабильно по глубине в отсутствие какой-либо скоростной границы.
На фигуре 5 показано волновое поле 501 и полученное время 503 пробега для скоростной модели, модели 2 из фигуры 3В, в которой скорость удваивается на половине максимальной глубины, при этом скоростная граница показана позицией 505. Действительная часть вычисленного волнового поля показана в виде карты на горизонтальной плоскости 501. Время пробега, полученное по фазе волнового поля, показано в виде поверхности 503, при этом время представлено возвышением над горизонтальной плоскостью.
На фигуре 5 показаны результаты, полученные на основании модели 2 с горизонтальной скоростной границей 505. Значение скорости ниже границы 505 удваивается по сравнению со значением выше границы. Как и ожидалось, наклон поверхности 503 времени пробега ниже границы уменьшается наполовину. Изолиниями 507 фазы на карте показано выпучивание волны при ее встрече со скоростной границей 505.
На фигуре 6 показана действительная часть волнового поля частотой 30 Гц в модели Marmousi с изохронами времен пробега с максимальными амплитудами. Набор синтетических данных Marmousi (Bourgeois et al., Proceedings of the 1990 EAEG Workshop on Practical Aspects of Data Inversion: Eur. Assoc. Expl. Geophys., 5-16, 1991) был получен в качестве теста для оценивания скорости. Набор данных часто используют для проверки миграции и алгоритмов обработки сейсмических данных с выделением скорости. Он представляет собой набор сложных акустических двумерных данных, базирующихся на геологии бассейна Cuanza в Анголе. Скоростная модель показана на фигуре 7. В структурном стиле преобладают конседиментационные разломы, которые поднимаются от соляного оползня и обуславливают сложную структуру скорости в верхней части модели. Основная цель построения изображения заключается в показе коллектора в антиклинальной структуре ниже соли.
Фигурой 8 иллюстрируется использование способа настоящего изобретения совместно с данными Marmousi. Данные Marmousi представляют собой мигрированные данные до суммирования с временами пробега, полученными по волновым полям частотой 30 Гц от точечного источника. Чистота и качество отраженных волн в нижней части отражений, получение которых является основной задачей картирования модели, свидетельствуют о высоком качестве миграции.
Монохроматическое волновое поле можно охарактеризовать как имеющее относительно высокоамплитудные потоки данных, например, на фигуре 6 показан высокоамплитудный поток 603, в котором наблюдается плавное монотонное возрастание фазы. Можно видеть, что промежутки между потоками отражают области данных с относительно низкой амплитудой. Эти промежутки существуют там, где вступления кратных волн перекрываются, создавая ослабляющую интерференцию, вследствие чего образуются только слабые отражения. Развертывание фазы, при осуществлении которой в высокоамплитудных областях получают соответствующие развернутые фазы и используют в качестве опорных в низкоамплитудных видимых промежутках, может быть полезно для повышения устойчивости процесса развертывания.
Альтернативный способ вычисления волнового поля в широкой апертуре заключается в вычислении волнового поля на расширяющейся многогранной оболочке. Например, представляется полезной сетка, обозначенная на двадцатиграннике, поскольку нормаль к каждой грани двадцатигранника является приблизительно радиальной. Волновые поля могут быть вычислены на приблизительно сферических многогранных оболочках при использовании методов конечной разности или других численных методов.
Вычисление времени пробега волны на основании монохроматического решения волнового уравнения может быть осуществлено несколькими различными путями. Решения волнового уравнения акустических волн могут включать в себя решения волнового уравнения акустических волн для пробега в одном направлении и решения волнового уравнения акустических волн для полного пробега. Совместно с этим изобретением могут быть использованы решения уравнения упругих волн. Решения уравнения упругих волн также включают в себя решения для пробега в одном направлении и решения для полного пробега. Численные методы решений включают в себя методы конечных разностей, методы конечных элементов и методы преобразования Фурье, а также других преобразований. Способы для развертывания фазы волны в заданной точке вычислений путем анализа уже развернутых фаз и неразвернутых фаз из набора соседних точек вычислений включают в себя: выбор соседних точек вычислений на основании относительного положения точки источника и точки вычислений, выбор соседних точек вычислений путем анализа локального градиента времени пробега или неразвернутой фазы, нахождение соседней точки вычислений с наивысшей амплитудой, нахождение наименьшей развернутой фазы соседней точки вычислений, подбор плоской волны для соседних точек вычислений, подбор взвешенной по амплитуде или иным образом взвешенной плоской волны для соседних точек вычислений и вычисление взвешенного по амплитуде или иным образом волнового импульса Гюйгенса, полученного на основании соседних точек вычислений.
Амплитуды миграции или весовые параметры амплитуд для миграции Кирхгофа могут быть получены из амплитуд, вычисленных при нахождении решений для монохроматического волнового поля. Миграцию Кирхгофа можно осуществлять, используя времена пробега, вычисленные так, как описано в настоящей заявке. Миграцию Кирхгофа можно осуществлять во многих частотных диапазонах, используя времена пробега для каждого диапазона, вычисленные на отдельной частоте или частотах в этом диапазоне.
Карты или таблицы времен пробега для глубинной миграции могут быть вычислены по монохроматическим волновым полям точечного источника или функциям Грина. Эти карты времен пробега представляют собой точные решения для волнового уравнения на частоте вычислений и представляют собой более точные приближения для соседнего частотного диапазона по сравнению с временами распространения, вычисленными с помощью высокочастотных асимптотических методов.
Времена пробега могут быть вычислены на нескольких частотах в полосе частот сейсмической разведки. Сейсмические данные могут быть разделены на диапазоны этих в непосредственной близости частот, и миграция данных в каждой полосе частот может быть осуществлена при использовании соответствующего времени пробега. Полное сейсмическое изображение может быть восстановлено путем суммирования изображений в этих ограниченных полосах частот, поскольку процесс построения изображений является линейным. При выборе некоторого количества полос можно прогнозировать дополнительное улучшение качества изображения наряду с дополнительным увеличением затрат вычислительных ресурсов.
Кратко излагая изобретение, задают скоростную модель и выбирают местоположение источника. Комплексное волновое поле вычисляют для каждой точки вычислений. Развернутую фазу вычисляют в каждой точке вычислений, например, используя функцию арктангенса. Итерационную петлю начинают в точке источника. Исходно развернутая фаза известна только в точке источника, поскольку она является нулевой. Итерации осуществляют ограниченно для точек вычислений, прилегающих к точке источника, поскольку существует только одна соседняя точка вычислений, которая имеет развернутую фазу при этой итерации. Итерации осуществляют ограниченно для верхнего ряда решетки точек вычислений, поскольку выше него нет ряда. Итерации могут быть осуществлены ограниченно на краях модели, если некоторые из используемых в общем случае соседних точек вычислений отсутствуют.
Общий случай используют после манипулирования с частными случаями. Выбирают точку вычислений вместе с соседними точками вычислений, которые уже имеют развернутые фазы. Порядок выбора точек вычислений определяется необходимостью иметь соседние точки вычислений в соответствующих положениях. Выбор положений происходит более или менее в радиальном направлении от точки источника. Опорную фазу вычисляют на основании развернутых фаз соседних точек вычислений. Вычисляют прогнозируемую развернутую фазу в точке вычислений на основании опорной фазы и задержки распространения. Выбирают значение, кратное 2π, для добавления к развернутой фазе точки вычислений для того, чтобы получающаяся в результате фаза была по возможности близка к прогнозируемой развернутой фазе или в качестве альтернативы была по возможности близка, но разность была больше 0.
Специалистам в области техники, к которой относится изобретение, должно быть понятно, что способ, описанный в настоящей заявке, может быть использован на практике как раскрытый, включающий в себя описанные варианты осуществления, но без ограничения ими. Кроме того, должно быть понятно, что изобретение не должно быть чрезмерно ограничено предшествующим описанием, которое изложено с иллюстративной целью. Для специалистов в области техники, к которой относится изобретение, должны быть очевидными различные модификации и варианты без отступления от истинного объема изобретения, определенного в нижеследующей формуле изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ С КОМПЕНСАЦИЕЙ ПОКАЗАТЕЛЯ КАЧЕСТВА | 2016 |
|
RU2693495C1 |
| СЕЙСМИЧЕСКАЯ ОТРАЖАТЕЛЬНАЯ Q-ТОМОГРАФИЯ | 2013 |
|
RU2598907C1 |
| ЭФФЕКТИВНОЕ ВЫЧИСЛЕНИЕ МИГРАЦИИ ПО ВОЛНОВОМУ УРАВНЕНИЮ УГЛОВЫХ СЕЙСМОГРАММ | 2011 |
|
RU2570825C2 |
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ ПРИ НАЛИЧИИ ПЛОЩАДНОГО И ТОЧЕЧНОГО ИСТОЧНИКОВ | 2017 |
|
RU2706831C1 |
| МОДЕЛИРОВАНИЕ СЕЙСМИЧЕСКИХ СКОРОСТЕЙ | 2019 |
|
RU2794968C1 |
| УСТОЙЧИВЫЙ МЕТОД ПОСТРОЕНИЯ ГЛУБИННЫХ ИЗОБРАЖЕНИЙ В СЕЙСМОРАЗВЕДКЕ НА ОСНОВАНИИ НАСТРОЙКИ ОПЕРАТОРА ПО ЭТАЛОННЫМ СЕЙСМОГРАММАМ | 2014 |
|
RU2577792C1 |
| СПОСОБ И СИСТЕМА ДЛЯ СОЗДАНИЯ КОНТРОЛЬНЫХ ТОЧЕК ВО ВРЕМЯ МОДЕЛИРОВАНИЯ | 2011 |
|
RU2573269C2 |
| СПОСОБ СБОРА МАССИВА СЕЙСМИЧЕСКИХ ДАННЫХ НА ИССЛЕДУЕМОМ УЧАСТКЕ И СООТВЕТСТВУЮЩАЯ СИСТЕМА | 2018 |
|
RU2738592C1 |
| ПРЕОБРАЗОВАНИЕ РАДОНА ВОЛНОВОГО ФРОНТА | 2009 |
|
RU2460095C2 |
| СПОСОБЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ГЕОЛОГИЧЕСКОЙ СРЕДЫ ПРИ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ И ОБРАТНОЙ МИГРАЦИИ ВО ВРЕМЕННОЙ ОБЛАСТИ | 2011 |
|
RU2545487C2 |
Изобретение относится к области геофизической разведки, а более конкретно: к способу определения времени пробега сейсмической волны от пункта на поверхности до, по меньшей мере, одной точки вычислений в геологической среде. Сущность: задают скоростную модель области. Вычисляют для по меньшей мере одной точки вычислений комплексную монохроматическую волновую функцию, используя скоростную модель. Определяют развернутую фазу сейсмической волны в соседней точке вычислений, ближайшей к по меньшей мере одной точке вычислений в геологической среде. Время пробега сейсмической волны до по меньшей мере одной точки вычислений определяют, используя развернутую фазу соседней точки вычислений, и вычисляют монохроматическое волновое поле для по меньшей мере одной точки вычислений. На основании определенных значений времен пробега могут быть образованы карты и таблица времен пробега. Технический результат: повышение точности получаемых результатов. 3 н. и 38 з.п.ф-лы, 8 ил.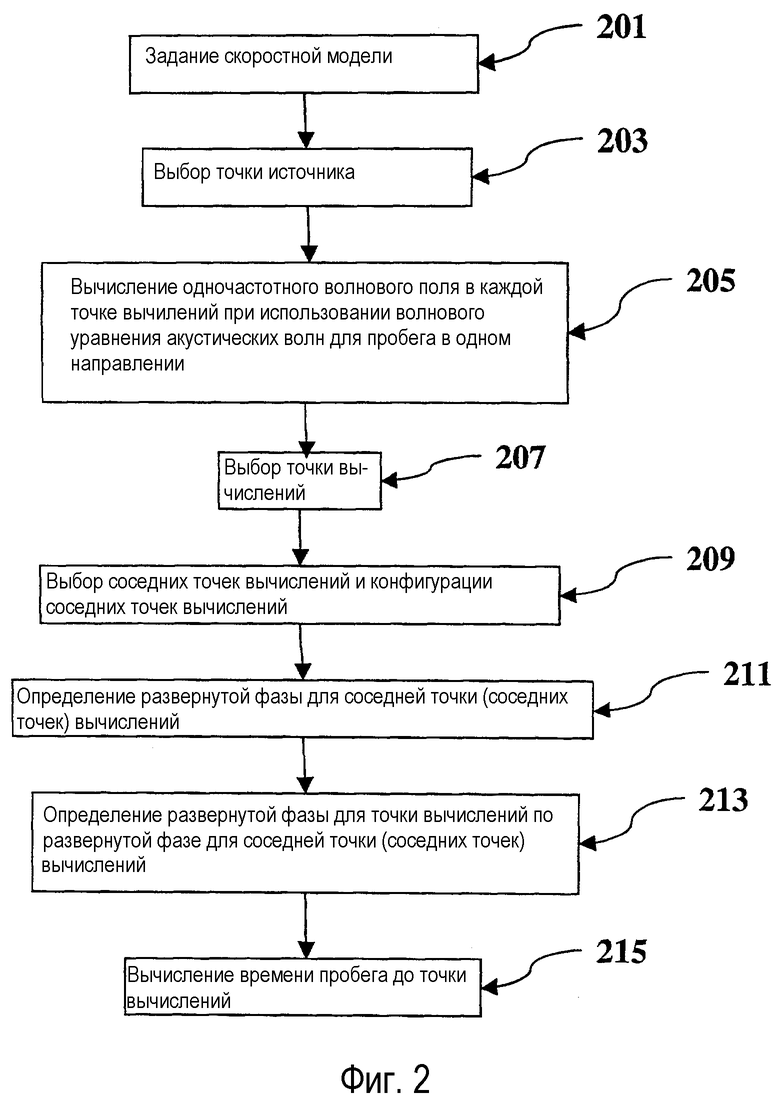
(a) задание скоростной модели области, включающей в себя указанное множество точек размещения в геологической среде;
(b) вычисление монохроматического волнового поля при использовании скоростной модели для, по меньшей мере, одной точки вычислений;
(c) определение развернутой фазы сейсмической волны в, по меньшей мере, одной соседней точке вычислений, ближайшей к, по меньшей мере, одной точке вычислений в указанном множестве точек размещения;
(d) определение времени пробега сейсмической волны до, по меньшей мере, одной точки вычислений по указанной определенной развернутой фазе и указанному вычисленному монохроматическому волновому полю для, по меньшей мере, одной точки вычислений,
(a) задание скоростной модели области, включающей в себя указанное множество точек размещения в геологической среде;
(b) вычисление монохроматического волнового поля при использовании скоростной модели для, по меньшей мере, одной точки вычислений;
(c) определение развернутой фазы сейсмической волны в, по меньшей мере, одной соседней точке вычислений, ближайшей к, по меньшей мере, одной точке вычислений в указанном множестве точек размещения;
(d) определение времени пробега сейсмической волны до, по меньшей мере, одной точки вычислений по указанной определенной развернутой фазе и указанному вычисленному монохроматическому волновому полю для, по меньшей мере, одной точки вычислений;
(e) сохранение значений времен пробега в виде карты.
(a) задание скоростной модели области, включающей в себя указанное множество точек размещения в геологической среде;
(b) вычисление волнового поля для, по меньшей мере, одной выбранной частоты при использовании скоростной модели для, по меньшей мере, одной точки вычислений;
(c) определение развернутой фазы сейсмической волны в, по меньшей мере, одной соседней точке вычислений, ближайшей к, по меньшей мере, одной точке вычислений в указанном множестве точек размещения; и
(d) определение времени пробега сейсмической волны до, по меньшей мере, одной точки вычислений по указанной определенной развернутой фазе и указанному вычисленному волновому полю для, по меньшей мере, одной точки вычислений.
| US 6081482 A, 27.06.2000 | |||
| Ванная стекловаренная печь | 1977 |
|
SU745870A1 |
| Роторно-лопастной двигатель внутреннего сгорания | 2019 |
|
RU2734069C1 |
| US 4340934 A, 20.07.1982 | |||
| СПОСОБ ПРОСТРАНСТВЕННОЙ СЕЙСМОРАЗВЕДКИ | 1994 |
|
RU2065182C1 |
Авторы
Даты
2007-06-10—Публикация
2002-12-30—Подача