Изобретение относится к области радиотехники и может найти применение в радиоприемных устройствах систем радиосвязи с шумоподобными сигналами, полученными манипуляцией фазы сигнала несущей частоты псевдослучайной последовательностью.
Когерентные методы приема и выделения информации обладают наиболее высокой помехозащищенностью, но они требуют точной оценки фазы входного сигнала. Поэтому одной из важных задач является определение способа фазовой синхронизации, обеспечивающего высокую точность слежения за фазой входного сигнала в условиях воздействия помех.
Шумоподобные сигналы, полученные в результате манипуляции фазы (на 0°, 180°) сигнала несущей частоты псевдослучайной последовательностью, имеют равномерный широкополосный спектр с подавленной несущей частотой. Отсутствие несущей частоты в спектре входного сигнала вызывает определенные сложности в реализации системы фазовой автоподстройки несущей частоты. Дополнительные сложности также могут быть обусловлены тем, что псевдослучайная последовательность, осуществляющая фазовую манипуляцию сигнала несущей частоты в передатчике, может быть дополнительно манипулировала по фазе от источника информации ["Системы связи с шумоподобными сигналами" Варакин Л.Е. М. «Радио и связь», 1985 г.].
Известен способ фазовой автоподстройки частоты при слежении за фазой фазоманипулированного сигнала, построенный на основе возведения в квадрат входного сигнала ["Системы синхронизации в связи и управлении" В.Линдсей, перевод с английского под редакцией Ю.Н.Бакаева, М.В.Капранова, М. «Советское радио», 1978 г., стр.100-101].
В данном способе фазовой автоподстройки частоты входной сигнал возводится в квадрат, а затем фильтруется узкополосным полосовым фильтром, настроенным на удвоенную частоту. При возведении в квадрат входного сигнала удваивается его частота, и фазовая манипуляция (0°, 180°) пропадает. Для фазовой автоподстройки частоты гетеродина используется классическая система фазовой автоподстройки частоты, работающая на удвоенной частоте входного сигнала. Для формирования сигнала гетеродина, когерентного с входным сигналом, выходной сигнал управляемого генератора кольца фазовой автоподстройки делится делителем частоты на два.
Недостатком данного способа фазовой автоподстройки частоты является низкая помехозащищенность. При возведении входного сигнала в квадрат, когда его величина меньше шума, шум значительно возрастает, а уровень сигнала относительно шума падает. Поэтому рассмотренный способ невозможно использовать для фазовой автоподстройки несущей частоты при отношении сигнал/шум на входе меньше единицы. Вторым недостатком известного способа является начальная неопределенность фазы сигнала на выходе делителя частоты, которая зависит от его начальной установки.
Известен также способ фазовой автоподстройки при слежении за фазой фазоманипулированного сигнала, использующий принцип фазоквадратурного кольца слежения «Система Костаса» ["Системы синхронизации в связи и управлении" В.Линдсей, перевод с английского под редакцией Ю.Н.Бакаева, М.В.Капранова, М. «Советское радио», 1978 г., стр.101-103].
В данном способе фазовой автоподстройки частоты на выходе управляемого генератора формируют два сигнала, сдвинутых относительно друг друга на 90° (синус и косинус). Входной сигнал умножается на опорный синусоидальный сигнал, а затем фильтруется фильтром нижних частот, на выходе которого выделяется сигнал разностной частоты. Одновременно входной сигнал умножается на опорный косинусоидальный сигнал и фильтруется другим фильтром нижних частот, на выходе которого выделяется другой сигнал разностной частоты. Полученные таким образом сигналы разностной частоты перемножаются между собой, фильтруются фильтром нижних частот, выходное напряжение которого подстраивает частоту управляемого генератора к частоте входного сигнала.
Недостатком известного способа является низкая помехозащищенность, так как он эквивалентен способу с возведением входного сигнала в квадрат ["Системы синхронизации в связи и управлении" В.Линдсей, перевод с английского под редакцией Ю.Н.Бакаева, М.В.Капранова, М. «Советское радио», 1978 г., стр.103].
Наибольшее применение в приемниках шумоподобных сигналов, сформированных в результате манипуляции фазы сигнала несущей частоты псевдослучайной последовательностью, получил способ фазовой автоподстройки частоты гетеродина, использующий двухкольцевую систему слежения.
Прототипом является способ, приведенный в книге "Системы связи с шумоподобными сигналами" автора Л.Е.Варакина, Москва «Радио и связь», 1985 г., стр.316.
Основным достоинством способа фазовой автоподстройки частоты гетеродина, использующего двухкольцевую систему слежения, является возможность работы при соотношениях сигнал/шум намного меньше единицы. В приемнике шумоподобного сигнала входной сигнал усиливается и преобразуется по частоте. Формируется псевдослучайная последовательность, совпадающая с псевдослучайной последовательностью, которой проманипулирован по фазе входной сигнал. Вычисляется комплексная функция корреляции R(τ)=(ReR(τ), ImR(τ)) входного сигнала с псевдослучайной последовательностью, сформированной в приемнике.
Определяется положение максимума 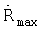 модуля
модуля 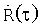 функции корреляции
функции корреляции
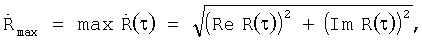
где 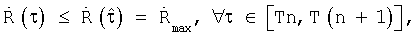
Т - период псевдослучайной последовательности, n=0, 1, 2, ...
Производится синхронизация сформированной в приемнике псевдослучайной последовательности с псевдослучайной последовательностью входного сигнала. Для этого псевдослучайная последовательность приемника сдвигается относительно псевдослучайной последовательности входного сигнала так, чтобы максимум функции корреляции попадал в зону дискриминационной характеристики системы подстройки временного сдвига. Двухкольцевая система фазовой автоподстройки содержит две системы автоматического регулирования. Одна из них предназначена для подстройки временного сдвига опорной псевдослучайной последовательности, сформированной в приемнике, по отношению к псевдослучайной последовательности входного сигнала. Другое кольцо слежения предназначено для компенсации фазового рассогласования между сигналом гетеродина приемника и несущей частотой входного сигнала. Система подстройки временного сдвига, за счет управления частотой тактовых импульсов генератора псевдослучайной последовательности, позволяет в приемнике сформировать псевдослучайную последовательность, совпадающую по времени с псевдослучайной последовательностью входного сигнала. Сформированная в приемнике такая псевдослучайная последовательность перемножается с входным сигналом, что позволяет снять с него фазовую манипуляцию. Разманипулированный сигнал перемножается в фазовом детекторе второго кольца (фазовой автоподстройки несущей частоты) с сигналом гетеродина приемника. Выходной сигнал детектора фильтруется фильтром нижних частот и управляет частотой гетеродина приемника, подстраивая его под частоту входного сигнала. Двухкольцевой способ фазовой автоподстройки частоты гетеродина имеет следующие недостатки.
1. Точность работы первого кольца влияет на точность работы второго кольца. Ошибки подстройки по времени псевдослучайных последовательностей (ПСП) при воздействии помех будут вызывать дополнительные ошибки подстройки фазы несущей частоты, и, наоборот, ошибки подстройки по фазе несущей частоты вызовут дополнительные ошибки в подстройке по времени ПСП.
2. Изменение уровня входного сигнала влияет на характеристики системы фазовой автоподстройки: быстродействие, помехозащищенность и устойчивость. Применение в приемнике системы автоматической регулировки усиления (АРУ) позволяет поддерживать заданный уровень сигнала, если аддитивная шумовая помеха значительно меньше уровня сигнала. Если уровень помехи по отношению к сигналу возрастет, то за счет работы системы АРУ, которая поддерживает постоянным уровень аддитивной смеси сигнала и шума, уровень сигнала на входе системы фазовой автоподстройки частоты будет уменьшаться. Если, например, шум на 20 дБ превышает уровень сигнала, то уровень сигнала будет почти на 20 дБ меньше по сравнению с уровнем сигнала, когда помеха отсутствует. Изменение уровня входного сигнала не позволяет оптимальным образом обеспечить требуемые характеристики фазовой автоподстройки частоты. При уменьшении уровня входного сигнала будет снижаться быстродействие, а при значительном возрастании уровня входного сигнала система фазовой автоподстройки может стать неустойчивой.
3. Способ фазовой автоподстройки частоты гетеродина не может использоваться в системах связи, в которых для передачи информации псевдослучайная последовательность проманипулирована по фазе от источника информации. Действительно, если псевдослучайная последовательность проманипулирована по фазе от источника информации, то, в зависимости от передаваемого бита информации (0 или 1), входной сигнал будет проманипулирован по фазе прямой или инверсной псевдослучайной последовательностью. После перемножения входного сигнала с псевдослучайной последовательностью, сформированной в приемнике, в сигнале на выходе перемножителя сохранится фазовая манипуляция, обусловленная передаваемыми битами информации. Поэтому второе кольцо, предназначенное для фазовой автоподстройки частоты гетеродина, работать не будет. Двухкольцевая система автоподстройки нашла применение в системах связи, в которых шумоподобный сигнал имеет две составляющие: синфазную и квадратурную (сдвинутую по фазе относительно синфазной составляющей на 90 градусов). Синфазная составляющая шумоподобного сигнала предназначена для работы системы синхронизации в приемнике и формируется фазовой манипуляцией сигнала несущей частоты псевдослучайной последовательностью. Квадратурная составляющая шумоподобного сигнала предназначена для передачи информации и формируется фазовой манипуляцией сигнала несущей частоты псевдослучайной последовательностью, которая проманипулирована по фазе от источника информации. Использование дополнительного сигнала для синхронизации снижает помехозащищенность системы связи. Это обусловлено тем, что энергия полученного суммарного сигнала распределяется между его синфазной и квадратурной составляющими.
Заявляемый способ фазовой автоподстройки частоты гетеродина в когерентном следящем приемнике шумоподобного сигнала позволяет устранить вышеперечисленные недостатки.
Это достигается за счет того, что в способе фазовой автоподстройки частоты гетеродина в когерентном следящем приемнике шумоподобного сигнала входной сигнал усиливают, смешивают с сигналом гетеродина и преобразуют по частоте. Затем вычисляют комплексную функцию корреляции входного сигнала с псевдослучайной последовательностью, сформированной в приемнике и вычисляют модуль функции корреляции. После определения максимума функции корреляции формируют сигнал фазового рассогласования, который фильтруют фильтром нижних частот, и управляют частотой сигнала гетеродина. Для формирования сигнала фазового рассогласования периодически вычисляют комплексную функцию корреляции и ее модуль. Затем выделяют действительную или мнимую составляющую комплексной функции корреляции в точке, соответствующей максимуму модуля комплексной функции корреляции, умножают на единицу со знаком другой составляющей и делят на максимальное значение модуля функции корреляции.
В заявляемом способе фазовой автоподстройки частоты в когерентном следящем приемнике шумоподобного сигнала входной фазоманипулированный сигнал усиливается, а затем преобразуется по частоте. Для преобразования по частоте входного сигнала формируется сигнал гетеродина. Усиленный входной шумоподобный сигнал смешивается с сигналом гетеродина. Из полученной смеси входного шумоподобного сигнала с сигналом гетеродина на разностной частоте выделяют синфазную и квадратурную составляющие. Затем в приемнике формируется псевдослучайная последовательность, являющаяся копией псевдослучайной последовательности, манипулирующей фазу входного сигнала. Через интервалы времени, равные периоду псевдослучайной последовательности, вычисляется комплексная функция корреляции R(τ)=(ReR(τ), ImR(τ)) входного сигнала с псевдослучайной последовательностью, сформированной в приемнике. Вычисляется модуль функции корреляции. Находится значение временного сдвига 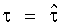 , при котором модуль
, при котором модуль  функции корреляции принимает максимальное значение
функции корреляции принимает максимальное значение 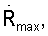 т.е.
т.е. 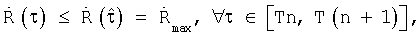 где: T - период псевдослучайной последовательности, n=0, 1, 2...
где: T - период псевдослучайной последовательности, n=0, 1, 2...
Для фазовой автоподстройки частоты гетеродина приемника можно использовать либо мнимую, либо действительную составляющую комплексной функции корреляции. Для этого из вычисленной комплексной функции корреляции 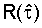 выбирается значение мнимой
выбирается значение мнимой 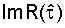 или действительной
или действительной 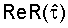 составляющей, полученное в точке
составляющей, полученное в точке 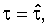 соответствующей максимуму модуля функции корреляции. Выбранное значение
соответствующей максимуму модуля функции корреляции. Выбранное значение 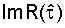 (или
(или 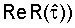 нормируется путем его деления на величину
нормируется путем его деления на величину 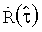 модуля функции корреляции в точке максимума
модуля функции корреляции в точке максимума 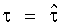 . Полученный результат умножается наsign
. Полученный результат умножается наsign (или sign
(или sign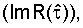 где
где 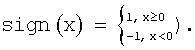 То есть умножается на единицу со знаком другой действительной или мнимой составляющей функции корреляции
То есть умножается на единицу со знаком другой действительной или мнимой составляющей функции корреляции 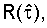 выбранной в точке
выбранной в точке 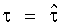 максимума ее модуля
максимума ее модуля 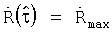 . Сформированный сигнал
. Сформированный сигнал 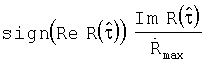
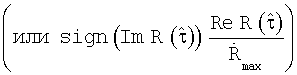 фильтруют фильтром нижних частот. Полученным сигналом на выходе фильтра нижних частот управляют частотой выходного сигнала гетеродина, компенсируя фазовое рассогласование между входным сигналом и сигналом гетеродина.
фильтруют фильтром нижних частот. Полученным сигналом на выходе фильтра нижних частот управляют частотой выходного сигнала гетеродина, компенсируя фазовое рассогласование между входным сигналом и сигналом гетеродина.
Техническим результатом при осуществлении способа фазовой автоподстройки частоты гетеродина в когерентном следящем приемнике шумоподобного сигнала является:
- повышение точности работы системы фазовой автоподстройки;
- исключение влияния изменения уровня входного сигнала на параметры кольца слежения;
- возможность производить фазовую автоподстройку частоты гетеродина без дополнительного сигнала синхронизации, когда широкополосный сигнал манипулирован по фазе псевдослучайной последовательностью и импульсной последовательностью источника информации.
Достигается это за счет того, что:
- используется только одно кольцо фазовой автоподстройки, в котором управляющее напряжение формируется из действительной или мнимой составляющей функции корреляции;
- производится нормирование действительной или мнимой составляющей функции корреляции, из которой формируется сигнал, управляющий частотой сигнала гетеродина;
- производится умножение нормированной составляющей функции корреляции на единицу со знаком второй составляющей.
Поясним на конкретном примере способ фазовой автоподстройки частоты гетеродина в когерентном следящем приемнике шумоподобного сигнала.
На вход радиоприемного устройства поступает входной сигнал, который имеет следующий вид
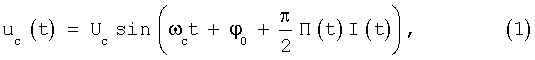
где Uc - амплитуда входного сигнала,
ωc - угловая частота входного сигнала,
ϕ0 - начальная фаза входного сигнала,
П(t) - псевдослучайная последовательность, манипулирующая фазу входного сигнала, П(t)∈{-1,1}, ∀t≥0,
I(t) - последовательность импульсов источника информации, I(t)∈{-1,1}, ∀t≥0.
В зависимости от поступающей информационной последовательности I(t) в моменты времени t∈[nT, (n+1)T), где n=0, 1, 2, ..., псевдослучайная последовательность П(t) может быть прямой или инверсной.
Для преобразования частоты входного сигнала в приемнике формируется квадратурный (комплексный) сигнал гетеродина
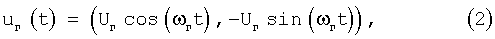
где Uг - амплитуда сигнала гетеродина,
ωг - угловая частота сигнала гетеродина.
Входной сигнал перемножается с синусной и косинусной составляющей сигнала гетеродина, а затем фильтруется фильтром нижних частот, который пропускает сигналы только разностной частоты
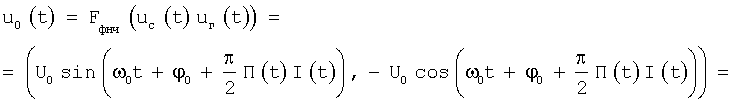
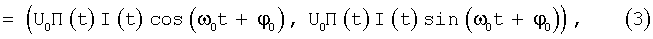
где u0(t) - выходной сигнал фильтра нижних частот, ω0=ωc-ωг, 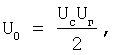
Fфнч. - функция, которая определяется характеристикой фильтра нижних частот.
В приемнике формируется псевдослучайная последовательность П0(t), которая должна быть копией последовательности, манипулирующей фазу входного сигнала. Вычисляется комплексная функция корреляции R(τ)=(ReR(τ), ImR(τ)) входного сигнала u0(t) с псевдослучайной последовательностью П0(t), сформированной в приемнике.
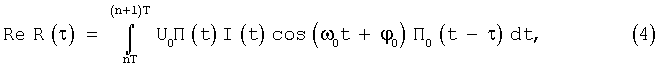
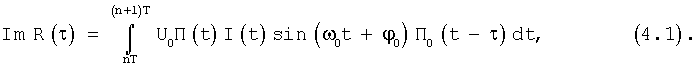
Частота гетеродина в приемнике близка к частоте входного сигнала, поэтому остаточное рассогласование по частоте определяется только суммарной нестабильностью генераторов приемника и передатчика, а также эффектом Доплера. Поэтому величина ω0=ωc-ωг близка к нулю.
Полагая, что ω0t+ϕ0≈ϕ[n], ∀t∈[nT, (n+1)T], а I(t)=In для ∀t∈[nT, (n+1)T], получим
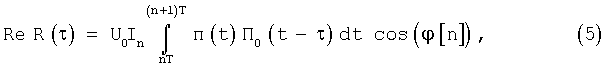
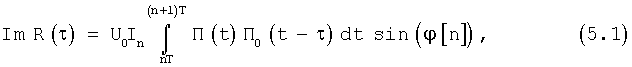
Вычисляем модуль 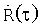 функции корреляции R(τ), который определяется равенством
функции корреляции R(τ), который определяется равенством
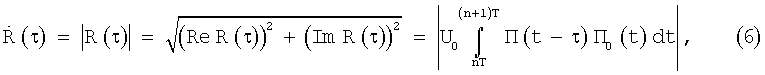 .
.
Определяем значение τ, при котором модуль 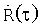 функции корреляции R(τ) принимает максимальное значение. Сформированная в приемнике псевдослучайная последовательность П0(t) отличается только временным сдвигом от формируемой в передатчике последовательности П(t). Учитывая, что П0(t)=П(t-τ0), где τ0 - задержка по времени псевдослучайной последовательности П(t) входного сигнала относительно формируемой в приемнике псевдослучайной последовательности П0(t), модуль
функции корреляции R(τ) принимает максимальное значение. Сформированная в приемнике псевдослучайная последовательность П0(t) отличается только временным сдвигом от формируемой в передатчике последовательности П(t). Учитывая, что П0(t)=П(t-τ0), где τ0 - задержка по времени псевдослучайной последовательности П(t) входного сигнала относительно формируемой в приемнике псевдослучайной последовательности П0(t), модуль 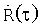 функции корреляции R(τ) будет иметь максимум в точке τ=τ0, т.е.
функции корреляции R(τ) будет иметь максимум в точке τ=τ0, т.е. 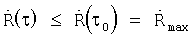 для ∀τ. В точке τ=τ0 функция корреляция определяется следующим равенством
для ∀τ. В точке τ=τ0 функция корреляция определяется следующим равенством
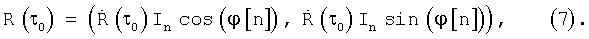
Делением действительной и мнимой составляющих функции корреляции на величину модуля функции корреляции в точке максимума, формируем нормированную функцию корреляции r(τ0), которая определяется равенством
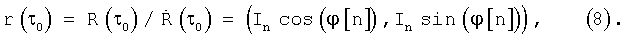
Составляющие Incos(ϕ[n]) и Insin(ϕ[n]) полученной нормированной функции корреляции r(τ0) не зависят от уровня входного сигнала приемника и коэффициента усиления его блоков. Они зависят только от величины фазовой ошибки ϕ[n] между входным сигналом и сигналом гетеродина, а также от передаваемой информации In в n-ом периоде формирования псевдослучайной последовательности. Можно управлять частотой сигнала гетеродина приемника, используя мнимую Insin(ϕ[n]) или действительную Incos[ϕ[n]) составляющую нормированной функции корреляции r(τ0). Если для подстройки частоты гетеродина использовать мнимую составляющую Insin(ϕ[n]) нормированной функции корреляции r(τ0), то, чтобы исключить влияние передаваемой информации In на сигнал управления, необходимо ее умножить на функцию sign(Incos(ϕ[n])), т.е. на единицу со знаком действительной составляющей. Если для подстройки частоты гетеродина использовать действительную составляющую Incos(ϕ[n]) нормированной функции корреляции r(τ0), то для исключения влияния передаваемой информации In на сигнал управления необходимо ее умножить на функцию sign(Insin(ϕ[n])), т.е. на единицу со знаком мнимой составляющей нормированной функции корреляции rn(τ0). Сформированный таким образом сигнал управления 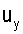 будет определяться равенством
будет определяться равенством
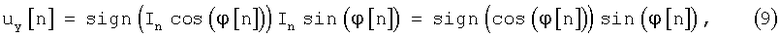
или
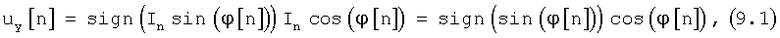
Сигнал управления uy обрабатывается фильтром нижних частот и управляет частотой гетеродина приемника. Сигнал на выходе фильтра нижних частот можно определить через его импульсную характеристику h[m], а именно:
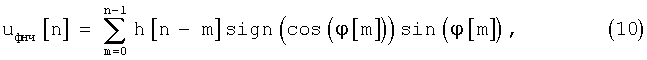
или
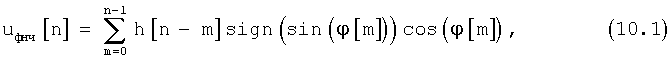
Приращение фазовой ошибки Δϕ[n]=ϕ[n+1]-ϕ[n] за временной интервал T, равный периоду псевдослучайной последовательности, определяется равенством
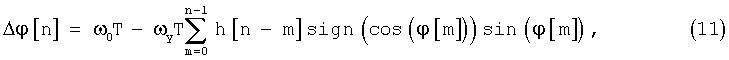
или
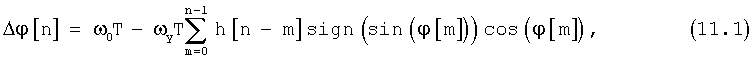
где ωy - приращение угловой частоты гетеродина приемника на единицу управляющего воздействия (рад/сек).
Поясним фазовую автоподстройку частоты гетеродина на простом примере, когда импульсная характеристика h[n] фильтра нижних частот определяется равенством
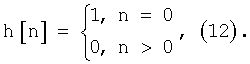
Для данной импульсной характеристики h[n] фильтра нижних частот уравнение (11) имеет вид
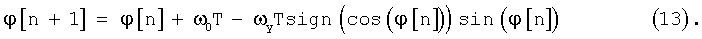
Уравнение (13) описывает изменение фазовой ошибки ϕ в моменты времени t=0, T, 2T, ...
Если 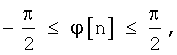 то sign(cos(ϕ[n]))=1. Уравнение (13) для фазовой ошибки ϕ можно записать в следующем виде
то sign(cos(ϕ[n]))=1. Уравнение (13) для фазовой ошибки ϕ можно записать в следующем виде
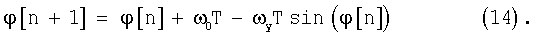
При выполнении неравенств ω0<ωy<1 из уравнения (14) получим последовательность ϕ[0], ϕ[1], ..., ϕ[n], ..., монотонно сходящуюся к точке устойчивого положения равновесия ϕ[∞]=ϕ0 +. Точка устойчивого положения равновесия ϕ0 + определяется равенством, полученным из уравнения (14) при условии ϕ[n+1]=ϕ[n]
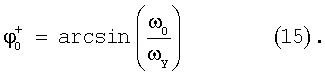
В установившемся режиме, когда ω0≪ωy и 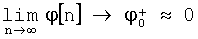 , для нормированной функции корреляции r(τ0) получим
, для нормированной функции корреляции r(τ0) получим
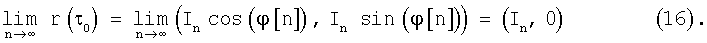
В установившемся режиме действительная составляющая Rer(τ0) нормированной функции корреляции r(τ0) совпадает с импульсной последовательностью передаваемой информации Rer(τ0)=In, а мнимая составляющая Imr(τ0)=0. Если для управления частотой гетеродина приемника использовать сигнал uy, определяемый равенством (9.1), то в установившемся режиме Imr(τ0)=In, а Rer(τ0)=0.
Если в уравнении (13) 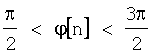 , то sign(cos(ϕ[n]))=-1.
, то sign(cos(ϕ[n]))=-1.
Для фазовой ошибки ϕ[n] в моменты времени t=nT, (где n=0, 1, 2, ...) запишем уравнение (13) в виде
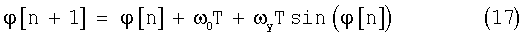
При выполнении неравенства, при котором ω0≪ωy<1, из уравнения (17) получим последовательность ϕ[0], ϕ[1], ..., ϕ[n], ..., которая будет монотонно сходиться к другой точке устойчивого положения равновесия ϕ[∞]=ϕ0 -.
Точка устойчивого положения равновесия определяется равенством, полученным из уравнения (17) при условии, что ϕ[n+1]=ϕ[n].
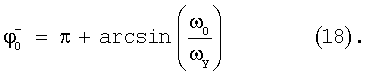
В установившемся режиме, когда ω0≪ωy, a 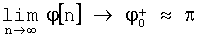 , для нормированной функции корреляции r(τ0) получим следующее равенство
, для нормированной функции корреляции r(τ0) получим следующее равенство
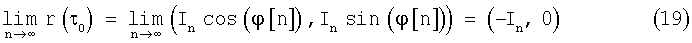
В установившемся режиме действительная составляющая Rer(τ0) нормированной функции корреляции r(τ0) совпадает с инверсной последовательностью импульсов передаваемой информации Rer(τ0)=-In, а мнимая составляющая Imr(τ0)=0. Если для управления частотой гетеродина приемника использовать сигнал uy, определяемый равенством (9.1), то можно показать, что в установившемся режиме Imr(τ0)=-In, a Rer(τ0)=0.
Более высокую точность в системе фазовой автоподстройки частоты гетеродина приемника можно получить, применяя активный пропорционально-интегрирующий фильтр. Если через активный пропорционально-интегрирующий фильтр подавать на вход управления частотой гетеродина сформированный сигнал управления uy (определяемый равенством 9), то, при наличии шума и нестабильности частоты входного сигнала, можно уменьшить фазовую ошибку ["Оценка точности работы фазовой синхронизации в условиях воздействия шума и нестабильности фазы входного сигнала" А.Р.Попов. Сборник докладов VIII международной конференции RLNC-2002, г. Воронеж].
Заявляемый в качестве изобретения способ фазовой автоподстройки частоты гетеродина в когерентном следящем приемнике шумоподобного сигнала обладает следующими преимуществами.
1. Позволяет обеспечить более высокую точность фазовой автоподстройки частоты гетеродина приемника. Она достигается за счет того, что заявляемый способ не требует применения дополнительной системы автоподстройки, компенсирующей рассогласование по времени псевдослучайных последовательностей. Неточность работы системы подстройки по времени приведет к дополнительным ошибкам, особенно при воздействии помех.
2. Позволяет исключить влияние уровня сигнала и коэффициентов усиления блоков приемника на характеристики фазовой автоподстройки частоты гетеродина в когерентном следящем приемнике. Достигается это за счет того, что производится нормирование составляющих функции корреляции, из которых формируется сигнал, управляющий частотой сигнала гетеродина.
3. Позволяет производить фазовую автоподстройку частоты гетеродина приемника, когда псевдослучайная последовательность входного шумоподобного сигнала манипулирована по фазе от источника информации и не требует применения дополнительного синхросигнала. Достигается это за счет того, что производится умножение нормированной составляющей функции корреляции на единицу со знаком второй составляющей.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ В СИСТЕМЕ СВЯЗИ С ШУМОПОДОБНЫМИ СИГНАЛАМИ | 2004 |
|
RU2286017C2 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ В СИСТЕМЕ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ | 2004 |
|
RU2279183C2 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ ШУМОПОДОБНЫМИ СИГНАЛАМИ В МОБИЛЬНОЙ СИСТЕМЕ СВЯЗИ ТАКТИЧЕСКОГО ЗВЕНА | 2016 |
|
RU2649418C2 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ ШУМОПОДОБНЫМИ СИГНАЛАМИ В СИСТЕМЕ ОПОЗНАВАНИЯ "СВОЙ-ЧУЖОЙ" | 2013 |
|
RU2532085C2 |
| УСТРОЙСТВО СИНХРОНИЗАЦИИ ПРИЕМНИКА ШУМОПОДОБНЫХ СИГНАЛОВ | 1980 |
|
SU1840647A1 |
| СПОСОБ ПРИЕМА ШУМОПОДОБНЫХ СИГНАЛОВ С МИНИМАЛЬНОЙ ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ | 2006 |
|
RU2307474C1 |
| СПОСОБ ПРИЕМА ШУМОПОДОБНЫХ ЧАСТОТНО-МАНИПУЛИРОВАННЫХ СИГНАЛОВ С НЕПРЕРЫВНОЙ ФАЗОЙ | 2006 |
|
RU2323536C1 |
| СПОСОБ И УСТРОЙСТВО ДЕМОДУЛЯЦИИ СИГНАЛОВ ГАЛИЛЕЯ С ПЕРЕМЕННОЙ БИНАРНОЙ СМЕЩЕННОЙ НЕСУЩЕЙ (ALTBOC) | 2004 |
|
RU2349049C2 |
| СПОСОБ ПОИСКА ШУМОПОДОБНЫХ СИГНАЛОВ С МИНИМАЛЬНОЙ ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ | 2007 |
|
RU2353064C1 |
| СПОСОБ ПОИСКА ШУМОПОДОБНЫХ СИГНАЛОВ С МИНИМАЛЬНОЙ ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ | 2012 |
|
RU2486683C1 |
Изобретение относится к области радиотехники и может быть использовано в радиоприемных устройствах систем радиосвязи с шумоподобными сигналами, полученными манипуляцией фазы сигнала несущей частоты псевдослучайной последовательностью (ПСП). В способе фазовой автоподстройки частоты (ФАПЧ) гетеродина в когерентном следящем приемнике шумоподобного сигнала входной сигнал усиливают, смешивают с сигналом гетеродина и преобразуют по частоте. Затем вычисляют комплексную функцию корреляции входного сигнала с ПСП, сформированной в приемнике и вычисляют модуль функции корреляции. После определения максимума функции корреляции формируют сигнал фазового рассогласования путем периодического вычисления комплексной функции корреляции и ее модуля, выделения действительной или мнимой составляющей комплексной функции корреляции в точке, соответствующей максимуму модуля комплексной функции корреляции, умножения на единицу со знаком другой составляющей и деления на максимальное значение модуля функции корреляции, который фильтруют фильтром нижних частот и управляют частотой сигнала гетеродина. Технический результат заключается в повышении точности ФАПЧ гетеродина приемника, а также в возможности производить фазовую автоподстройку частоты гетеродина приемника, когда ПСП входного шумоподобного сигнала манипулирована по фазе от источника информации.
Способ фазовой автоподстройки частоты гетеродина в когерентном следящем приемнике шумоподобного сигнала, в котором входной сигнал усиливают, смешивают с сигналом гетеродина, преобразуют по частоте, вычисляют комплексную функцию корреляции входного сигнала с псевдослучайной последовательностью, сформированной в приемнике, вычисляют модуль функции корреляции, определяют максимум функции корреляции, формируют сигнал фазового рассогласования, который фильтруют фильтром нижних частот и управляют частотой сигнала гетеродина, отличающийся тем, что для формирования сигнала фазового рассогласования периодически вычисляют комплексную функцию корреляции и ее модуль, выделяют ее действительную или мнимую составляющую в точке, соответствующей максимуму модуля комплексной функции корреляции, умножают на единицу со знаком другой составляющей и делят на максимальное значение модуля функции корреляции.
| ВАРАКИН Л.Е | |||
| Системы связи с шумоподобными сигналами | |||
| - М.: Радио и связь, 1985, с.316 | |||
| SU 12221762 А, 30.03.1986 | |||
| Устройство для приема частотно-манипулированных сигналов | 1987 |
|
SU1467784A2 |
| US 5280538 A, 18.01.1994. | |||
Авторы
Даты
2007-09-10—Публикация
2005-10-13—Подача