1. Способ распознавания форм рельефа местности по картине горизонталей, при котором создают трехмерную карту местности путем цифрования элементов земной поверхности, строят цифровую модель рельефа путем приписывания уровней высоты точкам земли, строят триангуляцию, связывающую элементы цифровой модели рельефа, и используют полученную триангулированную модель для распознавания форм рельефа, отличающийся тем, что построение цифровой модели рельефа дополнительно включает в себя построение и редактирование горизонталей, триангуляцию строят по совокупности отредактированных горизонталей таким образом, чтобы никакие части горизонталей не попадали внутрь получающихся треугольников, а при использовании триангулированной модели для распознавания форм рельефа строят неориентированный граф, множество вершин которого совпадает с некоторым подмножеством множества треугольников указанной триангуляции, причем множества вершин и ребер графа зависят от распознаваемых форм рельефа, после чего находят связные компоненты полученного графа и распознают указанные формы рельефа путем последовательного анализа всех связных компонент графа.2. Способ по п.1, отличающийся тем, что цифрование элементов земной поверхности выполняют путем построения стереомодели области земной поверхности и цифрования элементов рельефа с использованием построенной стереомодели.3. Способ по п.1, отличающийся тем, что цифрование элементов земной поверхности выполняют путем использования уже существующих тематических карт.4. Способ по п.1, отличающийся тем, что построение горизонталей производят по результатам цифрования элементов земной поверхности путем интерполяции указанных результатов цифрования, что дает функцию высоты, и путем автоматического нахождения линий уровня функции высоты.5. Способ по п.1, отличающийся тем, что редактирование горизонталей включает в себя их сглаживание.6. Способ по п.1, отличающийся тем, что редактирование горизонталей включает в себя согласование точек максимальной кривизны соседних горизонталей.7. Способ по п.1, отличающийся тем, что редактирование горизонталей включает в себя построение дополнительных и вспомогательных горизонталей.8. Способ по п.1, отличающийся тем, что редактирование горизонталей включает в себя согласование горизонталей с элементами гидрографии.9. Способ по п.1, отличающийся тем, что триангуляция является триангуляцией Делоне.10. Способ по п.1, отличающийся тем, что триангуляция является триангуляцией минимального периметра.11. Способ по п.1, отличающийся тем, что распознаваемыми формами рельефа являются вершины и впадины рельефа, а при использовании полученной триангулированной модели для распознавания вершин и впадин рельефа строят неориентированный граф, множество вершин которого совпадает с множеством треугольников указанной триангуляции, все три вершины которых являются вершинами одной и той же ломаной, изображающей какую-либо горизонталь рельефа, а две вершины графа соединяют ребром в том и только в том случае, если соответствующие им треугольники имеют общую сторону, не являющуюся частью никакого отрезка никакой ломаной, изображающей горизонталь рельефа, причем для каждой связной компоненты определяют совокупность тех сторон треугольников триангуляции, которые образуют периметр области, являющейся объединением треугольников, соответствующих вершинам данной связной компоненты, для каждой такой стороны треугольника определяют, является ли она частью какой-либо ломаной, определяющей какую-либо горизонталь рельефа, и если для данной связной компоненты оказывается, что все указанные стороны треугольников триангуляции являются частями одной и той же ломаной, определяющей горизонталь рельефа, то эту горизонталь рельефа берут в качестве горизонтали, ограничивающей очередную распознанную вершину или впадину рельефа.12. Способ по п.1, отличающийся тем, что распознаваемыми формами рельефа являются пропущенные горизонтали, а при использовании полученной триангулированной модели для распознавания пропущенных горизонталей выбирают сечение рельефа, являющееся максимальным расстоянием между горизонталями по высоте, и максимальное расстояние между соседними горизонталями в плане, затем строят неориентированный граф, множество вершин которого совпадает с множеством треугольников указанной триангуляции, для которых какие-либо две вершины лежат на разных горизонталях и либо разность высот этих горизонталей больше указанного сечения рельефа, либо эти две вершины удалены друг от друга на расстояние, превышающее указанное максимальное расстояние между соседними горизонталями в плане, а две вершины графа соединяют ребром в том и только в том случае, если соответствующие им треугольники имеют общую сторону, не являющуюся частью никакого отрезка никакой ломаной, изображающей горизонталь рельефа, причем для каждой связной компоненты определяют область, являющуюся объединением треугольников, соответствующих вершинам данной связной компоненты, и полученную область берут в качестве области, в которой пропущены горизонтали.13. Способ по п.1, отличающийся тем, что распознаваемыми формами рельефа являются седловины рельефа, а при использовании полученной триангулированной модели для распознавания седловин рельефа в предположении отсутствия пропущенных горизонталей строят неориентированный граф, множество вершин которого совпадает с множеством треугольников указанной триангуляции, имеющих по крайней мере одну горизонтальную сторону, не являющуюся частью никакой горизонтали, а две вершины графа соединяют ребром в том и только в том случае, если соответствующие им треугольники имеют общую сторону, являющуюся горизонтальной, причем для каждой связной компоненты определяют совокупность тех сторон треугольников триангуляции, которые образуют периметр области, являющейся объединением треугольников, соответствующих вершинам данной связной компоненты, выполняют обход указанного периметра области, разбивая его на совокупность замкнутых ломаных, одна из которых является внешним контуром области, а остальные - контурами границ дырок, затем для каждого звена каждой из указанных ломаных определяют направления ската рельефа при движении через данное звено ломаной из указанной области вовне ее, принимающее одно из трех значений: первое - понижение, второе - повышение и третье - неопределенное, затем выполняют обход каждой из указанных замкнутых ломаных, подсчитывая число переходов с первого значения направления ската на второе, игнорируя все третьи значения, и если результат подсчета оказывается больше 1 для хотя бы одной из указанных ломаных для данной связной компоненты, то указанную область берут в качестве области, в которой расположена седловина рельефа.14. Способ по п.1, отличающийся тем, что распознаваемыми формами рельефа являются несоответствия между горизонталями и отметками высот, а при использовании полученной триангулированной модели для распознавания несоответствия между горизонталями и отметками высот в предположении, что отсутствуют пропущенные ответные горизонтали, для каждого треугольника указанной триангуляции, содержащего хотя бы одну отметку высоты, определяют минимальное и максимальное допустимые значения высот точек внутри указанного треугольника, для чего последовательно просматривают все отметки высот, и для каждой отметки высоты определяют содержащий ее треугольник триангуляции, для этого треугольника сравнивают высоты трех его вершин и, если не все три его вершины имеют одну и ту же высоту, то приписывают минимальное и максимальное значения высоты для отметок высот, попадающих в данный треугольник, равные соответственно минимальному и максимальному значениям высот трех его вершин, а в противном случае помечают указанный треугольник как горизонтальный, затем, если после просмотра всех отметок высот хотя бы один треугольник оказался отмеченным как горизонтальный, строят неориентированный граф, множество вершин которого совпадает с множеством всех треугольников триангуляции, имеющих хотя бы одно горизонтальное ребро, не лежащее ни на какой горизонтали, включая и неотмеченные, а две вершины графа соединяют ребром в том и только в том случае, если соответствующие им треугольники имеют общую сторону, не являющуюся частью никакого отрезка никакой ломаной, изображающей горизонталь рельефа, причем находят множество существенных связных компонент графа, для чего просматривают все треугольники, отмеченные как горизонтальные, и для каждого такого треугольника отмечают связную компоненту графа, содержащую вершину, соответствующую указанному горизонтальному треугольнику, как существенную, после просмотра всех горизонтальных треугольников для каждой существенной связной компоненты определяют совокупность тех сторон треугольников триангуляции, которые образуют периметр области, являющейся объединением треугольников, соответствующих вершинам данной связной компоненты, и для каждой вершины полученного периметра области определяют ее высоту, затем вычисляют минимальное и максимальное значения высот указанных вершин полученного периметра области и по этим значениям для каждого треугольника указанной триангуляции, которому соответствует вершина графа, принадлежащая данной связной компоненте, и который помечен как горизонтальный, определяют минимальное и максимальное допустимые значения высоты для отметок высот, попадающих в данный треугольник, после окончания просмотра всех существенных связных компонент последовательно просматривают все отметки высот и для каждой отметки высоты определяют содержащий ее треугольник триангуляции, сравнивают значение высоты рассматриваемой отметки высоты с указанными минимальным и максимальным допустимыми значениями высот точек внутри указанного треугольника и, если значение высоты указанной отметки высоты оказывается меньшим указанного минимального допустимого значения или большим указанного максимального допустимого значения, то указанную отметку высоты отмечают как несоответствующую горизонталям рельефа.15. Способ по п.1, отличающийся тем, что распознаваемыми формами рельефа являются орографические линии, а при использовании полученной триангулированной модели для распознавания орографических линий строят неориентированный граф, множество вершин которого совпадает с множеством треугольников указанной триангуляции, для которых либо все вершины лежат на одной горизонтали, либо на двух горизонталях разной высоты, а две вершины графа соединяют ребром в том и только в том случае, если соответствующие им треугольники имеют общую сторону, не лежащую ни на какой горизонтали, причем для каждой связной компоненты, для которой треугольники, соответствующие элементам этой связной компоненты, имеют вершины, в совокупности не лежащие на одной горизонтали, определяют совокупность тех сторон треугольников триангуляции, которые образуют периметр области, являющейся объединением треугольников, соответствующих вершинам данной связной компоненты, и определяют совокупность отрезков горизонталей, лежащих на указанном периметре области, находят точки максимальной кривизны горизонталей, лежащие на указанных отрезках горизонталей, находят соответствие между двумя множествами точек максимальной кривизны указанных отрезков разных горизонталей, строят отрезки орографических линий, лежащие между соседними горизонталями и соединяющие пары соответствующих точек максимальной кривизны, затем после просмотра всех связных компонент производят объединение полученных отрезков орографических линий в окончательно распознанные орографические линии.16. Способ по п.1, отличающийся тем, что распознаваемыми формами рельефа являются несоответствия точек максимальной кривизны соседних горизонталей, а при использовании полученной триангулированной модели для распознавания несоответствия точек максимальной кривизны соседних горизонталей строят неориентированный граф, множество вершин которого совпадает с множеством треугольников указанной триангуляции, для которых либо все вершины лежат на одной горизонтали, либо на двух горизонталях разной высоты, а две вершины графа соединяют ребром в том и только в том случае, если соответствующие им треугольники имеют общую сторону, не лежащую ни на какой горизонтали, причем для каждой связной компоненты, для которой треугольники, соответствующие элементам этой связной компоненты, имеют вершины, в совокупности не лежащие на одной горизонтали, определяют совокупность тех сторон треугольников триангуляции, которые образуют периметр области, являющейся объединением треугольников, соответствующих вершинам данной связной компоненты, и определяют совокупность отрезков горизонталей, лежащих на указанном периметре области, находят точки максимальной кривизны горизонталей, лежащие на указанных отрезках горизонталей, находят соответствие между двумя множествами точек максимальной кривизны указанных отрезков разных горизонталей, строят отрезки орографических линий, лежащие между соседними горизонталями и соединяющие пары соответствующих точек максимальной кривизны, затем после просмотра всех связных компонент производят объединение полученных отрезков орографических линий в окончательно распознанные орографические линии, после чего находят такие места на орографических линиях, где при переходе от горизонтали к горизонтали меньшей высоты орографическая линия разветвляется по крайней мере на две орографические линии, которые при переходе к горизонтали еще меньшей высоты снова сливаются в одну орографическую линию, и отмечают все такие места как места несоответствия точек максимальной кривизны соседних горизонталей.17. Способ по п.1, отличающийся тем, что распознаваемыми формами рельефа являются направления его ската, а для определения направления ската рельефа при движении через данное звено ломаной из указанной области вовне ее определяют треугольник триангуляции, лежащий внутри области, одна из сторон которого совпадает с данным звеном ломаной, и, если не все три вершины этого треугольника имеют одну и ту же высоту, то для определения направления ската берут этот треугольник, в противном случае определяют второй треугольник триангуляции, одна из сторон которого совпадает с данным звеном ломаной, и при его наличии для определения направления ската берут этот второй треугольник, в противном случае направление ската определяют как неопределенное, в случае наличия треугольника для определения направления ската определяют точку А, совпадающую с серединой данного звена ломаной, и точку В, совпадающую с вершиной треугольника, не лежащей на данном звене ломаной, приписывают точке А высоту, равную полусумме высот концов данного звена ломаной, и, если выбранный треугольник лежит внутри области и высота точки В больше высоты точки А или если выбранный треугольник лежит вне области и высота точки В меньше высоты точки А, направление ската определяют как понижение, в противном случае - как повышение.18. Способ по п.9 или 10, отличающийся тем, что при построении триангуляции, связывающей элементы цифровой модели рельефа, строят триангуляцию по множеству всех точек на плоскости, являющихся вершинами ломаных, изображающих горизонтали рельефа, определяют все пересечения ребер всех треугольников полученной триангуляции с отрезками ломаных, изображающих горизонтали, после чего для каждого треугольника триангуляции определяют все выпуклые многоугольники, на которые он разбивается пересекающими его отрезками указанных ломаных, и выполняют триангуляцию каждого полученного выпуклого многоугольника, что дает совокупность более мелких треугольников, образующую нужную триангуляцию.19. Способ по п.13, отличающийся тем, что для указанной области, взятой в качестве области, в которой расположена седловина рельефа, дополнительно производят уточнение этой области, для чего строят второй неориентированный граф, множество вершин которого совпадает с указанной связной компонентой первого неориентированного графа, а две вершины второго графа соединяют ребром в том и только в том случае, если соответствующие им треугольники имеют общую сторону, являющуюся горизонтальной и не лежащую ни на какой горизонтали, затем находят множество связных компонент полученного второго графа, после чего для каждой полученной связной компоненты второго графа определяют совокупность тех сторон треугольников триангуляции, которые образуют периметр второй области, являющейся объединением треугольников, соответствующих вершинам указанной связной компоненты второго графа, затем определяют совокупность горизонталей, на которых лежат вершины ломаных, образующих периметр указанной второй области, далее из всех вторых областей, соответствующих связным компонентам второго графа, отбирают те вторые области, для которых указанная совокупность горизонталей содержит не менее двух горизонталей, и формируют объединение всех отобранных вторых областей в качестве результата уточнения области, в которой расположена седловина рельефа.20. Способ по п.14, отличающийся тем, что для определения минимального и максимального допустимых значений высоты для отметок высот, попадающих в треугольники указанной триангуляции, которым соответствуют вершины графа, принадлежащие данной связной компоненте, по минимальному и максимальному значениям высот вершин периметра указанной области, сравнивают указанные минимальное и максимальное значения и при их несовпадении определяют указанные минимальное и максимальное допустимые значения высоты равными указанным минимальному и максимальному значениям высот вершин периметра указанной области, а при их совпадении определяют все горизонтали, на которых лежат вершины периметра указанной области, определяют направления ската рельефа для этих горизонталей, далее, если ни для одной из указанных горизонталей не удалось определить направление ската, то оставляют указанные минимальное и максимальное допустимые значения высоты не определенными, а если хотя бы для одной из указанных горизонталей удалось определить направление ската и если указанная область лежит по ту же сторону от указанных горизонталей, что и указанные направления ската, то определяют указанное максимальное допустимое значение высоты равным значению высоты указанных горизонталей, а в противном случае определяют указанное минимальное допустимое значение высоты равным значению высоты указанных горизонталей.21. Способ по п.15 или 16, отличающийся тем, что при нахождении соответствия между точками максимальной кривизны на отрезках горизонталей разной высоты сначала находят и отмечают точки перегиба на указанных отрезках горизонталей, находят разбиение указанных отрезков горизонталей полученными точками перегиба на более мелкие отрезки, классифицируют указанные мелкие отрезки на хребты и лощины, считая хребтами те мелкие отрезки на более высокой горизонтали, которые выпуклы вовне области между двумя горизонталями, и те мелкие отрезки на более низкой горизонтали, которые выпуклы внутрь области между двумя горизонталями, а остальные мелкие отрезки - лощинами, далее выполняют генерализацию хребтов и лощин путем последовательного удаления отметок для некоторых пар соседних точек перегиба на каждой горизонтали, объединяя тем самым при каждом удалении указанной пары отметок пару хребтов с лощиной между ними в один генерализованный хребет или пару лощин с хребтом между ними в одну генерализованную лощину, выполняя это до тех пор, пока на обоих отрезках горизонталей не получится две одинаковые последовательности из генерализованных хребтов и генерализованных лощин, соответствующие друг другу, после чего последовательно рассматривают пары полученных генерализованных лощин и пары полученных генерализованных хребтов на первой и второй горизонталях, для каждой такой пары генерализованных лощин составляют список соответствующих пар точек максимальной кривизны исходных лощин, лежащих внутри соответствующих генерализованных лощин, и добавляют все такие пары в искомое соответствие, а также для каждой такой пары генерализованных хребтов составляют список соответствующих пар точек максимальной кривизны исходных хребтов, лежащих внутри соответствующих генерализованных хребтов, и добавляют все такие пары в искомое соответствие.22. Способ по п.15 или 16, отличающийся тем, что для построения отрезков орографических линий, лежащих между соседними горизонталями и соединяющих пары соответствующих точек максимальной кривизны, соединяют пары соответствующих точек максимальной кривизны отрезками прямых, которые берут в качестве отрезков орографических линий, и проверяют, что полученные отрезки пересекаются с горизонталями и между собой только в исходных точках максимальной кривизны горизонталей, причем при обнаружении недопустимых пересечений заменяют совокупность отрезков, соединяющих пары взаимно соответствующих точек максимальной кривизны соседних горизонталей, совокупностью более сложных ломаных, соединяющих указанные пары точек и представляющих отрезки орографических линий.23. Способ по п.16, отличающийся тем, что при обнаружении несоответствия точек максимальной кривизны соседних горизонталей выдают соответствующие места на карте на дисплей для восприятия оператором, производят визуальное рассмотрение этого места и делают вывод об отсутствии или наличии ошибки в изображении рельефа.24. Способ по п.20, отличающийся тем, что определяют величину h сечения рельефа, после этого, если для данной связной компоненты определена максимальная допустимая высота, то полагают неопределенное значение минимальной допустимой высоты для рассматриваемой связной компоненты равным результату вычитания h из максимальной допустимой высоты для рассматриваемой связной компоненты, а если для данной связной компоненты определена минимальная допустимая высота, то полагают неопределенное значение максимальной допустимой высоты для рассматриваемой связной компоненты равным результату прибавления h к минимальной допустимой высоте для рассматриваемой связной компоненты.25. Способ по п.20, отличающийся тем, что определяют величину h сечения рельефа, после чего, если для данной связной компоненты граница соответствующей области имеет вершины на одной и той же высоте, определяют, соответствует эта высота основным горизонталям или полугоризонталям в зависимости от того, является или нет эта общая высота кратной h, причем в первом случае полагают Δh=h, а во втором случае Δh=h/2, далее если для данной связной компоненты определена максимальная допустимая высота, то полагают неопределенное значение минимальной допустимой высоты для рассматриваемой связной компоненты равным результату вычитания Δh из максимальной допустимой высоты для рассматриваемой связной компоненты, а если для данной связной компоненты определена минимальная допустимая высота, то полагают неопределенное значение максимальной допустимой высоты для рассматриваемой связной компоненты равным результату прибавления Δh к минимальной допустимой высоте для рассматриваемой связной компоненты.26. Способ по любому из пп.20, 24, 25, отличающийся тем, что оставшиеся не определенными минимальные допустимые значения высоты и максимальные допустимые значения высоты полагают равными соответственно минимальному допустимому значению числа, представимому в компьютере, и максимальному допустимому значению числа, представимому в компьютере.27. Способ по п.20, отличающийся тем, что при использовании полученной триангулированной модели для распознавания направлений ската выбирают список горизонталей, для которых надо определить направление ската, выбирают одно из двух значений направления ската (влево или вправо) в качестве положительного направления ската, для каждой выбранной горизонтали обнуляют значение счетчика разности между числом случаев положительного направления ската и числом случаев отрицательного направления ската, затем просматривают все треугольники триангуляции, которые не являются горизонтальными, и для каждого негоризонтального ребра такого треугольника для каждой из двух горизонталей, на которой лежит один из концов указанного ребра треугольника, определяют, принадлежит ли эта горизонталь списку горизонталей, для которых надо определить направление ската, и если это так, то корректируют значение счетчика разности между числом случаев положительного направления ската и числом случаев отрицательного направления ската, увеличивая или уменьшая его на 1 в зависимости от положения указанного негоризонтального ребра относительно горизонтали, затем после окончания просмотра всех треугольников триангуляции для каждой выбранной горизонтали делают вывод о направлении ската для этой горизонтали в зависимости от знака значения счетчика разности между числом случаев положительного направления ската и числом случаев отрицательного направления ската, причем при нулевом значении указанного счетчика делают вывод о том, что указанная триангулированная модель рельефа не содержит достаточно информации для определения направления ската для данной горизонтали.28. Способ по п.21, отличающийся тем, что для выполнения генерализации хребтов и лощин путем последовательного удаления отметок для некоторых пар соседних точек перегиба на каждой горизонтали с целью получения двух одинаковых последовательностей из генерализованных хребтов и генерализованных лощин, соответствующих друг другу, строят двудольный граф, вершинами которого являются точки перегиба отрезка первой горизонтали и точки перегиба отрезка второй горизонтали, причем точку перегиба первой горизонтали соединяют ребром с точкой перегиба второй горизонтали, если одну из этих двух точек перегиба можно сместить вдоль прямой части соответствующей ломаной таким образом, чтобы отрезок, соединяющий две точки перегиба, лежал внутри области, заключенной между указанными двумя ломаными, после чего производят удаление точек перегиба на первой и второй ломаных, удаляя каждый раз по две соседние точки перегиба, выполняя это таким образом, чтобы в результате получился двудольный граф, вершины которого, лежащие на двух ломаных, оказались взаимно однозначно связаны ребрами, причем плата за удаление точек перегиба оказалась минимальной, при этом плату за удаление двух соседних точек перегиба Р и Q, лежащих на одной ломаной, определяют как площадь S(PQ) многоугольника, ограниченного замкнутой ломаной, образованной частью ломаной от точки Р до точки Q и отрезком QP, причем в случае, если часть ломаной от точки Р до точки Q пересекает отрезок QP не только на его концах, но и во внутренних точках, под площадью понимают сумму площадей простых многоугольников, на которые разбивается получаемый контур с самопересечениями, что дает взаимно однозначное соответствие между оставшимися точками перегиба на двух горизонталях, при котором хребты и лощины двух горизонталей взаимно однозначно соответствуют друг другу.29. Способ по п.21, отличающийся тем, что для выполнения генерализации хребтов и лощин путем последовательного удаления отметок для некоторых пар соседних точек перегиба на каждой горизонтали с целью получения двух одинаковых последовательностей из генерализованных хребтов и генерализованных лощин, соответствующих друг другу, выдают изображение карты с выделенными на ней двумя горизонталями, на которых отмечены точки максимальной кривизны и точки перегиба, на дисплей оператору, который на основании визуального анализа с учетом конфигурации соседних горизонталей определяет причину несоответствия точек максимальной кривизны двух выделенных горизонталей и исправляет несоответствие путем редактирования горизонталей, включающего в себя как удаление лишних хребтов и лощин путем спрямления линии горизонтали, так и добавление новых путем изгибания линии горизонтали, после окончания редактирования производят автоматическое распознавание отрезков орографических линий между отрезками двух отредактированных горизонталей и выдают их изображения на дисплей оператору, причем эти действия продолжают до тех пор, пока не будет получен результат, устраивающий оператора.30. Способ по п.22, отличающийся тем, что для замены совокупности отрезков, соединяющих пары взаимно соответствующих точек максимальной кривизны соседних горизонталей, совокупностью более сложных ломаных, соединяющих указанные пары точек и представляющими отрезки орографических линий, для каждой пары соответствующих точек максимальной кривизны строят соединяющую их ломаную, целиком лежащую внутри области между двумя горизонталями и не пересекающуюся с этими горизонталями ни в каких точках, кроме концевых точек ломаной, после чего исключают взаимные пересечения друг с другом всех таких ломаных путем замены участков одной из двух пересекающихся ломаной таким образом, чтобы либо этот участок стал проходить параллельно соответствующему участку второй ломаной, либо стал совпадать с соответствующим участком второй ломаной.31. Способ по п.24, отличающийся тем, что определяют величину сечения рельефа как минимальное значение ненулевых разностей значений высот треугольников.32. Способ по п.24 или 25, отличающийся тем, что величина сечения рельефа выбирается оператором.33. Способ по п.27, отличающийся тем, что для определения положение указанного ребра треугольника относительно горизонтали определяют положение конца указанного ребра треугольника, лежащего на данной горизонтали, относительно вершин ломаной, определяющих данную горизонталь: либо внутри отрезка ломаной, определяющей горизонталь, либо в вершине ломаной, определяющей данную горизонталь, далее, если указанный конец ребра треугольника лежит внутри отрезка ломаной, определяющей горизонталь, или если указанный конец негоризонтального ребра треугольника совпадает с вершиной ломаной, определяющей данную горизонталь, а эта горизонталь является незамкнутой и указанная вершина ломаной является ее началом или концом, то вычисляют векторное произведение двух векторов, из которых первый вектор направлен из указанного конца ребра треугольника в другой его конец, а второй вектор направлен из начала указанного отрезка ломаной, определяющей горизонталь, в конец этого отрезка, и по знаку векторного произведения определяют, слева или справа от горизонтали лежит указанное ребро треугольника, а если указанный конец негоризонтального ребра треугольника совпадает с вершиной ломаной, определяющей данную горизонталь, и указанная вершина ломаной не является ее началом или концом, то рассматривают два отрезка ломаной, сходящихся в указанном конце негоризонтального ребра треугольника, вычисляют векторное произведение двух векторов, из которых первый вектор направлен вдоль первого отрезка ломаной, а второй вектор направлен вдоль второго отрезка ломаной, определяющей горизонталь, в порядке направления обхода горизонтали, и по знаку векторного произведения определяют, происходит поворот горизонтали направо или налево, далее для каждого из двух указанных отрезков ломаной, определяющей горизонталь, вычисляют векторное произведение двух векторов, из которых первый вектор направлен из указанного конца негоризонтального ребра треугольника в другой его конец, а второй вектор направлен из начала отрезка ломаной, определяющей горизонталь, в конец этого отрезка, и по знаку векторных произведений определяют, слева или справа от каждого из двух отрезков ломаной лежит указанное ребро треугольника, после этого делают вывод о том, что ребро треугольника лежит слева от горизонтали, если оно либо лежит слева от каждого из двух отрезков ломаной, либо лежит слева от хотя бы одного из двух отрезков ломаной и происходит поворот горизонтали направо, а в остальных случаях делают вывод о том, что ребро треугольника лежит справа от горизонтали.34. Способ по п.28, отличающийся тем, что для определения удаляемых точек перегиба на первой ломаной и на второй ломаной сначала для всех хребтов и лощин указанных ломаных определяют все значения S(Ai, Ai+1) и S(Bi, Bi+1) указанной функции S для всех пар точек перегиба, являющихся концами указанных хребтов и лощин, после чего последовательно вычисляют все значения функции D(i,j) для тех пар (i, j) номеров точек перегиба первой и второй ломаной 1≤i≤m, 1≤j≤n, которые связаны ребром в указанном двудольном графе, где m и n - номера последних точек перегиба первой и второй ломаной соответственно, начиная с i=1, причем при каждом значении i последовательно вычисляют все требуемые (т.е. те, для которых (i, j) связаны ребром в указанном двудольном графе) значения D(i,j) в порядке возрастания j, используя указанное базовое условие и рекуррентное соотношение, причем если при вычислении D(i,j) минимум достигается на паре номеров точек (i1, j1), связанных ребром в указанном двудольном графе, то в искомые множества точек удаляемых точек перегиба для ломаных А0, ..., Ai и В0, ..., Bj включают все ранее найденные удаляемые точки перегиба для ломаных А0, ..., Аi1 и B0, ..., Bj1, а также все пары точек (Ai, Ai+1) и (Вi, Bi+1), для которых соответствующие члены S(Ai, Ai+1) и S(Bi, Bi+1) входят в суммы по k в определении D(i,j) для данного значения пары (i1, j1), дойдя до конца вычислений, то есть до значений i=m, j=n, получают требуемое соответствие между точками перегиба исходных ломаных и совокупность пар удаляемых точек перегиба, причем функция D(i,j) определяется базовым условием
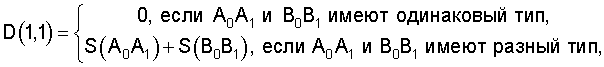
где типами отрезков ломаных между соседними точками максимальной кривизны являются «хребет» и «лощина», а рекуррентное соотношение имеет вид
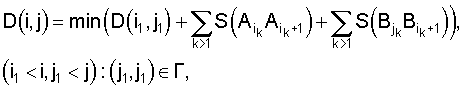
где Г - указанный двудольный граф, причем при пустом множестве {(i1<i, j1<j):(j1,j1)∈Г} значение D(i,j) полагают равным бесконечности, а последовательности индексов ik и jk при k>1 определяют следующим образом: если (i1, j1)∈Г и если отрезок первой ломаной от точки 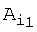 до точки
до точки  является хребтом, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки
является хребтом, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки  до точки
до точки 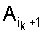 является лощиной, а если отрезок первой ломаной от точки
является лощиной, а если отрезок первой ломаной от точки  до точки
до точки  является лощиной, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки
является лощиной, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки 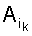 до точки
до точки  является хребтом.
является хребтом.
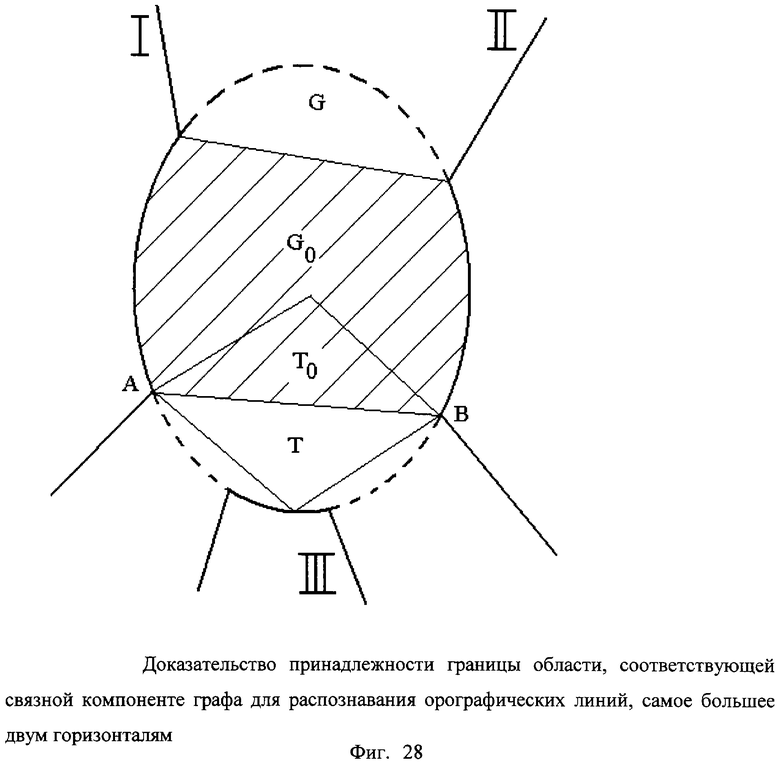
35. Способ по п.28, отличающийся тем, что для построения указанного двудольного графа удаляют все лишние вершины на горизонталях таким образом, чтобы никакие два соседних ребра ломаной, определяющей горизонталь, не лежали на одной прямой, строят двудольный граф Г1 видимости ребер ломаной, являющейся указанной частью второй горизонтали, из вершин ломаной, являющейся указанной частью первой горизонтали, причем вершинами графа Г1 являются точки перегиба отрезка первой горизонтали и замкнутые ребра ломаной, образующей указанную часть второй горизонтали, причем вершину графа Г1, соответствующую точке перегиба первой горизонтали, соединяют с вершиной графа Г1, соответствующей ребру ломаной, в том и только в том случае, если на этом ребре ломаной существует хотя бы одна точка, такая, что отрезок прямой, соединяющий эту точку с указанной точкой перегиба, целиком лежит внутри области, заключенной между указанными двумя ломаными, затем симметрично строят двудольный граф Г2 видимости ребер ломаной, являющейся указанной частью первой горизонтали, из вершин ломаной, являющейся указанной частью второй горизонтали, причем вершинами графа Г2 являются точки перегиба отрезка второй горизонтали и замкнутые ребра ломаной, образующей указанную часть первой горизонтали, причем вершину графа Г2, соответствующую точке перегиба второй горизонтали, соединяют с вершиной графа Г2, соответствующей ребру ломаной, в том и только в том случае, если на этом ребре ломаной существует хотя бы одна точка, такая, что отрезок прямой, соединяющий эту точку с указанной точкой перегиба, целиком лежит внутри области, заключенной между указанными двумя ломаными, наконец, строят указанный двудольный граф как граф, множество вершин которого совпадает с объединением множества T1 точек перегиба отрезка первой горизонтали и множества Т2 точек перегиба отрезка второй горизонтали, а вершины t1∈Т1 и t2∈Т2 соединяют ребром в том и только в том случае, если либо существует ребро s2 второй горизонтали, такое, что t2∈s2, причем t1 и s2 соединены ребром в графе Г1, либо существует ребро s1.36. Способ по п.35, отличающийся тем, что для построения указанных двудольных графов Г1 и Г2 видимости ребер ломаной перебирают все вершины ломаных, определяющих отрезки первой и второй горизонталей, и для каждой вершины используют вращательное заметание плоскости.





















































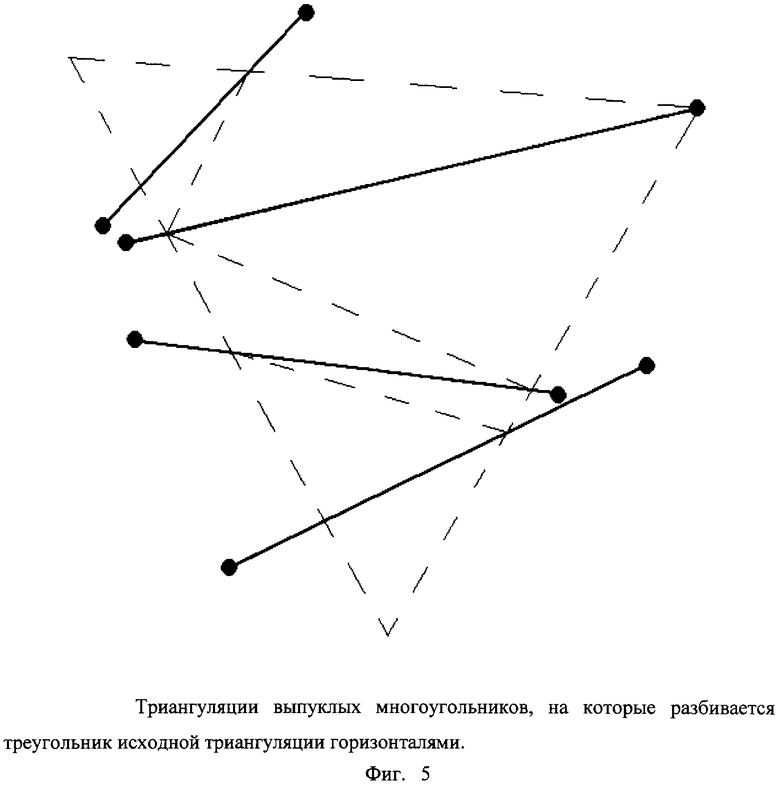























 до точки
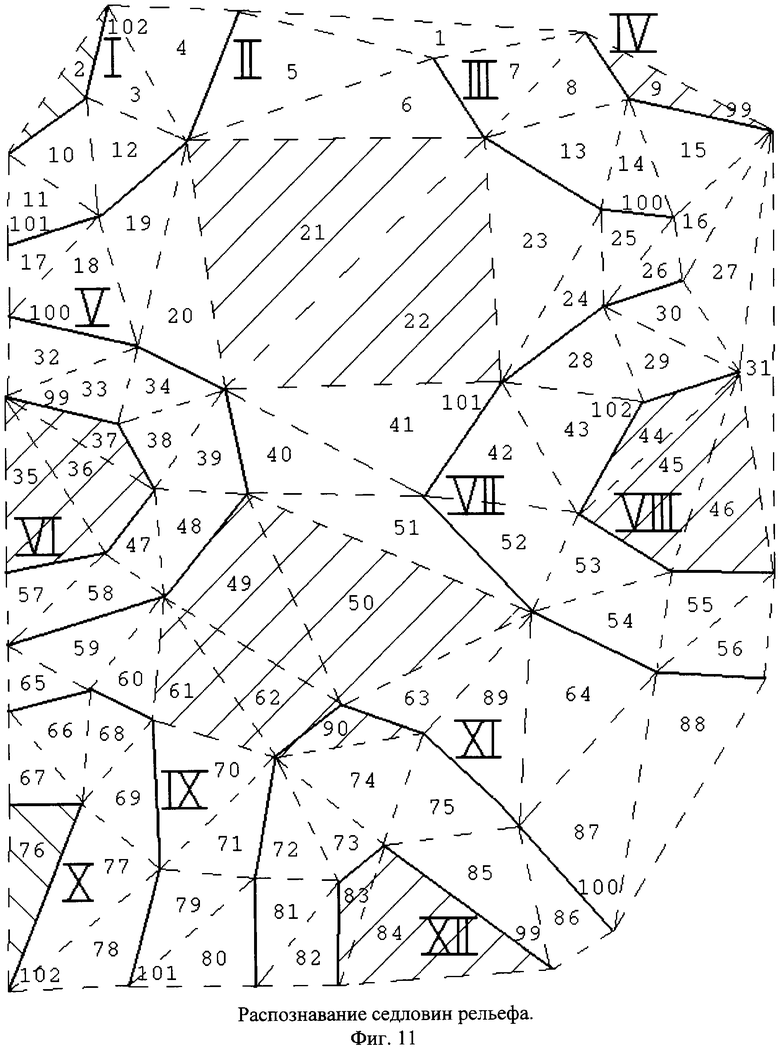
до точки  является хребтом, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки
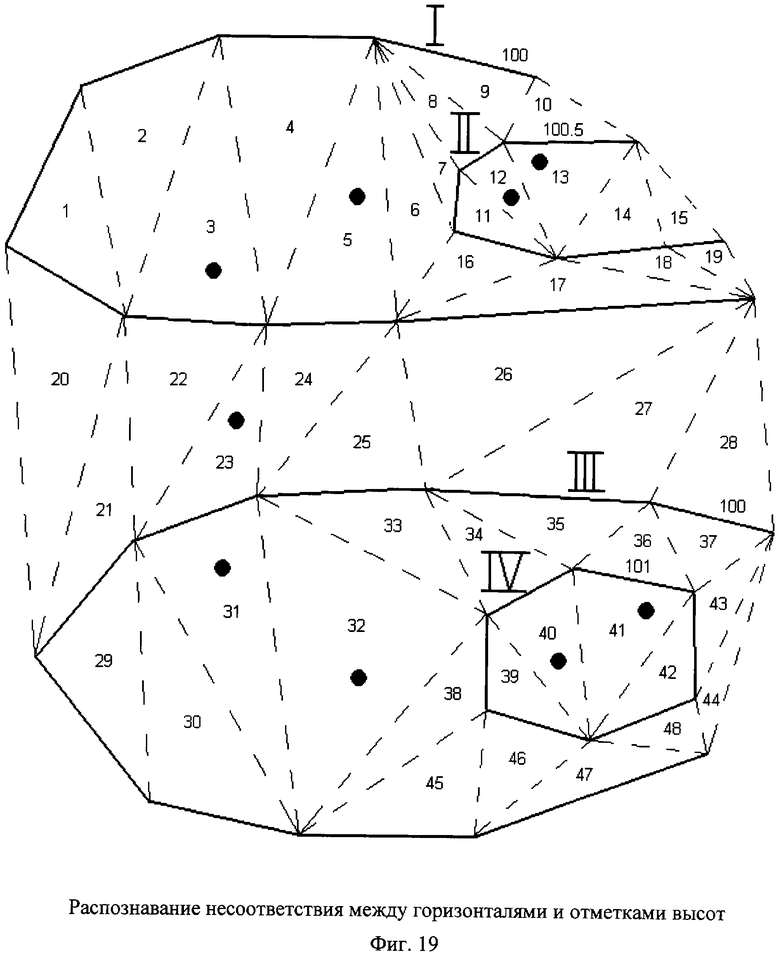
является хребтом, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки  до точки
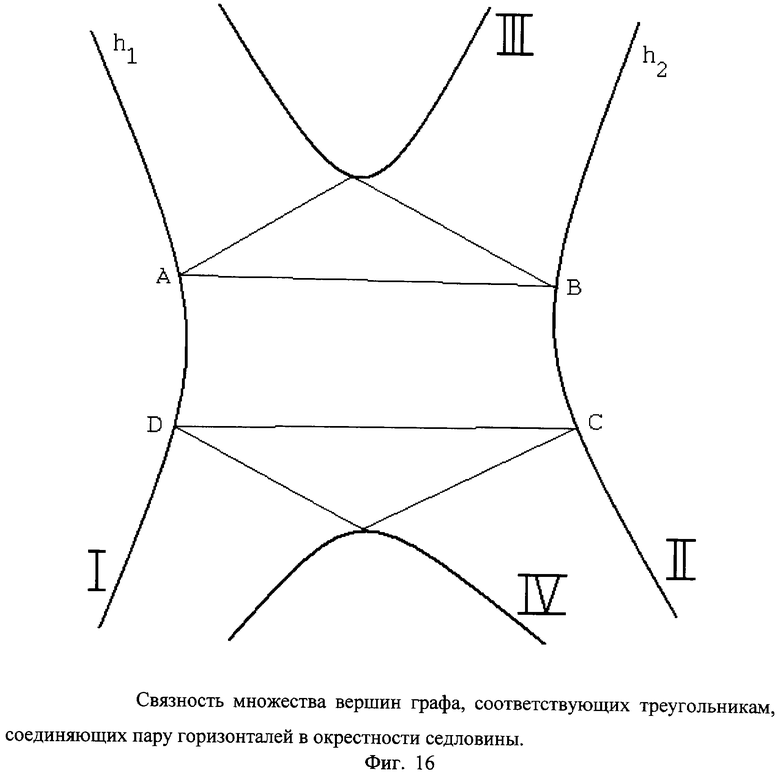
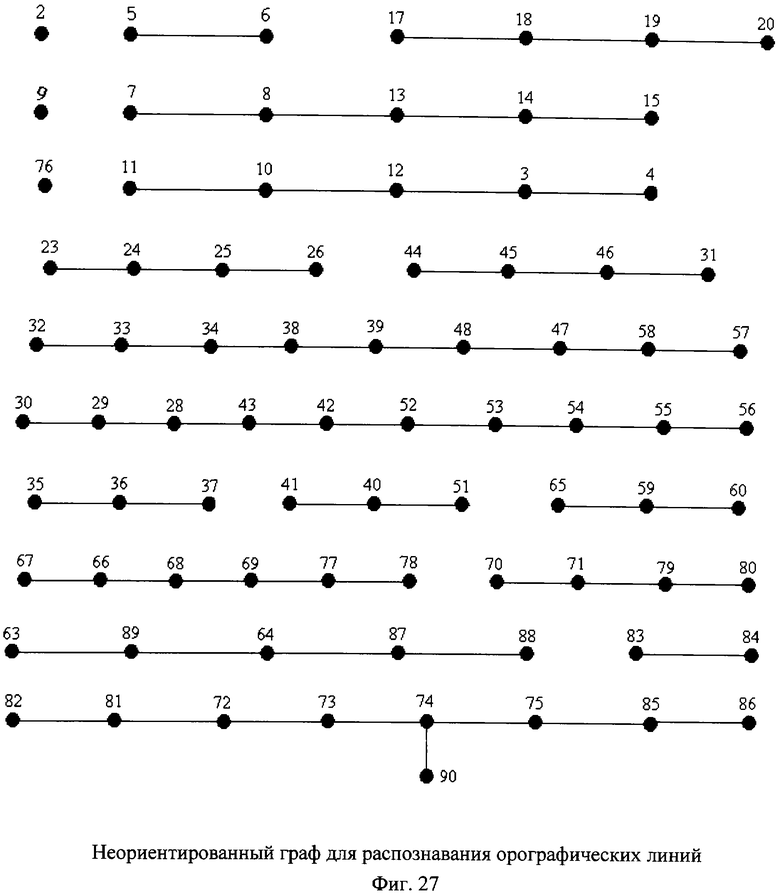
до точки  является лощиной, а если отрезок первой ломаной от точки
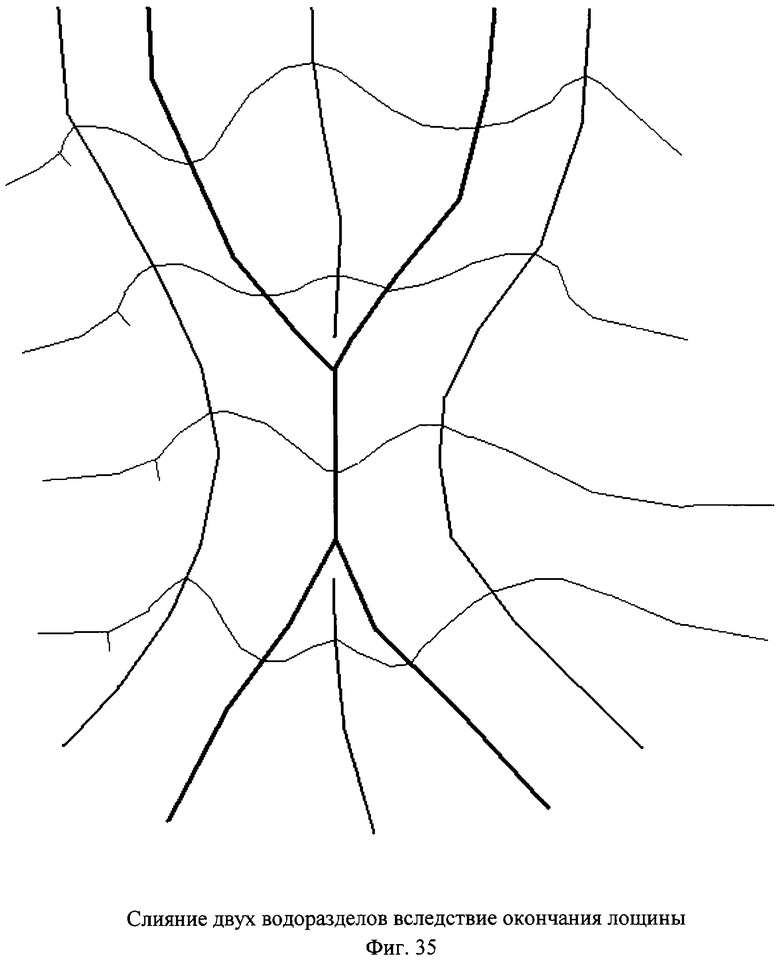
является лощиной, а если отрезок первой ломаной от точки  до точки
до точки  является лощиной, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки
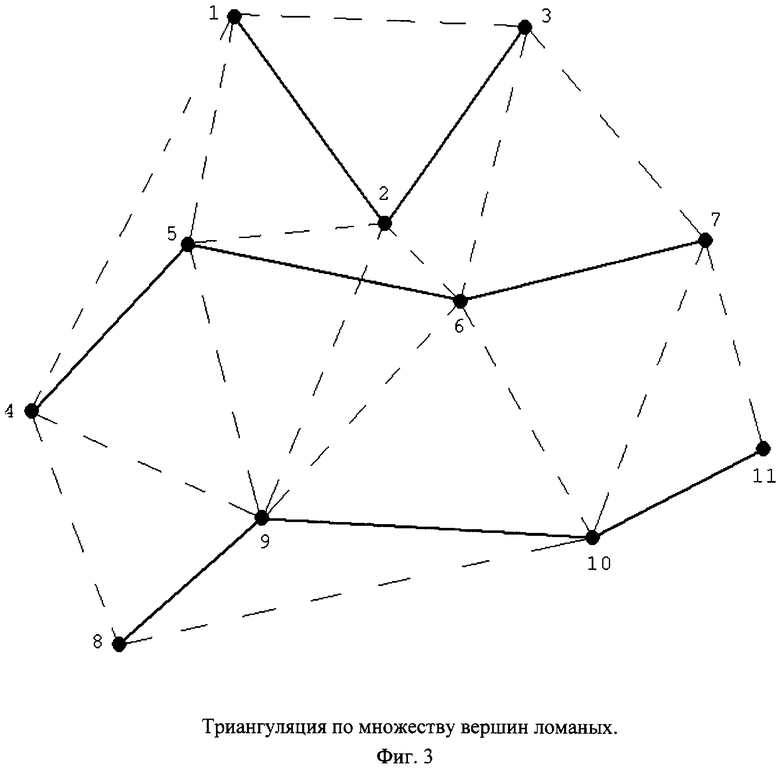
является лощиной, то в качестве значений индексов ik при k>1 берут все такие значения ik, для которых отрезок первой ломаной от точки  до точки
до точки  является хребтом.
является хребтом.