Изобретение относится к области двигателестроения, в частности к поршневым кольцам.
В двигателестроении известно несколько видов поршневых колец: круглые поршневые кольца - подразумевается, что распределение удельного радиального давления по всему объему поршневого кольца, когда оно вмонтировано в цилиндр, одинаково, а степень неравномерности и овальность равны нулю. Некруглые поршневые кольца - с постоянной степенью неравномерности - имеют во всех точках по объему различную силу давления. В случае максимально возможной, согласно теории Арнольда (Энглиш К. Поршневые кольца. М., 1962, с.57-58), степени неравномерности 0,9 величина давления составляет:
на 180°: 1,605 pm (здесь поршневые кольца имеют замок в свободном состоянии),
на 0°: 1,329 pm (диаметрально противоположно),
на 96°: 0,6147 pm (наименьшее),
где pm - единичное среднее радиальное давление для особого случая (n=0, l=1). Такое распределение удельного радиального давления называется яйцевидной формой. В противоположность этой форме, для двухтактных двигателей определяют сердцевидное распределение удельного радиального давления со следующими значениями:
на 180°: 0,379 pm,
на 0°: 0,671 pm,
на 96°: 1,385 pm.
Следовательно, сердцевидная форма распределения удельного радиального давления имеет, в противоположность яйцевидной, наименьшее давление в той точке на оси, которая проходит через замок поршневого кольца и соединяется с диаметрально противоположной точкой на кривой. Как видно, наибольшее удельное давление на 96°.
Некруглые поршневые кольца - с непостоянной степенью неравномерности - имеют также на каждой точке поверхности, которая определена внешним диаметром поршневого кольца во встроенном состоянии, неодинаковую интенсивность давления.
Характерные величины для степени неравномерности δр=1,9:
на 180°: 2,507 pm,
на 0°: 1,298 pm,
на 129°: 0,508 pm (наименьшее давление).
Такое распределение удельного радиального давления называется грушевидной формой и используется для четырехтактных двигателей. Соответствующей формой для двухтактных двигателей является распределение удельного радиального давления яблоковидной формы с характерными величинами давления:
на 180° - 0,593 pm.
Это неприемлемо, так как давление меньше 0 кг/см2, при этом поршневое кольцо "висит", протекание газов неизбежно. Чтобы избежать этого, необходимо выбрать меньшую степень неравномерности для двухтактных моторов (см. фиг.11 с. δр=-1,9, где представлено соответствующее решение):
на 0°: 0,7015 pm,
на 180°: 0,042 pm,
на 129°: 1,492 pm (наибольшее),
что подтверждается диаграммой распределения удельного радиального давления яблоко-сердцевидной формы и груше-яблоковидной формы (см.фиг.11).
При этом диаграмму давления надо читать следующим образом: например, для 180°: рϕ=2,507 pm, которое определяется следующим соотношением (100-50)/20 и это значение давления равно 2,5 кг/см2, где рm=р0=1 кг/см2 и представляет единичный вектор для круглых поршневых колец, без учета величины замка, характеристик поршневого кольца и модуля эластичности материала. При этом 50 - это радиус кольца в сжатом состоянии, а 20 - это масштаб графического изображения.
Определение диаметр кольца по оси Х (D2), проходящей через замок кольца, осуществляется следующим образом. Предварительно определяется D1:
 ,
,
где D1 - диаметр поршневого кольца в свободном состоянии по оси Y, которая перпендикулярна оси X, при этом ось Х проходит через замок поршневого кольца, при этом Δ=0,00381S′, а S′=1,15S для поршневых колец, которые копируются только по внешнему диаметру, a D - номинальный диаметр. После высечения и обработки внутреннего диаметра в сжатом состоянии величина раствора замка уменьшается примерно на 15% (Энглиш К. Поршневые кольца. М., 1962, с.373).
Величина раствора замка в свободном состоянии выбирается равной
 .
.
Уравнение (1) полностью соответствует точному расчету на основе теории упругости для круглых поршневых колец. Расчет верен и для отливки, и для модели, причем радиус увеличивается на припуск для обработки. При этом абсолютное значение 8 определяется процентным соотношением:
 .
.
где D=100 мм в данном случае.
При изготовлении отливки край замка должен соединиться с определенной точкой на оси Х, которая определяется следующим образом:
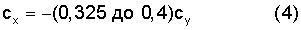
С выбранными значениями для cх и cу производится расчет для любой точки окружности поршневого кольца (а также шаблона, отливки, модели) и его радиуса. Полученный радиус определяет угол иссечения замка, который соединяется с точкой на оси X, и определяется выражением:
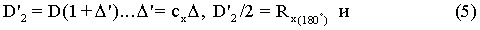
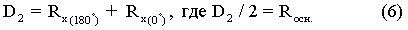
(см. фиг.5).
Это основной радиус, через который трансформируются яйцевидная форма в сердцевидную и обратно; грушевидная в яблоковидную и обратно.
Рассмотрим исходные положения распределения радиального удельного давления. Согласно уравнению 19 Лейбница (Энглиш К. Поршневые кольца. М., 1962, стр.29) для поршневых колец произвольной формы в свободном состоянии предполагается, что поршневое кольцо оказывает давление на стенку цилиндра по всему объему, исходя из уравнения:
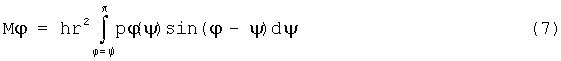 .
.
Продифференцировав это уравнение дважды по ϕ и решив дифференциальные уравнения второго порядка, он получил формулу для давления рϕ:
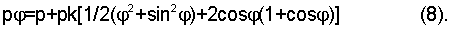
Арнольд положил в основу распределения радиального давления следующую функцию давления, которая удовлетворяет условиям равновесия в направлении осей Х и Y и требованию повышенного радиального давления на концах кольца (введя давление pm, соответственно pm1 и pm2), а через них определив коэффициенты n и l:
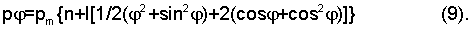
Арнольд отмечает, что эта функция давления ни в коем случае не может представлять собой идеальное распределение давлений; однако она позволяет осуществить благоприятные условия уплотнения и износа кольца (Энглиш К. Поршневые кольца. М., 1962, стр.57-58).
Это уравнение, как приблизительное решение, вполне довольно для контроля за просветом между поршневым кольцом и цилиндром и удовлетворяет условию равновесия: ∑X=0, ∑Y=0, ∑M=0.
Для частного случая, когда n=0, l=1 и рm=1 кг/см2, а степень неравномерности
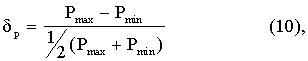
среднее радиальное давление вычисляется решением интеграла:
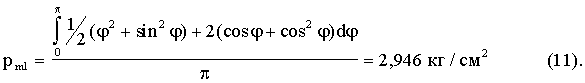
На фиг.6 показаны радиальные давления в прямоугольной системе координат, на которых видно, что 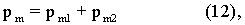
а на фиг.1 и фиг.2 показаны радиальные давления в полярной системе координат, при этом коэффициенты n и t заданы выражениями:


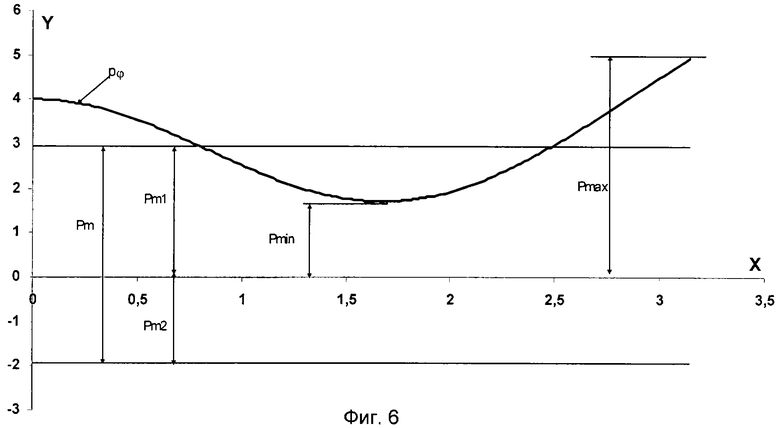
Для этого частного случая приводятся характерные величины средних давлений, которые видны на фиг.6, а расчет это подтверждает:
на 180° (раствор) pmax=4,940 кг/см2,
на 96° pmin=1,709 кг/см2,
на 0° Р=4 кг/см2.
Для всех практических случаев Арнольд определяет δр=0-0,9 как константу.
Известен также патент США №4957212, 18.09.1990 года, в котором поршневое некруглое кольцо для цилиндра двигателя, имеющего поверхность, которая контактирует с кольцом, цилиндр, имеющийся в двигателе, находящемся в холодном состоянии прежде, чем быть приведенным в действие, указанное кольцо, имеющее множество первичных круговых областей разнесенных вокруг указанного кольца, причем каждая из окружностей имеет радиус заданной кривизны, изменяющийся от первой области до следующей, и множество вторичных круговых областей, при этом каждая последующая расположена между двумя последующими и каждая сформирована таким образом, чтобы иметь возможность перемещения между радиусами кривизны двух последующих первичных областей, где указанные вторичные области формируются для создания радиального контактного давления в цилиндре, которое меньше чем в первичных областях, когда указанное кольцо установлено в цилиндре, и двигатель находится в его холодном состоянии.
Этот патент взят в качестве прототипа. К недостаткам прототипа относится то, что в нем рассматривается проблема измерения овальности поршневых колец с помощью тангенциальных сил, прилагаемых к стальной ленте. Этим способом рассчитывается перемещение точки по осям Х и У поршневого кольца в невстроенном состоянии, чем констатируется положительная или отрицательная овальность и ее роль во встроенном состоянии холодного и горячего (рабочее состояние) моторов.
Двигатель с такими поршневыми кольцами обладает рядом недостатков, ограничивающих их эффективность. Главный из них - это сильная вибрация поршневых колец при высоких оборотах двигателя. Вследствие чего появляется проникновение масла в газовую камеру, что вызывает ее загрязнение и ведет к образованию окалины, загрязнению атмосферы. Проникновение газов из камеры сгорания в масло приводит к ухудшению его смазочных свойств, к повышенному расходу горючего, снижению КПД двигателя, снижает его ресурс, а также вызывает шумы, превышающие нормы, установленные в развитых странах.
Сущностью заявленного изобретения является изготовление некруглого поршневого кольца с расширенным диапазоном распределения радиальных парциальных давлений с непостоянной степенью неравномерности, полученным математическим способом, вследствие чего поршневое кольцо некруглой формы отличается тем, что имеет величину раствора в свободном состоянии в диапазоне от 11% до 18%, от величины диаметра цилиндра, в котором это поршневое кольцо устанавливается в сжатом состоянии и при этом степень неравномерности распределения радиальных парциальных давлений δр находится в пределах от -5,175333187 до +2,339517464, в зависимости от материала поршневого кольца и поршневое кольцо имеет степень неравномерности распределения радиальных парциальных давлений δр в районе раствора (на 180°) в диапазоне от -1,3 до -1,9, а в точке, находящейся напротив раствора (на 0°), нижний предел степени неравномерности распределения радиальных парциальных давлений находится в пределах от -0,225 до -0,825, верхний предел степени неравномерности распределения радиальных парциальных давлений находится в пределах от 0 до -0,6.
Вариантом поршневого кольца является поршневое кольцо некруглой формы, которое отличается тем, что имеет величину раствора в свободном состоянии в диапазоне от 11% до 18%, от величины диаметра цилиндра, в котором это поршневое кольцо устанавливается в сжатом состоянии и при этом его степень неравномерности распределения радиальных парциальных давлений δр находится в пределах от -5,175333187 до +2,339517464, в зависимости от материала поршневого кольца и поршневое кольцо имеет степень неравномерности распределения радиальных парциальных давлений δр в районе раствора (на 180°) в диапазоне от 1,3 до 1,9, а в точке, находящейся напротив раствора (на 0°), нижний предел степени неравномерности распределения радиальных парциальных давлений находится в пределах от 0 до 0,6, верхний предел степени неравномерности распределения радиальных парциальных давлений находится в пределах от 0,225 до 0,825.
Предлагаемая разработка решает проблемы распределения парциальных радиальных давлений благодаря замене яйцевидной формы поршневого кольца на грушевидную форму в четырехтактном двигателе, и сердцевидной формы поршневого кольца на яблоковидную форму в двухтактном двигателе, сохранив при этом круглую форму в цилиндре, что приводит к достижению технического результата: значительному снижению вибрации поршневых колец, сохранению чистоты масла, устранению проникновения масла в камеру сгорания, снижению степени загрязнения атмосферы, снижению шумов, к уменьшению износа трущихся деталей, снижению специфицеского расхода топлива и, в конечном счете, к увеличению срока эксплуатации двигателя.
Расчеты формы поршневых колец позволяют значительно сократить время процесса изготовления колец любой заданной формы (диаметр, окно в свободном состоянии, степень неравномерности).
Новизна состоит в том, что впервые представлена возможность изготовления поршневого кольца некруглой формы с соответствующими характеристиками (диаметр, окно в свободном состоянии, степень неравномерности, тангенциальная сила) с абсолютным учетом коэффициента модуля эластичности материала, причем как с отрицательной, так и положительной степенями неравномерности распределения радиальных парциальных давлений.
Предложенная форма поршневого кольца дает повышение плотности прилегания к цилиндру, а также удовлетворяет условиям статически определенного носителя ∑x=0, ∑у=0 и ∑м=0. При этом можно получить любую величину овальности с помощью непостоянной степени неравномерности δр.
Расчет допускает два варианта:
1. изготовление поршневого кольца с твердой формы (традиционный метод),
2. изготовление формы на основе расчетов, минуя твердую форму, на станках с ЧПУ.
Расчет позволяет точно и быстро рассчитывать шаблоны для изготовления любых видов поршневых колец. Выведена математическая зависимость степени неравномерности от остальных коэффициентов. Найден предел +/- степени неравномерности для используемых материалов (серой чугун, стальное литье и др.), в области которого можно вывести кривую эластичности материалов.
При расчете формы шаблона указывается, какая должна быть проведена коррекция степени неравномерности δр, чтобы давление в критических точках вернулось в пределы коэффициентов эластичности материала со "свободным" выбором степени неравномерности δр.
Решена задача - получены нужные формы поршневого кольца при расширенных значениях степени неравномерности до границ, которые позволяют свойства используемого материала, а именно модуль эластичности. Каждая точка находится в границах коэффициента эластичности, определяемых законом Гука.
На чертежах изображено:
На фиг.1 представлены давления в полярной системе координат для степени неравномерности δр=0,9, постоянной по всему объему, где
1 - поршневое кольцо,
2 - распределение радиальных парциальных давлений яйцевидной формы - Pϕ,
3 - распределение радиальных парциальных давлений круглой формы.
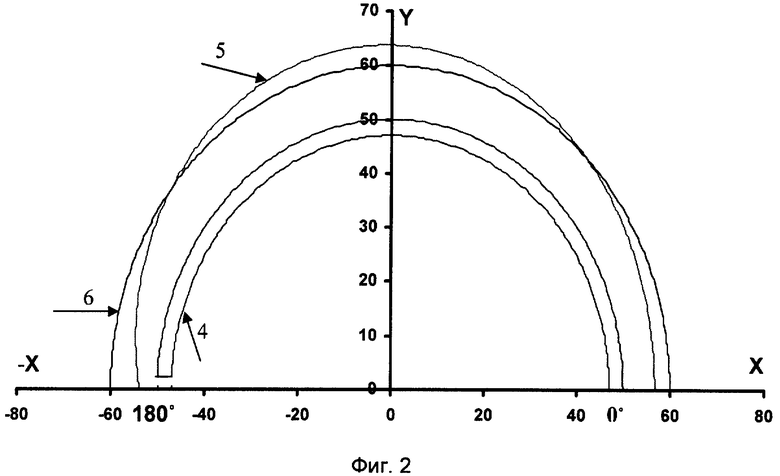
На фиг.2 представлены давления сердцевидной формы в полярной системе координат для степени неравномерности δр=0,9 постоянной по всему объему, где
4 - поршневое кольцо,
5 - распределение радиальных парциальных давлений яйцевидной формы Рϕ,
6 - распределение радиальных парциальных давлений круглой формы.
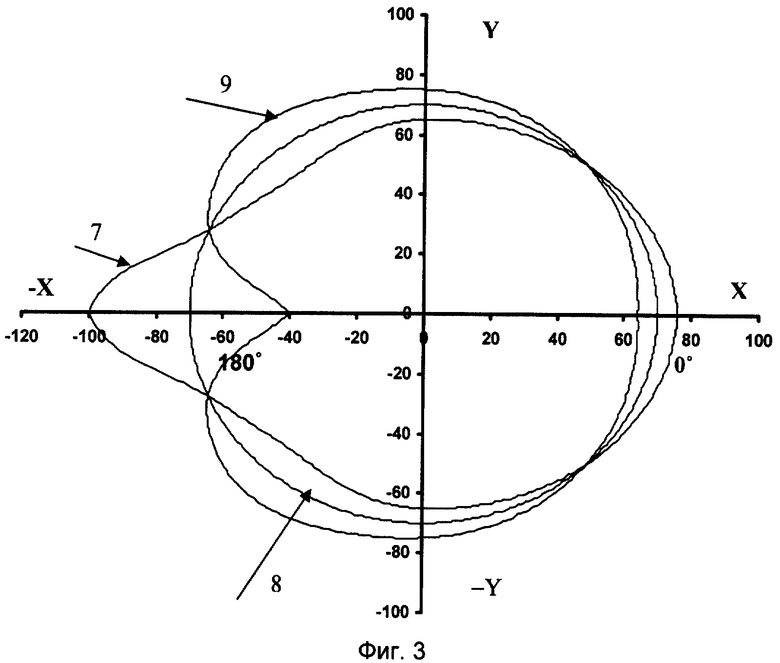
На фиг.3 представлены давления в полярной системе координат для степени неравномерности δр=1,9 для точки на 180°, где
7 - распределение радиальных парциальных давлений грушевидной формы Рϕ,
8 - распределение радиальных парциальных давлений круговидной формы Pϕ,
9 - распределение радиальных парциальных давлений яблоковидной формы Рϕ.
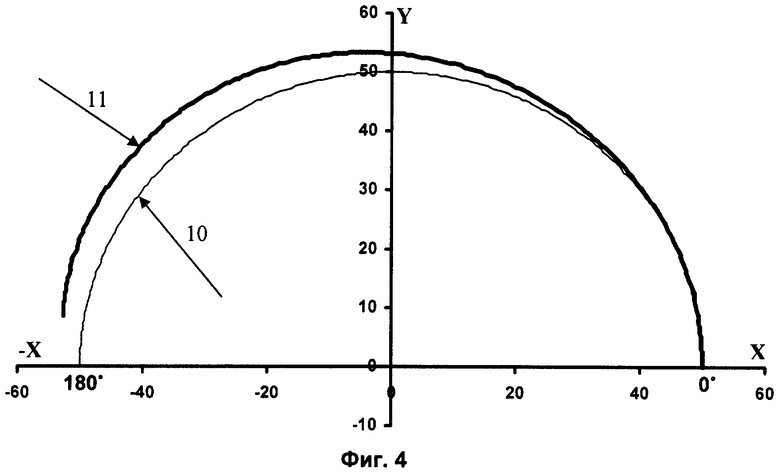
На фиг.4 представлен основной расчет шаблона, где
10 - основной радиус,
11 - шаблон.
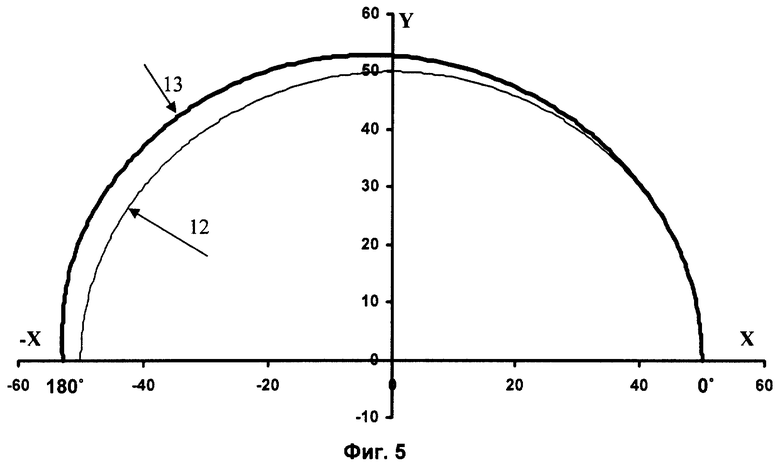
На фиг.5 представлен расчет диаметра D2 по оси Х (закрытый замок поршневого кольца в свободном состоянии), где
12 - основной радиус,
13 - шаблон.
На фиг.6 представлены значения радиальных парциальных давлений, используемых при расчете величин n и l (по Арнольду и Флоринну), где
Pϕ - радиальное парциальное давление,
Рmin - минимальное радиальное парциальное давление,
Рmax - максимальное радиальное парциальное давление,
Рm1 - среднее радиальное давление,
Рm2 - постоянная полоска давлений,
на оси Х представлены значения ϕrrad (угол, взятый в радианах).
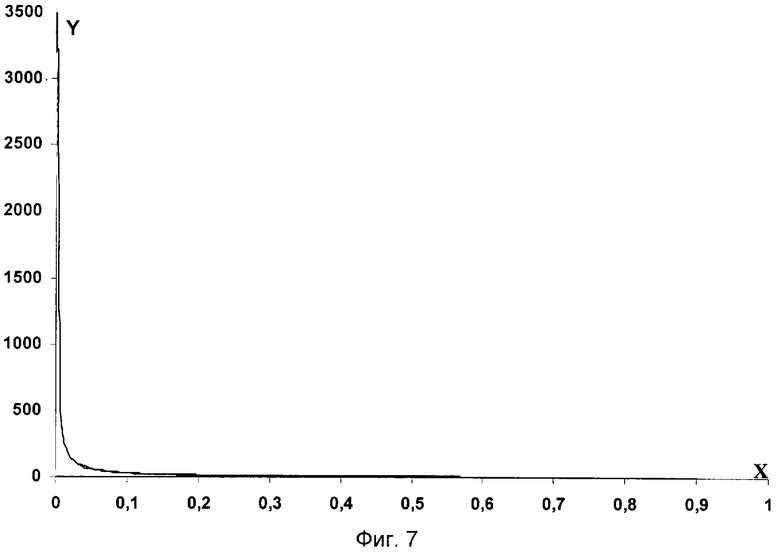
На фиг.7 показана функция степени неравномерности δр в пределах 0-0,9, используемая для расчета шаблона с постоянным δр, где
Рm - радиальное давление,
Рm1 - среднее радиальное давление,
Рm2 - постоянная полоска давлений.
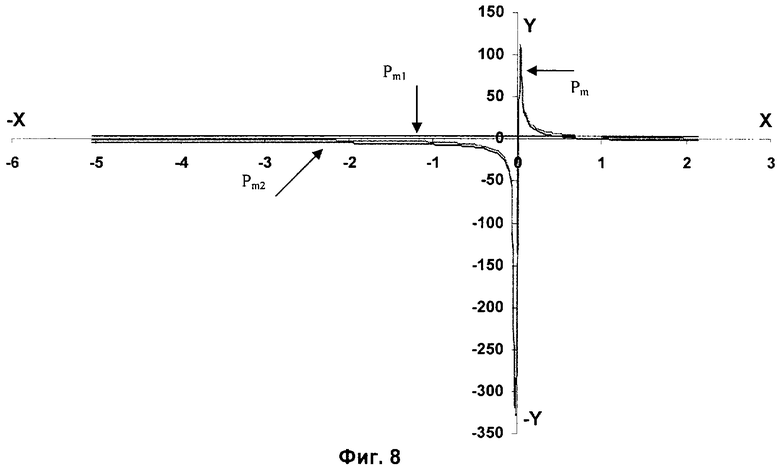
На фиг.8 представлена диаграмма значений давлений функции степени неравномерности для δр в пределах от - 5 до 2, где
Рm - радиальное давление,
Рm1 - среднее радиальное давление,
Рm2 - постоянная полоска давлений.
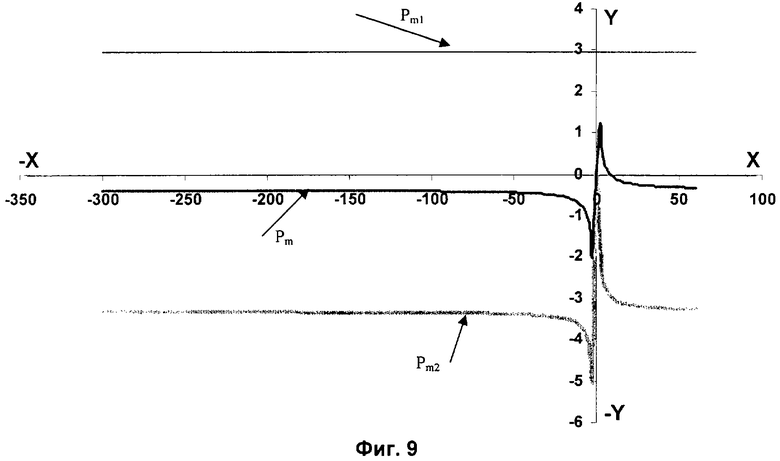
На фиг.9 представлена диаграмма значений давлений функции степени неравномерности δр в пределах от - 300 до 60, используемая для расчета шаблона с непостоянным δр, где
Рm - радиальное давление,
Рm1 - среднее радиальное давление,
Рm2 - постоянная полоска давлений.
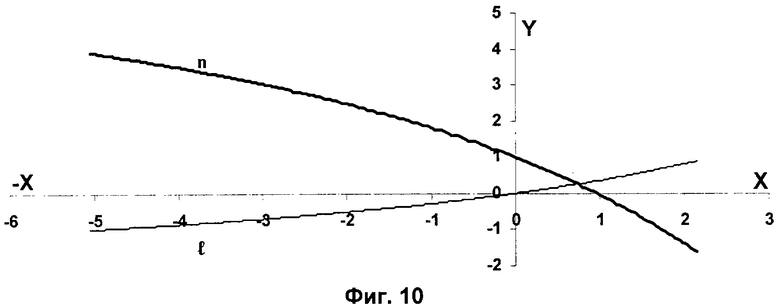
На фиг.10 представлена диаграмма значений n и l коэффициенты для расчета парциальных давлений, графическое изображение коэффициентов n и l, для расчета парциальных давлений для δр в пределах от - 5 до 2, используемая для расчета шаблона с непостоянной δр.
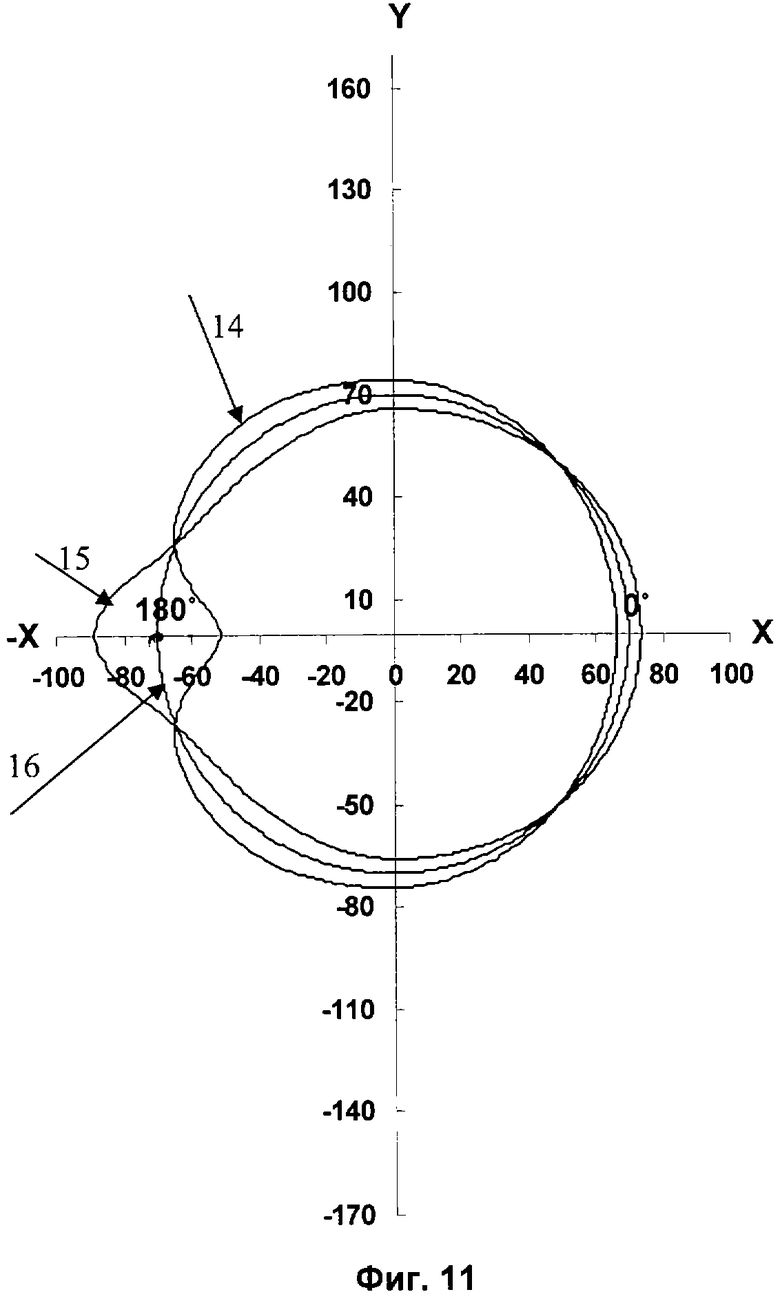
На фиг.11 представлена диаграмма распределения радиальных парциальных давлений для δр=-1,9 в точке 180°, где
14 - распределение радиальных парциальных давлений яблоковидной формы,
15 - распределение радиальных парциальных давлений грушевидной формы,
16 - распределение радиальных парциальных давлений круговидной формы.
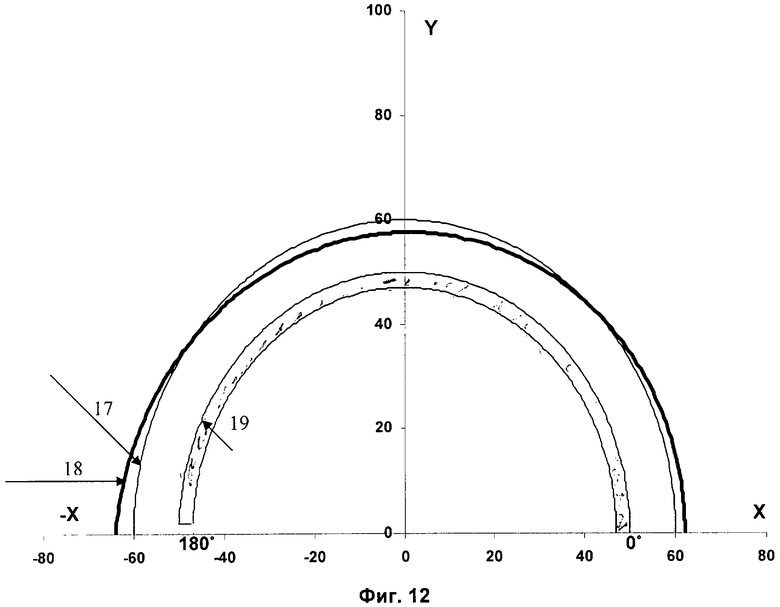
На фиг.12 - представлены распределения давления для δр=0,6, постоянной по всему объему в полярной системе координат, где
17 - распределение радиальных парциальных давлений круговидной формы Рϕ,
18 - распределение радиальных парциальных давлений яйцевидной формы Pϕ,
19 - поршневое кольцо.
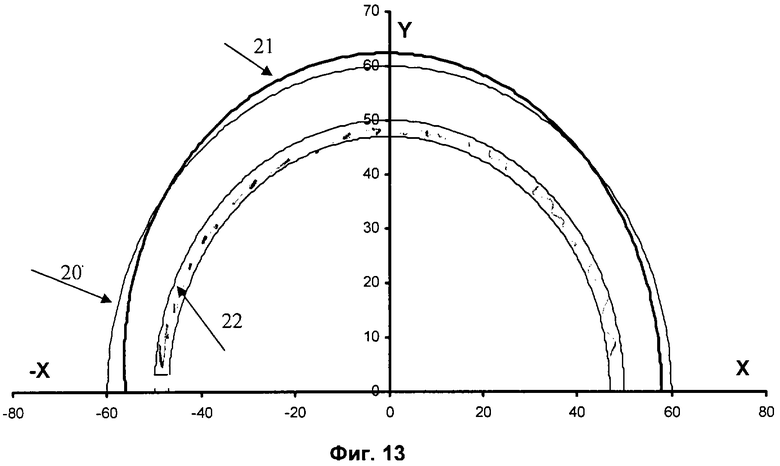
На фиг.13 приведены давления для δр=0,6 постоянной по объему полярной системе координат, где
20 - распределение радиальных парциальных давлений круговидной формы Рϕ,
21 - распределение радиальных парциальных давлений сердцевидой формы Pϕ,
22 - поршневое кольцо.
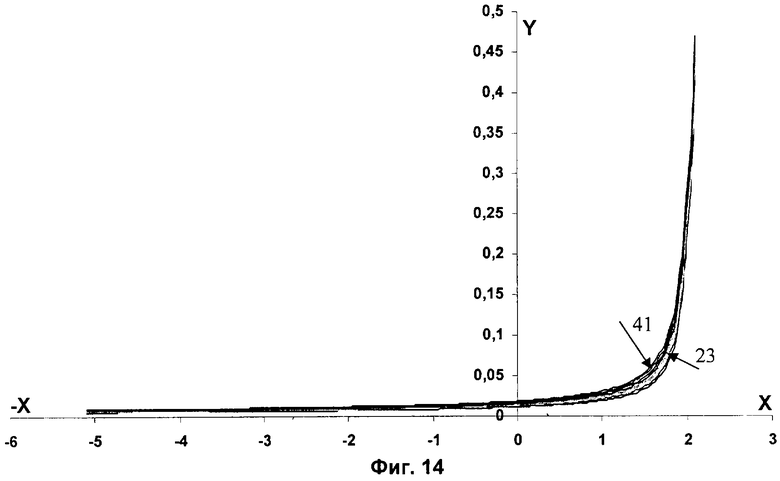
На фиг.14 представлена диаграмма значений коэффициента модуля эластичности k0 и величины раствора замка в процентах cу, где по оси Х отложены значения степени неравномерности δр, а по оси Y - величины коэффициента k0 в зависимости от величины раствора замка в процентах, где 23 - cу=0,11......41-су=0,18,
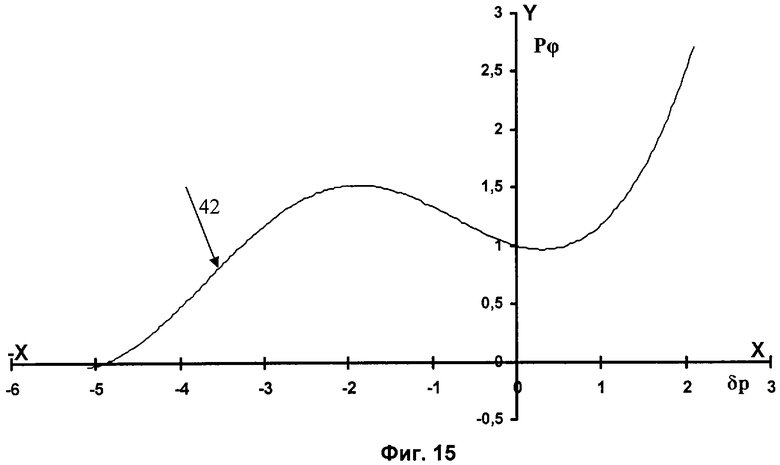
На фиг.15 - приведена диаграмма давлений Pϕ на цилиндр в функции степени неравномерности δр, представленная в прямоугольной системе координат, где 42 - давление Рϕ.
На фиг.16 - диаграмма формы шаблонов яблоковидной и грушевидной формы δр=1,6i для точки 180° в полярной системе координат, где
43 - шаблон яблоковидной формы,
44 - шаблон грушевидной формы.
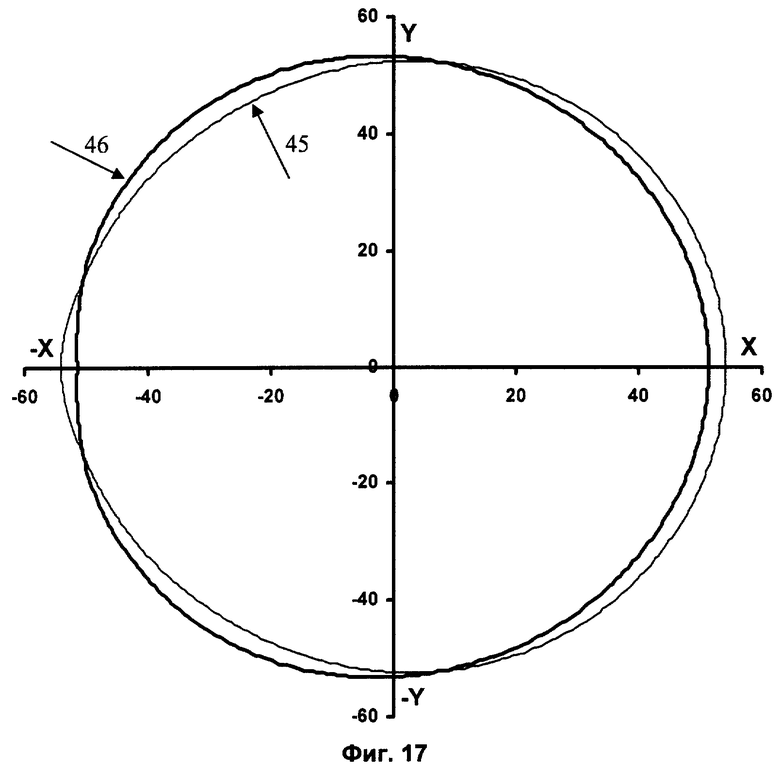
На фиг.17 - диаграмма формы шаблонов яблоковидной и грушевидной формы, δр=1,6а для точки 180° в полярной системе координат, где
45 - шаблон яблоковидной формы,
46 - шаблон грушевидной формы.
Для применения вышеприведенных расчетов необходимо определить степень неравномерности как функцию рm2:
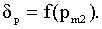
При этом степень неравномерности можно выбрать в границах ±∞, что позволяет спроектировать линию между двумя точками, которая может иметь неограниченное число вариантов. Задача, поставленная здесь, должна удовлетворять нескольким условиям:
1. достаточная плотность прилегания,
2. соблюдение условия равновесия X: ∑X=0, ∑Y=0, ∑M=0,
3. широкий диапазон между максимальной и минимальной величинами давления на одном поршневом кольце в сжатом состоянии в различных точках кривой.
Это приводит к максимальному снижению вибрации при соблюдении закона Гука для сопротивления материалов. Найденное решение позволяет установить: δр=-5,175333187 до +2.339517464.
Следующие диаграммы показывают изменение давления pm, pm1, pm2, то есть коэффициенты n и l в функции δр находятся в пределах от 0 до 0,9; от 5 до +2; от 300 до 60, которые представлены на фиг.7, фиг.8, фиг.9, при этом новый разброс степени неравномерности в границах δр≈7,5 не может быть выбран как константа. При применении упомянутого выше решения Арнольда (оно показано на фиг.1) возможно получить расчет со степенью неравномерности только от 0 до 0,9, включая и нулевую степень неравномерности.
Для постоянного δp, лежащего в пределах 0÷0,9, Арнольд дает уравнение для расчета координат Х и Y для любого градуса на окружности от 0° до 180° (этого диапазона достаточно, учитывая симметрию по оси Х), на основе которых он получил контур кривой поршневого кольца в свободном состоянии.
В уравнении введено по 8 корректирующих коэффициентов для расчета координат Х и Y, данные в виде таблицы для каждого градуса. Также введены два коэффициента n и l, на основе которых получены значения двух новых коэффициентов:
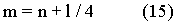
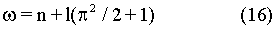
И в конце в уравнение введен коэффициент модуля эластичности k0,
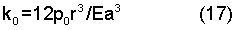
Этот коэффициент точен для круглых поршневых колец, но не может быть применен для некруглых поршневых колец. Наряду с этим, k0, как результирующая, может использоваться для расчета кривой с функциями: Δr и Δt. В том случае, когда контур кривой рассчитывается в координатах ΔX и ΔY, нужно произвести расчет со значениями: kx и ky для любой, сколь угодно малой части кривой и рассматривать ее как круглое кольцо, а это значит, что и р0 как среднее давление трансформируется в рϕ, чье значение также различно.
Проверка расчета кривой поршневого кольца в свободном состоянии, по приведенным данным в формуле (17), дает в результате замок в свободном состоянии ≅30% D, что технически невыполнимо.
Предлагается более эффективное решение с использованием непостоянной степени неравномерности распределения парциальных радиальных давлений с учетом свободного выбора степени неравномерности.
Предлагаемое техническое решение позволяет рассчитать форму поршневого кольца с учетом характеристик поршневого кольца, с величиной раствора замка и любого правильно определенного распределения радиального давления. Таким образом было спроектировано несколько типов поршневых колец со следующими вариантами распределения удельного радиального давления, которое удовлетворяет всем требованиям к характеристикам материалов:
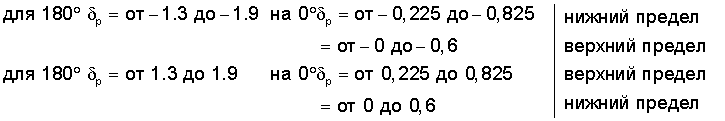
Между двумя этими пределами, как и полосами δр, возможно быстро и легко получить любую желаемую форму кривой распределения давлений для получения поршневых колец с заранее заданными характеристиками.
Согласно формуле 17 соотношение радиуса и радиальной толщины для стандартных поршневых колец является постоянным. Формула приобретает следующий вид:
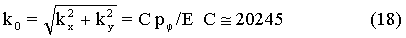
Коэффициент k0 и радиальные парциальные давления рϕ u расчет k0 для любой точки кривой видны на фиг.14 и фиг.15, модуль упругости материала получают лабораторным путем.
Например, возьмем данные по модулю эластичности для стального литья. На критической части кривой шаблона pϕ≅0,8 кг/см2, откуда следует, что возможно применение материала с k0=0,0077, при этом k0<0.0045, что определяет шаблон, а k0 должен быть больше или равен k0 материала, из которого изготовлено поршневое кольцо.
Следует коррекция исходного рассчитанного варианта таким образом, что степень неравномерности меняется и входит в границы между -5,175 - +2,339. Это делается для всех материалов с целью достичь максимально возможного проектируемого давления в точке 180° (для четырехтактных двигателей) или ≈129° (для двухтактных двигателей).
Получена система проектирования шаблона, которая позволяет легко и быстро получить формы распределения удельного радиального давления на поршневом кольце, вставленном в цилиндр.
Проверка периметра поршневого кольца, помещенного внутрь цилиндра до и после упомянутой коррекции, показала, что его форма осталась неизменной.
Таким образом, заявляемая форма поршневых колец позволяет кроме вышеуказанных преимуществ уменьшить расход горючего, масла и повысит КПД двигателя на 10% и выше.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБРАБОТКИ ПОРШНЕВЫХ КОЛЕЦ С КОНУСНЫМ РАБОЧИМ ПРОФИЛЕМ | 1997 |
|
RU2159697C2 |
| Поршневое кольцо | 1973 |
|
SU541060A1 |
| УПЛОТНИТЕЛЬНОЕ УСТРОЙСТВО ПОРШНЯ | 2000 |
|
RU2168082C1 |
| ДВОЙНОЙ ЦИЛИНДРОПОРШНЕВОЙ БЛОК ВЫСОКОГО ДАВЛЕНИЯ | 2009 |
|
RU2451831C2 |
| Портативный приводной инструмент для крепежа | 1982 |
|
SU1768024A3 |
| УСТРОЙСТВО ДЛЯ ТЕРМОФИКСАЦИИ ПОРШНЕВЫХ КОЛЕЦ В ПАКЕТЕ | 2006 |
|
RU2333262C2 |
| Уплотнение поршней | 2015 |
|
RU2656179C2 |
| УСТРОЙСТВО ДЛЯ ТЕРМОФИКСАЦИИ ПОРШНЕВЫХ КОЛЕЦ В ПАКЕТЕ | 2008 |
|
RU2371489C1 |
| Барабан для закрепления заготовок поршневых колец при их расточке | 1936 |
|
SU54877A1 |
| УСТРОЙСТВО ДЛЯ ТЕРМОФИКСАЦИИ ПОРШНЕВЫХ КОЛЕЦ В ПАКЕТЕ | 2008 |
|
RU2364635C1 |

Изобретение относится к двигателестроению. Поршневое кольцо имеет некруглую форму. Величина раствора кольца в свободном состоянии лежит в диапазоне от 11% до 18% от величины диаметра цилиндра, в котором это поршневое кольцо устанавливается. Степень неравномерности распределения радиальных парциальных давлений δp находится в пределах от -5,175333187 до +2,339517464. Кольцо имеет степень неравномерности в районе раствора от 1,3 до 1,9. Приведен другой вариант кольца. Такое выполнение снизит вибрацию колец, уменьшит износ трущихся деталей и увеличит срок эксплуатации двигателя. 2 н.п. ф-лы, 17 ил.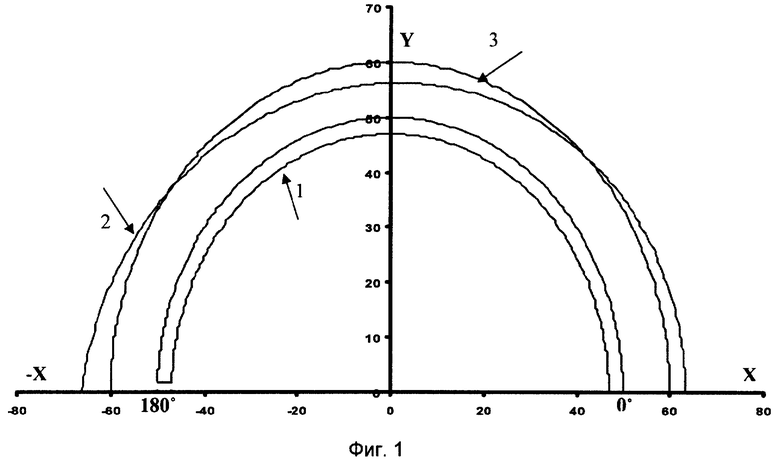
| ЭНГЛИШ К | |||
| Поршневые кольца | |||
| Теория, изготовление, конструкция и расчет, т.1 | |||
| : М | |||
| : Машгиз, с.47-73 | |||
| АФИНЕЕВСКИЙ С.А | |||
| и др | |||
| Особенности конструкций поршневых колец современных автомобильных двигателей | |||
| Обзорная информация | |||
| М | |||
| : НИИНавтопром, 1984, с.3-9 | |||
| Поршневое разрезное кольцо | 1947 |
|
SU72879A1 |
| US 4306730 А, 21.12.1981 | |||
| US 4198065 А, 15.04.1980 | |||
| Устройство для диагностики неисправностей технических объектов | 1976 |
|
SU714364A1 |
Авторы
Даты
2008-02-27—Публикация
2004-06-24—Подача