Изобретение относится к технике связи и может использоваться при проектировании, новых и модернизации существующих систем передачи дискретной информации. Заявленный способ может быть использован для декодирования помехоустойчивых блоковых кодов, обеспечивая высокую скорость и достоверность восстановления информации.
Заявленное техническое решение расширяет арсенал применения помехоустойчивых блоковых кодов.
Известны способы декодирования блоковых кодов (см., например, Дж.Кларк, мл., ДЖ Кейн «Кодирование с исправлением ошибок в системах цифровой связи» М.: Радио и связь, 1987, с.96-128), в которых комбинации ошибок отыскиваются путем отличным от процедуры умножения принятого кодового вектора на проверочную матрицу. Такие неалгебраические алгоритмы легко обобщаются на случай мягких решений и оказываются весьма полезными.
Недостатком таких способов является сложность декодера, которая сравнительно быстро возрастает с кратностью исправляемых ошибок. Поэтому они обычно оказываются бесполезными при исправлении более трех случайных ошибок или более одного пакета ошибок. Другим недостатком является сложность отыскания проверочного множества, покрывающего комбинацию ошибок или набора проверочных множеств, покрывающих все наборы ошибок данного типа (так называемого покрытия).
Наиболее близким по технической сущности к заявленному является способ декодирования по алгоритму Витерби (см., например, Скляр, Бернард «Цифровая связь. Теоретические основы и практическое применение». Изд.2-е, испр. М.: Изд. дом Вильямс, 2003, с.443, 444), в котором не используется метрика расстояния Хэмминга, имеющая ограниченное разрешение, а используется евклидово кодовое расстояние между точкой с шумом и точкой без шума за счет преобразования обрабатываемого двоичного вектора из двоичной системы счисления в числа с требуемой m-ичной системой счисления, например в восьмеричную.
Недостаток прототипа заключается в узкой области его применения. Он развит только на сверточные коды, хотя во многих практически важных приложениях широко используются блоковые коды, особенно в системах, не терпящих задержек при обмене информацией. Способ не приспособлен для исправления стираний, хотя при их исправлении корректирующие возможности кода повышаются в два раза.
Целью изобретения является разработка способа декодирования кодовых комбинаций блоковых кодов, позволяющая повысить скорость декодирования и достоверность принимаемой информации при исправлении ошибок и стираний.
Поставленная цель достигается тем, что при приеме двоичных символов, поступающих из канала связи, фиксируют показатель надежности каждого символа (например, показатель отношения функция правдоподобия - см. Скляр, Бернард «Цифровая связь. Теоретические основы и практическое применение» Изд.2-е, испр.: Пер. с англ. - М.: Издательский дом «Вильямс», 2003, с.500) и наименее надежные символы стирают, а по группе наиболее надежных символов определяют один из 2N кластеров (где N - натуральное число) (см. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. - 2-е изд., перераб. и доп. - М.: Юнити-Дана, 2004, с.496), к которому может принадлежать принятый кодовый вектор, при этом оставшуюся часть кодовой комбинации делят на две группы двоичных символов, переводя каждую группу в m-ичные целые числа общепринятым образом, от старших разрядов к младшим, и принимают их за две прямые координаты, принадлежащие плоскости выделенного кластера, а также в m-ичные целые числа от младших разрядов в группе к старшим, принимая их за инвариантные координаты того же кодового вектора, в ходе оценки принятого кодового вектора определяют конфигурацию стираний в каждой группе, устанавливая приоритеты исправления стертых символов, и в случае поражения стираниями старших разрядов прямых координат переходят к инвариантным координатам, определяя в любом случае по евклидовому расстоянию ближайший разрешенный кодовый вектор выделенного кластера.
Благодаря новой совокупности существенных признаков в заявленном способе при декодировании блоковых кодов учитываются показатели надежности принятых символов, на основании которых формируются стирания и определяются приоритеты их исправления за счет соотнесения принятого кодового вектора к тому или иному кластеру, в границах которого резко снижается число комбинаций, подлежащих анализу, что позволяет добиться более быстрого и точного восстановления стертых символов в принятой кодовой комбинации и таким образом расширяет область применения заявленного способа как для синхронных, так и для асинхронных систем передачи.
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна». Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретения соответствует условию патентоспособности «изобретательский уровень».
Иллюстрация способа осуществляется на примере кода БЧХ (15, 5, 7) и применима к любому блоковому коду.
Заявленный способ поясняется чертежами:
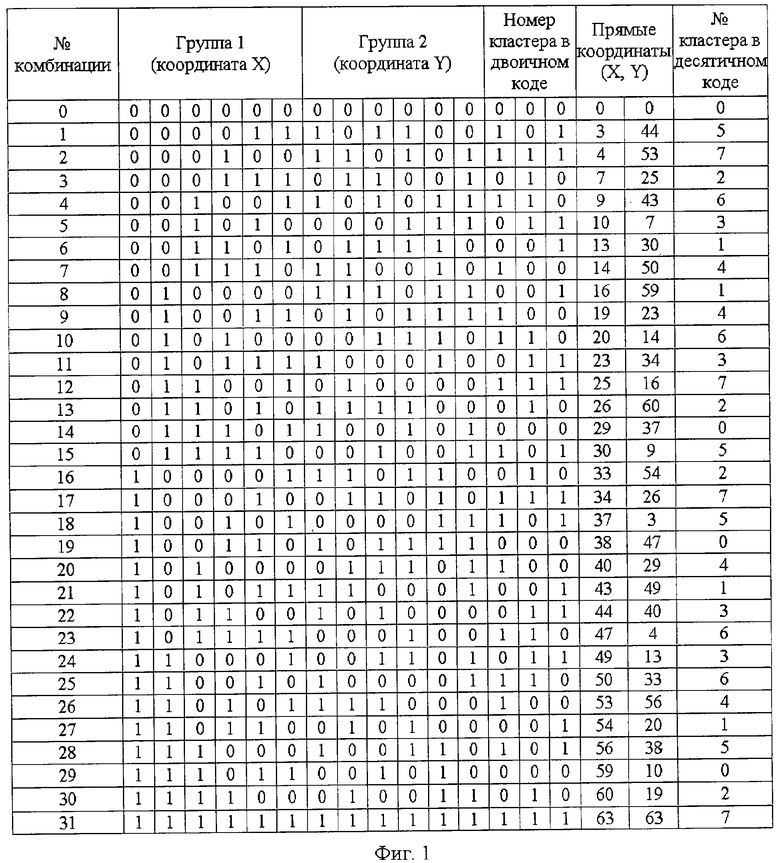
фиг.1 - таблица разрешенных кодовых комбинаций блокового кода (15, 5, 7);
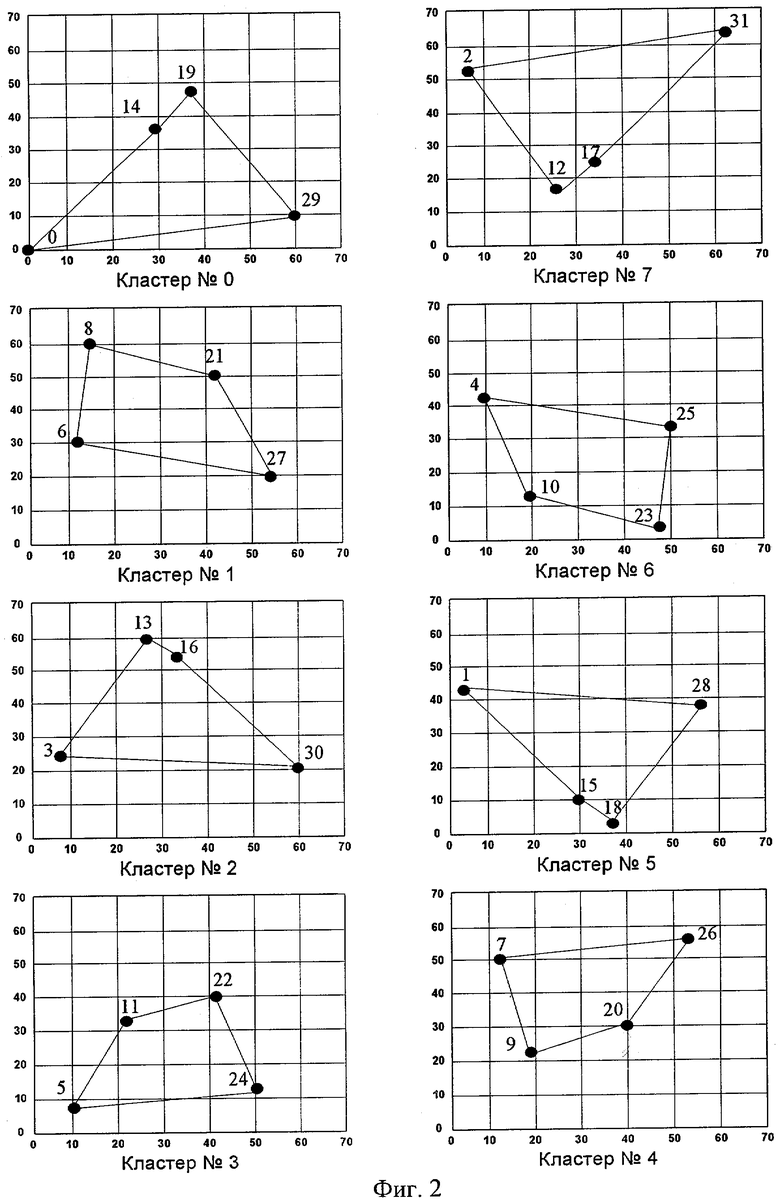
фиг.2 - конфигурация кластеров кода (15, 5, 7) в системе прямых координат;
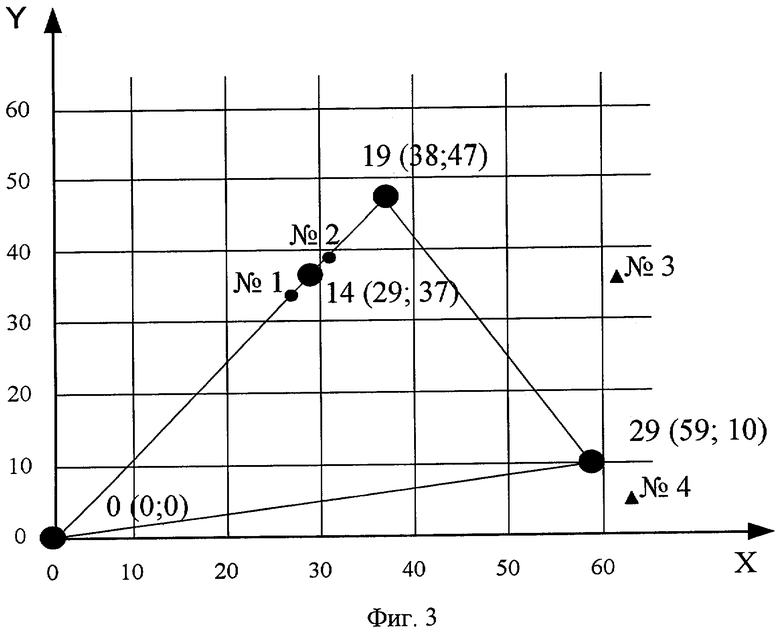
фиг.3 - комбинации кластера №0 в системе прямых координат;
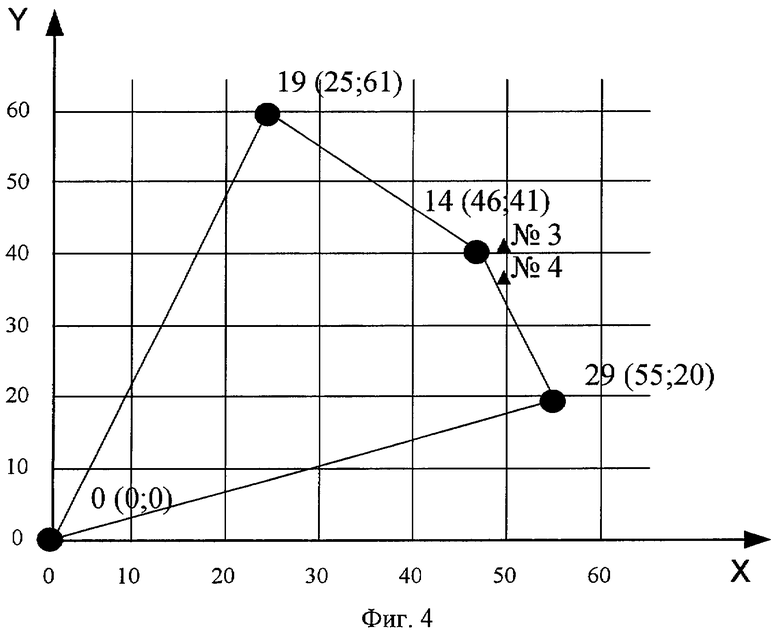
фиг.4 - комбинации кластера №0 в системе инвариантных координат.
Поставленная цель достигается следующим образом.
Множество кодовых комбинаций блокового кода разбивается на кластеры. В качестве признаков кластера может быть выбрано любое сочетание двоичных символов на длине кодовой комбинации. В приведенном примере в качестве такого признака выбрано сочетание соседних трех бит любой кодовой комбинации (см. фиг.1). Тогда оставшиеся 12 разрядов образуют две равные (не обязательное требование) группы двоичных символов. Первая группа бит представляет координату X, а вторая - координату Y. В каждой группе старший разряд в прямой системе координат находится слева. Преобразование значений координат из двоичной системы счисления в m-ичную осуществляется обычным способом. Например, принятая кодовая комбинация №14 имеет вид: 011101100101000 (старшие разряды слева). Последние три бита 000 - определяют принадлежность этой комбинации к кластеру №0. Символы: 011101 - определяют координату X, а символы: 100101 - определяют координату Y.
Запись произвольной координаты Х или Y в m-ичной позиционной системе счисления основывается на представлении этого целого числа в виде полинома.
Например,
Х10=anmn+an-1mn-1+...+a1m1+а0m0,
где каждый коэффициент аi может быть одним из базисных чисел и изображается одной цифрой (см. Острейковский В.А. Информатика: Учеб. для вузов. - Высш.шк., 2001, с.59). В нашем случае аi в зависимости от значения бита в Х или Y принимает значение либо 0, либо 1, а m=2.
Следовательно, преобразование значений координат из двоичной системы счисления в десятичную систему счисления имеет вид:
X=0111012=0·25+1·24+1·23+1·22+0·21+1·20=2910;
Y=1001012=1·25+0·24+0·23+1·22+0·21+1·20=3710.
Заметно, что цена каждого двоичного символа различна. Она зависит от места символа в группе и кратна значению 2Z, где Z - целое положительное, включая ноль. В последующем это свойство будет определять приоритеты в процедуре исправления стираний. В таблице (см. фиг.1) показаны номера кластеров и прямые координаты для всех векторов кода (15, 5, 7). Комбинации одного кластера для наглядности соединены непрерывной линией. Поскольку комбинации кода могут быть разбиты на ортогональные множества, то все кластеры образуют пары с определенным видом симметрии (см. фиг.2). Если выбранные двоичные символы, определяющие номер кластера, приняты не надежно, следует выбрать другие символы с высокими показателями надежности, например, в начале кодовой комбинации. В конфигурации кластеров изменений не последует из-за циклических свойств кода, однако комбинация №14 будет соотнесена с комбинациями других номеров, что не имеет принципиального значения.
На приемной стороне каждый бит кодового вектора сопровождается оценкой надежности. Символы с наименьшими оценками стираются, при этом возможно образование нескольких основных конфигураций стираний на длине групп Х и Y кодового вектора:
Вариант 1. Стирания отсутствуют.
Вариант 2. Все символы стерты.
Вариант 3. Стирания совпали с младшими разрядами групп, определяющих координаты Х и Y.
Вариант 4. Стирания совпали со старшими разрядами групп, определяющих координаты Х и Y.
Вариант 5. Стирания совпали с младшими разрядами, определяющими координату Х и старшими разрядами, определяющими координату Y.
Вариант 6. Стирания совпали со старшими разрядами, определяющими координату Х и младшими разрядами, определяющими координату Y
В первом случае декодирование кодовой комбинации не вызывает сомнений.
Во втором случае целесообразно отказаться от декодирования.
В третьем случае поиск переданной комбинации не вызывает затруднений, поскольку цена стираний невелика. Возможные варианты исправления стираний группируются возле значащей точки для i-й комбинации кластера. Например, для комбинации №14 нулевого кластера координаты Х и Y при восстановлении стираний могут иметь вид:
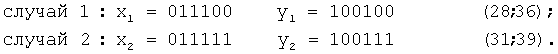
На фиг.3 показано незначительное отклонение в евклидовой метрике вариаций координат от истинного значения (29; 37), декодирование комбинации не вызывает сомнений и может производиться без процедуры перебора позиций стертых символов и умножения вектора на проверочную матрицу, что резко повышает производительность декодера.
В четвертом случае действия в прямых координатах могут привести к грубым ошибкам, поскольку цена стираний в старших разрядах велика. Например, в следующих случаях получаем:
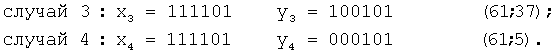
На фиг.3 в форме треугольников показаны точки №3 и №4, которые ошибочно идентифицируются с другими комбинациями кластера. Такое сочетание стираний в случае №3 легко трансформируется в комбинацию №19 (евклидова метрика равна ≈25 против аналогичной метрики ≈27 до комбинации №29 ) или в случае №4 в комбинацию №29 (заметно без дополнительных вычислений). Чтобы избежать ошибочного восстановления комбинации декодер при проявлении признаков, указанных в четвертом случае, переходит к инверсным координатам, т.е. определяет старшие разряды не слева, а справа. В этом случае кластер преобразуется и имеет вид, показанный на фиг.4. При этом ошибка восстановления комбинации №14 минимальна, а процедура декодирования аналогична для третьего случая. Например, на фиг.4 показано восстановление сочетаний стираний для случая 3 и случая 4, но в инвариантных координатах.
В пятом и шестом случае декодер оперирует с той координатой, у которой стирания сосредоточены в младших разрядах прямой системы координат, что позволяет однозначно декодировать принятый вектор. Успех декодирования основан на том, что ни в одном из восьми кластеров соседние точки, связанные с координатами разрешенных кодовых комбинаций, попарно не лежат на прямых, параллельных осям координат (см. фиг.2), т.е. не имеют одинаковых координат ни по X, ни по Y. Это позволяет утверждать, что в случае поражения одной их координат стертыми символами (шесть двоичных символов), комбинация восстанавливается по другой координате. По крайней мере, это не хуже, чем восстановление стираний в метрике Хемминга.
Применение предложенного способа декодирования комбинаций блоковых кодов со стираниями элементов позволяет исключить переборные методы восстановления стираний и повторяющуюся в таком случае процедуру умножения очередной версии процедуры перебора на проверочную матрицу. Способ позволяет целенаправленно использовать приоритеты стертых символов при исправлении той или иной их конфигурации, что повышает скорость восстановления кодовых комбинаций по стираниям и обеспечивает реализацию потенциальных возможностей кода по исправлению ошибок.
| название | год | авторы | номер документа |
|---|---|---|---|
| ДЕКОДЕР С ИСПРАВЛЕНИЕМ СТИРАНИЙ | 2007 |
|
RU2344556C1 |
| ДЕКОДЕР С ИСПРАВЛЕНИЕМ СТИРАНИЙ | 2008 |
|
RU2379841C1 |
| СИСТЕМА ИСПРАВЛЕНИЯ СТИРАНИЙ С ЗАЩИТОЙ НОМЕРА КЛАСТЕРА | 2012 |
|
RU2485702C1 |
| ДЕКОДЕР С УПОРЯДОЧЕННОЙ СТАТИСТИКОЙ СИМВОЛОВ | 2012 |
|
RU2490804C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ | 2015 |
|
RU2580797C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2010 |
|
RU2444127C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ С МЯГКИМИ РЕШЕНИЯМИ ДЛЯ ДВУХСТУПЕНЧАТОГО КАСКАДНОГО КОДА | 2012 |
|
RU2485683C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С СИСТЕМОЙ БЫСТРЫХ МАТРИЧНЫХ ПРЕОБРАЗОВАНИЙ | 2019 |
|
RU2718224C1 |
| СПОСОБ КОНТРОЛЯ КАЧЕСТВА КАНАЛА СВЯЗИ | 2005 |
|
RU2295196C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С ПАМЯТЬЮ | 2017 |
|
RU2672300C2 |
Изобретение относится к технике связи и может быть использовано в системах передачи дискретной информации. Технический результат - повышение скорости и достоверности восстановления информации. В способе при обработке двоичных символов, поступающих из канала связи, фиксируют показатель надежности каждого символа и наименее надежные символы стирают, а по группе наиболее надежных символов определяют один из 2N кластеров (где N - натуральное число), к которому может принадлежать принятый кодовый вектор, при этом оставшуюся часть кодовой комбинации делят на две группы двоичных символов, переводя каждую группу в m-ичные целые числа общепринятым образом, от старших разрядов к младшим, и принимают их за две прямые координаты, принадлежащие плоскости выделенного кластера, а также в m-ичные числа от младших разрядов в группе к старшим, принимая их за инвариантные координаты того же кодового вектора, в ходе оценки принятого кодового вектора определяют конфигурацию стираний в каждой группе, устанавливая приоритеты исправления стертых символов, и в случае поражения стираниями старших разрядов прямых координат переходят к инвариантным координатам, определяя в любом случае по евклидовому расстоянию ближайший разрешенный кодовой вектор выделенного кластера. 4 ил.
Способ декодирования блоковых кодов со стираниями элементов, заключающийся в том, что из канала связи принимают фиксированную последовательность двоичных символов, которую преобразуют в два m-х числа и принимают эти числа за координаты точки на плоскости, определяя место положение этой точки относительно наперед заданных точек этой плоскости в евклидовой метрике, отличающийся тем, что в ходе обработки двоичных символов поступающих из канала связи фиксируют показатель надежности каждого символа и наименее надежные символы стирают, а по группе наиболее надежных символов определяют один из 2N кластеров (где N - натуральное число), к которому может принадлежать принятый кодовый вектор, при этом оставшуюся часть кодовой комбинации делят на две группы двоичных символов, переводя каждую группу в m-е целые числа общепринятым образом, от старших разрядов к младшим, и принимают их за две прямые координаты, принадлежащие плоскости выделенного кластера, а также в m-е числа от младших разрядов в группе к старшим, принимая их за инвариантные координаты того же кодового вектора, в ходе оценки принятого кодового вектора определяют конфигурацию стираний в каждой группе, устанавливая приоритеты исправления стертых символов, и в случае поражения стираниями старших разрядов прямых координат переходят к инвариантным координатам, определяя в любом случае по евклидовому расстоянию ближайший разрешенный кодовой вектор выделенного кластера.
| СКЛЯР БЕРНАРД | |||
| Цифровая связь | |||
| Теоретические основы и практическое применение | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| - М.: Дом Вильямс, 2003, с.443, 444 | |||
| Устройство для формирования импульсов | 1990 |
|
SU1775850A1 |
| СПОСОБ ОЦЕНКИ КАЧЕСТВА КАНАЛА ПЕРЕДАЧИ ДАННЫХ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1995 |
|
RU2085045C1 |
| УСТРОЙСТВО ДЛЯ ДЕКОДИРОВАНИЯ СВЕРТОЧНОГО КОДА | 1991 |
|
RU2035124C1 |
| US 5446747, А, 29.08.1995 | |||
| DE 19918507, A1, 26.10.2000. | |||
Авторы
Даты
2008-06-20—Публикация
2006-03-21—Подача