ПАРАМЕТРИЧЕСКИЕ F-K-СПОСОБЫ ДЛЯ СЕЙСМИЧЕСКИХ ИССЛЕДОВАНИЙ Российский патент 2008 года по МПК G01V1/28 

Предпосылки создания изобретения

Записи сигналов от групп приемников используют для оценки волновых полей и выделения информации о среде, в которой распространяется волновое поле. В сейсмологии анализ сигналов от группы приемников применяют при оценивании распределения сейсмического рассеяния, при измерениях сейсмических волновых полей, связанных с вулканической активностью, при оценивании распространения разрушающей волны землетрясения и при выполнении других исследований.

Способы анализа сигналов от групп приемников можно разделить на две категории в зависимости от того, функционируют ли они в частотной области или во временной области. В частности, способы в частотной области обеспечивают возможность разрешения кратных волн, вступающих на группу приемников одновременно вследствие прохождения по многим путям или использования многочисленных источников.

Одним из наиболее простых частотно-волночисловых способов является формирование диаграммы направленности, или традиционный способ. При этом можно показать, что оцененный спектр мощности должен быть сверткой откликов группы приемников с истинным спектром мощности. В данном случае отклик группы приемников полностью определяется числом и пространственным распределением датчиков. Поскольку отклик сигналов (диаграмма направленности) группы приемников имеет широкий лепесток для волнового числа падающих волн и боковые лепестки, спектр мощности, оцененный с помощью традиционного способа, размазан откликом группы приемников.

При этом было показано, что неискажающий способ наименьшей дисперсии для единственной идентифицируемой волны обеспечивает значительно более высокое разрешение по сравнению с разрешением, обеспечиваемым способом, известным из уровня техники. Однако при наличии многих волн разрешающая способность неискажающего способа наименьшей дисперсии аналогична разрешающей способности способа, известного из уровня техники. Для разрешения кратных сигналов был предложен способ сигнального подпространства, названный способом разделения кратных сигналов (см., например, Johnson and Dudgeon Prentice-Hall Signal Processing Series, ISBN 0-13-048613-6). Ключевой момент способа разделения кратных сигналов заключается в разделении информации в пространственной перекрестной ковариантной матрице коэффициентов Фурье на два векторных подпространства, сигнальное подпространство и шумовое подпространство. Способ разделения кратных сигналов позволяет получать оценки спектра мощности с высоким разрешением, поскольку свертку истинного спектра с откликом группы приемников не осуществляют.

В области сейсмического анализа необходимы способы для формирования частотно-волночисловых спектров с высоким разрешением и спектров более высокой размерности в пространстве частота-волновое число-волновое число. Способами согласно настоящему изобретению решают указанные задачи.

Краткое описание изобретения

При анализе сейсмических данных чрезвычайно желательно использовать небольшое количество датчиков для получения частотно-волночисловых (f-k-) спектров с высоким разрешением и спектров более высокой размерности (f-k-k-) в пространстве частота-волновое число-волновое число, и такое использование найдет широкое применение. Такие применения включают в себя измерения локальных скоростей и обнаружение рассеивающих волн. При наличии относительно небольшого количества отсчетов параметрические способы обеспечивают лучшее разрешение волновых чисел по сравнению с обычным f-k-преобразованием. Параметрические способы, такие как способ разделения кратных сигналов, могут быть применены для получения на каждой частоте оценки области волновое число-волновое число или волнового числа и разработки f-k-k-алгоритма разделения кратных сигналов и f-k-алгоритма разделения кратных сигналов и многих других параметрических алгоритмов, предназначенных для использования при сейсмических исследованиях. Кроме того, параметрические способы могут быть распространены на f-k-k-k- или разреженные/нерегулярные группы датчиков. Способы согласно настоящему изобретению являются полезными в случае, когда оценку локальных скоростей осуществляют по данным с ограниченного числа приемников.

Поэтому в соответствии с настоящим изобретением разработан способ сейсмического анализа, включающий в себя временное преобразование Фурье и пространственное оценивание на основе параметрического алгоритма. В одном варианте осуществления настоящего изобретения параметрический алгоритм представляет собой алгоритм разделения кратных сигналов. В одной реализации этого варианта осуществления настоящего изобретения параметрический алгоритм применяют к данным, полученным при равномерной пространственной дискретизации. В другой реализации этого варианта осуществления настоящего изобретения параметрический алгоритм применяют к данным, полученным при разреженной пространственной дискретизации. В этом варианте осуществления данные вводят в параметрический алгоритм в виде матрицы MN×L, где MN - число датчиков в двумерной группе и L - число отсчетов на датчик. Кроме того, в этом варианте осуществления настоящего изобретения преобразование Фурье выполняют по каждой из трасс, а параметры, входящие в параметрический алгоритм, выбирают по порядку из группы, включающей в себя преобразование Фурье, частоту дискретизации, расстояние между приемниками в направлении x, расстояние между приемниками в направлении y, число источников или интервал f.

В альтернативных вариантах согласно настоящему изобретению применяют другие параметрические способы, включая, но без ограничения ими, алгоритм наименьшей дисперсии, алгоритм вычисления собственных векторов, алгоритм максимального правдоподобия, алгоритм Писаренко, алгоритм авторегрессионного скользящего среднего, алгоритмы авторегрессии или скользящего среднего и алгоритм максимальной энтропии.

Краткое описание чертежей

Более конкретное описание изобретения, кратко изложенного выше, можно получить при рассмотрении вариантов осуществления изобретения, описанных в настоящем описании и иллюстрированных приложенными чертежами. Однако следует отметить, что описание и приложенные чертежи иллюстрируют только некоторые варианты осуществления настоящего изобретения и поэтому не должны рассматриваться как ограничивающие его объем. В изобретении могут допускаться равнозначно эффективные варианты.

На чертежах:

фиг.1 - рабочая диаграмма одного варианта осуществления из способов настоящего изобретения;

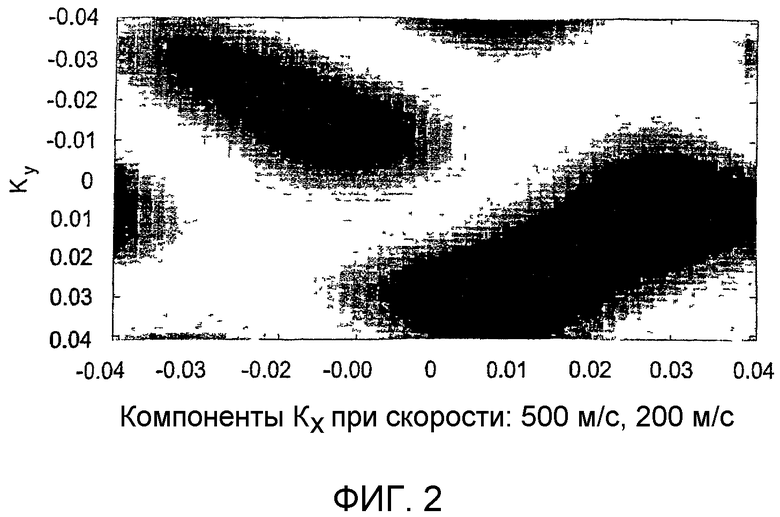
фиг.2 - иллюстрация того, что при оценивании k_x-k_y путем формирования диаграммы направленности на основе быстрого преобразования Фурье две волны не могут быть различены на частоте 9 Гц;

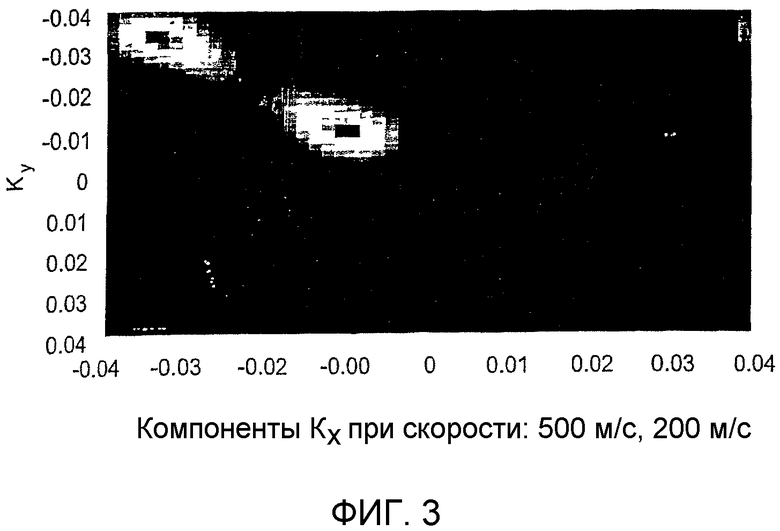
фиг.3 - иллюстрация того, что с помощью параметрического способа, способа разделения кратных сигналов, можно различить две волны согласно фиг.2; скорости находятся в приближенном соответствии со скоростями двух волн в синтетических данных; при этом группа содержит 2×2 элемента;

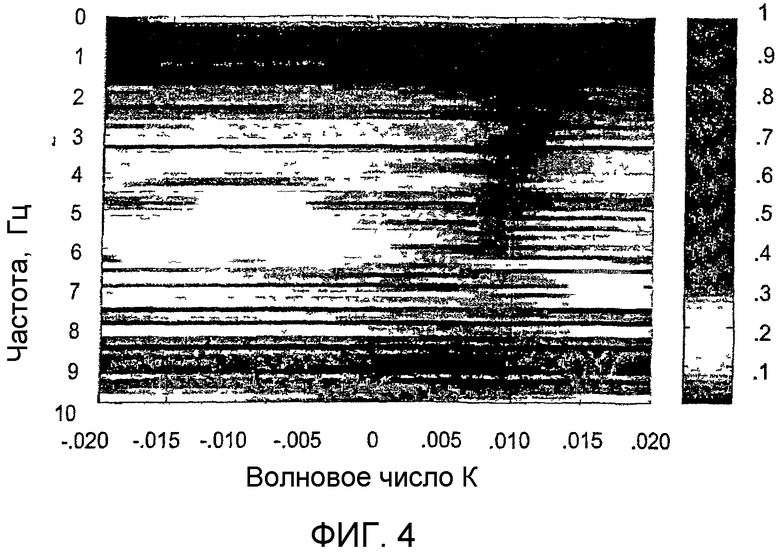
фиг.4 - график f-k для двух трасс; и

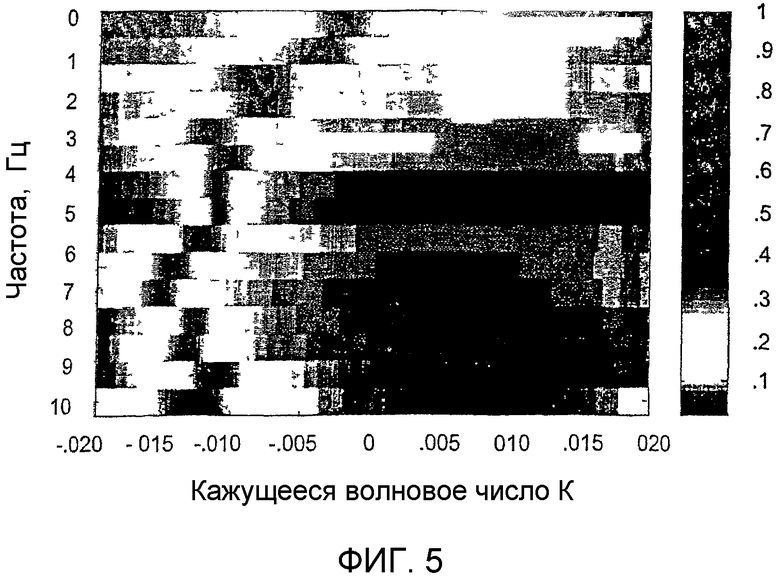
фиг.5 - оценка тех же самых трасс, что и на фиг.4, при использовании f-k-способа разделения кратных сигналов.

Подробное описание изобретения

Далее рассмотрим детали вариантов осуществления изобретения. Хотя изобретение будет описано применительно к этим вариантам осуществления, должно быть понятно, что описываемые варианты осуществления не подразумеваются ограничивающими изобретение. Наоборот, изобретение предполагается охватывающим варианты, модификации и эквиваленты, которые могут быть включены в рамки сущности и объема изобретения, определенные приложенной формулой изобретения.

В настоящем изобретении параметрические способы, такие как алгоритм разделения кратных сигналов, алгоритм наименьшей дисперсии, алгоритм вычисления собственных векторов, алгоритм максимального правдоподобия, алгоритм Писаренко, алгоритм авторегрессионного скользящего среднего, алгоритмы авторегрессии или скользящего среднего и алгоритм максимальной энтропии, используют для получения оценок в пространстве волновое число-волновое число или волновых чисел с целью разработки алгоритмов, таких как f-k-k-алгоритм разделения кратных сигналов и f-k-алгоритм разделения кратных сигналов, и других параметрических алгоритмов, полезных при сейсмических исследованиях. Используемый в настоящей заявке термин «параметрический алгоритм» относится к математическим моделям, которые описывают сигнал, и к использованию зарегистрированных данных для определения параметров модели. В обычных непараметрических способах нахождения спектральных оценок, подобных способу оценивания спектральной плотности мощности или статистике второго порядка, такой как автокорреляция, предполагается, что данные за пределами окна наблюдения являются нулевыми. При таком допущении ограничивается разрешение спектральных оценок. С другой стороны, в соответствии с моделью в параметрических способах относительно данных за пределами окна наблюдения предполагается, что в зависимости от модели данные могут быть описаны различными путями. Описание ненаблюдаемых данных основано, во-первых, на наличии информации относительно наблюдаемых данных и способа, использованного для получения наблюдаемых данных, и, во-вторых, на оцененных параметрах, специфических для принятой модели (см., например, Kay S., "Modern Spectral Estimation", Prentice-Hall Signal Processing Series, ISBN 0-13-598582-X).

На фиг.1 показана рабочая диаграмма, иллюстрирующая один общий вариант (100) осуществления способа согласно настоящему изобретению. Сначала на этапе 110 регистрируют сейсмические трассы, используя двумерную группу датчиков, а на этапе 120 к трассам применяют преобразование Фурье. Далее выбирают (106) частотный интервал относительно частоты F и формируют (108) пространственно-спектральную корреляционную матрицу, а затем производят разложение (110) матрицы на шумовое и сигнальное подпространства с помощью метода вычисления собственных векторов. На следующем этапе используют (112) параметрический способ с формированием диаграммы направленности в области волновых чисел и получают (114) двумерный параметрический спектр для конкретной частоты F. В этот момент может быть выбрана (116) другая частота, и этапы 106, 108, 110, 112 и 114 выполняют для этой новой частоты F. В качестве альтернативы из параметрического спектра, полученного на этапе 114, формируют (118) куб спектра и, наконец, осуществляют (120) анализ скорости.

В общем случае для f-k-спектра с высоким разрешением или для f-k-k-спектра требуются широкое временное и пространственное окно (период записи) и соответствующая дискретизация. Обычно при регистрации сейсмических данных не существует проблемы относительно временной дискретизации и периода записи, а частота дискретизации обычно намного выше по сравнению с рассматриваемыми частотами. Однако на пространственную дискретизацию часто накладываются ограничения. Кроме того, иногда желательно уменьшать пространственную протяженность при f-k-k- или f-k-преобразовании вследствие нестационарных в пространстве свойств данных и необходимости в анализе локальной оценки. В настоящем изобретении параметрические способы переработаны с целью получения высокоточных f-k-k-алгоритма разделения кратных сигналов и f-k-алгоритма разделения кратных сигналов при значительно меньшей пространственной апертуре.

Прежде всего, необходимо рассмотреть двумерную систему наблюдений. Двумерная система наблюдений может быть использована при оценивании небольших значений k_x-k_y. Одномерную систему наблюдений, или линейную группу приемников, можно считать частным случаем двумерной системы наблюдений. В настоящей заявке предполагается, что однородные двумерные группы имеют M×N элементов, в частном случае N=1; одномерная группа состоит по существу из М элементов. Однако элементы могут быть расположены с образованием разреженных или нерегулярных двумерных и одномерных групп. При применении параметрических способов к системам наблюдений с ограниченной апертурой и с очень небольшим числом приемников получают далекие от лучших оценки k_x-k_y, сравнимые с получаемыми классическими способами, такими как способ формирования диаграммы направленности на основе быстрого преобразования Фурье. Одно преимущество от использования f-k-k-способа разделения кратных сигналов или одномерного f-k-способа разделения кратных сигналов заключается в хорошем разрешении волн, которое обеспечивается этими конкретными способами.

Параметрические способы согласно настоящему изобретению, предназначенные для оценивания в координатах волновое число-волновое число (k-k), основаны на прикладной программе, аналогичной используемой в способах определения направления прихода (см., например, Nikias and Petropulu, Prentice-Hall Signal Processing Series, ISBN 0-13-678210-8). Различие между f-k-способами разделения кратных сигналов и способами определения направления прихода заключаются в том, что в способах определения направления прихода формирование диаграммы осуществляют при проходе возможных углов прихода, тогда в настоящем изобретении формирование диаграммы происходит в пространстве волнового числа k. Кроме того, в способах определения направления прихода скорость в среде полагают приблизительно постоянной, и поэтому в пространственной корреляционной матрице используют временные данные. Однако в настоящем изобретении для того, чтобы разрешить волновое число на каждой частоте, пространственно-спектральную матрицу образуют до формирования диаграммы направленности в области волновых чисел. Это позволяет получать оценки с помощью f-k-k-алгоритма разделения кратных сигналов и f-k-алгоритма разделения кратных сигналов или с помощью любого другого f-k-k- или f-k-алгоритма, при этом k оценивают, используя параметрические способы.

В случае двумерной группы датчиков путем двумерного преобразования Фурье результаты пространственных измерений сразу же преобразуют в пространственно-дискретизированные данные в области волновое число-волновое число (k-k), в которой каждая ось определена соответствующей пространственной дискретизацией. Если результаты измерений также непрерывно дискретизируют во времени, то путем трехмерного преобразования Фурье данные преобразуют в область f-k-k.

Оси волновых чисел охватывают как отрицательные, так и положительные волновые числа. Положительные и отрицательные волновые числа соответствуют противоположным направлениям прихода относительно нормальной линии, которая проходит через среднюю точку группы датчиков. Оси волновых чисел Найквиста определяются периодом пространственной дискретизации, то есть расстоянием между соседними датчиками в каждом направлении. В случае однородной прямоугольной двумерной группы датчиков, вытянутой в направлениях x и y, оси волновых чисел представляют кажущиеся (расчетные) волновые числа, измеренные с помощью датчиков, расположенных вдоль этих направлений.

Оси кажущихся волновых чисел охватывает базу [-1/(2dx) 1/(2dx)] и [-1/(2dy) 1/(2dy)], где dx и dy - расстояния между соседними датчиками в направлениях x и y. Если датчики расположены не на одинаковых расстояниях друг от друга, то dx и dy представляют собой наименьшие расстояния, имеющиеся в этих направлениях между любыми двумя соседними датчиками.

Разрешение, обеспечиваемое известными из уровня техники способами формирования диаграммы направленности, главный лепесток определяется размерами апертуры. В настоящем изобретении для повышения разрешения оценки волнового числа используют современные методы спектрального оценивания. Это повышение разрешения эквивалентно эффективному увеличению размеров апертуры.

Корреляционные матрицы подразделяют на два основных класса: пространственно-временные и пространственно-спектральные. Элементы R_ij в пространственно-временной корреляционной матрице определяют корреляцию между временными отсчетами, относящимися к датчику i, и временными отсчетами с датчика j. Пространственно-спектральные корреляционные матрицы традиционно формируют путем осуществления в первую очередь преобразования Фурье дискретизированного по времени ряда от каждого датчика до вычисления корреляционной матрицы. В таком случае каждый элемент в этой матрице будет определять взаимные спектры элементов i и j. Затем корреляционные задержки между датчиками преобразуют в зависимые от датчиков фазовые сдвиги в области Фурье.

Y=[Y₁₁Y₂₁...Y_i1...Y_M1...Y₁₂Y₂₂...Y_i2...Y_M2...Y_1NY_2N...Y_iN...Y_MN]^T,

где вектор Y_ij представляет собой быстрое преобразование Фурье временных отсчетов, относящихся к ij-тому датчику в двумерной группе.

Поэтому мы имеем R(ω)=Y(ω)·Y'(ω). Y' - сопряженный результат транспозиции Y. R(ω) - матрица MN×MN и зависит от угловой частоты ω. Используя управляющий вектор e в виде e'Re, где e' - сопряженный результат транспозиции вектора e, заданного как e=[exp(-jk.r₀)... exp(-jk.r_MN-1)]^T, получим пространственный оператор преобразования Фурье для k, квадратичную форму e'Re. При этом r задает положение датчика в плоскости xy. Эту величину называют квадратичной, поскольку P(k,ω)=e'Re=e'YY'e=|e'Y|². P(k, ω) представляет собой оценку мощности для k и ω. В случае k=(k_x, k_y) управляющий вектор определяется как:

e(k_x,k_y)=[exp(-j(k_xx₀+k_yy₀)......exp(-j(k_xx_MN-1+k_yy_MN-1)))]^T.

Поскольку сейсмический источник также является широкополосным, необходимо оценивать волновое число для каждой частотной компоненты. В настоящем изобретении выбирают пространственно-спектральную корреляционную матрицу вместо пространственно-временной матрицы для того, чтобы получить способ, который заменяет преобразования Фурье в пространстве, используемый совместно с результатами современных способов спектрального оценивания при получении оценок волновых чисел k_x и k_y.

Поскольку корреляционные матрицы имеют эрмитову симметрию (R'=R) и обычно являются положительно определенными (X'Rx>0 при ∀x≠0), то собственные векторы корреляционных матриц являются ортогональными по отношению к матрице, а собственные значения обычно являются положительными:

v_i'Rv_j=λ_iδ_ij и v_i'v_j=δ_ij.

Значение R может быть определено через его собственную систему:

R=∑_ij=1...MNλ_iv_i'v_j и R^-1=∑_ij=1...MNλ_i ^-1v_i'v_j.

Поэтому для двумерной группы с MN приемниками управляемая характеристика формирователя диаграммы направленности может быть записана в следующем виде:

e'Re=∑_i=1...MNλ_i|e'v_i|².

При осуществлении анализа собственных значений собственные значения сортируют по порядку величины их значений. В таком случае наименьшие собственные значения являются существенным признаком шума. Классификацию собственных значений по группам собственных значений, относящихся к сигналу или к шуму, осуществляют путем построения графика рассортированных значений и нахождения порога, который соответствует минимальному уровню шума. Осуществление операций (пространственных) регулярного преобразования Фурье до проведения анализа собственных значений может способствовать определению этого порога. Затем соответствующие собственные векторы упорядочивают в дополнение к их собственным значениям. Наибольшие собственные значения также подвергаются воздействию уровня шума. Однако собственные векторы, соответствующие наибольшим собственным значениям, определяются только направлением распространения волн. Поэтому пространство, задаваемое всеми собственными векторами, разделяют на шумовое и сигнальное подпространства. Поскольку величины собственных значений, соответствующих сигналам, также подвергаются воздействию уровня шума, то сигнальное подпространство часто называют сигнальным плюс шумовым подпространством. В настоящей заявке для исключения всякой неоднозначности сигнальное плюс шумовое подпространство будет называться сигнальным подпространством, в частности, когда амплитуда сигнала меньше по сравнению с оценкой по волновому числу.

Спектр наименьшей дисперсии может быть записан в членах собственных значений и собственных векторов корреляционной матрицы R в следующем виде:

P_MV(k)=[∑_i=1...Nsλ_i ^-1|e'(k)v_i|²+∑_i=Ns+1...MNλ_i ^-1|e'(k)v_i|²]^-1.

Ns - число различимых волновых чисел в сигнальном подпространстве. В приведенном выше выражении вторая «сумма» охватывает шумовое подпространство. Когда e(k) изменяют в направлении возрастания к правильному волновому числу, значение первой суммы возрастает, тогда как вторая сумма уменьшается. Поскольку исследуется обратная величина выражения внутри квадратных скобок, приравнивание к нулю выражения усиливает те максимумы, которые относятся к возрастанию волновых чисел. Это можно объяснить поведением второй «суммы» в этом выражении. Когда e(k) согласовано с правильным волновым числом, вторая сумма становится пренебрежимо малой и поэтому ее обратная величина становится заметной. При использовании терминологии направления прихода причина этого эффекта заключается в том, что любое направление распространения сигнала является идеально ортогональным к шумовому подпространству. Поэтому из способа собственного вектора следует:

P_EV(k)=[∑_i=Ns+1...MNλ_i ^-1|e'(k)v_i|²]^-1.

Путем отбеливания шумового подпространства и замены на 1 всех собственных значений, относящихся к шумовому подпространству, получаем параметрический способ разделения кратных сигналов (ПСРКС) (опять см. Johnson and Dudgeon, Prentice-Hall Signal Processing Series, ISBN 0-13-048513-6). Как понятно из выводов, сделанных для этого способа, в спектре имеются равные амплитуды для всех сигналов и равные минимальные уровни шума; таким образом, всякая информация об амплитуде теряется.

Р_ПСРКС=[∑_i=Ns+1...MN|e'(k)v_i|²]^-1.

Следовательно, в настоящем изобретении предложен алгоритм, предназначенный для применения в области сейсмических исследований, который заменяет трехмерное преобразование Фурье. При его использовании сохраняется временное преобразование Фурье, тогда как пространственные преобразования Фурье заменяются оцениванием на основе параметрических способов. Используя параметрические способы, получают f-k-k-оценки, подобные получаемым в f-k-k-способе разделения кратных сигналов или в частном случае одномерной группы датчиков, в f-k-способе разделения кратных сигналов.

Данные для алгоритма вводят в виде матрицы MN×L, где MN - число приемников (трасс), а L - число отсчетов на датчик. В этом алгоритме операция преобразования Фурье осуществляется по каждой трассе с обеспечением разрешения по частоте. В алгоритме задают порядок быстрого преобразования Фурье (число быстрого преобразования Фурье). Примерами таких чисел являются 8192 или 512 и т.д. (то есть 2ⁿ, где n - целое число).

Другими параметрами, входящими в алгоритм, являются Fs (частота дискретизации), dx (расстояние между приемниками в направлении x), dy (расстояние между датчиками в направлении y), число источников и «интервал f». Для алгоритма в его существующем виде приемлемы равноотстоящие пространственные отсчеты; однако алгоритм может быть легко распространен для работы с разреженными пространственными отсчетами и с различными геометриями.

После того как с помощью операции преобразования Фурье разрешены временные частоты, должны быть разрешены волновые числа. Разрешение интервала f, который в качестве параметра входит в алгоритм, определяет df или разрешение, выбранное в области временных частот для оценивания волновых чисел. Спектр волновых чисел оценивают внутри интервала df. Если число быстрого преобразования Фурье выбрано равным 8192, параметр интервала f может быть выбран, например, равным 10 с разделением пространства Найквиста на 4096/10 частей. Это трансформируется в разрешение df=10/4096 в пространстве Найквиста. При выборе числа быстрого преобразования Фурье, равного 512, выбор значения 2 для интервала f будет более подходящим, что дает df=2/256 в пространстве Найквиста. Волновые числа разрешаются внутри частотного интервала [f f+df]. При слишком большом значении df задача оценивания волнового числа внутри этого частотного окна может привести к получению неточных оценок. Векторы [f f+df] от каждой трассы используют для формирования пространственно-спектральной корреляционной матрицы, основной для всех способов формирования диаграммы направленности.

С помощью параметра «число источников» в алгоритм вводятся сведения относительно прогнозируемого количества различаемых волновых чисел. Этот параметр не может быть больше числа трасс. Если число источников выбрать равным 1, то это будет означать, что имеется только 1 собственное значение, относящееся к сигнальному подпространству. Соответственно модифицируют корреляционную матрицу, а затем корреляционную матрицу используют при реализации различных способов формирования диаграммы направленности.

На различных этапах с помощью алгоритма можно получать оценки по f-k-k-способу разделения кратных сигналов, f-k-k-методу наименьшей дисперсии, f-k-k-методу максимального правдоподобия и f-k-k-методу вычисления собственных значений. Выбор способа зависит, например, от отношения сигнала к шуму, числа используемых датчиков, вида шума и области применения. За исключением классического способа формирования диаграммы направленности, в том случае, когда используют очень много приемников, выходные сигналы могут иметь многочисленные побочные максимумы. В случае использования многих приемников f-k-k-процесс или связанный с ним классический способ формирования диаграммы направленности может быть оптимальным.

Пример. Применение параметрического f-k-k-способа (f-k-k-способа разделения кратных сигналов)

Согласно f-k-k-способу осуществляют формирование профиля k_x-k_y на каждой частоте. На отображение представляют разрез f-k-k-результатов на единственной частоте.

Результаты, представленные здесь, иллюстрируют, каким образом, используя параметрический способ, такой как способ разделения кратных сигналов, можно различить два отдельных вступления, когда это невозможно осуществить классическим способом формирования диаграммы направленности (основанным на быстром преобразовании Фурье). Получали синтетические данные для двух волн, распространяющихся со скоростью 200 и 500 м/с. Использовали группу 2×2. Для получения вступлений использовали импульс Рикера. Расстояния между приемниками, dx и dy, задавали равными 12,5 м. Результаты по способу формирования диаграммы направленности показаны на фиг.2. Из этой фигуры очевидно, что эти два вступления не могут быть различены. С другой стороны, на фиг.3 показаны результаты применения к этим синтетическим данным параметрического f-k-k-способа разделения кратных сигналов. Этим способом два вступления легко различаются. Зная, что группа состоит всего из 2×2 приемников, результат следует признать впечатляющим.

Параметрические способы (например, f-k-k-способ разделения кратных сигналов и f-k-способ разделения кратных сигналов) могут найти широкое применение, например, при анализе локальной скорости и оценивании волновых чисел. Кроме того, способы могут быть распространены на случай f-k-k-k- или разреженных/нерегулярных решеток. f-k-способ разделения кратных сигналов был применен к частному случаю одномерной группы. На фиг.4 показана зависимость f-k для двух трасс. На фиг.5 показаны данные f-k-способа разделения кратных сигналов для тех же самых двух трасс. При сравнении можно отчетливо видеть различие в разрешении.

Хотя настоящее изобретение было описано применительно к конкретным вариантам осуществления, специалистам в данной области техники, к которой относится изобретение, должно быть понятно, что могут быть выполнены различные модификации и замены эквивалентами без отступления от истинной сущности и объема изобретения. Кроме того, многочисленные модификации могут быть сделаны для приспособления конкретной ситуации, материала или процесса к задаче, сущности и объему настоящего изобретения. Все такие модификации подразумеваются находящимися в рамках объема изобретения.

В настоящей заявке все источники информации процитированы для содействия пониманию изобретения и с этой целью во всем своем объеме включены в настоящую заявку в качестве ссылок.

Настоящее изобретение относится к способам, предназначенным для использования при обработке сейсмических данных, направленным на решение проблем, встречающихся во время регистрации данных с ограниченного числа приемников, в частности на решение проблем размазанного спектра мощности. В настоящем изобретении параметрические способы используют для обеспечения высокого разрешения волновых чисел при использовании ограниченного числа приемников. 25 з.п. ф-лы, 5 ил.

1. Способ обработки сейсмических данных, включающий в себя регистрацию сейсмических данных от трехмерной группы датчиков, применение временного преобразования Фурье к сейсмическим данным для формирования Фурье преобразованных данных, при этом сейсмические данные вводят в параметрический алгоритм в виде MNO×L, где MNO - число сигналов в трехмерной группе и L - число отсчетов на датчик, применение оценки пространственного волнового числа, основанной на параметрическом алгоритме, к Фурье преобразованным данным, формирование спектра волновых чисел на основании параметрического алгоритма и использование спектра волновых чисел для осуществления одного или нескольких сейсмических применений.2. Способ по п.1, в котором применение оценки пространственного волнового числа включает в себя выбор частотного интервала относительно частоты F.3. Способ по п.1, в котором применение оценки пространственного волнового числа включает в себя формирование пространственно-спектральной корреляционной матрицы.4. Способ по п.3, в котором применение оценки волнового числа дополнительно включает в себя разложение пространственно-спектральной корреляционной матрицы на шумовое и сигнальное подпространства.5. Способ по п.4, в котором этап разложения выполняют используя метод разложения по собственным значениям.6. Способ по п.5, в котором в методе разложения по собственным значениям используют собственные значения с пороговой магнитудой.7. Способ по п.1, в котором параметрический алгоритм представляет собой алгоритм разделения кратных сигналов.8. Способ по п.1, в котором параметрический алгоритм представляет собой алгоритм наименьшей дисперсии, алгоритм вычисления собственных векторов, алгоритм максимального правдоподобия, алгоритм Писаренко, алгоритм авторегрессионного скользящего среднего, алгоритм авторегрессии или скользящего среднего, или алгоритм максимальной энтропии.9. Способ по п.1, в котором применение оценки пространственного волнового числа включает в себя выбор частотного интервала относительно частоты F, формирование пространственно-спектральной матрицы, разложение пространственно-спектральной матрицы на шумовое и сигнальное подпространства, и в котором параметрический алгоритм представляет собой алгоритм разделения кратных сигналов, алгоритм наименьшей дисперсии, алгоритм вычисления собственных векторов, алгоритм максимального правдоподобия, алгоритм Писаренко, алгоритм авторегрессионного скользящего среднего, алгоритм авторегрессии или скользящего окна, или алгоритм максимальной энтропии.10. Способ по п.1, в котором параметрический алгоритм применяют к данным с равноотстоящей пространственной дискретизацией.11. Способ по п.1, в котором параметрический алгоритм применяют к данным с разреженной пространственной дискретизацией.12. Способ по п.11, в котором параметры, входящие в параметрический алгоритм, выбирают по порядку из группы, включающей в себя преобразование Фурье, частоту дискретизации, расстояние между приемниками в направлении х, расстояние между приемниками в направлении у, число источников, интервал f.13. Способ по п.12, в котором интервал f, входящий в качестве параметра в параметрический алгоритм, определяет область временных частот, разрешающую спектр волновых чисел.14. Способ по п.12, в котором число источников входит в параметрический алгоритм.15. Способ по п.14, в котором число источников не больше числа сигналов.16. Способ по п.1, в котором сейсмические данные регистрируют от одномерной группы датчиков.17. Способ по п.16, в котором сейсмические данные вводят в параметрический алгоритм в виде матрицы M×L, где М - число сигналов в одномерной решетке и L - число отсчетов на датчик.18. Способ по п.16, в котором обобщенный спектр волновых чисел представляет собой одномерный ƒ-k-спектр для каждого частотного интервала.19. Способ по п.18, включающий в себя дополнительный этап формирования трехмерного объема ƒ-k-k-спектра.20. Способ по п.1, в котором сейсмические данные регистрируют от двумерной группы датчиков.21. Способ по п.19, в котором данные вводят в параметрический алгоритм в виде матрицы MN×L, где MN - число сигналов в двумерной группе и L - число отсчетов на датчик.22. Способ по п.19, в котором сформированный спектр волновых чисел представляет собой двумерный ƒ-k-k-спектр для каждого частотного интервала.23. Способ по п.21, дополнительно включающий в себя формирование трехмерного объема ƒ-k-k-спектра.24. Способ по п.1, в котором сформированный спектр волновых чисел представляет собой трехмерный ƒ-k-k-спектр для каждого частотного интервала.25. Способ по п.24, дополнительно включающий формирование четырехмерного изображения ƒ-k-k-k-спектра.26. Способ по п.1, в котором сейсмические применения включают осуществление анализа скоростей.