;Изобретение относится к способам определения скорости и направления ветра в нижних слоях атмосферы, используемым в приборах метеорологического обеспечения пуска ракет, стрельбы артиллерии и ведения звуковой разведки звукометрическими комплексами Сухопутных войск, т.к. ветер в нижних слоях атмосферы сильно влияет на полет ракет на активном участке траектории и снарядов, выпущенных реактивными системами залпового огня. Известны способы определения скорости и направления ветра в вышеуказанной области техники [1...4]. Техническая реализация способа, описанного в [1, 2], сложна, а устройства, его реализующие, не надежны в работе и дорогостоящие, а сам способ требует большого времени на получение скорости и направления ветра. Способ, предложенный в [3], не обеспечивает получения скорости среднего ветра и его направления при всевозможных направлениях ветра в приземном слое атмосферы, т.к. в его описании отсутствуют формулы расчета этих параметров ветра для указанных направлений ветра. Кроме того, отсутствуют программы автоматического вычисления данных параметров ветра, которые сократили бы время их определения. В настоящее время на практике применяются 2 способа определения скорости и направления среднего ветра: 1-й способ используется при составлении приближенного бюллетеня по данным метеорологического поста и заключается в измерении наземных температуры воздуха t (термометром-пращом или вентиляционным психрометром [4, c.8]) и давления атмосферы, скорости и направления наземного ветра (в приземном слое атмосферы), которые определяются, как среднеарифметические значения 10 измерений десантным метеорологическим комплектом ДМК-2 или ветромером в течение 5 минут, см. с.10, 21 и 22 работы [4], а потом по данным приложения 4 (см. с.28 работы [4]) определяются скорости среднего ветра и дирекционные углы (ДУ) его направлений в делениях угломера (окружность разбита на 6000 (60-00) малых делений угломера) для стандартных высот; 2-й способ используется при составлении приближенного бюллетеня по данным метеорологического поста и заключается в измерении наземных температуры воздуха и давления атмосферы аналогично 1-му способу, а скорость и направление ветра в слое атмосферы 0-200 м определяются с помощью ветрового ружья ВР-2, а потом по данным приложения 1 (см. с.23 работы [4]) определяются скорости среднего ветра и его дирекционные углы для стандартных высот. Последний способ определения скоростей среднего ветра и его дирекционных углов для стандартных высот используем в качестве прототипа. Этот способ определения скоростей среднего ветра и его дирекционных углов для стандартных высот не обеспечивает измерения этих параметров ветра при глубоком снежном покрове и высокой траве, т.к. упавшие в них «ветровые» пули с красной лентой (а производят 4-5 выстрелов, см. с.10 [4]), выстрелянные из этого ружья, не видны в этих случаях на поверхности земли, и особенно ночью, в тумане. Кроме того, этот способ требует и относительно большое время на определение рассматриваемых параметров, т.к. надо найти «среднюю точку падения не менее 3 пуль, см. с.10 [4]. При необходимости производят дополнительный выстрел». Визиром ветрового ружья «определяют ДУ на веху, что не обеспечивает высокой точности измерения направления среднего ветра, т.к. цена деления шкалы лимба ружья составляет 0-25 делений угломера, см. с.1 [6], а с помощью мерной ленты (мерного шнура) измеряют расстояние от ружья до вехи. За направление 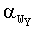 среднего ветра (откуда дует) в пределах высоты 200 м принимают значение ДУ на веху; направления среднего ветра для других 8 стандартных высот рассчитывают, используя данные приложения 1» и ДУ на веху, см. с.23 [4]. По дальности сноса ветровой пули (по удалению средней точки падения не менее 3 пуль) по приложению 1, см. с.23 прототипа [4], определяются скорости среднего ветра и приращения его дирекционного угла для всех стандартных высот. Дальности сноса ветровых пуль в этом приложении приведены через 10 м, реальные их значения будут в большинстве случаев дробными, поэтому требуется большое время на интерполяцию.
среднего ветра (откуда дует) в пределах высоты 200 м принимают значение ДУ на веху; направления среднего ветра для других 8 стандартных высот рассчитывают, используя данные приложения 1» и ДУ на веху, см. с.23 [4]. По дальности сноса ветровой пули (по удалению средней точки падения не менее 3 пуль) по приложению 1, см. с.23 прототипа [4], определяются скорости среднего ветра и приращения его дирекционного угла для всех стандартных высот. Дальности сноса ветровых пуль в этом приложении приведены через 10 м, реальные их значения будут в большинстве случаев дробными, поэтому требуется большое время на интерполяцию.
Для устранения указанных недостатков предлагается способ определения скорости и направления ветра в нижних слоях атмосферы, который может заменить вышеуказанные 2 способа и иллюстрируется следующими графическими материалами:
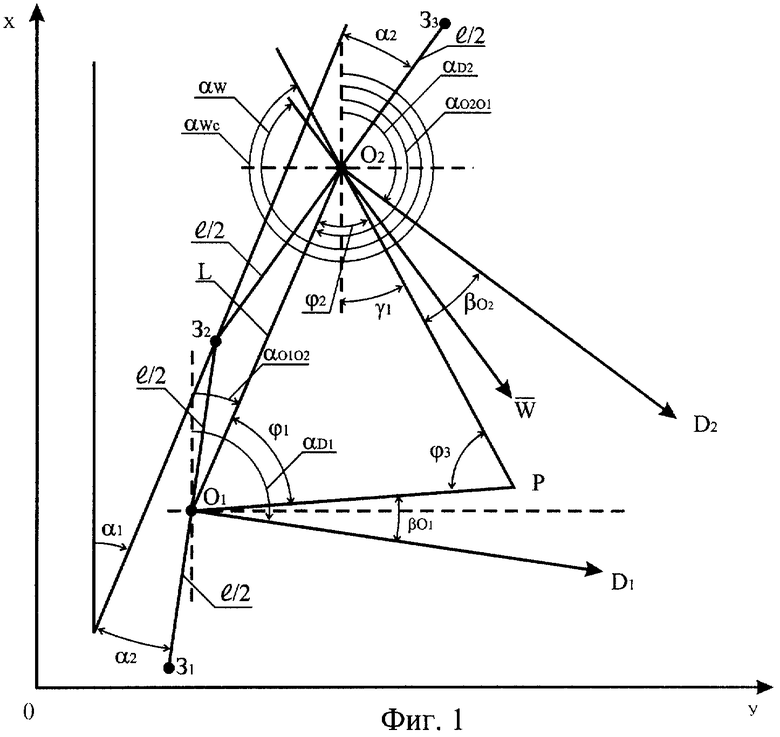
Фиг.1. Схема расположения акустических баз при северо-западном, западном и юго-западном направлениях ветра в приземном слое атмосферы.
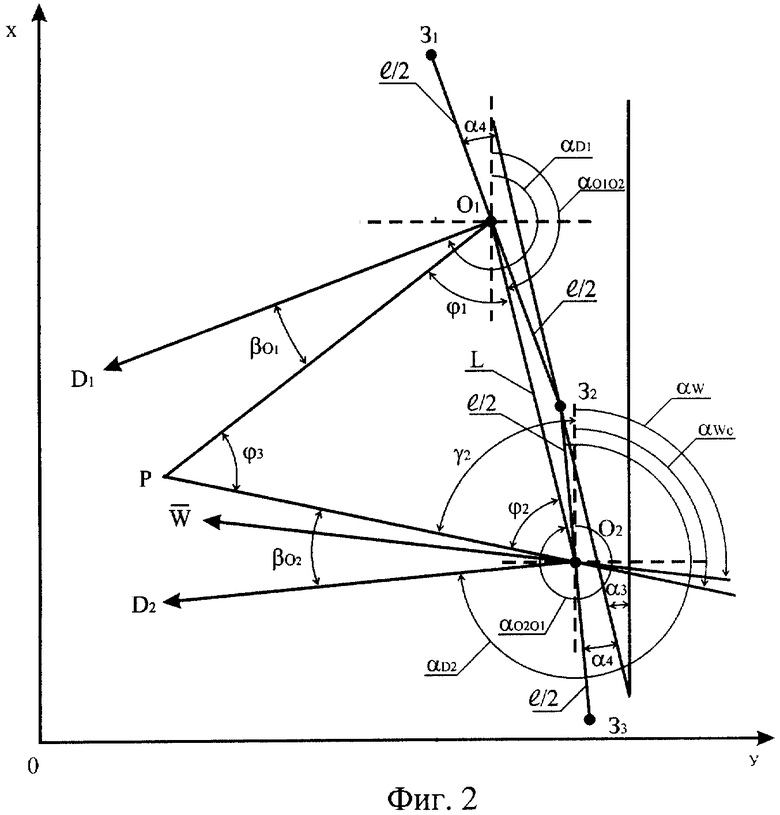
Фиг.2. Схема расположения акустических баз при северо-восточном, восточном и юго-восточном направлениях ветра в приземном слое атмосферы.
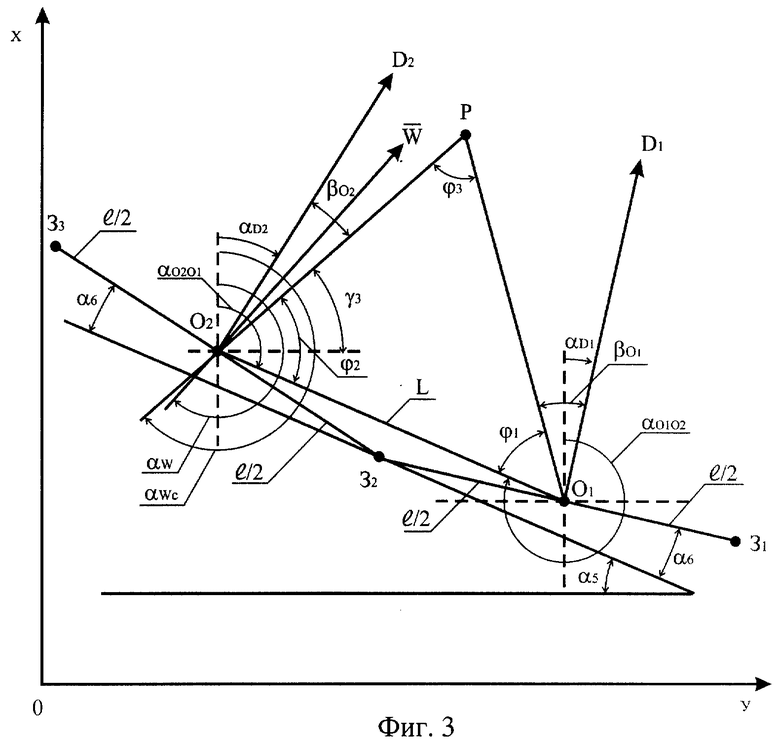
Фиг.3. Схема расположения акустических баз при юго-западном, южном и юго-восточном направлениях ветра в приземном слое атмосферы.
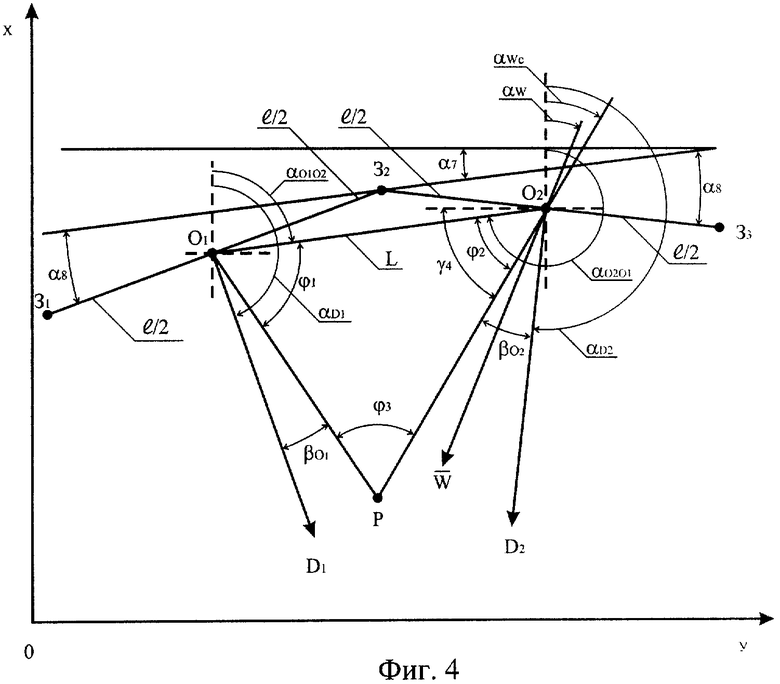
Фиг.4. Схема расположения акустических баз при северо-западном, северном и северо-восточном направлениях ветра в приземном слое атмосферы.
Он заключается в следующем, см. фиг.1...4. Выбирают открытый, ровный участок местности в направлении сноса пуль под действием ветра (куда дует наземный ветер) шириной около 100 м и протяженностью около 200 м от предполагаемой точки установки ветрового ружья, на котором развертывают 2 акустические базы (АБ) так, как показано на фиг.1...4. На стороне, противоположной направлению наземного ветра, вышеуказанного участка намечают воображаемую линию, расположенную относительно одной из осей топографической системы координат так, чтобы наземный ветер был направлен между предполагаемыми директрисами 2-х АБ O1D1 и O2D2. В случае северо-западного направления этого ветра (см. фиг.1) эта линия имеет ДУ α1. Затем примерно на средине этой линии, в точке З2, вбивают колышек, над этим колышком устанавливают перископическую артиллерийскую буссоль ПАБ-2А [5] так, чтобы отвес ее висел строго над этим колышком, производят горизонтирование, контролируя его по шаровому уровню, и ориентирование по странам света (днем и ночью при облачности используют для этого ориентир-буссоль, а ночью при отсутствии облачности - азимутальную насадку; по окончании ориентирования оптическая ось (OO) ее визира параллельна оси ОХ, а на шкале буссоли должен быть 0), потом поворачивают по направлению вращения часовой стрелки OO ее визира от этого направления на угол α1 и снимают отсчет со шкалы буссоли (на фиг.1 он равен примерно 24° или 4-00 делений угломера). Затем правее полученного направления на расстоянии 50 м (как показывают расчеты в этом случае обеспечивается точность измерения рассматриваемых параметров ветра, превосходящая точность определения этих параметров прототипом) устанавливают веху (начало мерного шнура крепится к колышку, над которым установлена буссоль, а конец прикреплен к основанию вехи, что обеспечивает сокращение времени развертывания АБ) и поворачивают ОО визира по направлению вращения часовой стрелки до совмещения его перекрестия с основанием вехи (совмещение перекрестия визира с основанием вехи повышает точность измерения угла α2) и снимают отсчет со шкалы буссоли суммы углов α1 и α2, затем из этой суммы углов вычесть значение угла α1, в результате получится значение угла α2 (на фиг.1 он примерно равен 15° или 2-50 делений угломера). После чего на средине мерного шнура установить ветровое ружье [6] и подготовить его к зондированию атмосферы, а на месте вехи установить звукоприемник (ЗП) №3, в точку З3. Затем повернуть OO визира по направлению вращения часовой стрелки на угол, равный (30-00-2α2) или (180°-2α2), это ДУ 1 АБ, что очевидно из фиг.1. После чего вышеуказанным мерным шнуром с вехой на OO визира на расстоянии 50 м установить эту веху и на месте вехи установить ЗП №1, в точку З1, а на месте буссоли установить ЗП №2, в точку З2. Методика определения параметров АБ может быть и другой. Потом вводят в ЭВМ значения углов α1, α2 (в малых делениях угломера), длину АБ 1, 10 значений скоростей наземного ветра, его 10 ДУ направлений и наземную температуру воздуха, производят 3 выстрела из ветрового ружья (после каждого выстрела проверяют вертикальность ствола по шаровому уровню) и определяют скорости и ДУ направлений среднего ветра для всех стандартных высот (200, 400, 800, 1200, 1600, 2000, 2400, 3000 и 4000 м), используя приложения 1...3, если направления ветра северо-западное, западное и юго-западное. Ветровая пуля должна быть по своим параметрам аналогична пули зондировочного патрона ЗП-2, но при падении на землю должна разрываться и создавать амплитуду звукового давления, равную примерно 2 Па, т.к., например, амплитуды баллистических волн составляют 2...10 Па и их акустические сигналы принимаются современными ЗП на дальностях, исчисляемых километрами, см. с.53 работы [7] и с.36...38 работы [8]. Зондировочный патрон должен быть по своим параметрам аналогичен патрону ЗП-2, но иметь вместо обычного капсула капсул - воспламенитель, корпус которого должен иметь электрическую изоляцию от корпуса ствола ружья.
Если направления наземного ветра другие в отличие от рассмотренного, то имеются некоторые особенности. При юго-восточном, восточном и северо-восточном направлениях этого ветра (см. фиг.2) ОО визира буссоли после ориентирования ее на север поворачивается против направления вращения часовой стрелки на угол α3, который определяется следующим образом: из 60-00 вычитается значение ДУ повернутой влево воображаемой линии (на фиг.2 этот угол примерно равен 2-00 или 12°), а угол α4 (на фиг.2 он примерно равен 1-00 или 6°) определяется, как разность показаний шкалы буссоли при первом повороте OO визира против направления вращения часовой стрелки на угол α3 и втором. Остальные параметры АБ определяются через эти углы. Может быть и другая методика определения этих углов. Тексты программ расчетов рассматриваемых параметров ветра с примерами приведены в приложениях 4 и 5.
При юго-западном, южном и юго-восточном направлениях наземного ветра (см. фиг.3) OO визира буссоли после ориентирования ее на север поворачивается против направления вращения часовой стрелки на угол 15-00 и снимается отсчет со шкалы буссоли (он должен быть равным 45-00), а потом 00 визира буссоли поворачивают по направлению вращения часовой стрелки на такой угол, чтобы наземный ветер из предполагаемой точки 02 был направлен между директрисами АБ, и снимают отсчет со шкалы буссоли, из этого значения вычитают 45-00, полученное значение и есть α5 (на фиг.3 он примерно равен 4-00 делений угломера или 24°). Затем ОО визира буссоли поворачивают по направлению вращения часовой стрелки до совмещения перекрестия визира с основанием вехи и снимают показание со шкалы буссоли, из полученного значения вычитают предыдущее значение угла (оно было равным 45-00+α5), в результате определяется угол α6 (на фиг.3 он примерно равен 2-00 делений угломера или 12°). Остальные параметры АБ определяются через эти углы. Может быть и другая методика определения этих углов. Тексты программ расчетов рассматриваемых параметров ветра с примерами приведены в приложениях 6 и 7.
При северо-западном, северном и северо-восточном направлениях наземного ветра (см. фиг.4) ОО визира буссоли после ориентирования ее на север поворачивается против направления вращения часовой стрелки на угол 15-00 и снимается отсчет со шкалы буссоли (он должен быть равным 45-00), а потом OO визира буссоли поворачивают еще против направления вращения часовой стрелки на такой угол, чтобы наземный ветер из предполагаемой точки 02 был направлен между директрисами АБ, и снимают отсчет со шкалы буссоли, из этого значения вычитают 45-00, полученное значение и есть α7 (на фиг.4 он примерно равен 1-00 делений угломера или 6°). Затем OO визира буссоли поворачивают еще против направления вращения часовой стрелки на такой угол, чтобы наземный ветер из предполагаемой точки 02 был также направлен между директрисами АБ, и снимают отсчет со шкалы буссоли, из полученного значения вычитают предыдущее значение угла (оно было равным 45-00-α7), в результате определяется угол α8 (на фиг.4 он примерно равен 2-00 делений угломера или 12°). Остальные параметры АБ определяются через эти углы. Может быть и другая методика определения этих углов. Тексты программ расчетов рассматриваемых параметров ветра с примерами приведены в приложениях 8 и 9.
После одного измерения наземной температуры воздуха, 10 измерений скорости и ДУ направления наземного ветра, а также измерения двух вышеуказанных углов они вводятся в ЭВМ, которая рассчитывает (при северо-западном, западном и юго-западном направлениях наземного ветра, см. фиг.1) следующие параметры:
1. Среднеарифметическое значение скорости наземного ветра при 10 измерениях

где Wi - скорость наземного ветра при i-м измерении.
2. Среднеарифметическое значение дирекционного угла направления наземного ветра в малых делениях угломера при 10 измерениях

где 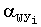 - ДУ направления наземного ветра в малых делениях угломера при i-м измерении.
- ДУ направления наземного ветра в малых делениях угломера при i-м измерении.
3. Среднеарифметическое значение дирекционного угла направления наземного ветра в радианах при 10 измерениях (учтя, что 3000 малых делений угломера составляют π радиан)

4. Значение угла α1У в радианах

5. Значение угла α2У в радианах

6. Дирекционный угол директрисы 2 АБ в радианах
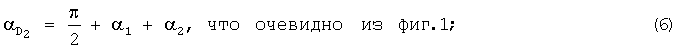
7. Дирекционный угол директрисы 1 АБ в радианах
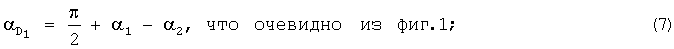
8. Угол при вершине равнобедренного треугольника O1З2O2 в радианах
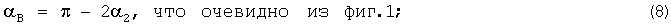
9. Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с
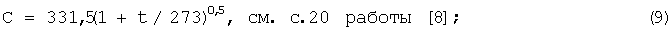
10. ДУ направления: средина 1 АБ - средина 2 АБ в радианах
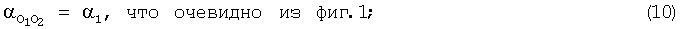
11. ДУ направления: средина 2 АБ - средина 1 АБ в радианах
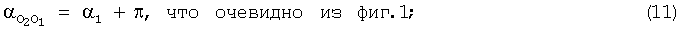
12. Геометрическая база в метрах
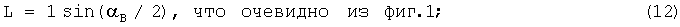
Нажатием кнопки устройства управления на короткое время подается постоянное напряжение на капсюль-воспламенитель, происходит 1-й выстрел из ветрового ружья, начинают работать временные счетчики всех 3 каналов обработки сигнала (КОС) ЗП №1...№3 и в это же время блокируются все эти каналы обработки сигнала, поэтому акустический сигнал (АС) от выстрела не влияет на работу системы. Перед моментом встречи пули с поверхностью земли автоматически открываются все 3 КОС и при падении ее на землю образующийся АС, поступает в КОС ЗП №1...№3 в моменты времени t1, t2 и t3 (из-за разных удалений ЗП от места разрыва пули эти времена разные), которые фиксирует ЭВМ и производит следующие расчеты:
1. Определяется запаздывание АС 1 АБ по формуле

2. Определяется звукометрический угол 1 АБ по формуле
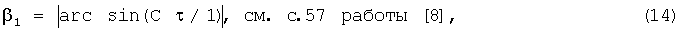
знак модуля здесь необходим потому, что АС при сносах ветровой пули сначала приходит к ЗП №1, а потом к ЗП №2, тогда значение τ1<0 и значение звукометрического угла β1 будет отрицательным, что будет вызывать ошибку при определении угла ϕ1, см. фиг.1;
3. Определяется общая поправка в звукометрический угол 1 АБ на ветер по формуле
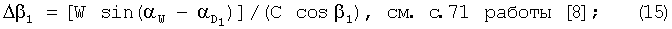
4. Определяется исправленный звукометрический угол 1 АБ по формуле

см. с.91 работы [8], но поправками на удаление и на превышение цели здесь пренебрегаем, т.к. АБ очень небольшие, а площадка выбирается ровной;
5. Рассчитывается угол ϕ1 по формуле:
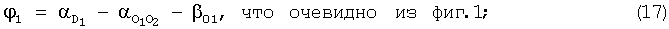
6. Определяется запаздывание АС 2 АБ по формуле:

7. Определяется звукометрический угол 2 АБ по формуле:
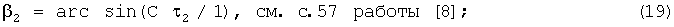
знак модуля в этой формуле не используется, т.к. 0≤τ2;
8. Определяется общая поправка в звукометрический угол 2 АБ на ветер по формуле:
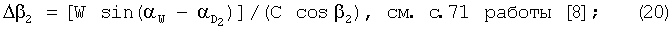
9. Определяется исправленный звукометрический угол 2 АБ по формуле

см. с.91 работы [8], но поправками на удаление и на превышение цели здесь пренебрегаем, т.к. АБ малы (l=50 м), а площадка выбирается ровной;
10. Рассчитывается угол ϕ2 по формуле
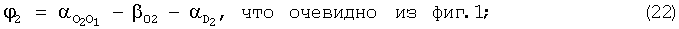
11. Рассчитывается угол ϕ3 по формуле
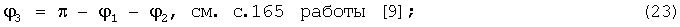
12. Рассчитывается расстояние до места разрыва 1 пули от ветрового ружья для стандартной высоты 200 м (величина сноса пули) по формуле
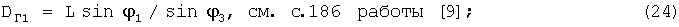
Далее производится 2-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 2-й ветровой пули DГ2, затем - 3-й и - дальность сноса 3-й ветровой пули DГ3.
Затем рассчитывается среднеарифметическое значение этих дальностей по формуле

Пусть D1=48,082 м (см. приложение 1). Далее из приложения 2 берется начальная дальность диапазона 40...50 м, т.е. DYH=40 м. Потом из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 40 м берется коэффициент kYH, равный 13,333, и затем из этого же приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 50 м берется коэффициент kYK, равный 12,5, которые подставляются в формулу
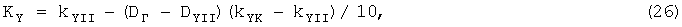
которая получена на основе уравнения прямой, что позволило автоматизировать процесс интерполяции при расчете скоростей среднего ветра для всех стандартных высот. Потом рассчитывается скорость среднего ветра для стандартной высоты 200 м по формуле

Аналогично рассчитываются скорости среднего ветра для остальных стандартных высот. Так скорости среднего ветра для стандартных высот 400, 800 и 1200 м вычисляются по формуле (27) с учетом - (26), где kYH=kYK=10, см. приложение 2. Скорости среднего ветра для стандартных высот 1600, 2000 и 2400 м вычисляются также по формуле (27) с учетом - (26), где kYH=10, a kYK=8,333, см. приложение 2. Скорости среднего ветра для стандартных высот 3000 и 4000 м вычисляются по формуле (27) с учетом - (26), где kYH=8, а kYK=8,333, см. приложение 2.
Текст программы расчета этих скоростей ветра при северо-западном, западном и юго-западном направлениях наземного ветра в среде Mathcad 2001i с примером расчета одного варианта приведен в приложении 1.
Затем вычисляются дирекционные углы направлений среднего ветра для всех вышеназванных стандартных высот следующим образом. Вычисляется угол γ1 в радианах по формуле
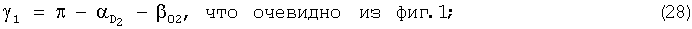
Потом вычисляется ДУ направления среднего ветра при 1-м выстреле для стандартной высоты 200 м в радианах по формуле

Затем вычисляется ДУ направления среднего ветра при 1-м выстреле для стандартной высоты 200 м в делениях угломера по формуле

Далее вычисляется ДУ направления среднего ветра при 2-м выстреле для стандартной высоты 200 м в радианах по формуле

Затем вычисляется ДУ направления среднего ветра при 2-м выстреле для стандартной высоты 200 м в делениях угломера по формуле

Потом вычисляется ДУ направления среднего ветра при 3-м выстреле для стандартной высоты 200 м в радианах по формуле

Затем вычисляется ДУ направления среднего ветра при 3-м выстреле для стандартной высоты 200 м в делениях угломера по формуле

Далее вычисляется среднеарифметическое значение ДУ направления среднего ветра для 3-х выстрелов для стандартной высоты 200 м в делениях угломера по формуле

Это значение в делениях угломера принимается за ДУ направления среднего ветра для стандартной высоты 200 м, т.е. αW200У.
Затем вычисляется ДУ направления среднего ветра в делениях угломера для стандартной высоты 400 м по формуле:
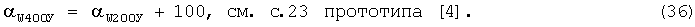
Потом вычисляется ДУ направления среднего ветра в делениях угломера для стандартной высоты 800 и 1200 м по формуле:
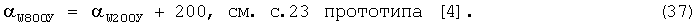
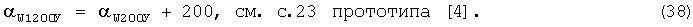
Затем вычисляется ДУ направления среднего ветра для стандартных высот 1600, 2000 и 2400 м по формулам:
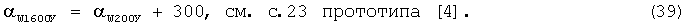
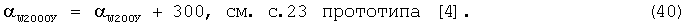
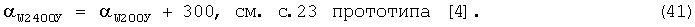
Потом вычисляется ДУ направления среднего ветра для стандартных высот 3000 и 4000 м по формулам:
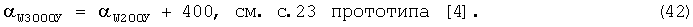

Приложение 2 получено на основе приложения 1, имеющегося в прототипе (см. с.23 [4]), путем деления дальностей сноса ветровых пуль на скорости среднего ветра. Это позволило на основе уравнения прямой получить интерполяционную формулу в общем виде, которая приведена в приложениях 1, 3...9, позволяющую автоматизировать процесс интерполяции при дробных значениях дальностей сноса ветровых пуль.
Текст программы расчета ДУ направлений среднего ветра для всех стандартных высот при северо-западном, западном и юго-западном наземном ветре в среде Mathcad 2001i с примером расчета одного варианта приведен в приложении 3.
Методики расчета скоростей и ДУ направлений среднего ветра для всех стандартных высот при остальных направлениях наземного ветра приведены в приложениях 4...9, которые отличаются от рассмотренной некоторыми формулами (они имеются в этих приложениях), корректность которых проверялась расчетами. Так, применительно к фиг.1 при этих расчетах увеличивалась скорость наземного ветра с 5 до 20 м/с. Из этой фигуры видно, что в этом случае увеличивается дальность сноса ветровых пуль, уменьшается исправленный звукометрический угол 1 АБ, а исправленный звукометрический угол 2 АБ остается неизменным, что и подтверждалось расчетами. Так были проверены все формулы и для остальных фигур. Формулы, содержащие параметры АБ, очевидны из фиг.1...4, что можно доказать.
Предлагаемый способ технически реализуем. Так, ветровое ружье ВР-2 можно легко модернизировать, подав на его корпус, например, минус источника постоянного тока, а вместо бойка затвора разместить провод с высокой электроизоляцией, подключенный к выходному контакту кнопки устройства управления, перископическая артиллерийская буссоль ПАБ-2А, ДМК-2 и ветромер имеются в штате метеорологического поста артиллерийских дивизионов армии РФ, см. с.5, 8, 9 прототипа [4]. Звукоприемники (приборы ПР-2) и акустические пеленгаторы (системы С-1) также имеются в армии РФ [10], а разрывную пулю можно разработать. В качестве ЭВМ можно использовать, например, Pentium IV 1700 MHz / 512 Mb DDR / 60 Gb HDD 7200 rpm. Запуск счетчиков времени ЗП №1...№3 и запрет обработки сигналов, образующихся при выстрелах из ветрового ружья можно обеспечить устройством управления, которое должно включать в себя аккумулятор, одновибратор (ждущий мультивибратор), инвертор и кнопку для подачи импульса напряжения на капсюль - воспламенитель зондировачного патрона ветрового ружья. Эти устройства выпускаются нашей промышленностью.
Список использованных источников
1. Радиолокационная метеорологическая станция РМС-1. Техническое описание. - БМ, 1960, - 259 с.
2. Радиолокационная станция ветрового зондирования атмосферы РВЗ-1 «Проба». Техническое описание. БМ, 1965.
3. Авторское свидетельство на изобретение №245909. Способ измерения скорости и направления ветра. / Теплухин В.А., Шмелев В.В. /. Приоритет изобретения 18.12.85 г.
4. Указания по работе метеорологического поста артиллерийского дивизиона. - М.: Воениздат МО СССР, 1975. - 32 с. Прототип.
5. Перископическая артиллерийская буссоль ПАБ 2А. Техническое описание и инструкция по эксплуатации, - БМ, 1988. - 39 с.
6. Ветровое ружье ВР-2. Техническое описание и инструкция по эксплуатации. - БМ, 1980. - 35 с.
7. Сергеев В.В. Основания устройства и элементы проектирования звукометрической аппаратуры. - Пенза: ПВАИУ, 1964. - 143 с.
8. Таланов А.В. Артиллерийская звуковая разведка. - М.: Воениздат министерства обороны Союза ССР, 1957. - 358 с.
9. Бронштейн И.Н., Семендяев К.А. Справочник по математике. - М.: Наука, 1964. - 608 с.
10. Система С-1. Альбом электрических принципиальных схем. - БМ, 1980.
Приложение 1. Текст программы автоматического расчета скоростей среднего ветра при северо-западном, западном и юго-западном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта.
Вариант расчета исходных данных при северо-западном направлении ветра в приземном слое атмосферы применительно к фиг.1.
Пусть температура воздуха в приземном слое атмосферы равна 5°С. Т.е.
t:=5°C.
Пусть скорости ветра в м/с в приземном слое атмосферы при 10 измерениях соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы в м/с при 10 измерениях будет равно
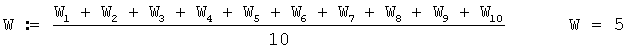
Пусть дирекционные углы (ДУ) ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=5141; α2WУ:=5161; α3WУ:=5450; α4WУ:=5632; α5WУ:=4812; α6WУ:=4711; α7WУ:=6731; α8WУ:=5532; α9WУ:=4811; α10WУ:=5351.
Тогда среднеарифметическое значение ДУ ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях будет равно
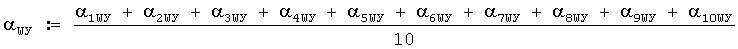
αWУ=5.333×103
Среднеарифметическое значение ДУ ветра в приземном слое атмосферы в радианах при 10 измерениях будет равно

Пусть угол α1 равен 4-00 делений угломера, т.е.
α1У:=400 малых делений угломера
Тогда значение этого угла в радианах будет равно

Пусть угол α2 равен 2-50 делений угломера, т.е.
α2У:=250 малых делений угломера
Тогда значение этого угла в радианах будет равно
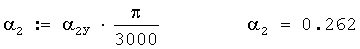
ДУ директрисы 2 акустической базы в радианах вычисляется по формуле
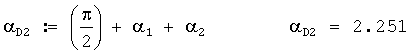
Пусть время прихода сигнала к 1-му звукоприемнику 1 акустической базы составляет
t1:=0.188 с.
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2:=0.158 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.218 с.
ДУ директрисы 1 акустической базы в радианах вычисляется по формуле
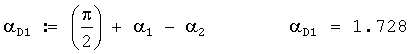
ДУ направления: средина 1 акустической базы - средина 2 акустической базы в радианах вычисляется по формуле
αO1O2:=α1 αO1O2=0.419
Пусть 1 и 2 акустические базы равны 50 м, т.е.
l:=50 м
Угол при вершине равнобедренного треугольника О1З2О2 в радианах вычисляется по формуле
αB:=π-2·α2 αB=2.618.
Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с определится по формуле
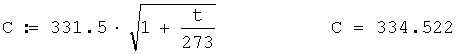
ДУ направления: средина 2 акустической базы - средина 1 акустической базы в радианах вычисляется по формуле
αO2O1:=α1+π αO2O1=3.56.
Геометрическая база в метрах вычисляется по формуле

Время запаздывания акустического сигнала 1 АБ в секундах вычисляется по формуле
τ1:=(t2-t1) τ1=0.06.
Звукометрический угол 1 АБ в радианах вычисляется по формуле
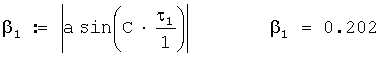
Общая поправка на ветер в звукометрический угол 1 АБ в радианах вычисляется по формуле
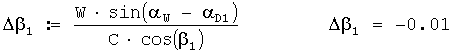
Исправленный звукометрический угол 1 АБ в радианах вычисляется по формуле
β01:=β1+Δβ1; β01=0.192.
Угол φ1 косоугольного треугольника в радианах вычисляется по формуле
φ1:=(αD1-αO1O2-β01); φ1=1.117.
Время запаздывания акустического сигнала 2 АБ в секундах вычисляется по формуле
τ2:=(t3-t2); τ2=0.06.
Звукометрический угол 2 АБ в радианах вычисляется по формуле
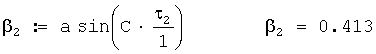
Общая поправка на ветер в звукометрический угол 2 АБ в радианах вычисляется по формуле
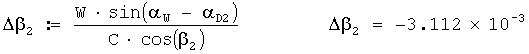
Исправленный звукометрический угол 2 АБ в радианах вычисляется по формуле
β02:=(β2+Δβ2); β02=0.41.
Угол φ2 косоугольного треугольника в радианах вычисляется по формуле
φ2:=(αO2O1-αD2-β02); φ2=0.899.
Угол φ3 косоугольного треугольника в радианах вычисляется по формуле
φ3:=(π-φ1-φ2); φ3=1.126.
Дальность сноса ветровых пуль в метрах при первом выстреле вычисляется по формуле

Далее производится 2-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 2-й ветровой пули. Пусть среднеарифметическое значение ДУ ветра в приземном слое атмосферы стало равным 52-33 делений угломера, а остальные параметры не изменились. Тогда дальность сноса ветровой пули составит 47,996 м. Т.е.
DГ2:=47.996.
Далее производится 3-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 3-й ветровой пули. Пусть среднеарифметическое значение ДУ ветра в приземном слое атмосферы стало равным 54-33 делений угломера, а остальные параметры не изменились. Тогда дальность сноса ветровой пули составит 48,155 м. Т.е.
DГ3:=48.155.
Затем определяется среднеарифметическое значение этих 3 рассчитанных дальностей сноса ветровых пуль.
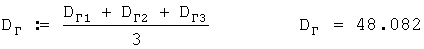
Затем определяется скорость среднего ветра для стандартной высоты 200 м.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 40 м берется коэффициент, равный 13,333, т.е.
kYH:=13.333.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 50 м берется коэффициент, равный 12,5, т.е.
kYK:=12.5.
Из приложения 2 берется начальная дальность диапазона, т.е.
DYH:=40, и рассчитывается скорость среднего ветра для стандартной высоты 200 м так
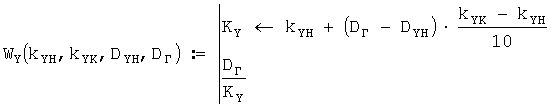
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(40)=3.798 м/с.
Аналогично рассчитываются скорости среднего ветра для остальных стандартных высот. Скорости среднего ветра для стандартных высот 400, 800 и 1200 м вычисляются по формуле
kYH:=10; kYK:=10; DYH:=40
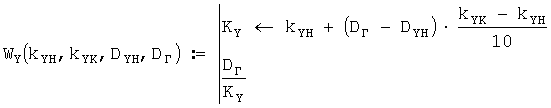
WY(DYH):=WY(kYH,kYK,DYH,DГ) ; WY(40)=4.808 м/с.
Скорости среднего ветра для стандартных высот 1600, 2000 и 2400 м вычисляются по формуле
kYH:=10; kYK:=8.333; DYH:=40
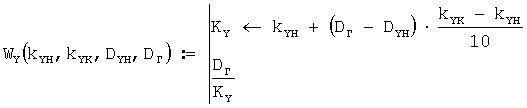
WY(DYH):=WY(kYH,kYK,DYH,DГ) ; WY(40)=5.557 м/с.
Скорости среднего ветра для стандартных высот 3000 и 4000 м вычисляются по формуле
kYH:=8; kYK:=8.333; DYH:=40
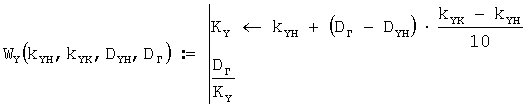
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(40)=5.815 м/с.
Приложение 2, Коэффициенты КY для определения скорости среднего ветра WY (м/сек) и приращения направления среднего ветра 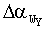 (дел. угл) в зависимости от дальности сноса ветровых пуль DГ с параметрами, идентичными параметрам пуль, выстреливаемых зондировочными патронами ЗП-2 и НЗП.
(дел. угл) в зависимости от дальности сноса ветровых пуль DГ с параметрами, идентичными параметрам пуль, выстреливаемых зондировочными патронами ЗП-2 и НЗП.
 увеличивают на
увеличивают на 
Приложение 3. Текст программы автоматического расчета дирекционного угла среднего ветра в нижних слоях атмосферы при северо-западном, западном и юго-западном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта
Вариант расчета исходных данных при северо-западном направлении ветра в приземном слое атмосферы.
Пусть температура воздуха в приземном слое атмосферы равна 5°С. Т.е.
t:=5°C.
Пусть скорости ветра в приземном слое атмосферы при 10 измерениях в м/с соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы при 10 измерениях в м/с будет равно
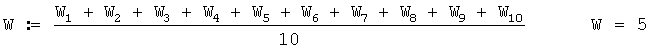
Пусть дирекционные углы ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=5141; α2WУ:=5161; α3WУ:=5450; α4WУ:=5632; α5WУ:=4812; α6WУ:=4711; α7WУ:=6731; α8WУ:=5532; α9WУ:=4811; α10WУ:=5351.
Тогда среднеарифметическое значение дирекционного угла ветра в приземном слое атмосферы при 10 измерениях в малых делениях угломера будет равно
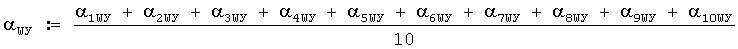
αWУ=5.333×103
Среднеарифметическое значение дирекционного угла ветра в приземном слое атмосферы при 10 измерениях в радианах будет равно

Пусть угол α1 равен 4-00 делений угломера, т.е.
α1У:=400 малых делений угломера.
Тогда значение этого угла в радианах будет равно

Пусть угол α2 равен 2-50 делений угломера, т.е.
α2У:=250 малых делений угломера
Тогда значение этого угла в радианах будет равно
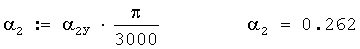
Дирекционный угол директрисы 2 акустической базы в радианах вычисляется по формуле
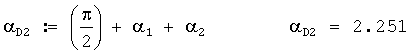
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2=0.158 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.218 с.
Пусть 1 и 2 акустические базы равны 50 м т.е. l:=50 м.
Скорость звука в атмосфере без учета влияния ветра определяется таким аналитическим выражением:
Тогда С=334.522 м/с 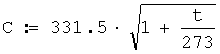
Время запаздывания акустического сигнала 2 акустической базы в секунда вычисляется по формуле
τ2:=(t3-t2); τ2=0.06.
Звукометрический угол 2 акустической базы в радианах вычисляется по формуле
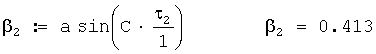
Общая поправка на ветер в звукометрический угол 2 акустической базы в радианах вычисляется по формуле
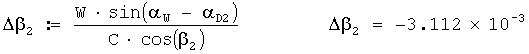
Исправленный звукометрический угол 2 акустической базы в радианах вычисляется по формуле
β02=(β2+Δβ2) β02=0.41.
Угол γ1 в радианах вычисляется по формуле
γ1=(π-αD2-β02) γ1=0.48.
Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в радианах вычисляется по формуле
α1WY:=2·π-γ1; α1WY=5.803.
Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в делениях угломера вычисляется по формуле

Далее производится 2-й выстрел из ветрового ружья, когда, например, среднеарифметическое значение дирекционный угол ветра в приземном слое атмосферы стало равным 50-00 делений угломера, а остальные параметры не изменились. Тогда дирекционный угол среднего ветра при 2-м выстреле для стандартной высоты 200 м в делениях угломера составит
α2WYУ:=5547.
Далее производится 3-й выстрел из ветрового ружья, когда, например, среднеарифметическое значение дирекционный угол ветра в приземном слое атмосферы стало равным 60-00 делений угломера, а остальные параметры не изменились. Тогда дирекционный угол среднего ветра при 3-м выстреле для стандартной высоты 200 м в делениях угломера составит
α3WYУ:=5532.
Потом вычисляется среднеарифметическое значение дирекционного угла среднего ветра для 3-х выстрелов для стандартной высоты 200 м в делениях угломера по формуле
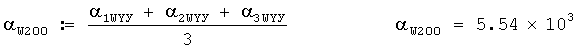
Это значение в делениях угломера принимается за дирекционный угол среднего ветра для стандартной высоты 200 м.
Затем вычисляется дирекционный угол среднего ветра для стандартной высоты 400 м по формуле
αW400:=αW200+100; αW400=5.64×103.
Затем вычисляется дирекционный угол среднего ветра для стандартных высот 800 и 1200 м по формулам
αW800:=αW200+200; αW800=5.74×103;
αW1200:=αW200+200; αW1200=5.74×103.
Затем вычисляется дирекционный угол среднего ветра для стандартных высот 1600, 2000 и 2400 м по формулам
αW1600:=αW200+300; αW1600=5.84×103;
αW2000:=αW200+300; αW2000=5.84×103;
αW2400:=αW200+300; αW2400=5.84×103.
Затем вычисляется дирекционный угол среднего ветра для стандартных высот 3000 и 4000 м по формулам
αW3000:=αW200+400 αW3000=5.94×103;
αW4000:=αW200+400 αW4000=5.94×103.
Приложение 4. Текст программы автоматического расчета скоростей среднего ветра при юго-восточном, восточном и северо-восточном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта.
Вариант расчета исходных данных при юго-восточном направлении ветра в приземном слое атмосферы применительно к фиг.2.
Пусть температура воздуха в приземном слое атмосферы равна 5°С. Т.е.
t:=5°C.
Пусть скорости ветра в м/с в приземном слое атмосферы при 10 измерениях соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы в м/с при 10 измерениях будет равно
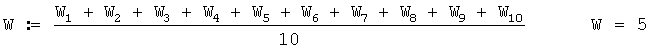
Пусть дирекционные углы (ДУ) ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=1610; α2WУ:=1602; α3WУ:=1600; α4WУ:=1610; α5WУ:=1612; α6WУ:=1611; α7WУ:=1631; α8WУ:=1640; α9WУ:=1718; α10WУ:=1538.
Тогда среднеарифметическое значение ДУ ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях будет равно
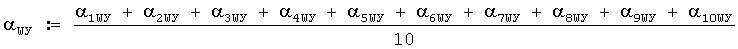
αWУ=1.617×103.
Среднеарифметическое значение ДУ ветра в приземном слое атмосферы в радианах при 10 измерениях будет равно

Пусть угол α3 равен 2-00 делений угломера, т.е.
α3У=200 малых делений угломера
Тогда значение этого угла в радианах будет равно
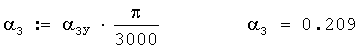
Пусть угол α4 равен 1-00 делений угломера, т.е.
α4У=100 малых делений угломера.
Тогда значение этого угла в радианах будет равно

ДУ директрисы 2 акустической базы в радианах вычисляется по формуле
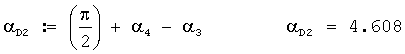
Пусть время прихода сигнала к 1-му звукоприемнику 1 акустической базы составляет
t1:=0.266 с.
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2:=0.215 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.258 с.
ДУ директрисы 1 акустической базы в радианах вычисляется по формуле
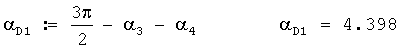
ДУ направления: средина 1 акустической базы - средина 2 акустической базы в радианах вычисляется по формуле
αО1О2:=π-α3; αО1О2=2.932.
Пусть 1 и 2 акустические базы равны 50 м т.е.
l:=50 м.
Угол при вершине равнобедренного треугольника О1З2О2 в радианах вычисляется по формуле
αВ:=π-2·α4; αВ=2.932.
Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с определится по формуле
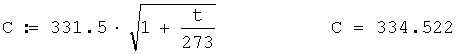
ДУ направления: средина 2 акустической базы - средина 1 акустической базы в радианах вычисляется по формуле
αО2О1:=αО1О2+π; αО2О1=6.074.
Геометрическая база в метрах вычисляется по формуле

Время запаздывания акустического сигнала 1 АБ в секундах вычисляется по формуле
τ1:=(t2-t1); τ1=-0.051.
Звукометрический угол 1 АБ в радианах вычисляется по формуле
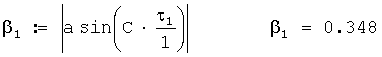
Общая поправка на ветер в звукометрический угол 1 АБ в радианах вычисляется по формуле
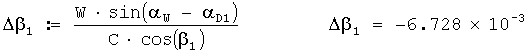
Исправленный звукометрический угол 1 АБ в радианах вычисляется по формуле
β01:=β1+Δβ1; β01=0.341.
Угол φ1 косоугольного треугольника O1З2O2 в радианах вычисляется по формуле
φ1:=(αD1-αO1O2-β01); φ1=1.125.
Время запаздывания акустического сигнала 2 АБ в секундах вычисляется по формуле
τ2:=(t3-t2); τ2=0.043.
Звукометрический угол 2 АБ в радианах вычисляется по формуле
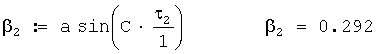
Общая поправка на ветер в звукометрический угол 2 АБ в радианах вычисляется по формуле
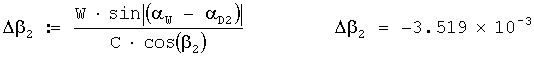
Исправленный звукометрический угол 2 АБ в радианах вычисляется по формуле
β02:=(β2+Δβ2); β02=0.295.
Угол φ2 косоугольного треугольника O1З2O2 в радианах вычисляется по формуле
φ2:=(αO2O1-αD2-β02); φ2=1.171.
Угол φ3 косоугольного треугольника O1З2O2 в радианах вычисляется по формуле
φ3:=(π-φ1-φ2); φ3=0.846.
Дальность сноса ветровых пуль в метрах при первом выстреле вычисляется по формуле
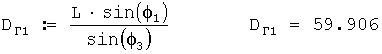
Далее производится 2-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 2-й ветровой пули. Пусть дальность сноса ветровой пули составит 60,032 м. Т.е.
DГ2:=60.032.
Далее производится 3-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 3-й ветровой пули. Пусть дальность сноса ветровой пули составит 60,656, т.е.
DГ3:=60.656.
Затем определяется среднеарифметическое значение этих 3 рассчитанных дальностей сноса ветровых пуль.
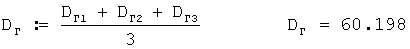
Затем определяется скорость среднего ветра для стандартной высоты 200 м.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 60 м берется коэффициент, равный 12, т.е.
kYH:=12.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 70 м берется коэффициент, равный 11,667 т.е.
kYK:=11.667.
Из приложения 2 берется начальная дальность 60 из диапазона 60...70 м и рассчитывается скорость среднего ветра для стандартной высоты 200 м так
DYH:=60
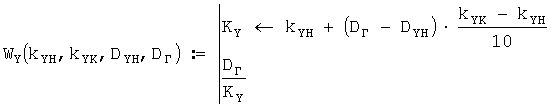
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(60)=5.019 м/с.
Аналогично рассчитываются скорости среднего ветра для остальных стандартных высот. Скорости среднего ветра для стандартных высот 400 и 800 м вычисляются по формуле
kYH:=10 ;kYK:=10
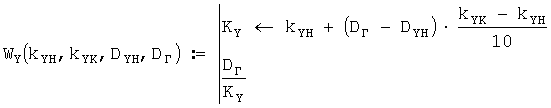
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(60)=6.02 м/с.
Скорости среднего ветра для стандартных высот 1200, 1600 и 2000 м вычисляются по формуле
kYH:=8.571; kYK:=8.75
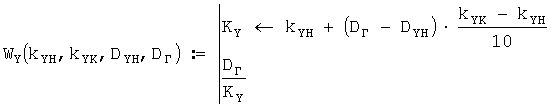
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(60)=7.021 м/с.
Скорости среднего ветра для стандартных высот 2400, 3000 и 4000 м вычисляются по формуле
kYH:=7.5; kYK:=7.778
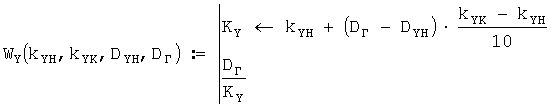
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(60)=8.021 м/с.
Приложение 5. Текст программы автоматического расчета дирекционного угла среднего ветра в нижних слоях атмосферы при юго-восточном, восточном и северо-восточном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта
Вариант расчета исходных данных при юго-восточном направлении ветра в приземном слое атмосферы применительно к фиг.2.
Пусть температура воздуха в приземном слое атмосферы равна 5°С. Т.е.
t=5°C.
Пусть скорости ветра в м/с в приземном слое атмосферы при 10 измерениях соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы в м/с при 10 измерениях будет равно
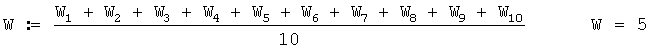
Пусть дирекционные углы (ДУ) ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=1610; α2WУ:=1602; α3WУ:=1600; α4WУ:=1610; α5WУ:=1612; α6WУ:=1611; α7WУ:=1631; α8WУ:=1640; α9WУ:=1718; α10WУ:=1538.
Тогда среднеарифметическое значение ДУ ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях будет равно
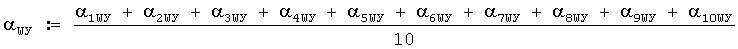
αWУ=1.617×103.
Среднеарифметическое значение ДУ ветра в приземном слое атмосферы в радианах при 10 измерениях будет равно

Пусть угол α3 равен 2-00 делений угломера, т.е.
α3У=200 малых делений угломера.
Тогда значение этого угла в радианах будет равно

Пусть угол α4 равен 1-00 делений угломера, т.е.
α4У=100 малых делений угломера.
Тогда значение этого угла в радианах будет равно

ДУ директрисы 2 акустической базы в радианах вычисляется по формуле
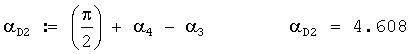
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2:=0.215 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.258 с.
Пусть 1 и 2 акустические базы равны 50 м, т.е.
l=50 м.
Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с определится по формуле
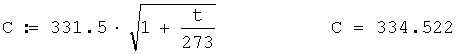
Время запаздывания акустического сигнала 2 АБ в секундах вычисляется по формуле
τ2:=(t3-t2); τ2=0.043.
Звукометрический угол 2 АБ в радианах вычисляется по формуле
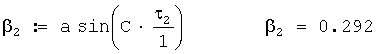
Общая поправка на ветер в звукометрический угол 2 АБ в радианах вычисляется по формуле
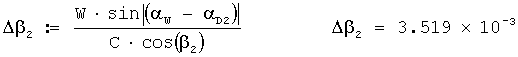
Исправленный звукометрический угол 2 АБ в радианах вычисляется по формуле
β02:=(β2+Δβ2); β02=0.295.
Вычисляется угол γ2 в радианах по формуле
γ2:=2·π-αD2; β02 γ2=1.38.
Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в радианах вычисляется по формуле
α1WY:=π-γ2; α1WY=1.761.
Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в делениях угломера вычисляется по формуле

Далее производится 2-й выстрел из ветрового ружья, когда, например, дирекционный угол среднего ветра в этом случае для стандартной высоты 200 м в делениях угломера составит
α2WYУ:=1600.
Потом производится 3-й выстрел из ветрового ружья, когда, например, дирекционный угол среднего ветра в этом случае для стандартной высоты 200 м в делениях угломера составит
α3WYУ:=1700.
Затем вычисляется среднеарифметическое значение дирекционного угла среднего ветра для 3-х выстрелов для стандартной высоты 200 м в делениях угломера по формуле
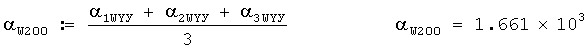
Это значение в делениях угломера принимается за дирекционный угол среднего ветра для стандартной высоты 200 м.
Затем вычисляется дирекционный угол среднего ветра в делениях угломера для стандартной высоты 400 м по формуле
αW400:=αW200+100; αW400=1.761×103.
Потом вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 800 и 1200 м по формулам
αW800:=αW200+200; αW800=1.861×103;
αW1200:=αW200+200; αW1200=1.861×103.
Затем вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 1600, 2000 и 2400 м по формулам
αW1600:=αW200+300; αW1600=1.961×103;
αW2000:=αW200+300; αW2000=1.961×103;
αW2400:=αW200+300; αW2400=1.961×103.
Потом вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 3000 и 4000 м по формулам
αW3000:=αW200+400; αW3000=2.061×103;
αW4000:=αW200+400; αW4000=2.061×103.
Приложение 6. Текст программы автоматического расчета скоростей среднего ветра при юго-западном, южном и юго-восточном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта.
Вариант расчета исходных данных при юго-западном направлении ветра в приземном слое атмосферы применительно к фиг.3.
Пусть температура воздуха в приземном слое атмосферы равна 5°С. Т.е.
t:=5°C.
Пусть скорости ветра в м/с в приземном слое атмосферы при 10 измерениях соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы в м/с при 10 измерениях будет равно
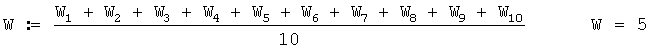
Пусть дирекционные углы (ДУ) ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=3790; α2WУ:=3761; α3WУ:=3790; α4WУ:=3750; α5WУ:=3760; α6WУ:=3720; α7WУ:=3731; α8WУ:=3732; α9WУ:=3711; α10WУ:=3751.
Тогда среднеарифметическое значение ДУ ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях будет равно
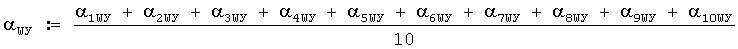
αWУ=3.75×103.
Среднеарифметическое значение ДУ ветра в приземном слое атмосферы в радианах при 10 измерениях будет равно

Пусть угол α5 равен 4-00 делений угломера, т.е.
α5У:=400 малых делений угломера.
Тогда значение этого угла в радианах будет равно

Пусть угол α6 равен 2-00 делений угломера, т.е.
α6У:=200 малых делений угломера.
Тогда значение этого угла в радианах будет равно
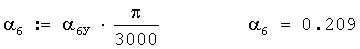
ДУ директрисы 2 акустической базы в радианах вычисляется по формуле
αD2:=α5+α6; αD2=0.628.
Пусть время прихода сигнала к 1-му звукоприемнику 1 акустической базы составляет
t1:=0.254 с.
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2:=0.203 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.224 с.
ДУ директрисы 1 акустической базы в радианах вычисляется по формуле
αD1:=α5-α6; αD1=0.209.
ДУ направления: средина 2 акустической базы - средина 1 акустической базы в радианах вычисляется по формуле

Пусть 1 и 2 акустические базы равны 50 м т.е.
l:=50 м.
Угол при вершине равнобедренного треугольника О1З2О2 в радианах вычисляется по формуле
αВ:=π-2·α6; αВ=2.723.
Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с определится по формуле
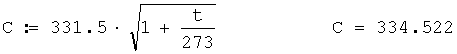
ДУ направления: средина 1 акустической базы - средина 2 акустической базы в радианах вычисляется по формуле
αО2О1:=αО1О2+π; αО2О1=5.131.
Геометрическая база в метрах вычисляется по формуле

Время запаздывания акустического сигнала 1 АБ в секундах вычисляется по формуле
τ1:=(t2-t1); τ1=-0.051.
Звукометрический угол 1 АБ в радианах вычисляется по формуле
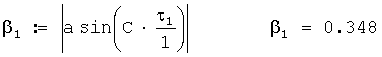
Общая поправка на ветер в звукометрический угол 1 АБ в радианах вычисляется по формуле
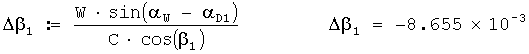
Исправленный звукометрический угол 1 АБ в радианах вычисляется по формуле
β01:=β1+Δβ1; β01=0.34.
Угол φ1 косоугольного треугольника О1З2О2 в радианах вычисляется по формуле
φ1:=(αD1-αO1O2-β01)+2·π φ1=1.022.
Время запаздывания акустического сигнала 2 АБ в секундах вычисляется по формуле
τ2:=(t3-t2); τ2=0.021.
Звукометрический угол 2 АБ в радианах вычисляется по формуле

Общая поправка на ветер в звукометрический угол 2 АБ в радианах вычисляется по формуле
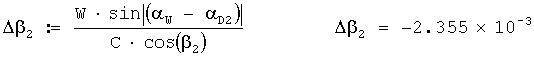
Исправленный звукометрический угол 2 АБ в радианах вычисляется по формуле
β02:=(β2+Δβ2); β02=0.139.
Угол φ2 косоугольного треугольника О1З2О2 в радианах вычисляется по формуле
φ2:=(αO2O1-αD2-β02); φ2=1.223.
Угол φ3 косоугольного треугольника О1З2О2 в радианах вычисляется по формуле
φ3:=(π-φ1-φ2); φ3=0.897.
Дальность сноса ветровых пуль в метрах при первом выстреле вычисляется по формуле
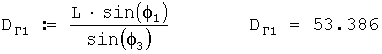
Далее производится 2-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 2-й ветровой пули.
Пусть дальность сноса ветровой пули составит 49,5 м. Т.е.
DГ2:=49.5.
Далее производится 3-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 3-й ветровой пули.
Пусть дальность сноса ветровой пули составит 48,155 м. Т.е.
DГ3:=48.155.
Затем определяется среднеарифметическое значение этих 3 рассчитанных дальностей сноса ветровых пуль.
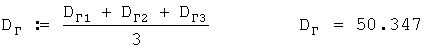
Потом определяется скорость среднего ветра для стандартной высоты 200 м.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 50 м берется коэффициент, равный 12,5, т.е.
kYH:=12.5.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 60 м берется коэффициент, равный 12, т.е.
kYK:=12.
Из приложения 2 берется начальная дальность диапазона 50...60 м, т.е. DYH=50, и рассчитывается скорость среднего ветра для стандартной высоты 200 м по формуле
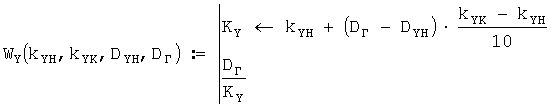
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(50)=4.033 м/с.
Аналогично рассчитываются скорости среднего ветра для остальных стандартных высот. Скорости среднего ветра для стандартных высот 400 и 800 м вычисляются по формуле
kYH:=10; kYK:=10
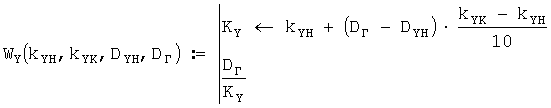
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(50)=5.035 м/с.
Скорость среднего ветра для стандартной высоты 1200 м вычисляется по формуле
kYH:=10; kYK:=8.571
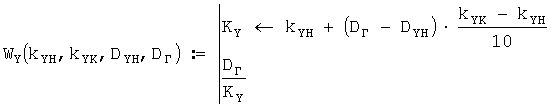
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(50)=5.06 м/с.
Скорости среднего ветра для стандартных высот 1600 и 2000 м вычисляются по формуле
kYH:=8.333; kYK:=8.571
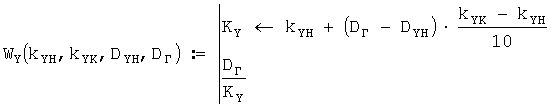
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(50)=6.036 м/с.
Скорости среднего ветра для стандартных высот 2400, 3000 и 4000 м вычисляются по формуле
kYH:=8.333; kYK:=7.5
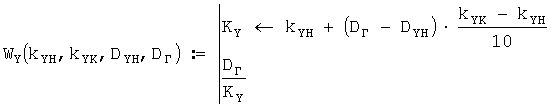
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(50)=6.063 м/с.
Приложение 7. Текст программы автоматического расчета дирекционного угла среднего ветра в нижних слоях атмосферы при юго-западном, южном и юго-восточном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта
Вариант расчета исходных данных при юго-западном направлении ветра в приземном слое атмосферы применительно к фиг.3.
Пусть температура воздуха в приземном слое атмосферы равна 5°С. Т.е.
t:=5°C.
Пусть скорости ветра в м/с в приземном слое атмосферы при 10 измерениях соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы в м/с при 10 измерениях будет равно
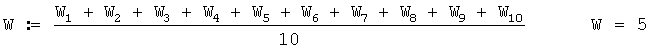
Пусть дирекционные углы (ДУ) ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=3790; α2WУ:=3761; α3WУ:=3790; α4WУ:=3750; α5WУ:=3760; α6WУ:=3720; α7WУ:=3731; α8WУ:=3732; α9WУ:=3711; α10WУ:=3751.
Тогда среднеарифметическое значение ДУ ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях будет равно
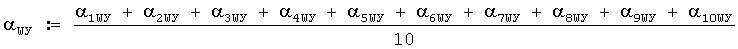
αWУ=3.75×103.
Среднеарифметическое значение ДУ ветра в приземном слое атмосферы в радианах при 10 измерениях будет равно

Пусть угол α5 равен 4-00 делений угломера, т.е.
α5У:=400 малых делений угломера.
Тогда значение этого угла в радианах будет равно

Пусть угол α6 равен 2-00 делений угломера, т.е.
α6У:=200 малых делений угломера.
Тогда значение этого угла в радианах будет равно
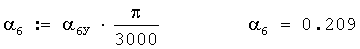
ДУ директрисы 2 акустической базы в. радианах вычисляется по формуле
αD2:=α5+α6; αD2=0.628.
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2:=0.203 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.224 с.
Пусть 1 и 2 акустические базы равны 50 м, т.е.
l:=50 м.
Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с определится по формуле
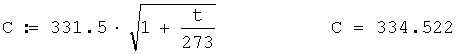
Время запаздывания акустического сигнала 2 АБ в секундах вычисляется по формуле
τ2:=(t3-t2); τ2=0.021.
Звукометрический угол 2 АБ в радианах вычисляется по формуле
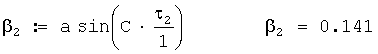
Общая поправка на ветер в звукометрический угол 2 АБ в радианах вычисляется по формуле
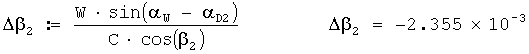
Исправленный звукометрический угол 2 АБ в радианах вычисляется по формуле
β02:=(β2+Δβ2); β02=0.139.
Вычисляется угол γ3 в радианах по формуле
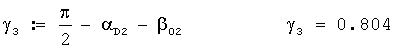
Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в радианах вычисляется по формуле

Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в малых делениях угломера вычисляется по формуле

Далее производится 2-й выстрел из ветрового ружья, когда, например, 3 дирекционный угол среднего ветра в этом случае для стандартной высоты 200 м в малых делениях угломера составит
α2WYУ:=3635.
Потом производится 3-й выстрел из ветрового ружья, когда, например, дирекционный угол среднего ветра в этом случае для стандартной высоты 200 м в малых делениях угломера составит
α3WYУ:=3725.
Затем вычисляется среднеарифметическое значение дирекционного угла среднего ветра для 3-х выстрелов для стандартной высоты 200 м в малых делениях угломера по формуле
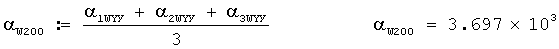
Это значение 36-97 в делениях угломера принимается за дирекционный угол среднего ветра для стандартной высоты 200 м.
Затем вычисляется дирекционный угол среднего ветра в делениях угломера для стандартной высоты 400 м по формуле
αW400:=αW200+100; αW400=3.797×103.
Потом вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 800 и 1200 м по формулам
αW800:=αW200+200; αW800=3.897×103;
αW1200:=αW200+200; αW1200=3.897×103.
Затем вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 1600, 2000 и 2400 м по формулам
αW1600:=αW200+300; αW1600=3.997×103;
αW2000:=αW200+300; αW2000=3.997×103;
αW2400:=αW200+300; αW2400=3.997×103.
Потом вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 3000 и 4000 м по формулам
αW3000:=αW200+400; αW3000=4.097×103;
αW4000:=αW200+400; αW4000=4.097×103.
Приложение 8. Текст программы автоматического расчета скоростей среднего ветра при северо-западном, северном и северо-восточном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта.
Вариант расчета исходных данных при северо-восточном направлении ветра в приземном слое атмосферы применительно к фиг.4.
Пусть температура воздуха в приземном слое атмосферы равна 5°С. Т.е.
t:=5°C.
Пусть скорости ветра в м/с в приземном слое атмосферы при 10 измерения соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы в м/с при 10 измерениях будет равно
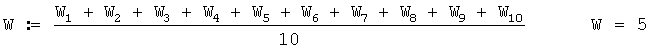
Пусть дирекционные углы (ДУ) ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=350; α2WУ:=340; α3WУ:=370; α4WУ:=375; α5WУ:=376; α6WУ:=362; α7WУ:=341; α8WУ:=325; α9WУ:=340; α10WУ:=321.
Тогда среднеарифметическое значение ДУ ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях будет равно
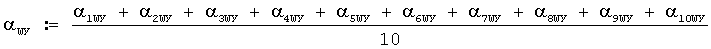
αWУ=350
Среднеарифметическое значение ДУ ветра в приземном слое атмосферы в радианах при 10 измерениях будет равно

Пусть угол α7 равен 1-00 делений угломера, т.е.
α7У:=100 малых делений угломера
Тогда значение этого угла в радианах будет равно
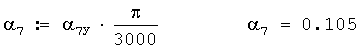
Пусть угол α8 равен 2-00 делений угломера, т.е.
α8У:=200 малых делений угломера.
Тогда значение этого угла в радианах будет равно

ДУ директрисы 2 акустической базы в радианах вычисляется по формуле
αD2:=π-α7+α8; αD2=3.246.
Пусть время прихода сигнала к 1-му звукоприемнику 1 акустической базы составляет
t1:=0.187 с.
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2:=0.152 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.218 с.
ДУ директрисы 1 акустической базы в радианах вычисляется по формуле
αD1:=π-α7-α8; αD1=2.827.
ДУ направления: средина 2 акустической базы - средина 1 акустической базы в радианах вычисляется по формуле
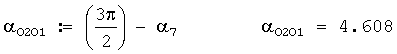
Пусть 1 и 2 акустические базы равны 50 м т.е.
l:=50 м.
Угол при вершине равнобедренного треугольника О1З2О2 в радианах вычисляется по формуле
αВ:=π-2·α8; αВ=2.723.
Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с определится по формуле
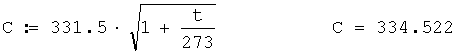
ДУ направления: средина 1 акустической базы - средина 2 акустической базы в радианах вычисляется по формуле
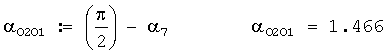
Геометрическая база в метрах вычисляется по формуле

Время запаздывания акустического сигнала 1 АБ в секундах вычисляется по формуле
τ1:=(t2-t1) τ1=-0.035
Звукометрический угол 1 АБ в радианах вычисляется по формуле
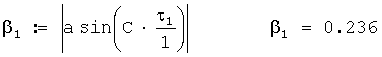
Общая поправка на ветер в звукометрический угол 1 АБ в радианах вычисляется по формуле

Исправленный звукометрический угол 1 АБ в радианах вычисляется по формуле
β01:=β1+Δβ1; β01=0.227.
Угол φ1 косоугольного треугольника О1З2О2 в радианах вычисляется по формуле
φ1:=(αD1-αO1O2-β01); φ1=1.135.
Время запаздывания акустического сигнала 2 АБ в секундах вычисляется по формуле
τ2:=(t3-t2); τ2=0.066.
Звукометрический угол 2 АБ в радианах вычисляется по формуле
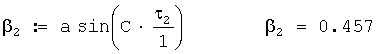
Общая поправка на ветер в звукометрический угол 2 АБ в радианах вычисляется по формуле
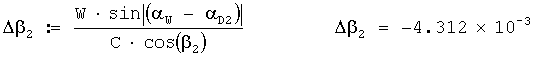
Исправленный звукометрический угол 2 АБ в радианах вычисляется по формуле
β02:=(β2+Δβ2); β02=0.453.
Угол φ2 косоугольного треугольника О1З2О2 в радианах вычисляется по формуле
φ2:=(αO2O1-αD2-β02); φ2=0.908.
Угол φ3 косоугольного треугольника О1З2О2 в радианах вычисляется по формуле,.
φ3:=(π-φ1-φ2); φ3=1.099.
Дальность сноса ветровых пуль в метрах при первом выстреле вычисляется по формуле
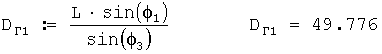
Далее производится 2-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 2-й ветровой пули.
Пусть дальность сноса ветровой пули составит 49,5 м. Т.е.
DГ2:=49.5.
Далее производится 3-й выстрел из ветрового ружья и автоматически определяется по данной программе дальность сноса 3-й ветровой пули.
Пусть дальность сноса ветровой пули составит 48,155 м. Т.е.
DГ3:=48.155.
Затем определяется среднеарифметическое значение этих 3 рассчитанных дальностей сноса ветровых пуль.
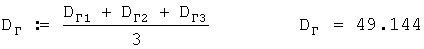
Потом определяется скорость среднего ветра для стандартной высоты 200 м.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 40 м берется коэффициент, равный 13,333 т.е.
kYH:=13.333.
Из приложения 2 на пересечении строки стандартной высоты 200 м и столбца дальности сноса ветровых пуль 50 м берется коэффициент, равный 12,5 т.е.
kYK:=12.5.
Из приложения 2 берется начальная дальность диапазона 40...50 м, т.е.
DYH:=40 и рассчитывается скорость среднего ветра для стандартной высоты 200 м по формуле
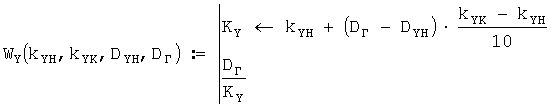
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(40)=3.909 м/с.
Аналогично рассчитываются скорости среднего ветра для остальных стандартных высот. Скорости среднего ветра для стандартных высот 400, 800 и 1200 м вычисляются по формуле
kYH:=10 kYK:=10
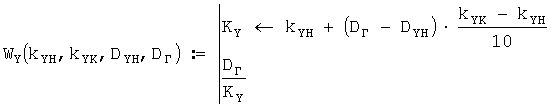
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(40)=4.914 м/с.
Скорости среднего ветра для стандартных высот 1600, 2000 и 2400 м вычисляются по формуле
kYH:=10; kYK:=8.333
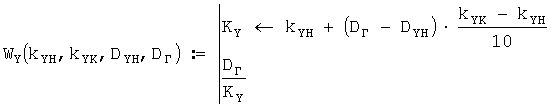
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(40)=5.798 м/с.
Скорости среднего ветра для стандартных высот 3000 и 4000 м вычисляют по формуле
kYH:=8; kYK:=8.333
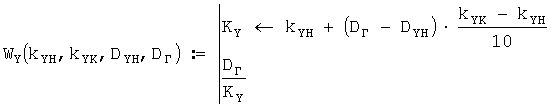
WY(DYH):=WY(kYH,kYK,DYH,DГ); WY(40)=5.918 м/с.
Приложение 9. Текст программы автоматического расчета дирекционного угла среднего ветра в нижних слоях атмосферы при северо-западном, северном и северо-восточном направлениях ветра в приземном слое атмосферы, разработанной в среде Mathcad 2001i, с примером расчета одного варианта
Вариант расчета данных при северо-восточном направлении ветра в приземном слое атмосферы применительно к фиг.4.
Пусть температура воздуха в приземном слое атмосферы равна 5°С, т.е.
t:=5°C.
Пусть скорости ветра в м/с в приземном слое атмосферы при 10 измерениях соответственно равны
W1:=3; W2:=3; W3:=4; W4:=4; W5:=5; W6:=5; W7:=6; W8:=10; W9:=6; W10:=4.
Тогда среднеарифметическое значение скорости ветра в приземном слое атмосферы в м/с при 10 измерениях будет равно
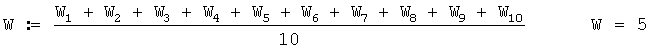
Пусть дирекционные углы (ДУ) ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях соответственно равны
α1WУ:=350; α2WУ:=340; α3WУ:=370; α4WУ:=375; α5WУ:=376; α6WУ:=362; α7WУ:=341; α8WУ:=325; α9WУ:=340; α10WУ:=321.
Тогда среднеарифметическое значение ДУ ветра в приземном слое атмосферы в малых делениях угломера при 10 измерениях будет равно
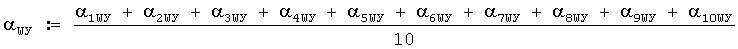
αWУ=350.
Среднеарифметическое значение ДУ ветра в приземном слое атмосферы в радианах при 10 измерениях будет равно

Пусть угол α7 равен 1-00 делений угломера, т.е.
α7У:=100 малых делений угломера
Тогда значение этого угла в радианах будет равно
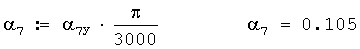
Пусть угол α8 равен 2-00 делений угломера, т.е.
α8У:=200 малых делений угломера.
Тогда значение этого угла в радианах будет равно

ДУ директрисы 2 акустической базы в радианах вычисляется по формуле (2)
αD2:=π-α7+α8; αD2=3.246.
Пусть время прихода сигнала к 1-му звукоприемнику 1 акустической базы составляет
t1:=0.187 с.
Пусть время прихода сигнала к 2-му звукоприемнику 1 и 2 акустических баз составляет
t2:=0.152 с.
Пусть время прихода сигнала к 3-му звукоприемнику 2 акустической базы составляет
t3:=0.218 с.
Пусть 1 и 2 акустические базы равны 50 м, т.е.
l:=50 м.
Скорость звука в приземном слое атмосферы без учета влияния ветра в м/с определится по формуле
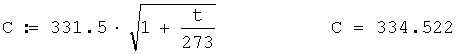
Время запаздывания акустического сигнала 2 АБ в секундах вычисляется по формуле
τ2:=(t3-t2); τ2=0.066.
Звукометрический угол 2 АБ в радианах вычисляется по формуле
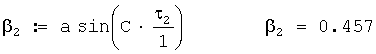
Общая поправка на ветер в звукометрический угол 2 АБ в радианах вычисляется по формуле
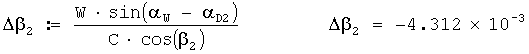
Исправленный звукометрический угол 2 АБ в радианах вычисляется по формуле
β02:=(β2+Δβ2); β02=0.453.
Вычисляется угол γ4 в радианах по формуле
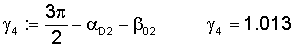
Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в радианах вычисляется по формуле

Дирекционный угол среднего ветра при 1-м выстреле для стандартной высоты 200 м в малых делениях угломера вычисляется по формуле

Далее производится 2-й выстрел из ветрового ружья, когда, например, дирекционный угол среднего ветра в этом случае для стандартной высоты 200 м в малых делениях угломера составит
α2WYУ:=635.383.
Потом производится 3-й выстрел из ветрового ружья, когда, например, дирекционный угол среднего ветра в этом случае для стандартной высоты 200 м в малых делениях угломера составит
α3WYУ:=722.
Затем вычисляется среднеарифметическое значение дирекционного угла среднего ветра для 3-х выстрелов для стандартной высоты 200 м в малых делениях угломера по формуле
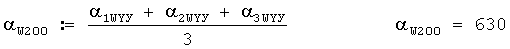
Это значение 6-30 в делениях угломера принимается за дирекционный угол среднего ветра для стандартной высоты 200 м.
Затем вычисляется дирекционный угол среднего ветра в делениях угломера для стандартной высоты 400 м по формуле
αW400:=αW200+100; αW400=730.
Потом вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 800 и 1200 м по формулам
αW800:=αW200+200; αW800=830;
αW1200:=αW200+200; αW1200=830.
Затем вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 1600, 2000 и 2400 м по формулам
αW1600:=αW200+300; αW1600=930;
αW2000:=αW200+300; αW2000=930;
αW2400:=αW200+300; αW2400=930.
Потом вычисляется дирекционный угол среднего ветра в делениях угломера для стандартных высот 3000 и 4000 м по формулам
αW3000:=αW200+400; αW3000=1.03×103;
αW4000:=αW200+400; αW4000=1.03×103.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ СКОРОСТИ И НАПРАВЛЕНИЯ ВЕТРА | 2006 |
|
RU2331904C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЕЛЕНГА ИСТОЧНИКА ЗВУКА | 2006 |
|
RU2323449C1 |
| АКУСТИЧЕСКИЙ ЛОКАТОР ИМПУЛЬСНЫХ ИСТОЧНИКОВ ЗВУКА | 2013 |
|
RU2529827C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЕЛЕНГА ИСТОЧНИКА ЗВУКА ПРИ РАЗМЕЩЕНИИ АКУСТИЧЕСКОЙ АНТЕННЫ АКУСТИЧЕСКОГО ЛОКАТОРА НА НАКЛОННЫХ ПЛОЩАДКАХ ПОВЕРХНОСТИ ЗЕМЛИ | 2014 |
|
RU2549919C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ИСТОЧНИКА ЗВУКА | 2004 |
|
RU2276383C2 |
| Способ определения отклонений реальных метеорологических условий от табличных, учитываемых при расчете установок для стрельбы артиллерии | 2019 |
|
RU2700709C1 |
| АКУСТИЧЕСКИЙ ПЕЛЕНГАТОР | 2004 |
|
RU2274873C2 |
| Способ определения координат стреляющих артиллерийских систем и разрывов снарядов звукометрическим комплексом | 2017 |
|
RU2676830C2 |
| Способ проведения метеорологической подготовки стрельбы артиллерии в горных условиях | 2016 |
|
RU2649052C2 |
| СПОСОБ ПРИСТРЕЛКИ ЦЕЛИ С ИСПОЛЬЗОВАНИЕМ КВАДРОКОПТЕРА | 2016 |
|
RU2642554C1 |
Изобретение относится к способам определения скорости и направления ветра, используемым в приборах метеорологического обеспечения пуска ракет, стрельбы артиллерии и ведения звуковой разведки звукометрическими комплексами Сухопутных войск. Сущность: выбирают в стороне от огневых и стартовых позиций артиллерии и пусковых установок ракет, в направлении сноса ветровых пуль, открытый ровный участок местности протяженностью до двухсот метров. Измеряют наземную температуру воздуха. Измеряют десятикратно скорость и направление наземного ветра. Рассчитывают среднеарифметические значения скорости и направления наземного ветра. Технический результат: повышение оперативности, точности, расширение функциональных возможностей. 4 ил.
Способ измерения скорости и направления ветра в нижних слоях атмосферы, заключающийся в том, что выбирают в стороне от огневых и стартовых позиций артиллерии и пусковых установок ракет в направлении сноса ветровых пуль открытый, ровный участок местности протяженностью до двухсот метров, измеряют наземную температуру воздуха, измеряют десятикратно скорость и направление наземного ветра, рассчитывают среднеарифметические значения скорости и направления наземного ветра, отличающийся тем, что на стороне, противоположной направлению наземного ветра вышеуказанного участка, намечают воображаемую линию, расположенную относительно одной из осей топографической системы координат так, чтобы наземный ветер был направлен между предполагаемыми директрисами двух акустических баз, устанавливают примерно на середине этой линии перископическую артиллерийскую буссоль, производят ее горизонтирование и ориентирование по странам света, измеряют угол наклона этой воображаемой линии к одной из осей топографической системы координат, определяемой направлением наземного ветра, поворачивают оптическую ось визира перископической артиллерийской буссоли в направлении сноса ветровых пуль на такой угол к воображаемой линии, чтобы наземный ветер был направлен между предполагаемыми директрисами двух акустических баз, измеряют этот угол, устанавливают на удалении двадцати пяти метров от точки установки буссоли второй акустической базы вдоль оптической оси визира перископической артиллерийской буссоли ветровое ружье и на удалении пятидесяти метров от точки установки буссоли этой акустической базы вдоль оптической оси визира перископической артиллерийской буссоли звукоприемник номер три, поворачивают оптическую ось визира перископической артиллерийской буссоли так, чтобы она совпадала с воображаемой линией и была направлена в сторону первой акустической базы, поворачивают оптическую ось визира перископической артиллерийской буссоли в сторону сноса ветровых пуль на угол, равный углу наклона второй акустической базы к воображаемой линии, устанавливают на удалении пятидесяти метров от точки установки буссоли вдоль оптической оси визира перископической артиллерийской буссоли первой акустической базы звукоприемник номер один, убирают перископическую артиллерийскую буссоль и на ее место устанавливают звукоприемник номер два, вычисляют дирекционные углы директрис первой и второй акустических баз, направлений с середины первой акустической базы на середину второй акустической базы и наоборот, геометрическую базу, выстреливают не менее трех ветровых пуль из ветрового ружья, измеряют при этом каждый раз времена прихода акустических сигналов ко всем трем звукоприемникам, рассчитывают каждый раз звукометрические углы первой и второй акустических баз, общие поправки на ветер в эти звукометрические углы, исправленные звукометрические углы первой и второй акустических баз, дальности сноса ветровых пуль для стандартной высоты двести метров, дирекционные углы среднего ветра для этой высоты, среднеарифметические значения дальности сноса ветровых пуль и дирекционного угла среднего ветра для этой высоты, рассчитывают по полученному среднеарифметическому значению дальности сноса ветровых пуль для стандартной высоты двести метров и скорости среднего ветра для всех девяти стандартных высот, рассчитывают по полученному среднеарифметическому значению дирекционного угла среднего ветра для стандартной высоты двести метров дирекционные углы среднего ветра для остальных восьми стандартных высот.
| Указания по работе метеорологического поста артиллерийского дивизиона | |||
| - М.: Воениздат, 1975 | |||
| Н.П.КРАСНЕНКО | |||
| Акустическое зондирование атмосферы | |||
| - Новосибирск: Наука, 1986, с.105-112 | |||
| Способ дистанционного измерения проекции скорости ветра на выбранное направление | 1979 |
|
SU812027A1 |
| СПОСОБ ДИСТАНЦИОННОГО ИЗМЕРЕНИЯ СКОРОСТИ И НАПРАВЛЕНИЯ ВЕТРА | 1992 |
|
RU2017169C1 |
| DE 3506591 А1, 28.08.1986. | |||
Авторы
Даты
2008-11-27—Публикация
2006-12-07—Подача