Изобретение относится к вычислительной технике и может быть использовано для коррекции радиальной и тангенциальной дисторсии на изображениях, полученных цифровыми фото-, видеокамерами и системами технического зрения, использующих в качестве приемников изображения матричные приемники изображения.
Известен способ определения дисторсии длиннофокусных объективов, описанный в патенте на изобретение №2276778, опубликованном 20.05.2006, Бюл. №14. Способ заключается в том, что производится измерение линейных величин изображений в фокальной плоскости оптической скамьи участков стеклянной шкалы, расположенных по полю зрения испытуемого объектива при помощи двух окуляр-микрометров.
Недостатком этого способа является невозможность компенсации дисторсии оптического объектива цифровой фотокамеры алгоритмическим путем поскольку он ориентирован на измерение только коэффициента радиальной дисторсии больших объективов с применением не автоматических методов измерений.
Известен способ автоматического определения и коррекции радиальной дисторсии на цифровом изображении, изложенный в патенте на изобретение №2351091, опубликованном 27.03.2009 Бюл. №9. Способ заключается в определении коэффициента дисторсии, выделении изображения контуров, их анализе, выборе трех точек на каждом контуре и расчете коэффициентов радиальной дисторсии, составлении гистограммы зависимости частот повторяемости найденных коэффициентов от их величин, определении значений коэффициента как среднего в окрестности значения коэффициента с максимальной частотой повторения, коррекции искажений, вызванных радиальной дисторсией.
Недостатками способа являются: неспособность компенсации периодических составляющих радиальной и тангенциальной составляющих дисторсии, а также низкая (пиксельная) точность определения коэффициента дисторсии.
Технической задачей изобретения является определение параметров дисторсии объектива и коррекции ее влияния на изображение. Технический результат при использовании заявляемого изобретения заключается в снижении влияния дисторсии на искажение изображения формируемого оптическим объективом.
Технический результат изобретения достигается тем, что в способе определения коэффициента дисторсии и коррекции искажений, вызванных радиальной дисторсией, основанный на выполнении экспозиции испытательного полигона в виде равномерно распределенных концентрических окружностей и радиусов посредством исследуемой фотокамеры, считываются координаты узлов полигона, осуществляется преобразование декартовых координат изображений узлов испытательного полигона на фотоматрице в полярные координаты, вычисляются коэффициенты математической модели дисторсии, которая представляет собой три разложения в ряды, один степенной и два ряда Фурье, последовательно выполняется компенсация радиальной дисторсии, периодических составляющих радиальной и тангенциальной дисторсии.
Сущность изобретения обусловлена выполнением следующих действий:
выполнение фотоэкспозиции испытательного полигона в виде равномерно распределенных концентрических окружностей и радиусов посредством исследуемой фотокамеры;
считывание координат узлов полигона посредством субпиксельной обработки изображения полигона;
преобразование декартовых координат изображений узлов испытательного полигона на фотоматрице в полярные координаты;
вычисление коэффициентов математической модели дисторсии;
последовательное выполнение компенсации радиальной дисторсии, периодических составляющих радиальной и тангенциальной дисторсии.
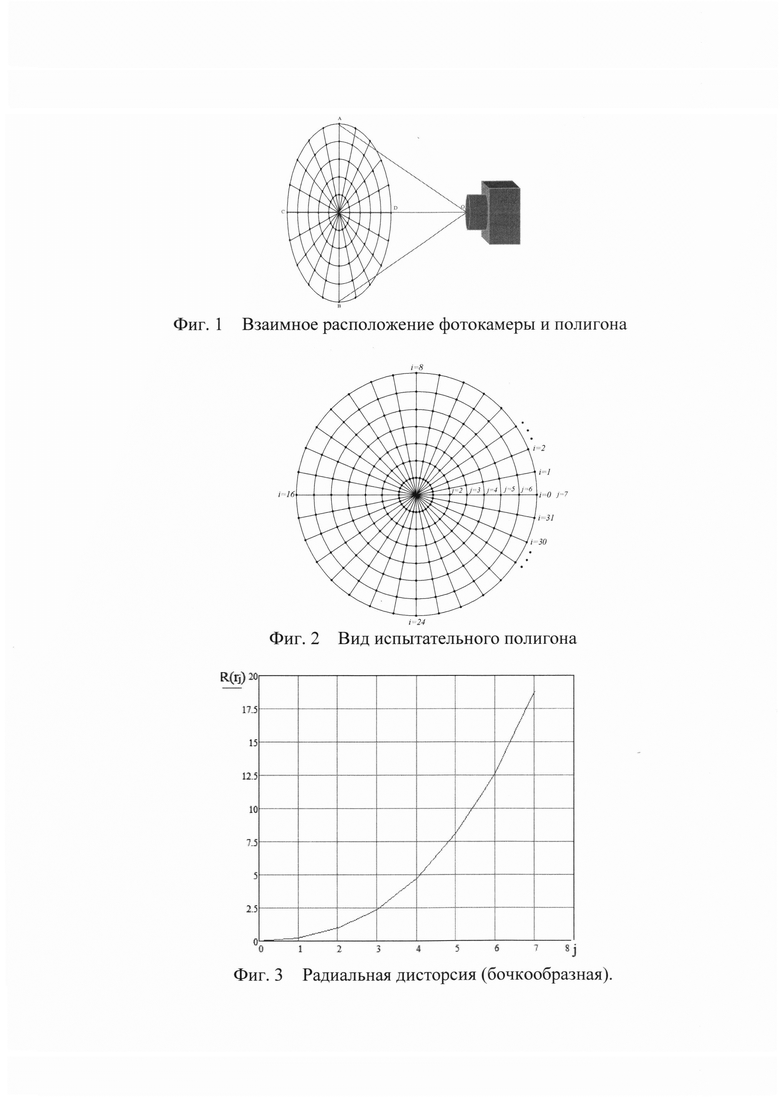
На фиг. 1 показано взаимное расположение фотокамеры и полигона:
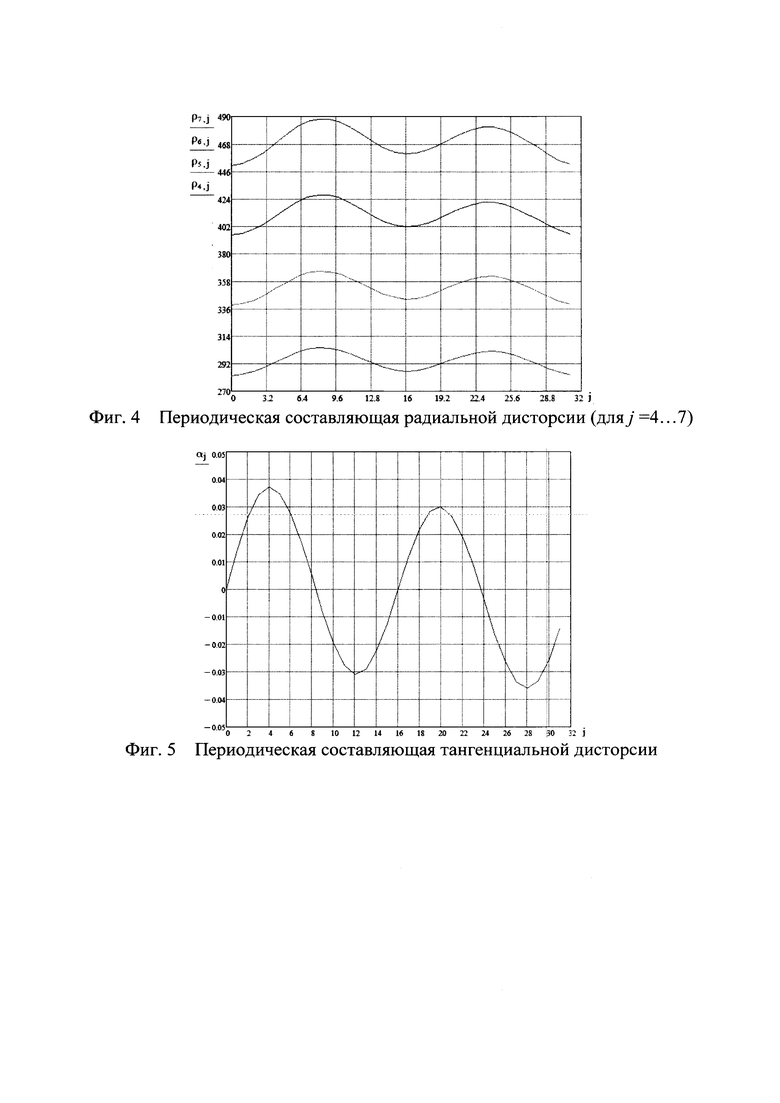
На фиг. 2 показан вид испытательного полигона, где i=0…31, j=1…8;
На фиг. 3 показан график зависимости радиальной дисторсии R(rj) от номера окружности i.
На фиг. 4 показан график зависимости периодической составляющей радиальной дисторсии ρ(λi) от номера радиуса i (для номера окружности j=4…7).
На фиг. 5 показан график периодической составляющей тангенциальной дисторсии представленной зависимостью угла отклонения радиусов αi от их номера.
Способ реализуется следующим образом.
В настоящее время во многих областях техники все большее распространение получают оптико-электронные системы, в состав которых часто входят цифровые фотокамеры, которые представляют собой уникальное измерительное средство способное функционировать дистанционно и в автоматическом режиме.
Однако оптические системы фотокамер как правило не соответствуют высоким требованиям, предъявляемым к измерительным приборам, поскольку они обычно разрабатываются с использованием предположения, что проецирование трехмерного пространства на плоскость фотоматрицы описывается моделью «камера-обскура». Одной из наиболее существенных причин погрешностей таких систем является дисторсия оптической системы, которая не только хорошо изучена, но и разработаны многочисленные способы ее минимизации. Существует ряд конструктивных способов компенсации аберраций до допустимых пределов, но этот путь совершенствования качества оптических систем ограничен существенным возрастанием их стоимости. Поэтому к настоящему времени разработаны способы алгоритмического исправления дисторсии, которые основаны на использовании математических моделей дисторсии и испытательного полигона в виде квадратной сетки со значительным количеством ячеек [Shang, J.J., Shi, Z.K.: Vision-based runway recognition for UAV autonomous landing. Int. J. Comput. Sci. Netw. Secur. 7(3), 112-117 (2007).].
Такой подход предполагает хранение в постоянном запоминающем устройстве калибровочной информации, а также значительных вычислений. Одной из наиболее распространенных моделей дисторсии является модель Брауна-Конради [Conrady, А. Е. Decentred lens-systems / А. Е. Conrady // Monthly notices of the royal astronomical society. - 1919. - т. 79, №5. - с. 384-390.] которая описывает следующие преобразования координат (xu, yu) точки на неискаженном изображении
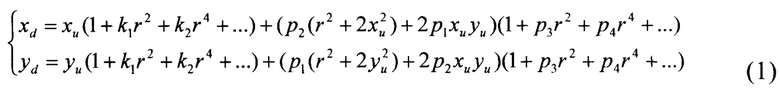
где (xd, yd) - координаты точки (xu, yu) на искаженном дисторсией изображении; 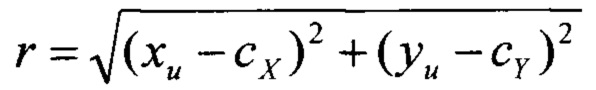 - расстояние от оптического центра (cX, cY) до точки (xu, yu); ki - коэффициенты радиальной дисторсии; ki - коэффициенты тангенциальной дисторсии.
- расстояние от оптического центра (cX, cY) до точки (xu, yu); ki - коэффициенты радиальной дисторсии; ki - коэффициенты тангенциальной дисторсии.
В библиотеке OpenCV [OpenCV: Open Source Computer Vision Library / GitHub. 2017. [Электронный ресурс] URL: https://github.com/opencv/opencv (дата обращения 10.07.2017).] (которая является мировым стандартом для компьютерной обработки изображений и видео в сфере свободного программного обеспечения) используется модель дисторсии, описанная соотношениями (2). Следует особо отметить, что в OpenCV коэффициенты радиальной дисторсии k4, k6 используются не в качестве коэффициентов при высших степенях полинома как в классическом описании (1), а в качестве коэффициентов аналогичного полинома в знаменателе. Такой вид функции радиальной дисторсии уменьшает вероятность превышения максимально возможного значения переменной при расчете двенадцатой степени числа r:
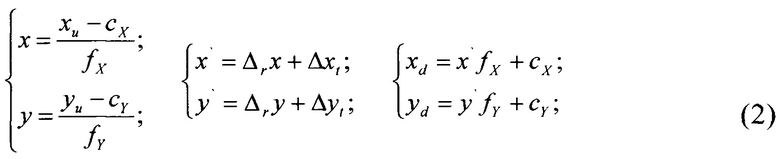
где 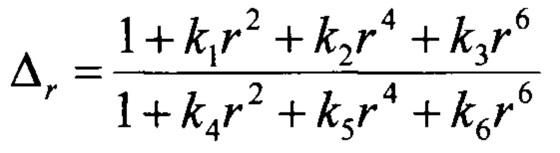 - смещение координат, вызванное радиальной дисторсией; Δх1=р2(r2+2х2)+2р1ху - смещение координаты x, вызванное тангенциальной дисторсией; Δу1=р1(r2+2у2)+2р2ху - смещение координаты y, вызванное тангенциальной дисторсией;
- смещение координат, вызванное радиальной дисторсией; Δх1=р2(r2+2х2)+2р1ху - смещение координаты x, вызванное тангенциальной дисторсией; Δу1=р1(r2+2у2)+2р2ху - смещение координаты y, вызванное тангенциальной дисторсией; 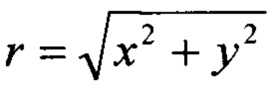 .
.
Исследование возможностей программного обеспечения из OpenCV для устранения дисторсии объектива фотокамеры показало, что оно не позволяет получить метрическую систему технического зрения, поскольку размеры «исправленных» изображений равных отрезков полигона имеют разброс порядка 1%. Поэтому необходимо дальнейшее улучшение такого алгоритмического подхода. Исследованиями было установлено, что имеется несколько причин не способности, известных программных продуктов к более существенному устранению дисторсии:
использование испытательного полигона в виде квадратной сетки, которая не соответствует геометрии оптической системы фотокамеры, представляющей собой совокупность линз в виде тел вращения с общей осью;
использование декартовой системы координат для описания математической модели дисторсии;
использование математической модели дисторсии, описывающей только наиболее существенные составляющие оптических искажений, то есть модель с ограниченной адекватностью.
Очевидно, что все три названных причины взаимосвязаны и нуждаются в полной замене. Поэтому предлагается испытательный полигон в виде концентрических окружностей и радиальных линий, который наилучшим образом соответствует характеру искажений, а полярные координаты наиболее просто и адекватно описывают искажения изображений. Численные исследования искажений реальных объективов показали, что радиальные искажения в полярных координатах содержат две составляющие, одна из которых хорошо известна и отлично описываются полиномиальным разложением, а вторая составляющая радиальных искажений, а также тангенциальные искажения имеют вид периодических функций. Таким образом, в полярных координатах дисторсия имеет следующее представление.

где ƒ1(r) и ƒ2(ϕ) - функциональные зависимости, описывающие радиальные искажения изображения, ƒ3(ϕ) - функция, описывающая тангенциальные искажения, (r, ϕ) и (r', ϕ') - полярные координаты точек изображения с искажениями и без них.
Особенно заметны эти искажения для короткофокусных объективов и проявляются они в виде эллипсоподобных изображений окружностей полигона, полуоси которых оказываются разноразмерными. Физической причиной этих искажений, существенно нарушающих симметрию изображения является несовпадение оптических осей линз объектива и неортогональность оптической оси объектива и плоскости фотоматрицы.
При фотоэкспонировании полигона весьма сложно выполнить идеальное взаимное расположение камеры и полигона, когда OABCD образует равнобедренную пирамиду в вершине которой размещается центр объектива фотокамеры (фиг. 1), в частности сложно разместить фотокамеру так чтобы центр изображения совпал с центром фотоматрицы, а изображение оси ОХ совпало с ее строкой. Для исправления этих технологических трудностей в методику включены дополнительные процедуры (пункты 3 и 5).
Методика компенсации искажений состоит в следующей последовательности действий:
1) Производится фотоэкспозиция испытательного полигона, исследуемой камерой, вид которого представлен на фиг. 2.
2) С помощью программы обработки изображения считываются координаты узлов полигона, которые представляются в виде двух матриц (xij)32×8 и (yij)32×8.
3) Посредством следующего очевидного преобразования декартовых координат изображения обеспечивается точное совпадение центра фотоматрицы и центра изображения полигона

где x00, y00 - координаты центра изображения полигона.
4) Осуществляется переход от декартовых координат изображений узлов испытательного полигона на фотоматрице к координатам в полярной системе по известным формулам:

где rij - полярный радиус координат изображения узла с номером i, j, ϕij -полярный угол изображения узла.
5) Выполняется малый поворот изображения 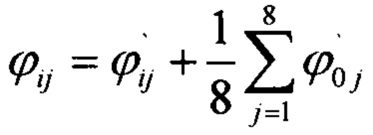 , позволяющий совместить нулевую строку фотоматрицы с изображением горизонтальной оси полигона. При этом использование среднего значения полярных углов узлов этой оси полигона позволяет уменьшить влияние погрешностей как обработки изображения полигона, так и погрешностей его изготовления.
, позволяющий совместить нулевую строку фотоматрицы с изображением горизонтальной оси полигона. При этом использование среднего значения полярных углов узлов этой оси полигона позволяет уменьшить влияние погрешностей как обработки изображения полигона, так и погрешностей его изготовления.
6) Экспериментальное исследование изображения полигона показало, что имеет место три характерных вида искажений:
- радиальное искажение известное как бочкообразная дисторсия, представленное на фиг. 3 успешно аппроксимируется посредством следующего степенного ряда
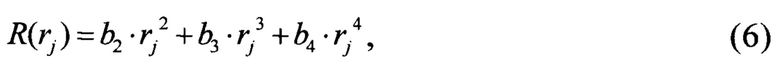
где 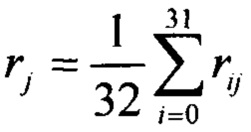 - статистическое среднее узлов j-й окружности (j=1…8);
- статистическое среднее узлов j-й окружности (j=1…8);
- радиальное периодическое отклонение изображения j-го контура полигона от окружности, показанное на фиг. 4. Эти искажения аппроксимируются рядом Фурье

где  - статистическое среднее угловых координат узлов i-го радиуса на изображении полигона, ck - коэффициенты разложения периодической составляющей радиальной дисторсии;
- статистическое среднее угловых координат узлов i-го радиуса на изображении полигона, ck - коэффициенты разложения периодической составляющей радиальной дисторсии;
- тангенциальное периодическое искажение, которое имеет особенность, связанную с тем, что прямые радиальные линии полигона остаются на изображении прямыми с точностью до 10-4 рад, а это дает основание для утверждения о том, что искажения внешней окружности изображения повторяются для всех концентрических окружностей полигона. Тангенциальные искажения (фиг. 5) описываются следующим выражением 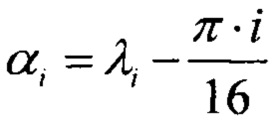 , где
, где 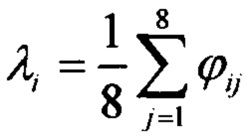 - статистическое среднее угловых координат узлов i-го радиуса.
- статистическое среднее угловых координат узлов i-го радиуса.
Периодический характер этой функциональной зависимости показывает, что ее аппроксимация может быть успешно выполнена с помощью ряда Фурье следующего вида
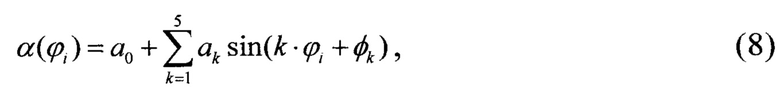
где ϕi - измеренные значения углового положения узлов полигона i=0…31.
Численные эксперименты с полигоном размерностью 32*8, отпечатанном на лазерном принтере, показали, что пять первых членов разложения (7) и (8) обеспечивают погрешность описания не хуже 0.1 пикс. Достижение только такой точности обусловлено тем, что именно таков порядок погрешности субпиксельной обработки изображения при определении координат центров изображений узлов полигона, поэтому увеличивать число членов разложения для достижения большей точности по условиям проведенного эксперимента не имеет смысла.
7) Для определения коэффициентов модели искажений и исправления изображения используется подход, основанный на методе наименьших квадратов.
В соответствии с методом наименьших квадратов для аппроксимации зависимостей описывающих три вида искажений взяты критерии качества K, L, М - минимум среднего квадрата отклонений искомых кривых от узлов изображения полигона, определенные выражениями:
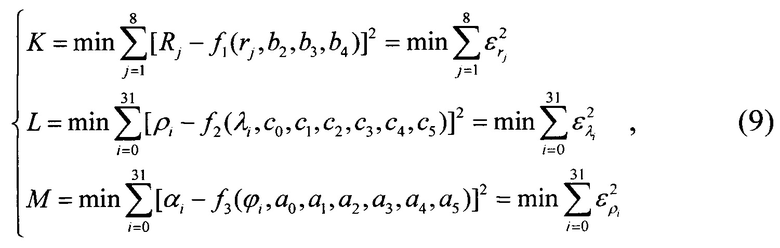
где ρi, Rj, αi - результаты эксперимента; ƒ1(rj, b2, b3, b4), ƒ2(λj, c0, c1, c2,…,c5, φ1, φ2, φ3, φ4, φ5), ƒ3(ϕi, α0, α1, α2,…,α5, ψ1, ψ2, ψ3, ψ4, ψ5) - определяемые аналитические зависимости; b2,b3,b4, c0, c1, c2,…,c5, φ1, φ2, φ3, φ4, φ5, ϕi, α0, α1, α2,…,α5, ψ1, ψ2, ψ3, ψ4, ψ5 - оцениваемые параметры; 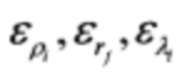 - ошибки измерений; (8*32) - размерность матрицы исходных данных.
- ошибки измерений; (8*32) - размерность матрицы исходных данных.
Для описания радиальной дисторсии используем первое равенство (9), которое совместно с (6) дает
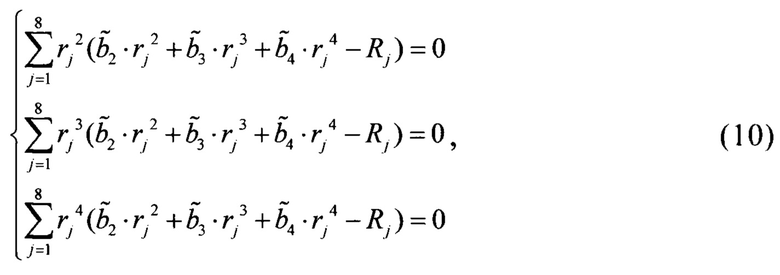
Решение этой системы нелинейных уравнений позволяет найти вектор оценок параметров  . Для фотокамеры USB500w02m, объектив которой имеет фокусное расстояние 3,6 мм. это разложение имеет вид
. Для фотокамеры USB500w02m, объектив которой имеет фокусное расстояние 3,6 мм. это разложение имеет вид
R(r)=4.1239114⋅10-9⋅r2+1.7218746⋅10-7⋅r3+7.1641887⋅10-11⋅r4.
В графическом виде эта зависимость представлена на фиг. 3. Устранение радиальной дисторсии выполняется посредством следующего соотношения

где r - радиальная координата точки.
Для описания периодической составляющей радиальной дисторсии используем 2 равенство системы (9), которое совместно с (7) дает
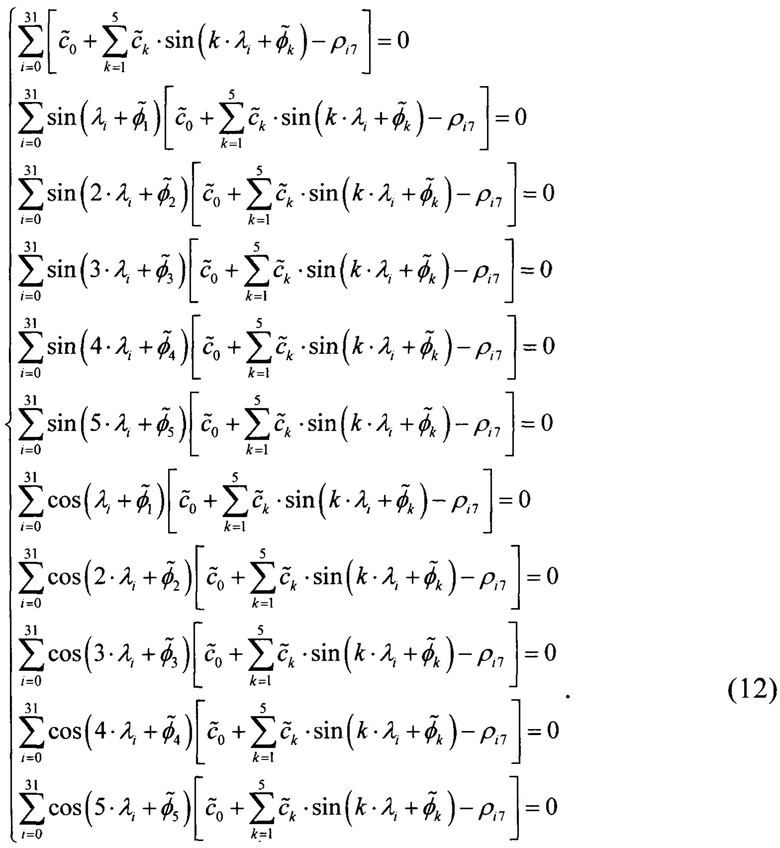
Решая эту систему нелинейных уравнений с использованием Mathcad находим вектор оценок параметров 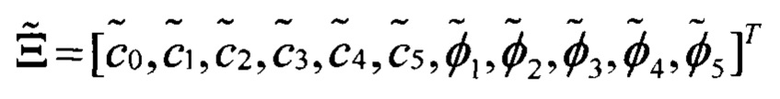
Для фотокамеры USB500w02m это разложение имеет вид
ρ(λ)=470.1601+5.4919sin(λ-0.9947)+14.6507sin(2λ-1.5867)-0.4726sin(3λ-0.0442)+0.0276sin(4λ-0.8495)-0.693sin(5λ+0.9902).
В графическом виде эта зависимость представлена на фиг. 4. Устранение радиальной периодической составляющей дисторсии выполняется посредством следующего соотношения

где r - исправленное значение радиуса текущей точки.
Минимизация критерия М обеспечивается при выполнении следующих условий

Решение этой системы нелинейных уравнений позволяет найти вектор оценок параметров 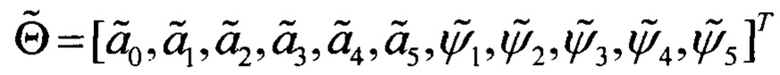 , минимизирующих среднее квадратическое отклонение аппроксимирующей кривой от совокупности вычисленных точек (αi, ϕi). Для фотокамеры USB500w02m (фокусное расстояние f=3.6 мм.) это разложение имеет вид
, минимизирующих среднее квадратическое отклонение аппроксимирующей кривой от совокупности вычисленных точек (αi, ϕi). Для фотокамеры USB500w02m (фокусное расстояние f=3.6 мм.) это разложение имеет вид
α(ϕ)=1.0689⋅10-4+4.494⋅10-3sin(ϕ+0.0916)+0.0335sin(2ϕ-6.5675⋅10-3)-3.5262⋅10-3sin(3ϕ+1.1168)-5.6304⋅10-4sin(4ϕ-0.0803)+1.1236⋅10-4sin(5ϕ+0.0958),
Устранение этих искажений для произвольной точки изображения с координатами (r, ϕ) выполняется посредством следующего соотношения

Для объектива, используемого в эксперименте дефекты неисправленного изображения имели разброс размеров равных отрезков строк и столбцов 35-50 пикс.
Разброс размеров равных отрезков для изображения, исправленного посредством средств OpenCV составил 4-5 пикс.
Разброс размеров равных отрезков для исправленного изображения посредством разработанной методики составил 0.2-0.25 пикс.
Таким образом, предложенный алгоритмический подход позволяет обеспечить высокую степень исправления физического несовершенства объективов, обусловленную наличием дисторсии.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ фотограмметрической калибровки для оценки коэффициентов радиальной и тангенциальной дисторсии объектива и матрицы внутренних параметров камеры | 2023 |
|
RU2808083C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТОВ ПО ИХ ЦИФРОВЫМ ИЗОБРАЖЕНИЯМ | 2018 |
|
RU2697822C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТЕЙ ДО ОБЪЕКТОВ ПО ИЗОБРАЖЕНИЯМ С ЦИФРОВЫХ ВИДЕОКАМЕР | 2016 |
|
RU2626051C2 |
| Тест-объект с радиально-кольцевым расположением реперных точек для оценки коэффициентов радиальной и тангенциальной дисторсии | 2023 |
|
RU2806654C1 |
| Тест-объект для оценки коэффициентов радиальной и тангенциальной дисторсии | 2023 |
|
RU2806669C1 |
| СПОСОБ ФОТОГРАММЕТРИЧЕСКОЙ КАЛИБРОВКИ ФОТОКАМЕР | 2006 |
|
RU2308001C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАССТОЯНИЯ ДО ОБЪЕКТА ПРИ ПОМОЩИ КАМЕРЫ (ВАРИАНТЫ) | 2014 |
|
RU2602729C2 |
| СПОСОБ ФОРМИРОВАНИЯ ПАНОРАМНЫХ ИЗОБРАЖЕНИЙ | 2006 |
|
RU2365998C2 |
| СПОСОБ КАЛИБРОВКИ ОПТИЧЕСКОЙ СИСТЕМЫ | 2008 |
|
RU2381474C2 |
| СПОСОБ ФОРМИРОВАНИЯ ОПТИЧЕСКОГО ИЗОБРАЖЕНИЯ В НЕКОГЕРЕНТНОМ СВЕТЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ (ВАРИАНТЫ) | 2000 |
|
RU2179336C1 |
Изобретение может быть использовано для коррекции радиальной и тангенциальной дисторсии на изображениях, полученных цифровыми фото-, видеокамерами и системами технического зрения, использующих в качестве приемников изображения матричные приемники изображения. Способ компенсации дисторсии объектива основан на определении радиальной и тангенциальной дисторсии и коррекции искажений, вызванных дисторсией. Производят экспозицию испытательного полигона в виде равномерно распределенных концентрических окружностей и радиусов посредством исследуемой фотокамеры, считывают координаты узлов полигона, осуществляют преобразование декартовых координат изображений узлов испытательного полигона на фотоматрице в полярные координаты, вычисляют коэффициенты математической модели дисторсии, которая представляет собой разложения в ряды, степенного и двух рядов Фурье, последовательно выполняют компенсацию радиальной дисторсии, периодических составляющих радиальной и тангенциальной дисторсии. Технический результат - снижении влияния дисторсии на искажение изображения. 5 ил.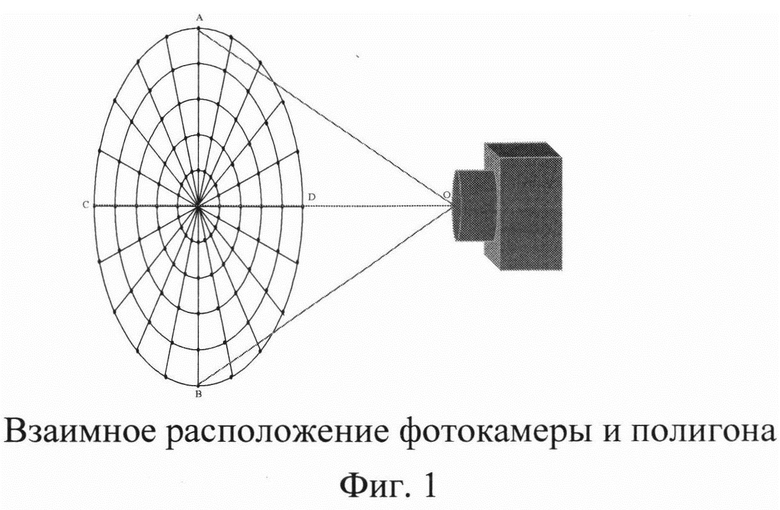
Способ компенсации дисторсии объектива, основанный на определении радиальной и тангенциальной дисторсии и коррекции искажений, вызванных дисторсией, отличающийся тем, что производят экспозицию испытательного полигона в виде равномерно распределенных концентрических окружностей и радиусов посредством исследуемой фотокамеры, считывают координаты узлов полигона, осуществляют преобразование декартовых координат изображений узлов испытательного полигона на фотоматрице в полярные координаты, вычисляют коэффициенты математической модели дисторсии, которая представляет собой разложения в ряды, степенного и двух рядов Фурье, последовательно выполняют компенсацию радиальной дисторсии, периодических составляющих радиальной и тангенциальной дисторсии.
| СПОСОБ АВТОМАТИЧЕСКОГО ОПРЕДЕЛЕНИЯ И КОРРЕКЦИИ РАДИАЛЬНОЙ ДИСТОРСИИ НА ЦИФРОВОМ ИЗОБРАЖЕНИИ | 2006 |
|
RU2351091C2 |
| US 2018122099 A1, 03.05.2018 | |||
| СПОСОБ АВТОМАТИЧЕСКОЙ НАСТРОЙКИ СИСТЕМЫ РАЗНЕСЕННЫХ В ПРОСТРАНСТВЕ ТЕЛЕКАМЕР ДЛЯ ФОРМИРОВАНИЯ ПАНОРАМНОГО ИЗОБРАЖЕНИЯ | 2019 |
|
RU2716896C1 |
| СПОСОБ КАЛИБРОВКИ ДИСТОРСИИ ОПТИКО-ЭЛЕКТРОННОГО УСТРОЙСТВА | 2006 |
|
RU2321888C1 |
| KR 2004053877 A, 25.06.2004. | |||
Авторы
Даты
2023-02-14—Публикация
2022-05-23—Подача