Изобретение относится к методам обработки цифровых изображений. В частности, к методам изменения размеров (масштаба) цифрового изображения, т.е. вычислению значений яркости в точках, не принадлежащих изначально исходному множеству точек, в которых значения яркости известны.
Существует большое разнообразие различных методов интерполяции. Все эти методы можно классифицировать по точности, критериям качества, мере приближения и применяемому математическому аппарату. В основе большинства алгоритмов интерполяции растрового изображения лежит замена неизвестной функции двумерного распределения яркости интерполируемого изображения функцией, близкой к неизвестной и обладающей свойствами, позволяющими легко производить те или иные аналитические или вычислительные операции. При этом в зависимости от выбора класса интерполирующих функций решение задачи интерполяции сводится к решению систем линейных или нелинейных уравнений.
Линейные методы исключительно важны для обработки изображений, поскольку они опираются на значительную совокупность хорошо изученных теоретических и практических результатов (см. патенты США № 5,671,298 [1], № 6,320,593 [2], № 6,496,609 [3], United States Patent 6965705 [4]).
Нелинейные методы (см. патент США № 6,823,091 [5]), хотя иногда и приводят к лучшим результатам, однако они не всегда предсказуемы, однозначны и по большей части недостаточно исследованы теоретически. Также существенным недостатком нелинейных методов по сравнению с линейными является повышенные требования к вычислительным ресурсам и низкая скорость интерполирования.
Дальнейшим развитием нелинейных методов интерполяции является применение адаптивных алгоритмов (см., например, патенты США № 5,532,950 [6], № 6,191,788 [7]), поведение которых изменяется в зависимости от статических свойств изображения внутри области действия интерполирующей функции. Как показывает практика, эффективность работы более сложных с вычислительной точки зрения адаптивных алгоритмов обычно лучше, чем у ранее рассмотренных методов, однако повышенные вычислительные требования при реализации адаптивных методов несмотря на высокую эффективность несколько снижают их область применения.
Из всех методов наиболее близкими к заявленному изобретению являются методы, основанные на линейной пространственной интерполяции. В качестве прототипа заявленного изобретения был выбран способ линейной кубической интерполяции, описанный в патенте США № 5,671,298 [8].
Интерполяция кубическими сплайнами заключается в поиске таких полиномов третьей степени на каждом из отрезков (границы которых являются соседними точками), у которых первая и вторая производные совпадают с первой и второй производной соседнего полинома. Таким образом, получающаяся непрерывная кусочно-полиномиальная функция обладает непрерывными первой и второй производной.
Существенным недостатком метода интерполяции, описанного в прототипе [8], является наличие характерных артефактов в интерполируемом изображении, ухудшающих точность масштабирования в области резких изменений яркости. Типичные артефакты включают в себя появление эффекта зубчатого края на наклонных линиях, размытие из-за ограничений при восстановлении высокочастотных составляющих интерполируемых данных, и эффект Гиббса, проявляющийся в виде паразитных волнообразных колебаний интерполяционной функции, отсутствующих у интерполируемого изображения.
Техническая задача, на решение которой направлено заявляемое изобретение, заключается в создании линейного пространственного метода интерполяции с улучшенными интерполяционными возможностями и со значительно меньшими артефактами, свойственными обычным линейным интерполяционным алгоритмам.
Поставленная задача решена путем разработки способа интерполяции изображения с увеличением частоты дискретизации цифрового изображения в t раз, состоящего из следующих шагов:
- осуществляют предварительную обработку изображения;
- определяют размер окна визирования m, степень интерполяционной функции n и масштабный коэффициент t;
- считывают вектор коэффициентов K, соответствующий заданной комбинации m, n, t;
- определяют для каждого пикселя исходного изображения m-1 ближайших соседей, которые вместе с этим пикселем образуют окно визирования m;
- осуществляют нормировку яркости пикселей, образующих окно визирования m до уровня k (k=1);
- рассчитывают яркость t2 пикселей с помощью m мерного интерполяционного полинома степени n, имеющего вектор K в качестве коэффициентов;
- присваивают каждому интерполированному пикселю новые координаты (x', y');
- повторяют все предыдущие шаги для каждой цветовой компоненты;
- проводят заключительную обработку изображения для уменьшения артефактов.
Таким образом, решение сводится к созданию линейного пространственного интерполианта на основе многомерного кусочно-непрерывного алгебраического многочлена (полиномиального сплайна). Размерность и степень многочлена выбираются исходя из требований точности восстановления сигнала и вычислительных возможностей.
Для функционирования полиномиального сплайна, отвечающего поставленной задаче, необходимо найти такие коэффициенты полинома, которые будут оптимально удовлетворять условию достижения максимальной точности интерполяционной функции
Способ по п.1 отличется тем, что коэффициенты определяют с применением множественного регрессионного анализа и набора эталонных изображений, которые искажены по тому же алгоритму, что и обрабатываемое изображение.
Их количество и вид выбирается исходя из выполнения условия достижения заданной точности интерполяционной функции. В общем случае для получения хороших результатов в качестве эталона достаточно использовать любое изображение с максимально широким диапазоном изменений локальных контрастов, однако наилучший результат с точки зрения минимизации погрешности интерполирования достигается только в случае рационального (репрезентативного) подбора эталонов.
Техническим результатом заявленного изобретения является создание линейного пространственного интерполяционного полинома путем реализации ряда модификаций метода интерполяции, описанного в прототипе. Указанные модификации базируются на следующих заключениях.
В основе бикубического метода лежит приближение многомерной интерполяционной функцией 3 степени в пределах окна 4×4 точек. Решая задачу определения значения интерполированного пикселя, после недолгих математических преобразований можно получить результирующее выражение, которое определяется как сумма значений 16 соседних интерполируемых пикселей, умноженных на соответствующие их расположению весовые коэффициенты аij.

Весовые коэффициенты aij для бикубического метода не зависят от значений функции f(xi, yi) и однозначно вычисляются исходя из соблюдения условий непрерывности внутри интервала самой интерполяционной функции, ее первой и второй производных и заданных значений первой или второй производной на границах интервала. Очевидно, что с математической точки зрения выражение (*) можно определить и как 16 мерный полином первой степени, в котором мономами являются значения яркости 16 соседних интерполируемых пикселей. Интересным является и тот факт, что как в случае использования интерполирующей функции любой другой степени, так и в случае более или менее жестких накладываемых условий вид выражения (*) остается неизменным, а все возможные варианты будут реализовываться только через весовые коэффициенты aij.
Предлагаемый метод является обобщением бикубического метода и дальнейшим его развитием, что выражается в следующих изменениях:
1. Количество учитываемых соседних интерполируемых пикселей уже не ограничивается 16, а может принимать любые значения.
2. Степень полинома уже не ограничивается первой, а может принимать любые другие целые и неотрицательные значения.
3. Коэффициенты аij определяются только условием обеспечения минимальной ошибки, и никакие другие условия (гладкости, например) не накладываются. При этом для их нахождения решается задача на основе метода множественного регрессионного анализа.
При этом становится очевидным, что предлагаемый метод не решает задачу нахождения интерполяционной функции. Поэтому данным методом нельзя воспользоваться в случае решения задач по нахождению функциональной зависимости. Наиболее важным и положительным свойством предлагаемого метода является сбалансированное сочетание таких качеств, как высокая скорость вычисления, которая свойственна обычным линейным методам, и высокое качество интерполирования, которое свойственно ресурсоемким нелинейным адаптивным методам.
Наиболее часто при решении задач масштабирования изображений используют различные алгоритмы интерполирования. Результатом работы таких алгоритмов является восстановленная с некоторой погрешностью свертка искомого изображения с масштабным окном. Для улучшения визуального качества часто используют различные алгоритмы, повышающие резкость. В результате из-за накопления ошибок результат работы таких методов несовершенен, а временные затраты существенны. Отличительной особенностью предложенного метода является то, что он базируется на решении обратной некорректной задачи и его работа аналогична инверсному фильтру. Существуют современные методы масштабирования, которые решают данную задачу схожим образом, используя, например, алгоритмы обратной свертки (деконволюции) с применением различных процедур регуляризации. Однако впервые для решения таких задач был применен многомерный кусочно-непрерывный многомерный алгебраический многочлен. В отличие от наиболее распространенных алгоритмов, в основе которых лежит поиск неизвестной функции двумерного распределения яркости интерполируемого изображения, в предлагаемом методе целью является нахождение закона изменения яркости интерполированного пикселя.
Для лучшего понимания существа заявляемого изобретения далее приводится его подробное описание с привлечением графических материалов.
Фиг.1. Блок-схема базовых компонентов системы.
Фиг.2. Иллюстрация задачи интерполирования элементарного пикселя изображения.
Фиг.3. Блок-схема этапов процесса расчета оптимальных коэффициентов полинома.
Фиг.4. Блок-схема этапов процесса интерполяции изображения.
Фиг.5. Примеры работы алгоритма.
Способ интерполяции изображения, то есть увеличение частоты дискретизации цифрового изображения в t раз, работает следующим образом:
1. Осуществляют предварительную обработку изображения, если необходимо;
2. Задают размер окна m, степень интерполяционной функции n и масштабный коэффициент t;
3. Загружают вектор коэффициентов K, соответствующий заданной комбинации m, n, t.
4. Для каждого пикселя исходного изображения определяют m-1 ближайших соседей, которые вместе с этим пикселем образуют окно визирования m;
5. Нормируют яркость пикселей, образующих окно визирования, до уровня k (k=1);
6. Рассчитывают яркости t2 пикселей с помощью m-мерного интерполяционного полинома степени n, имеющего вектор К в качестве коэффициентов;
7. Каждому интерполированному пикселю присваивают новые координаты (x', y');
8. Повторяют шаги 4-7 для каждой цветовой компоненты;
9. В случае необходимости производят последующую обработку изображения для уменьшения артефактов.
Метод может быть применен как к цветным, так и к черно-белым (с оттенками серого) изображениям и обеспечивает получение качественных и резких изображений с высоким пространственным разрешением.
Фиг.1. показывает основные компоненты системы, на которой данный метод может быть реализован. Реализацией способа управляют с помощью процессора 101, который выполняет программный код, хранящийся в памяти 102. Также в памяти 102 хранят исходную черно-белую или цветную фотографию. Изображение анализируют, создают новое изображение, пиксели которого вычисляют с помощью пикселей исходного изображения. Новое изображение передают на устройство отображения 104, или на устройство печати 103. Передачу информации в системе осуществляют по шине данных 106.
Далее описывается процесс создания интерполированного изображения.
Фиг.2. иллюстрирует задачу интерполирования изображения, где 2.1 и 2.2 - понижение дискретизации (downsampling), a 2.3 - повышение дискретизации (upsampling).
Пусть имеется изображение I(x, y), где x∈[1, xmax] y∈[1, ymax], которое было получено из Х после уменьшения (downsampling) известным способом в t раз. Несмотря на большое разнообразие допустимых способов уменьшения размеров изображений далее в качестве примера будет рассмотрен способ средних значений:
 ,
,
Тогда задача качественной интерполяции (upsampling) формулируется следующим образом. По имеющемуся изображению I, требуется получить такое изображение 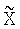 , которое бы согласно выбранному критерию близости в максимальной степени было близко к восстанавливаемому изображению X. Несмотря на возможность применения большого множества различных критериев близости в заявляемом способе предлагается использовать наиболее простой и самый распространенный критерий - метод наименьших квадратов (МНК):
, которое бы согласно выбранному критерию близости в максимальной степени было близко к восстанавливаемому изображению X. Несмотря на возможность применения большого множества различных критериев близости в заявляемом способе предлагается использовать наиболее простой и самый распространенный критерий - метод наименьших квадратов (МНК):
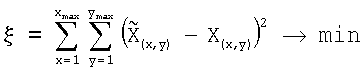 ,
,
Основой описываемого алгоритма является метод множественного регрессионного анализа с применением m мерного кусочно-непрерывного полинома степени n с фиксированными коэффициентами К вида:
 , при этом
, при этом  ,
,
где: 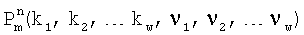 - m мерный полином степени n.
- m мерный полином степени n.
ν1, ν2, …νw образуют вектор V, вид которого определяется данным полиномом.
k1, k2, …kw образуют вектор K - коэффициенты полинома.
 - Приведенные к единому масштабу элементы изображения, принадлежащие оконной выборке, размер которой определяется параметром m. Ii∈[0, 1]
- Приведенные к единому масштабу элементы изображения, принадлежащие оконной выборке, размер которой определяется параметром m. Ii∈[0, 1]
d(x,y) - Масштабный коэффициент для текущего окна.
I(x,y) - Интерполируемый пиксель изображения.
Для каждого пикселя исходного изображения I(x,y) производят следующую процедуру: Выделяют m-1 ближайших соседей обрабатываемой точки I(x,y), которые образуют окно визирования m. После чего значения яркости внутри окна визирования приводят к единому масштабу нормировкой каждой переменной на диапазон разброса значений яркости внутри окна. В простейшем варианте это - линейное преобразование в единичный отрезок:
 ,
,
при этом: di=Ii,max-Ii,min,
где: Ii,max, и Ii,max - максимальное и минимальное значения яркости пикселей в заданном окне.
Длина w векторов V и K определяют по следующей формуле:
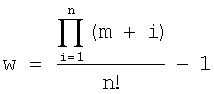 ,
,
Для нахождения вектора коэффициентов полинома методом МНК необходимо для каждого интерполируемого пикселя решить переопределенную систему линейных уравнений вида:
 , где
, где
 ,
,  ,
, 
Где S - матрица коэффициентов системы линейных уравнений размером [w, w].
U - вектор правой части системы уравнений размером [w].
K - вектор коэффициентов полинома размером [w].
Коэффициенты матрицы S, U определяют по следующим формулам:

Где r - число измерений: 
В случае m=9, n=2 и t=4 переменные аi и bi определяют следующими выражениями:
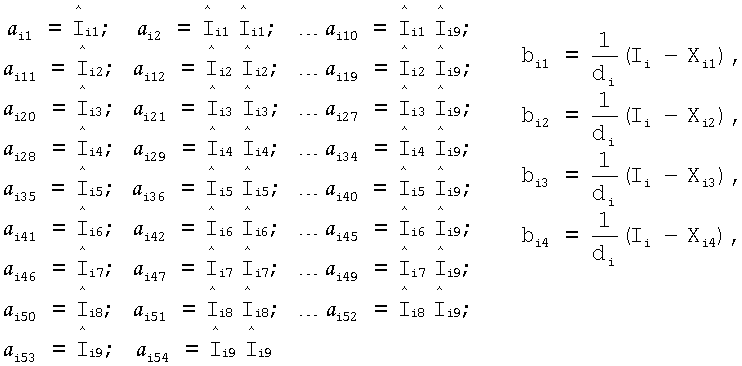
Элементарное окно для каждого пикселя исходного изображения I(x, y) для случая m=9 задают следующими формулами:
I1=I(x-1, y-1); I2=I(x, y-1); I3=I(x+1, y-1);
I4=I(x-1, y); I5=I(x, y); I6=I(x+1, y);
I7=I(x-1, y+1); I8=I(x, y+1); I9=I(x+1, y+1);
При этом x∈[2, xmax-1] и y∈[2, ymax-1]
После этого решают систему (1), каким-либо методом для однозначно определенных линейных систем, в частности, учитывающим симметрию СЛАУ. Решением системы является искомый вектор коэффициентов K.
Решения линейных систем уравнений большой размерности, как правило, является нетривиальной задачей по причине плохой их обусловленности. Система хорошо решается до тех пор, пока на погрешность алгоритма ее решения не начинает влиять вычислительная погрешность, которая неизбежна при любых компьютерных расчетах. Для получения достоверных результатов решения систем требуется использовать специальные методы, уменьшающие число обусловленности. Поскольку обусловленность системы прямо пропорционально ее размерности, выбор степени приближающего полинома и его размерности является важной задачей, которая сопряжена с определением таких оптимальных значений, при которых погрешность интерполяции минимальна, а вычислительные затраты приемлемы.
На Фиг.3 приведена блок-схема этапов реализация способа нахождения вектора оптимальных коэффициентов К для случая m=9, t=2, n=2.
Вначале необходимо задать масштабный коэффициент интерполяции t, а также в зависимости от требуемой точности и вычислительных возможностей необходимо определить степень (n) и размерность (m) применяемого интерполяционного полинома, 301.
После этого необходимо выбрать эталонное изображение X, удовлетворяющее требованию получения минимальной погрешности интерполяции и определить (или задать) масштабирующую передаточную функцию (например, способ средних значений), 301.
Затем производят операцию уменьшения эталонного изображения X в t раз известным способом, определенным масштабирующей функцией, 302. В результате после уменьшения изображения X получают изображения I.
Затем для каждой точки исходного изображения I(x, y), 303 производят следующую процедуру:
Выделяют m-1 ближайших соседей обрабатываемой точки 304, которые образуют окно визирования m, 305. Затем в определенной m окрестности определяют минимальное и максимальное значение яркости, затем окрестность масштабируется на сегмент [0, 1], 306.
 ,
,
где di=Ii,max-Ii,min,
Далее формируют вектор аргументов функции регрессии (S) и вектор (U), 307.
Накопление значений аргумента функции (S) и вектора (U), 308.
После этого, решая СЛАУ, определяют искомый вектор оптимальных коэффициентов K, 309.
На Фиг.4 приведена блок-схема этапов процесса интерполяции изображения сплайн-полиномом для случая m=9, t=2, n=2.
Вначале необходимо задать масштабный коэффициент интерполяции t, а также в зависимости от требуемой точности и допустимых временных и системных ресурсов определить степень (n) и размерность (m) применяемого интерполяционного полинома, 401.
В зависимости от выбранных параметров m, t и n загружают рассчитанный ранее вектор коэффициентов полинома K, 401.
Затем для каждого пикселя исходного изображения I(x, y) 402 выделяют m-1 ближайших соседей, 403. В результате образуется окно визирования размером m, 404. При этом в случае выхода границы окна за пределы интерполируемых данных недостающие пиксели (с отрицательной какой-либо координатой) в простейшем случае дублируют соседними значениями яркости, либо для получения лучших результатов рассчитывают линейной экстраполяцией.
Затем в полученной m окрестности определяют минимальное и максимальное значения яркости, после этого окрестность масштабируют на сегмент [0, 1], 405.
 ,
,
где di=Ii,mах-Ii,min,
Далее формируют вектор аргументов функции регрессии, 406.
После этого вычисляют полином и находят интерполированные значения пикселя, 407.
Затем полученные значения масштабируют обратно на сегмент [localmin, localmin]:

После чего полученным интерполированным значениям присваивают соответствующие координаты, 408.
Описанная процедура, а именно шаги 402-408, производится для каждой цветовой компоненты в пространстве RGB или YCrCb, 410. После того как условие 409 выполнено, изображение поступает на устройство вывода (принтер, дисплей или какое-либо другое) или сохраняется в память.
Фиг.5 иллюстрирует задачу интерполирования изображения в 4 раза двумя способами: бикубическим и новым методом, описанным выше, где 5.1 - исходные изображения, 5.2, 5.4 и 5.6 - изображения, интерполированные способом-прототипом, 5.3, 5.5, 5.7 - изображения, интерполированные заявляемым способом.
Следует иметь в виду, что указанный выше вариант выполнения изобретения изложен с целью иллюстрации и для специалистов очевидно, что возможны разные модификации, добавления и замены, не выходящие из объема и смысла настоящего изобретения, раскрытого в прилагаемом описании и формуле изобретения. Так, например, модифицировав метод для случая одномерных данных (изображение - двумерное распределение), можно использовать его для обработки звука, а модифицировав метод для случая трехмерных данных, можно использовать его для увеличения временного разрешения видеопоследовательностей. Также можно модифицировать алгоритм для реализации адаптивности метода к локальным особенностям интерполируемого изображения.
Изобретение относится к обработке цифровых изображений, в частности к способам изменения масштаба цифрового изображения, т.е. вычислению значений яркости в точках, не принадлежащих изначально исходному множеству точек, в которых значения яркости известны. Техническим результатом является создание линейного пространственного способа интерполяции с улучшенными возможностями и со значительно меньшими артефактами. Предложен способ интерполяции цифрового изображения с увеличением частоты дискретизации в t раз, состоящий из следующих шагов: осуществляют предварительную обработку изображения; определяют размер окна визирования m, степень интерполяционной функции n и масштабный коэффициент t; считывают вектор коэффициентов K, соответствующий заданной комбинации m, n, t; определяют для каждого пикселя исходного изображения m-1 ближайших соседей, которые вместе с этим пикселем образуют окно визирования m; осуществляют нормировку яркости пикселей, образующих окно визирования m до уровня k (k=1); рассчитывают яркость t2 пикселей с помощью m мерного интерполяционного полинома степени n, имеющего вектор K в качестве коэффициентов; присваивают каждому интерполированному пикселю новые координаты (x', y'); повторяют все предыдущие шаги для каждой цветовой компоненты; проводят заключительную обработку изображения для уменьшения артефактов. 5 з.п. ф-лы, 5 ил.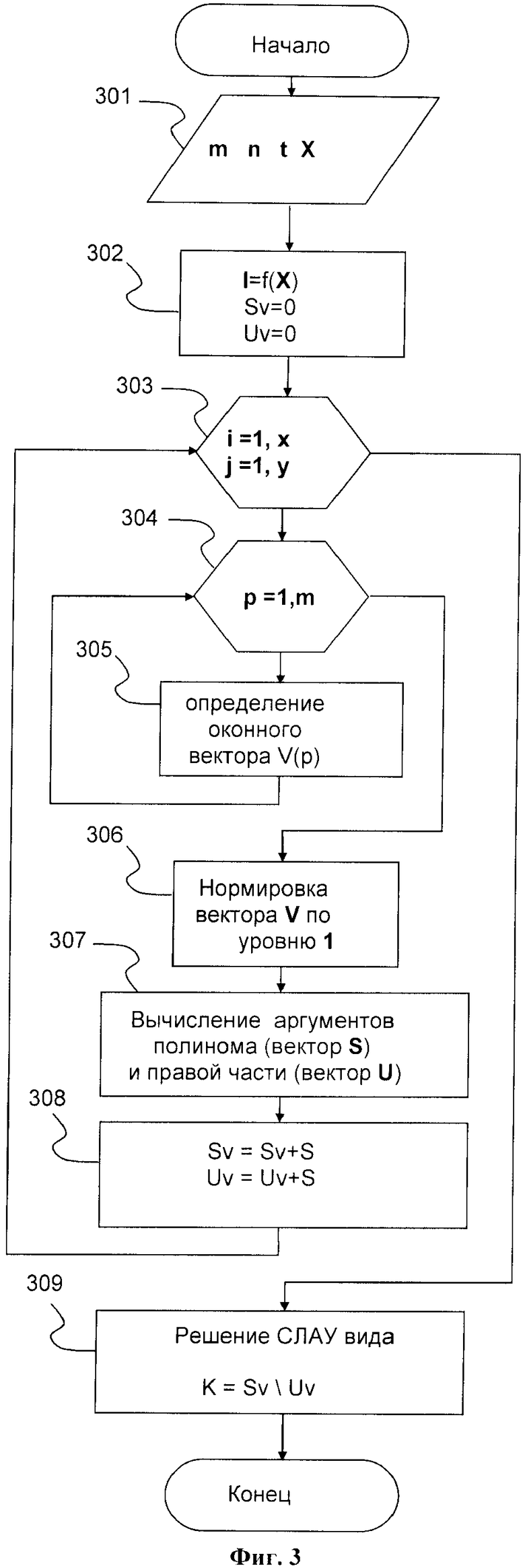
1. Способ интерполяции цифрового изображения с увеличением частоты дискретизации в t раз, состоящий из следующих шагов:
осуществляют предварительную обработку изображения;
определяют размер окна визирования m, степень интерполяционного полинома n и масштабный коэффициент t;
считывают вектор коэффициентов К, соответствующий заданной комбинации m, n, t;
определяют для каждого пикселя исходного изображения m-1 ближайших соседей, которые вместе с этим пикселем образуют окно визирования m;
осуществляют нормировку яркости пикселей, образующих окно визирования m до уровня k (k=1);
рассчитывают яркость t2 пикселей с помощью m мерного интерполяционного полинома степени n с фиксированными коэффициентами K вида: 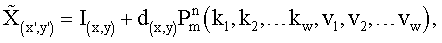 где
где  - m мерный полином степени n, v1, v2, … vw образуют вектор V, вид которого определяется данным полиномом, k1, k2, … kw - коэффициенты полинома, образующие вектор K, d(x, y) - масштабный коэффициент для текущего окна, I(х, у) - интерполируемый пиксель изображения;
- m мерный полином степени n, v1, v2, … vw образуют вектор V, вид которого определяется данным полиномом, k1, k2, … kw - коэффициенты полинома, образующие вектор K, d(x, y) - масштабный коэффициент для текущего окна, I(х, у) - интерполируемый пиксель изображения;
присваивают каждому интерполированному пикселю новые координаты (х', у');
повторяют все предыдущие шаги для каждой цветовой компоненты;
проводят заключительную обработку изображения для уменьшения артефактов.
2. Способ по п.1, отличающийся тем, что коэффициенты K m-мерного полинома рассчитывают, исходя из задачи уменьшения частоты дискретизации цифрового изображения в различное число раз и его обратного восстановления с условием близости результата восстановления цифрового изображения исходному цифровому изображению в смысле наименьших квадратов, при этом поиск коэффициентов К проводят с применением метода множественного регрессионного анализа с использованием упомянутого m-мерного кусочно-непрерывного полинома степени n с фиксированными коэффициентами К.
3. Способ по п.1, отличающийся тем, что коэффициенты K определяют с применением множественного регрессионного анализа и набора эталонных изображений, которые искажены по тому же алгоритму, что и обрабатываемое изображение.
4. Способ по п.1, отличающийся тем, что параметры полинома фиксированы и не зависят от интерполируемых данных.
5. Способ по п.1, отличающийся тем, что в качестве единственного критерия оптимальности принимают минимизацию погрешности масштабирования, для чего предварительно задают масштабный коэффициент интерполяции t, а также в зависимости от требуемой точности и вычислительных возможностей определяют степень (n) и размерность (m) применяемого интерполяционного полинома.
6. Способ по п.1, отличающийся тем, что расчет коэффициентов K полинома для каждого варианта интерполяционных параметров, в том числе размера окна визирования, степени полинома, масштабного коэффициента, выполняют один раз, при этом найденные параметры применяют для масштабирования произвольного изображения.
| US 5671298 B1, 23.09.1997 | |||
| RU 2002128369 A, 27.04.2004 | |||
| СПОСОБ ИНТЕРПОЛЯЦИИ ДВУХГРАДАЦИОННОГО ИЗОБРАЖЕНИЯ | 1997 |
|
RU2221275C2 |
| US 6603888 B1, 05.08.2003 | |||
| US 6577778 B1, 10.06.2003 | |||
| JP 2000207391 A, 28.07.2000. | |||
Авторы
Даты
2009-09-10—Публикация
2007-02-13—Подача