Изобретение относится к оптике и вычислительной технике и может быть использовано для определения внутренних (фокусное расстояние, дисторсия и другие геометрические и хроматические искажения) и внешних (положение в пространстве, направление оптической оси, расстояние до объекта) параметров ориентирования оптических систем, особенно для определения и коррекции дисторсии.
Проблема калибровки съемочной аппаратуры и, в частности, компенсации дисторсии вызывает широкий интерес, особенно в последнее время, когда она стала актуальной не только в фотограмметрии, но и в различных задачах, связанных с компьютерным зрением. Основы теории калибровки цифровых камер были заложены еще в восьмидесятые годы [1, 2]. Среди отечественных исследователей вопросы, касающиеся калибровки цифровых камер, теории учета систематических искажений неметрических снимков в своих работах рассматривали Р.Н.Гельман [3], В.И.Юрченко [4] и другие.
Чаше всего способы определения дисторсии основаны на использовании калибровочного объекта, состоящего обычно из контрастных точек - узлов квадратной сетки. Калибровочный объект фотографируется и по соответствию координат точек изображения и объекта определяется величина дисторсии в узлах сетки. Затем определяются полиномиальные коэффициенты дисторсии (в большинстве случаев только радиальной).
Довольно широкое распространение получил способ определения искажений снимков по степени кривизны линий, которые в природе прямые [1, 5].
Используется также метод компенсации дисторсии путем минимизации несоответствий положения точек объекта на разных изображениях [6].
Каждый из упомянутых способов предполагает использование какого-либо (в большинстве случаев полиномиального) приближения формы кривой дисторсии. В большинстве способов дисторсия полагается исключительно радиальной. Такие способы достаточны для исправления визуально заметной кривизны изображений, но для измерительных, фотограмметрических целей этого недостаточно. Для наиболее точной калибровки оптических систем используются прецизионные калибровочные стенды, требуется тонкая настройка положения калибруемой камеры. Затем следует достаточно сложный и долгий процесс обмера и расчетов. В НПП «Фотограмметрия», например, при налаженной поточной технологии процесс калибровки камеры занимает от двух дней до двух недель в зависимости от детальности исследования.
Классический способ определения дисторсии по соответствию положений реперов калибровочного объекта и положению их изображений на снимке является наиболее близким к заявляемому и может поэтому считаться его прототипом. Один из многочисленных вариантов решения данной задачи подобным способом довольно подробно изложен, например, в техническом отчете Microsoft Corporation [7]. В качестве плоского калибровочного объекта использовалась сетка черных и белых квадратов с известными геометрическими параметрами наподобие шахматной доски. Объект фотографировали, затем выделяли границы областей и вычисляли координаты узловых точек. Затем в предположении о монотонности, радиальной симметрии и локальной линейности функции дисторсии производили измерения несоответствия координат узлов калибровочного объекта и координат их изображения. Отказавшись, в отличие от большинства других исследователей, от попыток полиномиальной аппроксимации функции дисторсии, в данной работе исследователи получили график зависимости дисторсионного смещения точек изображения в зависимости от удаления точки от центра дисторсии. Этот способ позволяет определить параметры внутреннего ориентирования камеры, но для достаточно стабильного результата требуется обработка большого (порядка нескольких сотен) количества снимков. К тому же априорные предположения о виде дисторсионной зависимости (например, о радиальной симметрии) снижают достоверность результатов, так как в расчет не берется тангенциальная дисторсия, которая в некоторых оптических системах может быть заметной. Метод также не позволяет определять другие возможные искажения, например хроматическую аберрацию.
Задачей, на решение которой направлено заявляемое изобретение, является определение и последующее исключение геометрических искажений, вносимых системой регистрации изображений, предельно простым способом без использования прецизионных измерительных систем и стендов. При этом не делается никаких предварительных предположений о свойствах функции дисторсии, что повышает достоверность полученных результатов. Кроме того, способ позволяет определять хроматические искажения, вносимые оптической системой, что расширяет функциональные возможности способа.
Задача решается следующим образом.
Используется специальным образом синтезированный виртуальный калибровочный объект сплошного попиксельного заполнения информацией с двумерной функцией автокорреляции малого размера, напоминающий спекл-структуру, размер элемента которой порядка нескольких пикселей. Это может быть, например, сетка со случайным бинарным заполнением ячеек. То есть синтезируют файл в любом графическом формате (например, BMP или JPEG), содержащий случайное распределение черных и белых точек. Затем калибровочный объект (графический файл) распечатывают, и полученное печатное изображение фотографируют тестируемой оптической системой (камерой). Параметры ориентирования оптической системы (камеры) исключаются путем проективных преобразований, которые определяются из корреляционного соответствия выбранных реперных точек на фотографии и в исходном файле. Затем фотография объекта сравнивается корреляционным методом с содержимым исходного графического файла, приведенным в соответствие с ракурсом снимка с помощью проективных преобразований. Для каждого пикселя приемной матрицы оптической системы (камеры) вычисляется значение смещения по двум перпендикулярным осям относительно идеального положения (соответствующего изображению камерой-обскурой).
Полученную матрицу смещений можно использовать для коррекции изображений, получаемых при помощи данной оптической системы. Также при необходимости можно в явном виде определить параметры ориентирования камеры при съемке.
Для определения хроматической аберрации оптической системы производят сравнение цветовых каналов изображения. Полученную матрицу также можно использовать для коррекции изображений.
Искажения, вносимые печатающим устройством, пренебрежимо малы по сравнению с искажениями изображения при съемке (меньше в 30-50 раз). При необходимости их можно определить и исключить довольно простым способом.
Таким образом, отличие от прототипа состоит в том, что в данном методе не требуется измерения положений реперных точек и их изображений, не делается никаких априорных предположений о свойствах функции дисторсии. Используется виртуальный калибровочный объект, который поточечным корреляционным методом сравнивают с изображением данного объекта, полученным с использованием тестируемой оптической системы. С помощью данного способа можно получить не только радиальную компоненту дисторсии, но и другие виды искажений, возможные в оптической системе (например, тангенциальную компоненту дисторсии, величину хроматической аберрации) для любой заданной точки кадра. Для определения геометрических искажений, вносимых в изображение оптической системой, виртуальный калибровочный объект сравнивают с изображением, а для получения величины хроматических искажений сравнивают распределение интенсивности в цветовых каналах фотографии черно-белого объекта. В результате определяют двумерную матрицу смещений, которую можно использовать для коррекции снимков, полученных с помощью данной оптической системы.
Способ осуществляется следующим образом.
Пусть 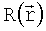 - известное бинарное распределение в плоскости объекта, a
- известное бинарное распределение в плоскости объекта, a 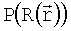 - преобразование исходного распределения, включающее в себя сдвиг, изменение масштаба, поворот и проективное преобразование. В случае отсутствия дисторсии (модель камеры-обскуры) это и будет распределение почернения в плоскости изображения.
- преобразование исходного распределения, включающее в себя сдвиг, изменение масштаба, поворот и проективное преобразование. В случае отсутствия дисторсии (модель камеры-обскуры) это и будет распределение почернения в плоскости изображения.
Обозначим через 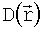 матрицу смещений положений пикселей изображения в результате различного рода геометрических искажений (дисторсии, отклонения точки пересечения оптической оси с приемной матрицей от центра матрицы и т.д.). Тогда
матрицу смещений положений пикселей изображения в результате различного рода геометрических искажений (дисторсии, отклонения точки пересечения оптической оси с приемной матрицей от центра матрицы и т.д.). Тогда 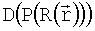 - распределение в плоскости изображения с учетом искажений. Чтобы выделить матрицу смещений D, мы сравниваем полученное в фотоаппарате изображение
- распределение в плоскости изображения с учетом искажений. Чтобы выделить матрицу смещений D, мы сравниваем полученное в фотоаппарате изображение 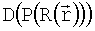 с исходным распределением, на которое наложено преобразование
с исходным распределением, на которое наложено преобразование 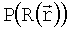 .
.
Первый шаг в осуществлении описываемого способа - это синтез калибровочного объекта. Пример заполнения части объекта случайной информацией показан на Фиг.1. Общее число информационных элементов объекта и размер его при печати зависят от расстояния, с которого предполагается проводить съемку, и от фокусного расстояния оптической системы. Практика показывает, что линейный размер изображения одного информационного элемента для оптимальной работы корреляционного метода должен быть не меньше трех пикселей приемной матрицы.
При съемке с некоторого расстояния под некоторым углом прямоугольный калибровочный объект виден не в виде прямоугольника, а в виде четырехугольника, все стороны которого, в общем случае, различны. Для удобства использования корреляционного метода мы снимаем калибровочный объект так, чтобы его границы не попадали в кадр. На Фиг.2 показана схема кадрирования при получении изображения калибровочного объекта, внутренняя рамка соответствует границам кадра. Это необходимо для определения характеристик искажений по всему полю зрения. При этом на прямоугольную матрицу оптической системы отображается часть плоскости, которая также, в общем случае, является неправильным четырехугольником. Слева на Фиг.3 изображена модель изображения калибровочного объекта, а справа - соответствующая ей область объекта, попавшая в кадр.
В общем случае виртуальная плоскость объекта и плоскость изображения связаны друг с другом преобразованиями поворота, сдвига, масштаба и проекции (т.е. степенью трапециевидности изображения прямоугольного объекта). Преобразование определяется восемью параметрами, из которых 2 отвечают за сдвиг, 1 - за поворот, 1 - за масштаб. Воспользуемся основной теоремой о проективном преобразовании плоскости (каковы бы ни были четыре точки А, В, С, D плоскости П, из которых никакие три не лежат на одной прямой, и четыре точки А', В', С', D' той же плоскости, из которых никакие три также не лежат на одной прямой, существует и притом только одно проективное преобразование, которое точки А, В, С, D переводит соответственно в точки А', В', С', D'). Таким образом, для полного определения параметров преобразования необходимо и достаточно найти попарное соответствие четырех точек в плоскости объекта и четырех точек в плоскости изображения, причем никакие три точки не должны лежать на одной прямой. Координаты х', у' точки в плоскости изображения связаны с координатами х, у в плоскости объекта дробно-линейными соотношениями:
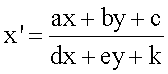
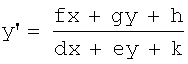
Параметров в этом преобразовании 9, но только 8 из них независимые, все параметры могут быть умножены на одно и то же число. Таким образом, найдя соответствие между четверками точек, мы знаем закон преобразования координат между плоскостью объекта и плоскостью изображения, т.е. преобразование P(R(r)). Теперь о выборе точек для определения параметров преобразования. Дело в том, что в плоскости изображения распределение соответствует не просто проективно преобразованному объекту, на проективное преобразование накладывается еще и дисторсионное искажение. Если в качестве реперных точек использовать угловые точки изображения, то при сравнении изображения и исходного калибровочного объекта, деформированного путем вышеуказанных преобразований для соответствия ракурсу съемки, мы получаем картину, изображенную на Фиг.4. Слева показана матрица горизонтальной составляющей смещения пикселей изображения за счет дисторсии, справа - вертикальная составляющая. Серый тон соответствует нулевому смещению, светлый - смещению налево (для горизонтальной компоненты) или вверх (для вертикальной компоненты), темный - смещению направо (вниз). На Фиг.5 показано распределение абсолютных значений смещений в зависимости от координат в кадре. Чем темнее тон, тем больше искажения. Неискаженными остаются угловые области, где мы выбрали реперные точки, и центр. Смещение центра неискаженной области относительно центра кадра соответствует смещению точки пересечения оптической оси камеры с приемной матрицей относительно центра матрицы. В первом приближении (когда оптическая ось камеры пересекает плоскость приемной матрицы строго в центре) картина сдвигов симметрична. Таким образом, выбор точек с априорно одинаковым значением дисторсии в качестве реперных приводит к нахождению истинных значений параметров проективного преобразования за исключением масштаба. Тем не менее, применение этой характеристики позволяет правильно провести коррекцию кривизны изображений. Масштаб же восстанавливается с помощью естественного предположения о том, что искажения изображения минимальны в центре кадра. После введения поправки к масштабному преобразованию мы получаем искомое преобразование P(R(r)). Теперь при сравнении изображения и калибровочного объекта, к которому применено преобразование для соответствия ракурсу съемки, мы получаем картину распределения величины дисторсионного искажения, показанную на Фиг.6. Слева - матрица горизонтальной составляющей смещения, справа - вертикальная составляющая. Чем светлее тон, тем больше смещение налево (вверх), чем темнее, тем больше смещение направо (вниз). На Фиг.7 показано распределение абсолютных значений смещения в зависимости от координат в кадре. Чем темнее тон, тем искажения больше. Видно, что в центральной части кадра искажения минимальны, сильнее всего дисторсия сказывается в угловых областях. Для обычных цифровых фотоаппаратов среднего класса максимальная величина смещения положения точек изображения относительно идеального составляет десятки пикселей, до трех-пяти процентов от линейного размера изображения.
Рассмотрим процедуру сравнения двух распределений интенсивности. Исходное виртуальное (неискаженное) распределение интенсивности в файле и второе, полученное при фотографировании, сравниваются при помощи корреляционного метода, который используется, например, для определения градиентов оптической толщины потоков [8, 9].
Итак, у нас имеется два распределения интенсивности - изображение, полученное на приемной матрице, и исходное рассчитанное распределение, находящееся в файле, к которому применено обратное проективное преобразование. Разница в положениях соответствующих точек этих двух распределений - это и есть искомая матрица смещений вследствие дисторсии. Для окрестности каждой точки (пикселя) изображения определим величину относительного смещения. Для этого рассмотрим взаимную корреляцию интенсивностей I0 пар небольших участков изображений:
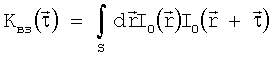 ,
,
где S - область, по которой проводится интегрирование. В случае жесткого смещения или выбора на картине участка такого небольшого размера, что изображение перемещается как целое, без деформации, функция взаимной корреляции принимает вид:
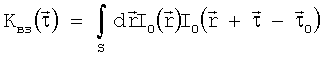 ,
,
где  - вектор смещения для всего изображения или вектор локального смещения в случае ограниченной области. Нетрудно видеть, что функция
- вектор смещения для всего изображения или вектор локального смещения в случае ограниченной области. Нетрудно видеть, что функция 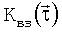 соответствует функции автокорреляции неискаженного изображения, смещенной на
соответствует функции автокорреляции неискаженного изображения, смещенной на  . Для окрестности точки изображения мы получаем функцию
. Для окрестности точки изображения мы получаем функцию 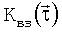 и по положению ее максимума определяем локальное значение
и по положению ее максимума определяем локальное значение  для этого участка, которое мы приписываем точке, соответствующей центру окна. Непрерывно сканируя окном изображение и выполняя в каждой точке описанную процедуру, мы строим поле смещений. Следует обратить внимание на то, что здесь мы получаем ориентированное смещение.
для этого участка, которое мы приписываем точке, соответствующей центру окна. Непрерывно сканируя окном изображение и выполняя в каждой точке описанную процедуру, мы строим поле смещений. Следует обратить внимание на то, что здесь мы получаем ориентированное смещение.
После обработки всего кадра мы получаем величину дисторсионного сдвига в каждой точке (пикселе). При этом смещение вычисляется с точностью, существенно меньшей размера пикселя в фотографическом изображении за счет аппроксимации функции взаимной корреляции.
Для определения матрицы смещений не требуется знания параметров внешнего ориентирования оптической системы. При желании их можно определить в явном виде.
Так как нам известно соответствие координат изображения и объекта, то путем очевидных геометрических расчетов мы можем определить положение центра проекции в системе координат, связанной с объектом, то есть положение оптической системы и углы наклона ее оптической оси по отношению к плоскости объекта.
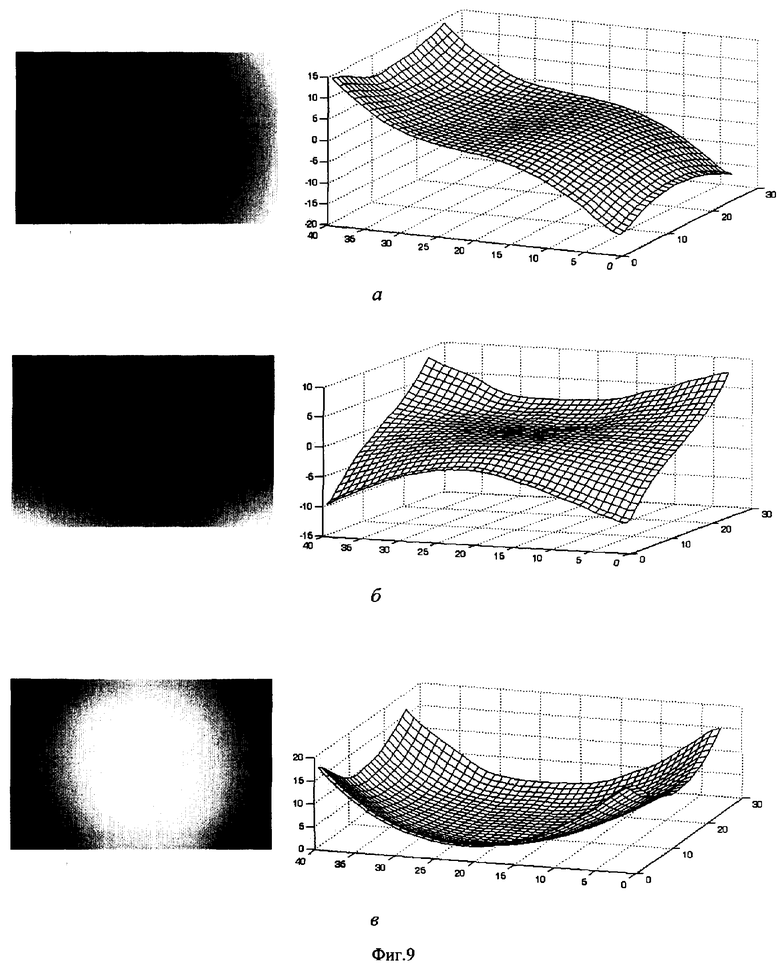
Приведем пример осуществления описанного способа калибровки оптической системы. Для проверки его работоспособности был прокалиброван ряд цифровых фотоаппаратов различных производителей. Фотографировался специально отпечатанный плоский калибровочный объект. Съемка проводилась «с руки», оптическая ось камеры была приблизительно перпендикулярна плоскости объекта. Для различных значений фокусных расстояний получены матрицы сдвига. На Фиг.8 приведены матрицы искажений для фотоаппарата Olympus SP350, а - горизонтальная составляющая сдвига в тоновом представлении и в виде поверхности, б - вертикальная составляющая, в - абсолютная величина искажения в зависимости от координаты. Данные приведены для размера кадра 1280×960 пикселей. По горизонтальным осям отложены условные координаты по плоскости кадра, по вертикальным осям графиков - величины искажения. На Фиг.9 показаны аналогичные матрицы для фотоаппарата Canon EOS 10D, а - горизонтальная составляющая сдвига, б - вертикальная составляющая, в - абсолютная величина искажения, размер кадра 1280×850 пикселей.
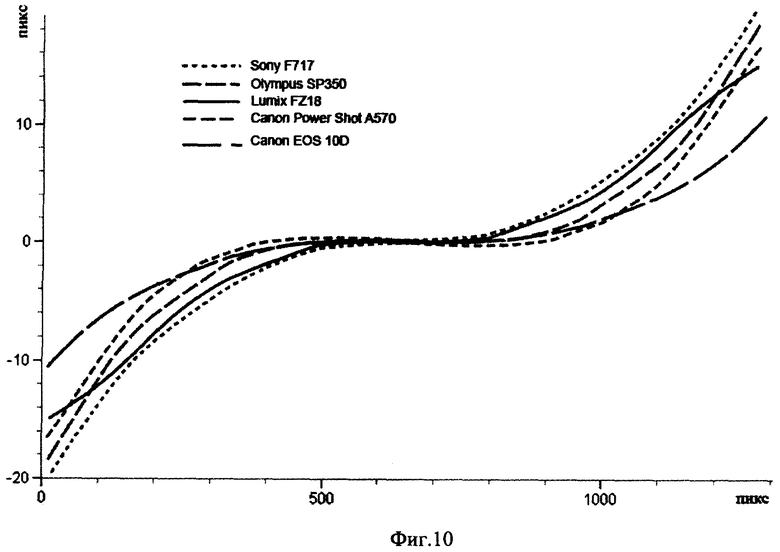
На Фиг.10 показаны центральные горизонтальные сечения матриц смещений для некоторых марок цифровых фотоаппаратов (для минимального фокусного расстояния и размера кадра 1280×960 пикселей). По оси х - номера пикселей приемной матрицы по центральной линии, от левого края кадра до правого, по оси у - величина горизонтальной составляющей матрицы смещений. Видно, что, хотя по порядку величины смещения в разных фотоаппаратах похожи, некоторые из моделей имеют свои особенности. Например, у фотоаппарата Canon EOS 10D (зеркальный со сменным объективом SIGMA UC-III) величина дисторсионного искажения почти в полтора-два раза меньше, чем у аппаратов со встроенными объективами. А у фотоаппарата Lumix FZ18 кривая дисторсии имеет перегиб.
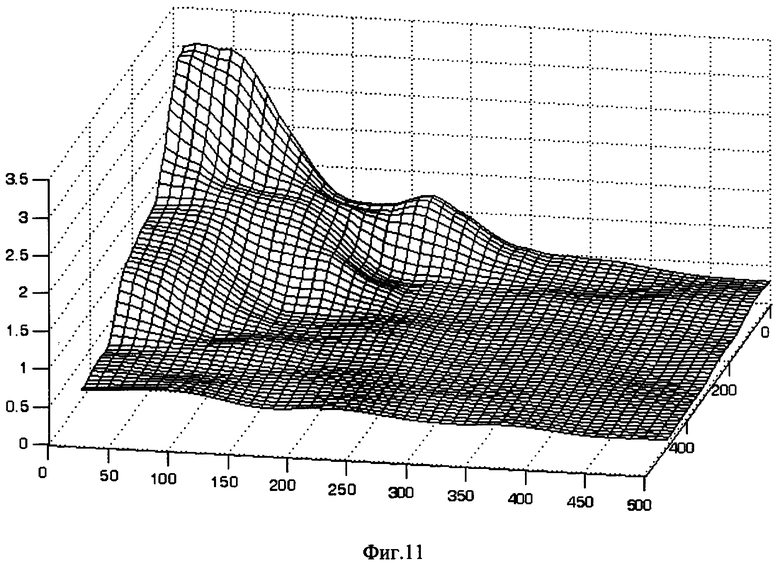
Если оптическая система дает хроматические искажения, их можно оценить путем сравнения цветовых каналов цифрового изображения. На Фиг.11 показана часть матрицы абсолютной величины хроматических искажений для фотоаппарата Olympus SP350. Изображена только угловая область размером 500×500 пикселей с максимальными искажениями (полный размер кадра 3264×2448). Сравнивались красный и синий каналы изображения, по вертикальной оси отложена абсолютная величина смещения содержимого каналов относительно друг друга в пикселях.
После определения матрицы смещений можно исправлять изображения, полученные этой же оптической системой при таком же фокусном расстоянии. Для иллюстрации на Фиг.12 приведены результаты восстановления описанным методом изображения, полученного с помощью фотоаппарата Canon Power Shot A570. На левом неисправленном снимке видно заметное бочкообразное искажение. Справа - исправленный с помощью рассчитанной матрицы искажений снимок. Нужно отметить, что функция геометрической корректировки изображения и сами матрицы искажений для различных фокусных расстояний могут быть зашиты во внутреннее программное обеспечение фотоаппарата еще на стадии изготовления, при этом получаемые с помощью этой функции изображения будут неискаженными.
Литература
1. D.С.Brown. Close-range camera calibration. Photogrammetric Engineering, 37(8):855-866, 1971.
2. R.Y.Tsai. "A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses", IEEE Trans. Rob. Autom, RA-3(4), p.323-344, 1987.
3. Гельман Р.Н., Дунц А.Л. Лабораторная калибровка цифровых камер с большой дисторсией. // Геодезия и картография. - 2002. - №7. - С.23-31.
4. Юрченко В.И. Способ аналитической обработки неметрических снимков. // Геодезия и картография. - 2000 - №11. - С.23-30.
5. H.Farid and A.C.Popescu. "Blind removal of lens distortion". Optical Society of America, Vol.18. №9, 2001.
6. G.Stein. Accurate internal camera calibration using rotation, with analysis of sources of error. In ICCV, pages 230-236, Cambridge, MA, June 1995.
7. R.Hartley and S.B.Kang. Parameter-free Radial Distortion Correction with Centre of Distortion Estimation. Texnical Report MSR-TR-2005-42. Microsoft Research, Microsoft Corporation.
8. Meier G.E.A. (2002) Computerized background-oriented schlieren. // Experiments in Fluids №33. P.181-187.
9. В.Н.Боркова, А.В.Крайский, Т.В.Миронова, Т.Т.Султанов. Измерение градиентов оптической длины с помощью корреляционной обработки цифровых фотографий случайных картин. Краткие сообщения по физике, 2006, №7, с.38-41
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ фотограмметрической калибровки для оценки коэффициентов радиальной и тангенциальной дисторсии объектива и матрицы внутренних параметров камеры | 2023 |
|
RU2808083C1 |
| Способ контроля пространственного положения участников спортивного события на игровом поле | 2016 |
|
RU2616152C1 |
| Способ калибровки видеосистемы для контроля объектов на плоской площадке | 2016 |
|
RU2610137C1 |
| СПОСОБ КАЛИБРОВКИ ЦИФРОВОЙ ВИДЕОКАМЕРЫ ДЛЯ АДАПТИВНОГО ПРОЦЕССА НАМОТКИ | 2005 |
|
RU2295109C2 |
| СПОСОБ АДАПТИВНОЙ КАЛИБРОВКИ РАДИАЛЬНОЙ ДИСТОРСИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2004 |
|
RU2289111C2 |
| Способ определения положения области поиска соответствий на дисторсионно-искажённых изображениях | 2020 |
|
RU2740435C2 |
| Способ калибровки подводной видеокамеры | 2022 |
|
RU2789190C1 |
| Способ измерения дальности до вагона на прямолинейном участке железнодорожного пути | 2021 |
|
RU2769453C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТЕЙ ДО ОБЪЕКТОВ ПО ИЗОБРАЖЕНИЯМ С ЦИФРОВЫХ ВИДЕОКАМЕР | 2016 |
|
RU2626051C2 |
| Система калибровки набора камер для задач оптического трекинга объектов в пространстве | 2023 |
|
RU2811363C1 |








Способ калибровки оптической системы, основанный на сравнении полученного этой системой изображения калибровочного объекта с самим объектом. Создают цифровой виртуальный калибровочный объект, напоминающий спекл-структуру и заполненный случайной информацией, причем линейный размер изображения информационного элемента калибровочного объекта не менее 3-х пикселей приемной матрицы. Затем его переносят на плоскую поверхность, получают с помощью тестируемой оптической системы его оцифрованное изображение, сравнивают корреляционным методом распределения интенсивности в оцифрованном изображении и в цифровом виртуальном калибровочном объекте, приведенном по ракурсу в соответствие с его оцифрованным изображением проективными преобразованиями, при этом определяют двумерную матрицу смещений положений точек указанного оцифрованного изображения относительно цифрового виртуального калибровочного объекта. Данный способ позволяет калибровать оптическую систему без измерения положений реперных точек и их изображений и без априорных предположений о свойствах функции дисторсии. 2 з.п. ф-лы, 16 ил.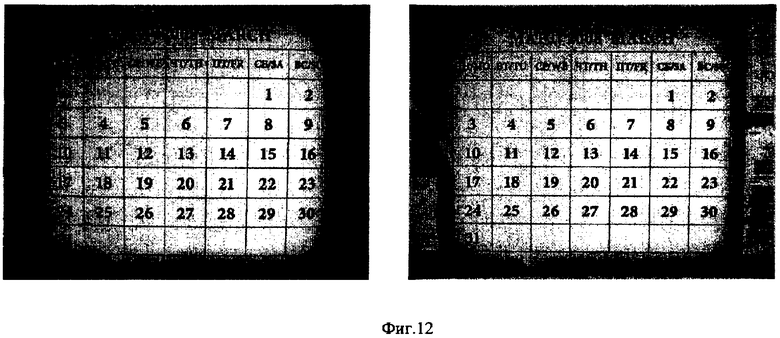
1. Способ калибровки оптической системы, основанный на сравнении полученного этой системой изображения калибровочного объекта с самим объектом, отличающийся тем, что создают цифровой виртуальный калибровочный объект, напоминающий спекл-структуру и заполненный случайной информацией, причем линейный размер изображения информационного элемента калибровочного объекта не менее 3 пикселей приемной матрицы, который переносят на плоскую поверхность, получают с помощью тестируемой оптической системы его оцифрованное изображение, сравнивают корреляционным методом распределения интенсивности в оцифрованном изображении и в цифровом виртуальном калибровочном объекте, приведенном по ракурсу в соответствие с его оцифрованным изображением проективными преобразованиями, при этом определяют двумерную матрицу смещений положений точек указанного оцифрованного изображения относительно цифрового виртуального калибровочного объекта.
2. Способ по п.1, отличающийся тем, что двумерную матрицу смещений положений точек оцифрованного изображения относительно цифрового виртуального калибровочного объекта используют для исправления геометрических искажений изображения.
3. Способ по п.1, отличающийся тем, что для определения хроматических искажений оцифрованного изображения цифрового виртуального калибровочного объекта сравнивают распределения интенсивности в цветовых каналах указанного изображения, получают матрицу хроматических искажений, которую можно использовать для коррекции изображения.
| СПОСОБ ФОТОГРАММЕТРИЧЕСКОЙ КАЛИБРОВКИ ФОТОКАМЕР | 2006 |
|
RU2308001C1 |
| СПОСОБ АДАПТИВНОЙ КАЛИБРОВКИ РАДИАЛЬНОЙ ДИСТОРСИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2004 |
|
RU2289111C2 |
| СПОСОБ КАЛИБРОВКИ ДИСТОРСИИ ОПТИКО-ЭЛЕКТРОННОГО УСТРОЙСТВА | 2006 |
|
RU2321888C1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
Авторы
Даты
2010-02-10—Публикация
2008-04-17—Подача