Изобретение относится к вычислительной технике и может быть использовано для оценки коэффициентов радиальной и тангенциальной дисторсии объектива и матрицы внутренних параметров камеры.
Известен способ фотограмметрической калибровки (Тюфлин Ю.С., Степаньянц Д.Г., Князь В.А., Желтов С.Ю. Предвычисление точности определения координат точек объекта в ближней фотограмметрии // Геодезия и картография. 2004. №11. С. 29-32), включающий определение координат точек плоского тест-объекта, фотографирование тест-объекта, измерение координат точек тест-объекта на снимках, вычисление элементов внутреннего ориентирования и параметров фотограмметрической дисторсии. Указанный способ основан на двукратном фотографировании тест-объекта одной фотокамерой из одной точки пространства. Тест-объект после первого фотографирования перемещают вдоль оптической оси фотокамеры на определенное расстояние, а величину перемещения при этом фиксируют с помощью отсчетного приспособления с высокой точностью. Далее на полученных снимках измеряют координаты точек тест-объекта. Элементы внутреннего ориентирования вычисляют совместно с элементами внешнего ориентирования снимков из решения уравнений коллинеарности, составленных для каждого изображения точки тест-объекта. Параметры фотограмметрической дисторсии определяют по остаточным расхождениям вычисленных и измеренных координат точек тест-объекта с учетом найденных элементов внешнего и внутреннего ориентирования снимков.
К недостатку способа следует отнести необходимость применения отсчетного приспособления для измерения величины перемещения тест-объекта с высокой точностью.
Из уровня техники известен способ фотограмметрической калибровки фотокамер (патент RU 2308001, опубликовано 10.10.2007, МПК: G01C 11/02 (2006.01)). Способ включает определение координат точек плоского тест-объекта, фотографирование тест-объекта, измерение координат точек тест-объекта на снимках, вычисление элементов внутреннего ориентирования и параметров фотограмметрической дисторсии. При этом плоский тест-объект создают на поверхности земли, фотографирование выполняют с самолета с двух высот фотографирования, разность высот определяют с помощью бортовой системы спутниковой навигации (GPS), при вычислении элементов внутреннего ориентирования координаты главной точки принимают равными координатам центральной точки кадра, а фокусное расстояние вычисляют по точкам тест-объекта, расположенным симметрично относительно центра кадра.
К недостатку способа следует отнести его применимость только к случаям калибровки камер, установленных на летательных аппаратах.
Известен способ калибровки видеодатчиков многоспектральной системы технического зрения (патент RU 2692970, опубликовано 28.06.2019, МПК: G06T 7/80 (2017.01)), в котором выполняют съемку тестового объекта с различных ракурсов, находят на снятых с различных ракурсов изображениях тестового объекта особые точки, выполняют оценку их координат с субпиксельной точностью, производят оценку матриц внутренних параметров камер, оценку векторов коэффициентов дисторсии объективов камер, оценку матриц внешних параметров, определяющих взаимное пространственное положение камер. Одновременную калибровку нескольких камер - как видимого, так и инфракрасного диапазонов - производят с использованием тестового объекта с калибровочным шаблоном с клетками в виде темных n-угольников на светлом поле, при этом на этапе инициализации алгоритма калибровки осуществляют ввод значений параметров тестового калибровочного шаблона: размера клетки, количества клеток по горизонтали и вертикали. При n=4 калибровочный шаблон представляет собой шахматное поле с априори известными в системе координат шаблона углами, что позволяет применять для калибровки классическую методику Джанга (Zhang Z. A flexible new technique for camera calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000. Vol. 22, No. 11. P. 1330-1334). В то же время применение для реализации способа универсальных, контрастных в различных спектральных диапазонах, тестовых шаблонов (патент RU 2672466, опубликовано 14.11.2018, МПК: G06T 7/80 (2017.01)), накладывает ряд ограничений, связанных, например, с необходимостью высокоточного нанесения полимерной пленки для формировании шахматного поля.
В качестве прототипа выбран наиболее близкий по совокупности признаков способ компенсации дисторсии объектива (патент RU 2790055, опубликовано 14.02.2023, МПК: G01M 11/02 (2006.01)). В способе прототипа для коррекции геометрических искажений изображения определяют коэффициенты радиальной и тангенциальной дисторсии с помощью калибровочного шаблона в виде полигона узловых точек, упорядоченных по концентрическим окружностям и с постоянным шагом по углу. При этом определяют декартовы пиксельные координаты узлов полигона, осуществляют их преобразование в полярные координаты, вычисляют коэффициенты математической модели дисторсии, которая представляет собой разложения в ряды - степенного и двух рядов Фурье, последовательно выполняют компенсацию радиальной дисторсии, периодических составляющих радиальной и тангенциальной дисторсии.
К недостаткам способа прототипа следует отнести следующее.
1) Необходимость центрирования декартовых координат узловых точек для обеспечения совпадения центра фотоматрицы и центра изображения полигона.
2) Для исключения проективных искажений изображения калибровочного полигона, которые могут быть в ходе калибровки трактованы как дисторсия объектива, необходимо обеспечить строго нормальное расположение плоскости полигона по отношению к оптической оси объектива калибруемой камеры. Аналогичное замечание касается и угловой юстировки калибровочного полигона по крену для обеспечения совмещения нулевой строки фотоматрицы с изображением горизонтальной оси полигона.
По этой причине для реализации способа необходимо прецизионное стендовое оборудование, обеспечивающее взаимное высокоточное позиционирование камеры и калибровочного полигона.
3) Как следует из описания прототипа, компенсация дисторсии после вычисления калибровочных коэффициентов по данному способу потребует сначала перехода к полярным координатам, т.е. вычисления обратной тригонометрической функции, затем вычисления тригонометрических функций для компенсации дисторсии, а также вычисления тригонометрических функций для возврата к декартовым координатам при визуализации изображения с компенсированной дисторсией. Таким образом, компенсация дисторсии по способу прототипа имеет большую вычислительную сложность по сравнению с известным из (Hartley R., Zisserman A. Multiple view geometry in computer vision: 2nd edition. Cambridge: Cambridge University Press, 2003. 656 p.) подходом, основанным на численном решении нелинейного уравнения для модели дисторсии Брауна-Конради (Brown D.C. Close-Range Camera Calibration // Photogrammetric Engineering. 1971. Vol. 37, No. 8. P. 855-866.) без вычисления тригонометрических функций: как прямых, так и обратных.
4) Известно, что радиальная дисторсия наиболее сильно проявляется на углах кадра. Однако радиально-кольцевое размещение узловых точек калибровочного полигона способа прототипа приводит к тому, что именно на углах кадра их количество на единицу площади кадра оказывается наименьшим, что может быть критичным при оценивании коэффициентов, характеризующих радиальную дисторсию, с помощью численных методов.
Техническая проблема, решаемая созданием заявленного изобретения, заключается в разработке способа калибровки, не требующего:
- центрирования изображения калибровочного полигона,
- высокоточного углового позиционирования оптической оси камеры коллинеарно нормали к плоскости полигона,
- вычисления вычислительно емких прямых и обратных тригонометрических функций в процедуре компенсации радиальной и тангенциальной дисторсии,
а также обеспечивающего высокую плотность узловых точек на краях кадра в процессе калибровки.
Технический результат изобретения заключается в решении переопределенной системы уравнений проективной геометрии для априори известных в системе координат калибровочного полигона пространственных координат его узловых точек.
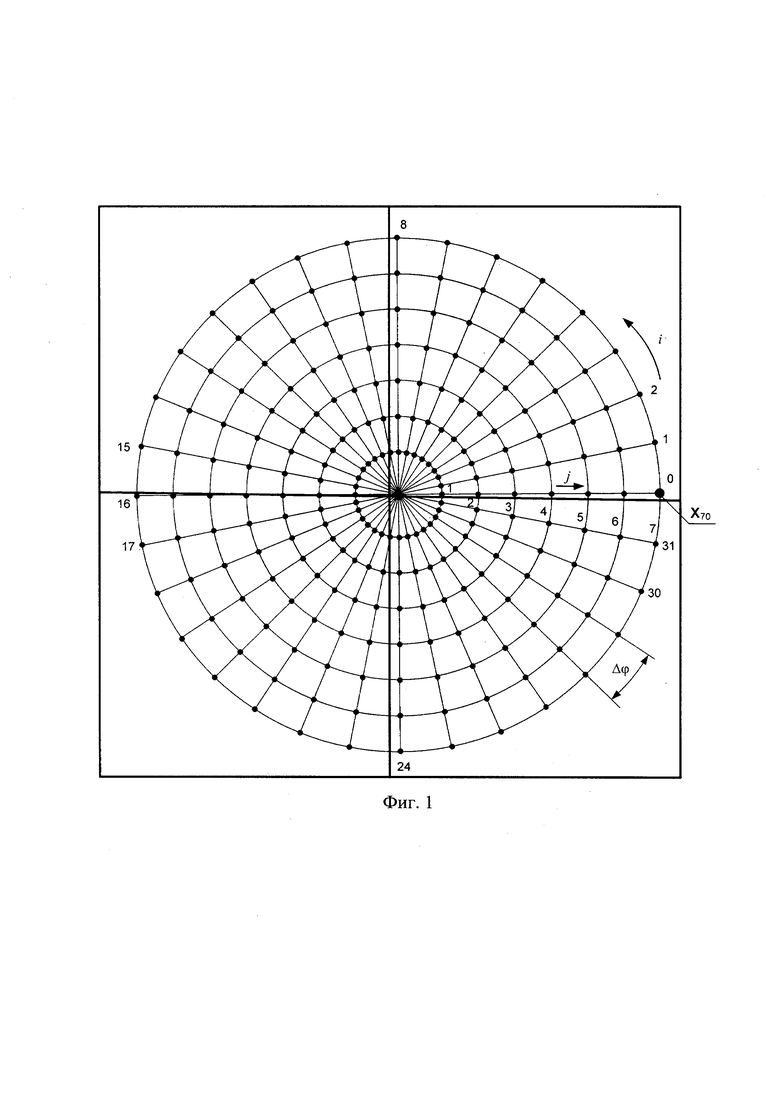
Технический результат достигается тем, что по аналогии с (Zhang Z. A flexible new technique for camera calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000. Vol. 22, No. 11. P. 1330-1334) калибровку выполняют не по единственному ракурсу съемки калибровочного радиально-кольцевого полигона способа прототипа, а по нескольким, но не менее чем двум. При этом взаимное позиционирование калибруемой камеры и калибровочного полигона не требует точного центрирования и выполнения условия совмещения нулевой строки фотоматрицы с изображением горизонтальной оси полигона: контролируется только полное попадание полигона в поле зрения камеры и его приблизительно симметричное расположение относительно центральных строки и столбца кадра камеры. Симметричность расположения может визуально контролироваться оператором путем выведения служебных маркеров в виде линейных мир (фиг. 1) поверх центральных строки и столбца изображения кадра с камеры (RU 2703492, МПК F41G 3/06 (2006.01), G02B 23/12 (2006.01), G01B 11/27 (2006.01), опубл. 17.10.2019). Критерием приблизительно симметричного расположения калибровочного полигона может выступать попадание центра перекрестия маркеров внутрь изображения окружности полигона с наименьшим радиусом (см. фиг. 1).
Начальное угловое положение калибровочного полигона по крену также может контролироваться с помощью маркеров. При этом критерием установки полигона в исходное положение с малым креном может выступать попадание горизонтального маркера в радиальные секторы «0-1», «15-16», «16-17» или «31-0». Таким образом, установка начального углового положения контролируется по попаданию маркера центра кадра по горизонтали в радиальные секторы полигона, прилегающие к его горизонтальной оси симметрии «0-Np/2», где Np - количество радиальных направлений полигона (для полигона из способа прототипа Np=32 и ось симметрии соответствует радиальным ветвям «0-16»).
Нормаль к плоскости полигона в процессе калибровки может быть и не коллинеарна оси калибруемой камеры. При съемке полигона это приведет к характерным для любой проективной камеры геометрическим искажениям.
После съемки калибровочного полигона в исходном положении выполняется его поворот по крену по или против часовой стрелки на угол

где m≥2 - общее количество калибровочных положений, а Δϕ - угловой размер радиального сектора полигона (для - способа прототипа Δϕ=360°/Np=360°/32=11,25°), и выполняется съемка следующего кадра.
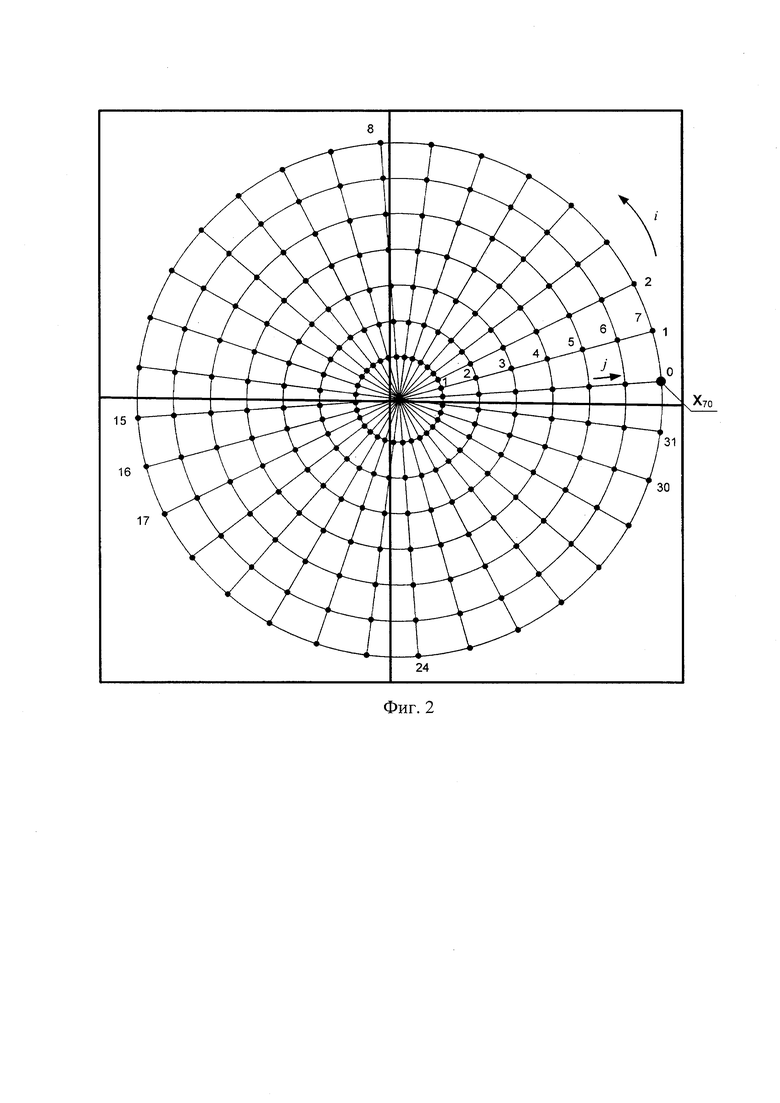
За счет углового перемещения полигона достигается увеличение общего количества узловых точек вблизи углов кадра. На фиг. 2 в качестве примера проиллюстрировано изменение изображения калибровочного полигона для второго калибровочного кадра при общем количестве ракурсов съемки m=3 и повороте по крену в направлении против часовой стрелки. Линейные миры позволяют оператору визуально контролировать выполнение условия (1).
Для случая автоматизированной калибровки, например, с применением устройств автоматизированного перемещения и вращения камеры относительно калибровочного полигона (патент RU 2645432, МПК: G01C 11/00 (2006.01), опубл. 21.02.2018; патент RU 2749363, МПК: G06T 7/80 (2017.01), опубл. 09.06.2021) можно обеспечить равенство левой и правой частей выражения (1) и отказаться от этапа контроля углового положения по крену по маркерам.
После съемки m кадров полигона, в каждом из которых его угловое положение по крену изменяется по сравнению с предыдущим согласно (1), с субпиксельной точностью (Shortis M.R, Clarke Т.A., Short Т. Comparison of some techniques for the subpixel location of discrete target images // Photonics for Industrial Applications. 1994. Vol. 2350. P. 239-250) оцениваются 2D координаты узловых точек Xjik в каждом k-м кадре, k=1, 2, …m, где j - номер радиуса концентрической окружности полигона, i - номер радиальной ветви; для фиг. 1 и фиг. 2 нумерация j={1, 2,…7}, i={0, 1,…,31}.
Далее устанавливается соответствие каждой узловой точки полигона с пространственными (3D) координатами в системе координат полигона Xjik, где j - номер радиуса концентрической окружности полигона, i - номер радиальной ветви, и ее 2D проекции на плоскость изображения камеры xjik. Для нахождения однозначного соответствия между 3D координатами узловых точек полигона априори известной конфигурации и их 2D проекциями в плоскости кадра с камеры изображение как минимум одной из узловых точек полигона, выбранной в качестве опорной, должно отличаться от остальных: например, иметь больший радиус. На фиг. 1 и 2 это точка Х70, радиус которой выбран вдвое большим радиуса остальных узловых точек полигона.
После установления соответствия между 3D координатами узловых точек полигона Xjik и их 2D проекциями xjik для совокупности т кадров численным методом, например, Левенберга-Марквардта (More J. The Levenberg-Marquardt algorithm: implementation and theory // Numerical Analysis. Lecture Notes in Mathematics. 1978. Vol. 630. P. 105-116), выполняется поиск псевдорешения {K, kд} системы уравнений проективной геометрии, минимизирующего квадрат ошибки репроекции (Zhang Z. А flexible new technique for camera calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000. Vol. 22, No. 11. P. 1330-1334; Hartley R., Zisserman A. Multiple view geometry in computer vision: 2nd edition. Cambridge: Cambridge University Press, 2003. 656 p):
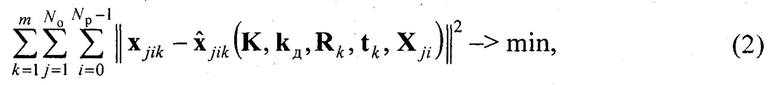
с учетом модели дисторсии Брауна-Конради:
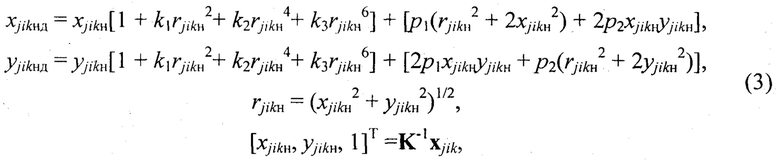
где No и Np - соответственно количество окружностей и радиальных направлений калибровочного полигона, К - матрица внутренних параметров камеры, kд=[k1, k2, k3, р1, р2]T - вектор коэффициентов дисторсии согласно модели Брауна-Конради, в которой kt, t=1…3, - коэффициенты радиальной дисторсии, pt, t=1,2, - коэффициенты тангенциальной дисторсии, (хjikнд, yjikнд). и (хjikн, yjikн) - соответственно нормированные пиксельные координаты узловых точек с дисторсией и без, Rk и tk - соответственно матрица поворота и вектор параллельного переноса (трансляции) системы координат калибруемой камеры относительно системы координат калибровочного полигона в k-м положении калибровочного полигона, k=1…m. Для случая применения калибровочного шаблона согласно способу прототипа No=7 и Np=32 (см. фиг. 1).
Поскольку в результате вращения по крену плоскость размещения узловых точек полигона не меняется, то оценка матрицы внутренних параметров 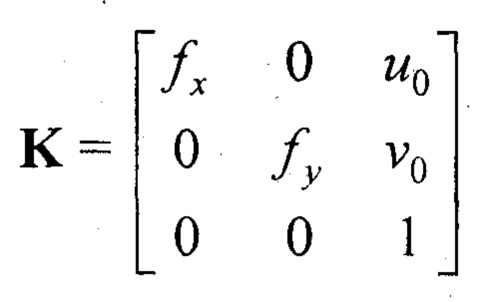 предполагает принятие следующих ограничений (Zhang Z., Matsushita Y., Ma Y. Camera calibration with lens distortion from low-rank textures // Proc. of Conf. on Computer Vision and Pattern Recognition CVPR'2011. - Colorado Springs, 2011. - P. 2321-2328):
предполагает принятие следующих ограничений (Zhang Z., Matsushita Y., Ma Y. Camera calibration with lens distortion from low-rank textures // Proc. of Conf. on Computer Vision and Pattern Recognition CVPR'2011. - Colorado Springs, 2011. - P. 2321-2328):
1) равенство фокусных расстояний ƒx и ƒy: ƒx=ƒy=ƒ;
2) координаты главной точки (u0,ν0) априори известны: как правило, принимают гипотезу (u0,ν0)=(0,5W,0,5H), где W и H -соответственно ширина и высота кадра камеры в пикселях.
Указанные ограничения приближенно справедливы для большинства выпускаемых камер, и, если точка обзора не является вырожденной, то калибровка по точкам полигона, лежащих в одной плоскости, корректно восстанавливает параметры дисторсии объектива kд и фокусное расстояние ƒ. Как показано в (Zhang Z., Matsushita Y., Ma Y. Camera calibration with lens distortion from low-rank textures // Proc. of Conf. on Computer Vision and Pattern Recognition CVPR'2011. - Colorado Springs, 2011. - P. 2321-2328), принятые ограничения не являются препятствием к успешной компенсации дисторсии.
Найденное в результате калибровки псевдорешение (2), т.е. набор параметров {ƒ, kд}, 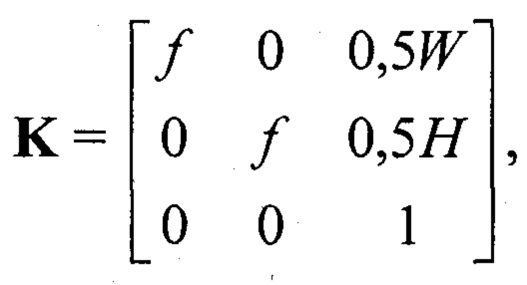 позволяет далее выполнить компенсацию дисторсии снятых камерой изображений путем численного решения (3) для каждого пикселя кадра (Hartley R., Zisserman A. Multiple view geometry in computer vision: 2nd edition. Cambridge: Cambridge University Press, 2003. 656 p). При этом тригонометрические функции в процессе поиска решения (3) не вычисляются.
позволяет далее выполнить компенсацию дисторсии снятых камерой изображений путем численного решения (3) для каждого пикселя кадра (Hartley R., Zisserman A. Multiple view geometry in computer vision: 2nd edition. Cambridge: Cambridge University Press, 2003. 656 p). При этом тригонометрические функции в процессе поиска решения (3) не вычисляются.
Поиск псевдорешения (2) обеспечивает (Zhang Z. A flexible new technique for camera calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000. Vol. 22, No. 11. P. 1330-1334) отнесение проективных геометрических искажений, вызванных установкой плоскости калибровочного полигона в общем случае не перпендикулярно линии визирования камеры, к параметрам {Rk, tk}, а не к коэффициентам дисторсии kд.
Изобретение относится к вычислительной технике и может быть использовано для оценки коэффициентов радиальной и тангенциальной дисторсии объектива и матрицы внутренних параметров камеры. Заявленный способ фотограмметрической калибровки для оценки коэффициентов радиальной и тангенциальной дисторсии объектива и матрицы внутренних параметров камеры основан на съемке испытательного полигона узловых точек, расположенных на пересечениях, равномерно распределенных No концентрических окружностей и Np радиальных направлений. По результатам съемки в кадрах с камеры выполняют оценку пиксельных координат узловых точек полигона с субпиксельной точностью и по ним вычисляют коэффициенты математической модели дисторсии и элементы матрицы внутренних параметров камеры. Съемку испытательного полигона производят m≥2 раз и перед каждым последующим экспонированием выполняют его поворот по крену на угол δϕ≈Δϕ/m, где Δϕ=360°/Νp - угловой размер радиального сектора полигона. При этом центрирование полигона выполняется по линиям маркеров центра кадра по вертикали и горизонтали и контролируется по попаданию точки пересечения маркеров в центр окружности наименьшего радиуса на изображении с камеры, а установка начального углового положения контролируется по попаданию линии маркера центра кадра по горизонтали в радиальные сектора изображения полигона, прилегающие к его горизонтальной оси симметрии, соответствующей радиальным ветвям полигона с номерами «0-Np/2». Технический результат – решение переопределенной системы уравнений проективной геометрии для априори известных в системе координат калибровочного полигона пространственных координат его узловых точек. 2 ил.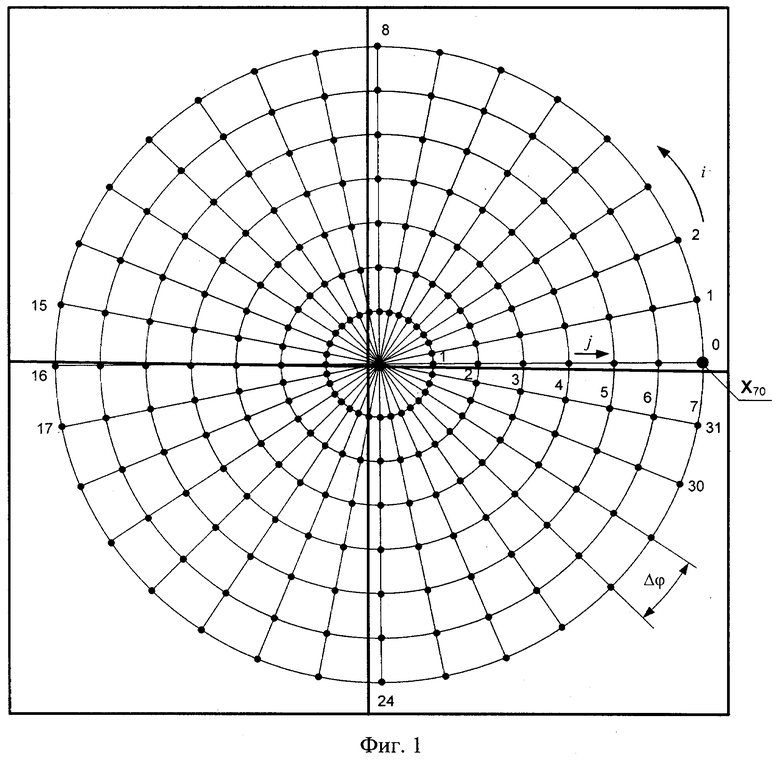
Способ фотограмметрической калибровки для оценки коэффициентов радиальной и тангенциальной дисторсии объектива и матрицы внутренних параметров камеры, в котором производят съемку испытательного полигона узловых точек, расположенных на пересечениях равномерно распределенных No концентрических окружностей и Np радиальных направлений, выполняют оценку пиксельных координат узловых точек полигона с субпиксельной точностью, вычисляют коэффициенты математической модели дисторсии и элементы матрицы внутренних параметров камеры, отличающийся тем, что съемку испытательного полигона производят m≥2 раз, при этом перед каждым последующим экспонированием полигона выполняют его поворот по крену на угол δϕ≈Δϕ/m, где Δϕ=360°/Np - угловой размер радиального сектора полигона, при этом центрирование калибровочного полигона выполняется по линиям маркеров центра кадра по вертикали и горизонтали и контролируется по попаданию точки пересечения маркеров в центр окружности наименьшего радиуса на его изображении с камеры, а установка начального углового положения контролируется по попаданию линии маркера центра кадра по горизонтали в радиальные сектора изображения полигона, прилегающие к его горизонтальной оси симметрии, соответствующей радиальным ветвям полигона с номерами «0-Np/2».
| СПОСОБ КОМПЕНСАЦИИ ДИСТОРСИИ ОБЪЕКТИВА | 2022 |
|
RU2790055C1 |
| СПОСОБ ФОТОГРАММЕТРИЧЕСКОЙ КАЛИБРОВКИ ФОТОКАМЕР | 2006 |
|
RU2308001C1 |
| DE 102018008539 A1, 05.12.2019 | |||
| УСТРОЙСТВО ДЛЯ ДЕЛЕНИЯ КОЛИЧЕСТВА ПОСЛЕДОВАТЕЛЬНЫХ ИМПУЛЬСОВ | 0 |
|
SU304706A1 |
| CN 104240262 A, 24.12.2014 | |||
| СПОСОБ АВТОМАТИЧЕСКОГО ОПРЕДЕЛЕНИЯ И КОРРЕКЦИИ РАДИАЛЬНОЙ ДИСТОРСИИ НА ЦИФРОВОМ ИЗОБРАЖЕНИИ | 2006 |
|
RU2351091C2 |
| KR 2004053877 A, 25.06.2004 | |||
| WO 2005073669 A1, 11.08.2005. | |||
Авторы
Даты
2023-11-23—Публикация
2023-05-02—Подача