Область техники, к которой относится изобретение
Настоящее изобретение относится к устройству криптографической обработки, способу криптографической обработки и его компьютерной программе, и более конкретно к устройству криптографической обработки с улучшенной устойчивостью к линейному анализу и дифференциальному анализу, известным как обработка анализа дешифрования и обработка атаки криптоанализа, способу криптографической обработки и его компьютерной программе.
Уровень техники
В настоящее время, в результате развития передачи данных по сетям и электронной коммерции, обеспечение безопасности при передачах данных становится жизненно важно проблемой. Криптографическая технология представляет собой одно из средств обеспечения безопасности, и в настоящее время при передаче данных на практике используют различные криптографические технологии.
Например, в практическое использование внедрена система, в которой установлен модуль криптографической обработки в виде небольшого устройства, такого как карта с интегральной микросхемой, при этом передачу данных и прием данных выполняют между картой с интегральной микросхемой и устройством считывания/записи, которое действует как устройство считывания и записи данных, при этом выполняют обработку аутентификации или шифрование/дешифрование передаваемых/принимаемых данных.
Существуют разные алгоритмы криптографической обработки, которые в широком смысле можно разделить на криптографическую систему с одним ключом, в которой установлены разные ключ шифрования и ключ дешифрования, например открытый ключ и секретный ключ, и криптографическую систему с общим ключом, в которой общий ключ установлен как ключ шифрования и как ключ дешифрования.
Также в криптографической системе с общим ключом существуют различные алгоритмы. Один из них представляет собой систему, в которой множество ключей генерируют с использованием общего ключа в качестве основания, и обработку преобразования данных многократно выполняют для каждого модуля блока (64 бита, 128 бит и т.д.) с использованием множества сгенерированных ключей. Типичный алгоритм, в котором используется такой способ генерирования ключа, и обработка преобразования данных представляет собой криптографический способ общий-ключ-блок.
В качестве типичного алгоритма криптографической обработки общий-ключ-блок, например, используется алгоритм DES (Стандарт шифрования данных), который представляет собой стандартный федеральный способ шифрования в Соединенных Штатах Америки и широко используется в различных областях.
Любой алгоритм, применяемый для криптографической обработки общий-ключ-блок, в соответствии со стандартом DES, в основном, может быть разделен на блок функции цикла, который выполняет преобразование входных данных, и блок планирования ключа, предназначенный для генерирования ключа, применяемого в каждом цикле части функции цикла (F-функции). Ключ (подключ) цикла, который должен применяться в каждом цикле в блоке функции цикла, генерируют в блоке планирования ключа, в который вводят один мастер-ключ (главный ключ), и применяют в каждой части функции цикла.
Однако при такой криптографической обработке с общим ключом возникает проблема возможной утечки ключа в результате криптоанализа. Известен дифференциальный анализ (также называемый способом дифференциального криптоанализа или атакой дифференциального криптоанализа), в котором анализируют прикладной ключ в каждой функции цикла путем анализа множества входных данных (открытый текст) и ее выходных данных (зашифрованный текст), и линейный анализ (также называемый способом линейного криптоанализа или атакой линейного криптоанализа), при котором выполняют анализ на основе открытого текста и соответствующего зашифрованного текста, в качестве типичной методики криптоанализа или методики атаки.
Простота анализа ключа средствами криптоанализа приводит к низкой безопасности криптографической обработки. В обычном алгоритме DES возникает проблема, состоящая в том, что поскольку обработка (матрица преобразования), применяемая в блоке линейного преобразования блока функции цикла (F-функции), эквивалентна в цикле каждого этапа, упрощается криптоанализ, и, следовательно, облегчается анализ ключа.
Сущность изобретения
Проблема, решаемая изобретением
Настоящее изобретение было выполнено с учетом указанных выше проблем, и целью его является создание устройства криптографической обработки, в котором реализован криптографический алгоритм общий-ключ-блок, обладающий высокой устойчивостью к линейному анализу и дифференциальному анализу, способ криптографической обработки и его компьютерная программа.
Средство решения проблемы
В первом аспекте настоящее изобретение направлено на устройство криптографической обработки, предназначенное для выполнения криптографической обработки общий-ключ-блок типа Фейстеля, имеющее структуру, которая повторно выполняет F-функцию SPN-типа, имеющую блок нелинейного преобразования и блок линейного преобразования в течение множества циклов, в котором каждый из блоков линейного преобразования F-функций, соответствующий каждому из множества циклов, выполнен с возможностью выполнения обработки линейного преобразования для входных n битов, выводимых из каждого из m блоков нелинейного преобразования, в сумме составляющих mn битов, в качестве обработки линейного преобразования, в которой используется квадратная матрица РМР, причем, по меньшей мере, в последовательных циклах с нечетными номерами и в последовательных циклах с четными номерами применяют разные квадратные матрицы РМР La, Lb, и матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1 для квадратных матриц РМР, является линейно независимой.
Кроме того, в одном варианте выполнения устройства криптографической обработки в соответствии с этим изобретением, устройство криптографической обработки отличается тем, что матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1, представляет собой квадратную матрицу РМР.
Кроме того, в одном варианте выполнения устройства криптографической обработки в соответствии с этим изобретением, устройство криптографической обработки отличается тем, что алгоритм криптографической обработки общий-ключ-блок типа Фейстеля представляет собой криптографический алгоритм с количеством циклов 2r, и блок линейного преобразования F-функции выполнен с возможностью выполнения линейного преобразования, в котором последовательно и повторно применяют q различных видов 2≤q≤r квадратных матриц РМР во всех r циклах с четными номерами и во всех r циклах с нечетными номерами.
Кроме того, в одном варианте выполнения устройства криптографической обработки в соответствии с этим изобретением устройство криптографической обработки отличается тем, что каждая из множества различных квадратных матриц РМР, предназначенных для применения в блоке линейного преобразования F-функции, представляет собой квадратную матрицу РМР, которая состоит из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, и является линейно независимой.
Кроме того, в одном варианте выполнения устройства криптографической обработки в соответствии с этим изобретением, устройство криптографической обработки отличается тем, что каждая из множества разных квадратных матриц РМР, предназначенных для применения в блоке линейного преобразования F-функции, представляет собой квадратную матрицу РМР, в результате чего матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, также представляет собой квадратную матрицу РМР.
Кроме того, в одном варианте выполнения устройства криптографической обработки в соответствии с этим изобретением, устройство криптографической обработки отличается тем, что каждая из множества разных квадратных матриц РМР, предназначенных для применения в блоке линейного преобразования F-функции, составлена из матрицы, которая составлена из векторов рядов, выделенных из матрицы M', которая состоит из векторов рядов, выбранных из квадратной матрицы М РМР, включающей все элементы, составляющие множество квадратных матриц РМР.
Во втором аспекте данное изобретение направлено на криптографический способ выполнения криптографической обработки общий-ключ-блок типа Фейстеля, содержащий следующие этапы: выполнения F-функции SPN-типа, предназначенной для выполнения обработки нелинейного преобразования и обработки линейного преобразования повторно в течение множества циклов; и при обработке преобразования F-функции, соответствующей каждому из множества циклов, выполнения линейного преобразования для n битов, поступающих с выхода m блоков нелинейного преобразования, что в сумме составляет mn битов, в качестве обработки линейного преобразования, в которой применяют квадратные матрицы РМР; в котором обработку линейного преобразования с квадратными матрицами РМР выполняют так, что, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетными номерами применяют разные квадратные матрицы РМР La, Lb, и матрица, составленная из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La-1, Lb-1 для квадратных матриц РМР, является линейно независимой и составляет квадратную матрицу РМР.
Кроме того, в одном варианте выполнения способа криптографической обработки в соответствии с этим изобретением, способ криптографической обработки отличается тем, что обработку линейного преобразования с использованием квадратных матриц РМР выполняют так, что матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1, представляет собой квадратную матрицу РМР.
Кроме того, в одном варианте выполнения способа криптографической обработки в соответствии с этим изобретением, способ криптографической обработки отличается тем, что алгоритм криптографической обработки общий-ключ-блок типа Фейстеля представляет собой криптографический алгоритм с количеством циклов, равным 2r, и при обработке линейного преобразования F-функции последовательно и повторно выполняют обработку линейного преобразования с использованием q видов разных квадратных матриц РМР 2≤q<r.
Кроме того, в одном варианте выполнения способа криптографической обработки в соответствии с этим изобретением, способ криптографической обработки отличается тем, что каждая из множества разных квадратных матриц РМР, предназначенных для применения при обработке линейного преобразования F-функции, выполнена так, что матрица, которая состоит из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, является линейно независимой и составляет квадратную матрицу РМР.
Кроме того, в одном варианте выполнения способа криптографической обработки в соответствии с этим изобретением, способ криптографической обработки отличается тем, что каждая из множества разных квадратных матриц РМР, предназначенных для применения при обработке линейного преобразования F-функции, представляет собой квадратную матрицу РМР так, что матрица, составленная из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, становится квадратной матрицей РМР.
Кроме того, в одном варианте выполнения способа криптографической обработки в соответствии с этим изобретением, способ криптографической обработки отличается тем, что каждая из множества разных квадратных матриц РМР, предназначенных для применения при обработке линейного преобразования F-функции, состоит из матрицы, составленной из векторов колонок, выделенных из матрицы M', состоящей из векторов рядов, выбранных из квадратной матрицы М РМР, включающей в себя все элементы, составляющие множество квадратных матриц РМР.
Настоящее изобретение также направлено на компьютерную программу, предназначенную для выполнения криптографической обработки общий-ключ-блок типа Фейстеля, которая содержит этап повторного выполнения F-функции SPN-типа, состоящий в выполнении обработки нелинейного преобразования и обработки линейного преобразования для множества циклов, в которой обработка линейного преобразования F-функции, соответствующей каждому из множества циклов, представляет собой этап линейного преобразования, состоящий в выполнении обработки линейного преобразования для входных n битов, поступающих из каждого из m блоков нелинейного преобразования, в сумме составляющих mn битов, в качестве обработки линейного преобразования, в которой применяют квадратные матрицы РМР (разделяемые с максимальным расстоянием). На этапе линейного преобразования, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетными номерами используют разные квадратные матрицы РМР La, Lb, и каждая из квадратных матриц РМР является такой, что матрица, составленная из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1 для квадратных матриц РМР, является линейно независимой.
Следует отметить, что компьютерная программа в соответствии с настоящим изобретением представляет собой компьютерную программу, которая установлена, например, в компьютерной системе, которая может выполнять различные программные коды с использованием любого из носителей данных и среды передачи данных в компьютеры, в форме, считываемой с ,например, носителей данных типа CD (компакт-диск), FD (гибкий диск), МО (магнитооптический диск) и т.д., или путем передачи по среде передачи данных, такой как сеть и т.д. Благодаря предоставлению такой программы в считываемой компьютером форме обработка, которая соответствует программе, может быть реализована в компьютерной системе.
Другие объекты, свойства и преимущества этого изобретения будут очевидны из следующего описания предпочтительных вариантов выполнения этого изобретения, которые иллюстрируются на прилагаемых чертежах. Следует отметить, что в этом описании система представляет такую систему, которая имеет структуру логической комбинации множества устройств, но которая не ограничивается такими системами, устройства которых установлены в одном корпусе.
В соответствии с конфигурацией этого изобретения, криптографическую обработку выполняют в соответствии с криптографической обработкой общий-ключ-блок типа Фейстеля, состоящей в выполнении F-функции SPN-типа, которая имеет блок нелинейного преобразования и блок линейного преобразования, повторно в течение множества циклов обработку линейного преобразования F-функции, соответствующую каждому из множества циклов, выполняют как обработку линейного преобразования, в которой используются квадратные матрицы РМР (разделяемые с максимальным расстоянием). И она выполнена с возможностью выполнения обработки линейного преобразования с квадратными матрицами РМР, в которых применяют квадратные матрицы PMP La, Lb, которые отличаются, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетными номерами, и матрица, состоящая из m векторов колонок, произвольно выбранных из векторов колонок, составляющих обратные матрицы La -1, Lb -1 квадратных матриц PMP, является линейно независимой или составляет квадратную матрицу PMP. В соответствии с этим повышается устойчивость к атакам линейного криптоанализа в шифре общий-ключ-блок, и увеличивается трудность при анализе ключа шифрования и т.д.; поэтому обеспечивается возможность реализации криптографической обработки с высоким уровнем защиты.
Кроме того, в соответствии с конфигурацией этого изобретения, при обработке, состоящей в криптографической обработке общий-ключ-блок типа Фейстеля, в которой повторно выполняют F-функцию SPN-типа, имеющую блок нелинейного преобразования и блок линейного преобразования в течение множества циклов, причем обработку линейного преобразования F-функции, соответствующую каждому из множества циклов, выполняют как обработку линейного преобразования, в которой используются квадратные матрицы PMP (разделяемые с максимальным расстоянием), в то время как обработку выполняют таким образом, что применяют квадратные матрицы PMP, которые отличаются, по меньшей мере, в последовательных циклах с нечетными номерами и в последовательных циклах с четными номерами, и сами эти квадратные матрицы PMP выполнены так, что проявляют линейную независимость или составляют квадратные матрицы PMP. Поэтому становится возможным гарантировать, что не будет возникать одновременное сокращение различий в результате вклада активных S-блоков, и следовательно, становится возможным увеличить минимальное количество активных S-блоков во всей криптографической функции, что представляет собой один из показателей устойчивости к атакам дифференциального криптоанализа в шифре общий-ключ-блок. Такая конфигурация повышает устойчивость как к атакам линейного криптоанализа, так и к атакам дифференциального криптоанализа, и позволяет реализовать криптографическую обработку с высокой степенью защиты.
Краткое описание чертежей
На фиг.1 показана схема, представляющая конфигурацию типичного шифра общий-ключ-блок, имеющего структуру Фейстеля.
На фиг.2А и 2В показаны схемы, поясняющие структуру F-функции, установленной как блок функции цикла. На фиг.2А показана схема, представляющая вход и выход F-функции 120 в одном цикле. На фиг.2В показана схема, подробно представляющая структуры F-функции 120.
На фиг.3 показана схема, представляющая пример квадратной матрицы, используемой для обработки линейного преобразования.
На фиг.4 показана схема, поясняющая одновременное сокращение различий трех этапов в шифре 128-битном блоком m=8 и n=8.
На фиг.5 показана схема, поясняющая конкретный пример генерирования выходного различия ΔYi F-функции путем выполнения линейного преобразования с квадратной матрицей РМР.
На фиг.6 показана схема, поясняющая одновременное сокращение различий на пяти этапах в шифре с 128-битным блоком при m=8 и n=8.
На фиг.7 показана схема, поясняющая определение одновременного сокращения различий для произвольного этапа в криптографической обработке общий-ключ-блок.
На фиг.8 показан пример квадратной матрицы РМР.
На фиг.9 показана схема, поясняющая пример установки квадратных матриц РМР в виде матриц линейного преобразования F-функций соответствующих циклов в криптографическом алгоритме общий-ключ-блок в соответствии с этим изобретением.
На фиг.10 показана блок-схема последовательности выполнения операций, поясняющая последовательность обработки установки квадратных матриц РМР в качестве матриц линейного преобразования F-функций соответствующих циклов в криптографическом алгоритме общий-ключ-блок, в соответствии с этим изобретением.
На фиг.11 показана блок-схема последовательности выполнения операций, поясняющая пример а1 обработки, состоящий в генерировании квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа, в качестве методики генерирования квадратных матриц РМР, которые представляют собой матрицы линейного преобразования, предназначенные для установки в F-функциях соответствующих циклов.
На фиг.12 показана блок-схема последовательности выполнения операций, поясняющая пример а2 обработки, состоящий в генерировании квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа, в качестве методики генерирования квадратных матриц РМР, которые представляют собой матрицы линейного преобразования, предназначенные для установки в F-функциях соответствующих циклов.
На фиг.13 показана блок-схема последовательности выполнения операций, поясняющая пример а3 обработки, состоящий в генерировании квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа, в качестве методики генерирования квадратных матриц РМР, которыепредставляют собой матрицы линейного преобразования, предназначенные для установки в F-функциях соответствующих циклов.
На фиг.14 показана схема, поясняющая конкретную методику примера а3 обработки, состоящую в генерировании квадратных матриц РМР, которые представляют собой матрицы линейного преобразования, предназначенные для установки в F-функциях соответствующих циклов.
На фиг.15 показана блок-схема последовательности выполнения операций, поясняющая пример b1 обработки, состоящей в генерировании квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам линейного криптоанализа, в качестве методики генерирования квадратных матриц РМР, которые представляют собой матрицы линейного преобразования, для установки в F-функциях соответствующих циклов.
На фиг.16 показана блок-схема последовательности выполнения операций, поясняющая пример обработки генерирования квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам линейного криптоанализа в качестве методики генерирования квадратных матриц РМР, которые представляют собой матрицы линейного преобразования, для установки в F-функциях соответствующих циклов.
На фиг.17 показана блок-схема последовательности выполнения операций, поясняющая пример обработки генерирования квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа и атакам линейного криптоанализа, в качестве методики генерирования квадратных матриц РМР, которые представляют собой матрицы линейного преобразования, предназначенные для установки в F-функциях соответствующих циклов.
На фиг.18 показана схема, представляющая пример конфигурации модуля с интегральной микросхемой, в качестве устройства криптографической обработки, предназначенного для выполнения криптографической обработки в соответствии с этим изобретением.
Подробное описание изобретения
Далее подробно описано устройство криптографической обработки в соответствии с этим изобретением, способ криптографической обработки и его компьютерная программа. Пояснения приведены в следующем порядке.
1. Обработка дифференциального анализа в криптографическом алгоритме общий-ключ-блок.
2. Обработка линейного анализа в криптографическом алгоритме общий-ключ-блок.
3. Криптографический алгоритм на основе этого изобретения:
(3-а) Пример генерирования квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа, и установки их в F-функциях,
(3-b) Пример генерирования квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам линейного криптоанализа, и установки их в F-функциях,
(3-е) Пример генерирования квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа и атакам линейного криптоанализа, и установки их в F-функциях.
[1. Обработка дифференциального анализа в криптографическом алгоритме общий-ключ-блок]
Вначале будет описана схема обработки дифференциального анализа в криптографическом алгоритме общий-ключ-блок, в соответствии с криптографической обработкой DES (Стандарт шифрования данных), с использованием обобщенной модели криптографической обработки общий-ключ-блок.
Алгоритм криптографической обработки общий-ключ-блок, в основном, может быть разделен на блок функции цикла, предназначенный для выполнения преобразования входных данных, и блок планирования ключа, предназначенный для генерирования ключа, который следует применять в каждом цикле части функции цикла. Ключ (подключ), применяемый в каждом цикле функции цикла, генерируют с помощью блока планирования ключа, в который вводят один мастер ключ (главный ключ), на основе него и используют в каждом цикле. Среди типичных систем такой криптографической системы с общим ключом можно назвать систему DES (Стандарт шифрования данных), используемую, как Федеральная стандартная система США.
Структура типичной криптографической обработки общий-ключ-блок, называемая структурой Фейстеля, будет описана со ссылкой на фиг.1.
Структура Фейстеля имеет конфигурацию преобразования открытого текста в зашифрованный текст путем простого повторения функции преобразования. Длина открытого текста установлена равной 2 mn(2×m×n) битов. Здесь m и n представляют целые числа. Вначале открытый текст размером 2mn битов разделяют на две части входных данных, PL (Открытая-левая) 101 из mn битов и PR (Открытая-правая) 102, содержащие mn битов, и их используют как входные значения.
Структуру Фейстеля выражают путем повторения основной структуры, и функцию преобразования данных, включаемую в каждом цикле, называют F-функцией 120. На фиг.1 показан пример конфигурации, состоящей из F-функций (функций цикла) 120, повторяемых для r-этапов.
Например, в первом цикле входные данные Х размером mn битов и ключ K1 103 цикла размером mn битов, подаваемый из блока генерирования ключа (не показан на чертеже), вводят в F-функцию 120, на выходе которой получают данные Y размером mn битов после выполнения в ней преобразования данных. Блок 104 исключающее ИЛИ выполняет операцию исключающее ИЛИ в отношении выходных данных и других частей входных данных, полученных на предыдущем этапе, и выводит результат операции размером mn битов в следующую функцию цикла. Криптографическую обработку заканчивают путем применения этой обработки, то есть F-функции, повторно в течение заданного количества (r) циклов, и выводят разделенные данные CL (Зашифрованные левые) и данные CR (Зашифрованные правые) в виде зашифрованного текста. Приведенная выше конфигурация приводит к тому, что для выполнения декодирования с использованием структуры Фейстеля необходимо только выполнить в обратном порядке последовательность ввода ключей цикла, которые не нужны для конфигурации обратной функции.
Структура F-функции 120, установленная как функция каждого цикла, будет описана со ссылкой на фиг.2. На фиг.2А показана схема, представляющая вход и выход F-функции 120 в одном цикле. На фиг.2В показана схема, подробно представляющая структуру F-функции 120. F-функция 120 имеет так называемую структуру SPN-типа, состоящую из уровня нелинейного преобразования и уровня линейного преобразования, соединенных вместе, как показано на фиг.2В.
F-функция 120 SPN-типа имеет множество S-блоков 121, предназначенных для выполнения обработки нелинейного преобразования, как показано на фиг.2В. Операцию исключающее ИЛИ выполняют в отношении входной величины Х размером mn бит из предыдущего этапа блока функции цикла, вместе с ключом Ki цикла, вводимым из блока планирования ключа, и ее вывод подают во множество (m) S-блоков, каждый из которых выполняет обработку нелинейного преобразования для n битов. Каждый из S-блоков выполняет обработку нелинейного преобразования, в которой применяют, например, таблицу преобразования.
Выходное значение Z размером mn битов, которое представляет собой выходные данные S-блока 121, вводят в блок 122 линейного преобразования 122 для выполнения обработки линейного преобразования, в ходе которой выполняют обработку линейного преобразования, например, обработку смены положений битов и т.д., и выводят выходное значение Y размером mn битов. Выходное значение Y вместе с входными данными из предыдущего этапа подвергают операции исключающее ИЛИ, и ее результат назначают входному значению F-функции следующего цикла.
В F-функции 120, показанной на фиг.2, битовая длина входа-выхода равна m×n (m, n - целые числа), уровень нелинейного преобразования имеет конфигурацию, в которой m S-блоков 121, каждый из которых выполняет функцию уровня нелинейного преобразования, вход и выход которых представляют n битов, расположенных параллельно, и блок 122 линейного преобразования, в качестве уровня линейного преобразования, выполняет обработку линейного преобразования на основе m-ой квадратной матрицы, которая имеет элементы в поле расширения GF (2n), определенные по n-ному несокращаемому полиному, как его элементы.
На фиг.3 показан пример квадратной матрицы, применяемой при обработке линейного преобразования в блоке 122 линейного преобразования. Квадратная матрица 125, показанная на фиг.3, представляет собой пример n=8 и m=8. Линейное преобразование выполняют для данных m n битов Z [1], Z [2]…,Z [m], выводимых из блока нелинейного преобразования (S-блок 121), в котором применяют заданную квадратную матрицу 125, и определяют Y [1], Y [2]…,Y [m] как выход F-функции (функции цикла). Следует отметить, что линейную операцию элементов матрицы каждых данных выполняют для заданного поля расширения GF (2n), равного 2.
Поскольку в используемом до настоящего времени шифре типа Фейстеля используют один и тот же уровень линейного преобразования для F-функций на всех этапах, он имеет свойство, состоящее в том, что множество различий сокращают одновременно, когда распространяют различия. Как было описано в параграфе "Уровень техники", в качестве типичной методики криптоанализа известен дифференциальный анализ (или методика дешифрования различий), в котором прикладной ключ для каждой функции цикла анализируют путем анализа множества входных данных (открытого текста) и ее выходных данных (зашифрованного текста). При обычной криптографической обработке общий-ключ-блок, такой как криптографический алгоритм DES, поскольку обработка (матрица преобразования), применяемая в блоку 122 линейного преобразования F-функции, 120 установлена эквивалентной в цикле на каждом этапе, легко выполнить дифференциальный анализ и в результате легко выполнить анализ ключа.
Пример, в котором множество различий сокращают одновременно во время распространения различий, поясняется со ссылкой на фиг.4. В этом описании, при выражении различий, различие обозначают путем добавления символа Δ (дельта).
На фиг.4 показана схема, поясняющая одновременное сокращение различий в трех этапах в блоке шифра 128-битов (m=8 и n=8). Следует отметить, что на чертеже данные размером 64 бита должны быть разделены побайтно, причем каждый из них должен быть выражен как вектор, и каждый элемент должен быть представлен в виде шестнадцатеричного числа.
Одновременное сокращение различий F-функции, имеющей структуру из трех этапов, происходит, например, на основе механизма установки следующих состояний 1-4 данных. Состояния данных, генерируемые механизмом, который поясняется ниже, представляют собой состояния данных, которые могут быть сгенерированы путем установки множества входных данных различия, то есть они могут быть сгенерированы при анализе ключа (ключа цикла) в так называемом дифференциальном анализе.
(Состояние 1)
Предположим, что левая половина входного различия для цикла i состоит из входных различий, всех равных нулю (ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00)), и правая его половина состоит из входных различий, всех равных нулю, за исключением входа только в один S-блок
(ΔХi-1=(34, 00, 00, 00, 00, 00, 00, 00)). Это состояние данных показывает, что путем установки множества различных входных данных, такое состояние данных может быть получено в цикле i.
Восемь элементов в ΔXi=(34, 00, 00, 00, 00, 00, 00, 00) соответствуют входным различиям соответствующих S-блоков (m=8), структурированных в F-функции. Различие (34) вводят в первый S-блок ((S1) по фиг.4), и (00) представляют собой входные различия в блоках со второго по восьмой.
Здесь выходное различие S-блока, имеющего входное различие, равное нулю (00), равно нулю (00). Что касается данных различия, S-блок, имеющий входное различие, равное нулю (00), не создает какой-либо эффект и, соответственно, называется S-блоком, который не является активным, то есть неактивным S-блоком. С другой стороны, S-блок, имеющий входное различие, не равное нулю (в примере по фиг.4, различие =34), генерирует результат нелинейного преобразования, соответствующий входному различию, не равному нулю и, соответственно, называется активным S-блоком.
В примере, показанном на фиг.4, генерируют выходное различие (b7) одного активного S-блока (S1), для которого вводят входное различие (34), не равное нулю. Другие неактивные S-блоки S2-S8 генерируют выходные различия (00) на основе их входных различий (00), равных нулю, соответственно, предоставляемых им, как входы различий в блоке линейного преобразования.
(Состояние 2)
Выходное различие S-блока, имеющего входное различие, не равное нулю, для цикла i (ниже называется активным S-блоком) рассеивают в уровне линейного преобразования и выводят из F-функции (выходное значение =ΔYi), которое становится входным различием ΔXi+1 для следующего цикла, в том виде, как оно есть.
Линейное преобразование в примере по фиг.4 выполняют таким образом, что линейное преобразование с использованием определенной конкретной квадратной матрицы 125, например, как показано на фиг.5, общей в F-функциях в соответствующих циклах, выполняют для вывода различия ΔYi=(98, с4, b4, d3, ас, 72, 32), в качестве выходного различия F-функции цикла i. Как можно понять по структуре линейного преобразования, показанной на фиг.5, выходное различие ΔYi=(98, с4, b4, d3, ас, 72, 32) определено как значение, зависящее только от выходного элемента Z [1]=b7 одного активного S-блока(S1).
Такие значения ΔYi=(98, с4, b4, d3, ас, 72, 32), используемые в качестве выходных различий F-функции в этом цикле i вместе с входными различиями, всеми равными нулю (ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00)), подвергают операции исключающее ИЛИ (XOR) в блоке 131 исключающее ИЛИ, показанном на фиг.4, и результат операции задают как ΔXi+1 для следующего цикла i+1.
Поскольку результаты операций исключающее ИЛИ (XOR) в отношении ΔYi=(98, с4, b4, d3, ас, 72, 32) в качестве выходных различий функции F цикла i и входных различий, всех равных нулю ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00), представляют собой ΔYi, входные различия ΔХi+1 для следующего цикла i+1 принимают равными ΔYi=(98, с4, b4, d3, ас, 72, 32).
(Состояние 3)
Выходное различие ΔYi+1 F-функции цикла i+1 имеет ненулевое значение только в положении активного S-блока в цикле i. Такое состояние данных обозначает, что такое состояние данных может быть получено путем установки множества входных данных различий.
То есть ΔYi+1=(ad, 00, 00, 00, 00, 00, 00, 00), и выходное различие ΔYi+1 имеет ненулевое значение только в положении S-блока (первого S-блока (S1)), который имеет ненулевое значение различия, аналогично циклу i. В частности, при этом понятно, что ad≠00.
(Состояние 4)
В случае, когда выходное различие активного S-блока (S1) в цикле i+2 соответствует выходному различию активного S-блока (S1) в цикле i, как показано на фиг.4, выходное различие активного S-блока (S1) в цикле i+2 становится равным b7 и соответствует выходному различию (b7) активного S-блока (S1). Это состояние данных показывает, что такое состояние данных может быть получено путем установки множества входных данных различий.
Когда возникает такое состояние данных, выходное различие ΔYi+2=(98, с4, b4, d3, ас, 72, 32) F-функции цикла i+2 будет соответствовать выходному различию ΔYi=(98, с4, b4, d3, ас, 72, 32), которое представляет собой F-функцию цикла i, представляющую собой предыдущий цикл через один цикл.
В качестве результата блок 133 исключающее ИЛИ будет выполнять операцию исключающее ИЛИ для ΔXi+1=ΔYi=(98, с4, b4, d3, ас, 72, 32) и ΔYi+2=(98, с4, b4, d3, ас, 72, 32), при этом они оба представляют одно и то же значение и выводят значения, все равные нулю, в результате операции исключающее ИЛИ.
В результате левое входное различие ΔХi+33 из предыдущего этапа (цикла i+2), которое приводит к получению выходного различия для следующего этапа (цикла i+3) становится равным ΔХi+3=(00, 00, 00, 00, 00, 00, 00,00).
Левый вход ΔХi+3=(00, 00, 00, 00, 00, 00, 00, 00) для этого цикла i+3 состоит из всех нулей, так же, как и у левого входного различия ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00) для цикла i, и при этом существует возможность, что та же обработка, что и в циклах от i до i+2 будет повторяться также в цикле i+3 и для следующих циклов.
Таким образом, возникает проблема, состоящая в том, что количество активных S-блоков не будет увеличиваться по мере увеличения номера цикла, и устойчивость к атакам дифференциального криптоанализа не будет значительно повышаться.
В шифре общий-ключ-блок минимальное количество активных S-блоков во всей криптографической функции известно как один из показателей устойчивости к атакам дифференциального криптоанализа. При этом определяют, что чем больше минимальное количество активных S-блоков, тем выше устойчивость к атакам дифференциального криптоанализа.
Как описано выше, дифференциальный анализ (атака дифференциального криптоанализа) представляет собой методику анализа применения ключа в каждой функции цикла путем установки множества входных данных (открытых текстов) с определенным различием и их выходных данных (зашифрованных текстов) с последующим анализом соответствия между ними. Если количество активных S-блоков может быть уменьшено при таком дифференциальном анализе, такой анализ становится простым, и количество процессов анализа при этом можно будет уменьшить
Хотя в примере, представленном со ссылкой на указанную выше фиг.4, показано состояние со структурой, в которой только первый S-блок (S1) представляет собой активный S-блок, возможна такая установка других S-блоков (S2-S8), когда каждый S-блок будет установлен как активный блок, путем установки входных данных дифференциального анализа. Поэтому при выполнении процесса дифференциального анализа такого типа становится возможным анализировать нелинейное преобразование каждого S-блока, и дополнительно анализировать ключ цикла, вводимый для F-функции.
Для повышения устойчивости к дифференциальному анализу такого типа необходимо поддерживать состояние, в котором количество активных S-блоков всегда велико, то есть, когда минимальное количество активных S-блоков велико.
В примере, описанном со ссылкой на фиг.4, в случае F-функции, вход в которую задают в направлении справа налево, то есть, когда учитывают только цикл 1 и цикл i+2, как циклы-объекты обработки расчета активного S-блока, количество активных S-блоков равно только двум в F-функциях, входы которых заданы в направлении слева направо, количество активных S-блоков в цикле i+1 равно восьми, но количество активных S-блоков становится равным нулю в результате одновременного сокращения различий, и, следовательно, становится простой обработка анализа, представляющая собой нелинейную обработку преобразования каждого S-блока, с использованием дифференциального анализа.
Криптографический алгоритм общий-ключ-блок, показанный на фиг.4, состоит в том, что матрицы линейного преобразования, применяемые в блоках линейного преобразования в соответствующих циклах, равны друг другу, и такая конкретная конфигурация приводит к возможности одновременного сокращения различий, вызванного только двумя активными S-блоками, в частности в F-функциях, вход которых задан в направлении справа налево. Поэтому возникает проблема, состоящая в том, что минимальное количество активных S-блоков недостаточно увеличивается по сравнению с ростом номера цикла, и устойчивость к атакам дифференциального криптоанализа не повышается в такой же степени.
Затем, аналогично конфигурации, в которой ту же линейную матрицу преобразования используют для F-функций всех этапов (циклов), со ссылкой на фиг.6 поясняется механизм возникновения одновременного сокращения различий для пяти циклов.
На фиг.6 показана схема, поясняющая одновременное сокращение различий для пяти этапов в шифре со 128-битным блоком, для которого m=8 и n=8. Следует отметить, что на фиг.6 данные размером 64 бита должны быть представлены как векторы путем побайтного их разделения, и каждый элемент должен быть представлен в шестнадцатеричной форме.
Одновременное сокращение различий в F-функции с конфигурацией для пяти этапов происходит, например, на основе следующего механизма установки состояний 1-7 данных. Состояние данных, генерируемое механизмом, описанным ниже, представляет собой состояние данных, которое может быть сгенерировано путем установки множества входных данных различий, и это состояние данных может быть сгенерировано при анализе ключа (ключа цикла) в так называемом дифференциальном анализе.
(Состояние 1)
Пусть левая половина входных различий для цикла i состоит из входных различий, всех равных нулю (ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00)), и правая половина входных различий состоит из входных различий, всех равных нулю, за исключением входа только в один S-блок (ΔХi=(34, 00, 00, 00, 00, 00, 00, 00)). Такое состояние данных показывает, что путем установки множества различий входных данных такое состояние данных может быть получено в цикле i.
Восемь элементов ΔХi=(34, 00, 00, 00, 00, 00, 00, 00) соответствуют соответствующим входным различиям для m (m=8) S-блоков, сконфигурированных в F-функциях. В первый S-блок ((S1) по фиг.6) вводят (34), и (00) вводят как входные различия для второго-восьмого блоков.
Как описано выше, выходное различие равно нулю (00) для любого S-блока, имеющего входное различие, равное (00). Что касается выходного различия, S-блок, имеющий входное различие, равное нулю, который не выполняет какую-либо операцию, соответственно, называется S-блоком, который не является активным, а именно неактивным S-блоком. С другой стороны, поскольку только S-блок (S1) с входным различием, не равным нулю (в примере по фиг.6 различие =34), генерирует результат нелинейного преобразования, соответствующий входному различию, не равному нулю, в качестве выходного различия, соответственно он называется активным S-блоком.
В примере, показанном на фиг.6, один вводимый активный S-блок (S1), входное различие (34) которого не равно нулю, генерирует выходное различие (b7), и другие неактивные S-блоки S2-S8 генерируют выходные различия (00) на основе входных различий (00), равных нулю, которые назначают как входные различия для блока линейного преобразования.
(Состояние 2)
Выходное различие S-блока (ниже называется активным S-блоком), который имеет входное различие, не равное нулю, для цикла i (в примере по фиг.4 различие =34) рассеивают на уровне линейного преобразования и выводят из F-функции (выходное значение =ΔYi), которое становится входным различием ΔХi+1 для следующего цикла в том виде, как оно есть.
В примере, показанном на фиг.6, линейное преобразование выполняют с определенной конкретной квадратной матрицей 125, которая является общей для каждого цикла, например такой, как показана на фиг.5, и выводят ΔYi=(98, с4, b4, d3, ас, 72, 0f, 32), как выходные различия F-функции для цикла i.
Значения ΔYi=(98, с4, b4, d3, ас, 72, 0f, 32) как выходные различия F-функции для цикла i, подвергают операции исключающее ИЛИ (XOR) в блоке 141 исключающее ИЛИ, показанном на фиг.6, вместе со входными различиями, всеми равными нулю
(ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00)), и результаты операции становятся входным различием для следующего цикла i+1.
Поскольку результаты операций исключающее ИЛИ (XOR) в отношении ΔYi=(98, с4, b4, d3, ас, 72, 0f, 32), в качестве выходных различий F-функции цикла i и входных различий, всех равных нулю, (ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00)) равны ΔYi, входные различия для следующего цикла i+1 становятся равными ΔХi+1=ΔYi=(98, с4, b4, d3, ас, 72, 0f, 32).
(Состояние 3)
Выходное различие ΔYi+1 F-функции в цикле i+1 имеет ненулевое значение только в положении активного S-блока в цикле i. Это состояние данных обозначает, что такое состояние данных может быть получено в результате установки множества входных данных различий.
То есть ΔYi+1 равно ΔYi+1=(34, 00, 00, 00, 00, 00, 00, 00) и имеет ненулевое значение только в положении S-блока (первого S-блока (S1)), который имеет значение различия, неравное нулю (в примере по фиг.6, различие =34) для цикла i.
(Состояние 4)
Вход в F-функцию для цикла i+2 представляет собой результат выполнения операции исключающее ИЛИ в блоке 142 исключающее ИЛИ для ΔXi=(34, 00, 00, 00, 00, 00, 00, 00) и ΔYi+1=(34, 00, 00, 00, 00, 00, 00, 00), которые представляют собой одни и те же данные и становятся входными данными, состоящими из всех нулей, ΔХi+2=(00, 00, 00, 00, 00, 00, 00, 00). В результате, выходное различие F-функции для цикла i+2 также становится входным различием, состоящим из всех нулей ΔYi+2=(00, 00, 00, 00, 00, 00, 00,00).
(Состояние 5)
Входы в F-функцию для цикла i+3 представляют собой результат операции исключающее ИЛИ, проведенной в блоке 143 исключающее ИЛИ для ΔXi+1=(98, с4, b4, d3, ас, 72, 0f, 32) и ΔXi+2=(00, 00, 00, 00, 00, 00, 00, 00), которые представляют собой выходные различия F-функции для цикла i+2, все равные нулю, и которые становятся входами ΔХi+3=ΔХi+1=(98, с4, b4, d3, ас, 72, 0f, 32) для F-функции в цикле i+3.
(Состояние 6)
Выходные различия F-функции для цикла i+3 становятся равными ΔYi+3=(43, 00, 00, 00, 00, 00, 00, 00). Операция исключающее ИЛИ в блоке 144 исключающее ИЛИ для этих различий вместе с ΔХi+2=(00, 00, 00, 00, 00, 00, 00, 00), состоящих из всех нулей, приводит к результату ΔХi+4=ΔYi+3=(43, 00, 00, 00, 00, 00, 00, 00), который становится входными различиями F-функции для цикла i+4.
(Состояние 7)
Когда выходное различие активного S-блока (S1) в цикле i+4 соответствует выходному различию активного S-блока (S1) в цикле i, выходное различие активного S-блока (S1) в цикле i+4 становится равным b7, как показано на фиг.6, в соответствии с выходным различием (b7) активного S-блока (S1) в цикле i. Это состояние данных указывает, что такое состояние данных может быть получено путем установки множества входных данных различий.
Когда возникает такое состояние данных, выходное различие ΔYi+4=(98, с4, b4, d3, ас, 72, 0f, 32) F-функции для цикла i+4 будет соответствовать выходному различию
ΔХi+3=(98, с4, b4, d3, ас, 72, 0f, 32) блока 143 исключающее ИЛИ для цикла i+2, который представляет собой предыдущий цикл через один.
В результате, в блоке 145 исключающее ИЛИ значения ΔXi+3=(98, с4, b4, d3, ас, 72, 0f, 32) и ΔYi+4=(98, с4, b4, d3, ас, 72, 0f, 32), которые оба имеют одно и то же значение, будут подвергнуты операции исключающее ИЛИ, на выходе которой будут получены все нули, в результате выполнения операции исключающее ИЛИ.
В соответствии с этим входные различия для следующего этапа (цикл i+5) будут установлены как ΔХi+5=(00, 00, 00, 00, 00, 00, 00, 00).
Такой вход слева в этот цикл i+5, ΔXi+5=(00, 00, 00, 00, 00, 00, 00, 00) состоит из всех нулей, так же, как и вход слева в цикл i
ΔХi-1=(00, 00, 00, 00, 00, 00, 00, 00), и при этом существует возможность, что одна и та же обработка, что и для цикла 1, будет повторена для цикла i+4, а также для цикла i+5 и в последующих циклах.
Вследствие этого возникает проблема, состоящая в том, что количество активных S-блоков не увеличивается по сравнению с увеличением номера цикла, и устойчивость к атакам дифференциального криптоанализа не повышается в такой же степени.
Как описано выше, дифференциальный анализ (атака дифференциального криптоанализа) представляет собой методику анализа прикладного ключа в каждой функции цикла путем установки множества входных данных (открытого текста), имеющих определенное различие, и его выходных данных (зашифрованного текста) и анализа соответствия между ними. При таком дифференциальном анализе, если количество активных S-блоков может быть уменьшено, анализ становится более простым, и количество процессов анализа можно сократить.
В примере, показанном на фиг.6, описанной выше, в случае F-функций, входы в которые передают в направлении справа налево, то есть в случае, когда цикл i, цикл i+2 и цикл i+4 рассматриваются как целевые циклы расчета активного S-блока, количество активных S-блоков равно только двум, сумма цикла i=1, цикла i+2=0 и цикла i+4=1. В случае F-функций, входы в которые передают в направлении слева направо, то есть в случае, когда цикл i+1 и цикл i+3 рассматриваются как целевые циклы, хотя количество активных S-блоков равно восьми, количество активных S-блоков в цикле i+5 становится равным нулю, в результате одновременного сокращения различий; поэтому анализ обработки нелинейного преобразования каждого S-блока с использованием дифференциального анализа и обработки криптоанализа во входном ключе цикла для F-функций, становится сравнительно простым.
Хотя в примере, описанном со ссылкой на фиг.6, представлено состояние возникновения структуры, в которой только первый S-блок (S1) представляет собой активный S-блок для других S-блоков (S2-S8), путем установки входных данных дифференциального анализа можно любой из этих других S-блоков установить как активный S-блок, поэтому выполнение такого процесса дифференциального анализа позволяет анализировать обработку нелинейного преобразования каждого S-блока и дополнительно анализировать ключ цикла, вводимый в F-функцию.
Хотя пример возникновения одновременного сокращения различий в случаях трех и пяти циклов был описан со ссылкой на фиг.4 и фиг.6, если эти случаи обобщить для произвольного количества циклов, для определения одновременного сокращения различий может быть приведено следующее определение. Определение одновременного сокращения различий для произвольного количества циклов будет описано со ссылкой на. фиг.7. На фиг.7 показаны последовательные циклы через один (i, i+2, i+4,…,i+2j) структуры Фейстеля, с помощью которых выполняют криптографическую обработку общий-ключ-блок в соответствии со структурой Фейстеля.
"Определение"
В процессе, в котором половина входных различий в структуре Фейстеля в цикле i состоит из нулей (фиг.7, ΔХi=(00, 00, 00, 00, 00, 00, 00, 00)) и каждое из них, а также каждое из выходных различий F-функции цикла i+2j подвергают операции исключающее ИЛИ в блоке исключающее ИЛИ, случай, когда результаты операции исключающее ИЛИ становятся равными нулю (по фиг.7, ΔХi+2j+i=(00, 00, 00, 00, 00, 00, 00, 00)), называется одновременным сокращением различий.
В это время активные S-блоки, существующие в F-функциях для циклов i, i+2, i+4,…,i+2k, называют активными S-блоками, которые приводят к одновременному сокращению различий. При определении количества ненулевых элементов вектора А в качестве веса Хемминга hw(A), количество "а" активных S-блоков, которые приводят к одновременному сокращению различий, можно выразить следующим уравнением.
[Уравнение 1]
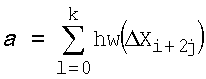
В описанных выше примерах из трех циклов и пяти циклов количество активных S-блоков, которые приводят к одновременному сокращению различий, в обоих случаях равно двум, то есть а=2.
Как описано выше, один из индексов устойчивости к атакам дифференциального криптоанализа в шифре общий-ключ-блок представляет собой минимальное количество активных S-блоков во всех криптографических функциях, и при этом определено, что чем больше минимальное количество активных S-блоков, тем выше становится устойчивость к атакам дифференциального криптоанализа.
Однако в конфигурации, в которой используют одну и ту же матрицу линейного преобразования для F-функций на всех этапах, как и в алгоритме DES, существует вероятность, что только два активных S-блока приведут к одновременному сокращению различий, как можно видеть из пояснений со ссылкой на фиг.4 и фиг.6. Существует проблема, состоящая в том, что, поскольку присутствует такое свойство, минимальное количество активных S-блоков увеличивается недостаточно, и устойчивость атакам дифференциального криптоанализа не будет в достаточной степени усилена.
[2. Обработка линейного анализа в криптографическом алгоритме общий-ключ-блок]
Обработка дифференциального анализа, как описано выше, требует, чтобы исполнитель анализа подготовил входные данные (открытый текст), имеющий постоянное различие, и проанализировал его соответствующие выходные данные (зашифрованный текст). Для обработки линейного анализа нет необходимости подготавливать входные данные (открытый текст), имеющий постоянное различие, и анализ выполняют на основе входных данных (открытый текст), количество которых равно или больше, чем заданное количество его соответствующих выходных данных (зашифрованный текст).
Как описано выше, в криптографическом алгоритме общий-ключ-блок подготавливают S-блоков в качестве блоков нелинейного преобразования, и при этом не существует линейной взаимосвязи между входными данными (открытый текст) и их соответствующими выходными данными (зашифрованный текст). При линейном анализе анализ выполняют путем линейной аппроксимации входа/выхода в таком S-блоке, анализируя линейную взаимосвязь между множеством входных данных (открытый текст) и составляющими их битовыми значениями соответствующих выходных данных (зашифрованный текст), с последующим сужением ключей, которые представляют собой предполагаемые кандидаты. При линейном анализе нет необходимости подготавливать входные данные с определенным различием, и анализ становится возможным только в результате подготовки большого количества открытых текстов и их соответствующих зашифрованных текстов.
[3. Криптографический алгоритм на основе данного изобретения]
Ниже поясняется криптографический алгоритм в соответствии с данным изобретением. Криптографический алгоритм в соответствии с данным изобретением имеет структуру, которая улучшает устойчивость к атакам линейного криптоанализа, атакам дифференциального криптоанализа, описанным выше, и т.п., то есть имеющий структуру, которая повышает трудность при анализе ключа и повышает безопасность.
Одно из свойств криптографического алгоритма в соответствии с данным изобретением состоит в том, что этот алгоритм построен путем установки множества различных квадратных матриц РМР (разделяемые с максимальным расстоянием), вместо структуры, в которой используется общая обработка (матрица преобразования) для блока линейного преобразования F-функции в каждом цикле, как в обычном алгоритме DES. В частности, этот алгоритм выполнен с возможностью выполнения обработки линейного преобразования с использованием квадратных матриц РМР, которые отличаются, по меньшей мере, в последующих циклах с четными номерами и в последующих циклах с нечетными номерами.
В криптографическом алгоритме, относящемся к данному изобретению, воплощена структура, с помощью которой не возникает одновременное сокращение различий на основе небольшого количества активных S-блоков или которая в меньшей степени склонна к возникновению с использованием свойств квадратных матриц РМР (разделяемых с максимальным расстоянием), в результате чего минимальное количество активных S-блоков увеличивается, и реализуется криптографическая обработка общий-ключ-блок, которая является более устойчивой к атакам дифференциального криптоанализа. В качестве альтернативы, в настоящем изобретении воплощается структура, которая затрудняет линейный анализ, выполняемый как известная атака криптоанализа открытого текста.
В криптографическом алгоритме в соответствии с этим изобретением применяют типичную криптографическую структуру общий-ключ-блок, которая называется структурой Фейстеля, имеющую F-функции SPN-типа, описанную со ссылкой на фиг.1 и 2, то есть используют структуру, которая преобразует открытый текст в зашифрованный текст или преобразует зашифрованный текст в открытый текст путем простого повторения F-функции SPN-типа, которая имеет блок нелинейного преобразования и блок линейного преобразования, в ходе множества циклов.
Например, длина открытого текста предполагается равной 2mn битов (здесь, m и n представляют собой целые числа). Эта структура разделяет открытый текст из 2mn битов на две части данных PL (Открытая-левая и Открытая-правая), каждая из которых содержит mn битов, и выполняет F-функцию в каждом цикле, используя эти данные как входные значения. F-функция представляет собой F-функцию SPN-типа, состоящую из блока нелинейного преобразования, состоящего из S-блоков, и блока линейного преобразования, соединенных вместе.
В конфигурации в соответствии с этим изобретением в качестве матрицы для обработки линейного преобразования, которую используют в блоке линейного преобразования F-функции, матрицы, выбранные из множества различных квадратных матриц РМР (разделяемые с максимальным расстоянием), установлены как матрицы для применения в блоках линейного преобразования F-функций в соответствующих циклах. В частности, используют квадратные матрицы РМР, которые отличаются, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетными номерами.
Далее поясняется квадратная матрица РМР. Квадратная матрица представляет собой матрицу, удовлетворяющую свойствам (а) и (b), приведенным ниже. (а) Матрица представляет собой квадратную матрицу. (b) Детерминанты всех подматриц, включенных в матрицу, не равны нулю, а именно det (submatrix)≠0.
Матрица, удовлетворяющая приведенным выше условиям (а) и (b), называется квадратной матрицей РМР. Длина входных/выходных битов для F-функции, выполняемой в каждом цикле криптографической обработки общий-ключ-блок, равна m×n битов (m, n: целые числа). На фиг.8 показан пример квадратной матрицы РМР в случае, когда блок нелинейного преобразования, выполняемый в F-функции, построен с m S-блоками, каждый из которых имеет n битов входа/выхода, и блок линейного преобразования выполняет обработку линейного преобразования на основе m квадратных матриц, каждая из которых имеет элементы поля расширения GF (2n) из 2 определенных по n-му несокращаемому полиному, в качестве ее элементов. Пример квадратной матрицы РМР, показанный на фиг.8, представляет собой пример квадратной матрицы РМР, для которой n=8 и m=8.
Если обозначить количество ненулевых элементов в векторе А по весу Хемминга hw(A), и квадратной матрице РМР с размером т, как М, и входной вектор для квадратной матрицы РМР М, как х, квадратная матрица РМР, удовлетворяющая приведенным выше условиям (а) и (b), удовлетворяет следующему неравенству (Уравнение 1).
hw (x)+hw (Mx)>m+l............ (Уравнение 1)
Приведенное выше выражение (Уравнение 1) показывает, что общее количество ненулевых элементов hw(x) входных данных х, которые должны быть линейно преобразованы в квадратной матрице (М) РМР, плюс количество ненулевых элементов hw(Mx) выходных данных Mx, которые были линейно преобразованы с использованием квадратной матрицы (М) РМР, больше, чем число m порядка квадратной матрицы РМР.
В частности, квадратная матрица РМР называется так, поскольку правая половина стандартной формы матрицы генерирования квадратного РМР-кода (разделяемый код с максимальным расстоянием) удовлетворяет указанным выше условиям.
Известно, что даже в обычной конфигурации, в которой одна матрица внедрена во все F-функции, использование квадратной матрицы РМР в качестве матрицы линейного преобразования обеспечивает возможность поддержания минимального количества активных S-блоков на относительно высоком уровне по сравнению со случаем, в котором используют другую матрицу вместо квадратной матрицы РМР.
В настоящем изобретении предложен способ использования матрицы, удовлетворяющей условиям квадратной матрицы РМР, для F-функций каждого цикла и дополнительно устанавливающий разные матрицы для соответствующих циклов. В частности, используют квадратные матрицы РМР, которые отличаются, по меньшей мере, в последующих циклах с четными номерами и в последующих циклах с нечетными номерами.
Ниже поясняется множество примеров конфигураций, в каждой из которых установлена более высокая устойчивость к атакам дифференциального криптоанализа в шифре общий-ключ-блок типа Фейстеля для количества этапов 2r (r представляет собой целое число).
В следующем описании MLTi обозначает матрицу линейного преобразования, которую применяют в блоке линейного преобразования F-функции для j-го этапа в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов 2r (количества цикла).
В конфигурации в соответствии с этим изобретением в качестве матрицы для обработки линейного преобразования, применяемой в блоке линейного преобразования F-функции на каждом этапе в криптографической структуре общий-ключ-блок типа Фейстеля на этапе с номером 2r (номер цикла), матрицы, выбранные из множества различных квадратных матриц РМР (разделяемые с максимальным расстоянием) установлены как матрицы, применяемые в блоках линейного преобразования F-функций соответствующих циклов. В частности, применяют квадратные матрицы РМР, которые отличаются, по меньшей мере, в последующих циклах с четными номерами и в последующих циклах с нечетными номерами.
В частности, в соответствии с криптографической структурой общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r генерируют q квадратных матриц РМР L1, L2,…Lq (q≤r). Затем, поскольку матрицы для обработки линейного преобразования применяют в блоках линейного преобразования в F-функциях на этапах с нечетными номерами в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r, повторно устанавливают q квадратных матриц РМР с обозначением L1, L2,…,Lq, L1, L2,… от верхнего этапа F-функций. Кроме того, для F-функций этапов с четными номерами повторно устанавливают q квадратных матриц РМР с обозначением L1, L2,…,Lq, L1, L2,… от нижнего этапа F-функций.
На фиг.9 показан пример конфигурации, в которой применяют такую установку. В качестве примера конфигурации, в которой три вида разных квадратных матриц РМР скомпонованы в криптографической структуре общий-ключ-блок типа Фейстеля для q=3, а именно для цикла номер 12, в случае, когда структура определена как криптографическая структура общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r=12, а именно для r=6, квадратные матрицы РМР (L1, L2, L3) будут установлены в блоках линейного преобразования F-функций в соответствующих циклах, представленных на фиг.9.
Конфигурация по фиг.9 представляет собой структуру, которая разделяет открытый текст из 2mn битов на две части данных PL (Открытая-левая) и PR (Открытая-правая), каждая из которых состоит из mn битов, и выполняет F-функцию в каждом цикле, с использованием их в качестве входных значений. F-функция в первом цикле, а также F-функции в других циклах представляют собой F-функции, каждая из которых является функцией SPN-типа, состоящей из блока нелинейного преобразования, состоящего из S-блоков, и блока линейного преобразования, соединенных вместе.
В примере установки по фиг.9 r=6 и q=3, где символ Ln, показанный в каждой F-функции, обозначает квадратную РМР матрицу 402. Таким образом, L1, L2 и L3 обозначают три вида взаимно различающихся квадратных матриц РМР, каждая из которых представляет собой квадратную матрицу РМР, применяемую для обработки линейного преобразования в блоке линейного преобразования в каждой из F-функций.
Последовательность обработки установки матрицы MLTi линейного преобразования поясняется со ссылкой на фиг.10.
[Этап S21]
Число q выбирают равным или меньшим, чем половина r количества 2r циклов, а именно q, удовлетворяющее условию q≤r. Здесь q представляет собой целое число, равное двум или больше.
[Этап S22]
Генерируют q квадратных матриц РМР с размером m L1, L2,…,Lq для GF(2n). Подробно q квадратных матриц РМР с размером m L1, L2,…,Lq для GF(2n) поясняют в следующем параграфе.
После того как q квадратных матриц РМР с размером m L1, L2,…,Lq для GF(2n) будут сгенерированы на этапе S22, выполняют обработку установки квадратной матрицы РМР, описанную ниже.
[Этап S23]
Матрицу MLT2i-1 линейного преобразования для этапа номер 2i-1 (1≤i≤r) устанавливают в L(I-1modq)+1.
[Этап S24]
Матрицу MLT2j линейного преобразования на этапе номер 2i(1≤i≤r) устанавливают в MLT2r-2i+1.
Например, в случае примерной конфигурации, показанной на фиг.9, то есть в случае, когда устройство криптографической обработки имеет 12 этапов (r=6) и q=3, установка будет представлять собой:
MLT1=L1, MLT2=L3, МLT3=L2, MLT4=L2, MLT5=L3, MLT6=L1, MLT7=L1, MLT8=L3, MLT9=L2, MLT10=L2, MLT11=L3, MLT12=L1.
Таким образом, в устройстве криптографической обработки в соответствии с данным изобретением используют следующую структуру. В соответствии с криптографической структурой общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r генерируют q квадратных матриц РМР, где q<r. Для F-функций на этапах с нечетными номерами q квадратных матриц РМР повторно устанавливают с последовательным определением L1, L2,…,Lq, L1, L2,… на основе F-функции верхнего этапа, и для F-функций с четными номерами этапов q квадратных матриц РМР повторно устанавливают с последовательным определением L1, L2,…,Lq, L1, L2,… по F-функции нижнего этапа.
Ниже подробно описаны q квадратных матриц РМР с размером m L1, L2,…,Lq для GF(2n) на этапе S22 в потоке обработки по фиг.10 и установка их по F-функциям. Пояснение будет приведено по следующим пунктам.
(3-а) Пример генерирования квадратных матриц РМР, которые позволяют реализовать улучшенную устойчивость к атакам дифференциального криптоанализа, и установки их по F-функциям.
(3-b) Пример генерирования квадратных матриц РМР, которые позволяют реализовать улучшенную устойчивость к атакам линейного криптоанализа, и установки их по F-функциям.
(3-е) Пример генерирования квадратных матриц РМР, которые позволяют реализовать улучшенную устойчивость к атакам дифференциального криптоанализа и к атакам линейного криптоанализа, и установки их по F-функциям.
Далее будет описан пример (3-а) генерирования квадратных матриц РМР, в котором реализуется улучшенная устойчивость к атакам дифференциального криптоанализа и установки их для F-функций. Вначале, в качестве примера генерирования квадратных матриц РМР, в которых реализуется улучшенная устойчивость к атакам дифференциального криптоанализа, и установки их для F-функций будут описаны три примера а1, а2 и а3 обработки.
(Пример а1 обработки)
Далее будет описан первый пример генерирования квадратных матриц РМР, в котором реализуется улучшенная устойчивость к атакам дифференциального криптоанализа, и установка их для F-функций. Вначале будет приведено пояснение обработки генерирования квадратной матрицы РМР со ссылкой на блок-схему последовательности выполнения операций, показанную на фиг.11.
[Этап S101]
Входные значения обозначают следующим образом: количество необходимых квадратных матриц РМР как q, порядок расширения как n, и размер матрицы как m, q квадратных матриц РМР с размером m L1, L2,…,Lq генерируют случайным образом для GF(2n). Блок-схема последовательности выполнения операций, показанная на фиг.11, представляет пример обработки для количества матриц РМР q=6, порядка расширения n=8 и размера матрицы m=8.
[Этап S102]
Проверяют, являются ли линейно независимыми произвольные qm векторов колонок, полученные из qm векторов колонок, включенных в q квадратных матриц РМР с размером m L1, L2,…,Lq. Если поток прошел проверку, он переходит на этап S103 если нет, поток возвращается на этап S 101.
[Этап S103] Эти q квадратных матриц РМР с размером m L1, L2,…,Lq выводят как квадратные матрицы РМР, предназначенные для применения в шифре общий-ключ-блок типа Фейстеля для количества циклов 2r.
В ходе выполнения приведенного выше процесса генерируют q квадратных матриц РМР с размером m L1, L2,…,Lq. Здесь q удовлетворяет условию q≤r.
Эти q квадратных матриц РМР с размером m L1, L2,…,Lq, сгенерированные таким образом, устанавливают как матрицы, предназначенные для применения в обработке линейного преобразования в блоке линейного преобразования F-функции на каждом этапе в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2 r, в соответствии с обработкой, выполняемой на [этапе S23] и на [этапе S24], которые были описаны выше со ссылкой на фиг.10. То есть для этапов с нечетными номерами q квадратных матриц РМР обозначены как L1, L2,…,Lq, L1, L2… последовательно и с повторением для F-функций верхнего этапа, и для этапов с четными номерами q квадратных матриц РМР, обозначенных, как L1, L2,…,Lq, L1, L2… последовательно и с повторением на основе F-функций нижнего этапа.
Таким образом, квадратные матрицы РМР для циклов с нечетными номерами и квадратные матрицы РМР для циклов с четными номерами расположены во взаимно противоположном порядке, соответственно, в результате чего гарантируется, что обработка шифрования и обработка дешифрования будут одинаковыми за исключением обработки замены последовательности ключей.
Такая конфигурация гарантирует следующее. (а) Матрица линейного преобразования каждой F-функции представляет собой квадратную матрицу РМР. (b) Произвольные m векторов колонок из матриц линейного преобразования, включенные в, по меньшей мере, q последовательных F-функций в циклах с нечетными номерами в криптографической функции, являются линейно независимыми (с) Произвольные m векторов колонок из матриц линейного преобразования, включенные, по меньшей мере, в q последовательных F-функций в циклах с четными номерами, являются линейно независимыми. Поскольку гарантируются отношения (а) - (с), гарантируется, что в криптографической структуре общий-ключ-блок типа Фейстеля, имеющей множество циклов, не происходит одновременное сокращение различий из-за m или меньше активных S-блоков. Поэтому минимальное значение количества активных S-блоков во всей криптографической функции будет увеличиваться.
Таким образом, такой пример обработки позволяет увеличить минимальное количество активных S-блоков во всей криптографической функции, что представляет собой один из показателей устойчивости к атакам дифференциального криптоанализа в шифре общий-ключ-блок. В результате, количество активных S-блоков при попытке применения дифференциального анализа (атака дифференциального криптоанализа) будет увеличиваться, что повышает трудность анализа. Поэтому реализуется криптографическая обработка с высокой надежностью с трудным для анализа ключом.
(Пример а2 обработки)
Второй пример генерирования квадратных матриц РМР, в которых реализуется улучшенная устойчивость к атакам дифференциального криптоанализа, и установки их в F-функции будет описан ниже. Обработка генерирования квадратных матриц РМР будет описана со ссылкой на блок-схемы последовательности выполнения операций, представленные на фиг.12.
[Этап S201]
Входные значения обозначают следующим образом: количество необходимых матриц РМР как q, порядок расширения как n, и размер матриц как m, при этом q квадратных матриц РМР с размером m L1, L2,…,Lq генерируют для случайного значения GF(2n). Блок-схема последовательности выполнения операций, показанная на фиг.12, представляет пример обработки для количества матриц РМР q=6, порядка расширения n=8 и размера матрицы m=8.
[Этап S202]
Проверяют, представляет ли собой матрица из m колонок, выбранных произвольно из qm колонок, включенных в q квадратных матриц РМР с размером m L1, L2,…,Lq, квадратную матрицу РМР. Если поток прошел проверку, он затем переходит на этап S203, если нет, поток возвращается на этап S201. Здесь квадратная матрица РМР означает матрицу, удовлетворяющую следующим свойствам, как описано выше. (а) Матрица представляет собой квадратную матрицу. (b) Детерминанты всех подматриц, включенных в матрицу, не равны нулю, то есть det (submatrix)≠0.
[Этап S203]
Эти q квадратных матриц РМР с размером m L1, L2,…,Lq выводят как квадратные матрицы РМР, предназначенные для применения в шифре общий-ключ-блок типа Фейстеля для количества циклов 2r.
При выполнении описанного выше процесса генерируют q квадратных матриц РМР с размером m L1, L2,…,Lq. Здесь q удовлетворяет условию q≤r.
При обработке генерирования квадратной матрицы РМР в приведенном выше примере обработки а1, как описано с использованием последовательности обработки со ссылкой на фиг.11, определяют линейную независимость матрицы, составленной из произвольных колонок, взятых из qm колонок, включенных в q квадратных матриц РМР с размером m L1, L2,…,Lq, на этапе S102. При обработке генерирования квадратной матрицы РМР в таком примере а2 обработки проверяют, является ли матрица, составленная из произвольных m-колонок, взятых из qm колонок, включенных в q квадратных матриц РМР с размером m L1, L2,…,Lq, квадратной матрицей РМР. То есть выполняют более строгую проверку.
Аналогично описанному выше примеру а1 обработки q квадратных матриц РМР с размером m L1, L2,…,Lq, генерируемых в результате обработки генерирования квадратных матриц РМР, которая следует после последовательности обработки, показанной на фиг.12, устанавливают как матрицы, применяемые для обработки линейного преобразования в блоках линейного преобразования F-функций на соответствующих этапах в криптографической структуре общий-ключ-блок типа Фейстеля, с количеством этапов (количеством циклов) 2r, в соответствии с обработкой по [этапу S23] и [этапу S24], которые описаны выше, со ссылкой на фиг.10. То есть для этапов с нечетными номерами q квадратных матриц РМР, повторно обозначенных как L1, L2,…,Lq, L1, L2,…, последовательно получают из F-функций на предыдущем этапе, и для этапов с четными номерами, q квадратных матриц РМР, повторно обозначенных как L1, L2,…,Lq, L1, L2,…, последовательно получают из F-функций на нижнем этапе.
Таким образом, квадратные матрицы РМР с циклами с четными номерами и квадратные матрицы РМР с циклами с нечетными номерами располагают во взаимно обратном порядке, соответственно, что гарантирует то, что обработка шифрования и обработка дешифрования будут одинаковыми, за исключением обработки замены последовательности ключей.
Такая конфигурация гарантирует следующее:
(a) Матрица линейного преобразования каждой F-функции представляет собой квадратную матрицу РМР.
(b) Произвольные m векторов колонок из матриц линейного преобразования, включенные, по меньшей мере, в q последовательных F-функций, в циклах с нечетными номерами составляют квадратную матрицу РМР.
(c) Произвольные m векторов колонок из матриц линейного преобразования, включенные, по меньшей мере, в q последовательных F-функций, в циклах с четными номерами составляют квадратную матрицу РМР.
Поэтому в криптографической структуре общий-ключ-блок типа Фейстеля с количеством циклов, состоящих из множества этапов, гарантируется, что не происходит одновременное сокращение различий из-за m или меньше активных S-блоков в последовательных 2q-1 циклах. Кроме того, гарантируется следующее.
(d) Количество ненулевых элементов значений различий, полученных в результате вклада "а" (а≤m) активных S-блоков, становится равным m+1-а или больше в результате свойства квадратной матрицы РМР. Поэтому минимальная величина количества активных S-блоков во всей криптографической функции увеличивается.
Таким образом, как показано на этом примере обработки, становится возможным увеличить минимальное количество активных S-блоков во всей криптографической функции, что представляет собой одни из индексов устойчивости к атакам дифференциального криптоанализа в шифре общий-ключ-блок и в результате количество активных S-блоков, в случае попытки дифференциального анализа (атаки дифференциального криптоанализа) будут увеличиваться, и трудность анализа будет повышаться. Таким образом, реализуется криптографическая обработка с высокой надежностью, ключи которой являются трудными для анализа.
(Пример а3 обработки)
Третий пример генерирования квадратных матриц РМР, в которых реализуются улучшенная устойчивость к атакам дифференциального криптоанализа и установка их для F-функций, поясняется ниже. Обработка генерирования квадратных матриц РМР будет описана со ссылкой на блок-схему последовательности выполнения операций по фиг.13.
[Этап S301]
Входные значения обозначают следующим образом: количество необходимых матриц РМР как q, порядок расширения как n, и размер матриц как m, при этом генерируют одну из q квадратных матриц РМР с размером m для GF(2n). Блок-схема последовательности выполнения операций, показанная на фиг.1, представляет пример обработки, в соответствии с которым количество матриц РМР q=6, порядок расширения n=8 и размер матрицы m=8.
[Этап S302]
m рядов выбирают и выделяют произвольно из одной квадратной матрицы РМР с размером qm, и составляют матрицу M' из m рядов и qm колонок
[Этап S303]
Такие qm векторов колонок, включенных в матрицу M', состоящую из m рядов и qm колонок, произвольно разделяют на q групп, каждая из которых состоит из m векторов колонок, так что любой один из векторов колонок не присутствует в двух или больше группах. Квадратную матрицу L1, L2,…, Lq с размером m выводят из векторов колонок, включенных в соответствующие группы, в виде квадратных матриц РМР, предназначенных для применения в шифре общий-ключ-блок типа Фейстеля с количеством циклов 2r.
В результате выполнения приведенной выше обработки генерируют q квадратных матриц РМР с размером m L1, L2,…,Lq. Здесь q удовлетворяет условию q≤r.
[0148] Методика 3 генерирования квадратной матрицы РМР в примере а3 обработки будет более конкретно описана со ссылкой на фиг.14.
[Этап S301]
Одну квадратную матрицу М РМР с размером qm генерируют для GF(2n). Как показано на фиг.14, генерируют квадратную матрицу М РМР размером qm×qm. Следует отметить, что порядок матрицы М, генерируемой на этом этапе S301, может быть выше, чем qm (порядок).
[Этап S302]
Как показано на фиг.14, m колонок выбирают и выделяют произвольно из квадратных матриц М РМР размером qm, и составляют матрицу М', состоящую из m рядов и qm колонок. Следует отметить, что хотя пример, показанный на фиг.14, представляет собой пример, в котором последовательно выбирают и выделяют m рядов, матрица М' из m рядов и qm колонок может быть составлена путем выбора и выделения произвольных m рядов, имеющих промежуток между ними, который составят квадратную матрицу М РМР с размером m.
[Этап S303]
qm векторов колонок, включенных в матрицу М' из m рядов и qm колонок, разделяют на х групп, каждая из которых имеет m векторов колонок так, что любой один вектор колонки не присутствует в двух или больше группах, и квадратные матрицы с размером m L1, L2,…,Lx генерируют из векторов колонок, включенных в соответствующие группы.
Как и в примерах обработки а1 и а2, которые были описаны выше, q квадратных матриц РМР с размером m L1, L2,...,Lq, генерируемых в результате обработки генерирования квадратной матрицы РМР, которая следует после последовательности обработки, описанной на фиг.13 и 14, устанавливают как матрицы, предназначенные для применения для обработки линейного преобразования блоков линейного преобразования F-функций на соответствующих этапах в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r, в соответствии с обработкой, выполняемой на [этапе S23] и на [этапе S24], которая была описана выше со ссылкой на фиг.10. То есть для этапов с нечетными номерами q квадратных матриц РМР соответственно обозначают как L1, L2…,Lq, L1, L2… последовательно из F-функций предыдущего этапа, и для этапов с четными номерами q квадратных матриц РМР, соответственно обозначают как L1, L2,…,Lq, L1, L2… последовательно их F-функций нижнего этапа.
Таким образом, квадратные матрицы РМР для циклов с четными номерами и квадратные матрицы РМР для циклов с нечетными номерами располагают во взаимно противоположном порядке, соответственно, в результате чего гарантируется, что обработка шифрования и обработка дешифрования будут одинаковыми, за исключением обработки замены последовательности ключей.
Такая конфигурация гарантирует следующее. (а) Матрица линейного преобразования каждой F-функции представляет собой квадратную матрицу РМР. (b) Произвольные m векторов колонок матрицы линейного преобразования, включенной, по меньшей мере, в последовательные q F-функций, в циклах с нечетными номерами в криптографической функции, являются линейно независимьми. (с) Произвольные m векторов колонок матрицы линейного преобразования, включенные, по меньшей мере, в q последовательных F-функций, в циклах с четными номерами являются линейно независимыми. Поскольку гарантируются такие отношения (а) - (с), гарантируется то, что одновременное сокращение различий в результате вклада m или меньше активных S-блоков не происходит в последовательных 2q - 1 циклах в криптографической структуре общий-ключ-блок типа Фейстеля с количеством циклов, равным множеству этапов. Кроме того, гарантируется следующее. (d) Исходя из свойства квадратной матрицы РМР количество ненулевых элементов в значениях различий, полученных за счет вклада "а" (а≤m) активных S-блоков, становится равным m+1-а или больше. Поэтому минимальная величина количества активных S-блоков во всей криптографической функции увеличивается.
Особенный эффект пример обработки а3 производит в случае, в котором m и r становятся большими, затраты времени, требуемые в системе обработки определения матрицы в соответствии с указанными выше примерами а1 и а2 обработки, становятся огромными, и, таким образом, становится трудно определить матрицу в пределах реального времени. Даже в этом случае, если используют методику генерирования квадратной матрицы РМР в соответствии с данным примером а3 обработки, становится возможной обработка генерирования матрицы в сравнительно короткое время.
Это происходит из-за того, что обеспечивается возможность в примере обработки а3 использовать систему, которая может выполнять обработку для достаточно больших значений m и r в течение реального времени, например способ генерирования предназначен для генерирования матрицы с кодом Рида - Соломона.
Кроме того, в этом примере а3 обработки, как описано выше, становится возможным увеличить минимальное количество активных S-блоков во всей криптографической функции, что представляет собой один из показателей устойчивости к атакам дифференциального криптоанализа в шифре с общим-ключом-блоком. В результате, в случае попытки дифференциального анализа (атаки дифференциального криптоанализа) количество активных S-блоков увеличивается, что повышает трудность анализа. Таким образом, реализуется криптографическая обработка с высокой степенью надежности, ключ которой является трудным для анализа.
[(3-b) Пример генерирования квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам линейного криптоанализа, и установки их в F-функциях]
Далее поясняются два примера b1, b2 обработки в качестве примеров генерирования квадратных матриц РМР, в которых реализуется улучшенная устойчивость к атакам линейного криптоанализа, и установки их для F-функций. (Пример b1 обработки)
Далее будет описан первый пример генерирования квадратных матриц РМР, в которых реализуется улучшенная устойчивость к атакам линейного криптоанализа и установки их для F-функций. Обработка генерирования квадратных матриц РМР поясняется со ссылкой на блок-схему последовательности выполнения операций, показанную на фиг.15.
[Этап S401]
Входные значения обозначают следующим образом: количество необходимых квадратных матриц РМР как q, порядок расширения как n и размер матриц как m, при этом q квадратных матриц РМР с размером m M1, M2,…, Mq генерируют случайным образом для GF (2n). Блок-схема последовательности выполнения операций, показанная на фиг.14, представляет пример обработки для количества квадратных матриц РМР q=6, порядка расширения n=8 и размера матрицы m=8.
[Этап S402]
Проверяют, являются ли произвольные m векторов рядов, взятые из 2m векторов рядов, включенных в две соседние обратные матрицы, после расчета обратных матриц M1-1, М2-1, …,Mq-1 для q квадратных матриц РМР с размером m M1, М2,…, Mq линейно независимыми. tR по фиг.15 обозначает транспонированный вектор для вектора ряда. Если поток проходит проверку, этот поток переходит на этап S403, если нет, поток возвращается на этап S401. Здесь матрицы М1-1, Mq-1 необходимо рассматривать как соседние матрицы.
[Этап S403]
Эти q квадратных матриц РМР с размером m L1, L2,…,Lq выводят как квадратные матрицы РМР, предназначенные для применения для шифра общий-ключ-блок типа Фейстеля, для количества циклов 2r.
В результате выполнения указанного выше процесса генерируют q квадратных матриц РМР с размером m L1, L2,…,Lq. Здесь q удовлетворяет условию q≤r.
Такие q квадратных матриц РМР с размером m, сгенерированные таким образом - L1, L2,…,Lq, устанавливают как матрицы, предназначенные для применения для обработки линейного преобразования в блоках линейного преобразования F-функций на соответствующих этапах в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r, в соответствии с обработкой, выполняемой на [этапе S23] и [этапе S24], которая была описана выше со ссылкой на фиг.10. Таким образом, для этапов с нечетными номерами q квадратных матриц РМР повторно обозначают как L1, L2,…,Lq, L1, L2… последовательно из F-функций верхнего этапа, и для этапов с четными номерами q квадратных матриц РМР повторно обозначают L1, L2,…,Lq, L1, L2… последовательно из F-функций нижнего этапа.
Квадратные матрицы РМР для циклов с четными номерами и квадратные матрицы РМР для циклов с нечетными номерами располагают во взаимно обратном порядке, соответственно, таким образом, в результате чего гарантируется, что обработка шифрования и обработка дешифрования будут одинаковыми, за исключением замены последовательности ключей.
Такая конфигурация гарантирует следующее. (а) Матрица линейного преобразования каждой F-функции представляет собой квадратную матрицу РМР, (b) m векторов колонок в обратной матрице, включенные последовательно в циклах с нечетными номерами, в криптографической функции и в обратной матрице, включенной последовательно в ее циклы с четными номерами, являются линейно независимыми. Эти свойства позволяют повысить трудность при анализе путем линейной аппроксимации в атаках линейного криптоанализа и реализовать криптографическую обработку с высокой надежностью, с повышенной трудностью анализа, то есть ключ которой является трудным для анализа.
(Обработка по примеру b2)
Второй пример генерирования квадратных матриц РМР, в котором реализуется улучшенная устойчивость к атакам линейного криптоанализа, и установка их для F-функций будет описан ниже. Пояснения будут приведены для обработки генерирования квадратной матрицы РМР со ссылкой на блок-схему последовательности выполнения операций, представленную на фиг.16.
[Этап S501]
Входные значения обозначают следующим образом: количество необходимых квадратных матриц РМР как q, порядок расширения как n и размер матриц как m, при этом q квадратных матриц РМР с размером m M1, M2,…,Mq генерируют случайным образом для GF (2n). В блок-схеме последовательности выполнения операций, показанной на фиг.16, представлен пример обработки для количества квадратных матриц РМР q=6, порядка расширения n=8 и размер матрицы m=8.
[Этап S502]
Проверяют, составляют ли квадратную матрицу РМР произвольные m векторов рядов, взятые из 2r векторов рядов, включенных в две соседние обратные матрицы, после расчета обратных матриц M1-1, M2-1,…,Mq-1, для q квадратных матриц РМР с размером m M1, М2,…,Mq. tR по фиг.16 обозначает транспонированный вектор для вектора ряда. Если поток проходит проверку, поток переходит на этап S503, если нет, поток возвращается на этап 401. Здесь M1-1, Mq-1 следует рассматривать как соседние матрицы. Квадратная матрица РМР представляет собой матрицу, удовлетворяющую следующим свойствам. (а) Эта матрица представляет собой квадратную матрицу. (b) Детерминанты всех подматриц, включенных в матрицу, не равны нулю, а именно det (submatrix)≠0.
[Этап S503]
Эти q квадратных матриц РМР с размером m L1, L2,…,Lq выводят как квадратные матрицы РМР, предназначенные для применения, в шифре общий-ключ-блок типа Фейстеля для количества циклов 2r.
В результате описанного выше процесса генерируют q квадратных матриц РМР с размером m L1, L2,…,Lq. Здесь q удовлетворяет условию q≤r.
При обработке генерирования квадратной матрицы РМР в примере b1 обработки, описанном выше, как поясняется последовательностью обработки, представленной на фиг.15, определяют линейную независимость при отборе произвольных m векторов колонок из qm векторов колонок, включенных в обратные матрицы M1 -1 M2 -1,…,Mq -1 для q квадратных матриц РМР с размером m M1, М2,…,Mq на этапе S402. При обработке генерирования квадратной матрицы РМР в таком примере b2 обработки проверяют, составляют ли квадратную матрицу РМР произвольные m векторов колонок, взятые из m векторов колонок, включенных в обратные матрицы M1 -1, M2 -1,…,Mq -1 для q квадратных матриц РМР с размером m M1, М2,…,Mq. Таким образом, выполняют более строгую проверку.
Так же, как в примере b1 обработки, описанной выше, q квадратных матриц РМР с размером m L1, L2,…,Lq, генерируемых в результате обработки генерирования квадратной матрицы РМР, которая соответствует последовательности обработки, показанной на этой фиг.16, устанавливают как матрицы, предназначенные для применения при обработке линейного преобразования в блоке линейного преобразования F-функций на соответствующих этапах в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количество циклов) 2r, в соответствии с обработкой на [этапе S23] и [этапе S24], которая была описана выше, со ссылкой на фиг.10. Таким образом, для этапов с нечетными номерами q квадратных матриц РМР обозначают как L1, L2,…,Lq, L1, L2… последовательно и с повторением из F-функций верхнего этапа, и для этапов с четными номерами q квадратных матриц РМР, обозначают как L1, L2,…,Lq, L1, L2… последовательно и с повторением из F-функций нижнего этапа.
Таким образом, квадратные матрицы РМР для циклов с четными номерами и квадратные матрицы РМР для циклов с нечетными номерами расположены во взаимно обратном порядке, соответственно, в результате чего гарантируется, что обработка шифрования и обработка дешифрования будут одинаковыми, за исключением обработки замены последовательности ключей.
Такая конфигурация гарантирует следующее. (а) Матрица линейного преобразования каждой F-функции представляет собой квадратную матрицу РМР. (b) Произвольные m векторов колонок из обратных матриц для матрицы линейного преобразования, включенных последовательно в циклы с нечетными номерами в криптографической функции, и/или матрица линейного преобразования, включенная последовательно в циклы четными номерами, составляют квадратную матрицу РМР. Эти свойства позволяют повысить трудность анализа путем линейной аппроксимации при атаках линейного криптоанализа, и при этом реализуется криптографическая обработка с высокой степенью надежности, которая повышает трудность анализа, то есть ключ которой является трудным для анализа.
[Пример (3-е) генерирования квадратных матриц РМР, в которых реализуется улучшенная устойчивость к атакам дифференциального криптоанализа и атакам линейного криптоанализа и установка их для F-функций]
Далее поясняется пример генерирования квадратных матриц РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа и атакам линейного криптоанализа и установка их для F-функций.
Криптографический алгоритм с устойчивостью к атакам дифференциального криптоанализа реализуют путем применения обработки, которая была описана выше со ссылкой на фиг.10-13, то есть путем установки квадратных матриц РМР, предназначенных для применения при линейном преобразовании в блоках линейного преобразования F-функций, путем применения любого одного из указанных выше примеров а1 (фиг.11))- а3 (фиг.13) обработки. Кроме того, криптографический алгоритм с устойчивостью к атакам линейного криптоанализа реализуют путем применения обработки, описанной выше со ссылкой на фиг.10 и фиг.14 и 15, то есть путем установки квадратных матриц РМР, предназначенных для применения в линейном преобразовании в блоках линейного преобразования F-функций, в результате применения любого из указанной выше примеров b1 обработки (фиг.14) и b2 (фиг.15).
Алгоритм, в котором используются квадратные матрицы РМР, которые реализуют улучшенную устойчивость к атакам дифференциального криптоанализа и атакам линейного криптоанализа, выполнен путем установки квадратных матриц РМР, сгенерированных в результате выполнения как одной из обработки по примерам а1 (фиг.11)- а3 (фиг.12) обработки и одной из обработки по примерам b1 (фиг.14) и b2 (фиг.15) обработки, в качестве матриц, предназначенных для применения при обработке линейного преобразования в блоках линейного преобразования F-функций соответствующих этапов в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количества циклов)2r.
Таким образом, q квадратных матриц РМР генерируют с помощью любой из следующих комбинаций: пример а1 обработки и пример b1 обработки; пример а1 обработки и пример b2 обработки; пример а2 обработки и пример b1 обработки; пример а2 обработки и пример b2 обработки; пример а3 обработки и пример b1 обработки; пример а3 обработки и пример b2 обработки; и устанавливают как матрицы, предназначенные для применения при обработке линейного преобразования блоков линейного преобразования F-функций на соответствующих этапах в криптографической структуре общий-ключ-блок типа Фейстеля с количеством циклов 2r. Таким образом, для этапов с нечетными номерами q квадратных матриц РМР повторно последовательно обозначают как L1, L2,…,Lq, L1, L2… на основе F-функций верхнего этапа, и для этапов с четными номерами q квадратных матриц РМР повторно последовательно обозначают как L1, L2,…,Lq, L1, L2… на основании F-функций нижнего этапа. При такой установке становится возможной криптографическая обработка, в которой реализуется улучшенная устойчивость к атакам дифференциального криптоанализа и атакам линейного криптоанализа.
Один пример обработки генерирования квадратных матриц РМР для воплощения криптографической обработки, которая реализует улучшенную устойчивость к атакам дифференциального криптоанализа и атакам линейного криптоанализа, поясняется со ссылкой на фиг.17. Такая обработка представляет собой комбинацию примера а2 обработки и примера b2 обработки, описанных выше.
[Этап S601]
Входные значения обозначают следующим образом: количество необходимых квадратных матриц РМР как q, порядок расширения как n и размер матрицы как m, при этом q квадратных матриц с размером m генерируют случайным образом для
GF (2n). Блок-схема последовательности выполнения операций, показанная на фиг.17, представляет пример обработки для количества квадратных матриц РМР q=6, порядка расширения n=8 и размера матрицы m=8.
[Этап S602]
Когда m колонок отбирают из qm колонок, включенных в q квадратных матриц РМР с размером m, M1, М2,…,Mq, проверяют, составляют ли они квадратную матрицу РМР. Если поток прошел проверку, он переходит на этап S603; если нет, поток возвращается на зтап S601. Здесь квадратная матрица РМР означает матрицу, удовлетворяющую следующим свойствам. (а) Она представляет собой квадратную матрицу. (b) Детерминанта любой из подматриц, включенных в матрицу, не равна нулю, а именно det (submatrix)≠0.
[Этап S603]
Обратные матрицы M1 -1, М2 -1,…,Mq -1 для q квадратных матриц РМР с размером mM1, М2,…,Mq рассчитывают и проверяют, составляют ли произвольные m векторов рядов, взятых из 2m векторов рядов, включенных в две соседние обратные матрицы, квадратную матрицу РМР. tR по фиг.17 обозначает транспонированный вектор для вектора ряда. Если поток обработки прошел эту проверку, поток переходит на этап S604; если нет, поток возвращается на этап S601. Здесь матрицы M1 -1, Mq -1 необходимо рассматривать как соседние матрицы.
[Этап S604]
Такие q квадратных матриц РМР с размером mL1, L2,…,Lq выводят как квадратные матрицы РМР, предназначенные для применения, в шифре с общим-ключом-блоком Типа Фейстеля с количеством циклов 2r.
Используя описанный выше процесс, генерируют q квадратных матриц РМР с размером m L1, L2,…,Lq. Здесь q удовлетворяет условию q≤r.
Эти q квадратных матриц РМР с размером m L1, L2,…,Lq, сгенерированные с использованием обработки генерирования квадратной матрицы РМР, после которой была выполнена последовательность обработки, показанная на фиг.17, устанавливают как матрицы, предназначенные для применения при обработке линейного преобразования блоков линейного преобразования блоков F-функций соответствующих этапов в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r, в соответствии с обработкой, выполняемой на [этапе S23] и [этапе S24], которые были описаны выше со ссылкой на фиг.10. То есть для этапов с нечетными номерами q квадратных матриц РМР, повторно последовательно обозначают как L1, L2,…,Lq, L1, L2… на основании F-функций верхнего этапа, и для этапов с четными номерами q квадратных матриц РМР повторно последовательно обозначают как L1, L2,…,Lq, L1, L2… из F-функций нижнего этапа.
Таким образом, квадратные матрицы РМР циклов с четными номерами и квадратные матрицы РМР циклов с нечетными номерами располагают во взаимно обратном порядке, соответственно, в результате чего гарантируется, что обработка шифрования и обработка дешифрования выполняются одинаково, за исключением обработки замены последовательности ключей.
Такая конфигурация гарантирует следующие соотношения (а) - (с). (а) Матрица линейного преобразования каждой F-функции представляет собой квадратную матрицу РМР. (b) Произвольные m векторов колонок матрицы линейного преобразования, включенные в, по меньшей мере, последовательные q F-функций в цикле с нечетным номером криптографической функции, составляют квадратную матрицу РМР. (с) Произвольные m векторов колонок матрицы линейного преобразования, включенные, по меньшей мере, в последовательные q F-функций в циклах с четными номерами, составляют квадратную матрицу РМР. Поскольку эти соотношения (а) - (с) гарантируются, в криптографической структуре общий-ключ-блок типа Фейстеля с количеством циклов, равным множеству этапов, гарантируется, что одновременное сокращение различий за счет вклада m или менее активных S-блоков не происходит в последовательных 2q - 1 циклах. Кроме того, (d), исходя из свойства квадратной матрицы РМР гарантируется, что количество ненулевых элементов в значениях различий, полученных в результате вклада "а" (а≤m) активных S-блоков, становится равным m+1-а или больше. Поэтому минимальное значение количества активных S-блоков во всей криптографической функции увеличивается. Кроме того, гарантируется следующее. (е) Произвольные m векторов колонок для обратных матриц в матрицах линейного преобразования, последовательно включенных в циклы с нечетными номерами, и матрицы линейного преобразования, последовательно включенные в циклы с четными номерами, в криптографической функции совместно составляют квадратную матрицу РМР. Эти свойства обеспечивают повышение трудности при анализе с использованием линейной аппроксимации при атаках линейного криптоанализа, и криптографическую обработку с высокой надежностью с увеличенной трудностью анализа, то есть реализуется трудность анализа всего ключа.
Таким образом, на основе такого примера обработки повышается трудность анализа как для атак дифференциального криптоанализа, так и для атак линейного криптоанализа, и реализуется криптографическая обработка с высокой надежностью, ключ которой является трудным для анализа. Пример, показанный на фиг.17, представляет собой, как описано выше, пример генерирования квадратных матриц РМР путем комбинирования примера а2 обработки и примера b2 обработки, описанных выше. Однако могут быть приняты другие варианты генерирования. То есть q квадратных матриц РМР генерируют путем комбинирования одной из следующих пар: пример а1 обработки и пример b1 обработки, пример а1 обработки и пример b2 обработки, пример а2 обработки и пример b1 обработки, пример а3 обработки и пример b1 обработки и пример а3 обработки и пример b2 обработки. Для этапов с нечетными номерами q квадратных матриц РМР повторно последовательно обозначают как L1, L2,…,Lq, L1, L2… из F-функций на верхнем этапе, и для этапов с четными номерами q квадратных матриц РМР повторно последовательно обозначают как L1, L2,…,Lq, L1, L2… из F-функций на более низком этапе в виде матрицы, предназначенной для применения в линейных блоках преобразования F-функций соответствующих этапов в криптографической структуре общий-ключ-блок типа Фейстеля для количества этапов (количества циклов) 2r; в результате чего становится возможным реализовать криптографическую обработку с высокой надежностью, которая имеет улучшенную трудность при анализе, как при атаках дифференциального криптоанализа, так и при атаках линейного криптоанализа, и ключ которых является трудным для анализа.
Хотя в приведенном выше пояснении предполагалось, что матрица линейного преобразования представляет собой матрицу размером m×m, определенную по GF (2n) и используемую в операции преобразования данных из mn битов в mn битов, эффект, аналогичный атакам дифференциального криптоанализа и атакам линейного криптоанализа, может быть эффективно получен даже в случае, когда используют матрицу размером mn×mn, определенную по GF (2). Фактически, произвольная матрица по GF (2n) может быть приведена во взаимное соответствие с матрицей по GF (2), обеспечивающей то же преобразование. Поэтому можно сказать, что матрица по GF (2) проявляет более общее представление. Матрица по GF (2) имеет mn колонок и mn рядов, которые n раз совпадают со случаем GF (2n). По этой причине первая колонка матрицы для GF (2n) соответствует с первой по n-ю колонкам матрицы для GF (2), и первый ряд матрицы для GF (2n) соответствует с первого по n-й ряд ее. То есть i-й ряд соответствует с [(i-1)+1]-го по [(i-1)+n]-го рядам, и i-я колонка соответствует с [(i -1)+1]-й по [(i-1)+n]-ю колонкам. Поэтому для выполнения операции выделения колонки или ряда для GF (2n), если используется матрица, определенная по GF (2), необходимо выполнить операцию выделения n рядов или n колонок, которые соответствуют колонке или ряду для GF (2), соответственно. Операция выделения m рядов или колонок для GF (2) требует выделения n рядов или колонок m раз для GF (2), и в результате может быть получена матрица mn×mn. Приведенная выше координация позволяет легко расширять матрицы до матриц, определенных для GF (2).
Наконец, на фиг.18 показан пример конфигурация модуля 600 с интегральной микросхемой, используемого в качестве устройства криптографической обработки, предназначенного для выполнения функции криптографической обработки. Указанную выше обработку выполняют в различных устройствах обработки информации, например ПК, карты с интегральной микросхемой, устройство считывания/записи и т.д. и модуль 600 с интегральной микросхемой, показанный на фиг.18, можно использовать как компонент этих различных устройств.
ЦПУ (центральное процессорное устройство) 601, показанное на фиг.18, представляет собой процессор, предназначенный для выполнения различных программ, таких как начало криптографической обработки, ее окончание, управление передачей/приемом данных, управление передачей данных между конфигурационными блоками и выполнение различных программ. Запоминающее устройство 602 состоит из ПЗУ (постоянное запоминающее устройство), предназначенного для сохранения программы, которую выполняет ЦПУ 601, или фиксированных данных, используемых в качестве операционных параметров, ОЗУ (оперативное запоминающее устройство), используемого как область сохранения программы, выполняемой при обработке ЦПУ 601, параметров, постоянно изменяющихся при обработке программы, и рабочей области и т.д. Причем запоминающее устройство 602 также можно использовать как область накопителя данных ключей, необходимых для криптографической обработки и т.д. Предпочтительно, чтобы область накопителя данных и т.д. была построена как запоминающее устройство, со структурой, устойчивой к взлому.
Блок 603 криптографической обработки выполняет шифрование, дешифрование и т.д. в соответствии с алгоритмом криптографической обработки, например общий-ключ-блок типа Фейстеля, описанный выше. Хотя был показан пример, в котором средство криптографической обработки выполнено как отдельный модуль, оно также может быть выполнено так, что, например, криптографическая программа будет записана в ПЗУ, и ЦПУ 601 будет считывать и выполнять сохраненную в ПЗУ программу без необходимости использования такого независимого криптографического модуля.
Генератор 604 случайного числа выполняет обработку генерирования случайных чисел, которые необходимы при генерировании ключа, то есть требуются для криптографической обработки и т.п.
Блок 605 передачи/приема представляет собой блок передачи данных, предназначенный для выполнения передачи данных с внешними устройствами, который выполняет передачу данных, например, из устройства считывания-записи и т.д. модуля с интегральной микросхемой, и который выводит зашифрованный текст, сгенерированный в модуле с интегральной микросхемой или вводит в него данные и т.д. из внешнего устройства считывания-записи и т.д.
В приведенном выше описании данное изобретение было подробно описано со ссылкой на конкретные варианты выполнения. Однако для специалистов в данной области техники будет очевидно, что возможно выполнить модификацию и замену варианта выполнения в пределах отхода от объема и сущности данного изобретения. То есть данное изобретение было описано в форме иллюстрации, и его не следует интерпретировать как ограничение. Для определения сущности этого изобретения следует учитывать колонку патентной формулы изобретения.
Следует отметить, что последовательность обработки, поясняемая в описании, может быть выполнена с использованием аппаратных средств, программных средств или с использование комбинации этих подходов. При выполнении обработки с помощью программных средств программа, в которой записана последовательность обработки, может выполняться путем установки ее в запоминающем устройстве, встроенном в специализированный компьютер, или может выполняться путем установки ее в компьютере общего назначения, который может выполнять различную обработку.
Например, программа может быть заранее записана на жесткий диск или в ПЗУ (постоянное запоминающее устройство), используемое как носитель записи. В качестве альтернативы, программа может быть временно или постоянно сохранена на съемном носителе записи, таком как гибкий диск, CD-ROM (постоянное запоминающее устройство на компакт-диске), МО диск (магнитооптический диск), DVD (цифровой универсальный диск), магнитный диск и полупроводниковая память. Такой съемный носитель записи может быть предоставлен в форме так называемого программного пакета.
Кроме установки программы в компьютере со съемного носителя записи, как описано выше, может быть принята следующая схема. Программа может быть передана по беспроводному каналу передачи данных в компьютер с сайта загрузки или может быть передана по кабелю в компьютер через сеть, такую как ЛВС (локальная вычислительная сеть) и сеть Интернет, в то время как компьютер принимает программу, передаваемую таким образом, и устанавливает ее на носителе записи, таком как внутренний жесткий диск.
Следует отметить, что различного рода обработка, записанная в описании, может быть выполнена параллельно или индивидуально в соответствии с возможностями обработки устройства, выполняющего обработку, или если необходимо, путем выполнения во временной последовательности в соответствии с описанием. Следует отметить, что в данном описании система представляет собой одну из систем, которая имеет структуру логической комбинации множества устройств, но не ограничивается системами, каждая из которых имеет собственные устройства в одном корпусе.
Как описано выше, в соответствии с конфигурацией этого изобретения, в криптографической обработке общий-ключ-блок типа Фейстеля, состоящей в выполнении F-функций SPN-типа, которая имеет блок нелинейного преобразования и блок линейного преобразования, повторно для множества циклов она сконфигурирована для выполнения следующего. При выполнении обработки линейного преобразования F-функции, соответствующей каждому из множества циклов, в качестве обработки линейного преобразования, в которой используется квадратные матрицы РМР (разделяемые с максимальным расстоянием), используют квадратные матрицы РМР La, Lb, которые отличаются, по меньшей мере, в последовательных циклах с нечетными номерами и в последовательных циклах с четными номерами, соответственно, и выполняют обработку линейного преобразования с квадратными матрицами РМР, в которой используют квадратные матрицы РМР La, Lb отличающиеся, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетным номерами, и матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1 для квадратных матриц РМР является линейно независимой или составляет квадратную матрицу РМР. Вследствие этого устойчивость к атакам линейного криптоанализа в шифре общий-ключ-блок улучшается, и трудность анализа ключа шифрования и т.д. повышается, в результате чего реализуется криптографическая обработка с высокой степенью защиты. Поэтому настоящее изобретение можно применять к устройству криптографической обработки, которое требуется для улучшения трудности анализа при поиске ключа, и которая имеет высокую степень надежности.
Кроме того, в соответствии с конфигурацией данного изобретения, в криптографической обработке общий-ключ-блок типа Фейстеля, в которой выполняют F-функцию SPN-типа, имеющую блок нелинейного преобразования и блок линейного преобразования, повторно, в течение множества циклов, конфигурируют для выполнения обработки линейного преобразования F-функции, соответствующей каждому из множества циклов, как обработку линейного преобразования, в которой используют квадратные матрицы РМР (разделяемые с максимальным расстоянием) и, в то же время, применяют квадратные матрицы РМР, которые отличаются, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетными номерами, в которой эти квадратные матрицы РМР проявляют линейную независимость или составляют квадратные матрицы РМР. Поэтому гарантируется, что не происходит одновременное сокращение различий в результате вклада активных S-блоков, и становится возможным увеличить минимальное количество активных S-блоков во всей криптографической функции, которая представляет собой один из показателей надежности для атак дифференциального криптоанализа в шифре общий-ключ-блок. При использовании такой конфигурации улучшается устойчивость как к атакам линейного криптоанализа, так и к атакам дифференциального криптоанализа, и, таким образом, воплощается криптографическая обработка с высокой степенью безопасности. Поэтому настоящее изобретение можно применять для устройства криптографической обработки, которое требуется для повышения трудности при анализе ключа и которое обладает высокой степенью защиты.
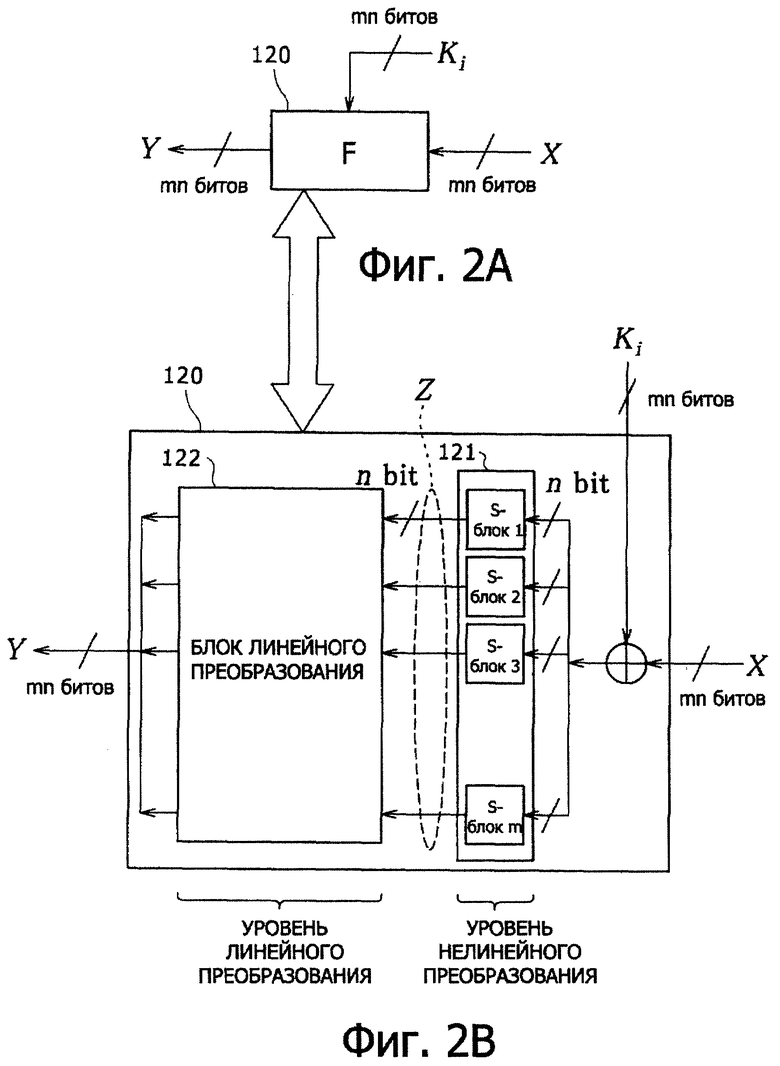
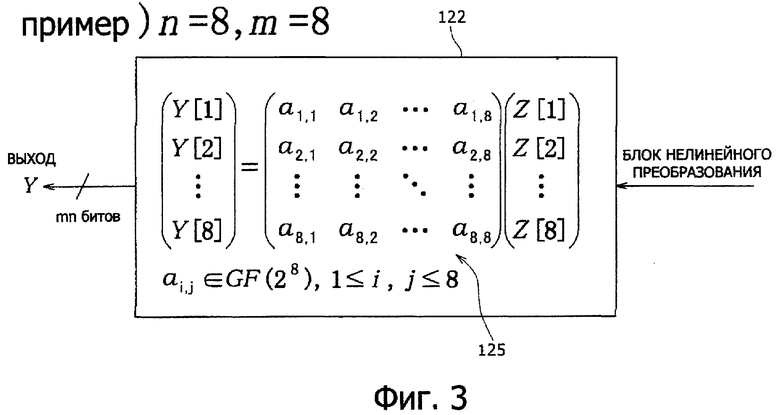
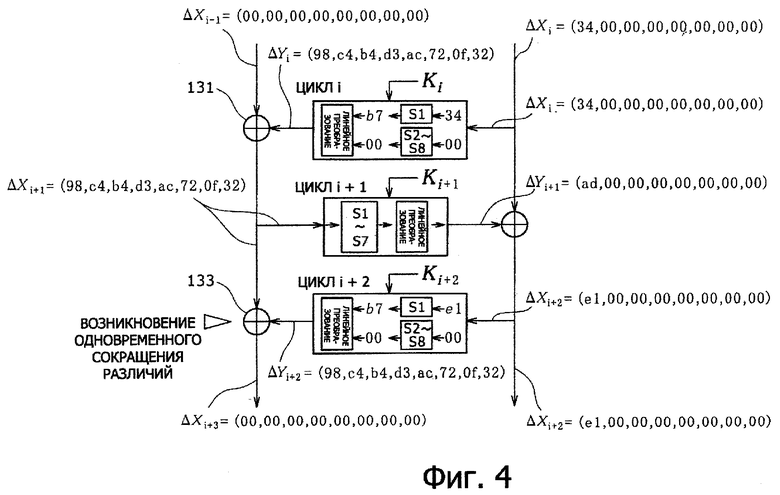
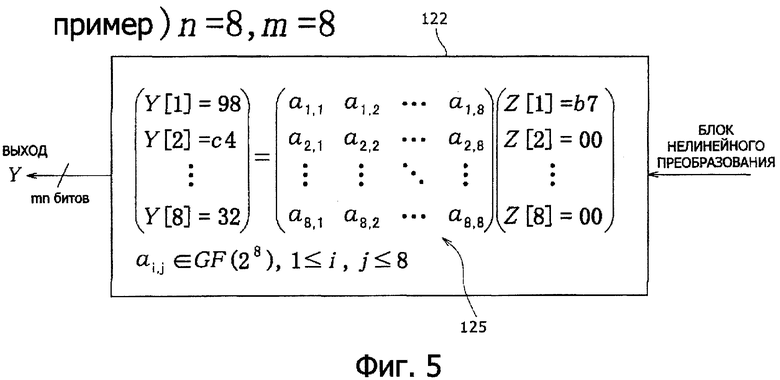
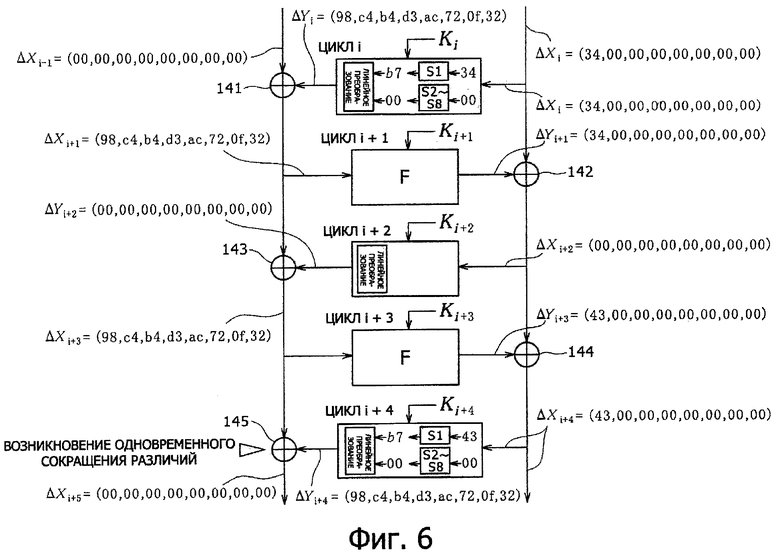
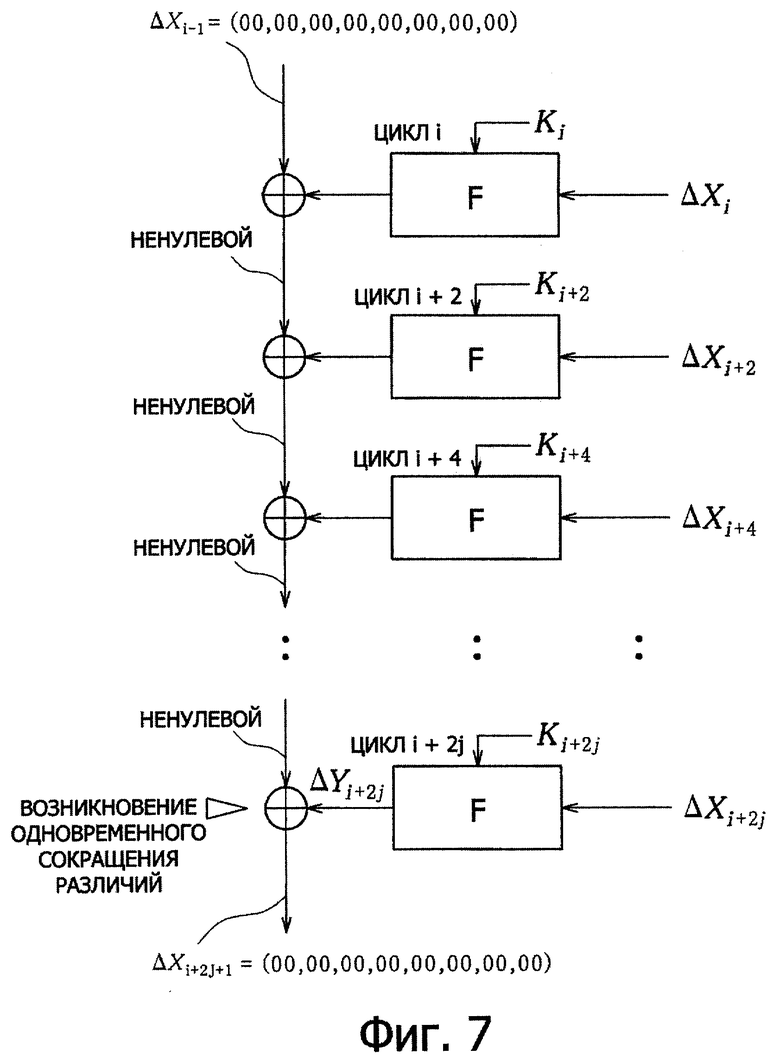

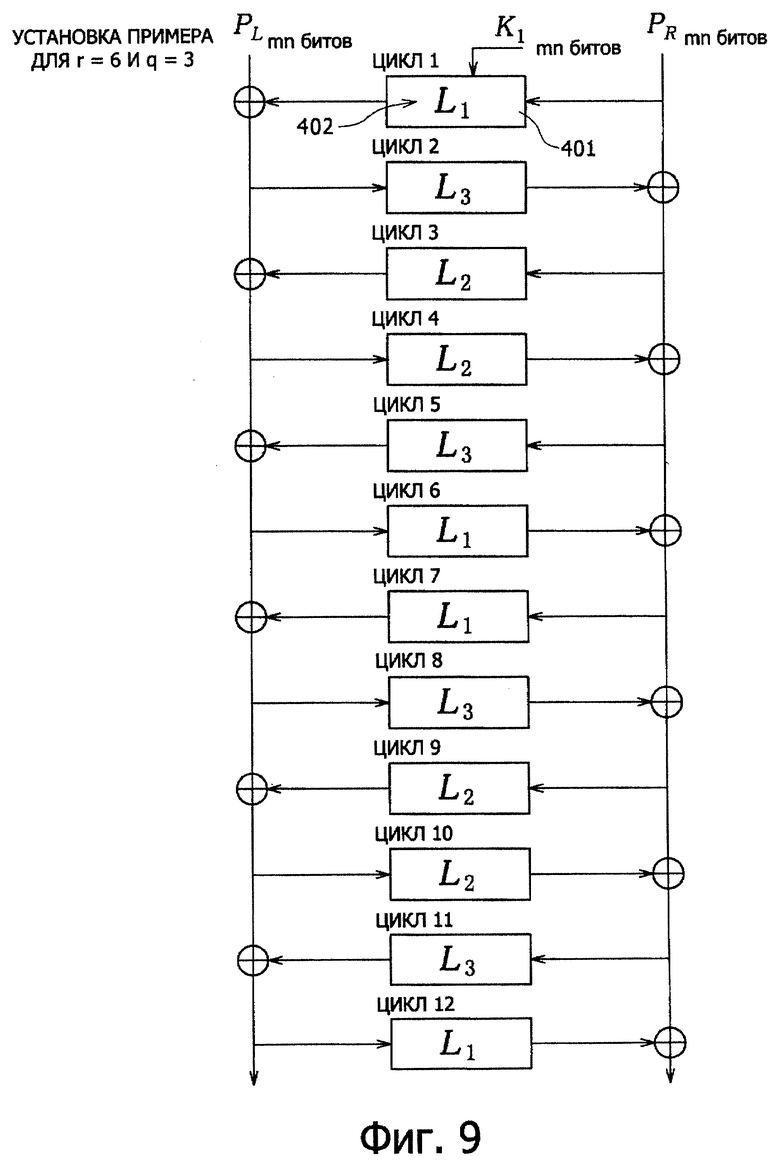
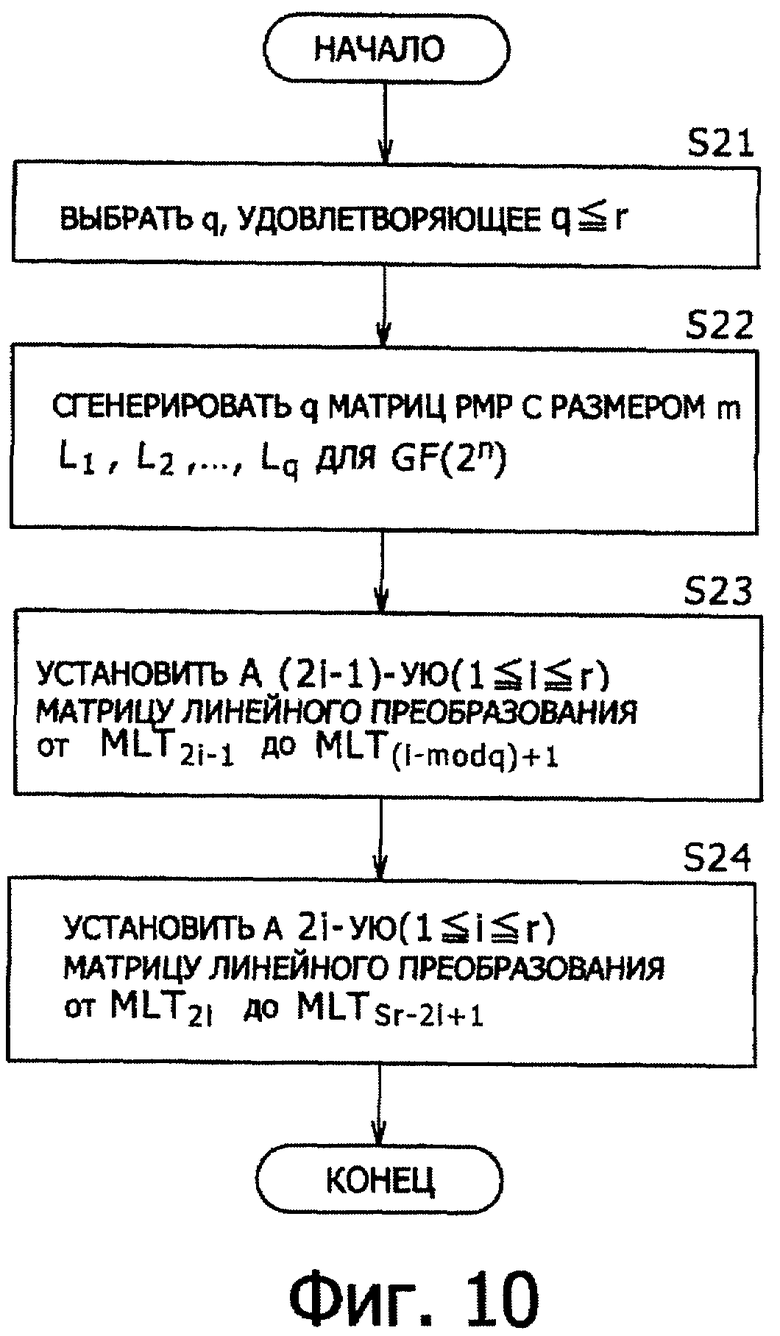
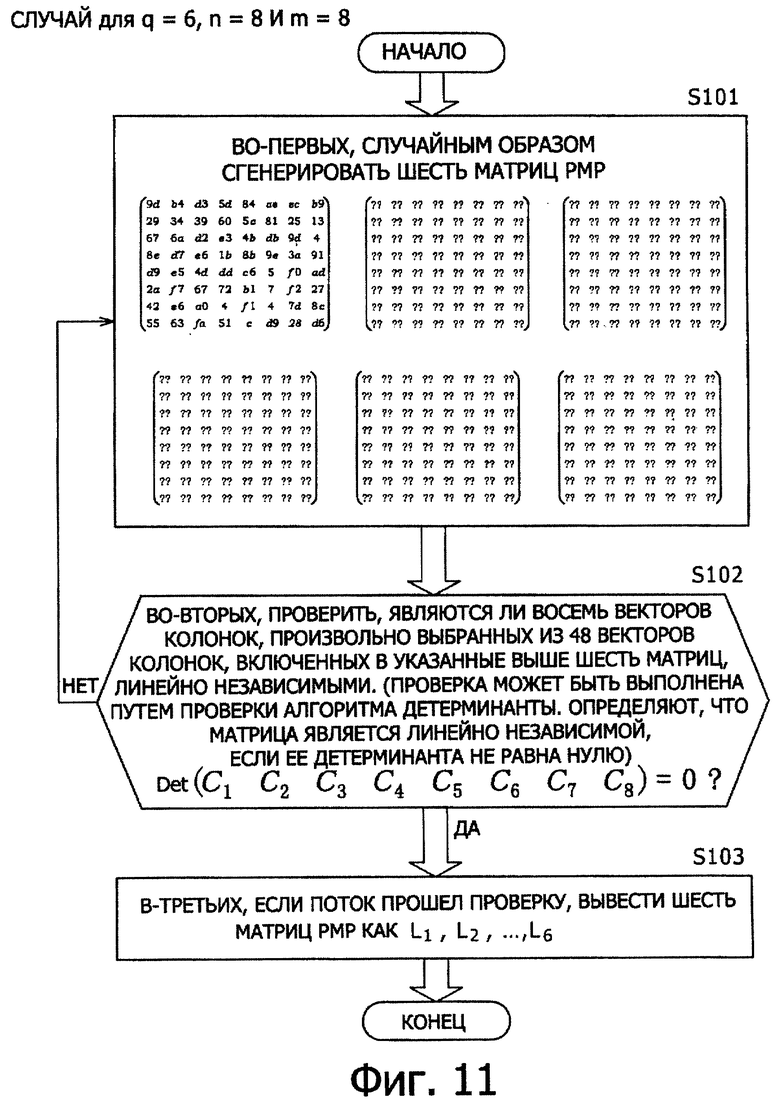
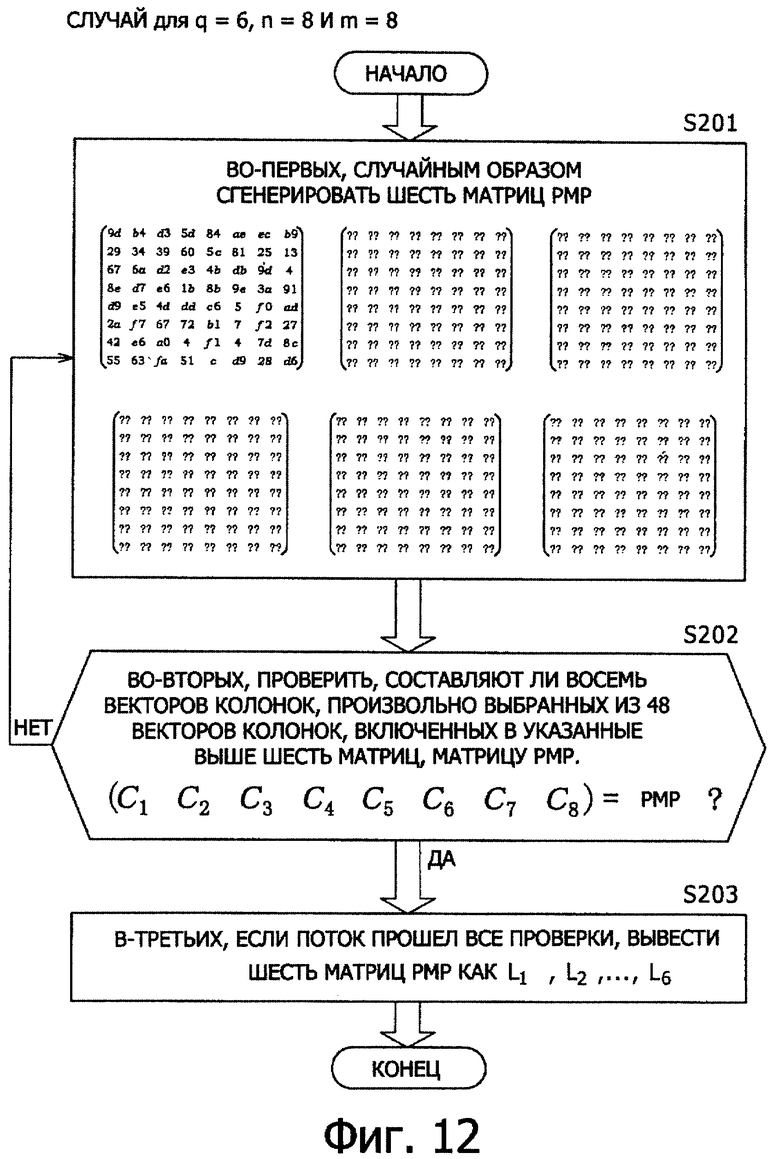
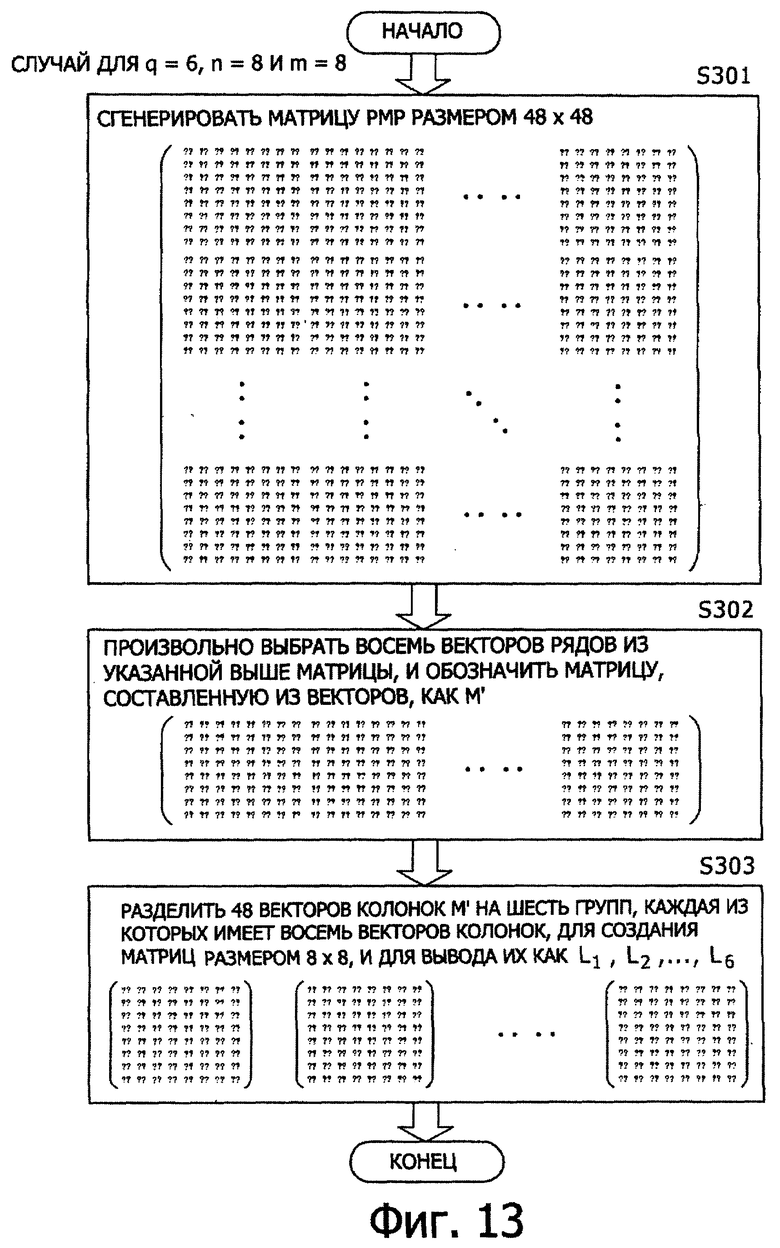
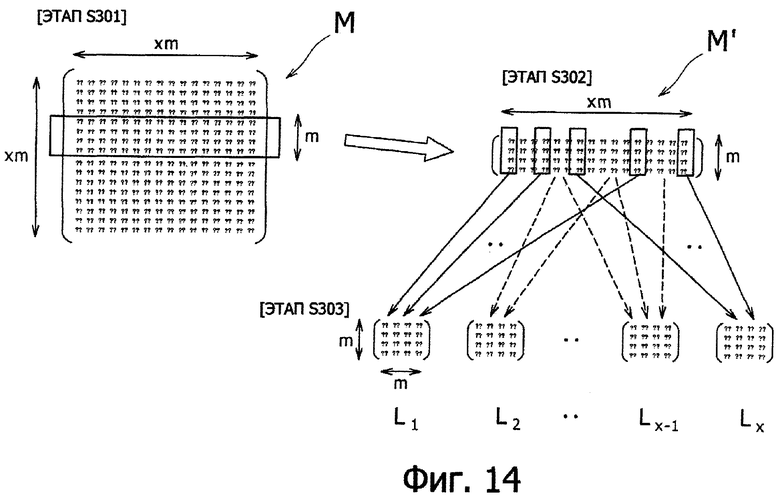
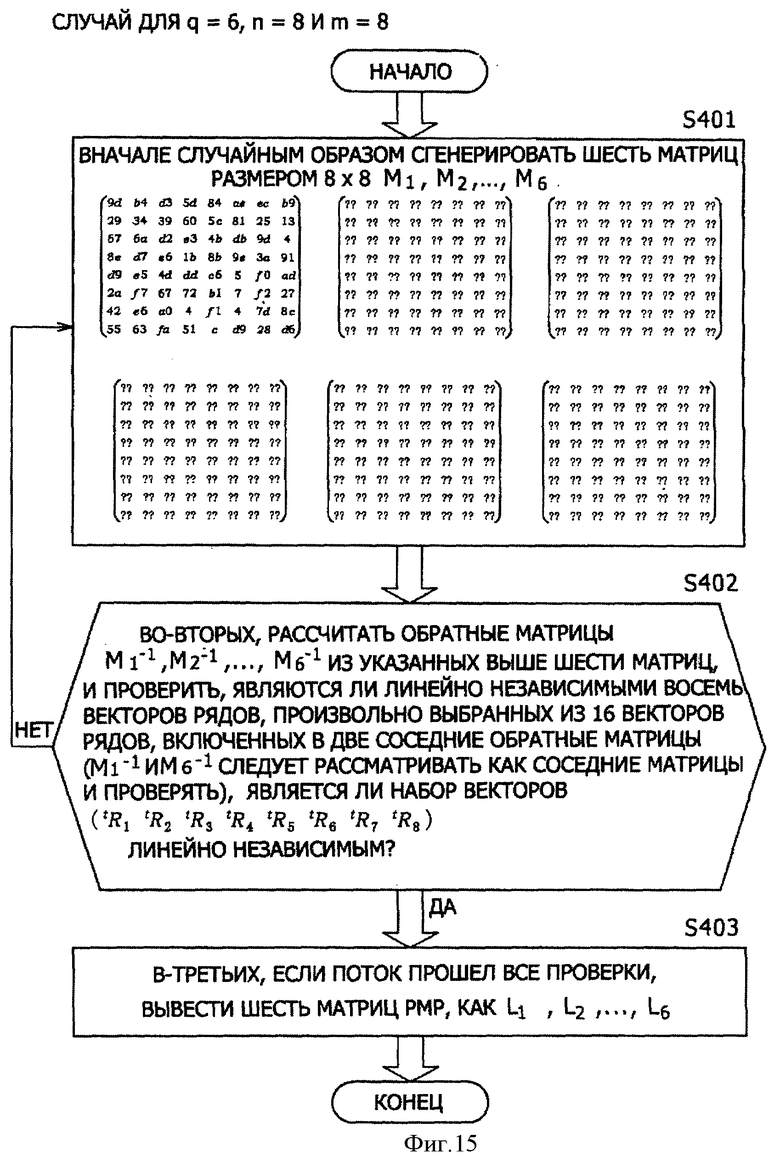
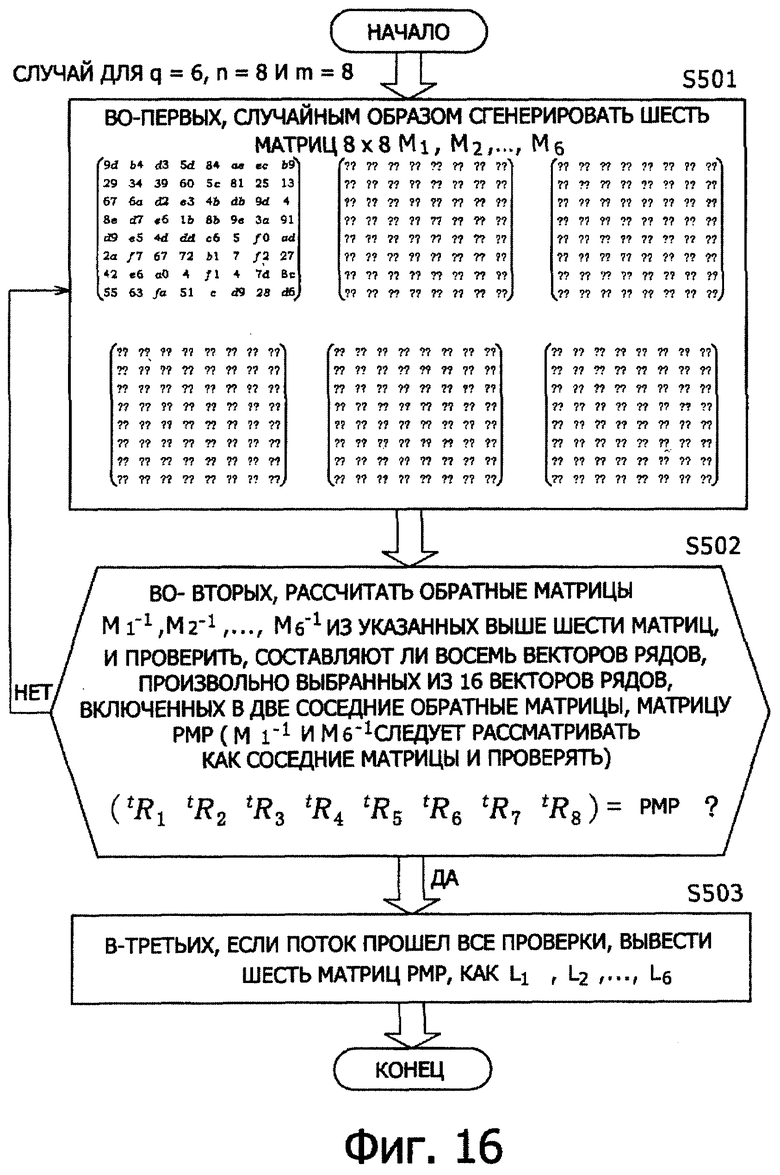
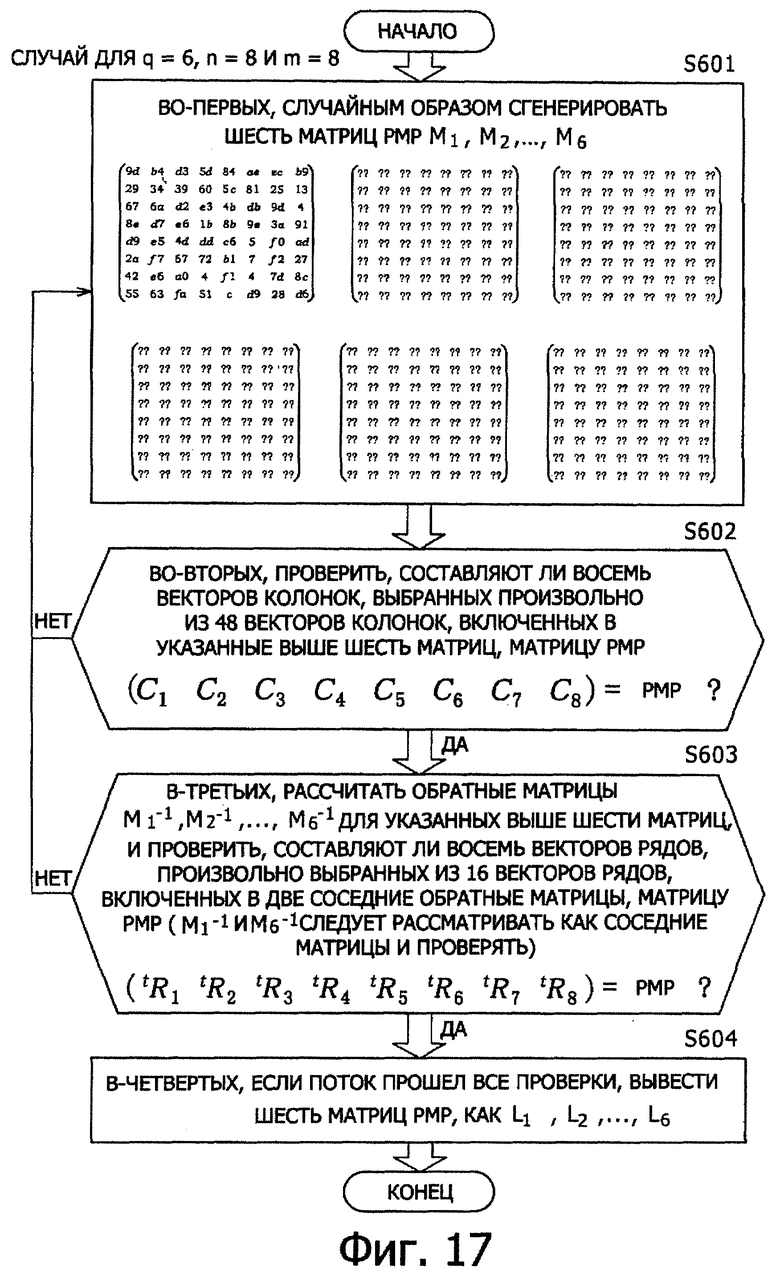
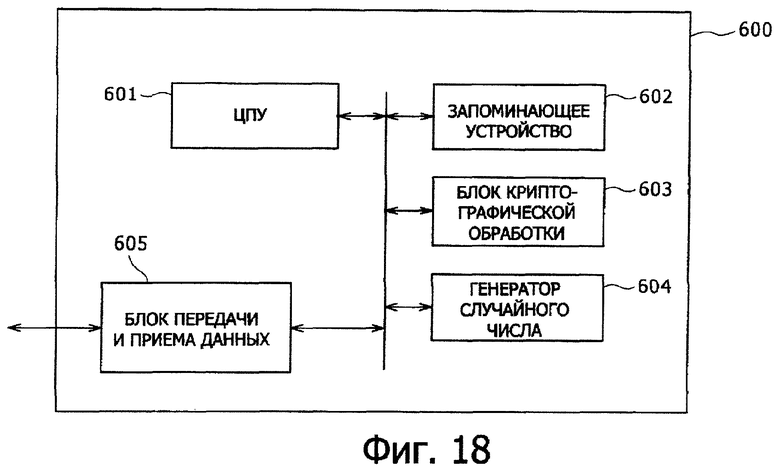
Изобретение относится к устройству криптографической обработки с высокой надежностью. В криптографической обработке общий-ключ-блок типа Фейстеля структура повторно выполняет F-функцию SPN-типа и имеет блок нелинейного преобразования и блок линейного преобразования в течение множества циклов. Обработку линейного преобразования F-функции, соответствующую каждому из множества циклов, выполняют путем обработки линейного преобразования, в которой используют квадратные матрицы РМР. Произвольные m векторов колонок, включенные в обратные матрицы для квадратных матриц РМР, устанавливаемых, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетными номерами, соответственно, составляют квадратную матрицу РМР. Техническим результатом изобретения является повышение устойчивости к атакам линейного криптоанализа в шифре с общим-ключом-блоком. 2 н. и 10 з.п. ф-лы, 18 ил.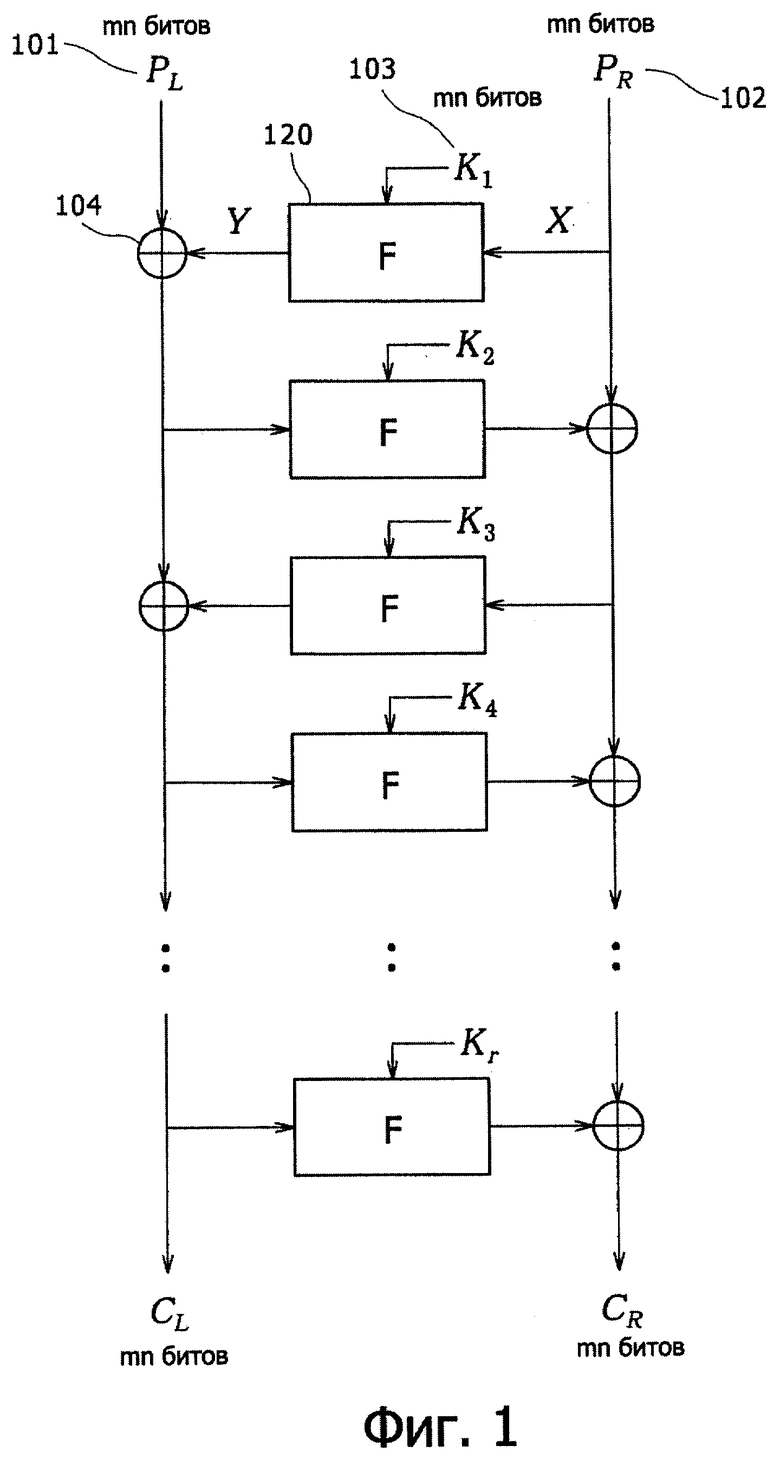
1. Устройство криптографической обработки, предназначенное для выполнения криптографической обработки общий-ключ-блок типа Фейстеля, имеющее структуру, которая повторно выполняет F-функцию SPN-типа, имеющую блок нелинейного преобразования и блок линейного преобразования в течение множества циклов, в котором каждый из блоков линейного преобразования F-функций, соответствующий каждому из множества циклов, выполнен с возможностью выполнения обработки линейного преобразования для входных n битов, выводимых из каждого из m блоков нелинейного преобразования, в сумме составляющих mn битов, в качестве обработки линейного преобразования, в которой используется квадратная матрица РМР, причем, по меньшей мере, в последовательных циклах с нечетными номерами и в последовательных циклах с четными номерами применяют разные квадратные матрицы РМР La, Lb, и матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1 для квадратных матриц РМР, является линейно независимой.
2. Устройство по п.1, в котором матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1, представляет собой квадратную матрицу РМР.
3. Устройство по п.1, в котором алгоритм криптографической обработки общий-ключ-блок типа Фейстеля представляет собой криптографический алгоритм с количеством циклов 2r, и блок линейного преобразования F-функции выполнен с возможностью выполнения линейного преобразования, в котором последовательно и повторно применяют q различных видов 2≤q≤r квадратных матриц РМР во всех r циклах с четными номерами и во всех г циклах с нечетными номерами.
4. Устройство по п.1, в котором каждая из множества различных квадратных матриц РМР, предназначенных для применения в блоке линейного преобразования F-функции, представляет собой квадратную матрицу РМР, которая состоит из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, и является линейно независимой.
5. Устройство по п.1, в котором каждая из множества разных квадратных матриц РМР, предназначенных для применения в блоке линейного преобразования F-функции, представляет собой квадратную матрицу РМР, в результате чего матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, также представляет собой квадратную матрицу РМР.
6. Устройство по п.1, в котором каждая из множества разных квадратных матриц РМР, предназначенных для применения в блоке линейного преобразования F-функции, составлена из матрицы, которая составлена из векторов рядов, выделенных из матрицы M', которая состоит из векторов рядов, выбранных из квадратной матрицы М РМР, включающей все элементы, составляющие множество квадратных матриц РМР.
7. Способ криптографической обработки, предназначенный для выполнения криптографической обработки общий-ключ-блок типа Фейстеля, содержащий следующие этапы: выполнения F-функции SPN-типа, предназначенной для выполнения обработки нелинейного преобразования и обработки линейного преобразования повторно в течение множества циклов; и при обработке преобразования F-функции, соответствующей каждому из множества циклов, выполнения линейного преобразования для n битов, поступающих с выхода m блоков нелинейного преобразования, что в сумме составляет mn битов, в качестве обработки линейного преобразования, в которой применяют квадратные матрицы РМР; в котором обработку линейного преобразования с квадратными матрицами РМР выполняют так, что, по меньшей мере, в последовательных циклах с четными номерами и в последовательных циклах с нечетными номерами применяют разные квадратные матрицы РМР La, Lb, и матрица, составленная из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1 для квадратных матриц РМР, является линейно независимой и составляет квадратную матрицу РМР.
8. Способ по п.7, в котором обработку линейного преобразования с использованием квадратных матриц РМР выполняют так, что матрица, состоящая из m векторов колонок, выбранных произвольно из векторов колонок, составляющих обратные матрицы La -1, Lb -1, представляет собой квадратную матрицу РМР.
9. Способ по п.7, в котором алгоритм криптографической обработки общий-ключ-блок типа Фейстеля представляет собой криптографический алгоритм с количеством циклов, равным 2r, и при обработке линейного преобразования F-функции последовательно и повторно выполняют обработку линейного преобразования с использованием q видов разных квадратных матриц РМР 2≤q<r.
10. Способ по п.7, в котором каждая из множества разных квадратных матриц РМР, предназначенных для применения при обработке линейного преобразования F-функции, выполнена так, что матрица, которая состоит из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, является линейно независимой и составляет квадратную матрицу РМР.
11. Способ по п.7, в котором каждая из множества разных квадратных матриц РМР, предназначенных для применения при обработке линейного преобразования F-функции, представляет собой квадратную матрицу РМР так, что матрица, составленная из m векторов колонок, выбранных произвольно из векторов колонок, составляющих множество квадратных матриц РМР, становится квадратной матрицей РМР.
12. Способ по п.7, в котором каждая из множества разных квадратных матриц РМР, предназначенных для применения при обработке линейного преобразования F-функции, состоит из матрицы, составленной из векторов колонок, выделенных из матрицы М', состоящей из векторов рядов, выбранных из квадратной матрицы М РМР, включающей в себя все элементы, составляющие множество квадратных матриц РМР.
| JP 2004245988 А, 02.09.2004 | |||
| JP 2002091295 A, 27.03.2002 | |||
| JP 2002091297 A, 27.03.2002 | |||
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 1992 |
|
RU2015575C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 1997 |
|
RU2140709C1 |
Авторы
Даты
2010-03-10—Публикация
2005-08-30—Подача