Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов и устройств для шифрования сообщений (информации).
В совокупности признаков заявляемого способа используются следующие термины:
- секретный ключ представляет из себя двоичную информацию, известную только законному пользователю;
- криптографическое преобразование - это преобразование цифровой информации, которое обеспечивает влияние одного бита исходных данных на многие биты выходных данных, например, с целью защиты информации от несанкционированного чтения, формирования цифровой подписи, выработки кода обнаружения модификаций; одними из важных видов криптографических преобразований являются одностороннее преобразование, хэширование и шифрование;
- хэширование информации есть некоторый способ формирования так называемого хэш-кода, размер которого является фиксированным (обычно 128 бит) для сообщения любого размера; широко применяются способы хэширования, основанные на итеративных хэш-функциях с использованием блочных механизмов криптографического преобразования информации [см. Lai X., Massey J.L. Hash Functions Based on Block Ciphers/Workshop on the Theory and Applications of Cryptographic Techniques. EUROCRYPT'92. Hungary, May 24-28, 1992. Proceedings. P. 53-66.].
- шифрование есть процесс, преобразования информации, который зависит от секретного ключа и преобразует исходный текст в шифртекст, представляющий собой псевдослучайную последовательность знаков, из которой получение информации без знания секретного ключа практически неосуществимо;
- дешифрование есть процесс, обратный процедуре шифрования; дешифрование обеспечивает восстановление информации по криптограмме при знании секретного ключа;
- шифр представляет собой совокупность элементарных шагов преобразования входных данных с использованием секретного ключа; шифр может быть реализован в виде программы для ЭВМ или в виде отдельного устройства;
- двоичный вектор - это некоторая последовательность нулевых и единичных битов, например 101101011; конкретная структура двоичного вектора может быть интерпретирована как двоичное число, если считать, что позиция каждого бита соответствует двоичному разряду, т.е. двоичному вектору может быть сопоставлено численное значение, которое определяется однозначно структурой двоичного вектора;
- криптоанализ - метод вычисления секретного ключа для получения несанкционированного доступа к зашифрованной информации или разработка метода, обеспечивающего доступ к зашифрованной информации без вычисления секретного ключа;
- одностороннее преобразование - это такое преобразование L-битового входного блока данных в L-битовый выходной блок данных, которое позволяет легко вычислить выходной блок по входному блоку, а вычисление входного блока, который бы преобразовывался в случайно выбранный выходной блок, является практически невыполнимой задачей;
- односторонняя функция - это функция, значение которой легко вычисляется по данному аргументу, однако вычисление аргумента по данному значению функции является вычислительно трудной задачей; односторонние функции реализуются как последовательность процедур одностороннего преобразования некоторого входного блока (аргумента), выходное значение которого принимается за значение функции;
- криптостойкость является мерой надежности защиты зашифрованной информации и представляет собой трудоемкость, измеренную в количестве элементарных операций, которые необходимо выполнить для восстановления информации по криптограмме при знании алгоритма преобразования, но без значения секретного ключа; в случае односторонних преобразований под криптостойкостью понимается сложность вычисления входного значения блока по его выходному значению;
- операции циклического сдвига, зависящие от преобразуемых подблоков или зависящие от двоичного вектора - это операции циклического сдвига на число бит, задаваемое значением подблока или значением двоичного вектора; операции циклического сдвига влево (вправо) обозначаются знаком "<<<"("<<<"), например, запись B1<<<B2 обозначает операцию циклического сдвига влево подблока B1 на число бит, равное значению двоичного вектора B2; подобные операции являются базовыми для шифра RC5;
- одноместная операция - это операция, выполняемая над одним операндом (блоком данных или двоичным вектором); значение подблока после выполнения некоторой данной одноместной операции зависит только от его начального значения; примером одноместных операций являются операции циклического сдвига;
- двухместная операция - это операция, выполняемая над двумя операндами; результат выполнения некоторой данной двухместной операции зависит от значения каждого операнда; примером двухместных операций являются операции сложения, вычитания, умножения и др.
Известны способы блочного шифрования данных, см. например стандарт США DES [National Bureau of Standards. Data Encryption Standard. Federal Information Processing Standards Publication 46, January 1977; см. также: С. Мафтик. Механизмы защиты в сетях ЭВМ. - М., Мир, 1993. С. 42-47]. В данном способе шифрование блоков данных выполняют путем формирования секретного ключа, разбиения преобразуемого блока данных на два подблока L и R и поочередного изменения последних путем выполнения операции поразрядного суммирования по модулю два на подблоком L и двоичным вектором, который формируется как выходное значение некоторой функции F от значения подблока R. После этого блоки переставляются местами. Функция F в указанном способе реализуется путем выполнения операций перестановки и подстановки, выполняемых над подблоком R. Данный способ обладает высокой скоростью преобразований при реализации в виде специализированных электронных схем.
Однако известный способ-аналог использует секретный ключ малого размера (56 бит), что делает его уязвимым к криптоанализу на основе подбора ключа. Последнее связано с высокой вычислительной мощностью современных ЭВМ массового применения.
Наиболее близким по своей технической сущности к заявляемому способу криптографического преобразования L-битовых входных блоков цифровых данных в L-битовые выходные блоки является способ, реализованный в шифре RC5 описанный в работе [R.Rivest, The RC5 Encryption Algorithm/ Fast Software Encryption, Second International Workshop Proceedings (Leuven, Belgium, December 14-16, 1994), Lecture Notes in Computer Science, v. 1008, Springer-Verlag, 1995, pp. 86-96] . Способ прототип включает в себя формирование секретного ключа в виде совокупности подключей, разбиение входного блока данных на подблоки A и B, и поочередное преобразование подблоков. Подблоки преобразуются путем выполнения над ними одноместных и двухместных операций. В качестве двухместных операций используются операции сложения по модулю 2n, где n = 8, 16, 32, 64, и операция поразрядного суммирования по модулю 2. В качестве одноместной операции используется операция циклического сдвига влево, причем число бит на которое сдвигается преобразуемый подблок зависит от значения другого подблока, это определяет зависимость операции циклического сдвига на текущем шаге преобразования подблока от исходного значения входного блока данных. Двухместная операция выполняется над подблоком и подключом, а также над двумя подблоками. Характерным для способа прототипа является использование операции циклического сдвига, зависящей от значения входного блока.
Подблок, например подблок B, преобразуют следующим путем. Выполняется операция поразрядного суммирования по модулю 2 над подблоками A и B и значение, получаемое после выполнения этой операции присваивается подблоку B. Это записывается в виде соотношения B ←_ B⊕V, где знак "←_" обозначает операцию присваивания и знак "⊕" обозначает операцию поразрядного суммирования по модулю 2. После этого над подблоком B выполняют операцию циклического сдвига на число бит, равное значению подблока A: B ←_ B ≪< A. Затем над подблоком и одним из подключей S выполняют операцию суммирования по модулю 2n, где n - длина подблока в битах: B ←_ B+S mod 2n. После этого аналогичным образом преобразуется блок A. Выполняется несколько таких шагов преобразования обоих подблоков.
Данный способ обеспечивает высокую скорость шифрования при реализации в виде программы для ЭВМ. Однако способ-прототип имеет недостатки, а именно при программной реализации для ЭВМ с 32-разрядными микропроцессором он не обеспечивает высокой стойкости криптографического преобразования данных к дифференциальному и линейному криптоанализу [Kaliski B. S., Yin Y.L. On Differential and Linear Cryptanalysis of the RC5 Encryption Algorithm. Advances in Cryptology - CRYPTO '95 Proceedings, Springer-Verlag, 1995, pp. 171-184] . Этот недостаток связан с тем, что эффективность использования операций, зависящих от преобразуемых данных с целью усложнения известных методов криптоанализа снижается тем, что операции циклического сдвига обусловливают слабо выраженный эффект рассеивания влияния исходной структуры подблока на структуру подблока после выполнения операции циклического сдвига.
В основу изобретения положена задача разработать способ криптографического преобразования блоков цифровых данных, в котором преобразование входных данных осуществлялось бы таким образом, чтобы выполнение операции, зависящей от преобразуемого блока, обеспечивало усиление эффекта рассеивания влияния исходной структуры подблока на структуру подблока после выполнения данной операции, благодаря чему повышается стойкость к дифференциальному и линейному криптоанализу.
Поставленная задача достигается тем, что в способе криптографического преобразования блоков цифровых данных, заключающемся в разбиении блока данных на N ≥ 2 подблоков, поочередном преобразовании подблоков путем выполнения над подблоком по крайней мере одной операции преобразования, которая зависит от значения входного блока, новым согласно изобретению является то, что в качестве операции зависящей от значения входного блока используется операция подстановки, выполняемая над k двоичными разрядами подблока, где 8 ≤ k ≤ 16, причем операции подстановок задаются таблицами подстановок, число которых T ≥ 2.
Благодаря такому решению обеспечивается усиление эффекта рассеивания влияния исходной структуры подблока на структуру подблока после выполнения операции, зависящей от преобразуемых данных, благодаря чему обеспечивается повышение стойкости криптографического преобразования к дифференциальному и линейному криптоанализу.
Новым является также то, что в качестве таблиц подстановки используются секретные таблицы подстановок.
Благодаря такому решению, обеспечивается дополнительное повышение криптостойкости к дифференциальному и линейному криптоанализу.
Новым является также то, что дополнительно формируют двоичный вектор V и для осуществления операции подстановки по значению V выбирают таблицу подстановки, причем двоичный вектор на текущем шаге преобразования формируют в зависимости от его значения на предшествующем шаге преобразования и от значения одного из подблоков.
Благодаря такому решению, обеспечивается дополнительное повышение криптостойкости к атакам, основанным на сбоях устройства шифрования.
Ниже сущность заявляемого изобретения более подробно разъясняется примерами его осуществления со ссылками на прилагаемые чертежи.
На фиг. 1 представлена обобщенная схема криптографического преобразования согласно заявляемому способу.
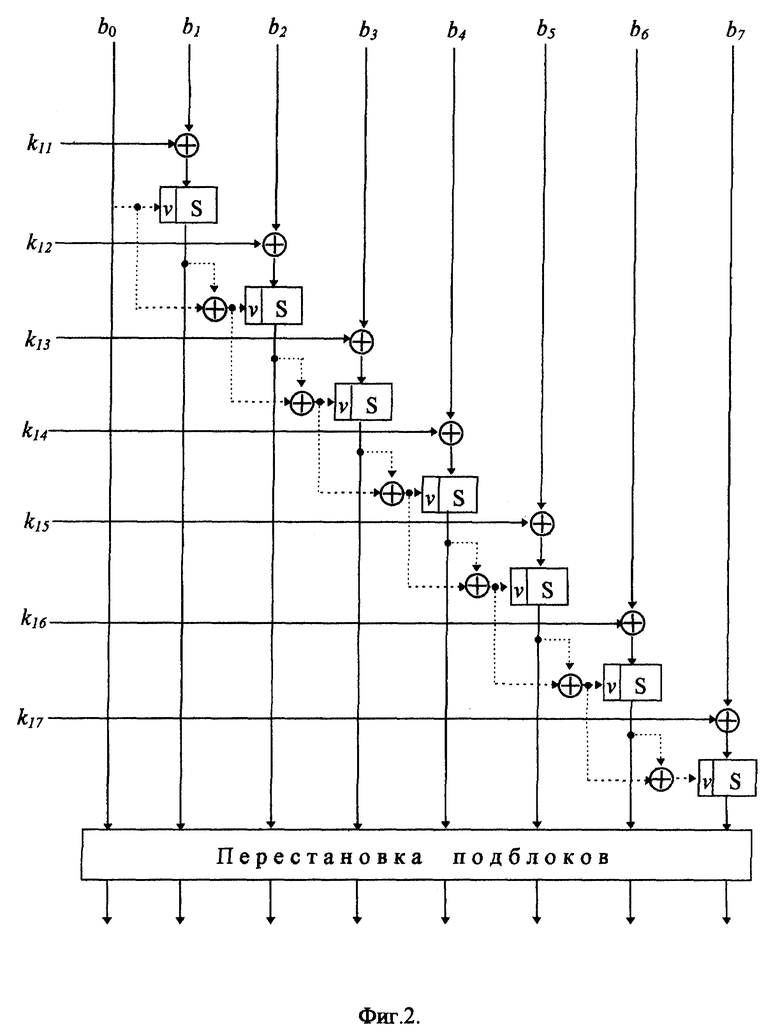
На фиг. 2 представлена схема шифрования, соответствующая примеру 1.
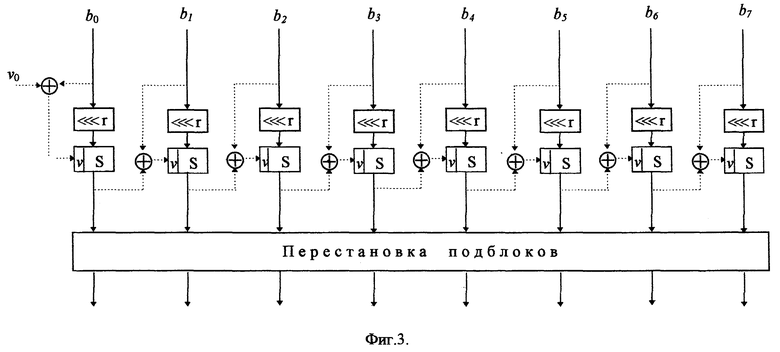
На фиг. 3 представлена схема одностороннего преобразования, соответствующая примру 2.
Изобретение поясняется обобщенной схемой криптографического преобразования блоков данных на основе заявляемого способа, которая представлена фиг. 1, где: B - преобразуемый блок, b1, b2, ..., bn - преобразуемые подблоки, S - операционный блок, осуществляющий над подблоками операцию подстановки, f - операционный блок, осуществляющий формирование двоичного вектора, v0 - начальное значение двоичного вектора. Сплошная линия соответствует передаче преобразуемых подблоков, пунктирная - передаче двоичного вектора.
Входной блок цифровых данных разбивается на N ≥ 2 подблоков. Подблоки поочередно преобразуются путем их изменения с помощью операционного блока S. который использует в преобразованиях значение двоичного вектора, что обусловливает зависимость выходного значения преобразуемого подблока от значения двоичного вектора. Операционный блок f для выполнения преобразования двоичного вектора использует значение подблока, преобразованного на предыдущем шаге, т.е. операционный блок f формирует двоичный вектор по структуре одного из преобразуемых подблоков и по значению двоичного вектора, которое он имел на предыдущем шаге преобразования подблока. Блок S для выполнения операции подстановки использует таблицу подстановки, выбираемую в зависимости от значения двоичного вектора. (Например, двоичный вектор формируют в соответствии с аналитическим соотношением V = (V' + b') mod T, где V' - значение двоичного вектора на предшествующем шаге преобразования, b' - выходное значение подблока, преобразованного на предшествующем шаге преобразования, T - количество используемых таблиц подстановки. Затем операцию подстановки осуществляют с помощью таблицы с номером V). Формирование двоичного вектора в зависимости от одного из преобразуемых подблоков обусловливает зависимость операции подстановки от преобразуемых данных.
Осуществление подстановки над подблоком будем называть одним шагом изменения подблока. Выполнение процедур преобразования, задаваемых функцией f, над двоичным вектором будем называть шагом формирования двоичного вектора. Шаг преобразования подблока включает шаг формирования двоичного вектора и шаг изменения подблока. Шаги преобразования выполняются последовательно над всеми подблоками, после чего осуществляется перестановка подблоков. В частных случаях реализация заявляемого способа перестановка подблоков может не использоваться. Выполнение N шагов изменения подблока, N шагов формирования двоичного вектора и перестановка подблоков, показанные на фиг. 1, составляют один раунд преобразования. Значение двоичного вектора после N-го шага формирования двоичного вектора служит начальным значением двоичного вектора для следующего раунда преобразования при построении односторонних функций преобразования блоков цифровых данных. При построении шифров начальное значение двоичного вектора для каждого раунда формируется в зависимости от секретного ключа.
Важным элементом является выполнение зависящей от двоичного вектора операции подстановки над подблоком. Такой тип подстановок может быть использован при задании множества различных таблиц подстановок, каждой из которых присвоен порядковый номер и для выполнения операции подстановки над подблоком используют таблицу номер которой выбирают в зависимости от значения V, например, если используются 32 таблицы подстановки, то номер таблицы можно вычислить по формуле v = V mod 25. Смысл выбора таблицы подстановки, которая используется для выполнения операции подстановки над подблоком на текущем шаге, по специально формируемому двоичному вектору состоит в том, чтобы сделать выбор таблицы подстановки непредопределенным для каждого шага преобразования подблоков, что повышает стойкость криптографического преобразования.
Под формированием двоичного вектора мы понимаем запись, например, в регистр или ячейку памяти вычислительного устройства некоторой последовательности единичных или нулевых битов. Под формированием двоичного вектора в зависимости от его структуры на предыдущем шаге преобразования подблока с использованием двоичного вектора мы понимаем задание зависимости текущего значения формируемого двоичного вектора от значения, которое двоичный вектор имел на предшествующем шаге использования при образовании подблока данных. Например, пусть подблок Bi был преобразован с использованием значения двоичного вектора V. Перед использованием двоичного вектора на некотором другом шаге преобразования, например, подблока Bj двоичный вектор может формироваться в соответствии с выражением V ←_ V+Qb, где b = Bimod 211 - номер подключа, вычисляемый в зависимости от значения подблока Bi.
Пусть операции подстановки выполняются над подблоками цифровых данных длиной k бит, где k - целое число. Тогда для задания операции подстановки, преобразующей k-битовый входной подблок в k-битовый выходной подблок требуется использование таблицы, содержащей две строки чисел: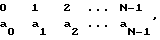
где N = 2k.
В данной таблице в нижней строке присутствуют все возможные значения k-битового блока ровно по одному разу, но в произвольном порядке. Очередность расположения чисел в нижней строке определяет конкретный вариант таблицы подстановки, а следовательно и конкретный вариант операции подстановки, выполняемой с использованием этой таблицы. Выполнение операции подстановки осуществляется следующим образом. Выбирается в верхней строке число, которое равно значению входного блока. Находящееся под этим числом значение в нижней строке берется в качестве выходного блока. Таким образом, таблицу подстановки можно разместить в оперативной памяти ЭВМ как последовательную запись k-битовых компьютерных слов, размещенных в ячейках с адресами w0, w1, w2, .. ., wN-1. В этом случае значение входного блока b служит для вычисления адреса w0 + b слова, которое берется в качестве выходного блока. Этот способ представления таблицы подстановки требует использования объема памяти, равного kN бит.
Выберем количество таблиц подстановки, равное 2L (объем требуемой памяти составит при этом 2LkN бит), и разместим таблицы подстановок непрерывно друг за другом. В качестве адреса таблицы с номером v возьмем значение адреса w0 ее первого k-битового слова. Пусть адрес таблицы с номером 0 есть s. В этом случае адрес таблицы подстановки с произвольным номером v равен s + vN. Если задан двоичный вектор, определяющий номер текущей таблицы подстановки v и текущий входной подблок для выполнения операции подстановки, то она выполняется заменой текущего входного блока на k-битовое слово, расположенное по адресу s + vN + b, где b - значение подблока, над которым выполняется текущая операции подстановки. Используя это соотношение легко задать выбор таблицы подстановки с номером v и выполнить подстановку над подблоком со значением b. В рассмотренном случае задание зависимости таблиц подстановок от значения двоичного вектора и выполнение операции подстановки осуществляется микропроцессором очень быстро при выборе соответствующих значений параметров L и k, например при L = 5 и k = 8. При указанных параметрах для размещения таблиц подстановки требуется 8 Кбайт оперативной памяти, что является приемлемым, поскольку современные ЭВМ обладают объемом оперативной памяти на многие порядки больше этой величины (от 1 до 64 Мбайт и более).
Возможность технической реализации заявляемого способа поясняется следующими конкретными примерами его осуществления.
Пример 1.
Пусть L = 5 и k = 8, т.е. даны 32 таблицы задающие операции подстановки над 8-битовыми подблоками данных. Таблицы будем предполагать известными, т. е. лицо пытающееся провести криптоанализ знает эти таблицы. Сформируем секретный ключ, представленный в виде совокупности из 7R 8-битовых подключей
где R - число раундов шифрования. На r-м раунде шифрования используется r-ая строка подключей.
Обозначим используемые таблиц подстановки следующим образом: T0, T1, T2, . . . , T31, а операцию подстановки, задаваемую таблицей Tv как Sv, где v = 0,1,2, . . .,31. Таблицы подстановок T0, T1, T2, ..., T15 могут быть выбраны произвольными, а таблицы T16, T17, ..., T31 берутся такими, чтобы операции подстановок Sv и S31-v были взаимно обратными. Последнее условие выполняется, если пары таблиц T16 и T15; T17 и T14; T18 и T13; ...; T31 и T0 будут задавать взаимно обратные операции подстановки. Для набора произвольных таблиц подстановки T0, T1, T2, ..., T15 легко составить таблицы, соответствующие обратным операциям подстановки. Например, для операции подстановки, задаваемой следующей таблицей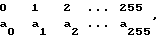
а обратная подстановка задается таблицей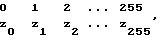
где строка (Z0, Z1, Z2, ..., Z255) получается как верхняя строка после упорядочения столбцов предыдущей таблицы в порядке возрастания чисел в нижней строке.
На фиг. 2 показана схема первого раунда шифрования. На фиг. 2 сплошная вертикальная линия соответствует передаче 8-битовых подблоков данных, пунктирная линия соответствует передаче 5-битовых подблоков, горизонтальная сплошная линия соответствует передаче 8-битового подключа. Операция поразрядного суммирования по модулю два обозначена знаком "⊕", v обозначает номер выбранной таблицы подстановки, блок S обозначает операцию подстановки, k11, k12, . .., k17 - подключи, используемые на первом раунде. Стрелки на линиях обозначают направление передачи сигналов. Пример 1 соответствует шифрованию блоков цифровых данных размером 64 бит. Шифрование выполняют следующим путем. Входной блок разбивают на 8 подблоков b0, b1, b2, ..., b7 размером 8 бит каждый. После этого формируют двоичный вектор v, имеющий значение 5 младших двоичных разрядов подблока b0: v ←_ b0 mod 25. Потом над подблоком b1 и подключом b11 выполняют операцию поразрядного суммирования по модулю 2 и выходное значение этой операции присваивают блоку b1, что можно записать аналитически следующим образом: b1 ←_ b1⊕r11. Затем по таблице подстановки с номером v выполняют операцию подстановки над подблоком b1: b1 ←_ Sv(b1). Затем по значению b1 формируют двоичный вектор v: v ←_ v⊕ (b1 mod 25), причем новое значение двоичного вектора зависит от его предыдущего значения. После этого выполняют преобразование подблока b2: b2 ←_ b2⊕k12 и затем b2 ←_ Sv(b2).
Аналогично выполняют преобразования подблоков b3, b4, b5, b6 и b7. На последнем шаге каждого раунда шифрования выполняют перестановку подблоков в обратном порядке, т.е. попарно меняются местами блоки b7 и b0, b6 и b1, b5 и b2, b4 и b3.
Второй раунд выполняется аналогично, за исключением того, что вместо первой строки подключей используется вторая строка подключей. Затем выполняется третий раунд шифрования с использованием третьей строки подключей и т. д. Всего выполняется R раундов шифрования, где R = 4. При программной реализации данный пример реализации заявляемого способа обеспечивает скорость шифрования около 25 Мбит/с для микропроцессора Pentium/200. При необходимости может быть задано и другое число раундов, например R = 2,3,5,6.
Пример 1 описывается следующим конкретным алгоритмом.
Алгоритм 1.
Вход: 64-битовый входной блок цифровых данных, представленный как конкатенация 8-битовых подблоков b0|b1|b2|b3|b4|b5|b6|b7, где знак "|" обозначает операцию конкатенации.
1. Установить число раундов шифрования R = 4 и счетчик числа раундов r = 1.
2. Установить счетчик i = 1.
3. Сформировать двоичный вектор v: v ←_ bi-1 mod 25.
4. Преобразовать подблок b1: bi ←_ bi⊕kri, bi ←_ Sv(bi), где операция подстановки Sv выполняется с помощью таблицы подстановки с номером v.
5. Сформировать двоичный вектор v: v ←_ v⊕ (b1 mod 25).
6. Если i ≠ 7, то прирастить i ←_ i+1 и перейти к п. 4.
7. Если r ≠ R, то прирастить r ←_ r+1. В противном случае СТОП.
8. Переставить подблоки в обратном порядке и перейти к п. 3.
Выход: 64-битовый блок шифртекста.
В этом примере видно, что номер используемой таблицы подстановки зависит от преобразуемых блоков и является непредопределенным для текущего шага преобразования, т.е. операция подстановки заранее неизвестна для всех шагов преобразования. Она определяется секретным ключом и блоком преобразуемых данных. Дешифрование осуществляется аналогично и описывается следующим алгоритмом.
Алгоритм 2.
Вход: 64-битовый входной блок шифртекста b0|b1|b2|b3|b4|b5|b6|b7.
1. Установить число раундов шифрования R = 4 и счетчик числа раундов r = 1.
2. Установить счетчик i = 1.
3. Сформировать двоичный вектор v: v ←_ bi-1 mod 25.
4. Сохранить значение b1 в переменной g: g ←_ bi. Преобразовать подблок b1: bi ←_ S31-v(bi), bi ←_ bi⊕kr′i, где r' = 5-r.
5. Сформировать двоичный вектор v: v ←_ v⊕ (g mod 25).
6. Если i ≠ 7, то прирастить i ←_ i+1 и перейти к п. 4.
7. Если r ≠ R, то прирастить r ←_ r+1. В противном случае СТОП.
8. Переставить подблоки в обратном порядке и перейти к п. 3.
Выход: 64-битовый блок исходного текста.
Приведенные алгоритмы шифрования и дешифрования могут быть легко модифицированы для преобразования блоков данных другого размера, например 125 и 256 бит.
Пример 2.
Данный пример относится к построению односторонней функции, основанной на заявляемом способе криптографического преобразования. Так же как и в примере 1 предполагается использование 32 таблиц подстановки T0, T1, T2, ... , T31. Таблицы подстановок предполагаются известными и секретные ключи не используются. Односторонняя функция задается алгоритмом 4. Последовательность операций преобразования подблоков данных для одного раунда преобразования показана на фиг. 2.
Алгоритм 3.
Вход: 64-битовый входной блок данных, представленный как конкатенация 8-битовых подблоков b0|b1|b2|...|b7.
1. Установить число раундов преобразования R = 8, счетчик числа раундов r = 1 и начальное значение двоичного вектора v = 13.
2. Установить счетчик i = 1.
3. Сформировать двоичный вектор v: v ←_ v⊕ (bi-1 mod 25).
4. Преобразовать подблок bi-1: 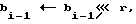 bi-1 ←_ Sv(bi-1).
bi-1 ←_ Sv(bi-1).
6. Если i ≠ 8, то прирастить i ←_ i+1 и перейти к п. 3.
7. Переставить подблоки b0, b1, ..., b7, в обратном порядке.
7. Если r ≠ R, то прирастить r ←_ r+1 и перейти к п. 2. В противном случае СТОП.
Выход: 64-битовое значение односторонней функции, заданное конкатенацией преобразованных подблоков b0|b1|b2|...|b7.
Аналогично может быть построена односторонняя функция для преобразования 128-битовых блоков данных, которая может быть использована для хэширования данных.
Пример 3.
Этот пример является аналогичным примеру 1, а отличие состоит только в том, что используемые 32 таблицы подстановок являются секретными, например они формируются в зависимости от секретного ключа. Этот вариант является легко реализуемым при использовании ЭВМ для шифрования данных путем формирования таблиц подстановок с помощью специальной программы при вводе секретного ключа в модуль шифрования. Формирование секретных таблиц может быть реализовано, например, путем модифицирования известных (заранее заданных) таблиц подстановки путем блочного шифрования по секретному ключу элементов нижней строки известных таблиц (поскольку блочное шифрующее преобразование является подстановкой, то модифицированные таблицы также будут являться таблицами подстановок).
Пример 4.
Данный пример также является аналогичным примеру 1. Отличие состоит в том, что блок цифровых данных разбивается на 16-битовые подблоки и используются 32 таблицы подстановок, соответствующие значению k = 16, т.е. они задают операцию подстановки над 16 двоичными разрядами преобразуемых подблоков. Объем оперативной памяти, необходимый для размещения одной таблицы, равен 2kk бит = 128 Кбайт. Для размещения 32 таблиц требуется 4 Мбайт, что может быть обеспечено современными ЭВМ массового применения. Могут быть использованы следующие два варианта записи таблиц подстановок в оперативную память ЭВМ: (1) известные таблицы хранятся на магнитных носителях информации и при запуске модуля шифрования копируются в оперативную память; (2) таблицы генерируются специальной программой, которая выполняется при запуске модуля шифрования. Во втором случае формирование таблиц подстановки может осуществляться в зависимости от секретного ключа, что позволяет использовать секретные подстановки над 16-битовыми подблоками для шифрования данных.
Приведенные примеры показывают, что предлагаемый способ криптографических преобразований блоков цифровых данных технически реализуем и позволяет решить поставленную задачу.
Заявляемый способ может быть реализован, например, на персональных ЭВМ и обеспечивает возможность создания на его основе скоростных программных модулей шифрования и замены дорогостоящей специализированной аппаратуры шифрования персональной ЭВМ, снабженной программной системой скоростного шифрования.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ШИФРОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 1997 |
|
RU2124814C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ L-БИТОВЫХ ВХОДНЫХ БЛОКОВ ЦИФРОВЫХ ДАННЫХ В L-БИТОВЫЕ ВЫХОДНЫЕ БЛОКИ | 1997 |
|
RU2188513C2 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ДАННЫХ | 1997 |
|
RU2106753C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ДВОИЧНЫХ ДАННЫХ | 1998 |
|
RU2141729C1 |
| СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 1998 |
|
RU2140711C1 |
| СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ ДИСКРЕТНЫХ ДАННЫХ | 1998 |
|
RU2140710C1 |
| ИТЕРАТИВНЫЙ СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ | 1999 |
|
RU2172075C1 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДИСКРЕТНЫХ ДАННЫХ | 2000 |
|
RU2186466C2 |
| СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1998 |
|
RU2140712C1 |
| СПОСОБ ШИФРОВАНИЯ БЛОКОВ ДАННЫХ | 1997 |
|
RU2111620C1 |
Способ относится к электросвязи и вычислительной технике, а конкретнее к криптографическим способам и устройствам для шифрования цифровых данных. Технический результат - повышение криптостойкости. Сущность способа заключается в разбиении блока данных на N ≥ 2 подблоков, поочередном преобразовании подблоков путем выполнения над подблоком по крайней мере одной операции преобразования, которая зависит от значения входного блока. В качестве операции, зависящей от значения входного блока, используется операция подстановки, выполняемая над k двоичными разрядами подблока, где 8 ≤ k ≤ 16, причем операции подстановок задаются таблицами подстановок, число которых T ≥ 2. В качестве таблиц подстановок используются секретные таблицы подстановок. Кроме того, в способе дополнительно формируют двоичный вектор V и для осуществления операции подстановки по значению V выбирают таблицу подстановки, причем вектор на текущем шаге преобразования формируют в зависимости от его значения на предшествующем шаге преобразования и от значения одного из подблоков. 2 з.п.ф-лы, 3 ил.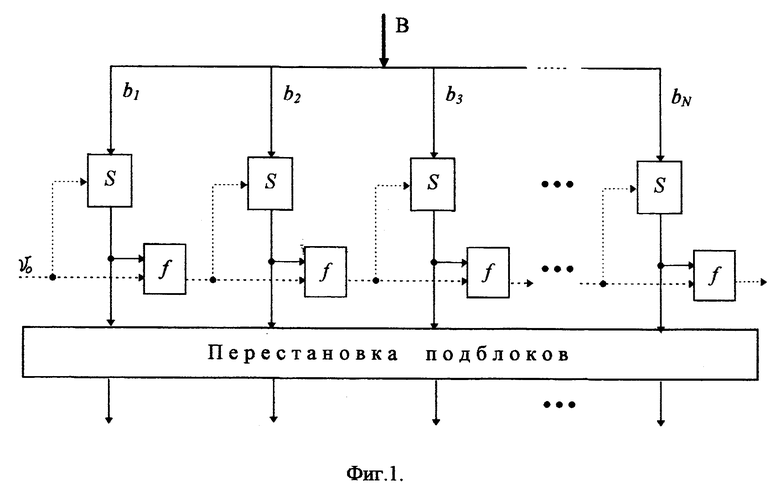
| R.Rivest | |||
| Кипятильник для воды | 1921 |
|
SU5A1 |
| ПЛУГ ДЛЯ РАЗГРУЗКИ БАЛЛАСТНЫХ ПЛАТФОРМ | 1923 |
|
SU1008A1 |
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2007884C1 |
| СПОСОБ ШИФРОВАНИЯ ЦИФРОВОЙ ПОДПИСИ ДВОИЧНОГО СООБЩЕНИЯ (АЛБЕР-ПОДПИСЬ) | 1991 |
|
RU2030836C1 |
| СПОСОБ ЗАСЕКРЕЧИВАНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 1995 |
|
RU2097930C1 |
| DE 2058285 B2, 28.06.79 | |||
| GB 1085168 A, 27.09.67 | |||
| US 3746799 A, 17.07.73. | |||
Авторы
Даты
1999-10-27—Публикация
1997-12-16—Подача