Изобретение относится к технологии подготовки к раскрою рулонных и листовых материалов с целью рационального размещения деталей кроя одежды и может быть использовано на различных предприятиях, в частности, швейной промышленности, в производственном цикле которых имеется необходимость получения деталей кроя большого количества комплектов различных размерных показателей из исходных материалов в виде рулонов или листов.
Известен способ подготовки к раскрою рулонных и листовых материалов, согласно которому на основе визуального анализа деталей кроя осуществляют их размещение на раскраиваемом материале в рамке раскладки с наиболее рациональным использованием исходных материалов в виде рулонов или листов (см. патент на изобретение №2084191, МПК A41H 3/00, опубл. 1997 г.). К недостаткам известного способа можно отнести большие как трудоемкость, так и расход рулонного или листового материала, так как, особенно при большом количестве деталей кроя различной конфигурации и размеров, очень трудно, тем более за небольшое время, разместить эти детали на раскраиваемом материале с реальными его изменениями по ширине рамки раскладки таким образом, чтобы в раскладке межлекальные промежутки были минимальны, и, соответственно, минимальным был бы расход исходного материала для раскроя всей партии изделий заказа.
Наиболее близким по технической сущности к предлагаемому способу относится способ подготовки к раскрою рулонных и листовых материалов, согласно которому определяют комплектность раскладок лекал на размерном поле заказа, строят в рамке раскладки, на основе визуального анализа, раскладку сочетаний комплектов лекал путем размещения лекал из комплектов различных размерных показателей. При этом деталям присваивают номера (в порядке убывания площади лекал, длины, ширины), которые служат основанием для определения последовательности их размещения в раскладке. Крупные детали укладывают рядами по ширине раскладки, стремясь к максимальному ее использованию, образуя секции одноименных деталей в порядке убывания их площади и длины. Мелкие детали располагают в межлекальных отходах, краевых и дополнительных секциях (см. кн. Инструкция по нормированию расхода материалов в массовом производстве швейных изделий. М.: ЦНИИ ТЭИ Легпром, 1988, с.9-11).
К недостаткам способа следует отнести:
- отсутствие обоснованности рационального выбора комплектности и сочетаний размеров лекал в раскладках;
- неоднозначность в оценке рациональности различий в конфигурациях раскладок;
- высокую трудоемкость способа при построении большого числа раскладок в одном заказе с отличающимися друг от друга конфигурациями.
При использовании традиционной технологии раскладки лекал в прямоугольной рамке в сочетаниях размеров лекал для всего размерного поля заказа их конфигурация (положение лекал в прямоугольной рамке раскладки относительно друг друга) изменяется от размера к размеру или от групп размеров к группам размеров. Подбор параметров четырех составляющих для каждой раскладки лекал заказа: комплектности, комбинаций сочетаний размеров, количества изделий в сочетаниях размеров, а также конфигураций раскладок, ведется оператором-раскладчиком простым эмпирическим путем, исходя из опыта работы раскладчика, полагаясь на субъективный фактор в принятии решений.
Предлагаемый способ направлен на решение задачи, состоящей в уменьшении трудоемкости построения раскладок большого количества комплектов лекал различных размерных показателей (в диапазоне заданных ширин рамки раскладки), а также расхода рулонного или листового материала посредством получения оптимальной конфигурации раскладок лекал при минимальной затрате времени.
Данная задача решается тем, что в способе подготовки к раскрою листовых и рулонных материалов, согласно которому определяют комплектность раскладок лекал на размерном поле заказа, строят в рамке раскладки, на основе визуального анализа, раскладку сочетаний комплектов лекал различных размерных показателей путем размещения лекал из комплектов различных размерных показателей, принимают за расчетное количество комплектов лекал, составляющих сочетания размерных показателей в раскладках, целое число, равное или ближайшее большее квадратному корню из полного количества номеров комплектов лекал всех необходимых в заказе размерных показателей, формируют размерный ряд комплектов лекал заказа в порядке возрастания с заданным шагом размерных показателей комплектов и присваивают каждому комплекту в размерном ряду лекал номер от наименьшего до наибольшего, выбирают номера комплектов лекал, составляющие сочетания размерных показателей в раскладке, из набора цифровых сочетаний в базе квадратных матриц, порядок которых равен расчетному количеству номеров комплектов лекал в сочетаниях, причем считают, что отсутствующие (нулевые) в заказе комплекты лекал с определенными размерными показателями имеют свои номера в числовой последовательности номеров, составляющих квадратные матрицы, но сами сочетания, включающие эти отсутствующие в заказе номера, не учитываются, выбирают в качестве оптимальных такие сочетания номеров комплектов лекал с размерными показателями, при которых количество комплектов лекал каждого размера равно или минимально превосходит заданное заказом количество, строят базовую раскладку как раскладку сочетания комплектов лекал среднего (базового) размерного показателя, количество комплектов лекал в этом сочетании равно порядку квадратной матрицы, строят раскладки комплектов лекал, производные от базовой, путем размещения в местах расположения лекал в базовой раскладке аналогичных по наименованию лекал из комплектов различных размерных показателей, номера которых соответствуют оптимальным сочетаниям.
В развитие и уточнение данной совокупности признаков целесообразно выбирать из всех возможных сочетаний размеров комплектов лекал, используя комплекты лекал одних и тех же размеров в различных сочетаниях, такие, использование которых обеспечивает получение каждого из комплектов лекал различных размерных показателей в количестве, равном или минимально превосходящем заданное количество в заказе.
Основой предлагаемого способа является использование системы свойств известного из математики магического квадрата.
Магический квадрат - это квадрат чисел, располагающихся таким образом, что их суммы по диагоналям или в любом ряду по горизонтали и вертикали всегда составляли одно и то же число - магическую константу. Порядок магического квадрата определяется количеством клеток или чисел в строке или столбце.
Магическая константа нормального квадрата зависит только от порядка квадратной матрицы n и определяется формулой
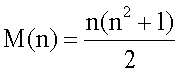
Первые значения магических констант приведены в следующей таблице:
Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы (http://www.krugosvet.ru/articles/15/1001543/1001543a1.htm). Найти все магические квадраты порядка n удается только для n≤4.
Правила образования квадрата с такими свойствами известны (кн. Н.Я.Виленкин. Популярная комбинаторика. Изд. Наука, 1975 г., с.38; http//www.synnegoria.com).
В первом магическом квадрате третьего порядка каждый из восьми наборов комбинаций, будучи вписан в естественном порядке в квадрат из девяти чисел (начиная с левого верхнего угла) (1), дает один из восьми квадратов третьего порядка (2):
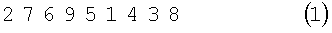

По тому же правилу (2) составляют остальные семь квадратов третьего порядка (3):

Все эти наборы квадратов получены один из другого либо поворотом вокруг центра, либо отображением относительно одной из осей симметрии.
Очевидно, что для составления квадратных матриц в рассматриваемом способе необходимо иметь последовательный ряд чисел, именуемых номерами комплектов лекал, знать их порядок и правила набора сочетаний чисел, имеющих равные суммы.
Если к ряду последовательных чисел магического квадрата прибавить любые другие числа, то получим нетрадиционную матрицу, называемую в нашем способе квадратной матрицей. Квадратная матрица также имеет одинаковое количество клеток по горизонтали и вертикали, в которые вписаны числа (номера) размерного ряда таким образом, чтобы суммы номеров в каждой строке, каждом столбце и на главных диагоналях были одинаковы. Порядок квадратной матрицы также определяется количеством клеток или чисел в строке или столбце.
Порядок квадратной матрицы можно определить как квадратный корень из общего количества чисел, составляющих матрицу. Общее количество чисел, из которых можно составить квадратную матрицу, должно быть равно общему количеству номеров комплектов лекал различных размерных показателей или быть больше этого количества, так как только в этом случае можно осуществить раскладку необходимого для выполнения заказа всего количества номеров комплектов. Отсюда следует, что за расчетное количество номеров комплектов лекал в сочетаниях принимают целое число, равное или ближайшее большее квадратному корню из полного количества номеров комплектов лекал всех необходимых размерных показателей, которое также равно порядку квадратной матрицы.
Например, при использовании квадратной матрицы третьего порядка можно охватить до девяти номеров комплектов лекал, из которых можно составить восемь сочетаний по три номера, сумма номеров которых будет одинакова. В случае использования квадратной матрицы четвертого порядка можно охватить уже до шестнадцати номеров комплектов лекал, из которых можно составить общее количество квадратных матриц, равное 7048 (что соответствует общему количеству магических квадратов четвертого порядка), включающих в себя сочетания, состоящие из четырех номеров каждое. На практике в подавляющем большинстве случаев массового производства швейных изделий (например, одежды) количество комплектов лекал различных размерных показателей в заказе не превышает шестнадцати. То есть для реализации подготовки производства заказа одежды в основном возможно использование квадратных матриц третьего или четвертого порядков. При этом в исключительных случаях большого количества комплектов лекал различных размерных показателей в заказе общее количество можно разбить на два или несколько количеств, из которых можно составить соответствующие квадратные матрицы, например одну третьего порядка, а другую - четвертого, две матрицы третьего порядка и т.п., либо перейти к использованию системы свойств квадратных матриц более высоких порядков (http//www.arbuz.uz/s_mk).
Формирование ряда комплектов лекал в порядке возрастания с определенным шагом размерных показателей комплектов лекал при присвоении каждому комплекту лекал номеров от наименьшего до наибольшего является операцией, которая позволяет в дальнейшем использовать при составлении квадратной матрицы обычную числовую последовательность, в которой каждому числу (номеру) будет соответствовать комплект лекал определенного размерного показателя, причем большему номеру соответствует комплект лекал большего размерного показателя.
При определении номеров комплектов лекал в сочетаниях из набора цифровых сочетаний в базе квадратных матриц, порядок которых равен расчетному количеству номеров комплектов лекал в сочетаниях, получается множество сочетаний размерных показателей, сумма которых одинакова, однако не все из этих сочетаний являются оптимальными для определенного заказа. Причем считают, что отсутствующие в заказе комплекты лекал (нулевые количества) определенных размерных показателей имеют свои номера в числовой последовательности номеров, составляющих квадратную матрицу, но сочетания, включающие эти номера, не учитываются. На практике в заказах на изготовление швейных изделий количество комплектов изделий различных размерных показателей может быть не только равным, но и быть различным, а в идеальном случае необходимо иметь раскладки сочетаний таких номеров комплектов, в которых необходимое по заказу количество изделий, входящих в сочетания различных номеров, одинаково. Соответственно, при наличии множества сочетаний номеров в качестве оптимальных следует выбрать такие сочетания номеров комплектов лекал, при которых количество комплектов изделий каждого номера равно или минимально превосходит заданное заказом количество. Данная процедура достаточно просто реализуется с использованием ЭВМ.
При этом возможен вариант, в котором удается получить либо равенство, либо приблизительное равенство по количеству комплектов не только различных номеров, составляющих сочетания, но и возможен вариант, в котором оптимальные сочетания номеров комплектов лекал различных размерных показателей включают в себя комплекты лекал одних и тех же номеров, но уже в различных сочетаниях, такие, использование которых обеспечивает получение каждого из комплектов лекал различных размерных показателей в количестве, равном или минимально превосходящем заданное заказом количество. Данная процедура также достаточно просто реализуется с использованием ЭВМ.
Построение базовой раскладки как раскладки сочетания комплектов лекал среднего размерного показателя в заказе, количество которых в этом сочетании равно порядку квадратной матрицы, позволяет в дальнейшем использовать конфигурацию этой раскладки для построения базовых раскладок того же количества комплектов лекал уже с другими размерными показателями (с большей или меньшей суммой чисел в сочетаниях размерных показателей) без изменения единой (общей) конфигурации базовой раскладки. Однако следует учесть, что при одной и той же ширине рамки раскладки нельзя без изменения единой конфигурации перестроить базовую раскладку нескольких комплектов лекал максимальных или близких к максимальным размерных показателей в раскладку аналогичного количества комплектов лекал меньших размерных показателей без больших межлекальных выпадов (без потери плотности раскладки), так же как невозможно перестроить базовую раскладку нескольких комплектов лекал минимальных размерных показателей в раскладку аналогичного количества комплектов лекал больших размерных показателей без выхода лекал за пределы рамки раскладки. Следовательно, в случае смещения средних размерных показателей в сочетаниях комплектов базовых раскладок либо в большую, либо в меньшую стороны размерного ряда заказа, используя при этом построении единую конфигурацию, необходимо подбирать ширину рамки раскладки, изменяя ее либо в большую, либо в меньшую стороны соответственно.
Следовательно, в случае изменения ширины рамки раскладки в большую, либо в меньшую стороны необходимо также смещение среднего размерного показателя в сочетаниях комплектов базовых раскладок либо в большую, либо в меньшую стороны размерного ряда заказа, используя в смещенных базовых раскладках размерах рядов единую конфигурацию раскладки.
Построение раскладок комплектов лекал, производных от принятой базовой, путем размещения в местах расположения в базовой раскладке аналогичных наименований лекал из комплектов различных размерных показателей, номера которых соответствуют оптимальным сочетаниям, обусловлено тем, что при одинаковой сумме номеров комплектов лекал различных размерных показателей, составляющих сочетания номеров из базы квадратных матриц, суммарное изменение определяющих размеров лекал в каждом таком сочетании равно нулю (как результат масштабирования лекал).
Показатели сумм в сочетаниях как по строкам, так и по столбцам есть показатель степени надежности размещения сочетания в производной раскладке относительно базовой.
Далее приведены примеры, реализующие способ с использованием системы свойств квадратных матриц.
Рассмотрим пример квадратной матрицы третьего порядка, составленной любыми другими числами и не обязательно числами от 1 до n2 (как у нормального квадрата), лишь бы он удовлетворял условию: суммы чисел по горизонталям, вертикалям и диагоналям равны. Такие квадраты, составленные из произвольных чисел, называют нетрадиционными или, в нашем случае, квадратной матрицей.
Рассматривая пример 1, формируем ранжированный ряд размерных показателей (4) с нижними индексами, которые обозначают номера размерных показателей комплектов лекал:

Далее преобразуем ряд размерных показателей в квадратную матрицу третьего порядка (5), оперируя правилом построения нормального квадрата из последовательного ряда натуральных чисел, являющихся номерами размерных показателей:
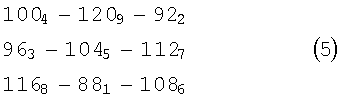
Получаем нетрадиционную квадратную матрицу третьего порядка, которая имеет одинаковое число клеток как по горизонтали, так и по вертикали. В каждую из клеток вписаны числа размерного ряда так, чтобы суммы чисел в каждой строке, каждом столбце и на главных диагоналях были одинаковы. Постоянная суммы квадратной матрицы в данном примере равна 312 и определяется как одинаковая сумма трех чисел в каждой строке, столбце и диагоналях.
Далее строят базовую раскладку комплекта лекал среднего размера или группы средних размеров лекал в размерном поле заказа. Размещают детали кроя, например, среднего размера (далее базовый размер) или группу средних размеров (далее базовая группа размеров) в сочетании размерных показателей заранее определенного порядка квадратной матрицы и ширины рамки раскладки.
Использование свойств системы квадратных матриц третьего порядка позволяет подбирать сочетания номеров базовых размеров лекал третьего порядка при условии неравенства ширины текстильного материала в рулонах, а следовательно, и ширины рамки раскладки.
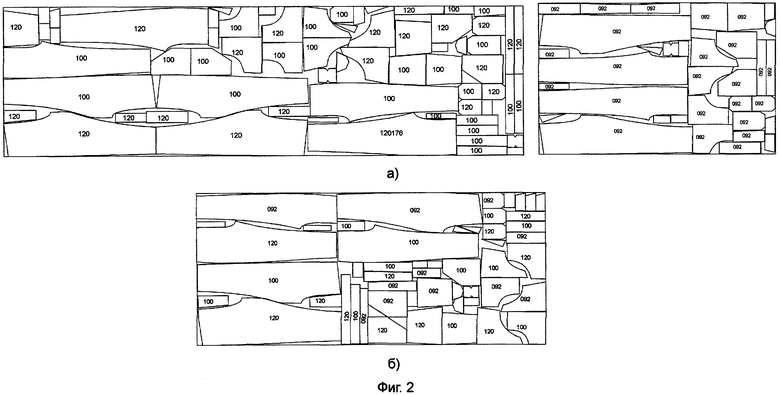
На фиг.1,а), б) и в) представлены три базовые полукомплектные раскладки (если традиционно, то полуторакомплектные раскладки) мужского полукомбинезона в сочетаниях размеров: (100-100-100), (104-104-104) и (108-108-108), при соответствующих ширинах рамки раскладки 1450 мм, 1490 мм, 1530 мм, выполненные по технологии единой (общей) конфигурации раскладки лекал с использованием системы свойств квадратной матрицы третьего порядка.
Строят базовую раскладку лекал, общую для указанных в примере трех ширин рамки раскладки: 1450 мм, 1490 мм, 1530 мм, смещая сочетания размеров в раскладках лекал в сторону увеличения размеров, если ширина материала увеличивается, и смещают сочетания размеров лекал в сторону уменьшения размеров, если ширина материала уменьшается, т.е. при ширине рамки раскладки, равной 1450 мм, сочетание базовой полукомплектной раскладки состоит из размеров 100-100-100; при ширине 1490 мм - из размеров 104-104-104; при ширине 1530 мм - из размеров 108-108-108.
Решение этой задачи обеспечивает устойчивость единой конфигурации раскладки к естественным, для текстильного материала, колебаниям параметра ширины рамки раскладки.
В примере 2 использование свойств системы квадратных матриц третьего порядка позволяет подбирать сочетания размерных показателей под заданную ширину рамки базовой раскладки лекал.
Эксперимент показал, что разброс экономических параметров базовых раскладок, при переменных ширинах материала, не выходит за пределы 0,2%.
Полный набор производных раскладок (6), по базовой конфигурации раскладки 3-х полукомплектов одного и того же размера (традиционно - полуторакомплектной раскладки), например, (100-100-100), получаем при ширине рамки раскладки, равной 1450 мм и постоянной сумме размеров, равной 300:

Затем, имея базовую конфигурацию раскладок размерности (104-104-104), несложно получить полный набор производных (7) при ширине рамки раскладки 1490 мм и постоянной сумме размеров, равной 312:

Не меняя общей, единой конфигурации раскладки, получают также полный набор производных раскладок (8) по базовой конфигурации раскладки (108-108-108) при ширине рамки раскладки 1530 мм и постоянной сумме размеров, равной 324:

Далее на фиг.2, фиг.3 и фиг.4 представлены примеры первых трех раскладок фиг.2,б), 3,б) и 4,б) (из полного набора, представленного выше), выполненные по единой конфигурации с суммой размеров, равной 312, соответственно (100-120-92); (96-104-112); (116-88-108), которые полностью закрывают всю шкалу, состоящую из 9-ти размеров заказа (от 88-го до 120-го) в сравнении с раскладками традиционной комплектности: двух- и однокомплектными, имеющими различные конфигурации фиг.2,а), 3,а) и 4,а), выполненными в реальных производственных условиях, на длину раскройного стола, равную 4500 мм.
Сравнительный анализ экономических параметров показал, с одной стороны, преимущество полукомплектных трехразмерных раскладок, выполненных по единой конфигурации над традиционной технологией двух- и однокомплектных раскладок по плотности в среднем до 1,5% и, с другой стороны, снижение трудоемкости подготовительно-раскройного производства, необходимой для выполнения раскладок на всем размерном поле всего заказа в среднем в 2-3 раза.
В примере 3 использование свойств системы квадратных матриц четвертого порядка позволяет выбирать сочетания номеров размеров лекал из базы квадратных матриц четвертого порядка, например в полукомплектных раскладках мужского полукомбинезона, при условии неравенства количества изделий по размерам в сочетаниях.
Ограничениями в решении данной задачи являются:
- отклонение от общего количества изделий в заказе, равного 161 ед. изделий, должно быть не более 10% (что отвечает традиционным требованиям формирования плана заказа для массового производства);
- количество раскладок должно быть минимальным при полном закрытии шкалы размеров и равняться, например, четырем.
Выстраивают в ряд с числовой последовательностью (9) проектное количество номеров в заказе по размерам лекал, где под нижним индексом 11 подразумевается рост 176 см, а под нижним индексом 4 - рост 182 см (10).
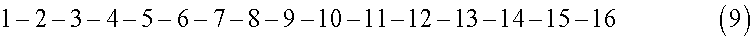
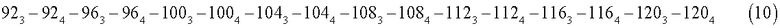
Приводят во взаимно однозначное соответствие с числовой последовательностью количество изделий (11), индексируя нижним индексом числовую последовательность (9), которая в свою очередь соответствует размерному ряду (10).

Далее подставляют количество комплектов изделий в ячейки с соответствующими размерами лекал в каждом сочетании квадратной матрицы в оптимальном сочетании наборов размеров (12), выбранных (любым путем, например, с использованием программного продукта) из базы данных сочетаний квадратных матриц четвертого порядка. Суммируют сначала реальное (чаще всего неравное) количество изделий в каждом из 4-х сочетаний, которые отвечают основному свойству - постоянная суммы равна 424 (в размерном выражении) и соответствуют по количеству в шкале заказа (13). Затем добавляют количество единиц в каждой ячейке, уравнивая их до максимального числа в каждом сочетании и суммируют уравненные (фактическое количество в раскрое) количества единиц изделий в каждом из 4-х сочетаний, представленные матрицей (14).

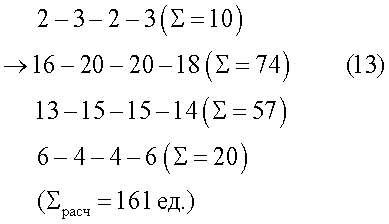
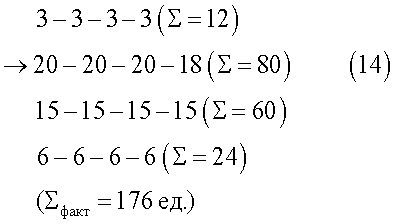
В результате рационального выбора комбинаций сочетаний размеров из базы, получено минимальное количество раскладок, равное 4-м, с минимальным отклонением суммарного количества размеров изделий в заказе, причем комбинации сочетаний размеров лекал в раскладках представлены в квадратной матрице (15) в данном примере построчно:

Количество полотен в настиле «лицом к лицу» в раскладке №1 составит 6 полотен, в раскладке №2 - 40 полотен, в раскладке №3 - 30 полотен и в раскладке №4 - 12 полотен. В результате, фактическое количество изделий при раскрое по раскладкам лекал в сочетаниях размеров (15) составит на 15 ед. больше, что соответствует 8,5% (при максимально допустимых 10%).
В примере 4 квадратной матрицы третьего порядка с отсутствующими двумя размерами 88 и 120 показана группа сочетаний номеров комплектов лекал различных размерных показателей, которая включает в себя комплекты лекал одних и тех же номеров, но уже в различных сочетаниях этой группы.
Формируем размерный ряд с нижними индексами (16), обозначающими количества изделий:
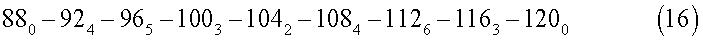
Выбираем из базы квадратных матриц третьего порядка такую, отсутствующие размеры в которой сосредоточены в одном сочетании размерных показателей, например, в первом столбце (17):
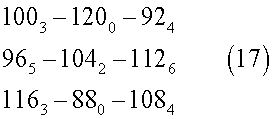
Выбираем оптимальные сочетания размерных показателей из структуры квадратной матрицы таким образом, чтобы количество комплектов изделий в каждом сочетании было равным, что становится возможным, представив размер с нижним индексом, указывающим на количество 965, как 963 и 962, а размер 1126, как 1124 и 1122. Таких оптимальных сочетаний в данном примере будет три (18):

Особенностью в данном примере является то, что в группе раскладок два размера повторяются дважды - это с одной стороны, а с другой стороны отсутствующие в размерном ряду размерные показатели не нарушают основной принцип способа: единая конфигурация раскладки для всего заказа.
Результатом технического решения комплексной задачи является создание конфигурации раскладки лекал, единой для сочетаний размеров на всем размерном поле, которая будет являться базовой для построения производных раскладок в заданных комбинациях сочетаний размеров лекал для заданных ширин рамки раскладки в заказе, минимальное количество раскладок лекал, а также увеличенная высота настилов, обеспечивающие в комплексе (при последующей реализации раскладок в самом раскрое заказа) снижение трудовых затрат, в основе которого лежит единый метод, базирующийся на использовании свойств системы квадратных матриц n-го порядка.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РАСКРОЯ ОТРЕЗКОВ БОЛЬШОЙ ПРОТЯЖЕННОСТИ НА ОТРЕЗКИ МАЛОЙ ДЛИНЫ | 2010 |
|
RU2445412C2 |
| СПОСОБ ПОДГОТОВКИ К РАСКРОЮ РУЛОННОГО МАТЕРИАЛА С ЛОКАЛЬНЫМИ И РАСПРОСТРАНЕННЫМИ ДЕФЕКТАМИ | 1995 |
|
RU2084191C1 |
| СПОСОБ ПОДГОТОВКИ К РАСКРОЮ РУЛОННЫХ И ЛИСТОВЫХ МАТЕРИАЛОВ (ВАРИАНТЫ) | 2006 |
|
RU2329750C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ДЕТАЛЕЙ КРОЯ ПЕРСОНИФИЦИРОВАННОЙ ОДЕЖДЫ | 1997 |
|
RU2118107C1 |
| Способ раскроя ткани для плечевой одежды | 1988 |
|
SU1639596A1 |
| Способ раскроя авровых тканей | 1989 |
|
SU1614789A1 |
| Способ изготовления листовых и рулонных материалов из малогабаритных элементов | 1992 |
|
SU1837817A3 |
| ОБЪЁМНОЕ ИГРОВОЕ УСТРОЙСТВО В ФОРМЕ КУБА "ЛАТИНСКИЙ КУБ" | 2017 |
|
RU2664247C1 |
| Способ раскроя ткани на швейные изделия | 1956 |
|
SU105364A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ОБЪЕМНОГО ИЗДЕЛИЯ | 1992 |
|
RU2038813C1 |



При подготовке к раскрою листовых и рулонных материалов определяют комплектность раскладок лекал на размерном поле заказа, строят в рамке раскладки, на основе визуального анализа, раскладку сочетаний комплектов лекал различных размерных показателей путем размещения лекал из комплектов различных размерных показателей, принимая за расчетное количество номеров комплектов лекал, составляющих сочетания, целое число, равное или ближайшее большее квадратному корню из полного количества номеров комплектов лекал всех необходимых размерных показателей. Формируют ряд комплектов лекал в порядке возрастания с определенным шагом размерных показателей комплектов и присваивают каждому комплекту лекал номер от наименьшего до наибольшего. Определяют номера комплектов лекал, составляющие сочетания, из набора цифровых сочетаний в базе квадратной матрицы, порядок которой равен расчетному количеству номеров комплектов лекал в сочетаниях. Причем считают, что отсутствующие в заказе комплекты лекал определенных размерных показателей имеют свои номера в числовой последовательности номеров, составляющих квадратную матрицу, но сочетания, включающие эти номера, не учитываются. Выбирают в качестве оптимальных такие сочетания номеров комплектов лекал, при которых количество комплектов лекал каждого номера равно или минимально превосходит заданное заказом количество. Строят базовую раскладку как раскладку сочетания комплектов лекал среднего размерного показателя, количество которых в этом сочетании равно порядку квадратной матрицы. Строят раскладки комплектов лекал, производные от базовой, путем размещения в местах расположения лекал базовой раскладки аналогичных лекал из комплектов различных размерных показателей, номера которых соответствуют оптимальным сочетаниям. Предусмотрен выбор из всех возможных сочетаний номеров комплектов лекал, используя комплекты лекал одних и тех же номеров в различных сочетаниях, такие, использование которых обеспечивает получение каждого из комплектов лекал различных размерных показателей в количестве, равном или минимально превосходящем заданное заказом количество. Изобретение обеспечивает уменьшение трудоемкости получения раскладок большого количества комплектов различных размерных показателей, а также расхода рулонного или листового материала при изменяющихся ширинах, путем получения оптимальной раскладки лекал за минимальное время. 1 з.п. ф-лы, 9 ил., 1 табл.
1. Способ подготовки к раскрою листовых и рулонных материалов, согласно которому определяют комплектность раскладок лекал на размерном поле заказа, строят в рамке раскладки на основе визуального анализа, раскладку сочетаний комплектов лекал различных размерных показателей путем размещения лекал из комплектов различных размерных показателей, отличающийся тем, что принимают за расчетное количество номеров комплектов лекал, составляющих сочетания размерных показателей в раскладке, целое число, равное или ближайшее большее квадратному корню из полного количества номеров комплектов лекал всех необходимых в заказе размерных показателей, формируют размерный ряд комплектов лекал заказа в порядке возрастания с заданным шагом размерных показателей комплектов и присваивают каждому комплекту в размерном ряду лекал номер от наименьшего до наибольшего, выбирают номера комплектов лекал, составляющие сочетания размерных показателей в раскладках, из набора цифровых сочетаний в базе квадратных матриц, порядок которых равен расчетному количеству номеров комплектов лекал в сочетаниях, причем считают, что отсутствующие (нулевые) в заказе комплекты лекал с определенными размерными показателями имеют свои номера в числовой последовательности номеров, составляющие квадратные матрицы, но сами сочетания, включающие эти отсутствующие в заказе номера, не учитываются, выбирают в качестве оптимальных такие сочетания номеров комплектов лекал с размерными показателями, при которых количество комплектов лекал каждого размера равно или минимально превосходит заданное заказом количество, строят базовую раскладку как раскладку сочетания комплектов лекал средних размерных показателей, количество комплектов лекал в этом сочетании равно порядку квадратной матрицы, строят раскладки комплектов лекал, производные от базовой, путем размещения в местах расположения лекал в базовой раскладке аналогичных по наименованию лекал из комплектов различных размерных показателей, номера которых соответствуют оптимальным сочетаниям.
2. Способ по п.1, отличающийся тем, что выбирают оптимальные сочетания номеров комплектов лекал различных размерных показателей, используя комплекты лекал одних и тех же номеров в различных сочетаниях, такие, использование которых обеспечивает получение каждого из комплектов лекал различных размерных показателей в количестве, равном или минимально превосходящем заданное заказом количество.
| Инструкция по нормированию расхода материалов в массовом производстве швейных изделий | |||
| - ЦНИИТЭИлегпром | |||
| - М., 1988, с.9-11 | |||
| СПОСОБ ПОДГОТОВКИ К РАСКРОЮ РУЛОННЫХ И ЛИСТОВЫХ МАТЕРИАЛОВ (ВАРИАНТЫ) | 2006 |
|
RU2329750C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ДЕТАЛЕЙ КРОЯ ПЕРСОНИФИЦИРОВАННОЙ ОДЕЖДЫ | 1997 |
|
RU2118107C1 |
| СПОСОБ ПОДГОТОВКИ К РАСКРОЮ РУЛОННОГО МАТЕРИАЛА С ЛОКАЛЬНЫМИ И РАСПРОСТРАНЕННЫМИ ДЕФЕКТАМИ | 1995 |
|
RU2084191C1 |
| US 4136452 А, 30.01.1979 | |||
| US 3816924 А, 18.06.1974 | |||
| US 5926966 А, 27.07.1999 | |||
| GB 701043 А, 16.12.1953 | |||
| Способ приготовления сахарного печенья | 2018 |
|
RU2668339C1 |
Авторы
Даты
2010-05-27—Публикация
2008-12-02—Подача