Область техники, к которой относится изобретение
Настоящее изобретение относится к способам управления сетями (логическими и физическими) в нескольких областях. Более конкретно, в настоящем изобретении описывается способ анализа сети, состоящей из любого количества сетевых узлов, соединенных связями.
Уровень техники
Почти любая социальная или физическая структура, отдельные объекты которой связаны отношениями некоторого типа, может быть проанализирована с сетевой точки зрения, будь то социальные группы, маршруты воздушных трасс или группы компьютеров. Сети - интересные объекты. Они имеют развитую структуру и в то же время они просты: они состоят, в простейшем случае, только из узлов, соединенных связями. Абстрактное представление сети, или граф (используются оба эти термина), является очень удобным и при моделировании структур, наблюдаемых в реальном мире. Таковы, например, социальные сети, системы связи, World Wide Web, метаболические и генетические сети в биологических системах, пищевые сети, сети болезней, энергетические сети. Более коротко, сеть представляет собой простую нетривиальную абстрактную структуру, увлекательную саму по себе и тесно связанную со многими отраслями науки и техники.
В области телекоммуникаций долгое время развивались теории управления сетями и теории сетевых структур. Крайне важно понимать сеть. Эффективность эксплуатации и обслуживания такой телекоммуникационной сети в значительной степени зависит от имеющихся знаний о рассматриваемой сети. Это важно как в отношении среднего времени между отказами, так и в отношении распространения вреда, такого как вирусы, саморазмножающиеся вирусы ("черви") и пр.
В сетях передачи данных имеет место аналогичная ситуация. Сходные соображения применимы и к эксплуатации сетей передачи электроэнергии, особенно в отношении безопасности. При планировании и эксплуатации электрической сети важно иметь устойчивую сеть во избежание ситуаций, при которых большая часть населения испытывает перебои в подаче электроэнергии. Анализ связности сети важен для оценки надежности.
Системное администрирование всегда включает в себя управление сетью, состоящей из связей нескольких типов. Это, например, физические связи между машинами, логические связи между пользователями и файлами, а также социальные связи между пользователями. Важным аспектом системного администрирования является обеспечение беспрепятственной передачи необходимой информации по сети, при этом задерживая поток вредной или разрушительной информации по этой же сети.
Структура сети играет в достижении этих двух, частично конфликтующих, целей системного администрирования критическую роль. Обе цели имеют дело с распространением информации по связям сети; следовательно, обе задачи сильно зависят от сетевой структуры. Ввиду этой зависимости понимание сетевой структуры может быть ценным компонентом эффективного системного администрирования.
Кроме того, естественно, существуют сети, которые являются одновременно социальными и технологическими. К таким сетям относятся телефонные сети, одноранговые сети (peer-to-peer) в Интернете, а также объединенная сеть компьютеров, файлов и пользователей, которая является объектом ежедневной работы любого системного администратора.
В этом случае безопасность снова представляется очевидной областью применения описанных принципов: требуется определить узлы, которым следует предоставить, например, наивысший приоритет в защите от вирусов.
Исследования сетей привлекли большое внимание приблизительно в последние десять лет. Большинство параметров описания сетевой структуры, изученных к настоящему времени [8], являются свойствами "целого графа", т.е. скалярными параметрами или распределениями, которые соответствуют графу в целом, и вычисляются путем усреднения. Примеры таких свойств целого графа включают в себя распределение степеней узлов, диаметр или среднюю длину пути, коэффициенты кластеризации и понятие "маленьких миров", которое базируется на предыдущих двух понятиях.
Свойства целого графа важны и полезны, однако они не могут дать полный ответ на вопрос "Как составить представление о структуре сети?"
Существует много ситуаций, в которых важно понимание сетей, имеющих более абстрактную форму по сравнению с сетями связи, сетями передачи данных или электрическими сетями. Например, в сфере эпидемиологии важно иметь представление о социальных сетях и о том, как эти сети способствуют распространению болезней. В сфере распространения информации важно знать механизмы, управляющие распространением информации в пределах популяции, будь то на местном или глобальном уровне.
При рассмотрении отношений между людьми или социальных сетей обращают внимание на связи между отдельными людьми, а не на их категории или характеризующие их параметры. Социальная сеть, таким образом, это любая группа людей, в которой между отдельными людьми имеются взаимоотношения некоторого типа. Люди с высокой степенью социального влияния в социальной сети часто именуются лидерами общественного мнения. Они имеют влияние на основании уровня знаний или социального положения. В любом случае это влияние часто проявляется наличием у лидеров общественного мнения большого числа социальных контактов; они связаны с большим числом людей. Это, разумеется, логично; иметь социальное влияние означает иметь возможность взаимодействия с большим количеством людей.
Применимость этого принципа для социальных сетей представляется очевидной [4]. Очевидно также, что интерес представляет идентификация сообществ в измеряемой социальной сети. Пример несколько другого вида - сеть сексуальных контактов. Здесь указанные принципы также могут быть весьма полезными при работе, связанной с ограничением распространения болезней, передающихся половым путем; скорее всего, здесь можно сосредоточиться на двух взаимодополняющих целях - (i) предотвращение заражения центральных узлов каждого сообщества и (ii) предотвращение передачи болезни между транзитными узлами.
Поэтому сети заслуживают серьезного исследования. Сеть - одна из самых простых абстракций структуры, допускающая исследование; с другой стороны, понимание структуры сети является нетривиальной задачей.
Известные решения
В научной области анализа сетей существует несколько путей измерения центральности сетевых узлов. Один из параметров такого измерения называется центральностью собственного вектора. Центральность собственного вектора (eigenvector centrality, EVC) была определена Бонасичем (Bonacich) [2] в начале семидесятых годов. Основной принцип EVC состоит в том, что важно не только количество людей, с которыми знаком некоторый индивид, но также и то, насколько важны (центральны) в свою очередь они, это определяет важность (центральность) самого индивида. Таким образом, появляется фактически рекурсивное определение: важность (центральность) индивида зависит от важности его соседей, которая, в свою очередь, зависит от его важности. Суть такого рекурсивного определения состоит в том, чтобы можно было определить те важнейшие узлы, которые на самом деле имеют заметное влияние в масштабах всей сети. Если по определению важность подсчитывается исходя только из количества имеющихся соседей, имеется риск появления ситуации, в которой важнейшими узлами сети будут названы центры изолированных кластеров. В социальных сетях эти центры имеют влияние в ограниченном масштабе, так как их влияние не выходит за пределы их непосредственных соседей.
Хотя работа Клейнберга (Kleinberg) [7] посвящена сетям с ориентированными связями, при этом в ней содержится достаточно перспективный взгляд. Клейнберг рассматривает ориентированный граф, определяет два различных типа ролей узлов графа и приводит способ вычисления индексов, определяющих количественную степень, в которой каждый узел играет роли этих двух типов. Таким образом, каждому узлу в ориентированном графе может быть присвоен показатель Источника и показатель Посредника. Важно отметить, что эти показатели могут базироваться исключительно на топологии графа независимо от содержания или смысла, а также любых "свойств" узлов.
Названия этих двух типов ролей отражают их значение. Узлы с высоким показателем Источника представляют собой важные узлы, поскольку на них указывают важные узлы, фактически узлы с высокими показателем Посредника. Последние получают высокие показатели Посредника за счет указания на хорошие Источники. Другими словами, Посредники указывают, Источники являются предметом указания. Эти принципы могут быть весьма полезными при анализе структуры WWW: Источники, вероятнее всего, будут хорошими конечными точками поиска информации, в то время как Посредники оптимальны для доведения поиска до Источников. Представляется очевидным, что подобные роли возникают в социальных сетях: в одних случаях индивидуум знает, кто имеет необходимую информацию (Источник), в других случаях ему необходимо осведомиться у хорошего Посредника.
Работа Клейнберга дает индексы для каждого узла в сети. Эти индексы представляют полезную информацию о роли (ролях), играемых узлом в сети. Такая информация весьма отлична от информации целого графа; тем не менее, она строится, по крайней мере в первоначальном варианте, исключительно на базе топологической структуры графа.
Другой аспект графа, который также отличается от свойств целого графа, - структура сообществ графа. В той же работе Клейнберг предлагает способ поиска таких сообществ в графах, таких как граф Web. Используемые математические инструменты - в основном те же, что и при поиске показателей Посредника/Источника; это, помимо прочего, означает, что разбитие графа на сообщества также базируется исключительно на структуре графа без привлечения данных или свойств узлов или связей. Кроме того, можно отметить, что разбиение графа на подсообщества дает новую информацию о ролях узлов: они могут быть членами сообщества X; они могут не принадлежать ни одному сообществу; они могут быть, в некотором смысле, "лидерами" своего сообщества; они могут находиться на "крае"; наконец, они могут играть важную роль в соединении нескольких сообществ.
Задаче поиска "естественных" сообществ в ориентированном графе, таком как Web, посвящено много других работ. Гирван (Girvan) и Ньюман (Newman) [5], напротив, рассмотрели этот вопрос для неориентированных графов. В основе их подхода лежит определение сообщества путем предварительного обнаружения их "границ", в частности путем поиска связей с высокой "промежуточностью", при удалении которых граф распадается на подсообщества.
Раскрытие изобретения
Задача, на решение которой направлено настоящее изобретение, состоит в создании способа анализа сетей, применимого как к физическим сетям, так и логическим сетям, существующим в форме сетей, наложенных на физические сети. Важным общим аспектом является идентификация связей (физических или логических), по которым может передаваться информация.
Другая задача настоящего изобретения состоит в создании "естественного" средства разбиения неориентированного графа на сообщества, базирующегося исключительно на топологии графа. Для узлов графа определяется набор ролей, такой что каждому узлу присваивается одна и только одна роль. Таким образом, в отличие от подхода Клейнберга, в настоящем приложении желательно, чтобы роли являлись бинарными (Да/Нет) и к тому же уникальными свойствами узлов.
В предшествующем уровне техники [13, 3] подробно описано применение описанного анализа для сетевых компьютеров со многими пользователями. В настоящем изобретении предлагается естественный способ разделения сети на хорошо связанные кластеры и назначения значимых ролей в потоке информации каждому узлу в сети.
В соответствии с изобретением решение поставленной задачи достигается путем создания способа анализа сети, раскрытого в пункте 1 прилагаемой формулы изобретения. В частности, настоящее изобретение включает в себя способ анализа способности сети к распространению информационного или физического трафика, причем указанная сеть содержит ряд сетевых узлов, соединенных связями, указанный способ включает в себя следующие шаги:
- составление карты топологии сети;
- вычисление значений силы связи между узлами;
- вычисление индекса центральности собственного вектора для всех узлов на основе указанных значений силы связи;
- идентификация узлов, имеющих локально максимальные индексы центральности собственного вектора, как центральных узлов;
- группирование узлов в области, окружающие каждый идентифицированный центральный узел;
- назначение роли каждому узлу в зависимости от его положения в области: центральный узел, элемент области, граничный узел, транзитный узел, пассивный узел;
- измерение способности сети к распространению на основе числа областей, их размера и структуры связей между ними.
Предпочтительные варианты осуществления изобретения описываются зависимыми пунктами формулы изобретения, приведенными далее.
Перечень фигур чертежей
Другие свойства и достоинства настоящего изобретения станут ясны из нижеследующего описания, содержащего ссылки на прилагаемые чертежи, которые иллюстрируют пример осуществления изобретения, не вносящий каких-либо ограничений.
На чертежах:
на фиг.1 представлена схема, показывающая Транзитный Узел (слева), а также Транзитный Узел и Пассивные Узлы(Danglers) (справа);
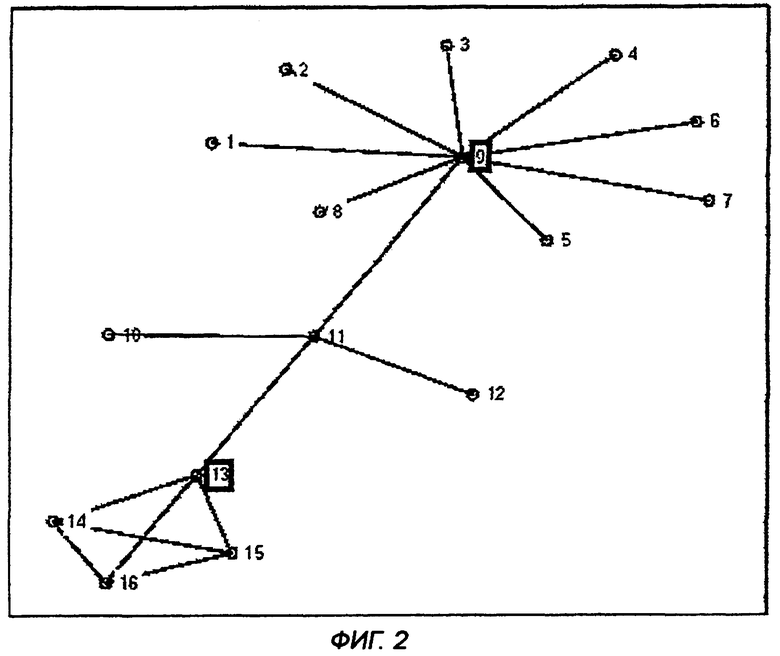
на фиг.2 показан простой граф с двумя областями;
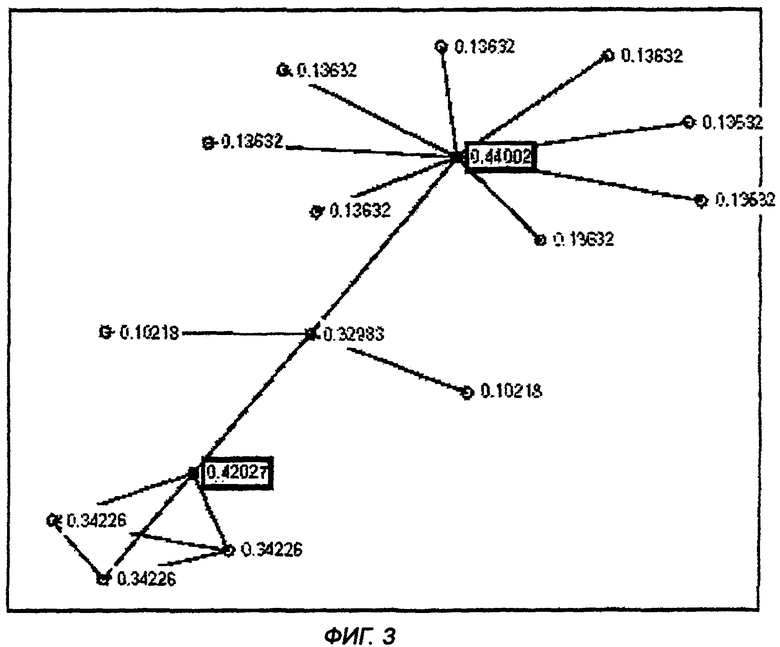
на фиг.3 показан тот же самый граф, что и на фиг.2, но с областями, определенными по другому правилу. Приведены значения EVC (Eigenvector Centrality, индекс центральности собственного вектора) для узлов;
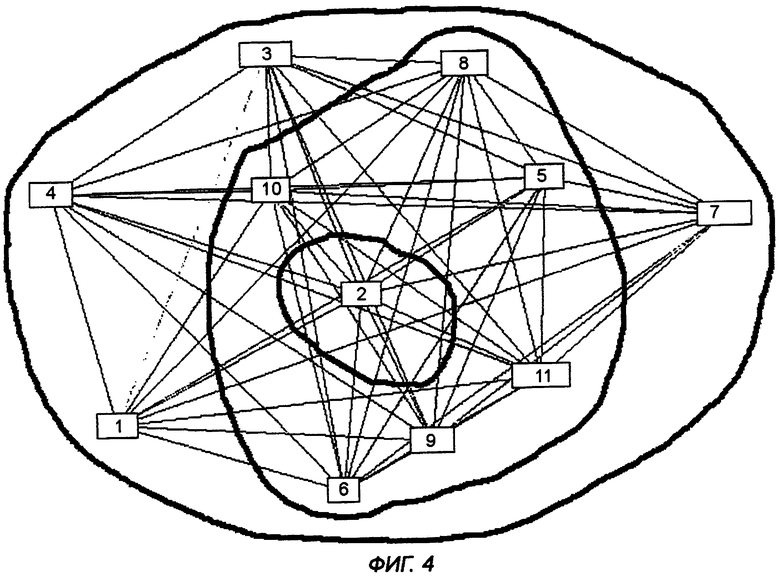
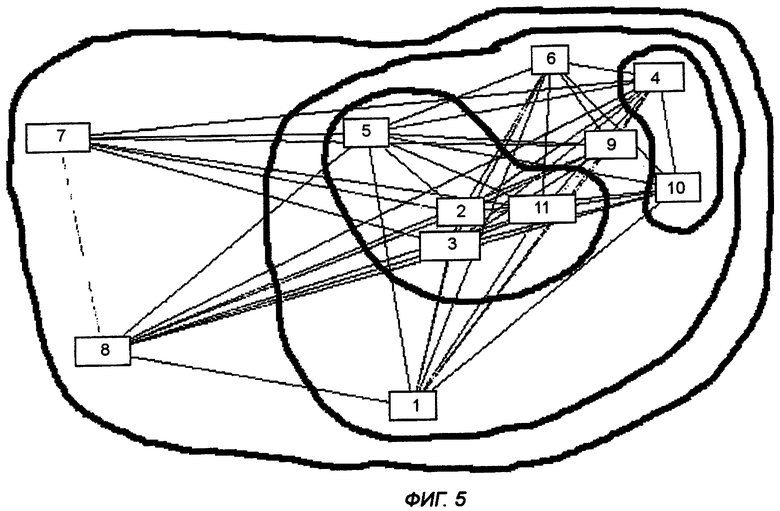
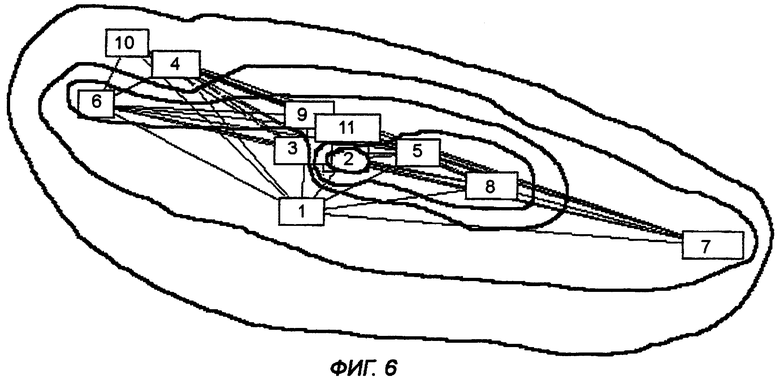
на фиг.4, 5, и 6 показаны результирующие графы проекта MANA [4] с использованием трех различных способов измерения силы связей;
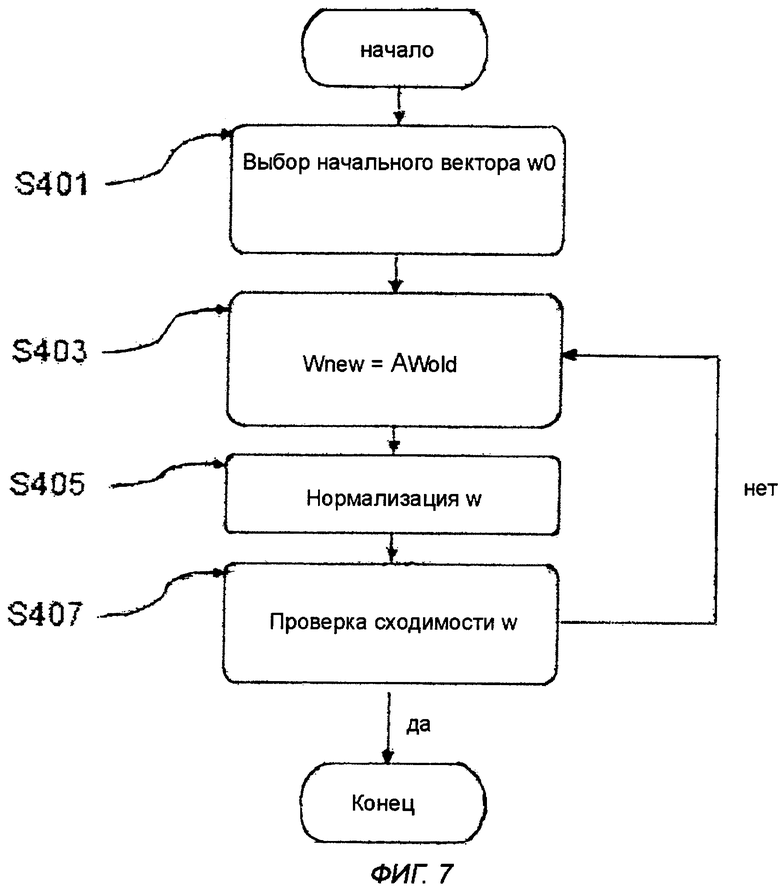
на фиг.7 приведена блок-схема способа вычисления индекса центральности собственного вектора.
Осуществление изобретения
В настоящем изобретении раскрываются полезные и интересные приложения принципов анализа сетей. Единственной предпосылкой является неориентированность связей в сетях. Под неориентированными связями подразумеваются связи, не имеющие определенного направления. Web-страница в системе World Wide Web может указывать на другую Web-страницу, но эта последующая страница не обязательно должна указывать на предыдущую. В данном случае страницы соединены ориентированной связью. Если бы обе страницы имели гиперссылки друг на друга, по одной ссылке на каждое направление, эти связи можно было бы объединить в одну неориентированную связь. Согласно настоящему изобретению все сети рассматриваются как состоящие из неориентированных связей.
Принцип, реализуемый в настоящем приложении, состоит в том, что "степень связности" может рассматриваться как функция высоты в дискретном пространстве (на графе). Если функция высоты по настоящему изобретению является достаточно гладкой, то можно использовать принципы, относящиеся к гладким поверхностям в непрерывном пространстве. А именно в соответствии с настоящим изобретением для определения областей в сети будет использоваться топографическая картина. Области будут соответствовать "горам", причем центр каждой области будет вершиной соответствующей горы. Границы между областями в этом случае определяются как точки, которые нельзя однозначно привязать к какой-либо области горы.
Определяются следующие роли: "лидер" сообщества (области); элемент сообщества; два типа ролей узлов в "граничном наборе", к которому относятся узлы, не принадлежащие к какому-либо сообществу.
Рассмотренный подход в определенной мере похож на подход Гирвана и Ньюмана [5]. Согласно настоящему изобретению анализ начинается не с "краев", а с "центров" сообществ. Исследование проводится от этой отправной точки "наружу", производится определение элементов и, в последнюю очередь, граничных узлов. Представленный набор ролей является полным и непротиворечивым в том смысле, что определения позволяют уникально и однозначно назначить единственную роль каждому узлу в графе.
Варианты осуществления изобретения
Люди, которые общаются друг с другом, образуют социальную сеть, связи в которой основаны на их общении. Эти связи можно различать по типу носителя связи, будь то телефония, личное общение или почта. Таким образом, социальная сеть может быть описана как мультиплексная, т.е. сеть, узлы в которой связаны друг с другом различными типами связей. Социальные отношения, связывающие различных людей, могут существовать независимо от типа носителя связи; тем не менее, тип носителя связи играет в определении связей важную роль, поскольку каждая среда является отдельным каналом для потока информации. В этом смысле различные средства связи подобны языкам. Например, человек, который хочет достичь много узлов в сети, должен иметь возможность общения посредством нескольких носителей связи - он должен говорить на "языке", предпочитаемом другими узлами. Описанный принцип дифференциации связей по носителям связи применим для большинства типов сетей: например, болезнь может распространяться посредством различных переносчиков инфекции, связи в транспортных сетях могут состоять из нескольких различных средств передвижения, таких как автомобили, самолеты или поезда.
Измерение силы связей и EVC
Силу связей в мультиплексной сети такого типа можно определять по-разному. Приведем четыре варианта:
1) Можно просто указывать, существует ли связь (любого типа) или нет. В цифровой форме это обозначается как 0 для "отсутствия связи" и 1 для наличия "некоторой связи".
2) Можно подсчитывать число различных носителей связи, соединяющих любую пару узлов, т.е. число различных носителей связи, по которым проходит любой поток веществ или информации между любыми двумя узлами в сети.
3) Можно измерять полный поток (трафик) между любыми двумя узлами в сети. Для этого необходимо преобразовать имеющиеся данные в обычные единицы измерения. Эти единицы измерения описывают таким образом общую интенсивность потока (например, в минутах или словах для средств связи) между любыми двумя узлами в сети.
4) В четвертом варианте определяется сила связей путем сочетания вариантов 2) и 3). При этом учитывается каждый носитель связи (как в варианте 2), но ее вклад определяется (как в варианте 3) долей потока для того носителя связи, которая используется данной парой.
Традиционный способ определения силы связи обозначен номером 1). Способ 3) также известен. Способы 2) и 4) являются новыми и инновационными способами определения силы связи.
Индекс центральности собственного вектора (EVC) математически определяется как главный собственный вектор матрицы. Наиболее простым и широко применяемым способом нахождения главного собственного вектора матрицы является степенной метод [14]. Этот метод основан на многократном умножении матрицы на вектор весов. Умножение матрицы на вектор весов эквивалентно так называемому "распространению весов": оно приводит к перераспределению набора весов по некоторому правилу. Повторяющееся перераспределение весов (с общей нормализацией полного веса) приводит к устойчивому распределению, которое представляет собой доминирующий или главный собственный вектор. В соответствии с настоящим изобретением эти показатели используются в качестве индекса центральности.
Для пояснения проиллюстрируем применение степенного метода на фиг.7. В данном случае процесс запускается с использованием описанных ранее уравнений и выбирается (S401) начальный вектор w0. При каждой итерации выполняется (S403) вычисление нового веса wnew путем перераспределения весов в соответствии с действием матричного оператора. Полученный новый вес нормализуется (S405). Далее производится (S407) проверка сходимости. Если вес сходится, процесс завершается. В противном случае выполняется вычисление нового веса, и процесс повторяется до тех пор, пока вес не сойдется.
Для анализа мультиплексных социальных сетей была создана обобщенная единица измерения EVC, включающая в себя три другие единицы сил связи (2-4), описанные выше. Модификация общего принципа EVC, примененная в новых способах 2) и 4), состоит в следующем: узел является центральным, если он имеет много соседей с высокой центральностью и использует множество различных типов носителей связи. Далее описана реализация этого общего принципа для каждого из четырех вышеописанных подходов к определению силы связи:
1) Традиционный подход, в котором матрица смежности 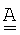 состоит только из значений 0 и 1, может использоваться совместно с мультиплексными сетями; но он полностью нечувствителен к числу носителей связи, используемых каждой парой узлов.
состоит только из значений 0 и 1, может использоваться совместно с мультиплексными сетями; но он полностью нечувствителен к числу носителей связи, используемых каждой парой узлов.
2) Матрица 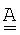 , все элементы которой имеют значение 0 или 1, заменяется матрицей
, все элементы которой имеют значение 0 или 1, заменяется матрицей 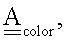 определенной следующим образом: элемент
определенной следующим образом: элемент 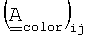 равен числу "цветов" (различных носителей связи), соединяющих узлы i и j.
равен числу "цветов" (различных носителей связи), соединяющих узлы i и j.
3) Единицы в традиционной матрице 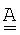 заменяются на положительное вещественное число, обозначающее полную интенсивность потока (просуммированную по всем носителям связи и приведенную к общей единице измерения) по некоторому данному интервалу времени. То есть
заменяются на положительное вещественное число, обозначающее полную интенсивность потока (просуммированную по всем носителям связи и приведенную к общей единице измерения) по некоторому данному интервалу времени. То есть 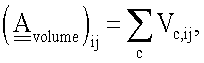 где с - индекс суммирования по "цветам" (носителям связи), Vc,ij - полная интенсивность коммуникационного потока в носителе связи с между узлами i и j.
где с - индекс суммирования по "цветам" (носителям связи), Vc,ij - полная интенсивность коммуникационного потока в носителе связи с между узлами i и j.
4) Наконец, в настоящем изобретении предлагается сочетание подходов 2) и 3), при котором весовой коэффициент присваивается как интенсивности потока, так и существованию нескольких носителей связи. Таким образом, для каждого носителя связи с и пары узлов ij назначается "показатель", который представляет собой долю (вносимую парой ij) полного коммуникационного потока, использующего носитель связи с в сети. Пусть VT,c обозначает полную интенсивность (по всей сети) коммуникационных потоков, использующих носитель связи с. Тогда "смешанную" измеренную силу связи можно записать как
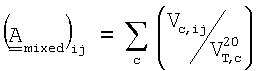
Способ по настоящему изобретению предполагает преобразование данных потока в матрицу смежности с использованием одного из четырех методов, описанных выше, для присвоения каждому элементу матрицы параметра силы связи. После этого вычисляется главный собственный вектор результирующей измененной матрицы смежности. Это позволяет назначить индекс (положительное число) всем узлам в сети, обозначающий их центральность согласно одной из описанных четырех систем измерения. Узлы с самыми высокими значениями центральности считаются самыми центральными узлами в сети. Это позволяет посредством данного способа построить список важнейших узлов сети и их непосредственных соседей. Индекс центральности также позволяет построить топографическую карту сетевой структуры, т.е. графический образ сети, на котором самые центральные узлы показаны как локальные "пики".
Роли в сетях
Последняя цель настоящего изобретения состоит в назначении естественной и уникальной роли каждому узлу в сети исключительно на основе топологии графа. Как отмечено выше, Клейнберг нашел две такие роли для ориентированных графов: Посредники и Источники. Посредники по определению указывают на хорошие Источники; Источники по определению являются объектами, на которые указывают хорошие Посредники. Уже из этих простых утверждений можно видеть, что в случае, когда дуги графа становятся неориентированными (т.е. при этом "указывающий" = "объект указания"), различие между Посредниками и Источниками исчезает. Математика дает тот же самый результат: в случае неориентированных дуг матрица смежности является симметричной, А=АT, следовательно, матрицы, определяющие Посредники и Источники, становятся одинаковыми.
Итак, для неориентированных графов два типа ролей сводятся к одной. Эта роль (точнее, индекс, определяющий степень, в которой узел играет роль) представляет собой центральность собственного вектора.
Оператор Посредника ААT и оператор Источника АTА становятся просто А2, главный собственный вектор которого совпадает с этим вектором для А.
Таким образом, оказывается, что две роли, связанные в работе Клейнберга с ориентированными графами, в случае неориентированного графа становятся одной ролью (типом роли). В следующих разделах этот тип роли называется степенью связности или центральностью собственного вектора. Далее рассматриваются различия между узлами неориентированного графа, другими словами, множество различных ролей, которые могут быть назначены любому данному узлу. Эти роли определены в следующем разделе. Центральность собственного вектора (EVC) является функцией высоты и, следовательно, отправной точкой.
Определения ролей
Необходимо пояснить различие между "типом роли" и "ролью". Каждому узлу могут быть присвоены вещественные индексы или "показатели": показатели Посредника и Источника в случае ориентированных связей и показатель EVC в случае неориентированных связей. Это и есть типы ролей; фактически можно сказать, что все три показателя представляют некоторый тип центральности. Все узлы имеют некоторую степень центральности; "центральность", разумеется, является типом роли. Ролью в настоящем документе называется бинарное (да/нет) различие, применяемое к каждому узлу, при этом каждый узел получает единственное "Да" и ему, следовательно, присваивается уникальная и однозначная роль. Центральность (тип роли) дает гладкую функцию высоты на графе, что позволяет назначить роль (Да или Нет) каждому узлу с использованием топографических критериев.
Центры
Для простоты и удобочитаемости сохранена картина гор, долин, седел и т.д. для функции высоты. Каждая гора может быть определена ее пиком. Пик представляет собой локальный максимум функции высоты. Тогда первая роль представляет собой вершину горы.
Центр: Центром называется любой узел, на который приходится локальный максимум центральности собственного вектора.
Области
Каждая вершина горы определяет гору. Следовательно, число Областей в графе равно числу центров (в дальнейшем, кроме как при определении ролей, заглавные буквы пропускаются; значение должно быть ясно из контекста). Области обычно состоят из более чем одного узла; следовательно, область не может быть ролью узла, ролью будет Элемент Области.
Элемент Области: каждый узел, который может быть единственным образом привязан к одному Центру по однозначному правилу, является элементом Области этого Центра и, следовательно, Элементом Области.
Остается определить "однозначное правило". Согласно настоящему изобретению возможны два варианта "однозначного правила".
Правило 1 (расстояние). Узел привязан к Центру С, если он находится ближе (в наименьшем числе переходов) к С, чем к любому другому Центру С0.
Правило 2 (крутейшее восхождение). Для каждого узла i путь крутейшего восхождения, начинающийся в i, завершится на одном (или нескольких) Центрах. Если он завершается на единственном Центре, то узел i привязан к этому Центру.
Эти правила являются дискретным вариантом процесса привязывания части области определения (базового пространства) к каждой вершине горы и, следовательно, определения каждой горы. При этом следует четко разделить определение области на две части: непосредственно определение, которое ссылается на правило, но не определяет его, и собственно правило. Это необходимо ввиду того, что в дискретном случае возможно наличие нескольких правил; при этом устанавливается определение области путем фиксирования принципа "гор", но правило остается неопределенным.
Оба вышеизложенных правила удовлетворяют интуитивно разумному критерию, состоящему в том, что ближайшие соседи центра должны (вообще говоря) относиться к его области (в конечном счете, высокий EVC центра обуславливается числом и связностью соседей центра). Кроме того, оба указанных правила легко реализовать на основе простого способа с итерациями: анализ начинается с центра и движется от них, при этом узлы "окрашиваются" в соответствии с областями (центрами), к которым они принадлежат. С другой стороны, правило крутейшего восхождения является наиболее адекватным топографической картине.
Границы между областями
На непрерывной топографической поверхности имеются точки, которые лежат между горами и не принадлежат одной отдельной горе. Аналогичные точки могут существовать и в дискретном случае.
Узлы, которые не могут быть связаны с единственной горой, вносятся в набор Граничных.
Граничные Узлы: любой узел, для которого однозначное правило принадлежности области дает болеее одного результата, является Граничным Узлом.
Граничные узлы интуитивно представляются как "узлы, соединяющие области". При более глубоком рассмотрении становится ясно, что в этом отношении не все граничные узлы одинаковы. Некоторые граничные узлы действительно играют важную роль в соединении двух или более областей: они лежат на путях, соединяющих соответствующие центры (и, следовательно, области). См. левую часть на фиг.1. Другие узлы могут быть удалены без какой-либо потери степени связанности между областями. См. правую часть на фиг.1. Следовательно, для набора граничных узлов естественно определить две различные роли.
Транзитный Узел: Граничный Узел, расположенный по крайней мере на одном не обратно-связном пути, соединяющем два Центра, называется Транзитным Узлом.
Пассивный узел: любой Граничный Узел, не являющийся Транзитным, называется Пассивным Узлом.
Разумеется, пассивные узлы могут вводить новую информацию в сеть, но они не играют существенной роли в передаче информации между областями.
Наконец, желательно выбрать класс связей, играющих важную роль в соединении областей. Причиной является то, что набор граничных узлов для правила крутейшего восхождения в общем случае очень мал или равен нулю. В этом случае однако целесообразно выделить сетевые элементы, соединяющие области. Отсюда определение:
Транзитные Связи: любая связь, конечные точки которой находятся в двух различных Областях, называется Транзитной Связью.
Транзитные связи возникают для любого правила определения области, описанного выше. Можно создать правила для определения областей с "толстыми" границами. Например, можно связать узлы с центрами следующим образом:
Правило 1' (расстояние с отсечкой). Узел связан с Центром С, если он находится ближе (по числу переходов) к С, чем к любому другому Центру С0, и его расстояние от С составляет не более h переходов.
"Толстые" границы возникают для этого правила по той причине, что может существовать много узлов, которые расположены дальше h переходов от любого центра. Вообще говоря, "толстые" границы возникают, если выбирается правило, предназначенное для избежания "совместного разрастания" областей от их соответствующих центров. Тогда расстояние, на которое допускается рост, может быть измерено в переходах (как в Правиле 1') или в единицах уменьшения EVC.
Согласно Правилу 1 границы являются "тонкими": фактически они имеют толщину в один узел. Границы согласно Правилу 2 еще более тонки: вообще говоря, они имеют толщину в 0 узлов, поскольку редко когда у узла будет два или более путей крутейшего возрастания, ведущих к различным локальным максимумам.
Математика
Математические задачи в соответствии с настоящим изобретением решаются в основном путем использования "гладких" функций на дискретном пространстве.
Предположим, что область определения непрерывна. Тогда наиболее гладкими функциями будут гармонические функции. Эти функции являются решениями уравнения Лапласа
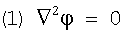
Для данного пространства получаются различные решения (1) в зависимости от различных граничных условий на φ. При этом сразу возникают проблемы в непрерывном случае. Одна проблема состоит в том, что отсутствуют максимумы и минимумы, кроме как на границе. Следовательно, топографическая картина согласно настоящему изобретению не может быть создана с использованием таких гладких функций: каждая вершина будет лежать на границе. Кроме того, в настоящем изобретении раскрывается естественный способ определения областей. "Естественный" в данном случае означает "в максимальной степени обусловленный топологией графа". Следовательно, нежелательно иметь необходимость присваивать значения данной функции φ на границе - эта задача предпочтительно должна решаться на основе топологии.
Последнюю задачу, разумеется, можно решить путем объявления φ=const, например нулю, на границе. Таким образом, границе лишь присваивается некоторое опорное номинальное значение. Это достаточно "естественно"; однако в этом случае φ=const на всем пространстве из-за свойства усреднения уравнения Лапласа.
Дискретная версия уравнения Лапласа:
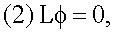
где L=К-А - матрица Лапласа, К=Diag(k1, k2, …) - диагональная матрица, i-й элемент которой является степенью узла ki, где ki - число связанных соседей узла i, А - матрица смежности, причем Аij=1, если от i к j имеется связь, и 0 в противном случае.
Отчетливо видно, что свойство усреднения действует и здесь: решения (2) подчиняются выражению
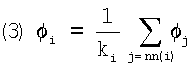
Здесь "nn" означает "около соседа". Дискретное уравнение Лапласа, таким образом, предлагает "наиболее гладкие" функции для дискретного случая; однако при этом сохраняются все проблемы, возникающие для непрерывных гармонических функций, и появляется еще одна. Новая проблема проистекает из того принципиального факта, что определение границы дискретного пространства не является единственным; фактически отсутствует естественный способ определить такую границу. Можно, разумеется, принять предположение (возможно, наименее произвольное) о том, что ни одна из точек не является граничной - все точки должны иметь некоторую высоту, определяемую структурой графа, но в этом случае вновь возникает состояние ϕi=const.
Центральность собственного вектора
В свете рассмотрения выражения (3) небольшое изменение картины в соответствии с (3) позволяет решить все проблемы сразу. Небольшое изменение следующее: используется функция высоты, которая подчиняется не свойству усреднения (3), а следующему правилу:
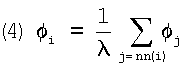
Таким образом, вместо использования точного среднего по всем соседям сумма соседей делится на константу λ, которая одинакова для всех узлов. Это уравнение можно записать следующим образом:
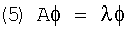
где А - матрица смежности. Теперь имеется уравнение для собственных значений, и функция высоты ϕ является собственным вектором матрицы смежности. В настоящем изобретении требуется фактически собственный вектор, представляющий собой устойчивое итерационное решение (4), так как высота должна отражать "степень связности". Таким образом, (4) представляет следующий принцип: степень связности узла i определяется в пределах константы масштаба λ степенью связности всех соседей i. Итеративная реализация этого требования с любым стартовым значением в конечном счете дает главный собственный вектор матрицы смежности. Этот собственный вектор дает устойчивое непротиворечивое решение (4); он также является положительным полуопределенным, поскольку таковой является матрица А.
В результате этого единственного изменения устраняются вышеописанные проблемы с уравнением Лапласа (дискретным или нет). EVC может иметь локальные максимумы не на границе. Поскольку он обозначает степень связности, локальные максимумы EVC фактически стремятся расположиться вдали от любых узлов, которые могут быть названы "граничными узлами". Кроме того, нет необходимости в определении значений на границе для дискретного случая: все узлы могут иметь значения EVC, определяемые уравнением (4) без введения значений в качестве "граничных условий".
Более конкретно, предлагаются следующие нововведения:
1) Две новые измененные формы матрицы смежности, которые дают два новых параметра центральности и позволяют проводить отбор сетевых центров.
2) Определение и способ идентификации сетевых областей.
3) Определения и способы назначения дискретных сетевых ролей каждому узлу в сети.
4) Применение новых единиц измерения центральности, областей и ролей в большом разнообразии приложений.
Примеры
Далее приводятся примеры вариантов осуществления настоящего изобретения, а также сравнения между двумя правилами определения областей.
На фиг.4, 5 и 6 показаны результаты научно-исследовательской работы MANA, представленные в [4]. Графы представляют небольшую социальную сеть - рабочую группу из 11 человек. На основе представленных способов измерения силы связи были получены индексы центральности на основе EVC для сети. Показатели центральности узлов выглядят на визуальном топографическом изображении как различия в высоте. На фиг.4 силы связей измеряются на основе числа различных носителей связи, используемых каждым узлом (способ 2). На фиг.5 представлен граф, силы связей в котором определяются на основе общей интенсивности потока между узлами (способ 3). Наконец, на фиг.6 представлен граф, который строится на основе сочетания вышеупомянутых способов определения сил связей, т.е. числа используемых сред и общей интенсивности потока (способ 4).
На фиг.2 показан простой граф с двумя центрами. Граница состоит из трех узлов. Один (узел 11) является транзитным узлом, который, очевидно, играет основную роль в соединении этих двух областей, остальные два узла являются пассивными.
Применение правила 2 к тому же графу дает результат, показанный на фиг.3. Можно видеть, что вся граница "поглощена" доминирующим центром (узел 9). Сравнительно периферийная роль узлов 10 и 12, ранее определенных как пассивные, теперь отражается в их расстоянии (2 перехода) от их центра (и, конечно, в их низком EVC).
Сравнение этих двух фигур, таким образом, подтверждает ожидания о различиях между двумя правилами: граничный набор с наличием пассивных узлов или без них, как правило, присутствует при использовании Правила 1, но отсутствует при использовании Правила 2.
Для иллюстрации применения этих принципов предположим, что узлами на фиг.2 и 3 являются пользователи в компьютерной сети, а связями - эффективные соединения между пользователями, по которым может проходить поток информации. Соединения названы "эффективными" ввиду того, что связи могут быть непрямыми: они могут устанавливаться через файлы, к которым имеют доступ по записи и чтению оба пользователя [3]. На основе анализа сразу можно заключить, что пользовательская система естественным образом состоит из двух основных групп. Кроме того, узел 9 является самым центральным в желтой группе, в то время как узел 13 является самым центральным для синей группы. Наконец, узел 11 является транзитным узлом, критичным для потока информации между двумя группами.
Предположим также, что представляет интерес безопасность этой небольшой системы. Тогда можно сразу указать, что узлы 9, 13, и 11 более всего нуждаются в защите от любых угроз системе. Должны быть защищены узлы 9 и 13, поскольку они являются центрами своих областей: в случае заражения такого узла имеется высокая вероятность заражения всей его области.
Кроме того, можно дать узлу 9 более высокий приоритет защиты по сравнению с узлом 13, так как его область имеет больший размер. Наконец, узел 11 нуждается в дополнительной защите: если он будет невосприимчив к угрозам, то не будет существовать готового канала их распространения из одной области в другую.
Следует отметить, что использование Правила 2 не предполагает выделения каких-либо граничных узлов для особой защиты даже при том, что узел 11, очевидно, играет важную роль в соединении этих двух областей. Однако в соответствии с Правилом 2 связь между 11 и 13 идентифицируется как транзитная связь. Очевидный вывод заключается в том, что узлы на каждом конце каждой транзитной связи нуждаются в специальных защитных мерах.
Эта проблема может быть и обратной: администратору необходимо обеспечить распространение требуемой информации по этой же небольшой сети. В этом случае на основе анализа предлагается эффективная стратегия решения этой задачи: вначале рассматриваются центры (узлы 9 и 13) и принимаются меры для широковещательного распространения требуемой информации от этих узлов.
Разумеется, следует ожидать, что правило расстояния и правило крутейшего восхождения дадут для некоторых узлов противоречивые результаты. Важный вывод, вытекающий из фиг.2-7, состоит в том, что общая качественная картина сравнительно нечувствительна к выбору правила определения областей. Можно ожидать, что это будет справедливо для большинства графов. Выбор центров не зависит от используемого правила; в свою очередь, эти центры существуют именно постольку, поскольку они находятся в области графа, имеющей некоторый "вес", т.е. некоторое число узлов, которые лучше связаны с друг другом, чем с их "окружением". Вкратце: различные правила, на первый взгляд определяющие области, фактически отличаются преимущественно тем, куда они помещают границы между областями, в то время как сами области являются довольно устойчивыми объектами.
Резюме определений ролей и областей в сетях
Основным критерием определения области (и ее центра) определена степень связности, измеряемая "гладкой" функцией графа, центральностью собственного вектора или EVC. В дополнение к определению естественных кластеров графа согласно описываемому подходу также производится назначение единственной роли каждому узлу в графе.
Два правила определения областей дают качественно сходную картину структуры графа в целом, но различные картины в терминах ролей узлов, присутствующих в анализе.
Именно Правило 1, по которому узлы привязываются к областям на основе только их удаленности от центров (в терминах наименьшего числа переходов), дает существенное число узлов в граничном наборе. Эти узлы, в свою очередь, могут быть отнесены к двум различным ролям: транзитные узлы и пассивные узлы (см. фиг.2). Правило 2 более близко к "топографической" природе подхода, описываемого в рамках данного приложения, и дает привязку узлов к центрам, с которыми они связаны путем крутейшего восхождения. Это правило обычно (в отсутствие специальной симметрии) не приводит к помещению каких-либо узлов в граничный набор; поэтому согласно Правилу 2 эти две роли (транзитные и пассивные узлы) по существу исключаются и все узлы являются либо центрами областей, либо элементами областей.
Можно установить и другие правила определения областей. Основная особенность подхода по настоящему изобретению состоит в том, что вначале идентифицируются центры, а затем области свободно "разрастаются" от этих центров. Оба правила в соответствии с настоящим изобретением соответствуют этому принципу. Подход Гирвана и Ньюмана позволяет иерархически разделять граф путем разбиения кластеров на подкластеры и т.д. Подобное иерархическое разделение также может выполняться согласно настоящему изобретению путем устранения граничных узлов и связей с последующим анализом полученных изолированных областей согласно настоящему изобретению. На основе описанных способов анализа могут быть определены дополнительные роли. В очень простом примере можно назначить узлам, связанным с граничными элементами (узлами или связями) роль "Край области". Другой тип роли Края может быть назначен узлам, являющимся "наиболее удаленными" от центра, но не связанным с какими-либо элементами границы.
Приложения
Далее описываются варианты применения способа и системы по настоящему изобретению. Очевидно, что наиболее центральные узлы и транзитные объекты (связи или узлы) могут быть выделены как требующие дополнительного внимания и принятия мер к предотвращению распространения повреждений. Наиболее центральные узлы скорее всего приведут к заражению своих областей; в свою очередь, транзитные объекты должны быть защищены соответствующим образом для предотвращения распространения инфекции из одной области в другие. Следовательно, целесообразно иммунизировать определенные элементы и таким образом гарантировать изоляцию инфекции в одной области. Для больших областей также целесообразно иммунизировать самые центральные узлы в каждой области, причем приоритет, разумеется, следует отдавать областям с наибольшим числом узлов. В некоторых случаях, например в одноранговых системах с высокой связностью, обеспечить защиту трудно, поскольку связь в них очень тесная. Это означает, что в каждой области имеется много узлов с примерно одинаковой центральностью и между областями есть много транзитных объектов (при наличии нескольких областей).
Использование описываемых системы и способа применимо ко многим другим типам графов - в принципе к любому неориентированному графу. Способ легко модифицируется, как описано в первом варианте осуществления, для связей с весами (помимо 0 и 1) между узлами. Способ и система по настоящему изобретению найдут применение в анализе социальных сетей, в которых можно (опять же) присвоить каждой связи (положительную) силу.
При представлении инновации (нового товара или услуги) населению распространение инновации происходит по стандартному образцу. Инновации обычно проходят апробацию в небольшой группе первых пользователей и через некоторое время, в зависимости от одобрения первых пользователей, инновации принимаются лидерами общественного мнения (или ведущими пользователями). Это - критический момент процесса распространения, поскольку принятие инновации большинством населения обычно зависит от ее одобрения лидерами общественного мнения [6]. Другими словами, принятие инновации приходит тогда, когда лидеры общественного мнения или социальные важнейшие узлы сети одобрят и примут эту инновацию.
Согласно способу, описанному в варианте осуществления и сопровождающих его примерах осуществления настоящего изобретения, используется измененная матрица смежности, основанная на данных потока, для вычисления меры центральности для каждого узла в социальной сети. Этот индекс центральности позволяет отбирать самые центральные узлы социальной сети, представленной данной матрицей смежности. В социальных сетях эти узлы - важнейшие узлы сети - соответствуют лидерам общественного мнения. Они, таким образом, являются оптимальными адресатами для распространения информации и т.д., поскольку они потенциально могут внести свой вклад в ускорение распространения этой информации. Очевидное приложение способа, таким образом, относится к сфере распространения инноваций.
Во вводном разделе упоминается эпидемиология, телекоммуникации, передача данных, системы передачи электроэнергии и т.д. Можно добавить, что результат анализа по настоящему изобретению имеет еще более широкий диапазон приложений. В качестве примера можно привести планирование расписаний в транспортных системах или системах транспортировки и распространения. Анализ потока трафика в дорожных сетях или железнодорожной системе позволяет установить наилучший расчет времени распространения с целью избежания пробок на дорогах. Аналогичным образом, планирование маршрутизации трафика в телекоммуникационных системах и системах передачи данных, как и планирование трафика в более широком смысле, является очевидным приложением настоящего изобретения, так как способ позволяет легко определять точки перегрузки или хорошие маршруты. На микроуровне он может использоваться при разработке компьютеров для анализа внутреннего трафика и, как следствие, оптимизации его компонентов и шин. Последнее применение особенно полезно в сфере параллельной обработки, поскольку позволяет уменьшить трафик между процессорами/компьютерами.
Следует отметить, что выше приведено подробное описание настоящего изобретения, однако следует понимать, что в пределы изобретения включаются соответствующие эквиваленты. Подробное описание в большой степени относится к теоретической стороне настоящего изобретения, однако эти теории имеют широкую область применения в случае неориентированных графов.
Таким образом, в общем случае способ по настоящему изобретению применим во множестве приложений и может использоваться для решения задач в этих сферах. Другие предпочтительные варианты осуществления настоящего изобретения описаны в зависимых пунктах прилагаемой формулы изобретения.
Библиография
1. G.D.BATISTA, P.EADES, R.TAMASSIA AND I.G.TOLLIS, Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, Upper Saddle River, New Jersey, 1999.
2. P.BONACICH, Factoring and weighting approaches to status scores and clique identification, Journal of Mathematical Sociology, 2 (1972), pp.113-120.
3. M.BURGESS, G.CANRIGHT AND K. ENGШ A graph theoretical model of computer security: from file access to social engineering. International Journal of Information Security, (2003). submitted for publication.
4. G.CANRIGHT, K.ENGШ - MONSEN AND Е. WELTZIEN, Multiplex structure of the communications network in a small working group, Social Networks - An International Journal of Structural Analysis, (2003) submitted for publication.
5. M.GIRVAN AND M.NEWMAN, Community structure in social and biological networks, Proc. Natl. Acad. Sci. USA, 99 (2002), pp.8271-8276.
6. E.M.ROGERS, Diffusion of Innovations. Free Press, Fifth Edition, 2003.
7. J.M.KLEINBERG, Authoritative sources in a hyperlinked environment, Journal of the ACM, 46 (1999), pp.604-632.
8. M.NEWMAN, The structure and function of complex networks, SIAM Review, 45 (2003), pp.167-256.
9. A.Y.NG, A.X.ZHENG AND M.I.JORDAN, Stable algorithms for link analysis, in Proc. 24th Annual Intl. ACM SIGIR Conference, ACM, 2001.
10. A.ORAM, ed., Peer-to-peer: Harnessing the Power of Disruptive Technologies, O'Reilly, Sebastopol, California, 2001.
11. L.PAGE, S.BRIN, R.MOTWANI AND T.WINOGRAD, The pagerank citation ranking: Bringing order to the web, tech. report, Stanford Digital Library Technologies Project, 1998.
12. R.PASTOR-SATORRAS AND A.VESPIGNANI, Epidemic spreading in scale-free networks, Phys. Rev. Lett., 86 (2001), pp.3200-3203.
13. Т.Н.STANG, F.POURBAYAT, M.BURGESS, G.CANRIGHT, K.ENGШ AND Ä. WELTZIEN, Archipelago: A network security analysis tool, in Proceedings of The 17th Annual Large Installation Systems Administration Conference (LISA 2003), San Diego, California, USA, October 2003.
14. G.Н.GOLUB AND С.Н.VAN LOAN, Matrix Computations. The Johns Hopkins University Press, Second Edition, 1989.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РАСПРОСТРАНЕНИЯ ИНФОРМАЦИИ И ПРЕДОТВРАЩЕНИЯ РАСПРОСТРАНЕНИЯ ИНФОРМАЦИИ В КОМПЬЮТЕРНОЙ СЕТИ | 2006 |
|
RU2408145C2 |
| СПОСОБ НЕЙРОСЕТЕВОЙ КЛАСТЕРИЗАЦИИ ПРОСТРАНСТВЕННО-РАСПРЕДЕЛЕННОЙ БЕСПРОВОДНОЙ СЕНСОРНОЙ СЕТИ | 2024 |
|
RU2836294C1 |
| СПОСОБ И СИСТЕМА ФОРМИРОВАНИЯ КЛАСТЕРОВ УЗЛОВ В КОМПЬЮТЕРНОЙ СЕТИ | 2023 |
|
RU2821054C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ СЕТИ СВЯЗИ С ПАМЯТЬЮ | 2020 |
|
RU2734503C1 |
| СПОСОБ И СИСТЕМА АВТОМАТИЧЕСКОГО ФОРМИРОВАНИЯ МУЛЬТИМОДАЛЬНЫХ СЕРВИСОВ ГРУЗОПЕРЕВОЗОК В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ | 2018 |
|
RU2695051C1 |
| СИСТЕМА И СПОСОБ ВЫЯВЛЕНИЯ ВЗАИМОДЕЙСТВИЯ И ВЛИЯНИЯ В СЕТЯХ | 2016 |
|
RU2742457C2 |
| Способ нахождения надежных кратчайших путей в сети связи | 2019 |
|
RU2700547C1 |
| Способ выбора безопасного маршрута в сети связи общего пользования | 2016 |
|
RU2640627C1 |
| Способ контроля состояния логической структуры сети связи | 2018 |
|
RU2672137C1 |
| СПОСОБ ВЫБОРА БЕЗОПАСНОГО МАРШРУТА В СЕТИ СВЯЗИ (ВАРИАНТЫ) | 2007 |
|
RU2331158C1 |

Изобретение относится к области сетей передачи данных. Технический результат заключается в идентификации физических или логических связей как физической сети, так и логической сети. Сущность изобретения заключается в том, что сеть содержит множество сетевых узлов, соединенных связями. Способ включает в себя: составление карты топологии сети, вычисление значений силы связи между узлами, вычисление индекса центральности собственного вектора для всех узлов на основе указанных значений силы связи; идентификацию узлов, имеющих локально максимальные индексы центральности собственного вектора, как центральных узлов; группирование узлов в области, окружающие каждый идентифицированный центральный узел; назначение роли каждому узлу в зависимости от его положения в области: центральный узел, элемент области, граничный узел, транзитный узел, пассивный узел; измерение способности сети к распространению на основе числа областей, их размера и структуры связей между ними, назначение роли элементов области в данной области всем узлам, для которых путь крутейшего возрастания на карте топологии заканчивается единственным образом на центральном узле этой области. 16 з.п. ф-лы, 7 ил.
1. Способ управления способностью сети к передаче информационного или физического графика, причем указанная сеть содержит ряд сетевых узлов, соединенных связями, включающий в себя следующие шаги:
составляют карту топологии сети;
вычисляют значения силы связи между узлами;
вычисляют индексы центральности собственного вектора для всех узлов на основе указанных значений силы связи;
назначают роль центрального узла узлам, представленным локальными максимумами вычисленного индекса центральности собственного вектора;
определяют область для каждого центрального узла;
назначают роль элемента области каждому узлу, который может быть ассоциирован единственным образом с единственным центральным узлом посредством однозначного правила;
управляют способность сети к распространению на основе числа областей, их размера и структуры связей между ними;
отличающийся тем, что указанное однозначное правило представляет собой правило крутейшего возрастания, в котором путь крутейшего возрастания для элементов области на карте топологии заканчивается единственным образом на центральном узле этой области.
2. Способ по п.1, отличающийся тем, что значение указанной силы связи вычисляют путем подсчета числа различных типов носителей, используемых при взаимодействии в любой паре узлов, причем в качестве единицы измерения силы связи используется число носителей.
3. Способ по п.1, отличающийся тем, что значение указанной силы связи вычисляют путем измерения графика между любыми двумя узлами, причем в качестве единицы измерения силы связи используется единица измерения графика.
4. Способ по п.1, отличающийся тем, что значение указанной силы связи вычисляют путем измерения графика в каждой паре узлов для каждого типа носителя посредством деления интенсивности графика в каждом типе носителя на полный график для данного типа носителя связи, после чего сумма полученных долей используется в качестве единицы измерения силы связи.
5. Способ по любому из пп.1-4, отличающийся тем, что указанные значения сил связей организуют в матрицу, матрицу смежности, и вычисляют индекс центральности собственного вектора как главный собственный вектор указанной матрицы смежности.
6. Способ по п.1, отличающийся тем, что всем узлам, не имеющим однозначной привязки к какому-либо центральному узлу, присваивают роль граничных узлов.
7. Способ по п.1, отличающийся тем, что всем узлам, для которых путь крутейшего на карге топологии заканчивается на двух или более центральных узлах, и находящимся по меньшей мере на одном не обратно-связном пути, соединяющем два центральных узла, присваивают роль транзитных узлов.
8. Способ по п.1, отличающийся тем, что всем узлам, для которых путь крутейшего на карге топологии заканчивается на двух или более центральных узлах, не находящимся на не обратно-связном пути, соединяющих два центральных узла, присваивают роль пассивных узлов.
9. Способ по п.1, отличающийся тем, что шаг управления включает в себя предотвращение распространения вирусов или вредной информации в указанной сети посредством определения нуждающихся в защите узлов.
10. Способ по п.1, отличающийся тем, что шаг управления включает в себя повышение восприимчивости сети к распространению информации.
11. Способ по п.1, отличающийся тем, что шаг управления включает в себя адаптацию архитектуры указанной сети с целью повышения по меньшей мере одного из следующих параметров: надежность, безопасность, эффективность связи в указанной сети.
12. Способ по п.1, отличающийся тем, что сеть представляет собой силовую сеть передачи электроэнергии, и шаг управления включает в себя повышение надежности указанной сети передачи электроэнергии.
13. Способ по п.1, отличающийся тем, что сеть представляет собой сеть распространения товаров и шаг управления включает в себя планирование распространения указанных товаров.
14. Способ по п.1, отличающийся тем, что сеть представляет собой транспортную сеть, и шаг управления включает в себя планирование указанной транспортной сети.
15. Способ по п.1, отличающийся тем, что дополнительно включает в себя шаг выборочного определения узлов для предотвращения распространения вредоносной информации в указанной сети.
16. Способ по п.7, отличающийся тем, что дополнительно включает в себя идентификацию связи между узлами, находящимися в двух различных областях, как транзитной связи, а также предотвращение распространения вредоносной информации или физического трафика посредством осуществления защитных мер для узлов, выбранных из по меньшей мере следующих: центральные узлы, граничные узлы, узлы, соединенные непосредственно по меньшей мере одной транзитной связью.
17. Способ по п.1, отличающийся тем, что шаг управления включает в себя выбор по меньшей мере одного из указанных центральных узлов и распространение информации от указанного по меньшей мере одного узла.
| WO 03075516 A1, 12.09.2003 | |||
| СПОСОБ АДМИНИСТРИРОВАНИЯ СЕТЕВЫХ КОМПЬЮТЕРНЫХ ПРИЛОЖЕНИЙ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ (ВАРИАНТЫ) | 1995 |
|
RU2143183C1 |
| US 2001049790 A1, 06.12.2001 | |||
| ВИБРАЦИОННАЯ УСТАНОВКА ДЛЯ ВЫГРУЗКИ СЫПУЧИХ ГРУЗОВ ИЗ КРЫТЫХ ЖЕЛЕЗНОДОРОЖНЫХ ВАГОНОВ | 0 |
|
SU211391A1 |
Авторы
Даты
2010-07-10—Публикация
2004-12-29—Подача