Изобретение относится к области телекоммуникационных сетей связи и может быть использовано для работы в составе контроллера маршрутизации.
Из уровня техники известен способ многопутевой маршрутизации, который включает этапы, на которых принимают промежуточной системой поток трафика данных, вычисляют два или более надежных маршрута в сети связи, для этого используют композицию алгоритмов Дейкстры, строят усеченное дерево событий, заполняют таблицы маршрутизации для двух или более надежных узлов в порядке уменьшения их надежности, формируют вектор величин расщепления потока трафика данных на два или более субпотоков с учетом вычисленных надежных маршрутов сети связи, пропускной способности каналов связи, загрузки каналов связи, расщепляют в промежуточной системе каждый поток на два или более субпотоков, маршрутизируют протокольные блоки данных или байты каждого, рекомбинируют в промежуточной системе каждый поток трафика данных, передают от промежуточной системы потоки трафика данных в оконечную систему получателя (патент РФ № 2636665, 27.11.2017).
Недостатком описанного в патенте способа нахождения надежных маршрутов (путей) в сети связи является невысокая скорость вычисления системой кратчайших маршрутов в сети связи. Это обусловлено тем, что для вычисления кратчайших маршрутов требуется многократный запуск алгоритма Дейкстры, для каждого ответвления дерева состояний. Таким образом, указанный способ характеризуется невысокой скоростью проведения расчетов.
Другим недостатком описанного в патенте способа является то, что при вычислении надежных маршрутов связи используется алгоритм Дейкстры, в котором матрица смежности, описывающая взвешенный граф, не учитывает кратные линии связи (ребра) между узлами сети. Таким образом, при соединении двух между собой двух узлов более, чем одной линией связи, указанный способ может не дать нужный результат, в результате чего снижается точность определения кратчайших надежных маршрутов и, как следствие, надежность способа в целом. Таким образом, возможность работы с сетями связи, содержащими кратные линии связи с применением указанного способа затруднена.
Еще одним недостатком описанного в патенте способа является то, в используемом алгоритме Дейкстры для расчета надежных k путей с использованием матрицы смежности в качестве весов ребер используется только один параметр – вероятность работоспособного состояния. Таким образом, применение алгоритма Дейкстры не позволяет учитывать более одного параметра, что существенно сужает функциональные возможности способа
Техническим результатом изобретения является повышение эксплуатационных характеристик способа, что достигается за счет ускорения процесса определения надежных кратчайших путей в сети связи, повышение надежности способа за счет точности расчета кратчайших маршрутов в сети связи, расширение функциональных возможностей способа.
Указанный технический результат достигается в способе нахождения надежных кратчайших путей в сети связи, заключающемся в том, что осуществляют алгоритм двойного поиска с помощью процессора, содержащего программное обеспечение, при этом алгоритм двойного поиска включает
формирование графа, содержащего в качестве вершин узлы сети связи, а в качестве ребер - функцию начального узла ребра, конечного узла ребра, весового вектора, при этом, ребра графа связывают вершины, а в качестве метрик ребер используют весовой вектор с последующим
формированием из графа матрицы расстояний (Матрицы DLU), каждый элемент которой представляет собой упорядоченный по возрастанию весового вектора набор путей до некоторого узла (или структура NodePathSet), учитывающей кратные дуги и весовые вектора W для каждой дуги,
инициализируют массивы данных матрицы расстояний (Матрицы DLU) и вектора наборов путей от начального узла до всех остальных узлов графа (вектора E, E1), с занесением в элемент Матрицы расстояний весового вектора ребра, соединяющего каждую пару вершин в графе,
формируют дополнительные матрицы, одна из которых содержит поддиагональные элементы матрицы расстояний и элементы, заполненные наборами пустых путей с бесконечными весами (W_INF) (Матрица L), а вторая содержит наддиагональные элементы матрицы расстояний и элементы, заполненные наборами пустых путей с бесконечными весами (W_INF) (Матрица U),
при этом массивы данных матрицы расстояний инициализируют на основе весов ребер, соединяющих каждую пару вершин в графе, а вектора наборов путей от начального узла до всех остальных узлов графа E, E1 инициализируют множеством пустых путей с бесконечными весами (W_INF),
последовательно запускают алгоритм обратного поиска, обрабатывающего элементы Матрицы L и элементы векторов E, E1 и алгоритм прямого поиска, обрабатывающего элементы Матрицы U и элементы векторов E, E1,
осуществляют проверку условий окончания итераций,
в случае положительной проверки завершают итерации и получают множество К кратчайших и надежных путей, упорядоченных по приоритету,
в случае отрицательной проверки условий окончания итераций осуществляют повторный запуск алгоритмов.
Оконечные и промежуточные системы представляют собой абстрактное представление технических средств (устройства коммутации и маршрутизации), удовлетворяющих тем требованиям стандартов ВОС, которые необходимы для функционирования открытой системы.
Все стадии алгоритма двойного поиска, в частности: формирование графа, матрицы расстояний, инициализация массивов данных, формирование дополнительных матриц, осуществление прямого и обратного поисков, осуществление проверки условий окончания итераций реализуются программно.
Все структуры, используемые для проведения вычислений в алгоритме двойного поиска: структура, описывающая путь до некоторого узла NodePath, список смежных ребер, представляющий путь от одного узла до другого P = (e_1, e_2…), весовой вектор W = (w_1,…,w_n), упорядоченный набор из K путей до некоторого узла: NodePathSet = (NodePath_1, …, NodePath_K), NodePath_i – структура типа NodePath, вектора наборов путей от начального узла BeginNode до всех остальных узлов графа E, E1 = (V_1, …, V_Nodes), вектор бесконечных весов размером n W_INF = (INF, …, INF), ребро e_i представляющее собой структуру
e_i = (node_begin, node_end, weights), также формируются программно автоматически из исходных данных, поступающих в программу.
В качестве исходных данных в системе содержатся следующие данные: число узлов в графе (Nodes), число ориентированных ребер в графе (Edges), вектор максимально допустимого отклонения весов (DeltaMetrics), начальный узел для поиска путей (BeginNode), искомое число путей (K), номер начального узла ребра (node_begin), номер конечного узла ребра (node_end), весовой вектор типа W (weights ), Graph – структура данных, описывающая структуру графа и представляющая собой вектор ребер Graph = (e_1,…,e_Edges).
Алгоритм двойного поиска, реализуемый в изобретении построен на векторных и матричных вычислениях. Каждый вектор – это метрика, приписываемая каждому ребру графа и каждому пути в графе. Таким образом, веса ребер графа представляют собой не скалярные значения, а векторы величин различной физической природы. Поиск К кратчайших путей по векторному критерию при реализации алгоритма двойного поиска может осуществляться с использованием весового вектора W.
Количество векторных метрик может быть любым, но одинаковым для всех ребер.
При этом, векторные и матричные вычисления, на которых построен алгоритм, могут быть реализованы с помощью параллельных программно-аппаратных вычислителей, что позволяет существенно повысить скорость находжения К надежных кратчайших путей в сети связи.
Применение в способе векторной метрики для поиска К кратчайших путей позволяет реализовывать алгоритм двойного поиска кратчайших путей с осуществлением поиска не по одному параметру, а по набору параметров, в результате чего достигается расширение функциональных возможностей способа.
Как правило, для реализации алгоритмов поиска путей в графе в качестве метрики используется один параметр – число хопов (ребер в пути) или время задержки пакетов. Однако, в настоящем изобретении в процессе осуществления алгоритма в качестве векторной метрики может использоваться целый набор разнородных параметров, например, измеряемые технические параметры (например, пропускная способности, время задержки, джиттер), стоимостные показатели или иные показатели, определяемые оператором телекоммуникационной сети. Это обусловлено возможностью применения векторной метрики в способе. При этом, возможно изменение вектора параметров при каждом запуске алгоритма в зависимости от потребности и задач. В результате применения векторной метрики в способе также возможно сделать отдельные параметры более значимыми или менее значимыми.
Таким образом, при реализации способа может учитываться большее число критериев для поиска путей, что позволяет достичь ускорения процесса определения надежных кратчайших путей в сети связи и, таким образом, приводит к повышению эксплуатационных характеристик способа в целом, а также повышения точности получения результата расчета кратчайших надежных маршрутов в сети связи, что приводит к повышению надежности способа. Кроме того, значимость критериев можно менять от запуска к запуску алгоритма без его перестройки.
Осуществление в алгоритме прямого и обратного поиска (в том числе при учете срезу нескольких критериев для поиска путей с использованием в качестве векторной метрики набора разнородных параметров) позволяет помимо ускорения процесса находить кратчайшие пути в сети связи с высокой степенью надежности. Кроме того, реализация алгоритма двойного поиска позволяет добиться ускорения процесса и, как следствие, эксплуатационных характеристик способа также за счет отсутствия необходимости многократного запуска алгоритма. Указанный алгоритм позволяет автоматически осуществлять прямой и обратный поиск надежный кратчайших путей до момента положительной проверки условий окончания итераций. Таким образом, алгоритм запускается однократно.
Настоящий способ нахождения надежных кратчайших путей в сети связи
обеспечивает возможность работы с сетями связи, содержащими кратные линии связи, а именно, в случае, когда два узла соединены между собой более, чем одной линией связи. При этом, несмотря на наличие кратных линий связи в настоящем способе обеспечивается точный расчет кратчайших надежных маршрутов в сети связи, что приводит к повышению надежности способа. Это обеспечивается тем, что среди множества линий связи, соединяющих два узла, процессором выбирается та из них, которая обладает меньшим весом. При этом, сравнение весовых векторов осуществляется процессором лексикографически, путем применения к векторам операции A lexE<B. Таким образом, возможность работы с сетями связи, содержащими кратные линии связи в настоящем способе также обеспечивает расширение функциональных возможностей способа.
Лексикографическое сравнение предусматривает следующие операции, осуществляемые процессором:
1. Операция лексикографического сравнения «меньше» над векторами весов W с учетом допустимого отклонения DeltaMetrics:
A lexE< B.
Исходные данные: A = (a1,…, an), B = (b1,…, bn) – весовые вектора типа W,
E = (e1,…,en) – вектор допустимых отклонений типа DeltaMetrics.
Результатом сравнения является логическое значение true/false.
При сравнении двух векторов типа W учитываются два правила.
1) Сравнение производится поэлементно в порядке следования компонентов вектора (т.е. учитывается их приоритет). Сначала сравниваются значения a1 и b1. Если a1 < b1, то дальнейшие сравнения не производятся, результат операции равен true. Если a1 > b2, то дальнейшие сравнения не производятся, результат операции равен false. Если a1 = b1, далее сравниваются значения a2 и b2 по тем же правилам. Переход к следующим компонентам векторов происходит в случае равенства предыдущих. Если an = bn, то результат операции равен false.
2) При сравнении двух компонент векторов учитывается их допустимое отклонение, задаваемое вектором E. Таким образом, если отклонение компонентов ai и bi друг от друга не превышает величину ei, то они считаются равными.
Алгоритм выполнения операции A lexE< B:
Для каждого i := 0…n:
Если |ai - bi| > ei то
Если bi > ai то
Результат := true
Иначе
Результат := false
Результат := false
2. Операция сравнения «меньше» над структурами NodePath:
A < B
Операнды A и B – структуры типа NodePath.
Результатом сравнения является логическое значение true/false.
Правило выполнения:
Операнды сравниваются по компоненту W структуры NodePath с помощью операции lexE<, т.е.
A.W lexE< B.W
При этом используется общий для всей сети вектор допустимых отклонений E.
3. Обобщенная операция минимизации:
C = common_min (A,B).
Операнды A и B – векторы типа NodePathSet размера K.
Результат C – вектор типа NodePathSet размера K.
Правило выполнения:
1) Строится множество S(A,B), состоящее из всех компонентов двух исходных векторов.
2) Множество S(A,B) сортируется по возрастанию. Для сортировки используется любой известный метод. В ходе сортировки сравнение элементов множества S(A,B) между собой осуществляется с помощью операции «меньше» над структурами NodePath (см. п.2).
3) Из множества S(A,B) удаляются элементы с одинаковыми весами.
4) Строится результирующий вектор C, составленный из первых K элементов множества S(A,B). Если множество S(A,B) содержит меньше K элементов, то недостающие компоненты вектора С заполняются структурами NodePath с весовым вектором W_INF.
Примеры (для упрощения, не искажая смысла операций, компоненты векторов A и B представлены только скалярными весами):
A = [-4, 0, 1, INF]
B = [1, 7, 8, 9]
S(A,B) = [-4, 0, 1, INF, 1, 7, 8, 9]
C = [-4, 0, 1, 7]
A = [1, INF, INF, INF]
B = [2, INF, INF, INF]
S(A,B) = [1, INF, INF, INF, 2, INF, INF, INF]
C = [1, 2, INF, INF]
4. Конкатенация путей:
C = concat(A,B)
Исходные данные: A = (a1,…, an), B = (b1,…, bm) – списки смежных ребер типа P.
Результат C = (a1,…, an, b1,…, bm) – список смежных ребер типа P.
Правило выполнения: результирующий путь C формируется путем добавления к списку ребер A списка ребер B.
5. Обобщенная операция сложения:
C = common_sum (A,B).
Операнды A и B – векторы типа NodePathSet размера K.
Результат C – вектор типа NodePathSet размера K.
Правило выполнения:
1) Строится множество S(A,B), состоящее из всех попарных сумм компонент двух исходных векторов. При вычислении каждой попарной суммы учитываются компоненты P и W структуры NodePath. При этом к компонентам P применяется операция конкатенации путей, а к компонентам W – операция поэлементного сложения двух векторов.
2) Множество S(A,B) сортируется по возрастанию. Для сортировки используется любой известный метод. В ходе сортировки сравнение элементов множества S(A,B) между собой осуществляется с помощью операции «меньше» над структурами NodePath (см. п.2).
3) Из множества S(A,B) удаляются элементы с одинаковыми весами.
4) Строится результирующий вектор C, составленный из первых K элементов множества S(A,B). Если множество S(A,B) содержит меньше K элементов, то недостающие компоненты вектора С заполняются структурами NodePath с весовым вектором W_INF.
Примеры (для упрощения, не искажая смысла операций, компоненты векторов A и B представлены только скалярными весами):
A = [-4, 0, 1, INF]
B = [1, 7, 8, 9]
S(A, B) = [-3, 1, 2, INF, 3, 7, 8, INF, 4, 8, 9, INF, 5, 9, 10, INF]
C = [-3, 1, 2, 3]
A = [1, INF, INF, INF]
B = [2, INF, INF, INF]
S(A, B) = [3, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF, INF,]
C = [3, INF, INF, INF]
Векторные метрики являются элементами более крупных структур – матрицы расстояний (Матрицы DLU) и векторов E, E1. Матрица DLU хранит векторы весов и список ребер K кратчайших путей до каждой вершины графа на текущем шаге итераций. Векторы E, E1 являются вспомогательными и используются для преобразования матрицы DLU на прямом и обратном шаге.
Матрица DLU и векторы E, E1 инициализируются исходя из значений векторных метрик ребер графа. В ходе работы алгоритма происходит итерационное преобразование матрицы DLU и векторов E, E1 до достижения результата. На каждой итерации алгоритма улучшаются кратчайшие пути до каждой из вершин графа, и, соответственно, пересчитываются их векторы весов.
Способ предназначен для реализации на ЭВМ и осуществляется следующим образом.
Вычисляют два или более маршрута в сети связи с помощью процессора, содержащего программное обеспечение, при этом используют алгоритм двойного поиска.
Алгоритм двойного поиска заключается в следующем.
Исходные данные, характеризующие сеть связи, содержащую совокупность из Х узлов, поступают в систему, после чего система, на основе исходных данных представляет сеть связи в виде графа (Graph) с использованием весового вектора W = (w_1,…,w_n) в качестве метрик ребер и путей в графе, где n – размер весового вектора, каждая величина w_i – целое или вещественное число,
При этом вершины графа представляют собой узлы сети связи. В качестве ребер граф содержит функцию начального узла ребра, конечного узла ребра, весового вектора, то есть, каждое ребро e_i представляет собой структуру (node_begin, node_end, weights), где
node_begin – номер начального узла ребра;
node_end – номер конечного узла ребра;
weights – весовой вектор типа W.
Размер весового вектора является одинаковым и постоянным для всех векторов.
Таким образом, каждое ребро e_i графа соединяет два смежных узла и характеризуется весовым вектором W = (w_1,…,w_n). Каждый вес w_i представляет собой числовой параметр линии связи. В качестве параметров линии связи могут использоваться:
- пропускная способность;
- время задержки;
- вероятность работоспособного состояния
- стоимость аренды.
Если в качестве i-го параметра линии используется пропускная способность, то в качестве веса w_i необходимо использовать эквивалентную величину
w_i = 1/q_i,
где q_i – пропускная способность линии.
Если в качестве i-го параметра линии используется вероятность работоспособного состояния, то в качестве веса w_i необходимо использовать эквивалентную величину
w_i = -ln(/p_i),
где p_i – вероятность работоспособного состояния линии.
Веса в векторе W должны быть упорядочены по приоритету.
Веса должны удовлетворять следующим условиям:
- аддитивность (или должны быть конвертированы к аддитивному виду); вес пути рассчитывается как сумма весов составляющих его смежных ребер;
- веса в векторе должны быть упорядочены по приоритету метрик. Пути сравниваются между собой лексикографически, т.е. путем последовательного сравнения весов в соответствии с приоритетом до первого найденного доминирования одного веса над другим (подробнее описано ниже);
- веса должны быть нормированы по критерию минимума, т.е. должно выполняться правило "меньший вес-лучше".
- однородность относительно ребер (т.е. набор весов должен быть одинаков для всех ребер графа).
Веса представляют собой вещественные числа или значения «бесконечность». Для обозначения бесконечного веса используется специальное значение INF, которое можно задать программно с помощью специального кода (например, 0xFFFFFFFF).
Для каждого узла графа создают упорядоченный по возрастанию весового вектора W упорядоченный набор из K путей до некоторого узла (структура NodePathSet). Для этого, упорядоченный набор из K путей до некоторого узла рассчитывают, как:
NodePathSet = (NodePath_1, …, NodePath_K),
где NodePath_i – структура типа NodePath,
NodePath - структура, описывающая путь до некоторого узла и равная (P, W),
где P – путь от начального узла BeginNode (начальный узел для поиска путей) до данного узла (список смежных ребер, представляющий путь от одного узла до другого) и равный (e_1, e_2…),
а e_i – номер ребра, при этом размер списка ребер – от 1 до Edges (число ориентированных ребер в графе. Если в графе есть неориентированные ребра, то они заменяются на два ориентированных – в прямом и обратном направлении);
W – весовой вектор пути P, рассчитывается как сумма векторов весов всех ребер пути.
Два вектора наборов путей от начального узла BeginNode до всех остальных узлов графа E, E1 равны (V_1, …, V_Nodes),
где каждый V_i – это структура типа NodePathSet.
Таким образом, для каждого узла графа создается упорядоченный по возрастанию весового вектора W набор путей NodePathSet.
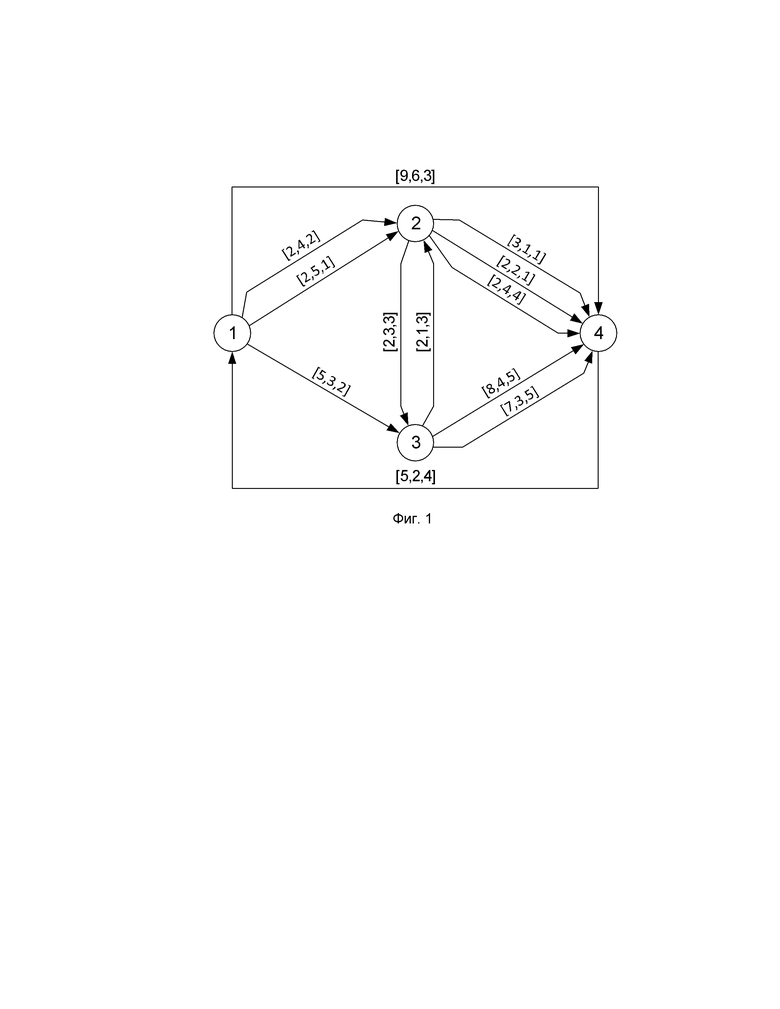
На фиг. 1 отражен пример структуры сети связи, узлы которой представлены вершинами графа и которая используется для построения матрицы расстояний. Линии связи представлены ориентированными дугами. Некоторые дуги кратные. Вес каждой дуги представлен вектором из трех значений.
Далее формируют матрицу расстояний - Матрицу DLU из исходного графа Graph. Graph является структурой данных, описывающей структуру графа и представляет собой вектор ребер Graph = (e_1,…,e_Edges). Размер вектора равен Edges.В процессе вычислений матрица расстояний DLU не изменяется. Матрица расстояний DLU – квадратная матрица размером Nodes x Nodes. При этом, Nodes – число узлов в графе. Каждый узел имеет порядковый номер от 1 до Nodes.
Матрица расстояний имеет вид: Матрица DLU = { D_i_j }, где i и j - номера узлов связи в графе. Каждый элемент матрицы D_i_j представляет собой структуру типа NodePathSet. Эта структура содержит K путей, содержащих только по одному ребру, соединяющих узлы с номерами i и j. Матрица DLU является аналогом матрицы весов, описывающей взвешенный граф, но учитывающий кратные дуги сети связи и весовой вектор W для каждой дуги. Структура NodePathSet в элементе D_i_j содержит упорядоченный набор линий связи, соединяющих два узла.
Ниже приведен пример матрицы расстояний, построенной на основе сети связи, представленной в виде графа и отраженной на фиг.1 (Пример Матрицы DLU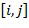 ).
).

Каждый элемент матрицы 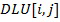
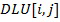 представляет собой упорядоченный массив из К (К – количество искомых путей) весовых векторов W. Каждый весовой вектор описывает отдельную линию связи, ведущую из вершины i в вершину j. Так, например, элемент
представляет собой упорядоченный массив из К (К – количество искомых путей) весовых векторов W. Каждый весовой вектор описывает отдельную линию связи, ведущую из вершины i в вершину j. Так, например, элемент
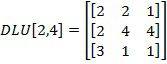
представляет собой 3-х кратную дугу, ведущую из вершины 2 в вершину 4 Веса дуг лексикографически упорядочены по возрастанию. Лексикографическое правило определяется операцией A lexE< B.
Далее инициализируют массивы данных DLU, E, E1. Перед началом итераций осуществляется инициализация массивов DLU, E, E1. Для инициализации используют исходные данные, поступившие на вход – структура Graph.
DLU инициализируют на основе весов ребер, соединяющих каждую пару вершин в графе. В элемент матрицы D_i_j заносится весовой вектор ребра, соединяющего пару узлов: i и j. Если узлы i и j соединены более, чем одним ребром, то в D_i_j заносится множество весовых векторов соответствующих ребер. Если узлы i и j не соединены ни одним ребром, то соответствующий элемент матрицы D_i_j содержит множество пустых путей с бесконечными весами W_INF.
Векторы E и E1 инициализируются множеством пустых путей с бесконечными весами W_INF.
Далее запускают алгоритм двойного (прямого и обратного) поиска, который осуществляют с использованием программного обеспечения.
Для реализации алгоритма двойного поиска используют две вспомогательные квадратные матрицы – L и U, каждая размером Nodes x Nodes.
Матрица L содержит поддиагональные элементы матрицы DLU, остальные элементы (диагональ) заполнены наборами пустых путей с весами W_INF (бесконечными векторами). Под пустыми путями подразумевается последовательность вершин, в которой вершины соединены между собой путями без ребер.
Матрица L, построенная на основе Матрицы DLU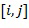
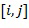 (Пример Матрицы DLU
(Пример Матрицы DLU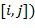
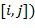 , имеет вид:
, имеет вид:

Матрица U содержит наддиагональные элементы матрицы DLU, остальные элементы (диагональ) заполнены наборами пустых путей с весами W_INF (бесконечными векторами), где W_INF = (INF, …, INF) - вспомогательная структура – вектор бесконечных весов размером n, а каждый элемент INF представляет собой значение бесконечности, которое можно задать программно с помощью специального кода (например, 0xFFFFFFFF). Матрица U, построенная на основе Матрицы DLU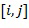
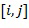 (Пример Матрицы DLU
(Пример Матрицы DLU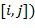
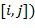 , имеет вид:
, имеет вид:

Для хранения матриц L и U дополнительная память может не выделяться, так как они легко могут быть получены непосредственно из матрицы DLU 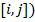
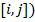 .
.
Строки матрицы L обрабатываются в обратном порядке: от последней к первому (шаг обратного поиска).
Шаг прямого поиска обрабатывает строки матрицы U в прямом порядке.
Шаг обратного поиска выполняется в соответствие со следующим алгоритмом:
Для каждого i от Nodes до 1:
Для каждого j от 1 до Nodes:
M := common_sum (E1j,Lij)
S := common_min (S,M)
E1i := common_min (S,Ei)
где:
Lij – элементы вспомогательной матрицы L, содержащей поддиагональные элементы матрицы DLU,
Ei и E1i – элементы векторов E и E1 соответственно.
Шаг прямого поиска выполняется в соответствие со следующим алгоритмом:
Для каждого i от 1 до Nodes:
Для каждого j от 1 до Nodes:
M := common_sum (Ej,Uij)
S := common_min (S,M)
Ei := common_min (S,E1i),
где
Uij – элементы вспомогательной матрицы U, содержащей наддиагональные элементы матрицы DLU,
Ei и E1i – элементы векторов E и E1 соответственно.
На каждой итерации векторы E и E1 изменяют свои значения. При этом предыдущие значения не сохраняются.
При этом, программное обеспечение осуществляет проверку условия окончания итераций путем проверки равенства векторов E и E1. Если векторы равны, то вычисления прекращаются. В противном случае выполняется еще один шаг итераций.
Программное обеспечение сравнивает вектора E и E1 сравниваются поэлементно. Вектора считаются равными при попарном равенстве всех их элементов. Если хотя бы одна пара элементов не равна, то вектора E и E1 считаются неравными.
В свою очередь, сравнение элементов векторов E и E1 также осуществляют поэлементно, поскольку они представляют собой множества типа NodePathSet. Поэлементное сравнение двух множеств NodePathSet выполняется относительно весовых векторов W структур NodePath.
Для сравнения двух весовых векторов W структур NodePath используется операция лексикографического сравнения «меньше» lexE< .
Результат вычислений представляет полученный в результате итераций вектор Е1, содержащий множество К найденных кратчайших и надежных путей, упорядоченных по приоритету.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ распределения симметричных ключей между узлами вычислительной сети с системой квантового распределения ключей | 2021 |
|
RU2764458C1 |
| СПОСОБ СТРУКТУРНО-ФУНКЦИОНАЛЬНОГО СИНТЕЗА ЗАЩИЩЕННОЙ ИЕРАРХИЧЕСКОЙ СЕТИ СВЯЗИ | 2013 |
|
RU2547627C2 |
| СИСТЕМА И СПОСОБ КОДИРОВАНИЯ ПРОИЗВОЛЬНО РАСПРЕДЕЛЕННЫХ ПРИЗНАКОВ В ОБЪЕКТЕ | 2005 |
|
RU2386168C2 |
| СПОСОБ МНОГОПУТЕВОЙ МАРШРУТИЗАЦИИ С ИСПОЛЬЗОВАНИЕМ РАСЩЕПЛЕНИЯ ПОТОКА ТРАФИКА ДАННЫХ | 2017 |
|
RU2636665C1 |
| СПОСОБ И СИСТЕМА ЦИКЛИЧЕСКОГО РАСПРЕДЕЛЕННОГО АСИНХРОННОГО ОБМЕНА СООБЩЕНИЯМИ СО СЛАБОЙ СИНХРОНИЗАЦИЕЙ ДЛЯ РАБОТЫ С БОЛЬШИМИ ГРАФАМИ | 2021 |
|
RU2761136C1 |
| СПОСОБ УСТОЙЧИВОЙ МАРШРУТИЗАЦИИ ДАННЫХ В ВИРТУАЛЬНОЙ СЕТИ СВЯЗИ | 2021 |
|
RU2757781C1 |
| СПОСОБ ИНТЕГРАЦИИ ПРОФИЛЕЙ ПОЛЬЗОВАТЕЛЕЙ ОНЛАЙНОВЫХ СОЦИАЛЬНЫХ СЕТЕЙ | 2011 |
|
RU2469389C1 |
| СПОСОБ НЕЙРОСЕТЕВОЙ КЛАСТЕРИЗАЦИИ БЕСПРОВОДНОЙ СЕНСОРНОЙ СЕТИ | 2014 |
|
RU2571541C1 |
| СПОСОБЫ И СИСТЕМЫ СЕГМЕНТАЦИИ ДОКУМЕНТА | 2018 |
|
RU2697649C1 |
| СПОСОБ И СИСТЕМА ДЛЯ ДИСТАНЦИОННОГО ВЫБОРА ОДЕЖДЫ | 2020 |
|
RU2805003C2 |
Изобретение относится к области сетей связи. Технический результат - ускорение процесса определения надежных кратчайших путей в сети связи и повышение точности расчета кратчайших маршрутов в сети связи. Для этого, в частности, в способе нахождения надежных кратчайших путей в сети связи осуществляют алгоритм двойного поиска с помощью процессора, содержащего программное обеспечение, где в алгоритме двойного поиска формируют граф, формируют из графа матрицы расстояний (Матрицы DLU), каждый элемент которой представляет собой упорядоченный по возрастанию весового вектора набор путей до некоторого узла (или структура NodePathSet), инициализируют массивы данных матрицы расстояний (Матрицы DLU) и вектора наборов путей от начального узла до всех остальных узлов графа (вектора E, E1) с занесением в элемент Матрицы расстояний весового вектора ребра, соединяющего каждую пару вершин в графе. 1 ил.
Способ нахождения надежных кратчайших путей в сети связи, характеризующийся тем, что осуществляют алгоритм двойного поиска с помощью процессора, содержащего программное обеспечение, при этом алгоритм двойного поиска включает формирование графа, содержащего в качестве вершин узлы сети связи, а в качестве ребер - функцию начального узла ребра, конечного узла ребра, весового вектора, при этом ребра графа связывают вершины, а в качестве метрик ребер используют весовой вектор с последующим формированием из графа матрицы расстояний, каждый элемент которой представляет собой упорядоченный по возрастанию весового вектора набор путей до некоторого узла, учитывающей кратные дуги и весовые вектора W для каждой дуги, инициализируют массивы данных матрицы расстояний и вектора E, E1 наборов путей от начального узла до всех остальных узлов графа, с занесением в элемент Матрицы расстояний весового вектора ребра, соединяющего каждую пару вершин в графе, формируют дополнительные матрицы, одна из которых содержит поддиагональные элементы матрицы расстояний и элементы, заполненные наборами пустых путей с бесконечными весами (W_INF) (Матрица L), а вторая содержит наддиагональные элементы матрицы расстояний и элементы, заполненные наборами пустых путей с бесконечными весами (W_INF) (Матрица U), при этом массивы данных матрицы расстояний инициализируют на основе весов ребер, соединяющих каждую пару вершин в графе, а вектора наборов путей от начального узла до всех остальных узлов графа E, E1 инициализируют множеством пустых путей с бесконечными весами (W_INF), последовательно запускают алгоритм обратного поиска, обрабатывающего элементы Матрицы L и элементы векторов E, E1 и алгоритм прямого поиска, обрабатывающего элементы Матрицы U и элементы векторов E, E1, осуществляют проверку условий окончания итераций, в случае положительной проверки завершают итерации и получают множество К кратчайших и надежных путей, упорядоченных по приоритету, в случае отрицательной проверки условий окончания итераций осуществляют повторный запуск алгоритмов.
| СПОСОБ МНОГОПУТЕВОЙ МАРШРУТИЗАЦИИ С ИСПОЛЬЗОВАНИЕМ РАСЩЕПЛЕНИЯ ПОТОКА ТРАФИКА ДАННЫХ | 2017 |
|
RU2636665C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ ПЕРЕДАЧЕЙ ПАКЕТОВ ДАННЫХ | 1998 |
|
RU2138128C1 |
| Устройство для поиска оптимальныхпуТЕй HA СЕТи | 1979 |
|
SU830409A1 |
| US 9374281 B2, 21.06.2016 | |||
| US 8730817 B2, 20.05.2014. | |||
Авторы
Даты
2019-09-17—Публикация
2019-01-09—Подача