Предлагаемое изобретение относится к области радиотехники и может быть использовано для оценки напряженности электромагнитного (или акустического) поля вблизи искажающих рассеивателей произвольной формы, размеров и материальных свойств.
Восстановление структуры электромагнитного (или акустического) поля может производиться с помощью различных алгоритмов, например, основанных на использовании свойств гармонических функций (описывающих скалярные и векторные поля), теории функций комплексного переменного, в частности, теории аналитических функций, аппроксимации поля во «внутренней» и «внешней» областях по отношению к контуру антенной решетки стационарного, мобильного или бортового базирования и т.д.
Известные способы учета и компенсации искажений структуры электромагнитного (или акустического) поля вблизи рассеивателя, как правило, основаны на формировании базы данных частотно-угловых зависимостей амплитудно-фазовых распределений поля в местах расположения элементов антенной решетки путем проведения большого количества натурных экспериментальных исследований. Эта база используется для нахождения максимальной корреляции измеренных в реальных условиях (при эксплуатации аппаратуры) амплитудно-фазовых распределений поля с «эталонными» зависимостями, хранящимися в базе данных (примеры реализации данного подхода описаны в статьях: Ашихмин А.В., Виноградов А.Д., Кондращенко В.Н., Рембовский А.М. Современные корреляционно-интерферометрические измерители пеленга и напряженности электромагнитного поля // Специальная техника. - 2002. - Спецвыпуск. - С.7-15; [2]. Ашихмин А.В., Козьмин В.А., Рембовский А.М. Наземные мобильные комплексы радиоконтроля и пеленгования // Специальная техника. - 2002. - Спецвыпуск. С.30-40.).
Этот подход не требует детальной информации о форме, размерах и материальных свойствах рассеивателя (в частности, корпуса мобильного носителя антенной решетки или стационарной опорной мачты с растяжками, блоками и другими местными предметами, рассеивающими волны и искажающими их структуру), но он характеризуется большими временными и материальными затратами на формирование базы данных. Это существенно снижает пропускную способность аппаратуры за счет необходимости проведения большого числа вычислительных операций при получении коэффициентов взаимной корреляции измеренных и эталонных амплитудно-фазовых распределений. Количество таких комбинаций может быть весьма значительным, к примеру, взяв за шаг дискретизации азимутального угла (от 0 до 360°), угла места (от 0 до 180°) и пространственной ориентации вектора напряженности электрической компоненты поля электромагнитной волны с линейной поляризацией (от 0 до 180°) величину, равную 1°, мы получаем более 11.6·106 возможных комбинаций на каждой из частот рабочего диапазона. Для итоговой оценки отметим, что современные радиопеленгаторы функционируют в области частот от нескольких десятков герц до сотен гигагерц.
Априорное незнание параметров рассеивателя и возможность их неконтролируемого изменения вызывает дополнительные проблемы. В реальных условиях зачастую трудно контролировать - открыта или закрыта дверь автомобиля, открыт или закрыт люк танка или бронетранспортера, поднята или опущена рея на судне. Кроме того, априорно неизвестно количество членов экипажа мобильного радиопеленгатора, положение их тел (также являющихся рассеивателями волн и искажающих их структуру).
Другой подход к учету и компенсации искажений структуры электромагнитного (или акустического) поля основан на создании физико-математических моделей и алгоритмов, позволяющих учесть искажения структуры падающих (или излучаемых) волн близлежащими рассеивателями (см., например, Demmel F. Short wave direction finding on ships // News of Rohde & Schwarz. - 1999. - №162. - P 29-30.).
Этот способ также является малоэффективным по следующим причинам. Даже при использовании самых современных высокопроизводительных ЭВМ решение задачи дифракции электромагнитных (или акустических) волн на рассеивателе с размерами, существенно большими длины волны в свободном пространстве и сложной геометрической формы (автомобиль, объект бронетехники, морское судно, летательный аппарат), связано с весьма существенными временными затратами. Проблема заключается в том, что коррекцию систематических погрешностей измерения напряженности поля необходимо, как правило, проводить в реальном масштабе времени. Заметим также, что при построении физико-математических моделей дифракции волн на сложных объектах многие факторы (качество электрического контакта деталей корпуса носителя, изменяющееся в зависимости от их окисления, налета пыли и др.), существенно влияющие на реальную искаженную картину поля, практически не поддаются учету.
Известен способ учета и компенсации искажений структуры электромагнитного (или акустического) поля вблизи рассеивателя, описанный в статье «Учет влияния корпуса носителя в алгоритме определения пеленга с помощью круговой ФАР». А.В.Ашихмин, В.Н.Кондращенко, К.Б.Меркулов, А.В.Останков, Ю.Г.Пастернак, В.И.Юдин. Теория и техника радиосвязи. 1998. №2. С.83-88. В этом способе рассеиватель электромагнитного поля (корпус мобильного носителя антенной решетки), примыкающий к контуру, на котором расположены элементы антенной решетки, может иметь лишь простую геометрическую форму и характеризоваться однородными материальными свойствами. Рассмотрена модель носителя в виде идеально проводящего прямоугольного параллелепипеда. Влияние рассеивателя на поле внутри и вне контура антенной решетки учитывается весьма приближенно (корпус носителя представляется в виде набора бесконечно тонких идеально проводящих лент, сходящихся к элементам антенной решетки). На лентах задается форма распределения тока, описывающаяся эвристической формулой. Оценка поля вблизи корпуса носителя антенной решетки производится по найденному распределению тока, протекающему по лентам.
Упрощенная модель рассеивателя приводит к существенной погрешности в оценке поля вблизи корпуса носителя (зачастую неприемлемой с точки зрения требований, предъявляемых в различных технических приложениях - радиолокация, радиопеленгация, связь и т.д.).
Таким образом, недостатком данного способа является значительное ограничение на геометрию и электрические размеры носителя, на расположение на нем элементов антенной решетки, а также наличие существенных погрешностей в оценке поля вблизи носителя.
Наиболее близким к предлагаемому решению является способ оценки (восстановления) напряженности электромагнитного поля в соответствии с принципом Гюйгенса-Кирхгофа, описанный в книге Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. - М., Наука, 1989. - 453 с.
Способ, принятый за прототип, позволяет вычислить значение любой скалярной компоненты электромагнитного поля Ф(х) в любой точке (с координатами х), лежащей внутри замкнутого контура L, на всех точках ξ∈L которого известны значения поля Ф(ξ) и его производной по нормали n, устремленной внутрь контура L, 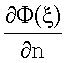 (фиг.1).
(фиг.1).
Материальная среда внутри контура предполагается однородной и изотропной (диэлектрическая проницаемость εr, магнитная проницаемость µr и проводимость σ не зависят от координат и от направления). При выполнении данных условий математическое описание принципа Гюйгенса-Кирхгофа дается с помощью формулы Грина [см. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1973. - 832 с., страница 484, формула 15.5-26]:
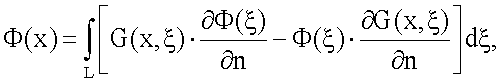
где
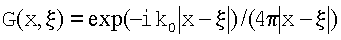 - скалярная функция Грина свободного пространства (функция излучения точечного источника).
- скалярная функция Грина свободного пространства (функция излучения точечного источника).
Согласно вышеприведенной формуле, поле внутри контура L (в произвольной точке) находится как сумма по всем точкам ξ контура L разностей произведения величины функции Грина G(х, ξ) на скорость изменения скалярной компоненты поля 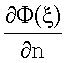 и произведения величины скалярной компоненты поля Ф(ξ) на скорость изменения поля точечного источника
и произведения величины скалярной компоненты поля Ф(ξ) на скорость изменения поля точечного источника  .
.
Недостатками данного способа оценки напряженности электромагнитного поля в соответствии с принципом Гюйгенса-Кирхгофа являются:
- необходимость однородности и изотропности среды внутри контура L, существенно ограничивающая применение данного подхода к аппроксимации поля в различных технических приложениях;
- должны быть известны не только значения скалярной компоненты поля в точках контура L, но и ее нормальная производная в этих точках;
- нахождение поля возможно только внутри контура L.
Задачей предлагаемого изобретения является уменьшение сложности и повышение точности оценки напряженности электромагнитного или акустического поля вблизи произвольного рассеивателя.
Для решения данной задачи предлагается два варианта способа оценки напряженности электромагнитного или акустического поля по сигналам элементов антенной решетки, расположенных вблизи искажающего поле рассеивателя.
Первый вариант заключается в том, что
1) на каждом элементе антенной решетки
- записывают сигнал на временном интервале [0, Т],
- формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру преобразования Фурье;
2) для каждой спектральной компоненты
- находят вектор В коэффициентов интерполяционной модели поля, удовлетворяющий матрично-векторному уравнению U(N)=QB, левая часть которого представляет собой вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки, а правая часть представляет собой произведение матрицы антенной решетки Q, элементы которой зависят от взаимного расположения элементов антенной решетки, и искомого вектора В коэффициентов интерполяционной модели поля,
- находят опорный вектор U(L) оценок напряженности поля спектральной компоненты для L эквидистантно расположенных опорных точек контура антенной решетки, перемножая матрицу F контура антенной решетки, зависящую от положения опорных точек контура, и найденного вектора В коэффициентов интерполяционной модели поля,
- определяют значение поля спектральной компоненты в плоскости антенной решетки в произвольной точке внутри ее контура, как скалярное произведение найденного опорного вектора U(L) оценок напряженности поля спектральной компоненты и вектора d оцениваемой точки, зависящего от комплексной разности между положениями соседних опорных точек контура антенной решетки и от разности комплексных положений опорных точек контура антенной решетки и оцениваемой точки,
- определяют вектор Y значений поля спектральной компоненты в плоскости антенной решетки в L точках внешнего контура по отношению к контуру антенной решетки, удовлетворяющий матрично-векторному уравнению U(L)=DY, левая часть которого представляет собой опорный вектор U(L) оценок напряженности поля спектральной компоненты, а правая часть представляет собой произведение матрицы внешнего контура D, элементы которой зависят от комплексной разности между положениями соседних точек внешнего контура и от взаимного расположения опорных точек контура антенной решетки и точек внешнего контура, в которых производится оценка, и искомого вектора Y значений поля спектральной компоненты внешнего контура.
Вектор В коэффициентов интерполяционной модели поля находят, например, как произведение матрицы, обратной матрице антенной решетки Q, на вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки.
Произвольный элемент матрицы антенной решетки Q, соответствующий n-ому столбцу и k-ой строке, определяют для случая кругового контура антенной решетки, например, как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-го элемента антенной решетки на отношение разности номера столбца и единицы к числу элементов антенной решетки.
Произвольный элемент матрицы F контура антенной решетки, соответствующий n-ому столбцу и k-ой строке, определяют для случая кругового контура антенной решетки, например, как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-ой опорной точки на отношение разности номера столбца и единицы к числу элементов антенной решетки.
Произвольный k-ый элемент вектора d оцениваемой точки определяют для случая кругового контура антенной решетки, например, как сдвинутое на -π/2 отношение радиуса контура антенной решетки к произведению числа опорных точек на разность комплексных координат k-ой опорной точки и оцениваемой точки внутри контура антенной решетки.
Произвольный элемент матрицы внешнего контура D, соответствующий n-ому столбцу и k-ой строке определяют для случая кругового внешнего контура, например, как сдвинутое на -π/2 отношение радиуса внешнего контура к произведению числа опорных точек на разность комплексных координат n-ой оцениваемой точки внешнего контура и k-ой опорной точки.
Вектор Y значений поля спектральной компоненты внешнего контура находят, например, как произведение матрицы, обратной матрице внешнего контура D, на опорный вектор U(L) оценок напряженности поля спектральной компоненты.
Второй вариант способа заключается в том, что
1) на каждом элементе антенной решетки
- записывают сигнал на временном интервале [0, T],
- формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру преобразования Фурье;
2) для каждой спектральной компоненты
- находят вектор В коэффициентов интерполяционной модели поля, удовлетворяющий матрично-векторному уравнению U(N)=QB, левая часть которого представляет собой вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки, а правая часть представляет собой произведение матрицы антенной решетки Q, элементы которой зависят от частоты и расположения элементов антенной решетки, и искомого вектора В коэффициентов интерполяционной модели поля,
- определяют значение поля спектральной компоненты в произвольной точке плоскости антенной решетки, как скалярное произведение найденного вектора В коэффициентов интерполяционной модели поля и вектора q, зависящего от частоты и положения этой оцениваемой точки.
Вектор В коэффициентов интерполяционной модели поля находят, например, как произведение матрицы, обратной матрице антенной решетки Q, на вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки.
Произвольный элемент матрицы антенной решетки Q, соответствующий n-ому столбцу и k-ой строке, определяют, например, как комплексную величину единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства на проекцию радиус-вектора k-го элемента антенной решетки, повернутого на угол, равный 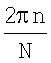 , на ось абсцисс.
, на ось абсцисс.
Произвольный n-ый элемент вектора q определяют, например, как комплексную величину единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства на проекцию радиус-вектора оцениваемой точки, повернутого на угол, равный 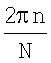 , на ось абсцисс.
, на ось абсцисс.
Отличительными (новыми) признаками заявляемого способа оценки напряженности электромагнитного или акустического поля по сигналам элементов антенной решетки, расположенных вблизи искажающего поле рассеивателя, относительно прототипа является то, что используют значения поля в конечном числе точек контура, не используют нормальную производную поля, оценка поля возможна не только внутри, но и вне контура.
Сопоставительный анализ заявляемого способа с другими техническими решениями в данной области техники не позволил выявить признаки, заявленные в формуле изобретения и направленные на уменьшение сложности и повышение точности оценки напряженности электромагнитного или акустического поля вблизи произвольного рассеивателя.
Графические материалы, представленные в материалах заявки
Фиг.1 - Пример определения значения скалярной компоненты электромагнитного поля в любой точке, лежащей внутри замкнутого контура.
Фиг.2 - Вариант реализации предлагаемого способа (первый вариант).
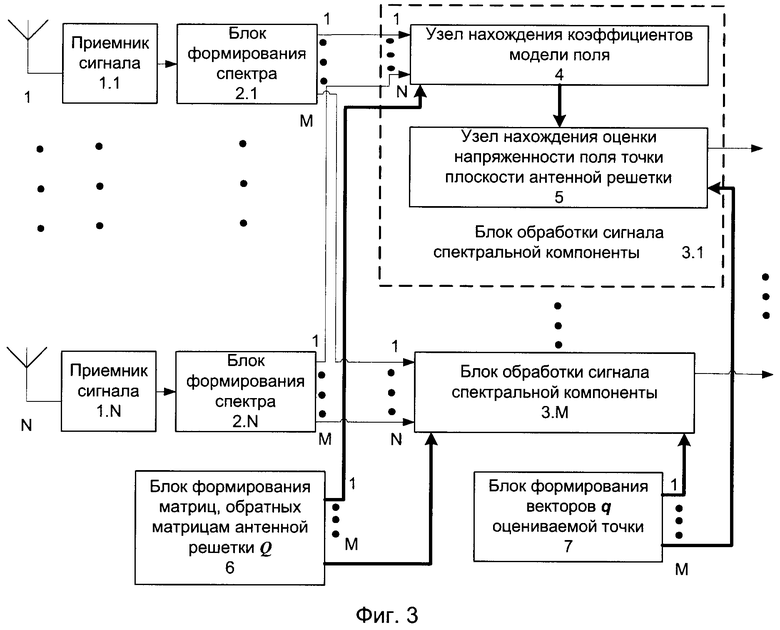
Фиг.3 - Вариант реализации предлагаемого способа (второй вариант).
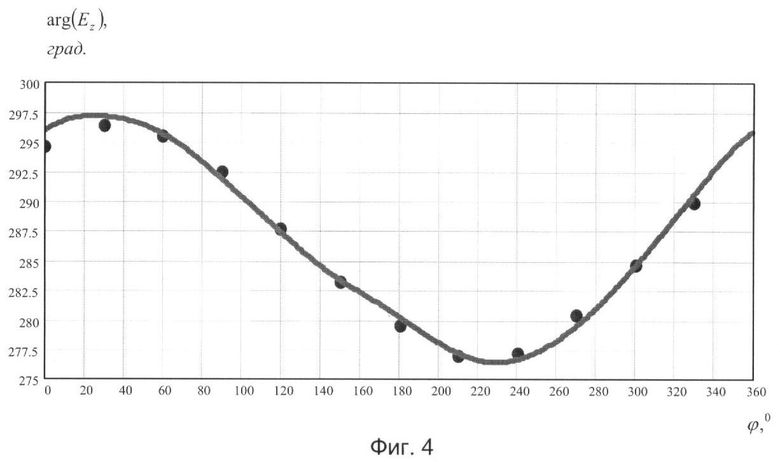
Фиг.4 - Результаты электродинамического моделирования значения напряженности электромагнитного поля.
Первый вариант предлагаемого способа заключается в следующем:
1) на каждом элементе антенной решетки
- записывают сигнал на временном интервале [0, Т],
- формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру преобразования Фурье;
2) для каждой спектральной компоненты
- находят вектор В коэффициентов интерполяционной модели поля, удовлетворяющий матрично-векторному уравнению U(N)=QB, левая часть которого представляет собой вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки, а правая часть представляет собой произведение матрицы антенной решетки Q, элементы которой зависят от взаимного расположения элементов антенной решетки, и искомого вектора В коэффициентов интерполяционной модели поля,
- находят опорный вектор U(L) оценок напряженности поля спектральной компоненты для L эквидистантно расположенных опорных точек контура антенной решетки, перемножая матрицу F контура антенной решетки, зависящую от положения опорных точек контура, и найденного вектора В коэффициентов интерполяционной модели поля,
- определяют значение поля спектральной компоненты в плоскости антенной решетки в произвольной точке внутри ее контура как скалярное произведение найденного опорного вектора U(L) оценок напряженности поля спектральной компоненты и вектора d оцениваемой точки, зависящего от комплексной разности между положениями соседних опорных точек контура антенной решетки и от разности комплексных положений опорных точек контура антенной решетки и оцениваемой точки,
- определяют вектор Y значений поля спектральной компоненты в плоскости антенной решетки в L точках внешнего контура по отношению к контуру антенной решетки, удовлетворяющий матрично-векторному уравнению U(L)=DY, левая часть которого представляет собой опорный вектор U(L) оценок напряженности поля спектральной компоненты, а правая часть представляет собой произведение матрицы внешнего контура D, элементы которой зависят от комплексной разности между положениями соседних точек внешнего контура и от взаимного расположения опорных точек контура антенной решетки и точек внешнего контура, в которых производится оценка, и искомого вектора Y значений поля спектральной компоненты внешнего контура.
Вектор В коэффициентов интерполяционной модели поля находят, например, как произведение матрицы, обратной матрице антенной решетки Q, на вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки.
Произвольный элемент матрицы антенной решетки Q, соответствующий n-ому столбцу и k-ой строке, определяют для случая кругового контура антенной решетки, например, как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-го элемента антенной решетки на отношение разности номера столбца и единицы к числу элементов антенной решетки.
Произвольный элемент матрицы F контура антенной решетки, соответствующий n-ому столбцу и k-ой строке определяют для случая кругового контура антенной решетки, например, как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-ой опорной точки на отношение разности номера столбца и единицы к числу элементов антенной решетки.
Произвольный k-ый элемент вектора d оцениваемой точки определяют для случая кругового контура антенной решетки, например, как сдвинутое на -π/2 отношение радиуса контура антенной решетки к произведению числа опорных точек на разность комплексных координат k-ой опорной точки и оцениваемой точки внутри контура антенной решетки.
Произвольный элемент матрицы внешнего контура D, соответствующий n-ому столбцу и k-ой строке определяют для случая кругового внешнего контура, например, как сдвинутое на -π/2 отношение радиуса внешнего контура к произведению числа опорных точек на разность комплексных координат n-ой оцениваемой точки внешнего контура и k-ой опорной точки.
Вектор Y значений поля спектральной компоненты внешнего контура находят, например, как произведение матрицы, обратной матрице внешнего контура D, на опорный вектор U(L) оценок напряженности поля спектральной компоненты.
Вариант устройства, реализующий предлагаемый способ, представлен на фиг.2. Устройство содержит N элементов антенной решетки, каждый из которых соединен с соответствующим приемником сигнала 1.1÷1.N. Выход каждого приемника сигнала 1.1÷1.N соединен с входом соответствующего блока формирования спектра 2.1÷2.N. Спектральные компоненты 1÷М с выходов блоков формирования спектра 2.1÷2.N поступают на соответствующие входы 1÷N блоков обработки сигнала спектральной компоненты 3.1÷3.М. Каждый блок обработки сигнала спектральной компоненты 3.1÷3.М содержит последовательно соединенные узел нахождения коэффициентов модели поля 4, узел нахождения оценок напряженности поля опорных точек 5, выход которого соединен со входом узла нахождения оценок напряженности поля внутри контура 6 и со входом узла нахождения оценок напряженности поля внешнего контура 7.
В состав устройства также входят блок формирования матрицы, обратной матрице антенной решетки Q, 8, блок формирования матрицы F контура антенной решетки 10, блок формирования матрицы, обратной матрице внешнего контура D, 9, блок формирования вектора d точки внутри контура 11. Выход блока формирования матрицы, обратной матрице антенной решетки Q, 8 соединен соответственно с входом узла нахождения коэффициентов модели поля 4 каждого из блоков обработки сигнала спектральной компоненты 3.1÷3.М, выход блока формирования матрицы F контура антенной решетки 10 соединен соответственно с входом узла нахождения оценок напряженности поля опорных точек 5 каждого из блоков обработки сигнала спектральной компоненты 3.1÷3.М. Выход блока формирования матрицы, обратной матрице внешнего контура D, 9 соединен соответственно с входом узла нахождения оценок напряженности поля внешнего контура 7 каждого из блоков обработки сигнала спектральной компоненты 3.1÷3.М, выход блока формирования вектора d точки внутри контура 11 соединен соответственно с входом узла нахождения оценок напряженности поля внутри контура 6 каждого из блоков обработки сигнала спектральной компоненты 3.1÷3.М. Выход узла нахождения оценок напряженности поля внутри контура 6 является выходом оценок напряженности поля внутри контура антенной решетки и первым выходом устройства. Выход узла нахождения оценок напряженности поля внешнего контура 7 является выходом оценок напряженности поля внешнего контура антенной решетки и вторым выходом устройства.
Работает данное устройство следующим образом. Сигнал с каждого элемента антенной решетки поступает на вход соответствующего приемника сигнала 1.1÷1.N, где производятся процедуры фильтрации, переноса на видеочастоту, аналого-цифрового преобразования и др. Видеосигналы с выходов приемников сигнала 1.1÷1.N поступают на входы соответствующих блоков формирования спектра 2.1÷2.N, где записываются на временном интервале [0, T]. Затем в блоках формирования спектра 2.1÷2.N формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру дискретного преобразования Фурье длиной М. Спектральные компоненты 1÷M с выходов блоков формирования спектра 2.1÷2.N поступают на соответствующие входы 1÷N блоков обработки сигнала спектральной компоненты 3.1÷3.М.
В блоке 8 сначала формируется матрица антенной решетки Q. Произвольный элемент матрицы антенной решетки Q, соответствующий n-ому столбцу и k-ой строке, определяют для случая кругового контура антенной решетки, например, как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-го элемента антенной решетки ξk на отношение разности номера столбца и единицы к числу элементов антенной решетки
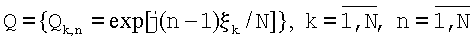 .
.
Далее в блоке 8 определяют матрицу, обратную матрице антенной решетки Q.
Для каждой спектральной компоненты в узле нахождения коэффициентов модели поля 4 находят вектор В коэффициентов интерполяционной модели поля. Вектор В коэффициентов интерполяционной модели поля находят как произведение матрицы, обратной матрице антенной решетки Q на вектор U(N)=[U1, U2, U3, …, UN]T напряженностей поля спектральной компоненты элементов антенной решетки, составленный из величин U1÷UN, поступивших с блоков 2.1÷2.N
В=Q-1U(N).
Найденный вектор В коэффициентов интерполяционной модели поля с выхода узла нахождения коэффициентов модели поля 4 поступает на вход узла нахождения оценок напряженности поля опорных точек 5. В узле 5 определяют опорный вектор U(L) оценок напряженности поля спектральной компоненты для L эквидистантно расположенных опорных точек контура антенной решетки, перемножая матрицу F контура антенной решетки, сформированную в блоке 10, на вектор В
U(L)=FB.
Произвольный элемент матрицы F контура антенной решетки, соответствующий n-ому столбцу и k-ой строке, определяют для случая кругового контура антенной решетки как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-ой опорной точки на отношение разности номера столбца и единицы к числу элементов антенной решетки
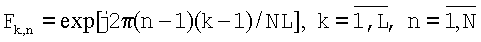 .
.
Опорный вектор U(L) оценок напряженности поля спектральной компоненты, вычисленный в узле 5, используют для определения оценок напряженности поля как внутри контура антенной решетки, так и вне этого контура. Значение поля спектральной компоненты в плоскости антенной решетки в произвольной точке внутри ее контура определяют как скалярное произведение найденного опорного вектора U(L) оценок напряженности поля спектральной компоненты и вектора d оцениваемой точки, сформированного в блоке формирования вектора d точки внутри контура 11
U(z)=dTU(L).
Произвольный k-ый элемент вектора d оцениваемой точки определяют для случая кругового контура антенной решетки как сдвинутое на -π/2 отношение радиуса контура антенной решетки R к произведению числа опорных точек на разность комплексных координат k-ой опорной точки и оцениваемой точки внутри контура антенной решетки z
 .
.
В блоке 9 формируют матрицу внешнего контура D. Произвольный элемент матрицы внешнего контура D, соответствующий n-ому столбцу и k-ой строке, определяют для случая кругового внешнего контура, например, как сдвинутое на -π/2 отношение радиуса внешнего контура r к произведению числа опорных точек на разность комплексных координат n-ой оцениваемой точки внешнего контура и k-ой опорной точки
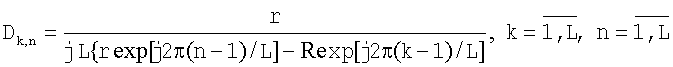 .
.
Затем в блоке 9 формируют матрицу, обратную матрице внешнего контура D.
Вектор Y значений поля спектральной компоненты в плоскости антенной решетки в L точках контура, внешнего по отношению к контуру антенной решетки, определяют в узле нахождения оценок напряженности поля внешнего контура 7 как произведение матрицы, обратной матрице внешнего контура D, на опорный вектор U(L) оценок напряженности поля спектральной компоненты
Y=D-1U(L).
Второй вариант способа заключается в том, что
1) на каждом элементе антенной решетки
- записывают сигнал на временном интервале [0, Т],
- формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру преобразования Фурье;
2) для каждой спектральной компоненты
- находят вектор В коэффициентов интерполяционной модели поля, удовлетворяющий матрично-векторному уравнению U(N)=QB, левая часть которого представляет собой вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки, а правая часть представляет собой произведение матрицы антенной решетки Q, элементы которой зависят от частоты и расположения элементов антенной решетки, и искомого вектора В коэффициентов интерполяционной модели поля,
- определяют значение поля спектральной компоненты в произвольной точке плоскости антенной решетки как скалярное произведение найденного вектора В коэффициентов интерполяционной модели поля и вектора q, зависящего от частоты и положения этой оцениваемой точки.
Вектор В коэффициентов интерполяционной модели поля находят, например, как произведение матрицы, обратной матрице антенной решетки Q, на вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки.
Произвольный элемент матрицы антенной решетки Q, соответствующий n-ому столбцу и k-ой строке, определяют, например, как комплексную величину единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства на проекцию радиус-вектора k-го элемента антенной решетки, повернутого на угол, равный 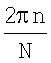 , на ось абсцисс.
, на ось абсцисс.
Произвольный n-ый элемент вектора q определяют, например, как комплексную величину единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства на проекцию радиус-вектора оцениваемой точки, повернутого на угол, равный 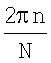 , на ось абсцисс.
, на ось абсцисс.
Вариант устройства, реализующий второй вариант предлагаемого способа, представлен на фиг.3. Устройство содержит N элементов антенной решетки, каждый из которых соединен с соответствующим приемником сигнала 1.1÷1.N. Выход каждого приемника сигнала 1.1÷1.N соединен с входом соответствующего блока формирования спектра 2.1÷2.N. Спектральные компоненты 1÷М с выходов блоков формирования спектра 2.1÷2.N поступают на соответствующие входы 1÷N блоков обработки сигнала спектральной компоненты 3.1÷3.М. Каждый блок обработки сигнала спектральной компоненты 3.1÷3.М содержит последовательно соединенные узел нахождения коэффициентов модели поля 4 и узел нахождения оценок напряженности поля точки плоскости антенной решетки 5.
В состав устройства также входят блок формирования матриц, обратных матрицам антенной решетки Q, 6 и блок формирования векторов q оцениваемой точки 7. Выходы блока формирования матриц, обратных матрицам антенной решетки Q, 6 соединены соответственно с входами узлов нахождения коэффициентов модели поля 4 каждого из блоков обработки сигнала спектральной компоненты 3.1÷3.М. Выходы блока формирования векторов q оцениваемой точки 7 соединены соответственно с входами узлов нахождения оценки напряженности поля точки плоскости антенной решетки 5 каждого из блоков обработки сигнала спектральной компоненты 3.1÷3.М. Выходы узлов нахождения оценки напряженности поля точки плоскости антенной решетки 5 являются выходами оценки напряженности поля точки плоскости антенной решетки и выходами устройства.
Работает устройство следующим образом.
Сигнал с каждого элемента антенной решетки поступает на вход соответствующего приемника сигнала 1.1÷1.N, где производятся процедуры фильтрации, переноса на видеочастоту, аналого-цифрового преобразования и др. Видеосигналы с выходов приемников сигнала 1.1÷1.N поступают на входы соответствующих блоков формирования спектра 2.1÷1.N, где записываются на временном интервале [0, Т]. Затем в блоках формирования спектра 2.1÷2.N формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру дискретного преобразования Фурье длиной М. Спектральные компоненты 1÷М с выходов блоков формирования спектра 2.1÷1.N поступают на соответствующие входы 1÷N блоков обработки сигнала спектральной компоненты 3.1÷3.М.
В блоке 6 сначала для каждой спектральной компоненты формируют матрицу антенной решетки Q. Произвольный элемент матрицы антенной решетки Q, соответствующий n-ому столбцу и k-ой строке, можно определить как комплексную величину единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства  , λ - длина волны, на проекцию радиус-вектора k-го элемента антенной решетки rk, повернутого на угол, равный
, λ - длина волны, на проекцию радиус-вектора k-го элемента антенной решетки rk, повернутого на угол, равный 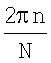 , на ось абсцисс
, на ось абсцисс
 .
.
Затем в блоке 6 для каждой спектральной компоненты находят матрицу, обратную матрице антенной решетки Q.
Для каждой спектральной компоненты в узле нахождения коэффициентов модели поля 4 находят вектор В коэффициентов интерполяционной модели поля. Вектор В находят как произведение матрицы, обратной матрице антенной решетки Q, на вектор U(N)=[U1, U2, U3, …, UN]T напряженностей поля спектральной компоненты элементов антенной решетки, составленный из величин U1÷UN, поступивших с блоков 2.1÷2.N
В=Q-1U(N).
Значение вектора В коэффициентов интерполяционной модели поля, определенное в узле нахождения коэффициентов модели поля 4, поступает на первый вход узла нахождения оценки напряженности поля точки плоскости антенной решетки 5. На второй вход узла нахождения оценки напряженности поля точки плоскости антенной решетки 5 поступает значение вектора q оцениваемой точки, которое формируется в блоке 7. Произвольный n-ый элемент вектора оцениваемой точки q может быть определен как комплексная величина единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства на проекцию радиус-вектора r оцениваемой точки, повернутого на угол, равный 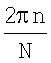 , на ось абсцисс
, на ось абсцисс
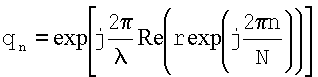 .
.
В узле нахождения оценки напряженности поля точки плоскости антенной решетки 5 определяют значение поля спектральной компоненты в произвольной точке плоскости антенной решетки как скалярное произведение найденного вектора В коэффициентов интерполяционной модели поля и вектора оцениваемой точки q
U(r)=BTq.
Результаты электродинамического моделирования, основанного на строгом решении задачи дифракции на структуре «корпус носителя - антенная решетка» падающей в азимутальной плоскости вертикально-поляризованной электромагнитной волны, показали, что измеренные антенной решеткой радиусом R=0.5 м напряженности Ez-компоненты электромагнитного поля могут быть использованы для аппроксимации суммарного поля (падающей и рассеянных волн) на окружностях радиуса r, вдвое и даже втрое большего радиуса, чем радиус антенной решетки R. На фиг.4. показаны полученные фазовые распределения Ez-компоненты поля на окружности радиусом r=1 м в ходе численного моделирования (маркер) и оцененные по второму варианту предложенного способа (сплошные линии).
Поставленная задача и технический результат достигается за счет того, что в предлагаемых способах оценки используют интерполяционные модели поля, что позволяет по конечному числу значений поля в анализируемых точках контура оценить поле как внутри, так и вне контура антенной решетки. Предложенные варианты способа позволяют уменьшить сложность и повысить точность оценки напряженности электромагнитного или акустического поля вблизи произвольного искажающего рассеивателя.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ "ВИРТУАЛЬНЫХ" КАНАЛОВ ПРИЕМА СИГНАЛОВ | 2013 |
|
RU2530320C2 |
| СПОСОБ ФОРМИРОВАНИЯ ТРЕХМЕРНОГО ИЗОБРАЖЕНИЯ ПОВЕРХНОСТИ НА БАЗЕ БОРТОВОГО РАДИОТЕПЛОЛОКАТОРА | 2008 |
|
RU2368918C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТРЕХМЕРНОГО ИЗОБРАЖЕНИЯ ЗЕМНОЙ ПОВЕРХНОСТИ И ВОЗДУШНОЙ ОБСТАНОВКИ С ПОМОЩЬЮ АНТЕННОЙ РЕШЕТКИ | 2013 |
|
RU2539558C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ГИДРОАКУСТИЧЕСКИХ ПОЛЕЙ | 1997 |
|
RU2116705C1 |
| Способ повышения точности пеленгования источников радиоизлучения обнаружителем-пеленгатором с многошкальной антенной системой | 2019 |
|
RU2713235C1 |
| Способ калибровки фазированной антенной решетки | 2022 |
|
RU2797790C1 |
| СПОСОБ ПОВЫШЕНИЯ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ БОРТОВОЙ СТАНЦИИ | 2011 |
|
RU2464680C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АМПЛИТУДНО-ФАЗОВОГО РАСПРЕДЕЛЕНИЯ ПОЛЯ ПРИНИМАЕМОГО СИГНАЛА В РАСКРЫВЕ ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ | 2007 |
|
RU2366968C1 |
| СПОСОБ ПЕЛЕНГОВАНИЯ ИСТОЧНИКА РАДИОСИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2010 |
|
RU2434239C1 |
| Способ адаптации антенной решетки градиентной процедурой с переменным шагом | 2021 |
|
RU2788589C1 |

Изобретение относится к области радиотехники. Техническим результатом является упрощение и повышение точности оценки напряженности электромагнитного или акустического поля. Предложенные способы оценки используют интерполяционные модели поля, что позволяет по конечному числу значений поля в анализируемых точках контура оценить поле как внутри, так и вне контура антенной решетки. 2 н. и 9 з.п. ф-лы, 4 ил.
1. Способ оценки напряженности электромагнитного или акустического поля по сигналам элементов антенной решетки, расположенных вблизи искажающего поле рассеивателя, заключающийся в том, что на каждом элементе антенной решетки записывают сигнал на временном интервале [0, Т], формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру преобразования Фурье, для каждой спектральной компоненты находят вектор В коэффициентов интерполяционной модели поля, удовлетворяющий матрично-векторному уравнению U(N)=QB, левая часть которого представляет собой вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки, а правая часть представляет собой произведение матрицы антенной решетки Q, элементы которой зависят от взаимного расположения элементов антенной решетки, и искомого вектора В коэффициентов интерполяционной модели поля, находят опорный вектор U(L) оценок напряженности поля спектральной компоненты для L эквидистантно расположенных опорных точек контура антенной решетки, перемножая матрицу F контура антенной решетки, зависящую от положения опорных точек контура, и найденного вектора В коэффициентов интерполяционной модели поля, определяют значение поля спектральной компоненты в плоскости антенной решетки в произвольной точке внутри ее контура, как скалярное произведение найденного опорного вектора U(L) оценок напряженности поля спектральной компоненты и вектора d оцениваемой точки, зависящего от комплексной разности между положениями соседних опорных точек контура антенной решетки и от разности комплексных положений опорных точек контура антенной решетки и оцениваемой точки, определяют вектор Y значений поля спектральной компоненты в плоскости антенной решетки в L точках внешнего контура по отношению к контуру антенной решетки, удовлетворяющий матрично-векторному уравнению U(L)=DY, левая часть которого представляет собой опорный вектор U(L) оценок напряженности поля спектральной компоненты, а правая часть представляет собой произведение матрицы внешнего контура D, элементы которой зависят от комплексной разности между положениями соседних точек внешнего контура и от взаимного расположения опорных точек контура антенной решетки и точек внешнего контура, в которых производится оценка, и искомого вектора Y значений поля спектральной компоненты внешнего контура.
2. Способ по п.1, отличающийся тем, что вектор В коэффициентов интерполяционной модели поля определяют как произведение матрицы, обратной матрице антенной решетки Q, на вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки.
3. Способ по п.1, отличающийся тем, что произвольный элемент матрицы антенной решетки Q, соответствующий n-му столбцу и k-й строке, определяют для случая кругового контура антенной решетки как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-го элемента антенной решетки на отношение разности номера столбца и единицы к числу элементов антенной решетки.
4. Способ по п.1, отличающийся тем, что произвольный элемент матрицы F контура антенной решетки, соответствующий n-му столбцу и k-й строке, определяют для случая кругового контура антенной решетки как комплексную величину единичной амплитуды, фаза которой равна произведению полярного угла k-й опорной точки на отношение разности номера столбца и единицы к числу элементов антенной решетки.
5. Способ по п.1, отличающийся тем, что произвольный k-й элемент вектора d оцениваемой точки определяют для случая кругового контура антенной решетки как сдвинутое на -π/2 отношение радиуса контура антенной решетки к произведению числа опорных точек на разность комплексных координат k-й опорной точки и оцениваемой точки внутри контура антенной решетки.
6. Способ по п.1, отличающийся тем, что произвольный элемент матрицы внешнего контура D, соответствующий n-му столбцу и k-й строке, определяют для случая кругового внешнего контура как сдвинутое на -π/2 отношение радиуса внешнего контура к произведению числа опорных точек на разность комплексных координат n-й оцениваемой точки внешнего контура и k-й опорной точки.
7. Способ по п.1, отличающийся тем, что вектор Y значений поля спектральной компоненты внешнего контура находят, например, как произведение матрицы, обратной матрице внешнего контура D, на опорный вектор U(L) оценок напряженности поля спектральной компоненты.
8. Способ оценки напряженности электромагнитного или акустического поля по сигналам элементов антенной решетки, расположенных вблизи искажающего поле рассеивателя, заключающийся в том, что на каждом элементе антенной решетки записывают сигнал на временном интервале [0, Т], формируют дискретный спектр напряженности поля, выполняя над записанным временным сигналом процедуру преобразования Фурье, для каждой спектральной компоненты находят вектор В коэффициентов интерполяционной модели поля, удовлетворяющий матрично-векторному уравнению U(N)=QB, левая часть которого представляет собой вектор U(N) напряженностей поля спектральной компоненты элементов антенной решетки, а правая часть представляет собой произведение матрицы антенной решетки Q, элементы которой зависят от частоты и расположения элементов антенной решетки, и искомого вектора В коэффициентов интерполяционной модели поля, определяют значение поля спектральной компоненты в произвольной точке плоскости антенной решетки как скалярное произведение найденного вектора В коэффициентов интерполяционной модели поля и вектора q, зависящего от частоты и положения этой оцениваемой точки.
9. Способ по п.8, отличающийся тем, что вектор В коэффициентов интерполяционной модели поля определяют как произведение матрицы, обратной матрице антенной решетки Q, на U(N) вектор напряженностей поля спектральной компоненты элементов антенной решетки.
10. Способ по п.8, отличающийся тем, что произвольный элемент матрицы антенной решетки Q, соответствующий n-му столбцу и k-й строке, определяют как комплексную величину единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства на проекцию радиус-вектора k-го элемента антенной решетки, повернутого на угол, равный 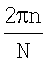 , на ось абсцисс.
, на ось абсцисс.
11. Способ по п.9, отличающийся тем, что произвольный n-й элемент вектора q определяют как комплексную величину единичной амплитуды, фаза которой равна произведению волнового числа свободного пространства на проекцию радиус-вектора оцениваемой точки, повернутого на угол, равный 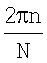 , на ось абсцисс.
, на ось абсцисс.
| НИКОЛЬСКИЙ В.В | |||
| и др | |||
| Электродинамика и распространение радиоволн | |||
| - М.: Наука, 1989, с.453 | |||
| СПОСОБ ИЗМЕРЕНИЯ НАПРЯЖЕННОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ РАДИОСИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2184980C1 |
| СПОСОБ ПЕЛЕНГАЦИИ РАДИОСИГНАЛОВ И МНОГОКАНАЛЬНЫЙ ПЕЛЕНГАТОР | 1999 |
|
RU2144200C1 |
| DE 4128191 A1, 25.02.1993. | |||
Авторы
Даты
2010-11-27—Публикация
2008-12-09—Подача